声明:虽然基础的提示技巧(如零样本/少样本示例或指令式提示)非常高效,但面对一些复杂难题(如数学/编程或需要多步骤逻辑推理的问题)时,更复杂的提示可能更为有效。由于大型语言模型(LLM)在处理这类问题时自然存在困难(其推理能力并不会随着模型规模的增大而单调提升),因此大部分关于提示设计的研究都聚焦于如何提升推理和解决复杂问题的能力上。简洁的提示足以应对大多数其他问题。
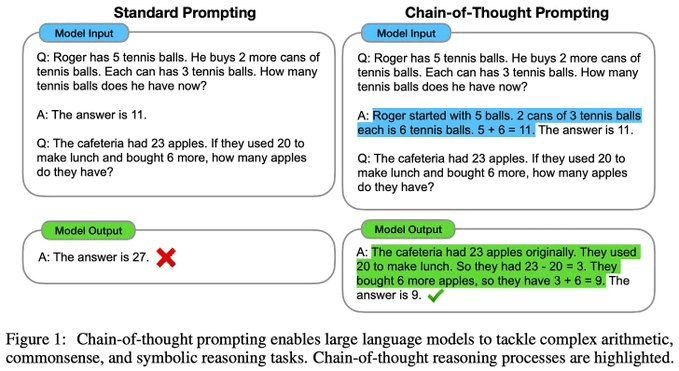
思维链(Chain of Thought [CoT])提示[1]通过在模型的提示中加入一串中间推理步骤,激活LLM的推理能力。通过为每个示例添加一个思维链,模型便可学会(通过上下文学习)在给出答案前自动生成类似的思维链条。[1]中的研究显示,明确阐释解决问题的推理过程实际上能有效提升模型的推理能力。

输入:
这组数中的奇数加起来是偶数:4、8、9、15、12、2、1。
A:将所有奇数相加(9、15、1)得到25。答案为False。这组数中的奇数加起来是偶数:17、10、19、4、8、12、24。
A:将所有奇数相加(17、19)得到36。答案为True。这组数中的奇数加起来是偶数:16、11、14、4、8、13、24。
A:将所有奇数相加(11、13)得到24。答案为True。这组数中的奇数加起来是偶数:17、9、10、12、13、4、2。
A:将所有奇数相加(17、9、13)得到39。答案为False。这组数中的奇数加起来是偶数:15、32、5、13、82、7、1。
A:输出:
将所有奇数相加(15、5、13、7、1)得到41。答案为False。
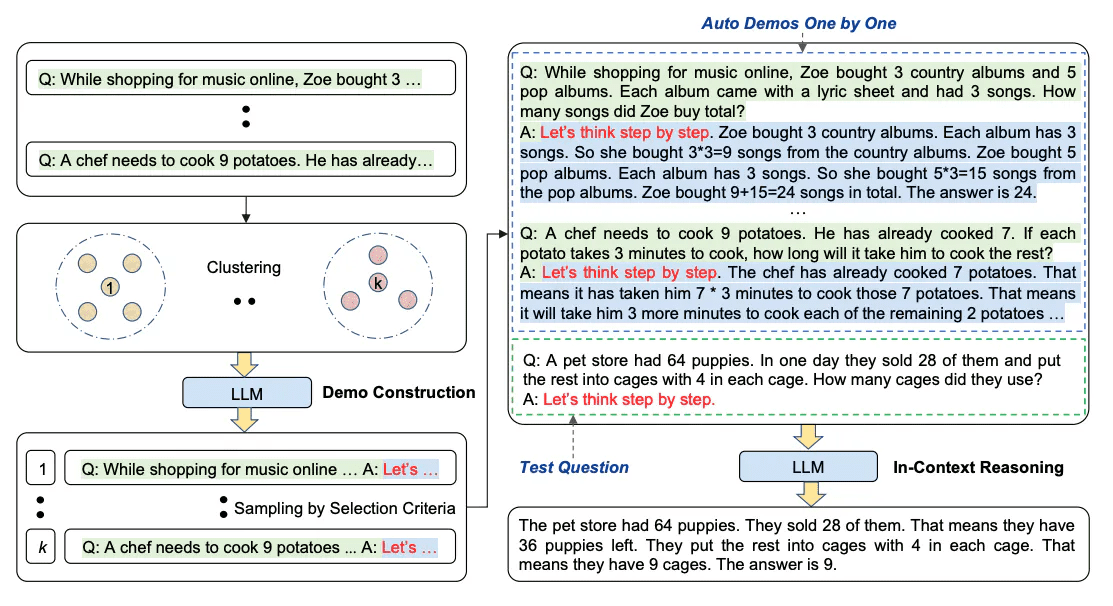
自动思维链(Auto-CoT)[8]:当使用思维链提示时,这个过程需要手工制作有效且多样化的例子。这种手动工作可能会导致次优解决方案。[8] 提出了一种消除人工的方法,即利用 LLMs “让我们一步一步地思考” 提示来生成一个接一个的推理链。这种自动过程仍然可能在生成的链中出现错误。为了减轻错误的影响,演示的多样性很重要。这项工作提出了Auto-CoT,它对具有多样性的问题进行采样,并生成推理链来构建演示。
Auto-CoT 主要由两个阶段组成:
阶段1:问题聚类:将给定问题划分为几个聚类
阶段2:演示抽样:从每组数组中选择一个具有代表性的问题,并使用带有简单启发式的 Zero-Shot-CoT 生成其推理链
简单的启发式方法可以是问题的长度(例如,60 个 tokens)和理由的步骤数(例如,5 个推理步骤)。这鼓励模型使用简单而准确的演示。
该过程如下图所示:
CoT变种:鉴于CoT提示的有效性及其受欢迎程度,多种衍生技术已被提出:
- 零样本示例 CoT[2]:去除少数示例并通过在提示末尾加上“让我们一步步来思考。”的方式,激励模型生成解题的逻辑推理。
输入:
我去市场买了10个苹果。我给了邻居2个苹果和修理工2个苹果。然后我去买了5个苹果并吃了1个。我还剩下多少苹果?
让我们逐步思考。
输出:
首先,您从10个苹果开始。
您给了邻居和修理工各2个苹果,所以您还剩下6个苹果。
然后您买了5个苹果,所以现在您有11个苹果。
最后,您吃了1个苹果,所以您还剩下10个苹果。
- 自我一致性(Self-Consistency)[3]:通过独立生成多条解题思路并对最终解答进行多数表决,增强了推理过程的鲁棒性。
输入:
Q:林中有15棵树。林业工人今天将在林中种树。完成后,将有21棵树。林业工人今天种了多少棵树?
A:我们从15棵树开始。后来我们有21棵树。差异必须是他们种树的数量。因此,他们必须种了21-15 = 6棵树。答案是6。
Q:停车场有3辆汽车,又来了2辆汽车,停车场有多少辆汽车?
A:停车场已经有3辆汽车。又来了2辆。现在有3 + 2 = 5辆汽车。答案是5。
Q:Leah有32块巧克力,她的姐姐有42块。如果他们吃了35块,他们总共还剩多少块?
A:Leah有32块巧克力,Leah的姐姐有42块。这意味着最初有32 + 42 = 74块巧克力。已经吃了35块。因此,他们总共还剩74-35 = 39块巧克力。答案是39。
Q:Jason有20个棒棒糖。他给Denny一些棒棒糖。现在Jason只有12个棒棒糖。Jason给Denny多少棒棒糖?
A:Jason有20个棒棒糖。因为他现在只有12个,所以他必须把剩下的给Denny。他给Denny的棒棒糖数量必须是20-12 = 8个棒棒糖。答案是8。
Q:Shawn有五个玩具。圣诞节,他从他的父母那里得到了两个玩具。他现在有多少个玩具?
A:他有5个玩具。他从妈妈那里得到了2个,所以在那之后他有5 + 2 = 7个玩具。然后他从爸爸那里得到了2个,所以总共他有7 + 2 = 9个玩具。答案是9。
Q:服务器房间里有9台计算机。从周一到周四,每天都会安装5台计算机。现在服务器房间里有多少台计算机?
A:从周一到周四有4天。每天都添加了5台计算机。这意味着总共添加了4 * 5 =
20台计算机。一开始有9台计算机,所以现在有9 + 20 = 29台计算机。答案是29。
Q:Michael有58个高尔夫球。星期二,他丢失了23个高尔夫球。星期三,他又丢失了2个。星期三结束时他还剩多少个高尔夫球?
A:Michael最初有58个球。星期二他丢失了23个,所以在那之后他有58-23 = 35个球。星期三他又丢失了2个,所以现在他有35-2 = 33个球。答案是33。
Q:Olivia有23美元。她用每个3美元的价格买了五个百吉饼。她还剩多少钱?
A:她用每个3美元的价格买了5个百吉饼。这意味着她花了15美元。她还剩8美元。
Q:当我6岁时,我的妹妹是我的一半年龄。现在我70岁了,我的妹妹多大?
A:输出1:
当我6岁时,我的妹妹是我的一半年龄,也就是3岁。现在我70岁了,所以她是70-3 = 67岁。答案是67。
输出2:
当叙述者6岁时,他的妹妹是他年龄的一半,也就是3岁。现在叙述者70岁了,他的妹妹应该是70-3 = 67岁。答案是67。
输出3:
当我6岁时,我的妹妹是我的一半年龄,也就是3岁。现在我70岁了,所以她是70/2 = 35岁。答案是35。
- 从简到繁(Least-to-Most)[4]:将问题拆解成多个部分,逐一解决,然后利用每个子问题的解答作为解决下一个子问题的上下文。
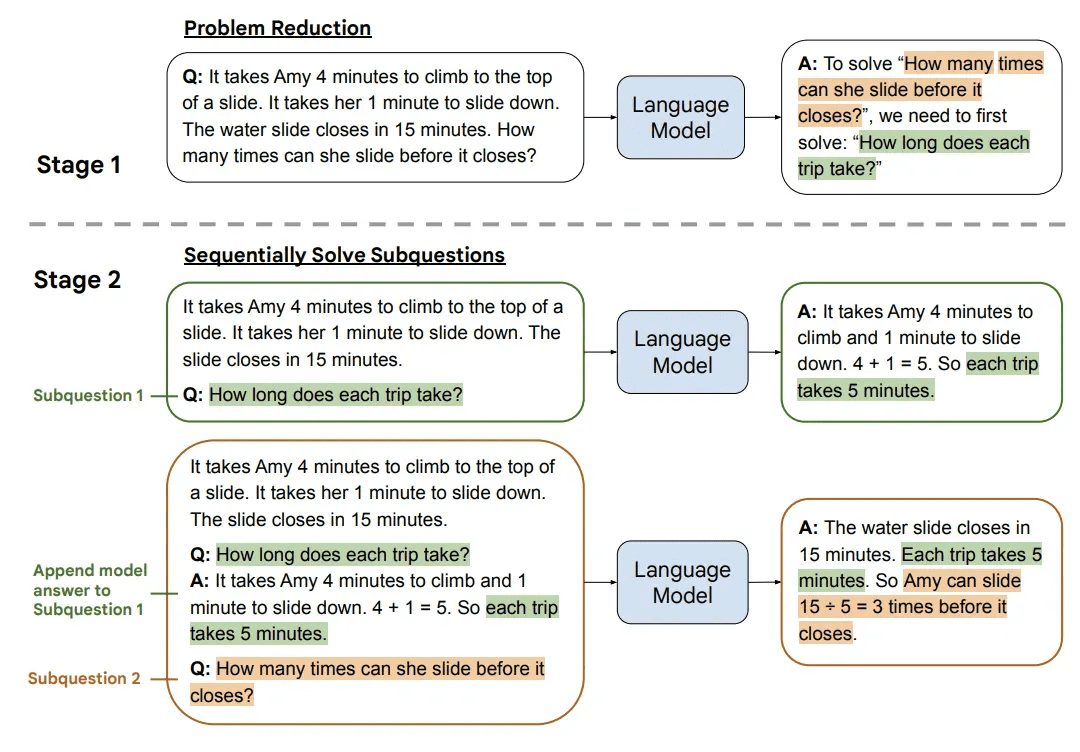
输入:
客户咨询:
我在3月1日购买了你们 Arnold 系列的一件T恤。我看到它有折扣,所以买了一件原价为 30 美元的衬衫,打了 6 折。我发现你们现在有一个新的T恤折扣活动,50% off。我想知道我是否可以退货,同时拥有足够的店内积分来购买两件你们的T恤?指令:
你是一名客户服务代表,负责友好地回复客户的查询。退货在 30 天内允许。今天是 3 月 29 日。目前所有衬衫都有 50% 的折扣。你的店里衬衫价格在 18-100 美元之间。请勿编造任何关于折扣政策的信息。
在回答这个问题之前,必须解决哪些子问题?输出:
1.客户购买衬衫的日期;
2.当前的折扣活动;
3.店内衬衫的价格范围;
4.客户是否有足够的店内积分;
5.客户退货的政策。输入:
客户咨询:
我在3月1日购买了你们 Arnold 系列的一件T恤。我看到它有折扣,所以买了一件原价为 30 美元的衬衫,打了 6 折。我发现你们现在有一个新的T恤折扣活动,50% off。我想知道我是否可以退货,同时拥有足够的店内积分来购买两件你们的T恤?指令:
你是一名客户服务代表,负责友好地回复客户的查询。退货在 30 天内允许。今天是 3 月 29 日。目前所有衬衫都有 50% 的折扣。你的店里衬衫价格在 18-100 美元之间。请勿编造任何关于折扣政策的信息。
确定客户是否在30天的退货期内。让我们一步一步来。输出:
尊敬的客户,非常感谢您对 Arnold 系列的支持!我们很高兴地向您提供服务。我们的退货政策是,客户可以在购买商品的 30 天内进行退货。由于您是在 3 月 1 日购买的,所以您仍然在退货期内,可以退货。
此外,我们目前正在举行一个 50% 的折扣活动,您可以使用您的店内积分购买两件 Arnold 系列的 T 恤。我们的衬衫价格在 18-100 美元之间,您可以根据自己的需求选择合适的衬衫。
如果您有任何其他问题,请随时与我们联系。我们将竭诚为您服务!
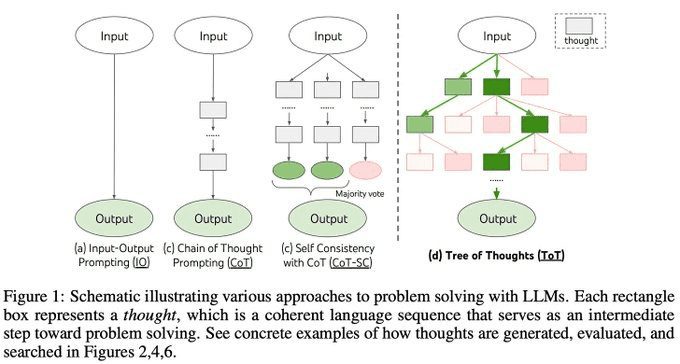
思维树(Tree of thoughts [ToT])提示[5]:CoT提示无法解决那些需要规划、战略预见、回溯以及并行探索多种解决方案的问题。ToT提示将复杂问题拆分成一系列更简单的问题(或“思考”)。LLM生成众多“思考”,并通过自然语言持续评估其向最终解决方案迈进的进度。利用模型对解决方案进展的自我评估,我们可以运用广泛使用的搜索算法(如宽度优先搜索或深度优先搜索)来促进探索过程,并在解决问题时允许进行预见/回溯。
假设三位不同的专家来回答这个问题。
所有专家都写下他们思考这个问题的第一个步骤,然后与大家分享。
然后,所有专家都写下他们思考的下一个步骤并分享。
以此类推,直到所有专家写完他们思考的所有步骤。
只要大家发现有专家的步骤出错了,就让这位专家离开。
请问...
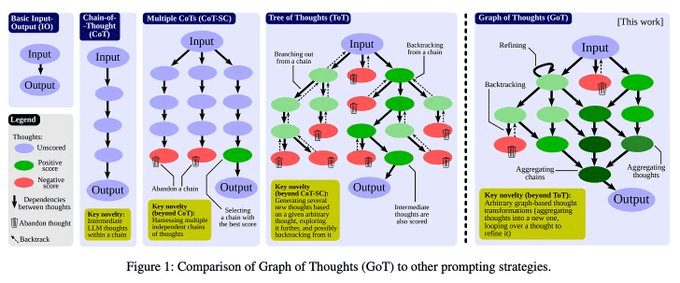
思维图(Graph of Thoughts [GoT])提示[6, 7]:后续的研究将ToT提示的工作推广到了基于图的推理策略。这些技术类似于ToT提示,但不假设生成解答的思维路径是线性的。我们可以重复使用思维,甚至在推导解决方案时对一系列的思维进行递归。尽管提出了多种基于图的提示策略,但这些技术以及ToT提示都因实用性不足而遭到批评。使用GoT提示解决一个推理问题可能需要LLM执行大量的推理步骤!
以下是上述所有引用论文的链接!
[1] https://arxiv.org/abs/2201.11903[2] https://arxiv.org/abs/2205.11916
[3] https://arxiv.org/abs/2203.11171
[4] https://arxiv.org/abs/2205.10625
[5] https://arxiv.org/abs/2305.10601
[6] https://arxiv.org/abs/2308.09687
[7]https://arxiv.org/abs/2305.16582[8]https://arxiv.org/abs/2201.11903
© 版权声明
文章版权归 AI分享圈 所有,未经允许请勿转载。
相关文章

暂无评论...