本测评结果仅用于学术研究。
10月22日,Anthropic正式推出升级版的大模型Claude 3.5 Sonnet以及新模型Claude 3.5 Haiku。
据Anthropic官方介绍,Claude 3.5 Sonnet在各项能力上全面超越前版本,特别是在智能体编码和工具使用任务方面表现显著提升。在SWE-bench Verified上,其编码性能从33.4%提高至49.0%,超越了包括 OpenAI o1-preview 在内的所有公开模型。
Anthropic同时推出一项突破性的新功能:计算机使用。开发人员可以通过 API控制 Claude 以人类的方式使用计算机,但该功能目前还处于实验阶段。
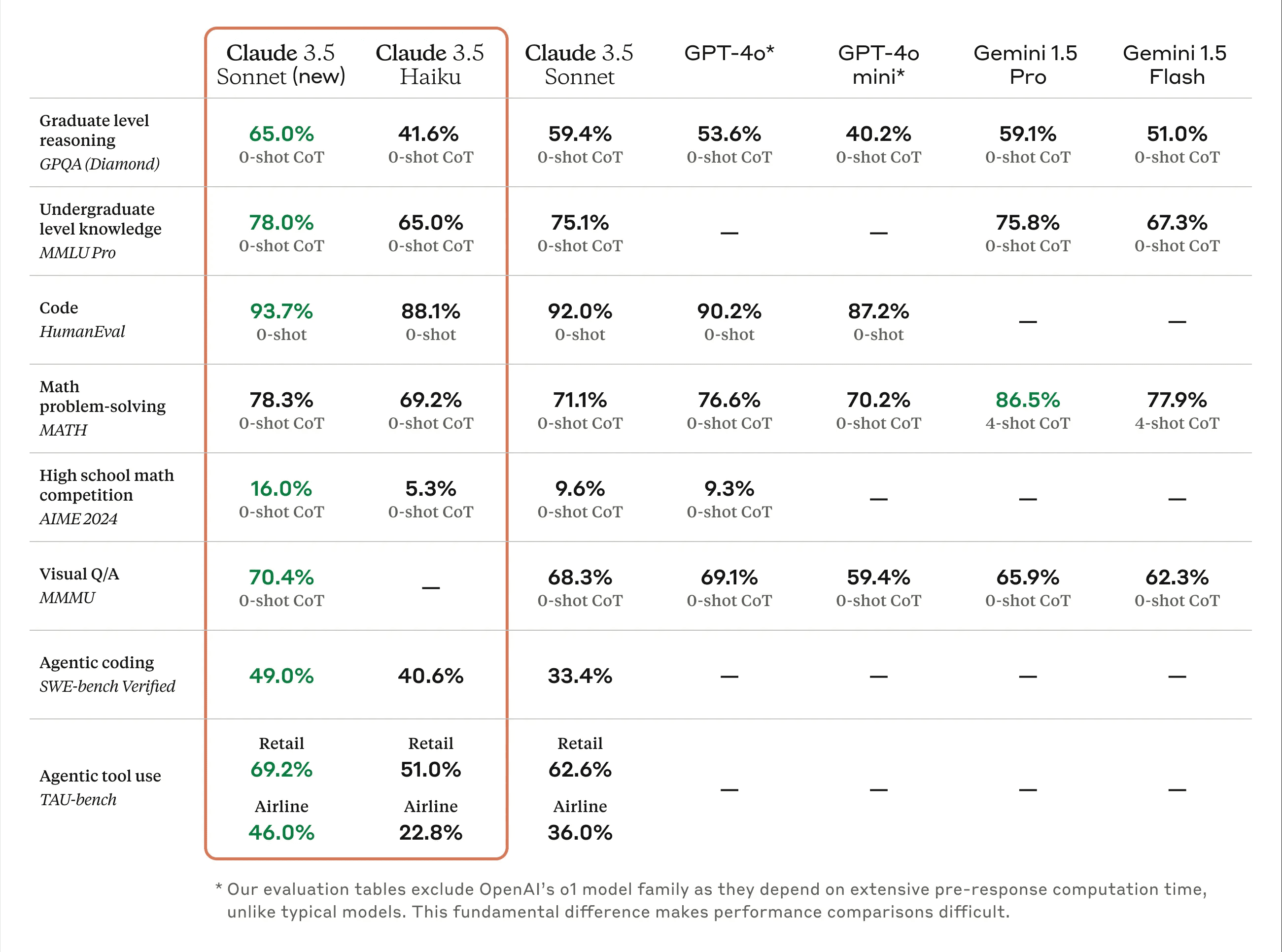
针对公众关注的Claude 3.5 Sonnet升级版,在中文场景下的推理和代码的性能问题,专业第三方测评机构SuperCLUE对Claude 3.5 Sonnet升级版进行了深入评估。
测评环境
参考标准:SuperCLUE-Reasoning中文高阶推理测评基准、SuperCLUE-Code3中文代码测评基准。
评测模型 :Claude 3.5 Sonnet(1022,POE最新模型快照)
模型GenerationConfig配置:
- 参考Claude详细说明文档:https://www.anthropic.com/news/3-5-models-and-computer-use
评测集:
1.SuperCLUE-Reasoning中文复杂任务高阶推理评测集。共302道题,包括多步推理、数字推理、推理计算、市场分析和最优化问题五个高难度推理任务。
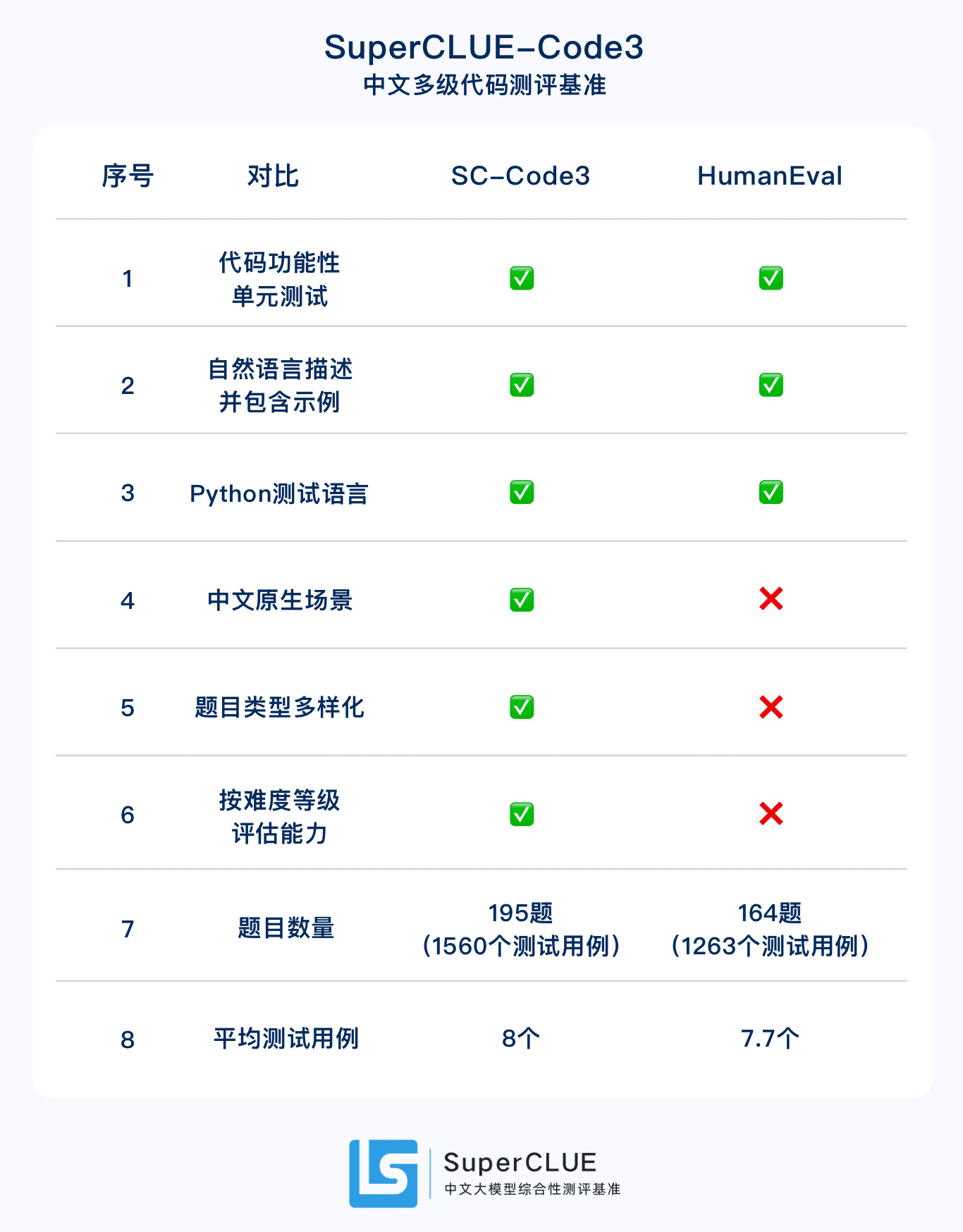
2.SuperCLUE-Code3中文原生代码评测集。HumanEval的中文升级版,共195道题,包括1560个测试用例,分为初级、中级和高级三类难度级别。
测评方法:
1.高阶推理:针对每一道推理题目,我们提供人工校验和核对后的参考答案和推理过程;然后根据设定的评估流程、评价标准和打分规则(1-5分),裁判模型对候选模型的答案进行评估。设定的评价标准包括:符合基本要求、推理准确性、结论合理性。
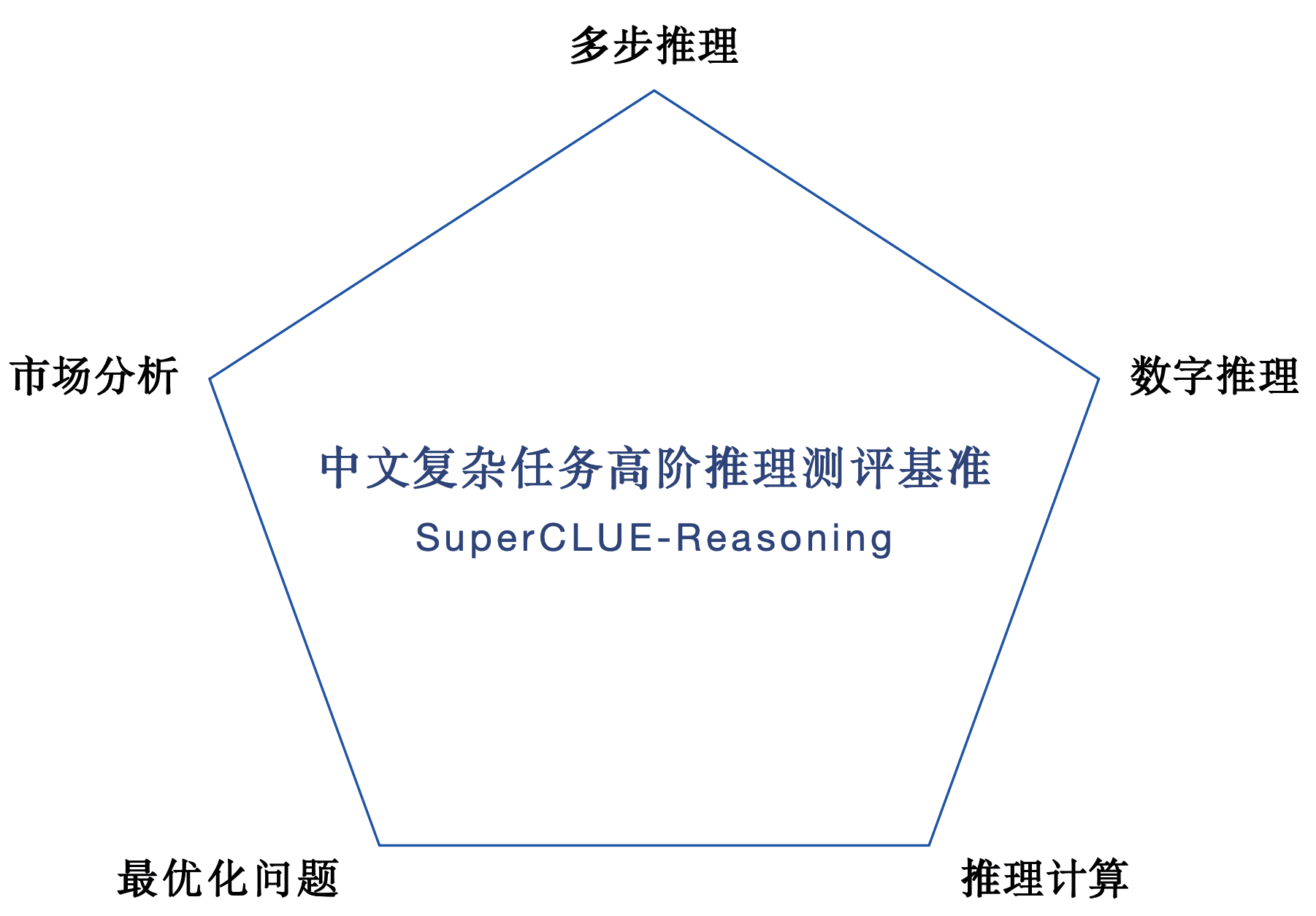
2.代码SC-Code3:通过功能性单元测试,专门设计来评估和提升中文大模型在代码生成方面的核心能力。
SuperCLUE-Code3:中文原生等级化代码能力测评基准
先说结论
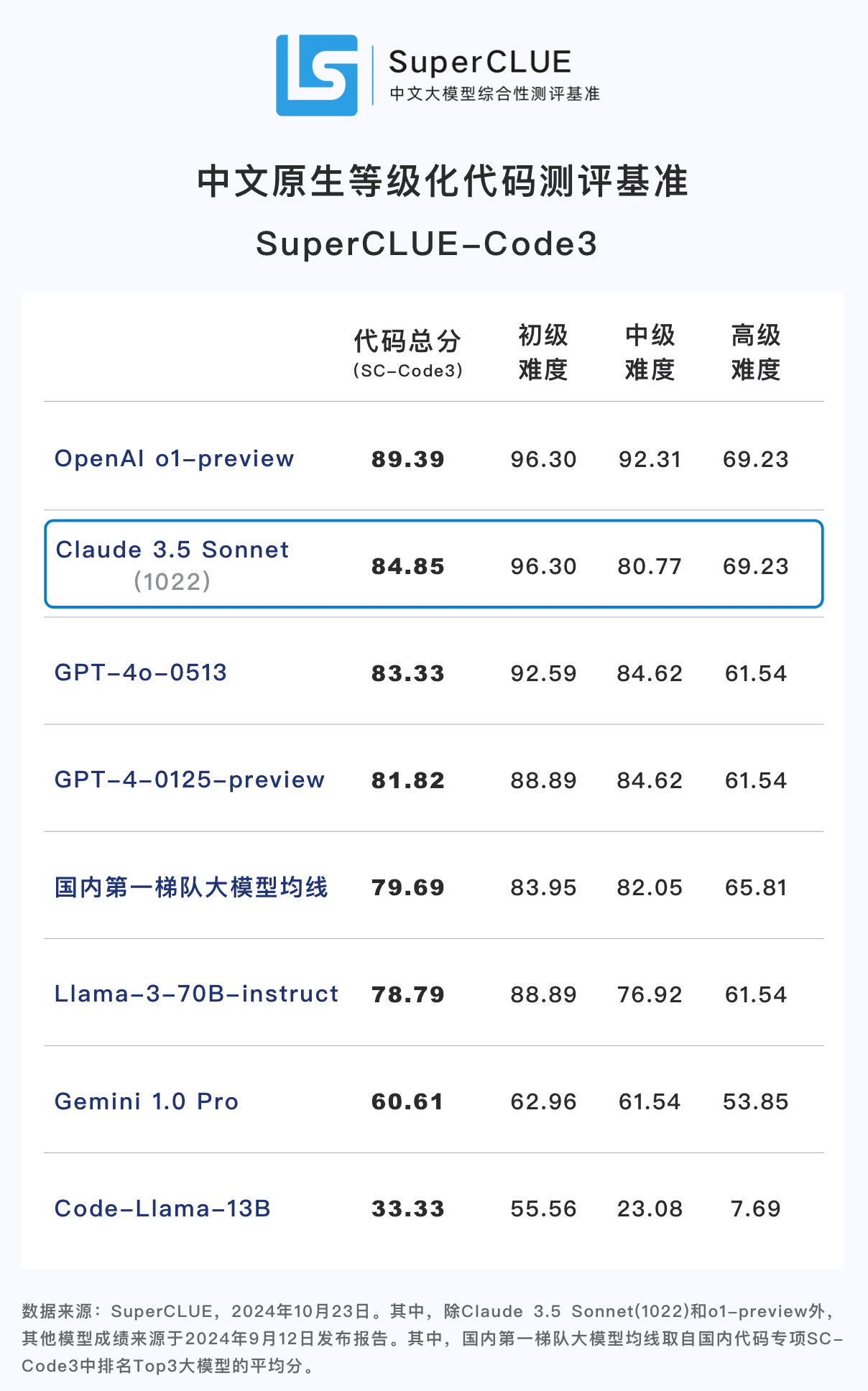
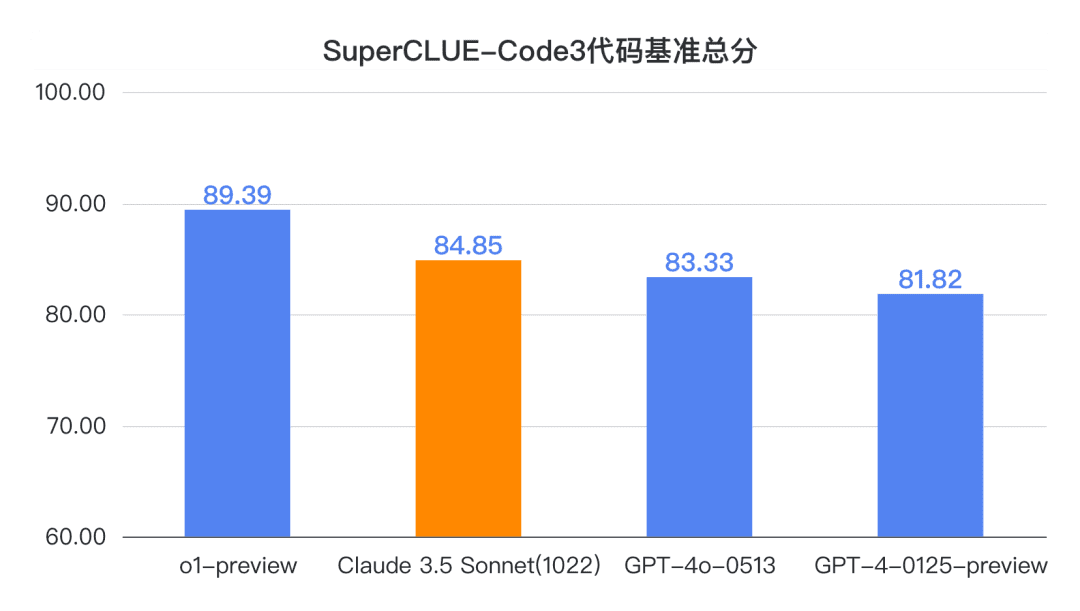
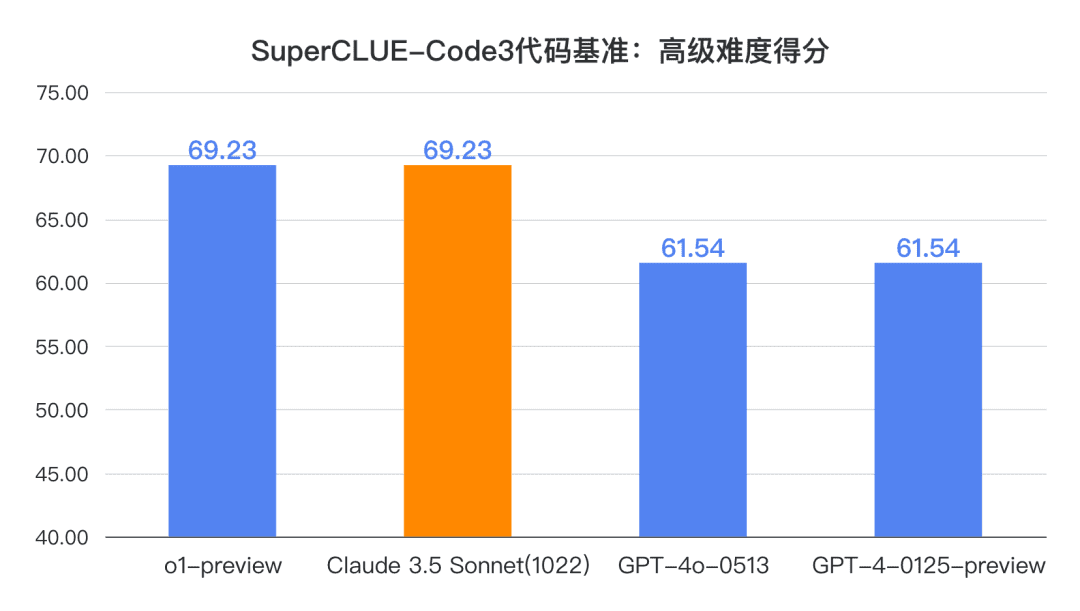
结论1: Claude 3.5 Sonnet(1022)在中文代码能力(SC-Code3)上表现不俗, 总分达到84.85分,较GPT-4o-0513高1.52分 ,较o1-preview低4.54分。其中,在高级代码任务上表现惊艳,得分69.23分,与o1-preview打平。
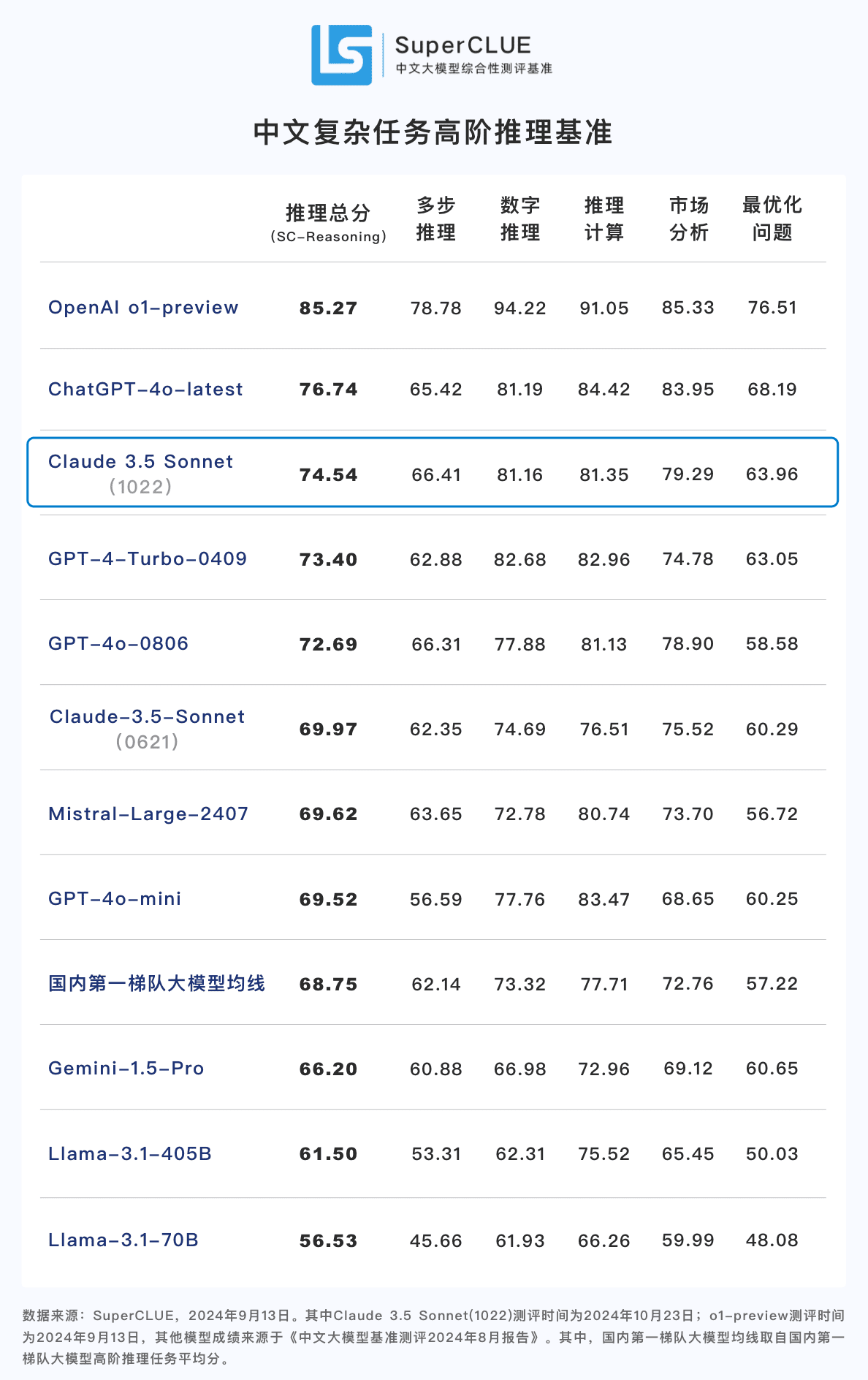
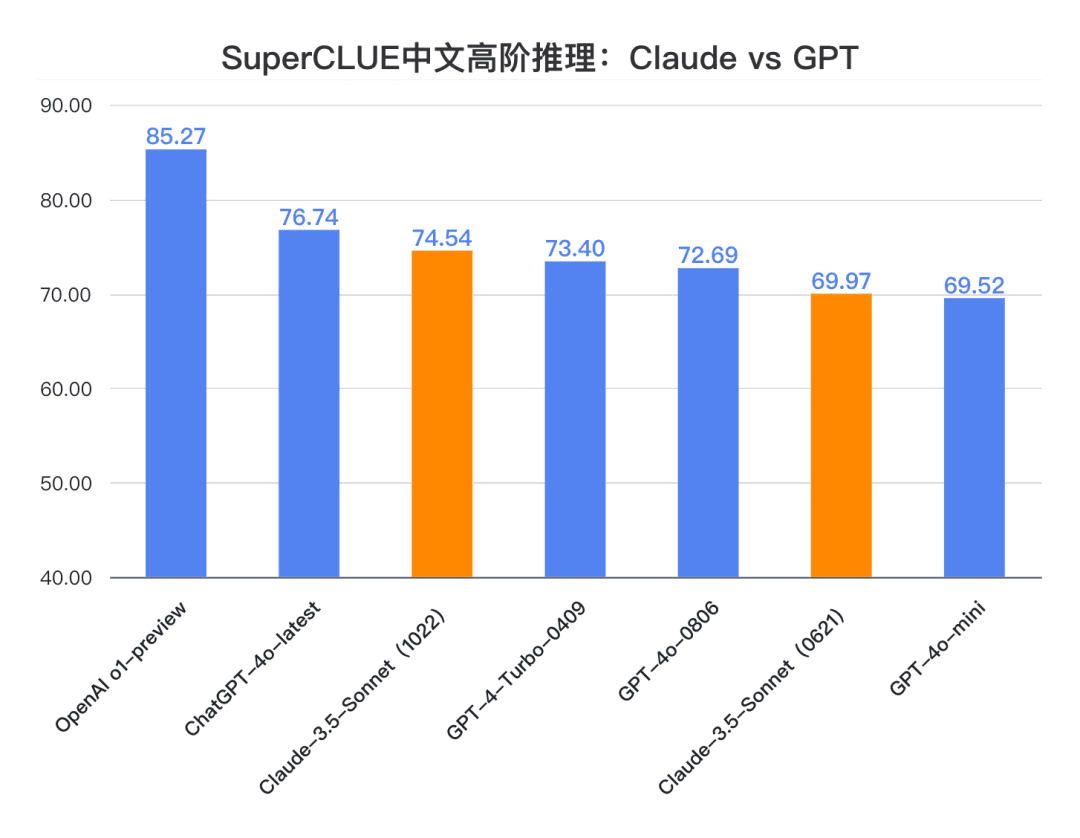
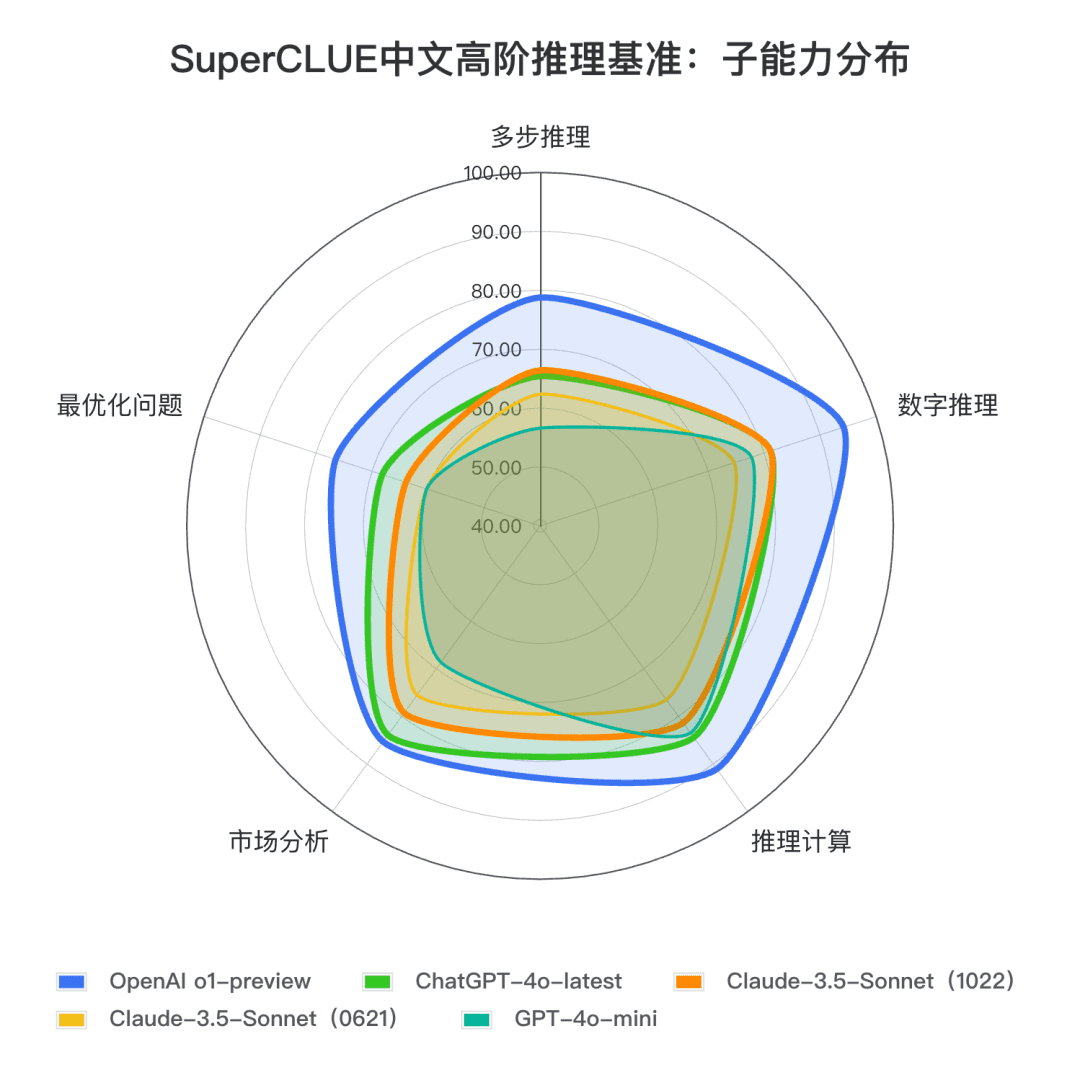
结论2: Claude 3.5 Sonnet(1022)在中文高阶推理任务上取得74.54分, 接近ChatGPT-4o-latest,相较o1-preview还有较大差距(-10.73分) 。其中,多步推理能力相对突出,有超过ChatGPT-4o-latest的表现。
**结论3:**相比上一代版本Claude 3.5 Sonnet(0621), Claude 3.5 Sonnet(1022)在推理任务中提升了4.57分 ,并在数字推理、计算推理等二级任务中有显著进步。
测评结果
对比分析
代码测评示例
示例1
Prompt:
from typing import List
def longest_peak_sequence(nums: List[int]) -> int:
"""
在一个整数数组中找出最长的"峰"序列的长度。
所谓"峰"序列,是指先严格递增然后严格递减的序列,且峰顶(即最大值)唯一。
至少包括三个数以上才能构成一个"峰"序列(即包含递增和递减的部分)。
返回数组中最长"峰"序列的长度。如果没有"峰"序列,则返回0。
示例:
>>> longest_peak_sequence([2, 1, 4, 7, 3, 2, 5])
5 # 最长的"峰"序列是 [1, 4, 7, 3, 2]
>>> longest_peak_sequence([5, 4, 3, 2, 1])
0 # 不存在"峰"序列,因为没有严格递增的部分
提示:
- 数组 `nums` 的长度范围为 [0, 10000]。
- 数组中的每个元素范围为 [-10000, 10000]。
"""
Claude 3.5 Sonnet(1022)答案:
from typing import List
def longest_peak_sequence(nums: List[int]) -> int:
if len(nums) < 3:
return 0
max_length = 0
# 从第二个元素遍历到倒数第二个元素
for i in range(1, len(nums) - 1):
# 检查当前位置是否是峰顶
if nums[i] > nums[i-1] and nums[i] > nums[i+1]:
# 找到一个峰顶,向两边扩展
left = i - 1
right = i + 1
# 向左扩展,寻找严格递增序列
while left > 0 and nums[left-1] < nums[left]:
left -= 1
# 向右扩展,寻找严格递减序列
while right < len(nums) - 1 and nums[right+1] < nums[right]:
right += 1
# 更新最长峰序列长度
current_length = right - left + 1
max_length = max(max_length, current_length)
return max_length
测试用例:
def check(candidate):
assert candidate( [1, 2, 3, 4, 5, 6])==0
assert candidate([1, 3, 5, 6, 4, 2, 0])==7
assert candidate( [5, 4, 3, 2, 1, 2, 3, 4, 1])==5
assert candidate([1, 3, 5, 3, 1])==5
assert candidate([1, 2, 3, 3, 2, 1])==0
assert candidate([2, 1, 3, 1, 2, 1, 3])==3
assert candidate([1, 3, 5, 4, 3, 2, 1])==7
if_passed**(是否通过):**通过。
示例2
Prompt:
from typing import List
def longest_increasing_path(matrix: List[List[int]]) -> int:
"""
给定一个整数矩阵,找到最长严格递增路径的长度。
路径被定义为从矩阵中的任意单元格开始,每次可以向上、下、左、右移动到相邻的单元格上,如果递增的话。
你不能在路径中移动到矩阵外面,也不能移动到不满足递增条件的单元格上。
路径的长度是路径上的单元格总数。
示例:
>>> longest_increasing_path([
[9, 9, 4],
[6, 6, 8],
[2, 1, 1]
])
4 # 最长递增路径是 [1, 2, 6, 9]
>>> longest_increasing_path([
[3, 4, 5],
[3, 2, 6],
[2, 2, 1]
])
4 # 最长递增路径是 [3, 4, 5, 6]或 [2, 4, 5, 6]
提示:
- 矩阵 `matrix` 的维度为 m x n。
- 矩阵 `matrix` 的每个元素是一个非负整数。
"""
Claude 3.5 Sonnet(1022)答案:
from typing import List
def longest_increasing_path(matrix: List[List[int]]) -> int:
if not matrix or not matrix[0]:
return 0
m, n = len(matrix), len(matrix[0])
# 缓存,用于存储每个位置的最长递增路径长度
cache = [[0] * n for _ in range(m)]
def dfs(i: int, j: int) -> int:
# 如果已经计算过,直接返回缓存结果
if cache[i][j] != 0:
return cache[i][j]
# 四个方向:上、下、左、右
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
# 当前位置的最长路径至少为1
max_length = 1
# 遍历四个方向
for di, dj in directions:
ni, nj = i + di, j + dj
# 检查是否在矩阵范围内且满足递增条件
if (0 <= ni < m and 0 <= nj < n and
matrix[ni][nj] > matrix[i][j]):
# 递归计算邻居位置的最长路径
curr_length = 1 + dfs(ni, nj)
max_length = max(max_length, curr_length)
# 存入缓存
cache[i][j] = max_length
return max_length
# 遍历矩阵中的每个位置,找到最长路径
result = 0
for i in range(m):
for j in range(n):
result = max(result, dfs(i, j))
return result
测试用例:
def check(candidate):
assert candidate([[1, 1], [1, 1]]) == 1
assert candidate([
[9, 9, 4],
[6, 6, 8],
[2, 1, 1]
]) == 4
assert candidate([
[3, 4, 5],
[3, 2, 6],
[2, 2, 1]
]) == 4
assert candidate([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
]) == 7
assert candidate([
[-1, -2, -3, 0],
[5, -6, 7, -8],
[-9, 0, -11, -12],
[13, 0, 15, -16]
]) == 4
assert candidate([
[5, 10, 6, 7, 9],
[6, 10, 2, 2, 3],
[4, 9, 8, 2, 8],
[3, 3, 3, 8, 8]
])==4
assert candidate([
[1, 3, 1, 4],
[1, 5, 1, 7],
[4, 2, 1, 1],
[1, 3, 2, 1]
])==3
assert candidate([
[1, 9, 2, 4],
[9, 6, 5, 3],
])==4
if_passed(是否通过):通过。
高阶推理示例
示例1:多步推理
问
某公司有七个员工分别是A, B, C, D, E, F和G。公司举行了一次评分活动,根据员工的成绩和以下条件,请推断出每个员工的具体排名:
- A的得分比B高,但比C低。
- D得分比E和G高,但低于A。
- G得分最低。
- B得分高于E和F。
- F的得分比E高。
- C得分最高。
- 每个员工的得分都不相同,D排在最中间。
请根据以上条件推断每个员工的具体得分。
Claude 3.5 Sonnet(1022)回答:
让我们通过逻辑分析来推断每个员工的排名:
- 从条件3知道:G排在最后(第7名)
- 从条件6知道:C排在最前(第1名)
- 从条件7知道:D排在第4名(中间位置)
- 从条件2知道:D比E和G高,但低于A,所以:
- E必须排在D之后(第5名或第6名)
- A必须排在D之前(第2名或第3名)
- 从条件1知道:A比B高但比C低,结合前面的分析:
- A排第2名
- B必须排第3名
- 从条件4和5知道:B比E和F高,F比E高,所以:
- F排第5名
- E排第6名
最终排名如下:
- C(第1名)
- A(第2名)
- B(第3名)
- D(第4名)
- F(第5名)
- E(第6名)
- G(第7名)
需要我为您展示详细的推理过程吗?
示例2:最优化问题
问
某城市有五个主要交通枢纽,城市规划部门希望优化公交线路的覆盖范围,确保每个枢纽都能被至少一条线路连接。已知各枢纽之间的建设成本,目标是以最小的成本连接所有枢纽。
数据:
- 枢纽之间的连接成本(单位:万元)
- 枢纽 1 和 枢纽 2:10 万元
- 枢纽 1 和 枢纽 3:15 万元
- 枢纽 2 和 枢纽 4:20 万元
- 枢纽 3 和 枢纽 4:25 万元
- 枢纽 3 和 枢纽 5:30 万元
- 枢纽 4 和 枢纽 5:18 万元
目标:确定哪些枢纽之间应连接线路,以最小化总建设成本,并确保所有枢纽相互连通。
Claude 3.5 Sonnet(1022)回答:
这是一个最小生成树问题,我会使用 Kruskal 算法来解决。让我们一步步分析:
- 首先,将所有连接按成本从小到大排序:
- 枢纽1-2:10万元
- 枢纽1-3:15万元
- 枢纽4-5:18万元
- 枢纽2-4:20万元
- 枢纽3-4:25万元
- 枢纽3-5:30万元
- 依次选择成本最低的连接,避免形成环:
- 选择 枢纽1-2 (10万元)
- 选择 枢纽1-3 (15万元)
- 选择 枢纽4-5 (18万元)
- 选择 枢纽2-4 (20万元)
最优方案:
- 连接枢纽1和枢纽2
- 连接枢纽1和枢纽3
- 连接枢纽4和枢纽5
- 连接枢纽2和枢纽4
总成本:10 + 15 + 18 + 20 = 63万元
这个方案确保了:
- 所有枢纽都被连接
- 没有形成环路
- 达到最小总成本
要不要我为您生成一个可视化图表来展示这个解决方案?
# 加入社群
更多详细Claude3.5最新大模型测评详情,可加入SuperCLUE-Claude交流群。
© 版权声明
文章版权归 AI分享圈 所有,未经允许请勿转载。
相关文章

暂无评论...