一种语言建模中 Transformer 的替代方案
Transformer 架构是大语言模型（LLMs）成功的关键组成部分。几乎所有今天使用的大语言模型都采用了该架构，从开源模型如 Mistral 到闭源模型如 ChatGPT。
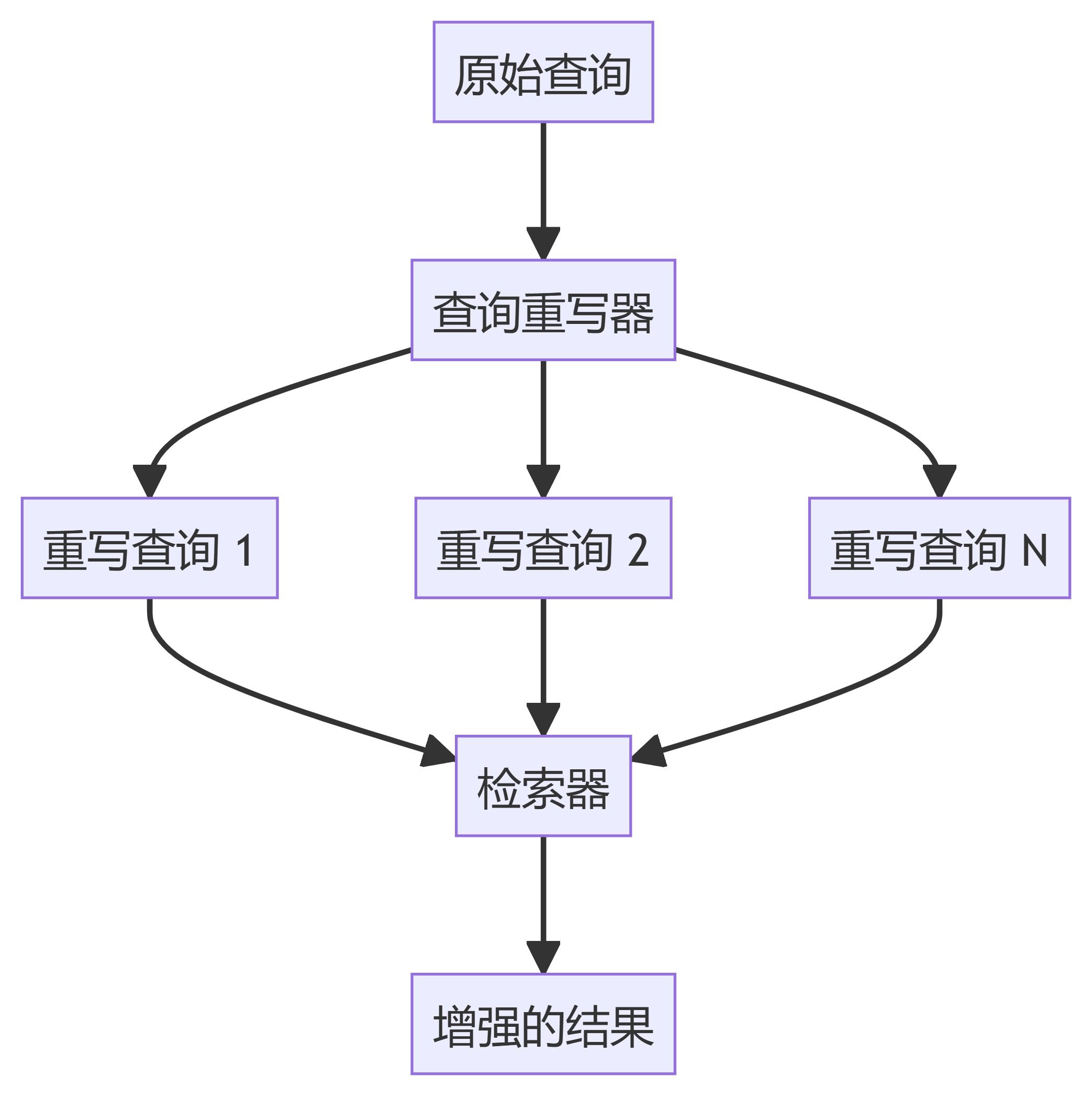
为了进一步改进大语言模型，新的架构被开发出来，这些架构可能甚至会超越 Transformer 架构。其中一种方法是 Mamba，一种 状态空间模型。
Mamba 在论文 Mamba: Linear-Time Sequence Modeling with Selective State Spaces1 中被提出。你可以在其 仓库 中找到其官方实现和模型检查点。
在这篇文章中，我将介绍在语言建模背景下的状态空间模型领域，并逐步探索各个概念，以帮助理解这一领域。然后，我们将讨论 Mamba 如何可能挑战 Transformer 架构。
作为一个视觉指南，本文将通过许多可视化内容来帮助理解 Mamba 和状态空间模型！
第 1 部分：Transformers 的问题
为了说明 Mamba 是多么有趣的架构，我们首先简要回顾一下 Transformers，并探索其一个缺点。
Transformer 将任何文本输入视为由 tokens 组成的 sequence。
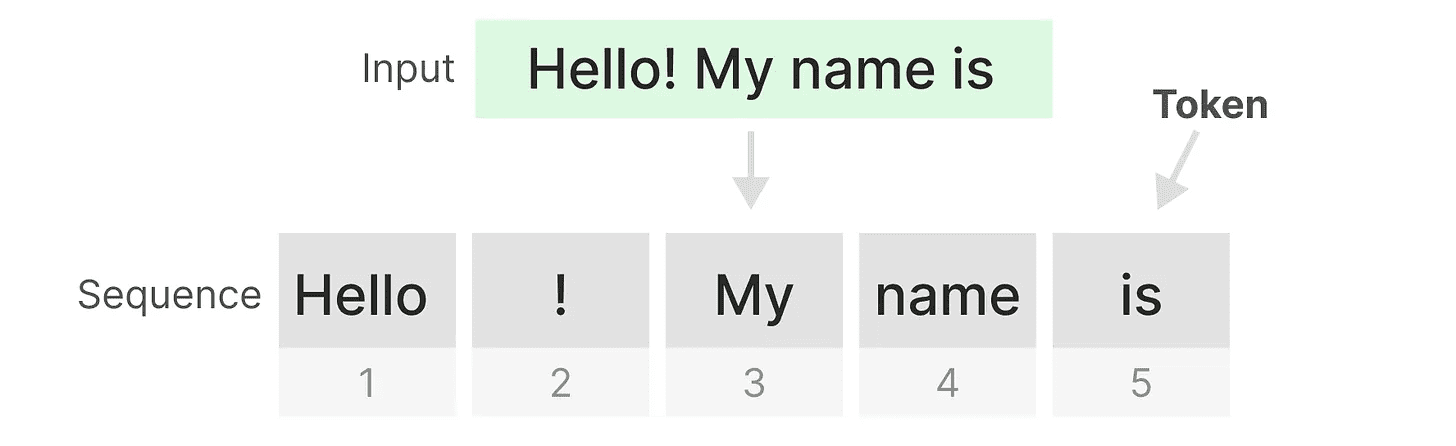Transformers 的一个主要优点是，无论它接收到什么输入，它都可以回溯到序列中任何早期的 tokens 来推导其表示。
Transformers 的核心组件
记住，Transformer 由两个结构组成，一个用于表示文本的编码器块集和一个用于生成文本的解码器块集。结合起来，这些结构可用于多个任务，包括翻译。
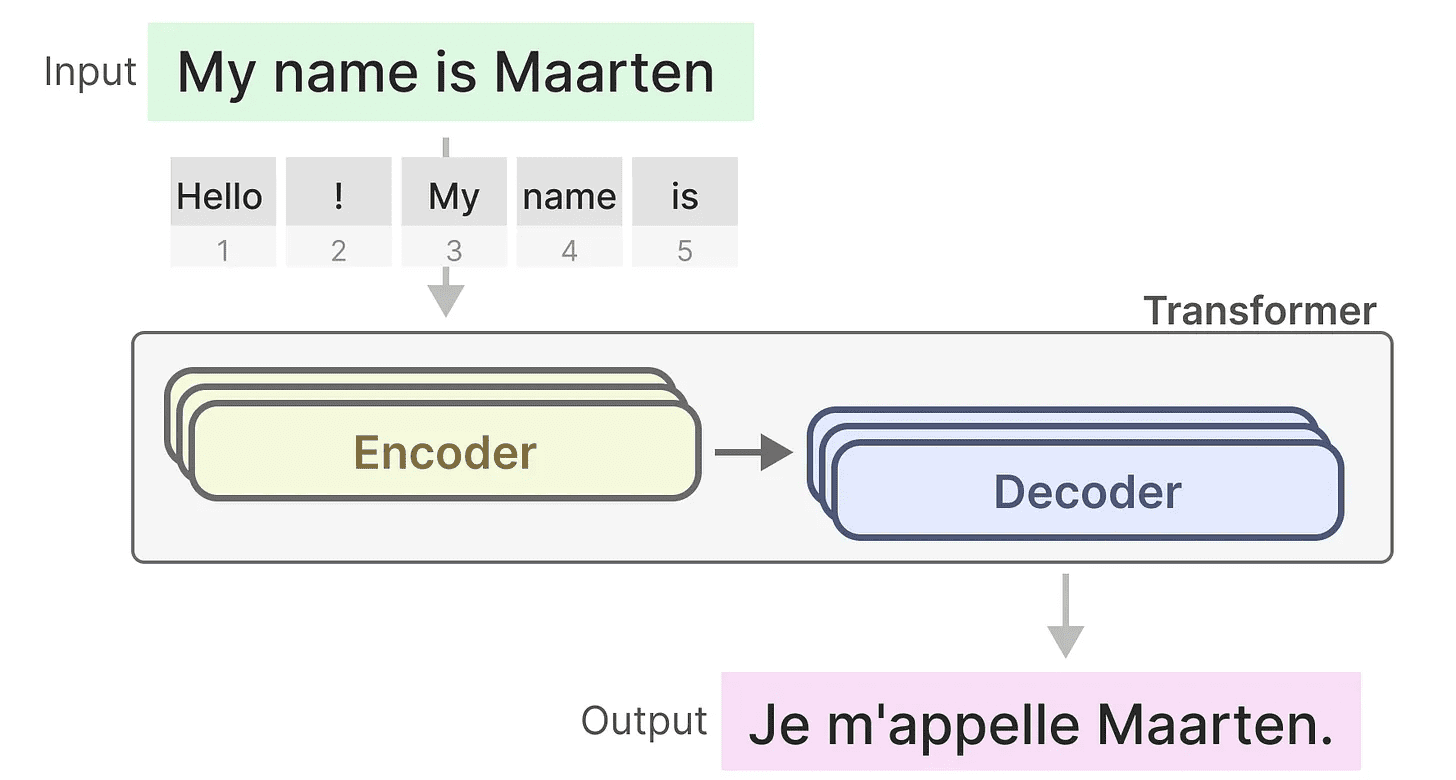我们可以采用这种结构，通过仅使用解码器来创建生成模型。这个基于 Transformer 的模型，生成式预训练 Transformer（GPT），使用解码器块来完成一些输入文本。
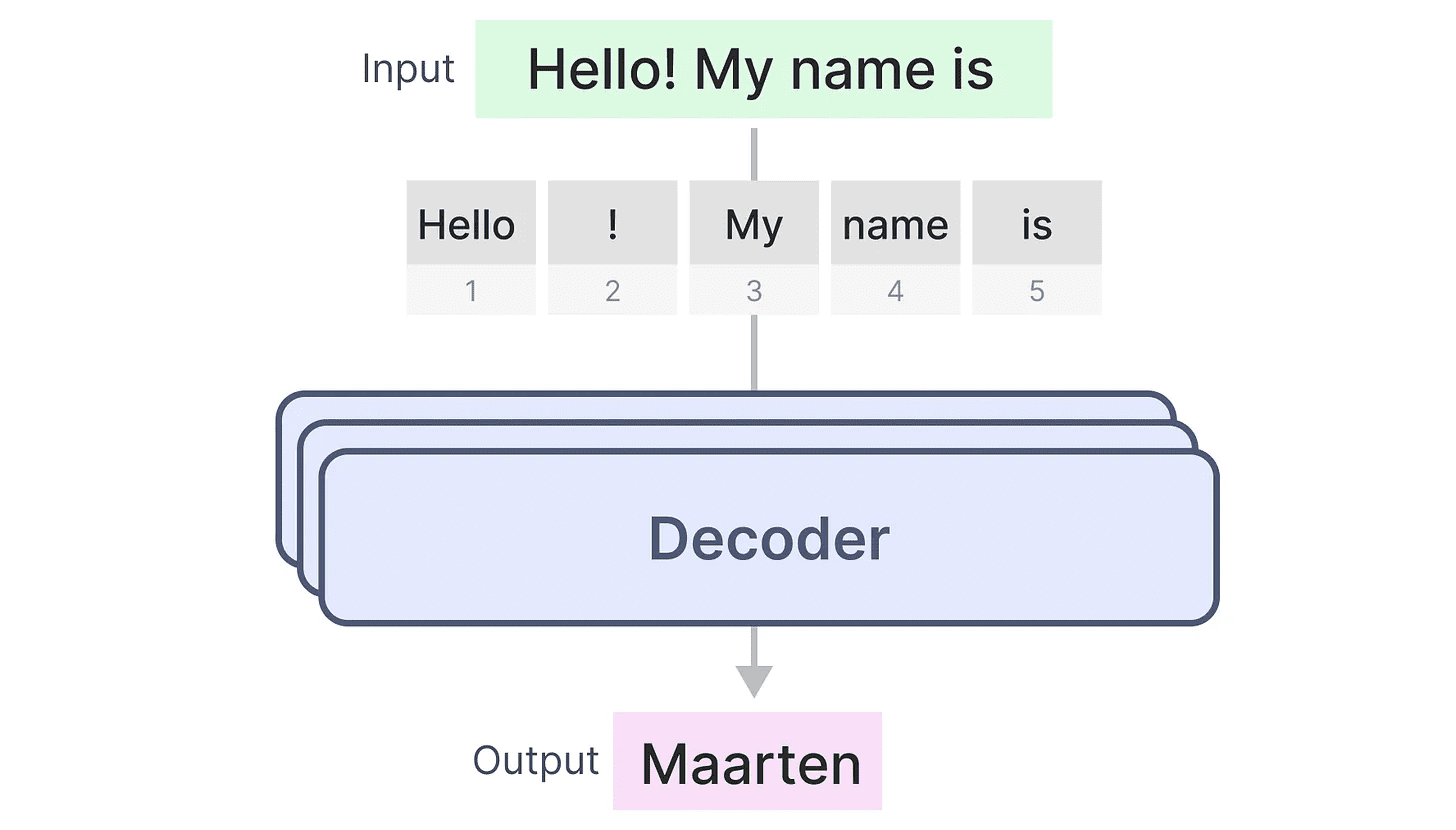让我们看看这是如何工作的！
训练中的祝福...
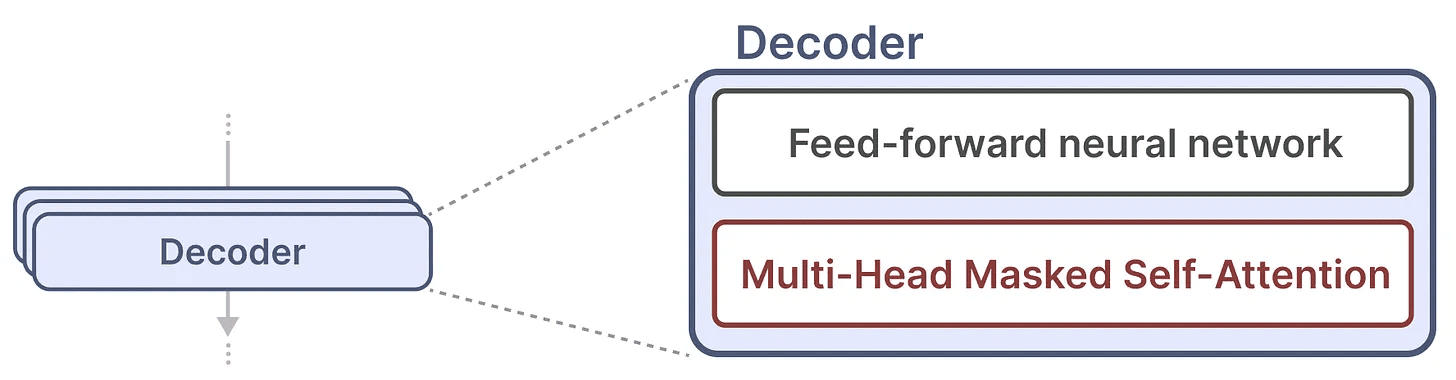
单个解码器块由两个主要组件组成，遮蔽的自注意力机制和前馈神经网络。
自注意力机制是这些模型工作得如此出色的一个重要原因。它使整个序列的未压缩视图得以实现，并且训练速度快。
那么它是如何工作的呢？
它创建了一个矩阵，将每个 Token 与之前的每个 Token 进行比较。矩阵中的权重取决于 Token 对彼此的相关性。
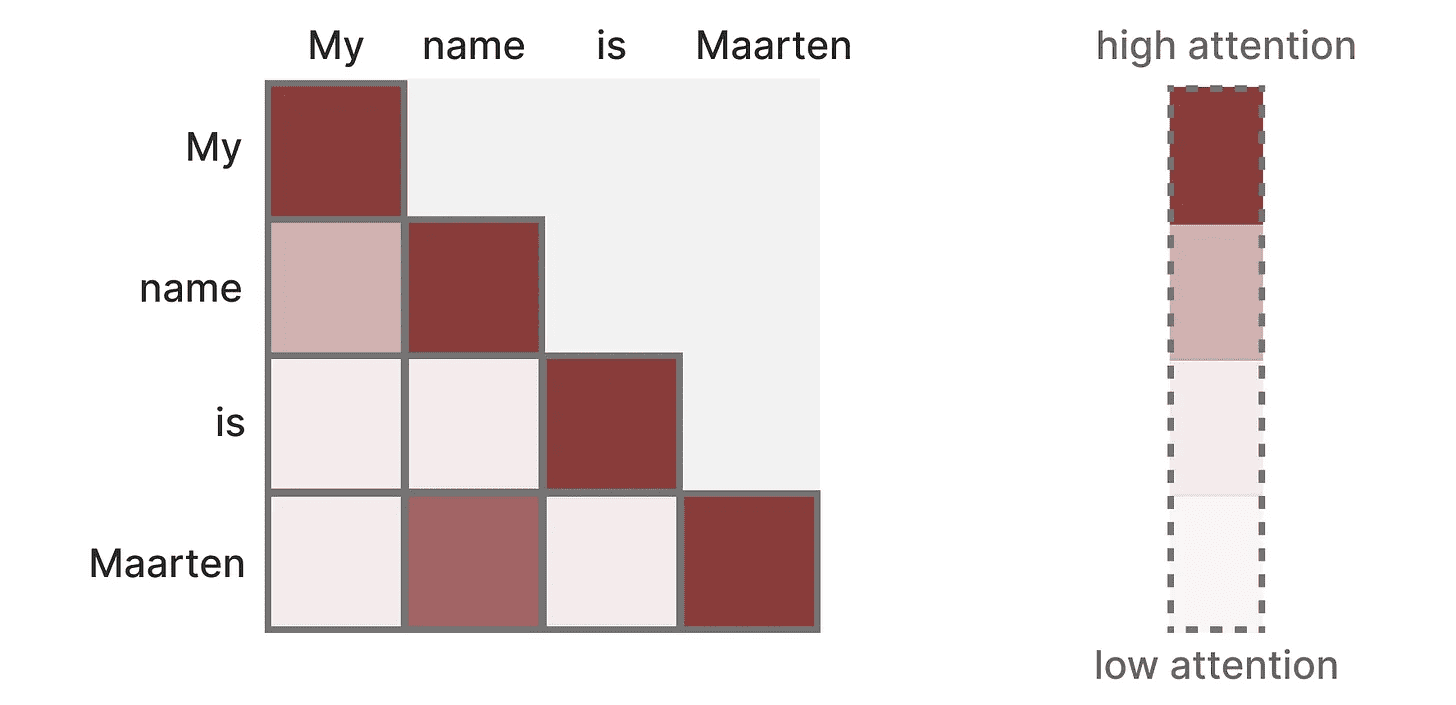在训练过程中，这个矩阵一次性创建。“My”和“name”之间的注意力不需要先计算，才能计算“name”和“is”之间的注意力。
它实现了并行化，这极大地加快了训练速度！
推理中的问题！
然而存在一个缺陷。当生成下一个 Token 时，我们需要重新计算整个序列的注意力，即使我们已经生成了一些 Token。
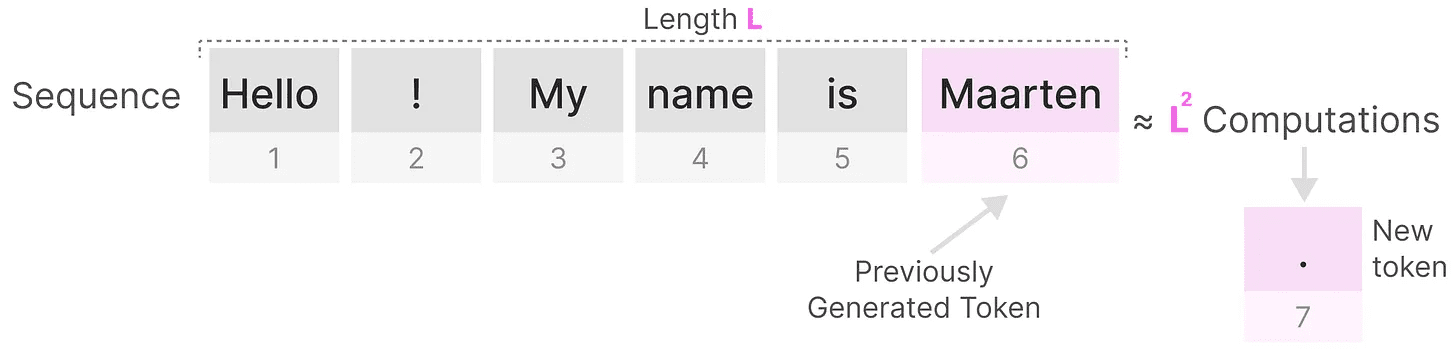生成长度为L的序列需要大约L²次计算，如果序列长度增加，计算代价会很高。
这种需要重新计算整个序列的情况是 Transformer 架构的主要瓶颈之一。
让我们看看一种“经典”技术——循环神经网络（Recurrent Neural Networks, RNN）是如何解决这个推理速度慢的问题。
RNN 是解决方案吗？
循环神经网络（RNN）是一种基于序列的网络。它在每个时间步中接收两个输入，即时间步t的输入和上一个时间步t-1的隐藏状态，用以生成下一个隐藏状态并预测输出。
RNN 有一个循环机制，允许它将信息从前一步传递到下一步。我们可以将这个可视化过程“展开”，使其更加明确。
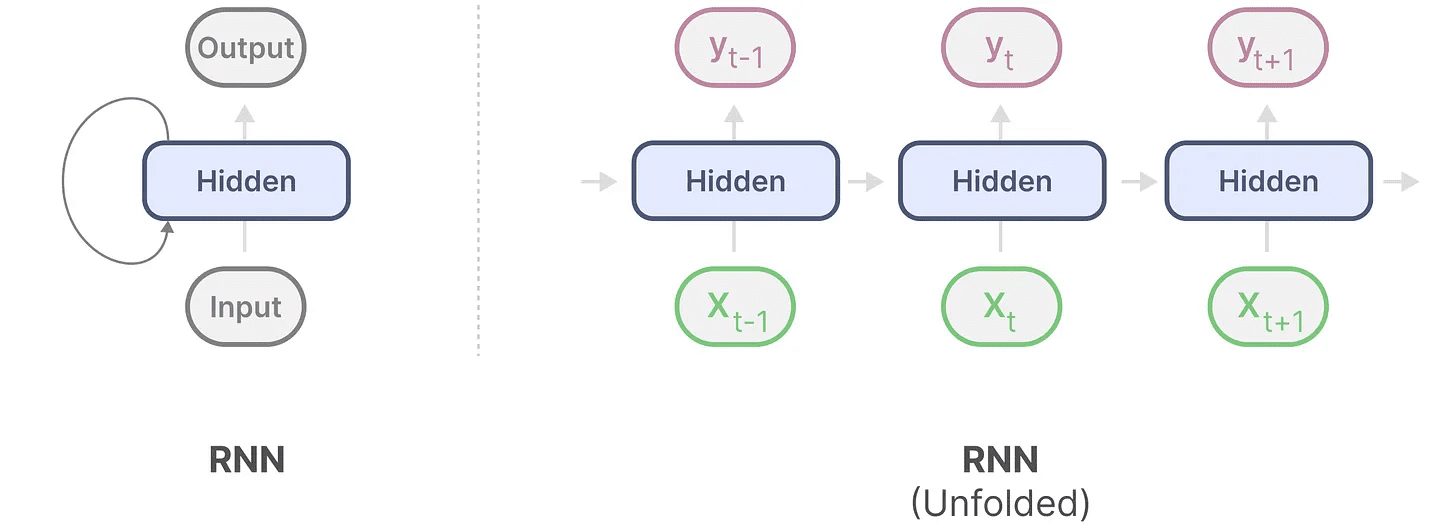在生成输出时，RNN 只需要考虑前一个隐藏状态和当前输入。它避免了 Transformer 所需的重新计算所有之前隐藏状态的问题。
换句话说，RNN 能够快速进行推理，因为它随着序列长度线性扩展！理论上，它甚至可以拥有无限的上下文长度。
为了说明这一点，让我们将 RNN 应用于我们之前使用的输入文本。
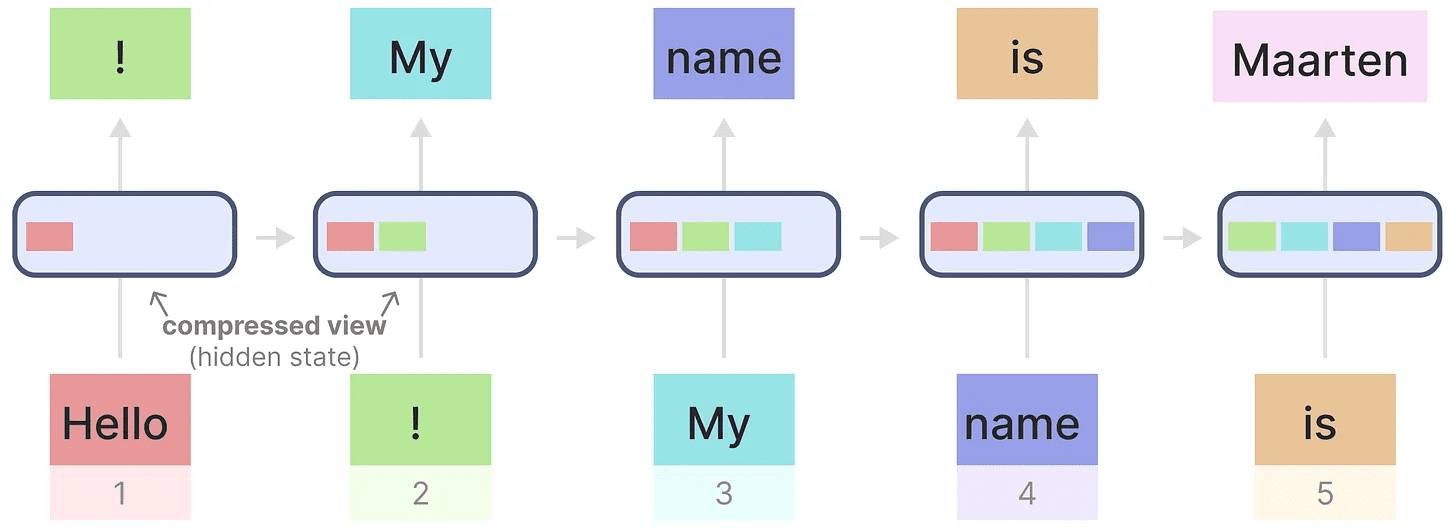每个隐藏状态都是所有之前隐藏状态的聚合，通常是一个压缩的视图。
然而，这里有一个问题……
注意，当生成名字“Maarten”时，最后一个隐藏状态已经不再包含关于单词“Hello”的信息了。RNN 随时间推移往往会忘记信息，因为它们只考虑上一个状态。
虽然 RNN 在训练和推理方面速度较快，但它们缺乏 Transformer 模型所能提供的精度。
因此，我们研究状态空间模型 (State Space Models) 来高效地使用 RNN（有时还会使用卷积）。
第 2 部分：状态空间模型 (SSM)
状态空间模型 (SSM) 像 Transformer 和 RNN 一样处理信息序列，比如文本和信号。在本节中，我们将介绍 SSM 的基本概念以及它们与文本数据的关系。
什么是状态空间？
状态空间包含完全描述一个系统所需的最少变量数。它是一种通过定义系统可能状态来数学表示问题的方法。
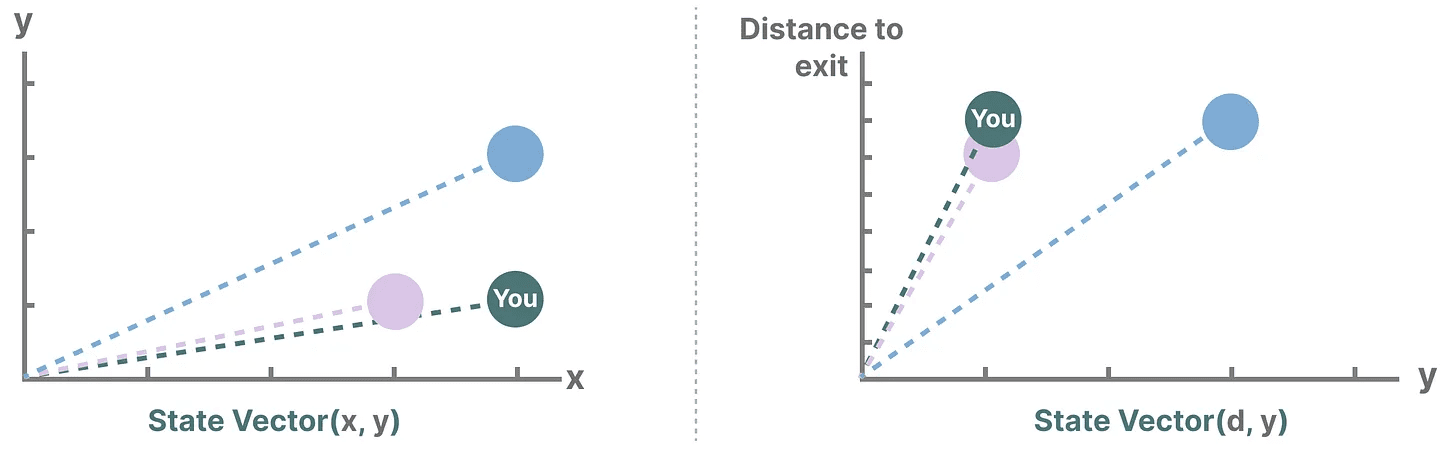
让我们简化一下。想象我们正在穿越迷宫。“状态空间”就是所有可能位置（状态）的地图。每个点代表迷宫中的一个独特位置，并带有特定的细节，比如你距离出口有多远。
“状态空间表示”是对这张地图的简化描述。它显示了你当前的位置（当前状态）、你可以前往的下一个位置（可能的未来状态）、以及你如何到达下一个位置（向右或向左移动）。
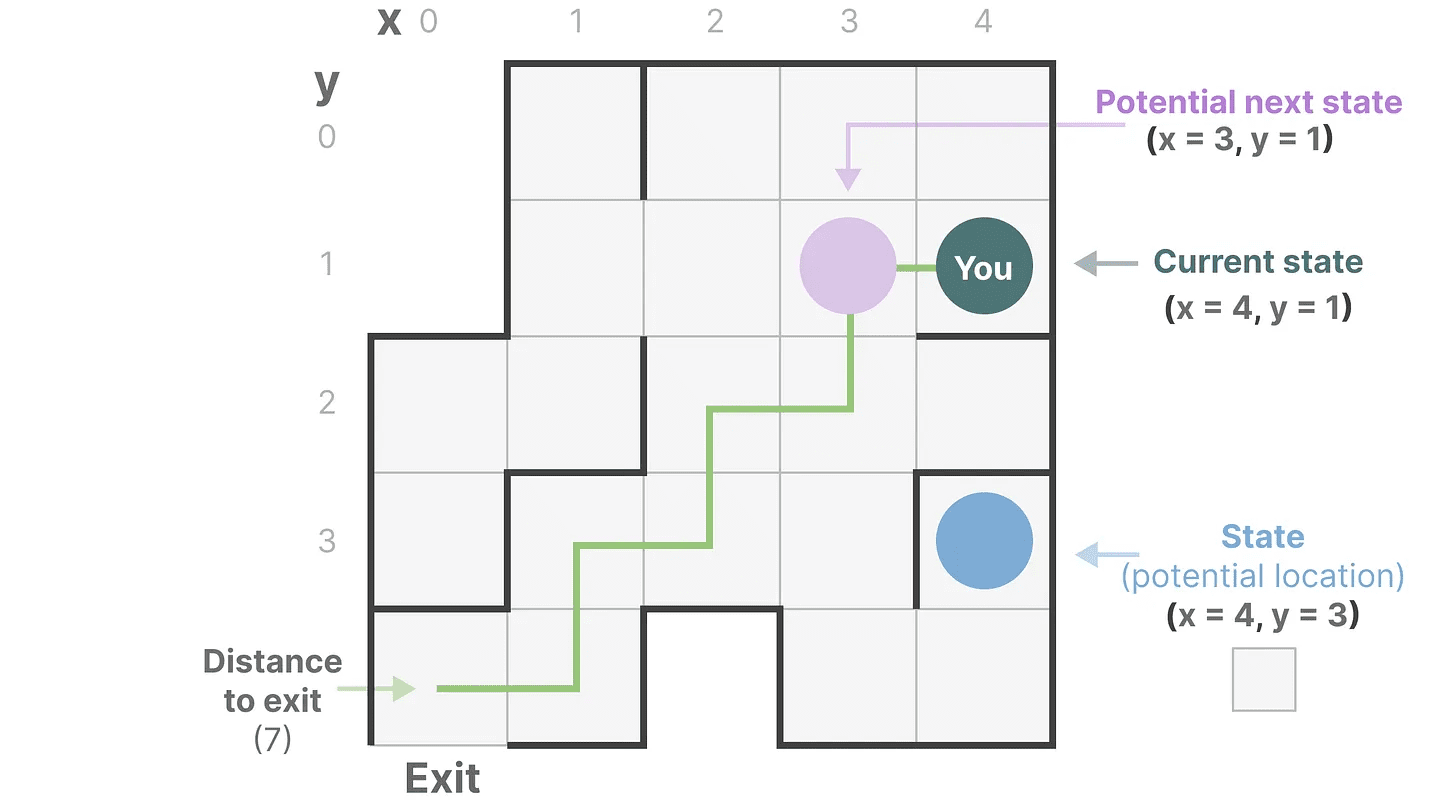虽然状态空间模型使用方程和矩阵来跟踪这种行为，但它实际上只是跟踪你在哪里、你可以去哪里、以及如何到达那里的一种方式。
变量描述了一个状态，在我们的例子中，X 和 Y 坐标，以及到出口的距离，可以表示为“状态向量”。
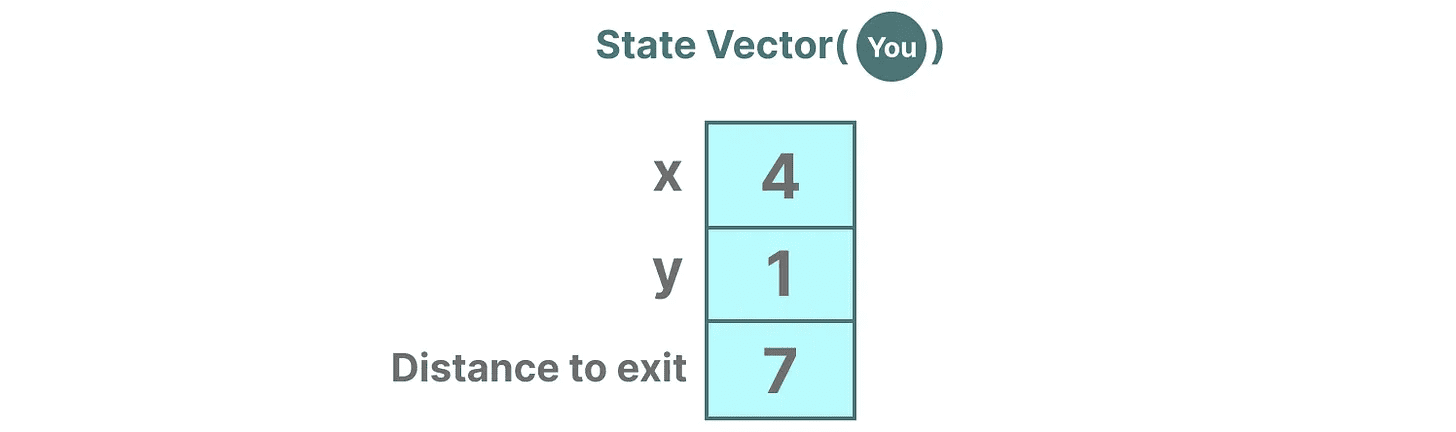
听起来很熟悉吗？这是因为在语言模型中，嵌入或向量也经常用于描述输入序列的“状态”。例如，描述你当前位置的向量（状态向量）可能类似于如下所示：
在神经网络中，“状态”通常指的是系统的隐藏状态，在大语言模型中，这是生成新 token 时最重要的方面之一。
什么是状态空间模型？
SSM（状态空间模型）是一类用于描述这些状态表示并预测其下一个状态的模型，预测基于某些输入。
传统上，在时间 t，SSM：
- 将输入序列 x(t)（例如，在迷宫中向左和向下移动）映射到潜在状态表示 h(t)（例如，到出口的距离和 x/y 坐标）
- 并推导出预测的输出序列 y(t)（例如，再次向左移动以更快到达出口）
然而，SSM 并不是使用离散序列（如向左移动一次），而是接受连续序列作为输入并预测输出序列。
SSM 假设动态系统（如在 3D 空间中移动的物体）可以通过时间 t 的状态和两个方程来预测。
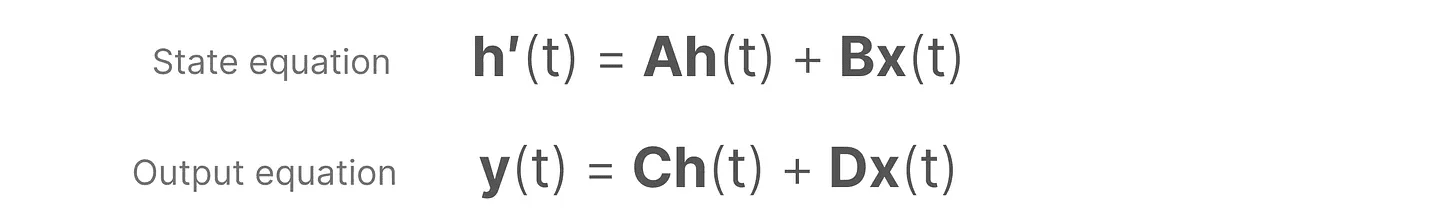通过求解这些方程，我们假设可以根据观测到的数据（输入序列和先前状态）揭示预测系统状态的统计原则。
其目标是找到这个状态表示 h(t)，使我们能够从输入到输出序列。
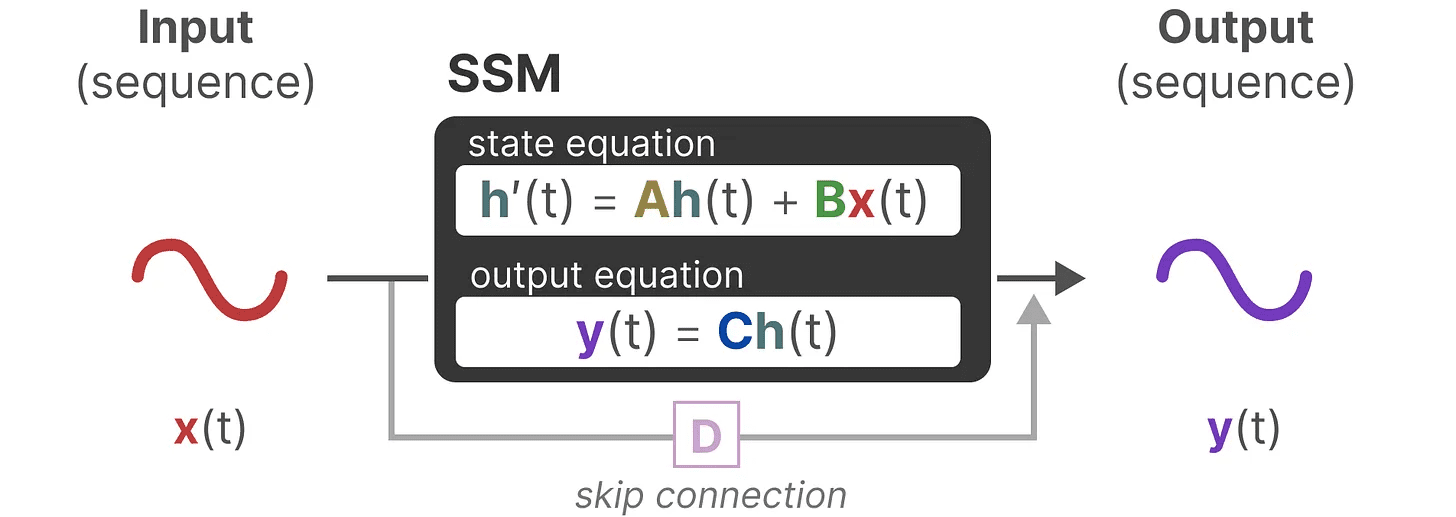
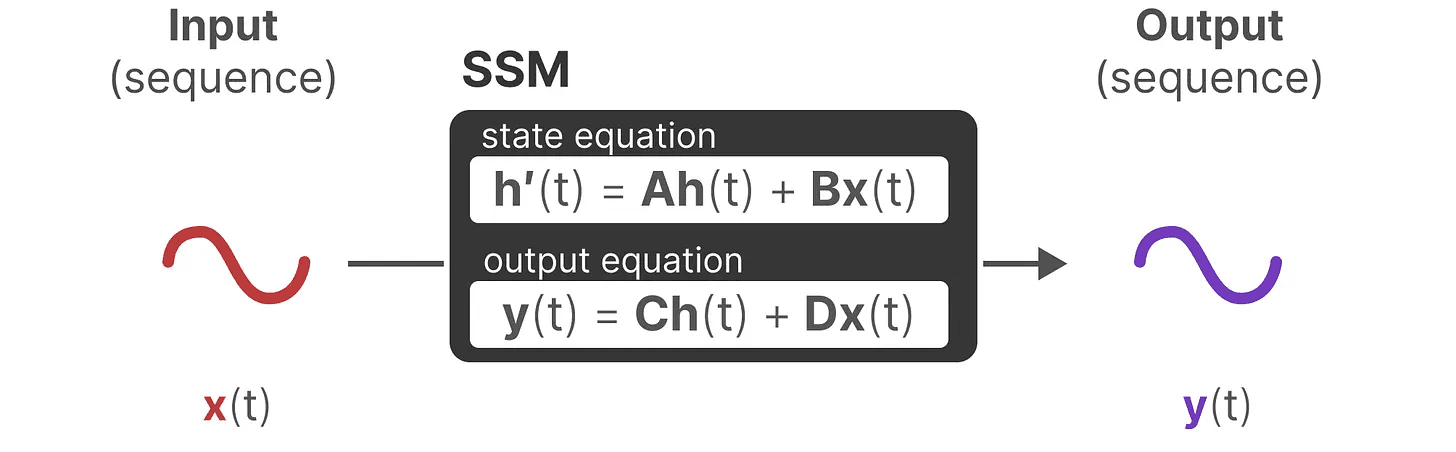这两个方程是状态空间模型的核心。
这两个方程将在整个指南中引用。为了让它们更直观，我们使用颜色编码，这样你可以快速引用它们。
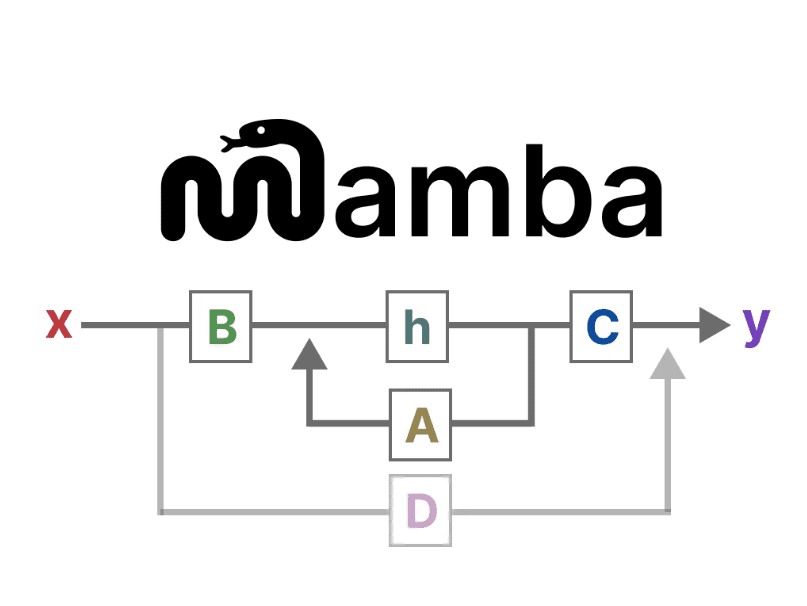
状态方程 描述了状态如何根据输入（通过 矩阵 B）影响状态（通过 矩阵 A）而变化。
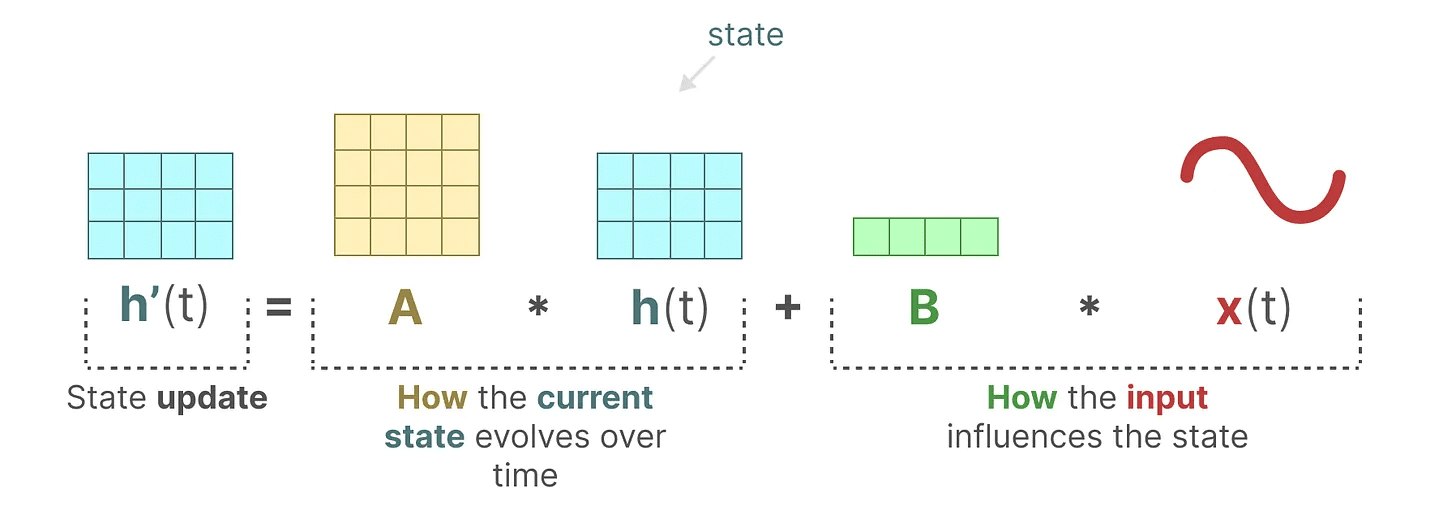如前所述，h(t) 指的是任意给定时间 t 的潜在状态表示，x(t) 指的是某个输入。
输出方程 描述了状态如何通过 矩阵 C 转换为输出，以及输入如何通过 矩阵 D 影响输出。
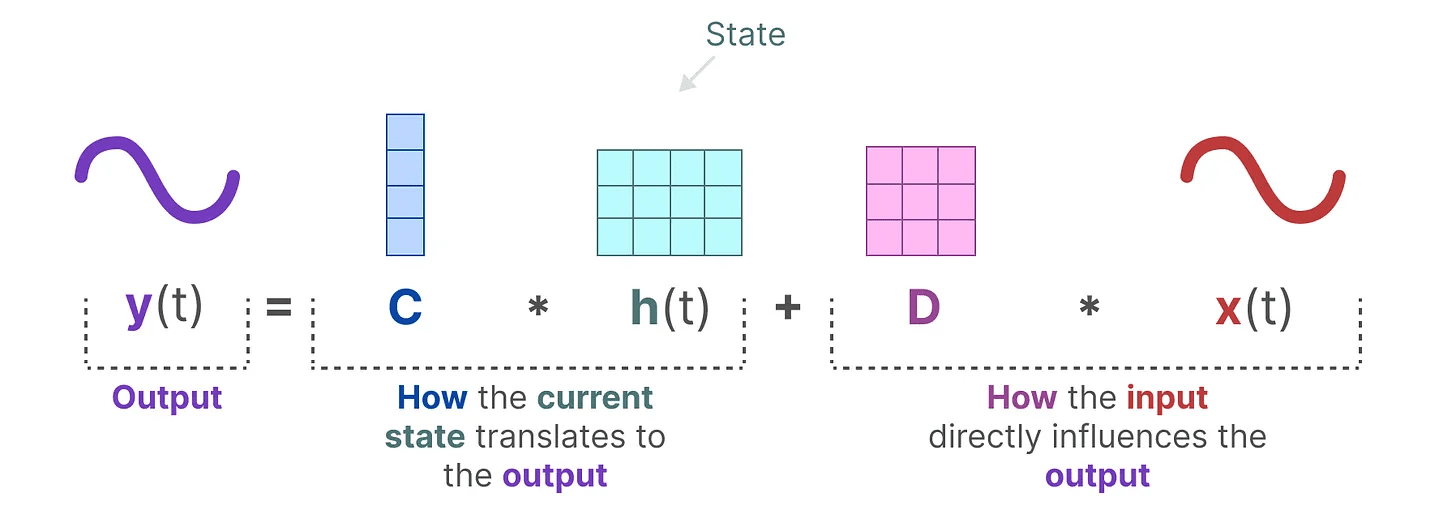
注意：矩阵 A、B、C 和 D 也常被称为 参数，因为它们是可学习的。
将这两个方程可视化，我们得到以下架构：
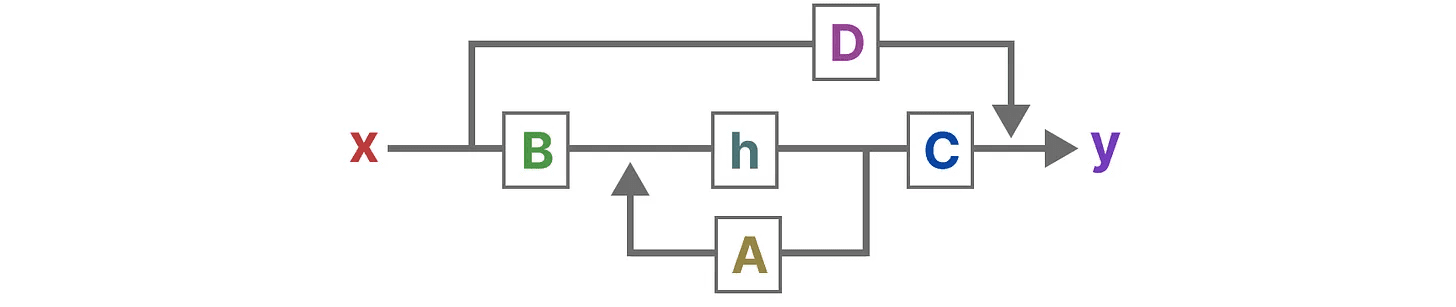让我们一步步了解这些矩阵如何影响学习过程。
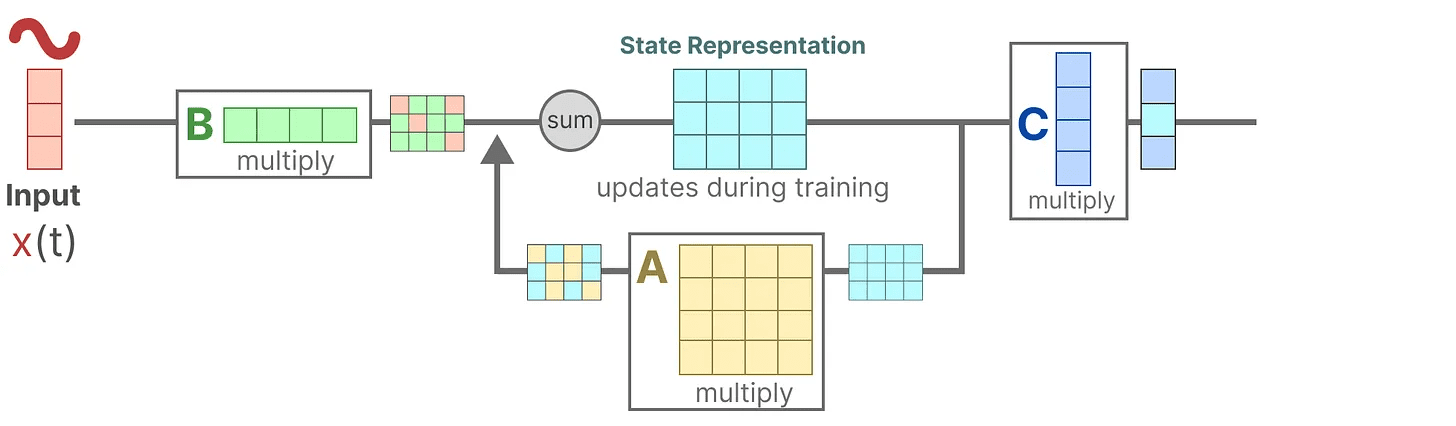
假设我们有一些输入信号 x(t)，该信号首先与 矩阵 B 相乘，矩阵 B 描述了输入如何影响系统。
更新后的状态（类似于神经网络的隐藏状态）是一个潜在空间，其中包含了环境的核心“知识”。我们将状态与 矩阵 A 相乘，该矩阵描述了所有内部状态之间的关联，表示系统的基本动态。
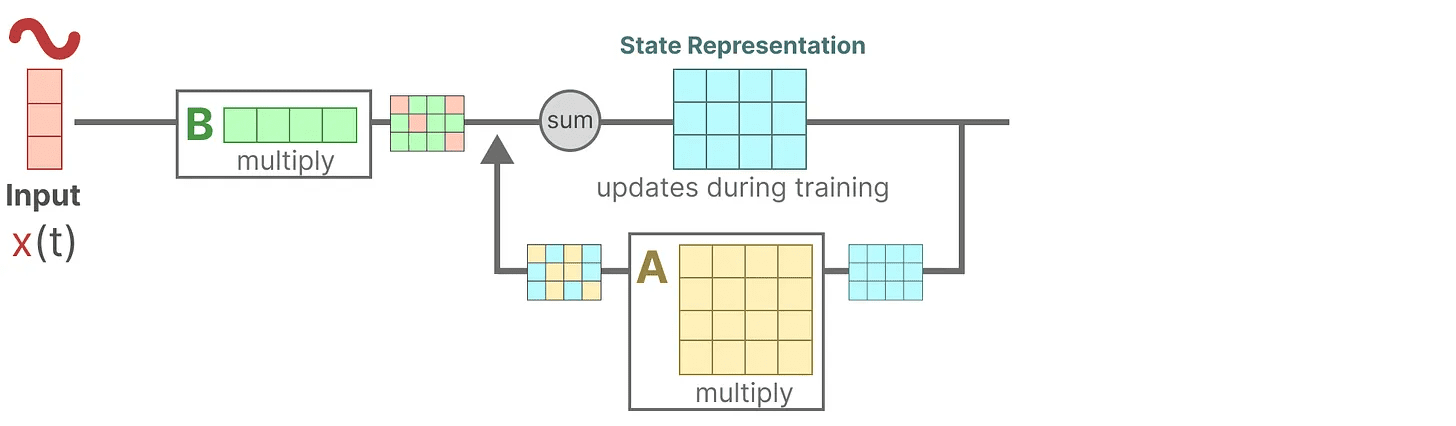你可能已经注意到，矩阵 A 在创建状态表示之前应用，并在状态表示更新后再次应用。
然后，我们使用 矩阵 C 来描述状态如何转换为输出。
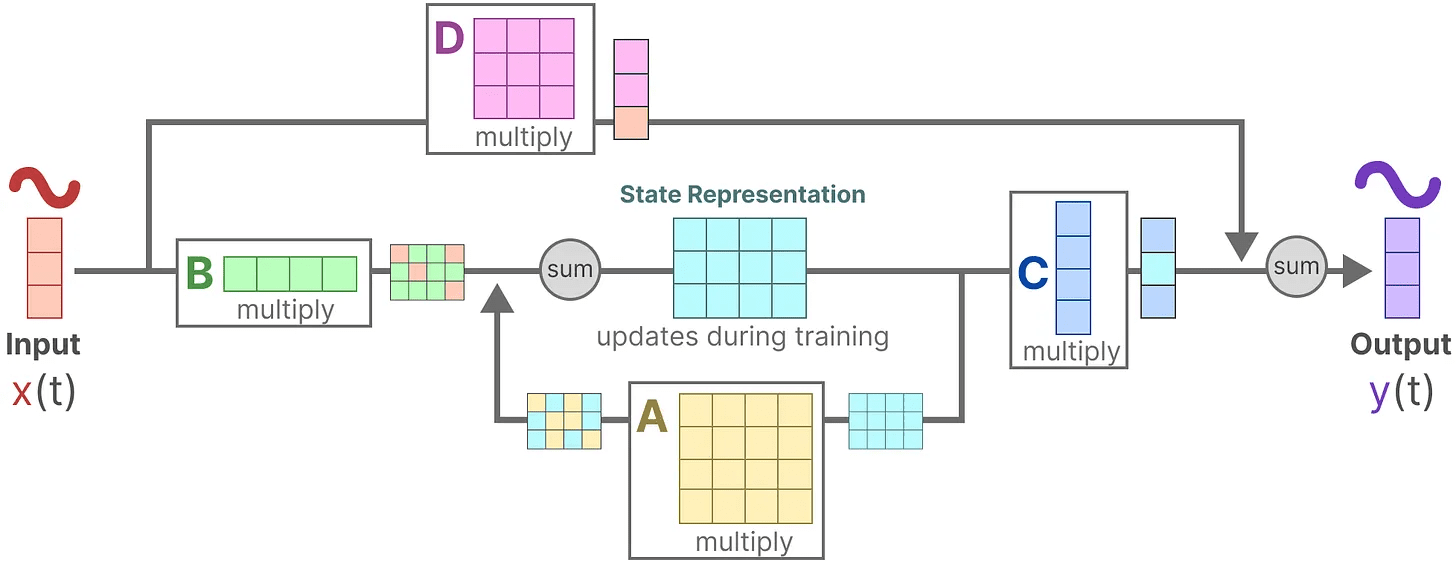
最后，我们可以使用 矩阵 D 提供从输入到输出的直接信号。这通常也被称为 跳跃连接。
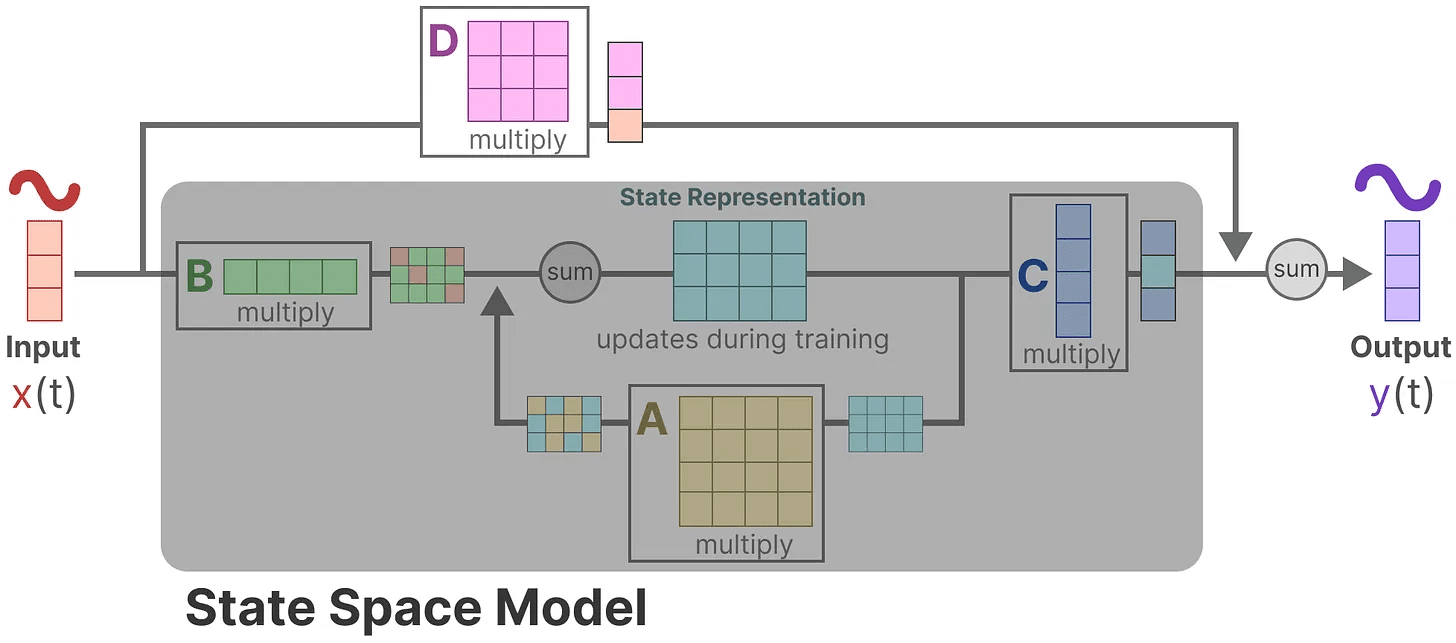
由于 矩阵 D 类似于跳跃连接，SSM 通常被认为是不包含跳跃连接的以下形式。
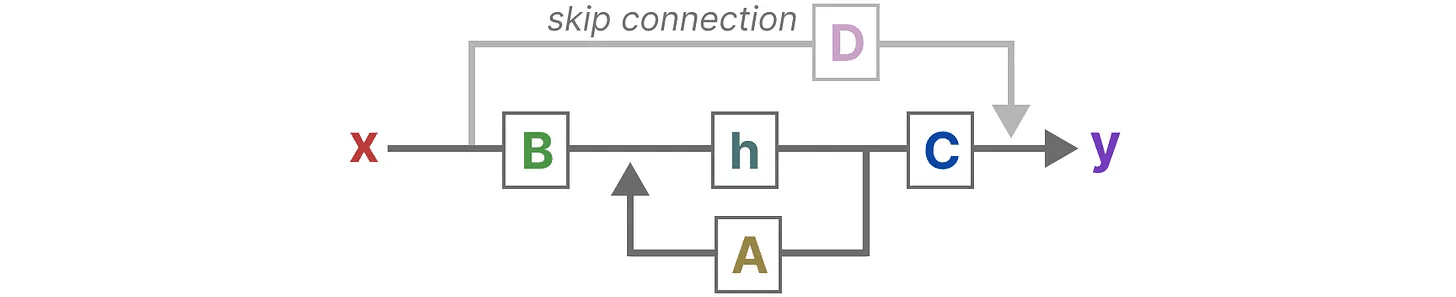
回到我们的简化视角，我们现在可以将重点放在矩阵 A、B 和 C 上，作为 SSM 的核心。
我们可以更新原始方程（并添加一些漂亮的颜色）来标明每个矩阵的用途，就像我们之前做的那样。
这两组方程一起旨在从观察数据中预测系统的状态。由于输入是连续的，SSM 的主要表示形式是 连续时间表示。
从连续信号到离散信号
如果你有一个连续信号，找到状态表示 h(t) 在解析上具有挑战性。此外，由于我们通常有离散输入（例如文本序列），我们希望对模型进行离散化。
为此，我们使用了 零阶保持技术。其工作原理如下：首先，每当我们接收到离散信号时，我们保持其值，直到我们接收到新的离散信号为止。这个过程会生成一个连续信号，供 SSM 使用：
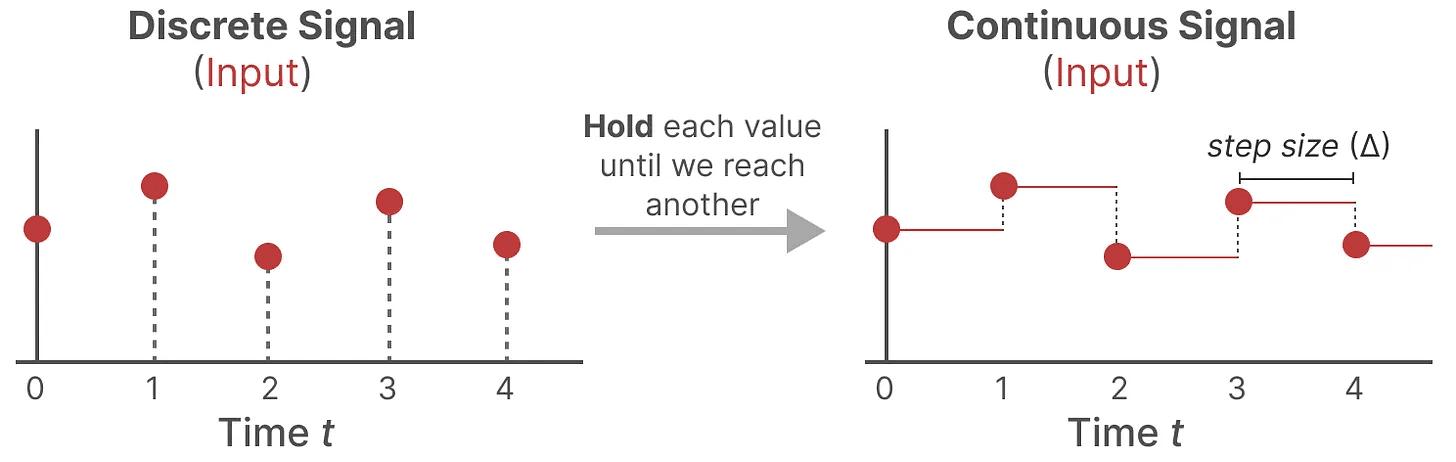我们保持数值的时间由一个可学习的新参数 步长 ∆ 表示。它表示输入的分辨率。
现在我们为输入生成了一个连续信号，接下来我们可以生成连续输出，并根据输入的时间步长对这些值进行采样。
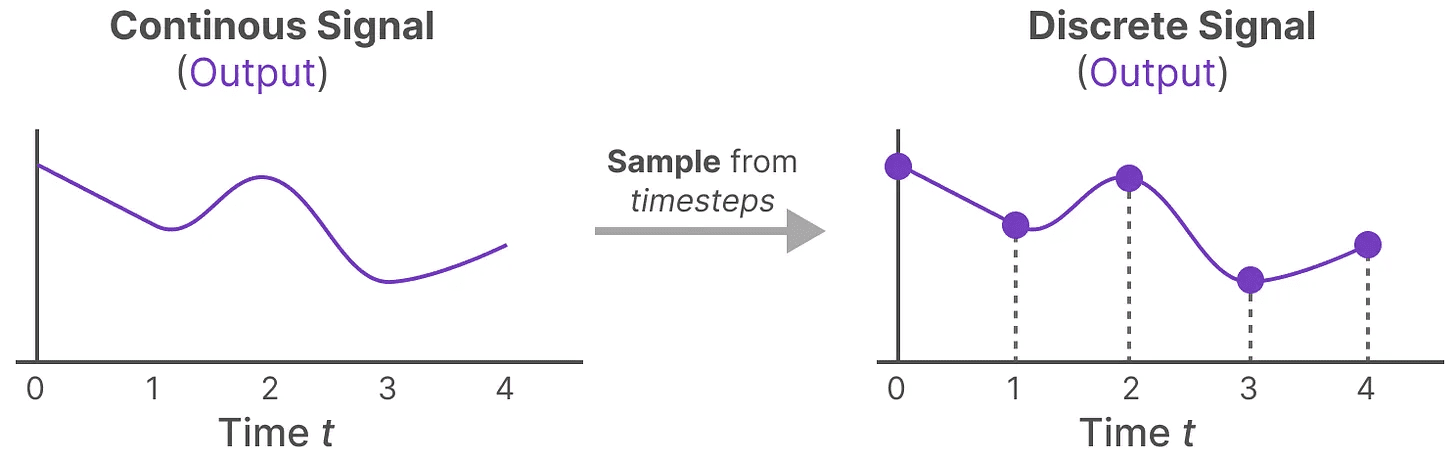这些采样的值就是我们离散化的输出！
从数学上讲，我们可以如下应用零阶保持：
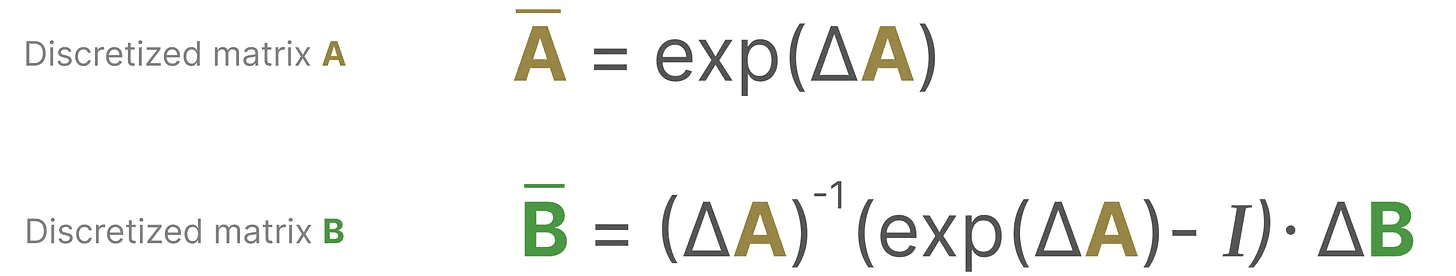它们共同使我们可以从一个连续的 SSM 过渡到一个离散的 SSM。此时模型不再是 函数对函数 x(t) → y(t)，而是 序列对序列 xₖ → y_ₖ：
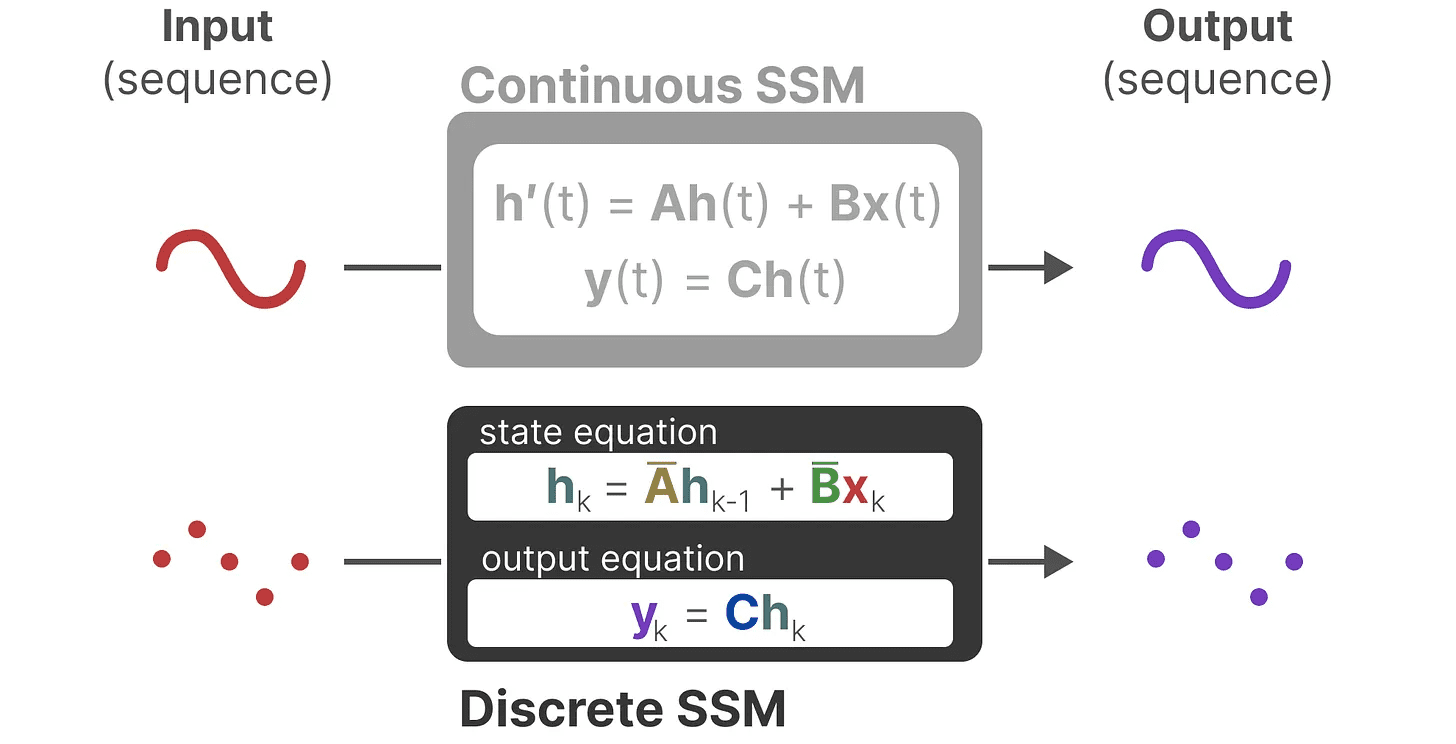这里，矩阵 A 和 B 现在表示模型的离散化参数。
我们用 k 来代替 t，以区分我们何时在谈论连续的 SSM 与离散的 SSM。
注意： 在训练期间，我们仍然保留 矩阵 A 的连续形式，而不是其离散化版本。在训练过程中，连续表示会被离散化。
现在我们已经有了一个离散化表示的公式，让我们探讨如何实际 计算 该模型。
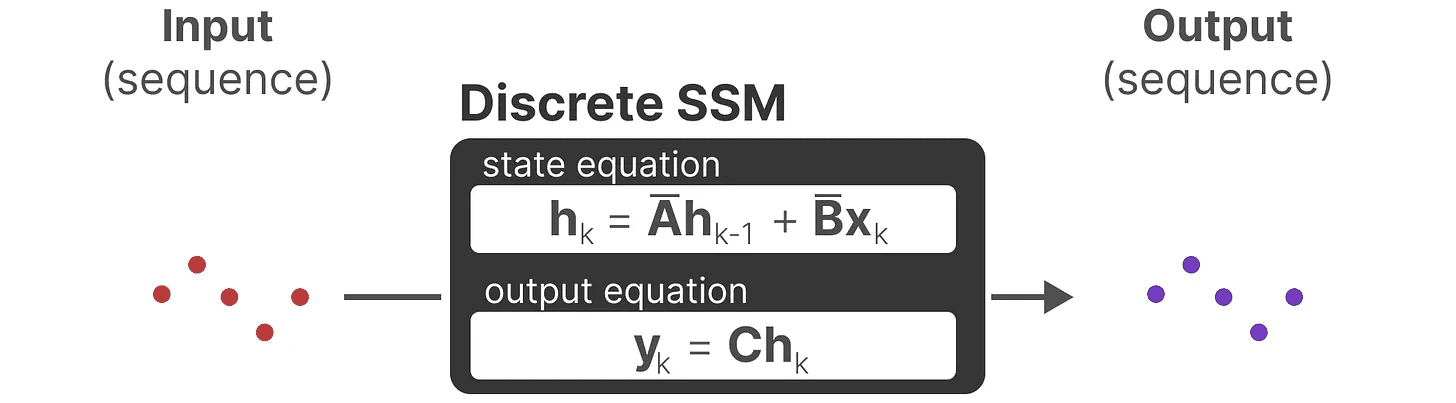
递归表示
我们的离散化 SSM 使我们能够在特定的时间步中，而不是连续信号中，构建问题。正如我们之前在 RNN 中看到的，递归方法在这里非常有用。
如果我们考虑离散的时间步而不是连续信号，我们可以使用时间步重新表述这个问题：
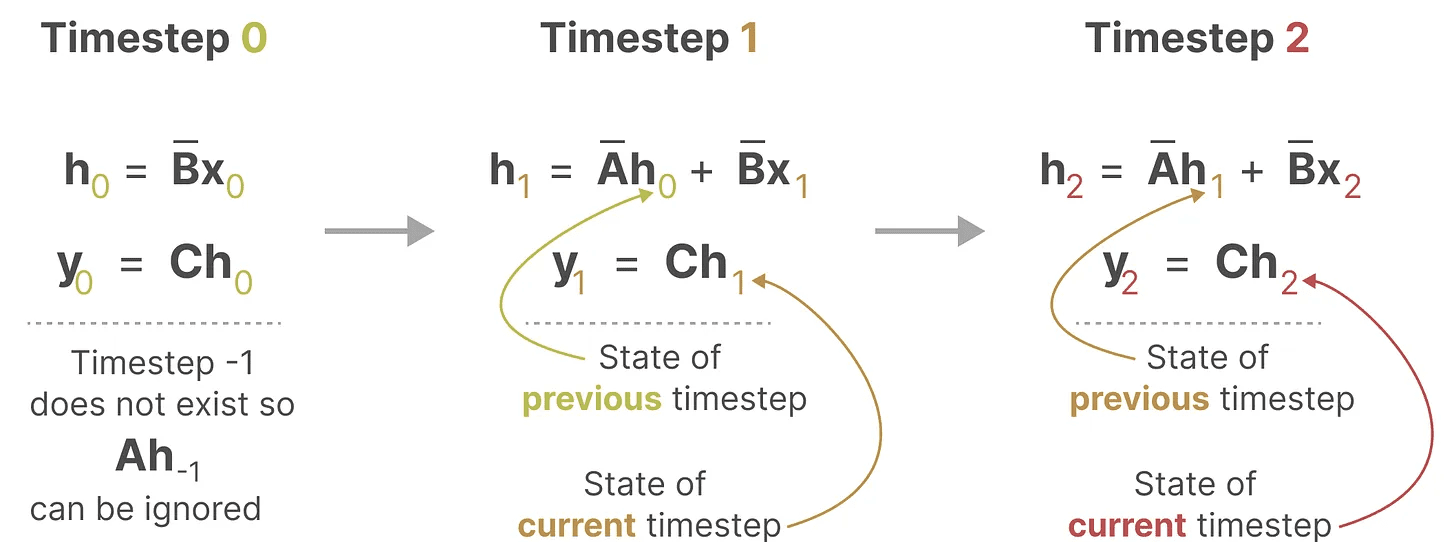
在每个时间步中，我们计算当前输入 (Bxₖ) 如何影响前一个状态 (Ahₖ₋₁)，然后计算预测输出 (Chₖ)。
这个表示可能已经让你感到熟悉！我们可以像之前对 RNN 的处理方法一样进行分析。
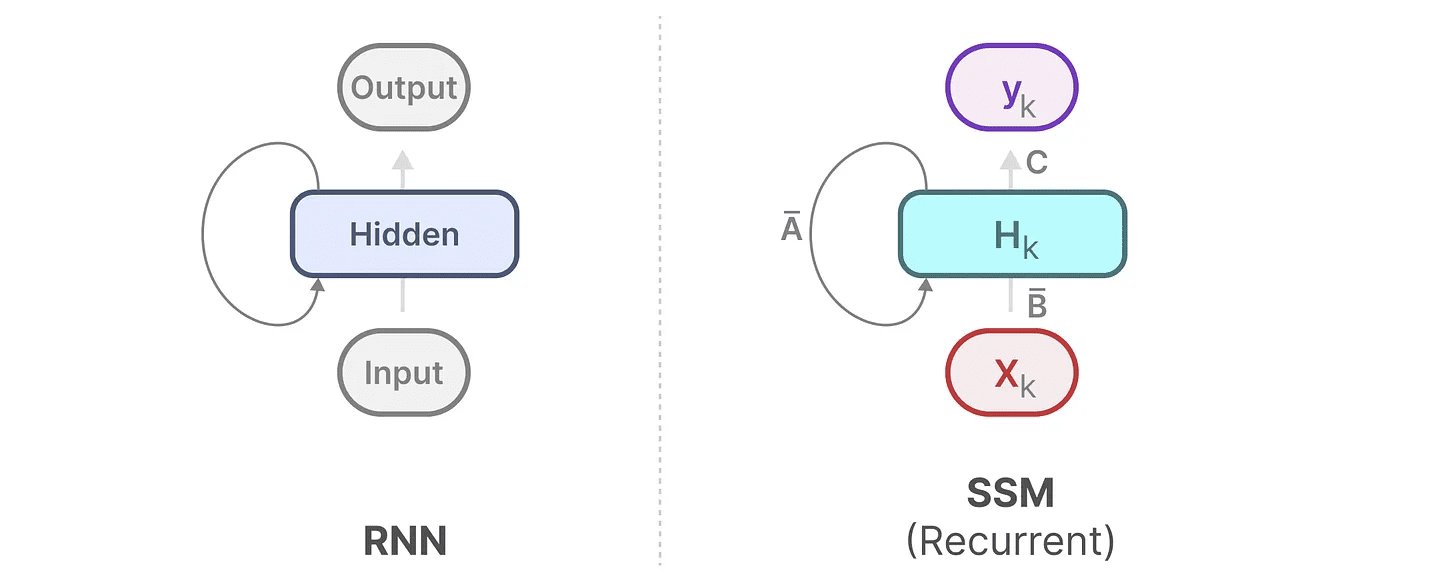我们可以将其展开（或展开成一系列时间步）如下：
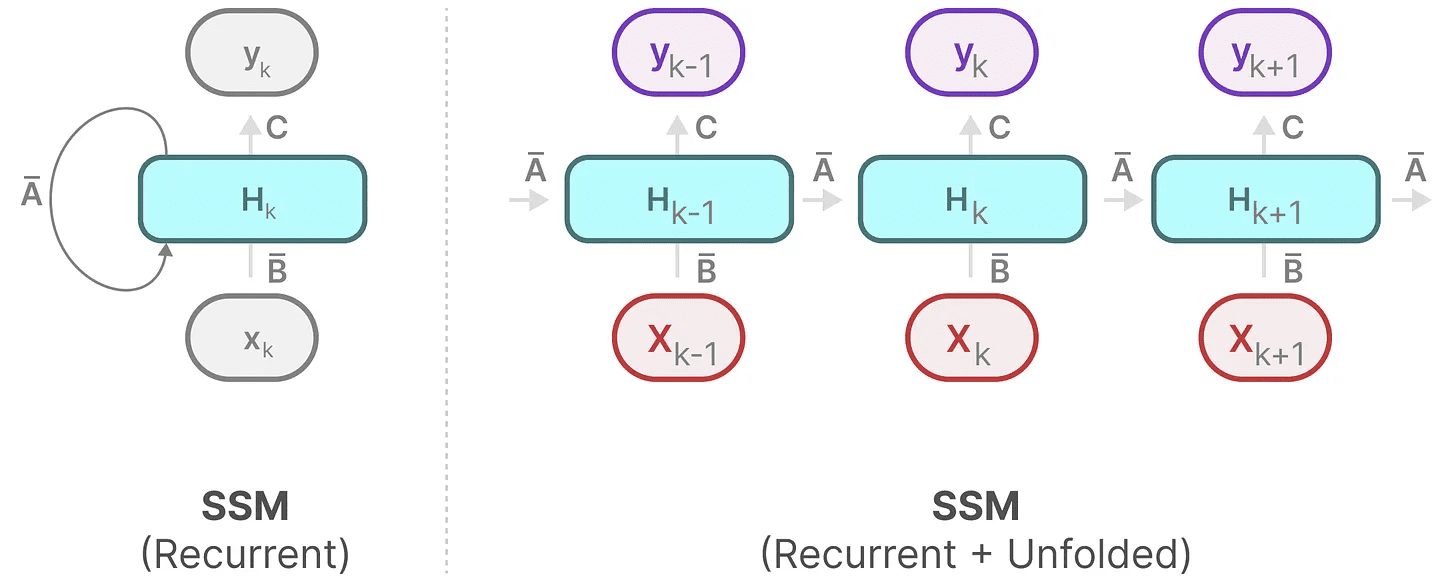请注意，我们可以使用 RNN 的基本方法来使用这种离散化的版本。
卷积表示
我们可以使用卷积来表示 SSM。记住在经典图像识别任务中，我们应用滤波器（kernels）来提取聚合特征：
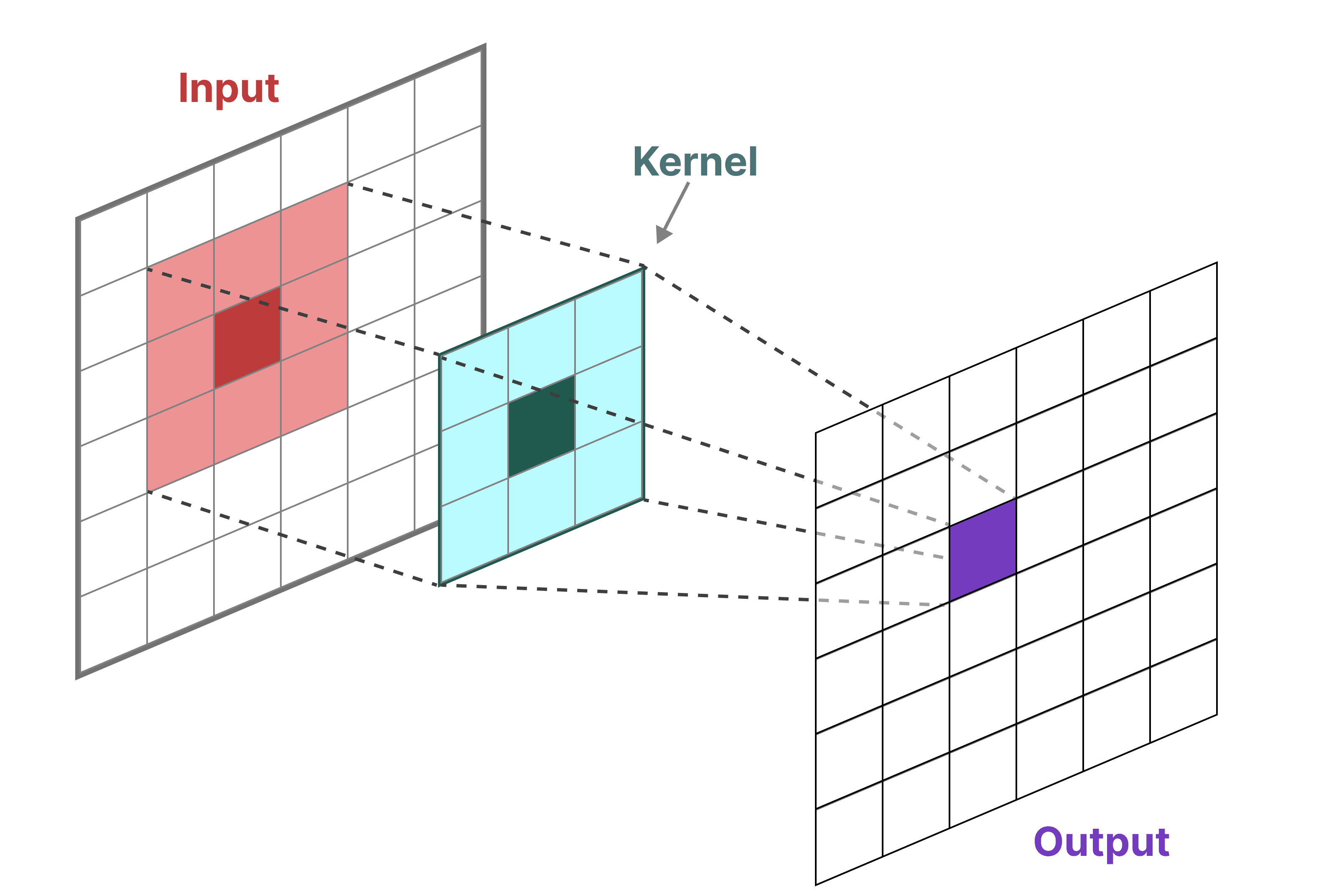由于我们处理的是文本而不是图像，我们需要使用一维视角：
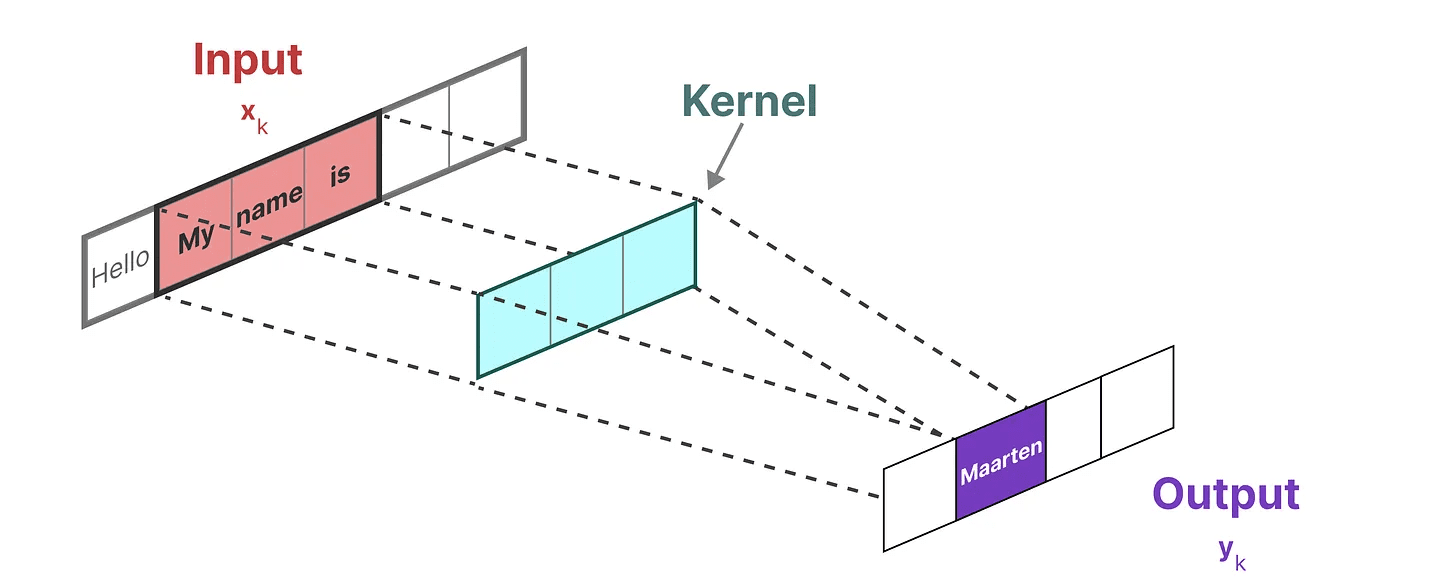我们用来表示这个“滤波器”的内核源自 SSM 公式：
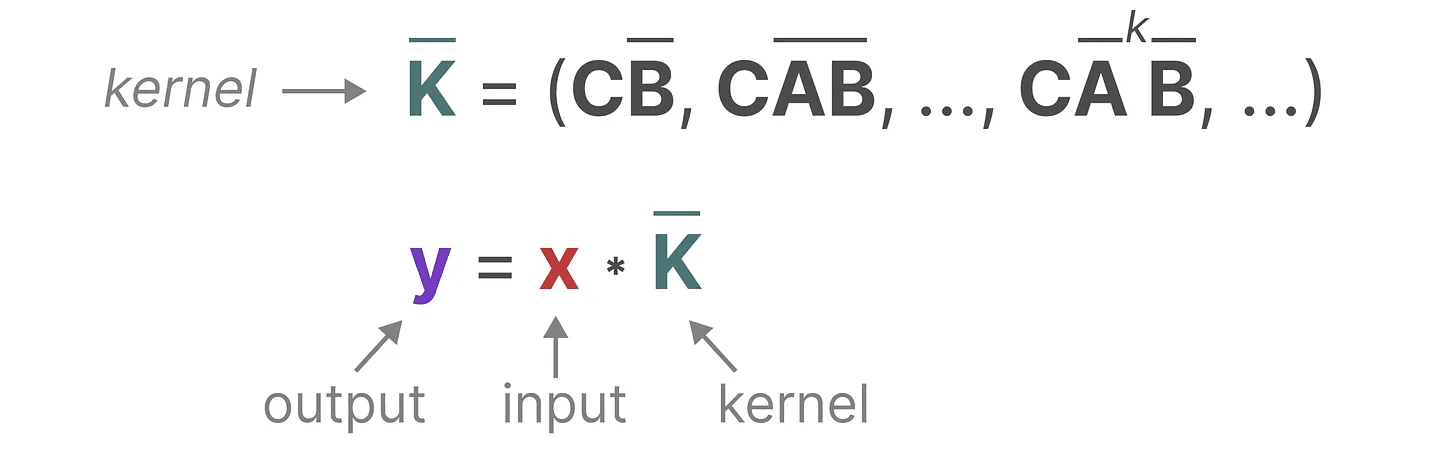让我们来看看这个内核在实践中的作用。像卷积一样，我们可以使用 SSM 内核遍历每组 tokens 并计算输出：
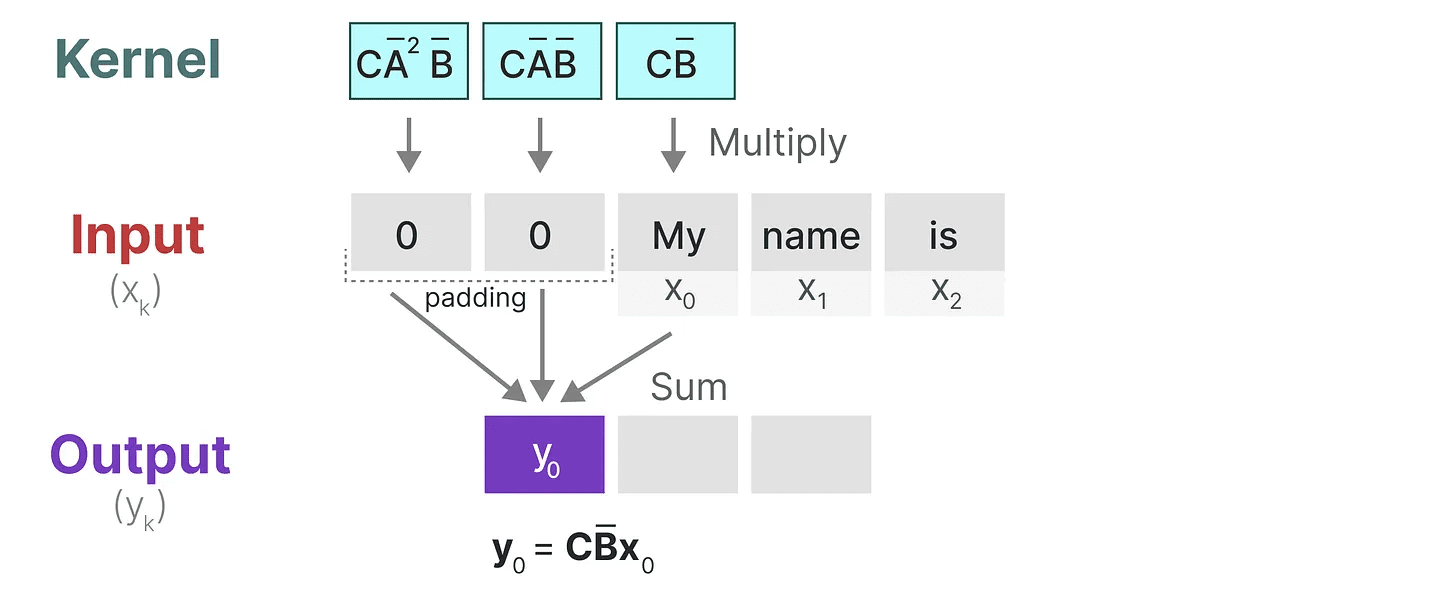这也展示了填充可能对输出产生的影响。我更改了填充的顺序以改善可视化，但我们通常在句子末尾应用填充。
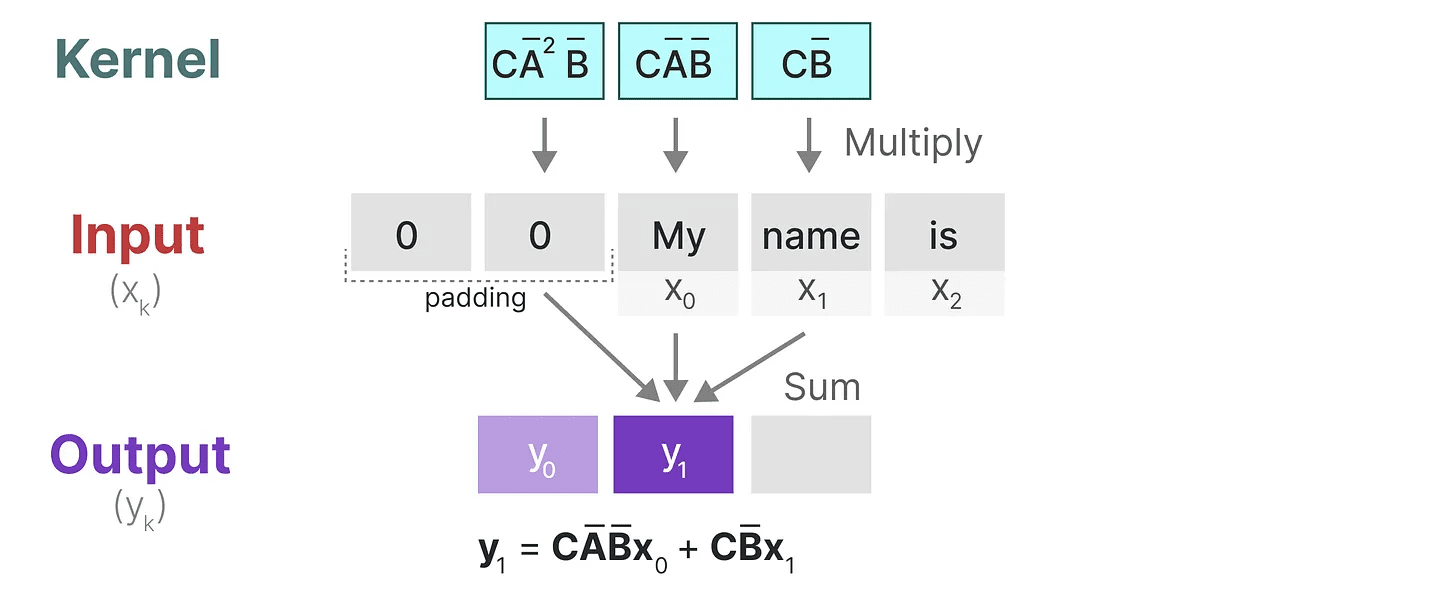
在下一步中，内核会移动一次以执行计算的下一步：
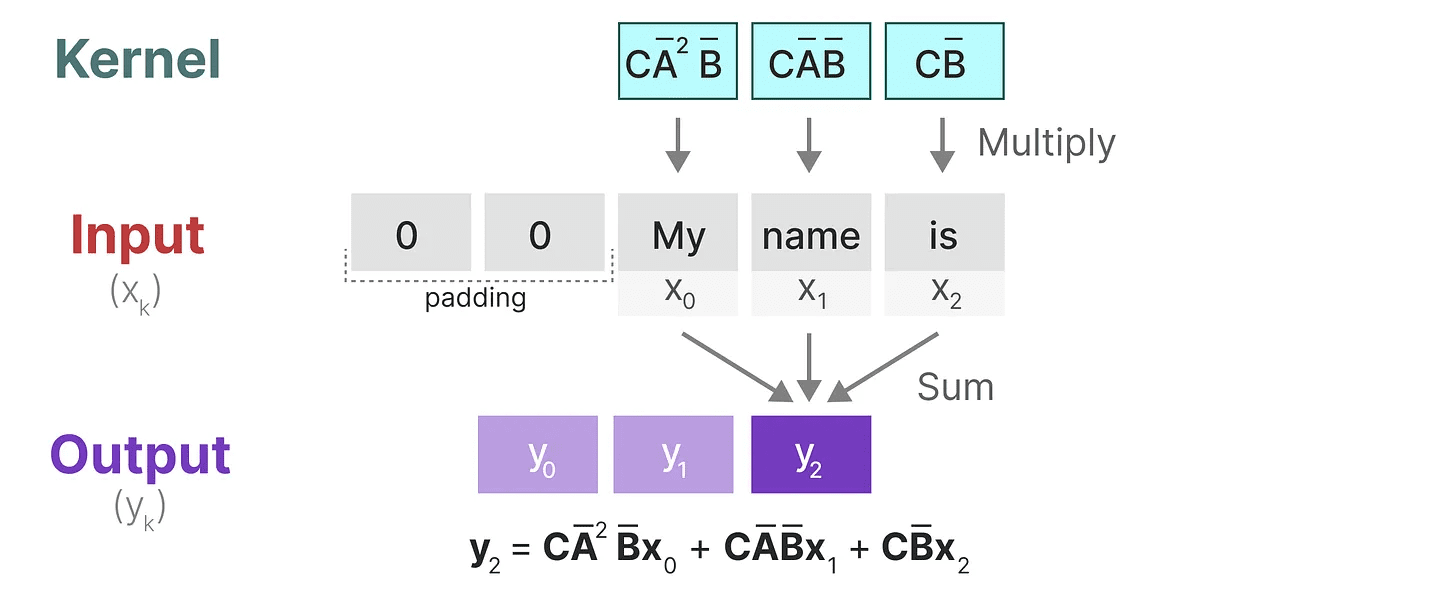
在最后一步中，我们可以看到内核的全部效果：
将 SSM 表示为卷积的一个主要好处是它可以像卷积神经网络（CNNs）一样并行训练。然而，由于内核大小固定，它们的推理速度不如 RNNs 快且不受限制。
三种表示方式
这三种表示方式——连续、递归 和 卷积 各有不同的优缺点：
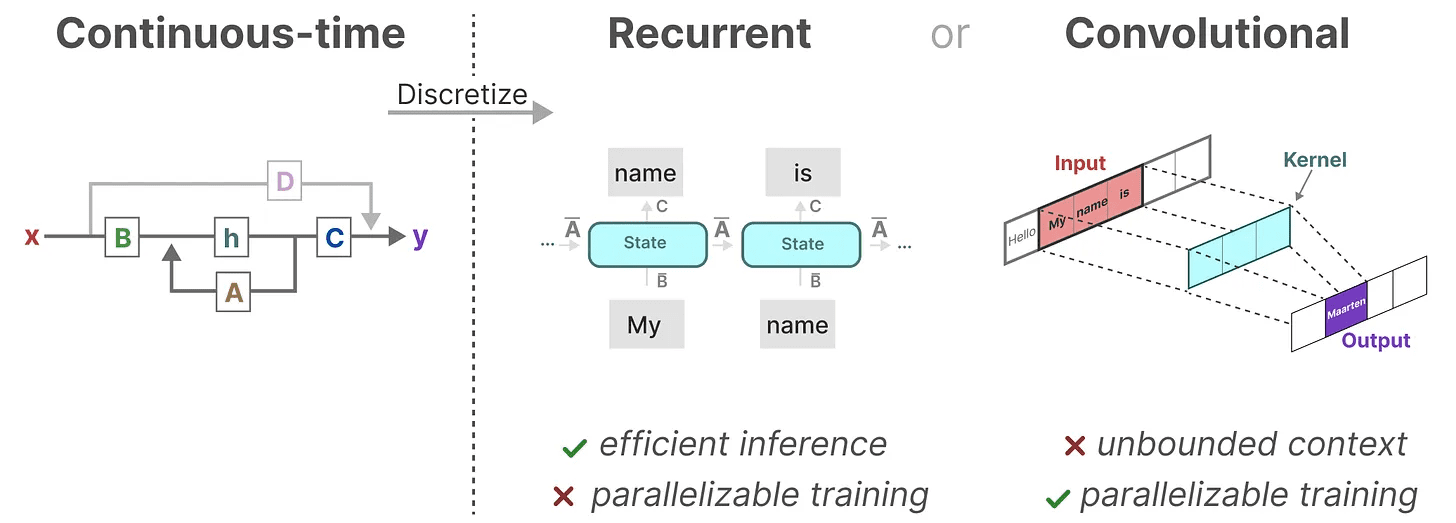有趣的是，我们现在可以利用递归 SSM 进行高效推理，同时利用卷积 SSM 进行并行训练。
利用这些表示方式，我们可以使用一个巧妙的技巧，即根据任务选择表示方式。在训练过程中，我们使用可以并行化的卷积表示，而在推理过程中，我们使用高效的递归表示：
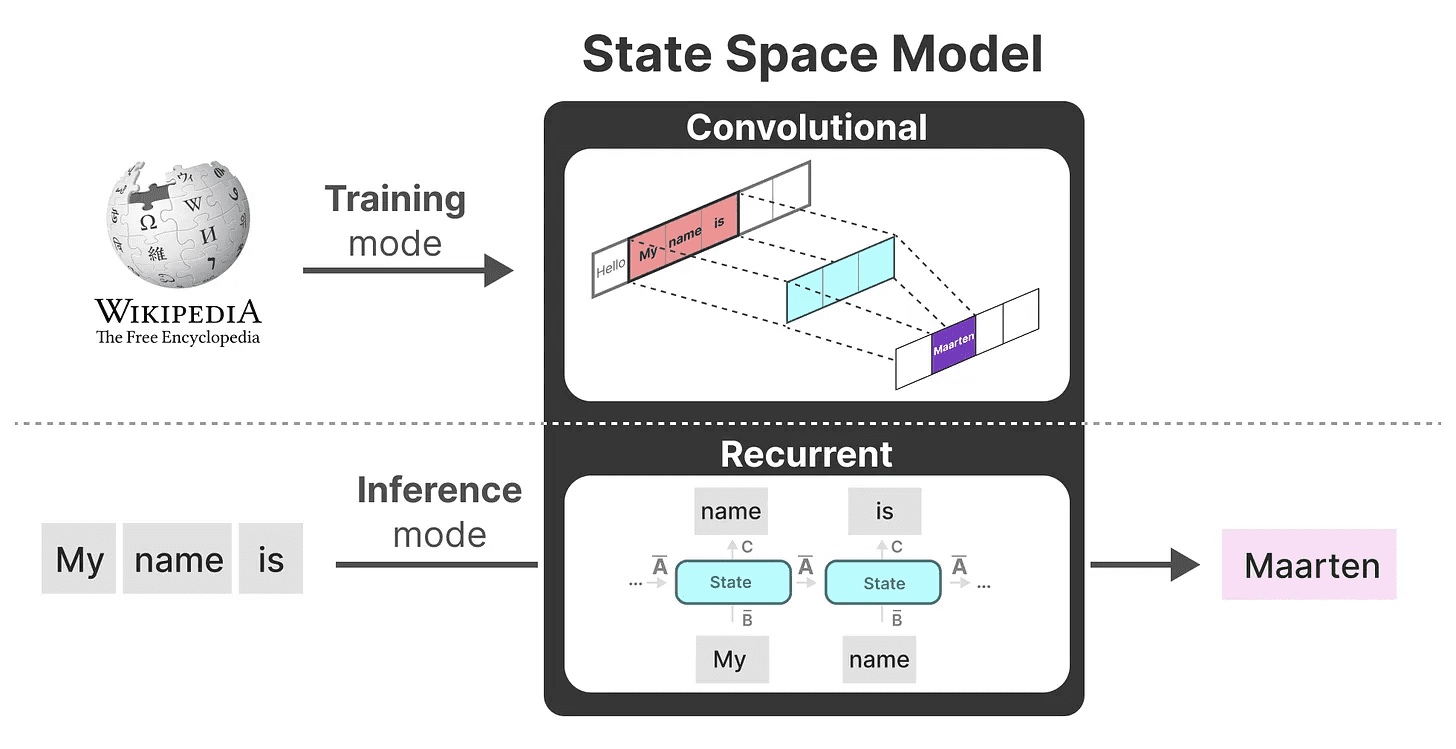这个模型被称为 线性状态空间层（LSSL）。 2
这些表示方式共享一个重要属性，即线性时间不变性（LTI）。LTI 表示 SSM 的参数 A、B 和 C 在所有时间步中都是固定的。这意味着矩阵 A、B 和 C 对每个生成的 Token 都是相同的。
换句话说，无论你给 SSM 任何序列，A、B 和 C 的值都保持不变。我们有一个不关心内容的静态表示方式。
在探讨 Mamba 如何解决这个问题之前，让我们探讨最后一个拼图碎片——矩阵 A。
矩阵 A 的重要性
可以说，SSM 公式中最重要的方面之一是 矩阵 A。正如我们之前在递归表示中看到的，它捕捉了有关 上一个 状态的信息，以构建 新的 状态。
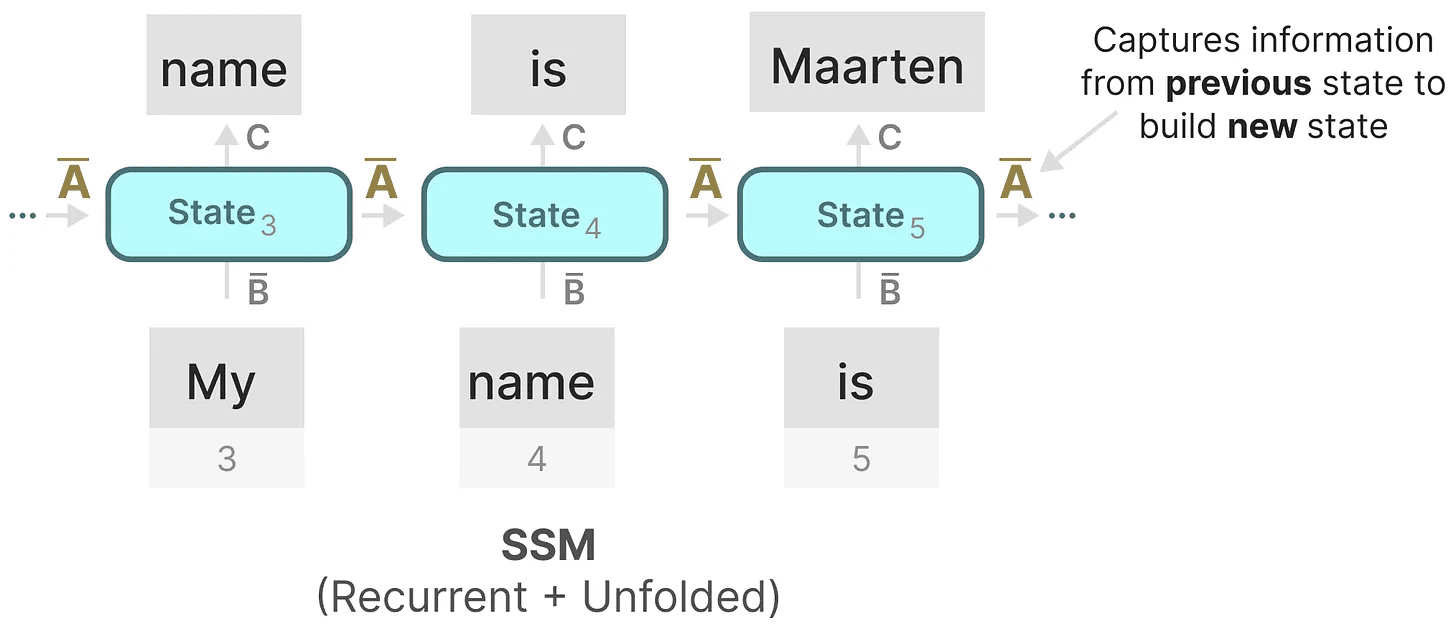本质上，矩阵 A 生成隐藏状态：
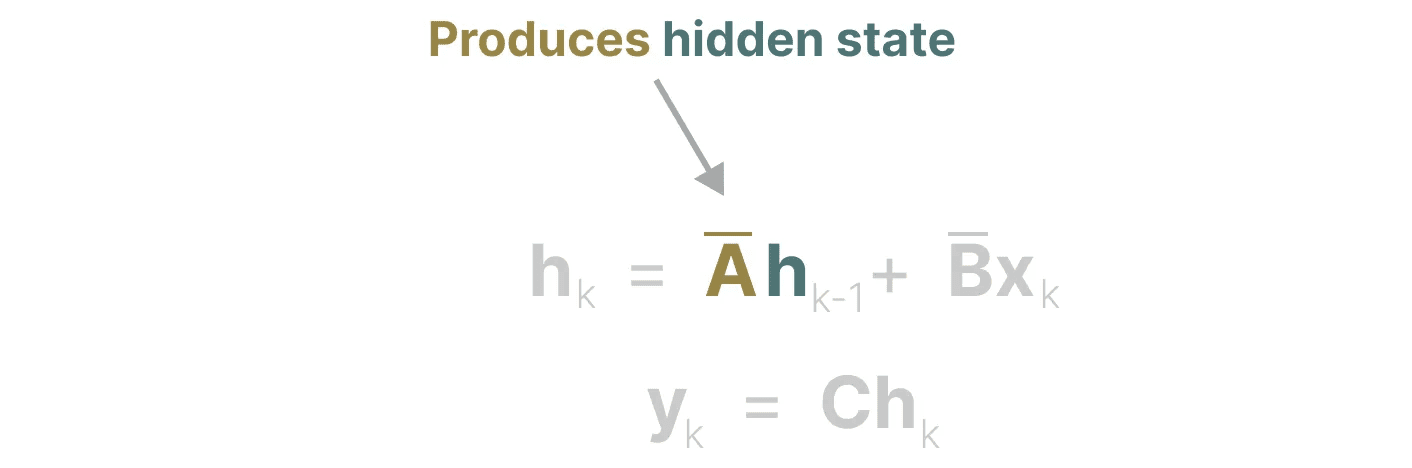因此，创建 矩阵 A 可能会决定我们能否记住仅仅几个之前的 token 或捕捉到我们迄今为止看到的每一个 token。特别是在递归表示的背景下，因为它只 回顾 上一个状态。
如何以保留大量记忆（上下文大小）的方式创建 matrix A？
我们使用 Hungry Hungry Hippo！或者 HiPPO3 来实现高阶 多项式 投影 运算符。HiPPO 试图将其至今看到的所有输入信号压缩为一个系数向量。
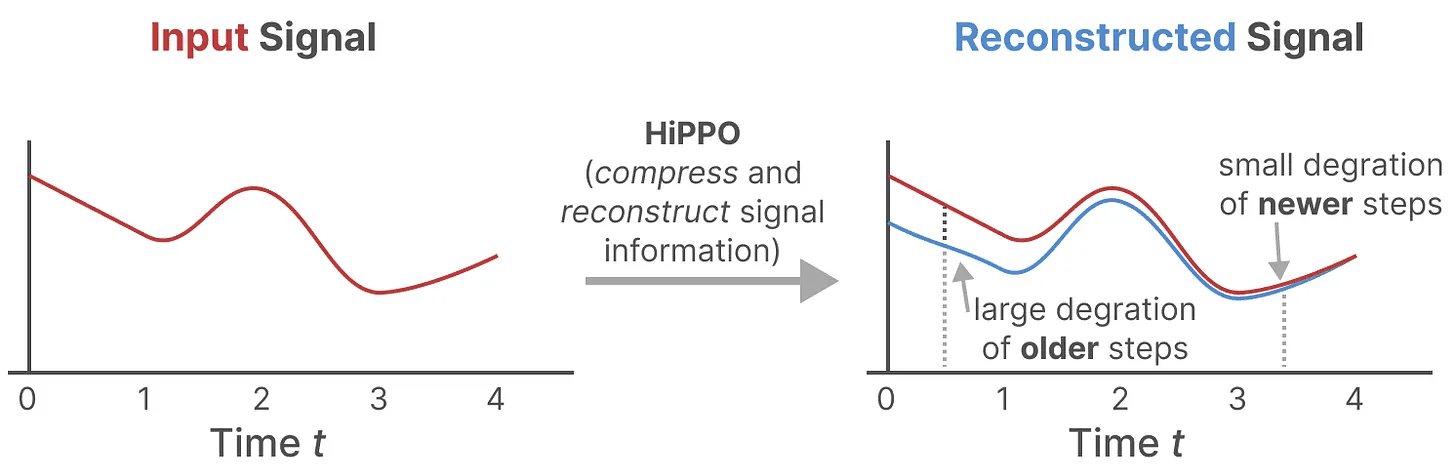它使用 matrix A 来构建一个状态表示，该表示能够较好地捕捉最近的 token，并衰减较旧的 token。其公式可以表示如下：
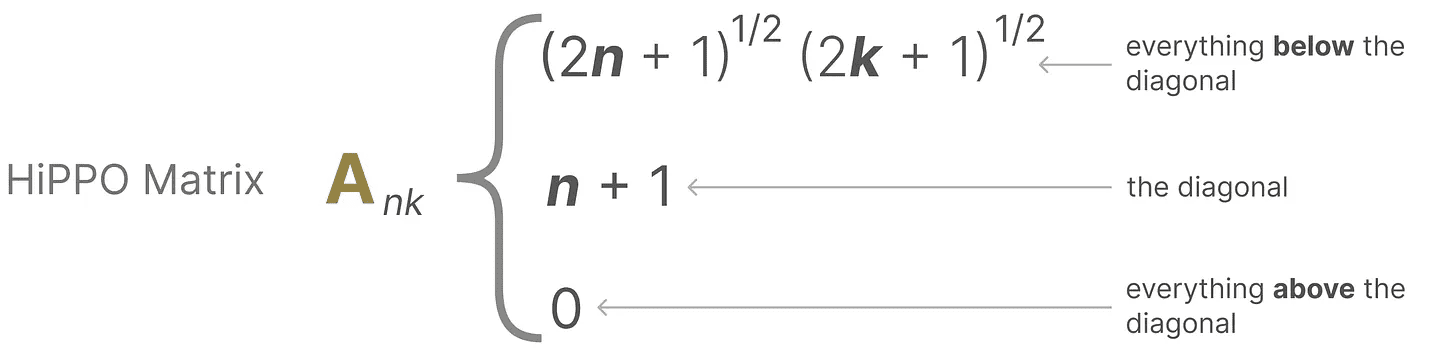假设我们有一个方阵 matrix A，这给我们提供了：
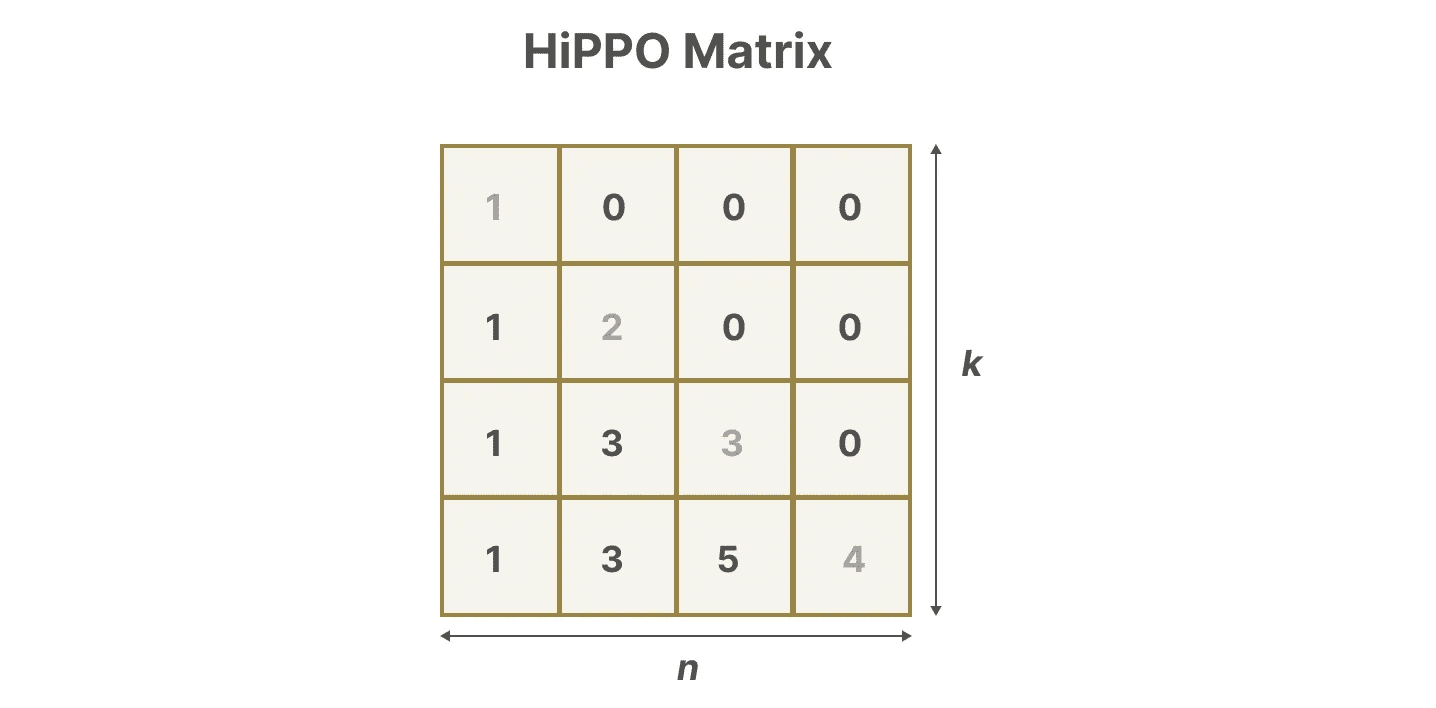使用 HiPPO 构建 matrix A 被证明比将其初始化为随机矩阵要好得多。因此，它在重建 更新 信号（最近的 token）方面比 较旧 信号（初始 token）更为准确。
HiPPO 矩阵的核心思想是生成一个记忆其历史的隐藏状态。
从数学上讲，它通过跟踪 Legendre 多项式 的系数来实现这一点，这使得它能够近似所有的历史记录。4
然后 HiPPO 被应用于我们之前看到的递归和卷积表示，以处理长距离依赖关系。结果是 Structured State Space for Sequences (S4)，一种可以高效处理长序列的 SSM 类。5
它由三部分组成：
- 状态空间模型
- HiPPO 用于处理 长距离依赖
- 离散化用于创建 递归 和 卷积 表示
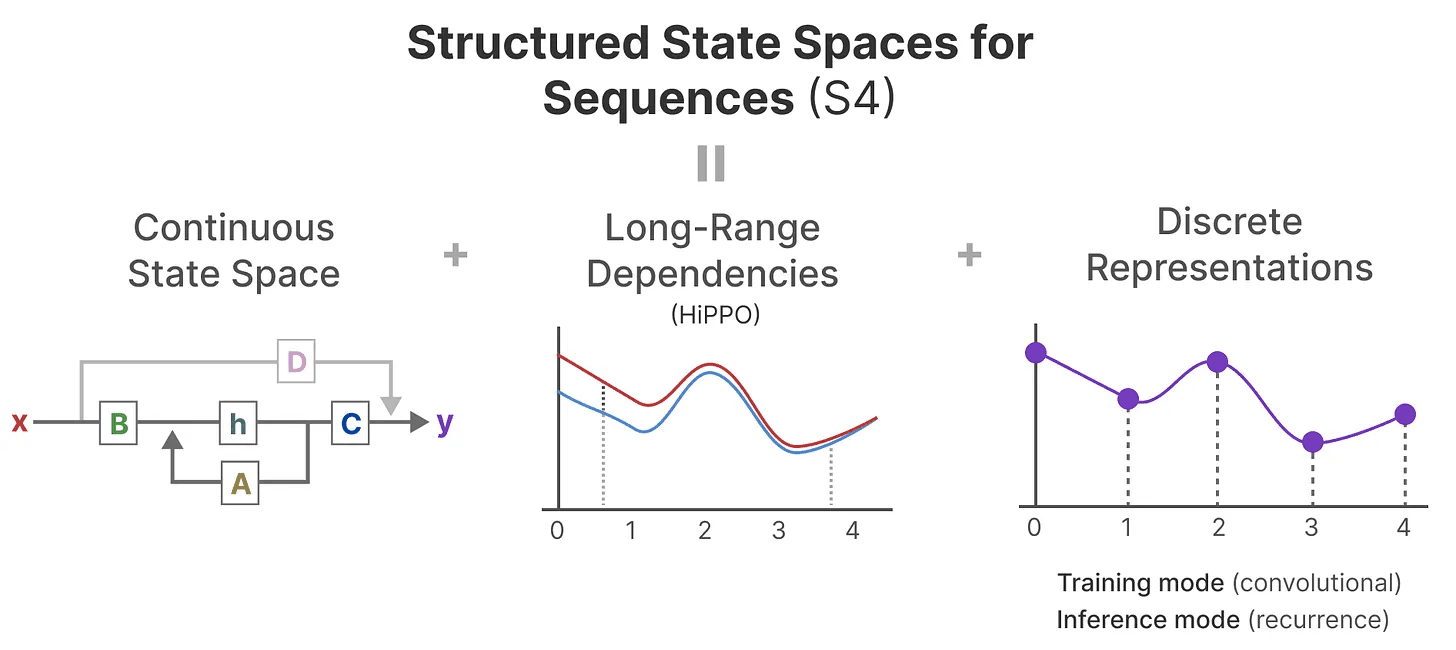这类 SSM 具有多个优点，具体取决于你选择的表示方式（递归与卷积）。它还可以处理长文本序列，并通过基于 HiPPO 矩阵来高效地存储记忆。
注意：如果你想深入了解如何计算 HiPPO 矩阵并自己构建 S4 模型，我强烈建议你阅读 Annotated S4。
第 3 部分：Mamba - 一种选择性状态空间模型
我们终于覆盖了理解 Mamba 特殊之处所需的所有基础知识。状态空间模型可以用于建模文本序列，但仍然有一系列我们希望避免的缺点。
在这一部分，我们将讨论 Mamba 的两个主要贡献：
- 一种 选择性扫描算法，允许模型筛选（不）相关信息
- 一种 硬件感知算法，通过 并行扫描、内核融合 和 重新计算 来高效存储（中间）结果。
这两者共同创建了 选择性状态空间模型 或 S6 模型，可以像自注意力一样用于创建 Mamba 块。
在探索这两个主要贡献之前，让我们首先探讨一下它们为何必要。
试图解决什么问题？
状态空间模型，甚至 S4（结构化状态空间模型），在语言建模和生成中某些关键任务上表现不佳，即 关注或忽略特定输入的能力。
我们可以用两个合成任务来说明这一点，即 选择性复制 和 诱导头。
在 选择性复制 任务中，SSM 的目标是复制输入的部分并按顺序输出：
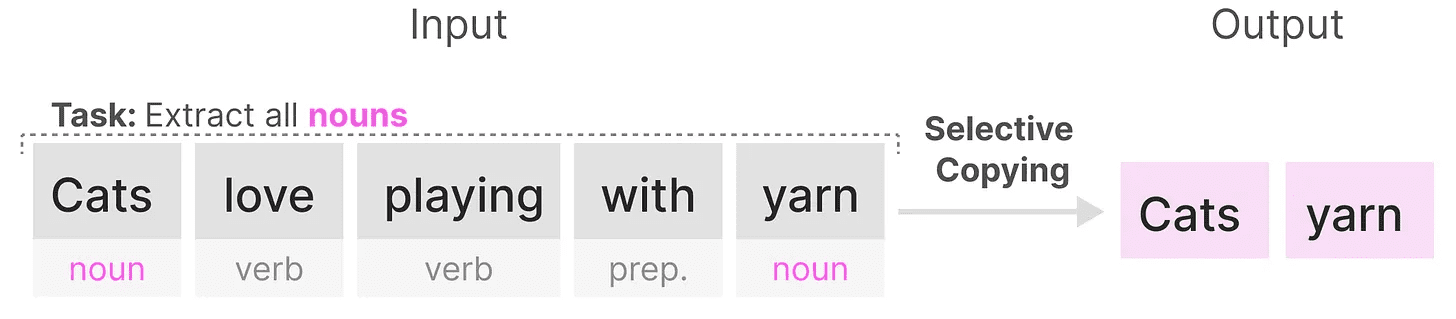然而，由于 SSM 是 线性时间不变的，它在这个任务上表现不佳。正如我们之前看到的，矩阵 A、B 和 C 对于 SSM 生成的每个 token 都是相同的。
因此，SSM 无法执行 内容感知推理，因为它由于固定的 A、B 和 C 矩阵而平等对待每个 token。这是一个问题，因为我们希望 SSM 对输入（提示）进行推理。
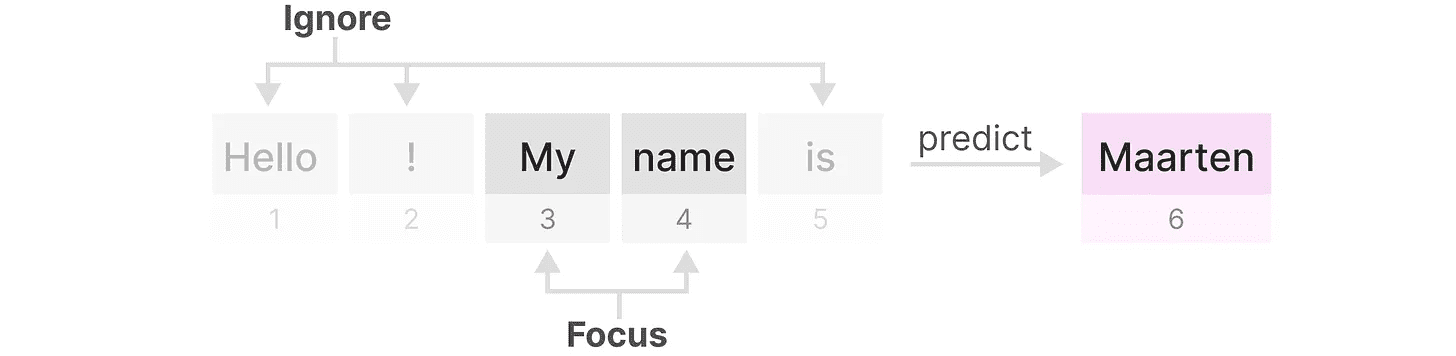
SSM 在另一个任务上表现不佳，即 诱导头，其目标是重现输入中找到的模式：
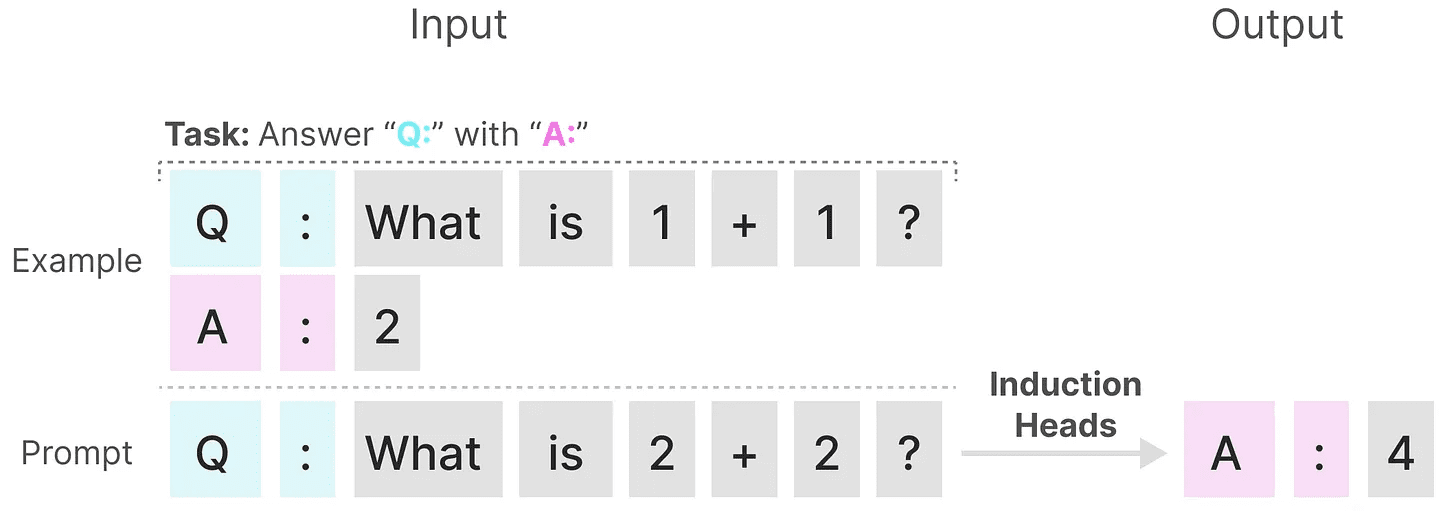在上面的示例中，我们本质上是在进行一次性提示，其中我们尝试“教”模型在每个 “Q:” 后提供一个 “A:” 响应。然而，由于 SSM 是时间不变的，它无法选择从历史中召回哪些先前的 tokens。
让我们通过关注 矩阵 B 来说明这一点。无论输入 x 是什么，矩阵 B 始终保持不变，因此与 x 无关：
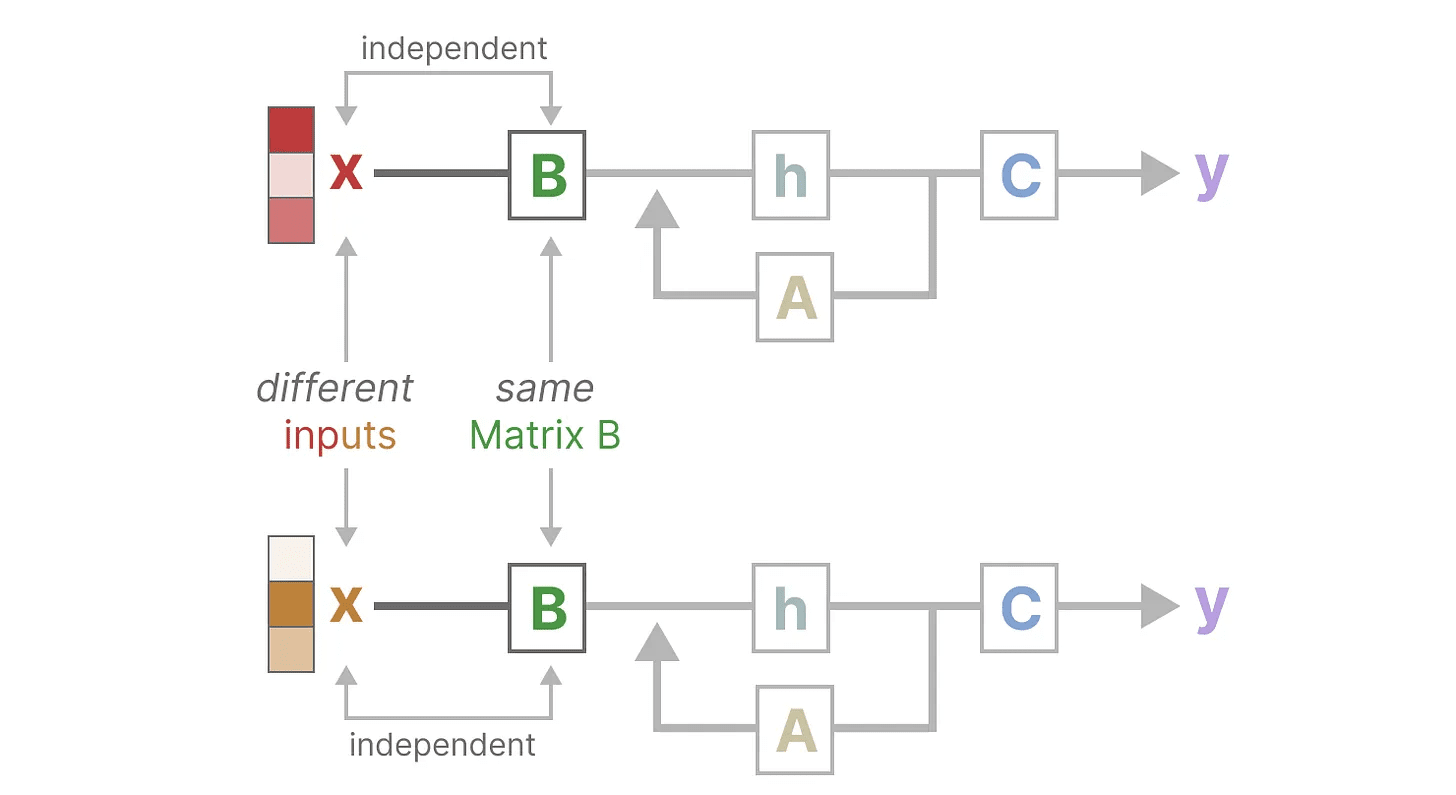同样，A 和 C 也始终保持固定，与输入无关。这表明我们迄今看到的 SSM 的 静态 特性。
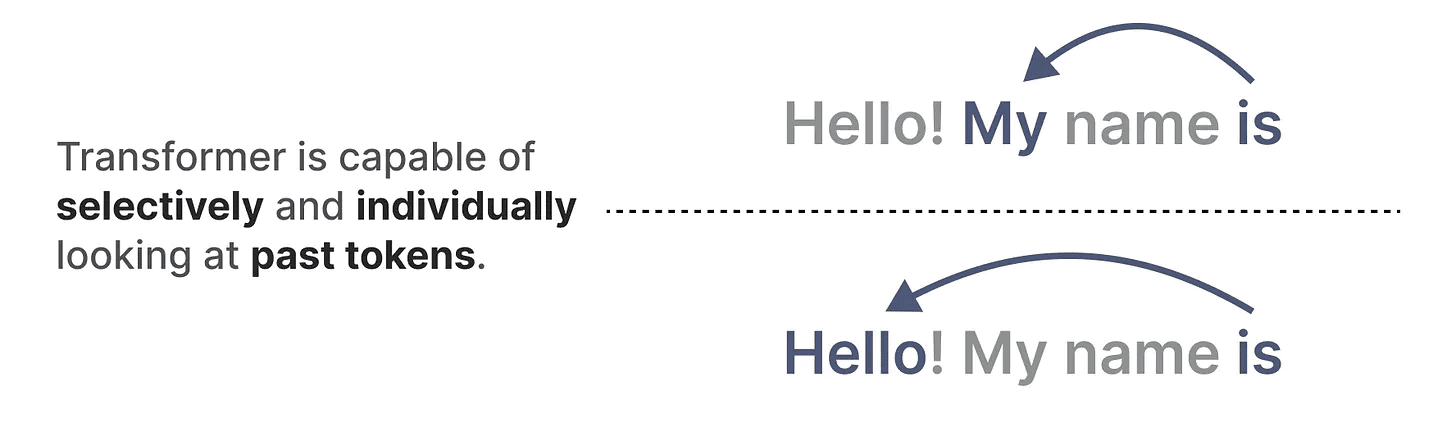
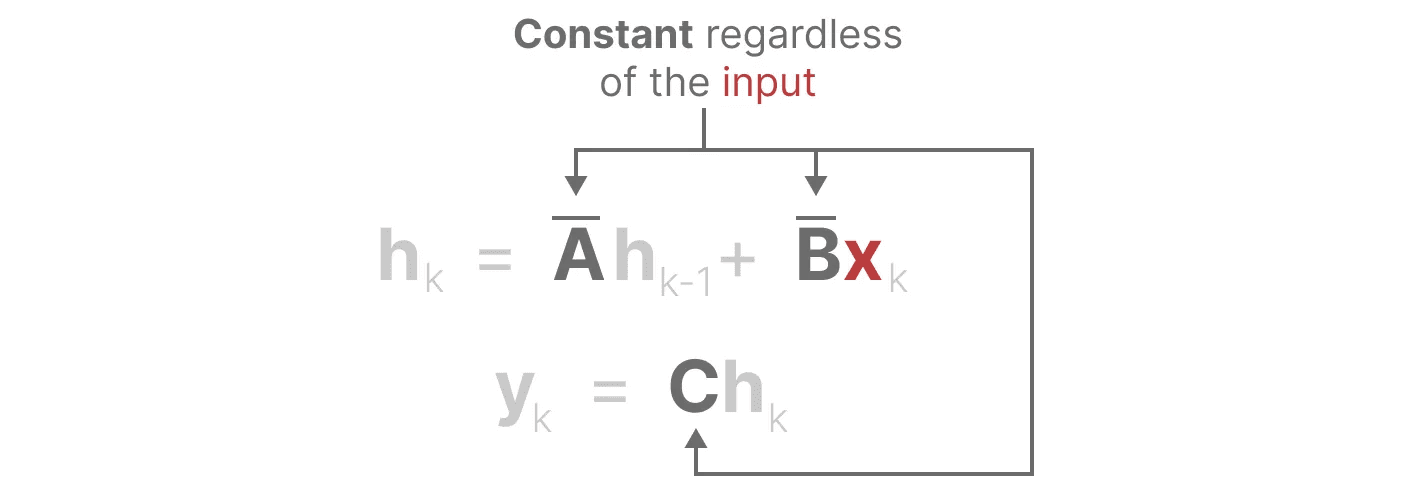相比之下，这些任务对于 Transformer 来说相对简单，因为它们根据输入序列 动态 改变注意力。它们可以选择性地“观察”或“关注”序列的不同部分。
SSM 在这些任务上的较差表现说明了时间不变 SSM 的潜在问题，矩阵 A、B 和 C 的静态特性导致了 内容感知 的问题。
选择性保留信息
SSM 的递归表示创建了一个较小的状态，这种状态非常高效，因为它压缩了整个历史。然而，与 Transformer 模型相比，Transformer 模型不会对历史进行压缩（通过注意力矩阵），因此它的能力更强。
Mamba 旨在兼具两者的优势。一个与 Transformer 状态一样强大的小状态：
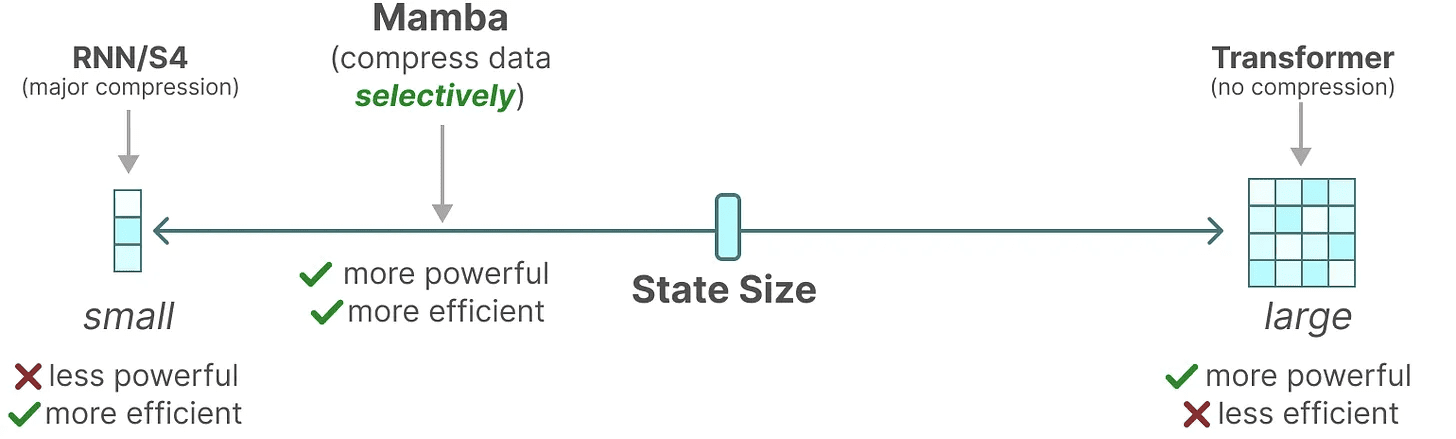如上所述，它通过选择性地将数据压缩到状态中来实现。当你有一个输入句子时，通常会有一些信息，例如停用词，没有太多意义。
为了选择性地压缩信息，我们需要参数依赖于输入。为此，让我们首先探索 SSM 在训练过程中输入和输出的维度：
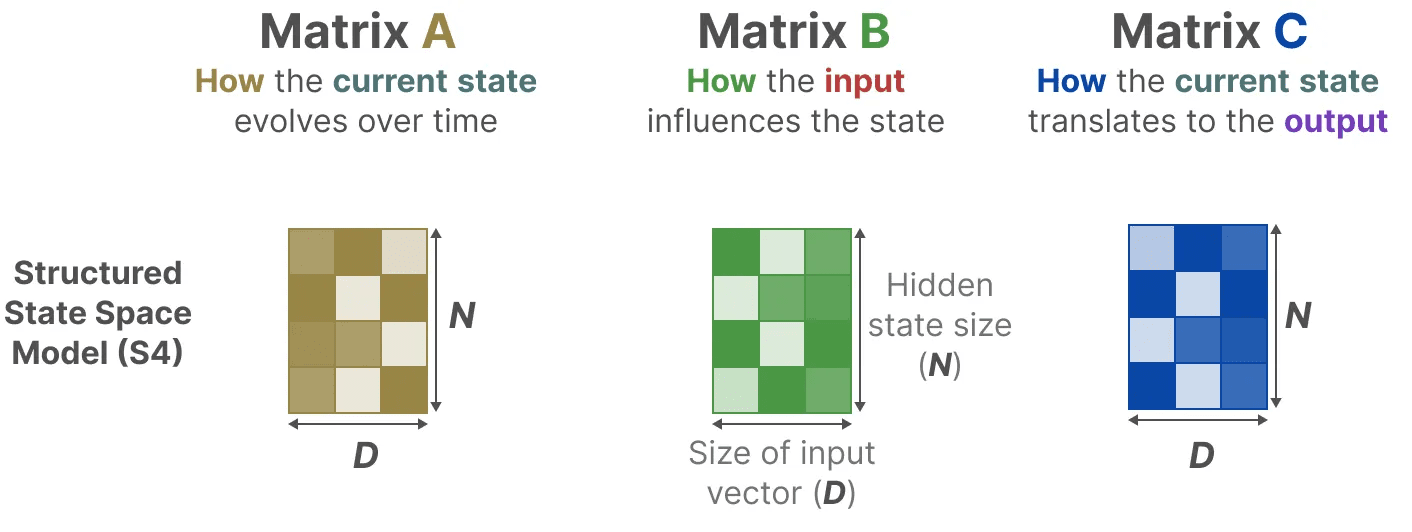
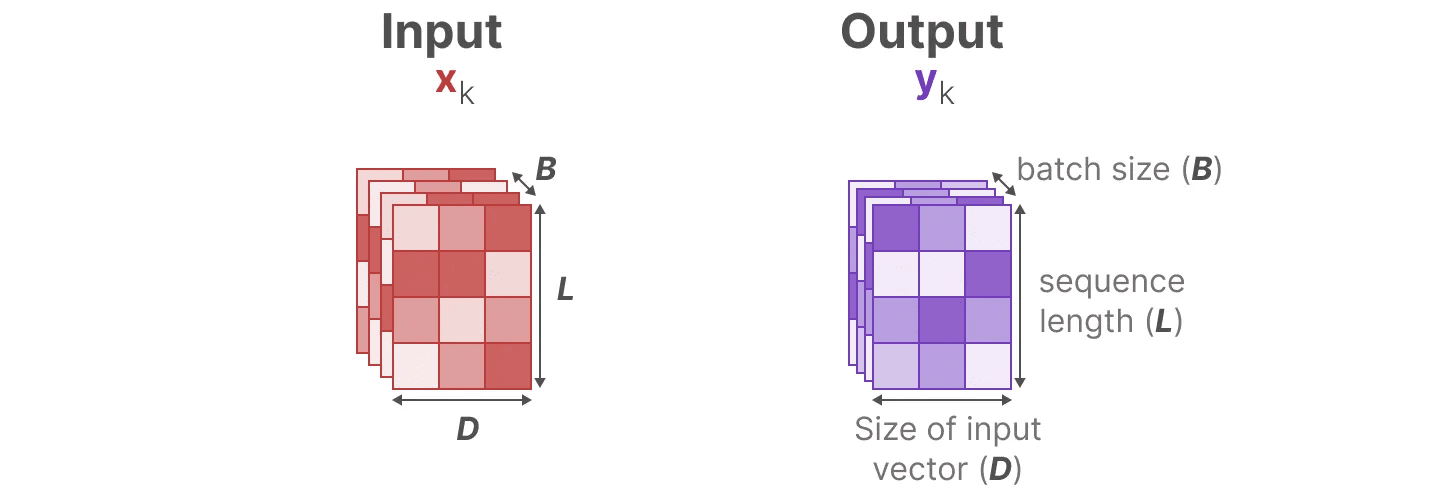在结构化状态空间模型（S4）中，矩阵 A、B 和 C 与输入无关，因为它们的维度 N 和 D 是静态的，不会改变。
相反，Mamba 通过结合输入的序列长度和批量大小，使矩阵 B 和 C，甚至 步长 ∆_，依赖于输入：
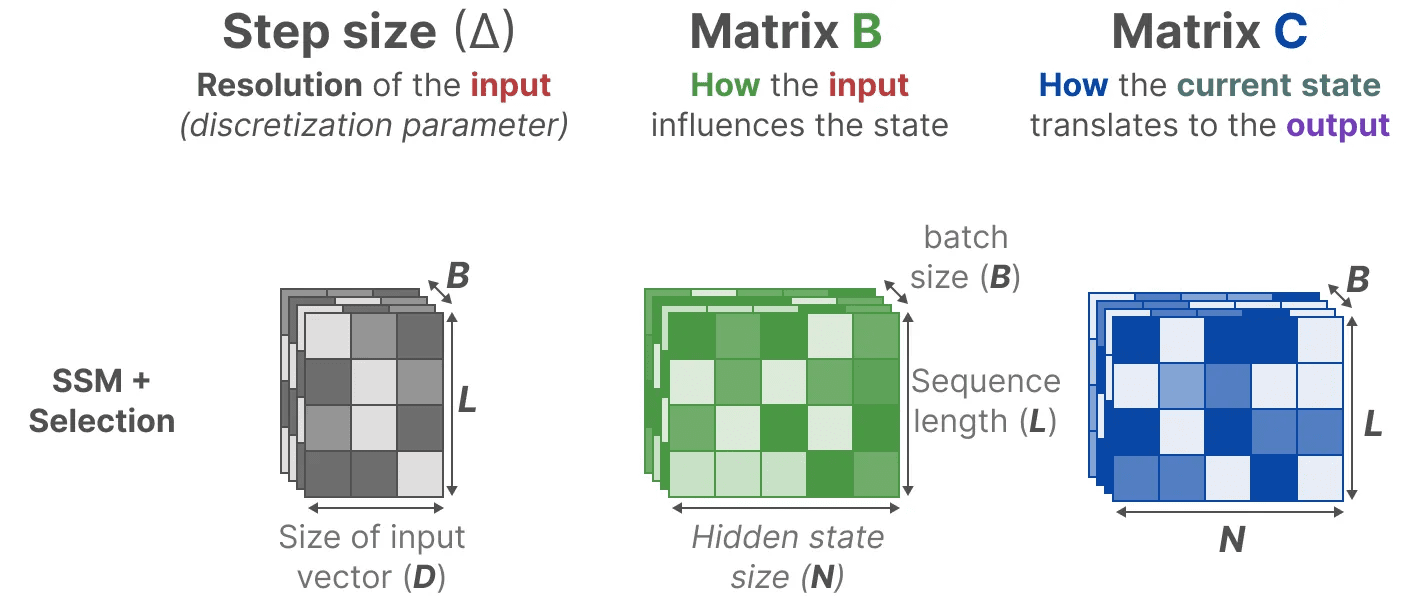这意味着对于每个输入 token，我们现在有不同的 B 和 C 矩阵，这解决了内容感知的问题！
注意：矩阵 A 保持不变，因为我们希望状态本身保持静态，但它的影响方式（通过 B 和 C）是动态的。
它们共同 选择性地 选择保留在隐藏状态中的内容和忽略的内容，因为它们现在依赖于输入。
较小的 步长 ∆ 导致忽略特定的词汇，而更多地使用之前的上下文，而较大的 步长 ∆ 则更加关注输入词汇，而不是上下文：
扫描操作
由于这些矩阵现在是 动态 的，它们不能使用卷积表示进行计算，因为卷积表示假设一个 固定 的卷积核。我们只能使用递归表示，这样就失去了卷积提供的并行化优势。
为了实现并行化，让我们探索如何使用递归计算输出：
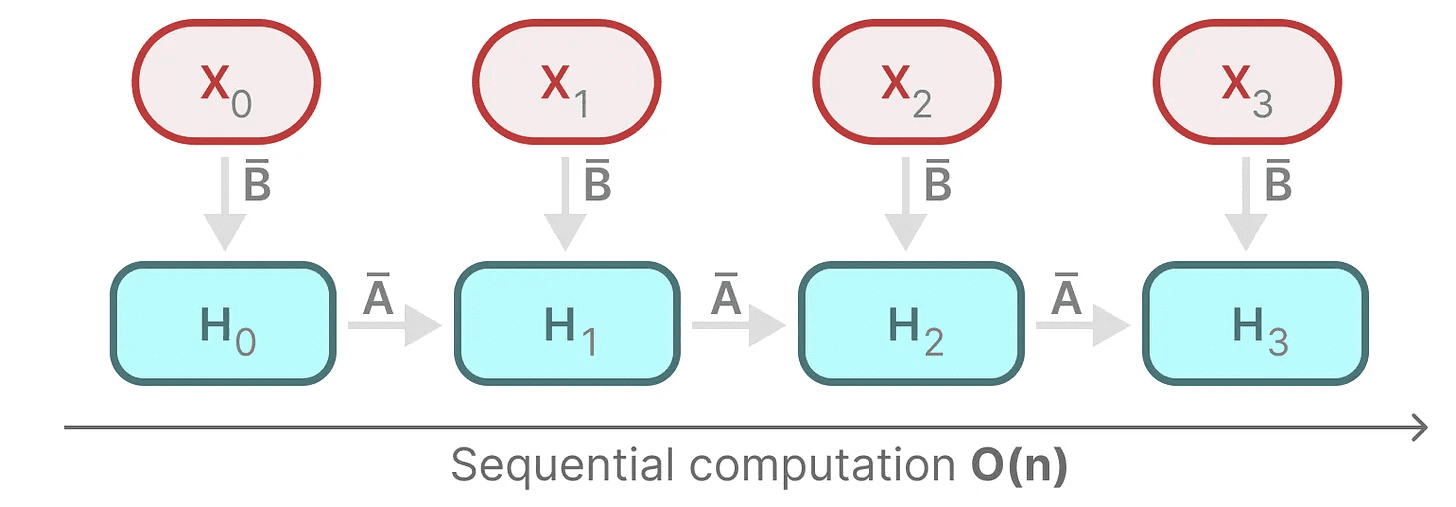每个状态都是前一个状态（乘以 A）与当前输入（乘以 B）的和。这被称为 扫描操作，可以通过 for 循环轻松计算。
相比之下，并行化似乎是不可能的，因为每个状态只能在有了前一个状态之后才可以计算。然而，Mamba 通过 并行扫描 算法使这一点成为可能。
它假设我们进行操作的顺序不重要，利用了结合律的属性。因此，我们可以将序列分成若干部分进行计算，然后迭代地将它们组合起来：
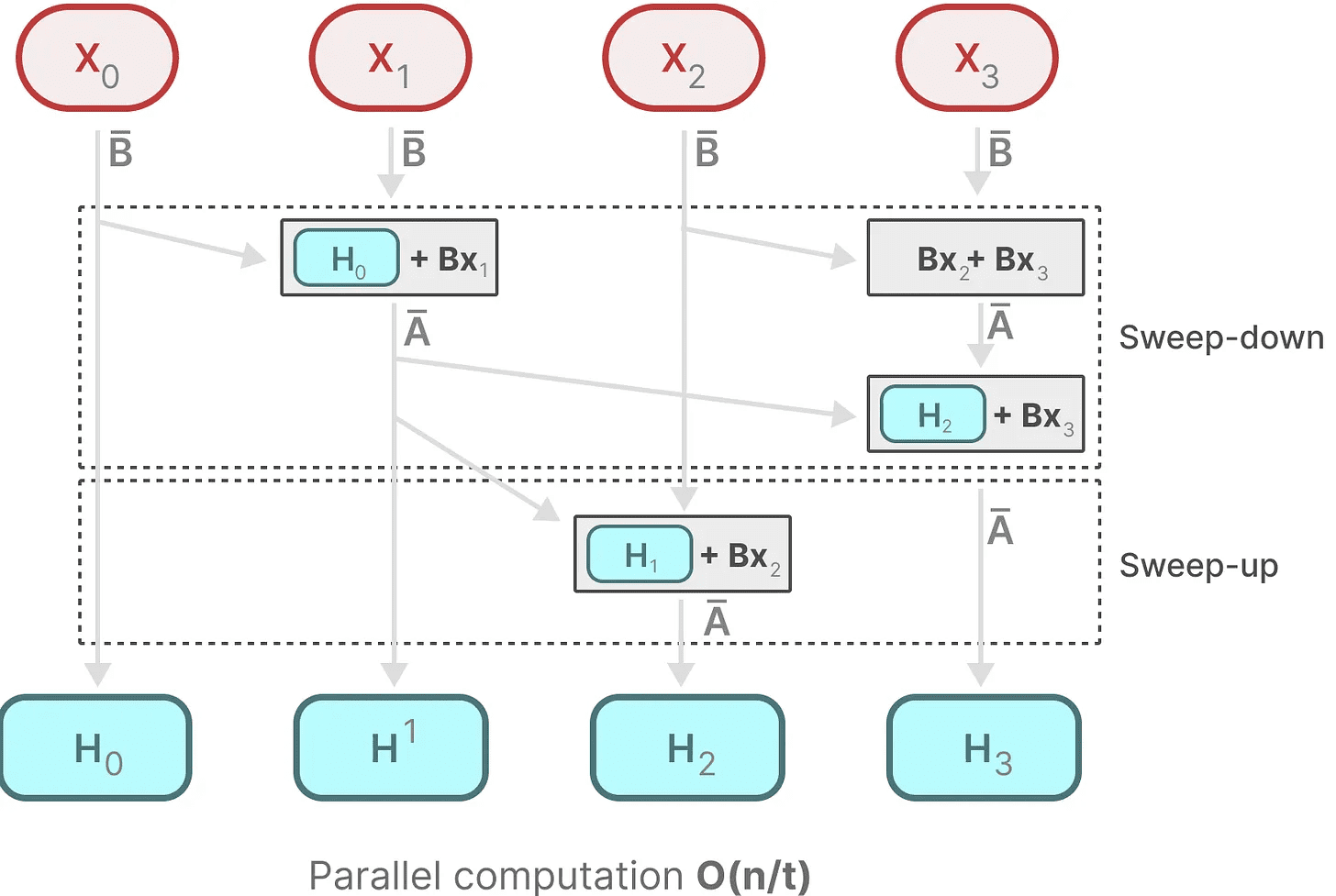动态矩阵 B 和 C 以及并行扫描算法共同创造了 选择性扫描算法，以表示使用递归表示的动态和快速特性。
硬件感知算法
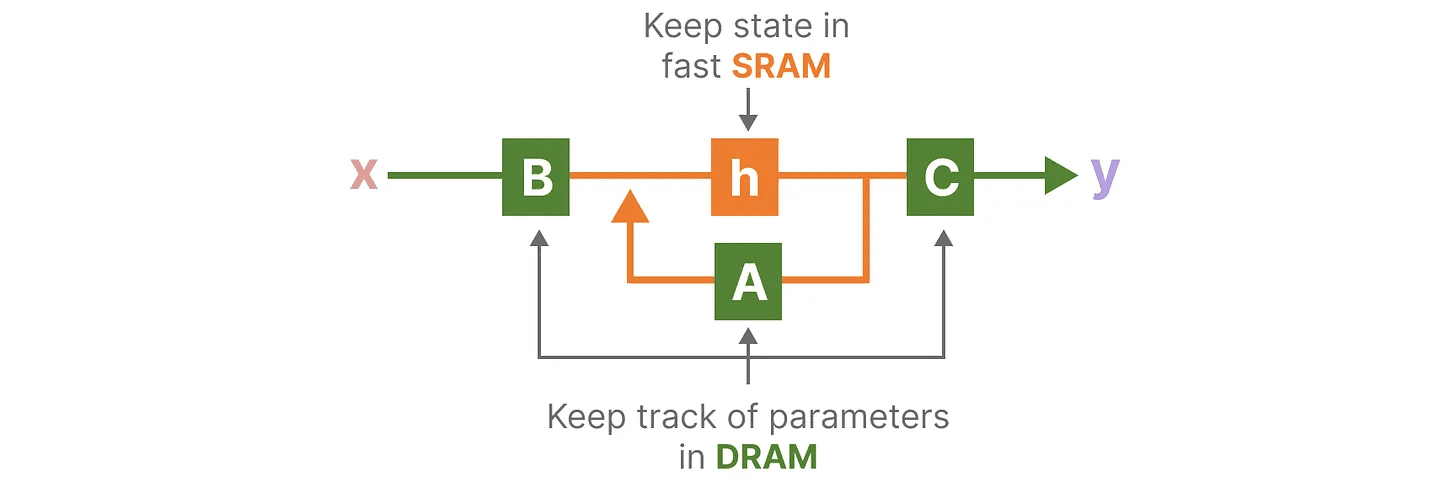
最近的 GPU 的一个缺点是它们的小型但高效的 SRAM 与大型但稍微不那么高效的 DRAM 之间的传输（IO）速度有限。频繁地在 SRAM 和 DRAM 之间复制信息会成为瓶颈。
Mamba 类似于 Flash Attention，试图限制从 DRAM 到 SRAM 及反向的次数。它通过 kernel fusion 实现这一点，允许模型防止写入中间结果，并持续执行计算直到完成。
我们可以通过可视化 Mamba 的基本架构来查看 DRAM 和 SRAM 分配的具体实例：
在这里，以下内容被融合成一个内核：
- 离散化步骤与 step size ∆
- 选择性扫描算法
- 与 C 的乘法
硬件感知算法的最后一部分是 recomputation。
中间状态不会被保存，但在反向传递中计算梯度时是必要的。相反，作者在反向传递期间重新计算这些中间状态。
尽管这看起来可能效率低下，但比从相对较慢的 DRAM 中读取所有这些中间状态要便宜得多。
我们现在已经涵盖了其架构的所有组件，该架构在其文章中的图像如下所示：
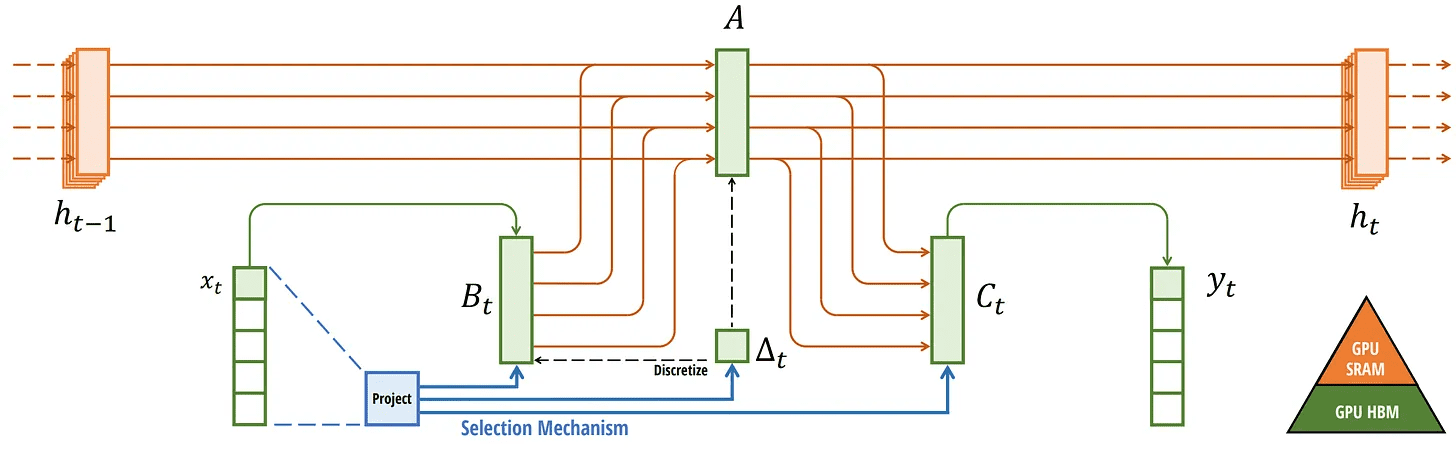选择性 SSM。 取自：Gu, Albert 和 Tri Dao. “Mamba: 具有选择性状态空间的线性时间序列建模。” arXiv 预印本 arXiv:2312.00752 (2023)。
这个架构通常被称为 选择性 SSM 或 S6 模型，因为它本质上是使用选择性扫描算法计算的 S4 模型。
Mamba 模块
我们迄今为止探索的 选择性 SSM 可以作为一个模块进行实现，就像我们可以在解码器模块中表示自注意力一样。
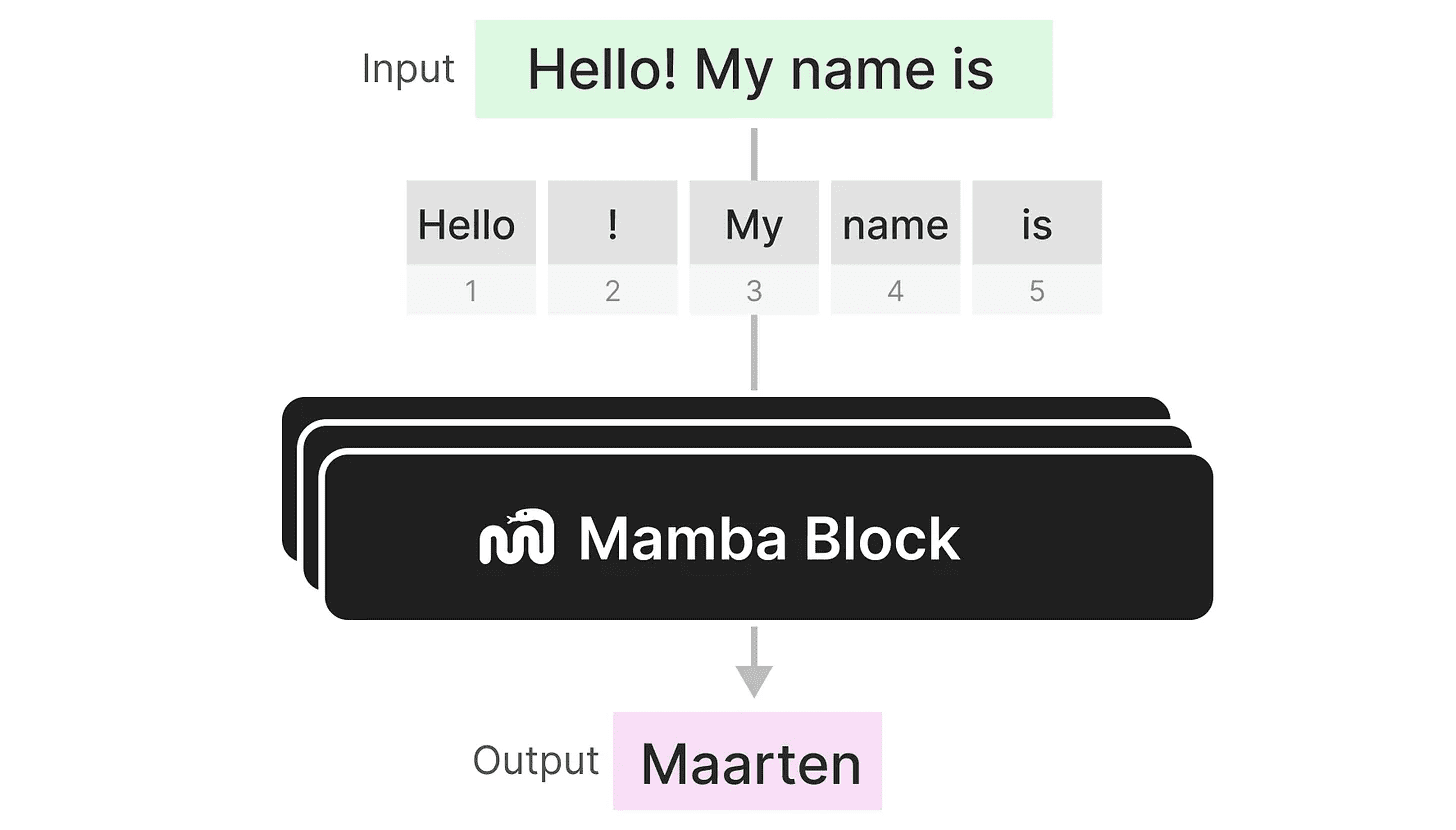像解码器一样，我们可以堆叠多个 Mamba 模块，并将它们的输出作为下一个 Mamba 模块的输入：
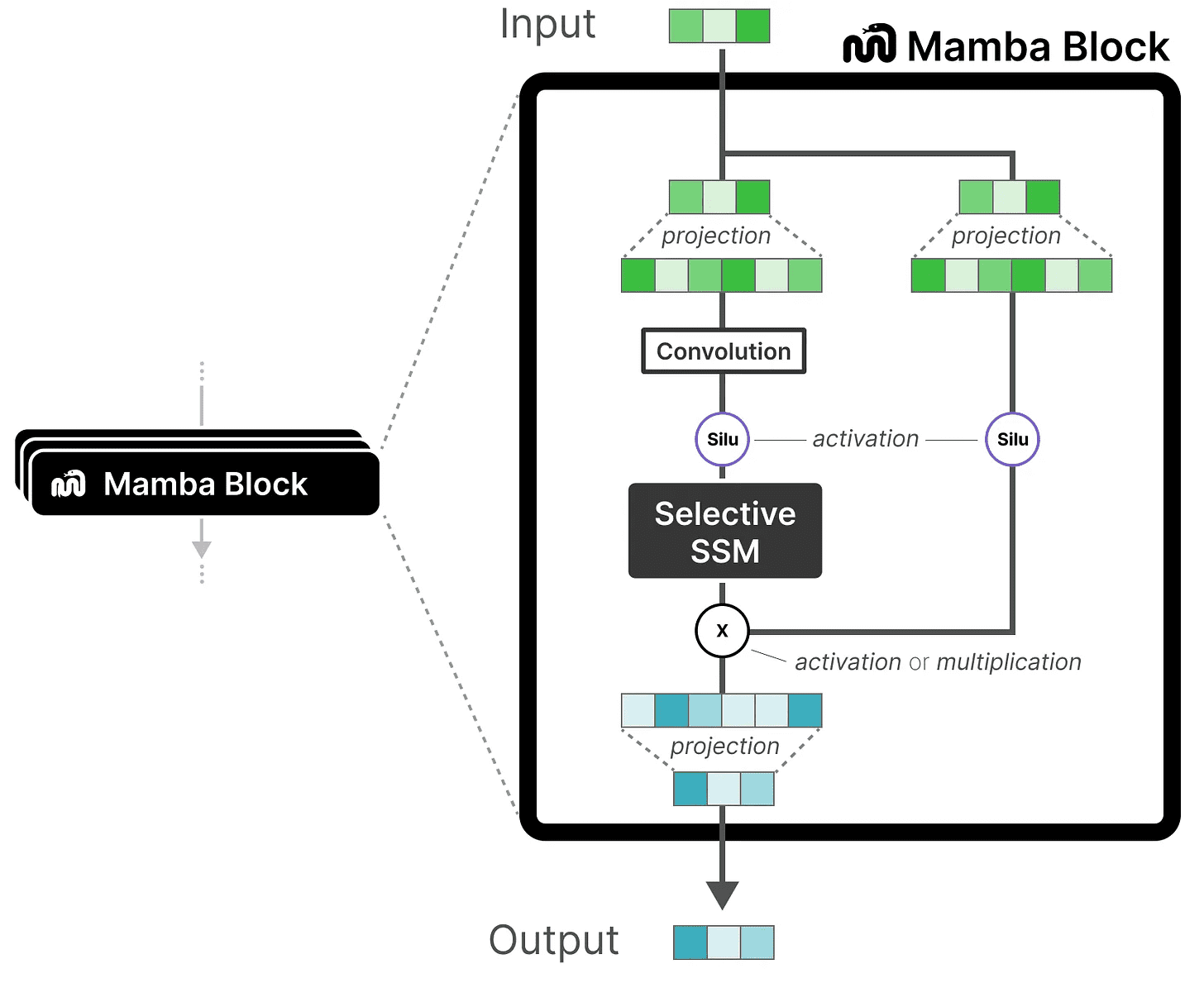它以线性投影开始，以扩展输入嵌入。然后，在 选择性 SSM 之前应用卷积，以防止独立的 token 计算。
选择性 SSM 具有以下特性：
- 通过 离散化 创建的 递归 SSM
- 在矩阵 A 上进行 HiPPO 初始化，以捕捉 长程依赖性
- 选择性扫描算法 以选择性地压缩信息
- 硬件感知算法 以加快计算速度
当我们查看代码实现时，我们可以对这个架构进行更多扩展，并探索一个端到端的示例会是什么样的：
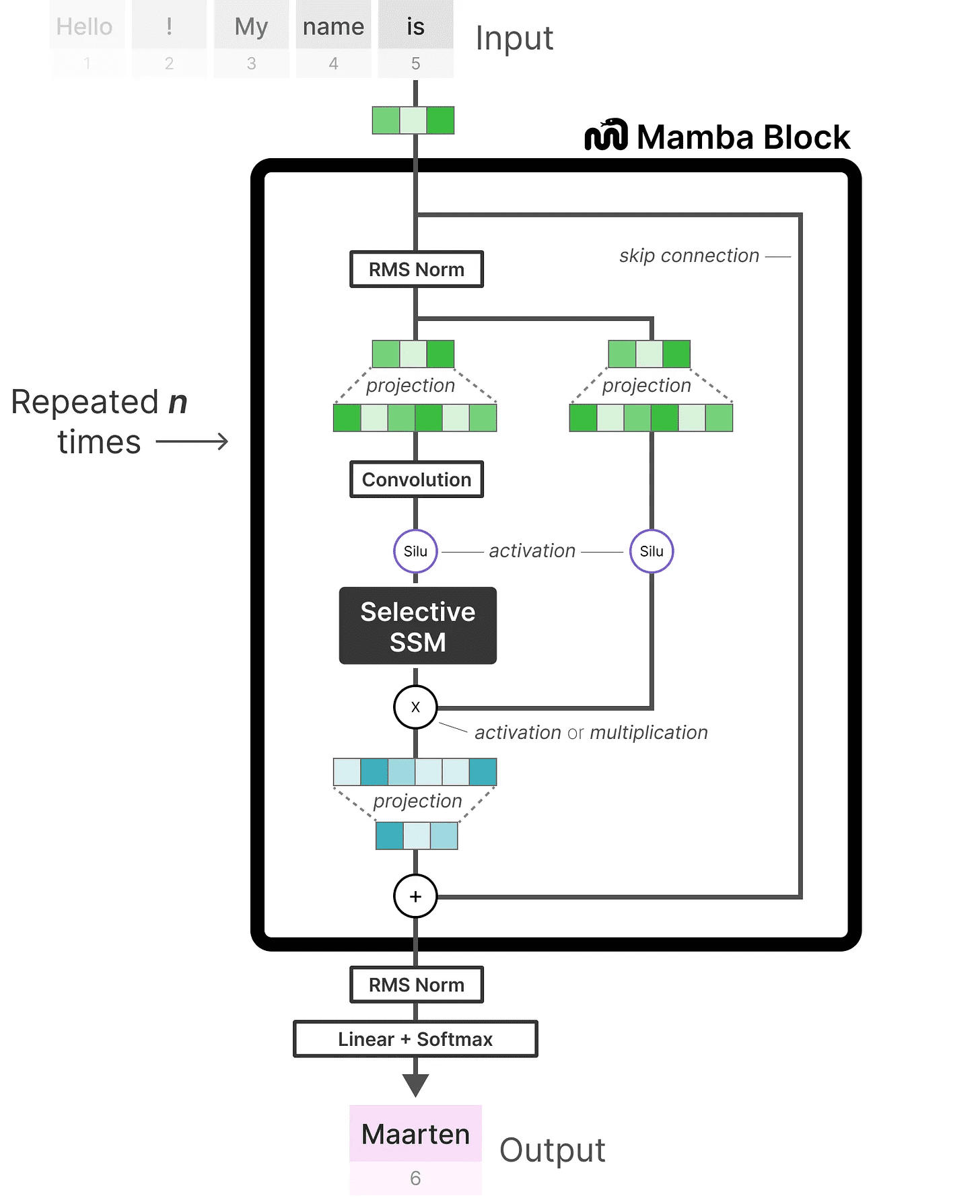注意一些变化，例如增加了归一化层和用于选择输出 token 的 softmax。
当我们将所有内容整合在一起时，我们得到了快速的推理和训练，甚至是无限上下文。使用这种架构，作者发现其性能与同等大小的 Transformer 模型相匹配，有时甚至超过！
结论
这就结束了我们对状态空间模型和令人难以置信的 Mamba 架构使用选择性状态空间模型的探索。希望这篇文章能让你更好地理解状态空间模型，特别是 Mamba。谁知道这是否会取代 Transformers，但现在，看到如此不同的架构获得应有的关注真是令人惊叹！
要查看更多与大语言模型相关的可视化内容并支持这份通讯，请查看我与 Jay Alammar 合著的书籍。
