今天读了一篇有意思的论文《Large Language Models as Analogical Reasoners 》,提到了一种新的 Prompt 方法——“类推提示法。
如果你对提示工程熟悉的话,一定听说过“思维链”(CoT,Chain of Thought),可以显著提升大语言模型(LLM)的推理能力。但使用 CoT 的时候,是需要我们需要提供相关的指导或推理示例来引导模型的。
常用的两种 CoT 方法是: “零示例 CoT(0-shot CoT)”“少示例 CoT(few-shot CoT)”,0-shot CoT 就是在 Prompt 里面明确给出推理步骤,让 LLM 参照步骤来完成推理。few-shot CoT 则是给出少量示例,让 LLM 参照示例来完成推理。
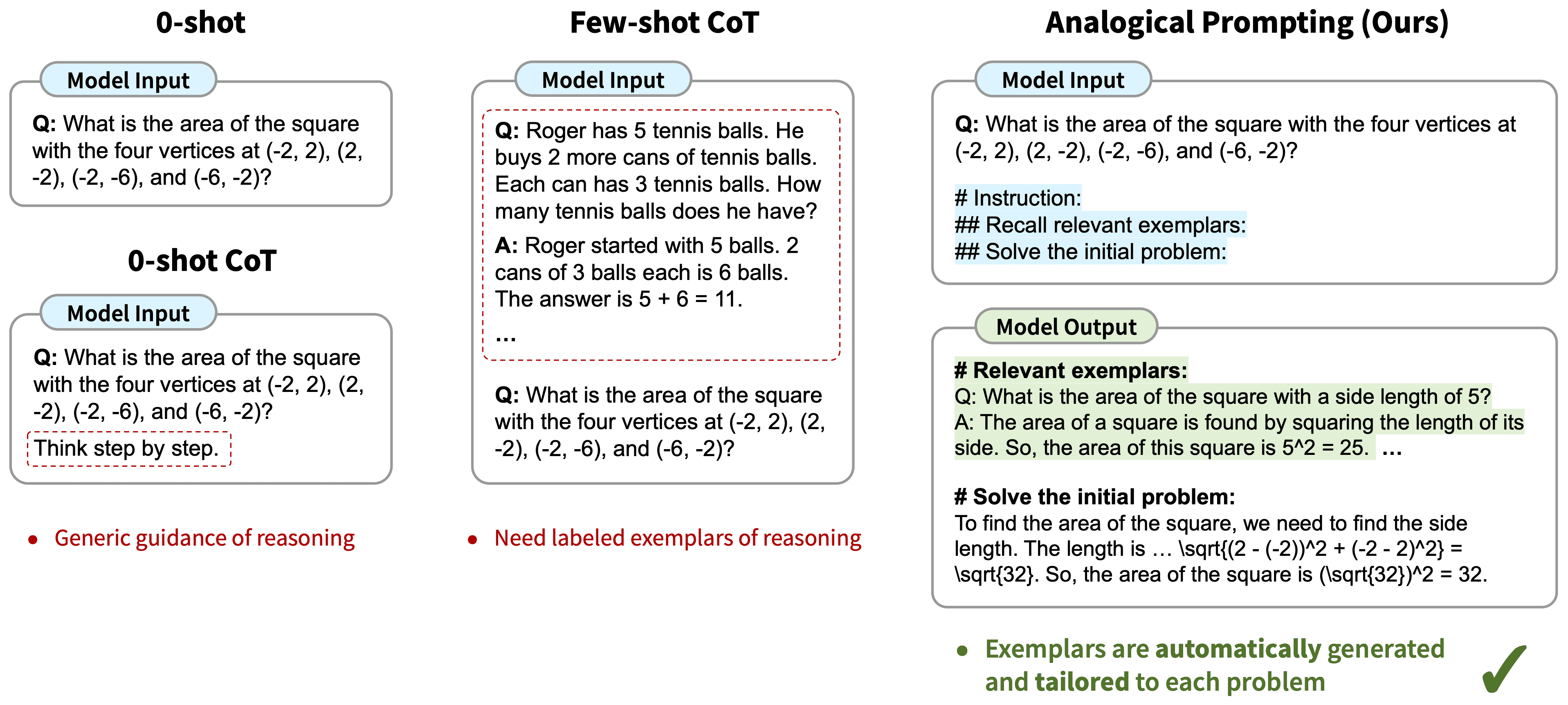
三种提示方法对比
举例来说,现在有一道数学题:”有一个正方形,它的四个顶点分别是 (-2, 2),(2, -2),(-2, -6) 和 (-6, -2),求这个正方形的面积是多少?“
如果不用 CoT,那么就是直接将问题扔给 LLM,让它得出答案。这个问题对于 GPT-4 来说应该可以解出来,但是对于 GPT-3.5 来说有可能会出错,至于其他推理弱一些的模型来说出错概率就更大了。
如果用 0-shot CoT,那么就是在 Prompt 里面明确给出推理步骤,比如:
请按照以下步骤来计算:
1、先计算任意两个相邻顶点的距离作为正方形边长
2、计算边长的平方得到正方形面积
按照这样的步骤,对于 GPT-3.5 这样的 LLM 来说应该能得到正确的结果。
如果用 few-shot CoT,那么就是给出少量示例,比如:
问:这里有一个正方形,它的四个顶点分别是 (0, 0),(1, 1),(0, 1) 和 (1, 0),求这个正方形的面积是多少?
答:我们从中选择两个相邻顶点,比如 (0, 0) 和 (1, 1),计算它们的距离得到边长为1,然后对边长计算平方得到面积为1。
问:有一个正方形,它的四个顶点分别是 (-2, 2),(2, -2),(-2, -6) 和 (-6, -2),求这个正方形的面积是多少?
我们在 Prompt 里面明确给出一个示例,告诉 LLM 应该参考示例的步骤来做,这样对于 GPT-3.5 这样的 LLM 来说应该也能得到正确的结果。
那么什么是”类推提示法“呢?
想想我们上学的时候学数学,如果做这样的数学题,会思考有没有做过类似的题目,尤其对于我这样的小镇做题家,当年不知道做了多少卷子,到后面看到题目就能想起以前做过类似的题目,然后就能很快得出答案。
对于 LLM 来说,它对于知识的储备方面比人类还要强,在训练时已经积累了各种知识,各种案例,所以我们要做的就是要“激发”LLM 去找出与问题相关的知识和案例,然后用这些知识和案例来推理解决问题。
所以”类推提示法“,就是让 LLM 先不要着急解题,而是先列出若干个与问题相关的例子,然后借助这些例子来推理解决问题。这相当于让 LLM 帮你去写 few-shot,帮你生成思维链。
类似于你拿到一道数学题,让它先按照这个数学题去找类似的例题和参考答案,然后让它按照这几个例题和参考答案去解原始题目。
Prompt 的结构如下:
初始问题:\<原始问题\>
相关问题:回想三个相关而独特的问题,并对每个问题及其解决方案进行描述。
解决初始问题:
让 LLM 在收到问题后,先回想三个相关而且独特的问题,并且列出每个问题和解决方案(最好包含步骤),并且一定要将中间过程打印出来。等 LLM 输出完这些相关例子后,再把原始问题打印一遍(防止遗忘),这样 LLM 就能用这些相关例子来推理解决原始问题了。
一个完整的使用类推提示法的 Prompt 参考:
你的任务是解数学题。当遇到一道数学题时,请你先回想一些相关的题目作为例子。然后,再去解决最开始的那个问题。
# 最开始的问题:
有一家航空公司为飞机上的每位乘客提供晚餐,乘客可以选择牛排或者鱼。六名机组人员中有三人可以选择牛排,三人可以选择鱼。如果食物是随机分配的,那么两名飞行员都拿到鱼的概率是多少呢?
# 操作指南:
你的答案中必须包含以下几点:
## 相关问题:
请你想出三个和最开始的问题相关的数学问题作为例子。注意,每个问题都应该和其它问题有所区别,包括和最开始的问题(比如,涉及不同的数字和名字)。每个问题都要按照以下的格式:
- “Q:” 后面写问题描述
- “A:” 后面写问题的解决方法,并把最终答案写在 \boxed 里。
## 解决最开始的问题:
说:“我们来解决下面这道数学题。” 然后按照以下的格式回答:
Q:把最开始的问题复制粘贴在这里。
A:解释解决方案,并把最终答案写在 \boxed 里。
LLM 会输出如下的结果:
## 相关问题:
### 问题1:
- **Q:** 在一个派对上,每个人都可以选择吃苹果派或香草冰淇淋。其中,五名女士可以选择吃苹果派,五名女士可以选择吃香草冰淇淋。如果甜点是随机分配的,那么两名女士都拿到香草冰淇淋的概率是多少?
- **A:** 使用组合计算来求解此问题。总的方式是从五名可以选择冰淇淋的女士中选择两名,这有 \( \binom{5}{2} = 10 \) 种方式。而总的分配方式是从十名女士中选择两名,即 \( \binom{10}{2} = 45 \) 种方式。所以概率是 \( \frac{10}{45} = \frac{2}{9} \)。最终答案是 \( \boxed{\frac{2}{9}} \)。
### 问题2:
- **Q:** 在一次晚宴上,每个人可以选择红酒或白酒。有四名男士可以选择红酒,四名男士可以选择白酒。如果酒是随机分配的,那么三名男士都拿到白酒的概率是多少?
- **A:** 采用类似的方法,从四名可以选择白酒的男士中选出三名,有 \( \binom{4}{3} = 4 \) 种方式。而总的分配方式是从八名男士中选择三名,即 \( \binom{8}{3} = 56 \) 种方式。所以概率是 \( \frac{4}{56} = \frac{1}{14} \)。最终答案是 \( \boxed{\frac{1}{14}} \)。
### 问题3:
- **Q:** 在咖啡馆,每个人可以选择拿铁或卡布奇诺。有三名顾客可以选择拿铁,三名顾客可以选择卡布奇诺。如果咖啡是随机分配的,那么一名顾客拿到卡布奇诺的概率是多少?
- **A:** 在这种情况下,我们选择一名可以喝卡布奇诺的顾客,有 \( \binom{3}{1} = 3 \) 种方式。总的分配方式是从六名顾客中选择一名,即 \( \binom{6}{1} = 6 \) 种方式。所以概率是 \( \frac{3}{6} = \frac{1}{2} \)。最终答案是 \( \boxed{\frac{1}{2}} \)。
## 我们来解决下面这道数学题。
### Q:有一家航空公司为飞机上的每位乘客提供晚餐,乘客可以选择牛排或者鱼。六名机组人员中有三人可以选择牛排,三人可以选择鱼。如果食物是随机分配的,那么两名飞行员都拿到鱼的概率是多少呢?
### A:我们可以使用类似的解决方案来处理这个问题。我们有三名可以选择鱼的飞行员,我们要选择其中的两名。这有 \( \binom{3}{2} = 3 \) 种方式。总的分配方式是从六名飞行员中选出两名,即 \( \binom{6}{2} = 15 \) 种方式。所以概率是 \( \frac{3}{15} = \frac{1}{5} \)。最终答案是 \( \boxed{\frac{1}{5}} \)。
© 版权声明
文章版权归 AI分享圈 所有,未经允许请勿转载。
相关文章

暂无评论...