模型量化是什么：FP32, FP16, INT8, INT4 数据类型详解

导读

在人工智能科技的浩瀚星空中，深度学习模型以其卓越的性能，驱动着诸多领域的创新发展。然而，模型规模的持续膨胀，如同双刃剑，在提升性能的同时，也带来了算力需求与存储压力的剧增。特别是在资源受限的应用场景中，模型的部署和运行面临严峻挑战。

面对这一困境，一种名为“量化”的技术应运而生，犹如一柄精巧的手术刀，在模型精度可接受的范围内，巧妙地降低模型大小，提升运算速度，并显著减少能耗。量化技术，能够将模型中高精度的 FP32 数据，转换为低精度的 INT4 数据，实现模型的“瘦身”与“加速”。本文将深入浅出地剖析量化技术的原理、方法及其在深度学习领域的应用，即使是技术初学者，亦能轻松理解其精髓。

1. 数字表示基础

1.1 二进制与十进制转换

在数字世界的基石——计算机科学中，所有数据皆以二进制形式存储。二进制系统仅包含 0 和 1 两个数字，而我们日常生活中所使用的十进制系统，则拥有 0 到 9 共十个数字。这两种进制之间的转换，犹如不同语言间的翻译，是理解计算机数据表示的关键。

以十进制数字 13 为例，转换为二进制形式为 1101。转换过程类似于将十进制的“整体”分解为二进制的“组成部分”。具体步骤如下：

13 除以 2，商为 6，余数为 1 （二进制最低位）
6 除以 2，商为 3，余数为 0
3 除以 2，商为 1，余数为 1
1 除以 2，商为 0，余数为 1 （二进制最高位）

余数从下往上排列：
↑1
↑0
↑1
↑1
得到二进制结果：1101

反之，将二进制 1101 转换回十进制，则如同将“组成部分”重新组合还原为“整体”。从右向左，每一位的权重以 2 的幂次方递增，最右位权重为 ，向左依次为 、 、 等。因此，二进制 1101 转换为十进制为： 1× + 1× + 0× + 1× = 8 + 4 + 0 + 1 = 13。

1.2 浮点数与整数区别

（一）整数类型（INT）

INT 是 Integer 的缩写，代表整数类型。整数，顾名思义，是不包含小数部分的数字，例如 1、2、3 等。

INT4 表示使用 4 位二进制数来表示一个整数，INT8 则使用 8 位二进制数表示整数。位数决定了整数的表示范围。

INT4 能够表示的整数范围是有限的，因为 4 位二进制数最多能表示 个不同的数。对于有符号 INT4，其表示范围通常为 -8 到 7；对于无符号 INT4，范围则为 0 到 15。INT8 亦然，有符号 INT8 的表示范围为 -128 到 127，无符号 INT8 的范围为 0 到 255，因为 8 位二进制数能表示 = 256 个不同的数。

（二）浮点数类型（FP）

FP 是 Floating Point 的缩写，即浮点数类型。浮点数，与整数相对，用于表示带有小数部分的数字。

浮点数由符号位、指数位和尾数位三部分构成。以 32 位浮点数（FP32）为例，它包含 1 位符号位、8 位指数位和 23 位尾数位。这种精巧的设计使得浮点数能够表示极其广泛的数值范围，从极小的数到极大的数，犹如一把伸缩自如的卷尺。

例如，FP32 可以表示极小的数（约 ），也可以表示极大的数（约 ）。而 INT8 (8 位整数) 仅能表示 -128 到 127 之间的整数。这种差异，如同使用固定长度的直尺（整数）与可伸缩的卷尺（浮点数）测量长度，浮点数在数值表示的灵活性和范围上远胜于整数。

（三）常用的数据类型

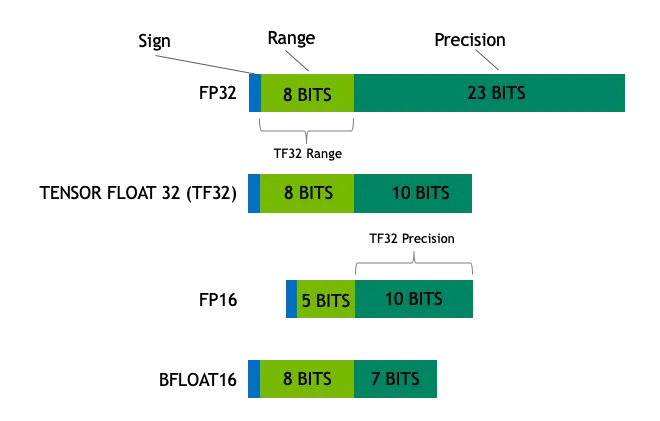
在深度学习和通用计算领域，常见的数据类型包括：

• Float32 (FP32): 这是标准的 32 位浮点数格式，以高精度和广阔的数值范围著称。FP32 运算因其通用性，得到广泛硬件的广泛支持，故而在模型训练和推理中占据主导地位。
• Float16 (FP16): FP16 是一种 16 位半精度浮点数，相较于 FP32，其精度有所降低，但内存占用显著减少，计算速度大幅提升。FP16 的数值表示范围相对较窄，可能面临上溢和下溢的风险。然而，在深度学习实践中，诸如损失缩放 (Loss Scaling) 等技巧的应用，能够有效缓解这些问题。
• BFloat16 (BF16): BF16 是另一种 16 位浮点数格式。其独特之处在于，BF16 保留了与 FP32 相同的 8 位指数位，从而拥有与 FP32 相当的动态范围。然而，BF16 的尾数位仅为 7 位，精度低于 FP16。在处理数值范围较大的场景时，BF16 表现出色，但在精度敏感型任务中，可能需要权衡考虑。
• Int8: INT8 是一种 8 位整数类型，其数值表示范围有限，但内存占用极低。INT8 主要应用于模型量化技术，通过将模型参数由高精度的 FP32 或 FP16 转换为 INT8，可以大幅降低模型存储空间需求和计算复杂度，为模型在资源受限设备上的高效部署铺平道路。

2. 量化概念

2.1 量化定义

量化指的是将模型中的数据从高精度表示转换为低精度表示，就像在画质和文件大小之间做权衡，将高精度的画作压缩成低精度的 JPEG 图像，在文件大小大幅降低的同时，画面主体信息仍然保留。在深度学习领域，量化通常指将模型权重和激活值从 FP32 (32 位浮点数) 降至 FP16 (16 位浮点数) 乃至 INT8 (8 位整数) 或更低精度。

FP32 作为一种高精度浮点数格式，以 32 位二进制位 (1 位符号位、8 位指数位、23 位尾数位) 精确表示数值。FP32 宛如一把精密的标尺，能够精确衡量微小至宏大的数值，但其高精度特性亦带来存储开销大、计算速度相对较慢的缺点。

FP16 作为一种半精度浮点数格式，仅需 16 位二进制位 (1 位符号位、5 位指数位、10 位尾数位) 即可表示数值。相较于 FP32，FP16 的精度有所牺牲，但换来了存储空间减半和计算效率提升。FP16 犹如一把刻度稍粗的标尺，在精度与效率之间实现了良好的平衡。

INT8 则是一种 8 位整数类型，仅能表示 -128 至 127 范围内的整数。INT8 以极低的存储空间占用和极高的计算速度为优势，但其数值表示精度亦是最低的。INT8 类似于一个简单的计数器，仅能进行整数计数，但胜在快速便捷。

2.2 量化目的

量化的核心目的在于降低模型的存储需求和计算复杂度，同时力求将精度损失控制在可接受范围内。具体而言，量化旨在实现以下目标：

降低存储需求: 现代深度学习模型，特别是参数规模庞大的大型模型，动辄拥有数亿乃至数千亿参数，对存储空间构成巨大压力。以 FP32 模型为例，每个参数占用 4 字节存储空间。若将模型量化为 FP16，则每个参数仅需 2 字节，存储需求立减一半。进一步量化至 INT8，每个参数仅需 1 字节，存储空间可缩减 75%。

提升计算效率: 量化后的模型在推理阶段，计算量显著降低，从而实现推理速度的提升。例如，FP32 模型在 GPU 上运行时，计算速度可能受限于内存带宽。而 FP16 或 INT8 模型，得益于硬件对低精度计算的优化加速，计算速度可大幅提升。尤其在边缘设备或移动设备等计算资源受限的场景中，量化所带来的性能提升尤为显著。

降低功耗: 模型计算资源需求的降低，直接转化为能耗的减少。对于移动设备和嵌入式系统而言，功耗是至关重要的考量因素。量化技术能够有效降低模型功耗，延长设备续航时间，并降低散热需求。

减少带宽需求: 在分布式计算系统中，模型体积的缩减亦意味着数据传输带宽需求的降低。在多服务器协同工作的场景下，量化模型能够以更快的速度完成模型分发和参数同步，从而提升整体数据传输效率。

3. INT4、INT8 量化

3.1 INT4 与 INT8 表示范围

INT4 和 INT8 均为整数类型的量化方法，它们在计算机系统中以二进制形式存储数据，但在数值表示范围和精度上存在差异。

• INT8: INT8 是一种 8 位整数类型，其表示范围为 -128 至 127。可以将其类比为一个 8 位计数器，每一位可以是 0 或 1，通过不同的 0/1 组合来表示不同的整数值。例如，在有符号 INT8 表示中，范围是 -128 到 127，二进制的 11111111 表示十进制的 -1。 如果是无符号 INT8，范围是 0 到 255，此时 11111111 则表示十进制的 255。INT8 的表示范围足以满足诸多应用场景的需求，例如图像处理中的像素值，通常在 0 至 255 范围内，INT8 即可有效表示。
• INT4: INT4 是一种 4 位整数类型，其表示范围较 INT8 更小，为 -8 至 7。INT4 以牺牲数值表示范围为代价，换取更小的存储空间占用和更快的计算速度。INT4 犹如一个更小巧的计数器，虽然数值表示范围受限，但“体积”更小，更节省资源。在一些对精度要求相对宽松的应用场景中，例如某些轻量级神经网络层，采用 INT4 量化能够显著降低存储和计算成本。例如，在移动端部署轻量级图像分类模型时，模型参数和中间计算结果可以使用 INT4 格式存储和计算，以减少内存占用和加速推理。

3.2 量化公式与示例

量化的过程，本质上是将高精度的浮点数映射转换为低精度的整数。以 FP32 量化至 INT8 为例，其量化公式如下：

是原始的浮点数。

是量化后的整数。

是缩放因子，用于将浮点数映射到整数范围。

表示四舍五入到最近的整数。

表示将结果限制在 INT8 的范围内，即 ［-128, 127］。

计算缩放因子

缩放因子 (scale) 的计算，通常依据浮点数绝对值的最大值确定。假设存在一组浮点数 ，计算步骤如下：

1. 找出该组浮点数的最大绝对值：
2. 计算缩放因子： 。

在实际应用中，缩放因子的计算方法有多种，例如最大值量化 (Max Quantization)、均值-标准差量化 (Mean-Std Quantization) 等。 最大值量化直接使用张量中的最大绝对值来计算缩放因子，实现简单，但可能对异常值敏感。 均值-标准差量化则利用数据的均值和标准差信息，更稳健地确定缩放因子，但计算复杂度稍高。选择合适的缩放因子计算方法，需要在精度和计算开销之间进行权衡。

示例

假设我们有一组浮点数 [-0.5, 0.3, 1.2, -2.1]，以下将逐步演示量化过程：

1. 计算最大绝对值：

2. 计算缩放因子：

3. 量化每个浮点数：

• 对于 -0.5:
• 对于 0.3:
• 对于 1.2:
• 对于 -2.1:

最终，量化后的 INT8 表示为 [-1, 1, 4, -7]。

通过上述步骤，我们可以清晰地看到量化技术如何将浮点数转换为整数。尽管量化过程不可避免地会引入一定的精度损失，但通过合理地选择缩放因子，可以在显著降低存储和计算成本的同时，最大限度地保持模型的性能水准。 为了进一步减小量化误差，还可以引入零点 (zero-point) 量化。 零点量化在量化公式中加入零点偏移，使得浮点数 0 精确映射到整数 0， 从而提高量化精度，尤其是在激活值中存在大量 0 值时。

4. FP8、FP16、FP32 量化

4.1 FP8、FP16、FP32 表示方法

FP8、FP16 和 FP32 均为浮点数表示格式，它们在计算机中以二进制形式存储，但因位宽不同，故而数值表示范围和精度各异。

FP32

FP32 作为一种标准 32 位浮点数格式，由以下三部分构成：

• 符号位 (1 位): 用于标识数值的正负，0 代表正数，1 代表负数。
• 指数位 (8 位): 用于定义数值的大小范围，使得 FP32 能够表示从极小到极大的数值。
• 尾数位 (23 位): 用于确定数值的精度，尾数位越多，精度越高。

FP32 拥有极宽广的数值表示范围，约为 至 ，其精度可达小数点后 6 位左右。FP32 宛如一把高精度的卷尺，既能量度细微至尘埃的尺度，亦可丈量广阔如山川的距离。 在科学计算、金融建模等对精度要求极高的领域，FP32 是不可或缺的数据类型。

FP16

FP16 是一种半精度浮点数格式，仅占用 16 位存储空间，为 FP32 的一半。FP16 的结构如下：

• 符号位 (1 位): 标识数值正负。
• 指数位 (5 位): 定义数值大小范围。
• 尾数位 (10 位): 决定数值精度。

FP16 的数值表示范围约为 到 ，精度相较 FP32 降低，约为小数点后 3 位。FP16 犹如一把刻度略粗的直尺，精度有所降低，但在存储空间和计算效率上更具优势。 FP16 常用于对计算速度和内存带宽有较高要求的深度学习模型训练和推理中。 尤其是在 GPU 加速的场景下，使用 FP16 可以充分利用 Tensor Core 等硬件加速单元， 从而实现显著的性能提升。

FP8

FP8 是一种新兴的低精度浮点数格式，主要应用于深度学习领域，旨在实现高效计算。FP8 的典型结构如下：

• 符号位 (1 位): 标识数值正负。
• 指数位 (3 位或 4 位): 定义数值大小范围 (存在两种 FP8 变体)。
• 尾数位 (4 位或 3 位): 决定数值精度 (与指数位位数对应)。

FP8 的数值表示范围和精度均进一步降低，但其优势在于更小的存储空间占用和更快的计算速度。如果说 FP32 是一把精密的卷尺，FP16 是刻度稍粗的直尺，那么 FP8 就像是一个只有厘米刻度的简易直尺，量程和精度都进一步降低，但在特定场合下，仍然可以快速完成测量任务。 FP8 作为一种极低精度的数据类型， 在对延迟和吞吐量有极致要求的场景中展现出巨大潜力，例如实时推理、边缘计算等。 但 FP8 的应用也对硬件和算法提出了更高的要求， 需要专门的硬件支持和量化策略来保证精度。

4.2 量化过程与公式

量化过程，是将高精度浮点数转换为低精度浮点数或整数的过程。以 FP32 量化至 FP16 为例，其量化公式如下：

是原始的浮点数。

是量化后的低精度浮点数。

是缩放因子，用于将浮点数映射到低精度范围。

表示四舍五入到最近的值。

计算缩放因子

缩放因子 (scale) 的计算，通常依据浮点数绝对值的最大值确定。假设存在一组浮点数 ，计算步骤如下：

1. 找出该组浮点数的最大绝对值：
2. 计算缩放因子： ，其中 是目标低精度格式的最大可表示绝对值。对于 FP16，这个值约为 65504。

类似于 INT8 量化， FP16 量化中缩放因子的计算方法也很多样， 可以根据不同的精度和性能需求进行选择。 此外， FP16 量化也常常结合混合精度训练 (Mixed Precision Training) 技术使用。 混合精度训练在模型训练过程中， 某些计算密集型操作 (如矩阵乘法、卷积) 使用 FP16， 而对精度要求较高的操作 (如损失计算、梯度更新) 仍使用 FP32， 从而在保证模型精度的前提下， 加速训练过程并减少内存占用。

示例

假设我们有一组 FP32 浮点数 [-0.5, 0.3, 1.2, -2.1]，以下将逐步演示 FP32 量化至 FP16 的过程：

1. 计算最大绝对值：

2. 计算缩放因子：

3. 量化每个浮点数：

• 对于 -0.5:
• 对于 0.3:
• 对于 1.2:
• 对于 -2.1:

最终，量化后的 FP16 表示为 [-0.5, 0.3, 1.2, -2.1]。

通过以上步骤，可以观察到量化技术如何将高精度浮点数转换为低精度浮点数。量化固然会带来一定的精度损失，但通过合理选择缩放因子，可以在降低存储和计算成本的同时，尽可能地维持模型的性能表现。 为了进一步提升 FP16 量化的精度， 可以采用动态量化 (Dynamic Quantization) 技术。 动态量化在推理过程中， 根据输入数据的实际范围， 动态调整缩放因子， 从而更好地适应数据的分布变化， 减小量化误差。

5. 量化应用与优势

5.1 在深度学习中的应用

量化技术在深度学习领域拥有广泛的应用前景，特别是在模型训练和推理阶段，其价值日益凸显。以下是量化技术在深度学习中的几项主要应用：

模型训练加速

在模型训练阶段，采用低精度数据类型 (如 FP16 或 FP8) 进行计算，能够显著加速训练进程。例如，NVIDIA Hopper 架构 GPU 支持 FP8 精度的 Tensor Core 运算。与传统的 FP32 训练相比，FP8 训练速度可提升 2 至 3 倍。这种训练加速对于参数规模庞大的模型尤为关键，能够大幅缩减训练时间和计算资源消耗。 例如， 训练 GPT-3 等大型语言模型时， 采用 FP16 或 BF16 混合精度训练， 可以显著缩短训练时间， 节省大量的计算资源。

以 Inflection AI 的 Inflection-2 模型为例，该模型采用了 FP8 混合精度训练策略，在 5000 块 NVIDIA Hopper 架构 GPU 上完成了训练，总计浮点运算次数高达 FLOPs。在多项标准人工智能性能基准测试中，Inflection-2 相较于同属训练计算类别的 Google 旗舰模型 PaLM 2，展现出卓越的性能优势。

模型推理优化

在模型推理阶段，量化技术能够显著降低模型的存储需求和计算复杂度，进而提升推理效率。例如，将 FP32 模型量化为 INT8，模型存储空间可减少 75%，推理速度可提升数倍。这对于在边缘设备或移动设备上部署深度学习模型至关重要，因为这些设备通常面临计算资源和存储空间受限的挑战。 例如， 在手机端部署图像识别模型时， 将模型量化为 INT8 可以有效降低模型大小， 减少内存占用， 并加速推理速度， 提升用户体验。

例如，Google 与 NVIDIA 团队紧密合作，将 TensorRT-LLM 优化技术应用于 Gemma 模型，并结合 FP8 技术实现了推理加速。实验结果表明，在使用 Hopper GPU 进行推理时，FP8 较之 FP16 在吞吐量方面实现了 3 倍以上的提升。

模型压缩与部署

量化技术亦可用于模型压缩和部署。通过将高精度模型量化为低精度模型，可以有效减小模型体积，从而 облегчить 模型在资源受限环境中的部署。例如，零一万物利用 NVIDIA 软硬件结合的技术栈，完成了大模型 FP8 训练和验证，其大模型训练吞吐量相较 BF16 提升了 1.3 倍。 除了 INT8 和 FP16/FP8 量化外， 还存在 INT4 甚至更低比特的量化技术， 例如二值化神经网络 (Binary Neural Network, BNN) 和三值化神经网络 (Ternary Neural Network, TNN)。 这些极低比特量化技术可以将模型压缩到极致， 但通常会带来较大的精度损失， 适用于对模型大小和速度有极端要求的场景。

此外，量化后的模型可以借助特定的硬件加速技术，进一步提升性能。例如，NVIDIA Transformer Engine 已被集成至 PyTorch、JAX、PaddlePaddle 等主流深度学习框架，为量化模型的推理提供了高效的硬件级支持。 除了 NVIDIA GPU 外， 其他硬件平台， 例如 ARM 架构 CPU、 移动端 NPU 等， 也针对量化计算进行了专门的优化和加速， 为量化模型的广泛部署提供了硬件基础。

5.2 优势与局限性

优势

计算效率提升: 低精度量化能够显著提升计算速度，降低计算资源消耗。FP16 和 FP8 的计算吞吐量均数倍高于 FP32。这种加速效应在大规模模型训练和推理中尤为突出。

存储需求降低: 量化技术可大幅降低模型存储需求。例如，将 FP32 模型量化为 INT8，存储空间可缩减 75%。这对于在存储资源受限的环境中部署模型具有重要意义。

功耗降低: 低精度计算所需计算资源更少，从而降低了设备能耗。在移动设备和嵌入式系统中，功耗是关键的设计考量因素。量化后的模型有助于延长设备电池续航时间，并减少散热需求。

模型优化: 量化技术推动模型在训练和推理过程中进行优化与压缩，从而进一步降低部署成本。例如，FP8 的应用促使模型在训练阶段进行更为精细的量化策略探索，进而提升模型整体效率。

局限性

精度损失: 量化过程不可避免地伴随精度损失，尤其是在采用极低精度格式 (如 FP8) 时，精度损失可能较为显著，并可能导致模型在特定任务上的性能下降。尽管可以通过精巧地选择缩放因子等手段在一定程度上缓解精度损失，但完全消除精度损失通常难以实现。 为了减轻量化带来的精度损失， 可以采用量化感知训练 (Quantization-Aware Training, QAT) 技术。 QAT 在模型训练过程中， 模拟量化操作， 将量化误差纳入训练的考量范围， 从而训练出对量化更鲁棒的模型。 QAT 通常能够显著提升量化模型的精度， 但训练成本也会相应增加。

硬件支持: 并非所有硬件平台均能全面支持低精度计算。例如，FP8 和 FP16 计算通常需要特定硬件 (如 NVIDIA Hopper 架构 GPU) 的支持。若硬件平台缺乏对低精度计算的优化，量化技术的优势将难以充分发挥。 随着低精度计算的普及， 越来越多的硬件平台开始支持 FP16、 BF16 甚至 FP8 等低精度数据类型， 为量化技术的广泛应用提供了更坚实的硬件基础。

复杂性提升: 量化流程本身会增加模型开发的复杂性。例如，量化过程需要精细地计算缩放因子，并可能需要对模型进行额外的校准和微调。这无疑增加了模型开发和部署的难度。 为了降低量化部署的复杂性， 业界也涌现出许多自动化量化工具和平台， 例如 NVIDIA TensorRT、 Qualcomm AI Engine 等， 这些工具可以帮助开发者快速、便捷地将模型量化并部署到目标硬件平台。

应用场景: 量化技术并非在所有应用场景下皆适用。在对精度要求极高的任务中 (如科学计算、金融建模等)，量化可能导致无法接受的精度损失。 对于精度敏感型任务， 可以尝试采用混合精度量化策略， 对模型中不同层或不同参数采用不同的量化精度， 例如对关键层或参数仍保持 FP32 或 FP16 精度， 而对其他层或参数则采用 INT8 或更低精度量化， 以在精度和效率之间取得更好的平衡。

综上所述，量化技术作为深度学习领域的一项关键技术，在提升计算效率、降低存储需求和功耗等方面展现出巨大的潜力。然而，量化技术亦存在精度损失和硬件依赖性等局限性。因此，在实际应用中，需根据具体的应用需求和场景特点，审慎选择量化策略，以期在模型性能与效率之间达到最优平衡。 未来， 随着硬件和算法的不断发展， 量化技术将在深度学习领域扮演更加重要的角色， 推动人工智能应用在更广泛的场景中落地生根。