Токенизация

Всем привет, сегодня мы рассмотрим технику причастий в Large Language Modelling (LLM). К сожалению, разотождествление является более сложной и запутанной частью современных топовых LLM, но понимание некоторых его деталей очень необходимо, потому что многие люди винят нейронные сети или другие кажущиеся загадочными причины в некоторых недостатках LLM, когда на самом деле источником этих проблем часто являются техники разотождествления.
Оригинальный текст:https://github.com/karpathy/minbpe

Ранее: сегментация на основе символов

Так что же такое подтекст? На самом деле в нашем предыдущем видео [Создание GPT с нуляВ [ ] мы говорили о семафоре, но это всего лишь очень простая и примитивная форма уровня символов. Если вы обратитесь к этому видео из [Google colab], вы увидите, что мы используем наши обучающие данные ([произведения Шекспира], что в Python является просто очень длинной строкой:

Первый гражданин: Прежде чем мы продолжим, пожалуйста, выслушайте меня.
Давайте, говорите.
Первый гражданин: Вы все решили умереть, а не голодать?
Все: Решительно. Решительный.
Первый гражданин: Прежде всего, вы знаете, что Гай Марций - враг народа номер один.
Мы знаем, мы знаем.

Но как ввести последовательности символов в языковую модель? Первым шагом в этом направлении является создание словарной таблицы, которая включает в себя все различные символы, встречающиеся в обучающем наборе данных:

``python# Это единственный символ, который встречается в тексте chars = sorted(list(set(text)))vocab_size = len(chars)print(''.join(chars))print(vocab_size)
# !$&',-.3:;?ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz# 65 ```

Сразу после этого мы создадим таблицу поиска для преобразования между отдельными символами и целыми словами, основываясь на словаре, перечисленном выше. Эта таблица поиска фактически является словарем Python:

``` pythonstoi = { ch:i for i,ch in enumerate(chars) }itos = { i:ch for i,ch in enumerate(chars) }# Encoder: принимает строку и выдает список соответствующих целых чисел encode = lambda s: [stoi[c ] for c in s]# Декодер: принимает список целых чисел и сводит его к строкеdecode = lambda l: ''.join([itos[i] for i in l])
print(encode("hii there")) print(decode(encode("hii there")))
# [46, 47, 47, 1, 58, 46, 43, 56, 43]# хий там``.

После преобразования последовательностей в целые числа мы увидим, что каждое целое число используется в качестве индекса в двумерной обучаемой матрице встраивания. Поскольку размер словаря составляет `vocab_size=65`, эта матрица встраивания также имеет 65 строк:

``pythonclass BigramLanguageModel(nn.Module).
def __init__(self, vocab_size):super(). __init__()self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
def forward(self, idx, targets=None):tok_emb = self.token_embedding_table(idx) # (B,T,C) ```

Здесь "целое число" извлекает строку из таблицы встраивания, которая является вектором, представляющим лексему. Этот вектор затем подается в трансформатор как вход для соответствующего временного шага (Трансформатор).

Токенизация "блоков символов" с помощью алгоритма кодирования пар байт (BPE)

Этого достаточно для простейшей языковой модели на уровне символов. Однако на практике современные языковые модели используют более сложные схемы построения словарей разметки. Эти схемы работают не на уровне символов, а на уровне блоков символов. Эти словари символьных блоков строятся с помощью алгоритмов типа Byte Pair Encoding (BPE), о которых мы расскажем подробнее ниже.
Если обратиться к истории развития этого подхода, то опубликованный в 2019 году документ OpenAI GPT-2 под названием "Language Models as Unsupervised Multitasking Learners" сделал алгоритмы BPE на уровне байтов популярными в маркировке языковых моделей. Прочитайте раздел 2.2 этой работы "Представление входных данных", чтобы узнать об описании и мотивации этого алгоритма. Вы увидите их упоминание в конце этого раздела:

Словарный запас был расширен до 50 257. Мы также увеличили размер контекста с 512 до 1024 лексем и использовали больший размер партии - 512.

Напомним, что на уровне внимания трансформатора каждый токен является вниманием к конечному числу токенов в предыдущей последовательности. В статье упоминается, что длина контекста в модели GPT-2 составляет 1024 лексемы, что является улучшением по сравнению с 512 лексемами в GPT-1. Другими словами, токены - это базовые единицы, которые служат входом в модель лингвистической долговременной памяти (LLM). Токенизация - это процесс преобразования необработанных строк в Python в списки токенов и наоборот. Еще один популярный пример повсеместного использования этой абстракции: если вы посмотрите на [Ллама 2В статье], опять же, выполните поиск по слову "маркеры" и получите 63 упоминания. Например, в статье утверждается, что они обучались на двух триллионах лексем и так далее.
Прежде чем мы углубимся в детали реализации, давайте вкратце объясним, зачем нам нужно углубляться в процесс токенизации. Токенизация лежит в основе многих странностей в LLM, и я бы рекомендовал не относиться к ней легкомысленно. Многие проблемы, которые кажутся связанными со структурой нейронных сетей, на самом деле возникают из-за токенизации. Вот несколько примеров:

• Почему LLM не может правильно писать слова?
• Почему LLM не может выполнять простые задачи по работе со строками, например, переворот строки?
• Почему LLM плохо работает с неанглийскими языками (например, с японским)?
• Почему LLM плохо работает при выполнении простых арифметических операций?
• Почему GPT-2 испытывает дополнительные трудности с программированием на Python?
• Почему мой LLM внезапно перестает работать, когда встречает строку ""?
• Что это за странное предупреждение, которое я получаю о "пробелах в конце"?
• Когда я спрашиваю о "SolidGoldMagikarp", почему LLM падает?
• Почему я должен предпочесть использовать YAML, а не JSON для взаимодействия с LLM?
• Почему LLM на самом деле не является настоящей сквозной моделью языка?
• Что именно является первопричиной страданий?

Мы вернемся к этим темам в конце видео.
Далее давайте загрузим этот [Онлайн-инструменты для токенизации] Преимущество этого онлайн-инструмента в том, что процесс токенизации происходит в реальном времени в вашем веб-браузере. Вы можете легко ввести текстовую строку в поле ввода и сразу же увидеть результат токенизации с правой стороны. В верхней части страницы показано, что в настоящее время мы используемgpt2токенизатор, мы видим, что строка в примере разбивается на 300 лексем. Эти лексемы отображаются разными цветами:

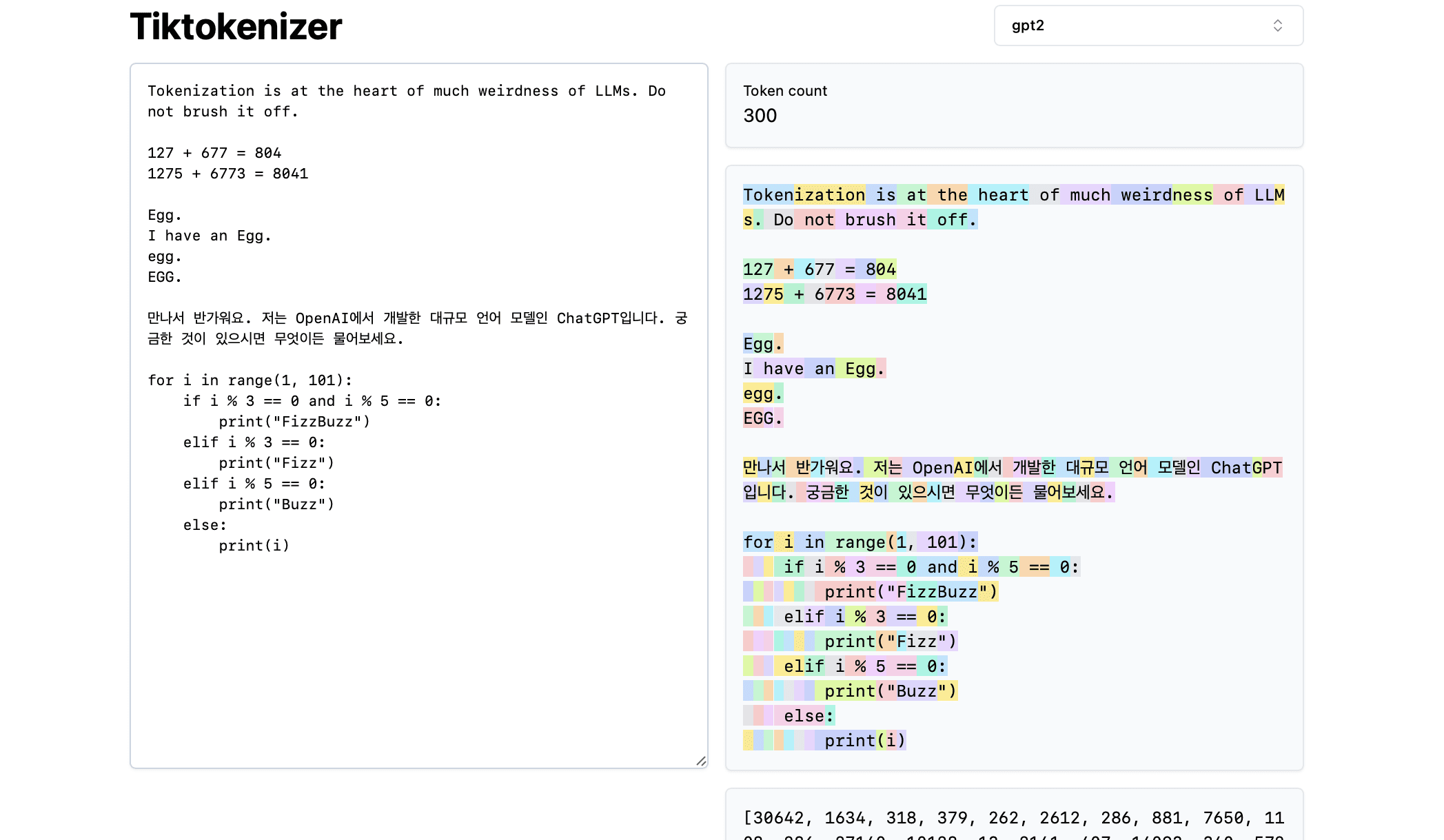
Например, строка "Tokenisation" кодируется как токен 30642, за которым следует токен 1634. индекс токена "is" (обратите внимание, что здесь три символа, включая предшествующий пробел, что очень важно!) ) индексируется как 318. Обратите внимание на пробел, так как он действительно присутствует в строке и должен быть токенизирован вместе со всеми остальными символами, но обычно опускается для визуальной наглядности. Вы можете переключить визуализацию пробелов в нижней части инструмента. Аналогично, лексема "at" равна 379, "the" - 262 и т. д.
Далее рассмотрим простой арифметический пример. Здесь мы видим, что числа могут разбиваться токенизатором непоследовательно. Например, число 127 разбивается на одну лексему, состоящую из трех символов, а число 677 разбивается на две лексемы: лексему " 6" (опять же, обратите внимание на пробел!) и лексема "77". Для понимания этой произвольности мы полагаемся на большие языковые модели. Модель должна узнать, как в своих параметрах, так и в процессе обучения, что эти две лексемы ("6" и "77") на самом деле объединяются и представляют число 677. Аналогично, если LLM хочет предсказать, что результатом сложения будет число 804, она должна вывести число в два этапа: сначала она выводит лексему "8", а затем лексему "04". Обратите внимание, что все эти разложения выглядят совершенно произвольными. В примере ниже мы видим, что 1275 разлагается на "12" и "75", 6773 на самом деле представляет собой две лексемы "6" и "773", а 8041 разлагается на "8" и "041".
(Продолжение следует...) (TODO: Если мы не найдем способ автоматически генерировать этот контент из видео, мы, вероятно, продолжим это).