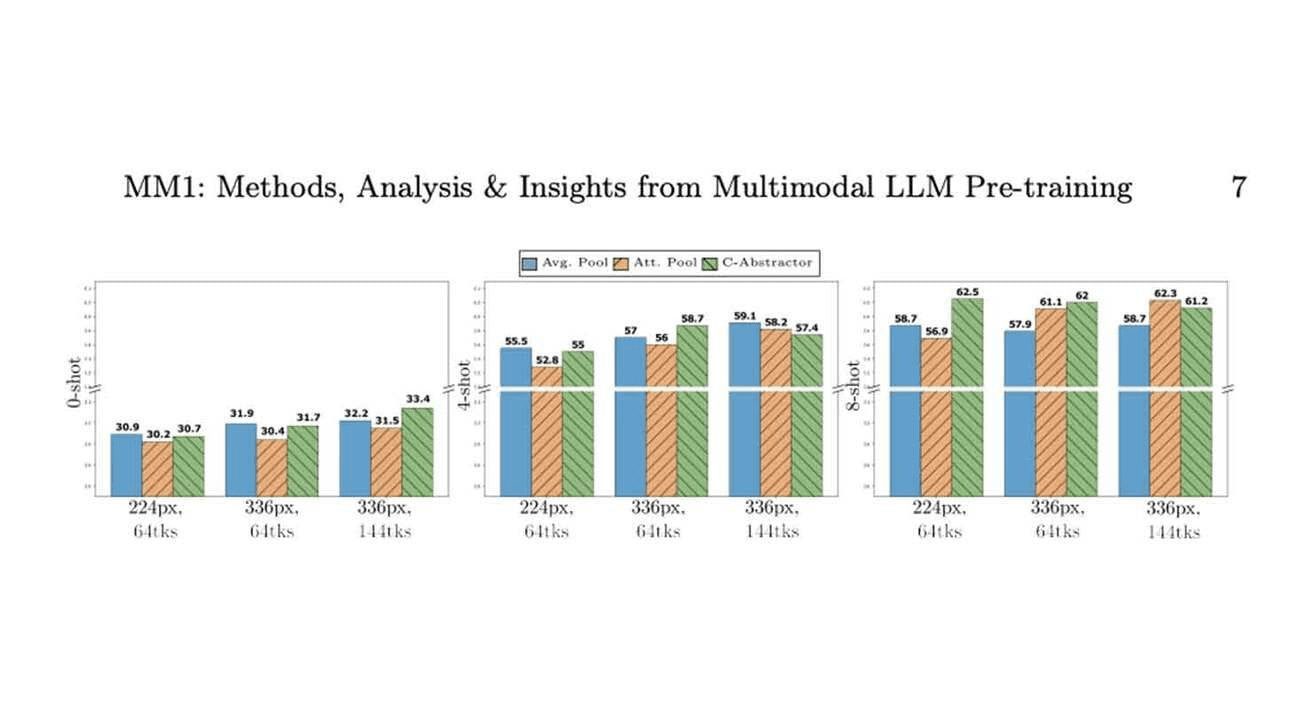
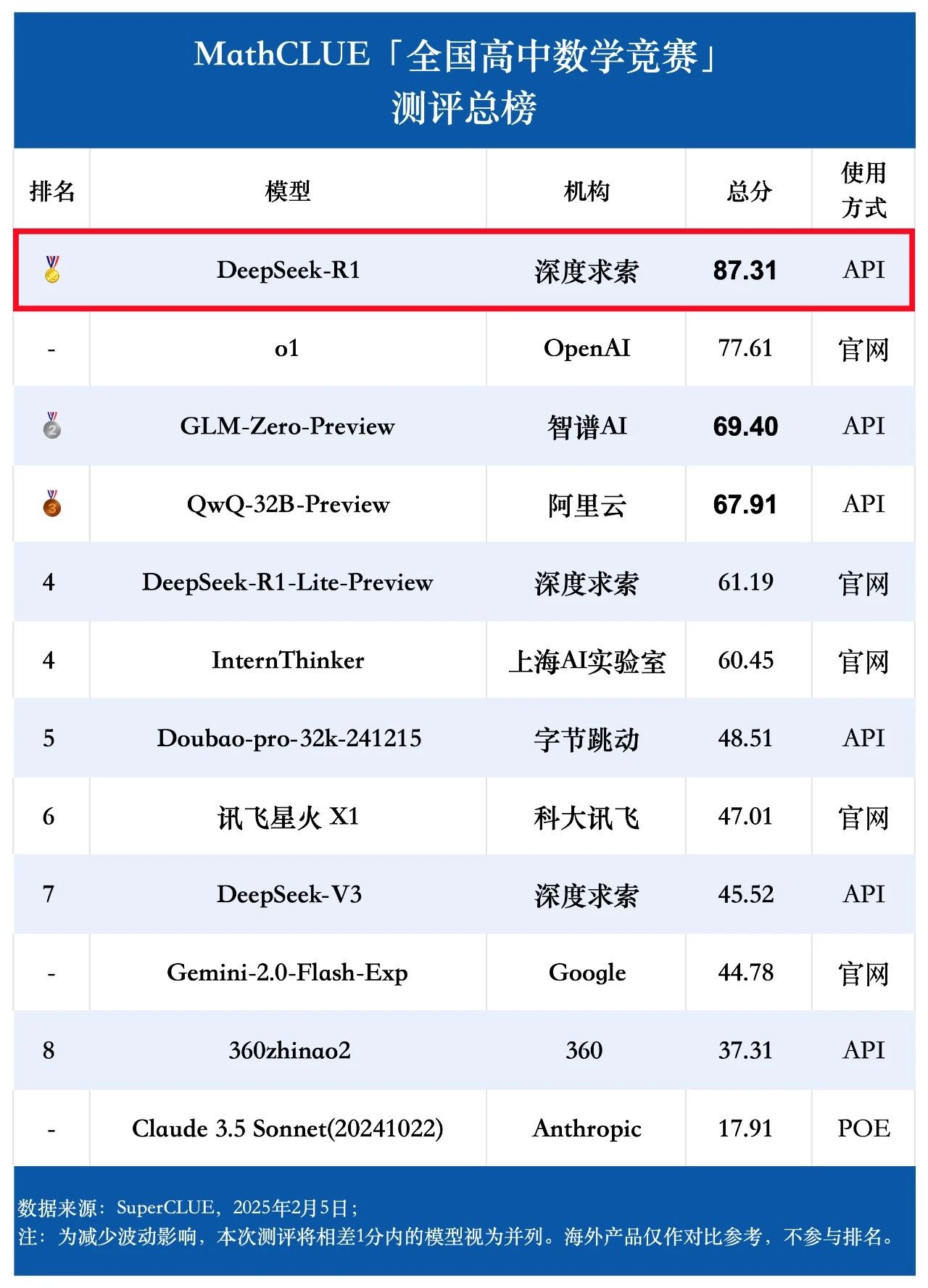
업그레이드된 클로드 3.5 소네트 중국어 벤치마크 평가가 공개되었습니다! 코드 능력은 GPT-4o를 능가하고, 고차 추론은 o1만큼 좋지 않습니다.
이 평가의 결과는 학술 연구용으로만 사용됩니다.
10월 22일, 앤트로픽은 업그레이드된 대형 모델 클로드 3.5 소넷과 새로운 모델 클로드 3.5 하이쿠를 공식 출시했습니다.
앤트로픽 관계자에 따르면 클로드 3.5 소네트는 모든 면에서 이전 버전보다 성능이 향상되었으며, 특히 스마트 바디 코딩 및 도구 사용 작업에서 성능이 크게 향상되었다고 합니다.SWE 벤치 검증에서 인코딩 성능은 33.41 TP3T에서 49.01 TP3T로 향상되어 OpenAI o1-preview를 포함한 모든 공개 모델보다 성능이 뛰어납니다.
또한, 앤트로픽은 획기적인 새 기능인 컴퓨터 사용 기능을 도입합니다. 개발자는 API를 통해 사람과 같은 방식으로 컴퓨터를 사용하도록 클라우드를 제어할 수 있지만, 이 기능은 현재 실험 단계에 있습니다.
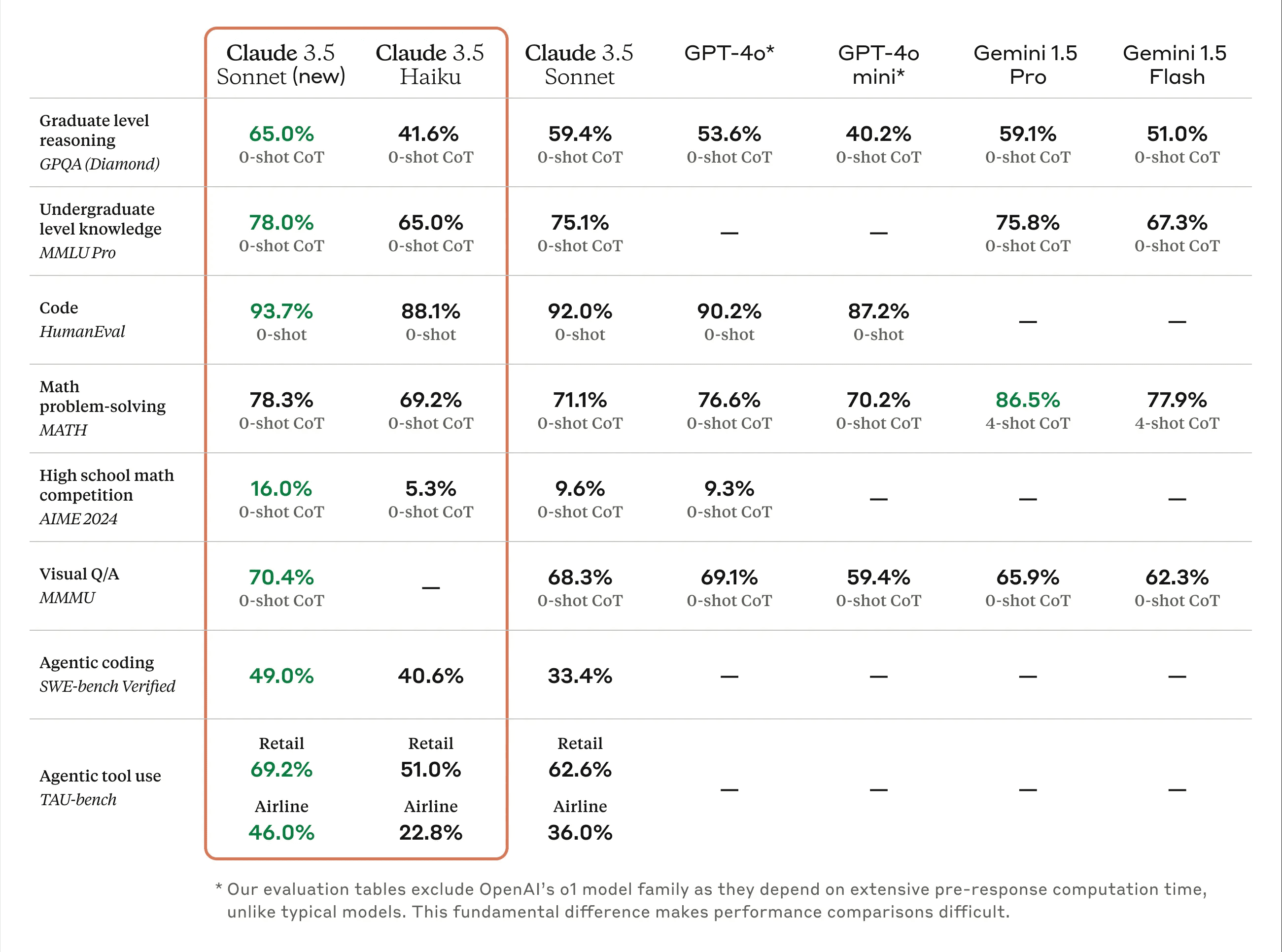
중국 시나리오의 추론 및 코드 측면에서 클로드 3.5 소네트 업그레이드의 성능에 대한 대중의 우려에 따라 전문 타사 평가 기관인 SuperCLUE에서 클로드 3.5 소네트 업그레이드에 대한 심층적인 평가를 실시했습니다.
평가 환경
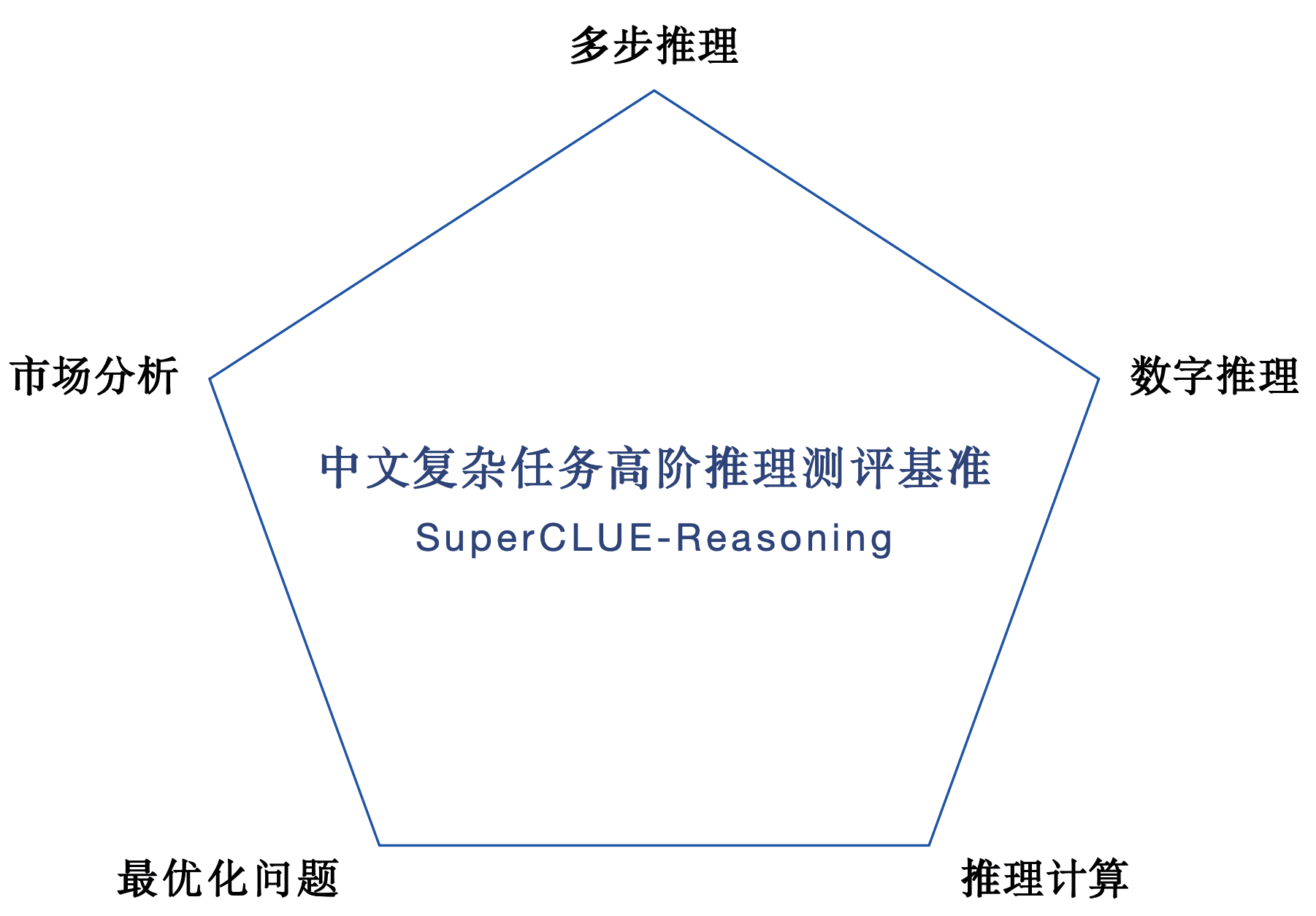
참조 표준: SuperCLUE-Reasoning 중국어 고차 추론 평가 벤치마크, SuperCLUE-Code3 중국어 코드 평가 벤치마크.
평가 모델 클로드 3.5 소네트(1022, POE 최신 모델 스냅샷)
모델 생성Config 구성:
- 클로드 세부 지침 문서를 참조하세요: https://www.anthropic.com/news/3-5-models-and-computer-use
에피소드 리뷰:
1.SuperCLUE-추리 중국어 고난도 추리 고난도 추리 복습 세트. 다단계 추론, 숫자 추론, 추론 계산, 시장 분석 및 최적화 문제 등 총 302개의 고난도 추론 과제 5문항이 포함되어 있습니다.
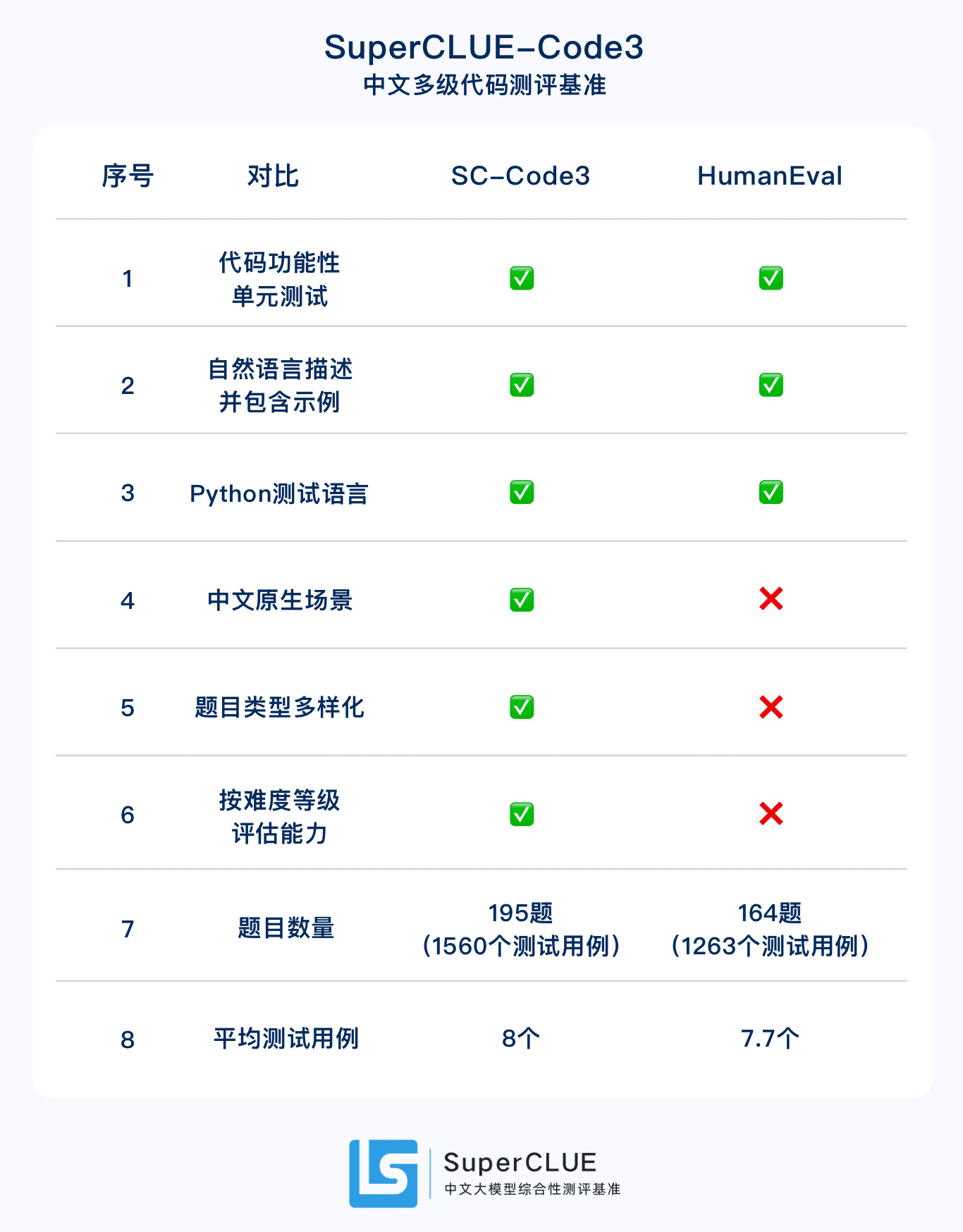
2. SuperCLUE-Code3 중국어 네이티브 코드 평가 세트.HumanEval의 중국어 업그레이드 버전으로, 1,560개의 테스트 사례를 포함한 총 195개의 문항이 기본, 중급, 고급 세 가지 난이도로 나뉘어 있습니다.
방법론::
1. 고차 추론: 각 추론 문항에 대해 수동 보정 및 확인을 거쳐 참조 답변과 추론 과정을 제공하고, 심판 모델은 정해진 평가 과정, 평가 기준 및 배점 규칙(1~5점)에 따라 후보 모델의 답변을 평가합니다. 설정된 평가 기준에는 기본 요건 준수, 추론의 정확성, 결론의 합리성 등이 포함됩니다.
2. 코드 SC-Code3: 기능 단위 테스트를 통해 코드 생성에서 중국 빅 모델의 핵심 기능을 평가하고 향상하도록 특별히 설계되었습니다.
SuperCLUE-Code3: 중국어 원어민 수준의 코드 숙련도 벤치마크
결론부터 말씀드리겠습니다.
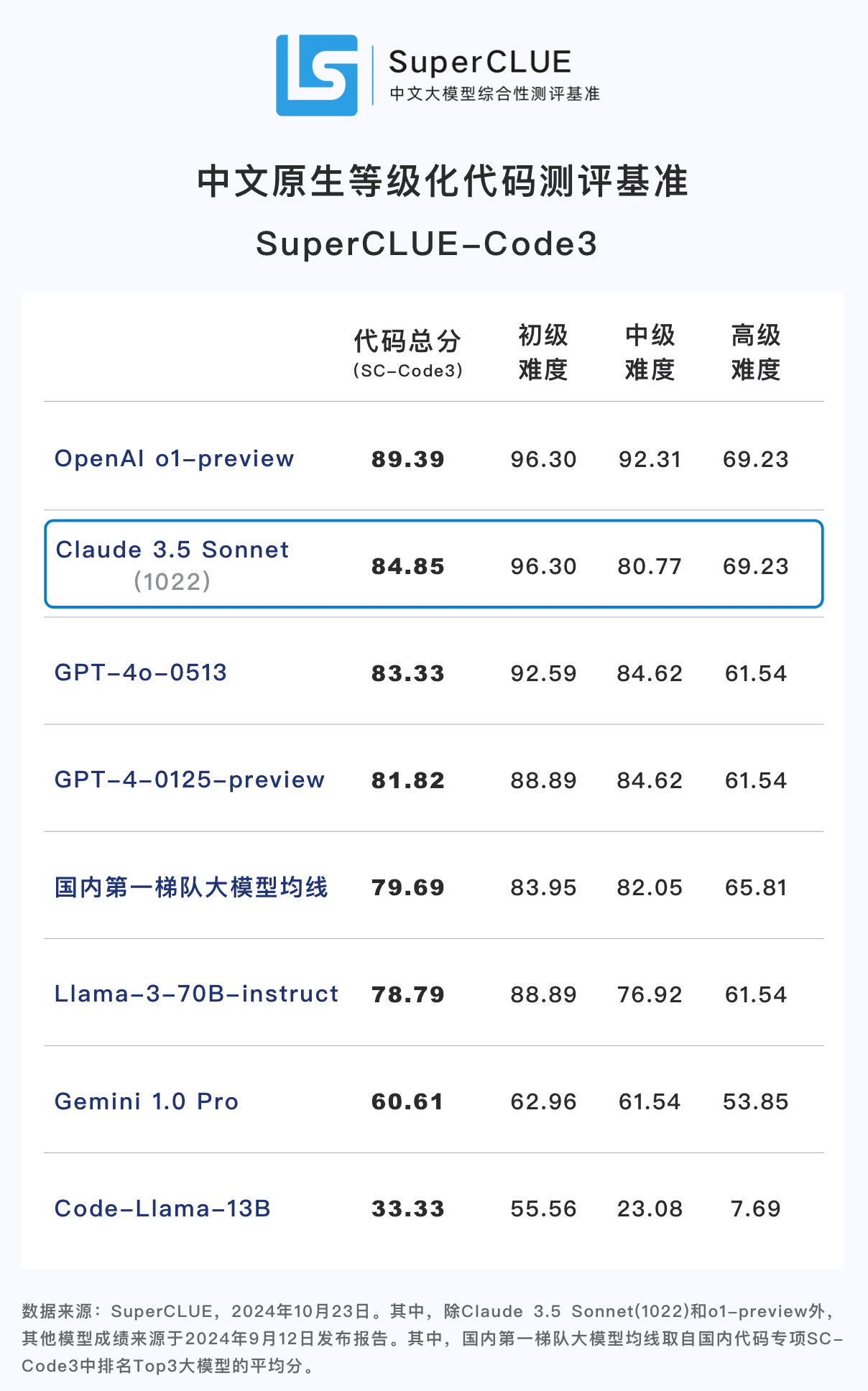
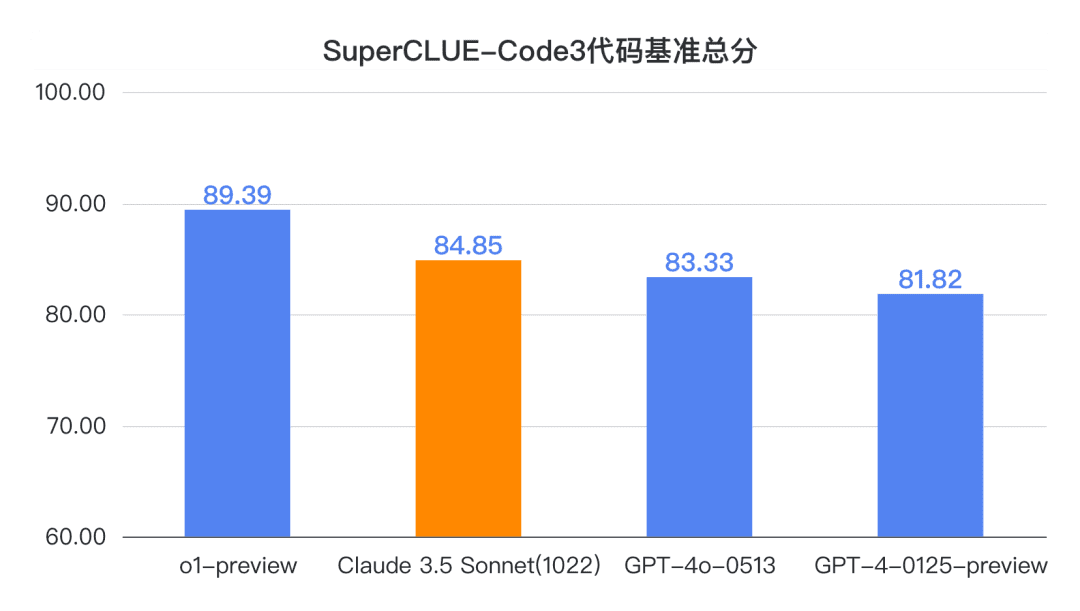
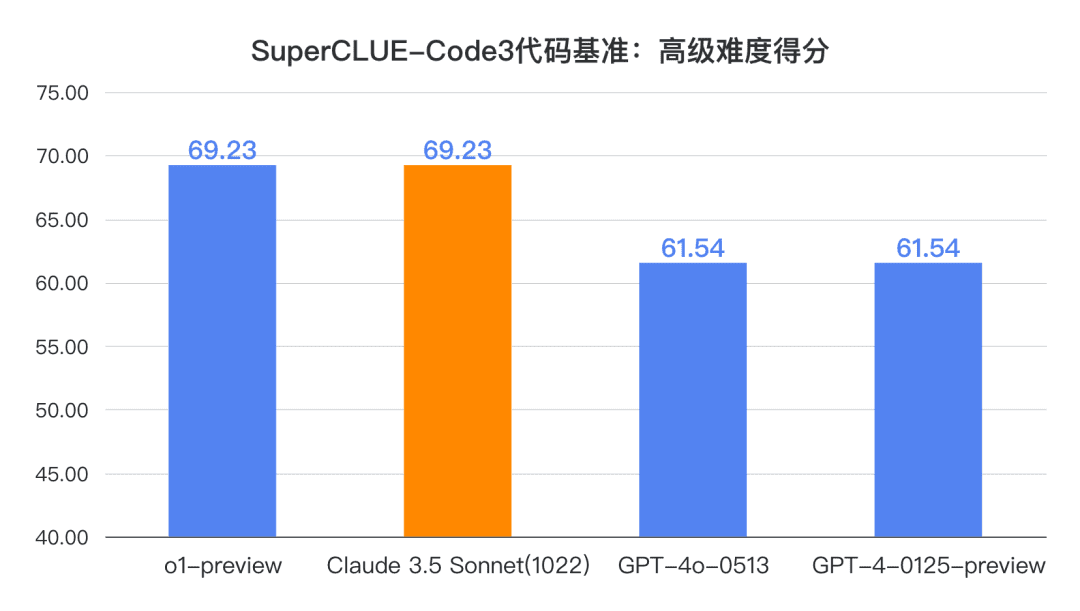
결론 1: 클로드 3.5 소네트(1022)는 중국어 코드 기능(SC-Code3) 측면에서 우수한 성능을 발휘합니다. 총 점수는 84.85점으로 GPT-4o-0513보다 1.52점 높았습니다. 보다 4.54점 낮은 점수입니다. 특히 고급 코드 작업에서 69.23점을 기록하여 o1-preview와 동점을 기록하는 등 놀라운 성과를 거두었습니다.
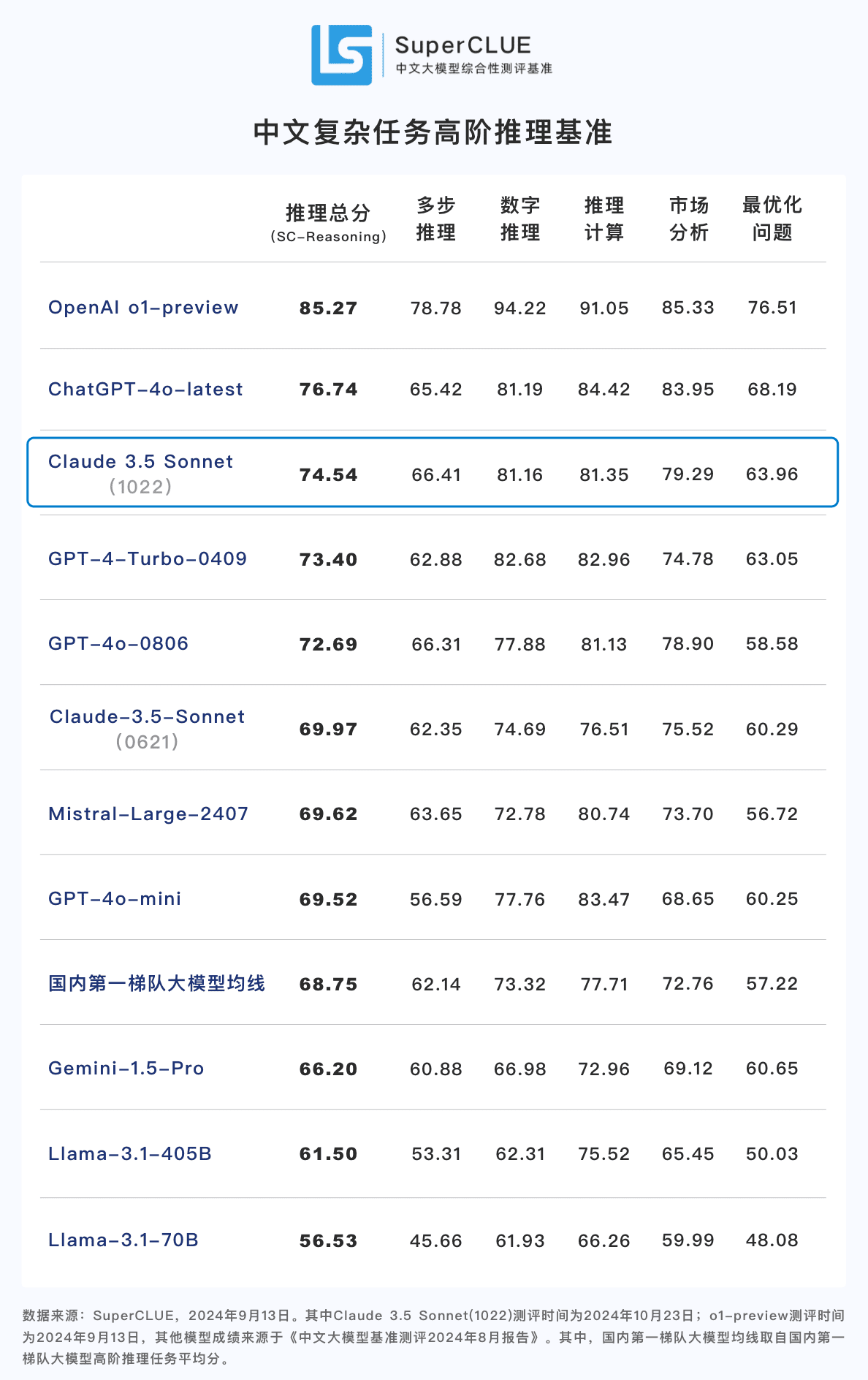
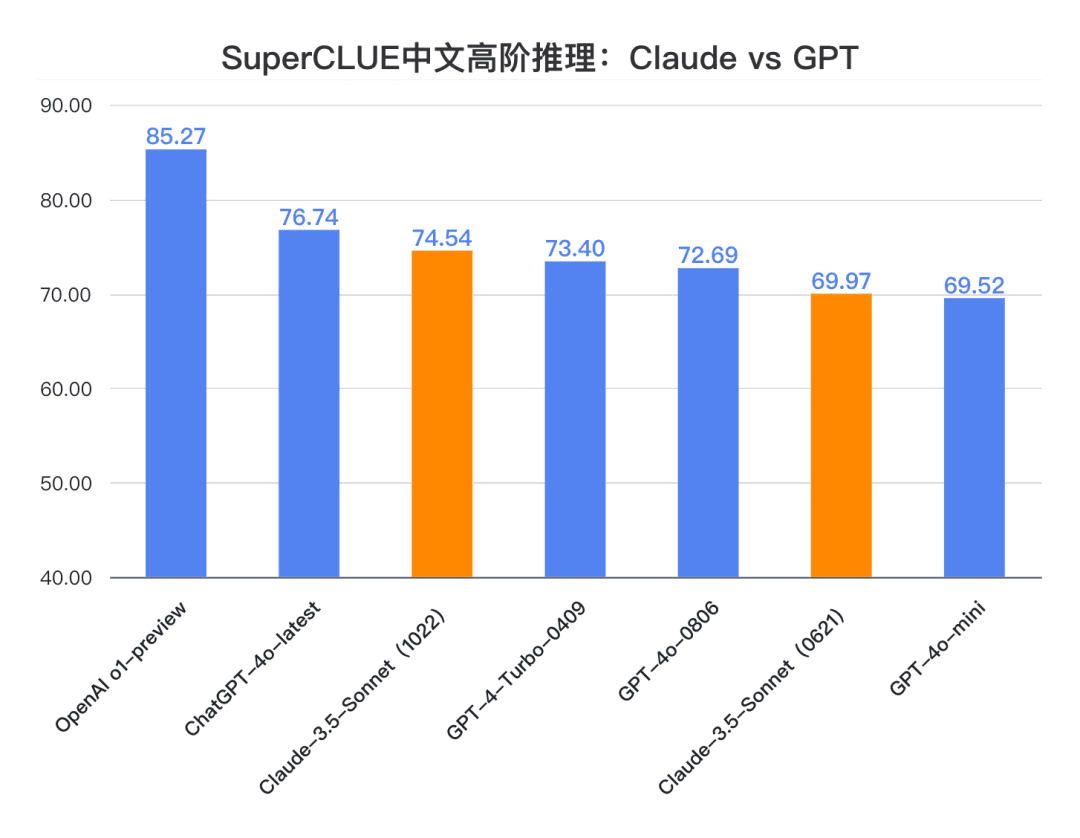
결론 2: 클로드 3.5 소네트(1022)는 중국어 고차 추론 과제에서 74.54점을 받았습니다. o1-프리뷰(-10.73점)에 비해 큰 격차로 ChatGPT-4o 최신 버전과 비슷합니다. . 그 중에서도 다단계 추론 능력은 상대적으로 뛰어나 최신 ChatGPT-4o를 능가하는 성능을 보입니다.
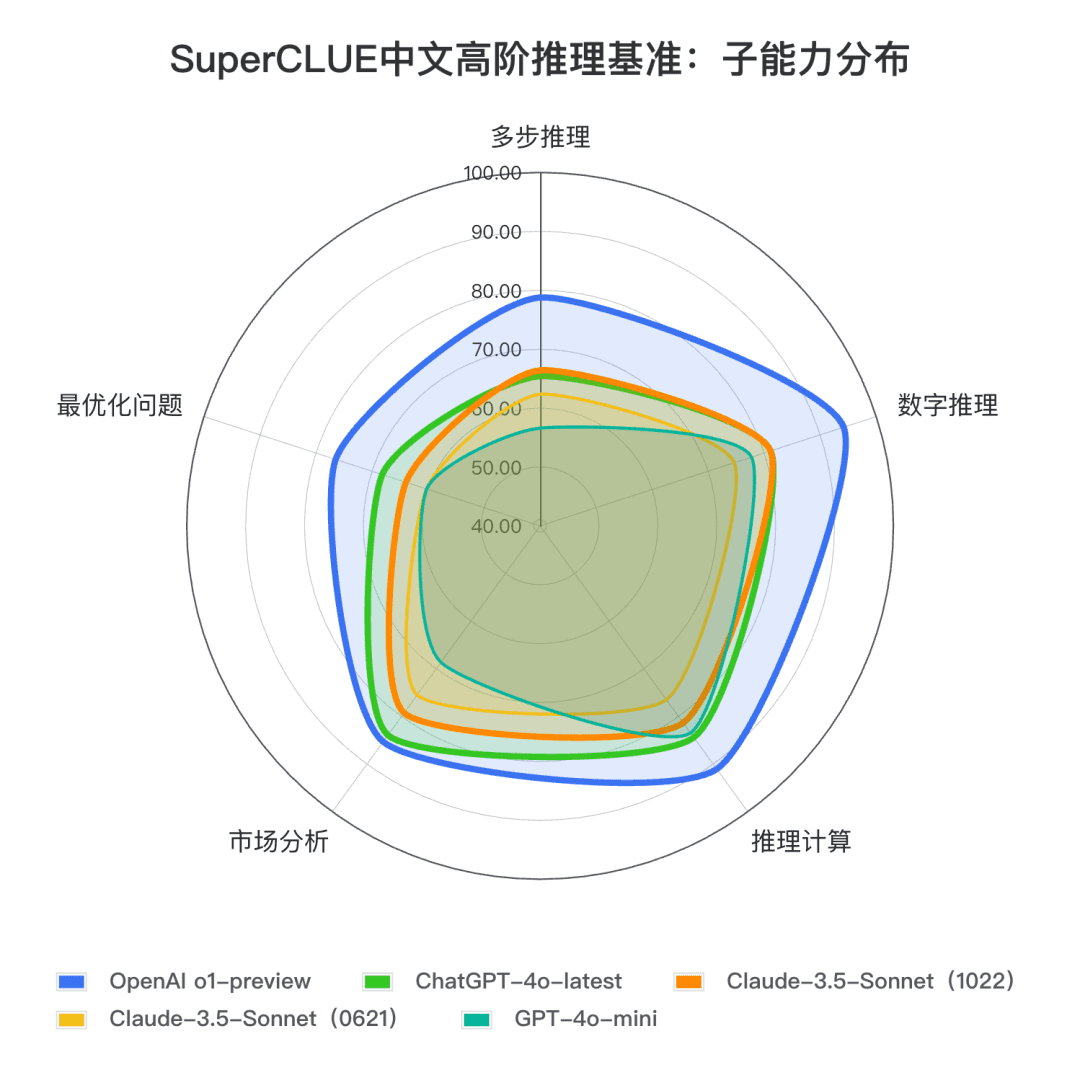
**결론 3:** 이전 버전인 클로드 3.5 소네트(0621)와 비교. 클로드 3.5 소네트(1022) 추론 과제에서 4.57점 향상 그리고 수치 추론과 계산 추론과 같은 보조 과제에서 상당한 진전을 이루었습니다.
평가 결과
비교 분석
코드 측정 예시
예제 1
프롬프트.
from typing import List
def longest_peak_sequence(nums: List[int]) -> int:
"""
在一个整数数组中找出最长的"峰"序列的长度。
所谓"峰"序列,是指先严格递增然后严格递减的序列,且峰顶(即最大值)唯一。
至少包括三个数以上才能构成一个"峰"序列(即包含递增和递减的部分)。
返回数组中最长"峰"序列的长度。如果没有"峰"序列,则返回0。
示例:
>>> longest_peak_sequence([2, 1, 4, 7, 3, 2, 5])
5 # 最长的"峰"序列是 [1, 4, 7, 3, 2]
>>> longest_peak_sequence([5, 4, 3, 2, 1])
0 # 不存在"峰"序列,因为没有严格递增的部分
提示:
- 数组 `nums` 的长度范围为 [0, 10000]。
- 数组中的每个元素范围为 [-10000, 10000]。
"""
클로드 3.5 소네트 (1022) 답변.
from typing import List
def longest_peak_sequence(nums: List[int]) -> int:
if len(nums) < 3:
return 0
max_length = 0
# 从第二个元素遍历到倒数第二个元素
for i in range(1, len(nums) - 1):
# 检查当前位置是否是峰顶
if nums[i] > nums[i-1] and nums[i] > nums[i+1]:
# 找到一个峰顶,向两边扩展
left = i - 1
right = i + 1
# 向左扩展,寻找严格递增序列
while left > 0 and nums[left-1] < nums[left]:
left -= 1
# 向右扩展,寻找严格递减序列
while right < len(nums) - 1 and nums[right+1] < nums[right]:
right += 1
# 更新最长峰序列长度
current_length = right - left + 1
max_length = max(max_length, current_length)
return max_length
테스트 케이스.
def check(candidate):
assert candidate( [1, 2, 3, 4, 5, 6])==0
assert candidate([1, 3, 5, 6, 4, 2, 0])==7
assert candidate( [5, 4, 3, 2, 1, 2, 3, 4, 1])==5
assert candidate([1, 3, 5, 3, 1])==5
assert candidate([1, 2, 3, 3, 2, 1])==0
assert candidate([2, 1, 3, 1, 2, 1, 3])==3
assert candidate([1, 3, 5, 4, 3, 2, 1])==7
if_passed**(채택 여부):**채택되었습니다.
예 2
프롬프트.
from typing import List
def longest_increasing_path(matrix: List[List[int]]) -> int:
"""
给定一个整数矩阵,找到最长严格递增路径的长度。
路径被定义为从矩阵中的任意单元格开始,每次可以向上、下、左、右移动到相邻的单元格上,如果递增的话。
你不能在路径中移动到矩阵外面,也不能移动到不满足递增条件的单元格上。
路径的长度是路径上的单元格总数。
示例:
>>> longest_increasing_path([
[9, 9, 4],
[6, 6, 8],
[2, 1, 1]
])
4 # 最长递增路径是 [1, 2, 6, 9]
>>> longest_increasing_path([
[3, 4, 5],
[3, 2, 6],
[2, 2, 1]
])
4 # 最长递增路径是 [3, 4, 5, 6]或 [2, 4, 5, 6]
提示:
- 矩阵 `matrix` 的维度为 m x n。
- 矩阵 `matrix` 的每个元素是一个非负整数。
"""
클로드 3.5 소네트 (1022) 답변.
from typing import List
def longest_increasing_path(matrix: List[List[int]]) -> int:
if not matrix or not matrix[0]:
return 0
m, n = len(matrix), len(matrix[0])
# 缓存,用于存储每个位置的最长递增路径长度
cache = [[0] * n for _ in range(m)]
def dfs(i: int, j: int) -> int:
# 如果已经计算过,直接返回缓存结果
if cache[i][j] != 0:
return cache[i][j]
# 四个方向:上、下、左、右
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
# 当前位置的最长路径至少为1
max_length = 1
# 遍历四个方向
for di, dj in directions:
ni, nj = i + di, j + dj
# 检查是否在矩阵范围内且满足递增条件
if (0 <= ni < m and 0 <= nj < n and
matrix[ni][nj] > matrix[i][j]):
# 递归计算邻居位置的最长路径
curr_length = 1 + dfs(ni, nj)
max_length = max(max_length, curr_length)
# 存入缓存
cache[i][j] = max_length
return max_length
# 遍历矩阵中的每个位置,找到最长路径
result = 0
for i in range(m):
for j in range(n):
result = max(result, dfs(i, j))
return result
테스트 케이스.
def check(candidate):
assert candidate([[1, 1], [1, 1]]) == 1
assert candidate([
[9, 9, 4],
[6, 6, 8],
[2, 1, 1]
]) == 4
assert candidate([
[3, 4, 5],
[3, 2, 6],
[2, 2, 1]
]) == 4
assert candidate([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
]) == 7
assert candidate([
[-1, -2, -3, 0],
[5, -6, 7, -8],
[-9, 0, -11, -12],
[13, 0, 15, -16]
]) == 4
assert candidate([
[5, 10, 6, 7, 9],
[6, 10, 2, 2, 3],
[4, 9, 8, 2, 8],
[3, 3, 3, 8, 8]
])==4
assert candidate([
[1, 3, 1, 4],
[1, 5, 1, 7],
[4, 2, 1, 1],
[1, 3, 2, 1]
])==3
assert candidate([
[1, 9, 2, 4],
[9, 6, 5, 3],
])==4
if_passed(채택 여부):채택되었습니다.
고차 추론의 예
예 1: 다단계 추론
ask
회사에는 A, B, C, D, E, F, G라는 7명의 직원이 있는데, 회사는 등급 매기기 행사를 열고 직원들의 성적과 다음 조건을 바탕으로 각 직원의 정확한 순위를 추론합니다:
- A는 B보다 점수가 높지만 C보다 낮습니다.
- D는 E와 G보다는 점수가 높지만 A보다는 낮습니다.
- G가 가장 낮은 점수를 받았습니다.
- B는 E와 F보다 점수가 높습니다.
- F는 E보다 높은 점수입니다.
- C가 가장 높은 점수를 받았습니다.
- 직원마다 점수가 다르며, 가장 중앙에 D가 있습니다.
위의 조건에 따라 각 직원의 구체적인 점수를 유추해 주세요.
클로드 3.5 소네트 (1022) 답장합니다:
논리적 분석을 통해 각 직원의 순위를 추정해 보겠습니다:
- 조건 3에서 알 수 있음: G가 최하위(7위)에 있음
- 조건 6에서 알 수 있음: C가 최상위(1위)에 있습니다.
- 조건 7에서 알 수 있음: D는 4위(중간 위치)입니다.
- 조건 2에서 D가 E와 G보다 높지만 A보다 낮다는 것을 알 수 있습니다:
- E는 D(5위 또는 6위) 다음 순위여야 합니다.
- A는 D(2위 또는 3위)보다 먼저 순위가 매겨져야 합니다.
- 조건 1에서 A가 B보다 높지만 C보다 낮다는 것을 알았으므로 이를 이전 분석과 결합합니다:
- A열 2위
- B는 3위를 차지해야 합니다.
- 조건 4와 5에서 B가 E와 F보다 높고, F가 E보다 높다는 것을 알 수 있습니다:
- F열 5위
- E 6위
최종 순위는 다음과 같습니다:
- C(1위)
- A(2위)
- B(3위)
- D (4위)
- F(5위)
- E (6위)
- G (7위)
자세한 추론 과정을 보여드릴까요?
예 2: 최적화 문제
ask
한 도시에 5개의 주요 교통 허브가 있고 도시 계획 부서에서 각 허브가 적어도 하나의 노선으로 연결되도록 버스 노선 범위를 최적화하려고 합니다. 허브 간의 건설 비용을 알고 있으며 최소한의 비용으로 모든 허브를 연결하는 것이 목표입니다.
데이터:
- 허브 간 연결 비용(백만 달러)
- 허브 1 및 허브 2: $100,000
- 허브 1 및 허브 3: $150,000
- 허브 2 및 허브 4: $200,000
- 허브 3 및 허브 4: $250,000
- 허브 3 및 허브 5: $300,000
- 허브 4 및 허브 5: $180,000
목표: 총 구축 비용을 최소화하고 모든 허브가 상호 연결되도록 하기 위해 어떤 허브를 서로 연결해야 하는지 결정합니다.
클로드 3.5 소네트 (1022) 답장합니다:
이것은 최소 스패닝 트리 문제이며 Kruskal의 알고리즘을 사용하여 해결하겠습니다. 단계별로 분석해 보겠습니다:
- 먼저, 모든 연결을 가장 작은 비용부터 가장 큰 비용 순으로 정렬합니다:
- 허브 1-2: $100,000
- 허브 1-3: $150,000
- 허브 4-5: $180,000
- 허브 2-4: $200,000
- 허브 3-4: $250,000
- 허브 3-5: $300,000
- 링 형성을 피하기 위해 가장 낮은 비용의 연결이 선택됩니다:
- 허브 1-2 선택($100,000)
- 허브 1-3 선택($150,000)
- 허브 4-5 선택(180,000달러)
- 허브 2-4 선택($200,000)
최적의 프로그램:
- 허브 1과 허브 2 연결
- 허브 1과 허브 3 연결
- 허브 4와 허브 5 연결
- 허브 2와 허브 4 연결
총 비용: 10 + 15 + 18 + 20 = $630,000
이 프로그램은 이를 보장합니다:
- 모든 허브가 연결됨
- 루프가 형성되지 않음
- 최소 총 소유 비용
이 솔루션의 비주얼라이제이션을 생성해 드릴까요?
# 커뮤니티 가입
더 자세한 클로드 3.5 최신 빅 모델 리뷰 내용을 보려면 SuperCLUE- 클로드 교환 그룹에 가입하세요.
© 저작권 정책
기사 저작권 AI 공유 서클 모두 무단 복제하지 마세요.
관련 문서

댓글 없음...