Вышел обновленный Claude 3.5 Sonnet Chinese benchmark evaluation! Кодовые способности превышают GPT-4o, рассуждения высшего порядка не так хороши, как o1

Результаты этой оценки будут использованы только для академических исследований.

22 октября компания Anthropic официально представила обновленную большую модель Claude 3.5 Sonnet, а также новую модель Claude 3.5 Haiku.

Клод

По словам представителей Anthropic, Claude 3.5 Sonnet превосходит предыдущую версию по всем параметрам, причем значительный прирост производительности наблюдается, в частности, в задачах кодирования "умного тела" и использования инструментов.На SWE-bench Verified производительность кодирования повысилась с 33,41 TP3T до 49,01 TP3T, опередив все общедоступные модели, включая OpenAI o1-preview.

Anthropic также представляет новую революционную функцию: использование компьютера. Разработчики могут управлять Клодом, чтобы он пользовался компьютером так же, как и человек, через API, но пока эта функция находится на стадии эксперимента.

В ответ на обеспокоенность общественности по поводу производительности обновления Claude 3.5 Sonnet с точки зрения рассуждений и кода в китайских сценариях, SuperCLUE, профессиональная сторонняя организация по оценке, провела углубленную оценку обновления Claude 3.5 Sonnet.

среда оценки

Эталоны: SuperCLUE-Reasoning Chinese Higher Order Reasoning Assessment Benchmark, SuperCLUE-Code3 Chinese Code Assessment Benchmark.

Модели оценки : Claude 3.5 Sonnet (1022, POE последняя модель)

Конфигурация Model GenerationConfig:

• См. документ с подробными инструкциями Claude: https://www.anthropic.com/news/3-5-models-and-computer-use.

Обзорный эпизод:

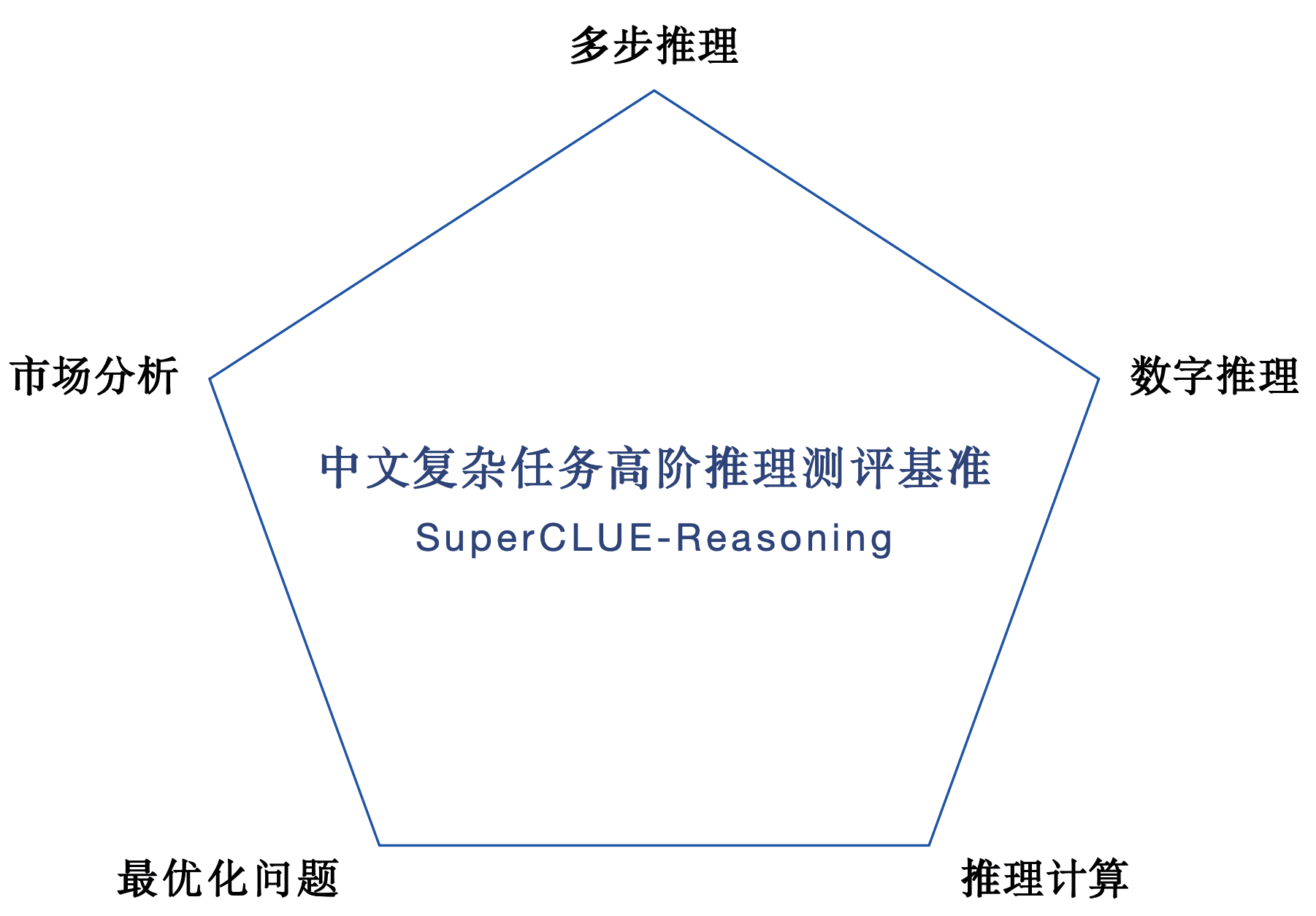
1.SuperCLUE-Reasoning Chinese Complex Tasks Higher Order Reasoning Review Set. Всего 302 вопроса, включая многоступенчатые рассуждения, числовые рассуждения, рассуждения-расчеты, анализ рынка и оптимизационные задачи, пять сложных задач на рассуждение.

2.Набор для оценки китайского родного кода SuperCLUE-Code3. Обновленная версия HumanEval на китайском языке, всего 195 вопросов, включая 1560 тестовых примеров, разделенных на начальную, среднюю и продвинутую три категории уровня сложности.

Методология::

1. рассуждения высшего порядка: для каждого вопроса мы предоставляем эталонные ответы и процессы рассуждений после ручной калибровки и проверки; затем судейская модель оценивает ответы моделей-кандидатов в соответствии с установленным процессом оценки, критериями оценки и правилами подсчета баллов (1-5 баллов). Установленные критерии оценки включают: соответствие основным требованиям, точность рассуждений и обоснованность выводов.

2. Code SC-Code3: специально разработан для оценки и расширения основных возможностей Китайской Большой Модели в генерации кода с помощью функционального модульного тестирования.

SuperCLUE-Code3: контрольные показатели уровня владения кодом для китайских аборигенов

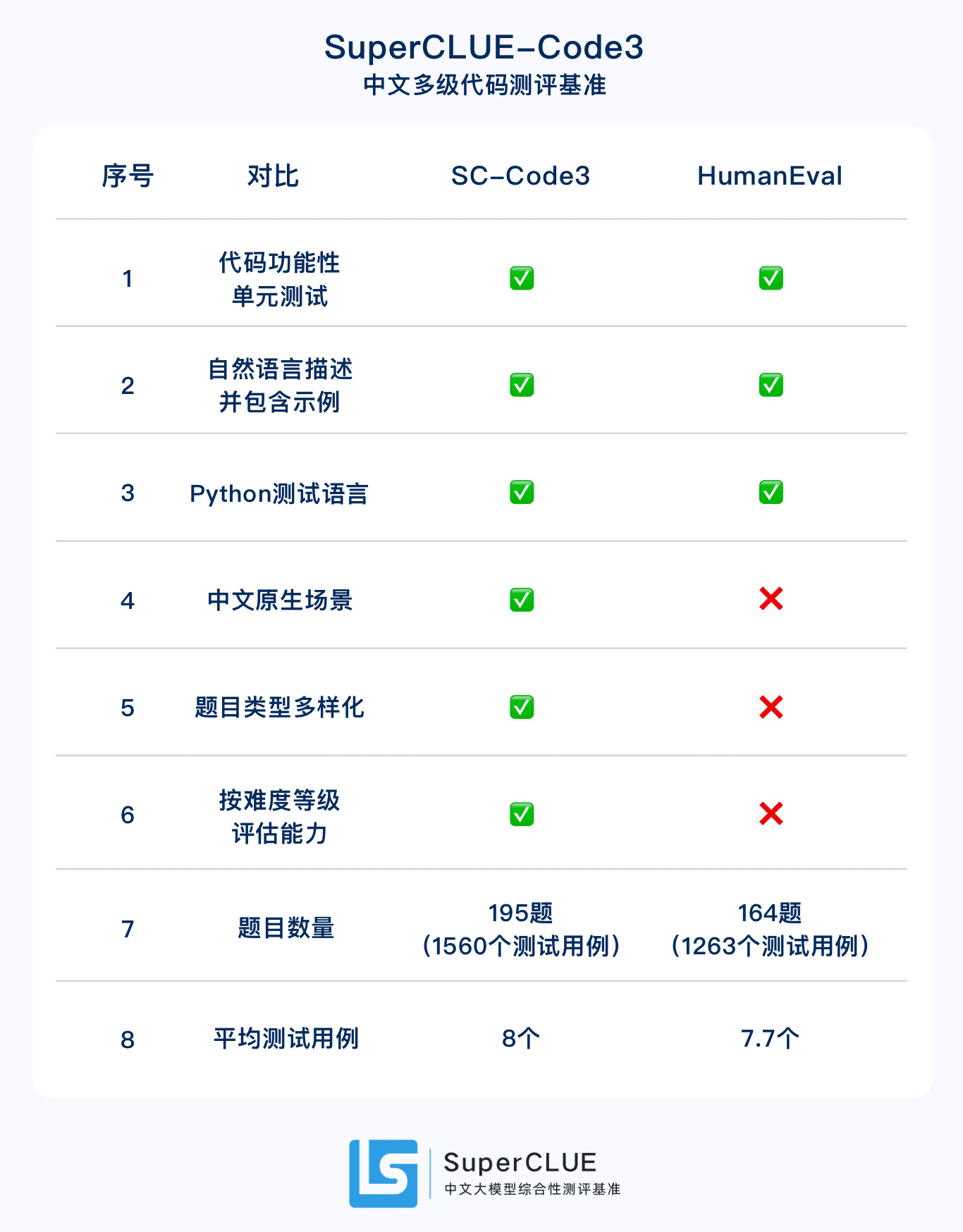
Давайте начнем с выводов.

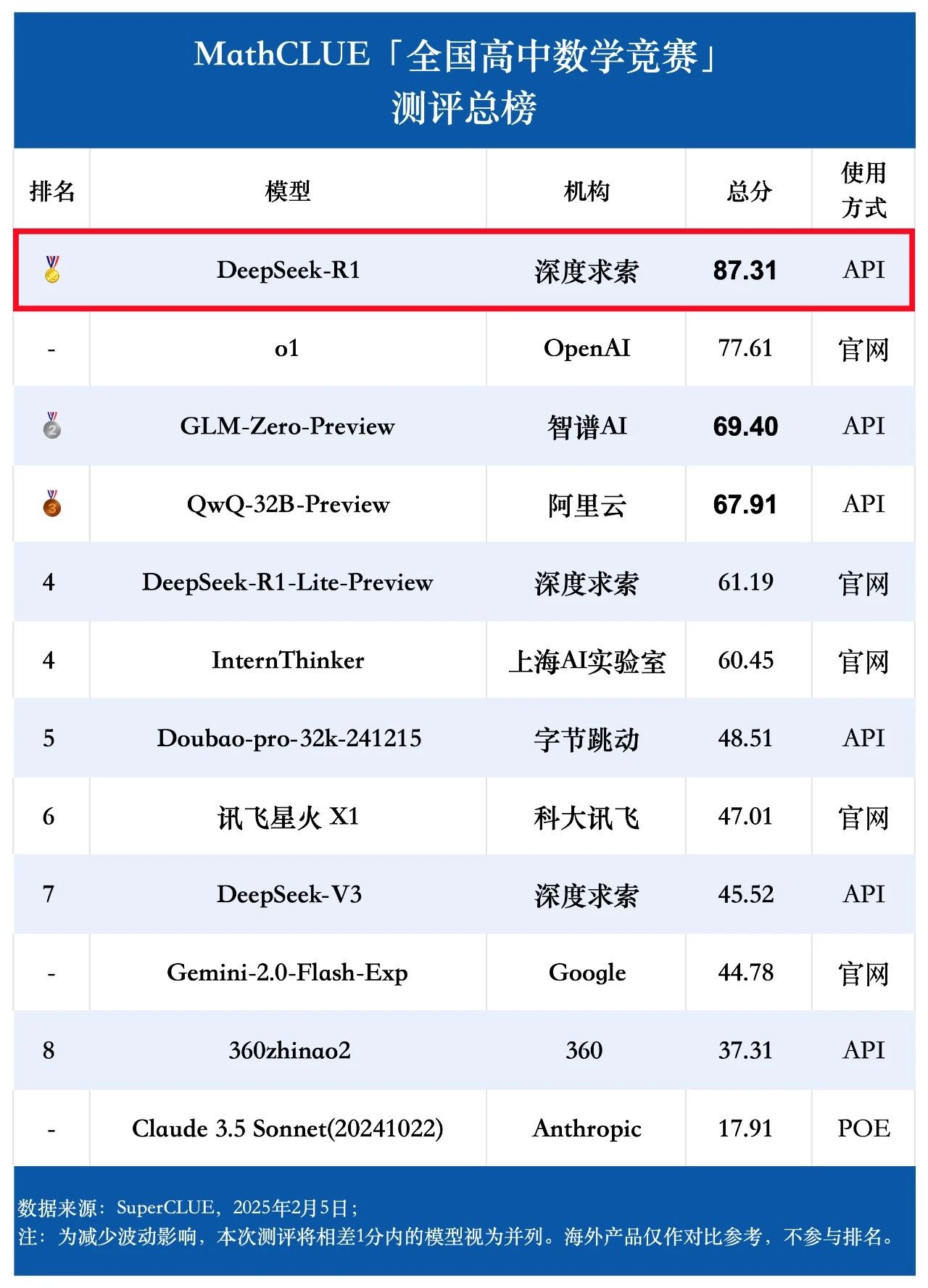
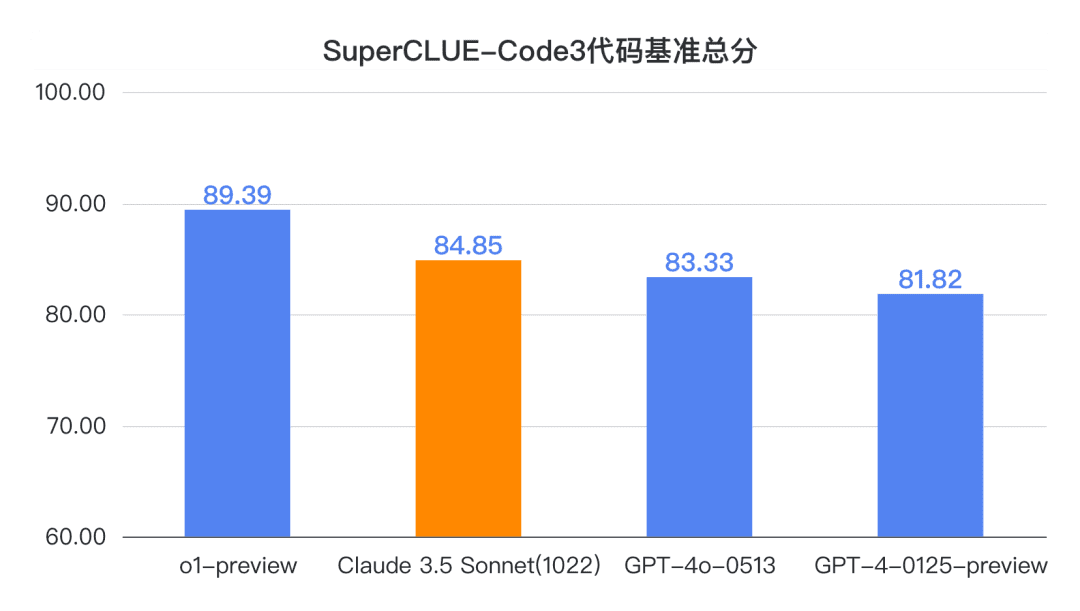
Вывод 1: Клод 3.5 Сонет (1022) демонстрирует хорошие результаты с точки зрения возможности использования китайского кода (SC-Code3). Общий балл достиг 84,85, что на 1,52 балла выше, чем у GPT-4o-0513. что на 4,54 балла ниже, чем у o1-preview. В частности, он показал потрясающие результаты в заданиях с расширенным кодом, набрав 69,23 балла, сравнявшись с o1-preview.

Заключение 2: Клод 3.5 Сонет (1022) набрал 74,54 балла в китайском задании "Рассуждения высшего порядка". Близко к ChatGPT-4o-latest, с большим отрывом от o1-preview (-10,73 балла) . Среди них можно выделить способность к многоступенчатому рассуждению, которая превосходит показатели ChatGPT-4o-latest.

**Вывод 3:** По сравнению с предыдущей версией Claude 3.5 Sonnet (0621). Клод 3.5 Сонет (1022) улучшил свои результаты на 4,57 балла в задании на рассуждение и значительный прогресс во вторичных заданиях, таких как числовые рассуждения и вычислительные рассуждения.

Результаты оценки

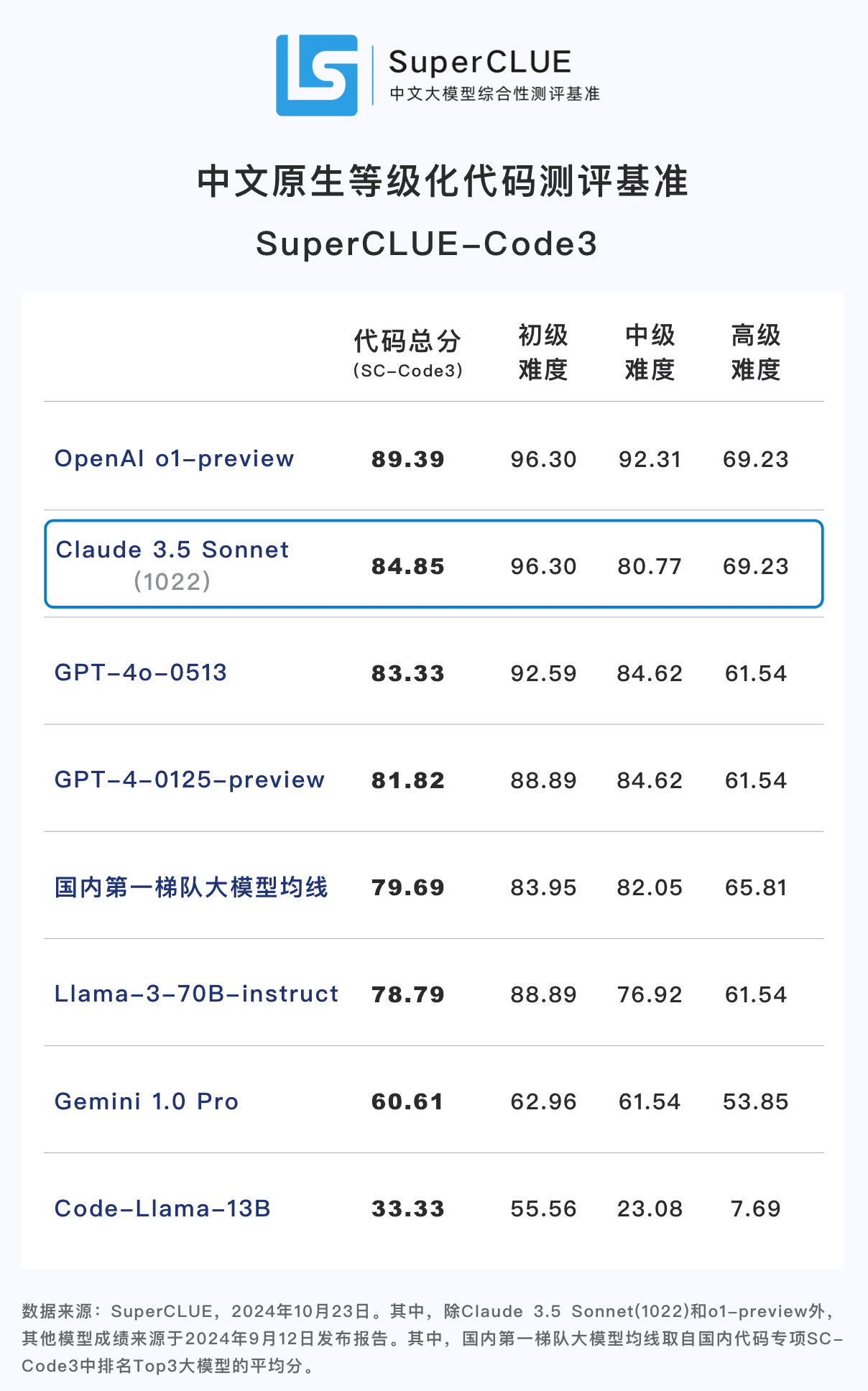
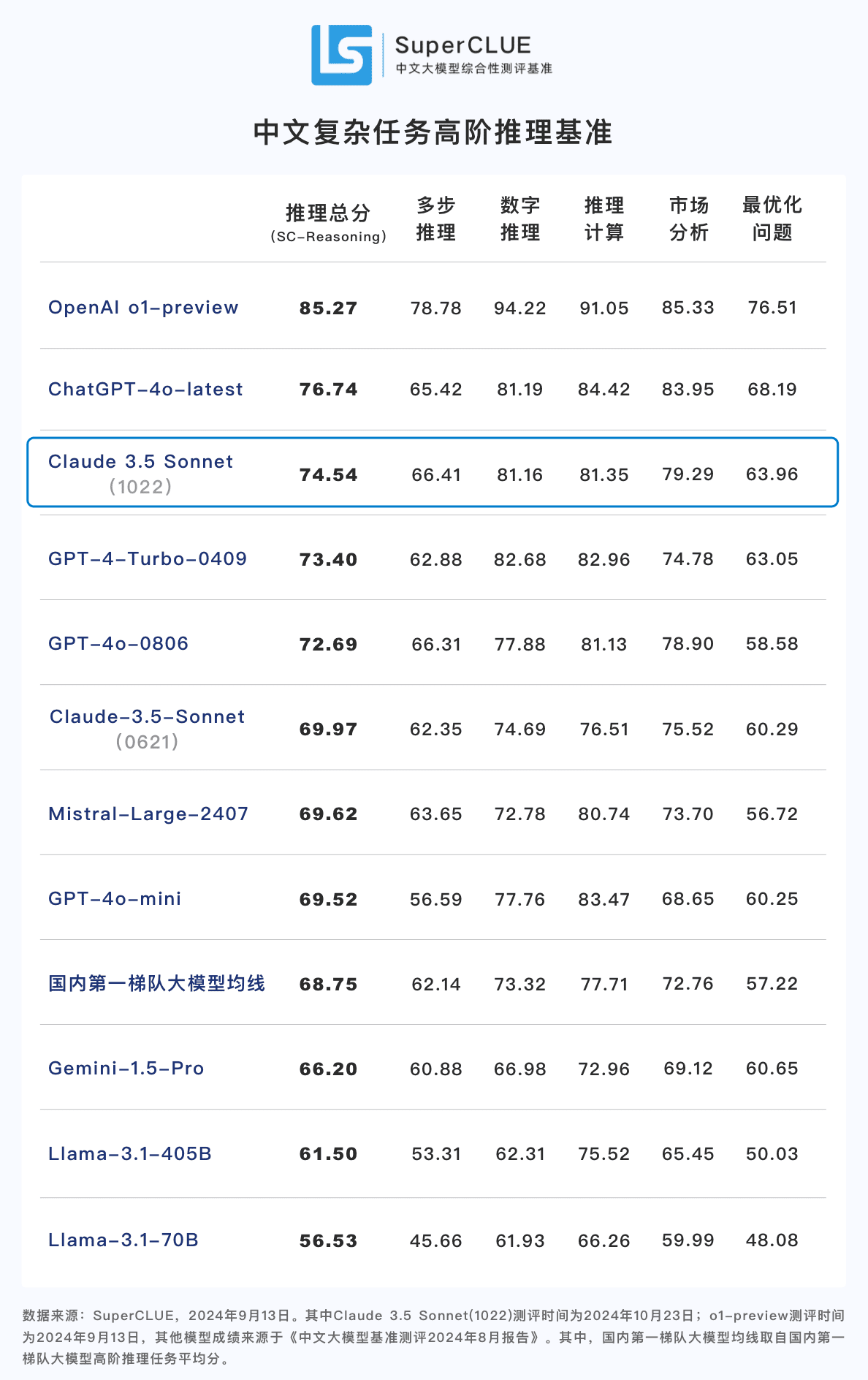
сравнительный анализ

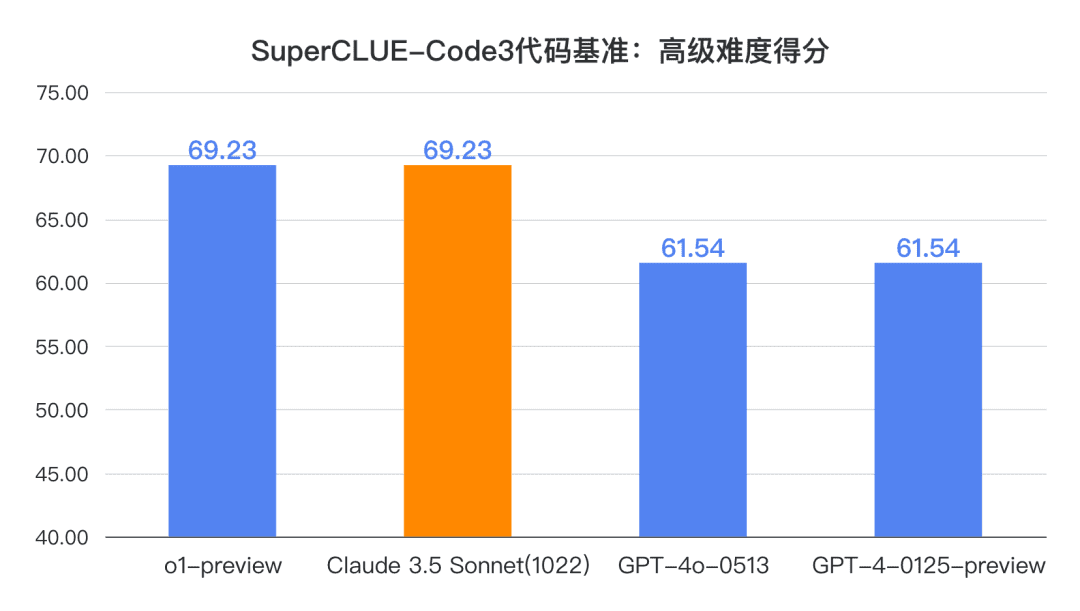
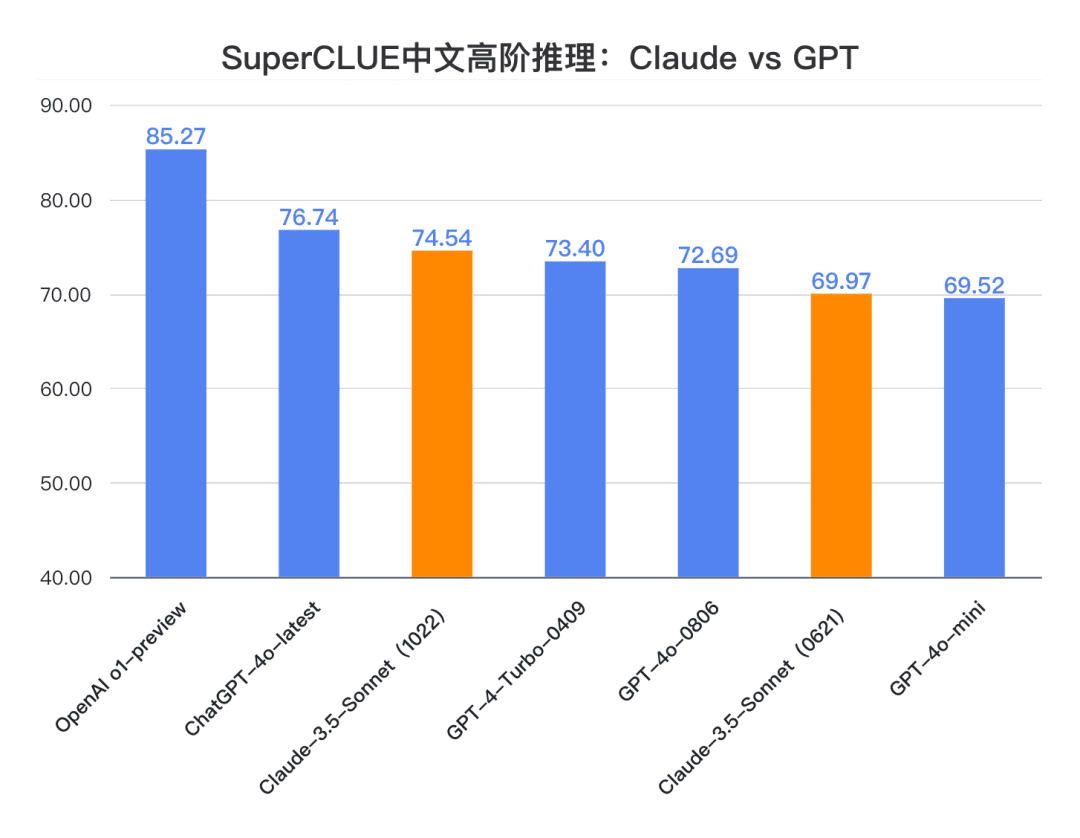
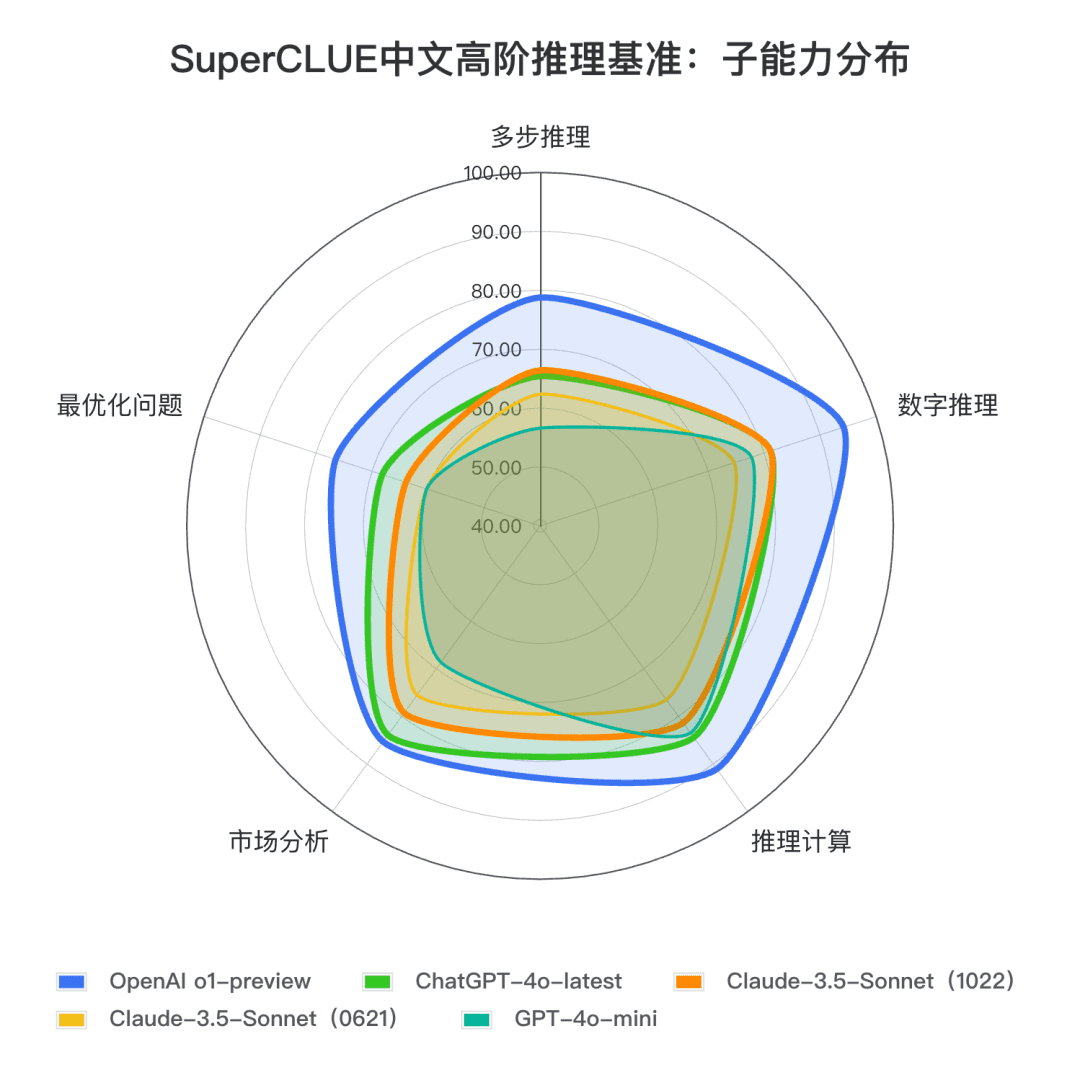
Пример измерения кода

Пример 1

Примета.

from typing import List


def longest_peak_sequence(nums: List[int]) -> int:
    """
    在一个整数数组中找出最长的"峰"序列的长度。
    所谓"峰"序列，是指先严格递增然后严格递减的序列，且峰顶（即最大值）唯一。
    至少包括三个数以上才能构成一个"峰"序列（即包含递增和递减的部分）。

    返回数组中最长"峰"序列的长度。如果没有"峰"序列，则返回0。


    示例:
    >>> longest_peak_sequence([2, 1, 4, 7, 3, 2, 5])
    5  # 最长的"峰"序列是 [1, 4, 7, 3, 2]


    >>> longest_peak_sequence([5, 4, 3, 2, 1])
    0  # 不存在"峰"序列，因为没有严格递增的部分

    提示:
    - 数组 `nums` 的长度范围为 [0, 10000]。
    - 数组中的每个元素范围为 [-10000, 10000]。
    """

Клод 3.5 Сонет (1022) Ответ.

from typing import List


def longest_peak_sequence(nums: List[int]) -> int:
    if len(nums) < 3:
        return 0

    max_length = 0

    # 从第二个元素遍历到倒数第二个元素
    for i in range(1, len(nums) - 1):
        # 检查当前位置是否是峰顶
        if nums[i] > nums[i-1] and nums[i] > nums[i+1]:
            # 找到一个峰顶，向两边扩展
            left = i - 1
            right = i + 1

            # 向左扩展，寻找严格递增序列
            while left > 0 and nums[left-1] < nums[left]:
                left -= 1

            # 向右扩展，寻找严格递减序列
            while right < len(nums) - 1 and nums[right+1] < nums[right]:
                right += 1

            # 更新最长峰序列长度
            current_length = right - left + 1
            max_length = max(max_length, current_length)

    return max_length

Тестовый пример.

def check(candidate):
    assert candidate( [1, 2, 3, 4, 5, 6])==0
    assert candidate([1, 3, 5, 6, 4, 2, 0])==7
    assert candidate( [5, 4, 3, 2, 1, 2, 3, 4, 1])==5
    assert candidate([1, 3, 5, 3, 1])==5
    assert candidate([1, 2, 3, 3, 2, 1])==0
    assert candidate([2, 1, 3, 1, 2, 1, 3])==3
    assert candidate([1, 3, 5, 4, 3, 2, 1])==7

if_passed**(усыновлен или нет):**Принято.

Пример 2

Примета.

from typing import List


def longest_increasing_path(matrix: List[List[int]]) -> int:
    """
    给定一个整数矩阵，找到最长严格递增路径的长度。
    路径被定义为从矩阵中的任意单元格开始，每次可以向上、下、左、右移动到相邻的单元格上，如果递增的话。
    你不能在路径中移动到矩阵外面，也不能移动到不满足递增条件的单元格上。
    路径的长度是路径上的单元格总数。

    示例:
    >>> longest_increasing_path([
            [9, 9, 4],
            [6, 6, 8],
            [2, 1, 1]
        ])
    4  # 最长递增路径是 [1, 2, 6, 9]


    >>> longest_increasing_path([
            [3, 4, 5],
            [3, 2, 6],
            [2, 2, 1]
        ])
    4  # 最长递增路径是 [3, 4, 5, 6]或 [2, 4, 5, 6]


    提示:
    - 矩阵 `matrix` 的维度为 m x n。
    - 矩阵 `matrix` 的每个元素是一个非负整数。


    """

Клод 3.5 Сонет (1022) Ответ.

from typing import List


def longest_increasing_path(matrix: List[List[int]]) -> int:
    if not matrix or not matrix[0]:
        return 0

    m, n = len(matrix), len(matrix[0])
    # 缓存，用于存储每个位置的最长递增路径长度
    cache = [[0] * n for _ in range(m)]

    def dfs(i: int, j: int) -> int:
        # 如果已经计算过，直接返回缓存结果
        if cache[i][j] != 0:
            return cache[i][j]

        # 四个方向：上、下、左、右
        directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]

        # 当前位置的最长路径至少为1
        max_length = 1

        # 遍历四个方向
        for di, dj in directions:
            ni, nj = i + di, j + dj

            # 检查是否在矩阵范围内且满足递增条件
            if (0 <= ni < m and 0 <= nj < n and 
                matrix[ni][nj] > matrix[i][j]):
                # 递归计算邻居位置的最长路径
                curr_length = 1 + dfs(ni, nj)
                max_length = max(max_length, curr_length)

        # 存入缓存
        cache[i][j] = max_length
        return max_length

    # 遍历矩阵中的每个位置，找到最长路径
    result = 0
    for i in range(m):
        for j in range(n):
            result = max(result, dfs(i, j))

    return result

Тестовый пример.

def check(candidate):
    assert candidate([[1, 1], [1, 1]]) == 1
    assert candidate([
    [9, 9, 4],
    [6, 6, 8],
    [2, 1, 1]
]) == 4
    assert candidate([
    [3, 4, 5],
    [3, 2, 6],
    [2, 2, 1]
]) == 4
    assert candidate([
        [1, 2, 3, 4],
        [5, 6, 7, 8],
        [9, 10, 11, 12],
        [13, 14, 15, 16]
]) == 7
    assert candidate([
        [-1, -2, -3, 0],
        [5, -6, 7, -8],
        [-9, 0, -11, -12],
        [13, 0, 15, -16]
]) == 4
    assert candidate([
    [5, 10, 6, 7, 9],
    [6, 10, 2, 2, 3], 
    [4, 9, 8, 2, 8],
    [3, 3, 3, 8, 8]
])==4
    assert candidate([
    [1, 3, 1, 4],
    [1, 5, 1, 7],
    [4, 2, 1, 1],
    [1, 3, 2, 1]
])==3
    assert candidate([
    [1, 9, 2, 4], 
    [9, 6, 5, 3],
])==4

if_passed(Усыновленные или нет):Принято.

Примеры рассуждений более высокого порядка

Пример 1: Многоступенчатое рассуждение

спросите

В компании работают семь сотрудников по имени A, B, C, D, E, F и G. Компания провела аттестацию и на основе оценок сотрудников и следующих условий вывела точный рейтинг каждого сотрудника:

1. Баллы A выше, чем B, но ниже, чем C.
2. D оценивается выше, чем E и G, но ниже, чем A.
3. G набрал меньше всего баллов.
4. B оценивается выше, чем E и F.
5. F оценивается выше, чем E.
6. C набрал наибольшее количество баллов.
7. Каждый сотрудник получает разную оценку, в самом центре находится D.

Пожалуйста, определите конкретный балл для каждого сотрудника, исходя из вышеперечисленных условий.

Клод 3.5 Сонет (1022) отвечает:

Давайте экстраполируем рейтинг каждого сотрудника с помощью логического анализа:

1. Известно из условия 3: G находится на последнем месте (7)
2. Известно из условия 6: C находится на вершине (1-е место)
3. Известно из условия 7: D занимает 4-е место (средняя позиция)
4. Из условия 2 мы знаем, что D выше, чем E и G, но ниже, чем A. Итак:
   • E должен занимать место после D (5-е или 6-е)
   • A должен занимать место перед D (2-е или 3-е)
5. Из условия 1 мы знаем: A выше, чем B, но ниже, чем C. Объедините это с предыдущим анализом:
   • 2-е место в ряду A
   • B должен занять 3-е место
6. Из условий 4 и 5 мы знаем: B выше, чем E и F, а F выше, чем E. Итак:
   • 5 место в ряду F
   • E 6 место

Итоговые рейтинги выглядят следующим образом:

1. C (1-е место)
2. A (2 место)
3. B (3-е место)
4. D (4)
5. F (5)
6. E (6)
7. G (7)

Хотите, я покажу вам подробный процесс рассуждений?

Пример 2: Оптимизационная задача

спросите

В городе пять крупных транспортных узлов, и департамент городского планирования хочет оптимизировать покрытие автобусных маршрутов, чтобы каждый узел был связан хотя бы одним маршрутом. Стоимость строительства между узлами известна, и задача состоит в том, чтобы соединить все узлы при минимальных затратах.

Данные:

• Расходы на связь между центрами (в млн. долл. США)
• Узловой центр 1 и Узловой центр 2: $100 000
• Узловой центр 1 и Узловой центр 3: $150,000
• Узловой центр 2 и Узловой центр 4: 200 000 долл.
• Узловой центр 3 и Узловой центр 4: 250 000 долл.
• Узловой центр 3 и Узловой центр 5: 300 000 долл.
• Хаб 4 и Хаб 5: $180 000

Цель: определить, какие узлы должны быть соединены друг с другом, чтобы минимизировать общую стоимость строительства и обеспечить соединение всех узлов.

Клод 3.5 Сонет (1022) отвечает:

Это задача о минимальном прячущемся дереве, которую я буду решать с помощью алгоритма Крускала. Давайте проанализируем ее шаг за шагом:

1. Сначала отсортируйте все соединения от наименьшей до наибольшей стоимости:
   • Узел 1-2: $100 000
   • Узлы 1-3: $150,000
   • Втулка 4-5: $180 000
   • Узлы 2-4: $200 000
   • Узел 3-4: $250 000
   • Узловые центры 3-5: $300 000
2. Чтобы избежать образования кольца, выбирается соединение с наименьшей стоимостью:
   • Выберите концентратор 1-2 ($100 000)
   • Выберите концентратор 1-3 ($150,000)
   • Select Hub 4-5 ($180 000)
   • Выберите концентратор 2-4 ($200 000)

Оптимальная программа:

• Подключение концентратора 1 и концентратора 2
• Подключение концентратора 1 и концентратора 3
• Подключение концентратора 4 и концентратора 5
• Подключение концентратора 2 и концентратора 4

Общая стоимость: 10 + 15 + 18 + 20 = $630 000

Эта программа обеспечивает:

1. Все концентраторы подключены
2. Петля не образуется
3. Минимальная совокупная стоимость владения

Хотите, чтобы я создал для вас визуализацию этого решения?

# Присоединяйтесь к сообществу

Для более подробного обзора Клод 3.5 последней большой модели, вы можете присоединиться к группе обмена SuperCLUE-Клод.