Новый метод подсказки - аналоговая подсказка

Сегодня я прочитал интересную статью под названием "TheБольшие языковые модели как аналоговые рассуждения Упоминается новый подход к подсказкам - "Аналоговые подсказки".

Если вы знакомы с инженерией подсказок, то наверняка слышали о CoT (Chain of Thought), которая может значительно улучшить способность к рассуждению больших языковых моделей (LLM). Однако при использовании CoT нам необходимо предоставлять соответствующие указания или примеры рассуждений, чтобы направлять модель.

Два широко используемых метода CoT: "0-shot CoT" и "few-shot CoT". 0-shot CoT - это явное указание шагов умозаключения в подсказке, и пусть LLM обращается к шагам для завершения умозаключения. 0-shot CoT - это явное указание шагов рассуждения в подсказке, и пусть LLM обращается к этим шагам для завершения рассуждения. few-shot CoT - это небольшое количество примеров, и пусть LLM обращается к этим примерам для завершения рассуждения.

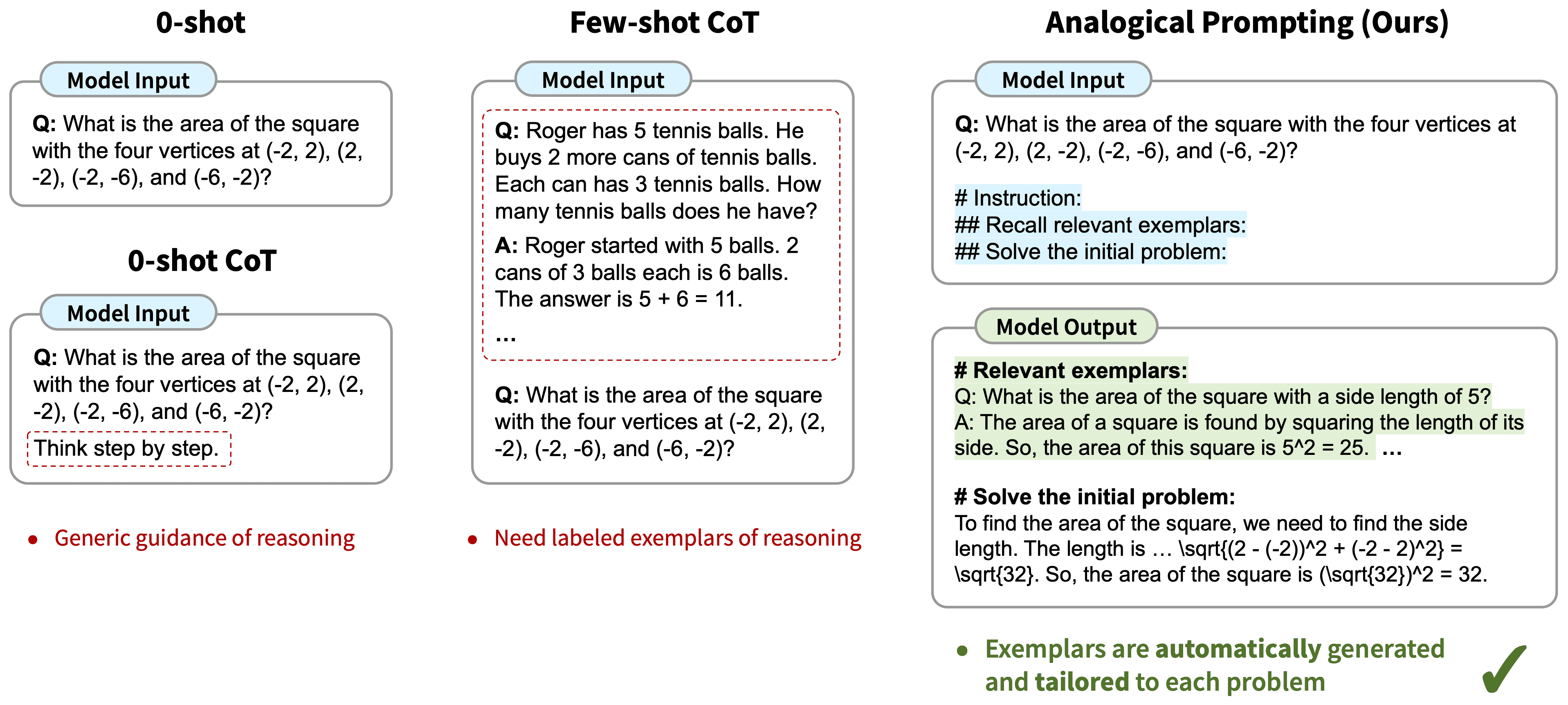
Сравнение трех методов подсказки

Например, сейчас есть вопрос по математике: "Существует квадрат, четыре вершины которого - (-2, 2), (2, -2), (-2, -6) и (-6, -2), найдите, какова площадь этого квадрата? "

Если вы не используете CoT, то вы просто бросаете задачу в LLM и позволяете ему найти ответ. Эта проблема должна быть решаема для GPT-4, но, скорее всего, будет ошибочной для GPT-3.5, и тем более для других моделей со слабыми рассуждениями.

Если вы используете 0-shot CoT, то в этом случае шаги умозаключения можно явно указать, например, в Prompt:

Для расчета выполните следующие действия:
1, сначала вычислите расстояние между любыми двумя соседними вершинами как длину стороны квадрата
2、 Вычислите квадрат длины стороны, чтобы получить площадь квадрата

Выполнение этих шагов должно дать правильные результаты для LLM с GPT 3,5.

Если вы используете малострельный CoT, то он дает небольшое количество примеров, например:

Вопрос: Вот квадрат, четыре вершины которого - (0, 0), (1, 1), (0, 1) и (1, 0). Какова площадь этого квадрата?
Ответ: Мы выбираем из него две соседние вершины, скажем (0, 0) и (1, 1), вычисляем расстояние между ними, чтобы получить длину ребра, равную 1, а затем вычисляем квадрат длины ребра, чтобы получить площадь, равную 1.
Вопрос: Имеется квадрат, четыре вершины которого - (-2, 2), (2, -2), (-2, -6) и (-6, -2). Какова площадь квадрата?

Мы явно приводим пример в подсказке, указывая LLM, что он должен следовать шагам в примере, чтобы получить правильный результат для LLM типа GPT-3.5.

Так что же такое "аналоговая подсказка"?

Вспомните, как мы изучали математику в школе: если мы решаем такой вопрос, мы подумаем, решали ли мы подобные вопросы, особенно для таких маленьких городских решателей задач, как я. Я не знаю, сколько работ я сделал тогда, поэтому, когда я вижу вопрос в конце комнаты, я могу вспомнить, что я решал подобный вопрос раньше, и тогда я могу придумать ответ очень быстро.

Запас знаний у LLM больше, чем у человека, и он накопил всевозможные знания и случаи в процессе обучения, поэтому нам нужно "стимулировать" LLM к поиску знаний и случаев, связанных с проблемой, а затем использовать их для рассуждений и решения проблемы.

Таким образом, "метод аналоговых подсказок" заключается в том, чтобы позволить LLM не бросаться решать проблему первым, а сначала перечислить ряд примеров, связанных с проблемой, а затем использовать эти примеры для рассуждений о решении проблемы. Это эквивалентно тому, как если бы LLM помог вам написать несколько предложений, помогая сформировать цепочку мыслей.

Это похоже на то, как если бы вы получили задачу по математике и попросили его сначала проследить за этой задачей, чтобы найти похожие примеры и эталонные ответы, а затем попросили бы его проследить за этими примерами и эталонными ответами, чтобы решить исходную задачу.

Структура Prompt выглядит следующим образом:

Первоначальный вопрос:\
Связанные проблемы: вспомните три связанные и уникальные проблемы и опишите каждую из них и ее решение.
Решите исходную задачу:

Пусть LLM, получив задачу, вспомнит три связанные и уникальные проблемы и перечислит каждую проблему и решение (желательно с шагами), и обязательно распечатает промежуточные процессы. Когда ЛЛМ закончит приводить примеры, распечатайте исходную задачу снова (чтобы не забыть), чтобы ЛЛМ мог использовать эти примеры для рассуждений об исходной задаче.

Полный справочник по Prompt с использованием аналогичных подсказок:

Ваша задача - решать математические задачи. Когда вам будет предложена математическая задача, вспомните несколько смежных тем в качестве примеров. Затем вернитесь и решите самую первую задачу.

# Самый первый вопрос:

Одна авиакомпания предлагает ужин каждому пассажиру самолета, который может выбрать стейк или рыбу. Три из шести членов экипажа могут выбрать стейк, а три - рыбу. Если блюда распределяются случайным образом, какова вероятность того, что оба пилота получат рыбу?

Руководство по эксплуатации #:

В вашем ответе должны быть указаны следующие пункты:

## Связанные вопросы:

Придумайте в качестве примера три математические задачи, связанные с самой первой задачей. Обратите внимание, что каждая задача должна отличаться от других, в том числе от самой первой (например, содержать разные числа и имена). Каждая задача должна соответствовать приведенному ниже формату:

- "Q:", за которым следует описание проблемы

- "A:" Далее следует решение задачи, а окончательный ответ запишите в \boxed.

## Решите проблему в самом начале:

Скажите: "Давайте решим следующую математическую задачу". Затем ответьте в следующем формате:

Вопрос: Скопируйте и вставьте сюда самый первый вопрос.

О: Объясните решение и запишите окончательный ответ в \boxed.

LLM выдаст следующее сообщение:

## Связанные вопросы:

### Вопрос 1:

- **Q:** На вечеринке каждый может выбрать яблочный пирог или ванильное мороженое. Пять дам выбирают яблочный пирог, а пять дам - ванильное мороженое. Если десерты распределяются случайным образом, какова вероятность того, что обе дамы получат ванильное мороженое?

- **A:** Для решения этой задачи используйте комбинаторные вычисления. Общее распределение состоит в том, чтобы выбрать двух из пяти дам, которые могут выбрать мороженое, что составляет \( \binom{5}{2} = 10 \) способов. А общее распределение состоит в том, чтобы выбрать двух из десяти дам, что составляет \( \binom{10}{2} = 45 \) способов. Таким образом, вероятность равна \( \frac{10}{45} = \frac{2}{9} \). Окончательный ответ \( \boxed{\frac{2}{9}} \).

### Вопрос 2:

- **Q:** На званом ужине каждый может выбрать красное или белое вино. Есть четыре человека, которые могут выбрать красное вино, и четыре человека, которые могут выбрать белое вино. Если вина распределяются случайным образом, какова вероятность того, что все трое мужчин получат белое вино?

- **A:** Используя аналогичный метод, из четырех мужчин, имеющих выбор белого вина, выбираются три человека \( \binom{4}{3} = 4 \) способами. А общее распределение производится путем выбора трех из восьми мужчин, т.е. \( \binom{8}{3} = 56 \) способов. Таким образом, вероятность равна \( \frac{4}{56} = \frac{1}{14} \). Окончательный ответ \( \boxed{\frac{1}{14}} \).

### Вопрос 3:

- **Q:** В кафе каждый человек может выбрать либо латте, либо капучино. Три клиента могут выбрать латте и три клиента могут выбрать капучино. Какова вероятность того, что клиент получит капучино, если выбор кофе происходит случайным образом?

- **A:** В данном случае существует \( \binom{3}{1} = 3 \) способов выбрать одного клиента, который может выпить капучино. Всего нужно выбрать одного клиента из шести, т.е. \( \binom{6}{1} = 6 \) способов. Таким образом, вероятность равна \( \frac{3}{6} = \frac{1}{2} \). Окончательный ответ \( \boxed{\frac{1}{2}} \).

## Давайте решим следующую математическую задачу.

### Q: Авиакомпания предоставляет ужин каждому пассажиру самолета, который может выбрать стейк или рыбу. Три из шести членов экипажа могут выбрать стейк, а три - рыбу. Если блюда распределяются случайным образом, какова вероятность того, что оба пилота получат рыбу?

### A: Мы можем использовать аналогичное решение для этой задачи. У нас есть три пилота, которые могут выбрать рыбу, и мы хотим выбрать двух из них. Это можно сделать \( \binom{3}{2} = 3 \) способами. Всего распределяется два из шести пилотов, что составляет \( \binom{6}{2} = 15 \) способов. Таким образом, вероятность равна \( \frac{3}{15} = \frac{1}{5} \). Окончательный ответ \( \boxed{\frac{1}{5}} \).