Что такое квантование моделей: объяснение типов данных FP32, FP16, INT8, INT4

руководство (например, книга или другой печатный материал)

На огромном звездном небосклоне технологий ИИ модели глубокого обучения способствуют инновациям и развитию многих областей благодаря своей превосходной производительности. Однако постоянное расширение масштабов моделей подобно обоюдоострому мечу, который приводит к резкому увеличению арифметических требований и нагрузки на систему хранения данных при одновременном повышении производительности. Особенно в сценариях применения с ограниченными ресурсами развертывание и эксплуатация моделей сталкиваются с серьезными проблемами.

Перед лицом этой дилеммы появилась технология "квантования", которая, подобно тонкому скальпелю, ловко уменьшает размер модели, повышает скорость вычислений и значительно снижает энергопотребление в пределах допустимого диапазона точности модели. Техника квантования позволяет преобразовывать высокоточные данные FP32 в модели в низкоточные данные INT4, тем самым осуществляя "похудение" и "ускорение" модели. В этой статье мы проанализируем принципы и методы квантования и его применение в области глубокого обучения, чтобы даже новички могли легко понять его суть.

1. Основы численного представления

1.1 Преобразование двоичной системы в десятичную

В информатике, краеугольном камне цифрового мира, все данные хранятся в двоичной форме. Двоичная система состоит только из двух чисел, 0 и 1, в то время как десятичная система, которую мы используем в повседневной жизни, состоит из десяти чисел от 0 до 9. Преобразование между этими двумя системами, подобно переводу между разными языками, является ключом к пониманию представления данных в компьютерах.

Например, десятичное число 13 преобразуется в двоичную форму как 1101. Процесс преобразования похож на разложение десятичного "целого" на его двоичные "компоненты". Шаги следующие:

13 Делится на 2, делитель равен 6, а остаток - 1 (младший двоичный разряд)
Если 6 разделить на 2, то получится 3, а остаток будет равен 0.
3 делится на 2, сумма 1, остаток 1
1 делится на 2, делитель равен 0, остаток - 1 (старший двоичный разряд)

Остатки перечислены снизу вверх:
↑1
↑0
↑1
↑1
Получите двоичный результат: 1101

И наоборот, преобразование двоичного числа 1101 обратно в десятичное - это как сборка "частей" для получения "целого". Справа налево вес каждого бита увеличивается на степень двойки, при этом самый правый бит имеет вес , , и так далее влево. Поэтому двоичное число 1101 переводится в десятичное следующим образом: 1× + 1× + 0× + 1× = 8 + 4 + 0 + 1 = 13.

1.2 Разница между числами с плавающей точкой и целыми числами

(i) Целочисленные типы (INT)

INT - это сокращение от Integer, обозначающее тип целого числа. Целые числа, как следует из названия, - это числа, не содержащие десятичных частей, например 1, 2, 3 и т. д.

INT4 означает, что для представления целого числа используется 4-битное двоичное число, а INT8 - 8-битное двоичное число. Количество битов определяет диапазон представления целых чисел.

Диапазон целых чисел, которые могут быть представлены INT4, ограничен, поскольку 4-битное двоичное число может представлять не более одного различного числа. Для знакового INT4 диапазон обычно составляет от -8 до 7, а для беззнакового INT4 - от 0 до 15. То же самое справедливо для INT8, диапазон которого составляет от -128 до 127, и для беззнакового INT8, диапазон которого составляет от 0 до 255, поскольку 8-битное двоичное число может представлять = 256 различных чисел.

(ii) Тип с плавающей точкой (FP)

FP означает Floating Point, тип числа с плавающей точкой. Числа с плавающей точкой, в отличие от целых чисел, используются для представления чисел с дробными частями.

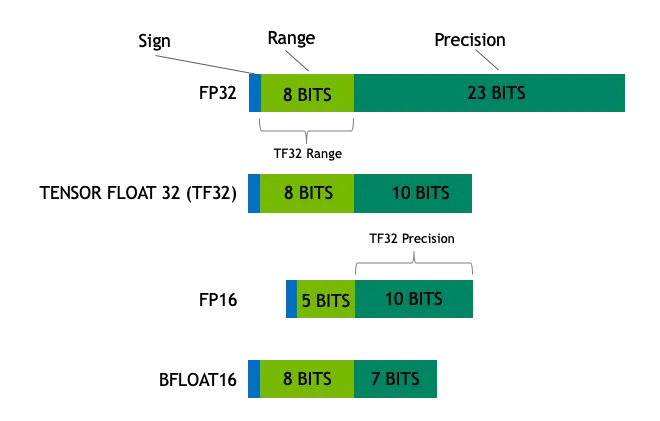
Число с плавающей точкой состоит из бита знака, бита экспоненты и бита мантиссы. Например, 32-битное число с плавающей точкой (FP32) состоит из 1 бита знака, 8 битов экспоненты и 23 битов мантиссы. Такая продуманная конструкция позволяет числам с плавающей точкой представлять чрезвычайно широкий диапазон значений, от очень маленьких до очень больших, как рулетка.

Например, FP32 может представлять очень маленькие числа (приблизительно) и очень большие числа (приблизительно). INT8 (8-битные целые числа), с другой стороны, может представлять только целые числа от -128 до 127. Эта разница аналогична измерению длины линейкой с фиксированной длиной (целые числа) и масштабируемой рулеткой (числа с плавающей точкой), где числа с плавающей точкой значительно превосходят целые числа в плане гибкости и диапазона числового представления.

(iii) Часто используемые типы данных

К распространенным типам данных в глубоком обучении и вычислениях общего назначения относятся:

• Float32 (FP32): Это стандартный 32-битный формат с плавающей точкой, известный своей высокой точностью и широким диапазоном значений. Операции FP32 доминируют в обучении и выводе моделей благодаря своей универсальности, которая поддерживается широким спектром аппаратных средств.
• Float16 (FP16)FP16 - это 16-битное число с плавающей точкой половинной точности, которое обладает меньшей точностью по сравнению с FP32, но при этом занимает значительно меньше места в памяти и имеет значительно более высокую скорость вычислений. FP16 имеет относительно узкий диапазон числовых представлений, что может быть чревато переполнением и недополнением. Однако в практиках глубокого обучения, таких какМасштабирование потерь Применение подобных методик позволяет эффективно решить эти проблемы.
• BFloat16 (BF16): BF16 - еще один 16-битный формат с плавающей запятой. Он уникален тем, что BF16 сохраняет тот же 8-битный бит экспоненты, что и FP32, и, таким образом, имеет тот же динамический диапазон, что и FP32, однако трейлинг-бит составляет всего 7 бит, что менее точно, чем FP16. Однако BF16 имеет только 7 младших битов, что менее точно, чем FP16. BF16 хорошо работает в сценариях с широким диапазоном значений, но в задачах, чувствительных к точности, может быть достигнут компромисс.
• Инт8INT8 - это 8-битный тип целых чисел с ограниченным диапазоном числового представления, но очень малым объемом памяти. INT8 в основном используется в методах квантования моделей, где преобразование параметров модели из высокоточных FP32 или FP16 в INT8 значительно сокращает объем памяти и вычислительную сложность модели, открывая путь для эффективного развертывания модели на устройствах с ограниченными ресурсами.

2. Количественные понятия

2.1 Количественные определения

Количественная обработка - это преобразование данных в модели из высокоточного представления в низкоточное, как в случае сКомпромисс между качеством изображения и размером файлаВ глубоком обучении квантование - это процесс сжатия изображения с высокой точностью в изображение JPEG с низкой точностью, что значительно уменьшает размер файла, сохраняя при этом основную информацию изображения. В области глубокого обучения квантование обычно означает уменьшение весов модели и значений активации с FP32 (32-битной плавающей точки) до FP16 (16-битной плавающей точки) или даже INT8 (8-битного целого числа) или более низкой точности.

FP32 - это формат с плавающей точкой высокой точности, который точно представляет значения в 32-битных двоичных разрядах (1 бит знака, 8 битов экспоненты и 23 бита мантиссы). FP32 - это точная шкала, которая может измерять от малых до больших значений, но ее высокая точность сопровождается большими затратами на хранение и относительно низкой скоростью вычислений.

FP16 - это формат с плавающей точкой половинной точности, для представления значения которого требуется всего 16 двоичных битов (1 бит знака, 5 битов экспоненты, 10 битов мантиссы). По сравнению с FP32, FP16 жертвует точностью ради вдвое меньшего объема памяти и повышенной эффективности вычислений, и напоминает немного более толстую шкалу, обеспечивая хороший баланс между точностью и эффективностью.

INT8 - это 8-битный целочисленный тип, который может представлять только целые числа в диапазоне от -128 до 127. Преимуществом INT8 является очень малая занимаемая память и очень высокая скорость вычислений, но при этом он обладает самой низкой точностью. INT8 похож на простой счетчик, который считает только целые числа, но при этом он быстрый и удобный.

2.2 Количественная цель

Основная цель количественной оценки заключается в том, чтобыСнижение требований к хранению и вычислительной сложности моделейи в то же время стремится удержать потерю точности в приемлемых пределах. В частности, количественная оценка направлена на достижение следующих целей:

Снижение требований к хранению: Современные модели глубокого обучения, особенно большие модели с огромным количеством параметров, часто имеют сотни миллионов или даже сотни миллиардов параметров, что создает огромную нагрузку на пространство для хранения данных. Если взять в качестве примера модель FP32, то каждый параметр занимает 4 байта пространства для хранения. Если модель квантована до FP16, то каждый параметр занимает всего 2 байта, что сокращает потребность в памяти вдвое. При дальнейшем квантовании модели до INT8 каждый параметр занимает всего 1 байт, а объем памяти может быть сокращен на 75%.

Повышение эффективности вычислений: Квантованная модель требует значительно меньше вычислительных затрат на этапе вывода, что позволяет увеличить скорость вывода. Например, когда модель FP32 работает на GPU, скорость вычислений может быть ограничена пропускной способностью памяти. С другой стороны, в моделях FP16 или INT8, благодаря оптимизированному аппаратному ускорению вычислений с низкой точностью, скорость вычислений может быть значительно увеличена. Повышение производительности за счет квантования особенно важно в сценариях, где вычислительные ресурсы ограничены, например, в пограничных или мобильных устройствах.

снижение энергопотребления: Снижение требований к вычислительным ресурсам модели напрямую ведет к снижению энергопотребления. Для мобильных устройств и встраиваемых систем энергопотребление является критически важным фактором. Методы квантования позволяют эффективно снизить энергопотребление модели, продлить срок службы устройства и снизить требования к рассеиванию тепла.

Снижение требований к пропускной способности:: В распределенных вычислительных системах уменьшение размера модели означает также уменьшение пропускной способности передачи данных. В сценарии с несколькими серверами количественные модели могут быть распределены и синхронизированы с большей скоростью, что повышает общую эффективность передачи данных.

3. Квантификация INT4, INT8

3.1 Диапазон представлений INT4 и INT8

INT4 и INT8 - оба метода квантования целочисленного типа, которые хранят данные в двоичной форме в компьютерных системах, но отличаются диапазоном и точностью числового представления.

• INT8INT8 - это 8-битный целочисленный тип с диапазоном представления от -128 до 127. Его можно сравнить с 8-битным счетчиком, где каждый бит может быть либо 0, либо 1, а различные целочисленные значения могут быть представлены различными комбинациями 0/1. Например, внотированный INT8 означает среднее значение в диапазоне от -128 до 127, а 11111111 в двоичном формате означает -1 в десятичном. Если этоunsigned (т.е. абсолютное значение, независимо от знака плюс или минус) INT8 в диапазоне от 0 до 255, в этом случае 11111111 представляет 255 в десятичной системе, достаточно для удовлетворения потребностей многих сценариев применения, таких как значения пикселей в обработке изображений, которые обычно находятся в диапазоне от 0 до 255 и могут быть эффективно представлены INT8.
• INT4INT4 - это 4-битный целочисленный тип с меньшим диапазоном представления от -8 до 7, чем у INT8. INT4 жертвует числовым диапазоном ради меньшего объема памяти и более быстрых вычислений. INT4 - это как меньший счетчик, с ограниченным числовым диапазоном, но меньшим "отпечатком", который более эффективен с точки зрения ресурсов. Он более эффективен с точки зрения ресурсов. В некоторых сценариях применения с относительно низкими требованиями к точности, например, в некоторых легких слоях нейронных сетей, использование квантования INT4 может значительно снизить затраты на хранение и вычисления.Например, при развертывании легкой модели классификации изображений на мобильном устройстве параметры модели и промежуточные результаты вычислений могут храниться и вычисляться с использованием формата INT4 для уменьшения занимаемой памяти и ускорения вывода.

3.2 Количественные формулы и примеры

Процесс квантования - это, по сути, преобразование карты чисел с плавающей точкой высокой точности в целое число низкой точности. Если в качестве примера взять квантование FP32 в INT8, то формула квантования выглядит следующим образом:

исходное число с плавающей запятой.

является квантованным целым числом.

коэффициент масштабирования, используемый для приведения чисел с плавающей точкой к целочисленному диапазону.

Указывает на округление до ближайшего целого числа.

Указывает, что результат ограничен диапазоном INT8, т.е. [-128, 127].

Вычисление коэффициента масштабирования

Масштабный коэффициент обычно вычисляется как максимальное абсолютное значение числа с плавающей точкой. Если имеется набор чисел с плавающей точкой, то процедура вычисления выглядит следующим образом:

1. Найдите максимальное абсолютное значение группы чисел с плавающей запятой:
2. Рассчитайте масштабный коэффициент: .

На практике существует несколько способов вычисления коэффициента масштабирования, таких как Max Quantization, Mean-Std Quantization и так далее. Максимальное квантование использует максимальное абсолютное значение тензора для вычисления коэффициента масштабирования, что просто в реализации, но может быть чувствительно к выбросам. Квантование Mean-Std использует информацию о среднем и стандартном отклонении данных для определения масштабного коэффициента более надежным способом, но вычислительная сложность при этом несколько выше. Выбор подходящего метода расчета коэффициента масштабирования требует компромисса между точностью и вычислительными затратами.

типичный пример

Если предположить, что у нас есть набор чисел с плавающей точкой [-0.5, 0.3, 1.2, -2.1], то ниже приводится пошаговая демонстрация процесса квантования:

1. Вычислите максимальное абсолютное значение:

2. Расчет масштабного коэффициента:

3. Количественно определите каждое число с плавающей запятой:

• Для -0,5.
• Для 0.3.
• Для 1.2.
• Для -2.1.

Окончательное, квантованное представление INT8 - это [-1, 1, 4, -7].

На примере описанных выше шагов мы можем наглядно увидеть, как техника квантования преобразует числа с плавающей запятой в целые числа. Хотя процесс квантования неизбежно влечет за собой определенную потерю точности, грамотный выбор коэффициента масштабирования позволяет максимально сохранить уровень производительности модели при значительном снижении затрат на хранение и вычисления. Для дальнейшего уменьшения ошибок квантования можно также использовать квантование с нулевой точкой. Квантование с нулевой точкой добавляет смещение нулевой точки в формулу квантования, что позволяет точно сопоставить нули с плавающей точкой с нулями целых чисел, тем самым повышая точность квантования, особенно если в значениях активации имеется большое количество нулей.

4. Количественная оценка FP8, FP16, FP32

4.1 Представления FP8, FP16, FP32

FP8, FP16 и FP32 - это числа с плавающей точкой, которые хранятся в компьютере в двоичном виде, но с разной шириной битов и, следовательно, с разным диапазоном и точностью.

FP32

FP32, как стандартный 32-битный формат с плавающей точкой, состоит из следующих трех частей:

• Бит знака (1 бит): Используется для обозначения положительных и отрицательных значений, при этом 0 означает положительное число, а 1 - отрицательное.
• Экспоненциальные цифры (8 цифр): используется для определения диапазона размеров значения, что позволяет FP32 представлять значения от очень маленьких до очень больших.
• Последняя цифра (23 бита): Используется для определения точности значения; чем больше цифр в конце строки, тем выше точность.

Имея широкий диапазон значений от примерно до , и точность около 6 знаков после запятой, FP32 напоминает высокоточную рулетку, которая может измерять масштабы, как маленькие пылинки, так и огромные расстояния, как горы. FP32 - незаменимый тип данных в научных вычислениях, финансовом моделировании и других областях, где требуется высокая степень точности.

FP16

FP16 - это формат с плавающей точкой половинной точности, занимающий всего 16 бит памяти, что вдвое меньше, чем FP32. Структура FP16 выглядит следующим образом:

• Бит знака (1 бит): Определяет положительные и отрицательные значения.
• Экспоненциальная цифра (5 цифр): Определяет диапазон размеров значений.
• Последняя цифра (10 цифр): Определяет числовую точность.

Диапазон FP16 составляет от примерно до , а точность уменьшена примерно до 3 десятичных знаков по сравнению с FP32. FP16 подобен линейке с немного более толстой шкалой, которая имеет меньшую точность, но имеет больше преимуществ в пространстве для хранения и эффективности вычислений. FP16 обычно используется для обучения и вывода моделей глубокого обучения, что требует высокой скорости вычислений и пропускной способности памяти. Особенно в сценариях с GPU-ускорением, FP16 может в полной мере использовать аппаратные ускорители, такие как Tensor Core, для достижения значительного повышения производительности.

FP8

FP8 - это новый формат чисел с плавающей точкой низкой точности, который в основном используется в области глубокого обучения и нацелен на эффективные вычисления:

• Бит знака (1 бит): Определяет положительные и отрицательные значения.
• Экспоненциальные цифры (3 или 4 цифры): Определите диапазон размеров значений (существует два варианта FP8).
• Последняя цифра (4 или 3 цифры): Определяет точность числа (соответствует количеству цифр индекса).

Диапазон и точность числового представления FP8 еще больше уменьшаются, но преимуществами являются меньший объем памяти и более высокая скорость вычислений. Если FP32 - это точная рулетка, а FP16 - линейка с чуть более толстой шкалой, то FP8 - более точная рулетка. Это как простая линейка с сантиметровой шкалой.Кроме того, дальность и точность измерений еще больше снижаются, но задача измерения все равно может быть решена быстро в конкретной ситуации. Будучи типом данных с чрезвычайно низкой точностью, FP8 демонстрирует большой потенциал в сценариях с экстремальными требованиями к задержке и пропускной способности, таких как выводы в реальном времени, пограничные вычисления и т. д. Однако FP8 также предъявляет повышенные требования к аппаратуре и алгоритмам. Однако применение FP8 также предъявляет повышенные требования к аппаратному обеспечению и алгоритмам, требуя специальной аппаратной поддержки и стратегий квантования для обеспечения точности.

4.2 Процесс количественной оценки и формулы

Квантование - это процесс преобразования числа с плавающей точкой высокой точности в число с плавающей точкой низкой точности или целое число. Если в качестве примера взять квантование FP32 в FP16, то формула квантования выглядит следующим образом:

исходное число с плавающей запятой.

квантованное число низкой точности с плавающей точкой.

коэффициент масштабирования, используемый для преобразования чисел с плавающей точкой в диапазоны более низкой точности.

Указывает на округление до ближайшего значения.

Вычисление коэффициента масштабирования

Масштабный коэффициент обычно вычисляется как максимальное абсолютное значение числа с плавающей точкой. Если имеется набор чисел с плавающей точкой, то процедура вычисления выглядит следующим образом:

1. Найдите максимальное абсолютное значение группы чисел с плавающей запятой:
2. Вычислите коэффициент масштабирования: , где - максимальное значение целевого формата низкой точности.Может быть выражена как абсолютная величина. Для FP16 это значение равно примерно 65504.

Как и в квантовании INT8, масштабные коэффициенты в квантовании FP16 могут быть рассчитаны различными способами, которые можно выбрать в соответствии с различными требованиями к точности и производительности. Кроме того, квантование FP16 часто используется в сочетании с обучением со смешанной точностью (MPT). В процессе обучения модели FP16 используется для некоторых вычислительно трудоемких операций (например, умножение матриц, свертка), а FP32 - для операций, требующих высокой точности (например, расчет потерь, обновление градиента), чтобы ускорить процесс обучения и уменьшить потребление памяти, гарантируя при этом точность модели.

типичный пример

Предположим, что у нас есть набор чисел с плавающей точкой FP32 [-0.5, 0.3, 1.2, -2.1], ниже приводится пошаговая демонстрация квантования FP32 в FP16:

1. Вычислите максимальное абсолютное значение:

2. Расчет масштабного коэффициента:

3. Количественно определите каждое число с плавающей запятой:

• Для -0,5.
• Для 0.3.
• Для 1.2.
• Для -2.1.

Окончательное количественное значение FP16 выражается как [-0,5, 0,3, 1,2, -2,1].

С помощью описанных выше шагов можно проследить, как методы квантования преобразуют числа с плавающей точкой высокой точности в числа с плавающей точкой низкой точности. Квантование, конечно, приводит к некоторой потере точности, но при грамотном выборе коэффициента масштабирования производительность модели может быть сохранена настолько, насколько это возможно, при этом снижаются затраты на хранение и вычисления. Для дальнейшего повышения точности квантования FP16 можно использовать динамическое квантование. Динамическое квантование динамически регулирует масштабный коэффициент в соответствии с фактическим диапазоном входных данных в процессе вывода, чтобы лучше адаптироваться к изменениям в распределении данных и уменьшить ошибку квантования.

5. Количественные приложения и преимущества

5.1 Применение в глубоком обучении

Количественные методы имеют широкий спектр перспективных применений в глубоком обучении, особенно на этапах обучения и вывода модели, где они приобретают все большую ценность. Ниже перечислены основные области применения количественных методов в глубоком обучении:

Ускорение обучения модели

На этапе обучения модели вычисления с низкоточными типами данных, такими как FP16 или FP8, могут значительно ускорить процесс обучения. Например, графические процессоры NVIDIA с архитектурой Hopper поддерживают операции Tensor Core с точностью FP8. Обучение на FP8 может быть в 2-3 раза быстрее, чем традиционное обучение на FP32. Такое ускорение обучения особенно важно для моделей с большим количеством параметров, значительно сокращая время обучения и расход вычислительных ресурсов. Например, при обучении крупномасштабных языковых моделей, таких как GPT-3, использование обучения со смешанной точностью FP16 или BF16 позволяет значительно сократить время обучения и сэкономить большое количество вычислительных ресурсов.

согласно Inflection AI Например, Inflection-2 обучался на 5 000 графических процессоров NVIDIA архитектуры Hopper с использованием стратегии обучения со смешанной точностью FP8, что составило FLOPs операций с плавающей запятой, и в ряде стандартных бенчмарков производительности ИИ Inflection-2 продемонстрировал превосходство над флагманской моделью Google PaLM 2, которая также относится к категории обучающих вычислений. В ряде стандартных эталонов производительности ИИ Inflection-2 продемонстрировал значительное превосходство над флагманской моделью Google PaLM 2 в той же категории обучающих вычислений.

Оптимизация вывода модели

На этапе вывода модели методы квантования позволяют значительно сократить объем памяти и вычислительную сложность модели, а значит, повысить эффективность вывода. Например, квантование модели FP32 до INT8 позволяет сократить объем памяти модели на 75% и увеличить скорость вывода в несколько раз. Это очень важно для развертывания моделей глубокого обучения на пограничных или мобильных устройствах, которые часто сталкиваются с проблемой ограниченных вычислительных ресурсов и пространства для хранения данных. Например, при развертывании моделей распознавания изображений на мобильных телефонах квантование модели в виде INT8 позволяет эффективно уменьшить размер модели, сократить потребление памяти, ускорить процесс вывода и повысить удобство работы пользователя.

Например, Google тесно сотрудничал с командой NVIDIA, чтобы применить технику оптимизации TensorRT-LLM к модели Gemma и объединить ее с технологией FP8 для ускорения вычислений. Результаты экспериментов показывают, что FP8 обеспечивает более чем 3-кратное увеличение пропускной способности по сравнению с FP16 при использовании GPU Hopper для вычислений.

Сжатие и развертывание моделей

Методы квантования также могут быть использованы для сжатия и развертывания моделей. Количественное преобразование высокоточных моделей в низкоточные позволяет эффективно уменьшить размер модели, что облегчает ее развертывание в средах с ограниченными ресурсами. Например, "ноль-один-всёиспользовать Объединенный стек аппаратных и программных технологий NVIDIA завершил обучение и проверку больших моделей FP8, увеличив производительность обучения больших моделей в 1,3 раза по сравнению с BF16. Помимо квантования INT8 и FP16/FP8, существуют также методы квантования INT4 и даже более низких битов, такие как двоичная нейронная сеть (BNN) и троичная нейронная сеть (TNN). Эти методы квантования с очень малым количеством бит могут сжимать модель до предела, но обычно с большой потерей точности, и подходят для сценариев с экстремальными требованиями к размеру и скорости модели.

Кроме того, квантованная модель может быть усовершенствована с помощью специальных методов аппаратного ускорения. Например, NVIDIA Трансформатор Движок интегрирован в основные фреймворки глубокого обучения, такие как PyTorch, JAX, PaddlePaddle и т.д., обеспечивая эффективную поддержку на аппаратном уровне для вывода количественных моделей. Помимо NVIDIA GPU, другие аппаратные платформы, такие как CPU архитектуры ARM и мобильные NPU, также оптимизированы и ускорены для количественных вычислений, обеспечивая аппаратную основу для широкого развертывания количественных моделей.

5.2 Сильные стороны и ограничения

доминирование

Повышение эффективности вычисленийНизкоточное квантование позволяет значительно ускорить вычисления и снизить потребление вычислительных ресурсов. И FP16, и FP8 имеют в несколько раз большую вычислительную производительность, чем FP32.

Низкие требования к хранению: Методы квантования могут значительно сократить требования к хранению моделей. Например, квантование модели FP32 до INT8 сокращает объем памяти на 75%, что важно для развертывания моделей в средах с ограниченными ресурсами хранения.

Сниженное энергопотребление:: Вычисления с низкой точностью требуют меньше вычислительных ресурсов, что снижает энергопотребление устройства. В мобильных устройствах и встраиваемых системах энергопотребление является ключевым фактором при проектировании. Количественные модели помогают продлить время автономной работы устройства и снизить требования к теплоотводу.

Оптимизация моделиМетоды квантования способствуют оптимизации и сжатию модели в процессе обучения и вывода, что еще больше снижает затраты на развертывание. Например, применение FP8 позволяет моделям исследовать более тонкие стратегии квантования на этапе обучения, что повышает общую эффективность модели.

ограничения

Потеря точности:: Процесс квантования неизбежно сопровождается потерей точности, которая может быть значительной, особенно при использовании форматов с очень низкой точностью (например, FP8), и может привести к ухудшению производительности модели на конкретной задаче. Хотя потерю точности можно в некоторой степени уменьшить, например, путем тщательного выбора коэффициентов масштабирования, полностью устранить потерю точности часто бывает трудно. Для снижения потерь точности, вызванных квантованием, можно использовать обучение с учетом квантования (QAT). QAT имитирует операцию квантования в процессе обучения модели и учитывает ошибку квантования в процессе обучения, чтобы обучить модель, которая более устойчива к квантованию. Как правило, QAT может значительно повысить точность моделей квантования, но при этом стоимость обучения соответственно возрастает.

Поддержка аппаратного обеспечения: Не все аппаратные платформы полностью поддерживают вычисления с низкой точностью. Например, для вычислений FP8 и FP16 часто требуется специальное оборудование (например, графические процессоры архитектуры NVIDIA Hopper). Если аппаратная платформа не оптимизирована для вычислений с низкой точностью, преимущества квантования не будут использованы в полной мере. С ростом популярности вычислений с низкой точностью все больше аппаратных платформ начинают поддерживать такие типы данных с низкой точностью, как FP16, BF16 и даже FP8, что обеспечивает более прочную аппаратную основу для широкого применения методов квантования.

Повышенная сложность:: Сам процесс количественной оценки может усложнить разработку модели. Например, процесс количественной оценки требует тонкого расчета масштабных коэффициентов и может потребовать дополнительной калибровки и тонкой настройки модели. Это, безусловно, повышает сложность разработки и развертывания модели. Чтобы снизить сложность развертывания квантования, в индустрии появилось множество автоматизированных инструментов и платформ для квантования, таких как NVIDIA TensorRT, Qualcomm AI Engine и т. д., которые помогают разработчикам быстро и легко проводить квантование и развертывать модели на целевых аппаратных платформах.

сценарий применения:: Методы квантования подходят не для всех сценариев применения. В задачах, требующих очень высокой точности (например, в научных вычислениях, финансовом моделировании и т. д.), квантование может привести к неприемлемой потере точности. Для задач, чувствительных к точности, можно попробовать стратегию квантования со смешанной точностью, когда к разным слоям или параметрам модели применяются разные точности квантования, например, FP32 или FP16 для ключевых слоев или параметров и INT8 или ниже для других слоев или параметров, чтобы достичь лучшего баланса между точностью и эффективностью.

В целом, методы квантования, как ключевая технология в области глубокого обучения, демонстрируют большой потенциал в повышении эффективности вычислений, снижении требований к хранению данных и энергопотреблению. Однако методы квантования имеют и свои ограничения, такие как потеря точности и аппаратная зависимость. Поэтому в практических приложениях стратегии квантования должны быть тщательно подобраны в соответствии с конкретными требованиями приложения и характеристиками сценария, чтобы достичь оптимального баланса между производительностью и эффективностью модели. В будущем, с непрерывным развитием аппаратного обеспечения и алгоритмов, количественные технологии будут играть все более важную роль в области глубокого обучения и способствовать укоренению применения искусственного интеллекта в более широком спектре сценариев.