CoRAG: MCTS(몬테카를로 트리)를 사용한 동적 연쇄 RAG 모델링

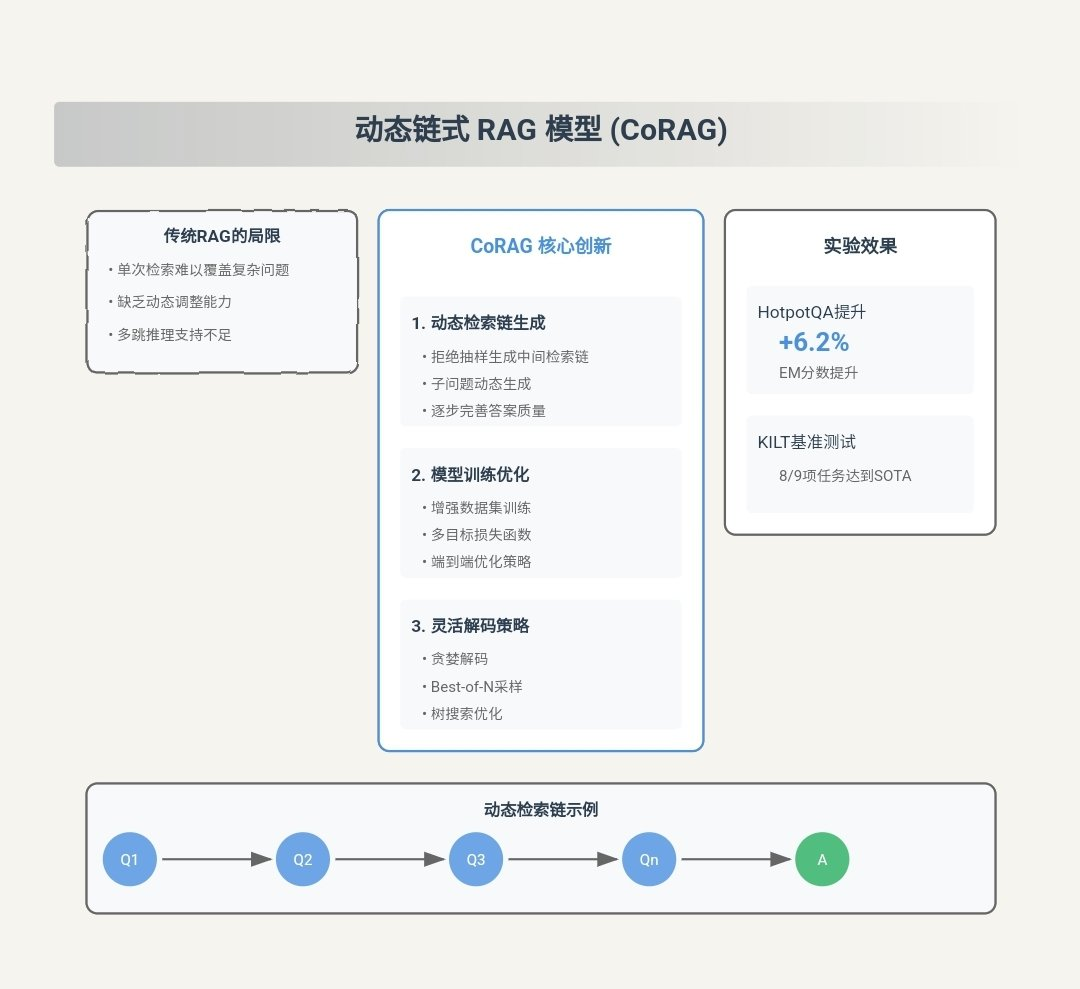
CORAG의 주요 기여 요약

CORAG(비용 제약) 검색 검색 증강 세대를 위한 최적화)는 기존의 검색 증강 세대(RAG) 문제를 해결하기 위해 설계된 혁신적인 검색 증강 세대(RAG) 시스템입니다. RAG 방법론의 주요 과제 다음은 CORAG의 주요 기여 사항입니다:

블록 간 연관성에 대한 종합적인 고려::
- 혁신 포인트CORAG는 RAG 작업에서 블록 조합 순서 최적화를 도입한 최초의 프레임워크입니다. 각 텍스트 블록을 독립적으로 처리하거나 클러스터링 수준에서만 블록을 고려하는 대신, CORAG는 기존 접근 방식과 달리 몬테카를로 트리 검색(MCTS) 를 사용하여 최적의 블록 조합 순서를 순차적으로 검색합니다. 이 접근 방식은 블록 간의 복잡한 연관성을 완벽하게 파악하고 중복 정보를 피하며 선택한 블록 조합이 사용자 쿼리에 완벽하게 응답하도록 보장합니다.
- 최첨단이러한 방식으로 CORAG는 보다 정확하고 관련성 높은 응답을 생성하여 생성 품질을 개선할 수 있습니다.
블록 유틸리티 비단조성 문제 해결하기::
- 혁신 포인트: CORAG는 예산 제약 예산 소진을 종료 조건으로 고려하지 않고 블록 포트폴리오의 최적화 프로세스에 통합합니다. 이 접근 방식은 다음과 같은 블록의 유용성을 고려합니다. 비단조로움즉, 블록을 더 많이 추가한다고 해서 최종 결과물의 품질이 항상 향상되는 것은 아닙니다.
- 최첨단최적화 프로세스 중 예산 사용량을 동적으로 조정함으로써 CORAG는 관련성이 없거나 중복된 블록이 과도하게 포함되는 것을 방지하여 생성된 응답의 정확성과 관련성을 개선할 수 있습니다.
다양한 문의 분야에 대한 적응::
- 혁신 포인트CORAG는 에이전트 구성하기상담원은 비교 학습 를 사용하여 다양한 쿼리 도메인에 맞게 MCTS 구성을 동적으로 조정할 수 있습니다. 에이전트는 최적의 리레인저 모델 노래로 응답 MCTS 구성.
- 최첨단이 접근 방식을 통해 CORAG는 간단한 키워드 쿼리부터 복잡한 추론 문제까지 다양한 쿼리 유형을 유연하게 처리할 수 있어 다양한 애플리케이션 시나리오에서 고품질의 응답을 보장합니다.
효율적이고 확장 가능한 검색 전략::
- 혁신 포인트CORAG는 노드 검색에 MCTS를 사용합니다. 병렬 확장 기술 검색 프로세스를 가속화합니다. 이 접근 방식은 기하급수적인 검색 공간을 선형으로 줄이고 효과적으로 탐색 노래로 응답 활용.
- 최첨단CORAG는 효율적인 검색을 유지하면서 대규모 데이터 세트를 처리하고 계산 비용과 검색 품질 간의 균형을 맞출 수 있습니다.
상당한 성능 향상::
- 실험적 검증실험 결과, CORAG는 여러 벤치마크 데이터 세트에서 기존 기준 방법보다 성능이 우수하여 ROUGE 점수를 약 20% 향상시켰습니다. 30%. 또한 CORAG는 효율성이 뛰어나 빠듯한 비용 제약 내에서 고품질의 응답을 제공합니다.

CORAG 워크플로 예시

다음은 CORAG가 사용자 쿼리를 처리하고 최종 응답을 생성하는 방법을 보여주는 전체 워크플로우 예시입니다. 각 단계에는 워크플로우의 앞뒤를 나타내는 입력과 출력이 포함되어 있습니다.

1단계: 사용자 쿼리 입력

가져오기예를 들어 사용자가 CORAG 시스템에 자연어 쿼리를 제출합니다:
```
"请解释光合作用的过程，并列出影响其效率的因素。"
```
수출쿼리가 쿼리 임베딩 모듈 처리 중입니다.

2단계: 쿼리 임베딩 생성

가져오기사용자 쿼리 텍스트.
거래사전 학습된 모델 임베딩(예: BGE-M3)는 쿼리 텍스트를 벡터 표현으로 변환합니다.
수출: 임베딩 벡터(예: 1024차원 벡터)를 쿼리합니다.
```
Query Embedding: [0.123, -0.456, 0.789, ..., -0.012]
```

3단계: 상담원 예측 구성

가져오기쿼리 임베딩 벡터 [0.123, -0.456, 0.789, ..., -0.012].
거래::
1. 특징 추출임베딩 벡터는 임베딩 벡터가 에이전트 구성하기 (명목식 형태로 사용됨) 코딩 네트워크 특징 추출은
2. 리랭거 예측최적의 네트워크 출력 예측 코드화 리레인저 모델예를 들면 다음과 같습니다. bge-reranker-large.
3. MCTS 구성 예측: 동시에 코딩 네트워크는 최적의 MCTS를 예측합니다. 구성 매개변수반복 횟수, 비용 계수, 탐색 계수 등입니다.
수출::
- 최적의 리레인저 모델::bge-reranker-large
- MCTS 구성 매개변수::
  - 반복 횟수:: 15
  - 비용 요소: 0.2
  - 탐색 요소: 2.5
```
Optimal Reranker: bge-reranker-large
MCTS Configuration:
- Iterations: 15
- Cost Coefficient: 0.2
- Exploration Coefficient: 2.5
```

4단계: 잠재적 텍스트 블록 가져오기

가져오기::
- 쿼리 임베딩 벡터 [0.123, -0.456, 0.789, ..., -0.012].
- 벡터 데이터베이스(예: 미리 분할된 텍스트 블록과 해당 임베딩 벡터 포함).

거래다음에 쿼리 임베딩 벡터를 사용합니다. 유사 검색를 사용하여 벡터 데이터베이스에서 가장 관련성이 높은 잠재적 텍스트 블록을 검색합니다. 다음은 검색된 처음 5개의 텍스트 블록의 예시입니다:텍스트 블록 1::

光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。

텍스트 블록 2::

光合作用主要发生在植物叶片的叶绿体中，分为光反应和碳反应两个阶段。

텍스트 블록 3::

影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。

텍스트 블록 4::

光照强度对光合作用的影响呈正相关，但过强的光照会导致光抑制现象，降低光合作用效率。

텍스트 블록 5::

二氧化碳是光合作用的原料之一，其浓度直接影响光合作用的速率。

수출잠재적인 텍스트 블록 및 임베딩 벡터 목록입니다.

Retrieved Chunks:
- Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。"
- Chunk 2: "光合作用主要发生在植物叶片的叶绿体中，分为光反应和碳反应两个阶段。"
- Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。"
- Chunk 4: "光照强度对光合作用的影响呈正相关，但过强的光照会导致光抑制现象，降低光合作用效率。"
- Chunk 5: "二氧化碳是光合作用的原料之一，其浓度直接影响光合作用的速率。"

5단계: MCTS 트리 검색

가져오기::
- 잠재적인 텍스트 블록 목록::
  - 청크 1: ...
  - 청크 2: ...
  - 청크 3: ...
  - 청크 4: ...
  - 청크 5: ...
- MCTS 구성 매개변수::
  - 반복 횟수:: 15
  - 비용 요소: 0.2
  - 탐색 요소: 2.5
- 리레인저 모델::bge-reranker-large
거래::
1. 루트 노드 초기화하기루트 노드는 텍스트 블록이 선택되지 않은 빈 상태를 나타냅니다.
2. 반복 확장::
  - 옵션사용 UCB 알고리즘 현재 유틸리티가 가장 높은 노드를 선택합니다. 예를 들어 청크 3은 쿼리와의 관련성이 가장 높기 때문에 첫 번째 반복에 선택됩니다.
  - 확장 프로그램: 가능한 모든 자식 노드(텍스트 청크의 새로운 조합)를 생성합니다. 예를 들어 청크 3의 자식은 청크 1, 청크 2, 청크 4, 청크 5가 될 수 있습니다.
  - 가치 평가사용 리레인저 모델 bge-reranker-large 모든 새로운 조합의 효용을 병렬로 평가합니다. 예를 들어 청크 3 + 청크 1, 청크 3 + 청크 2 등과 같은 조합의 효용을 평가합니다.
  - 업데이트노드 유틸리티 및 액세스 수를 업데이트하고 업데이트를 위쪽으로 전파합니다.
3. 반복최대 반복 횟수(15회)에 도달할 때까지 선택, 확장, 평가 및 업데이트 단계를 반복합니다.
4. 해지 조건: 최대 반복 횟수에 도달했습니다.

수출텍스트 블록을 결합하는 최적의 순서.

Optimal Chunk Combination:
- Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。"
- Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。"
- Chunk 2: "光合作用主要发生在植物叶片的叶绿体中，分为光反应和碳反应两个阶段。"

다음 사항에 유의하십시오.MCTS 프로세스 중 CORAG는 유틸리티에 따라 조합 순서를 동적으로 조정하고 최종적으로 최적의 조합 순서를 선택합니다.

6단계: 최종 응답 생성

가져오기::
- 텍스트 블록을 결합하는 최적의 순서::
  - 청크 3: "광합성 효율에 영향을 미치는 요인으로는 빛의 강도, 이산화탄소 농도, 온도, 물의 가용성 등이 있습니다."
  - 청크 1: "광합성은 식물, 조류 및 일부 박테리아가 빛 에너지를 사용하여 이산화탄소와 물을 포도당과 산소로 전환하는 과정입니다."
  - 청크 2: "광합성은 주로 식물 잎의 엽록체에서 일어나며, 빛 반응과 탄소 반응의 두 단계로 나뉩니다."
- 사용자 문의:: "광합성의 과정을 설명하고 효율성에 영향을 미치는 요인을 나열하세요."

거래::

빌드 팁텍스트 블록과 사용자 쿼리를 결합하는 최적의 순서를 결합하여 LLM 를 입력합니다. 예시:

用户查询：请解释光合作用的过程，并列出影响其效率的因素。
相关信息：
1. 影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。
2. 光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。
3. 光合作用主要发生在植物叶片的叶绿体中，分为光反应和碳反应两个阶段。

응답 생성하기사용 LLM(예: Llama3) 프롬프트에 대한 최종 응답을 생성합니다.

수출최종 자연어 응답입니다.

Final Response:
"光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。它主要发生在植物叶片的叶绿体中，分为光反应和碳反应两个阶段。影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。"

7단계: 응답 출력

가져오기최종 자연어 응답입니다.
거래: 사용자에게 응답을 표시합니다.
수출사용자 인터페이스에 응답 결과가 표시됩니다.

요약

위의 워크플로 예시를 통해 CORAG의 작동 원리를 다음 단계로 요약할 수 있습니다:

쿼리 임베딩 생성사용자 쿼리를 벡터 표현으로 변환합니다.
상담원 예측 구성: 최적의 재배치 모델과 MCTS 구성 매개변수를 예측합니다.
잠재적인 텍스트 블록 검색: 벡터 데이터베이스에서 가장 관련성이 높은 텍스트 블록을 검색합니다.
MCTS 트리 검색: MCTS를 사용하여 텍스트 블록을 결합하는 최적의 순서를 검색합니다.
최종 응답 생성: LLM을 사용하여 텍스트 블록의 최적 조합을 기반으로 최종 응답을 생성합니다.
응답 출력: 사용자에게 응답을 표시합니다.

이 단계는 CORAG가 검색, 향상, 생성의 세 단계를 효과적으로 결합하여 고품질의 자연어 응답을 제공하는 방법을 보여줍니다. 자세한 데이터 예시를 통해 독자들은 CORAG의 데이터 처리 프로세스와 작동 방식을 보다 명확하게 이해할 수 있습니다.

원본 텍스트:: https://arxiv.org/pdf/2411.00744

캡션:: CORAG: 검색 향상 생성을 위한 비용 제약이 있는 검색 최적화 시스템

작성자지팅 왕, 하이타오 위안, 웨이 동(난양공과대학교), 가오 콩(난양공과대학교), 페이페이 리(알리바바 그룹)

초록

대규모 언어 모델(LLM)은 생성 작업에서 뛰어난 역량을 보여 왔지만 최신 정보에 접근하기 어려워 환멸을 느낄 수 있는 경우가 많습니다. 검색 강화 생성(RAG)은 외부 데이터베이스의 지식을 통합하여 보다 정확하고 관련성 높은 응답을 도출함으로써 이 문제를 해결합니다. LLM의 컨텍스트 윈도우 제한으로 인해 전체 외부 데이터베이스 컨텍스트를 모델에 직접 입력하는 것은 비현실적입니다. 대신 가장 관련성이 높은 정보, 즉 '청크'(덩어리)만을 선택적으로 검색합니다. 그러나 현재 RAG 연구는 세 가지 주요 과제에 직면해 있습니다. 첫째, 기존 솔루션은 일반적으로 각 청크를 독립적으로 선택하기 때문에 청크 간의 잠재적 연관성을 무시합니다. 둘째, 실제로 청크의 효용은 "비단조적"이기 때문에 청크를 더 추가하면 전체 효용이 감소할 수 있습니다. 기존의 접근 방식은 포함된 블록의 수를 최대화하는 것을 강조하는데, 이는 의도치 않게 성능을 저하시킬 수 있습니다. 셋째, 각 유형의 사용자 쿼리에는 맞춤형 처리가 필요한 고유한 특성이 있는데, 현재의 솔루션은 이를 적절히 고려하지 못합니다.

이러한 문제를 극복하기 위해 검색 강화 생성을 위해 비용 제약이 있는 검색 최적화 시스템인 CORAG를 제안합니다. 최적의 블록 조합을 순차적으로 찾기 위해 몬테카를로 트리 탐색(MCTS) 기반 전략 프레임워크를 채택하여 블록 간의 연관성을 종합적으로 고려합니다. 또한, 예산 소진을 종료 조건으로 고려하는 대신 예산 제약을 블록 조합의 최적화 과정에 통합하여 블록 효용의 비단조성 문제를 효과적으로 해결합니다. 또한, 구성 에이전트를 설계하여 각 쿼리 유형에 대한 최적의 구성을 예측함으로써 적응성과 효율성을 향상시켰습니다. 실험 결과, 프레임워크는 기준 모델에 비해 최대 301 TP3T의 성능 향상을 보여줌으로써 긴 컨텍스트 애플리케이션에 대한 프레임워크의 효과, 확장성 및 적용 가능성을 강조했습니다.

PVLDB 참조 형식.

지팅 왕, 하이타오 위안, 웨이 동, 가오 콩, 페이페이 리. CORAG: 검색 증강 세대를 위한 비용 제약 검색 최적화 시스템 PVLDB, 14(1): xxx-xxx, 2020.
도이:XX.XX/XXX.XX

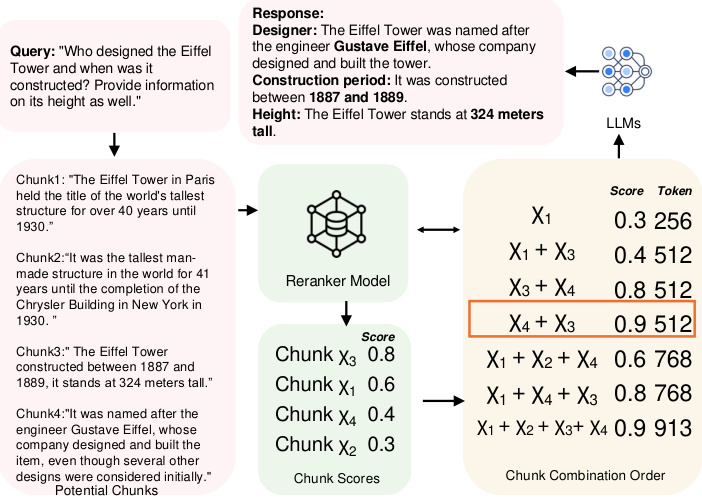
그림 1: 데이터 블록 조합 순서의 예시.

1 소개

LLM은 생성 작업에서 뛰어난 역량을 보여 왔지만, 최신 정보를 얻는 데 어려움을 겪는 경우가 많아 환각으로 이어질 수 있습니다[10, 38]. 이러한 문제를 해결하기 위해 RAG가 핵심 솔루션으로 부상했습니다. RAG는 외부 데이터 소스를 LLM에 통합함으로써 보다 정확하고 관련성 높은 최신 정보를 제공할 수 있습니다. 오늘날 RAG는 특히 질의응답 작업[2, 22, 29], 의료 정보 검색[1, 32], 시계열 분석[12, 26, 40]과 같이 업데이트된 외부 지식이 필요한 작업에서 LLM의 맥락에서 광범위하게 연구되고 있습니다. 외부 데이터 소스는 일반적으로 너무 커서 LLM에 직접 공급하는 것은 비현실적입니다. 이 문제를 해결하기 위해 일반적으로 데이터를 겹치지 않는 청크로 분할하여 벡터 데이터베이스에 저장한 다음, 사용자가 가장 유용한 청크를 쿼리하여 LLM에 대한 힌트를 구성합니다. 따라서 가장 관련성이 높은 청크를 찾기 위한 효율적이고 정확한 검색 구조와 알고리즘을 설계하는 것이 중요한 연구 주제가 되어 데이터베이스 [39, 48] 및 머신러닝 커뮤니티에서 광범위하게 연구되고 있습니다 [2, 35, 43].

하지만 기존 접근 방식에는 세 가지 주요 과제가 있습니다.

과제 1: 블록 간 연결 현재 가장 관련성이 높은 블록을 식별하는 데는 두 가지 주요 접근 방식이 있습니다. 첫 번째 접근 방식은 각 블록에 점수를 할당하고 점수에 따라 순위가 매겨진 대략적인 상위 k개의 블록을 선택하는 근사 근사 이웃(AKNN) 작업[41, 45]으로 문제를 공식화합니다. 두 번째 접근 방식은 블록을 클러스터링하고 쿼리에 대한 응답으로 가장 관련성이 높은 클러스터에 있는 모든 블록을 반환합니다[22, 29]. 그러나 두 방법 모두 블록 간의 잠재적 연관성을 무시합니다. 첫 번째 방법은 연관성을 완전히 무시하는 반면, 두 번째 방법은 각 클러스터의 모든 블록을 동등한 연관성으로 취급하여 피상적으로만 고려합니다. 결과적으로 이러한 방법은 여러 블록이 유사하거나 중복된 정보를 전달할 때 선택된 블록에 상당한 중복성을 유발합니다.

예를 들어 그림 1과 같이 에펠탑의 높이와 이력을 쿼리할 때 각 블록을 독립적으로 처리하면 욕심 방식은 처음 두 블록의 점수가 가장 높기 때문에 χ3와 χ1 블록을 선택합니다. 그러나 이 두 블록은 이력 정보만 제공하기 때문에 쿼리에 완전히 답하기에는 충분하지 않습니다. 쿼리에 더 잘 답하려면 χ4와 같이 빌더의 이름이 포함된 블록을 포함해야 합니다. 반면 클러스터링 방식은 χ1, χ2, χ3, χ4를 모두 반환하므로 중복성이 발생합니다. 최적의 솔루션은 중복 없이 필요한 정보를 제공하기 때문에 χ3과 χ4를 선택합니다. 또한, 연구[11, 19, 42]에 따르면 블록의 순서가 LLM의 성능에 영향을 미치는데, 이는 기존 방법에서도 무시되는 요소입니다. 예를 들어 에펠탑의 경우 블록 χ3과 χ4를 선택할 때 χ4를 첫 번째 위치에 배치하면 그 반대 순서에 비해 더 높은 점수를 얻게 됩니다. 그러나 두 경우 모두 사용 가능한 블록의 수에 따라 검색 공간이 기하급수적으로 증가하기 때문에 최적의 블록 조합 순서를 결정하는 것은 어려운 작업입니다. 이 백서에서는 이 문제가 NP-하드 문제임을 추가로 증명합니다(섹션 2.1 참조).

과제 2: 유틸리티의 비단조로움. 현재 솔루션은 더 많은 블록을 포함하면 항상 더 나은 최종 결과를 얻을 수 있다는 가정을 기반으로 합니다. 특히, AKNN 기반 접근 방식에서는 매번 정확히 k개의 블록이 결정론적으로 선택됩니다. 클러스터링 기반 접근 방식에서는 클러스터와 쿼리 사이의 거리 임계값을 설정하고 이 임계값 내에 있는 모든 클러스터를 반환합니다. 두 방식 모두 가능한 한 많은 블록을 반환합니다. 그러나 실제로는 블록의 유용성이 단조롭지 않습니다. 보다 구체적으로, 너무 많은 청크는 에지 관련 콘텐츠를 추가하여 핵심 정보를 희석시키고 명확성을 떨어뜨리는 노이즈를 생성합니다. 또한 블록 간의 충돌이나 미묘한 차이로 인해 모델이 혼동되어 응답 품질이 저하될 수 있습니다. 예를 들어, 그림 1에서 볼 수 있듯이 χ3과 χ4를 선택했을 때 블록 χ1을 추가하면 효용이 감소하는데, 이는 실제로 효용 점수가 일반적으로 단조롭지 않다는 사실을 강조합니다.

과제 3: 쿼리의 다양성. 사용자 쿼리에는 다양한 유형이 있으며, 각각 고유한 특성에 따라 다른 순위 지정 전략이 필요합니다[47]. 현재 RAG 시스템에서, 블록의 효용 점수는 일반적으로 할당된 리랭커 모델에 의해 결정됩니다. 현재까지 다양한 리랭커 모델이 존재하지만, 그 성능은 쿼리 유형에 따라 매우 다양하며, 모든 쿼리 변형에서 일관되게 다른 모델보다 우수한 성능을 보이는 고정된 리랭커 모델은 없습니다(자세한 내용은 섹션 6.3.4의 실험을 참조하세요). 현재의 접근 방식[20, 46]은 일반적으로 블록 랭킹을 위해 정적 리랭커 모델에 의존하며, 다양한 쿼리 컨텍스트에 적응할 수 있는 유연성이 부족합니다.

문제 설명: 모든 유형의 쿼리를 수용할 수 있으면서 블록 간의 연관성과 유틸리티의 비단조성을 충분히 고려하는 RAG 시스템이 존재하나요?

1.1 우리의 기여

이 백서에서는 RAG 시스템에서 블록 검색을 최적화하기 위한 새로운 MCTS 기반 정책 트리 프레임워크를 제안함으로써 이 질문에 긍정적으로 답합니다. 전반적으로 저희의 기여는 다음과 같이 요약할 수 있습니다:

- 저희는 RAG 작업에서 블록 조합의 순서를 고려하는 최초의 RAG 프레임워크를 제시합니다. 각 블록을 독립적으로 또는 클러스터링 수준에서 고려하는 대신 MCTS를 사용하여 최적의 블록 조합 순서를 순차적으로 검색할 수 있도록 지원합니다. 대략적인 아이디어는 다음과 같습니다. 먼저 루트 노드를 초기화합니다. 그런 다음 반복하는 동안 효용이 가장 높은 노드를 선택하고 해당 확장 노드의 효용을 계산하여 트리를 확장합니다. 각 확장 후에는 전체 정책 트리의 효용을 업데이트합니다. 이 과정에서 각 반복의 결정은 선택된 블록에 따라 달라지므로 블록 간의 연관성을 충분히 고려할 수 있습니다. 또한 MCTS는 지수적 탐색 공간을 선형으로 축소하고 병렬 확장 기법을 적용하여 계산 효율성을 더욱 높였습니다. 이 설계로 챌린지 1을 해결합니다.
- 예산 소진을 종료 조건으로 고려하는 기존 RAG 프레임워크와 달리, 저희는 블록 조합을 최적화하는 과정에 예산 제약을 통합하여 블록 효용의 비단조성을 충분히 고려하는 새로운 공식을 제안하여 과제 2를 해결합니다. 또한 상관관계가 높고 비용이 저렴한 블록의 우선순위를 정하고 토큰 길이를 고려함으로써, 저희는 계산 비용을 더욱 절감합니다. 계산 비용을 줄입니다.
- 우리는 쿼리에 맞게 MCTS 구성을 동적으로 조정하여 특정 쿼리 도메인에 맞게 재랭크 모델과 구성을 조정하는 비교 학습 기반 에이전트를 제안합니다. 이 접근 방식은 동적인 도메인별 쿼리에 유연성과 견고성을 제공하여 도전 과제 3에 부합합니다.
- 또한 프레임워크를 여러 최신 방법과 비교하는 종합적인 실험을 수행했습니다. 그 결과 우리 접근 방식의 효과성, 효율성, 확장성을 검증하고 기준선 대비 30%의 성능 향상을 확인했습니다.

2 준비 지식

이 섹션에서는 먼저 2.1절에서 블록과 블록 조합 순서와 같은 몇 가지 주요 개념의 정의를 소개합니다. 다음으로 블록 순서 최적화 문제에 대한 NP-하드 증명을 제시합니다. 마지막으로 2.3절에서 관련 작업에 대해 설명합니다.

2.1 주요 개념

헝겊 및 청크. RAG는 외부 말뭉치에서 관련 컨텍스트를 검색하여 생성 모델의 성능을 개선하는 효율적인 방법입니다. 이 접근 방식에서는 먼저 코퍼스를 블록이라는 더 작고 관리하기 쉬운 단위로 분할하여 벡터 데이터베이스에 저장합니다. 따라서 블록을 다음과 같이 공식적으로 정의할 수 있습니다:

정의 2.1(블록). C는 문서 말뭉치를 나타내고 블록 χ는 C에서 추출된 연속적인 텍스트 블록으로 정의합니다. 공식적으로 블록 χ는 토큰 시퀀스(t1, t2, ..., ... , tn)로 구성되며, 여기서 각 ti는 C의 토큰이고 크기 n은 사용자가 설정합니다.

RAG 시스템에서 각 블록은 블록의 의미적 의미를 파악하고 문맥상 유사한 콘텐츠를 검색할 수 있는 임베딩 모델을 사용해 벡터 표현에 임베드됩니다. 새로운 쿼리가 수신되면 벡터 데이터베이스는 유사성 검색을 수행하여 쿼리와 의미적으로 가장 연관성이 높은 블록을 식별합니다. 그런 다음 검색된 청크는 제너레이터(예: 대규모 언어 모델)로 전달되어 검색된 콘텐츠를 기반으로 최종 응답을 생성합니다. 특히, 블록에 포함된 토큰이 많을수록 생성기에 발생하는 비용이 높아집니다. 따라서 블록의 비용을 비용(χ) = |χ|로 정의하며, 이는 블록에 포함된 토큰의 수와 같습니다.

조합 순서를 차단합니다. RAG 시스템에서는 벡터 데이터베이스 검색 결과에 여러 블록이 포함될 수 있습니다. 그러나 생성 모델의 입력 제약으로 인해 이러한 블록을 모두 사용하는 것은 비현실적입니다. 따라서 주어진 비용 예산에 맞게 블록 조합이라고 하는 최적의 블록 하위 집합을 선택해야 합니다. 또한 조합 내 블록의 순서는 생성 모델의 성능에 큰 영향을 미칩니다. 블록 조합의 순서는 공식적으로 다음과 같이 정의할 수 있으며, 최적의 순서를 가진 블록 조합을 식별하는 것이 목표입니다:

정의 2.2(최적의 블록 조합 순서 선택). χ1, χ2, ... , χk}를 잠재적 블록의 집합, ℛ를 비용 예산, Φ = ⟨χφ1, ... , χφm⟩은 잠재적 블록 조합의 순서를 나타내며, 각 χφi는 블록이고 인덱스 φi는 Φ에서 해당 위치를 나타냅니다. U(Φ)는 리랭크 모델에 의해 할당된 효용 점수로, 임의적이거나 복합적일 수 있습니다. 우리의 목표는 최종 응답을 생성하기 위해 LLM에 공급하는 비용 제약 조건 하에서 효용 점수를 최대화하는 블록 조합의 순서를 찾는 것입니다(즉, 다음과 같이 검색).

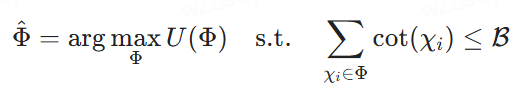
2.2 NP 난이도 증명

블록 조합 순차 선택이 NP-하드임을 보여주기 위해 최대 가중 하이퍼그룹 문제(MWHP)를 일반화합니다. MWHP는 NP-하드이므로 모든 MWHP 인스턴스를 다항식 시간 내에 블록 조합 최적화 인스턴스로 변환할 수 있음을 보여줍니다.

2.2.1 MWHP에 대한 문제 정의

V는 정점의 집합이고 E는 하이퍼엣지의 집합이며 각 하이퍼엣지는 V의 하위 집합을 포함하는 하이퍼그래프 ℋ = (V, E, w1, w2)가 주어지면 가중함수 w1: v → ℝ 및 w2: e → ℝ는 각 정점과 하이퍼엣지에 각각 가중치를 할당하는 함수입니다. 정점 V' ⊆ V의 하위 집합이 주어졌을 때, V'가 모든 정점을 포함하는 경우 하이퍼에지 e는 V'에 속한다고, 즉 e ∈ V'라고 합니다. 목표는 k개의 정점을 찾고 이 정점들과 이들이 커버하는 하이퍼엣지의 가중치의 합을 최대화하는 것입니다:

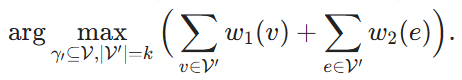
2.2.2 정규화 프로세스

이제 주어진 MWHP 인스턴스로부터 블록 조합 최적화 문제의 해당 인스턴스를 구축합니다. 각 노드 v ∈ V에 대해 해당 블록 Xv를 생성하고, 그 비용을 비용(Xv) ≡ 1로 정의합니다. 블록 조합 순서 Φ는 V(Φ) ⊆ V로 표시되는 V의 정점 하위 집합에 해당하며, 그 효용을 다음과 같이 정의합니다.

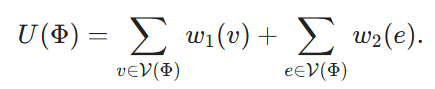
마지막으로 B = k를 설정하고 다음을 목표로 합니다.

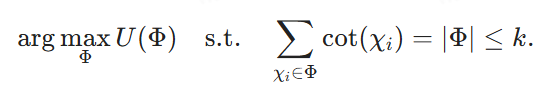
Φ가 (4)의 해를 나타낸다면, V(Φ)는 (2)의 해이며, 환원은 O(|V|-|E|) 시간 내에 수행할 수 있습니다.

이 유도법은 블록 조합 최적화 문제에서 재순위를 임의로 지정할 수 있다는 것을 전제로 하며, 이는 효용 점수 또한 임의로 할당할 수 있다는 것을 의미합니다. 리랭커에 대해 특정 가정을 하면 최적의 블록 조합 순서를 찾는 복잡성을 크게 줄일 수 있습니다. 예를 들어, 리랭커가 연관성을 고려하지 않고 각 블록의 효용 점수를 선형적으로 합산하면 각 블록을 독립적으로 평가할 수 있습니다. 그러나 이 백서에서는 가장 일반적인 경우를 다루며 리랭커 모델에 대한 어떠한 가정도 하지 않습니다.

2.3 관련 작업

2.3.1 강화 생성 가져오기

RAG[14, 20]는 지식 집약적인 NLP 작업을 처리하는 데 널리 사용됩니다. 일반적인 RAG 프로세스에서는 고밀도 임베딩 기반 리트리버가 외부 데이터베이스에서 관련 정보를 검색한 다음 생성 프로세스 중에 LLM에서 이를 사용합니다. 이 프로세스를 개선하기 위해 여러 연구[5, 18, 22, 35]에서는 LLM의 생성 요구에 더 적합하도록 리트리버를 조정하고, 다단계 검색 방법을 개발하고, 관련 없는 정보를 필터링하는 데 중점을 두었습니다. 많은 최신 검색기[8, 9, 15, 16, 27, 34]가 있지만, 엔드투엔드 프로세스에서 검색기와 LLM을 함께 최적화하는 것이 더 유망합니다[25, 31]. 예를 들어, 리트리버와 LLM을 동시에 또는 단계적으로 공동 훈련하는 연구[30]가 있지만, 이는 최적화를 위한 에이전트 손실이 필요하고 특히 임베디드 데이터베이스를 자주 재색인해야 하는 경우 훈련 프로세스를 복잡하게 만들어 높은 계산 비용을 발생시킵니다. 따라서 [5]와 같은 접근 방식은 복잡한 다단계 쿼리를 더 작은 하위 인텐트로 분해하여 빈번한 재색인 없이 응답의 포괄성을 향상시킵니다. 그러나 이러한 접근 방식은 일반적으로 블록 조합 순서의 중요한 역할을 무시하며, 이는 LLM의 전반적인 응답 품질에 상당한 영향을 미칠 수 있습니다. 저희가 아는 한, 이 논문은 RAG 작업에서 블록 조합 순서를 고려하는 최초의 접근 방식입니다.

2.3.2 RAG 순위 재조정

RAG 프로세스에서 검색 성능을 개선하려면 순위 재지정 방법이 필수적입니다 [43, 44, 51].

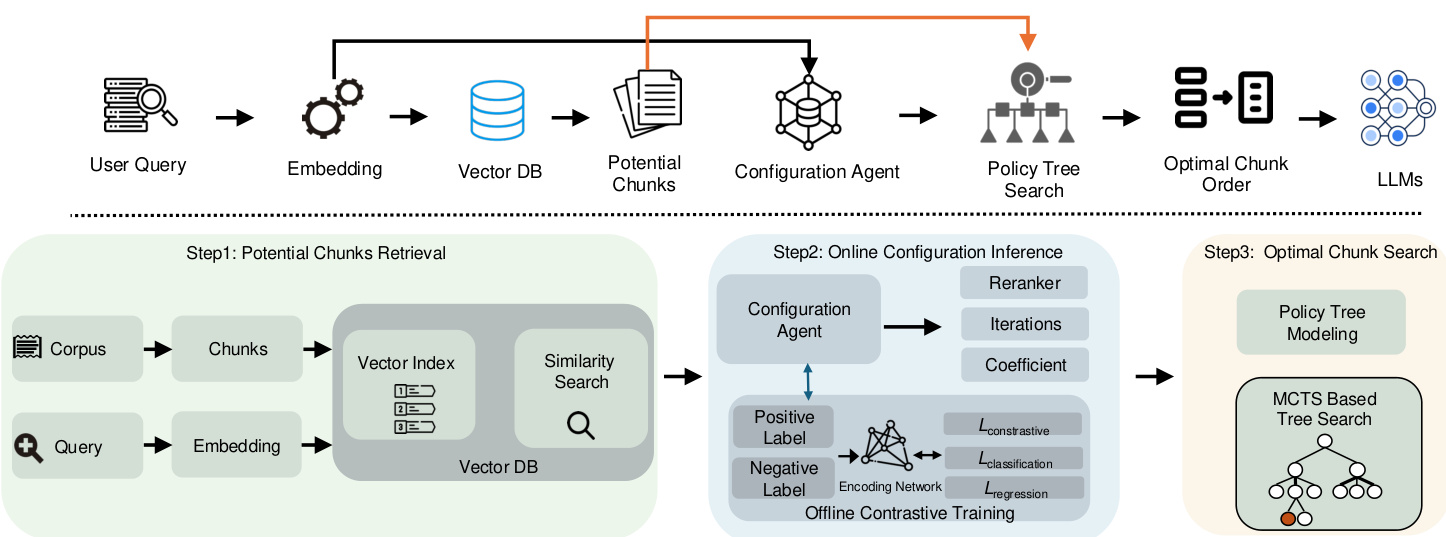
그림 2: CORAG 시스템 아키텍처 개요

기존의 재랭크 방법[33, 50]은 일반적으로 BERT 또는 T5와 같은 중간 규모의 언어 모델에 의존하여 검색된 컨텍스트의 순위를 매깁니다. 그러나 이러한 모델은 일반적으로 쿼리와 문맥 간의 의미 관계를 포착하는 데 어려움을 겪으며, 특히 표본이 0이거나 표본 수가 적은 환경에서는 더욱 그렇습니다. 따라서 최근 연구[43]에서는 노이즈가 많거나 관련 없는 정보가 있는 경우에도 문맥 재순위를 개선할 수 있는 명령어 조정 LLM의 잠재력을 강조했습니다. 이러한 발전에도 불구하고 RAG 시스템에서 LLM의 리랭크 기능은 여전히 제대로 활용되지 않고 있습니다. 특히, 블록 순위가 LLM의 성능에 영향을 미친다는 사실이 밝혀지면서[19] RAG 작업에서 블록 조합 순서를 고려해야 할 필요성이 강조되고 있습니다. 그러나 기존 모델은 고립된 블록이 아닌 최적의 검색을 위해 특정 순서나 블록의 조합이 필요한 상황에는 적합하지 않습니다. 따라서 향후 연구에서는 RAG 프레임워크 내에서 쿼리에 대한 응답으로 블록의 순서를 보다 효율적으로 정렬하기 위해 LLM을 더 잘 활용할 필요가 있습니다.

2.3.3 대규모 언어 모델을 위한 강화 학습

최근 강화 학습(RL)은 다양한 데이터 관리 및 RAG 작업에 점점 더 많이 사용되고 있으며, RL 기법은 검색 엔진과 같은 외부 지식 소스를 활용하여 대규모 언어 모델의 생성 능력을 향상시킬 수 있습니다[13, 23]. 특히, 사람의 피드백[4, 36, 37]을 통합하여 RL 프레임워크를 통해 모델이 보다 정확하고 맥락에 맞는 응답을 생성할 수 있도록 지원할 수 있습니다. 또한, 여러 쿼리 최적화 접근법[17, 21, 49]은 모델 성능이 쿼리 튜닝에 정보를 제공하고 궁극적으로 다운스트림 작업의 결과를 개선함으로써 검색 프로세스를 더욱 개선합니다. 이 연구에서는 RAG 시스템에서 블록 조합 순차 검색 프로세스를 최적화하기 위해 경량 RL 기법인 MCTS를 적용합니다. 또한 MCTS 검색 프로세스를 안내하는 구성 에이전트를 도입합니다. 저희가 아는 한, 이 특정 문제에 대한 접근 방식은 이것이 처음입니다.

3 시스템 개요

앞서 언급했듯이, 기존 RAG 프레임워크는 블록 간의 연관성과 블록 조합의 순차적 유용성의 비단조성을 적절히 고려하는 방법, 그리고 다양한 쿼리 도메인에 적응하는 방법이라는 세 가지 주요 과제에 직면해 있습니다. 이러한 문제는 출력 관련성 저하로 이어집니다. 이러한 문제를 해결하기 위해 쿼리 도메인과 사용자 예산을 모두 고려하여 최적의 블록 조합을 검색하도록 설계된 시스템인 CORAG를 도입했습니다. 이 시스템의 가장 중요한 구성 요소인 최적의 블록 조합 검색 모델을 소개합니다. 이 모델은 블록 조합 순서를 순차적으로 검색하기 위해 MCTS 기반 정책 트리를 사용하여 블록 간의 연관성(과제 1)과 블록 조합 순서 유틸리티의 비단조성(과제 2)을 충분히 고려할 수 있도록 합니다. 또한, 다양한 쿼리 도메인에 대해 최적의 MCTS 구성과 리랭커를 추천하는 구성 추론 모듈을 제안하여 챌린지 3을 해결합니다. 아래에서는 이 두 모듈에 대해 간략하게 설명합니다.

최적의 블록 조합 검색: 블록 연결을 고려하는 간단한 접근 방식은 벡터 데이터베이스에서 잠재적인 블록을 검색한 다음(1단계에 표시된 것처럼) 가능한 모든 블록 조합을 철저하게 탐색하는 것입니다. 그러나 이 접근 방식은 상당한 지연 시간과 계산 비용을 초래합니다. 이를 완화하기 위해 최적의 블록 조합 검색을 트리 내 노드 검색 문제로 재구성하는 전략 트리(2단계에 표시)를 구축합니다. 구체적으로 전략 트리의 루트 노드는 초기 비어 있는 상태를 나타내며, 각 하위 노드는 특정 블록 조합에 해당합니다. 예를 들어 루트 노드에 블록 χ1 을 나타내는 자식 노드가 있는 경우 자식 노드 중 하나는 χ1 + χ2 조합을 나타내고 다른 하나는 χ1 + χ3 을 나타낼 수 있습니다.

저희는 이 문제를 해결하기 위해 MCTS 기반 검색 알고리즘을 설계했습니다. 기존의 MCTS와 달리, 저희의 접근 방식은 가능한 모든 하위 노드를 평가하면서 각 반복에서 가장 효용성이 높은 노드를 확장합니다. 또한 전략 트리를 탐색하는 동안 비용과 예산 제약을 고려합니다. 노드 유틸리티는 탐색과 비용 관리의 균형을 맞춰 계산되며, 효율성과 정확성을 최적화합니다.

구성 추론: 구성 튜닝에 대한 간단한 해결책은 가능한 모든 구성을 열거하거나 순위를 재조정하고 결과를 병렬로 계산한 다음 최적의 구성을 선택하는 것입니다. 하지만 이렇게 하면 RAG 시스템의 비용이 비현실적으로 높아집니다. 정책 트리 검색 프로세스의 구성(즉, 반복 횟수, 비용 계수 및 탐색 계수)을 최적화하기 위해 쿼리 도메인을 기반으로 구성을 동적으로 생성하는 구성 에이전트를 도입합니다. 모델의 효율성을 보장하기 위해 양수 및 음수 레이블 쌍을 사용하는 비교 학습 접근 방식을 사용합니다. 양수 레이블은 동일한 최적 재랭크의 쿼리 임베딩에 해당하고 음수 레이블은 다른 최적 재랭크의 쿼리 임베딩에 해당합니다. 공동 손실 함수는 회귀(파라미터 튜닝용)와 대조 학습(라벨 판별력 향상용)을 동시에 최적화하는 데 사용됩니다.

요약. 프레임워크의 흐름은 그림 2에 나와 있습니다. 먼저 입력 쿼리에 대한 임베딩을 생성한 다음 이를 사용하여 벡터 데이터베이스에서 잠재적인 블록을 검색합니다. 이러한 쿼리 임베딩은 쿼리 필드를 기반으로 최적의 MCTS 구성을 동적으로 생성하는 구성 에이전트로도 전달됩니다. 이 최적 구성을 사용하여 정책 트리를 검색하여 검색된 잠재적 블록에서 최상의 블록 조합과 순서를 결정할 수 있습니다. 마지막으로, 이 최적의 블록 조합은 LLM에 대한 최종 힌트를 구성하는 데 사용됩니다.

4 블록 조합 검색

앞서 언급했듯이 블록 조합 순서는 LLM의 힌트 구성 효율에 큰 영향을 미칩니다. 특히 많은 수의 블록이 관련된 경우 잠재적인 조합의 수가 매우 많기 때문에 가능한 모든 블록 조합 순서를 열거하는 것은 불가능합니다. 이 섹션에서는 최적의 블록 조합 순서를 찾는 문제에서 효율성과 정확성의 균형을 맞추는 새로운 접근 방식을 제안합니다. 4.1절에서는 이 문제를 정책 트리에서 최적의 노드를 찾는 것으로 모델링합니다(4.1절). 그런 다음 이 노드 탐색 문제를 해결하기 위한 MCTS 기반 알고리즘을 제안합니다(섹션 4.2).

4.1 전략 트리 검색 모델링

최적의 조합 순서를 찾기 위한 첫 번째 단계는 가능한 모든 조합 순서를 효율적으로 열거할 수 있는 데이터 구조를 찾는 것입니다. 루트 노드에서 리프 노드로 이동하면서 모든 잠재적 답을 탐색할 수 있는 트리가 자연스러운 선택입니다.

전략 트리. 그림 3과 같이 벡터 데이터베이스에서 추출한 모든 가능한 블록 조합의 순서를 나타내는 전략 트리를 구성합니다. 구체적으로 루트 노드는 블록이 없는 초기 상태를 상징하며, 각 후속 노드는 잠재적 블록 중에서 선택된 블록을 나타냅니다. 따라서 자식 노드는 잠재적 블록의 대기열에서 사용 가능한 다음 블록을 선택하고 이를 조상 노드가 설정한 시퀀스에 병합하여 부모 노드에서 생성됩니다. 예를 들어 한 노드가 블록 조합 시퀀스 {χ1}을 나타내는 경우, 자식 노드는 {χ1, χ2}, {χ1, χ3} 또는 {χ1, χ4}와 같은 후속 조합 시퀀스를 포함할 수 있습니다. 따라서 전략 트리를 공식적으로 다음과 같이 정의합니다:

정의 4.1(전략 트리). 쿼리 q와 잠재적 블록 집합 {χ1, χ2, ... , ... , χn}이 주어지면 정책 트리 T를 구성합니다. T의 루트 노드는 블록이 없는 초기 상태를 나타냅니다. 이후의 각 비 루트 노드는 나머지 잠재 블록에서 새로 선택된 블록을 부모 노드의 시퀀스에 병합하여 블록 집합을 포함합니다. 이 프로세스는 각 비 루트 노드에서 순차적으로 블록의 순서대로 조합을 구성하며, 효용 점수가 가장 높은 노드를 찾는 것을 목표로 합니다.

전략 트리에서 우리의 목표는 최소한의 비용으로 최대의 이익을 제공하는 정렬된 블록을 포함하는 노드를 선택하는 것입니다. 이를 달성하기 위해서는 편익과 비용 간의 균형을 평가하는 효용 계산 함수를 설계해야 합니다. 이 함수는 아래에 설명된 대로 "노드 효용"이라고 정의하는 것으로 정량화됩니다.

노드 유틸리티. 유틸리티 메트릭은 블록 조합을 선택함으로써 얻을 수 있는 이점과 블록을 LLM의 프롬프트로 사용하는 데 드는 비용이라는 두 가지 구성 요소로 이루어져 있습니다. 구체적으로, 이점은 선택한 블록과 쿼리 간의 유사성을 측정하는 LLM에 의해 정량화됩니다. 특히, 이를 노드 값 V로 표시합니다. 다음으로, 노드 값 V(vi)와 검색 횟수 N(vi)의 탐색(탐색 횟수 N(vi)) 간의 균형을 맞추기 위해 상위 신뢰 한계(UCB)[3] 알고리즘을 사용합니다. 주어진 노드 vi에 대해 비용과 관련해서는 섹션 2에서 정의한 라벨링 비용을 고려하며, 할당된 총 예산 B에 대한 현재 블록 조합의 비용 비율로 측정합니다. 따라서 노드 유틸리티는 다음과 같이 정의됩니다:

정의 4.2(노드 유틸리티). 전략 트리와 비용 예산 B가 주어지면 비루트 노드의 효용은 다음과 같이 정의됩니다:

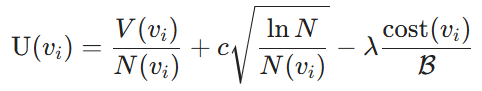
여기서 V(vi)는 훈련 모델에 의해 결정된 노드 vi에서 블록 조합의 예상 편익 값이고, N(vi)는 방문 횟수가 적은 노드의 탐색을 촉진하는 노드 vi의 방문 횟수이며, N은 탐색과 탐색 간의 균형을 유지하기 위해 정책 트리의 모든 노드에 대한 총 방문 횟수입니다. 또한 비용(vi)는 노드 vi의 라벨링 비용을 나타내고, B는 총 라벨링 예산, c는 탐색-탐색 트레이드오프를 조절하며, λ는 비용 효율성을 개선하기 위한 비용 패널티 요소로 사용됩니다.

최적의 노드 선택 모델링. 정의된 노드 유틸리티를 기반으로, 섹션 2에서 설명한 최적의 블록 조합 순서를 선택하는 작업은 정책 트리 T에서 최적의 노드를 선택하는 것으로 재구성됩니다. 주어진 예산 제약 조건 B 하에서, 목표는 vi와 관련된 총 비용이 B를 초과하지 않으면서 유틸리티 U(vi)를 최대화하는 노드 vi ⊆ T 를 식별하는 것입니다. 공식적으로는 다음과 같이 표현할 수 있습니다:

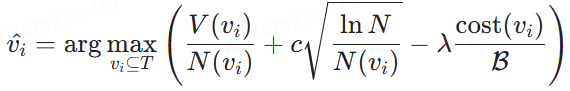
여기서 V(vi)는 노드 vi에서 블록 조합의 예상 편익을, cost(vi)는 관련 비용을 나타냅니다. 이 공식을 사용하면 주어진 예산 내에서 효용을 극대화하는 블록을 선택할 수 있습니다.

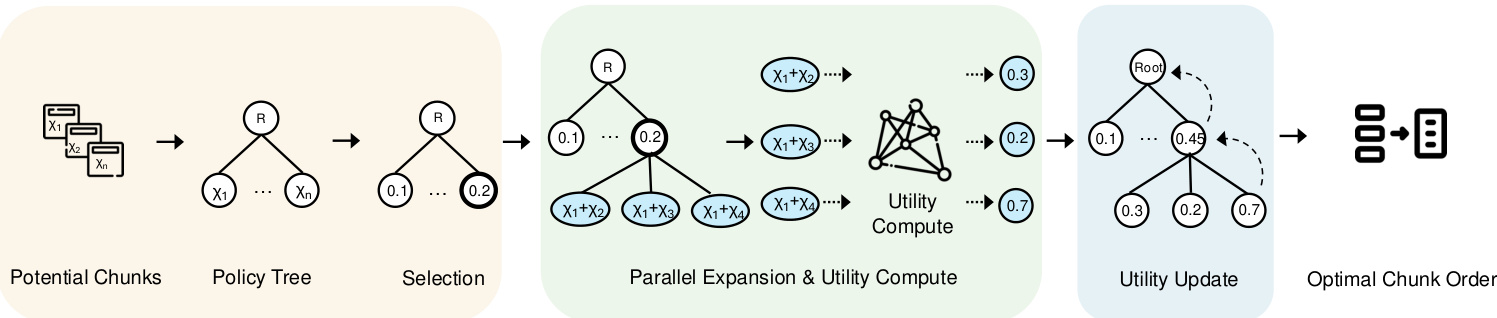
그림 3: MCTS 기반 블록 최적화 워크플로우

알고리즘 1 MCTS 기반 전략 트리 검색

4.2 MCTS 기반 정책 트리 검색

동기 부여. 정책 트리의 모든 노드를 열거하면 최적의 노드를 찾을 수 있지만 계산 비용이 많이 듭니다. 이 문제를 해결하기 위한 간단한 방법은 루트 노드에서 시작하여 트리를 반복적으로 탐색하는 욕심 전략을 적용하는 것입니다. 각 반복에서 가장 높은 이익을 가진 하위 노드를 선택하고 예산이 소진될 때까지 계속 진행합니다. 그러나 이 접근 방식은 최적이 아닌 결과를 초래할 가능성이 높습니다. 예를 들어 χ1이 χ2보다 약간 높은 편익을 가질 수 있지만 χ2 + χ3은 χ1 + χ3보다 훨씬 높은 편익을 가질 수 있습니다. 이 경우 욕심 많은 접근 방식은 차선의 결과를 초래할 수 있습니다. 따라서 효율성이 높은 상위 노드를 다시 살펴볼 필요가 있습니다. 동시에 효율성이 낮은 노드에 대한 탐색을 줄여야 합니다.

이러한 목표를 달성하기 위해 저희는 블록 조합을 효율적으로 선택하고 순위를 매기도록 설계된 MCTS 기반 전략 트리 검색 방법을 제안합니다. 이 접근 방식은 잠재적인 블록 시퀀스의 공간을 반복적으로 탐색하여 지정된 예산 제약 조건 내에서 주어진 쿼리를 최적화합니다.

개요. MCTS 기반 정책은 알고리즘 1에 설명되어 있습니다. 먼저 입력 쿼리를 사용하여 정책 트리의 루트 노드를 초기화합니다. 계산 예산이 소진되지 않으면 노드 선택과 유틸리티 업데이트라는 두 가지 주요 단계를 반복적으로 수행합니다. 반복 제한 또는 예산에 도달하면 프로세스를 중지하고 트리를 재귀적으로 검색하여 가장 높은 효용을 가진 노드를 찾습니다. 일반적으로 루트 노드에만 집중하는 기존의 MCTS 전략과 달리, 저희의 접근 방식은 블록 조합의 효용을 극대화하기 위해 유망한 중간 레벨 노드도 고려합니다.

주요 기능에 대한 자세한 설명. 이 두 가지 주요 기능에 대한 자세한 설명은 다음과 같습니다:

노드 선택(알고리즘 2). 최적의 블록 조합으로 이어질 가능성이 가장 높은 효용 가치가 가장 높은 노드를 재귀적으로 선택합니다. 구체적으로

알고리즘 2 노드 선택

알고리즘 3 유틸리티 업데이트

선택. 최대 효용 값을 가진 노드를 식별합니다. 𝑣가 아직 확장되지 않은 경우, 가능한 모든 하위 노드를 생성하여 전략 트리에 포함합니다. 𝑣가 확장된 경우, 추가 탐색을 위해 효용이 가장 높은 하위 노드를 선택합니다.
확장 프로그램. 활용도가 가장 높은 노드를 선택한 후, 모든 잠재적인 하위 노드를 생성하여 노드를 확장합니다. 각 하위 노드는 가능한 블록 조합의 새로운 순서를 나타냅니다. 저희의 접근 방식은 여러 하위 노드를 동시에 계산하고 평가하는 병렬 확장을 사용합니다. 이러한 병렬성은 단일 노드와 비슷한 계산 비용으로 여러 조합을 처리하는 가치 네트워크의 기능을 활용하여 검색의 효율성을 향상시킵니다.
계산된 유틸리티. 유틸리티 공식을 사용하여 각각의 새로운 자식 노드에 대한 유틸리티 값을 계산합니다. 리랭크 모델 R은 여러 블록 조합을 병렬로 처리하여 생성합니다.

5 에이전트 구성하기

사용자의 예산 내에서 블록 연결 처리의 효율성을 해결한 후 남은 작업은 각 쿼리의 도메인에 맞게 시스템을 설계하는 것입니다. MCTS 프로세스에는 재순위 선택, 반복 횟수, 탐색 계수, 비용 계수 등 몇 가지 주요 구성이 포함됩니다. 다양한 쿼리 유형에 걸쳐 이러한 구성을 최적화하는 것은 특히 어렵습니다. 이 문제를 해결하기 위해 각 쿼리에 대한 최적의 리랭커와 구성을 예측하는 구성 에이전트 프레임워크를 제안합니다. 이 섹션에서는 먼저 5.1절에서 에이전트 프레임워크를 소개한 다음 5.2절에서 모델 학습 프로세스를 간략하게 설명합니다.

5.1 모델링 프레임워크

동기 부여. 각 쿼리의 도메인에 맞게 조정하고 최적의 구성을 추천해야 하는 과제 3을 해결하기 위한 간단한 해결책은 MLP 분류기를 사용하여 각 쿼리를 최적의 재랭커에 할당하는 것입니다. 그러나 초기 실험에 따르면 MLP 분류의 성능이 좋지 않은 것으로 나타났습니다. 추가 분석 결과, 비슷한 유형의 쿼리가 동일한 최상의 리랭커와 구성을 공유하는 경향이 있는 것으로 나타났습니다. 따라서 대비 학습과 함께 샴 네트워크를 사용하여 같은 카테고리의 쿼리는 더 가깝게, 다른 카테고리의 쿼리는 더 멀리 밀어내는 것이 더 실현 가능한 접근 방식입니다.

그림 4는 입력을 특징 그래프로 변환하는 두 가지 주요 모듈로 구성된 에이전트의 개요를 보여줍니다. 먼저, 입력 임베딩 모듈은 입력 쿼리의 임베딩을 생성합니다. 그 후 인코딩 네트워크가 이러한 임베딩을 처리하여 피처 맵을 생성하고, 이 피처 맵은 MCTS 설정의 다양한 구성을 도출하는 데 사용됩니다.

다음 섹션에서는 각 구성 요소에 대해 자세히 설명하고 그 설계 근거를 설명합니다.

(1) 임베드된 쿼리를 입력합니다. 명시적 사실, 암묵적 사실, 해석 가능한 합리성, 숨겨진 합리성[47] 등 쿼리 유형의 다양성을 고려하여 다양한 쿼리의 요소를 효율적으로 포착하기 위해 BGE-M3[6] 임베딩 모델을 사용하여 각 쿼리에 대한 임베딩을 생성합니다. 이러한 임베딩은 유사한 유형의 쿼리를 동일한 리랭크 카테고리에 매핑하여 학습 프레임워크를 향상시킵니다. 1024차원 공간으로 표현되는 임베딩은 기본 의미적 특징을 포착하여 코딩 네트워크가 효율적으로 비교하고 분류할 수 있게 해줍니다. 이 단계는 다양한 쿼리 유형의 검색 관련성을 개선하는 데 도움이 됩니다. 또한 동일한 임베딩 모델을 사용하면 고유한 특징과 관련 메타데이터를 포함한 최적의 리랭크 주석 임베딩이 생성되어 모델이 쿼리를 최적의 리랭크에 정렬할 수 있습니다.

(2) 코드화된 네트워크를 사용하여 피처 맵 생성하기: 코드화된 네트워크의 재순위자 선택 작업을 최적화하고 다양한 쿼리 유형에 대해 각 쿼리에 가장 적합한 재순위자를 추천하기 위해, 분류와 구성 예측에 모두 유용한 표현을 효율적으로 학습하기 위해 코딩 네트워크를 사용합니다. 이 작업에는 완전히 연결된 세 개의 레이어로 구성된 샴 네트워크를 사용합니다. 이 네트워크는 차원 d = 1024의 입력 쿼리 임베딩을 처리하고 분류 출력과 MCTS 구성 예측(즉, 반복 횟수 및 λ)을 학습합니다. 인코딩 네트워크의 분기는 가중치를 공유하며, 각 분기는 선형 변환을 적용한 후 RELU를 활성화합니다. 순차적으로 첫 번째 숨겨진 계층은 차원을 512로, 두 번째 계층은 256으로, 세 번째 계층은 128로 줄이며, 최종 출력 계층은 각 쿼리에 대해 최상의 재순위를 지정하는 분류 예측과 검색 프로세스를 안내하는 가장 효율적인 MCTS 구성을 예측하는 데 사용되는 회귀 출력을 제공합니다. 분류 출력은 각 쿼리에 가장 적합한 리랭커를 식별하고, 회귀 출력은 최적의 MCTS 구성 설정을 결정합니다.

5.2 공동 교육

이 섹션에서는 구성 에이전트 개발을 위한 트레이닝 프로세스를 간략하게 설명합니다. 그림 4에서 볼 수 있듯이 모델의 학습 효율을 높이기 위해 세 가지 공동 학습 작업을 구현했습니다. 처음 두 작업은 각각 최적의 리랭커를 선택하고 MCTS 하이퍼파라미터의 최적 값을 예측하기 위한 분류와 회귀를 포함합니다. 또한 학습 프로세스를 더욱 개선하기 위해 비교 학습 접근 방식을 통합합니다.

5.2.1 분류 및 회귀 손실.

예측된 재랭크 레이블 Y(pred)와 그에 상응하는 실제 최적 재랭크 Y(true)가 주어지면 분류 손실 L(cla)는 다음과 같이 계산됩니다.

여기서 F(cla)는 예측된 리랭크 레이블과 실제 리랭크 레이블 사이의 교차 엔트로피 손실을 나타냅니다. 이 손실 함수는 각 쿼리에 대한 최적의 리랭커를 정확하게 분류하는 데 도움이 됩니다. 마찬가지로 회귀 손실 L(reg)은 다음과 같이 정의됩니다.

여기서 𝐹reg는 예측된 MCTS 파라미터 𝑝pred와 실제 MCTS 파라미터 𝑝true 사이의 평균 제곱 오차(MSE)입니다. 이 메트릭은 반복 횟수 및 𝜆 측면에서 MCTS 구성의 정확한 예측을 보장합니다.

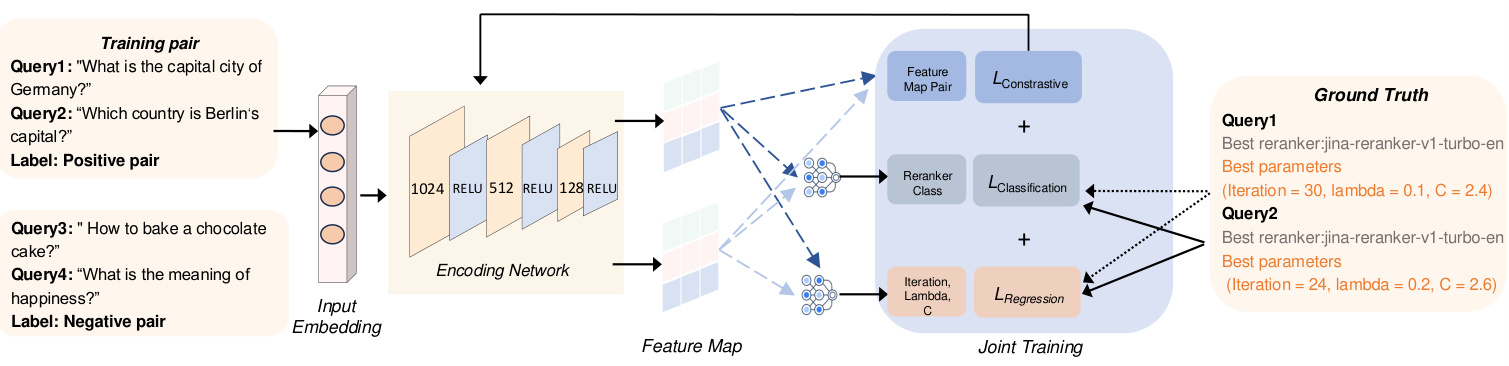
그림 4: 구성 에이전트 개요

5.2.2 대조 학습.

서로 다른 쿼리 도메인을 효율적으로 구분하고 각 쿼리에 가장 적합한 구성을 추천하기 위해 비교 학습을 사용하여 동일한 도메인의 쿼리를 서로 가깝게 배치하는 동시에 서로 다른 리랭크 클래스의 임베딩을 푸시아웃합니다.

비교 준비. 학습 데이터셋을 준비하기 위해서는 각 쿼리에 대한 최적의 리랭커와 구성을 결정해야 합니다. 본 연구에서는 다양한 설정에 대한 광범위한 실험을 통해 각 쿼리에 대한 최적의 리랭커와 해당 구성을 결정했습니다. 그 후 이러한 최적의 리랭커 주석을 기반으로 쿼리 쌍을 생성합니다. 포지티브 쌍은 동일한 최적의 리랭커를 공유하는 쿼리로 구성되며, 기능 공간에 포함되는 것을 최소화할 수 있습니다. 반대로, 네거티브 쌍은 서로 다른 리랭커를 가진 쿼리들로 구성되며, 이들 사이의 임베딩 거리를 최대화하는 것을 목표로 합니다. 일부 리랭커는 특정 쿼리에서 유사한 성능을 보이기 때문에, ROUGE-L이 10% 이상 차이가 나는 경우만 선택하여 훈련 데이터 세트를 구성합니다.

대비 손실. 그림 4와 같이, 주어진 양의 쌍(𝑥𝑖, 𝑥+)에 대해𝑖) 및 음수 쌍(𝑥𝑗, 𝑥-)𝑗), 먼저 코딩 모델을 사용하여 해당 피처 맵을 생성합니다. 그런 다음 이 피처 맵을 사용하여 대비 손실 𝐿con을 계산합니다. 구체적으로 이 프로세스는 다음과 같이 표현할 수 있습니다:

그중에서도.𝑓𝜃(𝑥) 는 임베딩 기능을 나타냅니다.𝐹con 는 두 가지 유형의 쌍에 적용되는 유사성 함수입니다. 양수 쌍(비슷한 재정렬자를 가진)과 음수 쌍(다른 재정렬자를 가진)입니다. 이 손실 함수는 같은 재정렬자가 있는 쿼리는 임베딩 공간에서 더 가깝게, 다른 재정렬자가 있는 쿼리는 더 멀리 배치되도록 설계되었습니다.

5.2.3 전체 교육 과정.

마지막으로 총 손실 함수 L(total)은 다음과 같이 비교, 분류 및 회귀 손실의 합입니다.

특히, 대비 손실 Lcon(θ)은 최적의 리랭크가 동일한 쿼리의 임베딩을 서로 가깝게 하고, 리랭크가 다른 쿼리의 임베딩을 멀리 밀어내는 역할을 합니다. 분류 손실 Lcla(θ)는 모델이 교차 엔트로피를 사용하여 리랭커를 정확하게 식별하는 데 도움이 되며, 회귀 손실 Lreg(θ)는 최적의 MCTS 구성을 예측할 때 발생하는 오류를 최소화합니다.

설명. 총 손실 L총계가 계산되면 학습 속도 η로 경사 하강을 사용하여 네트워크 파라미터 θ를 업데이트합니다. 이 최적화 프로세스는 여러 사이클 E와 배치에 걸쳐 반복되므로 시간이 지남에 따라 분류기와 매개변수 예측이 모두 개선됩니다.

6 실험

이 실험 연구는 다음과 같은 질문에 답하는 것을 목표로 합니다.
- RQ1 비용 제약이 있는 RAG 파이프라인에서 CORAG는 다른 방법과 어떻게 비교되나요?
- 블록 크기가 다른 RQ2 CORAG의 효율성은 어느 정도인가요?
- RQ3 현재 RAG의 병목 현상은 무엇인가요?
- RAG의 병목 현상은 무엇인가요?
- RQ4 다양한 데이터 세트 크기에 따라 CORAG의 확장성은 어느 정도인가요?
- RQ5 CORAG의 각 디자인은 얼마나 효과적인가요?

6.1 실험 설정

환경. 저희는 시스템을 인기 있는 RAG 프레임워크인 LlamaIndex와 통합했습니다. 실험은 인텔 코어 i7-13700K CPU(12코어, 24스레드, 5.3GHz), 64GB RAM 및 1TB NVMe SSD가 장착된 Linux 서버에서 실행되었습니다. 구성 에이전트 모듈은 PyTorch 2.0을 사용하여 24GB VRAM이 장착된 NVIDIA RTX 4090 GPU에서 구현되었습니다.

표 1: 실험에 사용된 통계 데이터.

데이터 집합	#트레인	#dev	#test	#p
MSMARCO	502,939	6,980	6,837	8,841,823
Wiki	3,332	417	416	244,136

데이터 세트.다양한 시나리오에서 CORAG의 성능을 평가하기 위해 작업 초점이 다른 두 가지 데이터 세트에서 실험을 수행했습니다. (1) WikiPassageQA [7]는 문단 수준 검색을 평가하기 위한 4,165개의 질문과 10만 개 이상의 텍스트 청크가 포함된 Q&A 벤치마크입니다. (2) MARCO [24]는 Q&A와 정보 검색에 중점을 둔 자연어 처리 작업 전용의 포괄적인 데이터 세트입니다. 표 1에서 볼 수 있듯이 WikiPassageQA와 MARCO는 모두 고품질 질문과 문단 주석을 제공하므로 검색 효과를 평가하는 데 적합합니다. 실험에서는 각 데이터 집합에 대한 실측 답변을 생성하도록 LLM에 요청합니다. 예를 들어, Llama3를 사용해 CORAG 성능을 평가하는 경우, 동일한 실험 설정에서 LLM의 특성에 맞게 공정성과 일관성을 유지하기 위해 Llama3를 사용해 지상 실측값을 생성하는 데도 사용합니다.

기준선.CORAG 성능을 두 가지 일반적인 RAG 기준선과 비교합니다:

- RAPTOR [29]: RAPTOR는 다단계 추상화를 위해 텍스트 블록을 재귀적으로 포함, 클러스터링, 요약하여 계층적 문서 요약 트리를 구성합니다. 이 접근 방식은 섹션 1에서 설명한 클러스터링 기반 접근 방식과 일치합니다. 대략적인 예산 제약 내에서 트리 구성을 완료합니다.
- NaiveRAG: 관련 블록을 검색하는 기본 방법입니다. 먼저 벡터 유사도 검색을 기반으로 벡터 데이터베이스에서 후보 블록을 검색한 다음 리랭크 모델을 사용하여 순위를 매깁니다. 이 방법은 섹션 1에서 언급한 AKNN 방식입니다. 비용 제약을 충족하기 위해 예산이 완전히 소진될 때까지 블록을 검색하는 탐욕스러운 예산 할당 전략을 사용합니다.

또한, 저희는 접근 방식에서 구성 에이전트를 제거하여 CORAG 성능에 미치는 영향을 평가하는 기준선으로 삼고 있으며, 이 버전을 CORAG w/o 에이전트라고 부릅니다. 마지막으로, 가능한 모든 블록 조합을 탐색하고 최상의 순서를 선택하여 상한을 설정하는 CORAG Upper라는 접근 방식을 구현합니다. 잠재적인 조합의 수가 많기 때문에 CORAG Upper의 경우 탐색을 6개 미만의 블록 조합으로 제한합니다.

비고.GraphRAG[22]와 같은 다른 접근 방식은 블록을 요약하고 인덱스를 구성하기 위해 LLM을 자주 호출하는 데 크게 의존하기 때문에 엄격한 비용 제약을 초과하는 막대한 비용(예: 수십억 개의 토큰)이 발생하게 됩니다. 따라서 이러한 접근 방식은 저희의 문제를 해결하는 데 적합하지 않습니다. 공정한 비교를 위해 이러한 유형의 RAG 접근 방식은 실험에서 제외했습니다.

하이퍼파라미터 설정: CORAG의 하이퍼파라미터는 구성 에이전트에 의해 자동으로 결정되는 반면, NaiveRAG는 하이퍼파라미터가 필요하지 않습니다. 다른 기준 방법의 경우, 공정한 비교를 위해 동일한 하이퍼파라미터를 사용하여 일관성을 보장합니다. 구체적으로 탐색 계수를 2.4로, 반복 횟수를 10으로, 비용 계수 λ를 0.1로 설정했습니다. 예비 실험 결과 이 구성이 기준선 성능을 최적화하는 것으로 나타났습니다. 또한 이러한 설정을 검증하기 위해 추가 제거 연구를 수행할 예정입니다.

매개변수 설정 학습. 이 접근 방식에서는 대비 학습을 사용하여 구성 에이전트를 학습시킵니다. 이 과정에서 사용되는 하이퍼파라미터에는 대비 손실(margin=1.0), 학습률(lr=0.001), 배치 크기(32), 주기 수(num_epochs=60), 임베딩 모델(즉, BAAI/bge-m3 [6]) 등이 있습니다.

평가 지표. 루즈-1, 루즈-2, 루즈-L을 평가 지표로 사용하여 실측 답변과 생성된 답변의 루즈 점수를 비교하여 효율성을 평가합니다. 효율성을 평가하기 위해 다양한 방법을 사용하여 쿼리에 응답하는 데 필요한 지연 시간을 측정합니다.

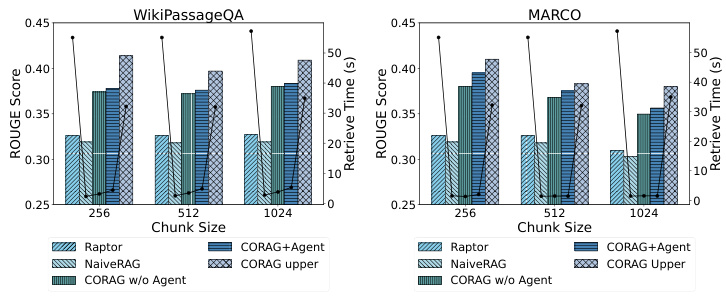
그림 5: 효율성 비교

6.2 성능 비교

6.2.1 RQ1: 루즈 비교.

그림 2에서 볼 수 있듯이, 우리는 주로 WikiPassageQA와 MARCO를 사용하여 다양한 데이터 세트에서 여러 기준선과 CORAG의 성능을 비교합니다. 평가는 세 가지 블록 크기에서 수행되며, Rouge-1, Rouge-2 및 Rouge-L 메트릭을 사용하여 우리의 검색 방법으로 인해 LLM에서 생성된 응답의 개선도를 평가합니다. 주류 RAG 방법(예: NaiveRAG 및 RAPTOR)에 비해 약 251 TP3 T의 상당한 개선을 보였습니다. 당연히 CORAG는 가능한 모든 조합 순서가 완전히 열거되어 비효율적이고 비실용적인 극단적인 경우를 나타내는 상한을 초과하지 않습니다. 결론적으로, CORAG는 기준선보다 성능이 뛰어나 검색 관련성을 향상시키는 동시에 검색 공간을 효과적으로 정리합니다.

6.2.2 RQ2: 효율성 평가.

그림 5에서 볼 수 있듯이, CORAG는 트리 검색 알고리즘을 기반으로 하기 때문에 에이전트는 주어진 쿼리에 대해 최적의 재순위와 파라미터를 예측하는 데 도움을 줍니다. 따라서 다양한 블록 크기와 데이터 세트가 검색 최적화 작업의 효율성에 미치는 영향을 평가하는 것이 중요합니다. 다양한 데이터 세트와 블록 크기를 사용해 효율성을 테스트한 결과, 전통적인 검색 방법을 사용하는 NaiveRAG는 검색 시간은 짧지만 루즈 점수는 낮았으며, CORAG는 루즈 점수는 높지만 전체 검색 공간을 탐색하기 때문에 효율성이 현저히 떨어지는 것으로 관찰되었습니다. 마찬가지로 RAPTOR는 요약에 외부 LLM을 사용하며 효율성이 떨어집니다. 이와 대조적으로, CORAG 접근 방식은 효율성과 검색 관련성 사이의 효과적인 절충점을 달성합니다.

6.2.3 RQ3: 성능 분해.

현재 RAG 시스템의 병목 현상을 강조하기 위해 기준이 되는 NaiveRAG의 성능 분해를 보여드립니다. 블록 조합의 최적 순서를 찾는 문제를 해결하기 위해 NaiveRAG를 사용하여 이를 구현하려면 a) 쿼리 임베딩 획득, b) 잠재적 블록 조합 검색, c) 잠재적 블록 조합의 순위 재조정, d) 큐 구체화 등의 단계가 필요합니다. 그림 6은 이전 실험 설정에서 각 단계의 평균 지연 시간을 보여줍니다.

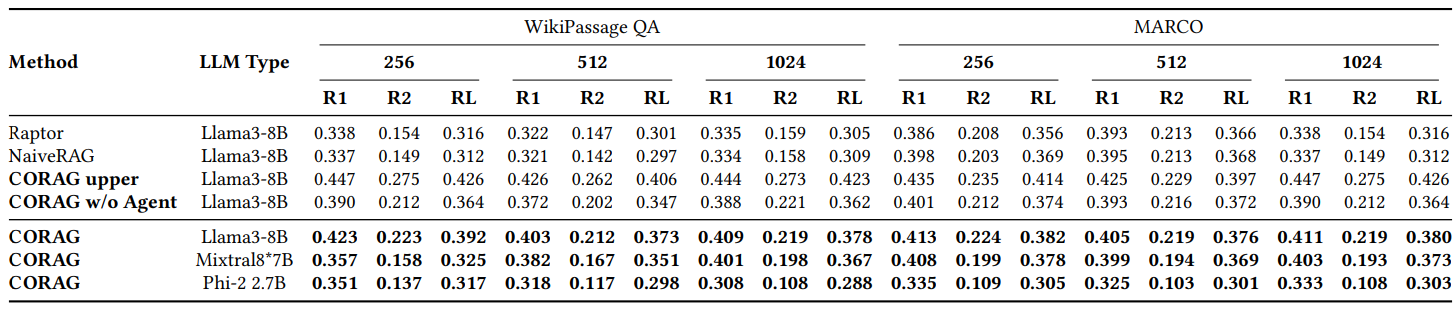
표 2: WikiPassage QA와 MARCO 데이터 세트의 루즈 비교

6.2.4 RQ4: 확장성 평가

CORAG는 특히 많은 수의 단락이 포함된 대규모 데이터셋(예: WikiPassageQA 및 MARCO)으로 작업할 때 뛰어난 확장성을 보여줍니다. 각 단락을 256개의 레이블이 지정된 청크로 분할하여 청크의 수를 10만 개 이상으로 쉽게 확장할 수 있습니다. 데이터 양이 크게 증가했음에도 불구하고 검색 시간은 기존 방식에 비해 10%밖에 증가하지 않아 대규모 검색 작업을 관리하는 데 있어 우리 시스템의 효율성을 입증했습니다. 특히, 저희 시스템은 검색 시간이 10분의 1밖에 걸리지 않으면서도 경쟁력 있는 ROUGE 점수를 제공함으로써 CORAG 상위 접근 방식보다 뛰어난 성능을 발휘합니다. 성능과 계산 오버헤드 사이의 이러한 효과적인 균형은 검색 공간을 효율적으로 정리하여 방대한 데이터 세트에서도 빠른 검색을 보장하는 시스템의 능력을 강조합니다. 따라서 이러한 접근 방식은 대규모 데이터 처리와 높은 검색 정확도가 필요한 시나리오에 매우 적합합니다.

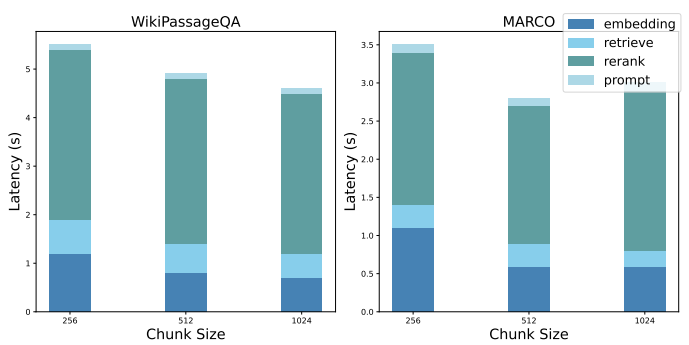
그림 6: 성능 분해

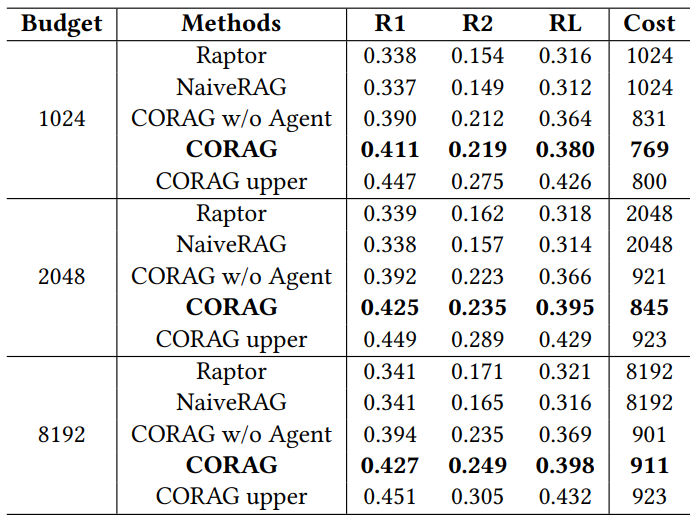
표 3: 다양한 예산에 따른 성과 비교

6.3 RQ5: 절제 연구

6.3.1 다양한 예산의 절제 연구

표 3에서 볼 수 있듯이, 저희는 비용 제약이 있는 시스템으로 CORAG를 평가하고 다양한 예산이 전체 성능에 미치는 영향을 조사했습니다. MARCO 데이터 세트를 사용하여 예산 한도를 1024, 2048, 8192 토큰으로 설정하고 ROUGE를 사용하여 결과를 평가한 결과, CORAG는 이러한 예산 수준에서 모든 기준선을 일관되게 능가하는 성능을 보였습니다. 특히, CORAG의 평균 태깅 비용은 각 예산 한도 이하로 유지되어 챌린지 2에서 강조한 것처럼 블록의 효용이 단조롭지 않음을 시사합니다. 예산이 증가함에 따라 CORAG는 단순히 블록 수를 늘리는 것이 아니라 검색 공간이 확장되어 더 많은 관련 정보를 포함할 수 있는 이점을 누리고 있습니다.

6.3.2 다양한 탐색 계수를 사용한 절제 연구

그림 7에서 볼 수 있듯이 다양한 탐사 계수가 시스템 성능에 미치는 영향을 평가하기 위해 제거 연구를 수행했으며, 특히 0, 1, 2, 3의 C 값을 테스트했습니다. 그 결과 약 2의 탐사 계수가 최상의 성능을 제공하여 탐색 과정에서 탐사와 개발 간의 최적의 균형을 이루는 것으로 나타났습니다. 이러한 균형을 통해 시스템은 잠재력이 높은 블록에 집중하면서 관련 정보를 효율적으로 발견할 수 있으며, 궁극적으로 RAG 응답이 개선됩니다. 반대로 탐사 계수가 낮을수록 탐사가 부족하여 최적의 결과를 얻지 못했고, 탐사 계수가 높을수록 초점이 과도하게 분산되어 최적의 결과를 얻지 못했습니다. 이러한 결과는 CORAG 검색 프로세스의 성능에서 탐색 계수의 중요한 역할을 강조하고 신중한 매개변수 조정의 중요성을 강조합니다.

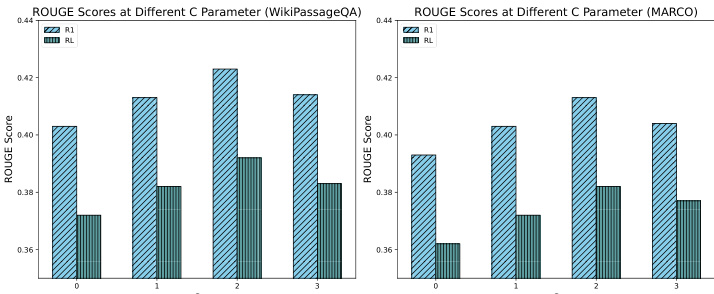
그림 7: 다양한 C 값 간의 ROUGE 비교

6.3.3 다양한 비용 요소를 사용한 절제 연구

그림 8에서 볼 수 있듯이, 다양한 비용 계수가 시스템 성능에 미치는 영향을 평가하기 위해 0, 0.1, 0.2, 0.3의 값을 테스트하는 제거 연구를 수행했습니다. 그 결과 유틸리티에 비용 계수를 도입하면 ROUGE 점수가 약간 감소하는 것으로 나타났습니다. 이러한 감소는 비용 제약이 없는 경우 CORAG가 비용 효율성을 희생하더라도 더 긴 출력을 생성하는 경향이 있기 때문입니다. 그러나 ROUGE 점수가 약간 감소했음에도 불구하고 감소폭은 51 TP3T 이내로 허용 가능한 수준입니다. 이러한 결과는 출력의 풍부함과 비용 제약의 균형을 맞추기 위해 비용 계수를 효율적으로 조정하는 것이 중요하다는 점을 강조하며, 효율적인 구성 튜닝을 통해 CORAG 성능을 최적화할 수 있는 구성 에이전트의 역할을 더욱 강조합니다.

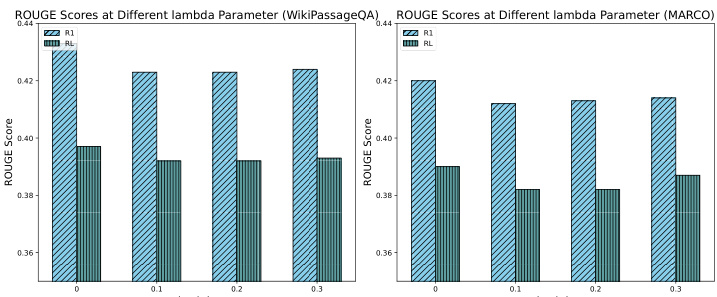
그림 8: 다양한 람다 값에 대한 ROUGE 비교

6.3.4 다양한 재배열기를 사용한 절제 연구

다양한 리랭커가 검색 성능에 미치는 영향을 평가하기 위해, 널리 알려진 6가지 리랭커 모델인 jina-reranker-v1-turbo-en, jina-reranker-v2-base-multilingual, bge-reranker-v2-m3, bge-. RER랭커-대형, BGE-RER랭커-베이스, GTE-멀티언어-RER랭커-베이스. 이러한 재배치기는 고정 비용 계수 0.1, 탐색 계수 2.4, 예산 제약 1024로 구성된 llama3-8B 모델을 사용하여 MARCO 데이터 세트에서 평가되었습니다.

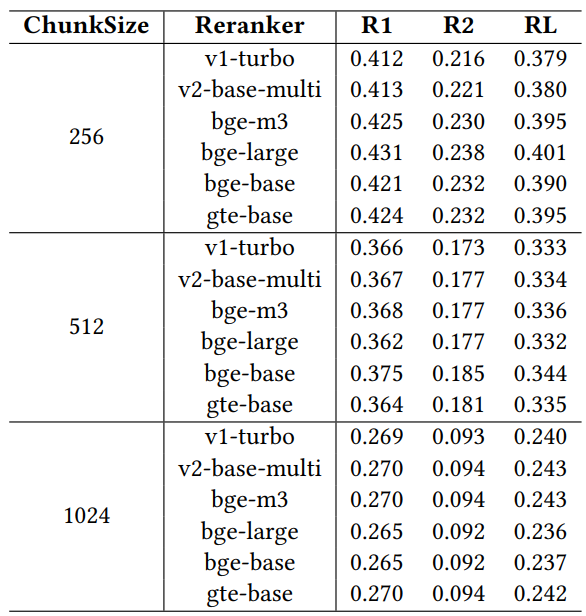
표 4: 다양한 리주더와의 성능 비교

표 4의 결과는 다양한 재랭커 간에 성능에 차이가 있음을 보여 주며, 특정 운영 제약 조건에서 RAG 시스템의 성능을 최적화하기 위해 재랭커를 신중하게 선택하는 것이 중요하다는 점을 강조합니다. 재랭커 중 gte-multilingual-reranker-base와 bge-reranker-large는 QA 작업에서 일관되게 강력한 성능을 보였으며, 이는 이러한 재랭커 모델이 다양한 QA 쿼리에 대한 관련 정보를 캡처하는 데 매우 효율적이라는 것을 시사합니다. 제거 연구에서 블록 크기가 커질수록 각 개별 재랭커가 다른 쿼리에 대한 권장 재랭커 측면에서 에이전트보다 성능이 떨어지는 것을 관찰했습니다. 이는 구성 에이전트가 검색 결과를 개선하기 위해 구성을 동적으로 조정함으로써 리랭커의 다양성을 효과적으로 활용하고 있음을 시사합니다. 더 나은 재배열 선택과 매개변수 구성을 추천하는 구성 에이전트의 기능은 특히 제한된 예산과 같은 제약 조건 하에서 RAG 시스템의 성능을 극대화하는 데 있어 그 역할을 강조합니다.

6.4 사례 연구

그림 9는 CORAG와 기존의 NaiveRAG 접근 방식의 검색 품질을 비교하는 세 가지 예를 보여 주며, 왜 우리의 접근 방식이 기준 접근 방식보다 성능이 뛰어난지를 강조합니다. 단순한 상위 k 검색과 재정렬로 인해 NaiveRAG는 쿼리와의 관련성보다는 키워드 매칭을 기반으로 청크를 검색하기 때문에 쿼리 의도와 관련된 중요한 정보를 놓치는 경우가 많습니다. 예를 들어, "잎이 많은 꽃은 관목인가요?"라는 쿼리의 경우 라는 쿼리의 경우 NaiveRAG는 일치하는 키워드를 포함하는 콘텐츠를 검색하지만 잎꽃의 실제 분류는 제공하지 못합니다. 반면, CORAG의 블록 조합 전략은 잎꽃의 카테고리를 포함하는 컨텍스트를 검색하여 LLM이 보다 정확한 응답을 제공할 수 있도록 합니다. 또 다른 사례에서 NaiveRAG는 '옥시플루오르펜'이 포함된 용어와 법률 조항을 검색했지만 쿼리 의도에 대한 이해가 부족한 반면, CORAG는 옥시플루오르펜을 면화의 사용 사례와 연결한 콘텐츠를 제공했기 때문에 NaiveRAG의 검색이 필요했습니다. 벡터 유사도 검색은 블록 간의 논리적 관계를 포착할 수 없었습니다. 마지막으로, "박테리아는 어디에서 왔을까?"라는 쿼리에 대해 알아보겠습니다. NaiveRAG는 "박테리아"라는 키워드가 포함된 청크를 검색하지만 그 기원은 다루지 않는 반면, CORAG는 박테리아의 기원과 번식 조건 등 보다 완전한 응답을 제공합니다. 이러한 사례는 논리적으로 연결된 정보를 검색하는 데 탁월한 CORAG가 단순한 키워드 매칭 이상의 기능을 필요로 하는 쿼리에 NaiveRAG보다 더 적합하다는 것을 보여줍니다.

그림 9: CORAG 사례 연구

RAG 및 향후 설계 옵션에 대한 7가지 인사이트

7.1 현재 RAG의 단점

현재 RAG 시스템에 대한 분석을 통해 검색(S1), 향상(S2), 생성(S3) 단계에서 직면한 성능 문제를 알려드립니다.

S1: 검색 오버헤드 현재의 RAG 시스템은 일반적으로 요약 및 색인 구조에 LLM을 사용하며, 외부 LLM과 관련된 계산 비용을 무시하기 때문에 계산 오버헤드가 증가합니다. 모델 기반 재정렬기는 검색 중 관련성을 향상시키지만 상당한 지연 시간을 발생시켜 지연 시간에 민감한 컨텍스트 효율성을 저해할 수 있습니다. 효율성과 성능의 균형을 맞추려면 비용 효율적인 인덱스 구성과 재정렬 최적화가 필수적입니다.

S2: 향상된 오버헤드 최적화된 블록 조합 순서 지정과 같은 검색 후 기술은 문맥 관련성을 향상시키지만 추가 계산이 필요합니다. 검색 공간을 최소화하고 조합 순서를 최적화하는 프루닝 전략은 계산 비용의 균형을 맞추고 문맥 관련성을 향상시키는 데 필수적입니다. 순서와 일관성에 중점을 둔 효율적인 블록 조합 최적화는 비용을 절감하고 검색 성능을 개선하는 데 필수적입니다.

S3: 세대 오버헤드 최적의 블록 조합을 위한 효율적인 힌트 엔지니어링에는 상당한 컴퓨팅 리소스가 필요합니다. 쿼리별 힌트 세분화 및 압축은 입력 관련성과 간결성을 유지하면서 오버헤드를 줄이는 데 필수적입니다. 다양한 쿼리 유형과 도메인별 요구 사항을 처리하기 위한 적응형 전략은 출력 품질을 저하시키지 않으면서도 프롬프트 효율성을 보장합니다.

7.2 디자인 옵션

위의 문제를 해결하기 위해 다음과 같은 설계를 통해 RAG 시스템의 성능을 최적화할 수 있습니다:

P1: 검색 및 재주문 프로세스의 공동 설계 CORAG에서는 트리 검색의 병렬 확장을 통해 쿼리 처리를 가속화하고 동시 검색과 재정렬을 가능하게 함으로써 지연 시간을 크게 줄였습니다. 향후 최적화를 통해 단계별 지연을 없애고 랭킹 효율성을 더욱 개선하여 병목 현상을 해결할 수 있습니다. 이러한 공동 설계 접근 방식은 블록 조합 순서를 효율적으로 관리하여 랭킹 프로세스 및 관련 점수를 개선합니다.

P2: 트리 구조 및 검색 반복 최적화 그 결과, 전략 트리 높이가 짧을수록 계산 오버헤드가 줄어들어 검색 효율성이 향상되며, 이는 대규모 데이터 세트에 특히 유용하다는 것을 보여줍니다. 트리 기반 검색에서 트리 높이를 최소화하면 문맥과 관련된 블록을 검색하는 속도가 향상되어 지연 시간과 계산 비용이 크게 줄어듭니다. 이 최적화 접근 방식은 대규모 데이터 세트에서 RAG 시스템의 성능을 향상시킵니다.

P3: 동적 팁 프로젝트 쿼리 유형에 따라 재정렬기를 선택하고 적응형 힌트 템플릿을 사용하면 LLM의 검색 관련성을 향상시킬 수 있습니다. 쿼리 의도와 도메인별 컨텍스트에 맞춰 동적 큐 구조를 조정하면 리소스 제약 내에서 출력 품질을 유지할 수 있습니다. 이러한 적응형 큐 엔지니어링 접근 방식은 효율성과 검색 품질 간의 효과적인 균형을 달성하여 RAG 시스템에서 쿼리의 동적 특성을 해결합니다.

8 결론

블록의 효용의 비단조성, 블록 간의 상관관계, 다양한 쿼리 도메인의 다양성을 고려하여 학습 기반 검색 최적화 시스템인 CORAG를 제안합니다.먼저 블록 조합의 순서를 정책 트리로 모델링하고 이 트리를 MCTS로 탐색하여 블록 조합의 최적 순서를 찾는 것을 목표로 합니다. 그리고 주어진 쿼리에 대한 최적의 구성과 재배치를 정확하게 예측하는 구성 에이전트를 도입합니다. 또한 각 반복에서 여러 노드를 확장하는 병렬 쿼리 확장 전략을 고안합니다. 실험 결과에 따르면 우리의 접근 방식은 비용 제약 내에서 최신 접근 방식보다 훨씬 뛰어난 성능을 보이며 효율성 측면에서도 뛰어납니다.