Problemas desafiantes de nivel olímpico: una revisión de 7 puntos de referencia de rendimiento en matemáticas chinas del LLM principal

La capacidad matemática, que abarca la derivación de fórmulas, la construcción de cadenas lógicas y el pensamiento abstracto, se considera desde hace tiempo un área clave para poner a prueba las capacidades de la Inteligencia Artificial (IA), en particular de los modelos lingüísticos a gran escala (LLM). Esto se debe a que no sólo pone a prueba la potencia de cálculo, sino que también profundiza en la capacidad del modelo para razonar, comprender y resolver problemas complejos.

Sin embargo, los resultados recientes de un equipo de la ETH de Zúrich muestran que incluso los mejores Modelos de Lenguaje Extenso (LLM) obtienen por lo general puntuaciones bajas cuando se enfrentan a preguntas difíciles de competiciones matemáticas, como los retos a nivel de la Olimpiada Matemática de EE.UU., lo que suscita un debate sobre las verdaderas capacidades de los LLM actuales en términos de razonamiento matemático riguroso.

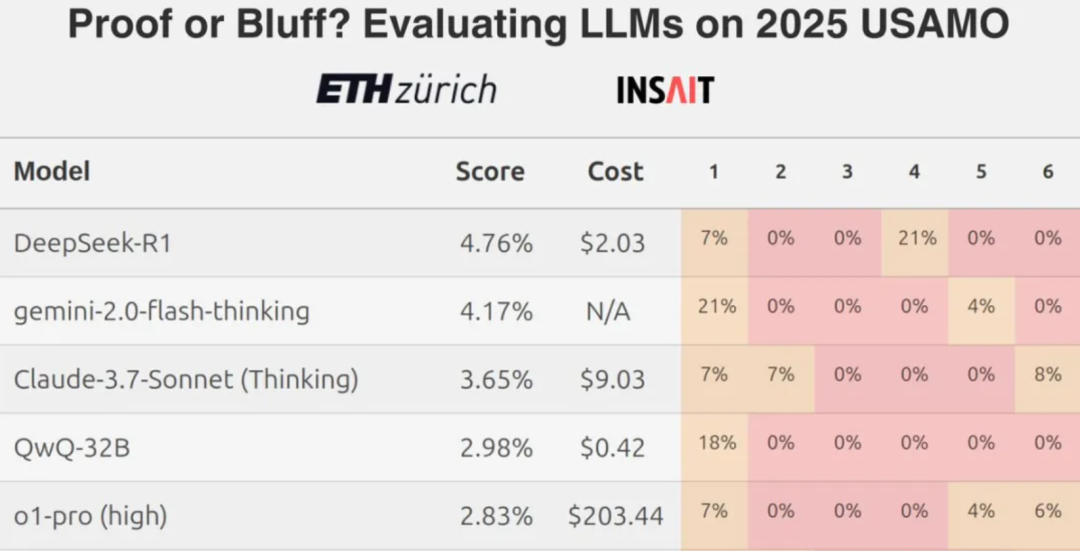
En este contexto, una pregunta natural es: ¿qué tal funcionan estos modelos cuando se enfrentan a problemas matemáticos formulados en chino? En esta revisión, se seleccionaron siete modelos lingüísticos a gran escala, tanto nacionales como extranjeros, para comparar sus capacidades matemáticas utilizando problemas de la Competición Mundial de Matemáticas de Alibaba y de la Olimpiada China de Matemáticas.

Entre los modelos que participan en la prueba figuran:

• Modelos domésticos:DeepSeek R1yHunyuan T1yTongyi Qwen-32B (texto original) 通义QwQ-32B),YiXin-Distill-Qwen-72B
• Modelización internacional:Grok 3 betayGemini 2.0 Flash Thinkingyo3-mini

Evaluación global de los resultados

La evaluación consta de 10 preguntas de alto nivel de dificultad, con un total de 13 preguntas puntuables. Los criterios de puntuación fueron: 1 punto por corrección completa, 0,5 puntos por corrección parcial y ningún punto por errores.

La corrección global de cada modelo en esta prueba es la siguiente:

Las distribuciones detalladas de las puntuaciones muestran las diferencias de rendimiento entre modelos:

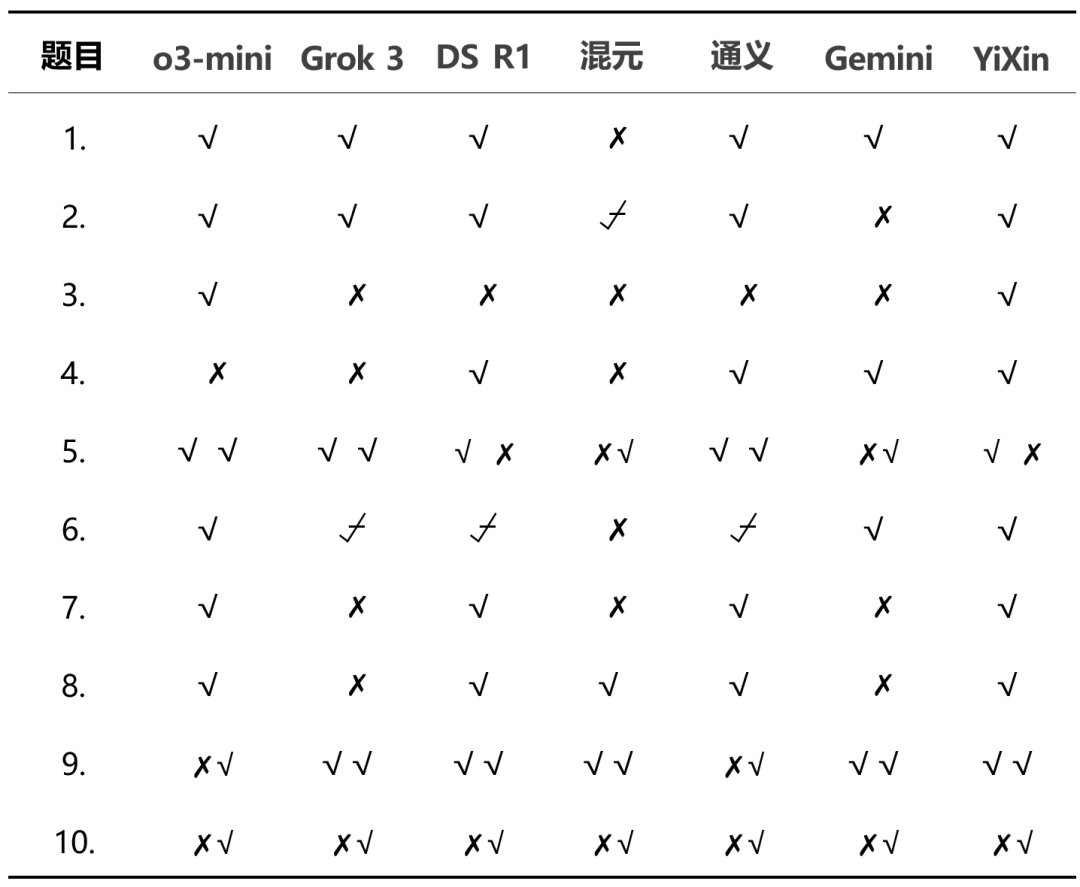
De los resultados globales.o3-mini responder cantando YiXin-Distill-Qwen-72B obtuvo buenos resultados en esta prueba, demostrando una gran capacidad para resolver problemas matemáticos. El rendimiento de los demás modelos varió.

A continuación se muestran las respuestas concretas a algunas de las preguntas del test.

Detalles de la medición

Ronda 1: El problema del cambio

Pregunta: El abuelo tiene 60 dólares y va al supermercado a comprar verduras por valor de 20 dólares, ¿cómo podría el cajero darle el cambio al abuelo?

Análisis: Se trata de una pregunta de aplicación de aritmética básica que examina la comprensión por parte del modelo de situaciones de la vida real y de habilidades básicas de cálculo monetario.

Resultados:
o3-mini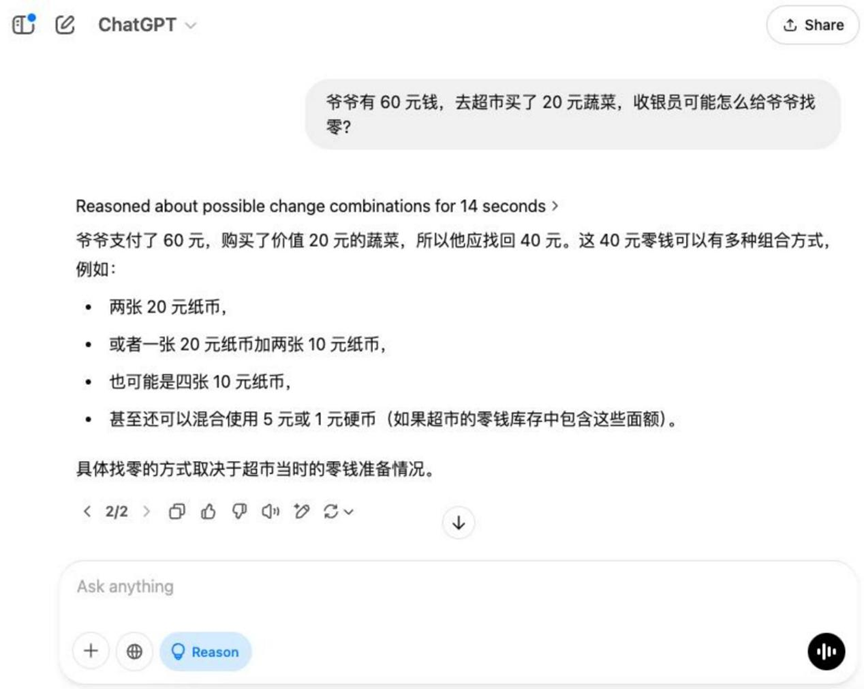

Grok 3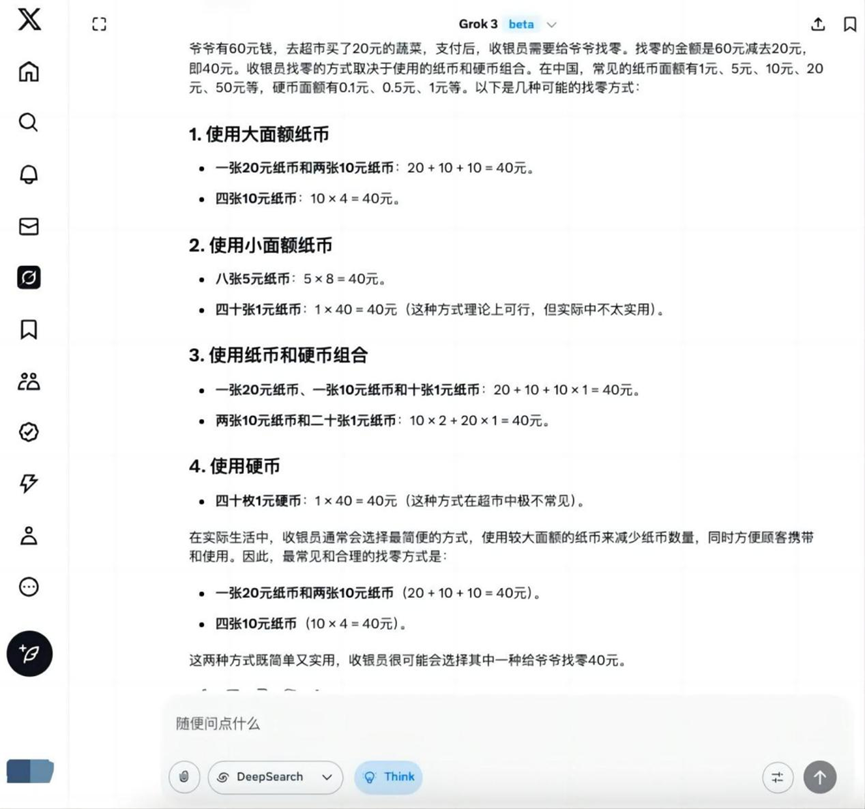

DeepSeek R1

Hunyuan T1

Gemini 2.0 Flash Thinking

YiXin-Distill-Qwen-72B

Sobre este tema básico, además de Hunyuan T1 Fuera de eso, el resto de los modelos dan la solución correcta para encontrar el cero.

Ronda 2: Cálculo de las distancias recorridas a pie y juicios metodológicos

Pregunta: Xiao Ming y Xiao Hua van andando al colegio todos los días. Ming camina 48 metros por minuto y Hua camina 55 metros por minuto. La casa de Xiaoming está a 384 metros de la escuela. Xiaohua tarda 4 minutos más que Ming en ir de casa a la escuela. ¿A qué distancia está la casa de Xiaohua de la escuela? ¿Cuál de los siguientes métodos es incorrecto y por qué?

Método 1: 55 × 4 = 220 (metros), 384 + 220 = 604 (metros)
Método 2: 384 / 48 = 8 (minutos), 55 × (8 + 4) = 660 (metros)

Análisis: Esta pregunta combina el cálculo de problemas de desplazamiento y el juicio lógico, exigiendo que el modelo sea capaz no sólo de calcular la respuesta correcta, sino también de analizar la corrección o incorrección de la solución dada, examinando el razonamiento en varios pasos y el discernimiento lógico.

Resultados:
DeepSeek R1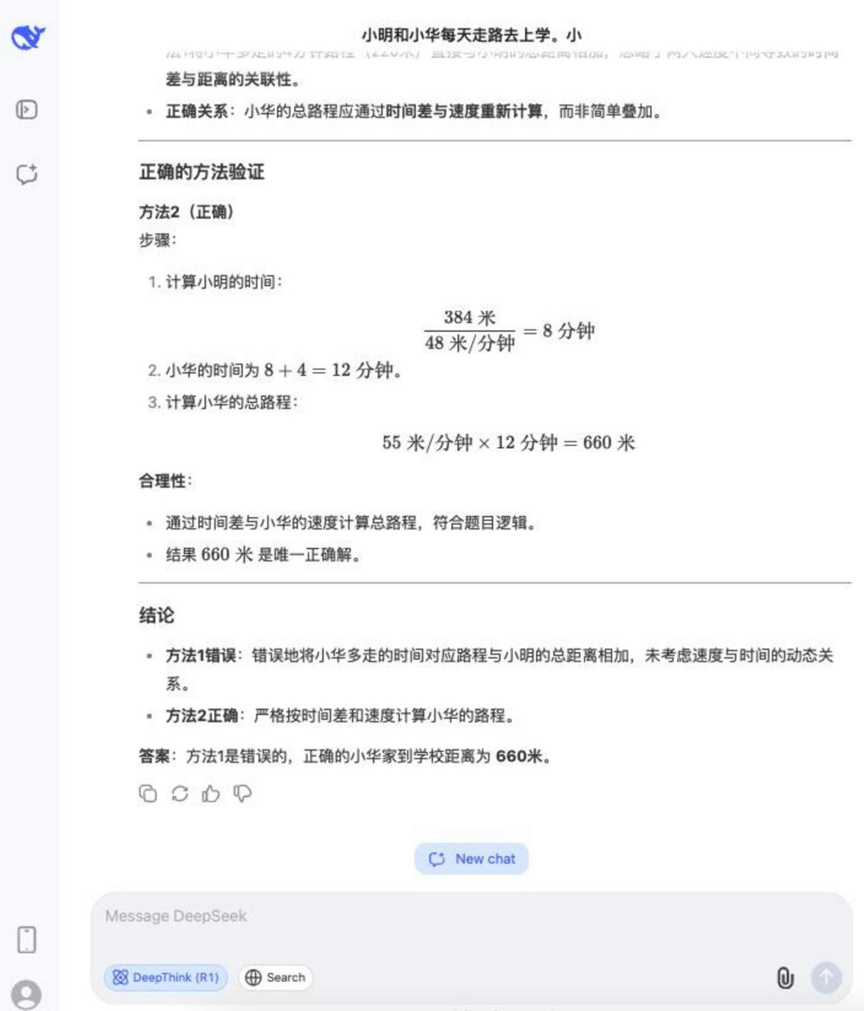

Tongyi Qwen-32B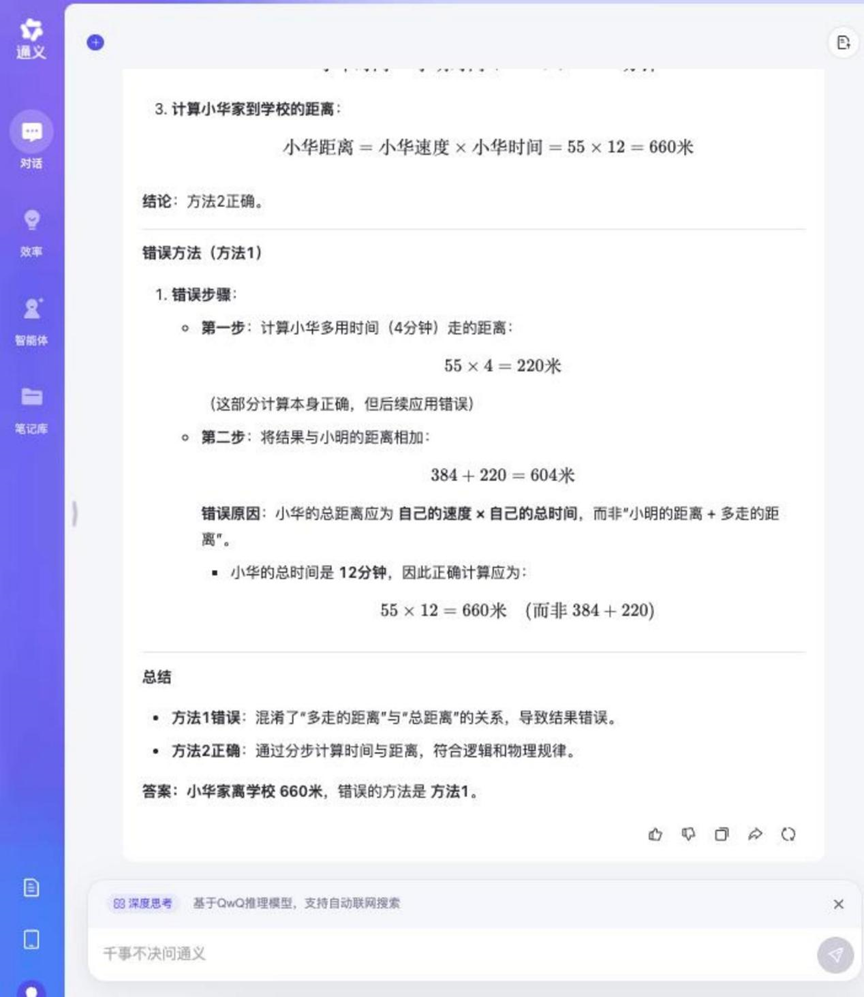

YiXin-Distill-Qwen-72B

El proceso de razonamiento de esta pregunta fue relativamente largo, pero la mayoría de los modelos que participaron en la prueba pudieron responderla correctamente y determinar el método incorrecto.

Ronda 3: Problema de oclusión geométrica (torres invisibles)

Pregunta: En una ciudad hay 6 torres situadas en los puntos A, B, C, D, E y F. Varios estudiantes forman un grupo viajero para ir de excursión a la ciudad. Al cabo de un rato, cada uno de los estudiantes se da cuenta de que sólo puede ver las 4 torres situadas en los puntos A, B, C y D, pero no las torres situadas en los puntos E y F. Se sabe que las posiciones de los alumnos y las torres se consideran puntos del mismo plano y que estos puntos no coinciden entre sí, y que 3 cualesquiera de los puntos A, B, C, D, E y F no comparten una línea común. La única posibilidad de no poder ver la torre es que la línea de visión esté bloqueada por otra torre. Por ejemplo, si un alumno se encuentra en un punto P que está situado junto a A y B, y A está en el segmento de recta PB, entonces el alumno no podrá ver la torre situada en B. Pregunte: ¿cuál es el número máximo de alumnos que puede haber en este grupo itinerante? a. 3 b. 4 c. 6 d. 12

Análisis: Se trata de una cuestión compleja de razonamiento geométrico y lógico que implica problemas de visibilidad, oclusión y configuración de conjuntos de puntos, lo que requiere un alto nivel de imaginación espacial y razonamiento lógico en el modelo.

Resultados:
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B

La dificultad de las preguntas ha aumentado considerablemente. En esta ronda de pruebas, sólo o3-mini responder cantando YiXin-Distill-Qwen-72B resuelto con éxito, los otros modelos no dieron una respuesta correcta.

Ronda 4: Problemas de probabilidad (Tigres y tigres)

Pregunta: Durante la Fiesta de la Primavera, una empresa lechera puso en marcha una actividad de cajas ciegas del Año Nuevo Chino: cada caja de leche viene con un "paquete rojo", que contiene "Tigre" "Sheng" Wei" uno de los tres dibujos. Juntando dos "Tiger", un "Sheng" y un "Wei" se puede deletrear "Tiger Tiger Sheng Wei" retrato de familia. Una vez lanzada la actividad, se convirtió en un éxito de Netflix y atrajo a mucha gente a participar. Las condiciones conocidas son las siguientes: los patrones de los paquetes rojos se distribuyen aleatoriamente de forma independiente y no pueden distinguirse unos de otros. La probabilidad de que aparezcan los tres dibujos "Tiger", "Sheng" y "Wei" es de 1/3. P: Para reunir un juego completo de "Tiger Tiger Sheng Wei P: ¿Cuántos cartones de leche hay que comprar por término medio para reunir un juego completo de fotos de familia "Tigre, Tigre, Poderoso"?

Análisis: Se trata de un típico problema de recaudación (variante del problema de recaudación de cupones), que requiere el uso de la teoría de la probabilidad y cálculos de expectativas, y examina la capacidad del modelo para tratar con modelos de probabilidad y realizar cálculos matemáticos de expectativas.

Resultados:
DeepSeek R1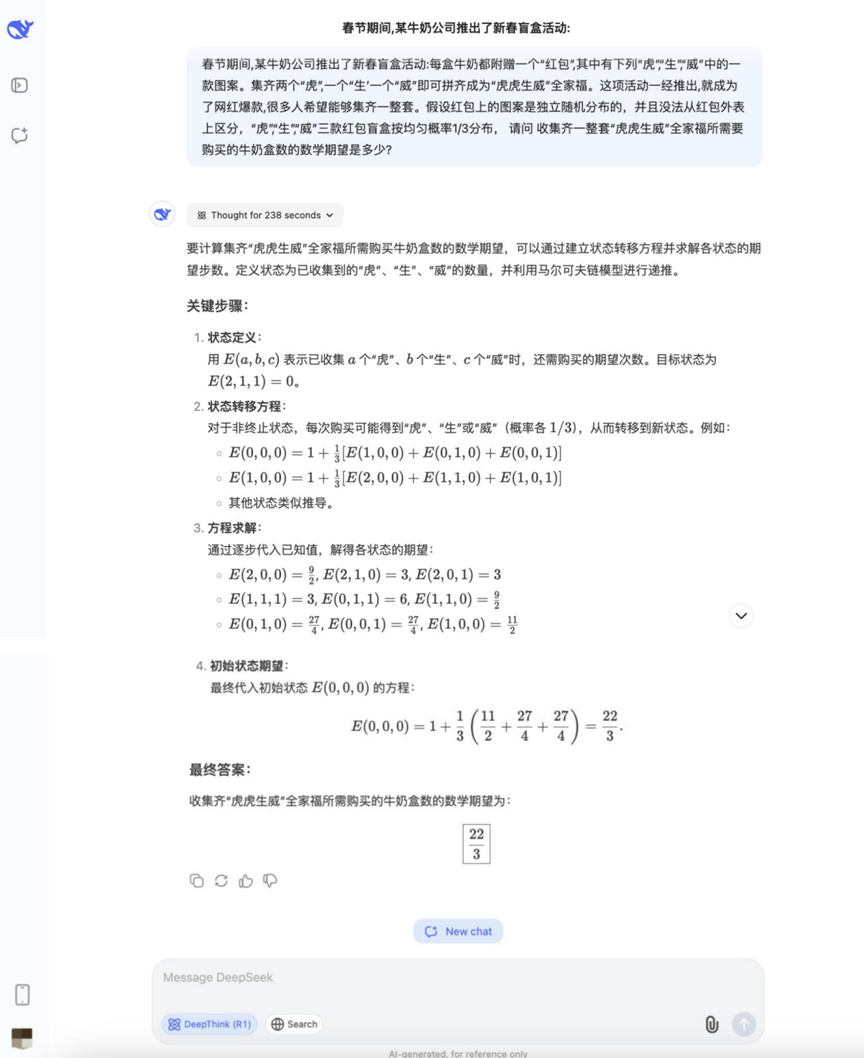

Hunyuan T1
 

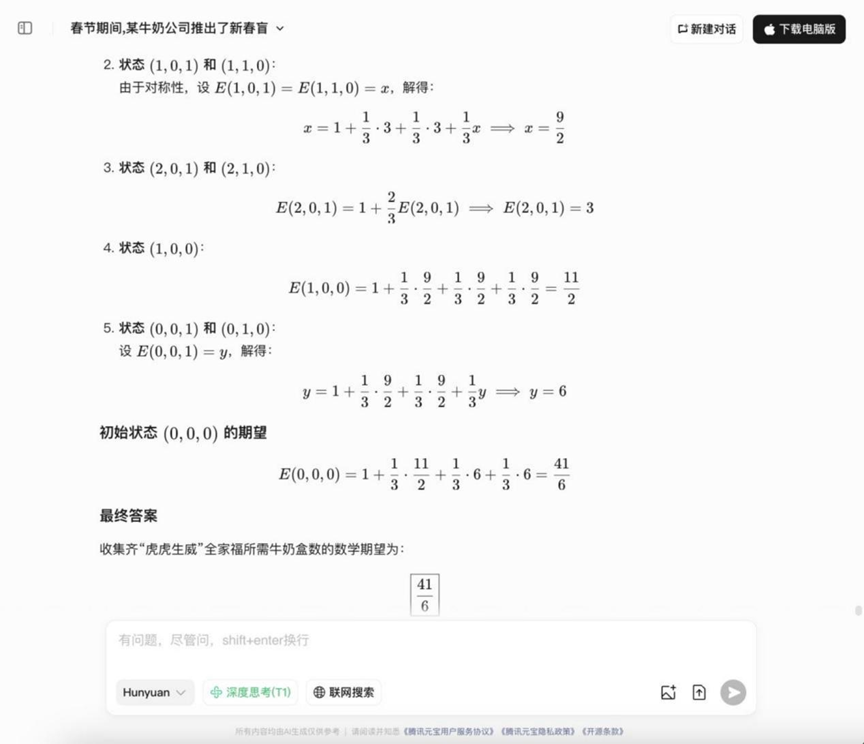
YiXin-Distill-Qwen-72B

Las respuestas a las preguntas sobre probabilidad en esta ronda empezaron a divergir, con algunos modelos capaces de enumerar correctamente las ideas y calcularlas.

Ronda 5: Geometría y planificación de trayectorias (Juegos de lucha)

Problema Descripción Imagen:

Análisis: Se trata de un problema que combina geometría, sistemas de coordenadas o cuadrículas y estrategias de camino más corto/óptimo, y puede requerir que el modelo comprenda la información gráfica y realice razonamientos y planificaciones espaciales.

Resultados:
o3-mini: Resolución satisfactoria

YiXin-Distill-Qwen-72B: Parcialmente correcto
 

Esta ronda de pruebas requiere un mayor grado de integración del modelo, ya que aproximadamente la mitad de los modelos probados se manejan de forma totalmente correcta.

Ronda 6: Problemas de Pruebas de Teoría de Números (Encontrar Mínimos No Factores)

Problema Descripción Imagen:

Análisis: Al entrar en el terreno de las preguntas de demostración, que requieren una deducción lógica rigurosa y una comprensión profunda de los conceptos de la teoría de números, estas preguntas son una prueba directa de la capacidad del modelo para razonar de forma abstracta.

Resultados:
o3-mini

YiXin-Distill-Qwen-72B
 

En la modelización doméstica, elYiXin-Distill-Qwen-72B Ha obtenido mejores resultados en esta ronda de preguntas de prueba. Las preguntas de prueba fueron mucho más difíciles para el modelo.

Ronda 7: Funciones y problemas de mapas (mapas en el círculo unitario)

Problema Descripción Imagen:

Análisis: Esta pregunta trata de los conceptos de funciones, cartografías y círculo unitario en matemáticas superiores, y examina la capacidad del modelo para comprender y aplicar definiciones matemáticas abstractas.

Resultados:
o3-mini

YiXin-Distill-Qwen-72B
 

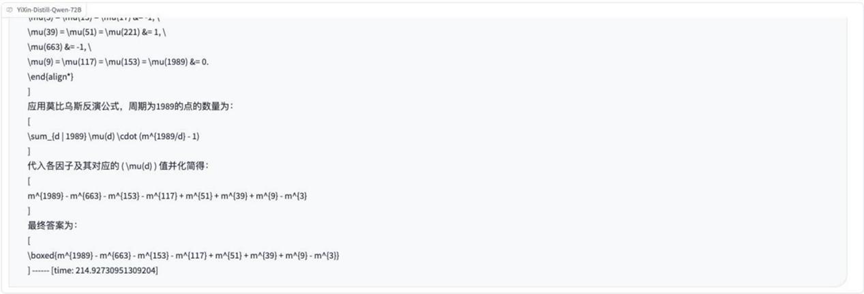
Aproximadamente la mitad de los modelos fueron capaces de resolver correctamente este problema relacionado con los mapas abstractos.

Ronda 8: Problemas de optimización combinatoria (triángulo máximo)

Pregunta: Hay 1989 puntos en el espacio, tres de los cuales no comparten una línea. Estos puntos se dividen en 30 grupos, cada uno con un número diferente de puntos. Se puede formar un triángulo tomando como vértice un punto cualquiera de tres grupos diferentes. P: ¿Cómo se puede distribuir el número de puntos de cada grupo para maximizar el número de triángulos formados?

Análisis: Se trata de un problema de optimización en matemáticas combinatorias que requiere un modelo para comprender los principios del recuento combinatorio y encontrar la estrategia de asignación óptima, lo que implica ideas más complejas de modelización matemática y optimización.

Resultados:
o3-mini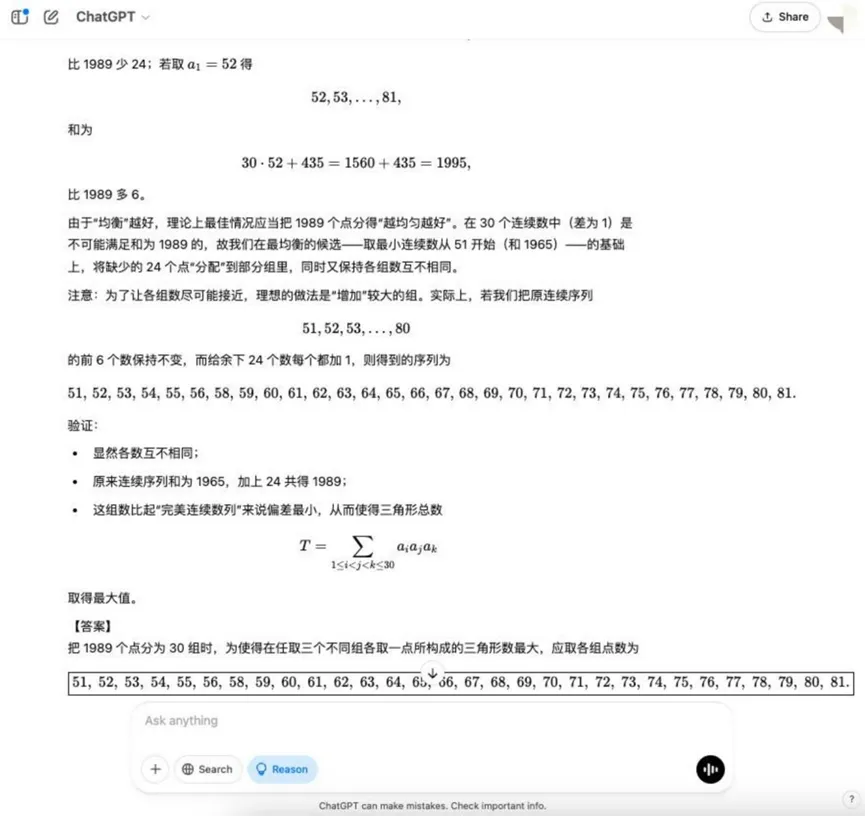

YiXin-Distill-Qwen-72B
 

Los problemas de optimización combinatoria aumentan aún más la dificultad y plantean mayores exigencias a las estrategias matemáticas y la capacidad de cálculo del modelo.

Ronda 9: Problemas de teoría de números (cadenas de factores)

Problema Descripción Imagen:

Análisis: De nuevo, intervienen conceptos de teoría de números, examinando la comprensión y aplicación por parte del modelo de relaciones como los factoriales y la integralidad, que pueden requerir pruebas constructivas o recuentos.

Resultados:
o3-mini: Parcialmente correcto

YiXin-Distill-Qwen-72BExacto.
 

YiXin-Distill-Qwen-72B Sólida actuación en este tema de recuento.

Ronda 10: Problemas geométricos (puntos de igual superficie)

Problema Descripción Imagen:

Análisis: La pregunta final es un problema geométrico que implica cálculos de áreas, trayectorias de puntos o pruebas de existencia, poniendo a prueba la intuición geométrica del modelo, las operaciones algebraicas y el razonamiento lógico.

Resultados:
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B
 

Las preguntas finales de geometría también mostraron diferencias entre los modelos en cuanto a su capacidad para resolver problemas geométricos complejos.

Observación y análisis

A partir de esta prueba de la capacidad matemática china en una serie de grandes modelos lingüísticos, pueden hacerse las siguientes observaciones:

1. Las habilidades matemáticas basadas en modelos mejoran significativamente: En comparación con los modelos anteriores, la generación actual de LLM muestra una mejora significativa en el manejo de problemas matemáticos que implican razonamiento en varios pasos, como la geometría, la probabilidad y algunos problemas de aplicación abierta. Esto puede atribuirse al aumento del tamaño del modelo, a la abundancia de datos de entrenamiento y a la aplicación de técnicas de mejora del razonamiento como el "encadenamiento de pensamientos".
2. Existen diferencias en los estilos de resolución de problemas: Los distintos modelos se comportan de forma diferente en cuanto al nivel de detalle del proceso de solución.
   • o3-mini, Grok 3 beta, Tongyi Qwen-32B El resultado es relativamente conciso y los pasos de inferencia son sencillos.
   • DeepSeek R1, Hunyuan T1, YiXin-Distill-Qwen-72B La tendencia a mostrar procesos de pensamiento más detallados, que a veces incluyen pasos de reflexión y corrección, es más "verbosa", pero esto puede ayudar a trazar la lógica de su razonamiento.
   • Gemini 2.0 Flash Thinking no sólo es largo, sino que además utiliza principalmente resultados en inglés, lo que sugiere que puede estar relativamente poco entrenado en corpus matemáticos chinos.
3. Robustez frente a errores de entrada: En las pruebas se observó que, aunque haya pequeños errores de notación o irregularidades de presentación en las descripciones de los problemas, algunos de los modelos siguen siendo capaces de entender correctamente el significado de las preguntas y responderlas, lo que demuestra cierto grado de robustez. Sin embargo, esto no significa que los modelos puedan ignorar siempre los errores, y los errores en la información crítica pueden seguir provocando fallos en las respuestas.
4. Futuras mejoras: especialización e integración de herramientas: A pesar de los evidentes avances, todavía hay margen de mejora en la precisión del LLM actual cuando se trata de problemas matemáticos complejos, especialmente en preguntas de competición difíciles y en escenarios que requieren pruebas rigurosas. Las futuras vías de mejora pueden incluir:
   • Integración de motores informáticos externos: Las deficiencias de LLM en el cálculo exacto y las operaciones simbólicas se compensan invocando herramientas de cálculo simbólico como Wolfram Alpha.
   • Ajuste fino exclusivo de campo: Construir conjuntos de datos afinados de alta calidad para la lógica matemática, ramas específicas de las matemáticas (por ejemplo, álgebra, geometría, teoría de la probabilidad) y reforzar los modelos de razonamiento experto y profundidad del conocimiento.
   • Aprendizaje y revisión interactivos: Desarrollar mecanismos que permitan al usuario guiar el proceso de solución, señalar los pasos en falso y permitir que el modelo ajuste dinámicamente la estrategia de solución.
5. Recomendaciones para los usuarios:
   • Estudiantes: El LLM puede utilizarse para ayudar al aprendizaje verificando rápidamente soluciones y respuestas a preguntas básicas. Sin embargo, en el caso de problemas complejos o creativos, hay que tener cuidado con la posibilidad de que el modelo diga "tonterías serias" (es decir, que dé con seguridad la respuesta incorrecta).
   • Educadores: Cuando se utiliza la enseñanza asistida por IA, es necesario diseñar preguntas que tengan más probabilidades de poner a prueba la comprensión profunda y las habilidades de pensamiento independiente de los alumnos, de modo que éstos no se basen en modelos para llegar a respuestas superficiales.
   • Promotor: Cuando se aplica el LLM para resolver problemas matemáticos, los límites del problema y los requisitos de la solución deben clarificarse optimizando la Ingeniería Prompt para reducir el razonamiento ineficaz o "lluvia de ideas" por parte del modelo debido a la comprensión difusa.

En conclusión, la aplicación de modelos lingüísticos a gran escala en matemáticas está pasando gradualmente de la fase exploratoria a la práctica. La futura dirección del desarrollo de modelos consistirá en buscar un mejor equilibrio entre simular la flexibilidad del pensamiento humano y garantizar el rigor de la lógica matemática.

Notas:
Los mejores de esta revisión YiXin-Distill-Qwen-72B La información sobre el modelo es la siguiente:

• Versión estándar: https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B
• AWQ Edición Cuantitativa: https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B-AWQ
• Requisitos de recursos para la implantación local: 72B Standard Edition requiere aproximadamente 8 tarjetas gráficas NVIDIA de la clase 4090; AWQ Quantitative Edition puede ejecutarse con 2 tarjetas de la misma clase.