Ya está disponible la evaluación comparativa actualizada de Claude 3.5 Sonnet Chinese. La capacidad de codificación supera a GPT-4o, el razonamiento de orden superior no es tan bueno como o1

Los resultados de esta evaluación se utilizarán únicamente con fines de investigación académica.

El 22 de octubre, Anthropic presentó oficialmente el modelo grande mejorado Claude 3.5 Sonnet, así como el nuevo modelo Claude 3.5 Haiku.

Claude

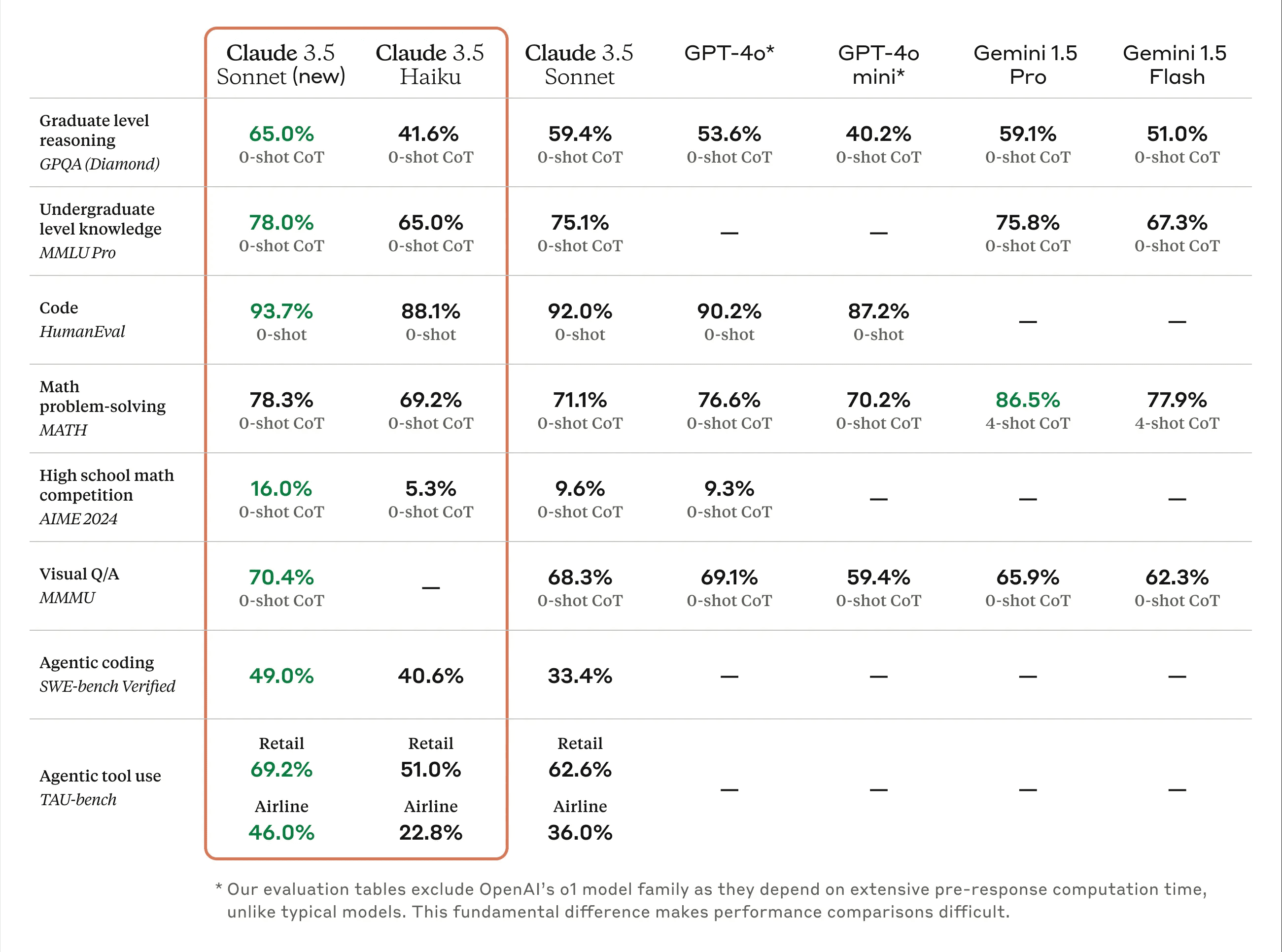
Según los responsables de Anthropic, Claude 3.5 Sonnet supera a la versión anterior en todos los aspectos, con importantes mejoras de rendimiento, especialmente en las tareas de codificación de cuerpos inteligentes y uso de herramientas.En SWE-bench Verified, su rendimiento de codificación mejora de 33,41 TP3T a 49,01 TP3T, superando a todos los modelos disponibles públicamente, incluido OpenAI o1-preview.

Anthropic también está introduciendo una nueva función innovadora: el uso del ordenador. Los desarrolladores pueden controlar a Claude para que utilice el ordenador del mismo modo que un humano a través de una API, pero la función se encuentra actualmente en fase experimental.

En respuesta a la preocupación pública sobre el rendimiento de la actualización a Claude 3.5 Sonnet, en términos de razonamiento y código en escenarios chinos, SuperCLUE, una organización profesional de evaluación de terceros, ha llevado a cabo una evaluación en profundidad de la actualización a Claude 3.5 Sonnet.

entorno de evaluación

Normas de referencia: SuperCLUE-Reasoning Chinese Higher Order Reasoning Assessment Benchmark, SuperCLUE-Code3 Chinese Code Assessment Benchmark.

Modelos de evaluación : Claude 3.5 Sonnet (1022, POE último modelo instantáneo)

Configuración del modelo GenerationConfig:

• Consulte el documento de instrucciones detalladas Claude: https://www.anthropic.com/news/3-5-models-and-computer-use

Episodio de revisión:

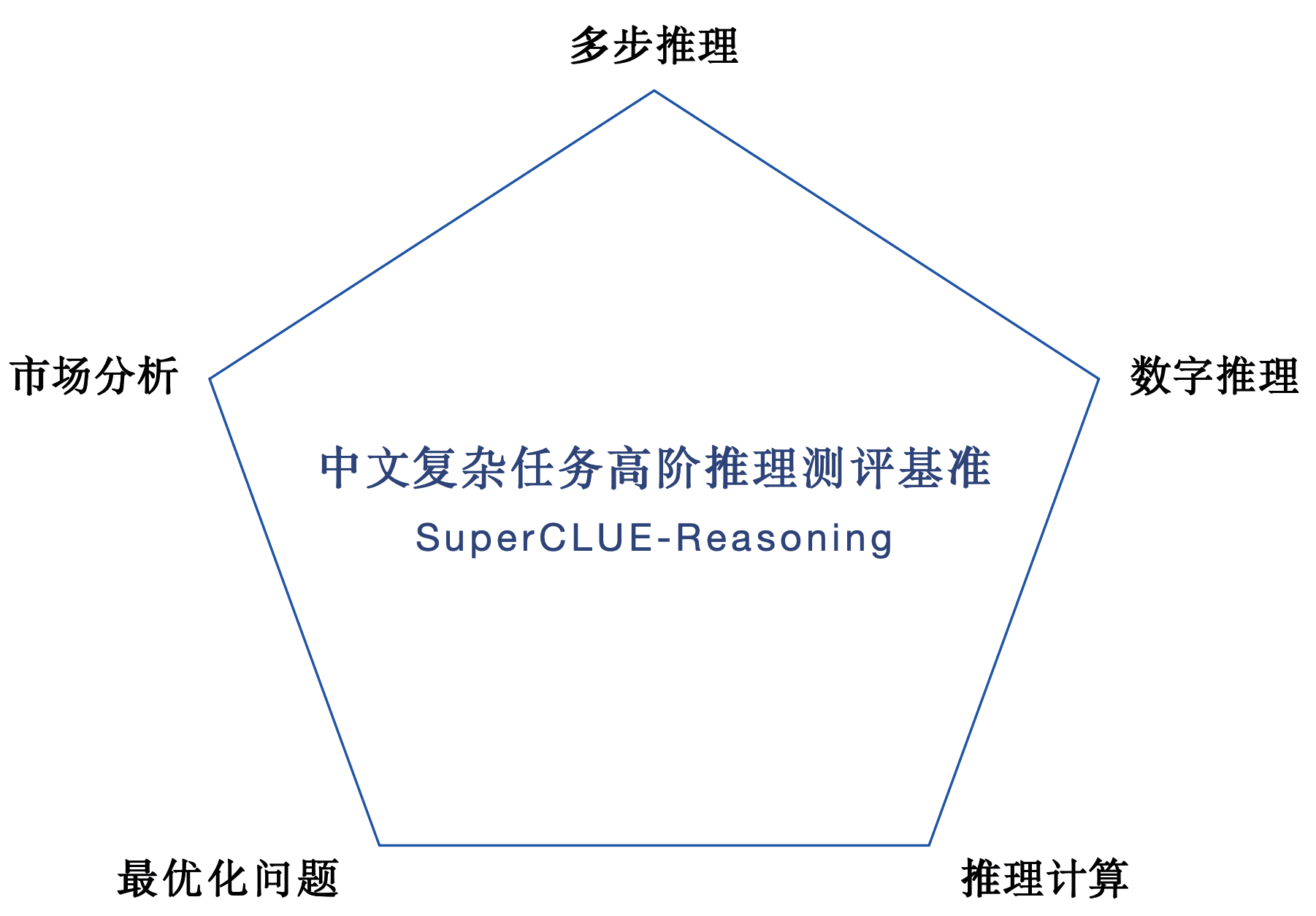
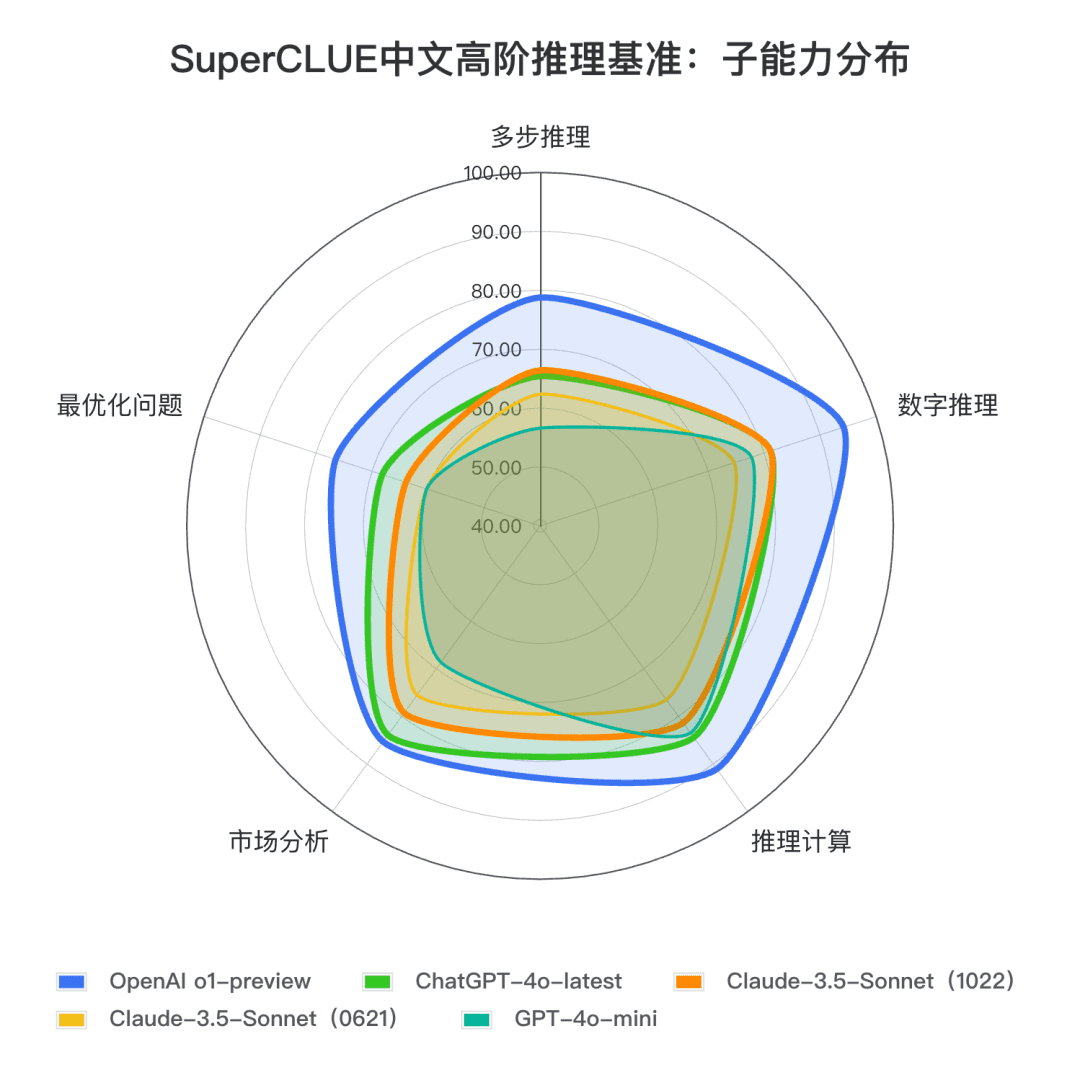
1.SuperCLUE-Reasoning Chinese Complex Tasks Higher Order Reasoning Review Set. Un total de 302 preguntas, incluyendo el razonamiento de varios pasos, razonamiento numérico, cálculos de razonamiento, análisis de mercado y problemas de optimización cinco tareas de razonamiento difíciles.

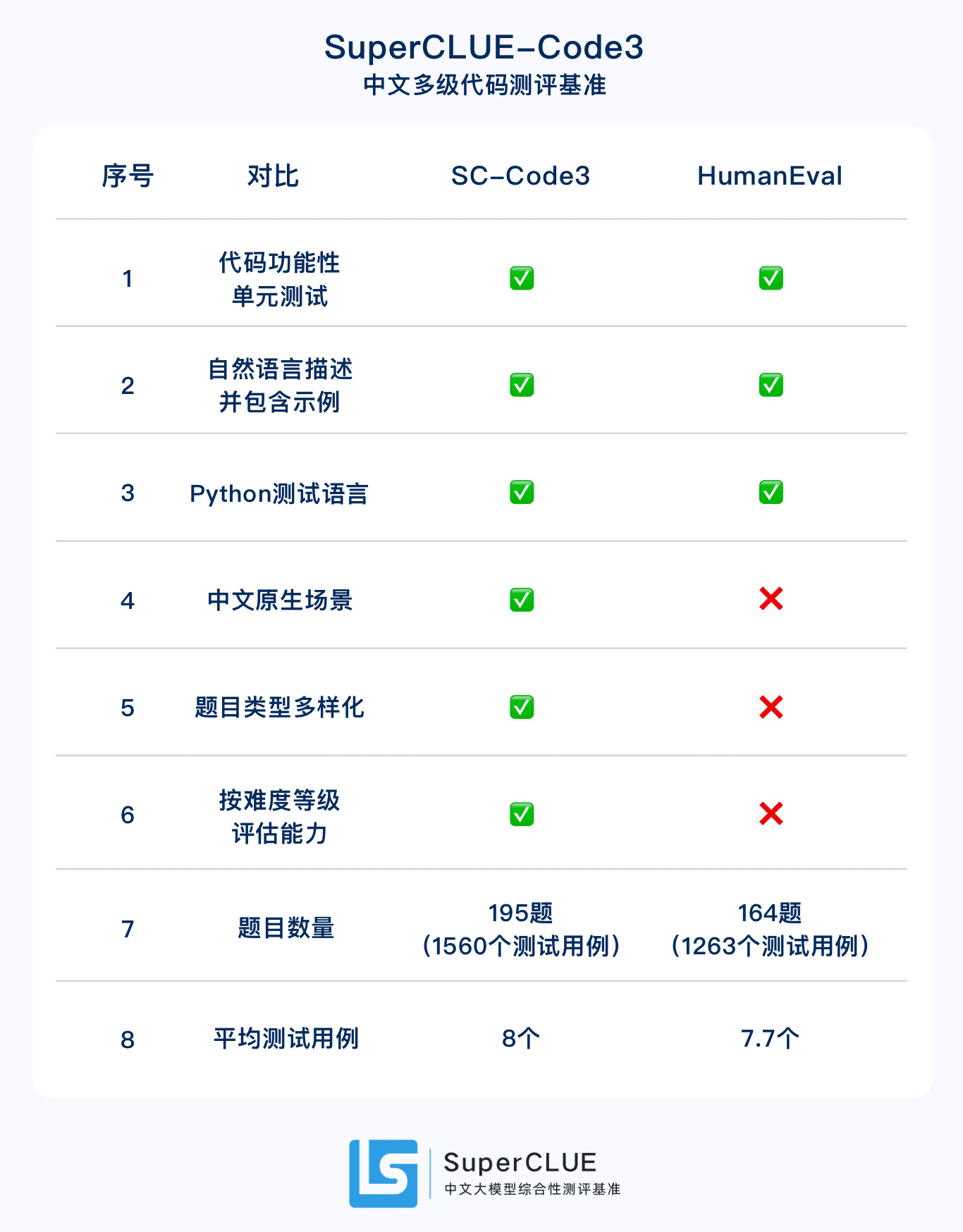
2.Conjunto de evaluación de código nativo chino SuperCLUE-Code3.Versión mejorada en chino de HumanEval, un total de 195 preguntas, incluidos 1.560 casos de prueba, divididos en tres categorías de nivel de dificultad: primario, intermedio y avanzado.

Metodología::

1. Razonamiento de orden superior: para cada pregunta de razonamiento, proporcionamos respuestas de referencia y procesos de razonamiento tras la calibración y comprobación manuales; a continuación, el modelo de referencia evalúa las respuestas de los modelos candidatos según el proceso de evaluación establecido, los criterios de evaluación y las reglas de puntuación (1-5 puntos). Los criterios de evaluación establecidos incluyen: cumplimiento de los requisitos básicos, precisión del razonamiento y razonabilidad de las conclusiones.

2. Código SC-Code3: diseñado específicamente para evaluar y mejorar las capacidades básicas del Gran Modelo Chino en la generación de código mediante pruebas funcionales unitarias.

SuperCLUE-Code3: evaluación comparativa de la competencia en código de los nativos chinos

Empecemos por las conclusiones

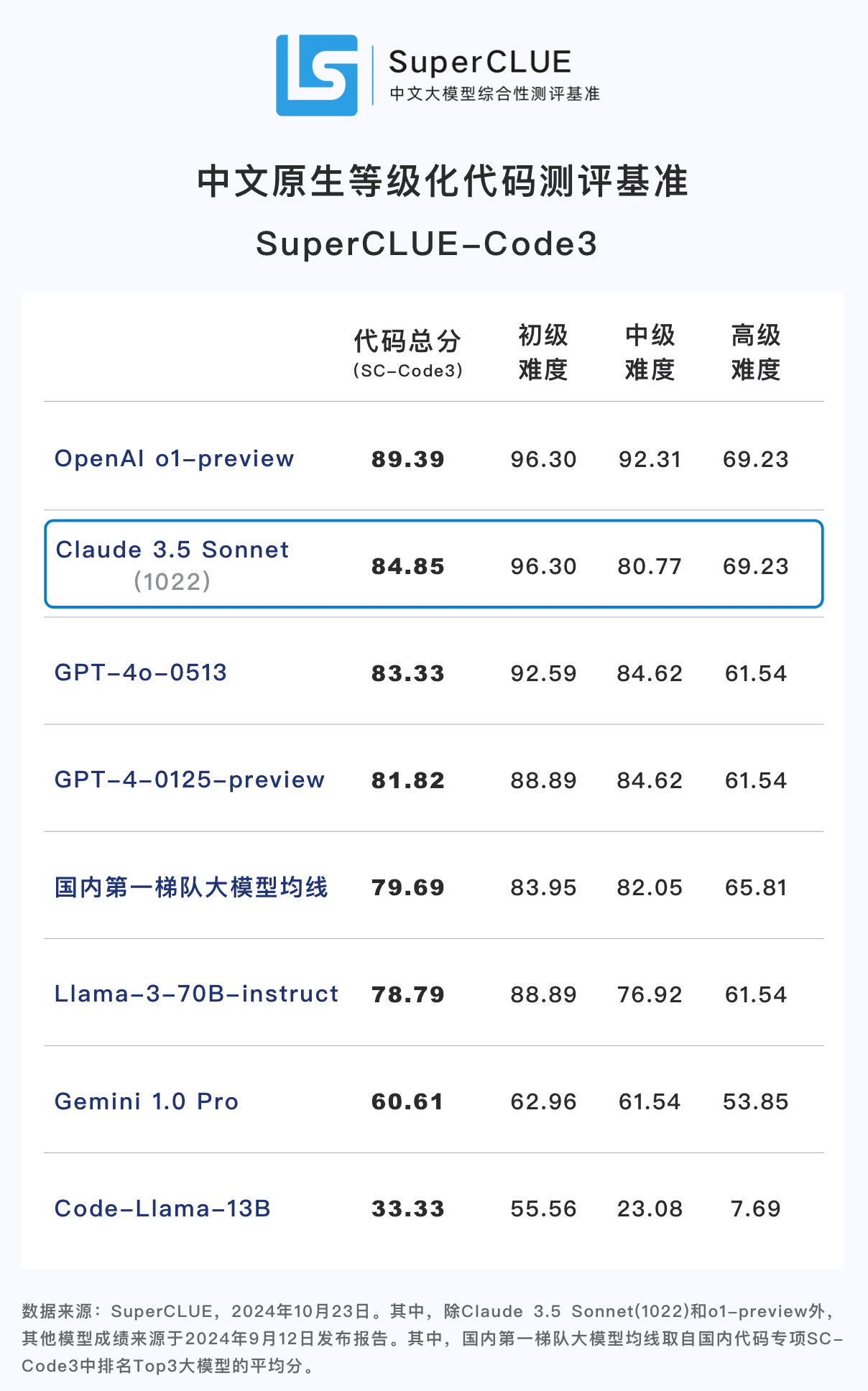
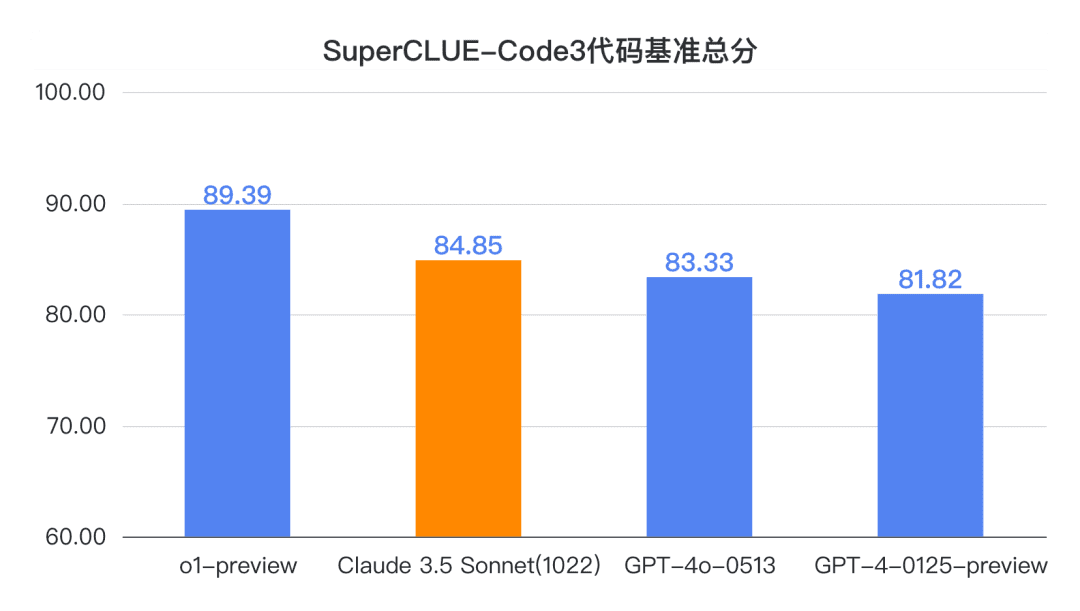
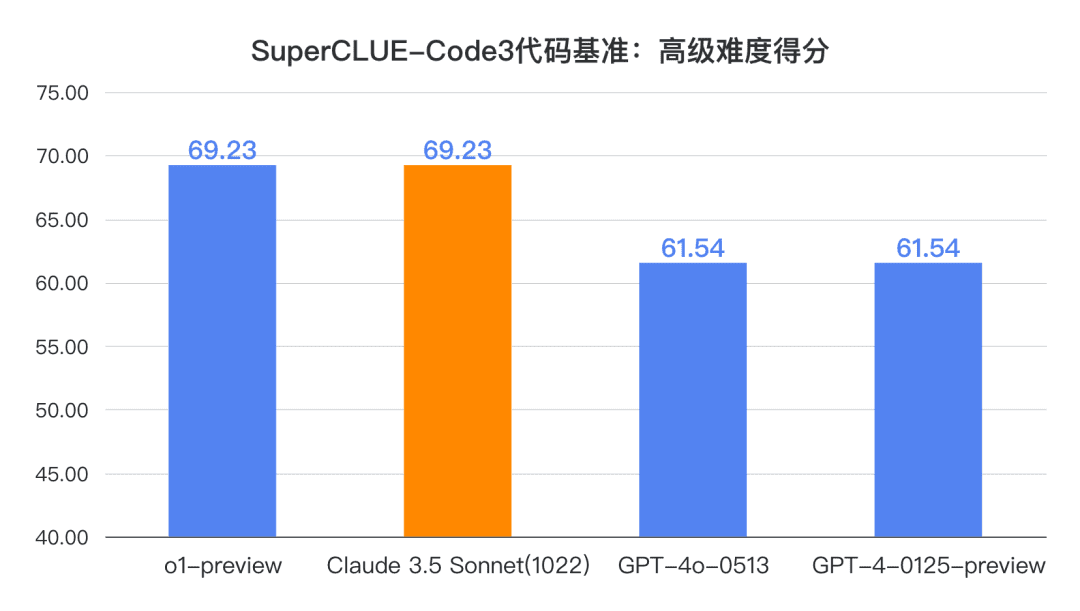
Conclusión 1: Claude 3.5 Sonnet (1022) obtiene buenos resultados en cuanto a capacidad de código chino (SC-Code3). La puntuación total alcanzó 84,85, 1,52 puntos más que GPT-4o-0513 lo que supone 4,54 puntos menos que o1-preview. En particular, obtuvo unos resultados sorprendentes en las tareas de código avanzadas, con una puntuación de 69,23, empatando con o1-preview.

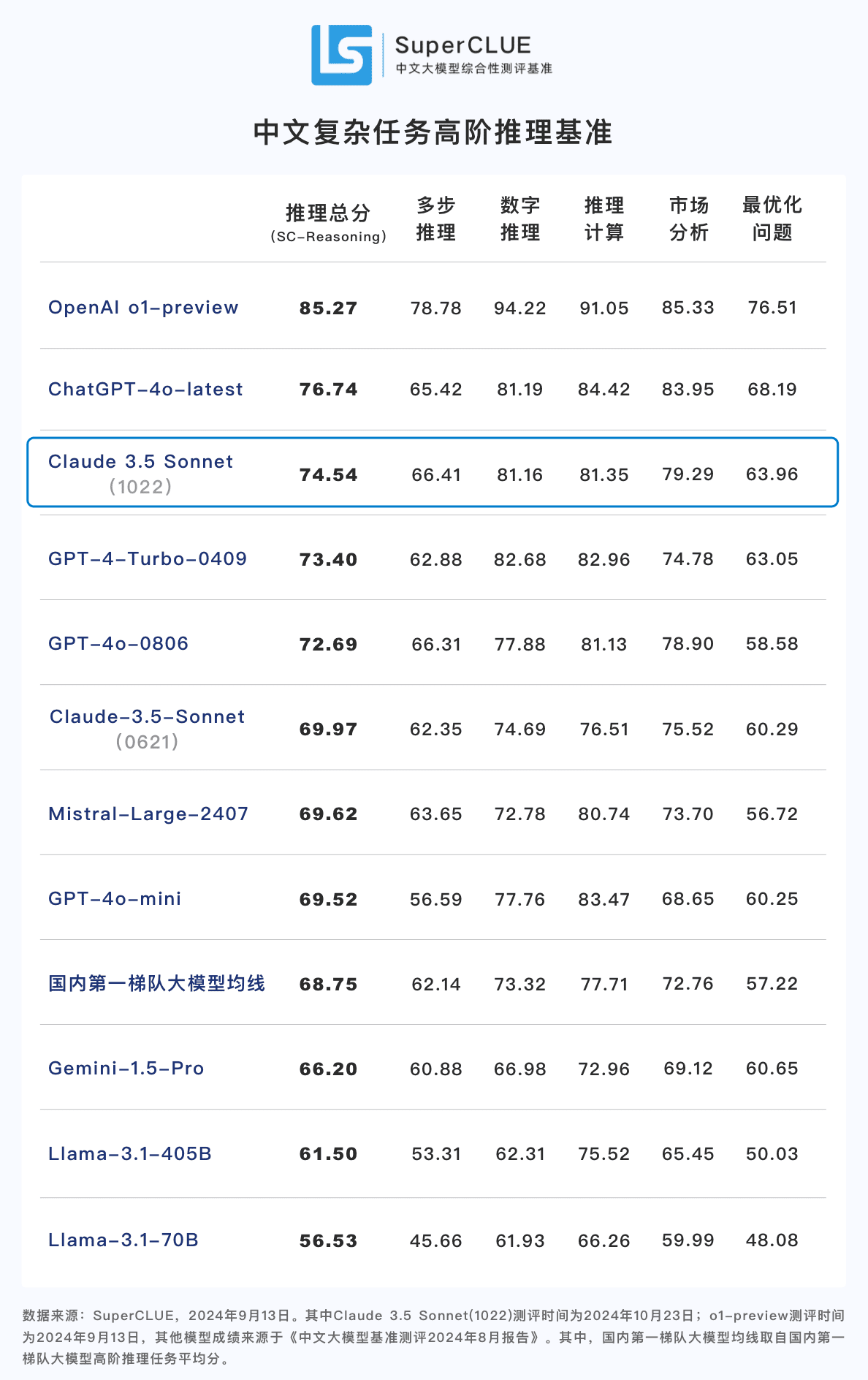
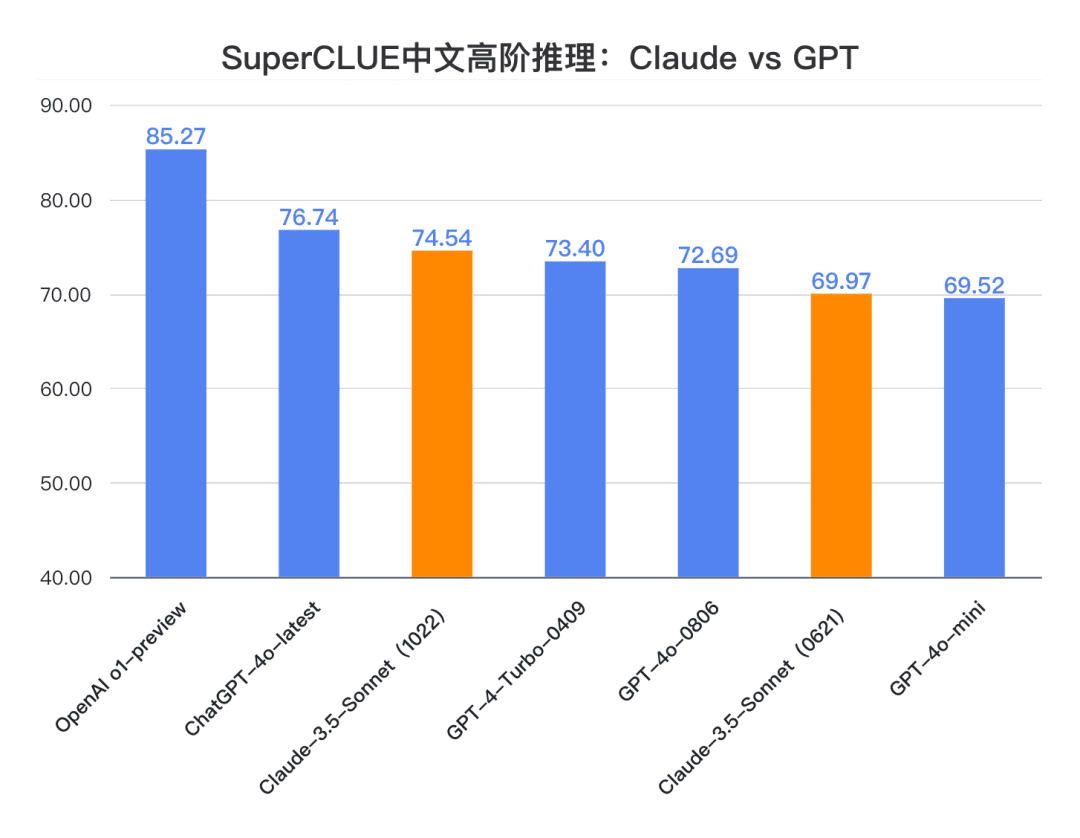
Conclusión 2: Claude 3.5 Sonnet (1022) obtuvo una puntuación de 74,54 en la tarea china de razonamiento de orden superior. Cerca de ChatGPT-4o-latest, con una gran diferencia respecto a o1-preview (-10,73 puntos) . Entre ellos, la capacidad de razonamiento multipaso es relativamente sobresaliente, con un rendimiento superior al ChatGPT-4o-latest.

**Conclusión 3:** En comparación con la versión anterior Claude 3.5 Sonnet (0621). Claude 3.5 Sonnet (1022) mejoró 4,57 puntos en la tarea de razonamiento y avances significativos en tareas secundarias como el razonamiento numérico y el razonamiento computacional.

Resultados de la evaluación

análisis comparativo

Ejemplo de medición de códigos

Ejemplo 1

Prompt.

from typing import List


def longest_peak_sequence(nums: List[int]) -> int:
    """
    在一个整数数组中找出最长的"峰"序列的长度。
    所谓"峰"序列，是指先严格递增然后严格递减的序列，且峰顶（即最大值）唯一。
    至少包括三个数以上才能构成一个"峰"序列（即包含递增和递减的部分）。

    返回数组中最长"峰"序列的长度。如果没有"峰"序列，则返回0。


    示例:
    >>> longest_peak_sequence([2, 1, 4, 7, 3, 2, 5])
    5  # 最长的"峰"序列是 [1, 4, 7, 3, 2]


    >>> longest_peak_sequence([5, 4, 3, 2, 1])
    0  # 不存在"峰"序列，因为没有严格递增的部分

    提示:
    - 数组 `nums` 的长度范围为 [0, 10000]。
    - 数组中的每个元素范围为 [-10000, 10000]。
    """

Claude 3.5 Soneto (1022) Respuesta.

from typing import List


def longest_peak_sequence(nums: List[int]) -> int:
    if len(nums) < 3:
        return 0

    max_length = 0

    # 从第二个元素遍历到倒数第二个元素
    for i in range(1, len(nums) - 1):
        # 检查当前位置是否是峰顶
        if nums[i] > nums[i-1] and nums[i] > nums[i+1]:
            # 找到一个峰顶，向两边扩展
            left = i - 1
            right = i + 1

            # 向左扩展，寻找严格递增序列
            while left > 0 and nums[left-1] < nums[left]:
                left -= 1

            # 向右扩展，寻找严格递减序列
            while right < len(nums) - 1 and nums[right+1] < nums[right]:
                right += 1

            # 更新最长峰序列长度
            current_length = right - left + 1
            max_length = max(max_length, current_length)

    return max_length

Caso de prueba.

def check(candidate):
    assert candidate( [1, 2, 3, 4, 5, 6])==0
    assert candidate([1, 3, 5, 6, 4, 2, 0])==7
    assert candidate( [5, 4, 3, 2, 1, 2, 3, 4, 1])==5
    assert candidate([1, 3, 5, 3, 1])==5
    assert candidate([1, 2, 3, 3, 2, 1])==0
    assert candidate([2, 1, 3, 1, 2, 1, 3])==3
    assert candidate([1, 3, 5, 4, 3, 2, 1])==7

si_pasado**(Adoptado o no)**Aprobado.

Ejemplo 2

Prompt.

from typing import List


def longest_increasing_path(matrix: List[List[int]]) -> int:
    """
    给定一个整数矩阵，找到最长严格递增路径的长度。
    路径被定义为从矩阵中的任意单元格开始，每次可以向上、下、左、右移动到相邻的单元格上，如果递增的话。
    你不能在路径中移动到矩阵外面，也不能移动到不满足递增条件的单元格上。
    路径的长度是路径上的单元格总数。

    示例:
    >>> longest_increasing_path([
            [9, 9, 4],
            [6, 6, 8],
            [2, 1, 1]
        ])
    4  # 最长递增路径是 [1, 2, 6, 9]


    >>> longest_increasing_path([
            [3, 4, 5],
            [3, 2, 6],
            [2, 2, 1]
        ])
    4  # 最长递增路径是 [3, 4, 5, 6]或 [2, 4, 5, 6]


    提示:
    - 矩阵 `matrix` 的维度为 m x n。
    - 矩阵 `matrix` 的每个元素是一个非负整数。


    """

Claude 3.5 Soneto (1022) Respuesta.

from typing import List


def longest_increasing_path(matrix: List[List[int]]) -> int:
    if not matrix or not matrix[0]:
        return 0

    m, n = len(matrix), len(matrix[0])
    # 缓存，用于存储每个位置的最长递增路径长度
    cache = [[0] * n for _ in range(m)]

    def dfs(i: int, j: int) -> int:
        # 如果已经计算过，直接返回缓存结果
        if cache[i][j] != 0:
            return cache[i][j]

        # 四个方向：上、下、左、右
        directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]

        # 当前位置的最长路径至少为1
        max_length = 1

        # 遍历四个方向
        for di, dj in directions:
            ni, nj = i + di, j + dj

            # 检查是否在矩阵范围内且满足递增条件
            if (0 <= ni < m and 0 <= nj < n and 
                matrix[ni][nj] > matrix[i][j]):
                # 递归计算邻居位置的最长路径
                curr_length = 1 + dfs(ni, nj)
                max_length = max(max_length, curr_length)

        # 存入缓存
        cache[i][j] = max_length
        return max_length

    # 遍历矩阵中的每个位置，找到最长路径
    result = 0
    for i in range(m):
        for j in range(n):
            result = max(result, dfs(i, j))

    return result

Caso de prueba.

def check(candidate):
    assert candidate([[1, 1], [1, 1]]) == 1
    assert candidate([
    [9, 9, 4],
    [6, 6, 8],
    [2, 1, 1]
]) == 4
    assert candidate([
    [3, 4, 5],
    [3, 2, 6],
    [2, 2, 1]
]) == 4
    assert candidate([
        [1, 2, 3, 4],
        [5, 6, 7, 8],
        [9, 10, 11, 12],
        [13, 14, 15, 16]
]) == 7
    assert candidate([
        [-1, -2, -3, 0],
        [5, -6, 7, -8],
        [-9, 0, -11, -12],
        [13, 0, 15, -16]
]) == 4
    assert candidate([
    [5, 10, 6, 7, 9],
    [6, 10, 2, 2, 3], 
    [4, 9, 8, 2, 8],
    [3, 3, 3, 8, 8]
])==4
    assert candidate([
    [1, 3, 1, 4],
    [1, 5, 1, 7],
    [4, 2, 1, 1],
    [1, 3, 2, 1]
])==3
    assert candidate([
    [1, 9, 2, 4], 
    [9, 6, 5, 3],
])==4

si_pasado(Adoptado o no):Aprobado.

Ejemplos de razonamiento de orden superior

Ejemplo 1: Razonamiento en varios pasos

pregunte a

Una empresa tiene siete empleados llamados A, B, C, D, E, F y G. La empresa ha realizado un ejercicio de clasificación y, basándose en las notas de los empleados y en las siguientes condiciones, deduce la clasificación exacta de cada empleado:

1. La puntuación de A es superior a la de B, pero inferior a la de C.
2. La puntuación de D es superior a la de E y G, pero inferior a la de A.
3. G obtuvo la puntuación más baja.
4. B obtiene una puntuación más alta que E y F.
5. La puntuación F es superior a la E.
6. C obtuvo la puntuación más alta.
7. Cada empleado obtiene una puntuación diferente, con la D en el centro.

Por favor, infiera la puntuación específica para cada empleado basándose en las condiciones anteriores.

Claude 3.5 Soneto (1022) responde:

Extrapolemos la clasificación de cada empleado mediante un análisis lógico:

1. Conocido a partir de la condición 3: G está en último lugar (7º)
2. Conocido a partir de la condición 6: C está en la cima (1er puesto)
3. Conocido a partir de la condición 7: D ocupa la 4ª posición (posición intermedia)
4. Sabemos por la condición 2: D es mayor que E y G, pero menor que A. Entonces:
   • E debe clasificarse después de D (5º o 6º)
   • A debe estar clasificado antes que D (2º o 3º)
5. Sabemos por la condición 1: A es superior a B pero inferior a C. Combina esto con el análisis anterior:
   • 2º puesto de la fila A
   • B debe ser el 3er clasificado
6. Sabemos por las condiciones 4 y 5: B es mayor que E y F, y F es mayor que E. Entonces:
   • 5º puesto de la fila F
   • E 6º puesto

Las clasificaciones finales son las siguientes:

1. C (1er puesto)
2. A (2º puesto)
3. B (3er puesto)
4. D (4º)
5. F (5º)
6. E (6º)
7. G (7º)

¿Quiere que le muestre el proceso de razonamiento detallado?

Ejemplo 2: Problema de optimización

pregunte a

Una ciudad tiene cinco grandes nudos de transporte y el departamento de urbanismo quiere optimizar la cobertura de las líneas de autobús para garantizar que cada nudo esté conectado al menos por una línea. Se conocen los costes de construcción entre los nudos y el objetivo es conectar todos los nudos con un coste mínimo.

Datos:

• Costes de conectividad entre nodos (en millones de dólares)
• Eje 1 y Eje 2: 100.000 dólares
• Eje 1 y Eje 3: 150.000 dólares
• Eje 2 y Eje 4: 200.000 dólares
• Eje 3 y Eje 4: 250.000 dólares
• Eje 3 y Eje 5: 300.000 dólares
• Eje 4 y Eje 5: 180.000 dólares

Objetivo: Determinar qué nodos deben conectarse entre sí para minimizar el coste total de construcción y garantizar que todos los nodos estén interconectados.

Claude 3.5 Soneto (1022) responde:

Se trata de un problema de árbol mínimo que resolveré mediante el algoritmo de Kruskal. Analicémoslo paso a paso:

1. En primer lugar, ordena todas las conexiones de menor a mayor coste:
   • Eje 1-2: 100.000 dólares
   • Ejes 1-3: 150.000 dólares
   • Eje 4-5: 180.000 dólares
   • Ejes 2-4: 200.000 dólares
   • Eje 3-4: 250.000 dólares
   • Ejes 3-5: 300.000 dólares
2. Se selecciona la conexión de menor coste para evitar que se forme un anillo:
   • Select Hub 1-2 (100.000 dólares)
   • Select Hub 1-3 (150.000 dólares)
   • Select Hub 4-5 (180.000 dólares)
   • Select Hub 2-4 (200.000 $)

Programa óptimo:

• Conexión del Hub 1 y el Hub 2
• Conexión de Hub 1 y Hub 3
• Conexión del Hub 4 y el Hub 5
• Conexión del Hub 2 y el Hub 4

Coste total: 10 + 15 + 18 + 20 = 630.000 $.

Este programa garantiza que:

1. Todos los concentradores están conectados
2. No se forma ningún bucle
3. Coste total de propiedad mínimo

¿Quiere que le genere una visualización para mostrarle esta solución?

# Únete a la Comunidad

Para obtener más información sobre el último gran modelo Claude 3.5, puedes unirte al grupo de intercambio SuperCLUE-Claude.