BoT: Pensamiento mejorado: resolución de problemas de ensayo y error con grandes modelos lingüísticos

resúmenes

El rendimiento del razonamiento de los Modelos de Lenguaje Amplio (LLM) en una amplia gama de problemas depende en gran medida de las indicaciones de pensamiento encadenado, lo que implica proporcionar algunas demostraciones de pensamiento encadenado como ejemplos en las indicaciones. Investigaciones recientes, por ejemplo, los árboles de pensamiento, han señalado la importancia de la exploración y la autoevaluación en la selección de los pasos de razonamiento en la resolución de problemas complejos. En este artículo, proponemos un marco automatizado de incitación denominado Boosting of Thoughts (BoT) que explora y autoevalúa de forma iterativa un gran número de árboles de pensamiento para obtener una colección de experiencias de razonamiento de prueba y error, que servirán como una nueva forma de incitación para la resolución de problemas complejos. Partiendo de pistas sencillas que no requieren ejemplos, BoT explora y evalúa iterativamente un gran número de pasos de razonamiento y, lo que es más importante, revisa explícitamente las pistas utilizando los análisis de errores que LLM hace de ellas para aumentar la generación de pasos de razonamiento hasta obtener una respuesta final. Nuestros experimentos con GPT-4 y Llama2 en una amplia gama de problemas matemáticos complejos demuestran que BoT consigue sistemáticamente tasas de resolución de problemas superiores o comparables a las de otros métodos de sugerencia del estado del arte. El código fuente está disponible en https://github.com/iQua/llmpebase的examples/BoTReasoning文件夹下获得.

1. Introducción

Los Modelos de Lenguaje Amplio (LLM) con un paradigma autorregresivo han logrado un rendimiento significativo en una variedad de tareas debido a su capacidad potencial de razonamiento. La garantía de esta capacidad en tareas complejas depende en gran medida de las pistas de pensamiento encadenado (CoT), que proporcionan ejemplos de razonamiento paso a paso. Este enfoque sugiere que la capacidad de razonamiento puede estimularse mediante una serie de pensamientos, en los que el pensamiento actúa como paso intermedio en la resolución de problemas.

Como resultado, los estudios de seguimiento, en particular el Tree of Thought (ToT), han sugerido formas de mejorar el CoT. Para garantizar su validez, las instrucciones de estos métodos suelen incluir anotaciones humanas para tareas específicas. Esta dependencia limita su escalabilidad. Los trabajos recientes que realizan una doble comprobación utilizando LLM para mejorar las respuestas o que mejoran las instrucciones basándose en los comentarios han demostrado ser muy prometedores. La bibliografía existente suele decantarse por descartar los pensamientos no válidos en las instrucciones. Sin embargo, los seres humanos suelen aprender continuamente analizando cuidadosamente los errores, adquiriendo así experiencia y mejorando gradualmente su rendimiento. Por lo tanto, planteamos la siguiente pregunta: ¿puede la generación de pensamiento de los LLM liberarse de las anotaciones humanas e imitar la resolución de problemas humana para un razonamiento eficaz en una variedad de tareas?

En este trabajo, proponemos un marco novedoso, mostrado en la Fig. 1, llamado Boosting of Thoughts (BoT), que implementa un mecanismo de refuerzo, incluyendo agregación y experiencia, para mejorar progresivamente los pasos de razonamiento poco fiables (pensamiento débil) aprendiendo de los errores, y finalmente resolver varios problemas. Partiendo de una simple sugerencia sin anotación humana, BoT puede obtener un pensamiento débil. Mediante la agregación, la BoT es capaz de derivar de ellos cadenas de pensamientos más lógicas y eficaces que conducen a mejoras posteriores. Esta orientación en nuestro marco se consigue adaptando las pistas, que son informes detallados de errores, sugerencias y orientación para cada paso de razonamiento obtenidos mediante el análisis de las cadenas agregadas utilizando LLM. A medida que dicha experiencia se acumula en las pistas, conduce gradualmente a un pensamiento más sólido.

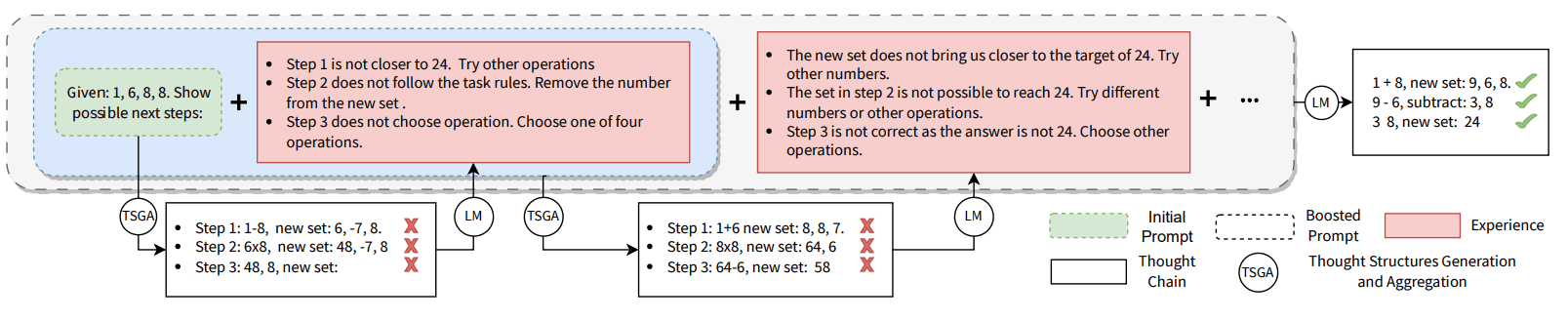
Figura 1: Mejora de las pistas mediante el aumento progresivo de la experiencia, que consiste en un análisis de las cadenas de pensamiento generadas por un gran modelo de lenguaje (LLM o LM). La experiencia contiene explícitamente la propia cadena de pensamiento, el correspondiente informe de error y sugerencias detalladas para revisar cada paso del razonamiento. Así, los pensamientos no válidos marcados con una cruz roja también pueden contribuir al perfeccionamiento de las instrucciones. Al acumular experiencia en las instrucciones, la SdT puede llegar a generar cadenas de pensamiento correctas a partir de instrucciones sencillas. El ejemplo que se presenta aquí es el resultado obtenido al aplicar GPT-4 con BoT a una tarea de juego de 24 puntos.

En concreto, BoT implementa este mecanismo de refuerzo como un proceso iterativo basado en la experiencia, tal y como se muestra en la Figura 1. En cada iteración, para una pista dada, BoT construye un gran número de estructuras de pensamiento simples en paralelo con LLM. En cada iteración, para una pista dada, BoT construye un gran número de estructuras de pensamiento simples en paralelo con LLM. Elegimos la estructura de árbol, como se muestra en ToT, pero para nuestros propósitos de refuerzo la modificamos significativamente para convertirla en un árbol binario ponderado con varias estrategias de crecimiento. Tras extraer las puntuaciones más altas de las ramas raíz-hoja de cada árbol, se ejecutó el componente de agregación de BoT para agregarlas en una única cadena de pensamientos. A continuación, esta cadena fue evaluada por el mismo LLM para extraer las lecciones aprendidas, que se añadieron a las indicaciones como guía para la generación de pensamientos en la siguiente iteración.

Nuestra contribución puede resumirse en tres puntos. En primer lugar, a diferencia de la generación de estructuras de pensamiento más complejas mediante instrucciones elaboradas, este artículo muestra que, basándose únicamente en instrucciones iniciales sencillas, los pensamientos débiles pueden mejorarse de forma incremental para resolver problemas basándose en la experiencia previa. En segundo lugar, para poner en práctica este mecanismo de mejora, proponemos un novedoso marco denominado Boosting of Thoughts (BoT), que lleva a cabo un proceso iterativo basado en la experiencia. Como empieza con instrucciones sencillas, BoT puede ampliarse a una gran variedad de tareas. Al tiempo que garantiza la validez, BoT es rápido porque construye estructuras de pensamiento sencillas en paralelo y converge a una solución tras unas pocas iteraciones. Por último, evaluamos el rendimiento de BoT en problemas matemáticos complejos utilizando GPT-4 y LlamaV2. Basándonos en GPT-4 OpenAI (2023) y LlamaV2 Touvron et al. (2023), evaluamos el rendimiento de BoT en problemas matemáticos complejos. Los índices de solución de problemas muestran que BoT con una estructura mental de árbol binario supera significativamente el estado del arte actual en GSM8K y AQuA, mientras que logra resultados de segundo mejor en otros conjuntos de datos. En particular, BoT supera al método líder ToT en 9,7% en la nueva tarea desafiante Juego de 24. Nuestro BoT demuestra así que los LLM pueden mantener un alto rendimiento en una amplia gama de tareas incluso sin anotaciones humanas aumentando las pistas, acumulando análisis de errores de cadenas de pensamiento no válidas y haciendo las sugerencias correspondientes.

2. Trabajos relacionados

inferencia multipaso.. Los trabajos más destacados sobre las instrucciones de pensamiento encadenado (CoT) sugieren que el comportamiento de razonamiento por pasos de los LLM puede estimularse proporcionando pasos de razonamiento intermedios en cada instrucción de problema. Un trabajo reciente, Tree of Thought (ToT), convierte el proceso de razonamiento secuencial en una estructura de árbol en la que cada pensamiento (nodo) puede considerar rutas de razonamiento previas para generar múltiples pensamientos siguientes. Mediante el retroceso y la exploración ampliada durante el proceso de razonamiento, ToT obtiene buenos resultados en problemas que desafían incluso a GPT-4. Teniendo en cuenta su gran capacidad, la estructura de pensamiento subyacente de BoT utiliza en gran medida la estructura de árbol de pensamiento de ToT. Y, debido al marco de refuerzo, la estructura de árbol generada por BoT en cada iteración es binaria y poco profunda, en lugar del árbol complejo de ToT en el que cada nodo corresponde a un gran número de nodos hijos. Sin embargo, la estructura subyacente no se limita a ToT. Por el contrario, BoT es flexible porque la estructura de pensamiento subyacente puede ser ToT, GoT Besta et al. (2023), o CR Zhang et al. (2023b), donde Thinking Graphs (GoT) Besta et al. (2023) es el trabajo más reciente sobre la extensión de la estructura de pensamiento a un formato gráfico. En este artículo, nos centraremos únicamente en ToT como estructura de pensamiento subyacente y dejaremos el uso de GoT como trabajo futuro.

autosugestión. Liberar a los humanos de las indicaciones específicas de la tarea atrae mucha atención. Para garantizar la capacidad de razonamiento de los LLM, los CoT tradicionales se basan en el conocimiento humano a priori para generar manualmente demostraciones específicas de la tarea como indicaciones. Sin embargo, el CoT cero demostró que, incluso sin ejemplos creados a mano, los LLM eran capaces de razonar paso a paso para obtener respuestas precisas simplemente añadiendo "pensemos paso a paso" a la indicación. Auto-CoT elimina el esfuerzo manual recuperando la cadena de razonamiento disponible generada por la CoT cero. Active-Prompt mide primero la incertidumbre de un conjunto de preguntas y, por tanto, selecciona sólo las preguntas inciertas que deben ser anotadas por un humano. posible. Nuestro artículo presenta un enfoque novedoso del refuerzo manual sin pistas. Partiendo de una pista simple, BoT la mejora de forma iterativa basándose en el análisis del pensamiento de los LLM.

Ingeniería de consejos a través de la retroalimentación. El uso de las respuestas de los LLM a las indicaciones de entrada como retroalimentación para posteriores revisiones de las indicaciones ha atraído mucha atención. Aquellos que revisan continuamente una indicación dada basándose en la descripción evaluada de la salida de los LLMs pretenden obtener respuestas precisas. Utilizando una idea de alto nivel similar a la de nuestro artículo, SELF-REFINE propone un algoritmo iterativo de auto-refinamiento que permite a los LLMs generar retroalimentación para refinar aún más su salida.PHP simplifica este proceso añadiendo la solución de la respuesta anterior directamente como una pista para las pistas posteriores.REFINER, también relacionado con nuestro artículo, evalúa cada paso de inferencia como una retroalimentación para producir una respuesta más razonable. razonable. Otra serie de estudios ha explorado la integración, concretamente el uso de mecanismos de refuerzo Freund et al. (1996) refinaron las pistas con la retroalimentación de un conjunto de ejemplos. Adaptaron la indicación añadiendo varios ejemplos inciertos a la iteración anterior, o se basaron en un proceso de retroalimentación-reflexión-refinamiento.APO Pryzant et al. (2023) refinaron iterativamente las indicaciones, utilizando el rendimiento de la indicación anterior para formar un lenguaje natural optimizado. Estos trabajos demuestran la eficacia de los mecanismos de refuerzo en la ingeniería de pistas. Sin embargo, nuestro trabajo es el primero en destacar la importancia del análisis de errores en la mejora de las pistas para generar cadenas de inferencia eficaces. La BoT propuesta amplía esta idea a un marco de sugerencias automatizado mediante la acumulación iterativa de una colección de experiencias de razonamiento de prueba y error.

3. Mejora del pensamiento

3.1 Antecedentes

El objetivo de la ingeniería de cue es diseñar un cue I que contenga múltiples secuencias lingüísticas que se utilizarán como entrada a través de este cue, y un Large Language Model (LLM) preentrenado denotado pθ, parametrizado por θ, que da acceso a las secuencias lingüísticas deseadas y. Así, el Input-Output (IO) estándar puede expresarse como y ∼ pθ (y|I (X, Q)), donde I (-) denota la instrucción de tarea envolvente del cue X y la la pregunta correspondiente Q.

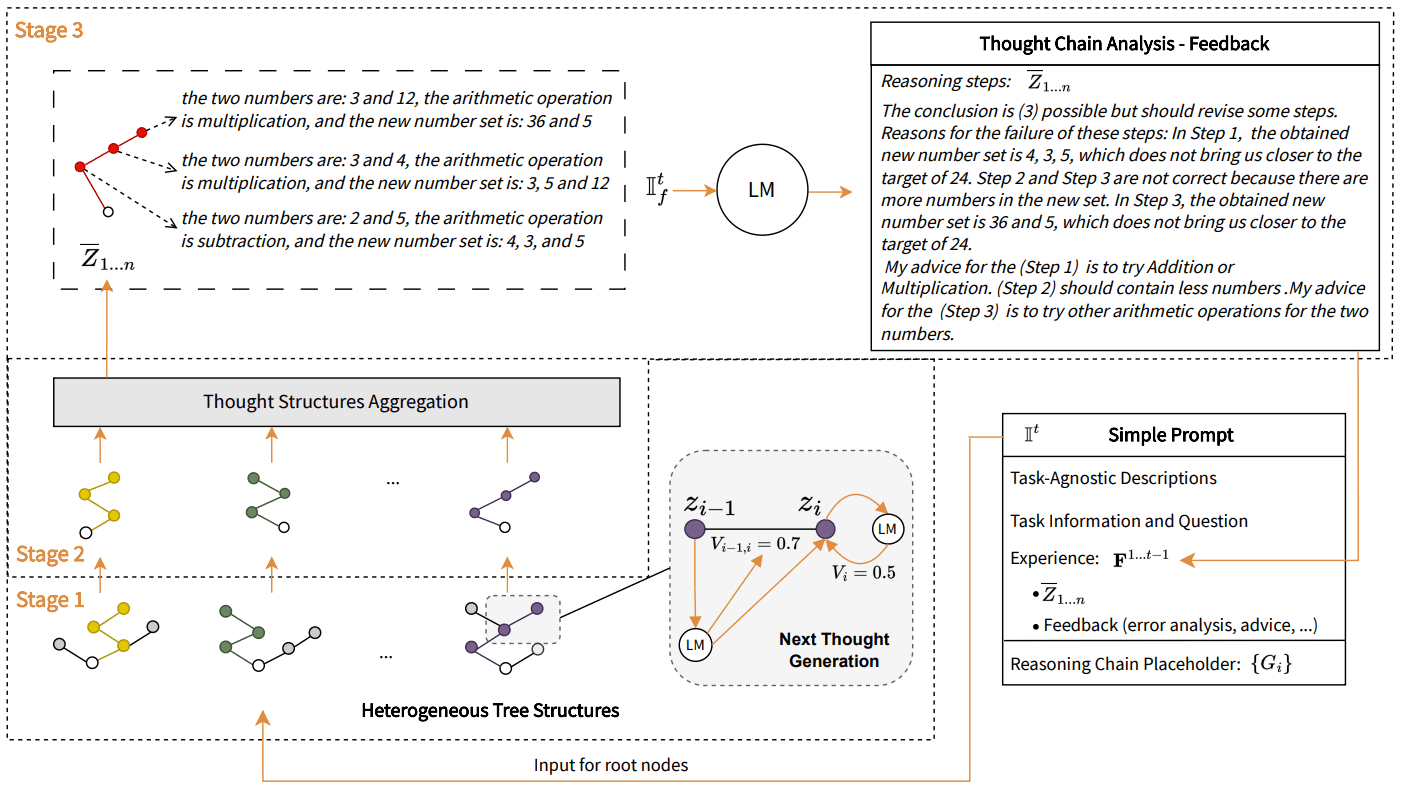
La imagen muestra una representación visual del proceso de pensamiento que subyace a la resolución de problemas mediante operaciones aritméticas. Se divide en tres partes principales: agregación de la estructura de pensamiento, generación del pensamiento siguiente y análisis de la cadena de pensamiento - retroalimentación.

La agregación de estructuras de pensamiento representa la combinación de diferentes etapas de razonamiento (Etapa 1, Etapa 2 y Etapa 3), cada una con su propia estructura numérica que describe los pasos dados para llegar a una conclusión.

La Generación del Pensamiento Siguiente se centra en una etapa específica, mostrando cómo el Modelado del Lenguaje (LM) puede utilizarse para predecir el pensamiento siguiente, teniendo en cuenta la experiencia previa (representada por los vectores Vi-1 y Vi) y generando una nueva cadena de razonamiento.

Análisis de la cadena de pensamiento - La retroalimentación proporciona un análisis detallado de los pasos de razonamiento realizados, señalando posibles errores y ofreciendo sugerencias de mejora. Critica los pasos evaluando si acercan al solucionador al número objetivo (en este caso 24) y sugiere otras operaciones aritméticas a probar.

Además, hay una breve sección de pistas en la que se describen las entradas al proceso de pensamiento, que incluyen descripciones no específicas de la tarea, información y preguntas sobre la tarea, y la experiencia adquirida en una cadena de razonamiento anterior que actúa como marcador de posición para generar nuevos pensamientos.

En conjunto, la imagen muestra un enfoque metodológicamente sólido del razonamiento y la resolución de problemas, que utiliza modelos lingüísticos para optimizar y mejorar iterativamente los procesos de pensamiento.

En concreto, veamos la sección Agregación de estructuras de pensamiento. En esta sección, podemos ver tres etapas, cada una con una estructura de árbol heterogénea coloreada. En la etapa 1, vemos algunas operaciones aritméticas, y la tendencia es "vi1 - 0,5". En la segunda etapa, se observan más operaciones aritméticas y la tendencia es "vi2 - 0,6". Por último, en la tercera etapa, vemos una secuencia de operaciones aritméticas con una tendencia de "vi3 - 0,4".

Para la siguiente sección de generación de pensamientos, se rastrea un nodo de pensamiento específico, Zi, y se muestra el peso que lo acompaña, vi, indicando la importancia de estos pensamientos en el contexto de la resolución de problemas.

En la sección Análisis de la cadena de pensamiento - Retroalimentación, se muestran varios pasos de razonamiento (Z1,Z2.... .Zn) y los evalúa. Para cada uno de estos pasos, "R1:-3, prueba +", "R2:+3, prueba -" y "R3: -1, prueba ×" representan la retroalimentación sobre el paso concreto retroalimentación, evaluación del razonamiento y sugerencias sobre cómo mejorar.

En la sección Pistas sencillas se pueden ver algunas pistas de entrada, como "Descripción no específica de la tarea 'Juega a un juego de números'", "Mensaje de tarea 'Intenta utilizar los cuatro números 1,3,4 ,6 (cada número sólo puede utilizarse una vez) y operaciones aritméticas (suma, resta, multiplicación y división) para llegar al número 24'", así como la cadena de razonamiento anterior Gi.

El resultado de esta canalización genera un nuevo proceso de pensamiento para el siguiente razonamiento.

Este diagrama representa el flujo lógico de un proceso de pensamiento y una metodología de razonamiento, mostrando cómo un Modelo de Lenguaje (LM) así como un mecanismo de retroalimentación/sugerencia pueden ser utilizados para avanzar en el problema, con retroalimentación crítica y evaluación en cada paso.

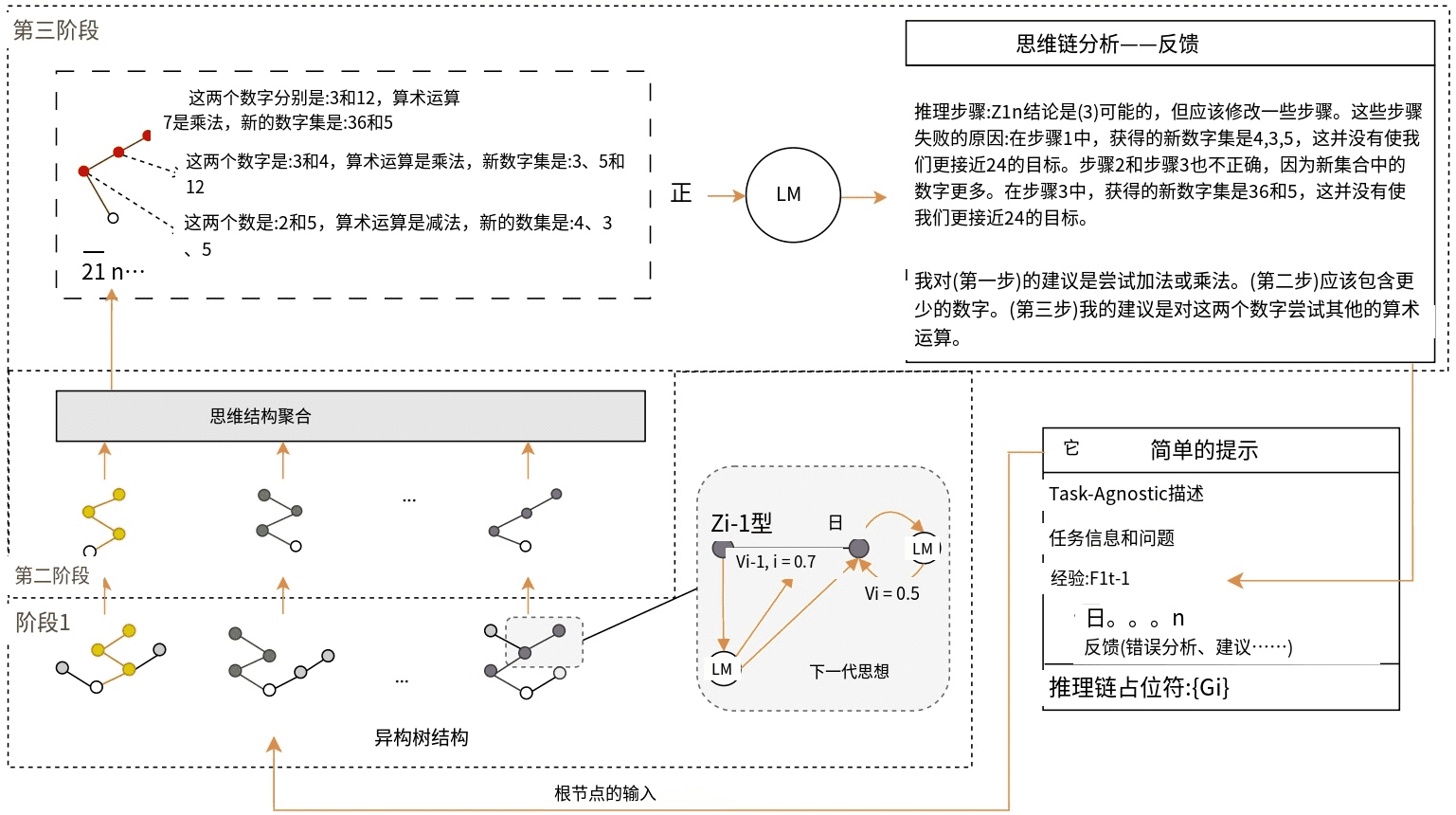
Figura 2: Muestra una visión general del proceso BoT en cada iteración. Para presentar cómo puede lograrse un aumento de la eficacia en este proceso iterativo de base empírica, mostramos los exhaustivos resultados intermedios obtenidos en un tipo de experimento sobre ChapGPT-4 en el conjunto de datos del juego de 24 puntos. Tras recibir el problema Q: "Los cuatro números proporcionados son: 2, 4, 5, 5", la BoT procede a través de tres fases consecutivas. Utilizando la pista simple It como entrada, la generación de estructuras de pensamiento (fase 1) produce una gran variedad de estructuras de pensamiento heterogéneas en forma de árbol. En la fase de agregación de estructuras de pensamiento (fase 2), se integran en una cadena de pensamientos z1.... .n y, a continuación, se analiza esta cadena de pensamientos en la Etapa 3 con el fin de generar experiencias que puedan utilizarse para reforzar aún más el indicio.

Las instrucciones pueden ser más elaboradas para guiar a los LLM a resolver el problema paso a paso. Cada paso intermedio del razonamiento se denomina zi (también conocido como pensamiento). El CdT proporciona varios ejemplos, cada uno de los cuales contiene una cadena de pensamientos z1.... .n. Esto conduce a y ∼ pθ y|I [z1 . .n]N , X, Q , donde N es el número de ejemplos incluidos en la pregunta.

En lugar de preparar ejemplos en el bootstrap, un enfoque más flexible es diseñar el bootstrap para llevar al LLM a generar gradualmente el pensamiento zi durante el proceso de razonamiento. esto se puede formalizar como zi ∼ pθ (zi |I(z1.... .i-1, X, Q)). Por último, la solución se formaliza como y ∼ pθ (y|I(z1.... .n, X, Q)).
De forma representativa, ToT Yao et al. (2024) amplían aún más este paso de razonamiento secuencial en una estructura de árbol en la que se pueden generar los siguientes pensamientos C. Así, la estructura de una reflexión puede ser encadenada o arborescente.

3.2 Marco

La literatura existente dirigida a generar pistas con ejemplos correctos de TdC o a diseñar estructuras de generación de pensamiento de grano fino adolece de tres limitaciones. En primer lugar, en estos enfoques se suele ignorar o descartar el pensamiento no válido. Sin embargo, los seres humanos, sobre todo los no expertos, y en particular en otros ámbitos, se basan en el análisis de errores anteriores para acumular más experiencia que les permita actuar correctamente en el siguiente intento. En segundo lugar, son menos escalables porque para cada tarea es necesario proporcionar en la pista ejemplos para generar el siguiente pensamiento, por ejemplo, I (z1|z0, X, Q). Por último, la generación de estructuras de pensamiento (por ejemplo, la estructura de árbol de Yao et al.) es demasiado compleja para explorar más pasos de razonamiento con el fin de obtener una solución mejor. Esto se debe principalmente a que las soluciones obtenidas no pueden revisarse más.

En este artículo, argumentamos que las indicaciones pueden mejorarse recogiendo continuamente análisis de estos pensamientos inválidos (pasos de razonamiento defectuosos en la cadena de pensamiento) de los LLM. Así, incluso una simple indicación, por ejemplo, I (X, Q), que puede conducir a un pensamiento inválido, puede mejorarse de forma incremental apoyándose en dichos análisis para obtener un pensamiento sólido que conduzca más cerca de una solución.

Proponemos un método denominadoPotenciación de los pensamientos (BoT)de un marco de cueing automatizado que permite mejorar el cueing a través de un proceso iterativo basado en la experiencia a partir delmás sencillode la señal de inicio. En resumen, como se muestra en la Figura 2, cada iteración t de BoT consta de tres fases. La fase de generación de estructuras de pensamiento es capaz de hacer un uso completo de las cadenas de inferencia generadas por los LLM, con las indicaciones de entrada como It. En la segunda fase, estas estructuras de pensamiento se agregan en una cadena de inferencia que será analizada por los LLM en la tercera fase para generar retroalimentación que contiene informes de errores y sugerencias de revisión detalladas. La cadena de razonamiento agregada se combina con los resultados de la retroalimentación para formar una nueva experiencia, denominada Ft. Así, al acumular estas experiencias a lo largo de las iteraciones F1.... .t, se mejora el indicio.

Consejos sencillos. Para cualquier tarea, en la iteración t = 0, creamos una pista inicial simple I0 ≡ {S, X, Q, F0, {Gi}}, donde S denota la descripción independiente de la tarea, mientras que X y Q denotan la información de la tarea y la pregunta, respectivamente. La parte empírica de la pregunta se denomina F0 y debe estar vacía al principio. {Gi}} es un marcador de posición que se rellenará al construir la estructura de pensamiento. En otras palabras, al generar el siguiente pensamiento zi, {Gi} se sustituirá por la cadena de pensamiento anterior z1.... ,i-1.

Generación de estructuras de pensamiento. Tras recoger la experiencia Ft-1 , el indicio para la iteración t puede ser It ≡ {S, X, Q, F1, .... ,t-1, {Gi}}. Basándose en esta pista, BoT genera en paralelo M estructuras de pensamiento. BoT es esencialmente capaz de contener cualquier estructura de pensamiento, por ejemplo, estructuras encadenadas de Wei et al. o estructuras arborescentes de Yao et al. Teniendo en cuenta la exploración de los pasos de razonamiento y los resultados experimentales, investigamos las estructuras de pensamiento arborescentes. Sin embargo, BoT introduce dos modificaciones novedosas que lo hacen más adecuado para el marco de elevación.

• árbol binario ponderado. Utilizando pistas sencillas en cada ronda, BoT construye mentes débiles con estructuras simples y de baja complejidad porque pueden revisarse posteriormente en el mecanismo de refuerzo. Así, cada estructura de pensamiento de BoT es un árbol binario ponderado poco profundo. Por simplicidad, mantenemos los símbolos z1.... .i-1 para denotar un pensamiento desde el nodo raíz hasta el padre del nodo i. Además de proporcionar a cada nodo i un pensamiento zi y su puntuación de evaluación del pensamiento Vi ∼ pθ (z1.... .i, Ia, X, Q), también incluimos una puntuación de arista Vi-1,i ∼ pθ (zi-1, zi, Ie, X, Q) entre un nodo hijo y su nodo padre, donde Ia e Ie se refieren a las descripciones guía del pensamiento y la evaluación de arista, respectivamente. vi-1,i denota el nivel de confianza de los LLM al generar este paso de razonamiento. Así, la generación del siguiente pensamiento de la BoT en esta estructura de árbol se formaliza como pθ (zi| (Vi-1,i, Vi, It, X, Q)).
• heterogeneidad de los árboles. A diferencia de ToT, que trata de encontrar soluciones en un gran árbol complejo, BoT pretende construir estructuras de pensamiento arborescentes muy heterogéneas. Así, para aumentar la heterogeneidad, la generación de estructuras de pensamiento emplea diferentes estrategias de crecimiento del árbol, como el crecimiento capa a capa y hoja a hoja. La primera enfatiza la exploración pero utiliza menos Chen & Guestrin (2016), mientras que la segunda es lo contrario Ke et al. (2017). Así, la estrategia hoja por hoja tiende a continuar razonando desde el mejor pensamiento actual hasta un mejor pensamiento final en comparación con el crecimiento capa por capa, pero también tiende a obtener cadenas monótonas de razonamiento. Además, se aplicaron LLM con diferentes ajustes de temperatura y Top p. Por último, utilizamos un valor de profundidad máxima pequeño en BoT y etiquetamos un nodo como hoja cuando los valores Vi-1,i y Vi estaban fuera del rango especificado [0,3, 0,8].

polimerización de la estructura de pensamiento. Tras obtener M estructuras de pensamiento, la BdT las agrega en una cadena de pensamientos, denotada z1.... .n. Para ello, por cada índice m de estructura de pensamiento, la BdT selecciona primero la cadena con la mayor puntuación de evaluación, es decir, zm 1.... .nm := arg maxz1.... .n∈Zm ∑i=1 Vi + Vi-1,i, donde Zm denota el conjunto de todas las cadenas de pensamiento del m-ésimo árbol. A continuación, existen dos estrategias para obtener z1.... .n.

• agregación del mejor primero.BoT depende de arg maxz1.... .n∈{Zm}M m=1 ∑i=1 Vi + Vi-1,i, y selecciona la mejor de las M estructuras de pensamiento como z1.... .n. Este algoritmo es rápido, pero puede conducir a una cadena ilógica que es difícil de guiar las mejoras posteriores.
• Agregación de codicia. se permite a la BoT realizar una búsqueda codiciosa en {Zm}M m=1 para ensamblar una nueva cadena de mentes que puede no existir, pero que puede ser globalmente óptima. Partiendo del pensamiento inicial, que suele ser el nodo raíz del árbol, la BoT obtiene z1 = arg maxzj ∈ {zm 1 } M m=1 Vj + Vj-1,j. Posteriormente, para obtener zi, la BoT busca todos los pensamientos en {Zm}M m=1 cuyo paso anterior fue zi-1.

análisis de la cadena de pensamiento. Para obtener información sobre lo que debería ajustarse para mejorar la clave y generar un mejor pensamiento, la SdT utiliza la capacidad de los LLM para autoevaluar z1.... .n. En concreto, con el indicio It f (z1.. .n, X, Q) como entrada, el LLM emite un párrafo de retroalimentación que contiene información sobre esta cadena de pensamientos z1.... .n con un informe del problema y sugerencias detalladas. Esta retroalimentación se añadirá a F1,.... ,t-1 como una nueva experiencia en la generación de pensamientos, dando como resultado F1,.... ,t.

Perfeccionamiento iterativo.. Mediante el mecanismo de refuerzo, F1,... ,t se utiliza para mejorar iterativamente el indicio, dando como resultado el indicio It+1 para la (t+1)ª iteración ≡ {S, X, Q, F1,.... t, {Gi}}. A medida que avanza la iteración, F1,.... t puede contener muchas cadenas de pensamiento típicas e ilógicas, así como otras más cercanas a la solución, todas ellas con resultados analíticos bien definidos. Así, incluso cuando se empieza con una pista simple, BoT refina iterativamente esta pista para producir los pasos de razonamiento correctos que conducen a una solución precisa. Después de T iteraciones, utilizamos It+1 como pista de entrada al LLM para la respuesta final.

4. Experimentación

conjunto de datos. Los experimentos se llevaron a cabo en conjuntos de datos de referencia que contenían diversos problemas matemáticos, como MMLU, SVAMP, GSM8K, AQuA y MATH.Además, incluimos una tarea de razonamiento matemático desafiante, Game of 24, en la que el objetivo era obtener 24 en 1 ecuación utilizando cuatro números y operaciones aritméticas básicas (suma, resta, multiplicación y división).Así, la solución consta de 3 pasos intermedios.

concurso. Además del método de referencia Entrada-Salida Estándar (IO), los métodos comparativos incluyen el Pensamiento Encadenado (CoT), CoT-SC y CoT Complejo, en los que las instrucciones de entrada contienen un puñado de ejemplos (8) y anotaciones humanas. Además, BoT se compara con otros trabajos relacionados, como los árboles de pensamiento (ToT), los avisos progresivos (PHP) y los CSV de última generación.Realizamos experimentos utilizando GPT-4 y Llama2.Se accedió a GPT-4 a través de la API de OpenAI, mientras que el modelo llama2-13b-chat se descargó de MetaAI para poder realizar los experimentos localmente. Para construir una estructura heterogénea de pensamiento arbóreo, BoT seleccionó aleatoriamente temperaturas en el intervalo [0,2, 0,4, 0,6, 0,7, 0,9, 1,1, 1,5] y el intervalo p superior [0,1, 0,3, 0,5, 0,7, 0,9].

establecer. A menos que se indique explícitamente, en todos los experimentos, BoT realiza T = 10 iteraciones y construye M = 15 estructuras de pensamiento, cada una de las cuales es un árbol binario ponderado, ya que esto tiende a producir los mejores resultados. Además, para estos conjuntos de datos de referencia, fijamos la profundidad del árbol en 5, mientras que la profundidad correspondiente en Juego de 24 era de 3. BoT + CoT significa que nuestra pista simple incluye 5 ejemplos de CoT. En los estudios de ablación, cuando no hay experiencia acumulada en el BoT, se proporcionarán 8 ejemplos de CoT en la indicación.

métrica. Medimos e informamos de los resultados de todos los experimentos en términos de la tasa de resolución de la tarea (%). A partir de la salida zT1.... .n de las respuestas objetivo, configuramos descripciones formateadas de las respuestas específicamente para los LLM. Para los conjuntos de datos de uso común, el formato de la respuesta se estableció en "La respuesta es:". Para el juego de 24 puntos, utilizamos "Índice del paso, conjunto actual:, dos números seleccionados:, operación:, nuevo número de la operación:, números restantes:, nuevo conjunto de números:". A continuación, comparamos los números del nuevo conjunto de números directamente con la verdad básica. En referencia a ToT Yao et al. (2024), utilizamos la tasa de solución contada a partir de 100 juegos difíciles como métrica.

4.1 Principales resultados

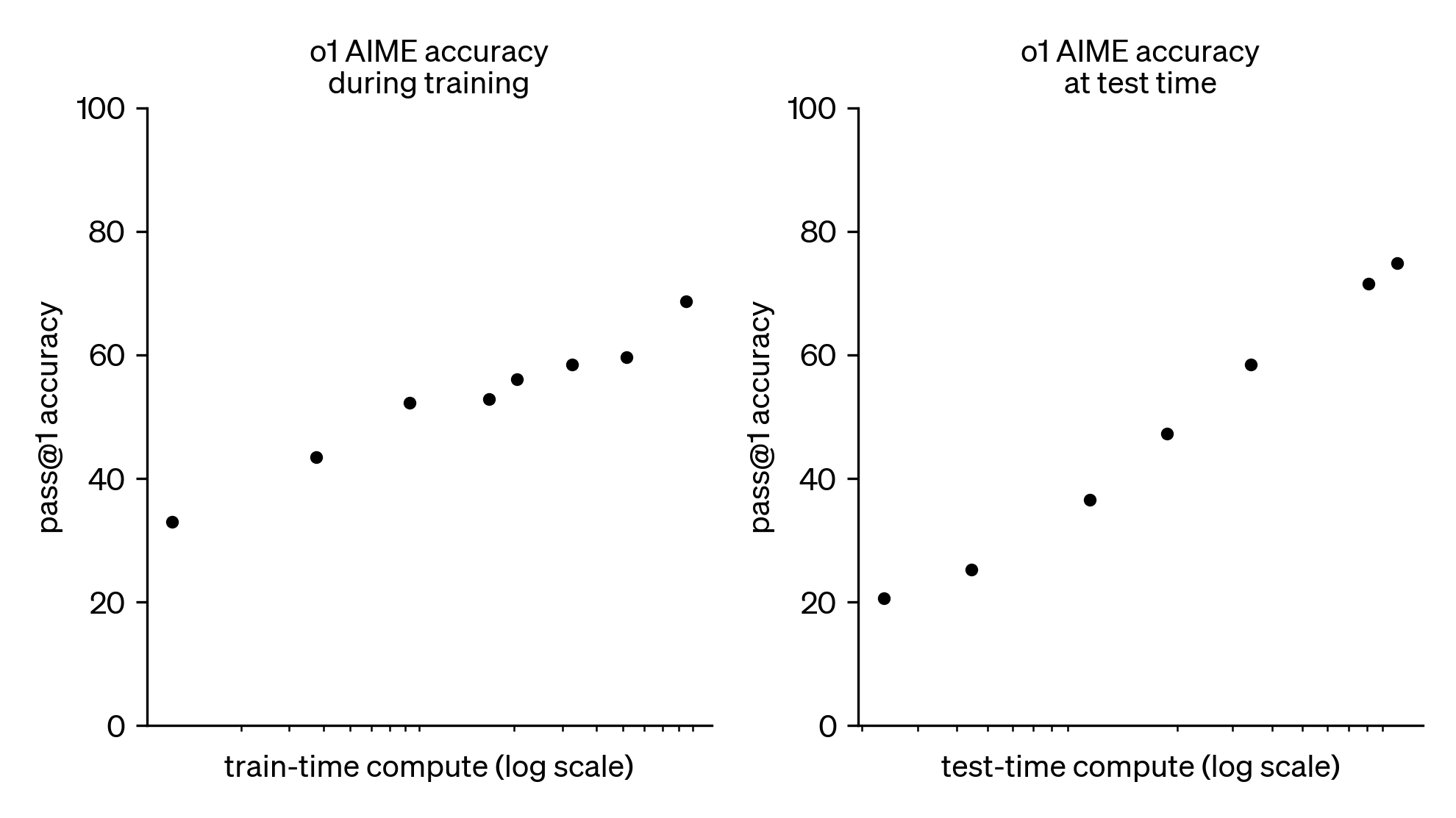
Los principales resultados experimentales se resumen en la Tabla 1 y la Figura 3, donde se ofrece información sobre el rendimiento global de la BoT. Nuestros resultados muestran que la BoT propuesta mediante la potenciación del mecanismo 1). Obtiene índices competitivos de resolución de problemas independientemente de las anotaciones humanas en la mayoría de los conjuntos de datos; 2). Alcanza un nuevo estado del arte al proporcionar ejemplos CoT. Sin embargo, los resultados experimentales también muestran que BoT depende en gran medida de la experiencia y, por tanto, es muy sensible a las capacidades de los LLM.

En concreto, en la Tabla 1, BoT comienza con pistas iniciales sencillas y acaba superando a CSV en 0,11 TP3T en términos de tasa de solución en GSM8K, que depende en gran medida del intérprete de código GPT-4. Si consideramos AQuA, BoT supera a SOTA en 2,51 TP3T. Considerando AQuA, BoT supera a SOTA en 2,51 TP3T. Esto demuestra que añadiendo análisis de errores y sugerencias a las pistas, sin depender de anotaciones humanas, los LLM pueden obtener buenos resultados en razonamientos complejos. La principal razón de ello es que las pistas sencillas pueden mejorarse de forma incremental acumulando experiencia previa para resolver problemas con precisión. Tras incluir ejemplos de CoT en las indicaciones, BoT+CoT es 1,3% superior a SOTA.Argumentamos que los ejemplos de CoT pueden considerarse casos de éxito en la experiencia, que guían directamente la generación de estructuras de pensamiento posteriores en BoT. Así, a través de la mejora iterativa, BoT+CoT alcanzó un nuevo SOTA.Mientras tanto, BoT y BoT+CoT, especialmente BoT, fueron al menos 181 TP3T inferiores a SOTA en MATH.Esta observación implica que los LLM débiles pueden no funcionar bien con BoT debido a la baja capacidad de los LLM para analizar cadenas de inferencia para experiencias válidas.

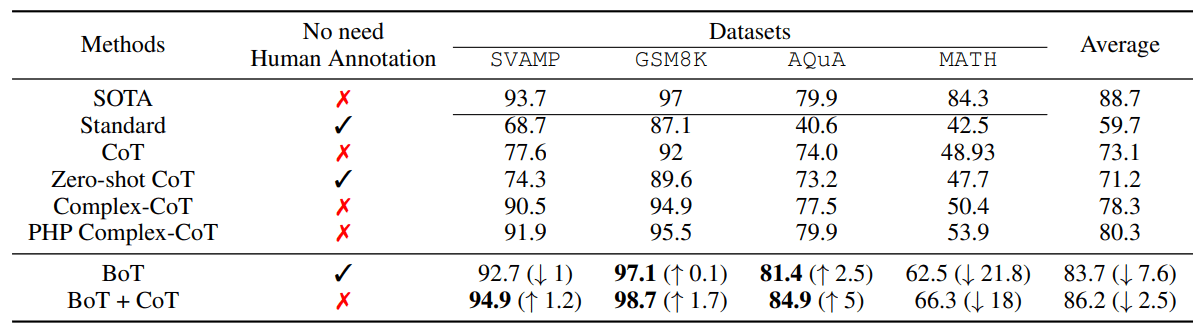
Tabla 1: El uso de BoT junto con GPT-4 mejora significativamente el rendimiento incluso sin anotación manual.
Cuando la pista inicial simple de BoT incluye ejemplos de CoT, el enfoque BoT+CoT correspondiente muestra tasas de solución más altas. Nuestro marco también se compara con enfoques líderes como Model Selection de Zhao et al. en 2023, PHP de Zheng et al. en 2023, y CSV de Zhou et al. en 2023, logrando un rendimiento de vanguardia (SOTA) en los conjuntos de datos SVAMP, AQuA y GSM8K & MATH, respectivamente.

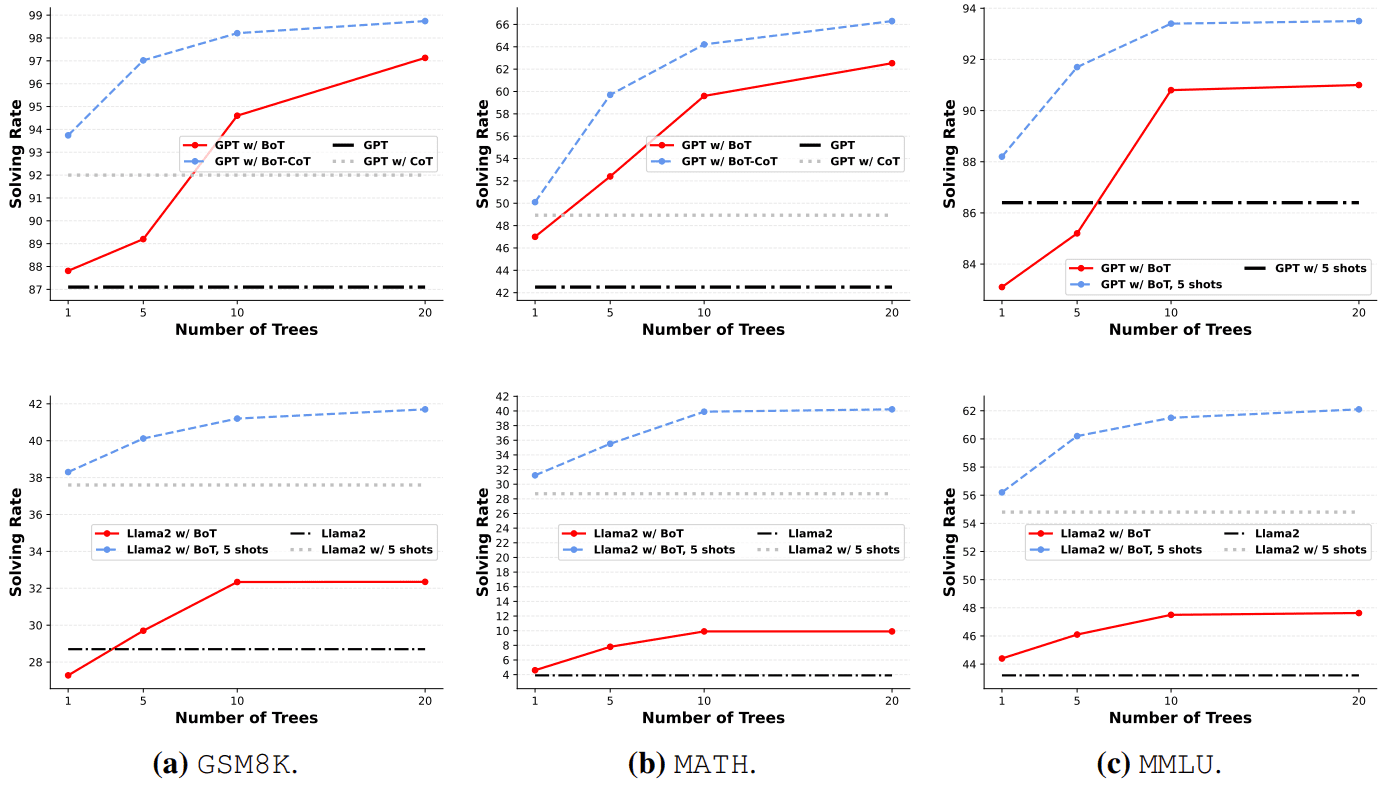
Figura 3: Uso de BoT y BoT+CoT para evaluar la tasa de resolución de problemas de GPT-4 OpenAI con Llama2 Touvron et al. en 2023.

Como puede verse en la Fig. 3, GPT-4 y Llama2 mejoran el rendimiento medio en 11,61 TP3T y 4,41 TP3T de media en los tres conjuntos de datos en condiciones BoT, respectivamente. Estas dos cifras muestran una tendencia clara de que BoT y BoT-CoT tienen un rendimiento similar cuando los LLM son más potentes, como se muestra en la figura 3. Además, a medida que el número de árboles cambia de 1 a 20, su rendimiento muestra una tendencia ascendente similar. Debido a la debilidad de Llama2, BoT no puede beneficiarse de sus análisis para realizar un proceso iterativo basado en la experiencia, como se muestra especialmente en la Fig. 3(a). Cuando se le proporcionan casos de éxito válidos, es decir, 5 pruebas, el BoT aún puede ayudar a Llama2 a resolver más problemas que la línea de base mediante mejoras incrementales, aunque con mejoras limitadas.

4,2 Partido de 24 puntos

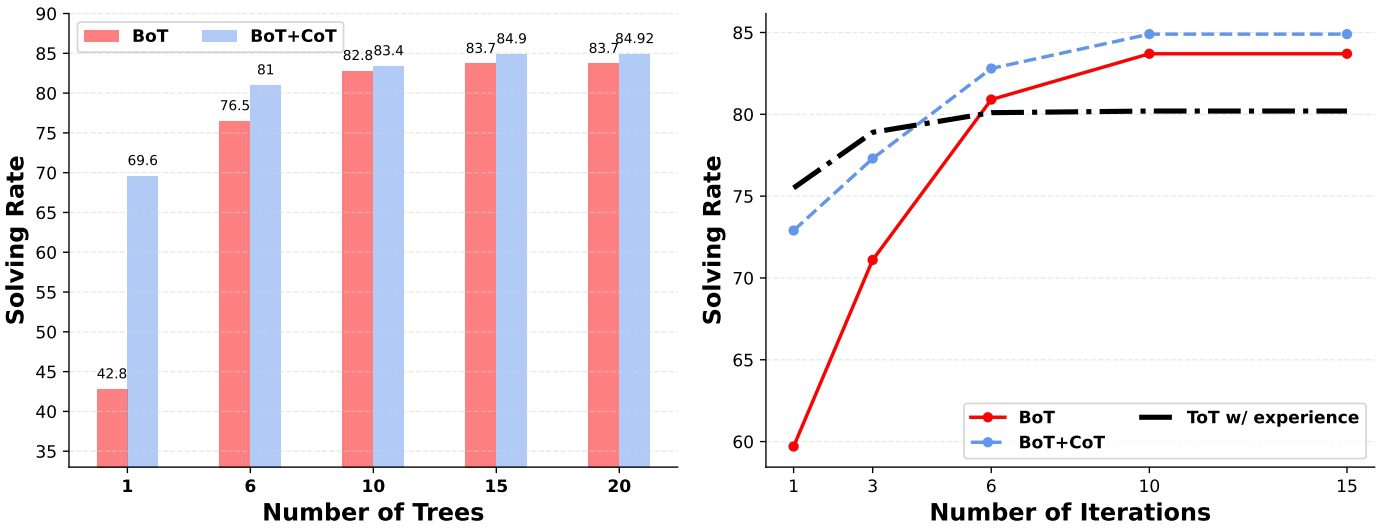
Fig. 4: Comparación de los tres métodos en diferentes números de árboles e iteraciones.

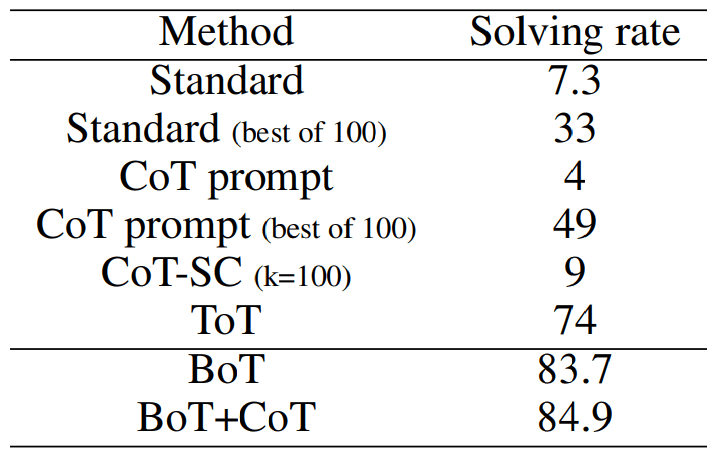
Tabla 2: Configuración de los diferentes métodos en el juego de 24 puntos siguiendo la configuración en ToT Yao et al. (2024), cuyos resultados se muestran aquí.

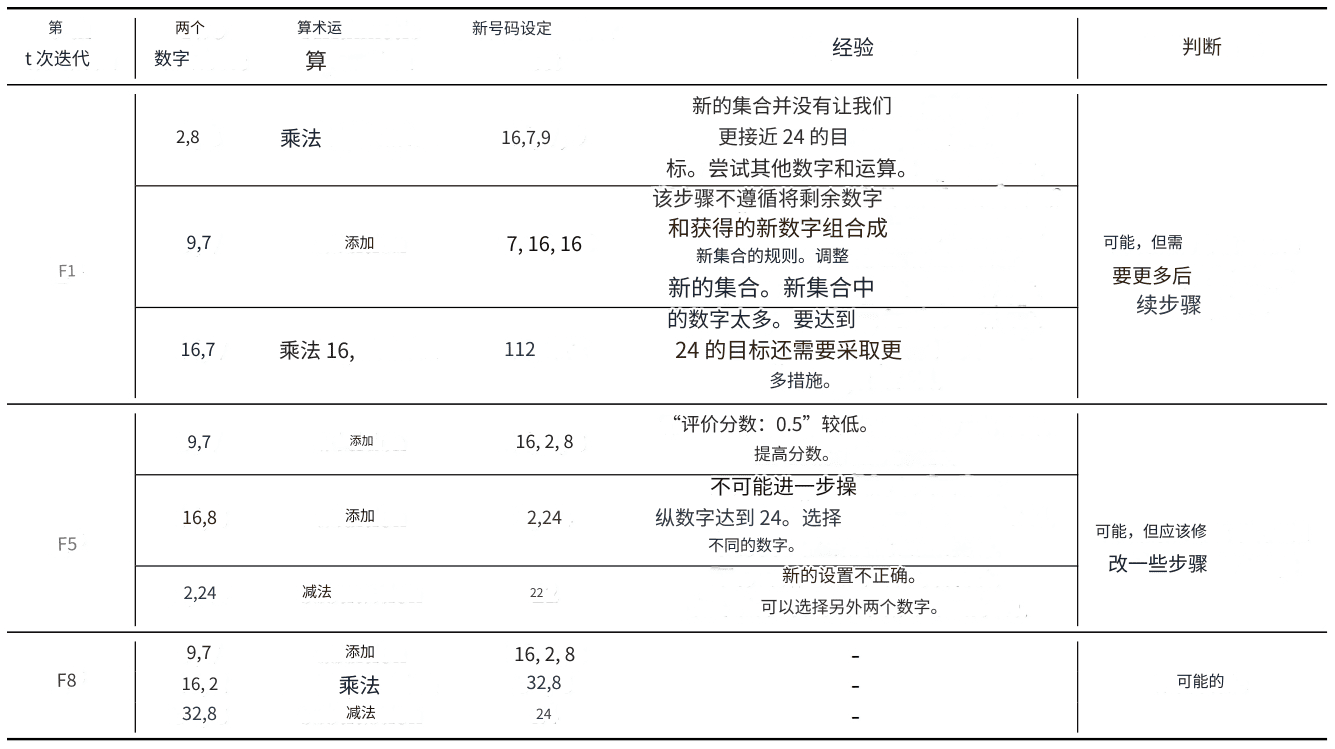
Tabla 3: Demuestra el proceso de reflexión acumulado y la experiencia adquirida durante la 1ª, 5ª y 8ª iteraciones. Los cuatro valores son: 2, 7, 8 y 9.

Debido a la dificultad del problema del Juego de los 24, tanto GPT-4 como Llama2 obtuvieron malos resultados en esta tarea, incluso al combinar los métodos CoT y CoT-SC. El modelo Llama2 fue incapaz de seguir siquiera las reglas correctas para resolver el problema, con lo que la tasa de solución fue aún más baja. Especialmente al aplicar BoT, que se basa en la experiencia, todos los resultados de Llama2 son inferiores a 5% sin mejoras significativas. Por lo tanto, sólo informamos del rendimiento de BoT con GPT-4. Para mantener una comparación justa, seguimos la configuración propuesta por ToT Yao et al. (2024).

Como se muestra en la Tabla 2, la BoT sin anotaciones humanas supera a la ToT que se basa en un ejemplo para mostrar todos los pasos siguientes posibles en 9,71 TP3 T. Además, la BoT+CoT que contiene 5 tomas de CoT supera a la BoT en 1,21 TP3 T. La proximidad de rendimiento entre la BoT y la BoT+CoT se atribuye al mecanismo de refuerzo, que revisa incrementalmente el pensamiento débil, como se discute en la Subsección 4.1. Utilizando un proceso iterativo basado en la experiencia, BoT muestra un rendimiento mejorado a medida que aumenta el número de árboles M y de iteraciones T. Como se muestra en la Fig. 4, BoT depende más de M y T que BoT+CoT porque requiere acumular experiencia a partir de mejores cadenas de pensamientos o iteraciones más largas. Otra observación es que cuando ToT está habilitado para operar con pistas experimentadas, la tasa de resolución de problemas aumenta de 72,51 TP3T en la primera iteración a 80,21 TP3T en la 10ª iteración.Esto sugiere que la experiencia -el análisis de cadenas de razonamiento previas- puede ser utilizada por los LLM para mejorar significativamente la tasa de resolución. Sin embargo, la puntuación obtenida por ToT sigue siendo 3,51 TP3T inferior a la de BoT. Esto se atribuye al hecho de que la fase de agregación de BoT producirá la cadena de razonamiento más representativa en la iteración actual, dirigiendo así una experiencia más significativa para mejorar el indicio. Lo comprobamos en la sección del estudio de ablación.

Para demostrar mejor cómo BoT aprende de los errores y las sugerencias anteriores, mostramos en la Tabla 3 que GPT-4 es capaz de evitar errores anteriores y generar sugerencias más específicas a medida que aumenta el número de iteraciones, lo que finalmente conduce a la solución correcta. En la primera iteración, debido a simples sugerencias, los LLM llegaron a cometer un error al seguir las reglas de la tarea, ya que el nuevo conjunto era incorrecto en el paso 3. Después de analizarlo, realizó la sugerencia correcta. Tras analizarlo, se hizo la sugerencia correcta para este error. Sin embargo, el análisis de la iteración inicial era vago, por ejemplo, "prueba con otros números y operaciones". Tras cinco iteraciones, la BdT sumó múltiples análisis de este tipo, lo que dio lugar a sugerencias más eficaces que llevaron a los LLM a elegir los números correctos 9 y 7. Además, las sugerencias fueron más específicas y útiles. Para esta elección correcta, la sugerencia consistía en aumentar la puntuación de la evaluación en consecuencia. Al acumular esta experiencia, BoT fue refinando gradualmente las sugerencias, generando finalmente la solución correcta directamente en la 8ª iteración.

4.3 Estudios de ablación

Tabla 4: Comparación de GPT-4 con distintas variantes de BoT empleadas en el juego de 24 puntos y el conjunto de datos AQuA.

Todas las estrategias de agregación producen altas tasas de solución cuando los problemas y las sugerencias se agrupan de forma "aditiva". Mantener una experiencia completa es especialmente importante para el pensamiento revisionista, sobre todo para el conjunto de datos AQuA, que abarca una gama más amplia de problemas de razonamiento matemático. Sin embargo, BoT(No), que utiliza todas las cadenas de razonamiento del árbol de spanning directamente sin agregación, obtiene los peores resultados en todos los contextos, especialmente cuando el tipo de experiencia es "acumulativa". En cada iteración de BoT se construyen 15 árboles, y juntarlos todos en un taco puede ocultar información importante, por no mencionar que la mayoría de ellos pueden no ser válidos o perjudiciales. Esa experiencia puede ser inválida o perjudicial.

Asesorarse es más decisivo para desencadenar el pensamiento que cualquier otra cosa.. En todos los ejemplos mencionados en la Tabla 4, la variante BoT que trata las sugerencias como experiencia consigue los mayores índices de solución. Por ejemplo, en el mismo caso de tipo "aditivo", sin sugerencias en la experiencia, el rendimiento bajó en más de 101 TP3T y 201 TP3T en el "juego de 24 puntos" y AQuA, respectivamente. por el contrario, incorporar problemas en la experiencia puede utilizarse como herramienta complementaria para ayudar a mejorar el rendimiento. Los TP con sugerencias sólo pueden alcanzar los mejores índices de resolución si se emparejan con problemas. Por ejemplo, en AQuA, la tasa de resolución de la BoT (método codicioso) aumentó en 4,41 TP3T.

Por razones de rendimiento, el Greedy Rally puede ser la única opción necesaria. Frente al enfoque de mayor prioridad de seleccionar una, o mantener todas, las cadenas de pensamiento existentes, las aglomeraciones codiciosas pueden fusionar de forma adaptativa la estructura de árbol en una cadena de pensamiento mejor, que puede no darse en la iteración actual. De este modo, LLM puede realizar análisis significativos de una cadena de pensamientos más robusta y, como resultado, generar lecciones importantes para aumentar el indicio. En AQuA, que contiene más problemas matemáticos, este número llega incluso a 101 TP3 T. Además, como hemos comentado en la Figura 4, aunque ToT tiene un mecanismo de refuerzo similar basado en la experiencia capaz de alcanzar 801 TP3 T, sigue estando por detrás de BoT. esto puede deberse a que no es capaz de realizar aglomeraciones codiciosas en su estructura de árbol único.

5. Conclusión

En este trabajo, validamos que una pista simple puede utilizarse para resolver tareas complejas mediante la acumulación gradual de análisis de errores de los pensamientos que genera. Proponemos un marco novedoso denominado Boosting of Thoughts (BoT) que permite este aumento gradual de pistas a través de un proceso iterativo basado en la experiencia para generar cadenas eficaces de pensamientos. Una sencilla cadena de pensamientos en forma de árbol, generada mediante la exploración iterativa y la autoevaluación, permite que un simple indicio inicial se vaya incrementando mediante una serie de experiencias de razonamiento de prueba y error que conducen a una solución precisa. Nuestros exhaustivos experimentos demuestran que BoT es capaz de alcanzar un rendimiento puntero en múltiples conjuntos de datos de referencia y supera a otros métodos punteros en la desafiante tarea de razonamiento matemático Juego de 24.

Un BoT de claves básicas y procesos de razonamiento

A1 BoT para el componente de generación de pensamiento

En esta sección se mencionan las pistas básicas utilizadas para la generación de razonamientos del Boosting of Thought (BoT) propuesto. Para obtener detalles específicos relacionados, puede visitar el archivo de ejemplo del código fuente: /examples/BoostingOfThought/BoT reasoner.py.

Consejo sobre el sistema:

Usted es un experto en problemas matemáticos. Realice razonamientos de resolución de problemas paso a paso aprendiendo de una serie de experiencias de razonamiento por ensayo y error. Estas experiencias de razonamiento de prueba y error incluyen específicamente informes de errores, así como sugerencias detalladas sobre cómo modificar los pasos de razonamiento anteriores. Es importante revisar estas experiencias enumeradas antes de generar nuevos pasos de razonamiento como forma de evitar repetir errores y, al mismo tiempo, utilizar los pasos correctos para generar mejores pasos de razonamiento para utilizar en la resolución de problemas.

 

Indicación del sistema S.

Eres un experto en problemas matemáticos. Realiza razonamientos paso a paso.
hacia la resolución de problemas aprendiendo primero de un conjunto de experiencias de razonamiento por ensayo y error.
Esta experiencia de razonamiento por ensayo y error contiene específicamente informes de errores y consejos detallados sobre
Cómo revisar los pasos del razonamiento histórico. Recuerde siempre estas experiencias enumeradas antes de generar un
nuevo paso de razonamiento, evitando así cometer los mismos errores y reutilizando los pasos correctos para generar
mejores pasos de razonamiento para resolver la tarea.

Generar un estímulo para el siguiente pensamiento:

f"""

{Alerta de Misión} \n

En primer lugar, recordar la experiencia de razonamiento anterior: \n\n

 

{Experiencia}\n

 

Por favor, introduzca el siguiente paso de razonamiento posible, y sólo puede haber uno. Este paso de razonamiento debe utilizarse como sucesor secuencial de los siguientes pasos ordenados y debe ir acompañado de una puntuación de evaluación correspondiente (las puntuaciones más altas indican una mayor probabilidad de completar la tarea):\n\t

{cadena pista}\n\n

 

Basándose en los pasos de inferencia del antecedente anteriores (o ignórelos si el espacio anterior está vacío), genere un único paso siguiente posible basado en las reglas de la tarea. (IMPORTANTE: Genere sólo el siguiente paso de razonamiento posible para un paso dado).

"""

f"""{solicitud de tarea}. \n En primer lugar , Recordar la experiencia histórica de razonamiento : \n\n {
experiencias} \n\n Por favor, haga un paso de razonamiento para generar sólo una próxima
Este siguiente paso de razonamiento es el paso secuencial desde El siguiente paso de razonamiento es el paso subsiguiente de
los siguientes pasos previos ordenados , acompañados de sus puntuaciones evaluadas (A
una puntuación más alta significa que el paso de razonamiento tiene más probabilidades de completar la tarea). : \n\t{
cadena prompt}\n\n Basándose en los pasos de razonamiento anteriores enumerados (ignórelos cuando el
el espacio anterior está vacío), genere un único paso siguiente posible tras la Tarea
regla . (Enfatizar: Por favor, genere sólo un único paso de razonamiento posible siguiente de
los pasos dados). """

La indicación de la tarea contiene la X y la Q de la tarea, y la experiencia histórica es F1..... La parte de "pista en cadena" es {Gi}, que es un marcador de posición que, cuando se realiza el pensamiento actual zi, se sustituye por la serie anterior de pensamientos z1...,i-1. ,i-1.

Consejos para reflexionar sobre la evaluación:

f"""

{Alerta de Misión} \n\n

A continuación se muestran los pasos de razonamiento en orden, acompañados de sus respectivas puntuaciones de evaluación. (Una puntuación más alta significa que el paso tiene más probabilidades de completar la tarea). \n

{pista de la cadena}\n

{Pensar}

¿Cuál es su puntuación para evaluar lo lógicos y correctos que son estos pasos de razonamiento, y lo útiles que son para la solución final? Por favor, elija una de las siguientes puntuaciones [0.1, 0.3, 0.5, 0.7, 0.9, 1.0], siendo las puntuaciones más altas las que indican mejores pasos de razonamiento. La puntuación debe colocarse después de ' Puntuación de la evaluación:' para que el usuario pueda leerla.""""

 

f"""{solicitud de tarea}. \A continuación se muestran los pasos de razonamiento generados, presentados por orden.
acompañadas de sus puntuaciones evaluadas (una puntuación más alta significa que el paso de razonamiento es
más probabilidades de completar la tarea). :\n{cadena de preguntas}\n{pensamiento}\n¿Cuál es su
puntuación de evaluación de la lógica , la corrección y el beneficio para llegar a un
solución para estos pasos de razonamiento? Por favor, seleccione un valor de [0,1, 0,3, 0,5,
0,7, 0,9, 1,0] como puntuación , donde una puntuación más alta significa mejores pasos de razonamiento . La dirección
puntuación debe colocarse después de ' Puntuación de evaluación :' para que los usuarios lean .""""

En este caso, el pensamiento es el pensamiento Zi que se está produciendo en ese momento.

A2 BoT para el componente de generación de experiencia

Para generar comentarios sobre cadenas agregadas, los LLM utilizan las siguientes indicaciones básicas. Para más información, visite también el código fuente examples/BoostingOfThought/BoT commenter.py.

System Prompt S: Usted es un revisor experto en IA para Maths Answers que trabaja en la evaluación de la cadena de razonamiento generada para resolver un problema matemático. Por favor, evalúe cada paso de esta cadena de razonamiento proporcionando un análisis detallado para determinar si el paso actual es una inferencia lógica del paso anterior y si el paso de razonamiento contribuye a la solución correcta. Para cada paso de razonamiento incorrecto, proporcione un informe de errores y las revisiones sugeridas correspondientes. Para cada paso de razonamiento correcto, proporcione una descripción de la recomendación o el rechazo.

Consejo sobre el sistema:

Tu papel es el de un hábil Revisor de Respuestas de Matemáticas AI, centrado en evaluar el proceso de razonamiento para resolver problemas matemáticos. Tendrás que juzgar cada paso de razonamiento mediante un análisis exhaustivo para ver si se basa en la lógica del paso anterior y si este paso contribuyó a encontrar la respuesta correcta. Si encuentra un paso de razonamiento incorrecto, deberá dar sugerencias y opciones para modificarlo. Para los pasos de razonamiento correctos, hay que afirmarlos o dar opciones diferentes.

 

Indicación del sistema S.

Eres un experto corrector de respuestas matemáticas, dedicado a evaluar las
cadena de razonamiento generada para abordar el problema matemático. Juzga cada razonamiento
paso de esta cadena de razonamiento proporcionando análisis detallados sobre si el paso actual es un paso lógico
inferencia del paso anterior y si el paso de razonamiento es beneficioso para la solución correcta.
Proporcionar consejos y sugerencias para cada paso de razonamiento con errores. Proporcionar recomendaciones o
descripciones de rechazo para cada paso de razonamiento correcto.

Sugerencia de retroalimentación:

f"""

Para la tarea dada:{pista de tarea}. \n

{Pistas de la Cadena de Razonamiento}\n\n

Por favor, evalúe esta cadena de razonamiento y proporcione una crítica detallada que incluya los siguientes puntos. \n

1. {Formato de retroalimentación de cadena}. 2. {Formato de retroalimentación de paso}. 3. {Formato de retroalimentación de confianza}. 4. {Formato de retroalimentación de paso}. \4. {Formato de Retroalimentación de Confianza}. 5. {Formato de Retroalimentación de Paso}.

Advertencia: {Caveat}

 

f"""Dada la tarea:{tarea prompt}. \Por favor, evalúe esta cadena de razonamiento.
mediante comentarios detallados con el siguiente contenido . \n 1.{
formato de retroalimentación en cadena }. 2.{ step feedback format }. 3.{ formato de retroalimentación de confianza }. \n
\Aviso: {Notice}.

incluidos entre estosPistas para la cadena de razonamientoes una cadena de inferencia agregada z1.... .n.

Formato de retroalimentación en cadena¿Puede esta cadena de razonamiento completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento? ¿Por qué? Escribe el análisis final en "Informe de análisis:".

Formato de respuesta paso a pasoPara cada paso de razonamiento, proporcione un análisis detallado de si el paso actual es una deducción lógica del paso anterior y si el paso de razonamiento contribuye a la solución correcta. Para cada paso de razonamiento incorrecto, facilite un informe de errores y las correspondientes recomendaciones de revisión. Para cada paso de razonamiento, describa la recomendación o el rechazo. Los comentarios deben ser concisos y seguir el siguiente formato: paso de razonamiento ⟨idx⟩. Análisis ⟨idx⟩. Recomendación:. Recomendación o rechazo Descripción:.

Formato de los comentarios de confianzaPuntuación: ¿Cuál es su puntuación de confianza para estas evaluaciones y reseñas? Seleccione un valor entre [0,1, 0,3, 0,5, 0,7, 0,9, 1,0] como puntuación para que el usuario la lea.

Con pistas de retroalimentación, los LLM generan Ft empíricos que contienen conclusiones y análisis de la cadena de razonamiento y de cada paso del razonamiento.

A3 Proceso de razonamiento

Para facilitar la comprensión del Boosting of Thoughts propuesto, resumimos el flujo de inferencia en la Tabla Algorítmica 1. El código fuente de este flujo se encuentra en el archivo examples/BoostingOfThought/BoT core.py.

BoT original

El contenido de la imagen es una representación algorítmica paso a paso de una teoría llamada "BoT", y lo que sigue es su traducción al chino, correspondiente a los siguientes pasos algorítmicos:

Algoritmo 1: Proceso principal de razonamiento de la SdT

Entradas: número de iteraciones T, número de estructuras de árbol M, problema Q.
Salida: cadena agregada z̄_1.... .n^T

1. Inicializar una pista simple I^0 (S, X, Q, F^0, {Gi}), donde F^0 será una cadena vacía.
2. Cada iteración t = 1, 2, ... , T.
3. Utilizar las claves I^t-1 (S, X, Q, F^t-1, {Gi}) con el LLMS (Low Latent Mixed Model) para crear M estructuras de pensamiento diferentes en un proceso llamado Generación de Estructuras de Pensamiento.
4. Extraer la cadena de pensamientos {z̄_i=1....n^m} de M estructuras de pensamiento, cada z̄_i=1.... .n^m}, cada z̄_i=1... .n^m es la mejor cadena de pensamiento de la m-ésima estructura de árbol.
5. Utilice el método "Best-First Aggregation" o "Greedy aggregation" para incorporar {z̄_i=1...n^m} en una única cadena de pensamiento z̄_1...n^m}. .n^m} en una única cadena de pensamiento z̄_1...n^t. .n^t.
6. Utilice LLMS para realizar un "Análisis de la cadena de pensamiento" en z̄_1.... .n^t, obtener la retroalimentación y combinarla con z̄_1.... .n^t y combinarla con z̄_1...n^t para obtener la experiencia F^t.
7. Actualice el taco acumulando F^t a I^t (S, X, Q, F^t-1,t, {Gi}).
8. Conclusión
9. Acceso a las soluciones z̄_1.... .n^T

B Ideas para mejorar el pensamiento

El refuerzo de los pensamientos se deriva de nuestra idea de que la capacidad de razonamiento de los Modelos de Lenguaje Amplio (LLM) para resolver problemas matemáticos se deriva directamente de experiencias que contienen análisis y sugerencias de errores anteriores. Una vez que las pistas contienen experiencias de razonamiento históricas válidas para que los LLM las recuerden antes de realizar el razonamiento, los pasos de razonamiento resultantes suelen ser más lógicos y racionales, como se muestra en la comparación de las Tablas 5 y 6. Estas ideas también nos llevaron a considerar que los LLM no necesitan depender en gran medida de indicaciones bien preparadas para cada tarea (varias demostraciones de cadenas de pensamiento en las indicaciones sirven como ejemplo). Sin embargo, dado que los LLM son capaces de aprender de la experiencia, podemos empezar con una instrucción sencilla que no requiera ejemplos ni contenido diseñado manualmente, e ir acumulando experiencia a medida que razonamos. En última instancia, al acumular experiencia en el indicio, los LLM logran un razonamiento robusto para resolver problemas complejos. Con estas ideas, se diseña el Boosting of Thoughts como un marco de ayuda automatizado que resuelve problemas mediante la recopilación iterativa de una colección de experiencias de razonamiento de prueba y error. Argumentamos que el BoT propuesto no es una aplicación de los LLM a una tarea específica, sino que se basa en la idea de que el poder de razonamiento de los LLM puede obtenerse directamente del análisis de errores de cadenas de inferencia incorrectas sin depender del conocimiento humano a priori.

Para destacar nuestros conocimientos, compartimos las siguientes tres observaciones clave, que se basan en el siguiente conjunto de datos de 24 partidos utilizando el modelo gpt-3.5-turbo con una temperatura de 0,7 y un valor p máximo de 0,7 aplicado.

La experiencia en la pregunta anima a los alumnos a explorar más la lógica en sus respuestas.Como se muestra en la Tabla 5, el modelo generó el mismo paso de razonamiento cinco veces cuando no se incluyó ninguna experiencia en la pista. Esta observación muestra un problema común con los LLM, a saber, la falta de automotivación para explorar diferentes lógicas de razonamiento. Así, a pesar de su gran potencial de razonamiento, los LLM pueden quedarse atascados en un ciclo que comienza con el paso de razonamiento más simple, que puede no conducir nunca a una solución final. La sección "Cadenas de razonamiento adquiridas" de la Tabla 5 ilustra cadenas de razonamiento erróneas. Creemos que, como en Tree of Thoughts Yao et al. (2024), donde los nodos del árbol se construyen generando múltiples respuestas como pensamientos, estos pasos de inferencia repetitivos pueden hacer que el algoritmo falle en algunos casos. Sin embargo, en la segunda iteración de BoT, la introducción de la experiencia en las indicaciones resultó en la generación de diferentes pasos de inferencia iniciales, como se muestra en la Tabla 6. La cadena de inferencia final puede llegar finalmente a la solución correcta partiendo de una gama más amplia de lógicas potenciales.Weng et al. (2023)

Los LLM evitan cometer errores similares destacados en la experiencia.Si no se incluye la experiencia en las indicaciones, que incluyen el análisis de errores, los LLM cometerán muchos errores, como desviarse de las reglas de la tarea y volver al paso de razonamiento inicial en el proceso final, como se muestra en la sección "Cadena de razonamiento adquirida" de la Tabla 5. Tras analizar esta cadena de razonamiento e incorporar su retroalimentación como experiencia en las instrucciones para la segunda iteración de la TdF, se puede observar en la Tabla 6 que los LLM aprenderán la experiencia mucho antes de razonar. En primer lugar, ninguna de las respuestas replicó los mismos pasos de razonamiento erróneos que los diversos pasos de razonamiento iniciales mostrados en "Cinco respuestas de gpt-3.5-turbo". En segundo lugar, los LLM evitaron con éxito todos los errores identificados anteriormente al atenerse estrictamente a las reglas de la tarea, eliminar el razonamiento incorrecto y realizar pasos de inferencia lógica. En tercer lugar, esto condujo finalmente a la solución correcta de la tarea "1 1 4 6" del Juego de los 24. Otros trabajos, como los de Weng et al. (2023); Madaan et al. (2023); Zheng et al. (2023), también han hecho hincapié en la importancia de aumentar las pistas a través de la retroalimentación, que es una autoevaluación de las respuestas anteriores. Sin embargo, BoT es un trabajo seminal basado en la idea de que la experiencia que incluye el análisis de errores puede conducir a un razonamiento sólido en los LLM.

Sin anotaciones humanas, los LLM organizan automáticamente cadenas de razonamiento eficaces para resolver problemas complejos basándose en la experiencia.BoT es la iniciativa pionera que propone un marco de sugerencias automatizado que aprovecha la idea de que los LLM pueden adquirir habilidades de razonamiento eficaces para la resolución de problemas mediante el análisis de errores y la orientación a través de la experiencia, sin necesidad de anotaciones humanas. Como se muestra en la Tabla 5, ésta es la primera iteración de BoT, y las sugerencias iniciales sólo contienen orientación básica sobre la tarea y preguntas sin ejemplos contextuales de aprendizaje como en CoT. Aunque las cadenas de inferencia obtenidas por los LLMs usando tales indicaciones contienen muchos errores y pasos de inferencia inválidos, sus análisis de errores y sugerencias pueden ser incluidos como lecciones aprendidas en las indicaciones de entrada para beneficiar la segunda iteración de inferencia, como se muestra en la Tabla 6. Se puede observar que sin una guía humana sobre el procedimiento de razonamiento correcto, los LLMs pueden obtener conocimiento de la experiencia, incluyendo análisis de errores y guía, que se obtienen de cadenas de razonamiento generadas previamente, lo que lleva a mejoras incrementales en la resolución de problemas de razonamiento.

Por lo tanto, nuestra TdC proporciona una orientación a largo plazo para la investigación, ya que demuestra la importancia del análisis de errores de recuerdo y sugerencias a la hora de permitir que los LLM generen procesos de razonamiento eficaces para tareas complejas. Con estos conocimientos, la investigación en ingeniería de pistas para inducir habilidades de razonamiento en los LLM puede centrarse en cómo generar experiencias en lugar de introducir más conocimiento humano a priori.

C Generación de estructuras de pensamiento

BoT es un marco de generación de pensamiento automatizado que acumula iterativamente la experiencia adquirida a partir de los análisis de las cadenas de inferencia. Como tal, BoT se generaliza a una variedad de métodos de generación de pensamiento y LLMs capaces de generar y evaluar pasos de inferencia.Además, el rendimiento de BoT depende de la eficacia de su estructura de generación de pensamiento. Por lo tanto, BoT utiliza la estructura más reciente, el Árbol de Pensamiento (Tree of Thought, ToT) Yao et al. (2024), como modelo base para generar cadenas de razonamiento en cada iteración. Como se menciona en el artículo principal, el modelo base de generación de pensamiento también podría ser un Gráfico de Pensamiento (Thinking Graph, GoT) Besta et al. (2023), es decir, BoT con GoT. sin embargo, debido a las limitaciones de tiempo y al hecho de que el GoT actual aún no se ha aplicado a problemas matemáticos, el diseño de BoT emplea exclusivamente ToT. además, al utilizarse como modelo base en el mecanismo de refuerzo, la estructura de pensamiento en cada iteración puede mantenerse ligera. En definitiva, el BoT propuesto genera estructuras de árbol heterogéneas, donde cada árbol es un árbol binario ligeramente ponderado.

C1 Generación de Next Thinking y cálculo del peso de las aristas

Utilizando la pista de generación del siguiente pensamiento discutida en la Sección A, los LLM pueden generar pistas combinando la experiencia F1.... .t y sustituyendo {Gi} por z1... ,i-1 sustituyendo {Gi} para generar el siguiente pensamiento posible para un paso de razonamiento zi. Para un paso de razonamiento zi, los LLM utilizan la pista de evaluación del pensamiento para generar puntuaciones de evaluación como pesos de arista entre zi y zi-1. Para un procedimiento detallado, véase el código fuente en examples/BoostingOfThought/BoT reasoner.py. Como ejemplo directo de BoT aplicado a '3 5 6 8' en Game of 24, usando gpt-3.5-turbo, las Tablas 7 y 8 muestran la generación del pensamiento, mientras que la Tabla 9 muestra cómo se calcula.

C2 Necesidad de estructuras de árbol heterogéneas

En cada iteración de BoT, la estructura de árbol heterogéneo se construye para explorar un espacio de búsqueda de inferencia más amplio y mejorar la robustez. Como se puede ver en el código fuente en examples/BoostingOfThought/BoT core.py, los valores de temperatura y Top p de los LLM de cada árbol se seleccionan entre los intervalos [0,2, 0,4, 0,6, 0,7, 0,9, 1,1, 1,5] y [0,1, 0,3, 0,5, 0,7, 0,9], respectivamente. La estrategia de crecimiento del árbol puede ser capa por capa u hoja por hoja. Observamos las dos ventajas siguientes de garantizar esta heterogeneidad.

La heterogeneidad amplía el espacio de búsqueda de inferencia y, por tanto, aumenta la velocidad de convergencia.Cuando se construyen árboles diferentes con propósitos distintos, por ejemplo, explorados mediante una estrategia capa por capa o explotados mediante una estrategia hoja por hoja, y basados en LLMs aleatorios o deterministas, los pasos de razonamiento generados y las cadenas de inferencia resultantes pueden mostrar diferencias significativas, abarcando efectivamente una gama más amplia de posibilidades de razonamiento. Por ejemplo, en una iteración, cuando los LLM generan el siguiente pensamiento con más confianza, se exploran continuamente pensamientos similares; de lo contrario, los LLM con más aleatoriedad tienden a generar pensamientos diversos. A menudo es difícil predecir si el razonamiento determinista o la aleatoriedad contribuirán a una solución. Por tanto, garantizar la heterogeneidad mezclando distintos tipos de pasos de razonamiento lógico nos permite explorar por completo el espacio de razonamiento en una sola iteración, lo que en última instancia facilita las iteraciones posteriores. En el estudio de ablación, comparamos el rendimiento de BoT entre estructuras de árbol heterogéneas y homogéneas.

La heterogeneidad reduce la probabilidad de generar cadenas de inferencia inválidas o incorrectas, aumentando así la robustez.A diferencia de la heterogeneidad, en los árboles con una configuración homogénea, los árboles individuales tienden a seguir un razonamiento lógico generativo coherente y a construir cadenas de inferencia con la misma estructura de árbol. Entonces, cuando la lógica es errónea o la estructura subyacente no es válida para el problema en cuestión, las cadenas de razonamiento de todos los árboles obtenidas por BoT en cada iteración sólo pueden contener pasos de razonamiento ruidosos e incorrectos. Incluso al agregarlos para obtener una cadena de razonamiento más refinada para su evaluación, la experiencia puede seguir desviándose significativamente de proporcionar consejos adecuados para la resolución de problemas. Por lo tanto, diseñar la estructura del árbol de razonamiento para que sea heterogénea puede ayudar a reducir la probabilidad de que no haya cadenas de razonamiento válidas disponibles para su evaluación en iteraciones posteriores de la BdT. Esta mayor robustez permite a la TdF resolver problemas de distintos niveles de dificultad.

Esta imagen muestra el proceso de "agregación de máxima prioridad" y "agregación codiciosa".

Entrada: m cadenas de inferencia, donde el paso de inferencia de una m-ésima cadena se denota z1i = 1m.
Salida: cadena polimérica z1..n.

1 - agregación de máxima prioridad
2 Para cada cadena m = 1, 2, ... . , M hacer
3 Calcula la suma de los pesos de arista de la cadena m-ésima como Vm = ∑i en el rango m1m Vi-1,i.
4 Finales
5 Obtenga la cadena óptima entre M cadenas realizando m* = arg maxm {Vm}
6 Asigne la cadena agregada como cadena óptima, z1.... .n := {z1i=1n*m*}

7 - Agregación codiciosa
8 z1 := z1 donde m* = arg maxm {V1m}.
9 Para cada paso de agregación i = 2, ... , n hacer
10 Para cada cadena m = 1, 2, ... . , M hacer
11 Recoger Jm = {j, sim(z1i-1, z1j) > 0,7; j ∈ n1m}.
12 Obtener j*,m = arg maxj∈Jm {Vj,j+1m}
13 Fin
14 Realice lo siguiente para obtener el siguiente paso de inferencia óptimo: zi = z1j*+1 donde j* = arg maxj∈{j*m}1M {Vj,j+1m}.
15 Finales
16 Obtener cadenas poliméricas z1.... .n.

Se trata básicamente de un diagrama de flujo algorítmico que describe cómo optimizar una cadena de datos o un nodo y obtener los mejores resultados mediante distintos métodos.

D Agregación de estructuras de pensamiento

Tras completar el razonamiento en una estructura arbórea heterogénea, el proceso de agregación de BoT extrae primero las mejores cadenas de razonamiento de cada árbol, y luego las combina en una única cadena de razonamiento utilizando los métodos de agregación best-first o greedy. Se puede encontrar información más detallada sobre estos dos métodos de agregación en el código fuente examples/BoostingOfThought/BoT aggregator.py.

Como se muestra en el primer bloque del algoritmo 16, la agregación del mejor primero es un método de agregación sencillo que extrae directamente la cadena con la mayor suma de pesos de arista. Este método es rápido y estable. Suele garantizar un rendimiento competitivo porque la experiencia posterior puede generarse analizando las cadenas óptimas obtenidas. Sin embargo, sólo puede seleccionar cadenas existentes sin un ajuste eficaz. La agregación codiciosa es más avanzada porque combina los pasos de inferencia en diferentes cadenas para producir una cadena de inferencia nueva y mejor con los pesos de arista más altos. El proceso de agregación codiciosa del algoritmo 16 consta de dos pasos. En primer lugar, recopila los pasos de inferencia que son similares al paso de inferencia agregado zi-1 . Por lo tanto, el siguiente paso de inferencia agregado se selecciona a partir del siguiente paso de inferencia de este conjunto de recopilación maximizando los pesos de las aristas. sim es una función de similitud que evalúa el porcentaje de palabras y números matemáticos iguales entre dos pasajes utilizando LLM. 0,7 es un umbral empírico obtenido a partir de los experimentos.

E Impacto de la información errónea

La retroalimentación obtenida al evaluar la cadena de inferencia agregada puede incluir un uso limitado de los análisis y conclusiones e informes de error completamente erróneos. Este problema suele deberse a la naturaleza de los LLM, que son modelos lingüísticos y no verifican intrínsecamente la exactitud del texto generado. Además, las capacidades de los LLM, como gpt-3.5-turbo, son limitadas cuando se utilizan como validadores de problemas matemáticos.

En el cuadro 7 se presenta un ejemplo sencillo. El análisis concluye que "el resultado final obtenido en el paso 3 es 80, que matemáticamente es igual a 24. "Peor aún, la experiencia contiene además que "la cadena de razonamiento es correcta" y que "no se encontraron errores en los pasos de razonamiento". se encontraron errores". Usando esta experiencia como pista de entrada, en la primera iteración, la BoT es engañada para generar el paso de inferencia incorrecto, y la cadena de agregación correspondiente puede verse al principio de la Tabla 8. Es evidente que la cadena de agregación es lógicamente incorrecta y no cumple ninguna de las reglas del Juego de 24.

Sin embargo, sostenemos que la retroalimentación errónea no se amplificará, sino que su impacto negativo en los pasos de razonamiento generados puede mitigarse o incluso corregirse por completo en iteraciones posteriores a través del mecanismo iterativo de la TdR. La razón principal es que los pasos de razonamiento erróneos generados se analizarán posteriormente para generar nuevas experiencias que se añadirán al taco. Concretamente, dado que estos pasos de razonamiento contienen errores fácilmente reconocibles y obvios, los LLM tienden a generar análisis de errores correctos y a proporcionar sugerencias de revisión eficaces. Con la nueva experiencia incluida en las pistas, la BdT es capaz de generar pasos de razonamiento correctos. Como muestran las experiencias de la Tabla 8, la SdT generó informes detallados de errores y sugerencias de revisión, lo que resultó en un proceso de generación de razonamientos racionales.

Las ventajas de BoT en la utilización de iteraciones para mitigar los efectos adversos de la retroalimentación de error son evidentes en la Figura 4. En particular, el rendimiento de BoT muestra una mejora consistente a medida que aumenta el número de iteraciones. En particular, el rendimiento de BoT mejora constantemente a medida que aumenta el número de iteraciones. Esto subraya la importancia de la experiencia acumulada y la capacidad de la experiencia posterior para corregir errores anteriores.

F Más resultados para matemáticas

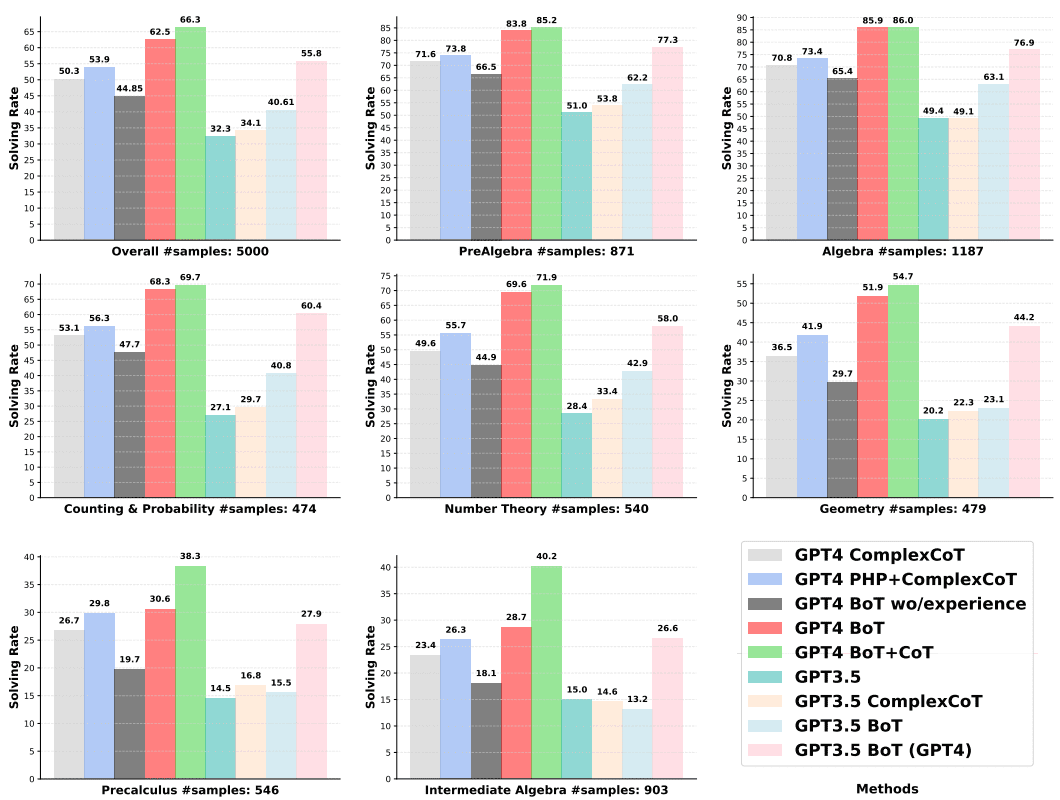
Fig. 5: Revela la eficacia del uso de diferentes estrategias para resolver todos los problemas categorizados en el conjunto de datos MATH. Las estrategias se comparan basándose en categorías que incluyen preálgebra, álgebra, cálculo y probabilidad, principios de teoría de números, geometría, precálculo y álgebra intermedia. El subgrupo denominado "global" muestra la tasa global de resolución de todos los problemas de todas las categorías.

En la Figura 5 se muestran los porcentajes de solución de los distintos métodos en cada categoría del conjunto de datos MATH. La complejidad y diversidad de los distintos problemas matemáticos de estas categorías proporcionan un punto de referencia más desafiante para el razonamiento matemático. Así, la complejidad y diversidad de los problemas en MATH requieren una amplia gama de habilidades de razonamiento para resolverlos. Por lo tanto, un examen detallado de nuestro enfoque y su comparación con otros enfoques en nuestro contexto puede proporcionar información valiosa.

LLMs.En los experimentos realizados con el conjunto de datos MATH se utilizaron modelos de grandes lenguajes (LLM) bien conocidos, a saber, GPT-3.5-Turbo, en lo sucesivo GPT3.5, y GPT-4, en lo sucesivo GPT4. Utilizamos directamente la API publicada por OPENAI.

Rivales.
- GPT4 ComplexCoT. que es un modelo de GPT4 que utiliza el método de incitación Complex CoT Fu et al. (2022). Se utilizan ejemplos de razonamiento en las pistas de inferencia, que se toman de la correspondiente publicación Complex CoT Fu et al. (2022). Dado que se utiliza decodificación codiciosa, no seguimos el enfoque autoconsistente de Wang et al. (2022) para el muestreo de rutas de inferencia.
- GPT3.5. se utilizan preguntas estándar y modelos GPT3.5 para generar respuestas.
- GPT3.5 ComplexCoT. similar a GPT4 ComplexCoT, pero con el modelo cambiado a GPT3.5.
- GPT4 PHP+ComplexCoT. Se trata del modelo GPT4 que utiliza PHP Zheng et al. (2023) + Complex CoTFu et al. (2022). Específicamente, en el marco de PHP Zheng et al. (2023), las respuestas base iniciales se generan utilizando indicaciones de Complex CoT, y luego PHP+Complex CoT puede desarrollar indicaciones de generación de respuestas posteriores a partir de estas respuestas base. Así, al principio de una interacción, las respuestas base pueden generarse pasando las pistas base de Complex CoT y la pregunta actual al LLM. A continuación, basándose en las sugerencias Complex CoT revisadas a la versión PHP con frases de sugerencia adicionales, el marco de sugerencias paso a paso se ejecuta sobre esta respuesta base para generar la respuesta correcta. Nos referimos a esto como la contrapartida PHP+Complex CoT del PHP-Complex CoT del trabajo original.
- GPT4 BoT sin experiencia. el modelo GPT4 se utiliza para realizar el razonamiento del marco BoT sin acumular experiencia. la configuración básica del BoT sigue las presentadas en el documento principal. Así, tras una iteración, se utilizarán cadenas agregadas como solución.
- GPT4 BoT. GPT4 se utiliza para realizar la versión completa del BoT que se muestra en el documento principal.
- GPT4 BoT + CoT.Además del marco BoT, las indicaciones incluían 5 ejemplos de razonamiento de la publicación CoT Wei et al. (2022). Así, en cada iteración, las instrucciones contienen no sólo la experiencia, sino también los 5 ejemplos adicionales de razonamiento CoT.
- GPT3.5 BoT. similar a GPT4 BoT, pero con el modelo cambiado a GPT3.5.
- GPT3.5 BoT (GPT4). En este experimento, utilizamos GPT3.5 para razonar y así generar cadenas de pensamientos en la generación de estructuras de pensamiento.

Sin embargo, el modelo GPT4 se utilizó para obtener información de evaluación y análisis al realizar la evaluación del pensamiento y la generación de experiencias en un análisis agregado de la cadena de pensamiento.

A partir de los resultados de la Figura 5, hacemos las siguientes observaciones adicionales.

Los excelentes resultados de la BoT en la resolución de problemas más complejos se deben en gran medida a la experiencia.Los métodos relacionados con BoT, como GPT4 BoT y GPT4 BoT + CoT, alcanzan sistemáticamente los mayores índices de resolución de problemas en las distintas subcategorías de MATH. En concreto, GPT4 BoT supera a la mejor solución disponible, GPT4 PHP + ComplexCoT, en 8,61 TP3T, mientras que GPT4 BOT + CoT lo hace en 12,41 TP3T.En el total de siete categorías, GPT4 BoT supera a GPT4 PHP + ComplexCoT en al menos 0,81 TP3T, con su problema algebraico Lo mismo ocurre con GPT3.5 BoT y GPT3.5 BoT + CoT. Sin embargo, cuando no hay experiencia acumulada en el marco BoT, todo el rendimiento en la resolución de problemas matemáticos se reduce drásticamente, como muestra la experiencia de GPT4 BoT wo/.

Además de la experiencia en el análisis de errores, la inclusión de ejemplos correctos, como ejemplos sencillos de CdT, es esencial para mejorar la eficacia de la CdT en la resolución de problemas matemáticos difíciles.GPT4 BoT supera significativamente a GPT4 PHP+ComplexCoT en la resolución de cada una de las cinco primeras subcategorías del problema MATH.Sin embargo, en las áreas de álgebra avanzada e intermedia, donde la necesidad de un razonamiento más complejo y de soluciones lógicas complejas paso a paso es mayor, las mejoras de BoT son sólo de 0,8% y 2,4%.Estas ganancias son relativamente limitadas en comparación con las mejoras significativas observadas en la resolución de las categorías de problemas más sencillos Estas ganancias son relativamente limitadas en comparación con las mejoras significativas observadas al resolver categorías de problemas más sencillas. Sin embargo, cuando se añadieron cinco instancias correctas de CoT directamente al prompt de entrada, la GPT-4 BoT + CoT mejoró enormemente su rendimiento en los dominios de álgebra avanzada e intermedia, superando a la GPT-4 BoT en 7,71 TP3T y 11,51 TP3T, respectivamente.La conclusión subyacente de estas observaciones es que para garantizar que la BoT alcanza el mejor rendimiento posible al resolver problemas matemáticos complejos, no es posible confiar únicamente en el análisis de ensayo-error para aprender a razonar. El análisis de errores para aprender a razonar no es suficiente y debería basarse en proporcionar respuestas correctas a los LLM en el prompt de entrada.

Aunque inicialmente la BoT ajustada GPT3.5 puede ser ligeramente inferior a la CoT GPT-4, cuando se genera experiencia utilizando la GPT-4 como herramienta de evaluación y análisis, es posible conseguir que la BoT GPT-3.5 (GPT-4) supere a la CoT Compleja GPT-4.Al utilizar GPT3.5, que tiene una capacidad menor que GPT4, como LLM, BoT obtuvo una tasa de solución al menos 7,71 TP3T inferior a GPT4 ComplexCoT (especialmente en la disciplina del álgebra). Está claro que BoT no puede superar a GPT4 ComplexCoT cuando los LLM de menor rendimiento producen análisis de prueba y error de menor calidad.Por lo tanto, después de utilizar GPT3.5 para generar sólo el paso de inferencia junto con la experiencia generada por GPT4, GPT3.5 BoT (GPT4) mostró una mejora significativa en todas las categorías, lo que llevó a una tasa de solución de 55,81 TP3T, que es superior a la de GPT4 ComplexCoT en 5,5%, e incluso 1,9% más que el estado actual de la técnica GPT4 PHP+ComplexCoT. Estas observaciones demuestran una vez más que la experiencia adquirida mediante la iteración sobre pistas es la principal razón del éxito del marco BoT.

G Resultados del razonamiento para el juego 24 puntos

En primer lugar, en las Tablas 5 a 9, mostramos las pistas detalladas utilizadas por BoT en el proceso de razonamiento, proporcionando así una comprensión global de lo que BoT hace en cada iteración. A continuación, a partir de la Tabla 10, mostramos ejemplos exactos que abarcan todo el proceso de razonamiento de BoT. Siguiendo la configuración básica mostrada en la sección Experimentos, estos experimentos se obtuvieron utilizando el modelo GPT-3.5-turbo con BoT.

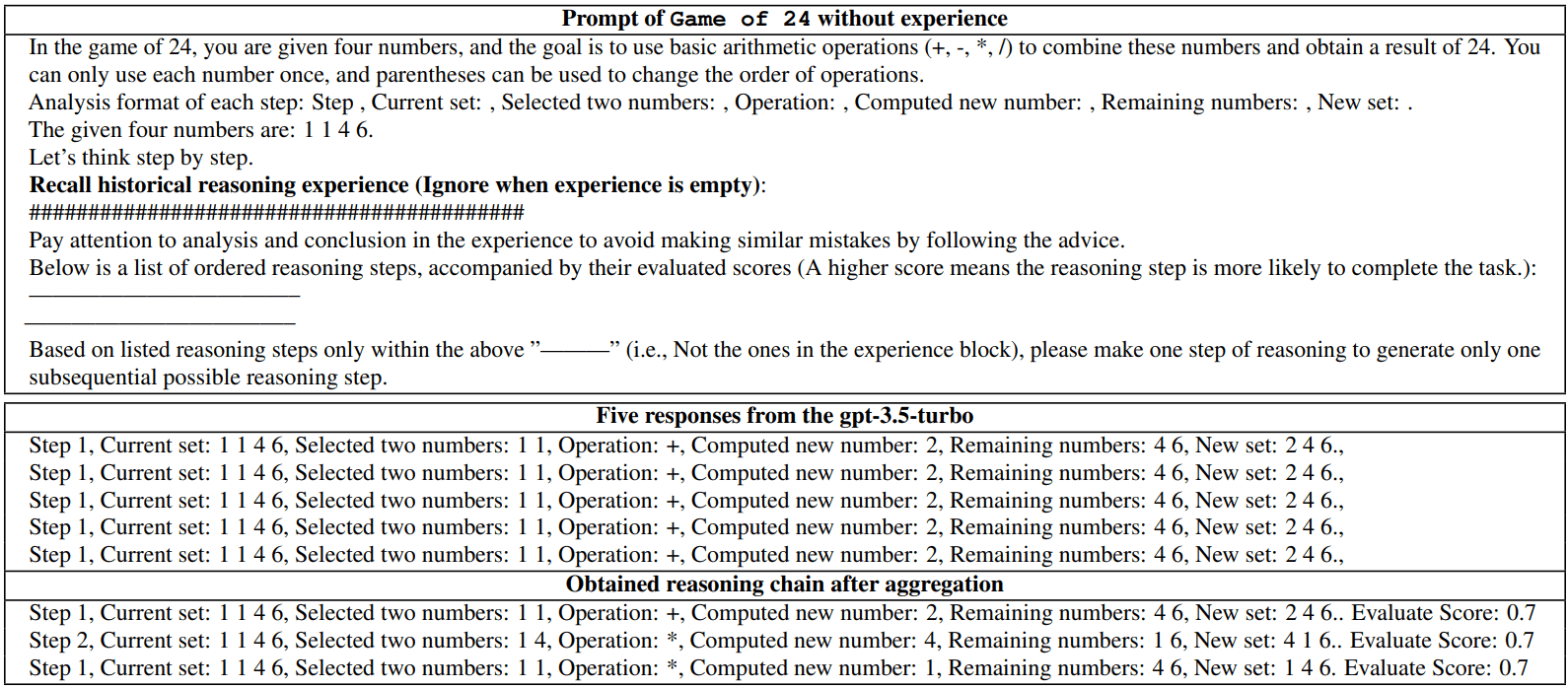
Tabla 5: Pasos de inferencia generados por gpt-3.5-turbo cuando no se incluye experiencia en la pregunta de entrada.Primero hacemos que el modelo genere cinco pasos de inferencia para comprobar la diversidad, y luego presentamos la cadena de inferencia final tras completar la primera iteración de la BoT.

Consejos para el juego 24:00, sin experiencia

En 24 Puntos se le dan cuatro números y el objetivo es utilizar operaciones aritméticas básicas (+, -, *, /) para combinar estos números y obtener el resultado 24. Sólo puedes utilizar cada número una vez y puedes utilizar paréntesis para cambiar el orden de las operaciones.

Analice cada paso del formato:
Paso X. Conjunto actual: XXXX, dos números seleccionados: XX XX, operación: XX, nuevo número obtenido por cálculo: XX, números restantes: XXXX, nuevo conjunto: XXXX.

Los cuatro números dados son: 1 1 4 6.
Pensemos paso a paso.

Recordar la experiencia histórica de razonamiento (ignorar cuando la experiencia es nula):
## ############### ######## ######## # # # #######
Presta atención a los análisis y conclusiones de la experiencia y evita cometer errores similares siguiendo las recomendaciones.
A continuación se muestra una serie de pasos de razonamiento ordenados, acompañados de sus puntuaciones de evaluación (las puntuaciones más altas significan que el paso de razonamiento tiene más probabilidades de completar la tarea). :

Basándose en los pasos de razonamiento enumerados en "_" más arriba (es decir, no en los pasos del bloque empírico), realice un paso de razonamiento para generar el único paso de razonamiento posterior posible.

Cinco respuestas de gpt-3.5-turbo
Paso 1, Conjunto actual: 1 1 4 6, Dos números elegidos: 1 1, Operación: +, Nuevo número calculado: 2, Números restantes: 4 6, Nuevo conjunto: 2 4 6., Puntuación de la evaluación: 0,7
Paso 1, Conjunto actual: 1 1 4 6, Dos números elegidos: 1 1, Operación: +, Nuevo número calculado: 2, Números restantes: 4 6, Nuevo conjunto: 2 4 6., Puntuación de la evaluación: 0,7
Paso 1, Conjunto actual: 1 1 4 6, Dos números elegidos: 1 1, Operación: +, Nuevo número calculado: 2, Números restantes: 4 6, Nuevo conjunto: 2 4 6., Puntuación de la evaluación: 0,7
Paso 1, Conjunto actual: 1 1 4 6, Dos números elegidos: 1 1, Operación: +, Nuevo número calculado: 2, Números restantes: 4 6, Nuevo conjunto: 2 4 6., Puntuación de la evaluación: 0,7
Paso 1, Conjunto actual: 1 1 4 6, Dos números elegidos: 1 1, Operación: *, Nuevo número calculado: 1, Números restantes: 4 6, Nuevo conjunto: 1 4 6., Puntuación de la evaluación: 0,7

Cadena de inferencia obtenida tras la agregación
Paso 1, Conjunto actual: 1 1 4 6, Dos números elegidos: 1 1, Operación: +, Nuevo número calculado: 2, Números restantes: 4 6, Nuevo conjunto: 2 4 6... Evaluar la fracción: 0.7
Paso 2, conjunto actual: 1 1 4 6, dos números elegidos: 1 4, operación: *, nuevo número calculado: 4, números restantes: 1 6, nuevo conjunto: 4 1 6... Puntuación de la evaluación: 0,7
Paso 1, Conjunto actual: 1 1 4 6, Dos números elegidos: 1 1, Operación: *, Nuevo número calculado: 1, Números restantes: 4 6, Nuevo conjunto: 1 4 6., Puntuación de la evaluación: 0,7

H Resultados de derivación para "GSM8K".

La BdT funciona utilizando instrucciones básicas y formatos específicos similares a los que se muestran en las Tablas 5 a 9. Lo único que cambiaría es la instrucción de tarea, como se muestra en la Tabla 15. Lo único que cambiaría es el prompt de la tarea, como se muestra en la Tabla 15. Y a partir de la Tabla 16, proporcionamos una serie de ejemplos detallados que contienen el proceso completo de razonamiento de BoT. Estos experimentos se basan en la configuración base mostrada en la sección Experimentos, utilizando el modelo GPT-3.5-turbo de BoT.

# Preguntas de razonamiento empírico para el juego 24

## En primer lugar, repasar la experiencia histórica del razonamiento:

### Cadena de inferencia 1 y sus comentarios

A continuación se muestra una cadena de pasos de razonamiento por orden:

---

### Paso 1
Conjunto actual: 1 1 4 6, dos números elegidos: 1 1, operación: +, nuevo número calculado: 2, números restantes: 4 6, nuevo conjunto: 2 4 6... Puntuación de la evaluación: 0,7

### Paso 2
Conjunto actual: 1 1 4 6, dos números elegidos: 1 4, operación: *, nuevo número calculado: 4, números restantes: 1 6, nuevo conjunto: 4 1 6... Puntuación de la evaluación: 0,7

### Paso 3
Conjunto actual: 1 1 4 6, dos números elegidos: 1 1, operación: *, nuevo número calculado: 1, números restantes: 4 6, nuevo conjunto: 1 4 6. Puntuación de la evaluación: 0,7

---

## ANÁLISIS: Esta cadena de razonamiento es incapaz de completar la tarea y alcanzar el objetivo correctamente. Hubo errores en los pasos de razonamiento que impidieron descubrir la solución correcta.

### Razonamiento Paso 1
Este paso es una extrapolación lógica del paso anterior, ya que sigue la regla de seleccionar dos números, realizar la operación y actualizar el conjunto en consecuencia. Sin embargo, este paso no contribuye a la solución correcta. El nuevo número 2 obtenido mediante el cálculo no conduce al resultado deseado 24.
**Sugerencia**: Prueba diferentes operaciones o combinaciones de números para obtener un nuevo número más cercano a 24.
**Descripción de la recomendación o el rechazo**: Rechazada.

### Razonamiento Paso 2
Hay un error en la descripción del paso de razonamiento. Se denomina incorrectamente "paso de razonamiento 2" dos veces. Sin embargo, suponiendo que sea el único paso, se trata de una deducción lógica del paso anterior. La operación de multiplicación (*) se aplica correctamente al número seleccionado y da como resultado el nuevo número 4. Los números restantes se actualizan en consecuencia.
**Descripción recomendada o rechazada**: Recomendada.

### Razonamiento Paso 3
Hay un error en la descripción del paso de razonamiento. Se denomina incorrectamente "Paso de razonamiento 1" en lugar de "Paso de razonamiento 3". Este paso no es una deducción lógica del paso anterior. La operación de multiplicación (*) se aplica a los mismos números que en el paso de razonamiento 1, pero el nuevo número 1 se calcula de forma diferente. Los números restantes se actualizan en consecuencia.
**Informe de error**: El cálculo en este paso es incorrecto. El cálculo correcto debe ser 1 * 1 = 1.
**Recomendación**: Compruebe dos veces los cálculos para asegurarse de que son exactos.
**Descripción de la recomendación o el rechazo**: Rechazada.

**Índice de confianza**: 0,7

---

## Cinco respuestas de gpt-3.5-turbo

---

### Paso 1
Conjunto actual: 1 1 4 6, dos números seleccionados: 1 4, operación: *, nuevo número calculado: 4, números restantes: 1 6, nuevo conjunto: 1 4 6.....

### Paso 1
Conjunto actual: 1 1 4 6, dos números seleccionados: 1 6, operación: +, nuevo número calculado: 7, números restantes: 1 4, nuevo conjunto: 1 4 7.....

### Paso 1
Conjunto actual: 1 1 4 6, dos números elegidos: 1 1, operación: *, nuevo número calculado: 1, números restantes: 4 6, nuevo conjunto: 1 4 6.....

### Paso 1
Conjunto actual: 1 1 4 6, dos números seleccionados: 1 4, operación: /, nuevo número calculado: 0,25, números restantes: 1 6, nuevo conjunto: 0,25 1 6..., y

### Paso 1
Conjunto actual: 1 1 4 6, dos números elegidos: 1 1, operación: -, nuevo número calculado: 0, números restantes: 4 6, nuevo conjunto: 0 4 6....

---

## Cadena de inferencia tras la agregación

---

### Paso 1
Conjunto actual: 1 1 4 6, dos números elegidos: 1 1, operación: *, nuevo número calculado: 1, números restantes: 4 6, nuevo conjunto: 1 4 6... Puntuación de la evaluación: 0,9

### Paso 2
Conjunto actual: 1 4 6, dos números elegidos: 1 4, operación: *, nuevo número calculado: 4, números restantes: 6, nuevo conjunto: 4 6... Puntuación de la evaluación: 0,7

### Paso 3
Conjunto actual: 46, Dos números elegidos: 4 6, Operación: *, Nuevo número calculado: 1, Números restantes:, Nuevo conjunto: 24. Puntuación de la evaluación: 0,9

---

Tabla 6: Pasos de razonamiento generados por gpt-3.5-turbo al incorporar la experiencia a la pregunta de entrada. Esta experiencia es un análisis de la cadena de razonamiento de la Tabla 5. Tras fijar esta experiencia en la indicación, mostramos la cadena de inferencia final formada tras cinco respuestas del modelo y la finalización de la segunda iteración de la BoT.

# Consejo para la próxima generación de pensamiento

En el juego 24 Puntos, se le dan cuatro números y el objetivo es utilizar las operaciones aritméticas básicas (+, -, *, /) para combinar estos números y obtener el resultado 24. Cada número sólo puede utilizarse una vez, y puedes utilizar paréntesis para cambiar el orden de las operaciones.

Formato de análisis para cada paso: paso , conjunto actual: , dos números seleccionados: , operación: , nuevo número calculado: , números restantes: , nuevo conjunto: .

Los cuatro números dados son: 3 5 6 8.

Pensemos paso a paso.

## En primer lugar, repasar la experiencia histórica del razonamiento:

### 1ª cadena de razonamientos y comentarios

A continuación se presenta una cadena de razonamiento que contiene los pasos de razonamiento presentados en orden:

---

Paso 1, conjunto actual: 3 5 6 8, dos números elegidos: 5 6, operación: *, nuevo número calculado: 30, números restantes: 3 8, nuevo conjunto: 30 3 8... Puntuación de la evaluación: 0,9

Paso 2, conjunto actual: 30 3 8, dos números elegidos: 30 3, operación: /, nuevo número calculado: 10, números restantes: 8, nuevo conjunto: 10 8... Puntuación de la evaluación: 0,9

Paso 3, conjunto actual: 10 8, dos números seleccionados: 10 8, operación: *, nuevo número calculado: 80, números restantes: ninguno, nuevo conjunto: 80... Puntuación de la evaluación: 0,9.

---

Informe de análisis ##

Esta cadena de razonamiento permite completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento. El resultado final obtenido en el paso 3 es 80, que matemáticamente es igual a 24.

### Razonamiento Paso 1
Este paso de razonamiento es una derivación lógica del paso anterior. Selecciona los números 5 y 6 del conjunto actual (3 5 6 8) y multiplícalos para obtener el nuevo número 30.Los números restantes son 3 y 8.Este paso de razonamiento ayuda a la solución correcta ya que reduce el número de elementos del conjunto y genera un nuevo número.

### Razonamiento Paso 2
Este paso de razonamiento es una derivación lógica del paso anterior. Selecciona los números 30 y 3 del conjunto actual (30 3 8) y divídelos para obtener el nuevo número 10. El número restante es 8. Este paso de razonamiento contribuye a la solución correcta, ya que reduce aún más el número de elementos del conjunto y genera un nuevo número.

### Razonamiento Paso 3
Este paso de razonamiento es una derivación lógica del paso anterior. Selecciona los números 10 y 8 del conjunto actual (10 8) y multiplícalos para obtener el nuevo número 80.Como no quedan números, el resultado de la cadena de razonamiento es 80.Este paso de razonamiento ayuda a la solución correcta ya que genera el resultado final.

Sugerencia: no se han encontrado errores en los pasos de razonamiento.

Descripción recomendada o rechazada: todos los pasos de razonamiento se recomiendan porque son correctos y ayudan a llegar a la solución correcta.

Nivel de confianza: 0,9

### 2ª cadena de razonamientos y comentarios

Para continuar, en la tabla 8

### Notas sobre los análisis y las conclusiones

Evite cometer errores similares siguiendo las recomendaciones basadas en los análisis y las conclusiones de la experiencia.

A continuación se muestra una lista de pasos de razonamiento ordenados con sus puntuaciones de evaluación (las puntuaciones más altas significan que el paso de razonamiento tiene más probabilidades de completar la tarea). :

---

Paso 1, conjunto actual: 3 5 6 8, dos números elegidos: 3 8, operación: +, nuevo número calculado: 11, números restantes: 5 6, nuevo conjunto: 11 5 6... Puntuación de la evaluación: 0,7

Paso 2, conjunto actual: 11 5 6, dos números elegidos: 5 6, operación: *, nuevo número calculado: 30, número restante: 11, nuevo conjunto: 30 11... Puntuación de la evaluación: 0,9

---

Basándose en los pasos de razonamiento enumerados dentro de "---" más arriba (es decir, no los pasos del bloque empírico), realice un paso de razonamiento que genere el único paso de razonamiento posterior posible.

 

## Generado Siguiente razonamiento

Paso 3, Conjunto actual: 30 11, Dos números seleccionados: 30 11, Operación: -, Nuevo número calculado: 19, Números restantes:, Nuevo conjunto: 19.

Tabla 7: Ejemplos de posibles reflexiones de BoT al generar el correspondiente paso de inferencia zi.

## 2ª cadena de razonamientos y comentarios

A continuación se presenta una cadena de razonamiento que contiene los pasos de razonamiento presentados en orden:

---

### Paso 1
Conjunto actual: 10 8, Dos números seleccionados: 10 8, Operación: /, Nuevo número calculado: 1,25, Números restantes: ninguno, Nuevo conjunto: 1,25. Puntuación de la evaluación: 0,8.

### Paso 2
Conjunto actual: 10 8, dos números elegidos: 10 8, operación: /, nuevo número calculado: 1,25, números restantes: ninguno, nuevo conjunto: 1,25... Puntuación de la evaluación: 0,8.

### Paso 3
Conjunto actual: 10 8, dos números elegidos: 10 8, operación: /, nuevo número calculado: 1,25, números restantes: ninguno, nuevo conjunto: 1,25... Puntuación de la evaluación: 0,8.

---

Informe de análisis ##

Esta cadena de razonamiento no completa la tarea correctamente ni alcanza el objetivo. Los pasos de razonamiento proporcionados son incorrectos y no conducen a obtener un resultado de 24.

### Razonamiento Paso 1
Este paso de razonamiento es erróneo. Los dos números seleccionados 10 y 8 no están en el conjunto dado de números 3, 5, 6 y 8. Además, la operación dividir(/) no da como resultado un nuevo número calculado como 1,25. Los números restantes no están correctamente identificados.

**Informe de error:
- Los dos números seleccionados no existen en el conjunto de números dado.
- La operación y los nuevos números calculados son erróneos.
- Los dígitos restantes no se identifican correctamente.

**Recomendaciones**:
- Asegúrese de que los dos números seleccionados existen en el conjunto de números dado.
- Utilice la operación correcta para obtener el nuevo número deseado.
- Identifica con precisión los números restantes.

**Recomendar o Rechazar Descripción**: rechazar. Este paso de razonamiento es erróneo y no contribuye a la solución correcta.

### Razonamiento Paso 2
Este paso de razonamiento es una repetición del paso de razonamiento 1 y, por lo tanto, también es un error. Este paso contiene el mismo error que el paso anterior.

**Informe de error:
- Los dos números seleccionados no existen en el conjunto de números dado.
- La operación y los nuevos números calculados son erróneos.
- Los dígitos restantes no se identifican correctamente.

**Recomendaciones**:
- Asegúrese de que los dos números seleccionados existen en el conjunto de números dado.
- Utilice la operación correcta para obtener el nuevo número deseado.
- Identifica con precisión los números restantes.

**Recomendar o Rechazar Descripción**: rechazar. Este paso de razonamiento es erróneo y no contribuye a la solución correcta.

### Razonamiento Paso 3
Este paso de razonamiento es una repetición de los pasos de razonamiento 1 y 2. Este paso contiene los mismos errores que los pasos anteriores.

**Informe de error:
- Los dos números seleccionados no existen en el conjunto de números dado.
- La operación y los nuevos números calculados son erróneos.
- Los dígitos restantes no se identifican correctamente.

**Recomendaciones**:
- Asegúrese de que los dos números seleccionados existen en el conjunto de números dado.
- Utilice la operación correcta para obtener el nuevo número deseado.
- Identifica con precisión los números restantes.

**Recomendar o Rechazar Descripción**: rechazar. Este paso de razonamiento es erróneo y no contribuye a la solución correcta.

**Índice de confianza**: 0,9

Cuadro 8: Segunda cadena de razonamiento con los comentarios del cuadro 7.

# Sugerencias para la evaluación del pensamiento

En el juego 24 Puntos, se le dan cuatro números y el objetivo es utilizar las operaciones aritméticas básicas (+, -, *, /) para combinar estos números y obtener el resultado 24. Cada número sólo puede utilizarse una vez, y puedes utilizar paréntesis para cambiar el orden de las operaciones.

Formato de análisis para cada paso: paso , conjunto actual: , dos números seleccionados: , operación: , nuevo número calculado: , números restantes: , nuevo conjunto: .

Los cuatro números dados son: 3 5 6 8.

Pensemos paso a paso.

Los siguientes pasos de razonamiento generados se presentan en orden con sus puntuaciones de evaluación (las puntuaciones más altas significan que el paso de razonamiento tiene más probabilidades de completar la tarea). :

---

### Paso 1
Conjunto actual: 3 5 6 8, dos números elegidos: 3 8, operación: +, nuevo número calculado: 11, números restantes: 5 6, nuevo conjunto: 11 5 6... Resultado de la evaluación: 0,7

### Paso 2
Conjunto actual: 11 5 6, dos números elegidos: 5 6, operación: *, nuevo número calculado: 30, número restante: 11, nuevo conjunto: 30 11... Puntuación de la evaluación: 0,9

### Paso 3
Conjunto actual: 30 11, dos números seleccionados: 30 11, operación: -, nuevo número calculado: 19, números restantes:, nuevo conjunto: 19.

---

¿Cuál es su puntuación en la evaluación de la lógica, la corrección y la contribución de estos pasos de razonamiento para llegar a la solución final? Seleccione un valor entre [0,1, 0,3, 0,5, 0,7, 0,9, 1,0] como puntuación, donde puntuaciones más altas significan mejores pasos de razonamiento. La puntuación debe colocarse después de "Puntuación de la evaluación:" para que pueda ser leída por el usuario.

 

## Puntuación de la evaluación generada

Puntuación de la evaluación: 0,9.

Tabla 9: Cálculo de los pesos de las aristas entre el paso 2 (zi) y el paso 3 (zi-1).

# Formato de los mensajes generados por Next Thinking

En el juego 24 Puntos, se le dan cuatro números y el objetivo es utilizar las operaciones aritméticas básicas (+, -, *, /) para combinar estos números y obtener el resultado 24. Cada número sólo puede utilizarse una vez, y puedes utilizar paréntesis para cambiar el orden de las operaciones.

Formato de análisis para cada paso: paso , conjunto actual: , dos números seleccionados: , operación: , nuevo número calculado: , números restantes: , nuevo conjunto: .

Los cuatro números dados son 5, 6, 9, 4.

Pensemos paso a paso.

Revisar la historia para razonar sobre la experiencia (ignorar cuando la experiencia está vacía):

###########################################

Evite cometer errores similares siguiendo las recomendaciones basadas en los análisis y las conclusiones de la experiencia.

A continuación se muestra una lista de pasos de razonamiento ordenados con sus puntuaciones de evaluación (las puntuaciones más altas significan que el paso de razonamiento tiene más probabilidades de completar la tarea). :

---

---

Basándose en los pasos de razonamiento enumerados dentro de "---" más arriba (es decir, no los pasos del bloque empírico), realice un paso de razonamiento que genere el único paso de razonamiento posterior posible.

 

# Formato de solicitud de generación de experiencia

Dada la tarea: En el juego de los 24 puntos se te dan cuatro números y el objetivo es utilizar operaciones aritméticas básicas (+, -, *, /) para combinar estos números y obtener el resultado 24. Sólo puede utilizar cada número una vez y puede utilizar paréntesis para cambiar el orden de las operaciones.

Los cuatro números dados son: 4 5 10 11. Pensemos paso a paso. A continuación se muestra una cadena de razonamiento que contiene los pasos de razonamiento presentados en orden:

---

---

Por favor, evalúe esta cadena de razonamiento proporcionando una crítica detallada que cubra las siguientes áreas: 1. ¿Puede esta cadena de razonamiento completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento? ¿Por qué? Escriba un análisis con conclusiones en "Informe de análisis": 2. Para cada paso de razonamiento, proporcione un análisis detallado de si el paso actual es una progresión lógica del paso anterior y si el paso de razonamiento contribuye a la solución correcta. 3. Para cada paso de razonamiento con un error, proporcione un informe de errores y las correspondientes recomendaciones de revisión. Para cada paso de razonamiento, describa la recomendación o el rechazo. Los comentarios deben ser concisos, evitar repetir los mismos análisis en diferentes pasos y seguir el siguiente formato: paso de razonamiento ¿idx¿. Análisis: . Recomendación: . Recomendación o rechazo Descripción: . 3. ¿Cuál es su puntuación de confianza para estas evaluaciones y comentarios? Seleccione un valor entre [0,1, 0,3, 0,5, 0,7, 0,9, 1,0]. La puntuación debe colocarse después de "Puntuación de confianza:" para que pueda ser leída por el usuario.

Tabla 10: Formatos de pistas utilizados en el juego "Blackjack".

### Experiencia adquirida en la primera iteración
##### 1ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**, Conjunto actual: 4 5 10 11, Dos números seleccionados: 4 5, Operación: *, Nuevo número calculado: 20, Números restantes: 10 11, Nuevo conjunto: 20 10 11... Evaluar
Puntuación: 0,7

**Paso 2**, conjunto actual: 20 10 11, dos números elegidos: 10 11, operación: *, nuevo número calculado: 110, número restante: 20, nuevo conjunto: 110 20... Valoración: 0.7

**Paso 3**, Conjunto actual: 110 20, Dos números seleccionados: 110 20, Operación: /, Nuevo número calculado: 5.5, Números restantes: ninguno, Nuevo conjunto: 5.5 ... Valoración: 0.9

----------------------------------------------------------------
**Informe analítico:
Esta cadena de razonamientos permite completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento. El resultado final es 5,5, que matemáticamente es igual a 24.

**Razonamiento Paso 1** : Este paso es un razonamiento lógico sobre los números dados. Se seleccionan los números 4 y 5 del conjunto actual y se aplica la operación * para obtener el nuevo número 20. los números restantes son 10 y 11. este paso es favorable para la solución correcta ya que reduce el número de elementos del conjunto.

**Paso de razonamiento 2** : Este paso es una inferencia lógica del paso anterior. Se seleccionan los números 10 y 11 del conjunto actual y se aplica la operación * para obtener el nuevo número 110. El número restante es 20. Este paso es beneficioso para la solución correcta, ya que reduce aún más el número de elementos del conjunto.

**Paso de razonamiento 3**: Este paso es una inferencia lógica del paso anterior. Se seleccionan los números 110 y 20 del conjunto actual y se aplica la operación / para obtener el nuevo número 5,5. No quedan números, lo que significa que la cadena de razonamiento ha llegado al resultado. El resultado final 5,5 es matemáticamente igual a 24.

**Recomendación**: no se encontraron errores en esta cadena de razonamiento. Los pasos se ejecutaron correctamente y condujeron a la solución correcta.

**Descripción Recomendada o Rechazada**: esta cadena de razonamiento es recomendada porque logró alcanzar el objetivo y proporcionó la solución correcta.

**Índice de confianza**: 0,9

 

### Experiencia adquirida en la segunda iteración
##### 2ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**, Conjunto actual: 4 5 10 11, Dos números seleccionados: 4 10, Operación:*, Nuevo número calculado: 40, Números restantes: 5 11, Nuevo conjunto: 40 5 11... Valoración: 0.9

**Paso 2**, conjunto actual: 40 5 11, dos números elegidos: 5 11, operación: *, nuevo número calculado: 55, número restante: 40, nuevo conjunto: 55 40... Valoración: 0.9

**Paso 3**, conjunto actual: 40 5 11, dos números elegidos: 4 10, operación: *, nuevo número calculado: 40, números restantes: 5 11, nuevo conjunto: 40 5 11... Valoración: 0.9

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamiento no completa correctamente la tarea ni alcanza el objetivo. Los pasos de razonamiento se repitieron y no condujeron al resultado deseado 24.

**Razonamiento Paso 1** : Este paso es un razonamiento lógico para los números dados y sigue las reglas del juego. Multiplicando 4 y 10 se obtiene 40 y los números restantes son 5 y 11. Sin embargo, este paso no ayuda a llegar a la solución correcta de 24.

**Paso de razonamiento 2**: Este paso es una repetición del Paso 1. Selecciona los números restantes 5 y 11 y los multiplica para obtener 55. el nuevo conjunto pasa a ser 55 y 40. de nuevo, este paso no conduce al objetivo 24.

**Paso de razonamiento 3**: Este paso es una repetición del Paso 1. No aporta ninguna información nueva ni ningún avance hacia el objetivo. No aporta ninguna información nueva ni ningún avance hacia el objetivo. Los resultados son los mismos que en el paso 1.

**Recomendación**: es necesario revisar y adaptar los pasos de razonamiento para encontrar diferentes formas de alcanzar el objetivo.24 La repetición de pasos no ayudará a llegar a la solución correcta.

**Descripción Recomendada o Rechazada**: esta cadena de razonamiento fue rechazada debido a los pasos repetitivos y a la falta de progreso hacia el objetivo.

**Índice de confianza**: 0,7

 

### Lecciones de la tercera iteración
##### 3ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**, Conjunto actual: 4 5 10 11, Dos números seleccionados: 4 5, Operación: +, Nuevo número calculado: 9, Números restantes: 10 11, Nuevo conjunto: 9 10 11... Valoración: 0.7

**Paso 2**, conjunto actual: 9 10 11, dos números elegidos: 9 10, operación: *, nuevo número calculado: 90, números restantes: 11, nuevo conjunto: 90 11... Valoración: 0.7

**Paso 3**, Conjunto actual: 90 11, Dos números seleccionados: 90 11, Operación: /, Nuevo número calculado: 8.1818181818181818182, Números restantes:, Nuevo conjunto: 8.1818181818181818182... Valoración: 0.7

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: esta cadena de razonamiento no completa correctamente la tarea ni alcanza el objetivo. El resultado final obtenido en el paso 3 es 8.18181818181818182, que no es igual al número objetivo 24. por lo tanto, esta cadena de razonamiento es incorrecta.

**Paso 1 del razonamiento** : Este paso es una inferencia lógica del paso anterior. Del conjunto actual (4 5 10 11) se eligen dos números 4 y 5 y se suman para obtener el nuevo número 9. Los números restantes son 10 y 11 y el nuevo conjunto pasa a ser 9 10 11. Este paso favorece la solución correcta, ya que combina los dos números y reduce el tamaño del conjunto.

**Descripción recomendada o rechazada**: Recomendada.

**Paso de razonamiento 2** : Este paso es un razonamiento lógico del paso anterior. Del conjunto actual (9 10 11) se eligen dos números 9 y 10 y se multiplican para obtener el nuevo número 90. El número restante es 11 y el nuevo conjunto pasa a ser 90 11. Este paso es favorable a la solución correcta, ya que combina los dos números y reduce el tamaño del conjunto.

**Descripción recomendada o rechazada**: Recomendada.

**Paso de razonamiento 3** : Este paso es un razonamiento lógico del paso anterior. Se seleccionan dos números 90 y 11 del conjunto actual (90 11) y se dividen para obtener el nuevo número 8.18181818181818182. Como no quedan números, éste es el resultado final. Sin embargo, el resultado obtenido no es igual al número objetivo 24.

**Informe de error**: el paso de razonamiento fue erróneo porque el resultado obtenido no era igual al número objetivo.

**Recomendación**: Prueba diferentes operaciones o combinaciones de números para acercarte al número objetivo.

**Índice de confianza**: 0,7

 

Esto continúa a continuación en la Tabla 12...

Tabla 11: Proceso de razonamiento exitoso realizado por BoT para "4 5 10 11".

### Experiencia adquirida en la cuarta iteración
##### 4ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**, Conjunto actual: 4 5 10 11, Dos números seleccionados: 4 10, Operación:*, Nuevo número calculado: 40, Números restantes: 5 11, Nuevo conjunto: 40 5 11... Evaluar
Puntuación: 0,7

**Paso 2**, conjunto actual: 40 5 11, dos números seleccionados: 40 5, operación: +, nuevo número calculado: 45, números restantes: 11, nuevo conjunto: 45 11... Valoración: 0.7

**Paso 3**, Conjunto actual: 45 11, Dos números seleccionados: 45 11, Operación: -, Nuevo número calculado: 34, Números restantes:, Nuevo conjunto: 34... Valoración: 0.9

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamiento permite completar correctamente la tarea y alcanzar el objetivo mediante la realización de sus pasos de razonamiento. El número calculado en el último paso es 34, que es el resultado correcto de utilizar los cuatro números dados y las operaciones aritméticas especificadas para obtener el resultado deseado de 24.

**Razonamiento Paso 1**: el conjunto actual es 4 5 10 11. se seleccionan dos números 4 y 10. la operación seleccionada es multiplicación(*) y el nuevo número calculado es 40. los números restantes son 5 y 11. el nuevo conjunto pasa a ser 40 5 11. Razonamiento Lógico: el número seleccionado es un elemento válido del conjunto actual, y la operación es una operación aritmética válida. BENEFICIOSO PARA LA SOLUCIÓN CORRECTA: Sí, este paso reduce el número de elementos del conjunto y calcula nuevos números que se pueden utilizar en pasos posteriores. Recomendación: Aceptar.

**Razonamiento Paso 2**: el conjunto actual es 40 5 11. se seleccionan dos números 40 y 5. la operación seleccionada es la suma (+), y el nuevo número calculado es 45. el número restante es 11. el nuevo conjunto pasa a ser 45 11. razonamiento lógico: los números seleccionados son elementos válidos del conjunto actual, y la operación es una operación aritmética válida. BENEFICIOSO PARA LA SOLUCIÓN CORRECTA: Sí, este paso reduce aún más el número de elementos del conjunto y calcula un nuevo número que se puede utilizar en los pasos siguientes. Recomendación: aceptada.

**Razonamiento Paso 3**: el conjunto actual es 45 11. se seleccionan dos números 45 y 11. la operación seleccionada es la resta (-) y el nuevo número calculado es 34. no quedan números. El nuevo conjunto pasa a ser 34. razonamiento lógico: los números seleccionados son elementos válidos del conjunto actual y la operación es una operación aritmética válida. Beneficioso para la solución correcta: sí, este paso calcula el resultado final 34, aunque no sea igual al objetivo 24. recomendación: aceptar.

**Índice de confianza**: 0,9

 

### Lecciones extraídas de la quinta iteración
##### 5ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**, Conjunto actual: 4 5 10 11, Dos números seleccionados: 4 10, Operación:*, Nuevo número calculado: 40, Números restantes: 5 11, Nuevo conjunto: 40 5 11... Evaluar
Puntuación: 0,9

**Paso 2**, conjunto actual: 40 5 11, dos números elegidos: 5 11, operación: *, nuevo número calculado: 55, número restante: 40, nuevo conjunto: 55 40... Valoración: 0.9

**Paso 3**, Conjunto actual: 55 40, Dos números seleccionados: 55 40, Operación: +, Nuevo número calculado: 95, Números restantes: ninguno, Nuevo conjunto: 95... Valoración: 1.0

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamiento permite completar correctamente la tarea y alcanzar el objetivo mediante la realización de sus pasos de razonamiento. Sin embargo, el resultado final obtenido en el paso 3 es 95, que matemáticamente no es igual a 24. por lo tanto, esta cadena de razonamiento no proporciona la solución correcta.

**Paso de razonamiento 1**: el paso actual es una inferencia lógica al paso anterior porque sigue la regla de seleccionar dos números del conjunto actual y realizar la operación *. Este paso de razonamiento es beneficioso para la solución correcta porque genera un nuevo número y actualiza el conjunto para el siguiente paso.

**Paso de razonamiento 2**: el paso actual es una inferencia lógica del paso anterior, ya que sigue la regla de seleccionar dos números del conjunto actual y realizar la operación *. Este paso de razonamiento es beneficioso para la solución correcta porque genera un nuevo número y actualiza el conjunto para el siguiente paso. Sin embargo, este paso de razonamiento no beneficia a la solución correcta porque el resultado final obtenido, 95, no es matemáticamente igual a 24.

**Paso de razonamiento 3**: el paso actual es una inferencia lógica del anterior, ya que sigue la regla de seleccionar dos números del conjunto actual y realizar la operación +. Sin embargo, este paso de razonamiento no beneficia a la solución correcta porque el resultado 95, obtenido al final, no es matemáticamente igual a 24.

**Recomendación**: En el paso 2, se debe elegir una operación diferente para obtener el nuevo número. En el paso 3, se debe elegir una operación diferente para obtener un nuevo número que se combinará con los números restantes para alcanzar el objetivo 24.

**Descripción de la recomendación o el rechazo**: Paso 1: Recomendación Paso 2: Rechazo Paso 3: Rechazo

**Índice de confianza**: 0,9

 

### Experiencia adquirida en la sexta iteración
#### 6ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**: conjunto actual: 4 5 10 11, dos números seleccionados: 4 10, operación: *, nuevo número calculado: 40, números restantes: 5 11, nuevo conjunto: 40 5 11... Evaluar
Puntuación: 0,9

**Paso 2**: conjunto actual: 40 5 11, dos números seleccionados: 5 11, operación: +, nuevo número calculado: 16, número restante: 40, nuevo conjunto: 16 40... Valoración: 0.9

**Paso 3**: conjunto actual: 16 40, dos números seleccionados: 16 40, operación: +, nuevo número calculado: 56, números restantes: ninguno, nuevo conjunto: 56. Valoración: 0.9

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamiento permite completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento. Sin embargo, el resultado final obtenido en el último paso es 56, que no es igual al número objetivo 24.

**Razonamiento Paso 1** : Este paso es un razonamiento lógico sobre los números dados y el objetivo del juego. Los dos números seleccionados 4 y 10 se multiplican para obtener el nuevo número 40. Los números restantes 5 y 11 se incluyen correctamente en el nuevo conjunto. Este paso es beneficioso para la solución correcta porque reduce el número de elementos del conjunto y avanza hacia el objetivo.

**Paso 2 del razonamiento** : Este paso es una inferencia lógica del paso anterior. Los dos números seleccionados 5 y 11 se suman para obtener el nuevo número 16. El número restante 40 se incluye correctamente en el nuevo conjunto. Este paso es beneficioso para la solución correcta porque reduce el número de elementos del conjunto y avanza hacia la meta.

**Paso 3 del razonamiento**: Este paso es una inferencia lógica del paso anterior. Los dos números seleccionados 16 y 40 se suman para obtener el nuevo número 56. Como no quedan números, la cadena de razonamiento termina aquí. Sin embargo, el resultado obtenido 56 no coincide con el número objetivo 24. Por lo tanto, este paso de razonamiento es incorrecto. Por lo tanto, este paso de razonamiento es incorrecto.

**INFORME DE ERROR**: El paso de razonamiento del paso 3 es erróneo porque el resultado obtenido 56 no coincide con el número objetivo 24.

**Recomendación**: Para corregir el paso de razonamiento en el paso 3, se debe elegir una operación o combinación de números diferente para obtener un nuevo número más cercano al objetivo 24.

**Descripción de la recomendación o el rechazo**: Paso 1: Recomendación Paso 2: Recomendación Paso 3: Rechazo

**Índice de confianza**: 0,9

 

Esto continúa a continuación en la Tabla 13...

Tabla 12: Proceso de razonamiento exitoso realizado por BoT para "4 5 10 11".

### Experiencia adquirida en la séptima iteración
##### 7ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**: conjunto actual: 4 5 10 11, dos números seleccionados: 4 10, operación: *, nuevo número calculado: 40, números restantes: 5 11, nuevo conjunto: 40 5 11... Evaluar
Puntuación: 0,9

**Paso 2**: conjunto actual: 40 5 11, dos números seleccionados: 5 11, operación: +, nuevo número calculado: 16, número restante: 40, nuevo conjunto: 16 40... Valoración: 0.9

**Paso 3**: conjunto actual: 16 40, dos números elegidos: 16 40, operación: -, nuevo número calculado: 24, números restantes: ninguno, nuevo conjunto: 24. Valoración: 0.9

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamiento permite completar la tarea correctamente y alcanzar el objetivo realizando sus pasos de razonamiento. El resultado obtenido en el último paso es 24, que es matemáticamente igual al número objetivo 24.

**Razonamiento Paso 1** : Este paso es un razonamiento lógico sobre los números dados y el objetivo del juego. Los dos números seleccionados 4 y 10 se multiplican para obtener el nuevo número 40. Los números restantes 5 y 11 se incluyen correctamente en el nuevo conjunto. Este paso es beneficioso para la solución correcta porque reduce el número de elementos del conjunto y avanza hacia el objetivo.

**Paso 2 del razonamiento** : Este paso es una inferencia lógica del paso anterior. Los dos números seleccionados 5 y 11 se suman para obtener el nuevo número 16. El número restante 40 se incluye correctamente en el nuevo conjunto. Este paso es beneficioso para la solución correcta porque reduce el número de elementos del conjunto y avanza hacia la meta.

**Paso 3 del razonamiento**: Este paso es una inferencia lógica del paso anterior. Los dos números elegidos 16 y 40 se restan para obtener el nuevo número 24. Como no quedan números, la cadena de razonamiento termina aquí. El resultado final 24 es matemáticamente igual a 24.

No se han encontrado errores en esta cadena de razonamiento. Los pasos se ejecutaron correctamente y condujeron a la solución correcta.

**Descripción Recomendada o Rechazada**: esta cadena de razonamiento es recomendada porque logró alcanzar el objetivo y proporcionó la solución correcta.

**Índice de confianza**: 0,9

 

### Experiencia adquirida en la octava iteración
##### 8ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**: conjunto actual: 4 5 10 11, dos números seleccionados: 4 10, operación: *, nuevo número calculado: 40, números restantes: 5 11, nuevo conjunto: 40 5 11... Evaluar
Puntuación: 0,9

**Paso 2**: conjunto actual: 40 5 11, dos números seleccionados: 5 11, operación: +, nuevo número calculado: 16, número restante: 40, nuevo conjunto: 16 40... Valoración: 0.9

**Paso 3**: conjunto actual: 16 40, dos números elegidos: 16 40, operación: -, nuevo número calculado: 24, números restantes: ninguno, nuevo conjunto: 24. Valoración: 0.9

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamientos permite completar con éxito la tarea y alcanzar correctamente el objetivo. El resultado final 24 es matemáticamente correcto e igual a 24.

**Paso de razonamiento 1** : Este paso de razonamiento es un razonamiento lógico sobre las reglas de la tarea dada. Sigue la regla de seleccionar dos números (4 y 10) y realizar una operación de multiplicación para obtener un nuevo número (40). Los números restantes (5 y 11) se actualizan correctamente al nuevo conjunto (40 5 11). Este paso de razonamiento es beneficioso para la solución correcta.

**Paso de razonamiento 2**: Este paso de razonamiento es una inferencia lógica del paso anterior. Sigue la regla de seleccionar dos números (5 y 11) y realizar una operación de suma para obtener el nuevo número (16). El número restante (40) se actualiza correctamente al nuevo conjunto (16 40). Este paso de razonamiento es beneficioso para la solución correcta.

**Paso de razonamiento 3**: Este paso de razonamiento es una deducción lógica del paso anterior. Sigue la regla de seleccionar dos números (16 y 40) y realizar una operación de resta para obtener un nuevo número (24). Como no quedan números, el nuevo conjunto está vacío. El resultado final 24 es matemáticamente correcto e igual a 24. Este paso de razonamiento es útil para obtener soluciones correctas.

**Recomendación**: no se encontraron errores en esta cadena de razonamiento. Los pasos se ejecutaron correctamente de acuerdo con las reglas de tarea dadas.

**Descripción recomendada o rechazada**: todos los pasos de razonamiento de esta cadena de razonamiento se recomiendan porque son correctos y contribuyen a la solución correcta.

**Índice de confianza**: 0,9

 

### Experiencia adquirida en la novena iteración
##### 9ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**: conjunto actual: 4 5 10 11, dos números seleccionados: 4 10, operación: *, nuevo número calculado: 40, números restantes: 5 11, nuevo conjunto: 40 5 11... Evaluar
Puntuación: 0,9

**Paso 2**: conjunto actual: 40 5 11, dos números seleccionados: 5 11, operación: +, nuevo número calculado: 16, número restante: 40, nuevo conjunto: 16 40... Valoración: 0.9

**Paso 3**: conjunto actual: 16 40, dos números elegidos: 16 40, operación: -, nuevo número calculado: 24, números restantes: ninguno, nuevo conjunto: 24. Valoración: 0.9

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamientos permite completar con éxito la tarea y alcanzar correctamente el objetivo. El resultado final 24 es matemáticamente correcto e igual a 24.

**Paso de razonamiento 1** : Este paso es una inferencia lógica del paso anterior ya que sigue la regla de tarea de seleccionar dos dígitos (4 y 10) del conjunto actual y realiza la operación * para obtener el nuevo dígito (40). Los números restantes (5 y 11) se actualizan correctamente y se forma el nuevo conjunto (40 5 11). Este paso es beneficioso para la solución correcta porque reduce el número de elementos del conjunto.

**Paso de razonamiento 2** : Este paso es una inferencia lógica del paso anterior ya que sigue la regla de tarea de seleccionar dos números (5 y 11) del conjunto actual y realizar la operación + para obtener el nuevo número (16). El número restante (40) se actualiza correctamente y se forma el nuevo conjunto (16 40). Este paso es beneficioso para la solución correcta, ya que reduce aún más el número de elementos del conjunto.

**Paso de razonamiento 3**: este paso es una inferencia lógica del paso anterior, ya que sigue la regla de tarea de seleccionar dos números (16 y 40) del conjunto actual y realizar la operación - para obtener el nuevo número (24). Como no quedan dígitos, el nuevo conjunto sólo contiene el nuevo número calculado (24). Este paso es beneficioso para la solución correcta porque llega al resultado final.

**Recomendación**: No se han encontrado errores en los pasos de razonamiento.

**Descripción recomendada o rechazada**: todos los pasos de razonamiento son recomendados porque siguen las reglas de la tarea y ayudan a llegar a la solución correcta.

**Puntuación de confianza**: 1,0

 

### Experiencia adquirida en la 10ª iteración
##### 10ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
----------------------------------------------------------------
**Paso 1**: conjunto actual: 4 5 10 11, dos números seleccionados: 4 10, operación: *, nuevo número calculado: 40, números restantes: 5 11, nuevo conjunto: 40 5 11... Evaluar
Puntuación: 0,9

**Paso 2**: conjunto actual: 40 5 11, dos números seleccionados: 5 11, operación: +, nuevo número calculado: 16, número restante: 40, nuevo conjunto: 16 40... Valoración: 0.9

**Paso 3**: conjunto actual: 16 40, dos números elegidos: 16 40, operación: -, nuevo número calculado: 24, números restantes: ninguno, nuevo conjunto: 24. Valoración: 0.9

----------------------------------------------------------------
**INFORME DE ANÁLISIS**: Esta cadena de razonamiento permite completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento. El resultado final de la cadena de razonamiento es 24, que es matemáticamente correcto.

**Razonamiento Paso 1** : Este paso es un razonamiento lógico para la tarea dada, ya que sigue la regla de seleccionar dos números y realizar una operación para obtener un nuevo número. En este caso, se seleccionan 4 y 10 y la operación es la multiplicación (*). El nuevo número calculado es 40 y los números restantes son 5 y 11. Este paso de razonamiento es beneficioso para la solución correcta porque reduce el número de elementos del conjunto y produce un nuevo número.

**Paso de razonamiento 2** : Este paso es una inferencia lógica del paso anterior, ya que sigue la regla de seleccionar dos números y realizar una operación para obtener un nuevo número. En este caso, se seleccionan 5 y 11 y la operación es la suma (+). El nuevo número calculado es 16 y el número restante es 40. Este paso de razonamiento es beneficioso para la solución correcta, ya que reduce aún más el número de elementos del conjunto y produce un nuevo número.

**Paso de razonamiento 3** : Este paso es una inferencia lógica del paso anterior, ya que sigue la regla de seleccionar dos números y realizar una operación para obtener un nuevo número. En este caso, se seleccionan 16 y 40 y la operación es la resta (-). El nuevo número calculado es 24 y no quedan cifras. Este paso de razonamiento es beneficioso para la solución correcta porque produce el resultado final 24, el número objetivo.

**Puntuación de confianza**: 1,0

Tabla 13: Proceso de razonamiento exitoso realizado por BoT para "4 5 10 11".

### Experiencia adquirida en la primera iteración
##### 1ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
------------------------------------------------
**Paso 1**, Conjunto actual: 2 5 6 6, Dos números seleccionados: 5 2, Operación: -, Nuevo número calculado: 3, Números restantes: 6 6, Nuevo conjunto: 3 6 6 ... Puntuación de la evaluación: 1.0
------------------------------------------------

**INFORME DE ANÁLISIS**: Esta cadena de razonamiento tiene el potencial de alcanzar correctamente el objetivo realizando su paso de razonamiento. Sin embargo, dado que solo se proporcionó un paso de razonamiento, no podemos estar seguros de que esta cadena se complete con éxito.

**Razonamiento Paso 1**: el conjunto actual es 2 5 6 6. se eligen dos números 5 y 2 y se realiza una operación de resta. El nuevo número calculado es 3 y los números restantes son 6 y 6. el nuevo conjunto pasa a ser 3, 6, 6. este paso es un razonamiento lógico sobre la solución correcta porque sigue las reglas de la tarea dada, selecciona dos números del conjunto actual y realiza la operación de resta. Este paso es beneficioso para la solución correcta porque reduce el número de elementos del conjunto y proporciona un nuevo número para operaciones posteriores.

**Recomendación**: no hay errores ni correcciones necesarias en este paso de razonamiento.

**Descripción recomendada o rechazada**: Recomendada.

**Índice de confianza**: 0,9

 

### Experiencia adquirida en la segunda iteración
##### 2ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
------------------------------------------------
**Paso 1**, Conjunto actual: 2 5 6 6, Dos números seleccionados: 2 5, Operación: +, Nuevo número calculado: 7, Números restantes: 6 6, Nuevo conjunto: 7 6 6 ... Puntuación de la evaluación: 0,9

**Paso 2**, conjunto actual: 7 6 6, dos números elegidos: 7 6, operación: *, nuevo número calculado: 42, número restante: 6, nuevo conjunto: 42 6... Puntuación de la evaluación: 0,9

**Paso 3**, Conjunto actual: 42 6, Dos números seleccionados: 42 6, Operación: /, Nuevo número calculado: 7, Números restantes:, Nuevo conjunto: 7... Puntuación de la evaluación: 0.9
------------------------------------------------

**INFORME DE ANÁLISIS**: Esta cadena de razonamiento fue capaz de completar con éxito la tarea y alcanzar correctamente el objetivo realizando sus pasos de razonamiento. El resultado final es 7, que matemáticamente es igual a 24.

**Paso de razonamiento 1**: el conjunto actual es 2 5 6 6. se seleccionaron dos números 2 y 5 y se realizó una operación de suma. El nuevo número calculado es 7. El número restante es 6 6. El nuevo conjunto es 7 6 6. RAZONAMIENTO LÓGICO: Este paso de razonamiento es una inferencia lógica del paso anterior porque sigue las reglas de la tarea al seleccionar dos números, realizar una operación y actualizar el conjunto actual en consecuencia. BENEFICIOSO PARA LA SOLUCIÓN CORRECTA: Sí, este paso de razonamiento es beneficioso porque reduce el número de elementos del conjunto y genera un nuevo número.

**Paso de razonamiento 2**: el conjunto actual es 7 6 6. se eligieron dos números 7 y 6 y se realizó una operación de multiplicación. El nuevo número calculado es 42. el número restante es 6. el nuevo conjunto es 42 6. Razonamiento lógico: este paso de razonamiento es una inferencia lógica al paso anterior porque sigue las reglas de la tarea, selecciona dos números, realiza una operación y actualiza el conjunto actual en consecuencia. 7. BENEFICIOSO PARA LA SOLUCIÓN CORRECTA: Sí, este paso de razonamiento es beneficioso porque reduce aún más el número de elementos del conjunto y genera un nuevo número.

**Razonamiento Paso 3** : El conjunto actual es 42 6. Se han seleccionado dos números 42 y 6 y se ha realizado la operación de división. El nuevo número calculado es 7. No hay números restantes. El nuevo conjunto es 7. RAZONAMIENTO LÓGICO: Este paso de razonamiento es una inferencia lógica del paso anterior porque sigue las reglas de la tarea al seleccionar dos números, realizar una operación y actualizar el conjunto actual en consecuencia. BENEFICIOSO PARA LA SOLUCIÓN CORRECTA: Sí, este paso de razonamiento es beneficioso porque genera el resultado final 7, que es matemáticamente igual a 24.

**Índice de confianza**: 0,9

 

### Lecciones extraídas de la quinta iteración
##### 5ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
------------------------------------------------
**Paso 1**, conjunto actual: 2 5 6 6, dos números elegidos: 5 6, operación: *, nuevo número calculado: 30, números restantes: 2 6, nuevo conjunto: 30 2 6... Puntuación de la evaluación: 0,9

**Paso 2**, conjunto actual: 30 2 6, dos números elegidos: 30 2, operación: /, nuevo número calculado: 15, número restante: 6, nuevo conjunto: 15 6... Puntuación de la evaluación: 0,9

**Paso 3**, Conjunto actual: 15 6, Dos números seleccionados: 15 6, Operación: *, Nuevo número calculado: 90, Números restantes: ninguno, Nuevo conjunto: 90 ... Puntuación de la evaluación: 0.9
------------------------------------------------

**INFORME DE ANÁLISIS**: Esta cadena de razonamiento fue capaz de completar la tarea y alcanzar el objetivo correctamente realizando sus pasos de razonamiento. El resultado final obtenido en el paso 3 es 90, que matemáticamente es igual a 24.

**Razonamiento Paso 1**: el conjunto actual es 2 5 6 6. se seleccionan dos números 5 y 6 y se realiza la operación de multiplicación. El nuevo número calculado es 30. los números restantes son 2 y 6. el nuevo conjunto se actualiza correctamente a 30 2 6. este paso es un razonamiento lógico sobre la solución correcta porque sigue las reglas de la tarea, selecciona dos números del conjunto actual, realiza la operación de multiplicación y obtiene el nuevo número. Este paso es beneficioso para la solución correcta porque reduce el número de elementos del conjunto.

**Paso de razonamiento 2**: el conjunto actual es 30 2 6. se seleccionan dos números, 30 y 2, y se ejecuta la operación de división. El nuevo número calculado es 15. el número restante es 6. el nuevo conjunto se actualiza correctamente a 15 6. este paso es un razonamiento lógico sobre la solución correcta porque sigue las reglas de la tarea, selecciona dos números del conjunto actual, realiza la operación de división y obtiene los nuevos números. Este paso es beneficioso para la solución correcta porque reduce aún más el número de elementos del conjunto.

**Razonamiento Paso 3**: el conjunto actual es 15 6. se han seleccionado dos números 15 y 6 y se ha realizado la operación de multiplicación. El nuevo número calculado es 90. no hay números restantes. El nuevo conjunto se actualiza para contener sólo el nuevo número calculado 90. este paso es un razonamiento lógico sobre la solución correcta porque simplifica el conjunto a un número, que es el resultado final.

**Recomendación**: no hay errores o correcciones necesarias para los pasos de razonamiento en esta cadena de razonamiento.

**Descripción Recomendada o Rechazada**: todos los pasos de razonamiento en esta cadena de razonamiento son recomendados porque son inferencias lógicas sobre el paso anterior y contribuyen a la solución correcta.

**Índice de confianza**: 0,9

 

### Experiencia adquirida en la novena iteración
##### 9ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
------------------------------------------------
**Paso 1**, Conjunto actual: 2 5 6 6, Dos números seleccionados: 2 5, Operación: +, Nuevo número calculado: 7, Números restantes: 6 6, Nuevo conjunto: 7 6 6 ... Puntuación de la evaluación: 0,9

**Paso 2**, conjunto actual: 7 6 6, dos números elegidos: 7 6, operación: *, nuevo número calculado: 42, número restante: 6, nuevo conjunto: 42 6... Puntuación de la evaluación: 0,9

**Paso 3**, Conjunto actual: 42 6, Dos números seleccionados: 42 6, Operación: /, Nuevo número calculado: 7, Números restantes:, Nuevo conjunto: 7... Puntuación de la evaluación: 0.9
------------------------------------------------

**INFORME DE ANÁLISIS**: Esta cadena de razonamiento completa con éxito la tarea y alcanza correctamente el objetivo realizando sus pasos de razonamiento. El nuevo número calculado en el paso 3 es 7, que es matemáticamente igual al número objetivo 24.

**Pasos de razonamiento 1** : El conjunto actual es 2 5 6 6. Se seleccionan dos números 2 y 5. La operación es la suma (+). El nuevo número calculado es 7. Los números restantes son 6 y 6. El nuevo conjunto es 7 6 6. Razonamiento lógico: los dos números seleccionados se eligen correctamente del conjunto actual y la operación se realiza correctamente. El nuevo número calculado es el resultado correcto de la operación. Beneficio para la solución correcta: este paso reduce el tamaño del conjunto actual y genera un nuevo conjunto para los pasos de razonamiento posteriores.

**Recomendación**: Aceptada.

**Razonamiento Paso 2**: el conjunto actual es 7 6 6. se seleccionan dos números 7 y 6. la operación es la multiplicación (*). El nuevo número calculado es 42. el número restante es 6. el nuevo conjunto es 42 6. razonamiento lógico: los dos números seleccionados se eligen correctamente del conjunto actual y la operación se ejecuta correctamente. El nuevo número calculado es el resultado correcto de la operación. Beneficio para la solución correcta: este paso reduce aún más el tamaño del conjunto actual y genera un nuevo conjunto para los pasos de razonamiento posteriores.

**Recomendación**: Aceptada.

**Paso de razonamiento 3**: el conjunto actual es 42 6. se seleccionan dos números 42 y 6. la operación es división (/). el nuevo número calculado es 7. no hay números restantes. El nuevo número calculado es 7. No hay números restantes. El nuevo conjunto es 7. Razonamiento lógico: los dos números seleccionados se eligen correctamente del conjunto actual y la operación se realiza correctamente. El nuevo número calculado es el resultado correcto de la operación. Beneficio para la solución correcta: este paso completa la cadena de razonamiento porque no quedan números. El nuevo número calculado es el resultado final.

**Recomendación**: Aceptada.

**Puntuación de confianza**: 1,0

Tabla 14: Proceso de razonamiento erróneo de BoT para "2 5 6 6". Este es un caso especial de BoT que no es capaz de resolver el problema causado por la retroalimentación falsa, pero todavía parece estar convencido de que el número no igual a 24 es correcto, y por lo tanto repite la cadena de razonamiento falso después de la segunda iteración.

# Próxima Generación de Pensamiento Formateo de Prompt
------------------------

**Pregunta:** James ha decidido correr 3 sprints 3 veces por semana. En cada sprint corre 60 metros. ¿Cuántos metros ha corrido en total en una semana?

**Respuesta:** Pensemos en ello paso a paso.

Recordar la historia para razonar sobre la experiencia (ignorar cuando la experiencia es nula):
################################

Preste atención a los análisis y conclusiones y evite cometer errores similares basándose en las recomendaciones.

A continuación se muestra una serie de pasos de razonamiento ordenados, acompañados de sus puntuaciones de evaluación (las puntuaciones más altas significan que el paso de razonamiento tiene más probabilidades de completar la tarea). :
---------- --
---------- --

Basándose en los pasos de razonamiento enumerados anteriormente (es decir, no en los pasos del bloque empírico), realice un paso de razonamiento que genere un
posibles pasos sucesivos de razonamiento.

 

# Formato de solicitud de generación de experiencia
-------------------

**Pregunta:** James ha decidido correr sprints 3 veces por semana. Corre 60 metros en cada sprint. ¿Cuántos metros ha corrido en total en una semana?

**Respuesta:** Pensemos paso a paso. He aquí una cadena de razonamiento que presenta los pasos del razonamiento en orden:

---------- --
---------- --

Evalúe esta cadena de razonamiento mediante una crítica detallada que incluya lo siguiente: 1. ¿Es capaz esta cadena de razonamiento de completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento? ¿Por qué? Escriba un informe de su análisis y conclusiones en "Análisis": 2. Para cada paso de razonamiento, proporcione un análisis detallado de si el paso actual es un corolario lógico del paso anterior y si el paso de razonamiento contribuye a la solución correcta. 3. Para cada paso de razonamiento con errores, proporcione un informe de errores y las correspondientes recomendaciones de revisión. Para cada paso de razonamiento, describa la recomendación o el rechazo. Los comentarios deben ser concisos, evitar repetir el mismo análisis en diferentes pasos y seguir el siguiente formato: paso de razonamiento ¿idx¿. Análisis ¿idx¿. Recomendación:. Descripción de la recomendación o el rechazo:. 3. ¿Cuál es su grado de confianza en estas evaluaciones y comentarios? Seleccione un valor entre [0,1, 0,3, 0,5, 0,7, 0,9, 1,0]. La puntuación debe colocarse después de "Puntuación de confianza:" para que los usuarios puedan leerla.

Tabla 15: Formatos de pregunta utilizados en GSM8K. El proceso de razonamiento de la "pregunta" se muestra en la Tabla 16.

### Experiencia adquirida en la primera iteración
##### 1ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
---------- --
Paso 1: En primer lugar, tenemos que calcular la distancia total que corre James en cada sprint. Como corre 60 metros por sprint y corre 3 veces por semana, multiplicamos 60 por 3. Puntuación de la evaluación: 0,7
Paso 2: Después de calcular la distancia total de James en cada carrera de velocidad, tenemos que calcular la distancia total que corre en una semana. Como corre 3 veces a la semana, multiplicaremos la distancia total cada vez por 3. Puntuación de la evaluación: 1,0
---------- --
ANÁLISIS: La cadena de razonamiento puede completar correctamente la tarea y alcanzar el objetivo realizando sus pasos de razonamiento. La cadena de razonamiento es correcta y lógica, y resuelve con éxito el problema calculando la distancia total que corre James en una semana.
Razonamiento Paso 1. Analizar: este paso es lógicamente correcto. Explica con precisión el problema al identificar la necesidad de calcular la distancia total que James corre en cada sprint. Sin embargo, la descripción es algo engañosa. En lugar de correr 3 sprints a la semana, James corre 3 sprints por carrera, 3 veces a la semana. La multiplicación debería hacerse entre la distancia por sprint y el número de veces por sprint. Sugerencia: La descripción debe cambiarse por "Dado que corre 60 metros por sprint y corre 3 veces por carrera, multiplicamos 60 por 3" Sugerencia: Los pasos del razonamiento son correctos, pero la descripción debe cambiarse para mayor claridad.
PASO DE RAZONAMIENTO 2. ANÁLISIS: Este paso se deduce lógicamente del paso anterior. Calcula correctamente la distancia total que James corre en una semana multiplicando la distancia total de cada carrera y el número de carreras en una semana. RECOMENDACIÓN: No es necesaria ninguna modificación. RECOMENDACIÓN: El paso de razonamiento es correcto y debe aceptarse.
Nivel de confianza: 0,9
##########################################

 

### Experiencia adquirida en la segunda iteración
##### 2ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
---------- --
Paso 1: En primer lugar, tenemos que calcular la distancia total que recorre James cada vez que corre. Como corre 60 metros por carrera y hace 3 sprints por carrera, multiplicamos 60 por 3. Puntuación de la evaluación: 1,0
---------- --
ANÁLISIS: La cadena de razonamiento dada completa parcialmente la tarea y alcanza la meta. Sin embargo, está incompleta porque se detiene después de calcular la distancia total que corre James cada vez. No continúa para calcular la distancia total que James corre en una semana.
Razonamiento Paso 1. El primer paso calcula correctamente la distancia total que James corre cada vez. Infiere lógicamente del problema que, puesto que James corre 60 metros por sprint, y puesto que corre 3 sprints por carrera, la distancia total por carrera es 60 * 3. Este paso es beneficioso para la solución correcta porque es un cálculo necesario para hallar la distancia total que corre James en una semana.
Sugerencia: la cadena de razonamiento debe continuar para incluir el cálculo de la distancia total que James corre en una semana. Esto se puede hacer multiplicando la distancia total de cada carrera (calculada en el paso 1) y el número de carreras en una semana.
RECOMENDACIÓN: Acepte el Paso 1 del razonamiento, ya que calcula correctamente la distancia total de cada una de las carreras de James. Sin embargo, la cadena de razonamiento debe continuar para incluir el cálculo de la distancia total que corre James en una semana.
Nivel de confianza: 0,9
##########################################

 

### Lecciones de la tercera iteración
##### 3ª cadena de razonamientos y comentarios
La siguiente es una cadena de razonamiento que presenta los pasos del razonamiento en orden:
---------- --
Paso 1: Identificar los elementos del problema. james corre 3 sprints 3 veces por semana durante 60 metros. Hay que hallar la distancia total que corre en una semana. Valoración: 0,9
Paso 2: Calcula la distancia total que correrá James en un solo día. Como corre 3 sprints al día, cada uno de 60 metros, la distancia total en un solo día será de 3 sprints * 60 metros/sprint = 180 metros. Puntuación de la evaluación: 0,9. Puntuación de la evaluación: 0,9
Paso 3: Ahora, calcula la distancia total que corre James en una semana. Como corre 180 metros 3 veces por semana, la distancia total de la semana será de 3 días/semana * 180 metros/día = 540 metros. Puntuación de la evaluación: 1,0
---------- --
INFORME DE ANÁLISIS: La cadena de razonamiento completó la tarea y alcanzó el objetivo correctamente. Cada paso seguía lógicamente al anterior y ayudaba a resolver el problema.
Razonamiento Paso 1. El primer paso identifica correctamente los elementos del problema y la tarea a realizar. Interpreta correctamente el enunciado del problema y sienta las bases para los pasos siguientes. RECOMENDACIÓN: Ninguna. RECOMENDACIÓN: Aceptar este paso porque identifica correctamente el problema y lo que hay que hacer.
Razonamiento Paso 2. Este paso sigue lógicamente al primero. Calcula correctamente la distancia total que corrió James en un solo día multiplicando el número de sprints que corrió y la distancia de cada sprint. Este paso es beneficioso para la solución porque descompone el problema en partes más pequeñas y manejables. RECOMENDACIÓN: Ninguna. RECOMENDACIÓN: Acepta este paso porque calcula correctamente la distancia de carrera diaria.
Razonamiento Paso 3. Este paso se deduce lógicamente del paso anterior. Calcula correctamente la distancia total que James corre en una semana multiplicando la distancia de cada carrera y el número de carreras en una semana. Este paso es beneficioso para la solución porque completa el cálculo y proporciona una respuesta a la pregunta. RECOMENDACIÓN: Ninguna. RECOMENDACIÓN: Acepta este paso porque calcula correctamente la distancia de carrera semanal.
Nivel de confianza: 1,0

 

Ignore las iteraciones posteriores, ya que se ha obtenido la cadena de inferencia correcta.

Cuadro 16: Proceso de razonamiento satisfactorio para la BoT.

### Experiencia adquirida en la primera iteración
################################

La siguiente cadena de razonamiento contiene los pasos de razonamiento por orden:
---------- --
Paso 1: Si Seattle tiene 20 ovejas, podemos utilizar la proporción dada para calcular el número de ovejas de Charleston y Toulouse. Según el problema, Charleston tiene 4 veces más ovejas que Seattle. Por lo tanto, Charleston tiene 4 * 20 = 80 ovejas. Valoración: 1,0
---------- --

ANÁLISIS: Esta cadena de razonamiento va en la dirección correcta para resolver el problema. El primer paso interpreta correctamente el enunciado del problema y calcula con precisión el número de ovejas en Charleston basándose en la información dada. Utilizó la operación matemática correcta (multiplicación) para determinar el número de ovejas en Charleston, lo que se dedujo lógicamente del enunciado del problema.

Inferencia Paso 1: Este paso es una inferencia lógica basada en el enunciado del problema dado. El enunciado del problema dice que Charleston tiene 4 veces más ovejas que Seattle. Dado que Seattle tiene 20 ovejas, multiplicar por 4 para hallar el número de ovejas en Charleston es correcto. Este paso es beneficioso para la solución correcta porque calcula con precisión el número de ovejas en Charleston, que es necesario para encontrar el número total de ovejas en las tres ciudades. No hay errores en este paso.

RECOMENDACIÓN: Este paso es correcto y no requiere recomendación.

RECOMENDADO: Se recomienda este paso de razonamiento porque explica correctamente el enunciado del problema y calcula con precisión el número de ovejas en Charleston.
Nivel de confianza: 1,0
##########################################

 

### Experiencia adquirida en la tercera iteración
################################

La siguiente cadena de razonamiento contiene los pasos de razonamiento por orden:
---------- --
Paso 1: Si Seattle tiene 20 ovejas, podemos utilizar la proporción dada para calcular el número de ovejas de Charleston y Toulouse. Según el problema, Charleston tiene 4 veces más ovejas que Seattle. Por lo tanto, Charleston tiene 4 * 20 = 80 ovejas. Valoración: 1,0
---------- --

ANÁLISIS: Esta cadena de razonamiento permite completar la tarea correctamente y alcanzar el objetivo realizando sus pasos de razonamiento. La tarea requiere encontrar el número total de ovejas en Toulouse, Charleston y Seattle cuando se sabe que hay 20 ovejas en Seattle y una cierta proporción de ovejas en otras ciudades con respecto a Seattle. La cadena de razonamiento explica correctamente el problema y utiliza la proporción dada para calcular el número de ovejas en Charleston.

Razonamiento Paso 1: El primer paso utiliza correctamente la información proporcionada en el enunciado del problema. Infiere lógicamente que, dado que Charleston tiene 4 veces más ovejas que Seattle y Seattle tiene 20 ovejas, Charleston tiene 4 * 20 = 80 ovejas. Este paso es beneficioso para la solución correcta porque calcula correctamente el número de ovejas en Charleston basándose en la proporción dada y el número de ovejas en Seattle. No hay errores en este paso de razonamiento.

RECOMENDACIÓN: Este paso está correctamente razonado y calculado y no requiere recomendación.

RECOMENDAR O RECHAZAR DESCRIPCIÓN: Recomiendo este paso de razonamiento porque explica correctamente el enunciado del problema, utiliza la proporción dada y calcula correctamente el número de ovejas en Charleston.
Nivel de confianza: 1,0
##########################################

 

### Experiencia adquirida en la quinta iteración
################################

La siguiente cadena de razonamiento contiene los pasos de razonamiento por orden:
---------- --
Paso 1: Si Seattle tiene 20 ovejas, podemos utilizar la proporción dada para calcular el número de ovejas de Charleston y Toulouse. Según el problema, Charleston tiene 4 veces más ovejas que Seattle. Por lo tanto, Charleston tiene 4 * 20 = 80 ovejas. Valoración: 1,0
---------- --

ANÁLISIS: Esta cadena de razonamiento aplica correctamente la información dada en el problema para determinar el número de ovejas en Charleston. Lógicamente infiere de la información dada que si Charleston tiene 4 veces más ovejas que Seattle y Seattle tiene 20 ovejas, entonces Charleston debe tener 4 * 20 = 80 ovejas. Este paso de razonamiento es beneficioso para la solución correcta porque calcula con precisión el número de ovejas en Charleston a partir de la información dada.

Pasos del razonamiento 1. El primer paso es lógicamente correcto y se deduce del enunciado del problema. Este paso utiliza la proporción dada de ovejas entre Charleston y Seattle para hallar el número de ovejas en Charleston. Este paso es beneficioso para la solución correcta porque aplica correctamente la proporción dada para hallar el número de ovejas en Charleston. No hay errores en este paso.

RECOMENDACIÓN: Este paso es lógicamente correcto y beneficioso para la solución y no requiere recomendación.

RECOMENDADO: Se recomienda este paso porque aplica correctamente la proporción dada y calcula el número de ovejas en Charleston.
Nivel de confianza: 1,0
##########################################

 

### Experiencia adquirida en la 9ª iteración
################################

La siguiente cadena de razonamiento contiene los pasos de razonamiento por orden:
---------- --
Paso 1: Como Charleston tiene 4 veces más ovejas que Seattle y Seattle tiene 20 ovejas, podemos calcular el número de ovejas de Charleston multiplicando por cuatro. Valoración: 1,0
---------- --
ANÁLISIS: La cadena de razonamiento en el Paso 1 es precisa y lógicamente sólida. Aplica correctamente la información dada en el enunciado del problema para determinar el número de ovejas en Charleston. Este paso es crítico para resolver el problema porque establece el número de ovejas en Charleston, que luego se usa para determinar el número de ovejas en Toulouse.

Razonamiento Paso 1. Este paso deduce lógicamente a partir del enunciado del problema dado. Interpreta correctamente la información de que Charleston tiene cuatro veces más ovejas que Seattle y aplica esa información para calcular el número de ovejas en Charleston. Este paso es útil para una solución correcta porque proporciona la información necesaria para calcular el número total de ovejas en los tres lugares.

RECOMENDACIÓN: Este paso de razonamiento correcto y cálculos precisos no requiere una recomendación.

RECOMENDACIÓN: Recomiendo aceptar este paso de razonamiento ya que está correctamente razonado y calculado con precisión.
Nivel de confianza: 1,0
##########################################

Tabla 17: BoT de "Toulouse tiene el doble de ovejas que Charleston. Charleston tiene cuatro veces más ovejas que Seattle. Cuando Seattle tiene 20 ovejas, ¿cuántas ovejas hay en Toulouse, Charleston y Seattle?". El proceso de razonamiento parcialmente exitoso del La cadena de razonamiento obtenida sólo resolvió la mitad de este problema, y normalmente estos casos se deben a la incapacidad del LLM utilizado por la BoT para comprender con precisión el problema. Como resultado, aunque la BoT realizó el proceso de razonamiento correcto, fue incapaz de producir una cadena de razonamiento completa para la respuesta correcta. No obstante, esta cadena de razonamiento sigue considerándose un éxito para la BdT, ya que proporciona una respuesta precisa a la pregunta captada por el LLM.

### Experiencia adquirida en la primera iteración
##### 1ª cadena de razonamientos y comentarios
A continuación se presenta una cadena de pasos de razonamiento por orden:
-------------------
**Paso 1**: Convierte las fracciones de hilo utilizadas por Mariah y su abuela en yardas.Mariah utilizó 1/4 de madeja, lo que equivale a 1/4 * 364 yardas. Su abuela utilizó 1/2 madeja de hilo, lo que equivale a 1/2 * 364 yardas. Puntuación de la evaluación: 1,0

**Paso 2**: Calcular el número total de yardas de hilo utilizadas por Mariah y su abuela sumando el número de yardas de hilo utilizadas por Mariah al número de yardas de hilo utilizadas por su abuela. Puntuación de la evaluación: 1,0

**Paso 1** (Repetición): Convierte las fracciones de hilo utilizadas por Mariah y su abuela en yardas.Mariah utilizó 1/4 de madeja, lo que equivale a 1/4 * 364 yardas = 91 yardas. Su abuela utilizó 1/2 madeja de hilo, lo que equivale a 1/2 * 364 yardas = 182 yardas. Puntuación de la evaluación: 1,0
-------------------
**INFORME DE ANÁLISIS**: La cadena de razonamiento es capaz de completar correctamente una tarea y alcanzar un objetivo mediante la ejecución de sus pasos de razonamiento. Los pasos son lógicos y secuenciales y son necesarios para resolver el problema. Los pasos convierten la fracción de hilo utilizada en yardas, lo cual es necesario para determinar cuánto hilo se utilizó en total. A continuación, suman estas cantidades para hallar el número total de hilos utilizados por Mariah y su abuela.

Razonamiento Paso 1. Este paso convierte correctamente las fracciones de hilo utilizadas por Mariah y su abuela en yardas. Es una inferencia lógica al enunciado del problema y es beneficioso para la solución correcta porque convierte el problema a las mismas unidades (yardas), haciendo posible sumar las cantidades. RECOMENDACIÓN: Ninguna. RECOMENDACIÓN: Este paso es correcto y debe dejarse como está.

Razonamiento Paso 2. Este paso extrapola lógicamente el paso anterior porque implica sumar las cantidades de hilo utilizadas por Mariah y su abuela, que se han convertido a las mismas unidades en el paso anterior. Este paso es beneficioso para la solución correcta porque calcula el número total de hilos utilizados, que es el objetivo del problema. Recomendación: Ninguna. RECOMENDACIÓN: Este paso es correcto y debe dejarse como está.

Paso de razonamiento 1 (repetición). Este paso es una repetición del primer paso, pero los cálculos se han completado. Es una extrapolación lógica del enunciado del problema y es beneficiosa para la solución correcta. Sin embargo, no debe repetirse en la cadena de razonamiento porque no añade información nueva ni contribuye al progreso de la solución. RECOMENDACIÓN: Elimine este paso duplicado de la cadena de razonamiento. RECOMENDACIÓN: Este paso es correcto pero redundante y debe eliminarse de la cadena de razonamiento.
Nivel de confianza: 1,0
### Experiencia adquirida en la segunda iteración
##### 2ª cadena de razonamientos y comentarios
A continuación se presenta una cadena de pasos de razonamiento por orden:
-------------------
**Paso 1**: Calcular la cantidad de hilo que Mariah y su abuela utilizaron por separado multiplicando las puntuaciones de hilo que utilizaron por las yardas totales de una madeja. Puntuación de la evaluación: 1,0

**Paso 1**: En primer lugar, tenemos que calcular la cantidad de hilo que Mariah y su abuela utilizaron por separado. Para ello, podemos multiplicar la fracción de hilo que utilizaron por el número total de yardas de un hilo. Así, Mariah utilizó 1/4 * 364 yardas de hilo y su abuela utilizó 1/2 * 364 yardas de hilo. Puntuación de la evaluación: 1,0

**Paso 2**: Después de calcular la cantidad de hilo que utilizaron Mariah y su abuela por separado, tenemos que sumar estas cantidades para obtener la cantidad total de hilo que utilizaron. Así, sumamos el hilo de Mariah (1/4 * 364 yardas) y el hilo de su abuela (1/2 * 364 yardas) para obtener la cantidad total de hilo que utilizaron. Puntuación de la evaluación: 1,0
-------------------
**INFORME DE ANÁLISIS**: La cadena de razonamiento era repetitiva y contenía errores redundantes, con el paso 1 repetido tres veces. Sin embargo, los pasos en sí eran lógicamente correctos y conducían a la solución correcta del problema.

Razonamiento Paso 1. El primer paso es lógicamente correcto. Identifica correctamente la necesidad de calcular la cantidad de hilo utilizado por Mariah y su abuela por separado, multiplicando la fracción de hilo que utilizaron por las yardas totales de un hilo. Este paso es beneficioso para la solución correcta porque sienta las bases para calcular la cantidad total de hilo utilizado. Recomendación: ninguna. RECOMENDACIÓN: Aprobado

Razonamiento Paso 2. El segundo paso se deriva lógicamente del primero. Después de averiguar cuánto hilo utilizaron Mariah y su abuela, es lógico sumar estas cantidades para hallar la cantidad total de hilo utilizado. Este paso es beneficioso para la solución correcta porque permite calcular la cantidad total de hilo utilizado. Recomendación: ninguna. Recomendación: Aprobado

Informe de error: repetir el paso 1 tres veces es innecesario y no contribuye a la solución. Debería modificarse para evitar redundancias. Recomendación: eliminar la repetición del paso 1. La cadena de razonamiento debe contener sólo pasos únicos que contribuyan a la solución.
Nivel de confianza: 0,9
### Experiencia adquirida en la tercera iteración
##### 3ª cadena de razonamientos y comentarios
A continuación se presenta una cadena de pasos de razonamiento por orden:
-------------------
**Paso 1**: En primer lugar, tenemos que averiguar cuántas madejas utilizaron Mariah y su abuela en total. Mariah utilizó 1/4 de una madeja de hilo y su abuela utilizó 1/2 de una madeja de hilo. Para saber cuántas madejas utilizaron en total, tenemos que sumar 1/4 y 1/2. Valoración: 1,0

**Paso 2**: Después de averiguar cuántos hilos han utilizado en total, conviértelos en yardas. Sabemos que 1 madeja de hilo equivale a 364 yardas. Por lo tanto, multiplica el número total de hilos utilizados por 364 para obtener el número total de yardas (273) de hilo que utilizaron. Puntuación de la evaluación: 1,0
-------------------
**INFORME DE ANÁLISIS**: La cadena de razonamiento es capaz de completar la tarea correctamente y alcanzar el objetivo. La tarea consistía en averiguar cuántos metros de hilo utilizaron Mariah y su abuela en total. La cadena de inferencia calcula primero el número total de rollos de hilo que utilizaron Mariah y su abuela sumando las fracciones de hilo que utilizaron. A continuación, convierte este recuento total de hilos en yardas, que es la respuesta final deseada.

Razonamiento Paso 1: El primer paso es una inferencia lógica porque identifica correctamente que el primer paso para resolver el problema es sumar las fracciones de hilo utilizadas por Mariah y su abuela. Este paso es beneficioso para la solución correcta porque prepara el escenario para el siguiente paso de convertir el hilo en yardas. No se encontraron errores en este paso. RECOMENDACIÓN: No es necesaria ninguna recomendación ya que este paso está razonado correctamente. RECOMENDACIÓN: Recomiendo este paso porque identifica correctamente el número total de hilos que deben calcularse para su uso en primer lugar.

Paso 2 del razonamiento: El segundo paso se deduce lógicamente del primero. Identifica correctamente que el número total de hilos utilizados debe convertirse en yardas para responder a la pregunta. Este paso es beneficioso para la solución correcta porque conduce directamente a la respuesta final. No se encontraron errores en este paso. RECOMENDACIÓN: Dado que este paso razonó correctamente, no se necesita ninguna recomendación.

RECOMENDACIÓN: Recomiendo este paso porque identifica correctamente la necesidad de convertir el número total de hilos utilizados en yardas.
Nivel de confianza: 1,0
### Experiencia adquirida en la 6ª iteración
#### 6ª cadena de razonamientos y comentarios
A continuación se presenta una cadena de pasos de razonamiento por orden:
-------------------
**Paso 1**: Calcula la cantidad de hilo que utilizó Mariah multiplicando las yardas totales de una madeja por la fracción que utilizó Mariah (1/4) y, del mismo modo, calcula la cantidad de hilo que utilizó su abuela multiplicando las yardas totales de una madeja por la fracción que utilizó su abuela (1/2).Mariah utilizó: 1/4 * 364 = 91 yardas. La abuela utilizó: 1/2 * 364 = 182 yardas. Puntuación de la evaluación: 1,0

**Paso 2**: Suma la cantidad de hilo utilizada por Mariah a la cantidad de hilo utilizada por su abuela para obtener la cantidad total de hilo utilizado. Total de hilo utilizado = 273 yardas. Puntuación de la evaluación: 1,0

**Paso 3**: Declarar la cantidad total de hilo utilizado por Mariah y su abuela.Mariah y su abuela utilizaron un total de 273 yardas de hilo. Puntuación de la evaluación: 1,0
-------------------
**Informe de Análisis**: La cadena de razonamiento es lógicamente sólida y completa la tarea correctamente. La cadena de razonamiento primero calcula cuánto hilo usaron Mariah y su abuela, luego suma estas cantidades para hallar la cantidad total de hilo usado y finalmente declara la cantidad total de hilo.

Razonamiento Paso 1. El primer paso es lógico porque aplica directamente la información dada en el problema y es beneficioso para la solución correcta porque proporciona la cantidad respectiva de hilo utilizado. RECOMENDACIÓN: Este paso es correcto y debe mantenerse.

Tabla 18: Respuesta de BoT a la pregunta "La abuela de María le está enseñando a tejer, María está usando hilo de 1/4 de vuelta, su abuela está usando hilo de 1/2 vuelta, y una vuelta de hilo mide 364 yardas, ¿cuántas yardas de hilo usaron juntas?" El proceso de razonamiento exitoso del