HuggingFace da marcha atrás en los detalles técnicos de o1 y abre su código fuente.

Si a los modelos pequeños se les da más tiempo para pensar, pueden superar a los grandes.

En los últimos tiempos, se ha despertado un entusiasmo sin precedentes en la industria por los modelos pequeños, con algunos "trucos prácticos" que les permiten superar en prestaciones a los modelos más grandes.

Se puede argumentar que centrarse en mejorar el rendimiento de los modelos más pequeños tiene su corolario. En el caso de los grandes modelos lingüísticos, el escalado del cómputo del tiempo de entrenamiento ha dominado su desarrollo. Aunque este paradigma ha demostrado ser muy eficaz, los recursos necesarios para el preentrenamiento de modelos cada vez más grandes se han vuelto prohibitivamente caros, y han surgido clusters multimillonarios.

Como consecuencia, esta tendencia ha despertado un gran interés por otro enfoque complementario, a saber, el escalado computacional en tiempo de prueba. En lugar de depender de presupuestos de preentrenamiento cada vez mayores, los métodos en tiempo de prueba utilizan estrategias de inferencia dinámica que permiten a los modelos "pensar durante más tiempo" en problemas más difíciles. Un ejemplo destacado de ello es el modelo o1 de OpenAI, que ha mostrado un progreso constante en problemas matemáticos difíciles a medida que aumenta la cantidad de cálculo en tiempo de prueba.

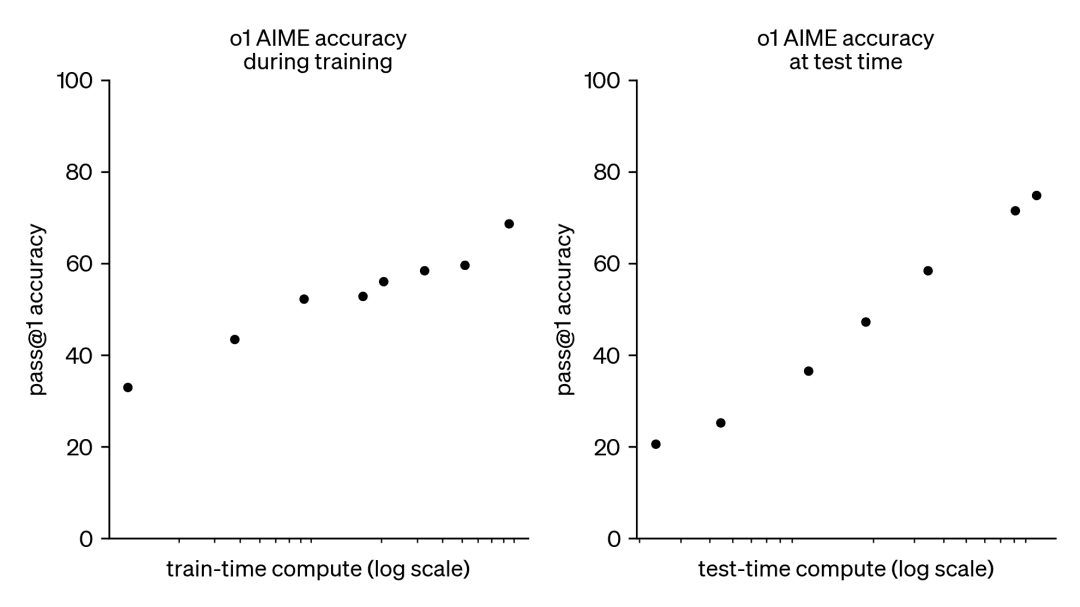
Aunque no sabemos exactamente cómo se entrena o1, investigaciones recientes de DeepMind sugieren que el escalado óptimo del cálculo en tiempo de prueba puede lograrse mediante estrategias como la auto-mejora iterativa o la búsqueda en el espacio de soluciones utilizando un modelo de recompensa. Al asignar de forma adaptativa el cálculo del tiempo de prueba en función de cada pregunta, los modelos más pequeños pueden igualar y, en ocasiones, incluso superar a los modelos más grandes que consumen muchos recursos. El escalado del tiempo de cálculo es especialmente beneficioso cuando la memoria es limitada y el hardware disponible es insuficiente para ejecutar modelos más grandes. Sin embargo, este prometedor enfoque se demostró utilizando un modelo de código cerrado y no se publicaron detalles de implementación ni código.

Documento de DeepMind: https://arxiv.org/pdf/2408.03314

En los últimos meses, HuggingFace se ha dedicado a intentar aplicar ingeniería inversa y reproducir estos resultados. Lo van a presentar en esta entrada del blog:

• Escalado óptimo computacional (compute-optimal scaling):Mejora la potencia matemática de los modelos abiertos en tiempo de prueba implementando trucos de DeepMind.
• Búsqueda en árbol de validadores de diversidad (DVTS):Se trata de una extensión desarrollada para la técnica de búsqueda en árbol bootstrap del validador. Este enfoque sencillo y eficiente aumenta la diversidad y proporciona un mejor rendimiento, especialmente cuando se prueba con un gran presupuesto computacional.
• Busca y aprende:Un conjunto de herramientas ligeras para aplicar estrategias de búsqueda utilizando LLM con el vLLM Consigue aumentos de velocidad.

¿Qué tal funciona en la práctica el escalado óptimo desde el punto de vista computacional? En el gráfico siguiente, los pequeñísimos modelos 1B y 3B de Llama Instruct superan a los modelos mucho más grandes de 8B y 70B en la exigente prueba MATH-500, si se les da suficiente "tiempo de reflexión".

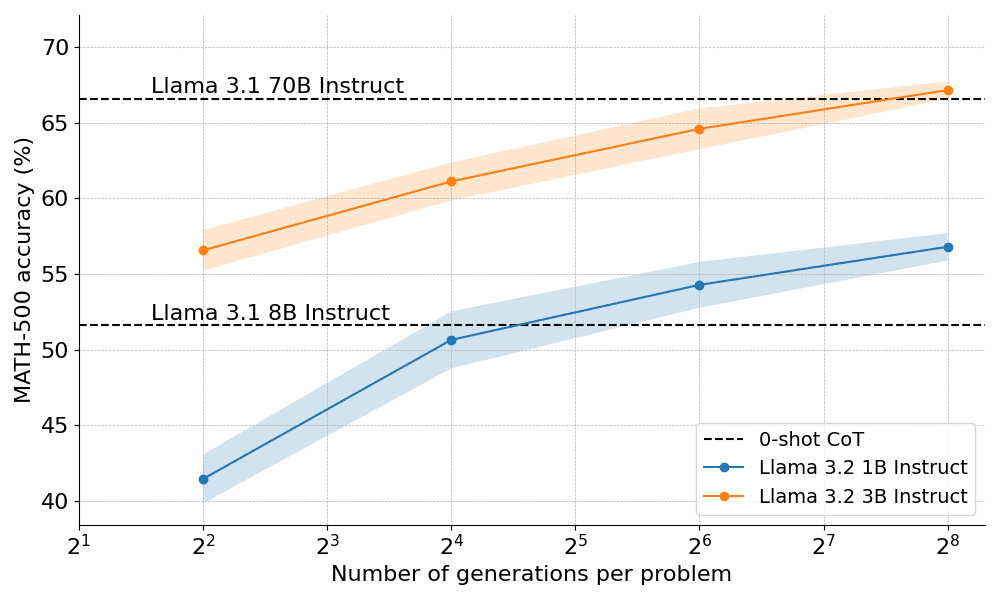
Sólo 10 días después del debut público de OpenAI o1, estamos encantados de desvelar una versión de código abierto de la revolucionaria tecnología que está detrás de su éxito: Extended Test-Time Computing", afirma Clem Delangue, cofundador y consejero delegado de HuggingFace. Al dar al modelo un "tiempo de reflexión" más largo, el modelo 1B puede vencer a 8B, y el modelo 3B a 70B. Por supuesto, la receta completa es de código abierto.

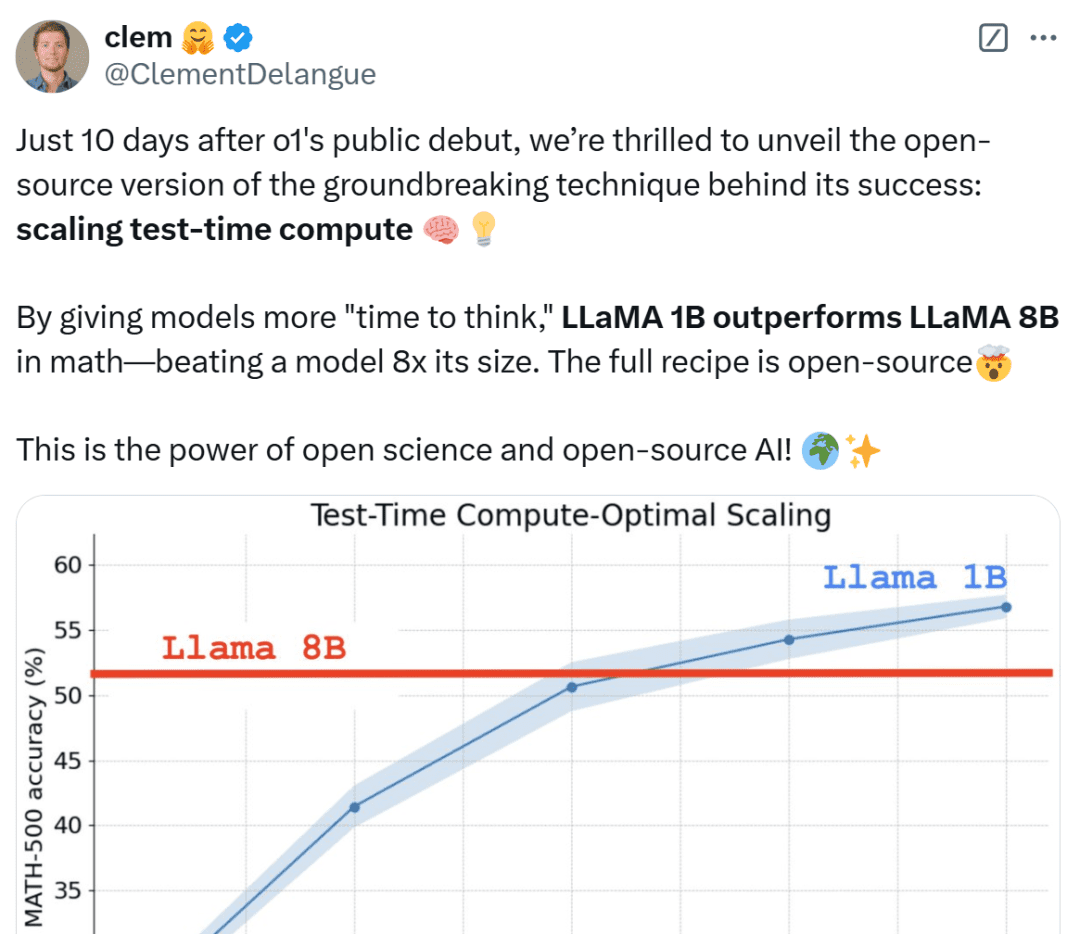
Internautas de toda condición no se tranquilizan al ver estos resultados, los califican de increíbles y lo consideran una victoria de las miniaturas.

A continuación, HuggingFace profundiza en las razones de estos resultados y ayuda a los lectores a comprender estrategias prácticas para aplicar el escalado computacional durante las pruebas.

Estrategia ampliada de cálculo del tiempo de prueba

Existen dos estrategias principales para ampliar el cómputo del tiempo de prueba:

• Autoperfeccionamiento: el modelo mejora iterativamente su resultado o "idea" identificando y corrigiendo errores en iteraciones posteriores. Aunque esta estrategia es eficaz en algunas tareas, suele requerir que el modelo disponga de un mecanismo de automejora incorporado, lo que puede limitar su aplicabilidad.
• Búsqueda contra un validador: este enfoque se centra en generar múltiples respuestas candidatas y utilizar un validador para seleccionar la mejor respuesta. Los validadores pueden basarse en heurísticos codificados o en modelos de recompensa aprendidos. En este artículo, nos centraremos en los validadores aprendidos, que incluyen técnicas como el muestreo Best-of-N y la búsqueda en árbol. Estas estrategias de búsqueda son más flexibles y pueden adaptarse a la dificultad del problema, aunque su rendimiento está limitado por la calidad del validador.

HuggingFace se especializa en métodos basados en búsquedas que son soluciones prácticas y escalables para la optimización computacional en tiempo de prueba. He aquí tres estrategias:

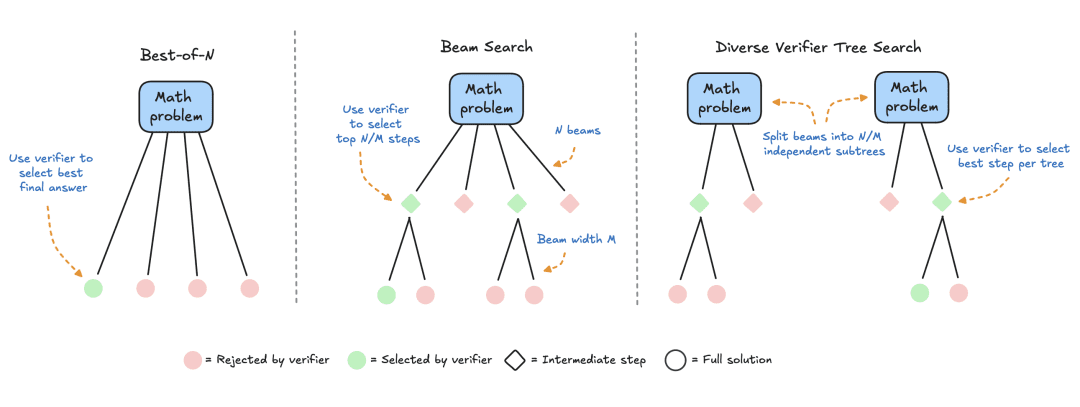
• Mejor de N: suele utilizar un modelo de recompensa para generar múltiples respuestas para cada pregunta y asigna una puntuación a cada respuesta candidata, para después seleccionar la respuesta con la recompensa más alta (o una variante ponderada, como se verá más adelante). Este enfoque hace hincapié en la calidad de la respuesta más que en la frecuencia.
• Búsqueda por conglomerados: método de búsqueda sistemática para explorar el espacio de soluciones, a menudo utilizado junto con los modelos de recompensa por procesos (PRM) para optimizar el muestreo y la evaluación de los pasos intermedios en la resolución de problemas. A diferencia de los modelos de recompensa tradicionales, que producen una única puntuación para la respuesta final, los PRM proporcionan una serie de puntuaciones, una para cada paso del proceso de razonamiento. Esta capacidad de retroalimentación precisa convierte a los PRM en una opción natural para los métodos de búsqueda LLM.
• Diversity Validator Tree Search (DVTS): una extensión de la búsqueda de clústeres desarrollada por HuggingFace que divide el clúster inicial en subárboles separados y, a continuación, expande estos subárboles con avidez utilizando PRM. Este enfoque mejora la diversidad y el rendimiento global de la solución, especialmente si el presupuesto computacional es elevado en el momento de la prueba.

Montaje experimental

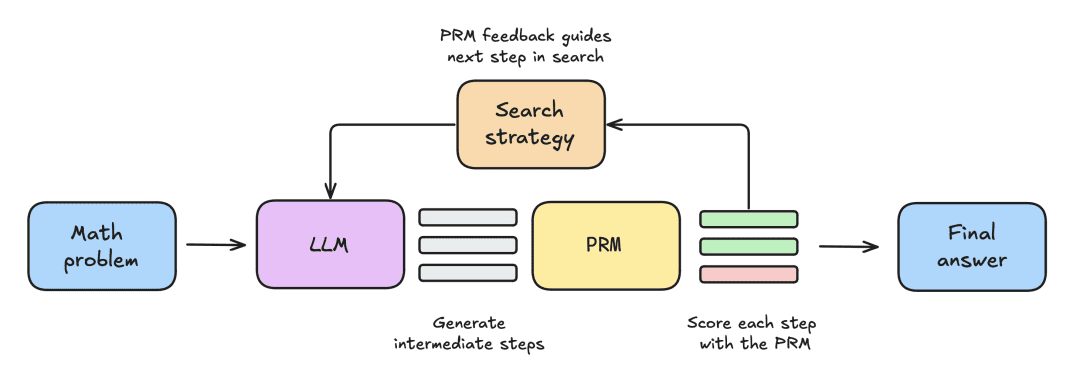
El montaje experimental consistió en los siguientes pasos:

• El LLM recibe primero un problema matemático para generar N soluciones parciales, por ejemplo, pasos intermedios en el proceso de derivación.
• Cada paso es puntuado por un PRM, que estima la probabilidad de que cada paso acabe con la respuesta correcta.
• Una vez finalizada la estrategia de búsqueda, la PMR clasifica las soluciones candidatas finales para obtener la respuesta definitiva.

Para comparar las distintas estrategias de búsqueda, en este documento se utilizan los siguientes modelos y conjuntos de datos de código abierto:

• Modelos: utilice meta-llama/Llama-3.2-1B-Instruct como modelo principal para los cálculos del tiempo de prueba ampliado;
• Modelo de recompensa por proceso PRM: para guiar la estrategia de búsqueda, este artículo utiliza RLHFlow/Llama3.1-8B-PRM-Deepseek-Data, un modelo de recompensa de 8.000 millones entrenado con supervisión por proceso. La supervisión de procesos es un método de entrenamiento en el que el modelo recibe retroalimentación en cada paso del proceso de razonamiento, no sólo en el resultado final;
• Conjunto de datos: Este trabajo se evaluó con el subconjunto MATH-500, un conjunto de datos de referencia MATH publicado por OpenAI como parte de un estudio supervisado por procesos. Estos problemas matemáticos abarcan siete temas y suponen un reto tanto para los humanos como para la mayoría de los modelos de grandes lenguajes.

Este artículo empezará con una base sencilla y luego irá incorporando gradualmente otras técnicas para mejorar el rendimiento.

voto mayoritario

La votación por mayoría es la forma más sencilla de agregar los resultados del LLM. Para un problema matemático dado, se generan N soluciones candidatas y se selecciona la respuesta con mayor frecuencia de aparición. En todos los experimentos, este trabajo muestrea hasta N=256 soluciones candidatas, con un parámetro de temperatura T=0,8, y genera hasta 2048 fichas para cada problema.

He aquí cómo se comportó la mayoría de los votos cuando se aplicaron a la Llama 3.2 1B Instruct:

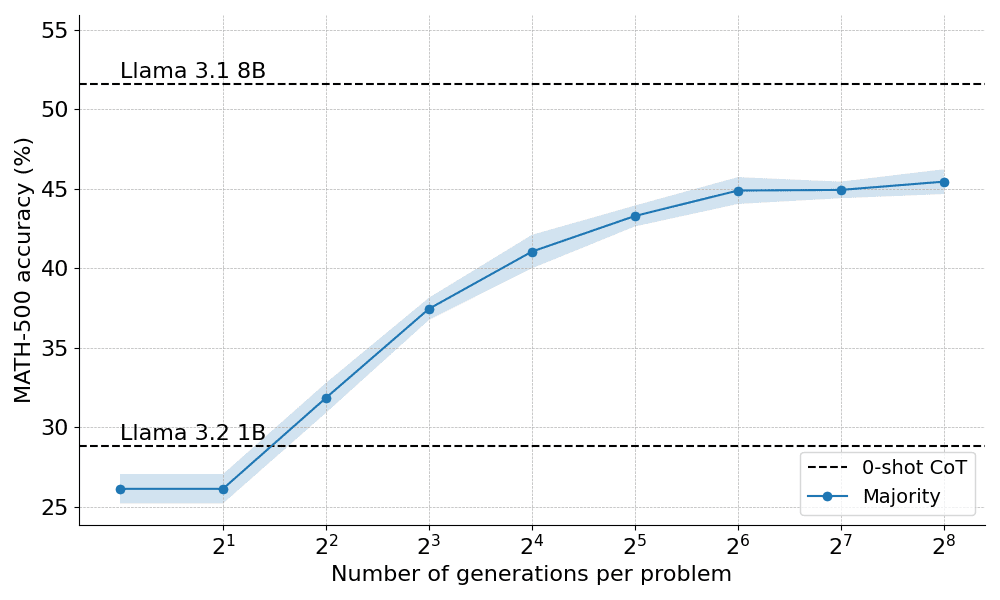
Los resultados muestran que la votación por mayoría proporciona una mejora significativa sobre la decodificación codiciosa de referencia, pero sus ganancias comienzan a estabilizarse después de aproximadamente N=64 generaciones. Esta limitación se debe a que la votación por mayoría tiene dificultades para resolver problemas que requieren un razonamiento cuidadoso.

Teniendo en cuenta las limitaciones de la votación por mayoría, veamos cómo podemos incorporar un modelo de recompensa para mejorar el rendimiento.

Más allá de la mayoría: Best-of-N

Best-of-N es una extensión sencilla y eficiente del algoritmo de votación por mayoría que utiliza un modelo de recompensa para determinar la respuesta más razonable. Existen dos variantes principales del método:

Best-of-N ordinario: Genera N respuestas independientes y elige la que tenga la mayor recompensa RM como respuesta final. Esto garantiza que se elige la respuesta con mayor confianza, pero no tiene en cuenta la coherencia entre las respuestas.

Mejor de N ponderada: resume las puntuaciones de todas las respuestas idénticas y selecciona la que tiene la recompensa total más alta. Este método da prioridad a las respuestas de alta calidad aumentando la puntuación mediante repeticiones. Matemáticamente, las respuestas se ponderan a_i:

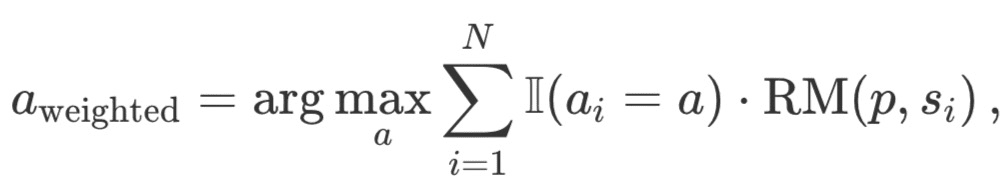
donde RM (p,s_i) es la puntuación del modelo de recompensa para la i-ésima solución s_i al problema p.

Normalmente, se utiliza el Modelo de Recompensa de Resultados (ORM) para obtener puntuaciones individuales a nivel de solución. Sin embargo, para realizar una comparación justa con otras estrategias de búsqueda, se utiliza el mismo PRM para puntuar las soluciones "mejor de N". Como se muestra en la siguiente figura, el PRM genera una secuencia acumulativa de puntuaciones a nivel de paso para cada solución, por lo que los pasos deben puntuarse estadísticamente (de forma reductiva) para obtener puntuaciones individuales a nivel de solución:

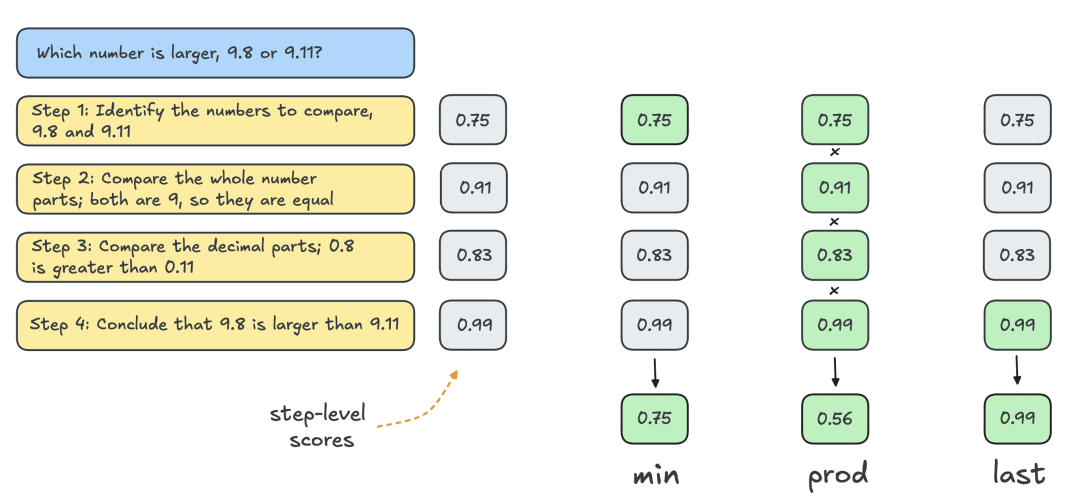
A continuación se enumeran los estatutos más comunes:

• Mínimo: Utiliza la puntuación más baja de todos los pasos.
• Prod: utiliza el producto de fracciones de paso.
• Último: Utiliza la puntuación final del paso. Esta puntuación contiene información acumulada de todos los pasos anteriores, por lo que trata a la PMR como una ORM capaz de puntuar soluciones parciales.

A continuación se muestran los resultados obtenidos aplicando las dos variantes de Best-of-N:

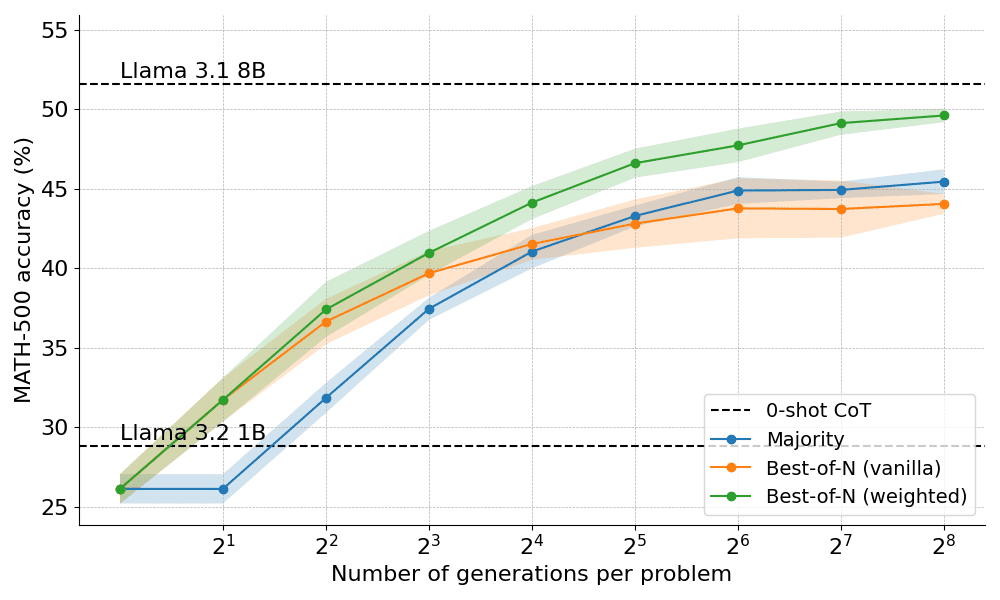
Los resultados revelan una clara ventaja: el Best-of-N ponderado supera sistemáticamente al Best-of-N normal, especialmente con presupuestos de generación mayores. Su capacidad para agregar las puntuaciones de respuestas idénticas garantiza que incluso las respuestas menos frecuentes pero de mayor calidad se prioricen eficazmente.

Sin embargo, a pesar de estas mejoras, sigue estando por debajo del rendimiento alcanzado por el modelo Llama 8B y el método Best-of-N empieza a estabilizarse a partir de N=256.

¿Pueden ampliarse los límites controlando gradualmente el proceso de búsqueda?

Búsqueda de agrupaciones mediante PMR

Como método de búsqueda estructurada, la búsqueda por conglomerados permite la exploración sistemática del espacio de soluciones, lo que la convierte en una potente herramienta para mejorar los resultados de los modelos en el momento de la prueba. Cuando se utiliza junto con la PMR, la búsqueda por conglomerados puede optimizar la generación y evaluación de pasos intermedios en la resolución de problemas. La búsqueda por conglomerados funciona de la siguiente manera:

1. Se generan iterativamente múltiples soluciones candidatas manteniendo un número fijo de "clusters" o caminos activos N .
2. En la primera iteración, se toman N pasos independientes del LLM con temperatura T para introducir diversidad en las respuestas. Estos pasos suelen definirse mediante un criterio de parada, por ejemplo, la terminación en la nueva fila n o el doble de la nueva fila nn.
3. Cada paso se puntúa utilizando PRM y los N/M mejores pasos se seleccionan como candidatos para la siguiente ronda de generación. Aquí M denota la "anchura de cluster" de una ruta de actividad dada. Como en el caso de Best-of-N, el "último" estatuto se utiliza para puntuar las soluciones parciales de cada iteración.
4. Amplíe los pasos seleccionados en el paso (3) muestreando M pasos posteriores en la solución.
5. Repita los pasos (3) y (4) hasta alcanzar el EOS. ficha o supera la profundidad máxima de búsqueda.

Al permitir que la PMR evalúe la corrección de los pasos intermedios, la búsqueda por conglomerados puede identificar y priorizar los caminos prometedores en una fase temprana del proceso. Esta estrategia de evaluación paso a paso es especialmente útil para tareas de razonamiento complejas como las matemáticas, debido a que la validación de soluciones parciales puede mejorar significativamente el resultado final.

Detalles de la aplicación

En los experimentos, HuggingFace siguió la selección de hiperparámetros de DeepMind y ejecutó la búsqueda de clústeres de la siguiente manera:

• Calcular N clusters al escalar a 4, 16, 64, 256
• Anchura de racimo fija M=4
• Muestreo a temperatura T=0,8
• Hasta 40 iteraciones, es decir, un árbol con una profundidad máxima de 40 pasos

Como se muestra en la siguiente figura, los resultados son asombrosos: con un presupuesto de tiempo de prueba de N=4, la búsqueda en clúster alcanza la misma precisión que Best-of-N con N=16, es decir, ¡una mejora de 4 veces en eficiencia computacional! Además, el rendimiento de la búsqueda en clústeres es comparable al de Llama 3.1 8B, que sólo requiere N=32 soluciones por problema. El rendimiento medio de los estudiantes de doctorado de Informática en matemáticas es de unos 40%, por lo que para el modelo 1B, ¡cerca de 55% es suficientemente bueno!

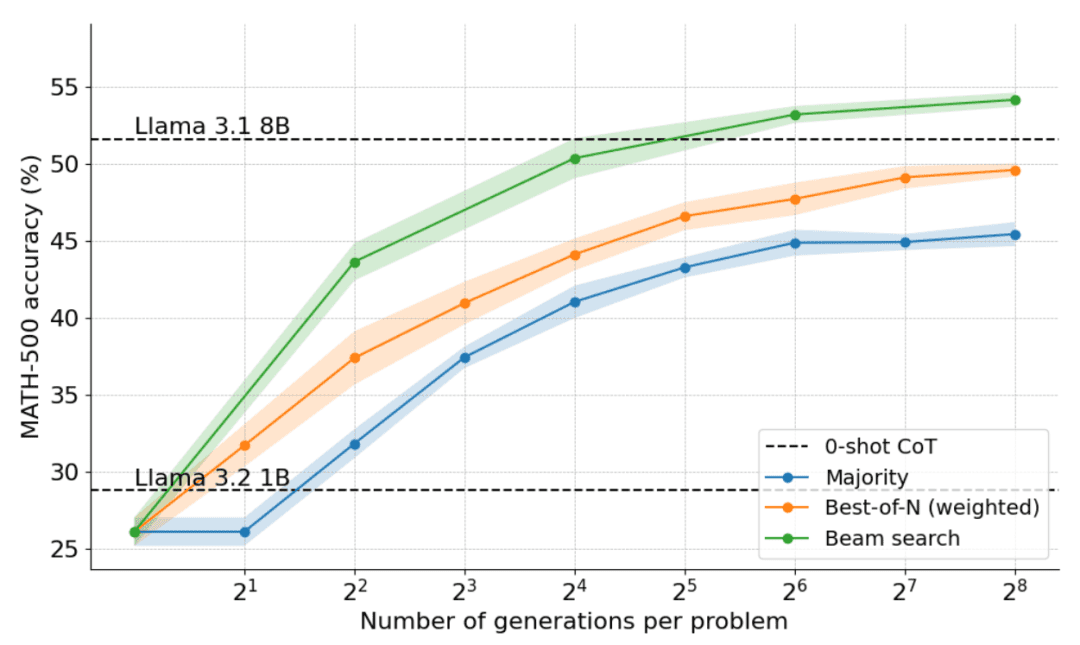
Qué problemas se resuelven mejor mediante la búsqueda en clústeres

Aunque en general está claro que la búsqueda por conglomerados es una estrategia de búsqueda mejor que la mejor de N o la votación por mayoría, el documento de DeepMind muestra que hay compensaciones para cada estrategia dependiendo de la dificultad del problema y del presupuesto computacional en el momento de la prueba.

Para saber qué problemas se adaptan mejor a cada estrategia, DeepMind calculó la distribución de la dificultad estimada de los problemas y dividió los resultados en quintiles. En otras palabras, cada problema fue asignado a uno de cinco niveles, con el nivel 1 indicando problemas más fáciles y el nivel 5 indicando los problemas más difíciles. Para estimar la dificultad del problema, DeepMind generó 2048 soluciones candidatas para cada problema con un muestreo estándar y, a continuación, propuso la siguiente heurística:

• Oráculo: Estimar las puntuaciones pass@1 de cada pregunta utilizando etiquetas de hechos básicos, clasificar la distribución de las puntuaciones pass@1 para determinar los quintiles.
• Modelización: los quintiles se determinan utilizando la distribución de las puntuaciones medias de PMR para cada problema. La intuición aquí es que las preguntas más difíciles tendrán puntuaciones más bajas.

La siguiente figura muestra un desglose de los distintos métodos basado en la puntuación pass@1 y el presupuesto N=[4,16,64,256] calculado sobre las cuatro pruebas:

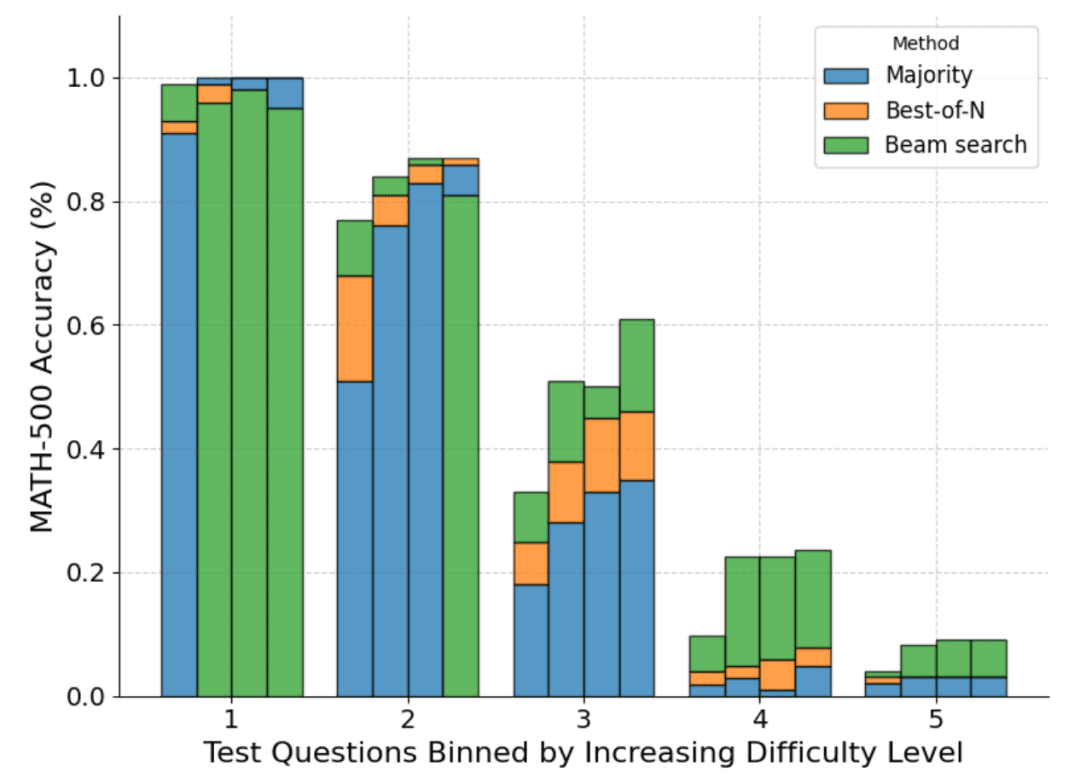
Como puede verse, cada barra representa el presupuesto calculado en el momento de la prueba y dentro de cada barra se muestra la precisión relativa de cada método. Por ejemplo, en las cuatro barras correspondientes al nivel de dificultad 2:

La votación por mayoría es el método con peores resultados de todos los presupuestos computacionales, excepto para N=256 (la búsqueda de clusters obtiene los peores resultados).

La búsqueda en clúster es mejor para N=[4,16,64], pero la mejor de N es mejor para N=256.

Cabe señalar que la búsqueda por conglomerados ha realizado progresos constantes en problemas de dificultad moderada y difícil (niveles 3-5), pero tiende a obtener peores resultados que Best-of-N (o incluso que la votación por mayoría) en problemas más sencillos, especialmente con presupuestos computacionales más elevados.

Al observar el árbol de resultados generado por la búsqueda en clústeres, HuggingFace se dio cuenta de que si a un solo paso se le asignaba una recompensa alta, todo el árbol se colapsaba en esa trayectoria, lo que afectaba a la diversidad. Esto les motivó a explorar una extensión de la búsqueda por clústeres que maximizara la diversidad.

DVTS: Mejorar el rendimiento mediante la diversidad

Como se ha visto anteriormente, la búsqueda en clúster ofrece un mejor rendimiento que Best-of-N, pero tiende a funcionar mal cuando se trata de problemas sencillos y grandes presupuestos computacionales en el momento de la prueba.

Para solucionar este problema, HuggingFace ha desarrollado una extensión denominada "Búsqueda en árbol de validadores de diversidad" (DVTS), cuyo objetivo es maximizar la diversidad cuando N es grande.

El DVTS funciona de forma similar a la búsqueda de clusters con las siguientes modificaciones:

• Para N y M dados, el conjunto inicial se expande en N/M subárboles independientes.
• Para cada subárbol, seleccione el paso con la puntuación PMR más alta.
• Generar M nuevos pasos a partir del nodo seleccionado en el paso (2) y seleccionar el paso con la puntuación PRM más alta.
• Repita el paso (3) hasta alcanzar el token EOS o la profundidad máxima del árbol.

El siguiente gráfico muestra los resultados de aplicar el DVTS a la Llama 1B:

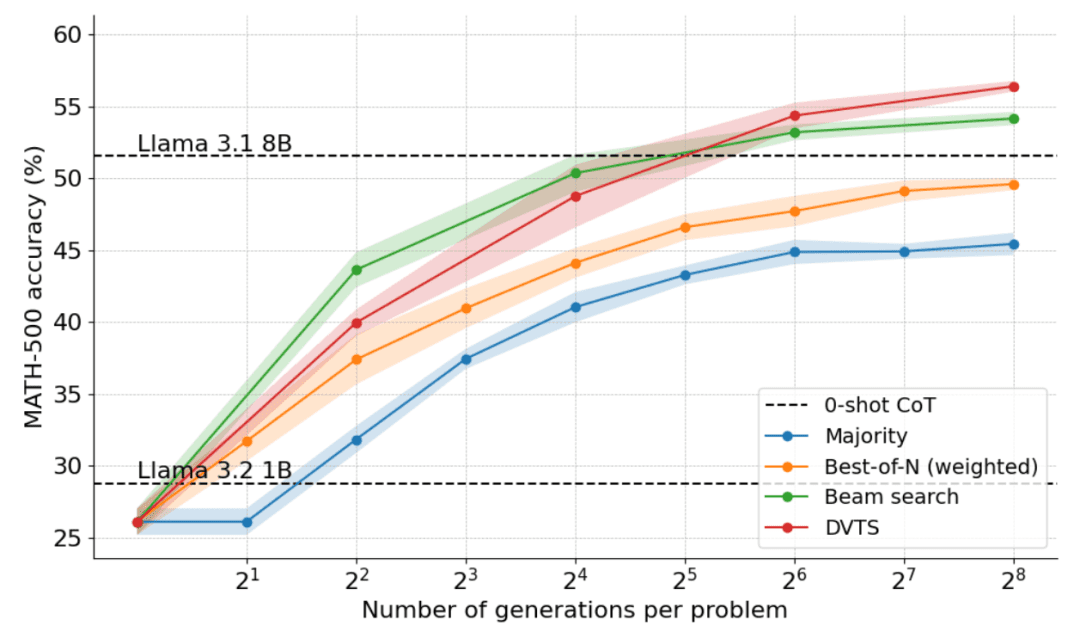
Se puede observar que el DVTS proporciona una estrategia complementaria a la búsqueda por conglomerados: con N pequeños, la búsqueda por conglomerados es más eficaz para encontrar la solución correcta; pero con N más grandes, la diversidad de candidatos DVTS entra en juego y se puede conseguir un mejor rendimiento.

Además, en el desglose de la dificultad del problema, DVTS mejora el rendimiento de los problemas simples/medios con N grande, mientras que la búsqueda en clústeres obtiene mejores resultados con N pequeño.

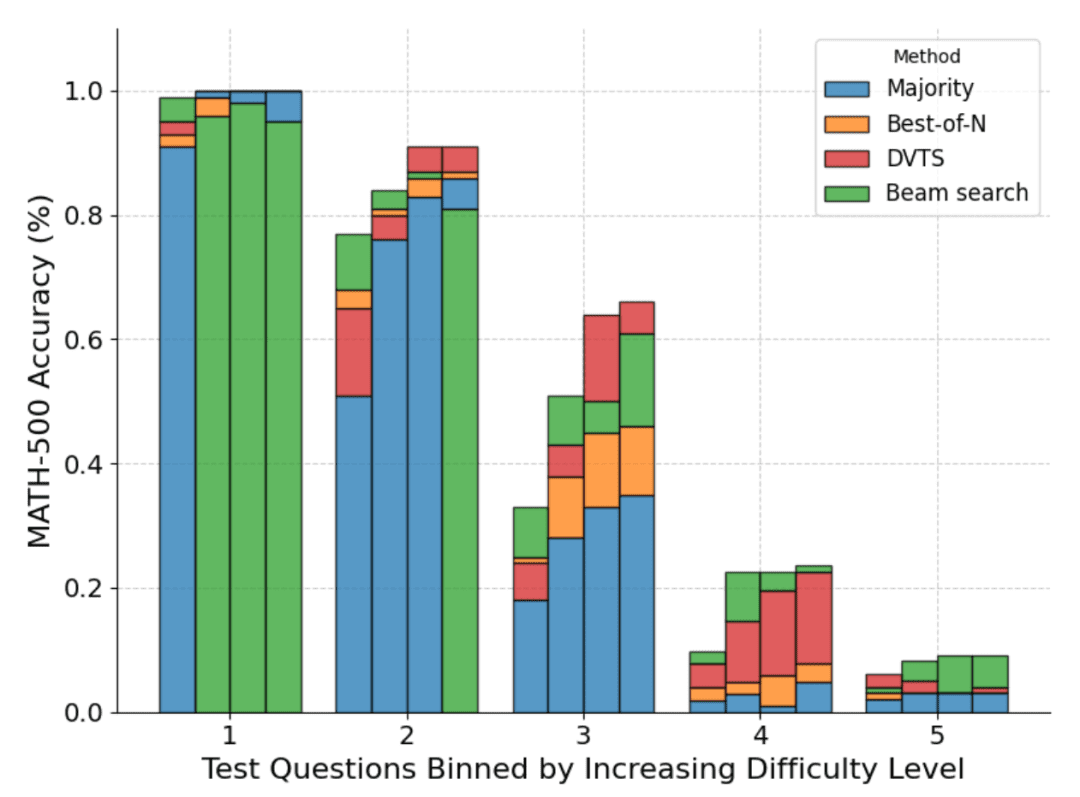
Escalado óptimo computacional (compute-optimal scaling)

Con una amplia variedad de estrategias de búsqueda, una pregunta natural es ¿cuál es la mejor? En el artículo de DeepMind (disponible como Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters ), proponen una estrategia de escalado computacionalmente óptima que selecciona el método de búsqueda y el parámetro hiper θ con el fin de lograr un rendimiento óptimo para un presupuesto computacional dado N :

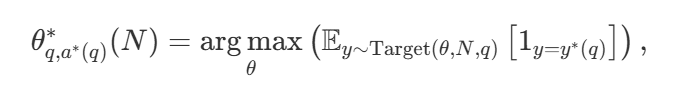
incluidos entre estos 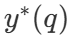es la respuesta correcta a la pregunta q. 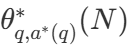Cálculo de representaciones - La estrategia de escalado óptimo. Dado que es sencillo calcular 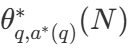Algo tramposo, DeepMind propone una aproximación basada en la dificultad del problema, es decir, asignar recursos computacionales durante las pruebas en función de qué estrategia de búsqueda consigue el mejor rendimiento en un nivel de dificultad determinado.

Por ejemplo, para problemas más sencillos y presupuestos computacionales más bajos, es mejor utilizar estrategias como Best-of-N, mientras que para problemas más difíciles, la búsqueda set shu es una mejor opción. La siguiente figura muestra la curva de optimización del cálculo.

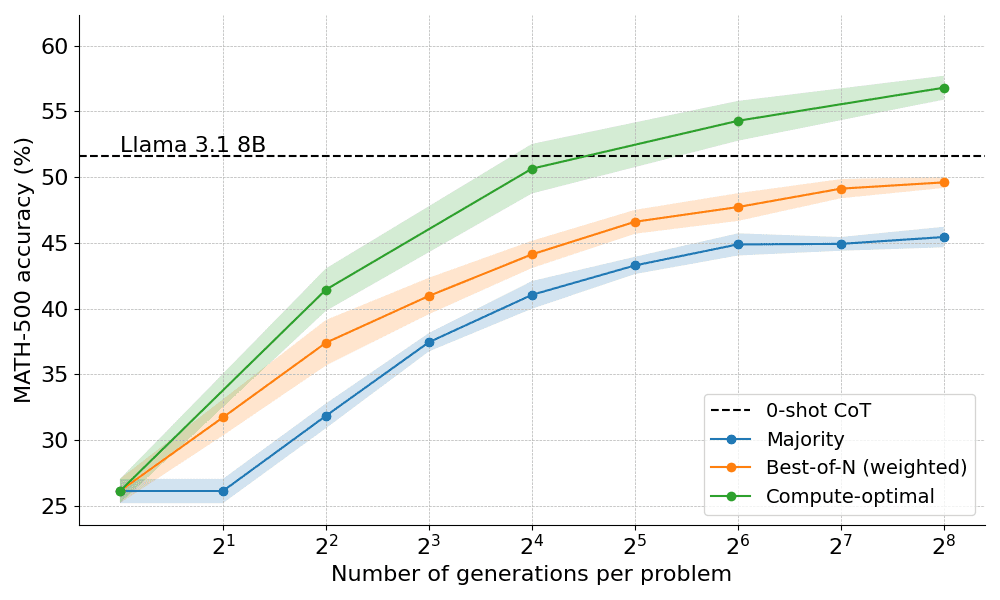
Ampliación a modelos más grandes

Este documento también explora la extensión del enfoque óptimo computacional al modelo Llama 3.2 3B Instruct para ver en qué punto la PMR empieza a debilitarse en comparación con la capacidad de la propia política. Los resultados muestran que la extensión óptima desde el punto de vista computacional funciona muy bien, y que el modelo 3B supera al Llama 3.1 70B Instruct (¡que es 22 veces más grande que el primero!). .

¿Y ahora qué?

La exploración del escalado computacional en tiempo de prueba revela el potencial y los retos de la utilización de enfoques basados en la búsqueda. De cara al futuro, este artículo sugiere varias direcciones interesantes:

• Validadores potentes: Los validadores potentes desempeñan un papel clave en la mejora del rendimiento, y mejorar la solidez y versatilidad de los validadores es fundamental para avanzar en estos planteamientos;
• Autovalidación: el objetivo final es lograr la autovalidación, es decir, que el modelo pueda validar de forma autónoma su propio resultado. Este enfoque parece ser el de modelos como o1, pero sigue siendo difícil de conseguir en la práctica. A diferencia del ajuste supervisado estándar (SFT), la autovalidación requiere una estrategia más matizada;
• (a) Integrar el pensamiento en el proceso: incorporar pasos intermedios explícitos o el pensamiento en el proceso generativo puede mejorar aún más el razonamiento y la toma de decisiones. Al incorporar el razonamiento estructurado al proceso de búsqueda, se puede conseguir un mejor rendimiento en tareas complejas;
• La búsqueda como herramienta de generación de datos: el método también puede actuar como un potente proceso de generación de datos para crear conjuntos de datos de entrenamiento de alta calidad. Por ejemplo, afinar un modelo como Llama 1B basándose en las trayectorias correctas generadas por la búsqueda puede aportar importantes beneficios. Este enfoque basado en estrategias es similar a técnicas como ReST o V-StaR, pero con la ventaja añadida de la búsqueda, lo que proporciona una dirección prometedora para la mejora iterativa;
• Reclamar más PMR: existen relativamente pocas PMR, lo que limita su aplicación generalizada. Desarrollar y compartir más PRM para distintos ámbitos es un área clave en la que la comunidad puede hacer una contribución significativa.