Hello everyone, today we're going to explore the technique of participles in large-scale language modeling (LLM). Unfortunately, disambiguation is a more complex and tricky part of current top LLMs, but understanding some of its details is essential because many people blame neural networks or other seemingly mysterious reasons for some of the shortcomings of LLMs, when in fact the source of these problems is often disambiguation techniques.
Original text:https://github.com/karpathy/minbpe
Before: Character-based Segmentation
So what is a subtext? Actually in our previous video [Building a GPT from scratchIn [ ], we've talked about the semaphore, but that's just a very simple and primitive form of character level. If you go to that video of [Google colab] page, you'll see that we're using our training data ([works of Shakespeare], which is just a very long string in Python:
First Citizen: Before we continue, please listen to me.All: Go ahead, say it.First Citizen: Are you all determined to die rather than starve?All: Determined. Determined.First Citizen: First of all, you know that Gaius Marcius is enemy number one of the people.All: We know, we know.
But how do we feed character sequences into the language model? The first step we take in doing so is to construct a vocabulary table that includes all the different characters we find throughout the training dataset:
``python# This is the only character that appears in the textchars = sorted(list(set(text)))vocab_size = len(chars)print(''.join(chars))print(vocab_size)# !$&',-.3:;?ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz# 65```
Immediately after that, we'll create a lookup table for converting between individual characters and integer words, based on the vocabulary listed above. This lookup table is actually a Python dictionary:
``pythonstoi = { ch:i for i,ch in enumerate(chars) }itos = { i:ch for i,ch in enumerate(chars) }# Encoder: receives a string and outputs a list of corresponding integersencode = lambda s: [stoi[c] for c in s]# Decoder: receives a list of integers and reduces back to a stringdecode = lambda l: ''.join([itos[i] for i in l])print(encode("hii there"))print(decode(encode("hii there")))# [46, 47, 47, 1, 58, 46, 43, 56, 43]# hii there```
After we convert the sequences to integers, we will see that each integer is used as an index in a two-dimensional trainable embedding matrix. Since the size of the vocabulary is `vocab_size=65`, this embedding matrix also has 65 rows:
``pythonclass BigramLanguageModel(nn.Module).def __init__(self, vocab_size).super(). __init__()self.token_embedding_table = nn.Embedding(vocab_size, n_embd)def forward(self, idx, targets=None).tok_emb = self.token_embedding_table(idx) # (B,T,C)```
Here, the "integer" extracts a row from the embedding table, which is a vector representing the token. This vector then enters the transformer as an input for the corresponding time step.
Tokenization of "character blocks" using the byte pair encoding (BPE) algorithm
This is good enough for a rudimentary character-level language model. In practice, however, state-of-the-art language models use more complex schemes for building markup vocabularies. These schemes do not work at the character level, but at the character block level. These character block vocabularies are constructed by using algorithms like Byte Pair Encoding (BPE), an approach we will explain in detail below.
Turning to the historical development of this approach, OpenAI's GPT-2 paper published in 2019, titled "Language Models as Unsupervised Multitasking Learners," has made byte-level BPE algorithms popular for the tokenization of language models. Read Section 2.2 of this paper on "Input Characterization" for their description and motivation for this algorithm. You will see them mentioned at the end of this section:
The vocabulary has been extended to 50,257. we have also increased the context size from 512 to 1024 tokens and used a larger batch size of 512.
Recall that at the attention (attention) layer of the Transformer, each token is an attention to a finite number of tokens in the previous sequence. The paper mentions that the context length of the GPT-2 model is 1024 tokens, which is an improvement over the 512 of GPT-1. In other words, tokens are the basic units that serve as input to the Linguistic Long-Term Memory (LLM) model. Tokenization is the process of converting raw strings in Python into lists of tokens and vice versa. To give one other popular example of the ubiquity of this abstraction, if you view [Llama 2The] paper, again, search for "markers" and you get 63 mentions. For example, the paper claims that they trained on two trillion markers and so on.
Before we dive into the implementation details, let's briefly explore why we need to delve into the tokenization process. Tokenization is at the heart of many of the oddities in LLMs, and I recommend that we don't take it lightly. Many problems that seem to be related to the structure of neural networks actually originate from tokenization. Here are a few examples:
- Why can't LLM spell words correctly?
- Why can't LLM accomplish simple string processing tasks such as string inversion?
- Why does LLM perform poorly when dealing with non-English languages (e.g. Japanese)?
- Why does LLM perform poorly when performing simple arithmetic operations?
- Why does GPT-2 have extra difficulty programming in Python?
- Why does my LLM suddenly stop working when it encounters the string ""?
- What is this strange warning I'm getting about "trailing spaces"?
- When I ask about "SolidGoldMagikarp", why does LLM crash?
- Why should I prefer to use YAML over JSON to interact with LLMs?
- Why is LLM not actually a true end-to-end language model?
- What exactly is the root cause of suffering?
We'll return to these topics at the end of the video.
Next, let's load this [Tokenization Online Tool] The advantage of this online tool is that the tokenization process takes place in real time in your web browser, so you can easily enter a text string into the input box and immediately see the results of the tokenization on the right side. The top of the page shows that we are currently using
gpt2tokenizer, we can see that the string in the example is being broken down into 300 tokens. These tokens are clearly displayed in different colors:
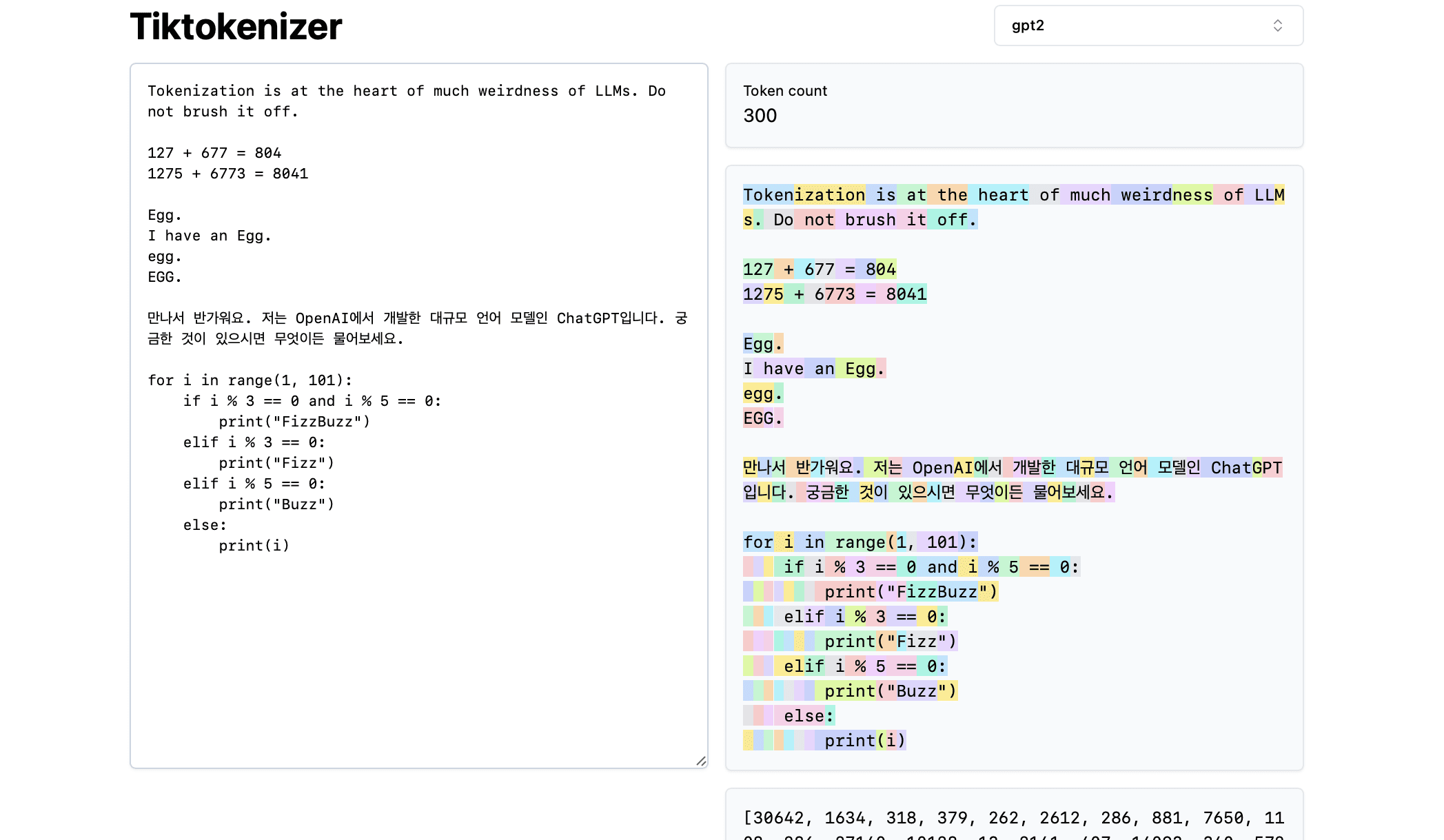
For example, the string "Tokenization" is encoded as token 30642, followed by token 1634. the index of the token "is" (note that there are three characters here, including the preceding space, which is important!) The index of the token is 318. note the space, as it is indeed present in the string and must be tokenized along with all other characters, but is usually omitted for visual clarity. You can toggle the visualization of spaces at the bottom of the tool. Similarly, the token "at" is 379, "the" is 262, and so on.
Next, let's look at a simple arithmetic example. Here we find that numbers may be broken down by the tokenizer in inconsistent ways. For example, the number 127 is broken down into a single token consisting of three characters, while the number 677 is broken down into two tokens: the token " 6" (again, note the leading space!) and the token "77". We rely on large language models to understand this arbitrariness. The model must learn, both in its parameters and during training, that the two tokens ("6" and "77") actually combine to represent the number 677. Similarly, if the LLM wants to predict that the result of this addition will be the number 804, it must output the number in two steps: first, it emits the token "8", and then the token "04". Note that all of these decompositions appear to be completely arbitrary. In the example below, we see that 1275 is decomposed into "12" and "75", 6773 is actually two tokens "6" and "773", and 8041 is decomposed into "8" and "041".
(To be continued...) (TODO: Unless we find a way to automatically generate this content from videos, we'll probably continue this.)
