Challenging Olympiad-Level Problems: 7 Mainstream LLM Chinese Math Performance Benchmark Reviews

Mathematical ability, which encompasses formula derivation, logic chain construction, and abstract thinking, has long been seen as a key area for testing the capabilities of artificial intelligence (AI), particularly large-scale language models (LLMs). This is because it does not only test computational power, but also delves deeper into the model's ability to reason, understand and solve complex problems.

However, recent findings from a team at ETH Zurich show that even the top Large Language Models (LLMs) generally score low when confronted with difficult mathematical competition questions, such as challenges at the level of the U.S. Mathematical Olympiad, which has sparked a discussion about the true capabilities of current LLMs in terms of rigorous mathematical reasoning.

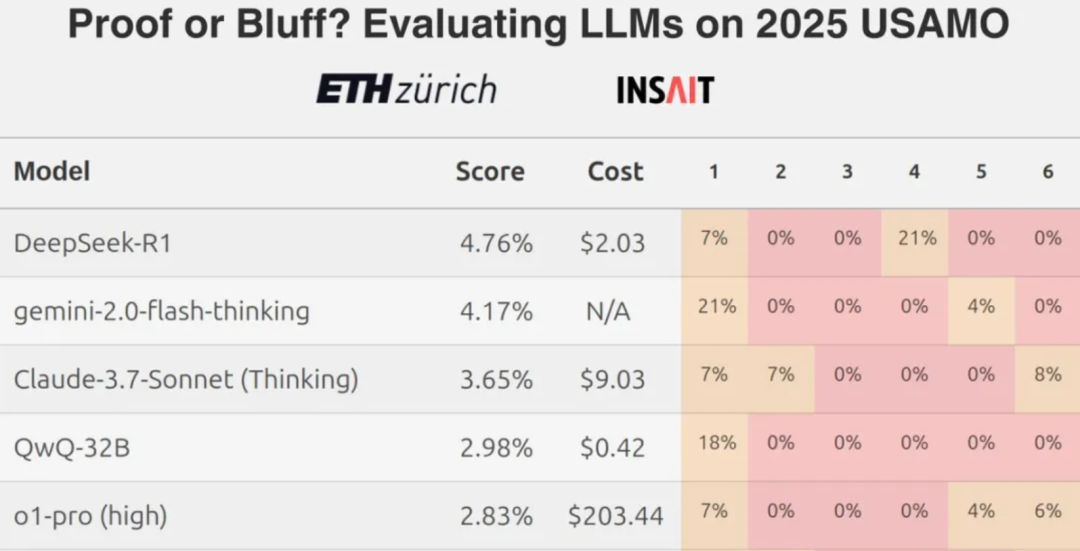
In this context, a natural question is: how well do these models perform when dealing with math problems formulated in Chinese? In this review, a total of seven mainstream or emerging large-scale language models from home and abroad are selected for a side-by-side comparison of their mathematical abilities using problems from the Alibaba Global Mathematics Competition and the Chinese Mathematics Olympiad.

The models involved in the test include:

• Domestic models:DeepSeek R1,Hunyuan T1,Tongyi Qwen-32B (original text) 通义 QwQ-32B),YiXin-Distill-Qwen-72B
• International models:Grok 3 beta,Gemini 2.0 Flash Thinking,o3-mini

Overall performance evaluation

The assessment consists of 10 challenging questions with 13 scoring questions. The scoring criteria are: 1 point for complete correctness, 0.5 points for partial correctness, and no points for errors.

The overall correctness of each model in this test is as follows:

The detailed score distribution shows the performance differences between models:

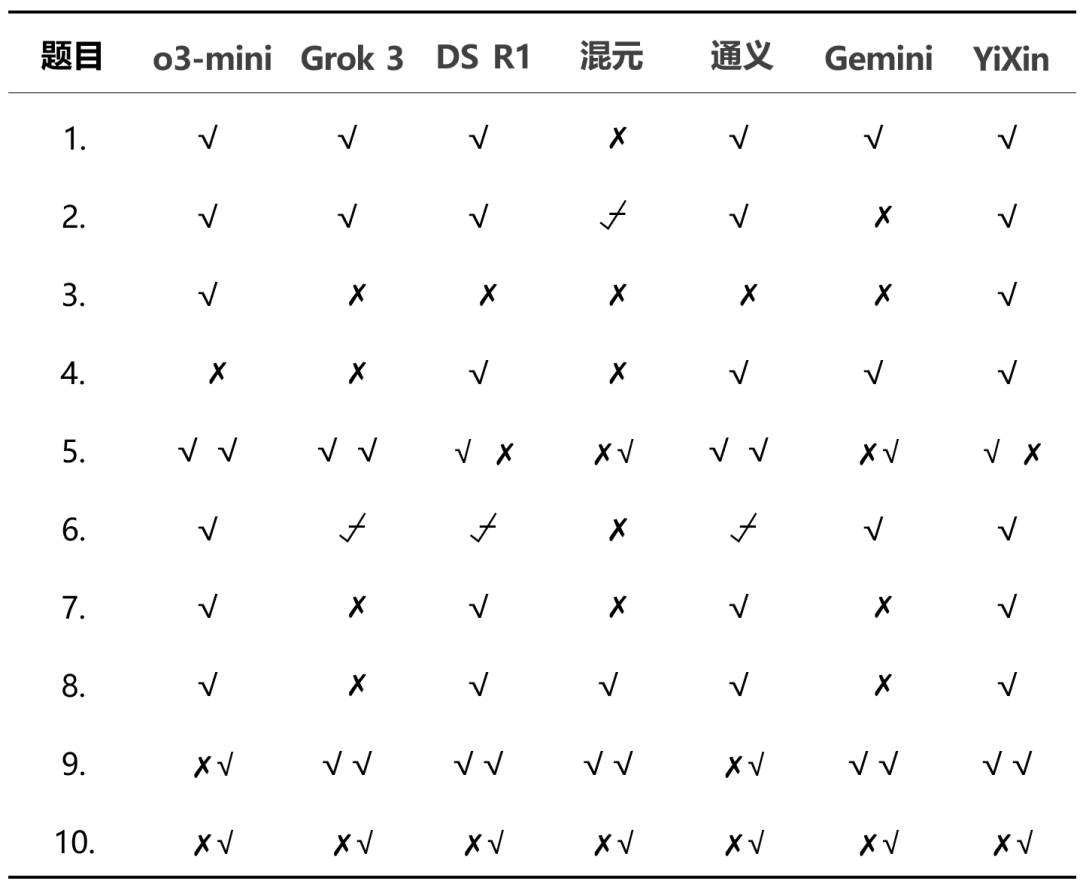
From the overall results.o3-mini cap (a poem) YiXin-Distill-Qwen-72B It performed well in this test, demonstrating strong math problem solving skills. The performance of the other models varied.

Specific answers to some of the test questions are shown next.

Measurement details

Round 1: The problem of change

Question: Grandpa has $60 and goes to the grocery store and buys $20 worth of vegetables. how might the cashier give grandpa his change?

Analysis: This is a basic arithmetic application question that examines the model's understanding of life scenarios and basic money calculation skills.

Results:
o3-mini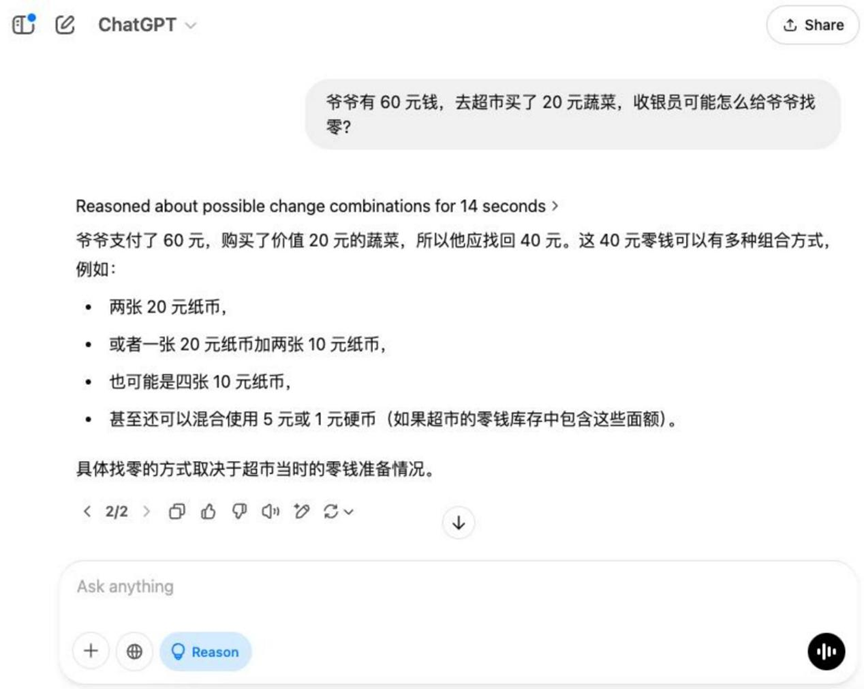

Grok 3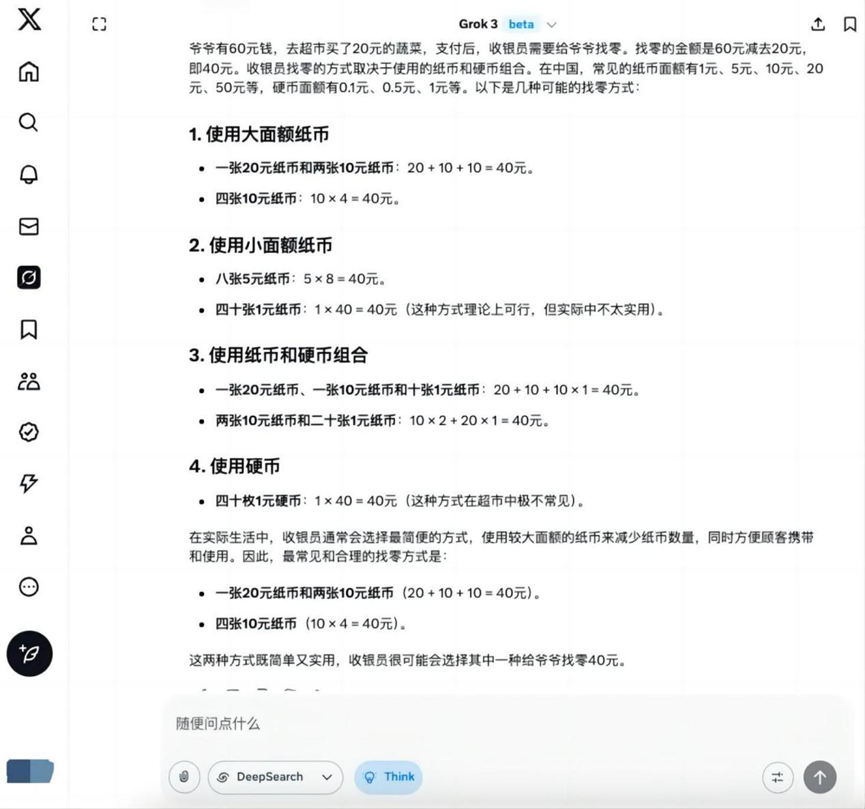

DeepSeek R1

Hunyuan T1

Gemini 2.0 Flash Thinking

YiXin-Distill-Qwen-72B

On this base topic, in addition to Hunyuan T1 Outside of that, the rest of the models give the correct solution for finding zero.

Round 2: Walking Distance Calculation and Method Judgment

Question: Xiaoming and Xiaohua walk to school every day. Ming walks 48 meters per minute and Hua walks 55 meters per minute. Xiaoming's house is 384 meters from the school. Xiaohua takes 4 minutes longer than Ming to get from home to school. How far is Xiaohua's house from the school? Which of the following methods is incorrect, and give your reasons.

Method 1: 55 × 4 = 220 (meters), 384 + 220 = 604 (meters)
Method 2: 384 / 48 = 8 (minutes), 55 × (8 + 4) = 660 (meters)

Analysis: This question combines itinerary problem calculation and logical judgment, requiring the model to not only calculate the correct answer, but also to be able to analyze the correctness or incorrectness of the given solution, examining multi-step reasoning and logical discernment skills.

Results:
DeepSeek R1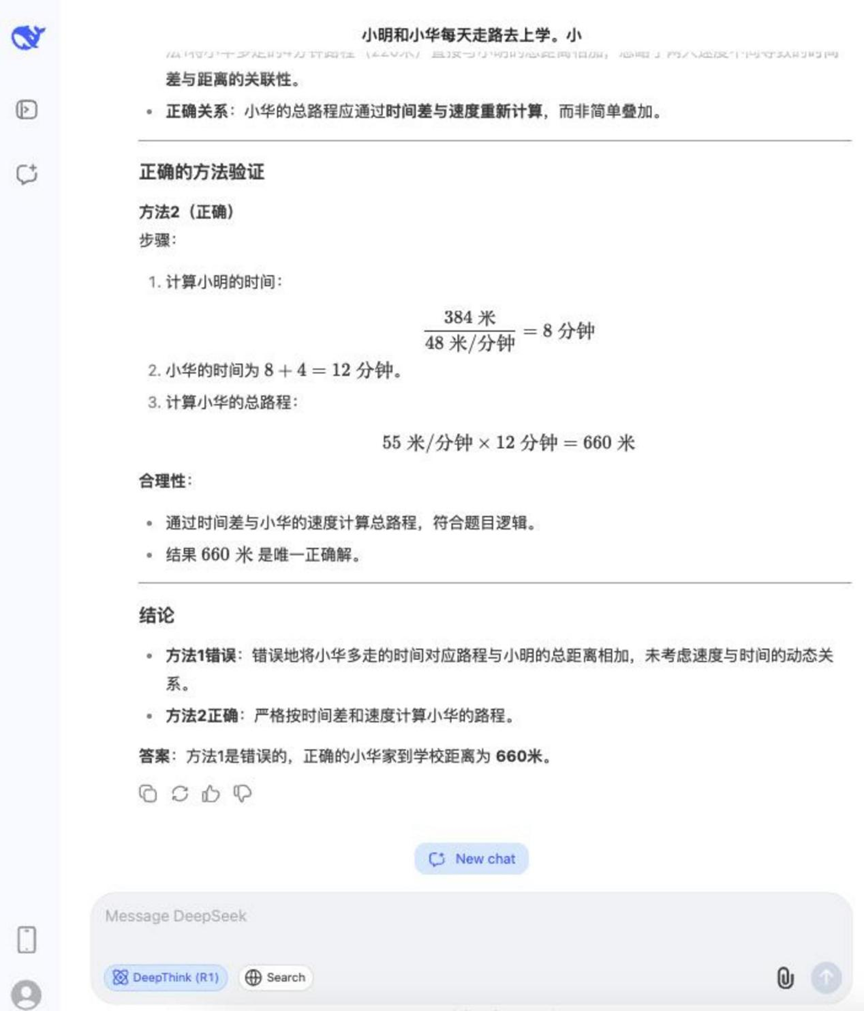

Tongyi Qwen-32B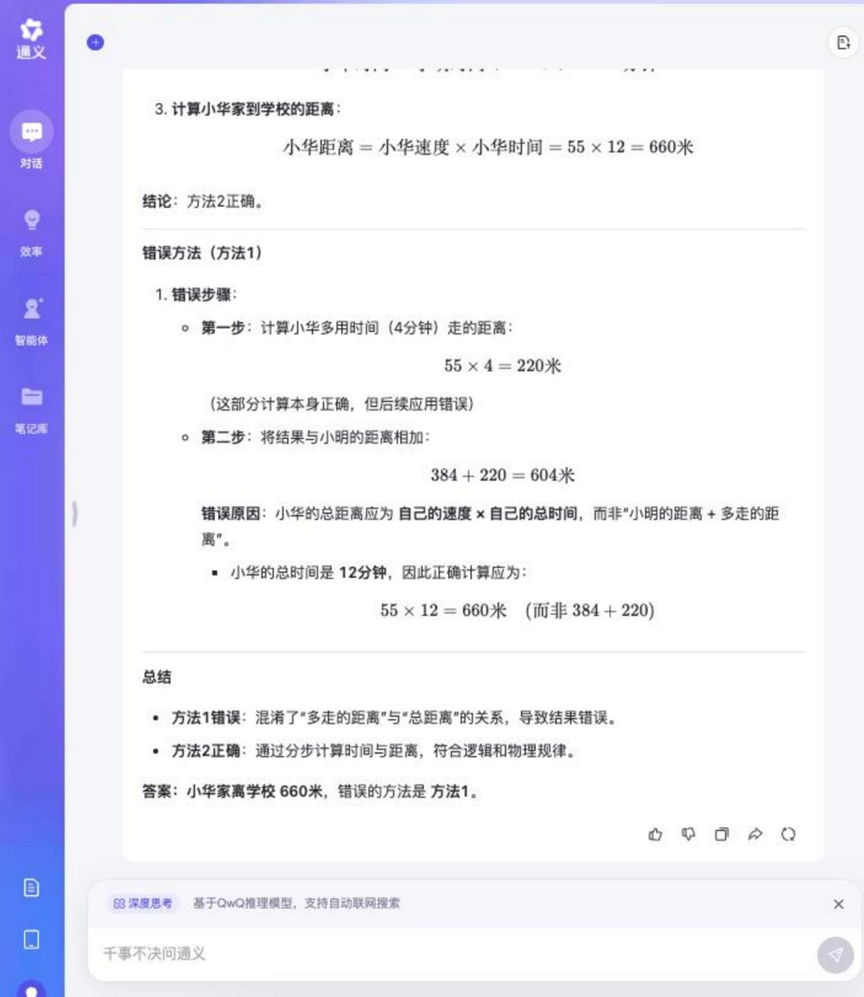

YiXin-Distill-Qwen-72B

The reasoning process for this question was relatively long, but most of the models involved in the test were able to answer it correctly and determine the wrong way to do it.

Round 3: Geometric Occlusion Problem (Invisible Towers)

Question: In a city there are 6 towers located at points A, B, C, D, E and F. Several students form a traveling group to go on a free trip to the city. After some time, each student realizes that he can only see the 4 towers located at points A, B, C, and D, but not the towers located at points E and F. The students can only see the towers located at points A, B, C, and D, but not the towers located at points E and F. It is known that the positions of the students and the towers are considered to be points on the same plane, and that these points do not coincide with each other. 3 of the points A, B, C, D, E, and F do not share a common line. The only possibility of not seeing the tower is that the line of sight is blocked by another tower. For example, if a student is at a point P that is co-located with A and B, and A is on the line segment PB, then that student cannot see the tower located at B. Ask: what is the maximum number of students who may be in this traveling group? a. 3 b. 4 c. 6 d. 12

Analysis: This is a complex geometric and logical reasoning problem involving visibility, occlusion, and point set configurations, which requires a high level of spatial imagination and logical reasoning for the model.

Results:
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B

The difficulty of the questions has increased significantly. In this round of testing, only o3-mini cap (a poem) YiXin-Distill-Qwen-72B successfully solved, the other models failed to give a correct answer.

Round 4: Probability Problems (Tigers and Tigers)

Question: During the Spring Festival, a milk company launched a Chinese New Year blind box activities: each box of milk comes with a "red packet", which contains "Tiger" "Sheng" "Wei" one of the three patterns. Wei" one of the three patterns. Collected two "Tiger", a "Sheng" and a "Wei" can be spelled out "Tiger Tiger Sheng Wei" family portrait. Once the activity was launched, it became a Netflix hit and attracted many people to participate. The known conditions are as follows: the patterns on the red packets are randomly distributed independently and cannot be distinguished from each other. The probability of the appearance of the three patterns "Tiger", "Sheng" and "Wei" is 1/3. Q: In order to collect a complete set of "Tiger Tiger Sheng Wei Q: How many cartons of milk do you need to buy on average in order to collect a complete set of "Tiger, Tiger, Mighty" family photos?

Analysis: This is a typical collector's problem (Coupon collector's problem variant) that requires the use of probability theory and expectation calculations, and examines the model's ability to handle probability models and perform mathematical expectation calculations.

Results:
DeepSeek R1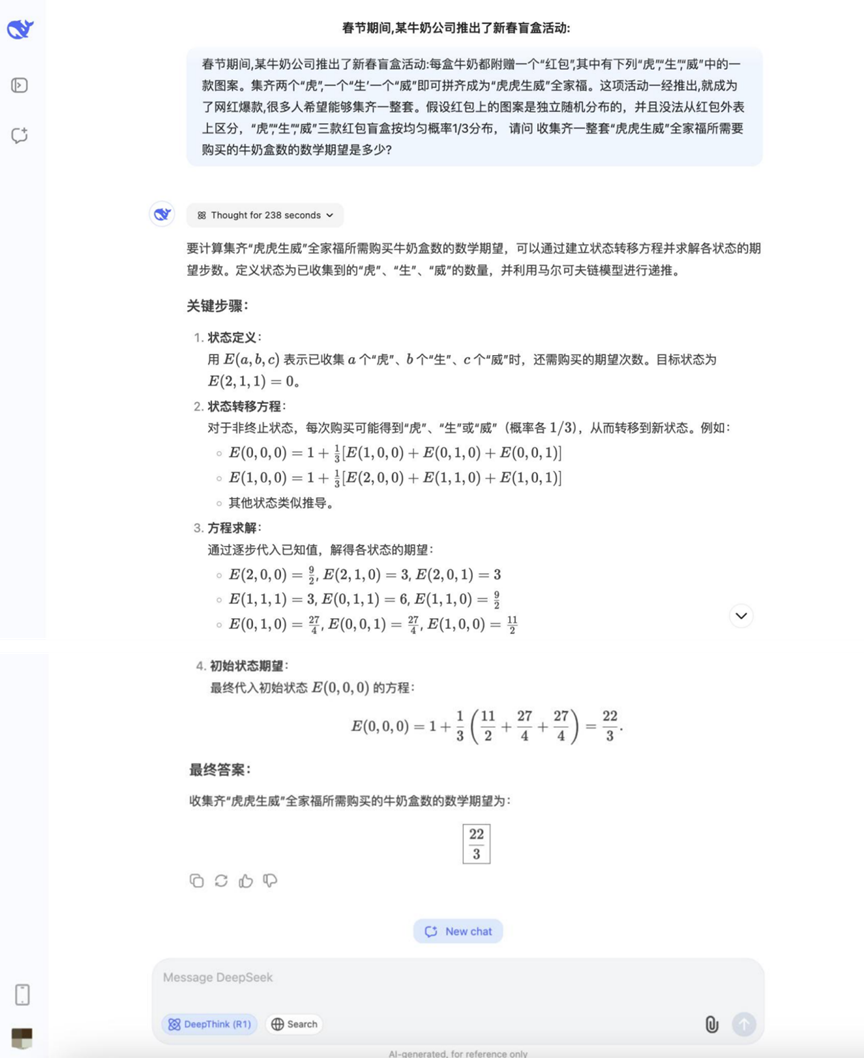

Hunyuan T1
 

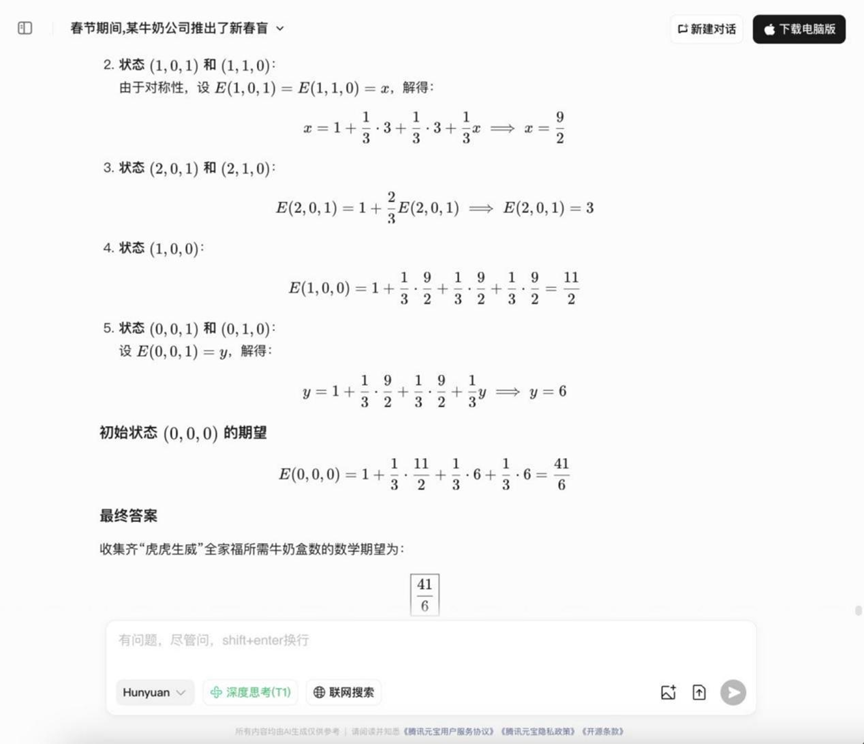
YiXin-Distill-Qwen-72B

The answers to the probability questions in this round began to diverge, with some models being able to correctly list ideas and calculate them.

Round 5: Geometry and Path Planning (Fighter Games)

Problem Description Picture:

Analysis: This is a problem that combines geometry, coordinate or grid systems, and shortest path/optimal strategies, and may require the model to understand the graphical information and perform spatial reasoning and planning.

Results:
o3-mini: Successful resolution

YiXin-Distill-Qwen-72B: Partially correct
 

This round of testing requires a higher level of model synthesis, with about half of the models tested being handled completely correctly.

Round 6: Number Theory Proof Problems (Finding Minimal Nonfactors)

Problem Description Picture:

Analysis: Moving into the realm of proof questions, which require rigorous logical deduction and a deep understanding of number theory concepts, is a direct test of a model's abstract reasoning ability.

Results:
o3-mini

YiXin-Distill-Qwen-72B
 

In the home-grown model, theYiXin-Distill-Qwen-72B Performed better in this round of proof questions. The proof questions were significantly more challenging to model.

Round 7: Functions and Mapping Problems (Mapping on the Unit Circle)

Problem Description Picture:

Analysis: This question involves the concepts of functions, mappings, and the unit circle in advanced mathematics and examines the model's ability to understand and apply abstract mathematical definitions.

Results:
o3-mini

YiXin-Distill-Qwen-72B
 

About half of the models were able to correctly handle this problem involving abstract mappings.

Round 8: Combinatorial Optimization Problems (Maximum Triangle)

Question: There are 1989 points in space, any three of which do not share a line. Divide these points into 30 groups, each with a different number of points. A triangle can be formed by taking a point as a vertex from any three different groups. Q: How can the number of points in each group be distributed so as to maximize the number of triangles formed?

Analysis: This is an optimization problem in combinatorial mathematics that requires a model to understand the principles of combinatorial counting and to find the optimal allocation strategy, which involves more complex mathematical modeling and optimization ideas.

Results:
o3-mini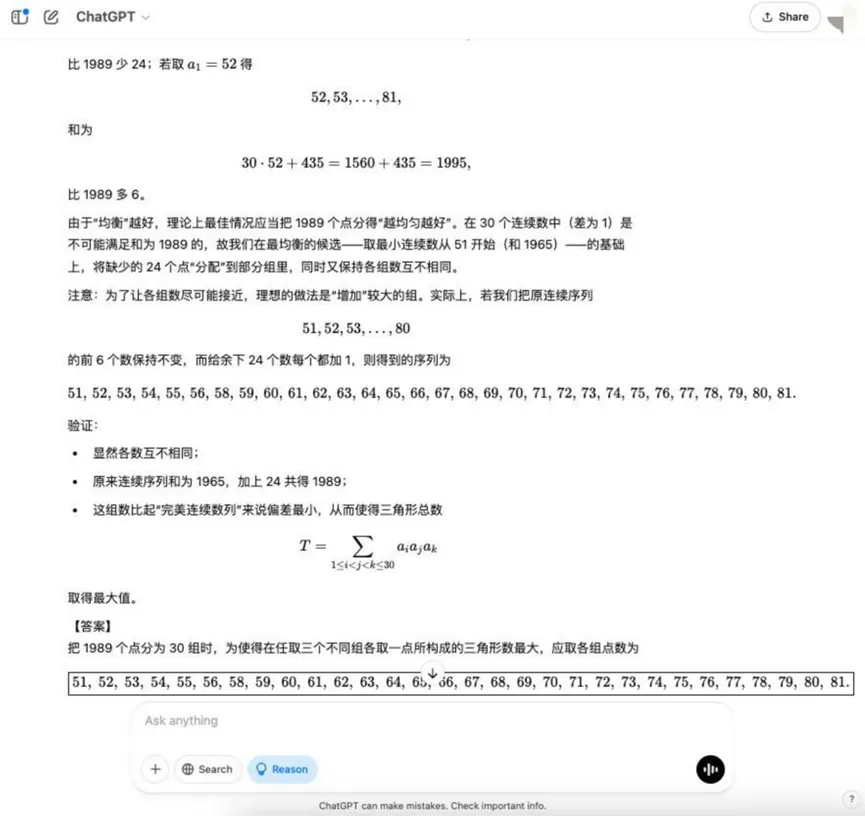

YiXin-Distill-Qwen-72B
 

Combinatorial optimization problems further increase the difficulty and place higher demands on the mathematical strategies and computational skills of the model.

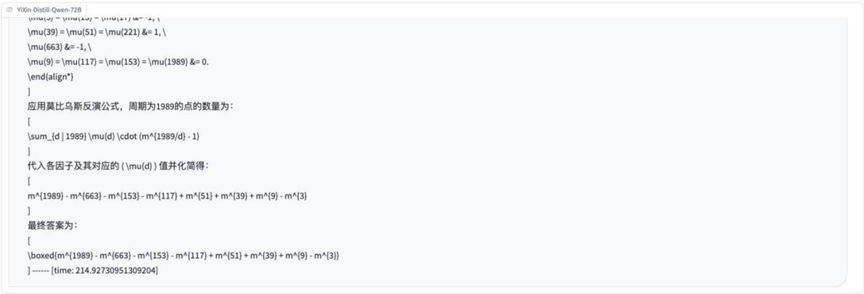
Round 9: Number Theory Problems (Factor Chains)

Problem Description Picture:

Analysis: Again, number theoretic concepts are involved, examining the model's understanding and application of relationships such as factorials and integrality, which may require constructive proofs or counting.

Results:
o3-mini: Partially correct

YiXin-Distill-Qwen-72B: Absolutely correct.
 

YiXin-Distill-Qwen-72B Solid performance on this counting topic.

Round 10: Geometric problems (equal area points)

Problem Description Picture:

Analysis: The final question is a geometric problem involving area calculations, trajectories of points, or existence proofs that test the model's geometric intuition, algebraic operations, and logical reasoning.

Results:
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B
 

The final geometry questions also showed differences between models in their ability to handle complex geometric problems.

Observation and analysis

Based on this Chinese math proficiency test on several large language models, the following observations can be made:

1. Modeling basic math skills improves significantly: Compared to earlier models, the current generation of LLMs shows significant improvement in handling mathematical problems involving multi-step reasoning, such as geometry, probability, and some open-ended application problems. This can be attributed to the increase in model size, the abundance of training data, and the application of reasoning enhancement techniques such as "thought chaining".
2. There are differences in problem solving styles: Different models behave differently in terms of the level of detail of the solution process.
   • o3-mini, Grok 3 beta, Tongyi Qwen-32B The output is relatively concise and the inference steps are straightforward.
   • DeepSeek R1, Hunyuan T1, YiXin-Distill-Qwen-72B The tendency to show more detailed thinking processes, sometimes including reflection and revision steps, is more "verbose", but this may help to trace the logic of their reasoning.
   • Gemini 2.0 Flash Thinking 's solution process is not only lengthy, but also uses mainly English output, suggesting that it may be relatively poorly trained on the Chinese math corpus.
3. Robustness to input errors: It is observed in the test that even if there are minor notation errors or presentation irregularities in the problem descriptions, some of the models are still able to understand the meaning of the questions correctly and answer them, showing a certain degree of robustness. However, this does not mean that the models can always ignore errors, and errors in key information can still lead to answer failure.
4. Future enhancements: specialization and tool integration: Despite the obvious progress, there is still room for improvement in the accuracy of the current LLM when dealing with complex math problems, especially in difficult competition problems and scenarios requiring rigorous proofs. Future enhancement paths may include:
   • Integration of external computing engines: The shortcomings of LLM in exact computation and symbolic operations are compensated by invoking symbolic computation tools such as Wolfram Alpha.
   • Domain-exclusive fine-tuning: Construct high-quality fine-tuned datasets for mathematical logic, specific branches of mathematics (e.g., algebra, geometry, probability theory), and strengthen the model's specialized reasoning and depth of knowledge.
   • Interactive learning and revision: Develop mechanisms that allow the user to guide the solution process, point out missteps and allow the model to dynamically adjust the solution strategy.
5. Advice to users:
   • Students: LLM can be used to assist learning by quickly verifying solutions and answers to basic questions. However, for complex or creative problems, be wary of the model's potential for "serious nonsense" (i.e., confidently giving the wrong answer).
   • Educators: When utilizing AI-assisted instruction, there is a need to design questions that are more likely to examine students' deeper understanding and independent thinking skills, so that students do not rely on models to arrive at superficial answers.
   • Developer: When applying LLM to solve mathematical problems, the problem boundaries and solution requirements should be clarified by optimizing Prompt Engineering to reduce ineffective reasoning or "brainstorming" due to ambiguous understanding of the model.

In conclusion, the application of large-scale language models in mathematics is gradually moving from the exploratory stage to the practicalization. The future direction of model development will be to seek a better balance between simulating the flexibility of human thinking and ensuring the rigor of mathematical logic.

Notes:
The better performers in this review YiXin-Distill-Qwen-72B The model information is as follows:

• Standard version: https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B
• AWQ Quantitative Edition: https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B-AWQ
• Local Deployment Resource Requirements: 72B Standard Edition requires approximately 8 NVIDIA 4090-class graphics cards; AWQ Quantized Edition can run on 2 cards of the same class.