BoT: Enhanced Thinking: Solving Trial and Error Problems with Large Language Models

summaries

The reasoning performance of Large Language Models (LLMs) on a wide range of problems relies heavily on chained-thinking cues, which involves providing some chained-thinking demonstrations as examples in the cues. Recent research, e.g., thinking trees, has pointed to the importance of exploration and self-assessment in the selection of reasoning steps in complex problem solving. In this paper, we propose an automated prompting framework called Boosting of Thoughts (BoT) that iteratively explores and self-assesses a large number of Thinking Trees to obtain a collection of trial-and-error reasoning experiences, which will serve as a new form of prompting for solving complex problems. Starting from simple hints that do not require examples, BoT iteratively explores and evaluates a large number of reasoning steps and, more importantly, explicitly revises the hints using LLM's error analysis of them to augment the generation of reasoning steps until a final answer is obtained. Our experiments using GPT-4 and Llama2 on a wide range of complex mathematical problems show that BoT consistently achieves higher or comparable problem-solving rates than other state-of-the-art hinting methods. The source code is available at https://github.com/iQua/llmpebase的examples/BoTReasoning文件夹下获得.

1. Introduction

Large Language Models (LLMs) with an autoregressive paradigm have achieved significant performance on a variety of tasks due to their potential reasoning capabilities. The assurance of this capability in complex tasks relies heavily on Chained Thinking (CoT) cues, which provide step-by-step reasoning examples. This approach suggests that reasoning ability can be stimulated by a series of thinking, where thinking serves as an intermediate step in problem solving.

As a result, follow-up studies, particularly the Tree of Thought (ToT), have suggested ways to improve the CoT. To ensure validity, the prompts of these methods usually include human annotations for specific tasks. This reliance limits their scalability. Recent work, either utilizing LLMs for double-checking to improve answers or enhancing prompts based on feedback, has shown significant promise. Existing literature typically favors discarding invalid thinking in prompts. However, humans can usually learn continuously by carefully analyzing errors, thus gaining experience and gradually improving performance. Thus, we pose the question: can the thought generation of LLMs be freed from human annotations and mimic human problem solving for effective reasoning in a variety of tasks?

In this paper, we propose a novel framework, shown in Fig. 1, called Boosting of Thoughts (BoT), which implements a boosting mechanism, including aggregation and experience, so as to progressively improve unreliable reasoning steps (weak thinking) by learning from errors, and ultimately solve various problems. Starting from a simple hint without human annotation, BoT may get weak thinking. Through aggregation, the BoT is able to derive from them more logical and effective chains of thoughts that lead to subsequent improvements. Such guidance in our framework is achieved by adapting hints, which are detailed error reports, suggestions, and guidance for each reasoning step obtained by analyzing the aggregated chains using LLMs. As such experience builds up in the prompts, it gradually leads to stronger thinking.

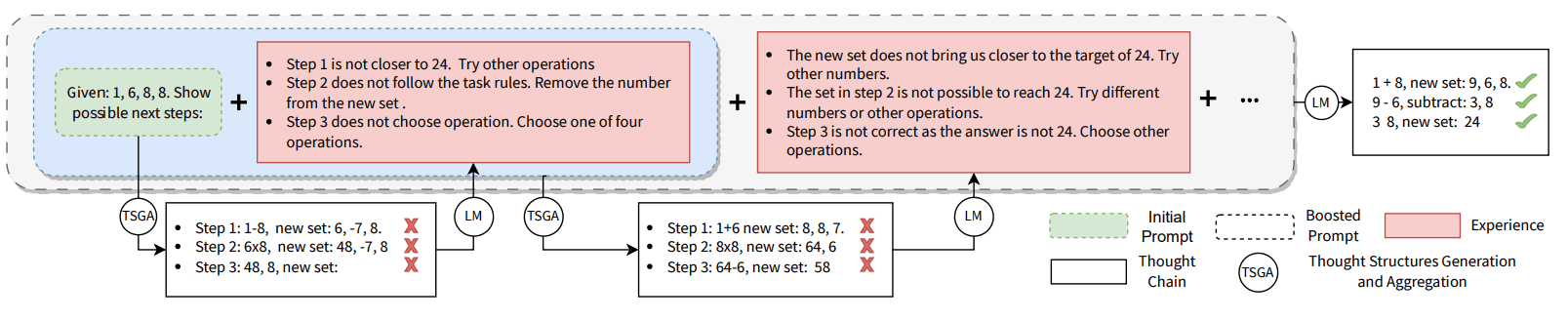
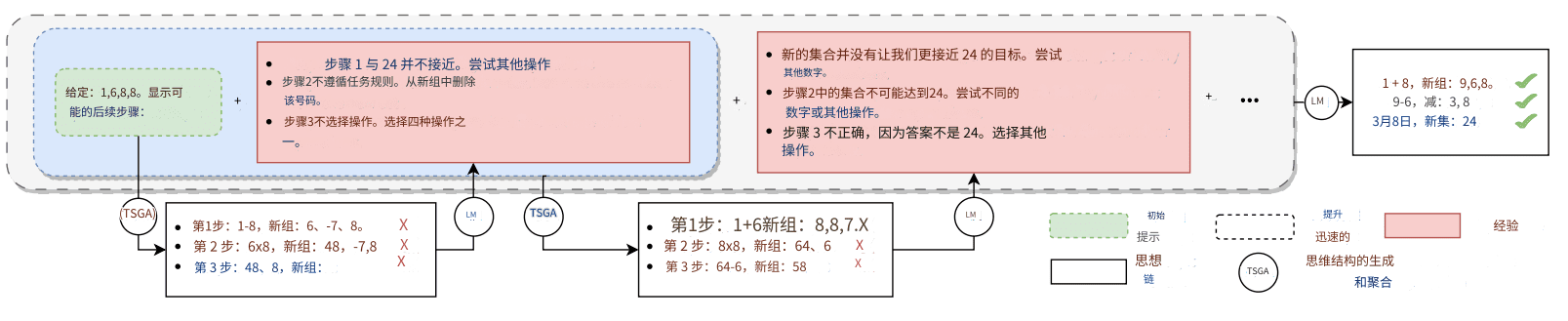
Figure 1: Enhancing cues by progressively augmenting the experience, which consists of an analysis of the generated thought chains by a large-scale language model (LLM or LM). The experience explicitly contains the chain of thoughts itself, the corresponding error reports and detailed suggestions for revising each reasoning step. Thus, those invalid thoughts marked with a red cross can also contribute to the refinement of the prompts. By accumulating experience in the prompts, the BoT can eventually generate correct thought chains starting from simple prompts. The example presented here is the result obtained by applying GPT-4 with BoT to a 24-point game task.

Specifically, BoT implements such a boosting mechanism as an experience-driven iterative process, as shown in Figure 1. In each iteration, for a given cue, BoT builds a large number of simple thought structures in parallel with LLM. We chose the tree structure, as shown in ToT, but for our boosting purposes, we modified it significantly to make it a weighted binary tree with various growth strategies. After extracting the highest scores of the root-to-leaf branches of each tree, the aggregation component of BoT was executed to aggregate them into a single chain of thoughts. This chain was then evaluated by the same LLM for lessons learned, which were added to the prompts as a guide for thought generation in the next iteration.

Our contribution can be summarized in three ways. First, unlike generating more complex thought structures using elaborate prompts, this paper shows that, relying only on simple initial prompts, weak thoughts can be incrementally improved to solve problems based on previous experience. Second, to realize this enhancement mechanism, we propose a novel framework called Boosting of Thoughts (BoT), which performs an experience-driven iterative process. Since it starts with simple prompts, BoT can be extended to a variety of tasks. While ensuring validity, BoT is fast because it builds simple thought structures in parallel and converges to a solution after a few iterations. Finally, we evaluated the performance of BoT on complex math problems using GPT-4 and LlamaV2. Relying on GPT-4 OpenAI (2023) and LlamaV2 Touvron et al. (2023), we evaluated the performance of BoT on complex math problems. Problem solution rates show that BoT, which employs a binary tree mindset structure, significantly outperforms the current state-of-the-art on GSM8K and AQuA, while achieving second-best results on other datasets. In particular, BoT outperforms the leading method ToT by 9.7% on the new challenging task Game of 24. Our BoT thus demonstrates that LLMs can maintain high performance across a wide range of tasks even without human annotations by augmenting cues, accumulating error analyses of ineffective chains of thought, and making corresponding suggestions.

2. Related work

multistep inference.. Prominent work on Chained Thinking (CoT) prompts suggests that the stepwise reasoning behavior of LLMs can be stimulated by providing intermediate reasoning steps in each problem prompt. Recent work, Tree of Thought (ToT) converts the sequential reasoning process into a tree structure in which each thought (node) may consider previous reasoning paths to generate multiple next thoughts. Through backtracking and extended exploration during the reasoning process, ToT performs well on problems that challenge even GPT-4. Considering its high capacity, the underlying thinking structure of BoT largely utilizes the thinking tree structure of ToT. And, due to the boosting framework, the tree structure generated by BoT in each iteration is binary and shallow, rather than ToT's complex tree in which each node corresponds to a large number of child nodes. However, the underlying structure is not limited to ToT. in contrast, BoT is flexible because the underlying thinking structure can be ToT, GoT Besta et al. (2023), or CR Zhang et al. (2023b), where Thinking Graphs (GoT) Besta et al. (2023) is the most recent work that extends the thinking structure to a graphical format. In this paper, we will focus only on ToT as the underlying thought structure and leave the use of GoT as future work.

auto-suggestion.. Releasing humans from task-specific cues attracts a lot of attention. In order to ensure the reasoning ability of LLMs, traditional CoTs rely on human a priori knowledge to manually generate task-specific demonstrations as prompts. However, zero CoT showed that even without hand-crafted examples, LLMs were able to reason step-by-step to obtain accurate answers by simply adding "let's think step-by-step" to the prompt. These insights spawned a series of follow-up studies.Auto-CoT eliminates manual effort by retrieving the available chains of reasoning generated by zero CoTs.Active-Prompt first measures the uncertainty of a set of questions, and thus selects only uncertain questions to be annotated by a human.ToT also reduces manual effort but, for each task, it still requires the expert to provide in the prompt the possible next thinking. Our paper introduces a novel approach to manual cue-free boosting. Starting with a simple cue, BoT iteratively enhances it based on LLMs analysis of the thinking.

Tip engineering through feedback. Much attention has been paid to utilizing LLMs' responses to input prompts as feedback for further prompt revisions. Those who continuously revise a given cue based on the LLMs' evaluated description of the output aim to obtain accurate answers. Using a high-level idea similar to our paper, SELF-REFINE proposes an iterative self-refinement algorithm that allows LLMs to generate feedback to further refine their output.PHP simplifies this process by adding the solution of the previous answer directly as a hint to subsequent hints.REFINER, also related to our paper, evaluates each inference step as a feedback to produce a more reasonable one. Another series of studies explored integration, specifically utilizing boosting mechanisms Freund et al. (1996) refined hints through feedback from a set of examples. They adapted the prompt by adding a few uncertain examples to the previous iteration, or relied on a feedback-reflection-refinement process.APO Pryzant et al. (2023) iteratively refined prompts, using the performance of the previous prompt to form an optimized natural language. These works demonstrate the effectiveness of boosting mechanisms in cue engineering. However, our work is the first to emphasize the importance of error analysis in enhancing hints to generate effective inference chains. The proposed BoT extends this insight to an automated prompting framework by iteratively accumulating a collection of trial-and-error reasoning experiences.

3. Enhanced thinking

3.1 Background

The goal of cue engineering is to design a cue I containing multiple language sequences to be used as input through this cue, and a pre-trained Large Language Model (LLM) denoted as pθ, parameterized by θ, which gives access to the desired language sequences y. Thus, the standard Input-Output (IO) can be expressed as y ∼ pθ (y|I (X, Q)), where I (-) denotes the cue wrapping task instruction X and the the corresponding question Q.

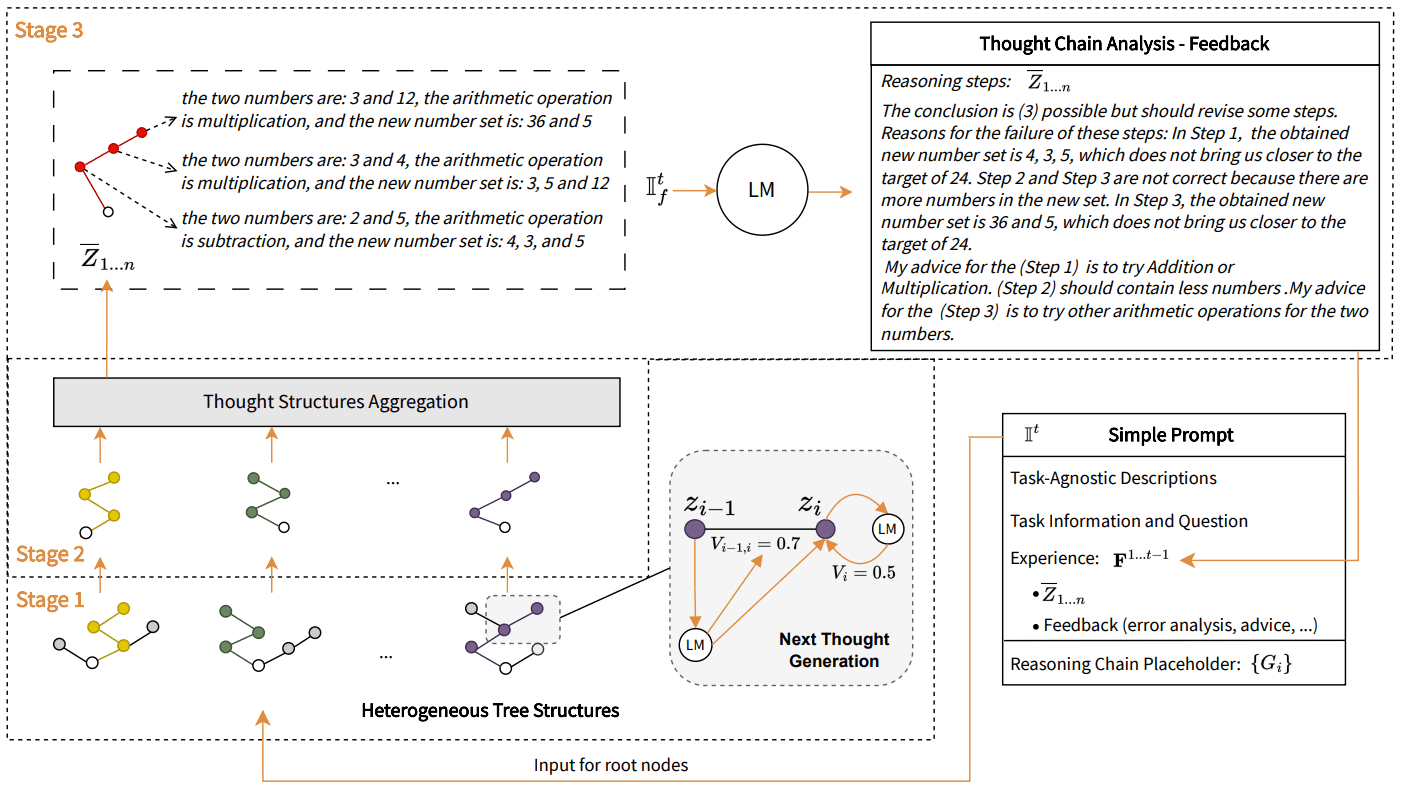
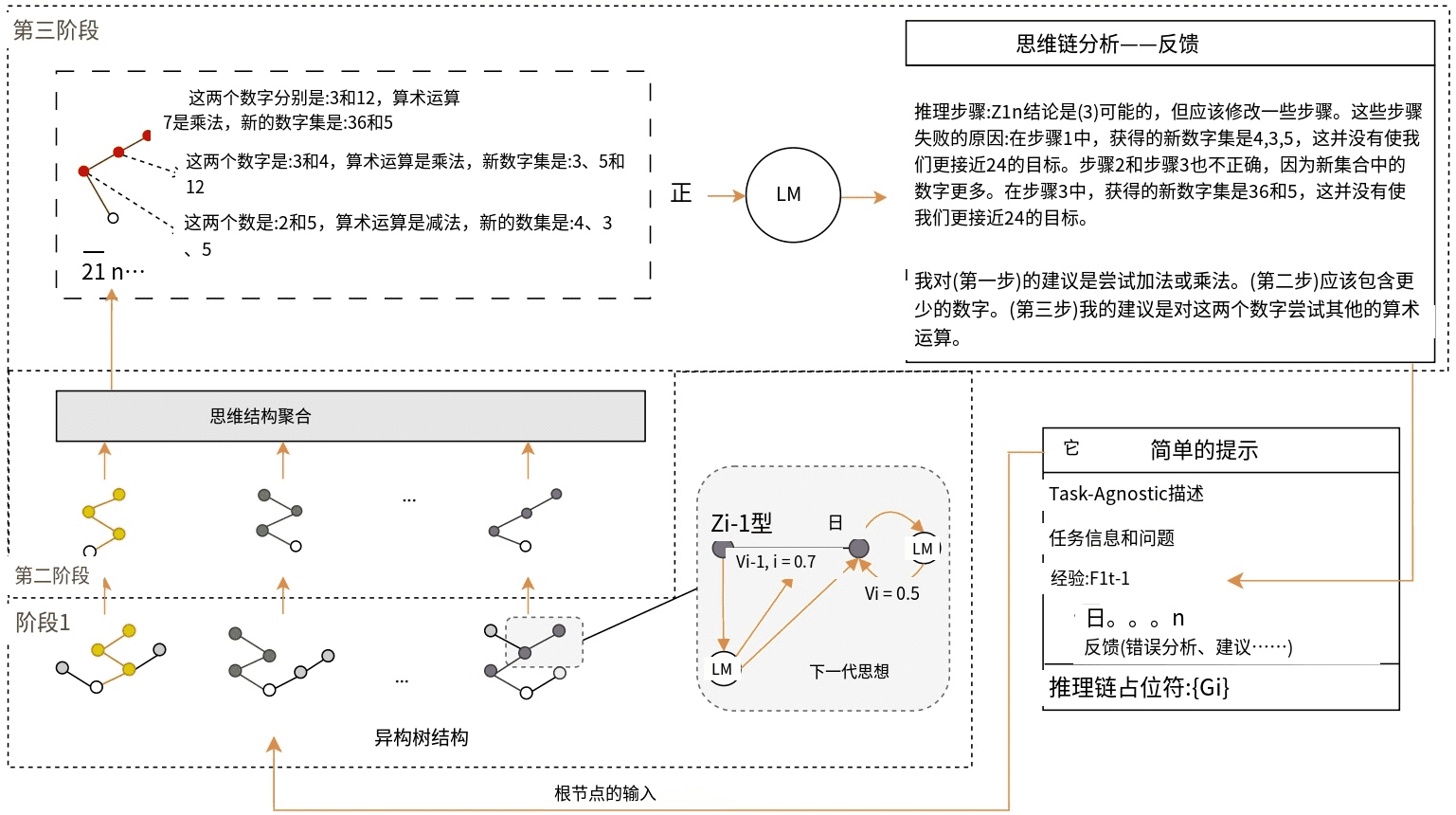
The image depicts a visual representation of the thinking process behind problem solving using arithmetic operations. It is divided into three main parts: thought structure aggregation, next thought generation and thought chain analysis - feedback.

Thought structure aggregation represents the combination of different stages of reasoning (Stage 1, Stage 2, Stage 3), each of which has its own number structure that describes the steps taken to reach a conclusion.

Next Thought Generation focuses on a specific stage, showing how to predict the next thought using a Language Model (LM), taking into account previous experience (represented by the vectors Vi-1 and Vi) and generating a new chain of reasoning.

Thought Chain Analysis - Feedback provides a detailed analysis of the reasoning steps taken, pointing out possible errors and offering suggestions for improvement. It critiques the steps by evaluating whether they bring the solver closer to the target number (in this case 24) and suggests other arithmetic operations to try.

In addition, there is a brief cueing section that outlines the inputs to the thinking process, which include task-unspecific descriptions, task information and questions, and experience gained from a previous chain of reasoning that acts as a placeholder for generating new thoughts.

Overall, the picture depicts a methodologically sound approach to reasoning and problem solving that utilizes language models to iteratively optimize and improve thought processes.

Specifically, let's look at the Thinking Structure Aggregation section. In this section, we can see three stages, each with a colored heterogeneous tree structure. In stage 1, we see some arithmetic operations, and the trend is "vi1 - 0.5". In stage two, we see more arithmetic operations and the trend is "vi2 - 0.6". Finally, in stage 3, we see a sequence of arithmetic operations with a trend of "vi3 - 0.4".

For the next thought generation section, a specific thought node, Zi, is tracked and its accompanying weight, vi, is shown, indicating the importance of these thoughts in the context of problem solving.

In the Thought Chain Analysis - Feedback section, several reasoning steps are shown (Z1,Z2.... .Zn) and evaluated. For each of these steps, "R1:-3, try +", "R2:+3, try -", and "R3: -1, try ×" represent feedback on the particular step feedback, evaluation of reasoning, and suggestions on how to improve.

In the Simple Hints section, some input hints can be seen, such as "Task non-specific description 'Play a number game'", "Task message 'Try to use the four numbers 1,3,4 ,6 (each number can only be used once) and arithmetic operations (addition, subtraction, multiplication, and division) to arrive at the number 24'" as well as the previous reasoning chain Gi.

The result of this pipeline generates a new thought process for the next reasoning.

This diagram represents the logical flow of a thinking process and reasoning methodology, showing how a language model (LM) as well as feedback/suggestion mechanisms can be used to move forward with the problem, with critical feedback and evaluation at each step.

Figure 2: Reveals an overview of the BoT process in each iteration. In order to present how an increase in effectiveness can be achieved in this empirically based iterative process, we show the exhaustive intermediate results obtained in one type of experiment on ChapGPT-4 on the 24-point game dataset. After being given the problem Q: "The four numbers provided are: 2, 4, 5, 5", the BoT proceeds through three consecutive phases. Using the simple cue It as input, Thought Structure Generation (Stage 1) outputs a large variety of heterogeneous tree-shaped thought structures. In Thought Structure Aggregation (Stage 2), they are integrated into a chain of thoughts z1.... .n, followed by analyzing this chain of thoughts in Stage 3 in order to generate experiences that can be used to further reinforce the cue.

The prompts can be designed to be more elaborate in order to guide LLMs to solve the problem in a step-by-step manner. Each intermediate reasoning step is denoted as a zi (also known as a thought).The CoT provides a handful of examples, each of whose answers contains a chain of thoughts z1.... .n. This leads to y ∼ pθ y|I [z1 . .n]N , X, Q , where N is the number of examples included in the prompt.

Instead of preparing examples in the bootstrap, a more flexible approach is to design the bootstrap to guide the LLM to gradually generate the thought zi in the reasoning process. this can be formalized as zi ∼ pθ (zi |I(z1.... .i-1, X, Q)). Finally, the solution is formalized as y ∼ pθ (y|I(z1.... .n, X, Q)).
Representatively, ToT Yao et al. (2024) further extend this sequential reasoning step into a tree structure in which C next thoughts can be generated. Thus, the structure of a reflection can be either chained or tree-like.

3.2 Framework

Existing literature aimed at generating cues with correct CoT examples or designing fine-grained thought generation structures suffers from three limitations. First, invalid thinking in these approaches is typically ignored or discarded. However, humans, especially non-experts, and in particular in other domains, rely on analyzing previous errors to gather more experience to perform correctly in the next attempt. Second, they are less scalable because for each task, examples for generating the next thought, e.g., I (z1|z0, X, Q), need to be provided in the cue. Finally, the generation of thought structures (e.g., the tree structure of Yao et al.) is too complex to explore more reasoning steps in order to obtain a better solution. This is mainly due to the fact that the obtained solutions may not be able to be revised further.

In this paper, we argue that prompts can be enhanced by continuously collecting LLMs' analyses of these invalid thoughts (faulty reasoning steps in the chain of thought). Thus, even a simple cue, e.g., I (X, Q), which may lead to invalid thinking, can be improved incrementally by relying on such analyses in order to obtain strong thinking that will lead closer to a solution.

We propose a method calledBoosting of Thoughts (BoT)'s automated cueing framework, which enables cue enhancement through an experience-driven iterative process from thesimplerthe start of the cue. To summarize as shown in Fig. 2, each iteration t of BoT consists of three phases. The thought structure generation phase is able to make full use of the inference chains generated by the LLMs with the input prompts as It. In the second phase, these thought structures are aggregated into an inference chain that will be analyzed by the LLMs in the third phase to generate feedback containing error reports and detailed revision suggestions. The aggregated chain of reasoning is combined with the feedback results to form a new experience, denoted Ft. Thus, by accumulating these experiences over the iterations F1.... .t, the cue is enhanced.

Simple Tips. For any task, at iteration t = 0, we create a simple initial cue I0 ≡ {S, X, Q, F0, {Gi}}, where S denotes the task-independent description, while X and Q denote the task information and question, respectively. The empirical part of the prompt is denoted F0 and should be empty at the beginning. {Gi}} is a placeholder that will be filled in when constructing the thought structure. In other words, when generating the next thought zi, {Gi} will be replaced with the previous thought chain z1.... ,i-1.

Thought Structure Generation. After collecting the experience Ft-1 , the cue for iteration t can be It ≡ {S, X, Q, F1, ... ,t-1, {Gi}}. Based on this cue, BoT generates in parallel M thought structures.BoT is essentially capable of containing any thought structure, e.g., chained Wei et al. structures or tree-like Yao et al. structures. Considering the exploration of reasoning steps and experimental results, we investigated tree-like thought structures. However, BoT introduces two novel modifications that make it more suitable for the lifting framework.

• weighted binary tree. Using simple cues in each round, BoT constructs weak minds with simple structures and low complexity because they can be further revised in the boosting mechanism. Thus, each thought structure of BoT is a shallow weighted binary tree. For simplicity, we keep the symbols z1.... .i-1 to denote a thought from the root node to the parent of node i. In addition to providing each node i with a thought zi and its thought evaluation score Vi ∼ pθ (z1.... .i, Ia, X, Q), we also include an edge score Vi-1,i ∼ pθ (zi-1, zi, Ie, X, Q) between a child node and its parent node, where Ia and Ie refer to the guiding descriptions of the thought and edge evaluation, respectively. vi-1,i denotes the confidence level of the LLMs in generating this reasoning step. Thus, the BoT's next thought generation in this tree structure is formalized as pθ (zi| (Vi-1,i, Vi, It, X, Q)).
• tree heterogeneity. Unlike ToT, which seeks to find solutions in a large complex tree, BoT aims to build highly heterogeneous tree-like thought structures. Thus, to increase heterogeneity, thought structure generation employs different tree growth strategies, such as layer-by-layer and leaf-by-leaf growth. The former emphasizes exploration but utilizes less Chen & Guestrin (2016), while the latter is the opposite Ke et al. (2017). Thus, the leaf-by-leaf strategy tends to continue reasoning from the current best thought to a better final thought compared to the layer-by-layer growth, but it also tends to get monotonous chains of reasoning. In addition, LLMs with different temperature and Top p settings were applied.Finally, we used a small maximum depth value in BoT and labeled a node as a leaf when Vi-1,i and Vi values were outside the specified range [0.3, 0.8].

thought structure polymerization. After obtaining M thought structures, the BoT aggregates them into a chain of thoughts, denoted z1.... .n. To accomplish this, for each thought structure index m, the BoT first selects the chain with the highest evaluation score, i.e., zm 1... .nm := arg maxz1... .n∈Zm ∑i=1 Vi + Vi-1,i, where Zm denotes the set of all thought chains of the mth tree. Subsequently, there exist two strategies to obtain z1.... .n.

• Best Priority Aggregation.BoT depends on arg maxz1.... .n∈{Zm}M m=1 ∑i=1 Vi + Vi-1,i, to select the best of the M thought structures as z1... .n. This algorithm is fast, but may lead to an illogical chain that is difficult to guide subsequent improvements.
• Greed Aggregation. the BoT is allowed to perform a greedy search on {Zm}M m=1 in order to assemble a new chain of minds that may not exist, but may be globally optimal. Starting from the initial thought, usually the root node of the tree, the BoT obtains z1 = arg maxzj ∈ {zm 1 } M m=1 Vj + Vj-1,j. Subsequently, in order to obtain zi, the BoT searches for all the thoughts in {Zm}M m=1 whose previous step was zi-1.

chain of thought analysis. To gain insight into what should be adjusted to enhance the cue to generate better thinking, the BoT utilizes the LLMs' ability to self-evaluate z1.... .n. Specifically, with the cue It f (z1 . .n, X, Q) as input, the LLM outputs a feedback paragraph containing information about this chain of thoughts z1.... .n with a problem report and detailed suggestions. This feedback will be added to F1,... ,t-1 as a new experience in thought generation, resulting in F1,... ,t.

Iterative refinement.. Through the boosting mechanism, F1,... ,t is used to iteratively enhance the cue, resulting in the cue It+1 for the (t+1)th iteration ≡ {S, X, Q, F1,... ,t, {Gi}}. As the iteration proceeds, F1,... ,t may contain many typical, illogical chains of thought, as well as those closer to the solution, all with well-defined analytic results. Thus, even when starting with a simple hint, BoT iteratively refines this hint to produce the correct reasoning steps that lead to an accurate solution. After T iterations, we use It+1 as the input hint to the LLM for the final answer.

4. Experimentation

data set. Experiments were conducted on benchmark datasets containing a variety of mathematical problems, including MMLU, SVAMP, GSM8K, AQuA, and MATH.In addition, we included a challenging mathematical reasoning task, Game of 24, where the goal was to obtain 24 in 1 equation using four numbers and basic arithmetic operations (addition, subtraction, multiplication, and division).Thus, the solution includes 3 intermediate steps.

competition. In addition to the benchmark method Standard Input-Output (IO), comparative methods include Chained Thinking (CoT), CoT-SC, and Complex CoT, where the input prompts contain a handful of examples (8) and human annotations. In addition, BoT is compared with related work such as thinking trees (ToT), progressive prompts (PHP), and state-of-the-art CSVs.We conducted experiments using GPT-4 and Llama2.GPT-4 was accessed via the OpenAI API, while the llama2-13b-chat model was downloaded from MetaAI to conduct experiments locally. To construct a heterogeneous tree-thinking structure, BoT randomly selected temperatures in the temperature range [0.2, 0.4, 0.6, 0.7, 0.9, 1.1, 1.5] and top p range [0.1, 0.3, 0.5, 0.7, 0.9].

set up. Unless explicitly stated, in all experiments, BoT performs T = 10 iterations and constructs M = 15 thought structures, each of which is a weighted binary tree, as this tends to yield the best results. In addition, for these benchmark datasets, we set the depth of the tree to 5, while the corresponding depth in Game of 24 was 3. BoT + CoT means that our simple cue includes 5 examples from CoT. In ablation studies, when there is no cumulative experience in the BoT, 8 CoT examples will be provided in the prompt.

metric. We measure and report the results of all experiments in terms of the resolution rate of the task (%). From the BoT output zT1.... .n from the target answers, we set up formatted descriptions of the answers specifically for LLMs. For commonly used datasets, the format of the answer was set to "The answer is:". For the game of 24 points, we use "Step index, current set:, two numbers selected:, operation:, new number from operation:, remaining numbers:, new set of numbers:". Then, we compare the numbers in the new set of numbers directly with the ground truth. Referring to ToT Yao et al. (2024), we use the solution rate counted from 100 difficult games as a metric.

4.1 Main results

The main experimental results are summarized in Table 1 and Figure 3, where we provide insights into the overall performance of the BoT. Our findings show that the proposed BoT by boosting the mechanism 1). Obtaining competitive problem solving rates independent of human annotations in most datasets; 2). Achieves new state-of-the-art when providing CoT examples. However, experimental results also show that BoT relies heavily on experience and is therefore very sensitive to the capabilities of LLMs.

Specifically, in Table 1, BoT starts with simple initial hints and eventually outperforms the current state-of-the-art CSV by 0.11 TP3T in terms of solution rate on GSM8K, which heavily relies on the GPT-4 code interpreter. Considering AQuA, BoT outperforms SOTA by 2.51 TP3T. this shows that by adding error analysis and suggestions to hints without relying on human annotations, LLMs can perform well on complex reasoning. The main reason for this is that simple hints can be improved gradually by accumulating previous experience to solve problems accurately. After the CoT examples were included in the prompts, BoT+CoT was 1.3% higher than SOTA.We argue that CoT examples can be regarded as successful cases in experience, which directly guide the generation of subsequent thought structures in BoT. Thus, through iterative improvement, BoT+CoT reached a new SOTA.Meanwhile, BoT and BoT+CoT, especially BoT, were at least 181 TP3T lower than SOTA on MATH.This observation implies that weak LLMs may not work well with BoT due to the low ability of LLMs to analyze the reasoning chain for valid experiences.

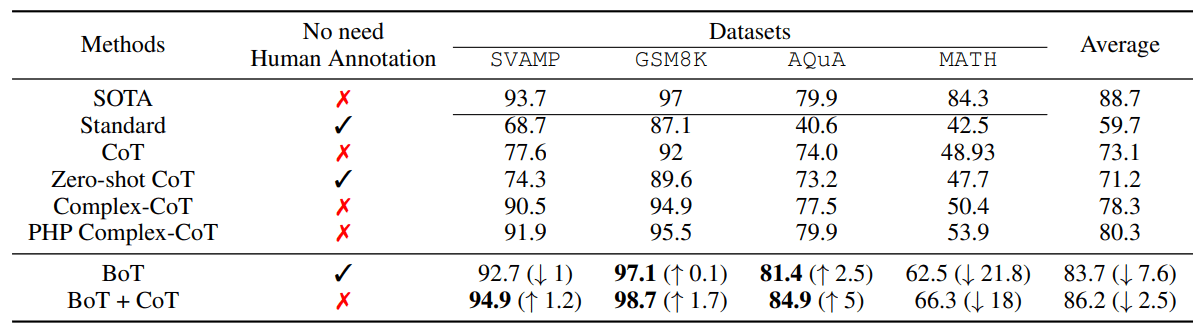
Table 1: Using BoT in conjunction with GPT-4 significantly improves performance even without manual labeling.
When BoT's simple initial cue includes CoT examples, the corresponding BoT+CoT approach exhibits higher solution rates. Our framework is also compared to leading approaches such as Model Selection by Zhao et al. in 2023, PHP by Zheng et al. in 2023, and CSV by Zhou et al. in 2023, achieving state-of-the-art (SOTA) performance on the SVAMP, AQuA, and GSM8K & MATH datasets, respectively.

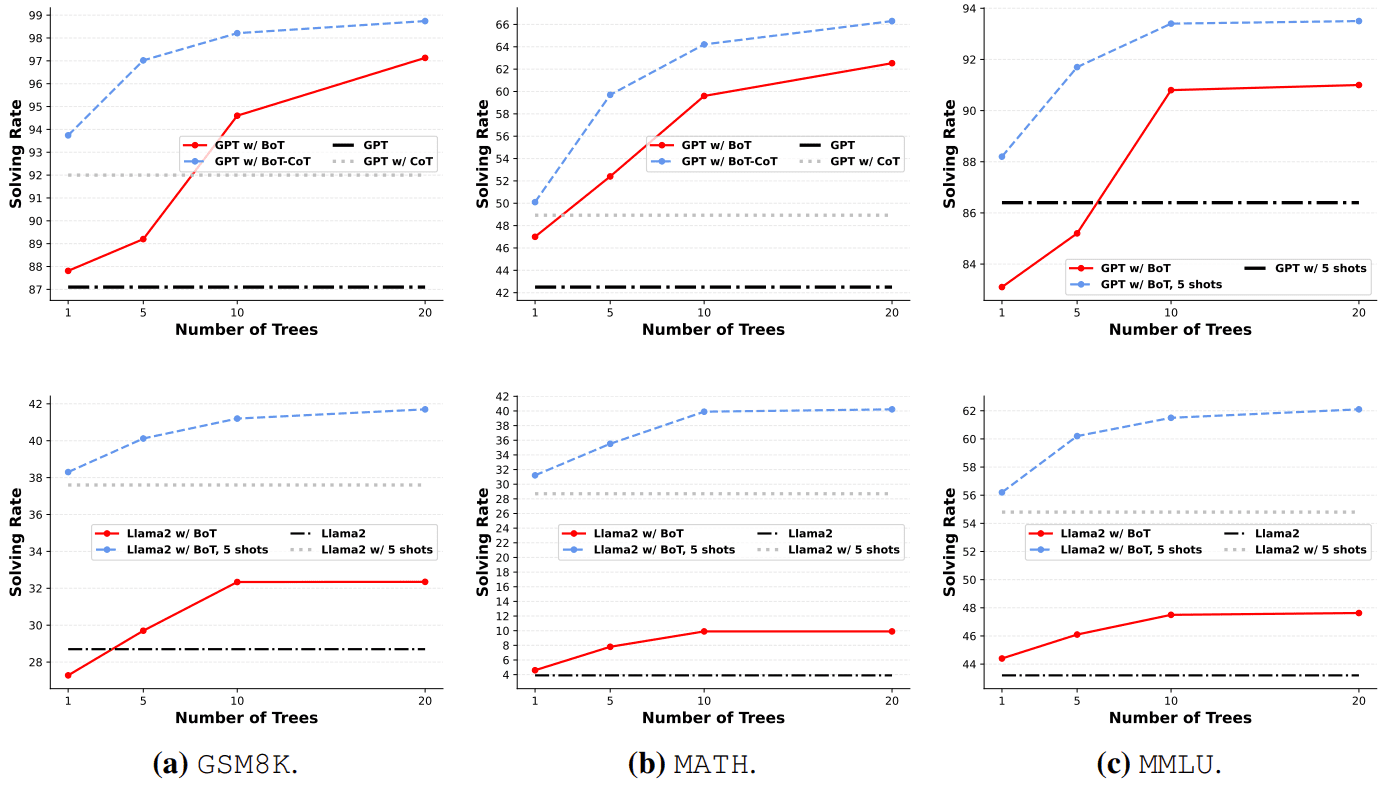
Figure 3: BoT and BoT+CoT are utilized to evaluate the problem solving rate of GPT-4 OpenAI with Llama2 Touvron et al. in 2023.

As can be seen in Fig. 3, GPT-4 and Llama2 improve the average performance of 11.61 TP3T and 4.41 TP3T on average across the three datasets under BoT conditions, respectively. These two figures show a clear trend that BoT and BoT-CoT perform similarly when LLMs are more powerful, as shown in Figure 3. In addition, their performance shows a similar upward trend as the number of trees changes from 1 to 20. Due to the weaker Llama2, BoT cannot benefit from its analysis to perform an experience-driven iterative process, especially shown in Fig. 3(a). When provided with valid success stories, i.e., 5 tests, the BoT can still help Llama2 solve more problems than the baseline through incremental improvements, albeit with limited improvements.

4.2 24-point game

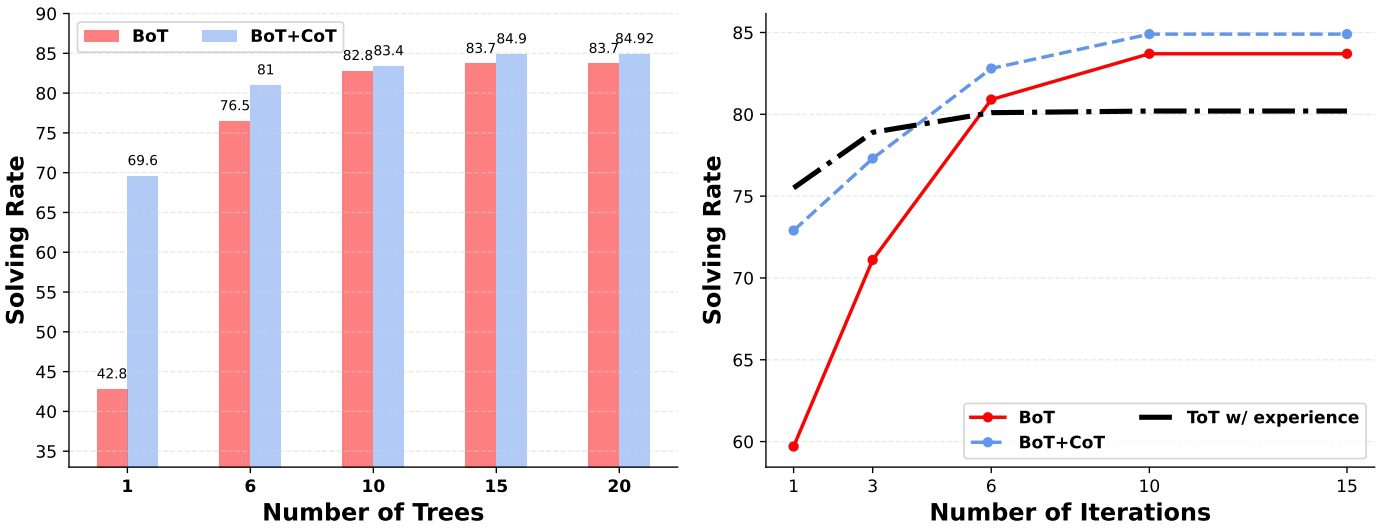
Fig. 4: Comparison of the three methods in different number of trees and iterations.

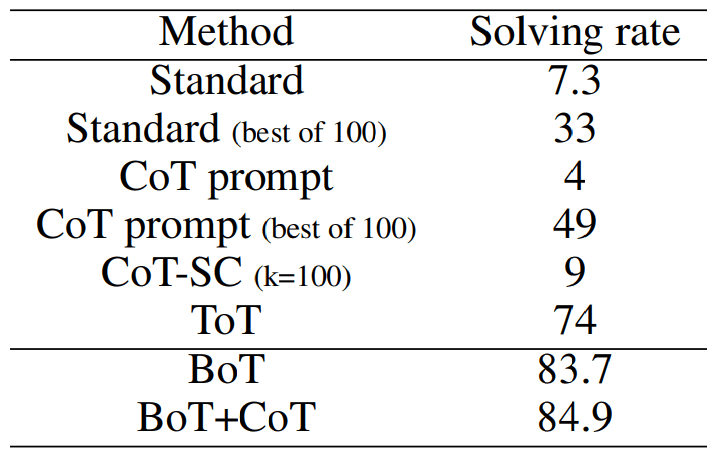
Table 2: Setup of the different methods in the 24-point game following the setup in ToT Yao et al. (2024), whose results are shown here.

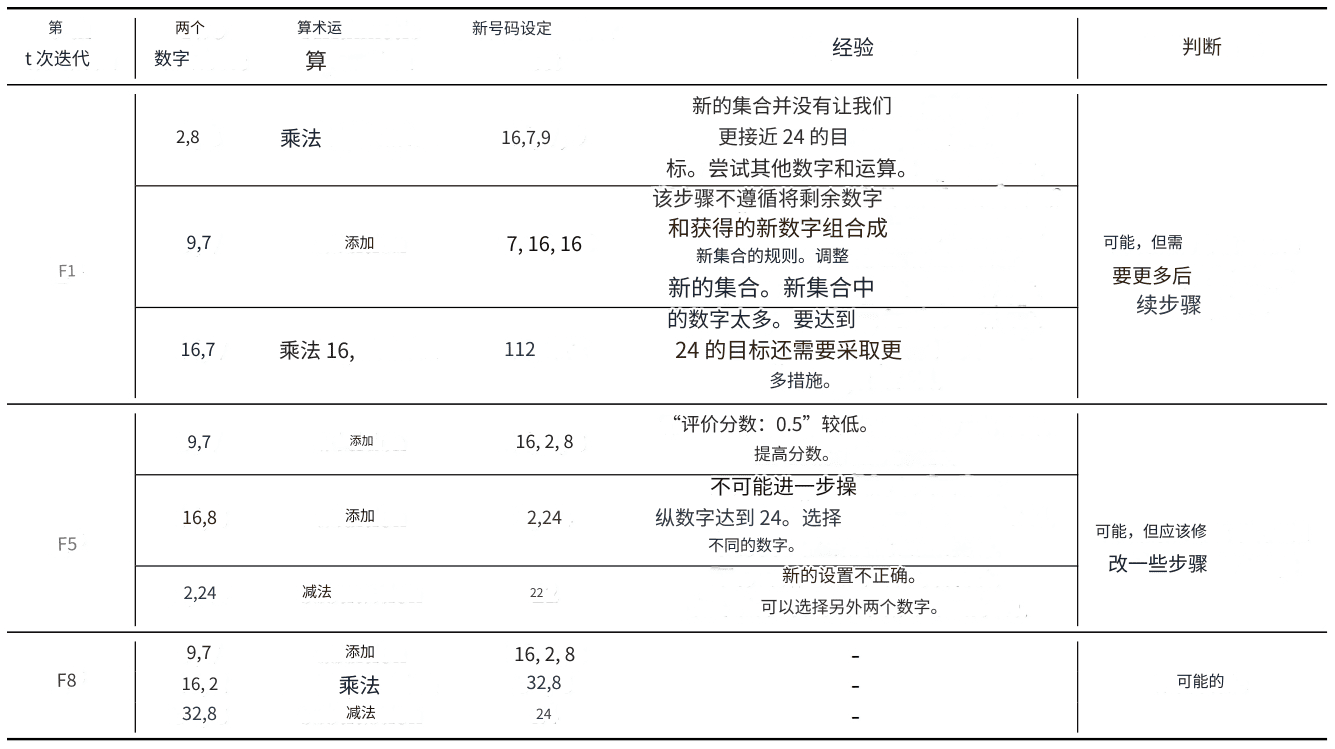
Table 3: Demonstrates the thought process that was accumulated and the experience that was able to be gained during the 1st, 5th, and 8th iterations. The four values given are: 2, 7, 8, and 9.

Due to the difficulty of the Game of 24 problem, both GPT-4 and Llama2 performed poorly on this task, even when combining the CoT and CoT-SC methods.The Llama2 model was unable to follow even the correct rules for solving the problem, making the solution rate even lower. Especially when applying BoT, which relies on experience, all the results of Llama2 are lower than 5% without significant improvement. Therefore, we only report the performance of BoT with GPT-4. To maintain a fair comparison, we follow the setup proposed by ToT Yao et al. (2024).

As shown in Table 2, the BoT without human annotations outperforms the ToT that relies on an example to show all possible next steps by 9.71 TP3 T. In addition, the BoT+CoT that contains 5 CoT shots outperforms the BoT by 1.21 TP3 T. The performance proximity between the BoT and the BoT+CoT is attributed to the boosting mechanism, which incrementally revises the weak mindset, as discussed in Subsection 4.1. Using an experience-driven iterative process, BoT exhibits enhanced performance when the number of trees M and iterations T increases. As shown in Fig. 4, BoT is more dependent on M and T than BoT+CoT because it needs to gather experience from a better chain of thoughts or longer iterations. Another observation is that when ToT is enabled to operate with experienced cues, the problem solving rate increases from 72.51 TP3T in the first iteration to 80.21 TP3T in the 10th iteration.This suggests that experience-an analysis of previous chains of reasoning-can be used by LLMs to significantly improve the solving rate. However, the score obtained by ToT is still 3.51 TP3T lower than that of BoT. this is attributed to the fact that the aggregation phase of BoT will produce the most representative chain of reasoning in the current iteration, thus channeling more meaningful experience to enhance the cue. We verified this in the ablation study section.

To better demonstrate how BoT learns from mistakes and previous suggestions, we show in Table 3 that GPT-4 is able to avoid previous mistakes and generate more specific suggestions as the number of iterations increases, eventually leading to the correct solution. In the first iteration, due to simple hints, the LLMs even made a mistake in following the task rules because the new set was wrong in step 3. After analyzing it, it made the correct suggestion for this error. However, the analysis of the initial iteration was vague, e.g. "try other numbers and operations". After five iterations, the BoT aggregated multiple such analyses, resulting in more effective hints that led the LLMs to choose the correct numbers 9 and 7. In addition, the suggestions were more specific and useful. For this correct choice, the suggestion was to increase the evaluation score accordingly. By accumulating such experience, BoT gradually refined the hints, eventually generating the correct solution directly in the 8th iteration.

4.3 Ablation studies

Table 4: Comparison of GPT-4 with different BoT variants utilized on the 24-point game and the AQuA dataset.

All aggregation strategies produce high solution rates when problems and suggestions are pooled in an "additive" fashion. Maintaining a complete experience is particularly important for revisionist thinking, especially for the AQuA dataset, which covers a wider range of mathematical reasoning problems. However, BoT(No), which uses all the reasoning chains of the spanning tree directly without aggregation, performs the worst in all contexts, especially when the cumulative type of experience is "cumulative." BoT builds 15 trees per iteration, and putting all of them together in a cue may obscure important information, not to mention most of the information that is not available in the cue. Such experience may be invalid or harmful.

Getting advice is more critical to triggering thinking than anything else.. In all the examples mentioned in Table 4, the BoT variant that treats suggestions as experience achieves the highest solution rates. For example, in the same "additive" type case, without suggestions in the experience, the performance slipped by more than 101 TP3T and 201 TP3T in the "24-point game" and AQuA, respectively. on the other hand, incorporating problems in the experience can be used as a complementary tool to help improve the performance. BoTs with suggestions can only achieve optimal resolution rates if they are paired with problems. For example, in AQuA, the solution rate of BoT (greedy method) increased by 4.41 TP3T.

For performance reasons, Greedy Rally may be the only option that is necessary. As opposed to the highest priority approach of selecting one, or sustaining all, of the existing thought chains, greedy agglomerations can adaptively merge the tree structure into a better thought chain, which may not occur in the current iteration. In this way, LLM can perform a meaningful analysis of a more robust chain of thoughts, and as a result, generate important lessons to enhance the cue. In AQuA, which contains more math problems, this number even reaches 101 TP3 T. Furthermore, as we discussed in Figure 4, while ToT has a similar experience-driven boosting mechanism capable of reaching 801 TP3 T, it still lags behind BoT. this may be due to its inability to perform greedy clustering in its single tree structure.

5. Conclusion

In this paper, we validate that a simple cue can be used to solve a complex task by gradually accumulating error analyses of the thoughts it generates. We propose a novel framework called Boosting of Thoughts (BoT) that enables this gradual cue augmentation through an experience-driven iterative process to generate effective chains of thoughts. A simple tree-like chain of thoughts generated through iterative exploration and self-assessment allows a simple initial cue to be incrementally augmented by a series of trial-and-error reasoning experiences that lead to an accurate solution. Our extensive experiments show that BoT is able to achieve state-of-the-art performance on multiple benchmark datasets and outperforms other leading methods on the challenging mathematical reasoning task of Game of 24.

A BoT of basic cues and reasoning processes

A1 BoT for the thought generation component

This section mentions the basic hints used for the reasoning generation of the proposed Boosting of Thought (BoT). For specific related details, you can visit the example file of the source code: /examples/BoostingOfThought/BoT reasoner.py.

System Tip:

You are an expert in math problems. Perform step-by-step problem-solving reasoning by learning from a series of trials and error reasoning experiences. Such trial-and-error reasoning experiences specifically include error reports, as well as detailed suggestions on how to modify previous reasoning steps. Before generating new reasoning steps, it is important to review these listed experiences as a way to avoid repeating mistakes while using the correct steps to generate better reasoning steps for problem solving.

 

System prompt S.

You are an expert on mathematical problems. Perform step-by-step reasoning
toward problem solving by first learning from an ensemble of trial-and-error reasoning experiences.
Such trial-and-error reasoning experience specifically contains error reports and detailed advice on
How to revise historical reasoning steps. Always recall these listed experiences before generating a
new reasoning step, thereby avoiding making the same mistakes and reusing correct steps to generate
better reasoning steps to solve the task.

Generate a prompt for the next thought:

f"""

{Mission Alert} \n

First, recall the previous reasoning experience: \n\n

 

{Experience}\n\n

 

Please introduce the next possible reasoning step, and there can only be one. This reasoning step should be used as a sequential successor to the following ordered steps and should be accompanied by a corresponding evaluation score (higher scores indicate a higher likelihood of completing the task):\n\t

{chain hint}\n\n

 

Based on the above antecedent inference steps (or ignore them if the above space is empty), generate a unique next possible step based on the task rules. (IMPORTANT: Please only generate the next possible reasoning step for a given step.)

"""

f"""{task prompt}. \n First of all , Recall historical reasoning experience : \n\n {
experiences} \n\n Please make one step of reasoning to generate only one next
This next reasoning step is the sequential step from This next reasoning step is the subsequential step from
the following ordered previous steps , accompanied by their evaluated scores (A
higher score means the reasoning step is more likely to complete the task .) : \n\t{
chain prompt}\n\n Based on listed previous reasoning steps (ignore them when the
above space is empty), generate one single next possible step following the Task
rule . (Emphasize: Please generate only one single next possible reasoning step of
the given steps .) """

The task prompt contains the X and Q of the task, and the historical experience is F1.... The "chain hint" part is {Gi}, which is a placeholder that, when the current thought zi is performed, is replaced by the previous series of thoughts z1...,i-1. ,i-1.

For tips on thinking about assessment:

f"""

{Mission Alert} \n\n

Below are the reasoning steps in order, accompanied by their respective assessment scores. (A higher score means that the step is more likely to complete the task.) \n

{chain hint}\n

{Think}\n\n

What is your score for evaluating how logical, correct, and helpful these reasoning steps are to the final solution? Please choose one of [0.1, 0.3, 0.5, 0.7, 0.9, 1.0] as the score, with higher scores indicating better reasoning steps. The score should be placed after ' Evaluation score:' for the user to read.""""

 

f"""{task prompt}. \n\n Below are the generated reasoning steps , presented in order ,
accompanied by their evaluated scores (A higher score means the reasoning step is
more likely to complete the task .) :\n{chain prompt}\n{thought}\n\nWhat is your
evaluation score for the logic , correctness , and benefit to reaching a final
solution for these reasoning steps ?
0.7, 0.9, 1.0] as the score , where a higher score means better reasoning steps . The
score should be placed after ' Evaluation score :' for users to read .""""

In this case, thinking is the thinking Zi that is currently going on.

A2 BoT for experience generation component

To generate feedback on aggregated chains, LLMs use the following basic prompts. For more information, also visit the source code examples/BoostingOfThought/BoT commenter.py.

System Prompt S: You are an AI expert reviewer for Math Answers working on evaluating the chain of reasoning generated to solve a math problem. Please evaluate each reasoning step of this reasoning chain by providing a detailed analysis to determine whether the current step is a logical inference from the previous step and whether the reasoning step contributes to the correct solution. For each incorrect reasoning step, please provide an error report and corresponding suggested revisions. For each correct reasoning step, provide a description of the recommendation or rejection.

System Tip:

Your role is that of a skilled AI math answer reviewer focused on evaluating the reasoning process of solving math problems. You need to judge each reasoning step through an exhaustive analysis to see if it is based on the logic of the previous step and if this step contributed to finding the correct answer. If you encounter an incorrect reasoning step, you need to give suggestions and options for modification. For correct reasoning steps, you need to affirm or give different options.

 

System prompt S.

You are an expert AI checker for math answers, dedicated to evaluating the
reasoning chain generated towards addressing the mathematical problem. Judge each reasoning
step of this reasoning chain by providing detailed analyses on whether the current step is a logical
inference of the previous step and whether the reasoning step is beneficial to the correct solution.
Provide advice and suggestions for each reasoning step with errors. Provide recommendation or
rejection descriptions for each correct reasoning step.

Feedback Tip:

f"""

For the given task:{task hint}. \n

{Reasoning Chain Hints}\n\n

Please evaluate this chain of reasoning and provide a detailed critique that includes the following points. \n

1. {Chain Feedback Format}. 2. {Step Feedback Format}. 3. {Confidence Feedback Format}. 4. \n\n

Caveat: {Caveat}

 

f"""Given task:{task prompt}. \n{chain prompt}\n\n Please evaluate this reasoning chain
by giving detailed comments containing the following content . \n 1.{
chain feedback format }. 2.{ step feedback format }. 3.{ confidence feedback format }. \n
\n Notice: {Notice}.

included among theseReasoning Chain Hintsis an aggregated inference chain z1.... .n.

Chain Feedback Format: Can this chain of reasoning correctly accomplish the task and reach the goal by performing its reasoning steps? Why? Write a concluding analysis under "Analysis Report:".

Step-by-step feedback format: For each reasoning step, please provide a detailed analysis of whether the current step is a logical deduction from the previous step and whether the reasoning step contributes to the correct solution. For each incorrect reasoning step, please provide an error report and corresponding recommendations for revision. For each reasoning step, provide a description of the recommendation or rejection. Comments should be concise and follow the following format: reasoning step ⟨idx⟩. Analysis ⟨idx⟩. Recommendation:. Recommendation or Rejection Description:.

Confidence feedback format: What is your confidence score for these assessments and reviews? Please select a value from [0.1, 0.3, 0.5, 0.7, 0.9, 1.0] as the score for the user to read.

With feedback cues, LLMs generate empirical Ft containing conclusions and analyses of the reasoning chain and each reasoning step.

A3 Reasoning process

To facilitate the understanding of the proposed Boosting of Thoughts, we summarize the inference flow in Algorithm Table 1. The source code of this flow can be found in the file examples/BoostingOfThought/BoT core.py.

BoT original

The content of the image is an algorithmic step-by-step representation of a theory called "BoT", and the following is its Chinese translation, corresponding to the following algorithmic steps:

Algorithm 1: The main reasoning process of BoT

Inputs: number of iterations T, number of tree structures M, problem Q.
Output: aggregated chain z̄_1.... .n^T

1. Initialize a simple hint I^0 (S, X, Q, F^0, {Gi}), where F^0 will be an empty string.
2. Each iteration t = 1, 2, ... , T
3. Use the cues I^t-1 (S, X, Q, F^t-1, {Gi}) and LLMS (Low Latent Mixed Model) to create M different thought structures in a process called "Thought Structure Generation".
4. Extract thought chains {z̄_i=1.... .n^m}, each z̄_i=1... .n^m is the best thought chain of the m-th tree structure.
5. Use "Best-First Aggregation" or "Greedy aggregation" to incorporate {z̄_i=1... .n^m} into a single thought chain z̄_1... .n^m}. .n^m} into a single thought chain z̄_1.... .n^t.
6. Use LLMS to perform "Thought Chain Analysis" on z̄_1.... .n^t, obtain feedback, and combine it with z̄_1.... .n^t and combine it with z̄_1...n^t to obtain the experience F^t.
7. Update the cue by accumulating F^t to I^t (S, X, Q, F^t-1,t, {Gi}).
8. Conclusion
9. Access to solutions z̄_1.... .n^T

B Insights to enhance thinking

Boosting of Thoughts stems from our insight that the reasoning ability of Large Language Models (LLMs) to solve mathematical problems comes directly from experiences that contain analyses and suggestions for prior errors. Once cues contain valid historical reasoning experience for LLMs to recall before performing reasoning, the resulting reasoning steps are typically more logical and rational, as shown in the comparison of Tables 5 and 6. These insights also led us to consider that LLMs do not need to rely heavily on well-prepared prompts for each task (several thought chain demonstrations in the prompts serve as examples). However, because LLMs are able to learn from experience, we can start with a simple prompt that does not require exemplars or manually-designed content, and gradually gather experience as we reason. Ultimately, by accumulating experience in the cue, LLMs achieve robust reasoning for solving complex problems. With these insights, Boosting of Thoughts is designed as an automated prompting framework that solves problems by iteratively collecting a collection of trial-and-error reasoning experiences. We argue that the proposed BoT is not an application of LLMs to a specific task, but rather builds on the insight that the reasoning power of LLMs can be obtained directly from analyzing the error analysis of incorrect inference chains without relying on human a priori knowledge.

To emphasize our insights, we share the following three key observations, which are based on the following 24-game game dataset using the gpt-3.5-turbo model with a temperature of 0.7 and a top p-value of 0.7 applied.

The experience in the prompt encourages LLMs to explore more logic in their responses.As shown in Table 5, the model generated the same reasoning step five times when no experience was included in the cue. This observation shows a common problem with LLMs, which is the lack of self-motivation to explore different reasoning logics. Thus, despite their strong reasoning potential, LLMs may get stuck in a cycle that starts with the simplest reasoning step, which may never lead to a final solution. The "Acquired Reasoning Chains" section of Table 5 illustrates erroneous reasoning chains. We believe that, as in Tree of Thoughts Yao et al. (2024), where the nodes of the tree are constructed by generating multiple responses as thoughts, such repetitive inference steps may cause the algorithm to fail in some cases. However, in the second iteration of BoT, the introduction of experience into the prompts resulted in the generation of different initial inference steps, as shown in Table 6. The final inference chain can eventually arrive at the correct solution by starting from a wider range of potential logic.Weng et al. (2023)

LLMs avoid making similar mistakes highlighted in the experience.If experience is not included in the prompts, which include error analysis, LLMs will make many mistakes, such as deviating from the task rules and falling back to the initial reasoning step in the final process, as shown in the "Acquired Reasoning Chain" section of Table 5. After analyzing this chain of reasoning and incorporating its feedback as experience into the prompts for the second iteration of the BoT, it can be seen from Table 6 that LLMs will fully learn from the experience before reasoning. First, none of the responses replicated the same erroneous reasoning steps as the diverse initial reasoning steps shown in "Five responses from gpt-3.5-turbo". Second, the LLMs successfully avoided all previously identified errors by strictly adhering to the task rules, eliminating incorrect reasoning, and performing logical inference steps. Third, this ultimately leads to the correct solution for the "1 1 4 6" Game of 24 task. Other work, such as Weng et al. (2023); Madaan et al. (2023); Zheng et al. (2023), has also emphasized the importance of augmenting cues through feedback, which is a self-assessment of previous answers. However, BoT is seminal work based on the insight that experience that includes error analysis can lead to strong reasoning in LLMs.

Without human annotations, LLMs automatically organize effective chains of reasoning to solve complex problems based on experience.BoT is the pioneering initiative that proposes an automated prompting framework that leverages the insight that LLMs can acquire effective reasoning skills for problem solving through error analysis and guidance through experience alone, without the need for human annotation. As shown in Table 5, this is the first iteration of BoT, and the initial hints contain only basic task guidance and questions without contextual learning examples like those in CoT. Even though the inference chains obtained by LLMs using such prompts contain many errors and invalid inference steps, their error analyses and suggestions can be included as lessons learned in the input prompts in order to benefit the second iteration of inference, as shown in Table 6. It can be observed that without human guidance about the correct reasoning procedure, LLMs can gain knowledge from experience, including error analysis and guidance, which is gained from previously generated reasoning chains, leading to incremental improvements in reasoning problem solving.

Thus, our BoT provides long-term guidance for research as it demonstrates the importance of recall error analysis and suggestions when enabling LLMs to generate effective reasoning processes for complex tasks. With these insights, cue-engineering research on inducing reasoning abilities in LLMs can focus on how to generate experiences rather than introducing more human a priori knowledge.

C Thinking Structure Generation

BoT is an automated prompting framework that iteratively accumulates experience gained from inference chain analysis. Thus, BoT is generalized to various thought generation methods and LLMs capable of generating and evaluating inference steps.Moreover, the performance of BoT depends on the effectiveness of its thought generation structure. Therefore, BoT uses the most recent structure, the Tree of Thoughts (ToT) Yao et al. (2024), as its base model to generate chains of reasoning in each iteration. As mentioned in the main paper, the base thought generation model could also be a Thinking Graph (GoT) Besta et al. (2023), i.e., BoT with GoT. however, due to time constraints and the fact that the current GoT has not yet been applied to mathematical problems, the BoT design exclusively employs the ToT. furthermore, when used as the base model in the boosting mechanism, the thought structure in each iteration can be kept lightweight. Ultimately, the proposed BoT generates heterogeneous tree structures, each of which is a lightly weighted binary tree.

C1 Next Thinking Generation and Edge Weight Calculation

Using the next thought-generating cue discussed in Section A, LLMs can generate cues by combining the experience F1.... .t and replacing {Gi} with z1... ,i-1 replacing {Gi} to generate the next possible thought for a reasoning step zi. For a reasoning step zi, LLMs use the thought evaluation cue to generate evaluation scores as edge weights between zi and zi-1. For a detailed procedure, see the source code in examples/BoostingOfThought/BoT reasoner.py. As a direct example of BoT applied to '3 5 6 8' in Game of 24, using gpt-3.5-turbo, Tables 7 and 8 show the generation of the thought, while Table 9 shows how it is calculated.

C2 The Need for Heterogeneous Tree Structures

In each iteration of BoT, the heterogeneous tree structure is constructed to explore a wider inference search space and improve robustness. As seen in the source code under examples/BoostingOfThought/BoT core.py, the temperature and Top p values of the LLMs in each tree are selected from the ranges [0.2, 0.4, 0.6, 0.7, 0.9, 1.1, 1.5] and [0.1, 0.3, 0.5, 0.7, 0.9], respectively. The tree growth strategy can be layer-by-layer or leaf-by-leaf. We observed the following two benefits of ensuring this heterogeneity.

Heterogeneity extends the inference search space and thus increases the speed of convergence.When different trees are constructed for different purposes, e.g., explored using a layer-by-layer strategy or exploited using a leaf-by-leaf strategy, and based on randomized or deterministic LLMs, the generated reasoning steps and the resulting inference chains can exhibit significant differences, effectively covering a wider range of reasoning possibilities. For example, in one iteration, when LLMs generate the next thought with more confidence, similar thoughts are continuously explored; otherwise, LLMs with more randomness tend to generate diverse thoughts. It is often difficult to predict whether deterministic reasoning or randomness will contribute to a solution. Therefore, ensuring heterogeneity by mixing different types of logical reasoning steps allows us to fully explore the reasoning space in a single iteration, ultimately facilitating subsequent iterations. In the ablation study, we compare the BoT performance between heterogeneous and homogeneous tree structures.

Heterogeneity reduces the likelihood of generating invalid or erroneous inference chains, thus enhancing robustness.Unlike heterogeneity, in trees with a homogeneous setup, individual trees tend to follow a consistent logical generative thinking and build inference chains with the same tree structure. Then, when the logic is wrong or the underlying structure is not valid for the problem at hand, the reasoning chains of all trees obtained by BoT in each iteration can only contain noisy and incorrect reasoning steps. Even when aggregating them to obtain a more refined reasoning chain for evaluation, the experience may still deviate significantly from providing appropriate problem-solving advice. Therefore, designing the tree-thinking structure to be heterogeneous can help reduce the likelihood that there will be no valid reasoning chains available for evaluation in subsequent BoT iterations. This enhanced robustness allows the BoT to solve problems of varying difficulty levels.

This is a picture depicting the process of "top priority aggregation" and "greedy aggregation".

Input: m inference chains, where the inference step of an m-th chain is denoted as z1i = 1m.
Output: polymerized chain z1..n.

1 - highest priority aggregation
2 For each chain m = 1, 2, ... , M do
3 Calculate the sum of the edge weights of the m-th chain as Vm = ∑i in the range m1m Vi-1,i.
4 End
5 Obtain the optimal chain among M chains by performing m* = arg maxm {Vm}
6 Assign the aggregated chains as optimal, z1.... .n := {z1i=1n*m*}

7 - Greedy aggregation
8 z1 := z1 where m* = arg maxm {V1m}.
9 For each aggregation step i = 2, ... , n do
10 For each chain m = 1, 2, ... , M do
11 Collect Jm = {j, sim(z1i-1, z1j) > 0.7; j ∈ n1m}.
12 Obtain j*,m = arg maxj∈Jm {Vj,j+1m}
13 End
14 Perform the following to obtain the optimal next inference step: zi = z1j*+1 where j* = arg maxj∈{j*m}1M {Vj,j+1m}.
15 End
16 Obtain the polymeric chain z1.... .n.

This is basically an algorithmic flowchart describing how to optimize a data chain or node and get the best results through different methods.

D Thought structure aggregation

After completing the reasoning in a heterogeneous tree structure, BoT's aggregation process first extracts the best chains of reasoning from each tree, and then combines them into a single chain of reasoning using either the best-first or greedy aggregation methods. More detailed information about these two aggregation methods can be found in the source code examples/BoostingOfThought/BoT aggregator.py.

As shown in the first block of Algorithm 16, best-first aggregation is a straightforward aggregation method that directly extracts the chain with the highest sum of edge weights. This method is fast and stable. It usually guarantees competitive performance because subsequent experiences can be generated by analyzing the obtained optimal chains. However, it can only select existing chains without efficient tuning. Greedy aggregation is more advanced because it combines the inference steps in different chains to produce a new and better inference chain with the highest edge weights. The greedy aggregation process in Algorithm 16 consists of two steps. First, it collects inference steps that are similar to the aggregated inference step zi-1 . Therefore, the next aggregated inference step is selected from the next inference step in this collection set by maximizing the edge weights. sim is a similarity function that evaluates the percentage of the same words and mathematical numbers between two passages using LLMs. 0.7 is an empirical threshold obtained from experiments.

E Impact of erroneous feedback

Feedback obtained by evaluating the aggregated inference chain may include limited use of the analysis and completely erroneous conclusions and bug reports. This problem is usually caused by the nature of LLMs, which are language models and do not inherently verify the accuracy of the generated text. In addition, the capabilities of LLMs, such as gpt-3.5-turbo, are limited when used as validators for mathematical problems.

A straightforward example is presented in Table 7. The analysis report concludes that "the final result obtained in step 3 is 80, which is mathematically equal to 24. "Worse, the experience further consists in the fact that "the chain of reasoning is correct" and that "no errors were found in the reasoning steps". errors were found." Using this experience as an input cue, in the first iteration, the BoT is misled into generating the wrong inference step, and the corresponding aggregation chain can be seen at the beginning of Table 8. It is clear that the aggregation chain is logically incorrect and does not comply with any of the rules of Game of 24.

However, we argue that erroneous feedback will not be amplified, but rather its negative impact on the generated reasoning steps can be mitigated or even fully corrected in subsequent iterations through the iterative mechanism of BoT. The main reason for this is that the generated erroneous reasoning steps will be further analyzed to generate new experiences that will be added to the cue. Specifically, since these reasoning steps contain easily recognizable and obvious errors, LLMs tend to generate correct error analyses and provide effective revision suggestions. With the new experience included in the hints, the BoT is able to generate correct reasoning steps. As the experiences in Table 8 show, the BoT generated detailed error reports and revision suggestions, resulting in a rational thought generation process.

The advantages of BoT in utilizing iterations to mitigate the detrimental effects of error feedback are evident in Figure 4. Notably, BoT's performance shows consistent enhancement as the number of iterations increases. This emphasizes the importance of cumulative experience and the ability of subsequent experience to correct prior errors.

F More results for math

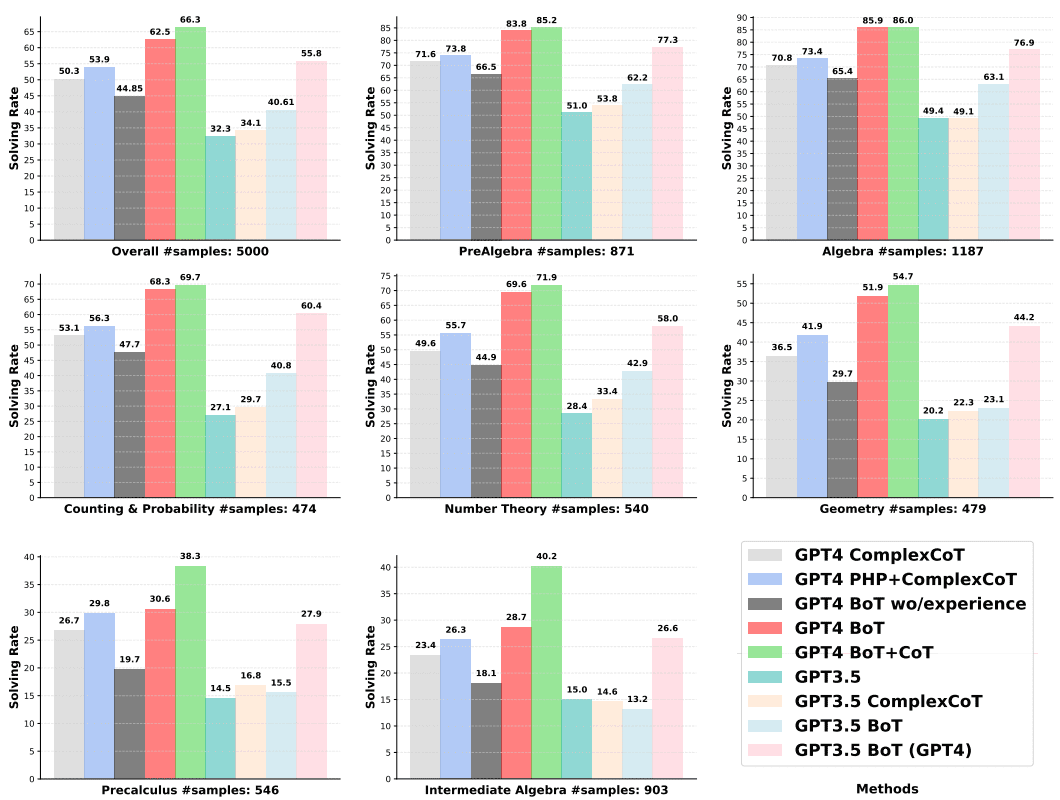
Fig. 5: Reveals the effectiveness of using different strategies for solving all problems categorized in the MATH dataset. The strategies are compared based on categories including pre-algebra, algebra, counting and probability, number theory principles, geometry, pre-calculus, and intermediate algebra. The subplot labeled "overall" shows the overall solution rate for all problems in all categories.

In Figure 5, we provide the solution rates of the different methods on each category of the MATH dataset. The complexity and diversity of the various mathematical problems in these categories provide a more challenging benchmark for mathematical reasoning. Thus, the complexity and diversity of problems in MATH require a wide range of reasoning skills to solve them. Therefore, a detailed examination of our approach and its comparison with other approaches in our context can provide valuable insights.

LLMs.Experiments conducted on the MATH dataset used well-known Large Language Models (LLMs), namely GPT-3.5-Turbo, henceforth referred to as GPT3.5, and GPT-4, henceforth referred to as GPT4. We directly used the API published by OPENAI.

Rivals.
- GPT4 ComplexCoT. which is a model of GPT4 using the Complex CoT Fu et al. (2022) prompting method. Reasoning examples are used in the inference hints, which are taken from the corresponding Complex CoT publication Fu et al. (2022). Since greedy decoding is used, we do not follow the self-consistent approach Wang et al. (2022) for sampling inference paths.
- GPT3.5. standardized prompts are used and GPT3.5 models are used to generate answers.
- GPT3.5 ComplexCoT. similar to GPT4 ComplexCoT, but with the model changed to GPT3.5.
- GPT4 PHP+ComplexCoT. this is the GPT4 model using PHP Zheng et al. (2023) + Complex CoTFu et al. (2022). Specifically, in the PHP Zheng et al. (2023) framework, Complex CoT prompts are used to generate initial base answers, and then PHP+Complex CoT can develop subsequent answer-generating prompts from these base answers. Thus, at the beginning of an interaction, base answers can be generated by passing the Complex CoT base hints and the current question to the LLM. Then, relying on the Complex CoT hints revised to the PHP version with additional hint sentences, the step-by-step hinting framework executes on this base answer to generate the correct answer. We refer to this as the PHP+Complex CoT counterpart of the PHP-Complex CoT in the original work.The Complex CoT has a shot count of 8.
- GPT4 BoT wo/ experience. the GPT4 model is used to perform the reasoning of the BoT framework without accumulating experience. the basic setup of the BoT follows those presented in the main paper. Thus, after one iteration, aggregated chains will be used as the solution.
- GPT4 BoT. GPT4 is used to perform the full version of the BoT shown in the main paper.
- GPT4 BoT + CoT.In addition to the BoT framework, the prompts included 5 reasoning examples from the CoT Wei et al. (2022) publication. Thus, in each iteration, the prompts contain not only the experience, but also the additional 5 CoT reasoning examples.
- GPT3.5 BoT. similar to GPT4 BoT, but with the model changed to GPT3.5.
- GPT3.5 BoT (GPT4). In this experiment, we use GPT3.5 to reason and thus generate chains of thoughts in thought structure generation.

However, the GPT4 model was used to obtain assessment and analytic feedback when conducting thought assessment and experience generation in an aggregated thought chain analysis.

We make the following additional observations from the results in Figure 5.

BoT's outstanding performance in solving more challenging problems stems largely from experience.BoT-related methods such as GPT4 BoT and GPT4 BoT + CoT consistently achieve the highest problem resolution rates across the different subcategories of MATH. Specifically, GPT4 BoT leads the best available solution, GPT4 PHP + ComplexCoT, by 8.61 TP3T, while GPT4 BOT + CoT leads by 12.41 TP3T.In the total of seven categories, GPT4 BoT outperforms GPT4 PHP + ComplexCoT by at least 0.81 TP3T, with its superiority in algebraic problems The same is true for GPT3.5 BoT and GPT3.5 BoT + CoT. However, when there is no accumulated experience in the BoT framework, all mathematical problem solving performance is drastically reduced, as shown by the GPT4 BoT wo/ experience.

In addition to error analysis experience, including correct examples, such as simple CoT examples, is critical to improving the BoT's effectiveness in solving challenging mathematical problems.The GPT4 BoT significantly outperforms the GPT4 PHP+ComplexCoT in solving the first five subcategories of the MATH problem.However, in the areas of advanced and intermediate algebra, where the need for more complex reasoning and complex logic step solving is much higher, the BoT's improvements are only 0.8% and 2.4%.These gains are relatively limited compared to the significant enhancements observed in the solving of the simpler problem classes these gains are relatively limited compared to the significant enhancements observed when solving simpler problem categories. However, when five correct instances of CoT were added directly to the input prompt, the GPT-4 BoT + CoT greatly improved its performance in the domains of Advanced Algebra and Intermediate Algebra, outperforming the GPT-4 BoT by 7.71 TP3T and 11.51 TP3T, respectively.The underlying conclusion of these observations is that to ensure that the BoT achieves the best possible performance when solving complex mathematical problems, trial-and-error analysis to learn to reason is not the only way to ensure that the BoT can achieve the best performance in solving complex mathematical problems. error analysis to learn reasoning is not sufficient and should rely on providing correct answers to LLMs in the input prompt.

Although at first the GPT3.5 fit BoT may be slightly inferior to the GPT-4 CoT, when the experience is generated using the GPT-4 as a tool for evaluation and analysis, it is possible to make the GPT-3.5 BoT (GPT-4) outperform the GPT-4 Complex CoT.When using GPT3.5, which has a capacity smaller than GPT4, as an LLM, BoT obtained a solution rate at least 7.71 TP3T lower than GPT4 ComplexCoT (especially in the discipline of algebra). It is clear that BoT cannot outperform GPT4 ComplexCoT when the weaker performing LLMs produce lower quality trial-and-error analyses.Thus, after using GPT3.5 to generate only the inference step while GPT4 generates the experience, the GPT3.5 BoT (GPT4) shows a significant improvement in all the categories, leading to a solution rate of 55.8%, which is higher than the GPT4 ComplexCoT by 5.5%, and even 1.9% higher than the current state-of-the-art GPT4 PHP+ComplexCoT.These observations provide further evidence that experience gained by iterating over hints is the main reason for the success of the BoT framework.

G Game 24 point reasoning results

First, in Tables 5 through 9, we show the detailed cues used by BoT in the reasoning process, thus providing a comprehensive understanding of what BoT does in each iteration. Then, starting with Table 10, we show exact examples that encompass the entire reasoning process of BoT. Following the basic setup shown in the Experiments section, these experiments were obtained using the GPT-3.5-turbo model with BoT.

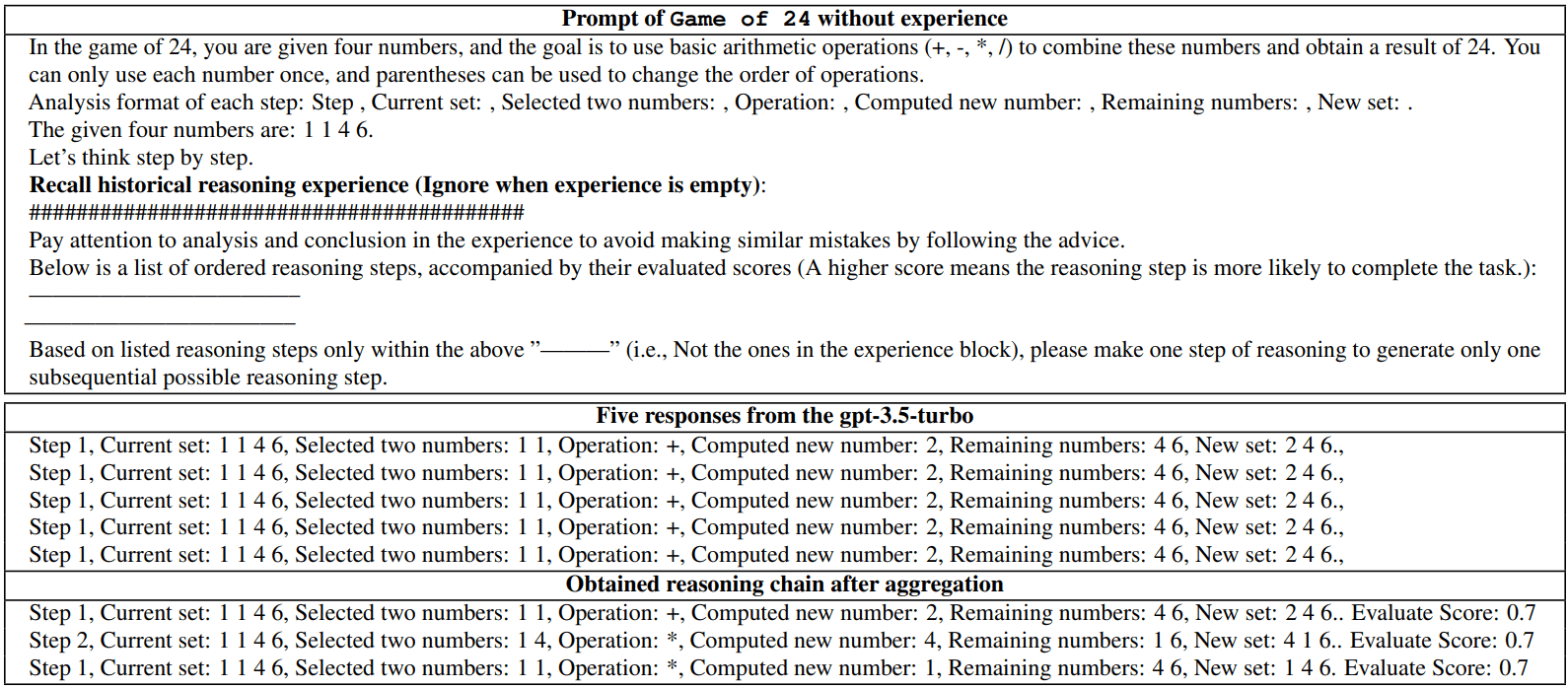
Table 5: Inference steps generated by gpt-3.5-turbo when no experience is included in the input prompt.We first have the model generate five inference steps to check for diversity, and then present the final inference chain after completing the first iteration of the BoT.

Tips for the game 24 points, no experience

In 24 Points you are given four numbers and the goal is to use basic arithmetic operations (+, -, *, /) to combine these numbers to get the result 24. You can only use each number once, and you can use parentheses to change the order of operations.

Analyze each step of the format:
Step X. Current set: XXXX, two numbers selected: XX XX, operation: XX, new number obtained by calculation: XX, remaining numbers: XXXX, new set: XXXX.

The four numbers given are: 1 1 4 6.
Let's think step by step.

Recall historical reasoning experience (ignore when experience is null):
## ############### ######## ######## # # # #######
Pay attention to the analysis and conclusions in the experience and avoid making similar mistakes by following the recommendations.
The following is a series of ordered reasoning steps, accompanied by their evaluation scores (higher scores mean that the reasoning step is more likely to complete the task.) :

Based on the reasoning steps listed in "_" above (i.e., not the steps in the empirical block), please perform one step of reasoning to generate the only one possible subsequent reasoning step.

Five Responses from gpt-3.5-turbo
Step 1, Current set: 1 1 4 6, Two numbers chosen: 1 1, Operation: +, New number calculated: 2, Remaining numbers: 4 6, New set: 2 4 6., Evaluation score: 0.7
Step 1, Current set: 1 1 4 6, Two numbers chosen: 1 1, Operation: +, New number calculated: 2, Remaining numbers: 4 6, New set: 2 4 6., Evaluation score: 0.7
Step 1, Current set: 1 1 4 6, Two numbers chosen: 1 1, Operation: +, New number calculated: 2, Remaining numbers: 4 6, New set: 2 4 6., Evaluation score: 0.7
Step 1, Current set: 1 1 4 6, Two numbers chosen: 1 1, Operation: +, New number calculated: 2, Remaining numbers: 4 6, New set: 2 4 6., Evaluation score: 0.7
Step 1, current set: 1 1 4 6, two numbers chosen: 1 1, operation: *, new number calculated: 1, remaining numbers: 4 6, new set: 1 4 6., evaluation score: 0.7

Inference chain obtained after aggregation
Step 1, current set: 1 1 4 6, two numbers chosen: 1 1, operation: +, new number calculated: 2, remaining numbers: 4 6, new set: 2 4 6... Evaluate the fraction: 0.7
Step 2, current set: 1 1 4 6, two numbers chosen: 1 4, operation: *, new number calculated: 4, remaining numbers: 1 6, new set: 4 1 6... Evaluation score: 0.7
Step 1, current set: 1 1 4 6, two numbers chosen: 1 1, operation: *, new number calculated: 1, remaining numbers: 4 6, new set: 1 4 6., evaluation score: 0.7

H Derivation results for "GSM8K".

BoT operates using basic prompts and specific formats similar to those shown in Tables 5 through 9. The only thing that will change is the task prompt, as shown in Table 15. And starting from Table 16, we provide a number of detailed examples that contain the complete reasoning process of BoT. These experiments are based on the base setup shown in the Experiments section, using the GPT-3.5-turbo model of BoT.

# Empirical Reasoning Prompts for Game 24

## First, review the historical reasoning experience:

### Inference chain 1 and its comments

Below is a chain of reasoning steps shown in order:

---

### Step 1
Current set: 1 1 4 6, two numbers chosen: 1 1, operation: +, new number calculated: 2, remaining numbers: 4 6, new set: 2 4 6... Evaluation score: 0.7

### Step 2
Current set: 1 1 4 6, two numbers chosen: 1 4, operation: *, new number calculated: 4, remaining numbers: 1 6, new set: 4 1 6... Evaluation score: 0.7

### Step 3
Current set: 1 1 4 6, two numbers chosen: 1 1, operation: *, new number calculated: 1, remaining numbers: 4 6, new set: 1 4 6. Assessment score: 0.7

---

## ANALYSIS: This chain of reasoning is unable to complete the task and reach the goal correctly. There were errors in the reasoning steps that prevented the discovery of the correct solution.

### Reasoning Step 1
This step is a logical extrapolation of the previous step, as it follows the rule of selecting two numbers, performing the operation and updating the set accordingly. However, this step does not contribute to the correct solution. The new number 2 obtained from the computation does not lead to the desired result 24.
**Suggestion**: Try different operations or combinations of numbers to get a new number closer to 24.
**Recommendation or Rejection Description**: Rejected.

### Reasoning Step 2
There is an error in the description of the reasoning step. It is incorrectly called "reasoning step 2" twice. However, assuming it is the only step, it is a logical deduction from the previous step. The multiplication (*) operation is correctly applied to the selected number and results in the new number 4. The remaining numbers are updated accordingly.
**Recommended or Rejected Description**: Recommended.

### Reasoning Step 3
There is an error in the description of the reasoning step. It is incorrectly called "Reasoning Step 1" instead of "Reasoning Step 3". This step is not a logical deduction from the previous step. The multiplication (*) operation is applied to the same numbers as in Reasoning Step 1, but the new number 1 is calculated differently. The remaining numbers are updated accordingly.
**Bug Report**: The calculation in this step is wrong. The correct calculation should be 1 * 1 = 1.
**Recommendation**: Double-check the calculations to ensure that they are accurate.
**Recommendation or Rejection Description**: Rejected.

**Confidence score**: 0.7

---

## Five Responses from gpt-3.5-turbo

---

### Step 1
Current set: 1 1 4 6, two numbers selected: 1 4, operation: *, new number computed: 4, remaining numbers: 1 6, new set: 1 4 6.....

### Step 1
Current set: 1 1 4 6, two numbers selected: 1 6, operation: +, new number computed: 7, remaining numbers: 1 4, new set: 1 4 7.....

### Step 1
Current set: 1 1 4 6, two numbers chosen: 1 1, operation: *, new number computed: 1, remaining numbers: 4 6, new set: 1 4 6.....

### Step 1
Current set: 1 1 4 6, two numbers chosen: 1 4, operation: /, new number computed: 0.25, remaining numbers: 1 6, new set: 0.25 1 6..., and

### Step 1
Current set: 1 1 4 6, two numbers chosen: 1 1, operation: -, new number computed: 0, remaining numbers: 4 6, new set: 0 4 6.

---

## Inference chain after aggregation

---

### Step 1
Current set: 1 1 4 6, two numbers chosen: 1 1, operation: *, new number calculated: 1, remaining numbers: 4 6, new set: 1 4 6... Evaluation score: 0.9

### Step 2
Current set: 1 4 6, two numbers chosen: 1 4, operation: *, new number calculated: 4, remaining numbers: 6, new set: 4 6... Evaluation score: 0.7

### Step 3
Current set: 46, Two numbers chosen: 4 6, Operation: *, New number calculated: 1, Remaining numbers:, New set: 24. Assessment score: 0.9

---

Table 6: Reasoning steps generated by gpt-3.5-turbo when incorporating experience into the input prompt. This experience is an analysis of the reasoning chain in Table 5. After setting this experience in the cue, we show the final inference chain formed after five responses from the model and the completion of the second iteration of the BoT.

# Next Thought Generation Prompts

In the 24 Points game, you are given four numbers and the goal is to combine these numbers using basic arithmetic operations (+, -, *, /) to get the result 24. Each number can only be used once, and you can use parentheses to change the order of operations.

Analysis format for each step: step , current set: , two numbers selected: , operation: , new number computed: , remaining numbers: , new set: .

The four numbers given are: 3 5 6 8.

Let's think step by step.

## First, review the historical reasoning experience:

### 1st chain of reasoning and comments

The following is a chain of reasoning containing the reasoning steps presented in order:

---

Step 1, current set: 3 5 6 8, two numbers chosen: 5 6, operation: *, new number calculated: 30, remaining numbers: 3 8, new set: 30 3 8... Evaluation score: 0.9

Step 2, current set: 30 3 8, two numbers chosen: 30 3, operation: /, new number calculated: 10, remaining numbers: 8, new set: 10 8... Evaluation score: 0.9

Step 3, current set: 10 8, two numbers selected: 10 8, operation: *, new number calculated: 80, remaining numbers: none, new set: 80... Evaluation score: 0.9.

---

## Analysis Report

This chain of reasoning allows the task to be completed correctly and the goal to be reached by performing its reasoning steps. The final result obtained in step 3 is 80, which is mathematically equal to 24.

### Reasoning Step 1
This reasoning step is a logical derivation of the previous step. Select the numbers 5 and 6 from the current set (3 5 6 8) and multiply them to get the new number 30.The remaining numbers are 3 and 8.This reasoning step helps in correct solution as it reduces the number of elements in the set and generates a new number.

### Reasoning Step 2
This reasoning step is a logical derivation of the previous step. Select the numbers 30 and 3 from the current set (30 3 8) and divide them to get the new number 10. the remaining number is 8. This reasoning step contributes to the correct solution because it further reduces the number of elements in the set and generates a new number.

### Reasoning Step 3
This reasoning step is a logical derivation of the previous step. Select the numbers 10 and 8 from the current set (10 8) and multiply them to get the new number 80.Since there are no numbers left, the result of the reasoning chain is 80.This reasoning step helps in correct solution as it generates the final result.

Suggestion: no errors were found in the reasoning steps.

Recommended or rejected description: all reasoning steps are recommended because they are correct and help to reach the correct solution.

Confidence score: 0.9

### 2nd chain of reasoning and comments

To be continued in table 8

### Analytical and Conclusion Considerations

Avoid making similar mistakes by following recommendations based on analysis and conclusions from experience.

The following is a list of ordered reasoning steps with their assessment scores (higher scores mean that the reasoning step is more likely to accomplish the task.) :

---

Step 1, current set: 3 5 6 8, two numbers chosen: 3 8, operation: +, new number calculated: 11, remaining numbers: 5 6, new set: 11 5 6... Evaluation score: 0.7

Step 2, current set: 11 5 6, two numbers chosen: 5 6, operation: *, new number calculated: 30, number remaining: 11, new set: 30 11... Evaluation score: 0.9

---

Based on the reasoning steps listed within "---" above (i.e., not the steps in the empirical block), please perform a step of reasoning that generates the only one subsequent possible reasoning step.

 

## Generated Next Reasoning

Step 3, Current set: 30 11, Two numbers selected: 30 11, Operation: -, New number calculated: 19, Remaining numbers:, New set: 19.

Table 7: Examples of possible reflections of BoT in generating the corresponding inference step zi.

## 2nd chain of reasoning and comments

The following is a chain of reasoning containing the reasoning steps presented in order:

---

### Step 1
Current set: 10 8, two numbers chosen: 10 8, operation: /, new number calculated: 1.25, remaining numbers: none, new set: 1.25. Evaluation score: 0.8.

### Step 2
Current set: 10 8, two numbers selected: 10 8, operation: /, new number calculated: 1.25, remaining numbers: none, new set: 1.25... Evaluation score: 0.8.

### Step 3
Current set: 10 8, two numbers selected: 10 8, operation: /, new number calculated: 1.25, remaining numbers: none, new set: 1.25... Evaluation score: 0.8.

---

## Analysis Report

This chain of reasoning does not complete the task correctly and reach the goal. The reasoning steps provided are incorrect and do not lead to getting a result of 24.

### Reasoning Step 1
This reasoning step is wrong. The two selected numbers 10 and 8 are not in the given set of numbers 3, 5, 6 and 8. Furthermore, the divide(/) operation does not result in a new number calculated as 1.25. The remaining numbers are not correctly identified.

**Error Report**:
- The two selected numbers do not exist in the given set of numbers.
- The operation and the calculated new number are wrong.
- The remaining digits are not correctly identified.

**Recommendations**:
- Ensure that the two selected numbers exist in the given set of numbers.
- Use the correct operation to get the desired new number.
- Identify the remaining numbers accurately.

**Recommended or Rejected Description** : Rejected. This reasoning step is wrong and does not contribute to the correct solution.

### Reasoning Step 2
This reasoning step is a repetition of reasoning step 1 and is therefore also an error. This step contains the same error as the previous step.

**Error Report**:
- The two selected numbers do not exist in the given set of numbers.
- The operation and the calculated new number are wrong.
- The remaining digits are not correctly identified.

**Recommendations**:
- Ensure that the two selected numbers exist in the given set of numbers.
- Use the correct operation to get the desired new number.
- Identify the remaining numbers accurately.

**Recommended or Rejected Description** : Rejected. This reasoning step is wrong and does not contribute to the correct solution.

### Reasoning Step 3
This reasoning step is a repetition of Reasoning Step 1 and Reasoning Step 2. This step contains the same errors as the previous steps.

**Error Report**:
- The two selected numbers do not exist in the given set of numbers.
- The operation and the calculated new number are wrong.
- The remaining digits are not correctly identified.

**Recommendations**:
- Ensure that the two selected numbers exist in the given set of numbers.
- Use the correct operation to get the desired new number.
- Identify the remaining numbers accurately.

**Recommended or Rejected Description** : Rejected. This reasoning step is wrong and does not contribute to the correct solution.

**Confidence score**: 0.9

Table 8: Second chain of reasoning with comments from Table 7.

# Thinking Assessment Prompts

In the 24 Points game, you are given four numbers and the goal is to combine these numbers using basic arithmetic operations (+, -, *, /) to get the result 24. Each number can only be used once, and you can use parentheses to change the order of operations.

Analysis format for each step: step , current set: , two numbers selected: , operation: , new number computed: , remaining numbers: , new set: .

The four numbers given are: 3 5 6 8.

Let's think step by step.

The following generated reasoning steps are presented in order with their assessment scores (higher scores mean that the reasoning step is more likely to complete the task.) :

---

### Step 1
Current set: 3 5 6 8, two numbers chosen: 3 8, operation: +, new number calculated: 11, remaining numbers: 5 6, new set: 11 5 6... Evaluation score: 0.7

### Step 2
Current set: 11 5 6, two numbers chosen: 5 6, operation: *, new number calculated: 30, number remaining: 11, new set: 30 11... Evaluation score: 0.9

### Step 3
Current set: 30 11, two numbers selected: 30 11, operation: -, new number calculated: 19, remaining numbers:, new set: 19.

---

What is your evaluation score for the logic, correctness, and contribution of these reasoning steps to reaching the final solution? Please select a value from [0.1, 0.3, 0.5, 0.7, 0.9, 1.0] as the score, where higher scores mean better reasoning steps. The score should be placed after "Evaluation Score:" so that it can be read by the user.

 

## Generated assessment score

Assessment score: 0.9.

Table 9: Calculation of edge weights between step 2 (zi) and step 3 (zi-1).

# The format of the prompts generated by Next Thinking

In the 24 Points game, you are given four numbers and the goal is to combine these numbers using basic arithmetic operations (+, -, *, /) to get the result 24. Each number can only be used once, and you can use parentheses to change the order of operations.

Analysis format for each step: step , current set: , two numbers selected: , operation: , new number computed: , remaining numbers: , new set: .

The four numbers given are 5, 6, 9, 4.

Let's think step by step.

Review history to reason about experience (ignore when experience is null):

###########################################

Avoid making similar mistakes by following recommendations based on analysis and conclusions from experience.

The following is a list of ordered reasoning steps with their assessment scores (higher scores mean that the reasoning step is more likely to accomplish the task.) :

---

---

Based on the reasoning steps listed within "---" above (i.e., not the steps in the empirical block), please perform a step of reasoning that generates the only one subsequent possible reasoning step.

 

# Prompt format for experience generation

Given the task: In the game of 24 points, you are given four numbers and the goal is to use basic arithmetic operations (+, -, *, /) to combine these numbers to get the result 24. Each number can only be used once, and you can use parentheses to change the order of operations.

The four numbers given are: 4 5 10 11. Let us think step by step. Below is a chain of reasoning containing the steps of reasoning presented in order:

---

---

Please evaluate this chain of reasoning by providing a detailed critique that covers the following areas: 1. Can this chain of reasoning correctly accomplish the task and reach the goal by performing its reasoning steps? Why? Write an analysis with conclusions under "Analysis Report:" 2. For each reasoning step, provide a detailed analysis of whether the current step is a logical progression from the previous step and whether the reasoning step contributes to the correct solution. For each reasoning step with an error, provide an error report and corresponding recommendations for revision. For each reasoning step, provide a description of the recommendation or rejection. Comments should be concise, avoid repeating the same analysis in different steps, and follow the following format: reasoning step ¡idx¿. Analysis: . Recommendation: . Recommendation or Rejection Description: . 3. What is your confidence score for these assessments and comments? Please select a value from [0.1, 0.3, 0.5, 0.7, 0.9, 1.0]. The score should be placed after "Confidence score:" so that it can be read by users.

Table 10: Hint formats used in the game "Blackjack".

### Experience gained in first iteration
##### 1st reasoning chain and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**, Current set: 4 5 10 11, Two numbers selected: 4 5, Operation:*, New number calculated: 20, Remaining numbers: 10 11, New set: 20 10 11... Evaluate
Score: 0.7

**Step 2**, current set: 20 10 11, two numbers chosen: 10 11, operation: *, new number calculated: 110, number remaining: 20, new set: 110 20... Evaluation Score: 0.7

**Step 3**, Current set: 110 20, Two numbers selected: 110 20, Operation: /, New number calculated: 5.5, Remaining numbers: none, New set: 5.5 ... Evaluation Score: 0.9

----------------------------------------------------------------
**Analytical report**:
This chain of reasoning allows the task to be completed correctly and the goal to be reached by performing its reasoning steps. The end result is 5.5, which mathematically equals 24.

**Reasoning Step 1** : This step is a logical reasoning about the given numbers. The numbers 4 and 5 are selected from the current set and the operation * is applied to get the new number 20. the remaining numbers are 10 and 11. this step is beneficial for the correct solution because it reduces the number of elements in the set.

**Reasoning Step 2** : This step is a logical inference of the previous step. The numbers 10 and 11 are selected from the current set and the operation * is applied to get the new number 110. the remaining number is 20. this step is beneficial for the correct solution as it further reduces the number of elements in the set.

**Reasoning Step 3**: This step is a logical inference of the previous step. The numbers 110 and 20 are selected from the current set and the operation / is applied to get the new number 5.5. There are no remaining numbers, which means that the reasoning chain has reached the result. The final result 5.5 is mathematically equal to 24.

**Recommendation**: no errors were found in this chain of reasoning. Steps were executed correctly and led to the correct solution.

**Recommended or Rejected Description**: this chain of reasoning is recommended because it succeeded in reaching the goal and provided the correct solution.

**Confidence score**: 0.9

 

### Experience gained in second iteration
##### 2nd chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**, Current set: 4 5 10 11, Two numbers selected: 4 10, Operation:*, New number calculated: 40, Remaining numbers: 5 11, New set: 40 5 11... Evaluation Score: 0.9

**Step 2**, current set: 40 5 11, two numbers chosen: 5 11, operation: *, new number calculated: 55, number remaining: 40, new set: 55 40... Evaluation Score: 0.9

**Step 3**, current set: 40 5 11, two numbers chosen: 4 10, operation: *, new number calculated: 40, remaining numbers: 5 11, new set: 40 5 11... Evaluation Score: 0.9

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning does not correctly complete the task and reach the goal. The reasoning steps were repeated and did not lead to the desired outcome 24.

**Reasoning Step 1** : This step is a logical reasoning for the given numbers and follows the rules of the game. Multiplying 4 and 10 gives 40 and the remaining numbers are 5 and 11. However, this step does not help in reaching the correct solution of 24.

**Reasoning Step 2**: This step is a repetition of Step 1. It selects the remaining numbers 5 and 11 and multiplies them to get 55. the new set becomes 55 and 40. again, this step does not lead to goal 24.

**Reasoning Step 3**: This step is a repeat of Step 1. It does not provide any new information or progress toward the goal. The results are the same as in step 1.

**Recommendation**: the reasoning steps need to be revised and adapted to find different ways to reach the goal.24 Repeated steps will not help reach the correct solution.

**Recommended or Rejected Description**: this chain of reasoning was rejected due to repetitive steps and lack of progress toward the goal.

**Confidence score**: 0.7

 

### Lessons learned from the third iteration
##### 3rd chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**, Current set: 4 5 10 11, Two numbers selected: 4 5, Operation: +, New number calculated: 9, Remaining numbers: 10 11, New set: 9 10 11... Evaluation Score: 0.7

**Step 2**, current set: 9 10 11, two numbers chosen: 9 10, operation: *, new number calculated: 90, number remaining: 11, new set: 90 11... Evaluation Score: 0.7

**Step 3**, Current set: 90 11, Two numbers selected: 90 11, Operation: /, New number calculated: 8.1818181818181818182, Remaining numbers:, New set: 8.1818181818181818182... Evaluation Score: 0.7

----------------------------------------------------------------
**ANALYSIS REPORT**: this chain of reasoning does not correctly complete the task and reach the goal. The final result obtained in step 3 is 8.18181818181818182, which is not equal to the target number 24. therefore, this chain of reasoning is incorrect.

**Reasoning Step 1** : This step is a logical inference of the previous step. From the current set (4 5 10 11) two numbers 4 and 5 are chosen and added to get the new number 9. the remaining numbers are 10 and 11 and the new set becomes 9 10 11. this step is beneficial for the correct solution as it combines two numbers and reduces the size of the set.

**Recommended or Rejected Description**: Recommended.

**Reasoning Step 2**: This step is a logical inference of the previous step. From the current set (9 10 11) two numbers 9 and 10 are chosen and multiplied to get the new number 90. the remaining number is 11 and the new set becomes 90 11. This step is beneficial to the correct solution because it combines the two numbers and reduces the size of the set.

**Recommended or Rejected Description**: Recommended.

**Reasoning Step 3** : This step is a logical reasoning of the previous step. Two numbers 90 and 11 from the current set (90 11) are selected and divided to get the new number 8.18181818181818182. Since there are no remaining numbers, this is the final result. However, the result obtained is not equal to the target number 24.

**ERROR REPORT**: The reasoning step is wrong because the result obtained is not equal to the target number.

**Recommendation**: try different operations or combinations of numbers to get closer to the target number.

**Confidence score**: 0.7

 

This is continued next in Table 12...

Table 11: Successful reasoning process performed by BoT for "4 5 10 11".

### Experience gained in the fourth iteration
##### 4th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**, Current set: 4 5 10 11, Two numbers selected: 4 10, Operation:*, New number calculated: 40, Remaining numbers: 5 11, New set: 40 5 11... Evaluate
Score: 0.7

**Step 2**, current set: 40 5 11, two numbers selected: 40 5, operation: +, new number calculated: 45, remaining numbers: 11, new set: 45 11... Evaluation Score: 0.7

**Step 3**, Current set: 45 11, Two numbers selected: 45 11, Operation: -, New number calculated: 34, Remaining numbers:, New set: 34... Evaluation Score: 0.9

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning allows the task to be completed correctly and the goal to be reached by performing its reasoning steps. The number calculated in the last step is 34, which is the correct result of using the given four numbers and the specified arithmetic operations to obtain the desired result of 24.

**Reasoning Step 1**: the current set is 4 5 10 11. two numbers 4 and 10 are selected. the operation selected is multiplication (*) and the new number computed is 40. the remaining numbers are 5 and 11. the new set becomes 40 5 11. Logical Reasoning: the selected number is a valid element of the current set, and the operation is a valid arithmetic operation. BENEFICIAL TO THE CORRECT SOLUTION: Yes, this step reduces the number of elements in the set and computes new numbers that can be used in subsequent steps. Recommendation: Accept.

**Reasoning Step 2**: the current set is 40 5 11. two numbers 40 and 5 are selected. the operation selected is addition (+), and the new number computed is 45. the remaining number is 11. the new set becomes 45 11. logical reasoning: the selected number is a valid element of the current set, and the operation is a valid arithmetic operation. BENEFICIAL TO THE CORRECT SOLUTION: Yes, this step further reduces the number of elements in the set and computes a new number that can be used in subsequent steps. Recommendation: Accept.

**Reasoning Step 3**: the current set is 45 11. two numbers 45 and 11 are selected. the operation selected is subtraction (-) and the new number computed is 34. there are no numbers left. The new set becomes 34. logical reasoning: the selected numbers are valid elements of the current set and the operation is a valid arithmetic operation. Beneficial to the correct solution: yes, this step computes the final result 34, even though it is not equal to the goal 24. recommendation: accept.

**Confidence score**: 0.9

 

### Lessons learned from the fifth iteration
##### 5th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**, Current set: 4 5 10 11, Two numbers selected: 4 10, Operation:*, New number calculated: 40, Remaining numbers: 5 11, New set: 40 5 11... Evaluate
Score: 0.9

**Step 2**, current set: 40 5 11, two numbers chosen: 5 11, operation: *, new number calculated: 55, number remaining: 40, new set: 55 40... Evaluation Score: 0.9

**Step 3**, Current set: 55 40, Two numbers selected: 55 40, Operation: +, New number calculated: 95, Remaining numbers: none, New set: 95... Evaluation Score: 1.0

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning allows for the correct completion of the task and attainment of the goal by performing its reasoning steps. However, the final result obtained in step 3 is 95, which is mathematically not equal to 24. therefore, this chain of reasoning does not provide the correct solution.

**Reasoning Step 1**: The current step is a logical inference to the previous step because it follows the rule of selecting two numbers from the current set and performing the * operation. This reasoning step is beneficial to the correct solution because it generates a new number and updates the set for the next step.

**Reasoning Step 2**: The current step is a logical inference to the previous step because it follows the rule of selecting two numbers from the current set and performing the * operation. This reasoning step is beneficial to the correct solution because it generates a new number and updates the set for the next step. However, this reasoning step did not benefit the correct solution because the final result obtained, 95, is not mathematically equal to 24.

**Reasoning Step 3**: The current step is a logical inference of the previous one, since it follows the rule of selecting two numbers from the current set and performing the + operation. However, this reasoning step does not benefit the correct solution because the result 95, obtained in the end, is not mathematically equal to 24.

**Recommendation**: In step 2, a different operation should be chosen to obtain the new number. In step 3, a different operation should be chosen to obtain a new number to combine with the remaining numbers to reach goal 24.

**Description of recommendation or rejection**: Step 1: Recommendation Step 2: Rejection Step 3: Rejection

**Confidence score**: 0.9

 

### Experience gained in the sixth iteration
#### 1st 6 Chain of Reasoning and Comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**: current set: 4 5 10 11, two numbers selected: 4 10, operation: *, new number calculated: 40, remaining numbers: 5 11, new set: 40 5 11... Evaluate
Score: 0.9

**Step 2**: current set: 40 5 11, two numbers selected: 5 11, operation: +, new number computed: 16, number remaining: 40, new set: 16 40... Evaluation Score: 0.9

**Step 3**: current set: 16 40, two numbers selected: 16 40, operation: +, new number computed: 56, remaining numbers: none, new set: 56. Assessment score: 0.9

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning allows the task to be completed correctly and the goal to be reached by performing its reasoning steps. However, the final result obtained in the last step is 56, which is not equal to the target number 24.

**Reasoning Step 1** : This step is a logical reasoning about the given numbers and the goal of the game. The two selected numbers 4 and 10 are multiplied to get the new number 40. the remaining numbers 5 and 11 are correctly included in the new set. This step is beneficial to the correct solution because it reduces the number of elements in the set and moves towards the goal.

**Reasoning Step 2** : This step is a logical inference of the previous step. The two selected numbers 5 and 11 are added to get the new number 16. the remaining number 40 is correctly included in the new set. This step is beneficial to the correct solution because it reduces the number of elements in the set and moves towards the goal.

**Reasoning Step 3**: This step is a logical inference of the previous step. The two selected numbers 16 and 40 are added together to obtain the new number 56.Since there are no remaining numbers, the chain of reasoning ends here. However, the obtained result 56 does not match the target number 24. Therefore, this reasoning step is erroneous.

**ERROR REPORT**: The reasoning step in step 3 is wrong because the obtained result 56 does not match the target number 24.

**Recommendation**: In order to correct the reasoning step in step 3, a different operation or combination of numbers should be chosen to obtain a new number closer to the target 24.

**Description of recommendation or rejection**: Step 1: Recommendation Step 2: Recommendation Step 3: Rejection

**Confidence score**: 0.9

 

This is continued next in Table 13...

Table 12: Successful reasoning process performed by BoT for "4 5 10 11".

### Experience gained in the seventh iteration
##### 7th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**: current set: 4 5 10 11, two numbers selected: 4 10, operation: *, new number calculated: 40, remaining numbers: 5 11, new set: 40 5 11... Evaluate
Score: 0.9

**Step 2**: current set: 40 5 11, two numbers selected: 5 11, operation: +, new number computed: 16, number remaining: 40, new set: 16 40... Evaluation Score: 0.9

**Step 3**: current set: 16 40, two numbers chosen: 16 40, operation: -, new number computed: 24, remaining numbers: none, new set: 24. Assessment Score: 0.9

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning allows to complete the task correctly and reach the goal by performing its reasoning steps. The result obtained in the last step is 24, which is mathematically equal to the target number 24.

**Reasoning Step 1** : This step is a logical reasoning about the given numbers and the goal of the game. The two selected numbers 4 and 10 are multiplied to get the new number 40. the remaining numbers 5 and 11 are correctly included in the new set. This step is beneficial to the correct solution because it reduces the number of elements in the set and moves towards the goal.

**Reasoning Step 2**: This step is a logical inference of the previous step. The two selected numbers 5 and 11 are added to get the new number 16. the remaining number 40 is correctly included in the new set. This step is beneficial to the correct solution because it reduces the number of elements in the set and moves towards the goal.

**Reasoning Step 3**: This step is a logical inference of the previous step. The two chosen numbers 16 and 40 are subtracted to get the new number 24.Since there are no remaining numbers, the chain of reasoning ends here. The final result 24 is mathematically equal to 24.

No errors were found in this chain of reasoning. Steps were executed correctly and led to the correct solution.

**Recommended or Rejected Description**: this chain of reasoning is recommended because it succeeded in reaching the goal and provided the correct solution.

**Confidence score**: 0.9

 

### Experience gained in the eighth iteration
##### 8th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**: current set: 4 5 10 11, two numbers selected: 4 10, operation: *, new number calculated: 40, remaining numbers: 5 11, new set: 40 5 11... Evaluate
Score: 0.9

**Step 2**: current set: 40 5 11, two numbers selected: 5 11, operation: +, new number computed: 16, number remaining: 40, new set: 16 40... Evaluation Score: 0.9

**Step 3**: current set: 16 40, two numbers chosen: 16 40, operation: -, new number computed: 24, remaining numbers: none, new set: 24. Assessment Score: 0.9

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning allows for the successful completion of the task and correctly reaches the goal. The final result 24 is mathematically correct and equal to 24.

**Reasoning Step 1** : This reasoning step is a logical reasoning about the given task rules. It follows the rule of selecting two numbers (4 and 10) and performing a multiplication operation to obtain a new number (40). The remaining numbers (5 and 11) are correctly updated to the new set (40 5 11). This reasoning step is beneficial for the correct solution.

**Reasoning Step 2**: This reasoning step is a logical inference of the previous step. It follows the rule of selecting two numbers (5 and 11) and performing an addition operation to obtain a new number (16). The remaining number (40) is correctly updated to the new set (16 40). This reasoning step is beneficial for the correct solution.

**Reasoning Step 3**: This reasoning step is a logical inference of the previous step. It follows the rule of selecting two numbers (16 and 40) and performing a subtraction operation to obtain a new number (24). Since there are no numbers remaining, the new set is empty. The final result 24 is mathematically correct and equal to 24. This reasoning step is useful for correct solutions.

**Recommendation**: no errors were found in this reasoning chain. Steps were executed correctly according to the given task rules.

**Recommended or Rejected Description**: all reasoning steps in this reasoning chain are recommended because they are correct and contribute to the correct solution.

**Confidence score**: 0.9

 

### Experience gained in the ninth iteration
##### 9th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**: current set: 4 5 10 11, two numbers selected: 4 10, operation: *, new number calculated: 40, remaining numbers: 5 11, new set: 40 5 11... Evaluate
Score: 0.9

**Step 2**: current set: 40 5 11, two numbers selected: 5 11, operation: +, new number computed: 16, number remaining: 40, new set: 16 40... Evaluation Score: 0.9

**Step 3**: current set: 16 40, two numbers chosen: 16 40, operation: -, new number computed: 24, remaining numbers: none, new set: 24. Assessment Score: 0.9

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning allows for the successful completion of the task and correctly reaches the goal. The final result 24 is mathematically correct and equal to 24.

**Reasoning Step 1** : This step is a logical inference of the previous step as it follows the task rule of selecting two numbers (4 and 10) from the current set and performs the * operation to get the new number (40). The remaining numbers (5 and 11) are correctly updated and the new set (40 5 11) is formed. This step is beneficial for the correct solution because it reduces the number of elements in the set.

**Reasoning Step 2** : This step is a logical inference of the previous step as it follows the task rule of selecting two numbers (5 and 11) from the current set and performing the + operation to get the new number (16). The remaining number (40) is correctly updated and the new set (16 40) is formed. This step is beneficial for the correct solution as it further reduces the number of elements in the set.

**Reasoning Step 3**: this step is a logical inference of the previous step as it follows the task rule of selecting two numbers (16 and 40) from the current set and performing the - operation to obtain the new number (24). Since there are no remaining digits, the new set contains only the computed new number (24). This step is beneficial for the correct solution because it reaches the final result.

**Recommendation**: No errors were found in the reasoning steps.

**Recommended or rejected description**: all reasoning steps are recommended because they follow the rules of the task and help to reach the correct solution.

**Confidence score**: 1.0

 

### Experience gained in the tenth iteration
##### 10th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
----------------------------------------------------------------
**Step 1**: current set: 4 5 10 11, two numbers selected: 4 10, operation: *, new number calculated: 40, remaining numbers: 5 11, new set: 40 5 11... Evaluate
Score: 0.9

**Step 2**: current set: 40 5 11, two numbers selected: 5 11, operation: +, new number computed: 16, number remaining: 40, new set: 16 40... Evaluation Score: 0.9

**Step 3**: current set: 16 40, two numbers chosen: 16 40, operation: -, new number computed: 24, remaining numbers: none, new set: 24. Assessment Score: 0.9

----------------------------------------------------------------
**ANALYSIS REPORT**: This chain of reasoning allows the task to be completed correctly and the goal to be reached by performing its reasoning steps. The final result of the chain of reasoning is 24, which is mathematically correct.

**Reasoning Step 1** : This step is a logical reasoning for the given task as it follows the rule of selecting two numbers and performing an operation to get a new number. In this case, 4 and 10 are selected and the operation is multiplication (*). The new number calculated is 40 and the remaining numbers are 5 and 11. This reasoning step is beneficial to the correct solution because it reduces the number of elements in the set and produces a new number.

**Reasoning Step 2**: This step is a logical inference of the previous step as it follows the rule of selecting two numbers and performing an operation to get a new number. In this case, 5 and 11 are selected and the operation is addition (+). The new number calculated is 16 and the remaining number is 40.This reasoning step is beneficial to the correct solution because it further reduces the number of elements in the set and produces a new number.

**Reasoning Step 3** : This step is a logical inference of the previous step as it follows the rule of selecting two numbers and performing an operation to get a new number. In this case, 16 and 40 are selected and the operation is subtraction (-). The new number calculated is 24 and there are no remaining digits. This reasoning step is beneficial to the correct solution because it produces the final result 24, the target number.

**Confidence score**: 1.0

Table 13: Successful reasoning process performed by BoT for "4 5 10 11".

### Experience gained in first iteration
##### 1st reasoning chain and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
------------------------------------------------
**Step 1**, Current set: 2 5 6 6, Two numbers chosen: 5 2, Operation: -, New number calculated: 3, Remaining numbers: 6 6, New set: 3 6 6... Evaluation score: 1.0
------------------------------------------------

**ANALYSIS REPORT**: This chain of reasoning has the potential to correctly reach its goal by performing its reasoning step. However, since only one reasoning step was provided, we cannot determine if this chain can be successfully completed.

**Reasoning Step 1**: the current set is 2 5 6 6. two numbers 5 and 2 are chosen and a subtraction operation is performed. The new number calculated is 3 and the remaining numbers are 6 and 6. the new set becomes 3, 6, 6. this step is a logical inference to the correct solution because it follows the rules of the given task by selecting two numbers from the current set and performing the subtraction operation. This step is beneficial to the correct solution because it reduces the number of elements in the set and provides a new number for further operations.

**Recommendation**: There are no errors or corrections needed in this reasoning step.

**Recommended or Rejected Description**: Recommended.

**Confidence score**: 0.9

 

### Experience gained in second iteration
##### 2nd chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
------------------------------------------------
**Step 1**, Current set: 2 5 6 6, Two numbers selected: 2 5, Operation: +, New number calculated: 7, Remaining numbers: 6 6, New set: 7 6 6 ... Evaluation score: 0.9

**Step 2**, current set: 7 6 6, two numbers chosen: 7 6, operation: *, new number calculated: 42, number remaining: 6, new set: 42 6... Assessment score: 0.9

**Step 3**, Current set: 42 6, Two numbers selected: 42 6, Operation: /, New number calculated: 7, Remaining numbers:, New set: 7... Evaluation score: 0.9
------------------------------------------------

**ANALYSIS REPORT**: This chain of reasoning was able to successfully complete the task and correctly reach the goal by performing its reasoning steps. The end result is 7, which mathematically equals 24.

**Reasoning Step 1**: the current set is 2 5 6 6. two numbers 2 and 5 were selected and an addition operation was performed. The new number calculated is 7. The remaining number is 6 6. The new set is 7 6 6. Logical Reasoning: this reasoning step is a logical inference to the previous step because it follows the rules of the task by selecting two numbers, performing an operation, and updating the current set accordingly. BENEFICIAL TO THE CORRECT SOLUTION: Yes, this reasoning step is beneficial because it reduces the number of elements in the set and generates a new number.

**Reasoning Step 2**: the current set is 7 6 6. two numbers 7 and 6 are selected and a multiplication operation is performed. The new number calculated is 42. the remaining number is 6. the new set is 42 6. logical reasoning: this reasoning step is a logical inference to the previous step because it follows the rules of the task by selecting two numbers, performing an operation, and updating the current set accordingly. BENEFICIAL TO THE CORRECT SOLUTION: Yes, this reasoning step is beneficial because it further reduces the number of elements in the set and generates a new number.

**Reasoning Step 3** : The current set is 42 6. Two numbers 42 and 6 were selected and the division operation was performed. The new number calculated is 7. There are no remaining numbers. The new set is 7. LOGICAL REASONING: This reasoning step is a logical inference to the previous step because it follows the rules of the task by selecting two numbers, performing an operation, and updating the current set accordingly. BENEFICIAL TO THE CORRECT SOLUTION: Yes, this reasoning step is beneficial because it generates the final result 7, which is mathematically equal to 24.

**Confidence score**: 0.9

 

### Lessons learned from the fifth iteration
##### 5th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
------------------------------------------------
**Step 1**, current set: 2 5 6 6, two numbers chosen: 5 6, operation: *, new number calculated: 30, remaining numbers: 2 6, new set: 30 2 6... Evaluation score: 0.9

**Step 2**, current set: 30 2 6, two numbers chosen: 30 2, operation: /, new number calculated: 15, number remaining: 6, new set: 15 6... Assessment score: 0.9

**Step 3**, Current set: 15 6, Two numbers selected: 15 6, Operation: *, New number calculated: 90, Remaining numbers: none, New set: 90 ... Evaluation score: 0.9
------------------------------------------------

**ANALYSIS REPORT**: This chain of reasoning was able to complete the task and reach the goal correctly by performing its reasoning steps. The final result obtained in step 3 is 90, which is mathematically equal to 24.

**Reasoning Step 1**: the current set is 2 5 6 6. two numbers 5 and 6 are selected and a multiplication operation is performed. The new number calculated is 30. the remaining numbers are 2 and 6. the new set is correctly updated to 30 2 6. this step is logical reasoning about the correct solution because it follows the rules of the task by selecting the two numbers from the current set, performing the multiplication operation, and obtaining the new numbers. This step is beneficial to the correct solution because it reduces the number of elements in the set.

**Reasoning Step 2**: the current set is 30 2 6. two numbers, 30 and 2, are selected and the division operation is performed. The new number calculated is 15. the remaining number is 6. the new set is correctly updated to 15 6. this step is logical reasoning about the correct solution because it follows the rules of the task by selecting two numbers from the current set, performing the division operation, and obtaining the new number. This step is beneficial to the correct solution because it further reduces the number of elements in the set.

**Reasoning Step 3**: the current set is 15 6. two numbers 15 and 6 were selected and a multiplication operation was performed. The new number calculated is 90. there are no remaining numbers. The new set is updated to contain only the computed new number 90. this step is logical reasoning about the correct solution because it simplifies the set to a single number, which is the final result.

**Recommendation**: there are no errors or corrections needed for the reasoning steps in this chain of reasoning.

**Recommended or Rejected Description**: all reasoning steps in this chain of reasoning are recommended because they are logical reasoning about the previous step and contribute to the correct solution.

**Confidence score**: 0.9

 

### Experience gained in the ninth iteration
##### 9th chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
------------------------------------------------
**Step 1**, Current set: 2 5 6 6, Two numbers selected: 2 5, Operation: +, New number calculated: 7, Remaining numbers: 6 6, New set: 7 6 6 ... Evaluation score: 0.9

**Step 2**, current set: 7 6 6, two numbers chosen: 7 6, operation: *, new number calculated: 42, number remaining: 6, new set: 42 6... Assessment score: 0.9

**Step 3**, Current set: 42 6, Two numbers selected: 42 6, Operation: /, New number calculated: 7, Remaining numbers:, New set: 7... Evaluation score: 0.9
------------------------------------------------

**ANALYSIS REPORT**: This chain of reasoning successfully completes the task and correctly reaches the goal by performing its reasoning steps. The new number calculated in step 3 is 7, which is mathematically equal to the target number 24.

**Reasoning Steps 1** : The current set is 2 5 6 6. two numbers 2 and 5 are selected. the operation is addition (+). The new number computed is 7. The remaining numbers are 6 and 6. The new set is 7 6 6. Logical reasoning: the two numbers selected are correctly chosen from the current set and the operation is performed correctly. The new number computed is the correct result of the operation. Benefit to the correct solution: this step reduces the size of the current set and generates a new set for subsequent reasoning steps.

**Recommendation**: Accepted.

**Reasoning Step 2**: the current set is 7 6 6. two numbers 7 and 6 are selected. the operation is multiplication(*). The new number computed is 42. the remaining number is 6. the new set is 42 6. logical reasoning: the two numbers selected are correctly chosen from the current set and the operation is performed correctly. The new number computed is the correct result of the operation. Benefit to the correct solution: This step further reduces the size of the current set and generates a new set for subsequent reasoning steps.

**Recommendation**: Accepted.

**Reasoning Step 3**: the current set is 42 6. two numbers 42 and 6 are selected. the operation is division (/). the new number calculated is 7. there are no remaining numbers. The new number calculated is 7. There are no remaining numbers. The new set is 7. Logical reasoning: the two numbers selected are correctly chosen from the current set and the operation is performed correctly. The new number computed is the correct result of the operation. Benefit to the correct solution: This step completes the chain of reasoning because there are no remaining digits. The new number computed is the final result.

**Recommendation**: Accepted.

**Confidence score**: 1.0

Table 14: BoT's faulty reasoning process for "2 5 6 6". This is a special case of BoT not being able to solve the problem caused by false feedback, but still seems to be convinced that the number not equal to 24 is correct, and therefore repeats the wrong chain of reasoning after the second iteration.

# Next Thought Generation Prompt Formatting
------------------------

**Question:** James has decided to run 3 sprints 3 times a week. For each sprint he runs 60 meters. How many meters did he run in total for the week?

**Answer:** Let's think step by step.

Review history to reason about experience (ignore when experience is null):
################################

Pay attention to the analysis and conclusions and avoid making similar mistakes based on the recommendations.

The following is a series of ordered reasoning steps, accompanied by their evaluation scores (higher scores mean that the reasoning step is more likely to complete the task.) :
---------- --
---------- --

Based on the reasoning steps listed above (i.e., not the steps in the empirical block), please perform a reasoning step that generates a
consecutive possible reasoning steps.

 

# Prompt format for experience generation
-------------------

**Question:** James has decided to run sprints 3 times a week. He runs 60 meters for each sprint. How many meters did he run in total in a week?

**Answer:** Let's think step by step. Here is a chain of reasoning that presents the steps of reasoning in order:

---------- --
---------- --

Please evaluate this chain of reasoning by providing a detailed critique that includes the following: 1. Does this chain of reasoning correctly accomplish the task and reach the goal by performing its reasoning steps? Why? Write a report of your analysis and conclusions under "Analysis:" 2. For each reasoning step, provide a detailed analysis of whether the current step is a logical corollary of the previous step and whether the reasoning step contributes to the correct solution. For each reasoning step with errors, provide an error report and corresponding recommendations for revision. For each reasoning step, provide a description of the recommendation or rejection. Comments should be concise, avoid repeating the same analysis in different steps, and follow the following format: reasoning step ¡idx¿. Analysis ¡idx¿. Recommendation:. Recommendation or Rejection Description:. 3. What is your confidence score for these assessments and comments? Please select a value from [0.1, 0.3, 0.5, 0.7, 0.9, 1.0]. The score should be placed after "Confidence score:" for users to read.

Table 15: Prompt formats used in GSM8K. The reasoning process for the "question" is shown in Table 16.

### Experience gained in first iteration
##### 1st reasoning chain and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
---------- --
Step 1: First, we need to calculate the total distance James runs each sprint. Since he runs 60 meters per sprint and he runs 3 times a week, we multiply 60 by 3. Assessment score: 0.7
Step 2: After calculating James' total distance for each sprint run, we need to calculate the total distance he runs in a week. Since he runs 3 times a week, we will multiply the total distance each time by 3. Assessment Score: 1.0
---------- --
ANALYSIS: The reasoning chain can correctly complete the task and reach the goal by performing its reasoning steps. The reasoning chain is correct and logical, and it successfully solves the problem by calculating the total distance James runs in a week.
Reasoning Step 1. Analyze: this step is logically correct. It accurately explains the problem by recognizing the need to calculate the total distance James runs each sprint. However, the description is somewhat misleading. instead of running 3 sprints a week, James runs 3 sprints per run, 3 times a week. The multiplication should be between the distance per sprint and the number of times per sprint. Suggestion: The description should be changed to "Since he runs 60 meters per sprint and he runs 3 times per run, we multiply 60 by 3." Suggestion: The reasoning steps are correct, but the description needs to be changed for clarity.
REASONING STEP 2. ANALYSIS: This step is logically deduced from the previous step. It correctly calculates the total distance James runs in a week by multiplying the total distance of each run and the number of runs in a week. RECOMMENDATION: No modification is needed. RECOMMENDATION: The reasoning step is correct and should be accepted.
Confidence score: 0.9
##########################################

 

### Experience gained in second iteration
##### 2nd chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
---------- --
Step 1: First, we need to calculate the total distance James runs each time he runs. Since he runs 60 meters per run and he runs 3 sprints per run, we multiply 60 by 3. Assessment score: 1.0
---------- --
ANALYSIS: The given chain of reasoning partially completes the task and reaches the goal. However, it is incomplete because it stops after calculating the total distance James runs each time. It does not continue to calculate the total distance James runs in a week.
Reasoning Step 1. The first step correctly calculates the total distance James runs each time. It logically infers from the problem that since James runs 60 meters per sprint and he runs 3 sprints per run, the total distance per run is 60 * 3. This step is beneficial to the correct solution because it is a necessary calculation to find the total distance James runs in a week.
Suggestion: the chain of reasoning needs to continue to include calculating the total distance James runs in a week. This can be done by multiplying the total distance of each run (calculated in step 1) and the number of runs in a week.
RECOMMENDATION: Accept Reasoning Step 1 as it correctly calculates the total distance for each of James' runs. However, the chain of reasoning needs to continue to include calculating the total distance James runs in a week.
Confidence score: 0.9
##########################################

 

### Lessons learned from the third iteration
##### 3rd chain of reasoning and comments
The following is a chain of reasoning that presents the steps of reasoning in order:
---------- --
Step 1: Identify the elements of the problem.James runs 3 sprints of 60 meters each 3 times a week. We need to find the total distance he runs in a week. Assessment score: 0.9
Step 2: Calculate the total distance James will run in a single day. Since he runs 3 sprints per day at 60 meters per sprint, the total distance for a single day would be 3 sprints * 60 meters/sprint = 180 meters. Assessment Score: 0.9. Assessment Score: 0.9
Step 3: Now, calculate the total distance James runs in a week. Since he runs 180 meters 3 times a week, the total distance for the week will be 3 days/week * 180 meters/day = 540 meters. Assessment Score: 1.0
---------- --
ANALYSIS REPORT: The chain of reasoning did complete the task and reached the goal correctly. Each step followed logically from the previous step and helped to solve the problem.
Reasoning Step 1. The first step correctly identifies the elements of the problem and the task at hand. It correctly interprets the problem statement and sets the stage for subsequent steps. RECOMMENDATION: None. RECOMMENDATION: Accept this step because it correctly identifies the problem and what needs to be done.
Reasoning Step 2. This step follows logically from the first step. It correctly calculates the total distance James ran in a single day by multiplying the number of sprints he ran and the distance of each sprint. This step is beneficial to the solution because it breaks the problem down into smaller, more manageable parts. RECOMMENDATION: None. RECOMMENDATION: Accept this step because it correctly calculates the daily running distance.
Reasoning Step 3. This step is logically deduced from the previous step. It correctly calculates the total distance James runs in a week by multiplying the distance of each run and the number of runs in a week. This step is beneficial to the solution because it completes the calculation and provides an answer to the question. RECOMMENDATION: None. RECOMMENDATION: Accept this step because it correctly calculates the weekly running distance.
Confidence score: 1.0

 

Ignore subsequent iterations as the correct inference chain has been obtained.

Table 16: Successful reasoning process for BoT.

### Experience gained in first iteration
################################

The following reasoning chain containing the reasoning steps is presented in order:
---------- --
Step 1: If Seattle has 20 sheep, then we can use the given ratio to calculate the number of sheep in Charleston and Toulouse. According to the problem, Charleston has 4 times as many sheep as Seattle. Therefore, Charleston has 4 * 20 = 80 sheep. Assessment Score: 1.0
---------- --

ANALYSIS: This chain of reasoning is moving in the right direction to solve the problem. The first step correctly interprets the problem statement and accurately calculates the number of sheep in Charleston based on the given information. It used the correct math operation (multiplication) to determine the number of sheep in Charleston, which was logically inferred from the problem statement.

Reasoning Step 1: This step is a logical inference based on the given problem statement. The problem statement states that Charleston has 4 times as many sheep as Seattle. Given that Seattle has 20 sheep, multiplying by 4 to find the number of sheep in Charleston is correct. This step is beneficial to the correct solution because it accurately calculates the number of sheep in Charleston, which is needed to find the total number of sheep in all three cities. There are no errors in this step.

RECOMMENDATION: This step is correct and does not require a recommendation.

RECOMMENDED: This reasoning step is recommended because it correctly interprets the problem statement and accurately calculates the number of sheep in Charleston.
Confidence score: 1.0
##########################################

 

### Experience gained in third iteration
################################

The following reasoning chain containing the reasoning steps is presented in order:
---------- --
Step 1: If Seattle has 20 sheep, then we can use the given ratio to calculate the number of sheep in Charleston and Toulouse. According to the problem, Charleston has 4 times as many sheep as Seattle. Therefore, Charleston has 4 * 20 = 80 sheep. Assessment Score: 1.0
---------- --

ANALYSIS: This chain of reasoning allows the task to be completed correctly and the goal to be reached by performing its reasoning steps. The task requires finding the total number of sheep in Toulouse, Charleston, and Seattle when it is known that there are 20 sheep in Seattle and a certain ratio of sheep in other cities to Seattle. The chain of reasoning correctly explains the problem and uses the given ratio to calculate the number of sheep in Charleston.

Reasoning Step 1: The first step correctly uses the information provided in the problem statement. It logically infers that since Charleston has 4 times as many sheep as Seattle and Seattle has 20 sheep, Charleston has 4 * 20 = 80 sheep. This step is beneficial to the correct solution because it correctly calculates the number of sheep in Charleston based on the given ratio and the number of sheep in Seattle. There are no errors in this reasoning step.

RECOMMENDATION: This step is correctly reasoned and calculated and does not require a recommendation.

RECOMMEND OR REJECT DESCRIPTION: I recommend this reasoning step because it correctly explains the problem statement, uses the given ratio, and correctly calculates the number of sheep in Charleston.
Confidence score: 1.0
##########################################

 

### Experience gained in fifth iteration
################################

The following reasoning chain containing the reasoning steps is presented in order:
---------- --
Step 1: If Seattle has 20 sheep, then we can use the given ratio to calculate the number of sheep in Charleston and Toulouse. According to the problem, Charleston has 4 times as many sheep as Seattle. Therefore, Charleston has 4 * 20 = 80 sheep. Assessment Score: 1.0
---------- --

ANALYSIS: This chain of reasoning correctly applies the information given in the problem to determine the number of sheep in Charleston. It logically infers from the given information that if Charleston has 4 times as many sheep as Seattle and Seattle has 20 sheep, then Charleston must have 4 * 20 = 80 sheep. This reasoning step is beneficial to the correct solution because it accurately calculates the number of sheep in Charleston from the given information.

Reasoning Steps 1. The first step is logically correct and follows from the problem statement. This step uses the given ratio of sheep between Charleston and Seattle to find the number of sheep in Charleston. This step is beneficial to the correct solution because it correctly applies the given ratio to find the number of sheep in Charleston. There are no errors in this step.

RECOMMENDATION: This step is logically correct and beneficial to the solution and does not require a recommendation.

RECOMMENDED: This step is recommended because it correctly applies the given ratio and calculates the number of sheep in Charleston.
Confidence score: 1.0
##########################################

 

### Experience gained in 9th iteration
################################

The following reasoning chain containing the reasoning steps is presented in order:
---------- --
Step 1: Since Charleston has 4 times as many sheep as Seattle and Seattle has 20 sheep, we can calculate the number of sheep in Charleston by multiplying by four. Assessment Score: 1.0
---------- --
ANALYSIS: The chain of reasoning in Step 1 is accurate and logically sound. It correctly applies the information given in the problem statement to determine the number of sheep in Charleston. This step is critical to solving the problem because it establishes the number of sheep in Charleston, which is then used to determine the number of sheep in Toulouse.

Reasoning Step 1. This step logically infers from the given problem statement. It correctly interprets the information that Charleston has four times as many sheep as Seattle and applies that information to calculate the number of sheep in Charleston. This step is beneficial to the correct solution because it provides the necessary information needed to calculate the total number of sheep in all three locations.

RECOMMENDATION: This step of correct reasoning and accurate calculations does not require a recommendation.

RECOMMENDATION: I recommend accepting this reasoning step because it reasons correctly and calculates accurately.
Confidence score: 1.0
##########################################

Table 17: BoT for "Toulouse has twice as many sheep as Charleston. Charleston has four times as many sheep as Seattle. When Seattle has 20 sheep, how many sheep are there in Toulouse, Charleston, and Seattle?" The partially successful reasoning process of the The chain of reasoning obtained only solved half of this problem, and usually such cases are due to the inability of the LLM used by the BoT to accurately understand the problem. As a result, although the BoT performed the correct reasoning process, it was unable to produce a complete chain of reasoning for the correct answer. Nonetheless, this chain of reasoning is still considered a success for BoT because it gives an accurate answer to the question captured by the LLM.

### Experience gained in first iteration
##### 1st reasoning chain and comments
Below is a chain of reasoning steps presented in order:
-------------------
**Step 1**: Convert the fractions of yarn used by Mariah and her grandmother into yards.Mariah used 1/4 of a skein, which equals 1/4 * 364 yards. Her grandmother used 1/2 skein of yarn, which equals 1/2 * 364 yards. Assessment Score: 1.0

**Step 2**: Calculate the total number of yards of yarn used by Mariah and her grandmother by adding the number of yards of yarn used by Mariah to the number of yards of yarn used by her grandmother. Assessment Score: 1.0

**Step 1** (Repeat): Convert the fractions of yarn used by Mariah and her grandmother into yards.Mariah used 1/4 of a skein, which equals 1/4 * 364 yards = 91 yards. Her grandmother used 1/2 skein of yarn, which equals 1/2 * 364 yards = 182 yards. Assessment Score: 1.0
-------------------
**ANALYSIS REPORT**: The chain of reasoning enables the correct completion of tasks and the attainment of goals through the execution of its reasoning steps. The steps are logical and clearly sequenced and are necessary to solve the problem. The steps convert the fraction of yarn used into yardage, which is necessary to determine how much yarn was used in total. They then add these amounts to find the total number of yarns used by Mariah and her grandmother.

Reasoning Step 1. This step correctly converts the fractions of yarn used by Mariah and her grandmother into yards. It is a logical inference to the problem statement and is beneficial to the correct solution because it converts the problem to the same units (yards), making it possible to add the quantities. RECOMMENDATION: None. RECOMMENDATION: This step is correct and should be left as is.

Reasoning Step 2. This step logically extrapolates from the previous step because it involves adding the amounts of yarn used by Mariah and her grandmother, which have been converted to the same units in the previous step. This step is beneficial to the correct solution because it calculates the total number of yarns used, which is the goal of the problem. Recommendation: None. RECOMMENDATION: This step is correct and should be left as is.

Reasoning step 1 (repeat). This step is a repetition of the first step, but the calculation has been completed. It is a logical extrapolation of the problem statement and is beneficial to the correct solution. However, it should not be repeated in the reasoning chain because it does not add new information or contribute to the progress of the solution. RECOMMENDATION: Remove this duplicate step from the reasoning chain. RECOMMENDATION: This step is correct but redundant and should be removed from the reasoning chain.
Confidence score: 1.0
### Experience gained in second iteration
##### 2nd chain of reasoning and comments
Below is a chain of reasoning steps presented in order:
-------------------
**Step 1**: Calculate the amount of yarn Mariah and her grandmother used separately by multiplying the yarn score they used by the total yardage of a skein. Assessment Score: 1.0

**Step 1**: First, we need to calculate the amount of yarn Mariah and her grandmother used separately. To do this, we can multiply the fraction of yarn they used by the total number of yards of a yarn. So, Mariah used 1/4 * 364 yards of yarn and her grandmother used 1/2 * 364 yards of yarn. Assessment Score: 1.0

**Step 2**: After figuring out the amount of yarn used by Mariah and her grandmother separately, we need to add these quantities together to find the total amount of yarn they used. So, we add Mariah's yarn (1/4 * 364 yards) and her grandmother's yarn (1/2 * 364 yards) to get the total amount of yarn they used. Assessment Score: 1.0
-------------------
**ANALYSIS REPORT**: The chain of reasoning was repetitive and contained redundant errors, with step 1 being repeated three times. However, the steps themselves were logically correct and led to the correct solution of the problem.

Reasoning Step 1. The first step is logically correct. It correctly identifies the need to calculate the amount of yarn used by Mariah and her grandmother separately by multiplying the fraction of yarn they used by the total yardage of a yarn. This step is beneficial to the correct solution because it sets the stage for calculating the total amount of yarn used. RECOMMENDATION: None. RECOMMENDATION: Approved

Reasoning Step 2. The second step follows logically from the first. After finding out how much yarn Mariah and her grandmother each used, it is logical to add these amounts to find the total amount of yarn used. This step is beneficial to the correct solution because it allows the total amount of yarn used to be calculated. RECOMMENDATION: None. Recommendation: Approved

Bug report: repeating step 1 three times is unnecessary and does not contribute to the solution. It should be modified to avoid redundancy. Recommendation: Eliminate the repetition of step 1. The reasoning chain should contain only unique steps that contribute to the solution.
Confidence score: 0.9
### Experience gained in third iteration
##### 3rd chain of reasoning and comments
Below is a chain of reasoning steps presented in order:
-------------------
**Step 1**: First, we need to figure out how many skeins Mariah and her grandma used in total.Mariah used 1/4 of a skein and her grandma used 1/2 of a skein. To find out how many skeins they used in total, we need to add 1/4 and 1/2. Assessment Score: 1.0

**Step 2**: After finding out how many total skeins of yarn they used, convert that to yards. We know that 1 skein of yarn equals 364 yards. So, multiply the total number of yarns used by 364 to find the total number of yards (273) of yarn they used. Assessment Score: 1.0
-------------------
**ANALYSIS**: The reasoning chain is able to complete the task correctly and reach the goal. The task was to find out how many yards of yarn Mariah and her grandmother used in total. The inference chain first calculates the total number of rolls of yarn Mariah and her grandmother used by adding up the fractions of yarn they used. It then converts this total yarn count to yards, which is the desired final answer.

Reasoning Step 1: The first step is a logical inference because it correctly recognizes that the first step in solving the problem is to add the yarn fractions used by Mariah and her grandmother. This step is beneficial to the correct solution because it sets the stage for the next step of converting yarn to yardage. No errors were found in this step. RECOMMENDATION: No recommendation is needed as this step is reasoned correctly. RECOMMENDATION: I recommend this step because it correctly identifies the total number of yarns that need to be calculated for use in the first place.

Reasoning Step 2: The second step is logically extrapolated from the first step. It correctly recognizes that the total number of yarns used needs to be converted to yards to answer the question. This step is beneficial to the correct solution because it leads directly to the final answer. No errors were found in this step. RECOMMENDATION: Since this step reasoned correctly, no recommendation is needed.

RECOMMENDATION: I recommend this step because it correctly identifies the need to convert the total number of yarns used to yards.
Confidence score: 1.0
### Experience gained in 6th iteration
#### 1st 6 Chain of Reasoning and Comments
Below is a chain of reasoning steps presented in order:
-------------------
**Step 1**: Calculate the amount of yarn Mariah used by multiplying the total yardage of a skein by the fraction Mariah used (1/4), and similarly, calculate the amount of yarn her grandma used by multiplying the total yardage of a skein by the fraction her grandma used (1/2).Mariah used: 1/4 * 364 = 91 yards. Grandma used: 1/2 * 364 = 182 yards. Assessment Score: 1.0

**Step 2**: Add the amount of yarn used by Mariah to the amount of yarn used by her grandmother to find the total amount of yarn used. Total amount of yarn used = 273 yards. Assessment Score: 1.0

**Step 3**: Declare the total amount of yarn used by Mariah and her grandmother.Mariah and her grandmother used a total of 273 yards of yarn. Assessment Score: 1.0
-------------------
**ANALYSIS REPORT**: The chain of reasoning is logically sound and completes the task correctly. The chain of reasoning first calculates how much yarn Mariah and her grandmother each used, then adds these amounts to find the total amount of yarn used, and finally declares the total amount of yarn.

Reasoning Step 1. The first step is logical because it directly applies the information given in the problem and is beneficial to the correct solution because it provides the respective amount of yarn used. RECOMMENDATION: This step is correct and should be maintained.

Table 18: BoT's answer to the question "Maria's grandmother is teaching her to knit, Maria is using 1/4 twist yarn, her grandmother is using 1/2 twist yarn, and one twist of yarn is 364 yards long, how many yards of yarn are they using together?" The successful reasoning process of

The layman's guide to getting started with AI

Help you learn how to utilize AI tools at a low cost and from a zero base.AI, like office software, is an essential skill for everyone. Mastering AI will give you an edge in your job search and half the effort in your future work and studies.

View Details>