HuggingFace reverses out the technical details behind o1 and open-sources it!

If small models are given longer to think, they can outperform larger models.

In recent times, there has been an unprecedented amount of enthusiasm in the industry for small models, with a few 'practical tricks' to allow them to outperform larger scale models in terms of performance.

Arguably, there is a corollary to focusing on improving the performance of smaller models. For large language models, the scaling of train-time compute has dominated their development. While this paradigm has proven to be very effective, the resources required for pre-training larger and larger models have become prohibitively expensive, and multi-billion dollar clusters have emerged.

As a result, this trend has sparked a great deal of interest in another complementary approach, namely test-time compute scaling. Instead of relying on ever-larger pre-training budgets, test-time methods use dynamic inference strategies that allow models to 'think longer' on harder problems. A prominent example is OpenAI's o1 model, which has shown consistent progress on difficult math problems as the amount of test-time computation increases.

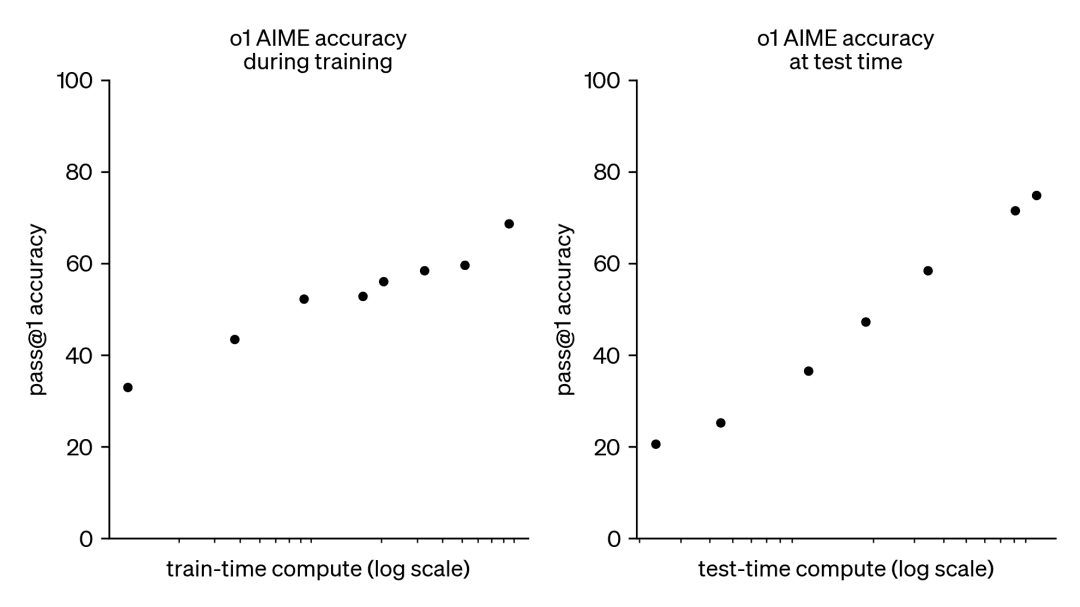
While we do not know exactly how o1 is trained, recent research from DeepMind suggests that optimal scaling of test-time computation can be achieved through strategies such as iterative self-improvement or searching over the solution space using a reward model. By adaptively allocating test-time computation on a prompt-by-prompt basis, smaller models can match and sometimes even surpass larger, resource-intensive models. Scaling time-to-computation is especially beneficial when memory is limited and available hardware is insufficient to run larger models. However this promising approach was demonstrated with closed-source models and no implementation details or code was released.

DeepMind paper: https://arxiv.org/pdf/2408.03314

Over the past few months, HuggingFace has been delving into trying to reverse engineer and reproduce these results. They are going to present in this blog post:

• Compute-optimal scaling (compute-optimal scaling):Enhance the mathematical power of open models at test time by implementing DeepMind tricks.
• Diversity Validator Tree Search (DVTS):It is an extension developed for the validator bootstrap tree search technique. This simple and efficient approach increases diversity and provides better performance, especially when tested with a large computational budget.
• Search and learn:A lightweight toolkit for implementing search strategies using LLM with the vLLM Realize the speed increase.

So how well do computationally optimal scaling work in practice? In the figure below, the very small 1B and 3B Llama Instruct models outperform the much larger 8B, 70B models on the challenging MATH-500 benchmark, if you give them enough 'thinking time'.

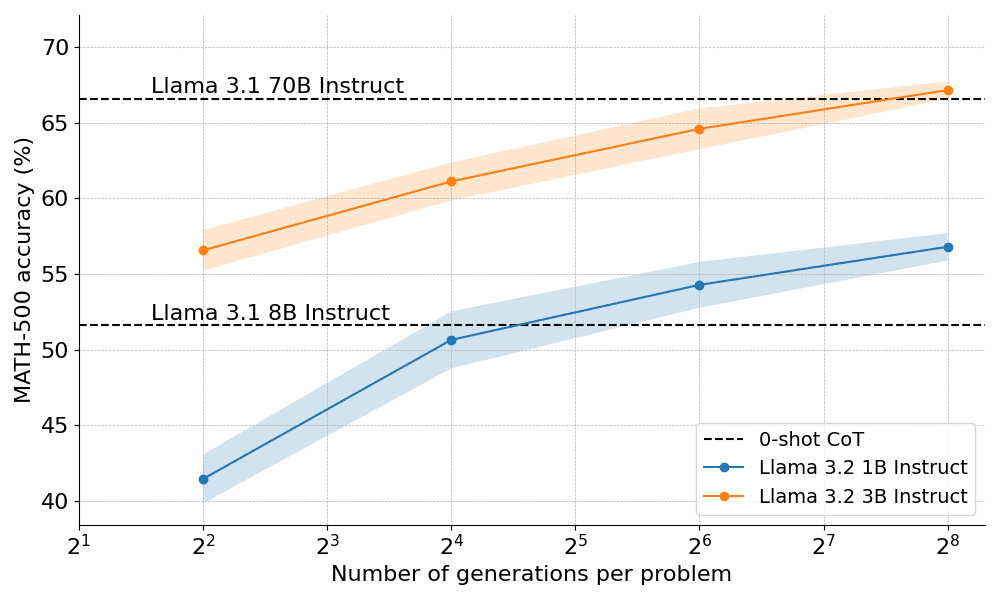
Only 10 days after the public debut of OpenAI o1, we're excited to unveil an open source version of the breakthrough technology behind its success: Extended Test-Time Computing," said Clem Delangue, Co-Founder and CEO of HuggingFace. By giving the model longer "thinking time", the 1B model can beat 8B, and the 3B model can beat 70B. Of course, the full recipe is open source.

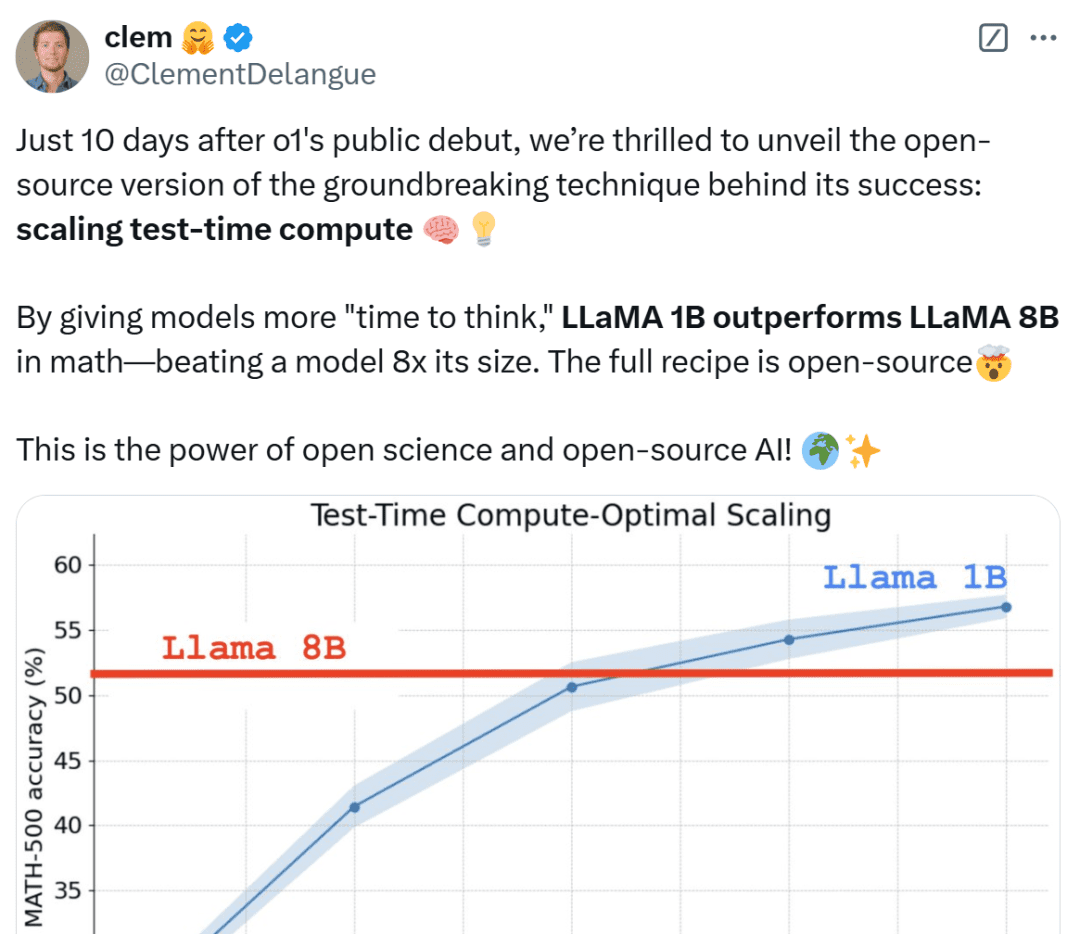
Various netizens are not calm when they see these results, calling them unbelievable and considering it a victory for the miniatures.

Next, HuggingFace delves into the reasons behind these results and helps readers understand practical strategies for implementing computational scaling while testing.

Extended test-time computation strategy

There are two main strategies for extending the test-time computation:

• Self-improvement: the model iteratively improves its output or 'idea' by recognizing and correcting errors in subsequent iterations. While this strategy is effective on some tasks, it usually requires the model to have a built-in self-improvement mechanism, which may limit its applicability.
• Search against a validator: this approach focuses on generating multiple candidate answers and using a validator to select the best answer. Validators can be based on hard-coded heuristics or learned reward models. In this paper, we will focus on learned validators, which include techniques such as Best-of-N sampling and tree search. Such search strategies are more flexible and can be adapted to the difficulty of the problem, although their performance is limited by the quality of the validator.

HuggingFace focuses on search-based methods that are practical and scalable solutions for computational optimization at test time. Here are three strategies:

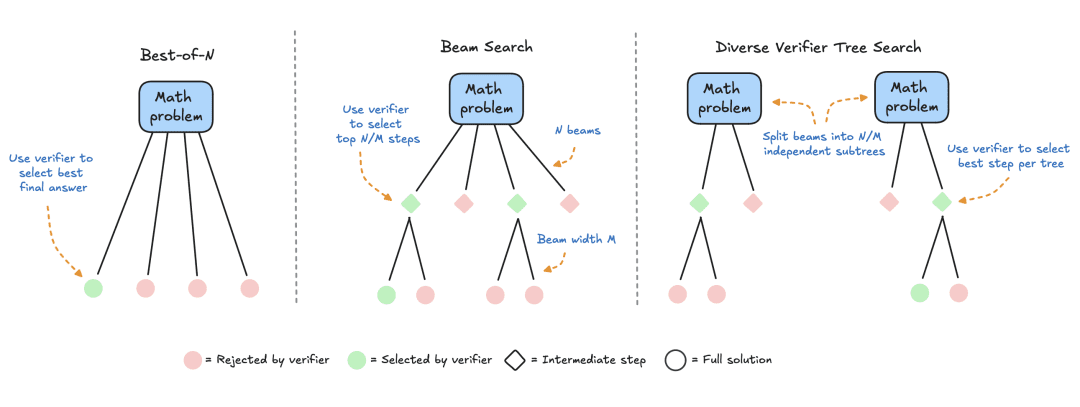
• Best-of-N: Typically uses a reward model to generate multiple responses for each question and assigns a score to each candidate answer, then selects the answer with the highest reward (or a weighted variant as discussed later). This approach emphasizes answer quality over frequency.
• Cluster Search: A systematic search method for exploring the solution space, often used in conjunction with Process Reward Models (PRMs) to optimize the sampling and evaluation of intermediate steps in problem solving. Unlike traditional reward models that produce a single score for the final answer, PRMs provide a series of scores, one for each step of the reasoning process. This fine-grained feedback capability makes PRMs a natural choice for LLM search methods.
• Diversity Validator Tree Search (DVTS): a cluster search extension developed by HuggingFace that splits the initial cluster into separate subtrees and then greedily expands these subtrees using PRM. This approach improves the diversity and overall performance of the solution, especially if the computational budget is large at the time of testing.

Experimental setup

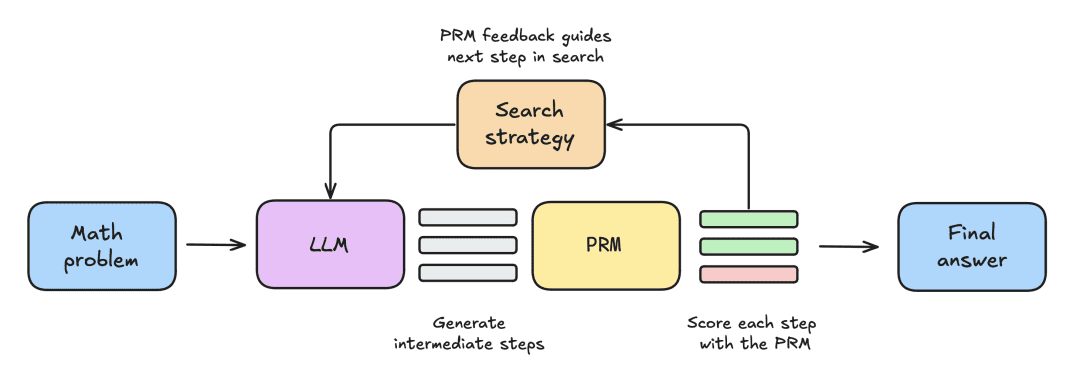
The experimental setup consisted of the following steps:

• The LLM is first given a mathematical problem to generate N partial solutions, e.g., intermediate steps in the derivation process.
• Each step is scored by a PRM, which estimates the probability that each step will end up with the correct answer.
• Once the search strategy is complete, the final candidate solutions are sorted by the PRM to produce the final answer.

To compare various search strategies, the following open source models and datasets are used in this paper:

• Models: use meta-llama/Llama-3.2-1B-Instruct as the primary model for extended test-time computation;
• Process Reward Model PRM: To guide the search strategy, this paper uses RLHFlow/Llama3.1-8B-PRM-Deepseek-Data, an 8 billion reward model trained with process supervision. Process supervision is a training method where the model receives feedback at every step of the reasoning process, not just the final result;
• Dataset: This paper was evaluated on the MATH-500 subset, a MATH benchmark dataset released by OpenAI as part of a process-supervised study. These math problems cover seven subjects and are challenging for humans and most large language models.

This article will start with a simple baseline and then gradually incorporate other techniques to improve performance.

majority vote

Majority voting is the most straightforward way to aggregate LLM output. For a given math problem, N candidate solutions are generated and the answer that occurs most frequently is selected. In all experiments, this paper samples up to N=256 candidate solutions, with a temperature parameter T=0.8, and generates up to 2048 tokens for each problem.

Here's how the majority of votes performed when applied to the Llama 3.2 1B Instruct:

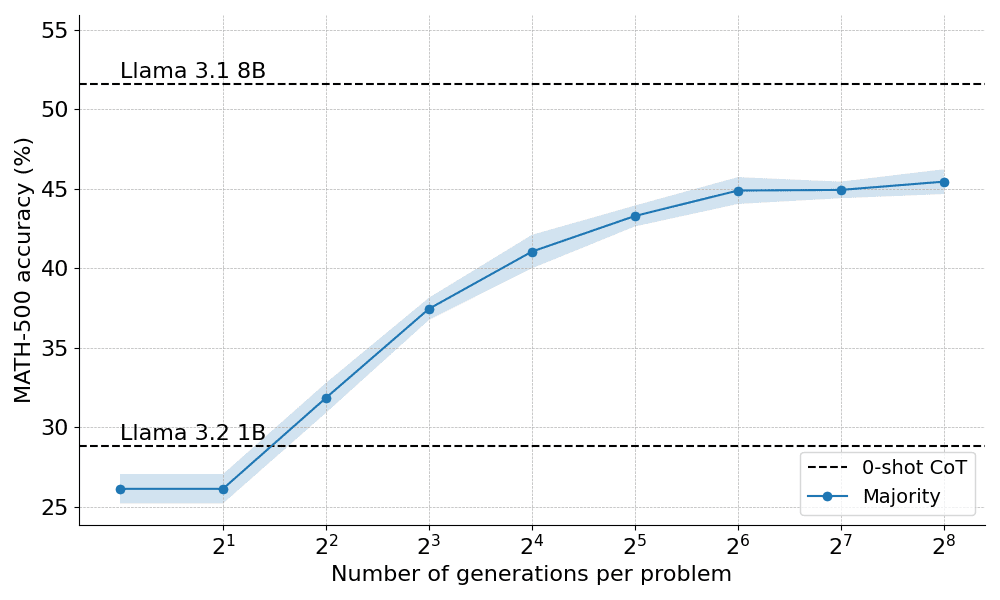
The results show that majority voting provides a significant improvement over the greedy decoding baseline, but its gains begin to level off after about N = 64 generations. This limitation arises because majority voting has difficulty solving problems that require careful reasoning.

Based on the limitations of majority voting, let's see how we can incorporate a reward model to improve performance.

Beyond the Majority: Best-of-N

Best-of-N is a simple and efficient extension of the majority voting algorithm that uses a reward model to determine the most reasonable answer. There are two main variants of the method:

Ordinary Best-of-N: Generate N independent responses and choose the one with the highest RM reward as the final answer. This ensures that the response with the highest confidence is chosen, but it does not take into account consistency between responses.

Weighted Best-of-N: Summarizes the scores of all identical responses and selects the answer with the highest total reward. This method prioritizes high-quality responses by increasing the score through repeated occurrences. Mathematically, responses are weighted a_i:

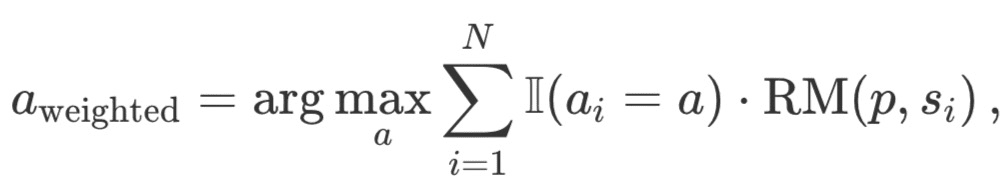
where RM (p,s_i) is the reward model score for the ith solution s_i to problem p.

Typically, one uses the Outcome Reward Model (ORM) to obtain individual solution-level scores. However, for a fair comparison with other search strategies, the same PRM is used to score Best-of-N solutions. As shown in the figure below, the PRM generates a cumulative sequence of step-level scores for each solution, and therefore steps need to be statistically (reductively) scored to obtain individual solution-level scores:

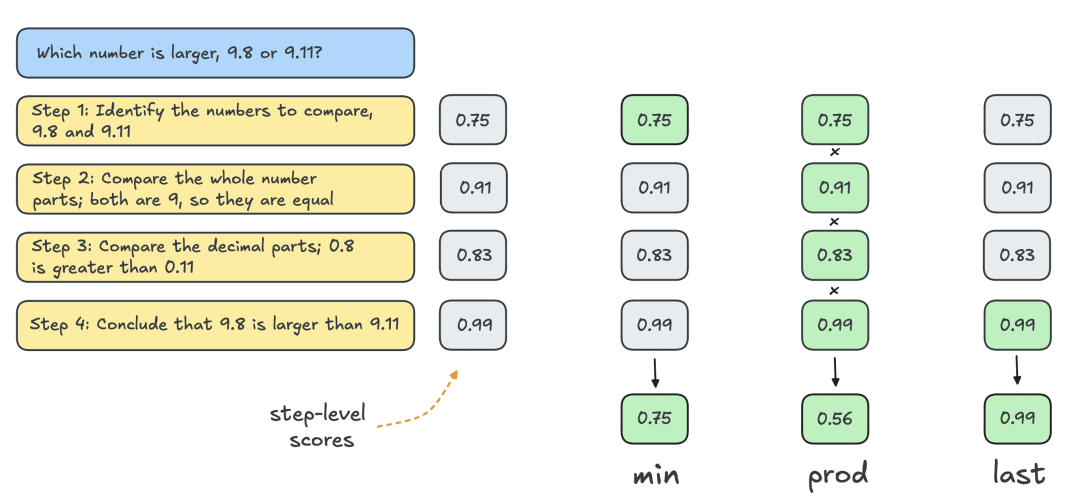
The most common statutes are listed below:

• Min: Use the lowest score from all steps.
• Prod: use the product of step fractions.
• Last: Use the final score from the step. This score contains cumulative information from all previous steps, thus effectively treating the PRM as an ORM capable of scoring partial solutions.

Below are the results obtained by applying the two variants of Best-of-N:

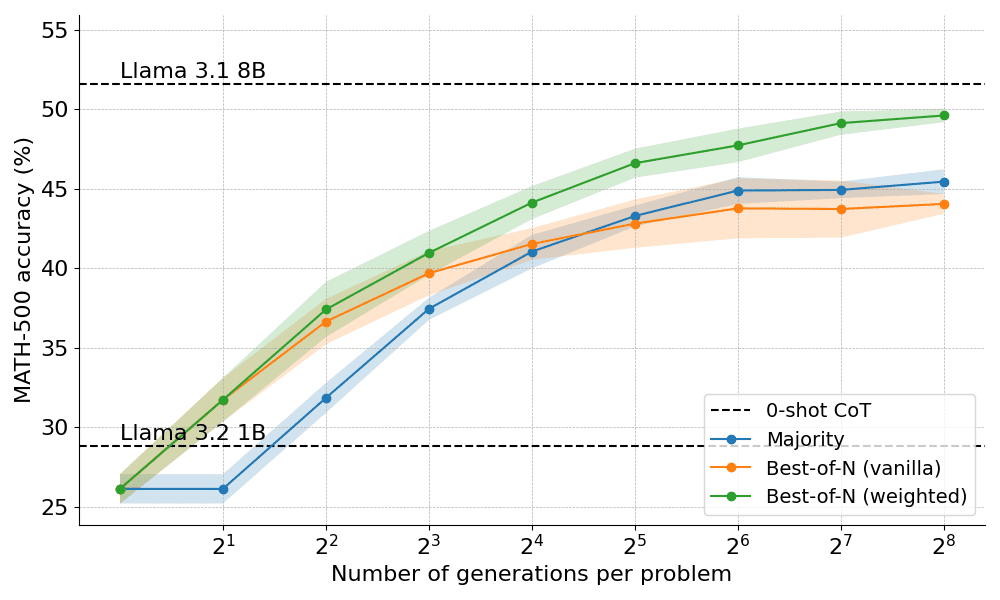
The results reveal a clear advantage: weighted Best-of-N consistently outperforms regular Best-of-N, especially with larger generation budgets. Its ability to aggregate the scores of identical answers ensures that even less frequent but higher quality answers are effectively prioritized.

However, despite these improvements, it still falls short of the performance achieved by the Llama 8B model and the Best-of-N method begins to stabilize at N=256.

Can the boundaries be pushed further by progressively monitoring the search process?

Cluster Search with PRM

As a structured search method, cluster search allows for the systematic exploration of the solution space, making it a powerful tool for improving model outputs at test time. When used in conjunction with PRM, cluster search can optimize the generation and evaluation of intermediate steps in problem solving. Cluster search works in the following way:

1. Multiple candidate solutions are iteratively generated by keeping a fixed number of 'clusters' or active paths N .
2. In the first iteration, N independent steps are taken from the LLM with temperature T to introduce diversity in the responses. These steps are usually defined by a stopping criterion, such as termination at new row n or double new row nn.
3. Each step is scored using PRM and the top N/M steps are selected as candidates for the next round of generation. Here M denotes the "cluster width" of a given activity path. As with Best-of-N, the "last" statute is used to score partial solutions for each iteration.
4. Extend the steps selected in step (3) by sampling M subsequent steps in the solution.
5. Repeat steps (3) and (4) until EOS is achieved token or exceeds the maximum search depth.

By allowing the PRM to evaluate the correctness of intermediate steps, cluster search can identify and prioritize promising paths early in the process. This step-by-step evaluation strategy is particularly useful for complex reasoning tasks such as math, due to the fact that validating partial solutions can significantly improve the final result.

Realization details

In the experiments, HuggingFace followed DeepMind's hyperparameter selection and ran the cluster search as follows:

• Calculate the N clusters when scaling to 4, 16, 64, 256
• Fixed cluster width M=4
• Sampling at temperature T=0.8
• Up to 40 iterations, i.e. a tree with a maximum depth of 40 steps

As shown in the figure below, the results are astounding: with a test time budget of N=4, cluster search achieves the same accuracy as Best-of-N with N=16, i.e., a 4x improvement in computational efficiency! Furthermore, the performance of cluster search is comparable to that of Llama 3.1 8B, requiring only N=32 solutions per problem. The average performance of computer science PhD students in math is about 40%, so close to 55% is pretty good for a 1B model!

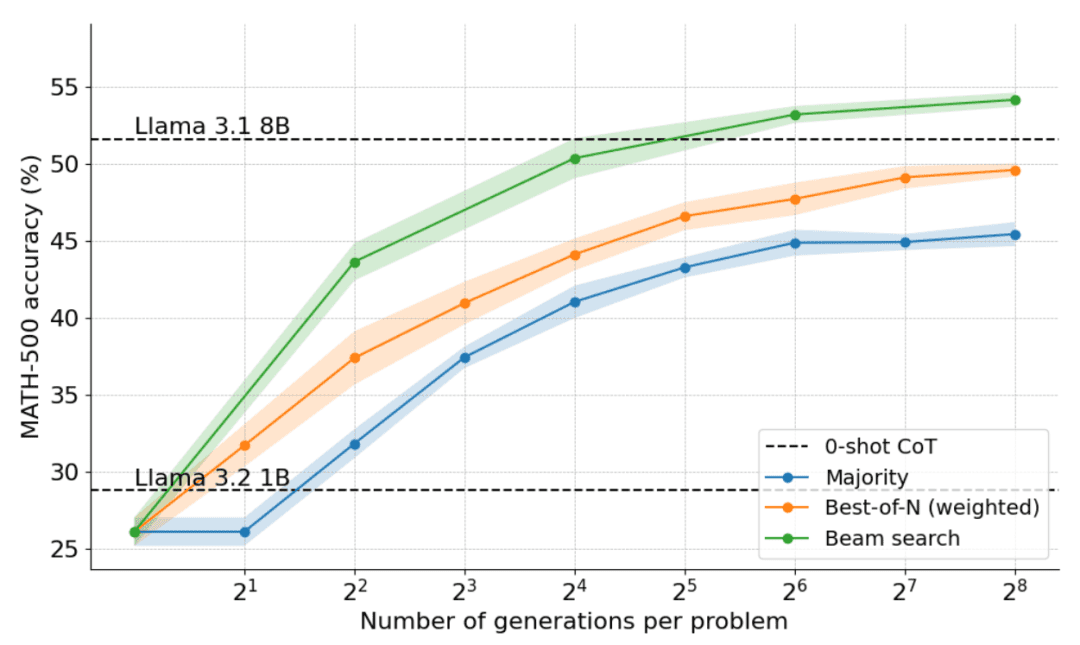
Which problems are best solved by cluster search

While it's clear overall that cluster search is a better search strategy than Best-of-N or majority voting, DeepMind's paper shows that there are tradeoffs for each strategy, depending on the difficulty of the problem and the computational budget at the time of testing.

To understand which problems are best suited for which strategy, DeepMind computed the distribution of estimated problem difficulty and divided the results into quintiles. In other words, each problem was assigned to one of five levels, with level 1 indicating easier problems and level 5 indicating the most difficult problems. To estimate the problem difficulty, DeepMind generated 2048 candidate solutions for each problem with standard sampling and then proposed the following heuristic:

• Oracle: Estimate pass@1 scores for each question using basic fact labels, and categorize the distribution of pass@1 scores to determine quintiles.
• Modeling: use the distribution of mean PRM scores for each problem to determine quintiles. The intuition here is that harder problems will have lower scores.

The following figure shows a breakdown of the various methods based on the pass@1 score and the budget N=[4,16,64,256] computed over the four tests:

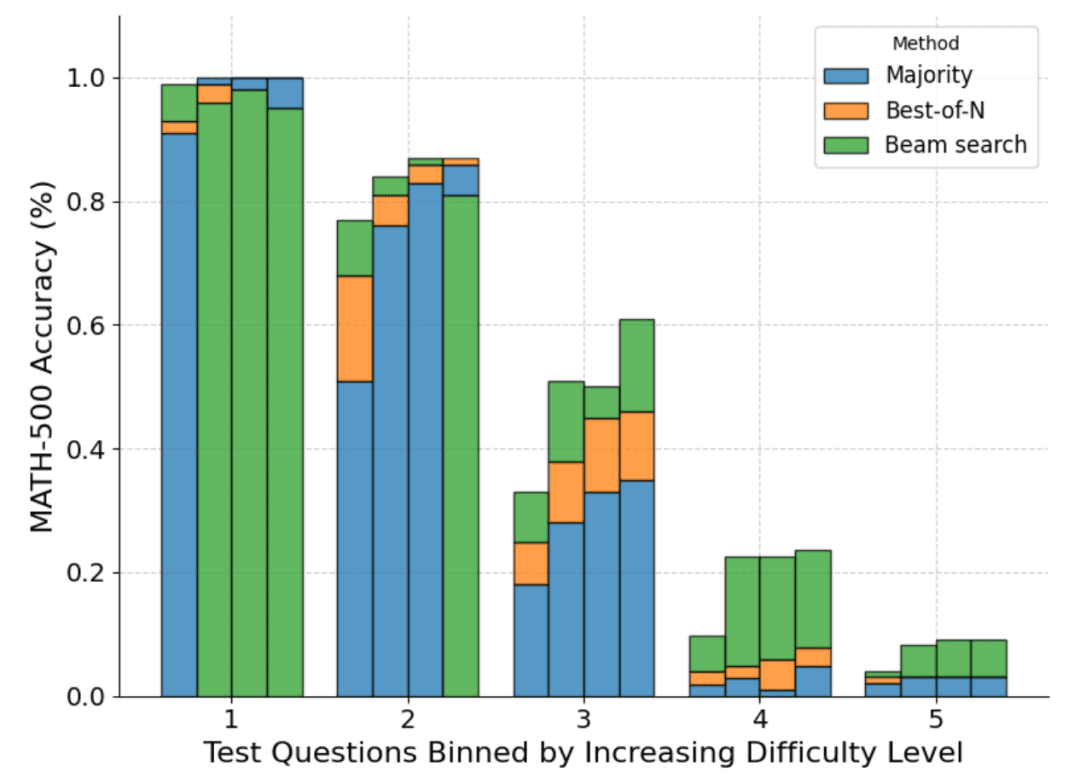
As can be seen, each bar represents the budget calculated at the time of the test and the relative accuracy of each method is shown within each bar. For example, in the four bars for difficulty level 2:

Majority voting is the worst performing method of all computational budgets, except for N=256 (cluster search performs worst).

Cluster search is best for N=[4,16,64], but Best-of-N is best for N=256.

It should be noted that cluster search has made consistent progress in moderately and difficult difficulty problems (levels 3-5), but it tends to perform worse than Best-of-N (or even majority voting) on simpler problems, especially with larger computational budgets.

By looking at the result tree generated by cluster search, HuggingFace realized that if a single step was assigned a high reward, then the entire tree collapsed on that trajectory, thus affecting diversity. This motivated them to explore a cluster search extension that maximizes diversity.

DVTS: Enhancing Performance through Diversity

As seen above, cluster search has better performance than Best-of-N, but tends to perform poorly when dealing with simple problems and large computational budgets at the time of testing.

To address this problem, HuggingFace has developed an extension called 'Diversity Validator Tree Search' (DVTS), which aims to maximize diversity when N is large.

DVTS works in a similar way to cluster search with the following modifications:

• For a given N and M, the initial set is expanded into N/M independent subtrees.
• For each subtree, select the step with the highest PRM score.
• Generate M new steps from the node selected in step (2) and select the step with the highest PRM score.
• Repeat step (3) until the EOS token or maximum tree depth is reached.

The following graph shows the results of applying DVTS to Llama 1B:

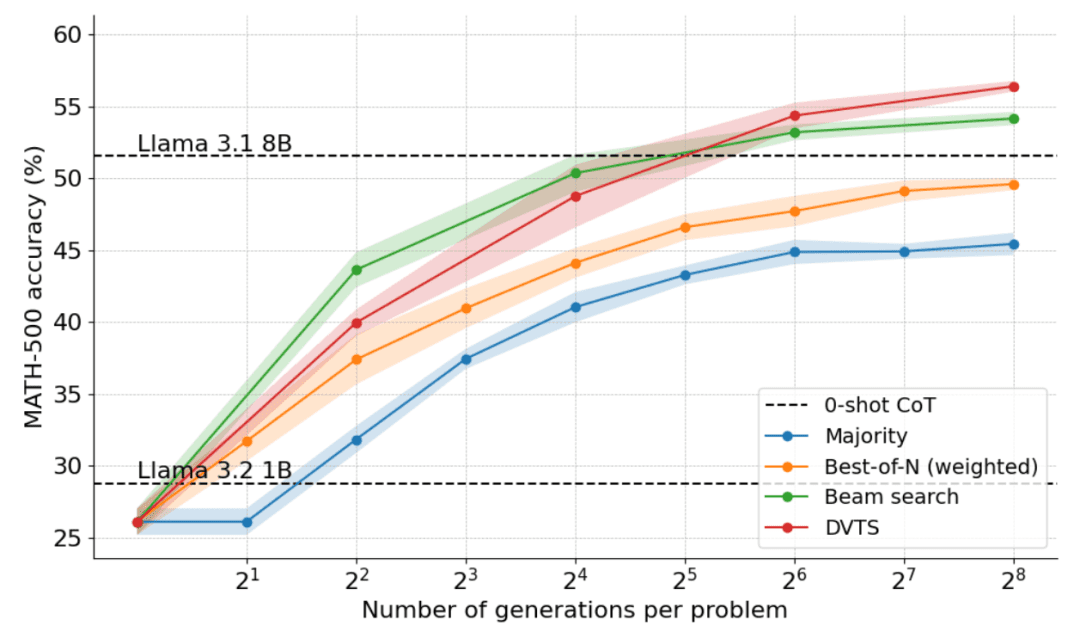
It can be seen that DVTS provides a complementary strategy to cluster search: at small N, cluster search is more effective in finding the correct solution; but at larger N, the diversity of DVTS candidates comes into play and better performance can be achieved.

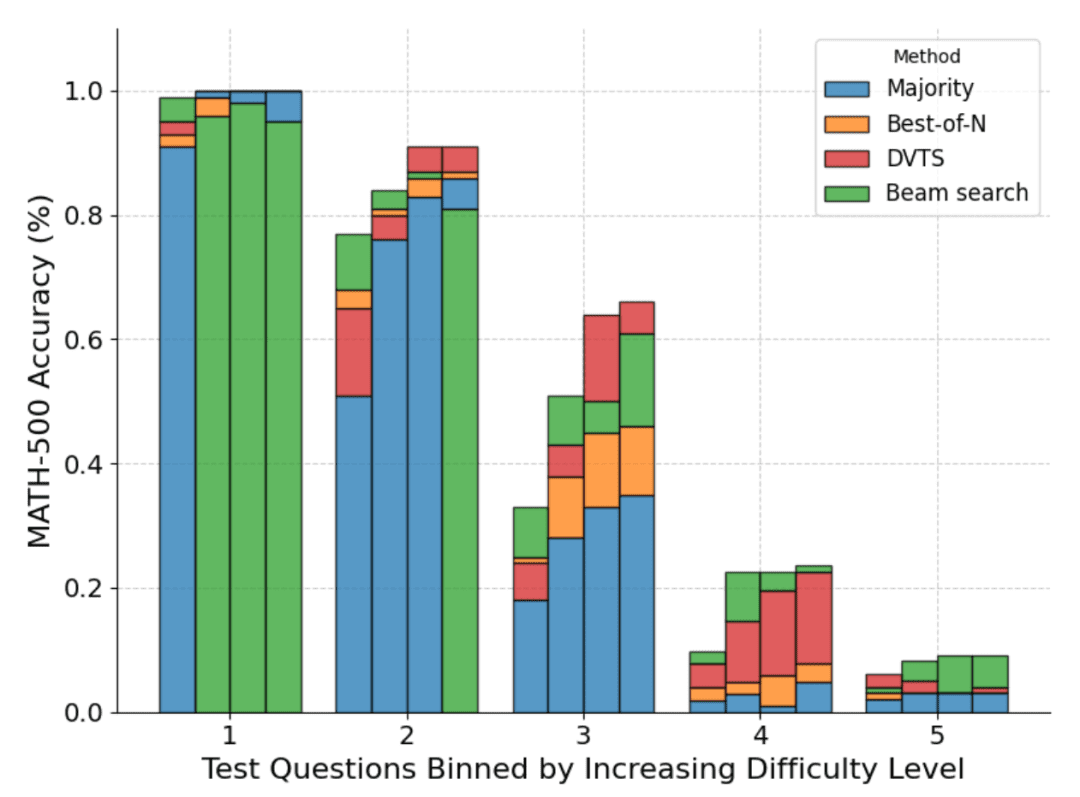
In addition in the problem difficulty breakdown, DVTS improves the performance of simple/medium problems with large N, while cluster search performs best with small N.

Compute-optimal scaling (compute-optimal scaling)

With a wide variety of search strategies, a natural question is which one is the best? In DeepMind's paper (available as Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters ), they propose a computationally-optimal scaling strategy that selects the search method and the hyper parameter θ in order to achieve optimal performance for a given computational budget N :

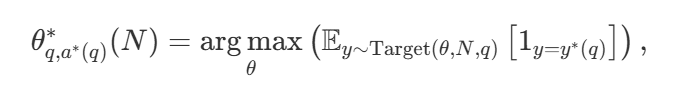
included among these 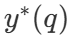is the correct answer to question q. 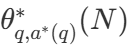Representation Computing - The Optimal Scaling Strategy. Since it is straightforward to compute 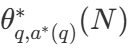Somewhat tricky, DeepMind proposes an approximation based on the difficulty of the problem, i.e., allocating computational resources for testing based on which search strategy achieves the best performance at a given difficulty level.

For example, for simpler problems and lower computational budgets, it is better to use strategies such as Best-of-N, while for harder problems, set shu search is a better choice. The figure below shows the computation-optimization curve!

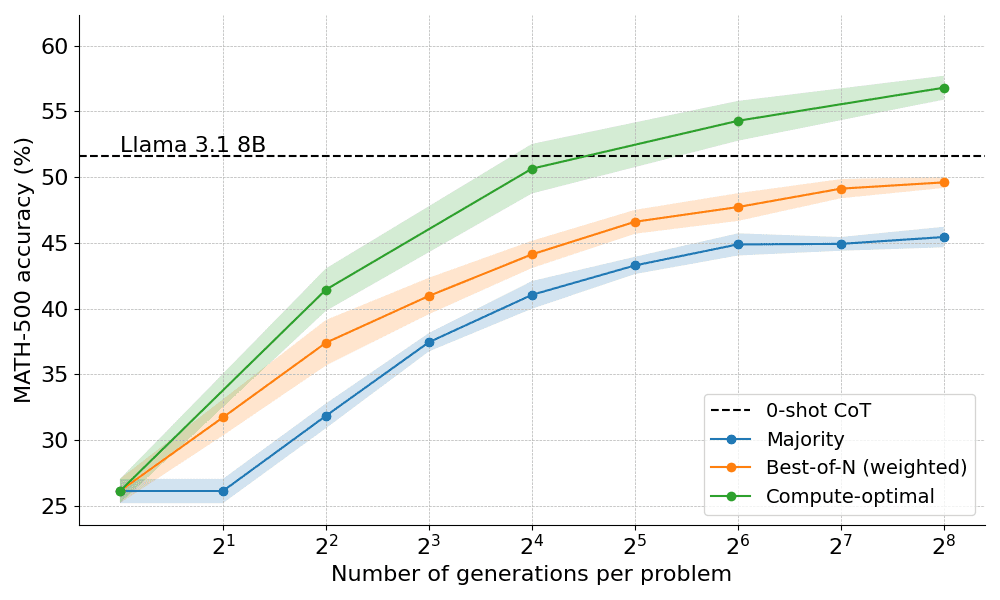
Extension to larger models

This paper also explores the extension of the compute-optimal approach to the Llama 3.2 3B Instruct model to see at which point the PRM starts to weaken when compared to the capacity of the policy itself. The results show that the computational-optimal extension works very well, with the 3B model outperforming the Llama 3.1 70B Instruct (which is 22 times the size of the former!). .

What's next?

The exploration of test-time computational scaling reveals the potential and challenges of utilizing search-based approaches. Looking ahead, this paper suggests several exciting directions:

• Strong Validators: Strong validators play a key role in improving performance, and improving the robustness and generalizability of validators is critical to advancing these approaches;
• Self-validation: the ultimate goal is to achieve self-validation, i.e. the model can autonomously validate its own output. This approach seems to be what models such as o1 are doing, but is still difficult to achieve in practice. Unlike standard supervised fine-tuning (SFT), self-validation requires a more elaborate strategy;
• (a) Integrating thinking into the process: Incorporating explicit intermediate steps or thinking into the generative process can further enhance reasoning and decision-making. By incorporating structured reasoning into the search process, better performance on complex tasks can be achieved;
• Search as a data generation tool: the method can also act as a powerful data generation process to create high quality training datasets. For example, fine-tuning a model such as Llama 1B based on the correct trajectories generated by search can provide significant benefits. This strategy-based approach is similar to techniques such as ReST or V-StaR, but with the added benefit of search, providing a promising direction for iterative improvement;
• Calling more PRMs: There are relatively few PRMs, limiting their wider application. Developing and sharing more PRMs for different domains is a key area where the community can make a significant contribution.