Herausfordernde Probleme auf Olympia-Niveau: Eine Überprüfung von 7 Mainstream-LLM-Mathematik-Leistungsbenchmarks für China

Mathematische Fähigkeiten, die die Ableitung von Formeln, die Konstruktion logischer Ketten und abstraktes Denken umfassen, gelten seit langem als Schlüsselbereich für die Prüfung der Fähigkeiten von Künstlicher Intelligenz (KI), insbesondere von groß angelegten Sprachmodellen (LLM). Dies liegt daran, dass nicht nur die Rechenleistung getestet wird, sondern auch die Fähigkeit des Modells, komplexe Probleme zu denken, zu verstehen und zu lösen.

Jüngste Ergebnisse eines Teams an der ETH Zürich zeigen jedoch, dass selbst die besten Large Language Models (LLMs) im Allgemeinen schlecht abschneiden, wenn sie mit schwierigen mathematischen Wettbewerbsfragen konfrontiert werden, wie z. B. bei der US-Mathematikolympiade, was eine Diskussion über die wahren Fähigkeiten der derzeitigen LLMs in Bezug auf strenges mathematisches Denken auslöste.

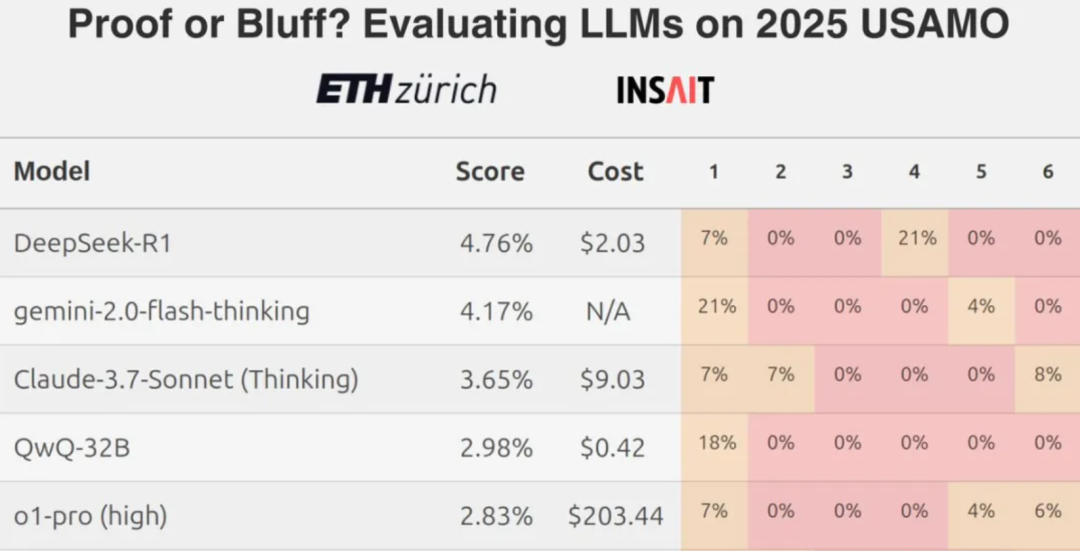
In diesem Zusammenhang stellt sich natürlich die Frage: Wie gut schneiden diese Modelle bei der Bewältigung mathematischer Probleme ab, die in chinesischer Sprache formuliert sind? In dieser Untersuchung wurden insgesamt sieben gängige oder neu entstehende großsprachige Modelle aus dem In- und Ausland ausgewählt, um ihre mathematischen Fähigkeiten anhand von Problemen aus dem Alibaba Global Maths Competition und der chinesischen Mathematik-Olympiade zu vergleichen.

Zu den an dem Test beteiligten Modellen gehören:

• Inländische Modelle:DeepSeek R1undHunyuan T1undTongyi Qwen-32B (Originaltext) 通义 QwQ-32B),YiXin-Distill-Qwen-72B
• Internationale Modellierung:Grok 3 betaundGemini 2.0 Flash Thinkingundo3-mini

Bewertung der Gesamtleistung

Der Test besteht aus 10 Fragen mit hohem Schwierigkeitsgrad und insgesamt 13 Fragen, die mit Punkten bewertet werden. Die Bewertungskriterien waren: 1 Punkt für vollständige Korrektheit, 0,5 Punkte für teilweise Korrektheit und keine Punkte für Fehler.

Die Gesamtkorrektheit der einzelnen Modelle in diesem Test ist wie folgt:

Detaillierte Punkteverteilungen zeigen die Leistungsunterschiede zwischen den Modellen:

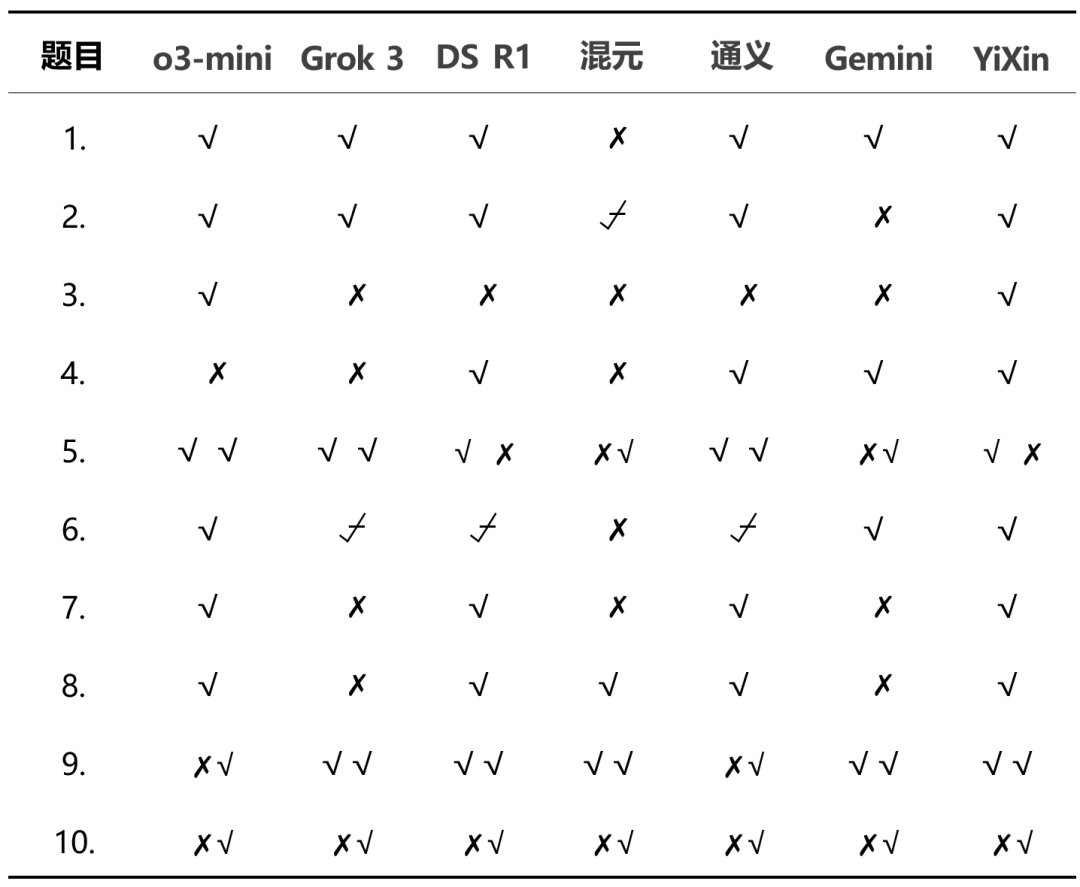
Aus den Gesamtergebnissen.o3-mini im Gesang antworten YiXin-Distill-Qwen-72B schnitt in diesem Test gut ab und bewies starke mathematische Problemlösungskompetenzen. Die Leistungen der anderen Modelle waren unterschiedlich.

Nachfolgend finden Sie spezifische Antworten auf einige der Testfragen.

Details zur Messung

Runde 1: Das Problem des Wandels

Frage: Opa hat 60 Dollar und geht in den Supermarkt, um Gemüse im Wert von 20 Dollar zu kaufen. Wie könnte der Kassierer Opa sein Wechselgeld geben?

Analyse: Bei dieser Frage handelt es sich um eine grundlegende arithmetische Anwendungsfrage, die das Verständnis des Modells für Lebensszenarien und grundlegende Geldberechnungsfähigkeiten prüft.

Ergebnisse:
o3-mini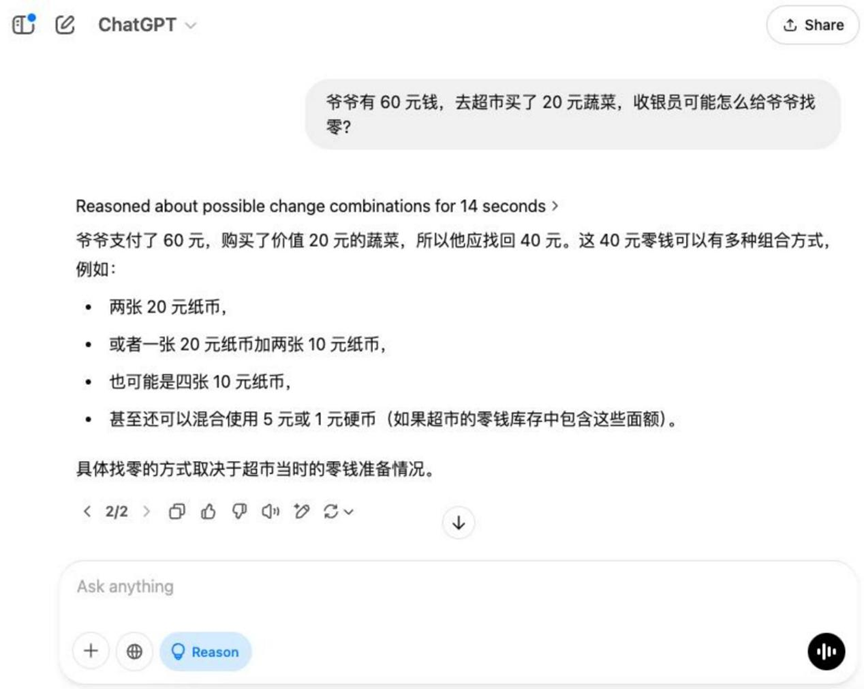

Grok 3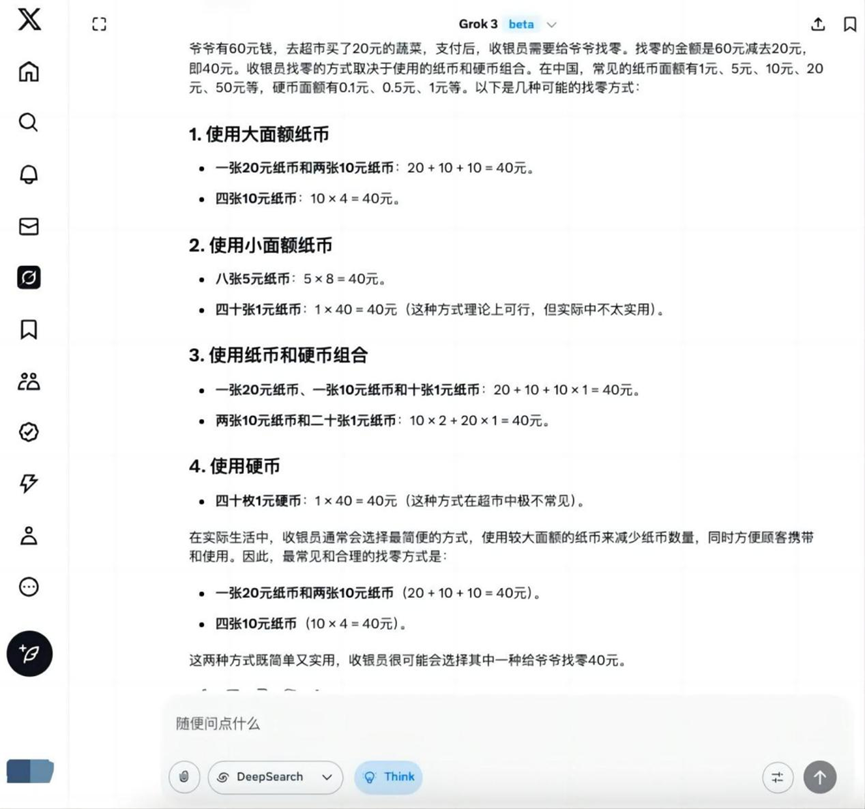

DeepSeek R1

Hunyuan T1

Gemini 2.0 Flash Thinking

YiXin-Distill-Qwen-72B

Zu diesem grundlegenden Thema, zusätzlich zu Hunyuan T1 Abgesehen davon ergeben die übrigen Modelle die richtige Lösung, um die Null zu finden.

Runde 2: Berechnung der Gehstrecken und methodische Beurteilungen

Frage: Xiao Ming und Xiao Hua gehen jeden Tag zur Schule. Ming geht 48 Meter pro Minute und Hua geht 55 Meter pro Minute. Das Haus von Xiaoming ist 384 Meter von der Schule entfernt. Xiaohua braucht 4 Minuten länger als Ming, um von zu Hause zur Schule zu kommen. Wie weit ist Xiaohuas Haus von der Schule entfernt? Welche der folgenden Methoden ist falsch, und warum?

Methode 1: 55 × 4 = 220 (Meter), 384 + 220 = 604 (Meter)
Methode 2: 384 / 48 = 8 (Minuten), 55 × (8 + 4) = 660 (Meter)

Analyse: Diese Frage kombiniert die Berechnung von Reiseproblemen und logisches Urteilsvermögen, wobei das Modell nicht nur in der Lage sein muss, die richtige Antwort zu berechnen, sondern auch in der Lage sein muss, die Richtigkeit oder Unrichtigkeit der gegebenen Lösung zu analysieren, wobei mehrstufiges Denken und logisches Unterscheidungsvermögen geprüft werden.

Ergebnisse:
DeepSeek R1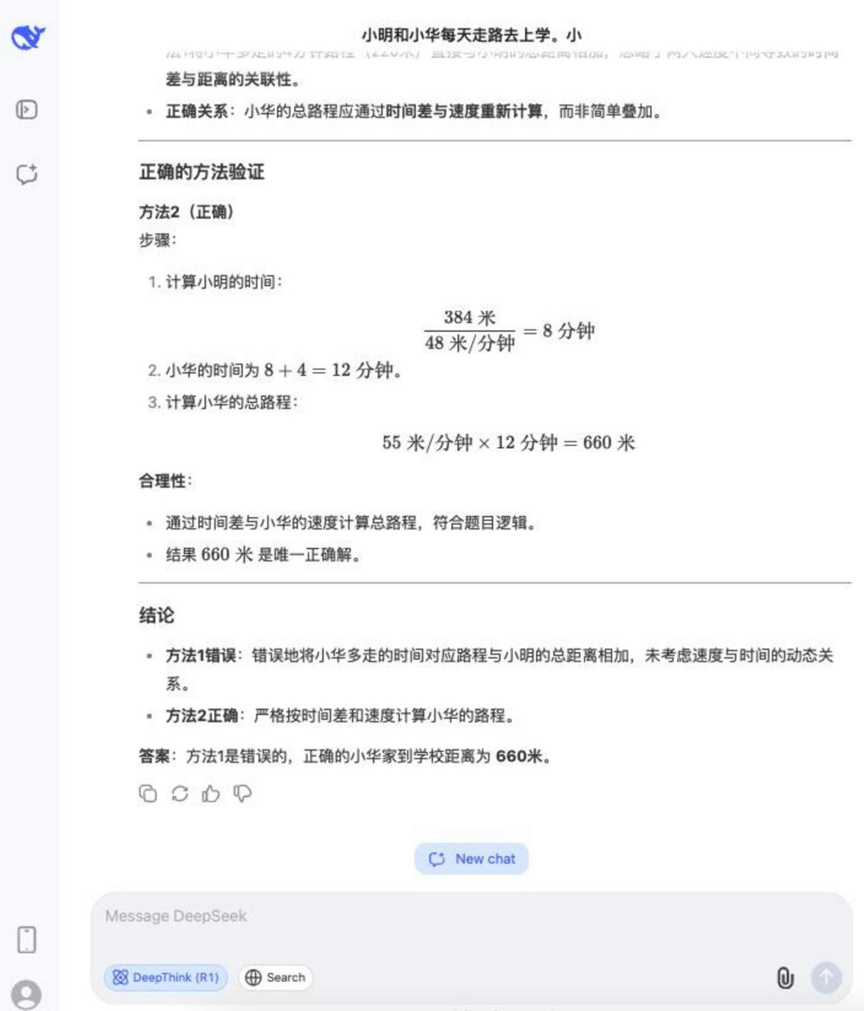

Tongyi Qwen-32B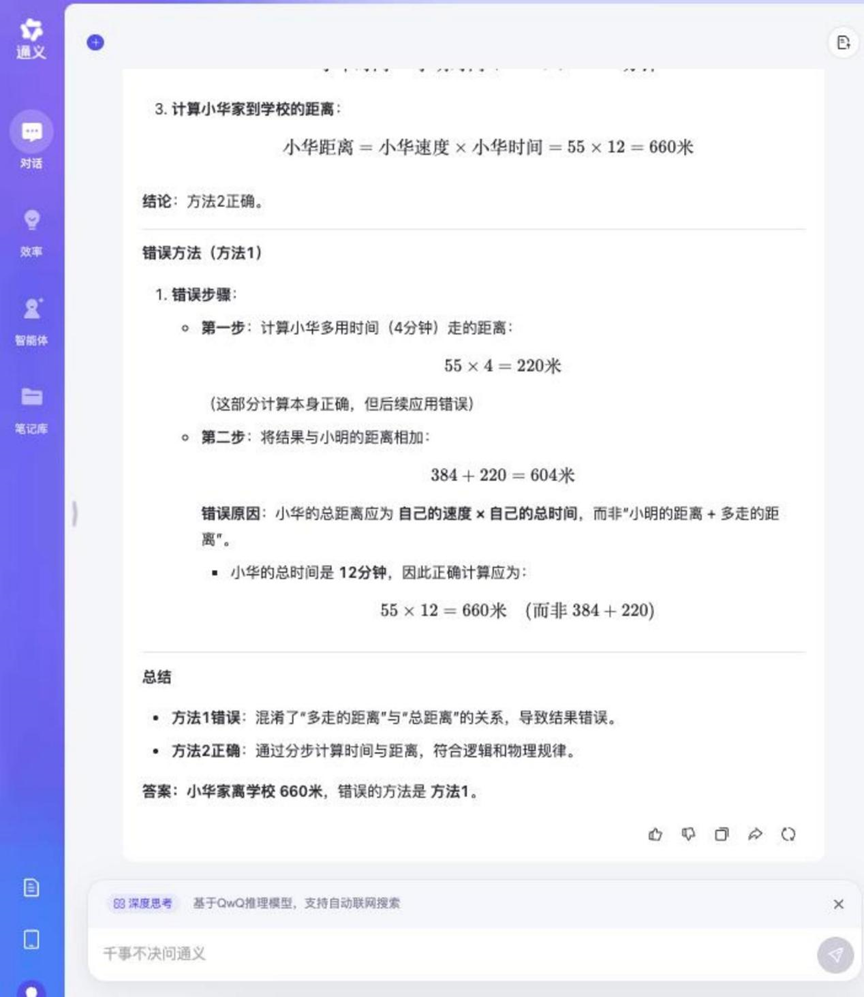

YiXin-Distill-Qwen-72B

Der Denkprozess für diese Frage war relativ lang, aber die meisten der am Test beteiligten Modelle waren in der Lage, sie richtig zu beantworten und die falsche Methode zu bestimmen.

Runde 3: Geometrisches Okklusionsproblem (Unsichtbare Türme)

Frage: In einer Stadt gibt es 6 Türme an den Punkten A, B, C, D, E und F. Mehrere Schüler bilden eine Reisegruppe, um einen kostenlosen Ausflug in die Stadt zu unternehmen. Nach einiger Zeit stellt jeder der Studenten fest, dass sie nur die 4 Türme an den Punkten A, B, C und D sehen können, nicht aber die Türme an den Punkten E und F. Die Studenten sind nicht in der Lage, die Türme an den Punkten A, B, C und D zu sehen. Es ist bekannt, dass die Positionen der Schüler und der Türme als Punkte in derselben Ebene betrachtet werden und dass diese Punkte nicht miteinander übereinstimmen, und dass drei der Punkte A, B, C, D, E und F keine gemeinsame Linie haben. Die einzige Möglichkeit, den Turm nicht sehen zu können, besteht darin, dass die Sichtlinie durch einen anderen Turm blockiert wird. Befindet sich ein Schüler zum Beispiel an einem Punkt P, der mit A und B zusammen liegt, und A liegt auf dem Linienabschnitt PB, dann kann der Schüler den Turm bei B nicht sehen. Fragen Sie: Wie viele Schüler können sich maximal in dieser Reisegruppe befinden? a. 3 b. 4 c. 6 d. 12

Analyse: Hierbei handelt es sich um eine komplexe geometrische und logische Fragestellung, bei der es um Fragen der Sichtbarkeit, der Verdeckung und der Konfiguration von Punktmengen geht, was ein hohes Maß an räumlichem Vorstellungsvermögen und logischem Denken im Modell erfordert.

Ergebnisse:
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B

Der Schwierigkeitsgrad der Fragen hat sich deutlich erhöht. In dieser Testrunde wurden nur o3-mini im Gesang antworten YiXin-Distill-Qwen-72B erfolgreich gelöst, die anderen Modelle gaben keine richtige Antwort.

Runde 4: Wahrscheinlichkeitsprobleme (Tiger und Tigerinnen)

Frage: Während des Frühlingsfestes startete ein Milchunternehmen eine Blindbox-Aktion zum chinesischen Neujahrsfest: Jeder Milchpackung liegt ein "rotes Päckchen" bei, das mit "Tiger" "Sheng""" Wei", eines der drei Muster. Wenn man zwei "Tiger", einen "Sheng" und einen "Wei" sammelt, kann man das Familienporträt "Tiger Tiger Sheng Wei" erstellen. Sobald die Aktion gestartet wurde, wurde sie ein Netflix-Hit und zog viele Leute zum Mitmachen an. Die bekannten Bedingungen sind wie folgt: Die Muster auf den roten Päckchen sind unabhängig voneinander zufällig verteilt und können nicht voneinander unterschieden werden. Die Wahrscheinlichkeit des Auftretens der drei Muster "Tiger", "Sheng" und "Wei" beträgt 1/3. F: Um ein komplettes Set "Tiger Tiger Sheng Wei" zu sammeln F: Wie viele Kartons Milch muss man im Durchschnitt kaufen, um einen kompletten Satz von "Tiger, Tiger, Mighty"-Familienfotos zu sammeln?

Analyse: Hierbei handelt es sich um ein typisches Sammlerproblem (Coupon-Sammlerproblem-Variante), das die Anwendung der Wahrscheinlichkeitstheorie und Erwartungsberechnungen erfordert und die Fähigkeit des Modells untersucht, mit Wahrscheinlichkeitsmodellen umzugehen und mathematische Erwartungsberechnungen durchzuführen.

Ergebnisse:
DeepSeek R1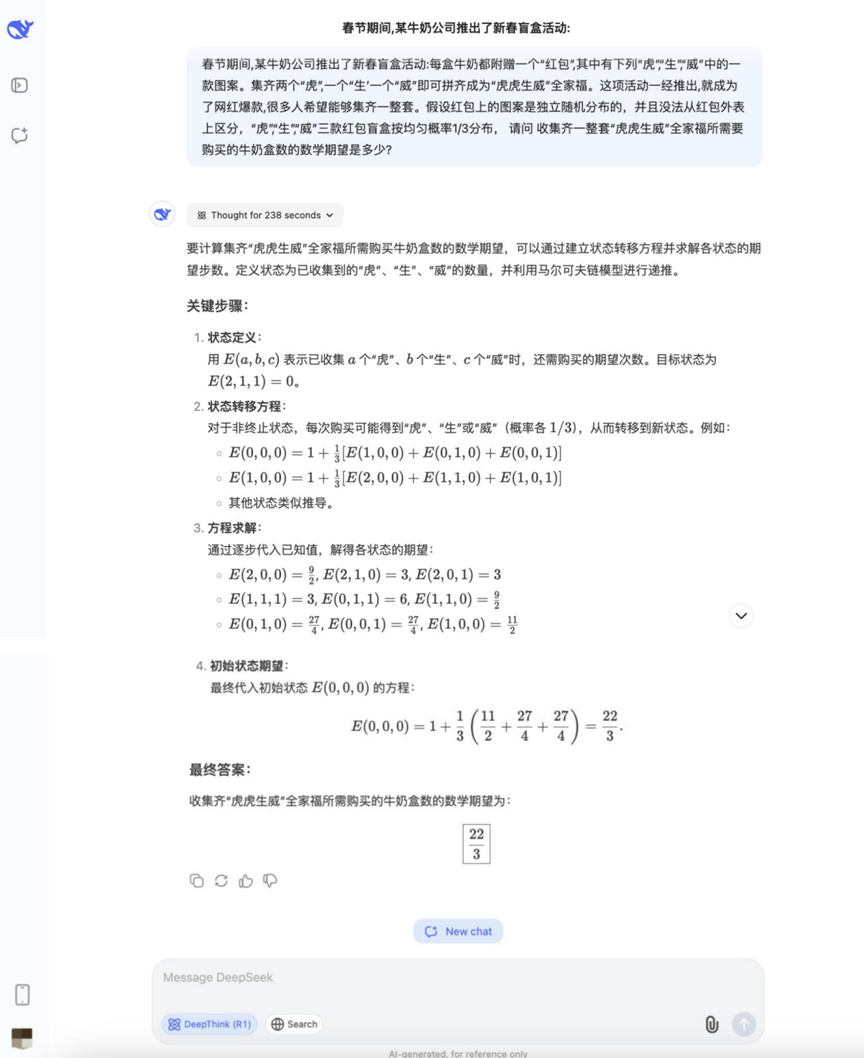

Hunyuan T1
 

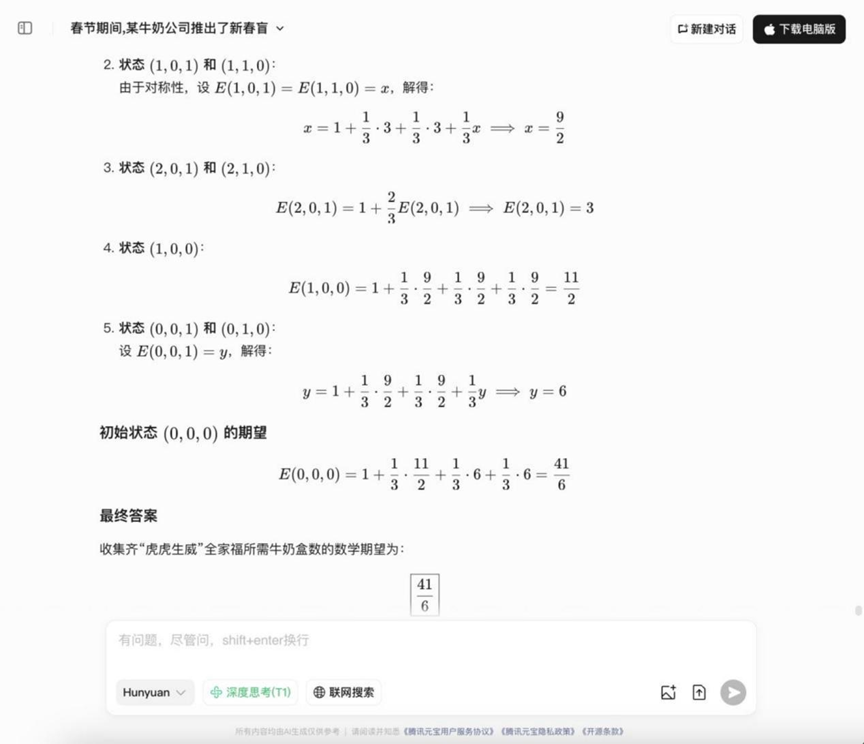
YiXin-Distill-Qwen-72B

Die Antworten auf die Wahrscheinlichkeitsfragen in dieser Runde begannen zu divergieren, wobei einige Modelle in der Lage waren, Ideen korrekt aufzulisten und zu berechnen.

Runde 5: Geometrie und Pfadplanung (Kampfspiele)

Problembeschreibung Bild:

Analyse: Es handelt sich um ein Problem, das Geometrie, Koordinaten- oder Gittersysteme und kürzeste Wege/optimale Strategien kombiniert und von dem Modell verlangen kann, dass es die grafischen Informationen versteht und räumliche Überlegungen und Planungen durchführt.

Ergebnisse:
o3-mini: Erfolgreiche Auflösung

YiXin-Distill-Qwen-72B: Teilweise korrekt
 

Diese Testrunde erfordert einen höheren Grad an Modellintegration, wobei etwa die Hälfte der getesteten Modelle vollständig korrekt gehandhabt wurde.

Runde 6: Zahlentheoretische Beweisprobleme (Minimale Nicht-Faktoren finden)

Problembeschreibung Bild:

Analyse: Wenn man in den Bereich der Beweisfragen eintritt, die eine strenge logische Schlussfolgerung und ein tiefes Verständnis der Konzepte der Zahlentheorie erfordern, sind diese Fragen ein direkter Test für die Fähigkeit des Modells, abstrakt zu denken.

Ergebnisse:
o3-mini

YiXin-Distill-Qwen-72B
 

Bei der Modellierung im Inland ist dieYiXin-Distill-Qwen-72B Hat in dieser Runde der Beweisfragen besser abgeschnitten. Die Beweisfragen waren für das Modell deutlich anspruchsvoller.

Runde 7: Funktionen und Mapping-Probleme (Mapping auf dem Einheitskreis)

Problembeschreibung Bild:

Analyse: Diese Frage befasst sich mit den Konzepten von Funktionen, Abbildungen und dem Einheitskreis in der höheren Mathematik und prüft die Fähigkeit des Modells, abstrakte mathematische Definitionen zu verstehen und anzuwenden.

Ergebnisse:
o3-mini

YiXin-Distill-Qwen-72B
 

Etwa die Hälfte der Modelle war in der Lage, dieses Problem mit abstrakten Zuordnungen korrekt zu lösen.

Runde 8: Kombinatorische Optimierungsprobleme (Maximales Dreieck)

Frage: Es gibt 1989 Punkte im Raum, von denen drei beliebige nicht auf einer Linie liegen. Diese Punkte sind in 30 Gruppen unterteilt, jede mit einer anderen Anzahl von Punkten. Ein Dreieck kann gebildet werden, indem ein Punkt aus drei beliebigen Gruppen als Scheitelpunkt genommen wird. F: Wie kann die Anzahl der Punkte in jeder Gruppe so verteilt werden, dass die Anzahl der gebildeten Dreiecke maximiert wird?

Analyse: Hierbei handelt es sich um ein Optimierungsproblem in der kombinatorischen Mathematik, das ein Modell erfordert, um die Grundsätze der kombinatorischen Zählung zu verstehen und die optimale Zuweisungsstrategie zu finden, was komplexere mathematische Modellierungs- und Optimierungsideen erfordert.

Ergebnisse:
o3-mini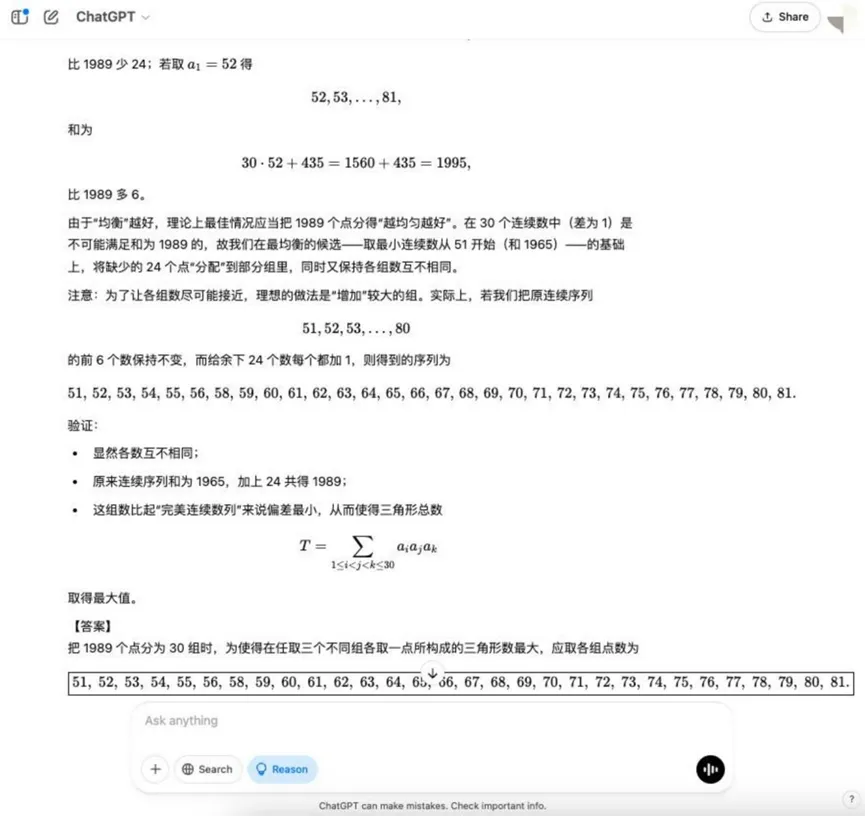

YiXin-Distill-Qwen-72B
 

Kombinatorische Optimierungsprobleme erhöhen den Schwierigkeitsgrad weiter und stellen höhere Anforderungen an die mathematischen Strategien und Rechenfähigkeiten des Modells.

Runde 9: Zahlentheoretische Probleme (Faktorketten)

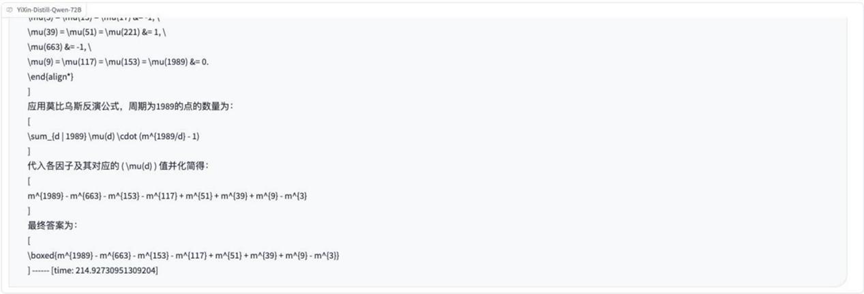
Problembeschreibung Bild:

Analyse: Auch hier geht es um zahlentheoretische Konzepte, wobei das Verständnis des Modells und die Anwendung von Beziehungen wie Faktoren und Ganzheitlichkeit geprüft werden, was konstruktive Beweise oder Zählungen erfordern kann.

Ergebnisse:
o3-mini: Teilweise korrekt

YiXin-Distill-Qwen-72B: Absolut richtig.
 

YiXin-Distill-Qwen-72B Eine solide Leistung zu diesem Thema der Zählung.

Runde 10: Geometrische Probleme (Punkte mit gleicher Fläche)

Problembeschreibung Bild:

Analyse: Bei der letzten Frage handelte es sich um eine geometrische Frage, bei der es um Flächenberechnungen, Flugbahnen von Punkten oder Existenzbeweise ging, wobei die geometrische Intuition des Modells, algebraische Operationen und logisches Denken geprüft wurden.

Ergebnisse:
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B
 

Auch bei den abschließenden Geometriefragen zeigten sich Unterschiede zwischen den Modellen hinsichtlich ihrer Fähigkeit, komplexe geometrische Probleme zu lösen.

Beobachtungen und Analysen

Auf der Grundlage dieses Tests der mathematischen Fähigkeiten der Chinesen an einer Reihe von großen Sprachmodellen lassen sich die folgenden Feststellungen treffen:

1. Die Modellierung mathematischer Grundkenntnisse verbessert sich erheblich: Im Vergleich zu früheren Modellen zeigt die aktuelle Generation von LLMs deutliche Verbesserungen bei der Bewältigung mathematischer Probleme, die mehrstufiges Denken erfordern, wie Geometrie, Wahrscheinlichkeit und einige offene Anwendungsprobleme. Dies kann auf die Vergrößerung des Modells, die Fülle an Trainingsdaten und die Verwendung von Techniken zur Verbesserung des logischen Denkens, wie z. B. "Gedankenketten", zurückgeführt werden.
2. Es gibt Unterschiede in den Problemlösungsstilen: Verschiedene Modelle verhalten sich unterschiedlich, was den Detaillierungsgrad des Lösungsprozesses angeht.
   • o3-mini, Grok 3 beta, Tongyi Qwen-32B Die Ausgabe ist relativ übersichtlich und die Schlussfolgerungsschritte sind einfach.
   • DeepSeek R1, Hunyuan T1, YiXin-Distill-Qwen-72B Die Tendenz, detailliertere Denkprozesse zu zeigen, die manchmal auch Reflexions- und Korrekturschritte beinhalten, ist eher "wortreich", aber das kann helfen, die Logik ihrer Argumentation nachzuvollziehen.
   • Gemini 2.0 Flash Thinking Der Problemlösungsprozess ist nicht nur langwierig, sondern verwendet auch hauptsächlich englische Ausgaben, was darauf hindeutet, dass er möglicherweise relativ schlecht auf den chinesischen mathematischen Korpus trainiert ist.
3. Robustheit gegenüber Eingabefehlern: Im Test wurde festgestellt, dass einige Modelle selbst bei kleineren Notationsfehlern oder Unregelmäßigkeiten in der Problembeschreibung die Bedeutung der Frage richtig verstehen und die Frage beantworten können, was ein gewisses Maß an Robustheit zeigt. Dies bedeutet jedoch nicht, dass die Modelle Fehler immer ignorieren können, und Fehler bei kritischen Informationen können immer noch zu einem Antwortversagen führen.
4. Künftige Erweiterungen: Spezialisierung und Tool-Integration: Trotz des offensichtlichen Fortschritts ist die Genauigkeit des derzeitigen LLM bei komplexen mathematischen Problemen noch verbesserungswürdig, insbesondere bei schwierigen Wettbewerbsfragen und Szenarien, die strenge Beweise erfordern. Zukünftige Verbesserungsmöglichkeiten können sein:
   • Integration von externen Rechenmaschinen: Die Unzulänglichkeiten von LLM in Bezug auf exakte Berechnungen und symbolische Operationen werden durch den Einsatz von symbolischen Berechnungswerkzeugen wie Wolfram Alpha kompensiert.
   • Domänenexklusive Feinabstimmung: Konstruktion hochwertiger, fein abgestimmter Datensätze für die mathematische Logik, bestimmte Zweige der Mathematik (z. B. Algebra, Geometrie, Wahrscheinlichkeitstheorie) und Stärkung von Modellen für die Argumentation von Experten und die Tiefe des Wissens.
   • Interaktives Lernen und Wiederholung: Entwicklung von Mechanismen, die es dem Benutzer ermöglichen, den Lösungsprozess zu steuern, auf Fehltritte hinzuweisen und dem Modell zu erlauben, die Lösungsstrategie dynamisch anzupassen.
5. Empfehlungen für Benutzer:
   • Studenten: LLM kann zur Unterstützung des Lernens eingesetzt werden, indem Lösungen und Antworten auf grundlegende Fragen schnell überprüft werden. Bei komplexen oder kreativen Problemen sollte man sich jedoch vor dem Potenzial des Modells für "ernsthaften Unsinn" hüten (d. h., dass es mit Sicherheit die falsche Antwort gibt).
   • Pädagogen: Beim Einsatz von KI-gestütztem Unterricht ist es notwendig, Fragen zu entwickeln, die eher das tiefere Verständnis und die Fähigkeiten zum eigenständigen Denken der Schüler testen, damit die Schüler sich nicht auf Modelle verlassen, um zu oberflächlichen Antworten zu gelangen.
   • Entwickler: Bei der Anwendung von LLM zur Lösung mathematischer Probleme sollten die Problemgrenzen und Lösungsanforderungen durch eine Optimierung von Prompt Engineering geklärt werden, um ineffektive Schlussfolgerungen oder "Brainstorming" durch das Modell aufgrund von unscharfem Verständnis zu reduzieren.

Zusammenfassend lässt sich sagen, dass die Anwendung von groß angelegten Sprachmodellen in der Mathematik allmählich aus dem Stadium der Erforschung in die Praxis übergeht. Die zukünftige Richtung der Modellentwicklung wird darin bestehen, ein besseres Gleichgewicht zwischen der Simulation der Flexibilität des menschlichen Denkens und der Strenge der mathematischen Logik zu finden.

Anmerkungen:
Die besten Leistungen in dieser Überprüfung YiXin-Distill-Qwen-72B Die Modellinformationen lauten wie folgt:

• Standardausführung: https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B
• AWQ Quantitative Ausgabe: https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B-AWQ
• Ressourcenanforderungen für die lokale Bereitstellung: 72B Standard Edition erfordert etwa 8 NVIDIA-Grafikkarten der Klasse 4090; AWQ Quantitative Edition kann auf 2 Karten derselben Klasse ausgeführt werden.