この評価結果は学術研究のみに使用される。
10月22日、Anthropicはバージョンアップした大型モデル「Claude 3.5 Sonnet」と新モデル「Claude 3.5 Haiku」を正式に発表した。
Anthropicの関係者によると、クロード3.5ソネットは、あらゆる能力において前バージョンを上回っており、特にスマートボディのコーディングとツール使用タスクにおいて大幅な性能向上が見られたという。SWEベンチ検証では、エンコード性能が33.4%から49.0%に向上し、OpenAI o1-previewを含むすべての公開モデルを上回った。
Anthropicはまた、コンピュータの使用という画期的な新機能を導入している。開発者はAPIを介してクロードをコントロールし、人間と同じようにコンピュータを使用することができるが、この機能は現在実験段階である。
クロード3.5ソネットアップグレードの中国語シナリオにおける推論とコードのパフォーマンスに関する一般的な懸念に対応するため、プロの第三者評価機関であるSuperCLUEは、クロード3.5ソネットアップグレードの詳細な評価を実施しました。
アセスメント環境
参考基準：SuperCLUE-Reasoning中国語高次推論評価基準、SuperCLUE-Code3中国語コード評価基準。
評価モデル クロード3.5ソネット（1022、POE最新モデルスナップショット）
Model GenerationConfigの設定：
- クロード詳細説明書（https://www.anthropic.com/news/3-5-models-and-computer-use）をご参照ください。
レビュー・エピソード
1.SuperCLUE-推論中国語複合課題高次推論復習セット。多段階推理、数値推理、推理計算、市場分析、最適化問題5つの難問推理を含む全302問。
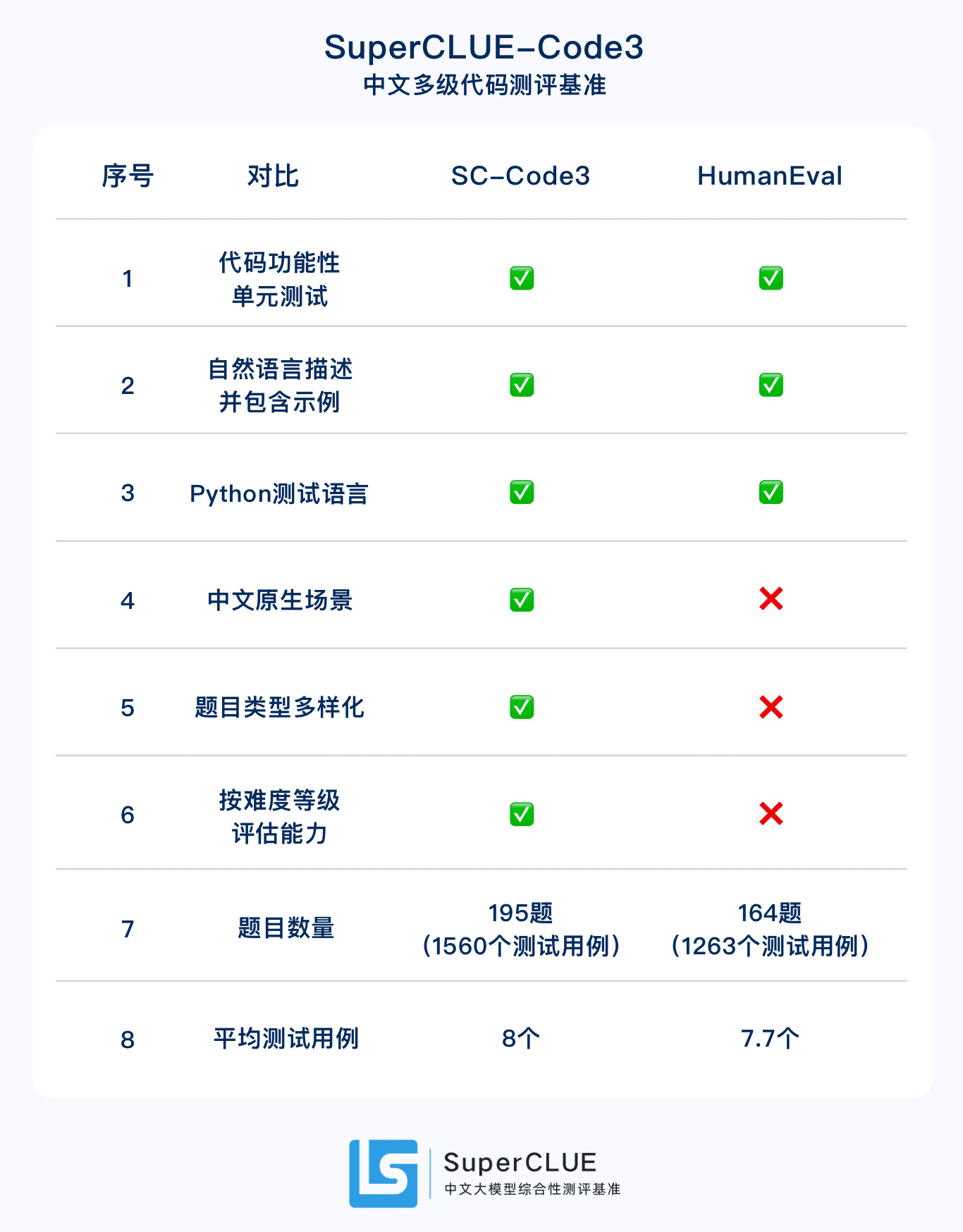
2.SuperCLUE-Code3中国語ネイティブコード評価セット.HumanEvalの中国語アップグレード版、合計195問、1,560のテストケースを含み、初級、中級、上級の3つの難易度に分かれています。
方法論::
1.高次推論：各推論問題に対して、手動校正・チェック後の参考解答と推論プロセスを提供し、レフェリーモデルが設定された評価プロセス、評価基準、採点ルール（1〜5点）に従って、候補モデルの解答を評価する。評価基準は、基本要件への適合性、推論の正確性、結論の妥当性です。
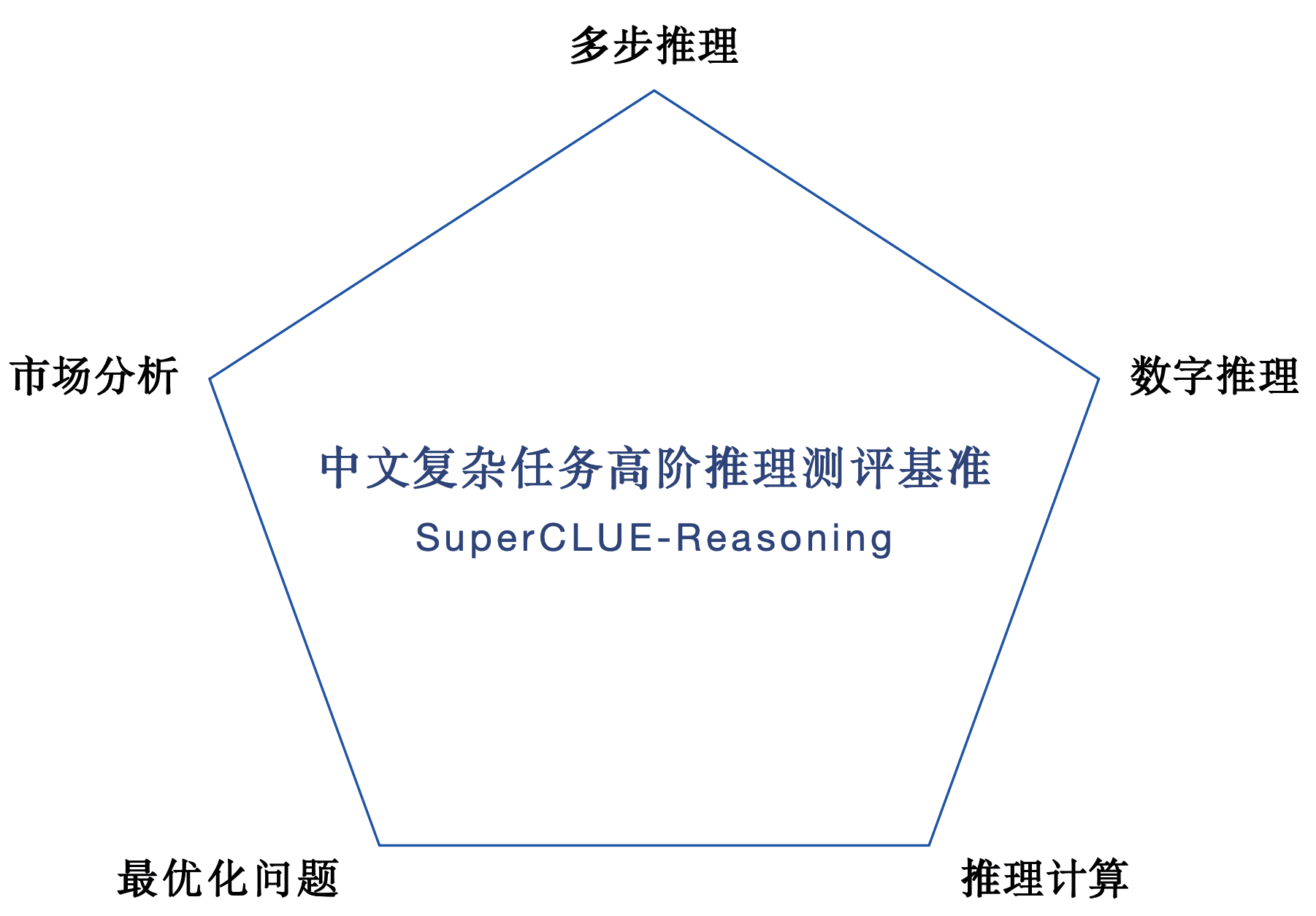
2.コードSC-Code3：特に、機能ユニットテストを通じてコード生成における中国ビッグモデルのコア機能を評価し、強化するために設計された。
SuperCLUE-Code3：中国語ネイティブレベル・コード能力ベンチマーク
結論から言おう。
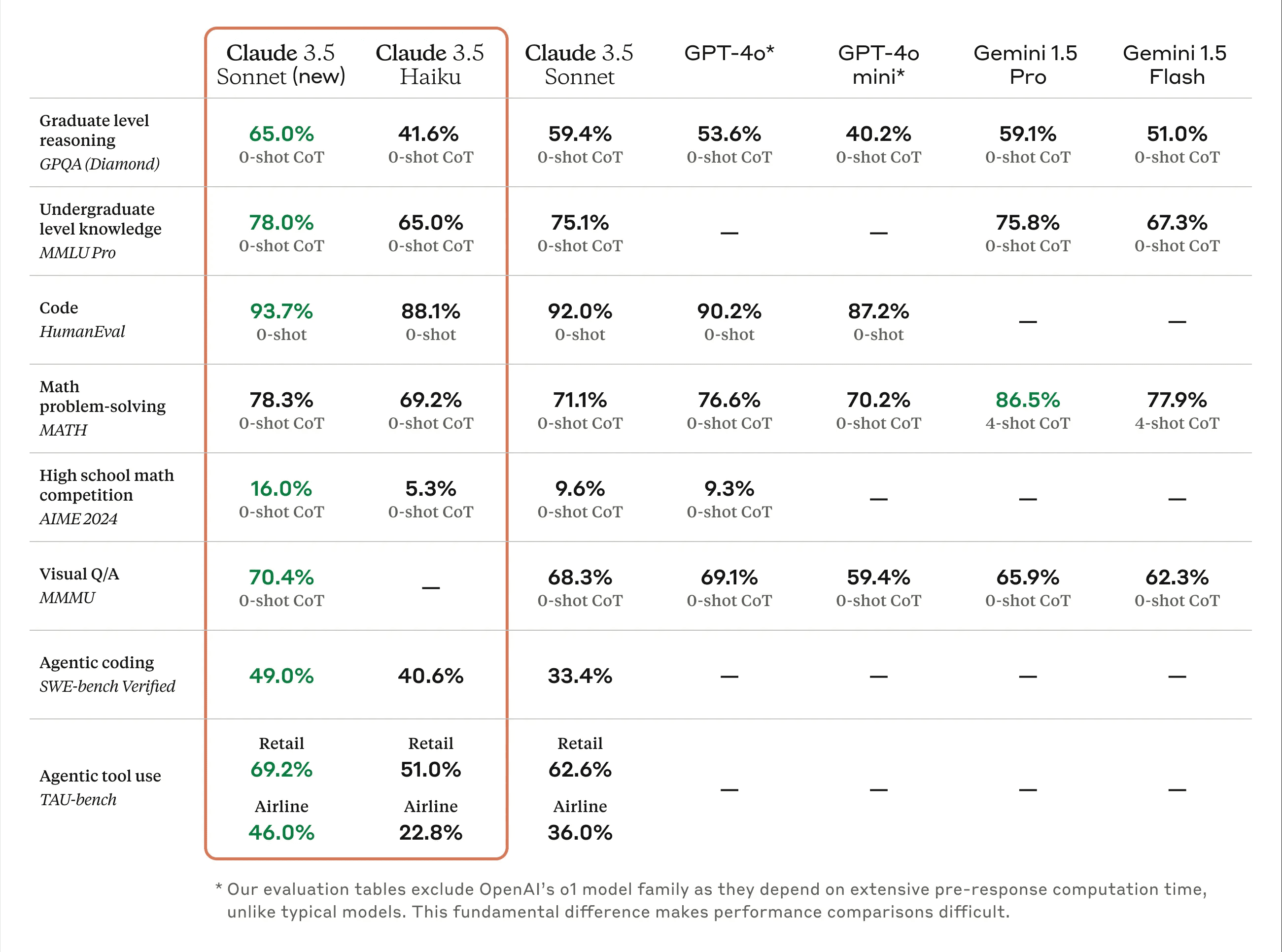
結論 1： Claude 3.5 Sonnet (1022)は、中国語コード能力（SC-Code3）の点で良い結果を出している。 総合得点は84.85点に達し、GPT-4o-0513より1.52点高かった。 これはo1-previewより4.54ポイント低い。特に高度なコード・タスクでは、o1-previewと並ぶ69.23点を獲得し、素晴らしい結果を残した。
結論 2： クロード3.5ソネット(1022)は中国の高次推理課題で74.54点を獲得した。 ChatGPT-4o-latestに近く、o1-preview（-10.73ポイント）との差は大きい。 .その中でも、多段階推理能力は比較的優れており、ChatGPT-4o-latestを上回るパフォーマンスを持っています。
**結論3:**前バージョンのクロード3.5ソネット(0621)との比較。 クロード 3.5 ソネット (1022) 推論タスクで 4.57 ポイント向上 また、数的推理や計算推理といった二次的な課題においても大きな進歩を遂げた。
評価結果
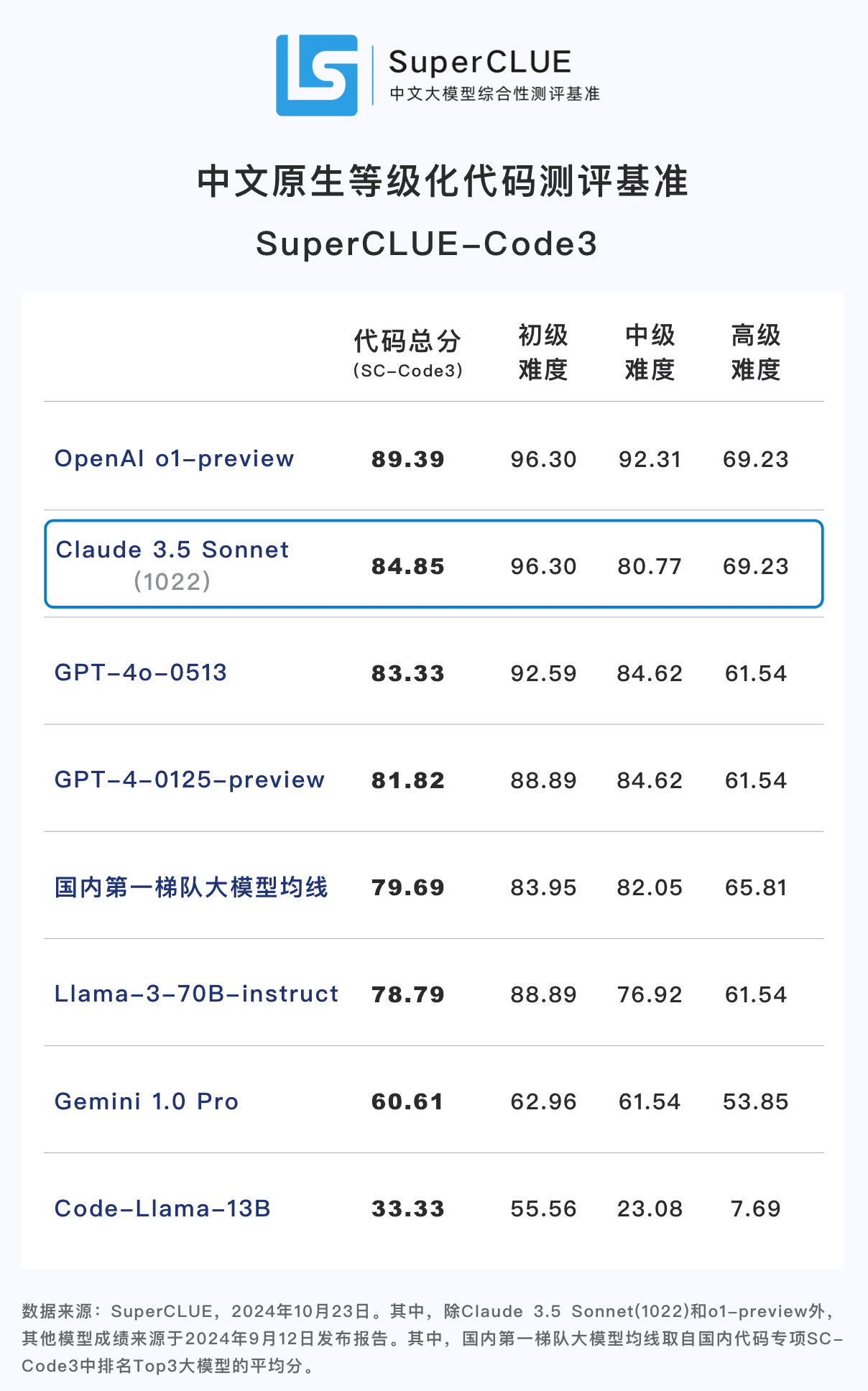
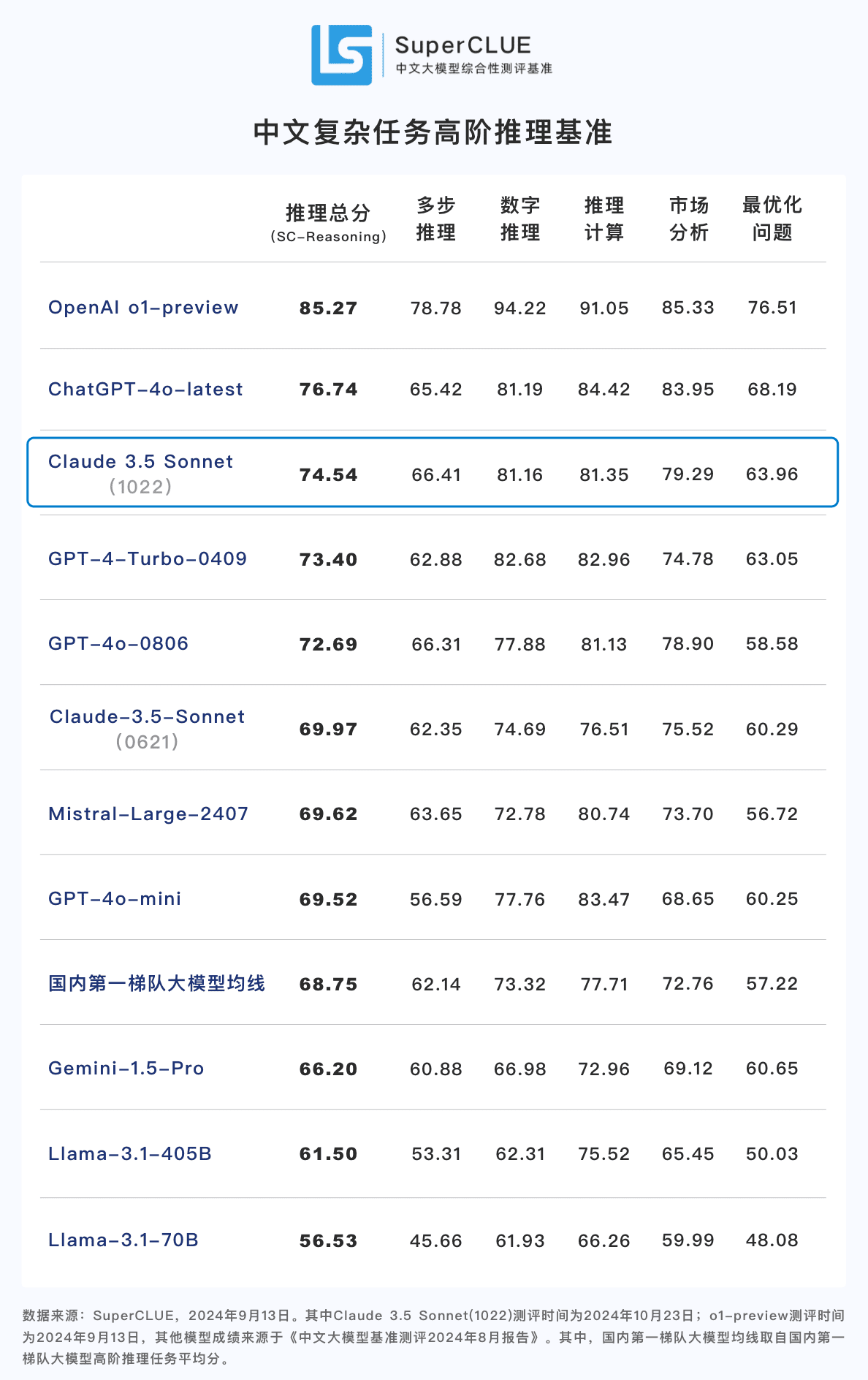
比較分析
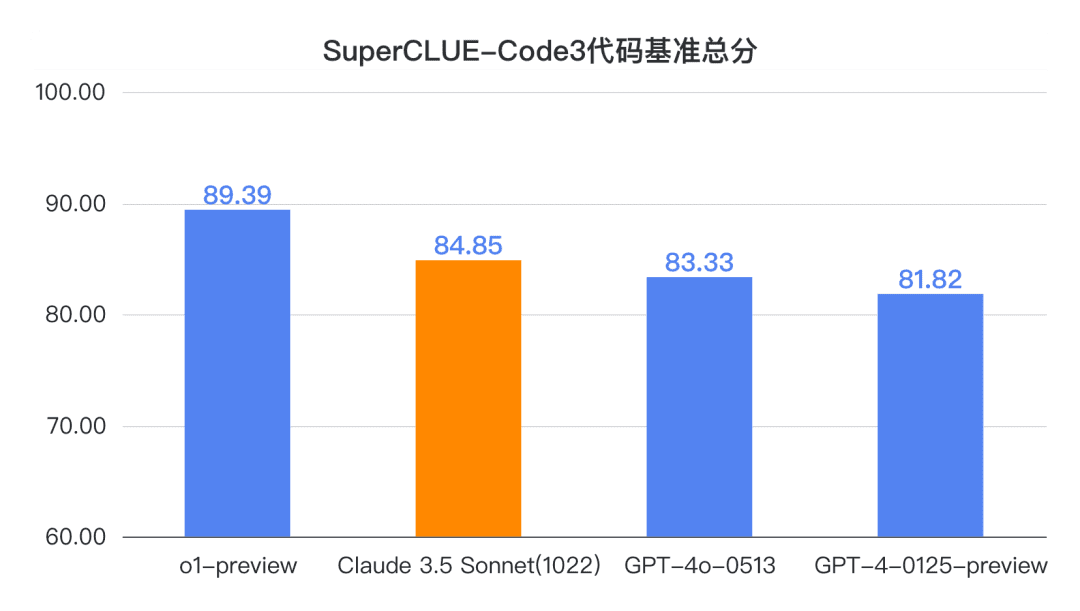
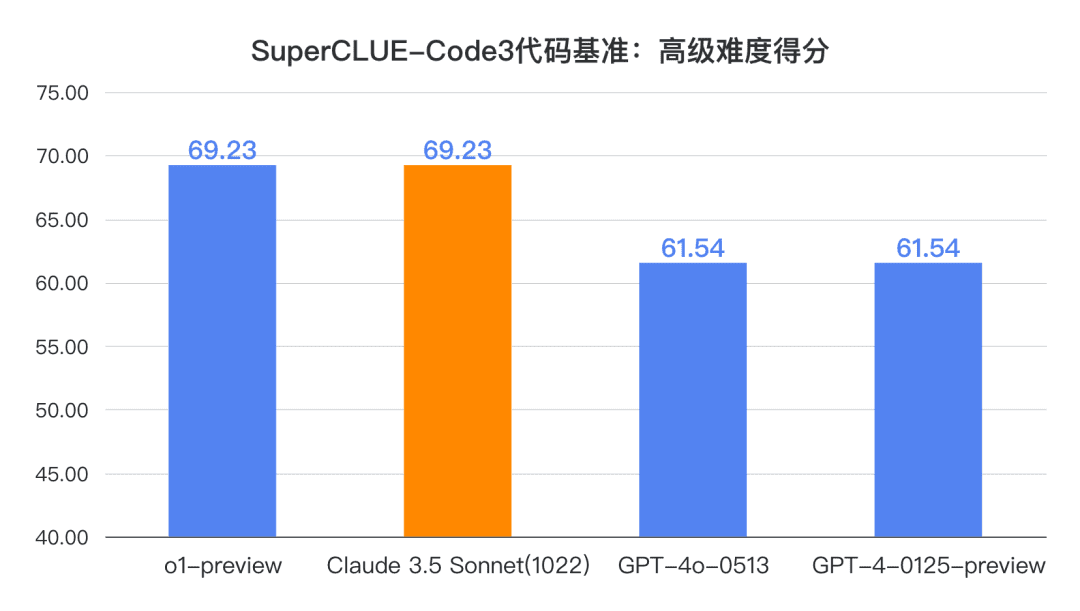
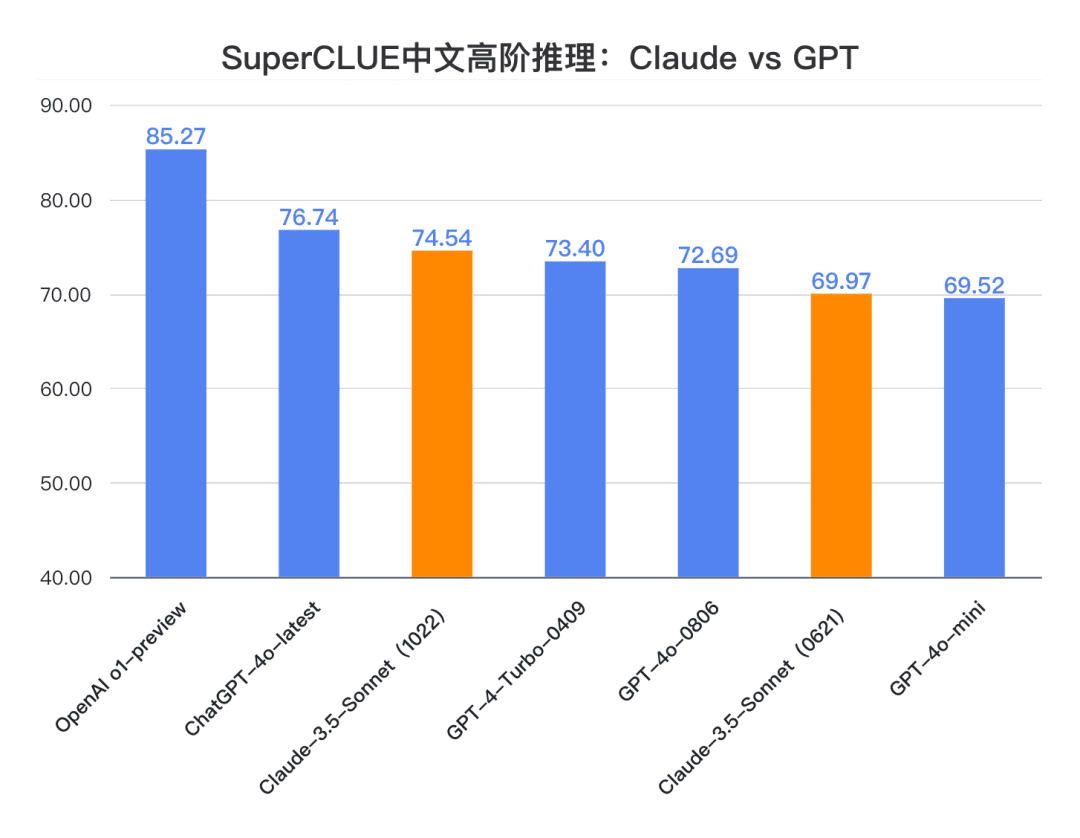
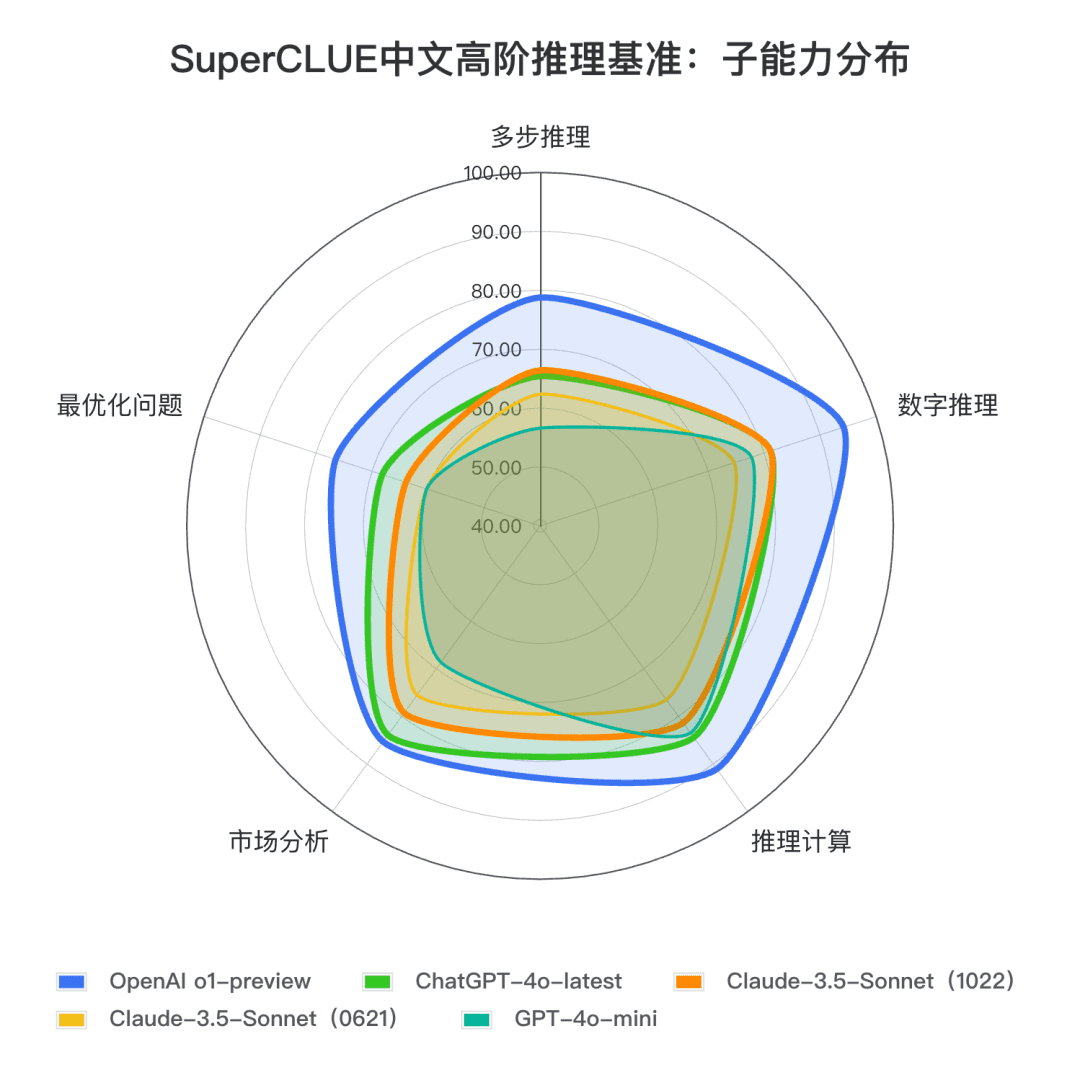
コード測定例
例1
プロンプト
from typing import List
def longest_peak_sequence(nums: List[int]) -> int:
"""
在一个整数数组中找出最长的"峰"序列的长度。
所谓"峰"序列，是指先严格递增然后严格递减的序列，且峰顶（即最大值）唯一。
至少包括三个数以上才能构成一个"峰"序列（即包含递增和递减的部分）。
返回数组中最长"峰"序列的长度。如果没有"峰"序列，则返回0。
示例:
>>> longest_peak_sequence([2, 1, 4, 7, 3, 2, 5])
5 # 最长的"峰"序列是 [1, 4, 7, 3, 2]
>>> longest_peak_sequence([5, 4, 3, 2, 1])
0 # 不存在"峰"序列，因为没有严格递增的部分
提示:
- 数组 `nums` 的长度范围为 [0, 10000]。
- 数组中的每个元素范围为 [-10000, 10000]。
"""
クロード3.5ソネット（1022）の答え。
from typing import List
def longest_peak_sequence(nums: List[int]) -> int:
if len(nums) < 3:
return 0
max_length = 0
# 从第二个元素遍历到倒数第二个元素
for i in range(1, len(nums) - 1):
# 检查当前位置是否是峰顶
if nums[i] > nums[i-1] and nums[i] > nums[i+1]:
# 找到一个峰顶，向两边扩展
left = i - 1
right = i + 1
# 向左扩展，寻找严格递增序列
while left > 0 and nums[left-1] < nums[left]:
left -= 1
# 向右扩展，寻找严格递减序列
while right < len(nums) - 1 and nums[right+1] < nums[right]:
right += 1
# 更新最长峰序列长度
current_length = right - left + 1
max_length = max(max_length, current_length)
return max_length
テストケース。
def check(candidate):
assert candidate( [1, 2, 3, 4, 5, 6])==0
assert candidate([1, 3, 5, 6, 4, 2, 0])==7
assert candidate( [5, 4, 3, 2, 1, 2, 3, 4, 1])==5
assert candidate([1, 3, 5, 3, 1])==5
assert candidate([1, 2, 3, 3, 2, 1])==0
assert candidate([2, 1, 3, 1, 2, 1, 3])==3
assert candidate([1, 3, 5, 4, 3, 2, 1])==7
if_passed**養子縁組の有無）：***。採用された。
例2
プロンプト
from typing import List
def longest_increasing_path(matrix: List[List[int]]) -> int:
"""
给定一个整数矩阵，找到最长严格递增路径的长度。
路径被定义为从矩阵中的任意单元格开始，每次可以向上、下、左、右移动到相邻的单元格上，如果递增的话。
你不能在路径中移动到矩阵外面，也不能移动到不满足递增条件的单元格上。
路径的长度是路径上的单元格总数。
示例:
>>> longest_increasing_path([
[9, 9, 4],
[6, 6, 8],
[2, 1, 1]
])
4 # 最长递增路径是 [1, 2, 6, 9]
>>> longest_increasing_path([
[3, 4, 5],
[3, 2, 6],
[2, 2, 1]
])
4 # 最长递增路径是 [3, 4, 5, 6]或 [2, 4, 5, 6]
提示:
- 矩阵 `matrix` 的维度为 m x n。
- 矩阵 `matrix` 的每个元素是一个非负整数。
"""
クロード3.5ソネット（1022）の答え。
from typing import List
def longest_increasing_path(matrix: List[List[int]]) -> int:
if not matrix or not matrix[0]:
return 0
m, n = len(matrix), len(matrix[0])
# 缓存，用于存储每个位置的最长递增路径长度
cache = [[0] * n for _ in range(m)]
def dfs(i: int, j: int) -> int:
# 如果已经计算过，直接返回缓存结果
if cache[i][j] != 0:
return cache[i][j]
# 四个方向：上、下、左、右
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
# 当前位置的最长路径至少为1
max_length = 1
# 遍历四个方向
for di, dj in directions:
ni, nj = i + di, j + dj
# 检查是否在矩阵范围内且满足递增条件
if (0 <= ni < m and 0 <= nj < n and
matrix[ni][nj] > matrix[i][j]):
# 递归计算邻居位置的最长路径
curr_length = 1 + dfs(ni, nj)
max_length = max(max_length, curr_length)
# 存入缓存
cache[i][j] = max_length
return max_length
# 遍历矩阵中的每个位置，找到最长路径
result = 0
for i in range(m):
for j in range(n):
result = max(result, dfs(i, j))
return result
テストケース。
def check(candidate):
assert candidate([[1, 1], [1, 1]]) == 1
assert candidate([
[9, 9, 4],
[6, 6, 8],
[2, 1, 1]
]) == 4
assert candidate([
[3, 4, 5],
[3, 2, 6],
[2, 2, 1]
]) == 4
assert candidate([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
]) == 7
assert candidate([
[-1, -2, -3, 0],
[5, -6, 7, -8],
[-9, 0, -11, -12],
[13, 0, 15, -16]
]) == 4
assert candidate([
[5, 10, 6, 7, 9],
[6, 10, 2, 2, 3],
[4, 9, 8, 2, 8],
[3, 3, 3, 8, 8]
])==4
assert candidate([
[1, 3, 1, 4],
[1, 5, 1, 7],
[4, 2, 1, 1],
[1, 3, 2, 1]
])==3
assert candidate([
[1, 9, 2, 4],
[9, 6, 5, 3],
])==4
if_passed(採用されたかどうか）：採用された。
高次の推論の例
例1：多段階推論
尋ねる
ある会社には、A、B、C、D、E、F、Gという7人の従業員がいる。この会社は、従業員の等級付けを行い、その等級と以下の条件に基づいて、各従業員の正確な順位を推論した：
- AはBより高いが、Cより低い。
- DはEとGより高いが、Aより低い。
- Gは最低点だった。
- BはEとFより高いスコア。
- Fの方がEよりスコアが高い。
- Cが最高点。
- 各従業員によってスコアは異なり、Dが最も中央に位置する。
上記の条件に基づいて、各従業員の具体的なスコアを推測してください。
クロード3.5ソネット（1022）が答える：
各従業員の順位を論理的に分析してみよう：
- 条件3から判明：Gは最下位（7位）
- 条件6から判明：Cがトップ（1位）
- 条件7から判明：Dは4位（真ん中の位置）
- つまり、DはEとGより高く、Aより低い：
- EはDの次（5位か6位）にランクされなければならない。
- AはD（2位または3位）より前にランクされなければならない。
- 条件1から、AはBより高く、Cより低いことがわかる：
- A列2位
- Bは3位でなければならない
- 条件4と5から、BはEとFより高く、FはEより高いことがわかる：
- F組5位
- E 6位
最終順位は以下の通り：
- C（1位）
- A（2位）
- B（3位）
- D（4位）
- F（5位）
- E（6位）
- G（7位）
詳しい推理の過程をお見せしましょうか？
例2：最適化問題
尋ねる
ある都市には5つの主要な交通拠点があり、都市計画部門は、各拠点が少なくとも1つの路線で結ばれるように、バス路線のカバー範囲を最適化したいと考えている。ハブ間の建設コストは既知であり，最小コストですべてのハブを結ぶことが目的である．
データ
- ハブ間の接続コスト（単位：百万ドル）
- ハブ1とハブ2：10万ドル
- ハブ1とハブ3：15万ドル
- ハブ2とハブ4：20万ドル
- ハブ3およびハブ4：25万ドル
- ハブ3およびハブ5：30万ドル
- ハブ4とハブ5：180,000ドル
目的：総工費を最小限に抑え、すべてのハブを確実に相互接続するために、どのハブ同士を接続すべきかを特定する。
クロード3.5ソネット（1022）が答える：
これは最小スパニングツリーの問題で、クラスカルのアルゴリズムを使って解く。順を追って分析してみよう：
- まず、すべての接続をコストの小さいものから大きいものへとソートする：
- ハブ1-2：10万ドル
- ハブ1～3：15万ドル
- ハブ4-5：180,000ドル
- ハブ2～4：20万ドル
- ハブ3-4：25万ドル
- ハブ3～5：30万ドル
- リングの形成を避けるため、最も低コストの接続が選択される：
- セレクト・ハブ1-2（10万ドル）
- セレクト・ハブ1～3（15万ドル）
- セレクト・ハブ4-5（18万ドル）
- セレクト・ハブ2-4（20万ドル）
最適なプログラム
- ハブ1とハブ2の接続
- ハブ1とハブ3の接続
- ハブ4とハブ5の接続
- ハブ2とハブ4の接続
総費用：10＋15＋18＋20＝63万ドル
このプログラムは、以下のことを保証する：
- すべてのハブが接続されている
- ループが形成されない
- 最小の総所有コスト
この解決策を示すビジュアライゼーションを作成しましょうか？
# コミュニティに参加する
より詳細なクロード3.5最新大型モデルのレビューの詳細については、SuperCLUE-クロード交流グループに参加することができます。
日本語 
简体中文 
English 
Deutsch 
Português do Brasil