BoT：強化された思考：大規模言語モデルによる試行錯誤の問題解決

抄録

大規模言語モデル(LLM)の様々な問題に対する推論性能は、連鎖思考プロンプトに大きく依存しており、プロンプトの中でいくつかの連鎖思考デモを例として提供する必要がある。シンキングツリーなどの最近の研究では、複雑な問題解決における推論ステップの選択における探索と自己評価の重要性が指摘されている。本論文では、複雑な問題を解決するための新しいプロンプティングの形として、多数のシンキングツリーを繰り返し探索し、自己評価することで、試行錯誤的な推論経験のコレクションを得る、BoT（Boosting of Thoughts）と呼ばれる自動プロンプティングフレームワークを提案する。BoTは、例を必要としない単純なヒントから出発し、多数の推論ステップを反復的に探索・評価し、さらに重要なことに、LLMのエラー分析を用いてヒントを明示的に修正し、最終的な答えが得られるまで推論ステップの生成を補強する。GPT-4とLlama2を用いた幅広い複雑な数学的問題に対する我々の実験によると、BoTは常に他の最先端のヒンティング手法よりも高い、あるいは同等の問題解決率を達成している。ソースコードはhttps://github.com/iQua/llmpebase的examples/BoTReasoning文件夹下获得。

1.はじめに

自己回帰パラダイムを持つ大規模言語モデル(LLM)は、その潜在的な推論能力により、様々なタスクにおいて重要な性能を達成してきた。複雑なタスクにおけるこの能力の保証は、ステップバイステップの推論例を提供する連鎖思考（CoT）キューに大きく依存している。このアプローチは、思考が問題解決の中間段階として機能する一連の思考によって、推論能力が刺激されることを示唆している。

その結果、特にTree of Thought (ToT)と呼ばれるフォローアップ研究が、CoTを改善する方法を提案してきた。妥当性を確保するために、これらの手法のプロンプトには通常、特定のタスクに対する人間の注釈が含まれている。この依存性は拡張性を制限する。最近の研究では、LLMをダブルチェックに利用して回答を改善したり、フィードバックに基づいてプロンプトを強化したりすることで、大きな可能性が示されている。既存の文献では、プロンプトにおいて無効な思考を排除することが一般的に支持されている。しかし、人間は通常、エラーを注意深く分析することで継続的に学習し、経験を積んで徐々にパフォーマンスを向上させることができる。そこで我々は、LLMの思考生成を人間の注釈から解放し、人間の問題解決を模倣することで、様々なタスクにおいて効果的な推論を行うことは可能か？

本論文では、図1に示すようなBoosting of Thoughts(BoT)と呼ばれる新しいフレームワークを提案する。BoTは、集計と経験を含むブースティング機構を実装し、エラーから学習することで信頼性の低い推論ステップ(弱い思考)を漸進的に改善し、最終的に様々な問題を解決する。BoTは、人間の注釈のない単純なヒントから出発するため、弱い思考になる可能性がある。BoTはそれらを集約することで、より論理的で効果的な思考の連鎖を導き出し、その後の改善を導くことができる。私たちのフレームワークにおけるこのようなガイダンスは、LLMを使用して集約された連鎖を分析することによって得られる各推論ステップの詳細なエラー報告、提案、ガイダンスであるヒントを適応することによって達成されます。このような経験がプロンプトに蓄積されることで、徐々に強い思考へと導かれる。

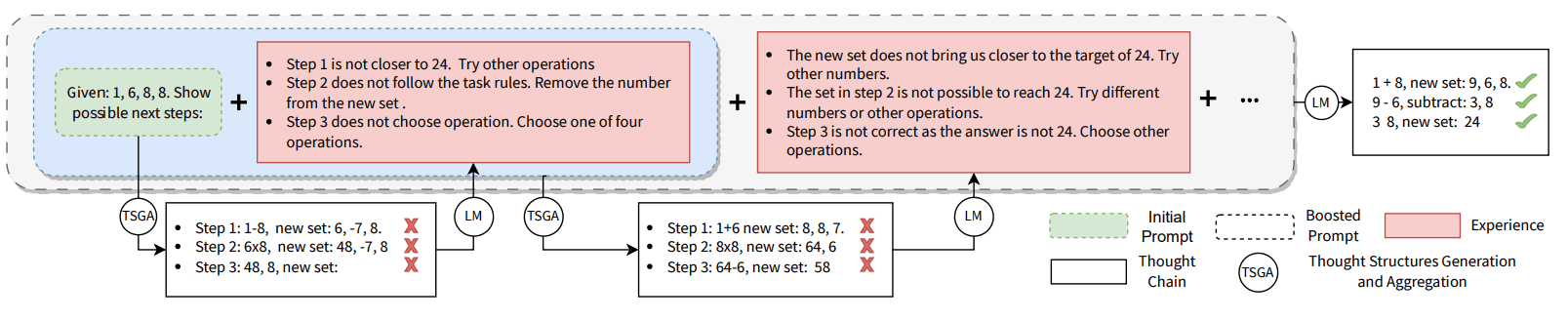
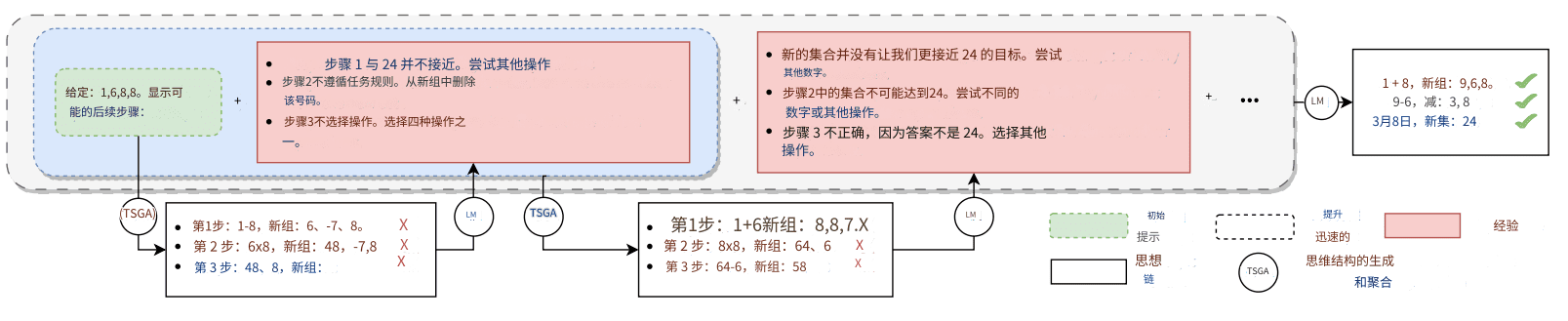
図1: 大規模言語モデル(LLMまたはLM)による生成された思考連鎖の分析からなる経験を段階的に増大させることで、キューを強化する。経験には、思考連鎖そのもの、対応するエラーレポート、および各推論ステップを修正するための詳細な提案が明示的に含まれる。従って、赤いバツ印が付けられた無効な思考も、プロンプトの改良に貢献することができる。プロンプトの経験を蓄積することで、BoTは最終的に単純なプロンプトから正しい思考連鎖を生成できるようになる。ここで紹介する例は、GPT-4とBoTを24ポイントのゲームタスクに適用した結果である。

具体的には、BoTはこのようなブースティング・メカニズムを、図1に示すような経験駆動型の反復プロセスとして実装している。各反復において、与えられた手がかりに対して、BoTはLLMと並行して多数の単純な思考構造を構築する。私たちはToTで示されるようなツリー構造を選択したが、ブースティングの目的のために、それを大幅に修正し、さまざまな成長戦略を持つ重み付きバイナリーツリーにした。各樹木の根から葉への枝について最高スコアを抽出した後、BoTの集約コンポーネントを実行して、それらを1つの思考の連鎖に集約した。この連鎖を同じLLMで評価し、得られた教訓を次の反復における思考生成のガイドとしてプロンプトに追加した。

我々の貢献は3つに要約できる。第一に、精巧なプロンプトを使用してより複雑な思考構造を生成するのとは異なり、本論文は、単純な最初のプロンプトに頼るのみで、弱い思考を過去の経験に基づいて問題を解決するために段階的に改善できることを示す。第二に、この強化メカニズムを実装するために、経験主導の反復プロセスを実行する、思考のブースト（BoT）と呼ばれる新しいフレームワークを提案する。BoTは単純なプロンプトから始まるため、様々なタスクに拡張可能である。BoTは単純な思考構造を並列に構築し、数回の反復で解に収束するため、妥当性を確保しながらも高速である。最後に、GPT-4とLlamaV2を用いて、複雑な数学的問題に対するBoTの性能を評価した。GPT-4 OpenAI (2023)とLlamaV2 Touvron et al. (2023)に依拠し、複雑な数学的問題に対するBoTの性能を評価した。問題の解答率は、バイナリーツリーのマインドセット構造を持つBoTが、GSM8KとAQuAにおいて現在の最先端技術を大幅に上回り、他のデータセットでは2番手の結果を達成したことを示している。このように、LLMは、キューを補強し、無効な思考連鎖のエラー分析を蓄積し、対応する提案を行うことで、人間の注釈がなくても、幅広いタスクで高いパフォーマンスを維持できることを実証している。

2.関連作品

多段階推論..連鎖思考（CoT）プロンプトに関する著名な研究は、各問題プロンプトに中間的な推論ステップを提供することにより、LLMの段階的な推論行動を刺激できることを示唆している。最近の研究であるTree of Thought (ToT)は、逐次的な推論プロセスをツリー構造に変換し、各思考(ノード)は複数の次の思考を生成するために以前の推論パスを考慮することができる。推論プロセス中のバックトラックと拡張探索により、ToTはGPT-4さえも挑戦する問題で優れた性能を発揮する。その高い能力を考慮すると、BoTの基本的な思考構造は、ToTの思考ツリー構造を大きく利用している。また、ブースティングのフレームワークにより、各反復でBoTが生成するツリー構造は、各ノードが多数の子ノードに対応するToTの複雑なツリーではなく、2進数の浅いツリーである。しかし、基礎となる構造はToTに限定されない。対照的に、BoTは、基礎となる思考構造がToT、GoT Bestaら（2023）、またはCR Zhangら（2023b）であることができるので柔軟である。ここで、思考グラフ（GoT）Bestaら（2023）は、思考の構造をグラフ形式に拡張した最新の研究である。本稿では、基礎となる思考構造としてToTのみに焦点を当て、GoTの利用は今後の課題として残す。

自己暗示.タスク固有の手がかりから人間を解放することが注目されている。LLMの推論能力を保証するために、従来のCoTは人間の先験的知識に依存し、タスク固有のデモをプロンプトとして手動で生成していた。しかし、zero CoTでは、手作業で作成した例題がなくても、プロンプトに「ステップ・バイ・ステップで考えよう」と付け加えるだけで、LLMがステップ・バイ・ステップで推論し、正確な回答を得られることが示された。Active-Promptは、まず質問セットの不確実性を測定し、不確実な質問のみを選択し、人間がアノテーションする。を提供する必要がある。本論文では、キューを使わない手動ブースティングの新しいアプローチを紹介する。BoTは単純なキューから開始し、LLMの思考分析に基づいてそれを反復的に強化する。

フィードバックによる先端技術.入力プロンプトに対するLLMの応答を、プロンプトを修正するためのフィードバックとして利用することが注目されている。LLMが評価した出力の記述に基づいて、与えられた手がかりを継続的に修正することで、正確な解答を得ることを目指している。SELF-REFINEは、我々の論文に類似した高レベルのアイデアを用いて、LLMがフィードバックを生成して出力をさらに洗練させる反復的な自己洗練アルゴリズムを提案する。PHPは、前回の解答を直接後続のヒントのヒントとして追加することで、このプロセスを単純化する。より合理的なものを生成する。Freundら(1996)は例題からのフィードバックによりヒントを改良した。APO Pryzant et al. (2023)は、最適化された自然言語を形成するために、前のプロンプトのパフォーマンスを使用して、プロンプトを反復的に改良した。これらの研究は、キューエンジニアリングにおけるブースティング機構の有効性を示している。しかし、効果的な推論連鎖を生成するためにヒントを強化する際のエラー分析の重要性を強調したのは、我々の研究が初めてである。提案するBoTは、試行錯誤の推論経験を反復的に蓄積することで、この洞察を自動プロンプトフレームワークに拡張する。

3.強化された思考

3.1 背景

キューエンジニアリングの目標は、複数の言語シーケンスを含むキューIを設計することであり、このキューを入力として使用することで、pθとして示される事前に訓練された大規模言語モデル（LLM）をθでパラメータ化することで、所望の言語シーケンスyを得ることができます。 したがって、標準的な入出力（IO）は、y〜pθ（y｜I（X，Q））と定式化することができ、I（-）は、タスク命令Xと対応する質問Qを包むキューを示します。対応する質問Qを表す。

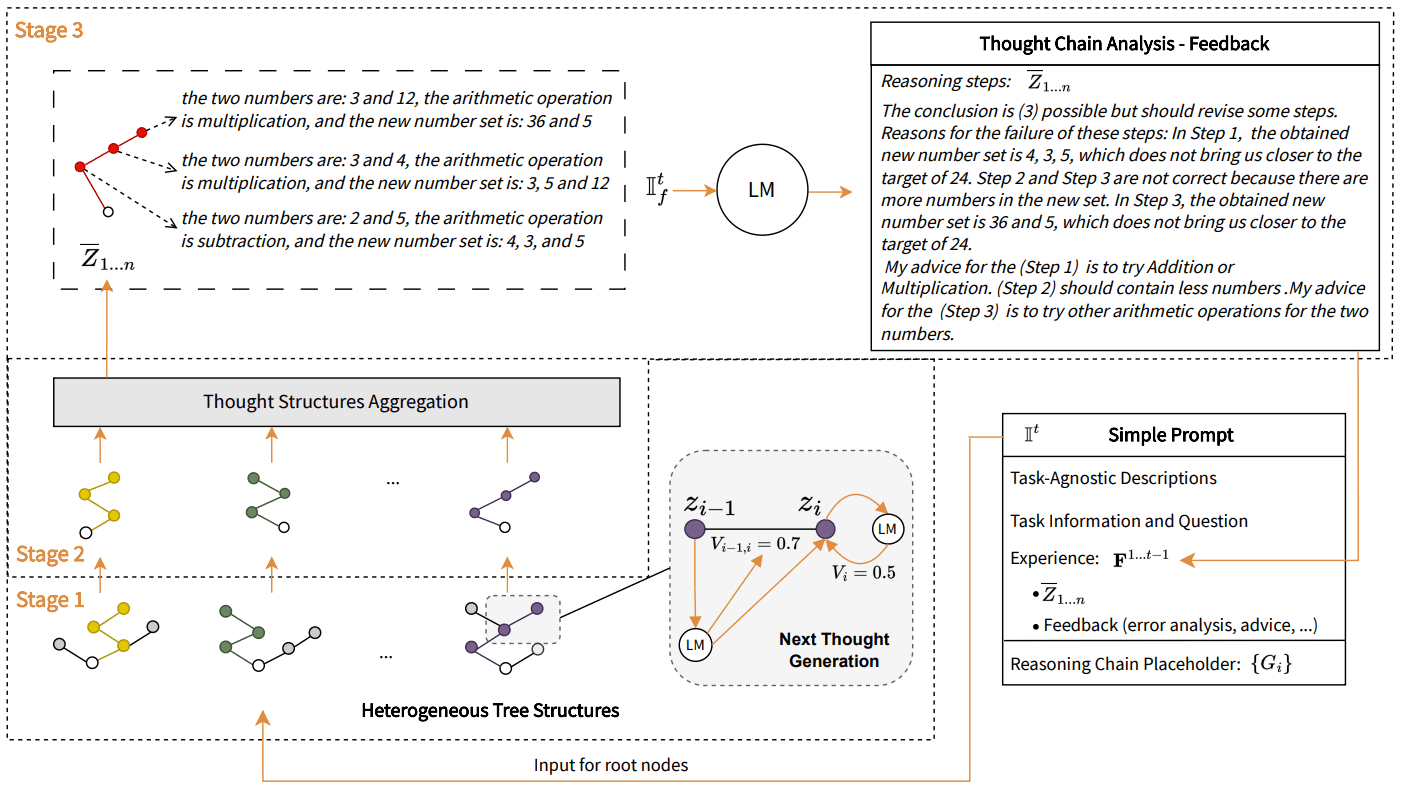
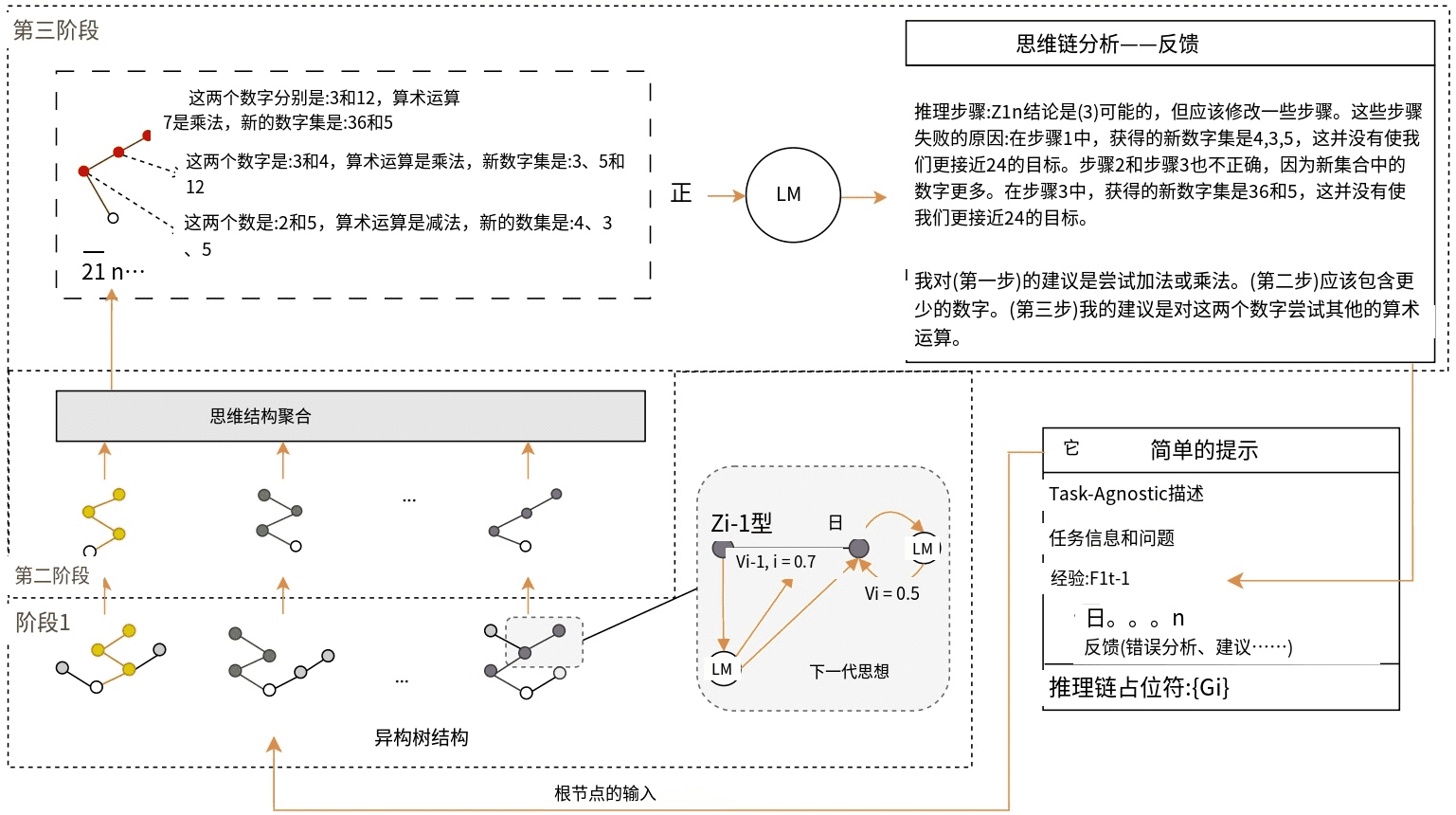
この図は、算術演算を用いた問題解決の思考プロセスを視覚的に表したものである。思考構造の集約、次の思考の生成、思考の連鎖の分析-フィードバックの3つの部分に大別される。

思考構造の集約は、推論の異なるステージ（ステージ1、ステージ2、ステージ3）の組み合わせを表し、それぞれのステージは、結論に達するまでのステップを記述する独自の数構造を持つ。

次の思考生成は特定の段階に焦点を当て、言語モデリング（LM）をどのように使って次の思考を予測し、以前の経験（ベクトルVi-1とViで表される）を考慮に入れ、新しい推論の連鎖を生成するかを示す。

思考連鎖分析 - フィードバックでは、推論のステップを詳細に分析し、考えられるエラーを指摘し、改善のための提案を行います。ステップの批評では、解答者が目標数（この場合は24）に近づいたかどうかを評価し、他の算術演算を試すよう提案します。

さらに、思考プロセスへのインプットを概説する簡単なキューセクションがあり、これには、タスクに特化していない説明、タスク情報や質問、新しい思考を生み出すためのプレースホルダーとして機能する、以前の推論の連鎖から得られた経験などが含まれる。

全体として、思考プロセスを反復的に最適化し改善するために言語モデルを使用する、推論と問題解決への方法論的に健全なアプローチが描かれている。

具体的には、「思考構造の集約」のセクションを見てみよう。このセクションには3つのステージがあり、それぞれに色のついた異種ツリー構造が見られる。第1段階では、いくつかの算術演算が見られ、その傾向は「vi1 - 0.5」である。第2段階では、より多くの算術演算が見られ、トレンドは「vi2 - 0.6」である。最後に、ステージ3では、「vi3 - 0.4」の傾向を持つ一連の算術演算が見られる。

次の思考生成セクションでは、特定の思考ノードZiが追跡され、それに付随する重みviが示され、問題解決の文脈におけるこれらの思考の重要性が示される。

思考連鎖分析-フィードバックのセクションでは、いくつかの推論ステップ（Z1,Z2.....Zn）を示し、それらを評価する。これらの各ステップについて、「R1:-3, try +」、「R2:+3, try -」、「R3: -1, try ×」は、特定のステップに関するフィードバックを表します。フィードバック、推論の評価、改善方法の提案。

簡単なヒント」では、「タスク非特定の説明『数字ゲームをする』」、「タスクメッセージ『1,3,4,6の4つの数字（各数字は1回のみ使用可能）と算術演算（足し算、引き算、掛け算、割り算）を使って、24という数字になるようにしなさい。6(各数字は一度しか使えない)と算術演算(足し算、引き算、掛け算、割り算)を使って24という数字になるようにしなさい。

このパイプラインの結果は、次の推論のための新たな思考プロセスを生み出す。

この図は、思考プロセスと推論方法論の論理的な流れを表しており、言語モデル（LM）だけでなく、フィードバック/提案メカニズムが、各ステップで批判的なフィードバックと評価を行いながら、問題を前進させるためにどのように使用できるかを示している。

図2：各反復におけるBoTプロセスの概要を明らかにする。この経験則に基づく反復プロセスにおいて、どのように有効性の向上が達成されるかを示すために、ChapGPT-4における24点ゲームデータセットの1種類の実験で得られた網羅的な中間結果を示す。問題Q「与えられた4つの数字は2、4、5、5である」が与えられた後、BoTは3つの連続した段階を経る。単純な手がかりItを入力とする思考構造生成（第1段階）では、多種多様な異種ツリー状の思考構造が出力される。思考構造集約（ステージ2）では、それらを思考の連鎖z1.....nに統合され、続いてステージ3でこの思考の連鎖を分析し、手がかりをさらに強化するために使用できる経験を生成する。

プロンプトは、LLMがステップバイステップで問題を解くように導くために、より精巧に設計することができる。各中間的な推論ステップはzi (思考とも呼ばれる)と表記される。CoTは一握りの例を提 供し、それぞれの回答は思考の連鎖z1 ... .nを含む。これはy ∼ pθ y|I [z1 ..n]N , X, Q , ここで N はプロンプトに含まれる例の数である。

ブートストラップで例を準備するよりも、より柔軟なアプローチは、推論プロセス中にLLMが徐々に思考ziを生成するようにブートストラップを設計することである。これはzi ∼ pθ (zi |I(z1.....i-1, X, Q))と定式化できる。最後に、解はy ∼ pθ (y|I(z1.....n, X, Q))と定式化される。
代表的な例として、ToT Yaoら（2024）は、この逐次推論ステップを、C個の次の思考を生成できるツリー構造にさらに拡張している。このように、反射の構造は連鎖状にもツリー状にもなる。

3.2 フレームワーク

正しいCoT例を手がかりに生成したり、きめ細かな思考生成構造を設計したりすることを目的とした既存の文献には、3つの限界がある。第一に、これらのアプローチでは無効な思考は通常無視されるか、破棄される。しかし、人間、特に非専門家、そして特に他の領域では、次の試行で正しく実行するためにより多くの経験を収集するために、過去の誤りを分析することに依存している。第2に、タスクごとに、次の思考を生成するための例、例えばI (z1|z0, X, Q)をキューで提供する必要があるため、拡張性が低い。最後に、思考構造（例えばYaoらのツリー構造）の生成は複雑すぎるため、より良い解を得るために推論ステップを増やすことはできない。これは主に、得られた解をさらに修正できない可能性があることによる。

本稿では、このような無効思考（思考の連鎖における誤った推論ステップ）の分析をLLMから継続的に収集することで、プロンプトを強化できることを主張する。従って、例えばI (X, Q)のような、無効な思考を導く可能性のある単純な手がかりであっても、このような分析に依存することで、解に近づく強い思考を得るために段階的に改善することができる。

という方法を提案する。思考を高める（BoT）自動キューイング・フレームワークは、経験主導の反復プロセスを通じて、キューイングの強化を可能にする。よりシンプルにキューが始まる。図 2 に示すように、BoT の各反復 t は 3 つのフェーズから構成される。第2フェーズでは、これらの思考構造が推論チェーンに集約され、第3フェーズでLLMによって分析され、エラー報告と詳細な修正提案を含むフィードバックが生成される。集約された推論の連鎖はフィードバックの結果と組み合わされ、Ftと表記される新しい経験となる。.t、キューは強化される。

簡単なヒント.ここで、Sはタスクに依存しない説明を表し、XとQはそれぞれタスク情報と質問を表す。プロンプトの経験的な部分はF0とし、最初は空でなければならない。{Gi}}は思考構造を構築する際に埋められるプレースホルダである。言い換えると、次の思考 zi を生成するとき、{Gi} は前の思考チェーン z1....,i-1.

思考構造の生成.経験Ft-1を収集した後、反復tのキューはIt≡ {S, X, Q, F1, ....t-1, {Gi}}である。このキューに基づいて、BoTはM個の思考構造を並列に生成する。BoTは基本的に、連鎖したWeiらの構造やツリー状のYaoらの構造など、あらゆる思考構造を含むことができる。推論ステップの探索と実験結果を考慮し、ツリー状の思考構造を検討した。しかし、BoTはリフティング・フレームワークにより適した2つの新しい修正を導入している。

• 加重バイナリツリー.BoTは各ラウンドで単純なキューを使用し、ブースティング機構でさらに修正できるため、構造が単純で複雑性の低い弱いマインドを構築する。したがって、BoTの各思考構造は浅い重み付き2進木である。簡単のため、z1.....i-1という記号を残して、ルート・ノードからノードiの親への思考を表す。各ノードiに思考ziとその思考評価スコアVi ∼ pθ (z1.....i、Ia、X、Q）に加えて、子ノードとその親ノード間のエッジスコアVi-1,i ∼ pθ (zi-1, zi, Ie, X, Q)も含める。ここで、IaとIeはそれぞれ思考のガイド記述とエッジ評価を指す。したがって、このツリー構造におけるBoTの次の思考生成は、pθ (zi| (Vi-1,i, Vi, It, X, Q))として形式化される。
• 樹木の不均質性.大きな複雑な木の中で解を見つけようとするToTとは異なり、BoTは高度に不均一な木のような思考構造を構築することを目的としている。したがって、異質性を高めるために、思考構造生成は、層ごとや葉ごとの成長など、異なるツリー成長戦略を採用する。前者は探索を重視するが利用は少ない Chen & Guestrin (2016)、後者は逆である Ke et al.したがって、リーフ・バイ・リーフ戦略は、レイヤー・バイ・レイヤー成長と比べて、現在の最良の思考からより良い最終的な思考へと推論を続ける傾向があるが、推論の連鎖が単調になる傾向もある。最後に、BoTの最大深度値を小さくし、Vi-1,iとViの値が指定された範囲[0.3, 0.8]外にあるノードをリーフとした。

思考構造重合.M個の思考構造を得た後、BoTはそれらをz1....nと示す思考の連鎖に集約する。これを達成するために、BoTはまず、各思考構造インデックスmについ て、最も高い評価スコアを持つチェーンを選択する。.nm := arg maxz1.....n∈Zm ∑i=1 Vi + Vi-1,i、ここでZmはm番目のツリーのすべての思考チェーンの集合を示す。続いて、z1...nを得るための2つの戦略が存在する。.n.

• ベストファースト集計.BoTはarg maxz1....に依存する。.n∈{Zm}M m=1 ∑i=1 Vi + Vi-1,iに依存し、M個の思考構造の中から最良のものをz1... .nとして選択する。このアルゴリズムは高速だが、非論理的な連鎖につながる可能性があり、その後の改良を導くのが難しい。
• 欲の集約BoTは、｛Zm｝M m=1上で貪欲に探索を行い、存在しないかもしれないが大域的に最適な新しい思考 の連鎖を組み立てることができる。BoTは、通常ツリーのルート・ノードである最初の思考から始めて、z1 = arg maxzj∈{zm 1 } M m=1 Vj + Vj-1,jを得る。

思考連鎖分析.BoTは、より良い思考を生み出すためにキューを強化するために何を調整すべきかについての洞察を得るために、LLMのz1....nを自己評価する能力を利用する。具体的には、手がかりIt f (z1.....n, X, Q）を入力として、LLMはこの思考の連鎖z1.....nに関する情報を含むフィードバックパラグラフを出力する。このフィードバックはF1,....t-1は思考生成の新たな経験としてF1,... ,t-1に追加される。,t.

反復的改良..ブースティング・メカニズムにより、F1,...tは反復的にキューを強化するために使用され、(t+1)番目の反復≡ {S, X, Q, F1,... ,t, {Gi}}のためのキューIt+1が得られる。t, {Gi}}となる。反復が進むにつれて、F1,...tには、解に近いものだけでなく、典型的で非論理的な思考の連鎖が多数含まれる可能性があり、そのすべてが明確に定義された解析結果を持つ。このように、単純なヒントから始めても、BoTはこのヒントを反復的に改良し、正確な解を導く正しい推論ステップを生成する。T回繰り返した後、It+1をLLMへの入力ヒントとして使用し、最終的な解答を得る。

4.実験

データセット.実験は、MMLU、SVAMP、GSM8K、AQuA、MATHなど、さまざまな数学的問題を含むベンチマーク・データセットで実施された。さらに、4つの数と基本的な算術演算（足し算、引き算、掛け算、割り算）を使って、1つの方程式で24を求めるという、難易度の高い数学的推論課題Game of 24も含まれた。は3つの中間ステップからなる。

コンペティション.ベンチマーク手法であるStandard Input-Output (IO)に加え、入力プロンプトに一握りの例(8)と人間の注釈が含まれるChained Thinking (CoT)、CoT-SC、Complex CoTを比較対象とした。GPT-4はOpenAI API経由でアクセスし、llama2-13b-chatモデルはローカルで実験を行うためにMetaAIからダウンロードした。異種ツリー思考構造を構築するために、BoTは温度範囲[0.2、0.4、0.6、0.7、0.9、1.1、1.5]とトップp範囲[0.1、0.3、0.5、0.7、0.9]の中からランダムに温度を選択した。

セットアップ.また、BoT+CoT は、BoT+CoT に対応する深さが 3 であるのに対し、BoT+CoT は深さが 5 である。BoT＋CoTは、単純な手がかりにCoTの5つの例が含まれることを意味する。BoTの累積経験がないアブレーション研究では、8つのCoT例がプロンプトで提供される。

メトリック.すべての実験結果をタスクの解決率（%）で測定し、報告する。BoTの出力zT1.....nから、LLMのために特別にフォーマットされた解答の記述を設定した。よく使われるデータセットでは、解答の書式を「解答は：」に設定した。24点のゲームでは、「ステップインデックス、現在の集合：、選択された2つの数字：、操作：、操作による新しい数字：、残りの数字：、新しい数字の集合：」とする。そして、新しい数字集合の数字を直接グランドトゥルースと比較する。ToT Yao et al.(2024)を参考に、難易度100のゲームの解答率を指標とする。

4.1 主な結果

主な実験結果を表 1 と図 3 にまとめ、BoT の全体的な性能についての洞察を示す。我々の知見は、メカニズムをブーストすることによって提案されたBoTが1).ほとんどのデータセットにおいて、人間のアノテーションに依存しない競争力のある問題解決率を達成した。）CoT事例を提供する際に、新たな最先端を達成すること。しかし、実験結果は、BoTが経験に大きく依存し、LLMの能力に非常に敏感であることも示している。

具体的には、表1において、BoTは単純な初期ヒントから開始し、GPT-4コードインタプリタに大きく依存するGSM8Kでの解答率において、最終的に現在の最先端CSVを0.11 TP3T上回る。AQuAを考慮すると、BoTはSOTAを2.51 TP3T上回る。これは、人間のアノテーションに頼らずにヒントにエラー分析と提案を追加することで、LLMが複雑な推論で優れた性能を発揮できることを示している。この主な理由は、単純なヒントは過去の経験を積み重ねることで段階的に改善され、正確に問題を解くことができるためである。CoT例をプロンプトに含めた後、BoT+CoTはSOTAより1.3%高い。我々は、CoT例は経験における成功事例とみなすことができ、BoTにおける後続の思考構造の生成を直接導くと主張する。一方、BoTとBoT+CoT、特にBoTは、MATHのSOTAより少なくとも18%低かった。この観察結果は、LLMが有効な経験に対する推論の連鎖を分析する能力が低いため、弱いLLMはBoTとうまく機能しない可能性があることを示唆している。

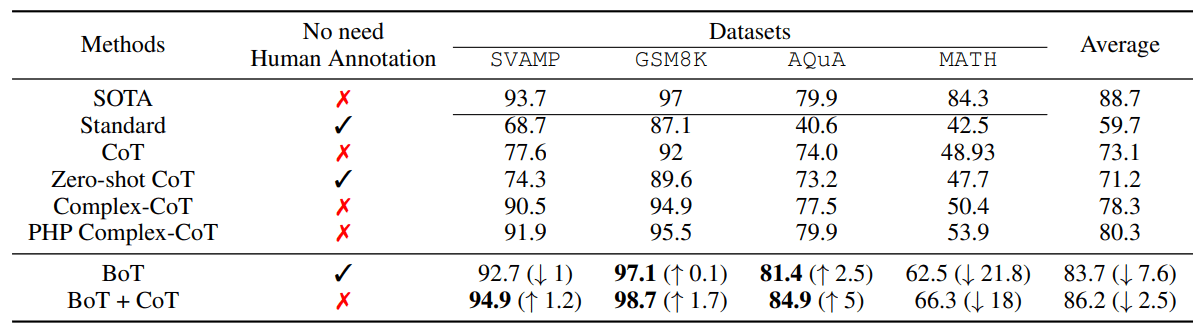
表1：BoTとGPT-4を併用することで、手動アノテーションなしでもパフォーマンスが大幅に向上する。
BoTの単純な初期手がかりにCoT例が含まれる場合、対応するBoT+CoTアプローチはより高い解答率を示す。我々のフレームワークはまた、2023年のZhaoらのModel Selection、2023年のZhengらのPHP、2023年のZhouらのCSVのような主要なアプローチとも比較され、それぞれSVAMP、AQuA、GSM8K & MATHデータセットで最先端の（SOTA）性能を達成している。

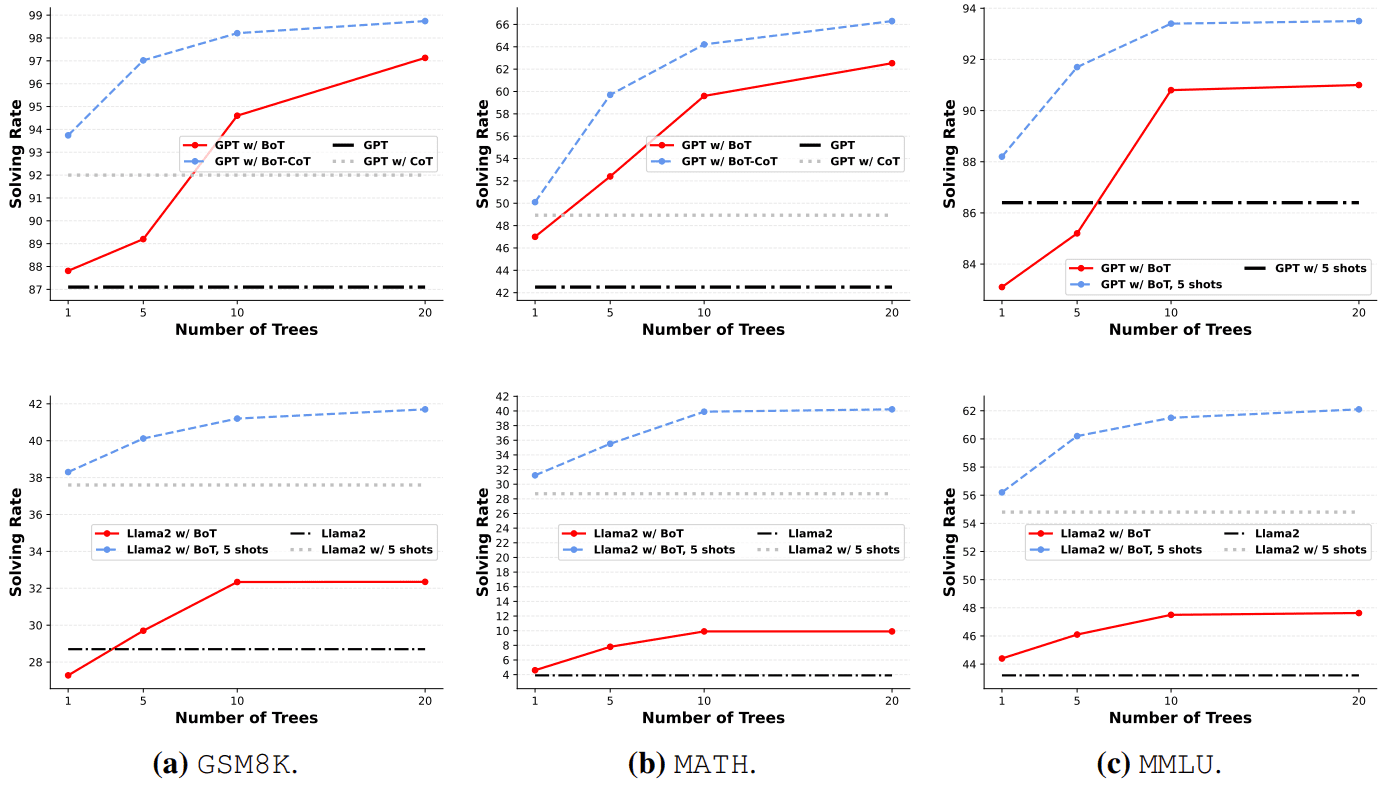
図3：BoTとBoT+CoTを用いて、2023年におけるGPT-4 OpenAIの問題解決率をLlama2 Touvronらと評価。

図3からわかるように、GPT-4とLlama2は、BoT条件下で、3つのデータセットの平均でそれぞれ11.61 TP3Tと4.41 TP3Tの性能を改善している。これら2つの図は、図3に示すように、LLMがより強力な場合、BoTとBoT-CoTが同様の性能を発揮するという明確な傾向を示しています。さらに、木の本数が1本から20本に変わると、両者の性能は同様の上昇傾向を示す。Llama2が弱いため、BoTは特に図3(a)に示すように、経験主導の反復プロセスを実行するための分析の恩恵を受けることができない。有効な成功事例、すなわち5つのテストが提供された場合、BoTは、限定的な改善ではあるが、漸進的な改善を通じて、Llama2がベースラインよりも多くの問題を解決するのを助けることができる。

4.2 24点ゲーム

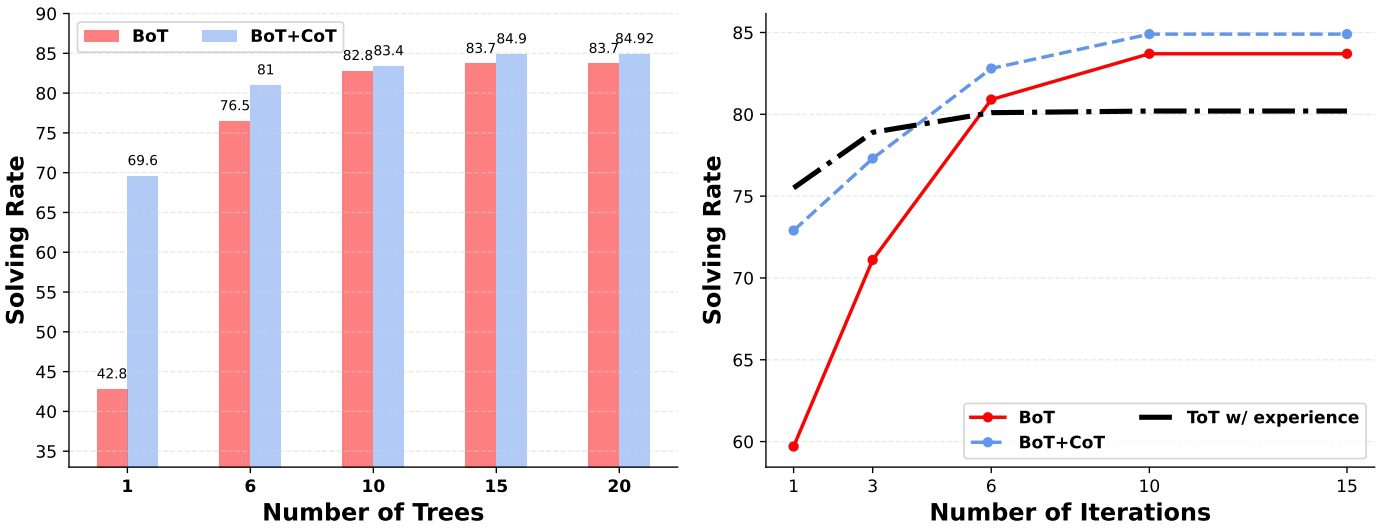
図4：木の本数と反復回数を変えた場合の3つの方法の比較。

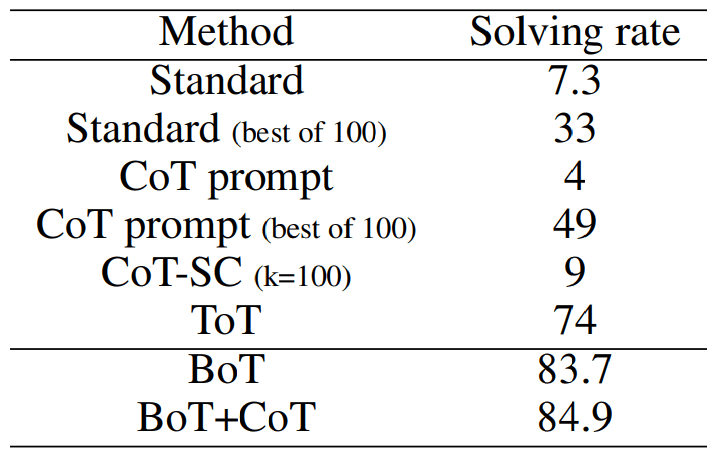
表2：ToT Yaoら(2024)の設定に従った24点ゲームにおける異なる方法の設定。

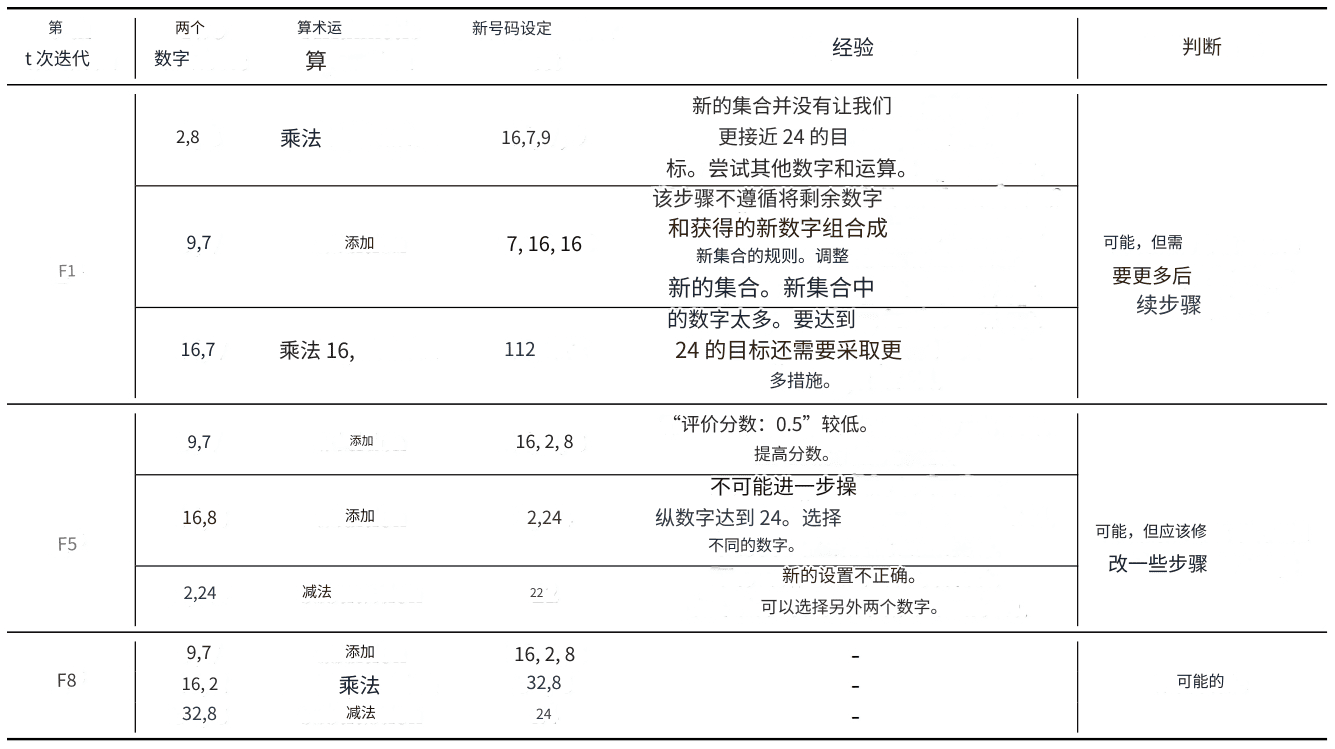
表3：1回目、5回目、8回目の反復で蓄積された思考プロセスと得られた経験を示す。与えられた4つの値は、2、7、8、9である。

Llama2モデルは問題を解くための正しいルールにさえ従うことができず、解答率はさらに低くなった。特に経験に依存するBoTを適用した場合、Llama2の結果はすべて5%より低く、大きな改善は見られなかった。そこで、GPT-4を用いたBoTの性能のみを報告する。公平な比較を維持するため、ToT Yaoら(2024)が提案したセットアップに従う。

表 2 に示すように、人間による注釈のない BoT は、すべての可能な次のステップを示すために例に依存する ToT を 9.71 TP3 T 上回った。さらに、5 つの CoT ショットを含む BoT+CoT は BoT を 1.21 TP3 T 上回った。経験駆動型の反復プロセスを使用するBoTは、木の本数Mと反復回数Tが増えるにつれて性能が向上する。図4に示すように、BoTはBoT+CoTよりもMとTに依存する。これは、より良い思考の連鎖や長い反復から経験を集める必要があるためである。このことは、LLMが経験、すなわち過去の推論の連鎖の分析を利用することで、解答率を大幅に向上させることができることを示唆している。しかし、ToTで得られるスコアはBoTより3.5%低い。これは、BoTの集計フェーズが現在の反復で最も代表的な推論の連鎖を生成するため、より有意義な経験をキュー強化に向けることに起因する。このことは、アブレーション研究のセクションで検証した。

BoTがミスや以前の提案からどのように学習するかをよりよく示すために、GPT-4が反復回数が増えるにつれて以前のミスを回避し、より具体的な提案を生成できるようになり、最終的に正しい解を導くことを表3に示す。最初の反復では、単純なヒントにより、LLMはステップ3で新しいセットが誤っていたため、タスクルールに従うというミスさえ犯した。それを分析した後、この誤りに対して正しい提案を行った。しかし、最初の反復の分析は、「他の数や演算を試す」など曖昧なものだった。5回の反復の後、BoTはこのような複数の分析を集約し、その結果、LLMが正しい数字9と7を選択するよう導く、より効果的なヒントを作成した。この正しい選択に対しては、それに応じて評価点を上げるという提案だった。このような経験を積み重ねることで、BoTはヒントを徐々に洗練させ、最終的には8回目の反復で正解を直接生成した。

4.3 アブレーション研究

表4：24ポイントゲームとAQuAデータセットで採用された異なるBoTバリエーションとGPT-4の比較。

すべての集約戦略は、問題と提案が「加算的」にプールされたときに高い解答率を生み出す。完全な経験を維持することは、特に数学的推論問題のより広い範囲をカバーするAQuAデータセットでは、修正主義的思考にとって特に重要である。しかし、スパニングツリーのすべての推論連鎖を集約せずに直接使用するBoT(No)は、特に経験の累積タイプが「累積」である場合、すべての文脈で最悪のパフォーマンスを示す。BoTの各反復で15本のツリーが構築され、それらをすべてキューにまとめると、重要な情報が不明瞭になる可能性があることはもちろん、そのほとんどが有効でなかったり有害であったりする可能性がある。そのような経験は無効または有害であるかもしれない。

アドバイスを得ることは、考えるきっかけを作る上で何よりも重要だ。.表4に挙げたすべての例において、提案を経験として扱うBoT変形が最も高い解答率を達成している。例えば、同じ「加法」型のケースで、経験にサジェスチョンがない場合、「24ポイントゲーム」では101 TP3T以上、AQuAでは201 TP3T以上パフォーマンスが低下した。一方、経験に問題を組み込むことは、パフォーマンスを向上させるための補完ツールとして使用できる。提案のあるBoTは、問題とペアになって初めて最高の解決率を達成することができる。例えば、AQuAでは、BoT（貪欲法）の解決率は4.41 TP3T増加した。

パフォーマンス上の理由から、グリーディ・ラリーは必要な唯一のオプションかもしれない。.貪欲な凝集は、既存の思考の連鎖の中から1つを選択する、あるいはすべてを維持するという最優先のアプローチとは対照的に、ツリー構造をより良い思考の連鎖に適応的にマージすることができる。このようにして、LLMはよりロバストな思考の連鎖について意味のある分析を行い、その結果、キューを補強するための重要な教訓を生成することができる。さらに、図4で説明したように、ToTは801 TP3 Tに達することができる同様の経験駆動型ブースティング・メカニズムを持っているものの、BoTに遅れをとっている。これは、ToTが単一ツリー構造で貪欲な凝集を実行できないことが原因であると考えられる。

5.結論

本論文では、単純な手がかりが、それが生成する思考のエラー分析を徐々に蓄積することによって、複雑なタスクを解決するために使用できることを検証する。我々は、効果的な思考の連鎖を生成するための経験主導型の反復プロセスを通じて、この漸進的なキューの増強を可能にする、思考のブースト（BoT）と呼ばれる新しいフレームワークを提案する。反復的な探索と自己評価を通じて生成される単純なツリー状の思考の連鎖により、単純な初期手がかりが、一連の試行錯誤的な推論経験によって漸進的に増強され、正確な解答へと導かれる。我々の広範な実験により、BoTは複数のベンチマークデータセットで最先端の性能を達成でき、「24のゲーム」という難易度の高い数学的推論タスクにおいて他の主要な手法を凌駕することが示された。

基本的なプロンプトと推論プロセスのBoT

A1 思考生成コンポーネントのBoT

このセクションでは、提案するBoosting of Thought(BoT)の推論生成に使用する基本的なヒントについて述べます。具体的な詳細については、ソースコードのサンプルファイル/examples/BoostingOfThought/BoT reasoner.pyを参照してください。

システムのヒント

あなたは数学問題のエキスパートです。一連の試行錯誤の推論経験から学ぶことで、段階的な問題解決の推論を実行します。この試行錯誤の推論経験には、具体的にエラー報告や、以前の推論ステップの修正方法に関する詳細な提案が含まれています。新しい推論ステップを生成する前に、これらのリストアップされた経験を確認することが重要である。

 

システムプロンプト S.

あなたは数学的問題の専門家です。 段階的な推論を行います。
試行錯誤の推論経験のアンサンブルからまず学ぶことによって、問題解決に向かう。
このような試行錯誤の推論経験には、具体的には、エラーレポートと詳細なアドバイスが含まれている。
歴史的な推論のステップを修正する方法。 歴史的な推論を生み出す前に、必ずこれらの経験を思い出してください。
新たな推論ステップを導入することで、同じミスを避け、正しいステップを再利用することができる。
タスクを解決するために、より良い推論のステップ。

次の思考のためのプロンプトを生成する：

f"""

{ミッションアラート｝ \n

まず、前の推理経験を思い出してください。

 

経験

 

次に考えられる推論ステップを紹介してください。この推理ステップは、次の順序付けられたステップの連続的な後継として使用され、対応する評価スコア（スコアが高いほど、タスクを完了する可能性が高いことを示す）を伴う必要があります。

{チェーンヒント

 

上記の先行推論ステップに基づいて(または上記のスペースが空の場合は無視して)、タスクルールに基づいてユニークな次の可能なステップを生成します。(重要: 与えられたステップに対して、次に可能な推論ステップのみを生成してください)。

"""

f"""{タスクプロンプト}. \まず、過去の推論経験を思い出してください。
次の推論を1つだけ生成するために、1ステップの推論をしてください。
この次の推論ステップは、次のステップからの順次ステップである。 次の推論ステップは
次の順序で前のステップに進み、その評価点（A
スコアが高いほど、推論ステップがタスクを完了する可能性が高いことを意味する) :ε≦ε≦ε≦ε≦ε≦ε≦ε
chain prompt}n Based on listed previous reasoning steps (ignore them when
上記のスペースは空である）、タスクに続く次の可能なステップを1つ生成する。
ルール (強調：次の可能な推論ステップを1つだけ生成してください。
与えられたステップ.) """

タスクプロンプトはタスクのXとQを含み、過去の経験はF1...である。連鎖ヒント」部分は{Gi}で、これはプレースホルダであり、現在の思考 zi が実行されると、前の一連の思考 z1...,i-1.,i-1.

評価を考えるヒント

f"""

{ミッションアラート｝\

以下に、推論ステップを順番に、それぞれの評価スコアとともに示します。(スコアが高いほど、そのステップでタスクを完了できる可能性が高いことを意味する）。\n

{チェーンヒント}n

{Thinking｝

これらの推論ステップがどの程度論理的で正しいか、また、最終的な解答にどの程度役立っているかを評価するための点数を教えてください。0.1、0.3、0.5、0.7、0.9、1.0]のいずれかを選んでください。スコアは' 評価スコア:'の後に配置し、ユーザーが読めるようにしてください。""""

 

f"""{タスクプロンプト}. \以下に、生成された推論ステップを順に示します。
評価された点数（点数が高いほど、推論ステップが高いことを意味する。
タスクを完了する可能性が高い。） :チェーンプロンプト}n{思考}nWhat is your
論理性、正しさ、そして最終的な利益を評価する。
これらの推論ステップの解答は？ 0.1,0.3,0.5.から一つ選んでください、
0.7、0.9、1.0] をスコアとし、スコアが高いほど推論ステップが優れていることを意味する。 ここで
スコアは、ユーザーが読みやすいように ' 評価スコア :' の後に置くべきである。

この場合の思考とは、現在進行中の思考ジーのことである。

経験生成コンポーネントのA2 BoT

集約されたチェーンに対するフィードバックを生成するために、LLMは以下の基本的なプロンプトを使用します。詳しくは、ソースコードexamples/BoostingOfThought/BoT commenter.pyを参照してください。

システムプロンプトS：あなたは数学の問題を解くために生成された推論の連鎖を評価するMaths AnswersのAIエキスパートレビュアーです。この推論チェーンの各推論ステップを、現在のステップが前のステップからの論理的推論であるかどうか、推論ステップが正しい解答に寄与しているかどうかを判断するための詳細な分析を提供することによって評価してください。間違った推論ステップごとに、エラーレポートとそれに対応する修正案を提示してください。正しい推論ステップごとに、推奨または却下の説明を提供してください。

システムのヒント

あなたの役割は、数学の問題を解く推論プロセスを評価することに焦点を当てた、熟練したAI数学解答レビュアーです。各推論ステップが前のステップの論理に基づいているか、このステップが正解を導くのに貢献しているかを徹底的に分析し、判断する必要があります。間違った推論ステップに遭遇した場合は、修正のための提案や選択肢を与える必要があります。正しい推論ステップについては、肯定するか、別の選択肢を与える必要があります。

 

システムプロンプト S.

あなたは、数学の解答を評価するエキスパートAIチェッカーです。
数学的問題に取り組むために生成された推論の連鎖。
この推論チェーンのステップでは、現在のステップが論理的であるかどうかについての詳細な分析を提供する。
前のステップの推論と、推論ステップが正しい解答に有益かどうか。
各推論ステップについて、誤りを含むアドバイスや提案をする。 推奨事項や提案をする。
それぞれの正しい推論ステップに対する拒絶の説明。

フィードバックのヒント

f"""

与えられたタスク:{タスクヒント}に対して。\n

{推論連鎖のヒント

この一連の推論を評価し、以下の点を含む詳細な批評を行ってください。\n

1. {チェーンフィードバック形式}. 2. {ステップフィードバック形式}. 3. {自信フィードバック形式}. 4.\4.

警告：{Caveat}。

 

f"""与えられたタスク:{タスクプロンプト}。\この推論連鎖を評価してください。
以下の内容を含む詳細なコメントを与えることによって。\n 1.{
チェーンフィードバック形式｝ 2.{ステップフィードバック形式}。 3.{信頼度フィードバック形式}。\n
\お知らせ: {お知らせ}です。

この中には推論チェーンのヒントは集約された推論連鎖z1.....n.

チェーン・フィードバック・フォーマットこの推論の連鎖は、その推論のステップを実行することで、タスクを正しく完了し、ゴールに到達することができますか？なぜか？分析レポート：」の下に結論となる分析を書いてください。

ステップ・バイ・ステップのフィードバック形式各推論ステップについて、現在のステップが前のステップからの論理的な推論であるかどうか、推論ステップが正しい解答に寄与しているかどうかについての詳細な分析を提供してください。各推論ステップの誤りについては、エラーレポートとそれに対応する修正勧告を提示してください。各推論ステップについて、推奨または却下の説明を提供してください。コメントは簡潔で、次の形式に従ってください：推論ステップ ⟨ IDX ⟩.分析⟩.推奨：.推奨または却下の説明：.

自信のフィードバック形式: これらの評価やレビューに対する信頼度は何点ですか？0.1,0.3,0.5,0.7,0.9,1.0]から選んでください。

フィードバックを合図に、LLMは推論チェーンと各推論ステップの結論と分析を含む経験的なFtを生成する。

A3 推論プロセス

提案するBoosting of Thoughtsの理解を容易にするために、推論フローをアルゴリズム表1にまとめる。このフローのソースコードはexamples/BoostingOfThought/BoT core.pyにあります。

BoTオリジナル

画像の内容は、「BoT」と呼ばれる理論を段階的にアルゴリズムで表現したもので、以下はその中国語訳であり、以下のアルゴリズムのステップに対応している：

アルゴリズム1：BoTの主な推論プロセス

入力: 反復回数 T, 木構造の数 M, 問題 Q.
出力：集約されたチェーン z̄_1.....n^T

1.単純なヒントI^0 (S, X, Q, F^0, {Gi})を初期化する。
2.各反復 t = 1, 2, ... , T., T.
3.手がかりI^t-1 (S, X, Q, F^t-1, {Gi})をLLMS(低潜在混合モデル)を使って、思考構造生成と呼ばれるプロセスでM個の異なる思考構造を作成する。
4.M個の思考構造から思考の連鎖{z↪Mn_i=1...n^m} を抽出、各z↪Mn_i=1.....n^m}、各z̄=1.....n^mはm番目の木構造の最良の思考連鎖である。
5.ベスト・ファースト集約法または貪欲集約法を使用して、{z_i=1...n^m}を一つの思考鎖 z̄_1...n^m} に組み込む。.n^m} を単一の思考鎖 z̄_1...n^t..n^t.
6.LLMSを使ってz̄_1...n^tに対して「思考連鎖分析」を行う。.n^tで「思考連鎖分析」を実行し、フィードバックを得、z̄_1.....n^tと組み合わせ、z̄_1...n^t と組み合わせて経験値F^tを得る。
7.F^tをI^t（S,X,Q,F^t-1,t,{Gi}）に累積してキューを更新する。
8.結論
9.解へのアクセス z̄_1.....n^T

B 思考力を高める洞察

思考のブーストは、数学的問題を解くための大規模言語モデル（LLM）の推論能力は、過去のエラーに対する分析と示唆を含む経験から直接得られるという我々の洞察に由来する。LLMが推論を実行する前に思い出すべき有効な過去の推論経験がキューに含まれていれば、表5と表6の比較に示されているように、結果として得られる推論ステップは通常より論理的で合理的である。また、これらの洞察から、LLMは各タスクにおいて、十分に準備されたプロンプトに大きく依存する必要はないと考えるに至った（プロンプト中のいくつかの思考連鎖のデモンストレーションがその例となる）。しかし、LLMは経験から学習することができるため、模範解答や人手でデザインしたコンテンツを必要としないシンプルなプロンプトから始め、推論しながら徐々に経験を蓄積していくことができる。最終的には、キューの経験を蓄積することで、LLMは複雑な問題を解決するための強固な推論を達成する。これらの洞察により、Boosting of Thoughtsは、試行錯誤的な推論経験を繰り返し収集することで問題を解決する自動プロンプトフレームワークとして設計される。提案するBoTは、LLMを特定のタスクに応用したものではなく、LLMの推論力は、人間の先験的知識に頼ることなく、誤った推論連鎖のエラー分析から直接得られるという洞察に基づいていると主張する。

我々の洞察を強調するために、以下の3つの重要な見解を共有します。これらは、温度0.7、p値0.7のgpt-3.5-turboモデルを使用したアプリケーションから得られた以下の24試合のゲームデータセットに基づいています。

プロンプトにある経験は、LLMの回答がより論理的なものになるよう促す。表5に示すように、経験がキューに含まれていない場合、モデルは同じ推論ステップを5回生成した。この観察結果は、LLMに共通する問題、すなわち、さまざまな推論論理を探求する自己動機付けの欠如を示している。このように、LLMは強い推論の可能性を持っているにもかかわらず、最も単純な推論ステップから始まるサイクルにはまり込み、最終的な解決に至らないことがある。表5の「獲得された推論チェーン」のセクションは、誤った推論チェーンを示している。我々は、Tree of Thoughts Yao et al.(2024)のように、ツリーのノードが思考として複数の回答を生成することで構築されるため、このような推論ステップの繰り返しにより、場合によってはアルゴリズムが失敗する可能性があると考える。しかし、BoTの2回目の反復では、プロンプトに経験を導入した結果、表6に示すように、異なる初期推論ステップが生成された。最終的な推論チェーンは、より幅広い潜在的論理から出発することで、最終的に正しい解に到達することができる。

LLMは、この経験で強調されたような間違いを犯さないようにする。エラー分析を含むプロンプトに経験が含まれていない場合、LLMは表5の「習得した推論の連鎖」に示すように、タスクルールから逸脱したり、最終プロセスで最初の推論ステップに後退したりするなど、多くのミスを犯す。この推論の連鎖を分析し、そのフィードバックを経験としてBoTの2回目の反復のプロンプトに取り入れた結果、表6から、LLMは推論の前に経験をしっかり学習することがわかる。まず、どの回答も「gpt-3.5-turboからの5つの回答」で示した多様な最初の推論ステップと同じ誤った推論ステップを再現していない。第二に、LLMはタスクルールを厳密に守り、誤った推論を排除し、論理的な推論ステップを実行することで、これまでに確認されたすべての誤りを回避することに成功した。第三に、これは最終的に「1 1 4 6」の24のゲームのタスクの正しい解答につながった。Wengら(2023); Madaanら(2023); Zhengら(2023)のような他の研究も、以前の解答の自己評価であるフィードバックを通じて手がかりを補強することの重要性を強調している。しかし、BoTは、エラー分析を含む経験が、LLMの強力な推論につながるという洞察に基づく画期的な研究である。

人間の注釈がなくても、LLMは自動的に効果的な推論の連鎖を組織し、経験に基づいて複雑な問題を解決する。BoTは、人間のアノテーションを必要とせず、LLMがエラー分析と経験によるガイダンスだけで、問題解決のための効果的な推論スキルを習得できるという洞察を活用した自動プロンプティングフレームワークを提案する先駆的な取り組みである。表5に示すように、これはBoTの最初の反復であり、最初のヒントには、CoTのような文脈的な学習例がなく、基本的なタスクガイダンスと質問のみが含まれている。このようなプロンプトを使用してLLMが得た推論チェーンには、多くのエラーや無効な推論ステップが含まれているにもかかわらず、表6に示すように、彼らのエラー分析や提案は、2回目の推論の反復に役立つように、入力プロンプトに教訓として含めることができる。正しい推論手順に関する人間のガイダンスがなくても、LLMは過去に生成された推論チェーンから得られるエラー分析やガイダンスを含む経験から知識を得ることができ、推論問題解決の漸進的な改善につながることが観察される。

このように、我々のBoTは、LLMが複雑なタスクに対して効果的な推論プロセスを生成できるようにする際の想起エラー分析と示唆の重要性を示しており、研究の長期的な指針となる。これらの洞察により、LLMに推論能力を誘導するための手がかり工学的研究は、より人間的な先験的知識を導入するのではなく、どのように経験を生成するかに焦点を当てることができる。

C思考構造の生成

BoTは、推論連鎖分析から得られた経験を反復的に蓄積する自動プロンプトフレームワークである。さらに、BoTの性能は思考生成構造の有効性に依存する。したがって、BoTは、各反復で推論の連鎖を生成するための基本モデルとして、最新の構造であるTree of Thought（ToT）Yaoら（2024）を使用する。さらに、ブースティング機構のベースモデルとして使用する場合、各反復における思考構造を軽量に保つことができる。最終的に、提案されたBoTは、それぞれが軽量に重み付けされたバイナリーツリーである異種ツリー構造を生成する。

C1 次世代思考とエッジの重み計算

セクションAで説明した次の思考生成の手がかりを使えば、LLMは経験F1.....tを組み合わせ、{Gi}をz1... ,i-1に置き換えることで、推論ステップziの次に可能な思考を生成する。i-1を{Gi}に置き換えて、推論ステップziの次に可能な思考を生成する。推論ステップziに対して、LLMは思考評価キューを使用して、ziとzi-1の間のエッジ重みとして評価スコアを生成する。詳細な手順については、examples/BoostingOfThought/BoT reasoner.pyのソースコードを参照してください。gpt-3.5-turboを用いて、BoTをGame of 24の'3 5 6 8'に適用した直接の例として、表7と表8に思考の生成を、表9にその計算方法を示す。

C2 異種ツリー構造の必要性

BoTの各反復において、より広い推論探索空間を探索し、頑健性を向上させるために、異種ツリー構造が構築される。examples/BoostingOfThought/BoT core.pyのソースコードにあるように、各ツリーのLLMの温度とTop p値はそれぞれ[0.2, 0.4, 0.6, 0.7, 0.9, 1.1, 1.5]と[0.1, 0.3, 0.5, 0.7, 0.9]の範囲から選択される。木の成長戦略は、層ごとでも葉ごとでもよい。このような異質性を確保することで、以下の2つの利点がある。

異質性は推論探索空間を拡張し、収束速度を向上させる。異なるツリーが異なる目的のために構築される場合、例えば、レイヤ ーごとの戦略を使用して探索される場合、リーフごとの戦略を使用して探索 される場合、ランダムまたは決定論的なLLMに基づく場合、生成される推論ステッ プと結果として得られる推論チェーンは大きな違いを示し、効果的に推論の可 能性の広い範囲をカバーすることができる。例えば、ある反復において、LLMがより確信を持って次の思考を生成する場合、類似した思考が連続的に探索される。そうでない場合、よりランダム性の高いLLMは多様な思考を生成する傾向がある。決定論的推論とランダム性のどちらが解に寄与するかを予測するのは難しいことが多い。したがって、異なるタイプの論理的推論ステップを混ぜることによって異質性を確保することで、1回の反復で推論空間を完全に探索することができ、最終的にその後の反復が容易になる。アブレーション研究では、異種ツリー構造と同種ツリー構造のBoT性能を比較する。

異質性は、無効な推論連鎖や誤った推論連鎖を生み出す可能性を減らし、ロバスト性を高める。異質性とは異なり、均質な設定を持つツリーでは、個々のツリーは一貫した論理的生成思考に従い、同じツリー構造で推論チェーンを構築する傾向がある。そのため、論理が間違っていたり、基礎となる構造が手元の問題に対して妥当でない場合、各反復でBoTによって得られたすべての木の推論チェーンには、ノイズの多い誤った推論ステップしか含まれなくなる。それらを集約してより洗練された推論チェーンを得て評価する場合でも、その経験は適切な問題解決アドバイスの提供から大きく逸脱する可能性がある。したがって、ツリー思考構造を異種構造に設計することで、後続のBoT反復で評価に利用できる有効な推論チェーンがない可能性を減らすことができる。このようにロバスト性を高めることで、BoTはさまざまな難易度の問題を解決できるようになる。

これは "最優先集約 "と "貪欲集約 "のプロセスを描いたものである。

入力: m個の推論連鎖。m番目の連鎖の推論ステップをz1i = 1mとする。
出力：ポリマー鎖z1...n。

1 - 最優先アグリゲーション
2 各チェーンm = 1, 2, ... に対してM
3 m1m Vi-1,iの範囲でm番目のチェーンのエッジ重みの合計をVm = ∑iとして計算する。
4 終了
5 m* = arg maxm {Vm}を実行することにより、M個の鎖の中から最適な鎖を得る。
6 集約されたチェーンを最適なものとして割り当てる。.n := {z1i=1n*m*} とする。

7 - 貪欲な集約
8 z1 := z1 ここで、m* = arg maxm {V1m}である。
9 各集計ステップ i = 2, ... についてn
10 各チェーンm = 1, 2, ... , についてM
11 Jm = {j, sim(z1i-1, z1j) > 0.7; j∈n1m} を集める。
12 j*,mを得る = arg maxj∈Jm {Vj,j+1m}。
13エンド
14 最適な次の推論ステップを得るために以下を実行する： zi = z1j*+1 ここで、j* = arg maxj∈{j*m}1M {Vj,j+1m}。
15エンド
16 ポリマー鎖z1.....n.

これは基本的に、データチェーンやノードを最適化し、さまざまな方法によって最良の結果を得る方法を説明するアルゴリズムのフローチャートである。

D 思考構造の集約

異種ツリー構造で推論を完了した後、BoTの集約プロセスでは、まず各ツリーから推論の最良の連鎖を抽出し、最良優先または貪欲な集約メソッドのいずれかを使用して、それらを単一の推論の連鎖に結合します。これら2つの集約方法に関する詳細な情報は、ソースコードexamples/BoostingOfThought/BoT aggregator.pyに記載されています。

アルゴリズム16の最初のブロックに示すように、ベスト・ファースト集約は、エッジ重みの合計が最も大きいチェーンを直接抽出する、簡単な集約方法である。この方法は高速で安定している。得られた最適な連鎖を分析することで、後続の経験を生成することができるため、通常、競争力のある性能を保証する。しかし、効率的なチューニングを行うことなく、既存の連鎖を選択することしかできない。貪欲な集約は、異なる連鎖の推論ステップを組み合わせて、最も高いエッジ重みを持つ新しいより良い推論連鎖を生成するため、より高度である。アルゴリズム16の貪欲な集約プロセスは2つのステップからなる。まず、集約された推論ステップ zi-1 に類似する推論ステップを集める。simはLLMを用いて2つの文章間で同じ単語や数学的数値の割合を評価する類似度関数であり、0.7は実験から得られた経験的閾値である。

E 誤ったフィードバックの影響

集約された推論チェーンを評価することで得られるフィードバックには、解析の利用が制限されたり、完全に誤った結論やエラーレポートが含まれることがある。この問題は通常、言語モデルであり、生成されたテキストの正確さを本質的に検証しないLLMの性質に起因する。加えて、gpt-3.5-turboのようなLLMの機能は、数学的問題のバリデーターとして使用する場合には限界がある。

わかりやすい例を表7に示す。この分析では、「ステップ3で得られた最終結果は80であり、数学的には24に等しい」と結論づけている。さらに悪いことに、この経験には「推論の連鎖は正しい」「推論のステップでエラーは見つからなかった。エラーが見つかった"この経験を入力キューとして使用すると、最初の反復で、BoTは間違った推論ステップを生成するように惑わされ、対応する集計チェーンは表8の最初に見ることができる。集計チェーンが論理的に正しくなく、ゲーム・オブ・24のどのルールにも準拠していないことは明らかである。

しかし、誤ったフィードバックが増幅されることはなく、BoTの反復メカニズムによって、生成された推論ステップへの悪影響が軽減されたり、その後の反復で完全に修正されることもあると主張する。その主な理由は、生成された誤った推論ステップは、キューに追加される新しい経験を生成するためにさらに分析されるからである。具体的には、これらの推論ステップには容易に認識できる明白な誤りが含まれているため、LLMは正しい誤り分析を生成し、効果的な修正案を提供する傾向がある。新しい経験がヒントに含まれることで、BoTは正しい推論ステップを生成できる。表8の経験が示すように、BoTは詳細なエラー報告と修正提案を生成し、合理的な思考生成プロセスをもたらした。

エラー・フィードバックの悪影響を軽減するために反復を利用するBoTの利点は、図4を見れば明らかである。注目すべきは、反復回数が増えるにつれてBoTのパフォーマンスが一貫して向上していることである。これは、累積経験の重要性と、後続の経験が以前のエラーを修正する能力を強調している。

F 数学の検索結果をもっと見る

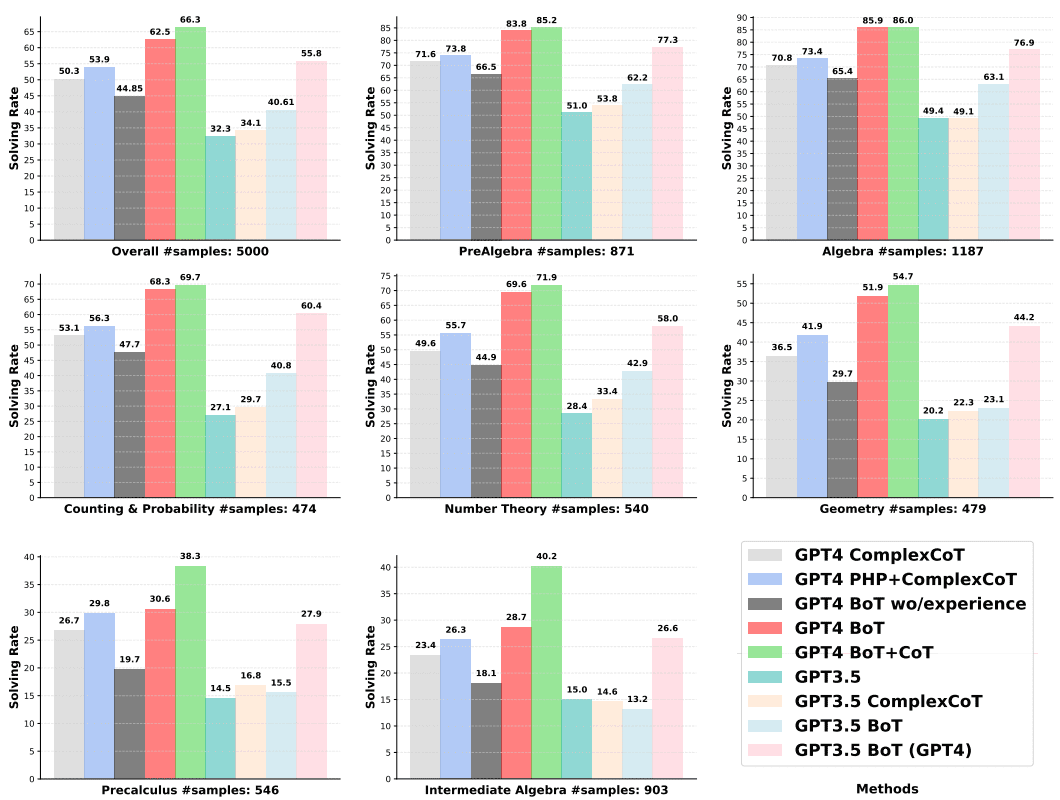
図5：MATHデータセットに分類されたすべての問題を解くために、異なる戦略を使用することの有効性を明らかにする。プレ代数、代数、計数と確率、数論原理、幾何、プレ微積分、中級代数を含むカテゴリーに基づいて、ストラテジーを比較している。全体」とラベル付けされたサブプロットは、すべてのカテゴリーにおけるすべての問題の全体的な解答率を示している。

図5では、MATHデータセットの各カテゴリーにおける異なる手法の解答率を示している。これらのカテゴリーに含まれる様々な数学的問題の複雑さと多様性は、数学的推論のより困難なベンチマークを提供する。このように、MATHの問題の複雑さと多様性は、それらを解くための幅広い推論能力を必要とする。したがって、我々のアプローチの詳細な検討と、我々の文脈における他のアプローチとの比較は、貴重な洞察を提供することができる。

LLM。GPT-3.5-Turbo(以下GPT3.5)とGPT-4(以下GPT4)という、よく知られた大規模言語モデル(LLM)を使用しました。 OPENAIが公開しているAPIを直接使用しました。

ライバルたち
- GPT4 ComplexCoT.は、Complex CoT Fuら（2022）のプロンプト法を用いたGPT4のモデルである。推論ヒントには推論例を用いており、これは対応するComplex CoTの出版物であるFu et al.（2022）から引用している。貪欲なデコーディングを使用しているため、推論経路のサンプリングについてはWang et al.
- GPT3.5.標準プロンプトが使用され、GPT3.5モデルが答えを生成するために使用されます。
- GPT3.5 ComplexCoT。GPT4 ComplexCoTに似ているが、モデルはGPT3.5に変更されている。
- これは、PHP Zheng et al. (2023) + Complex CoTFu et al. (2022) を使用した GPT4 モデルである。具体的には、PHP Zheng et al. (2023)のフレームワークでは、Complex CoTプロンプトが最初のベース回答を生成するために使用され、PHP+Complex CoTはこれらのベース回答から後続の回答生成プロンプトを開発することができる。したがって、インタラクションの最初に、Complex CoTのベースヒントと現在の質問をLLMに渡すことで、ベースアンサーを生成することができる。その後、ヒント文を追加したPHPバージョンに改訂されたComplex CoTヒントに基づき、ステップバイステップのヒンティングフレームワークがこのベースアンサー上で実行され、正しい答えが生成されます。これを、原著のPHP-Complex CoTと対をなすPHP+Complex CoTと呼ぶ。Complex CoTのショット数は8である。
- GPT4 BoT wo/ experience. GPT4モデルは、経験を蓄積することなくBoTフレームワークの推論を実行するために使用される。BoTの基本的な設定は、メインペーパーで提示されたものに従う。したがって、1回の反復の後、集約された連鎖が解として使用される。
- GPT4 BoT。GPT4は、本論文で示したBoTの完全版を実行するために使用される。
- GPT4 BoT + CoT.BoTフレームワークに加えて、プロンプトにはCoT Wei et al.(2022)の出版物から5つの推論例が含まれていた。したがって、各反復において、プロンプトには経験だけでなく、追加の5つのCoT推論例も含まれている。
- GPT3.5 BoT。GPT4 BoTに似ているが、モデルはGPT3.5に変更されている。
- GPT3.5 BoT（GPT4）。この実験では、GPT3.5を使って推論を行うことで、思考構造生成における思考の連鎖を生み出す。

しかし、GPT4モデルは、思考連鎖分析の集計で思考評価と経験生成を行う際に、評価と分析フィードバックを得るために使用された。

図5の結果から、我々は次のような追加的観察を行った。

BoTがより困難な問題を解決する際、傑出したパフォーマンスを発揮するのは、経験によるところが大きい。GPT4 BoTやGPT4 BoT + CoTなどのBoT関連手法は、MATHのさまざまなサブカテゴリで一貫して最高の問題解決率を達成しています。具体的には、GPT4 BoT は利用可能な最良の解決策である GPT4 PHP + ComplexCoT を 8.61 TP3T 上回り、GPT4 BOT + CoT は 12.41 TP3T 上回りました。7 つのカテゴリの合計では、GPT4 BoT は GPT4 PHP + ComplexCoT を少なくとも 0.81 TP3T 上回り、その代数問題GPT3.5 BoTとGPT3.5 BoT + CoTも同様である。しかし、BoTフレームワークの経験が蓄積されていない場合、GPT4 BoT wo/経験で示されるように、すべての数学的問題解決のパフォーマンスが激減する。

エラー分析の経験に加え、簡単なCoTの例題のような正しい例題を含めることは、難しい数学的問題を解くBoTの効果を高めるために不可欠である。GPT4のBoTは、MATH問題の最初の5つのサブカテゴリを解く際に、GPT4のPHP+ComplexCoTを大幅に上回った。しかし、より複雑な推論と複雑な論理的ステップバイステップの解法の必要性が高い上級および中級代数の分野では、BoTの改善はわずか0.8%と2.4%である。これらの向上は、より単純な問題カテゴリーを解いたときに観察された大幅な向上と比較すると、比較的限定的である。しかし、CoTの5つの正しいインスタンスが入力プロンプトに直接追加された場合、GPT-4 BoT + CoTは、上級代数と中級代数のドメインでそのパフォーマンスを大幅に向上させ、それぞれ7.71 TP3Tと11.51 TP3TでGPT-4 BoTを上回りました。これらの観察の根本的な結論は、BoTが複雑な数学的問題を解く際に最高のパフォーマンスを達成できるようにするには、推論を学習するための試行錯誤分析だけでは不十分であるということです。推論を学習するためのエラー分析は十分ではなく、入力プロンプトのLLMに正しい答えを提供することに頼るべきである。

当初はGPT3.5フィットBoTはGPT-4CoTにやや劣るかもしれないが、GPT-4を評価・分析ツールとして経験を積めば、GPT-3.5BoT（GPT-4）をGPT-4コンプレックスCoTを凌駕させることも可能である。GPT4よりも容量が小さいGPT3.5をLLMとして使用した場合、BoTはGPT4 ComplexCoTよりも少なくとも7.71 TP3T低い解答率を得た（特に代数の分野で）。したがって、GPT3.5を使用して推論ステップのみを生成し、GPT4で生成された経験と並行させた後、GPT3.5 BoT（GPT4）はすべてのカテゴリで大幅な改善を示し、解答率は55.81 TP3Tとなり、GPT4 ComplexCoTを5.81 TP3T上回りました。これは、GPT4 ComplexCoTよりも5.5%高く、さらに現在の最先端GPT4 PHP+ComplexCoTよりも1.9%高い。これらの観察結果は、ヒントの反復を通じて得られた経験がBoTフレームワークの成功の主な理由であることを示すさらなる証拠となる。

G 試合の推理結果 24点

まず、表5から表9に、推論プロセスでBoTが使用する詳細なキューを示し、各反復でBoTが何を行うかを包括的に理解できるようにする。次に表10から、BoTの推論プロセス全体を網羅する正確な例を示す。実験セクションに示した基本セットアップに従い、これらの実験はBoTを搭載したGPT-3.5-turboモデルを使用して得られた。

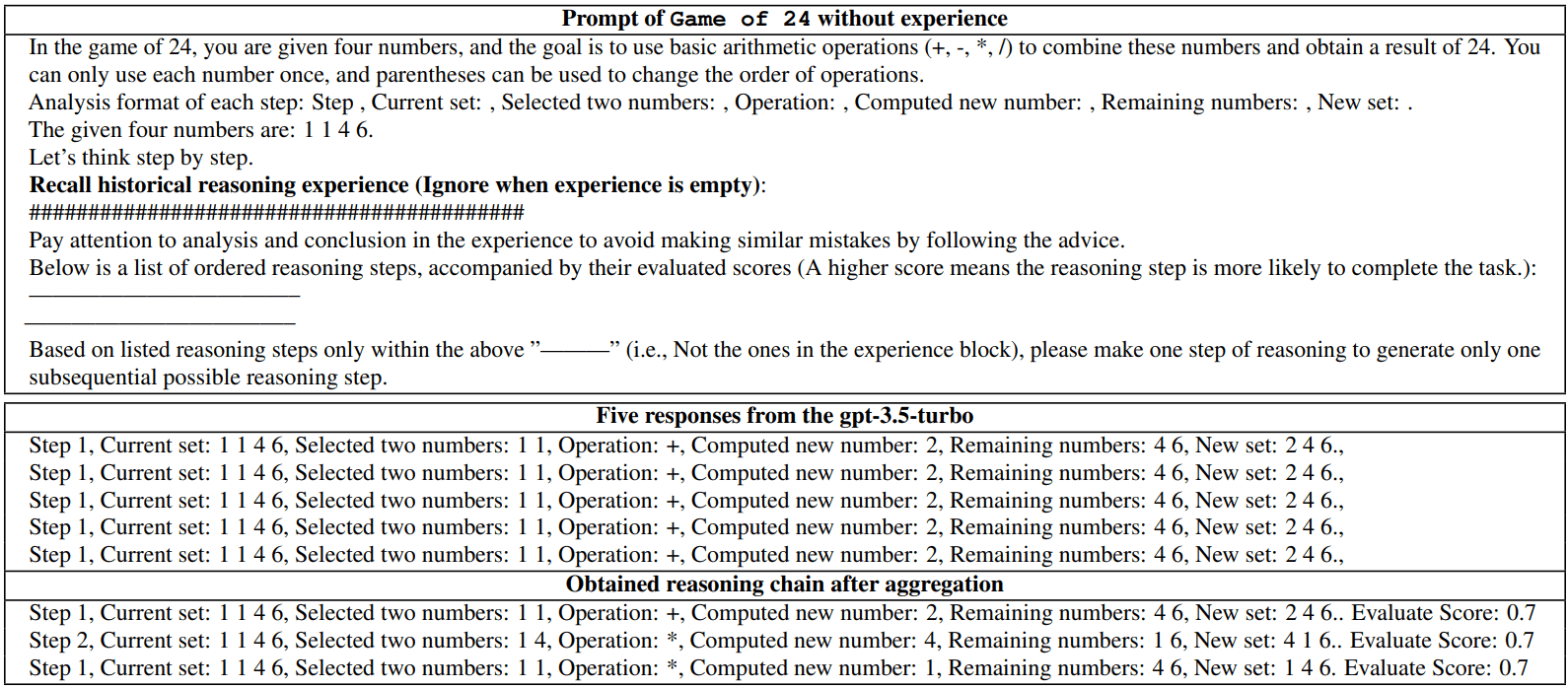
表5：入力プロンプトに経験が含まれていない場合にgpt-3.5-turboが生成する推論ステップ。まず、多様性をチェックするためにモデルに5つの推論ステップを生成させ、BoTの最初の反復を完了した後に最終的な推論チェーンを提示する。

試合のヒント 24:00、経験なし

24ポイントでは、4つの数字が与えられ、基本的な算術演算（+、-、*、/）を使ってこれらの数字を組み合わせ、24という結果を得ることを目標とする。各数値は一度しか使用できず、括弧を使って演算の順序を変えることができる。

フォーマットの各ステップを分析する：
ステップX 現在のセット：XXXX、選択された2つの数字：XX XX、操作：XX、計算によって得られた新しい数字：XX、残りの数字：XXXX、新しいセット：XXXX。

与えられた4つの数字は、1 1 4 6。
ステップ・バイ・ステップで考えよう。

歴史的な推論経験を思い起こす（経験が無効の場合は無視）：
## ############### ######## ######## # # # #######
体験談にある分析と結論に注意を払い、提言に従って同じような過ちを犯さないようにしよう。
以下は、順番に並んだ推論ステップとその評価スコアである(スコアが高いほど、その推論ステップがタスクを完了する可能性が高いことを意味する)。:

に記載された推論ステップ（すなわち、経験的ブロックのステップではない）に基づいて、1つの推論ステップを実行し、1つだけ可能な後続の推論ステップを生成してください。

gpt-3.5-turboからの5つの回答
ステップ1: 現在のセット: 1 1 4 6, 2つの数字を選択: 1 1, 操作: +, 新しい数字を計算: 2, 残りの数字: 4 6, 新しいセット: 2 4 6, 評価スコア: 0.7.
ステップ1: 現在のセット: 1 1 4 6, 2つの数字を選択: 1 1, 操作: +, 新しい数字を計算: 2, 残りの数字: 4 6, 新しいセット: 2 4 6, 評価スコア: 0.7.
ステップ1: 現在のセット: 1 1 4 6, 2つの数字を選択: 1 1, 操作: +, 新しい数字を計算: 2, 残りの数字: 4 6, 新しいセット: 2 4 6, 評価スコア: 0.7.
ステップ1: 現在のセット: 1 1 4 6, 2つの数字を選択: 1 1, 操作: +, 新しい数字を計算: 2, 残りの数字: 4 6, 新しいセット: 2 4 6, 評価スコア: 0.7.
ステップ1、現在のセット：1 1 4 6、選ばれた2つの数字：1 1、操作：*、計算された新しい数字：1、残りの数字：4 6、新しいセット：1 4 6、評価点：0.7。

集約後に得られる推論チェーン
ステップ1、現在の集合：1 1 4 6、選ばれた2つの数：1 1、操作：+、計算された新しい数：2、残りの数：4 6、新しい集合：2 4 6... 分数を評価する： 0.7
ステップ2、現在の集合：1 1 4 6、選ばれた2つの数：1 4、操作：*、計算された新しい数：4、残りの数：1 6、新しい集合：4 1 6... 評価スコア：0.7
ステップ1、現在のセット：1 1 4 6、選ばれた2つの数字：1 1、操作：*、計算された新しい数字：1、残りの数字：4 6、新しいセット：1 4 6、評価点：0.7。

H "GSM8K "の派生結果。

BoTは、表5から表9に示すような基本的なプロンプトと特定のフォーマットを使用して動作する。変わるのは、表15に示すように、タスクプロンプトだけである。そして表16から、BoTの完全な推論プロセスを含む詳細な例を多数提供する。これらの実験は、BoTのGPT-3.5-turboモデルを使用し、実験セクションに示した基本セットアップに基づいている。

# 第24戦のための経験的推論のプロンプト

##まず、歴史的な推論経験を振り返る：

### 推論連鎖1とそのコメント

以下は、推論ステップの連鎖を順番に示したものである：

---

### ステップ1
現在の集合：1 1 4 6、選ばれた2つの数：1 1、操作：+、計算された新しい数：2、残りの数：4 6、新しい集合：2 4 6... 評価スコア：0.7

### ステップ2
現在の集合：1 1 4 6、選ばれた2つの数：1 4、操作：*、計算された新しい数：4、残りの数：1 6、新しい集合：4 1 6... 評価スコア：0.7

### ステップ3
現在のセット：1 1 4 6、選ばれた2つの数字：1 1、操作：*、計算された新しい数字：1、残りの数字：4 6、新しいセット：1 4 6。

---

##分析：この推論の連鎖は課題を完了し、ゴールに正しく到達することができない。推論のステップに誤りがあり、正しい解決策の発見を妨げています。

### 推論ステップ1
このステップは、2つの数を選択し、演算を実行し、それに応じて集合を更新するというルールに従っているので、前のステップの論理的な外挿である。しかし、このステップは正しい解答には貢献していない。計算によって得られた新しい数2は、望ましい結果24にはつながらない。
**提案**：24に近い新しい数字を得るために、さまざまな操作や数字の組み合わせを試してみてください。
**推薦または不採用の内容**：不採用。

### 推論ステップ2
推論ステップの説明に誤りがあります。推論ステップ2」と2回間違っている。しかし、それが唯一のステップであると仮定すると、それは前のステップからの論理的な演繹である。乗算(*)操作は選択された数字に正しく適用され、新しい数字4になります。
**推薦または不採用の内容**：推薦する。

### 推論ステップ3
推論ステップの説明に誤りがあります。推論ステップ3」ではなく「推論ステップ1」と間違っています。このステップは前のステップからの論理的な推論ではありません。乗算(*)演算は推論ステップ1と同じ数に適用されますが、新しい数1の計算方法は異なります。残りの数字はそれに応じて更新される。
**バグレポート**：このステップの計算が間違っています。正しい計算は 1 * 1 = 1 です。
**推奨**：計算が正確であることを再確認すること。
**推薦または不採用の内容**：不採用。

**信頼度**：0.7

---

## gpt-3.5-turboからの5つの回答

---

### ステップ1
現在のセット：1 1 4 6、選択された2つの数字：1 4、操作：*、計算された新しい数字：4、残りの数字：1 6、新しいセット：1 4 6......。

### ステップ1
現在のセット：1 1 4 6、選択された2つの数字：1 6、操作：＋、計算された新しい数字：7、残りの数字：1 4、新しいセット：1 4 7......。

### ステップ1
現在のセット：1 1 4 6、選ばれた2つの数字：1 1、操作：*、計算された新しい数字：1、残りの数字：4 6、新しいセット：1 4 6......。

### ステップ1
現在のセット：1 1 4 6、選択された2つの数字：1 4、操作：/、計算された新しい数字：0.25、残りの数字：1 6、新しいセット：0.25 1 6...、そして

### ステップ1
現在のセット：1 1 4 6、選ばれた2つの数字：1 1、操作：-、計算された新しい数字：0、残りの数字：4 6、新しいセット：0 4 6......。

---

## 集約後の推論チェーン

---

### ステップ1
現在の集合：1 1 4 6、選ばれた2つの数：1 1、操作：*、計算された新しい数：1、残りの数：4 6、新しい集合：1 4 6... 評価スコア：0.9

### ステップ2
現在の集合：1 4 6、選ばれた2つの数：1 4、操作：*、計算された新しい数：4、残りの数：6、新しい集合：4 6... 評価スコア：0.7

### ステップ3
現在のセット：46、選ばれた2つの数字：4 6、操作：*、新たに計算された数字：1、残りの数字：、新しいセット：24。 評価スコア：0.9

---

表6: 経験を入力プロンプトに組み込んだときにgpt-3.5-turboが生成する推論ステップ。この経験は表5の推論連鎖を分析したものである。この経験をキューに設定した後、モデルからの5つの応答とBoTの2回目の反復の完了後に形成される最終的な推論チェーンを示す。

# 次世代思想のヒント

24ポイントゲームでは、4つの数字が与えられ、基本的な算術演算（+、-、*、/）を使ってこれらの数字を組み合わせ、24という結果を得ることが目標です。各数字は一度しか使用できず、括弧を使って演算の順序を変えることができます。

各ステップの分析フォーマット：ステップ、現在のセット：、選択された2つの数字：、操作：、計算された新しい数字：、残りの数字：、新しいセット： 。

与えられた4つの数字は、3 5 6 8。

ステップ・バイ・ステップで考えよう。

##まず、歴史的な推論経験を振り返る：

###最初の推論とコメントの連鎖

以下は、順番に示された推論ステップを含む推論の連鎖である：

---

ステップ1、現在の集合：3 5 6 8、選ばれた2つの数：5 6、操作：*、計算された新しい数：30、残りの数：3 8、新しい集合：30 3 8... 評価スコア：0.9

ステップ2、現在の集合：30 3 8、選ばれた2つの数：30 3、操作：/、計算された新しい数：10、残りの数：8、新しい集合：10 8... 評価スコア：0.9

ステップ3、現在のセット：10 8、選択された2つの数字：10 8、操作：*、計算された新しい数字：80、残りの数字：なし、新しいセット：80... 評価スコア：0.9。

---

##分析レポート

この推論の連鎖により、タスクは正しく完了し、その推論ステップを実行することでゴールに到達することができる。ステップ3で得られた最終結果は80であり、数学的には24に等しい。

### 推論ステップ1
この推論ステップは、前のステップの論理的派生である。残りの数は3と8である。この推論ステップは、集合の要素数を減らして新しい数を生成するので、正しい解答に役立つ。

### 推論ステップ2
この推論ステップは、前のステップの論理的派生である。現在の集合（30 3 8）から数30と3を選択し、それらを割って新しい数10を得る。

### 推論ステップ3
この推論ステップは前のステップの論理的派生である。現在のセット（10 8）から数字10と8を選択し、新しい数字80を得るためにそれらを乗算します。

提案：推論ステップにエラーは見つからなかった。

推奨または不承認の記述：すべての推論ステップは正しく、正しい解答に到達するのに役立つため、推奨される。

信頼度スコア：0.9

###2番目の推論とコメントの連鎖

続きは表8で

### 分析と結論に関する注記

経験からの分析と結論に基づく提言に従うことで、同じような失敗を避けることができる。

以下は、順番に並んだ推論ステップのリストとその評価点である(点数が高いほど、その推論ステップがタスクを完了する可能性が高いことを意味する)。:

---

ステップ1、現在の集合：3 5 6 8、選ばれた2つの数：3 8、操作：+、計算された新しい数：11、残りの数：5 6、新しい集合：11 5 6... 評価スコア：0.7

ステップ2、現在の集合：11 5 6、選ばれた2つの数：5 6、操作：*、計算された新しい数：30、残った数：11、新しい集合：30 11... 評価スコア：0.9

---

上記の「---」内に記載されている推論ステップ（すなわち、経験ブロック内のステップではない）に基づいて、後続の可能な推論ステップを1つだけ生成する推論ステップを実行してください。

 

##生成された次の推論

ステップ3、現在のセット：30 11、選択された2つの数字：30 11、操作：-、計算された新しい数字：19、残りの数字：、新しいセット：19。

表7：対応する推論ステップziを生成する際にBoTが反映される可能性のある例。

## 2番目の推論とコメントの連鎖

以下は、順番に示された推論ステップを含む推論の連鎖である：

---

### ステップ1
現在のセット：10 8、選択された2つの数字：10 8、操作：/、計算された新しい数字：1.25、残りの数字：なし、新しいセット：1.25。 評価スコア：0.8。

### ステップ2
現在の集合：10 8、選ばれた2つの数：10 8、操作：/、計算された新しい数：1.25、残りの数：なし、新しい集合：1.25... 評価スコア：0.8。

### ステップ3
現在の集合：10 8、選ばれた2つの数：10 8、操作：/、計算された新しい数：1.25、残りの数：なし、新しい集合：1.25... 評価スコア：0.8。

---

##分析レポート

この推論の連鎖は、タスクを正しく完了し、ゴールに到達していない。提供された推論のステップは間違っており、24という結果を得ることにつながらない。

### 推論ステップ1
この推論ステップは間違っている。選択された2つの数10と8は、与えられた数3、5、6、8の集合の中にはない。さらに、divide(/)操作は1.25として計算される新しい数にはならない。

**エラー報告**：
- 選択された2つの数字は、与えられた数字の集合の中には存在しない。
- 操作と計算された新しい数字が間違っている。
- 残りの数字は正しく識別されていない。

**おすすめは**：
- 選択された2つの数字が、与えられた数字の集合の中に存在することを確認する。
- 正しい操作で、希望する新しい番号を取得する。
- 残りの数字を正確に特定する。

**推薦または却下 説明**：却下。この推論ステップは間違っており、正しい解答に貢献していません。

### 推論ステップ2
この推論ステップは推論ステップ1の繰り返しであり、したがってこれも誤りである。このステップは前のステップと同じ誤りを含んでいる。

**エラー報告**：
- 選択された2つの数字は、与えられた数字の集合の中には存在しない。
- 操作と計算された新しい数字が間違っている。
- 残りの数字は正しく識別されていない。

**おすすめは**：
- 選択された2つの数字が、与えられた数字の集合の中に存在することを確認する。
- 正しい操作で、希望する新しい番号を取得する。
- 残りの数字を正確に特定する。

**推薦または却下 説明**：却下。この推論ステップは間違っており、正しい解答に貢献していません。

### 推論ステップ3
この推理ステップは推理ステップ1と推理ステップ2の繰り返しである。このステップには、前のステップと同じ誤りが含まれています。

**エラー報告**：
- 選択された2つの数字は、与えられた数字の集合の中には存在しない。
- 操作と計算された新しい数字が間違っている。
- 残りの数字は正しく識別されていない。

**おすすめは**：
- 選択された2つの数字が、与えられた数字の集合の中に存在することを確認する。
- 正しい操作で、希望する新しい番号を取得する。
- 残りの数字を正確に特定する。

**推薦または却下 説明**：却下。この推論ステップは間違っており、正しい解答に貢献していません。

**信頼度**：0.9

表8：表7のコメントによる第2の推理の連鎖。

#思考評価プロンプト

24ポイントゲームでは、4つの数字が与えられ、基本的な算術演算（+、-、*、/）を使ってこれらの数字を組み合わせ、24という結果を得ることが目標です。各数字は一度しか使用できず、括弧を使って演算の順序を変えることができます。

各ステップの分析フォーマット：ステップ、現在のセット：、選択された2つの数字：、操作：、計算された新しい数字：、残りの数字：、新しいセット： 。

与えられた4つの数字は、3 5 6 8。

ステップ・バイ・ステップで考えよう。

以下の生成された推論ステップは、その評価スコアとともに順番に示されている(スコアが高いほど、その推論ステップはタスクを完了する可能性が高いことを意味する)。:

---

### ステップ1
現在の集合：3 5 6 8、選ばれた2つの数：3 8、操作：+、計算された新しい数：11、残りの数：5 6、新しい集合：11 5 6... 評価スコア：0.7

### ステップ2
現在の集合：11 5 6、選ばれた2つの数：5 6、操作：*、計算された新しい数：30、残った数：11、新しい集合：30 11... 評価スコア：0.9

### ステップ3
現在のセット：30 11、選択された2つの数字：30 11、操作：-、計算された新しい数字：19、残りの数字：、新しいセット：19。

---

これらの推論ステップの論理性、正しさ、最終解に到達するまでの貢献度について、あなたの評価点を教えてください。0.1、0.3、0.5、0.7、0.9、1.0]の中から選んでください。スコアは "評価スコア: "の後に記述してください。

 

## 評価スコアの生成

評価スコア：0.9

表9：ステップ2（zi）とステップ3（zi-1）間のエッジ重みの計算。

# Next Thinkingが生成するプロンプトのフォーマット

24ポイントゲームでは、4つの数字が与えられ、基本的な算術演算（+、-、*、/）を使ってこれらの数字を組み合わせ、24という結果を得ることが目標です。各数字は一度しか使用できず、括弧を使って演算の順序を変えることができます。

各ステップの分析フォーマット：ステップ、現在のセット：、選択された2つの数字：、操作：、計算された新しい数字：、残りの数字：、新しいセット： 。

与えられた4つの数字は5、6、9、4。

ステップ・バイ・ステップで考えよう。

経験を推論するために歴史を見直す（経験が空っぽのときは無視する）：

###########################################

経験からの分析と結論に基づく提言に従うことで、同じような失敗を避けることができる。

以下は、順番に並んだ推論ステップのリストとその評価点である(点数が高いほど、その推論ステップがタスクを完了する可能性が高いことを意味する)。:

---

---

上記の「---」内に記載されている推論ステップ（すなわち、経験ブロック内のステップではない）に基づいて、後続の可能な推論ステップを1つだけ生成する推論ステップを実行してください。

 

# 経験値生成のためのプロンプトフォーマット

与えられた課題：24点のゲームでは、4つの数字が与えられ、基本的な算術演算（+、-、*、/）を使ってこれらの数字を組み合わせ、24という結果を得ることが目標である。各数字は一度しか使えず、括弧を使って演算の順序を変えることができる。

ステップ・バイ・ステップで考えよう。以下は、推論のステップを順番に示した推論の連鎖である：

---

---

この推論の連鎖は、次の領域をカバーする詳細な批評を提供することによって評価してください： 1.この推論の連鎖は、その推論のステップを実行することによって、タスクを正しく完了し、ゴールに到達することができますか？なぜですか？各推論ステップについて、現在のステップが前のステップからの論理的な進行であるかどうか、また、推論ステップが正しい解答に寄与しているかどうかを詳細に分析してください。エラーのある推論ステップごとに、エラーレポートとそれに対応する修正勧告を提供する。各推論ステップについて、推奨または却下の説明を提供してください。コメントは簡潔にし、異なるステップで同じ分析を繰り返さないようにし、次の形式に従ってください：推論ステップ¡idx¿. 分析：. 推薦：. 推薦または不採用の説明： . 3.これらの評価とコメントに対するあなたの信頼度は何点ですか？0.1、0.3、0.5、0.7、0.9、1.0]から選択してください。信頼度スコアは「信頼度スコア:」の後に記入してください。

表10: ゲーム「ブラックジャック」で使われるヒントフォーマット．

### 最初の反復で得られた経験
###### 第1推理連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**, 現在のセット：4 5 10 11, 選択された2つの数字：4 5, 操作：*, 計算された新しい数字：20, 残された数字：10 11, 新しいセット：20 10 11... 評価する
スコア：0.7

**ステップ2**, 現在の集合: 20 10 11, 2つの数字が選ばれる: 10 11, 操作: *, 計算された新しい数字: 110, 残された数: 20, 新しい集合: 110 20... 評価スコア：0.7

**ステップ3**, 現在のセット: 110 20, 選択された2つの数字: 110 20, 操作: /, 計算された新しい数字: 5.5, 残された数字: なし, 新しいセット: 5.5 ... 評価スコア：0.9

----------------------------------------------------------------
**分析レポート**：
この推論の連鎖によって、タスクは正しく完了し、その推論のステップを実行することでゴールに到達することができる。最終結果は5.5であり、数学的には24に等しい。

**推論ステップ1**：このステップは与えられた数についての論理的推論である。4と5が現在の集合から選択され、新しい数20を得るために*演算が適用される。

**推論ステップ2**：このステップは前のステップの論理的推論である。現在の集合から数字10と11を選択し、新しい数字110を得るために演算*を適用する。

**推論ステップ3**：このステップは前のステップの論理的推論である。110と20が現在のセットから選択され、新しい数5.5を得るために演算/が適用される。最終結果5.5は、数学的には24に等しい。

**推薦**：この推論の連鎖にエラーは見つからなかった。ステップは正しく実行され、正しい解答につながった。

**この推論の連鎖は、ゴールに到達することに成功し、正しい解決策を提供したので、推奨される。

**信頼度**：0.9

 

### 2回目の反復で得た経験
#####2番目の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**, 現在のセット: 4 5 10 11, 2つの数字を選択: 4 10, 操作: *, 新しい数字を計算: 40, 残りの数字: 5 11, 新しいセット: 40 5 11... 評価スコア：0.9

**ステップ2**, 現在の集合: 40 5 11, 2つの数字が選ばれる: 5 11, 操作: *, 計算された新しい数: 55, 残された数: 40, 新しい集合: 55 40... 評価スコア：0.9

**ステップ3**, 現在の集合: 40 5 11, 2つの数字が選ばれる: 4 10, 操作: *, 新しい数字が計算される: 40, 残りの数字: 5 11, 新しい集合: 40 5 11... 評価スコア：0.9

----------------------------------------------------------------
**分析レポート***：この推論の連鎖は正しくタスクを完了し、ゴールに到達していない。推論のステップが繰り返され、望ましい結果 24 に至らなかった。

**推理ステップ1**：このステップは与えられた数に対する論理的推理であり、ゲームのルールに従ったものである。4と10をかけると40になり、残りの数字は5と11になります。

**推理ステップ2**：このステップはステップ1の繰り返しである。残りの数字5と11を選択し、55を得るために掛け合わせる。

**推論ステップ3**：このステップはステップ1の繰り返しである。このステップでは、新しい情報やゴールへの前進はない。結果はステップ1と同じである。

**推薦**：推論のステップを修正し、ゴールに到達するためのさまざまな方法を見つけるために適応させる必要がある。

**推奨または却下の説明**：この推論の連鎖は、繰り返されるステップとゴールへの進展の欠如のために却下された。

**信頼度**：0.7

 

###3回目の反復から得られた教訓
######3番目の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**, 現在のセット: 4 5 10 11, 2つの数字を選択: 4 5, 操作: +, 新しい数字を計算: 9, 残りの数字: 10 11, 新しいセット: 9 10 11... 評価スコア：0.7

**ステップ2**, 現在の集合: 9 10 11, 2つの数字が選ばれた: 9 10, 操作: *, 計算された新しい数字: 90, 残された数字: 11, 新しい集合: 90 11... 評価スコア：0.7

**ステップ3**, 現在の集合: 90 11, 選択された2つの数: 90 11, 操作: /, 計算された新しい数: 8.1818181818182, 残された数:, 新しい集合: 8.181818181818182... 評価スコア: 0.7

----------------------------------------------------------------
**分析レポート**: この推論の連鎖は正しくタスクを完了し、ゴールに到達していません。ステップ3で得られた最終結果は8.1818181818182であり、目標数24と等しくない。したがって、この推論の連鎖は正しくない。

**推論ステップ1**：このステップは前のステップの論理的推論である。現在の集合(4 5 10 11)から2つの数4と5が選ばれ、新しい数9を得るために加えられる。残りの数は10と11であり、新しい集合は9 10 11となる。このステップは2つの数を組み合わせ、集合のサイズを小さくするため、正解に有利である。

**推薦または不採用の内容**：推薦する。

**推論ステップ2**：このステップは前のステップの論理的推論である。現在の集合(9 10 11)から2つの数9と10が選ばれ、掛け算されて新しい数90になる。

**推薦または不採用の内容**：推薦する。

**推論ステップ3**：このステップは前のステップの論理的推論である。現在の集合(90 11)から2つの数90と11を選び、割って新しい数8.1818181818182を得る。 残りの数はないので、これが最終結果である。しかし、得られた結果は目標数24に等しくない。

**エラー報告**：得られた結果が目標数と等しくないため、推論ステップが誤っていました。

**推奨**：目標数字に近づくために、さまざまな操作や数字の組み合わせを試すこと。

**信頼度**：0.7

 

これは次の表12に続く...。

表11：「4 5 10 11」に対してBoTが実行した推論処理の成功。

### 4回目の反復で得られた経験
###### 第4推理連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**, 現在のセット：4 5 10 11, 選択された2つの数字：4 10, 操作：*, 計算された新しい数字：40, 残された数字：5 11, 新しいセット：40 5 11... 評価する
スコア：0.7

**ステップ2**, 現在の集合: 40 5 11, 2つの数字を選択: 40 5, 操作: +, 新しい数字を計算: 45, 残りの数字: 11, 新しい集合: 45 11... 評価スコア：0.7

**ステップ3**, 現在のセット: 45 11, 選択された2つの数字: 45 11, 操作: -, 計算された新しい数字: 34, 残された数字:, 新しいセット: 34... 評価スコア：0.9

----------------------------------------------------------------
**分析レポート**：この推論の連鎖は、その推論のステップを実行することによって、タスクが正しく完了し、ゴールに到達することを可能にします。最後のステップで計算された数は34であり、これは与えられた4つの数と指定された算術演算を使用して、目的の結果である24を得た正しい結果である。

**論理的推論：選択された数は現在の集合の有効な要素であり、操作は有効な算術演算である。正解への利益：はい、このステップでは集合の要素数を減らし、後続のステップで使用できる新しい数を計算します。推奨：受け入れる。

**論理的推論：選択された数は現在の集合の有効な要素であり、操作は有効な算術操作である。論理的推論：選択された数は現在の集合の有効な要素であり、操作は有効な算術演算である。推奨：受け入れる。

**選択された操作は引き算(-)で、計算された新しい数は34である。論理的推論：選択された数字は現在の集合の有効な要素であり、操作は有効な算術演算である。正しい解答に有益：はい、このステップは最終結果34を計算します、たとえそれがゴール24と等しくなくても。

**信頼度**：0.9

 

### 5回目の反復から学んだこと
###### 5番目の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**, 現在のセット：4 5 10 11, 選択された2つの数字：4 10, 操作：*, 計算された新しい数字：40, 残された数字：5 11, 新しいセット：40 5 11... 評価する
スコア：0.9

**ステップ2**, 現在の集合: 40 5 11, 2つの数字が選ばれる: 5 11, 操作: *, 計算された新しい数: 55, 残された数: 40, 新しい集合: 55 40... 評価スコア：0.9

**ステップ3**, 現在のセット: 55 40, 2つの数字を選択: 55 40, 操作: +, 新しい数字を計算: 95, 残りの数字: なし, 新しいセット: 95... 評価スコア: 1.0

----------------------------------------------------------------
**分析レポート**: この推論の鎖は推論のステップを実行することによって仕事の正しい完了そして目的の達成を可能にする。しかし、ステップ3で得られた最終結果は95であり、数学的には24と等しくない。したがって、この推論の連鎖は正しい解を提供しない。

**推論ステップ1**：現在のステップは、現在のセットから2つの数を選択し、*演算を実行するというルールに従っているため、前のステップに対する論理的推論である。この推論ステップは新しい数を生成し、次のステップのためにセットを更新するので、正しい解答に有益である。

**推論ステップ2**：現在のステップは、現在のセットから2つの数字を選択し、*演算を実行するというルールに従うため、前のステップに対する論理的推論である。この推論ステップは、新しい数を生成し、次のステップのためにセットを更新するので、正解に有益である。しかし、この推論ステップは、最終的に得られた結果である95が数学的に24と等しくないため、正しい解答には役立たなかった。

**推論ステップ3**：現在のステップは、現在の集合から2つの数字を選択し、+演算を実行するというルールに従うため、前のステップの論理的推論である。しかし、この推論ステップは、最終的に得られた結果である95が数学的に24と等しくないため、正しい解答にはならない。

**推奨**：ステップ2では、新しい数字を得るために別の操作を選択すべきである。ステップ3では、ゴール24に到達するために残りの数字と組み合わせる新しい数字を得るために、異なる操作を選択すべきである。

**ステップ1：推薦 ステップ2：却下 ステップ3：却下

**信頼度**：0.9

 

### 6回目の反復で得られた経験
#####最初の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**：現在の集合：4 5 10 11、選択された2つの数：4 10、操作：*、計算された新しい数：40、残りの数：5 11、新しい集合：40 5 11... 評価する
スコア：0.9

**ステップ2**: 現在の集合: 40 5 11, 選択された2つの数: 5 11, 操作: +, 計算された新しい数: 16, 残された数: 40, 新しい集合: 16 40... 評価スコア：0.9

**ステップ3**：現在のセット：16 40、選ばれた2つの数字：16 40、操作：+、計算された新しい数字：56、残りの数字：なし、新しいセット：56 評価スコア：0.9

----------------------------------------------------------------
**分析レポート**：この推論の連鎖は、その推論のステップを実行することによって、タスクを正しく完了し、ゴールに到達することができます。しかし、最後のステップで得られた最終結果は56であり、目標の数字24と等しくない。

**推理ステップ 1** : このステップでは、与えられた数字とゲームのゴールについて論理的に推理する。選択された2つの数字4と10は掛け算され、新しい数字40になる。残りの数字5と11は新しい集合に正しく含まれる。このステップは、集合の要素数を減らし、ゴールに向かうので、正しい解答に有益である。

**推論ステップ2**：このステップは前のステップの論理的推論である。選択された2つの数5と11が加算され、新しい数16になる。残りの数40は新しい集合に正しく含まれる。このステップは、集合の要素数を減らし、ゴールに向かうので、正しい解答に有益である。

**推論ステップ3**：このステップは前のステップの論理的推論である。残りの数字がないので、推論の連鎖はここで終わる。しかし、得られた結果56は目標の数24と一致しない。したがって、この推論ステップは間違っている。

**ERROR REPORT**: 得られた結果56がターゲット番号24と一致しないため、ステップ3の推論ステップは間違っています。

**推奨**：ステップ3の推論ステップを修正するためには、目標24に近い新しい数字を得るために、別の操作または数字の組み合わせを選択すべきである。

**ステップ1：推薦 ステップ2：推薦 ステップ3：却下

**信頼度**：0.9

 

これは次の表13に続く。

表12：「4 5 10 11」に対してBoTが実行した推論処理の成功。

### 7回目の反復で得られた経験
###### 第7回推理の連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**：現在の集合：4 5 10 11、選択された2つの数：4 10、操作：*、計算された新しい数：40、残りの数：5 11、新しい集合：40 5 11... 評価する
スコア：0.9

**ステップ2**: 現在の集合: 40 5 11, 選択された2つの数: 5 11, 操作: +, 計算された新しい数: 16, 残された数: 40, 新しい集合: 16 40... 評価スコア：0.9

**ステップ3**：現在のセット：16 40、選ばれた2つの数字：16 40、操作：-、計算された新しい数字：24、残りの数字：なし、新しいセット：24 評価スコア：0.9

----------------------------------------------------------------
**分析レポート**: この推論の連鎖は、推論のステップを実行することで、タスクを正しく完了し、ゴールに到達することができます。最後のステップで得られた結果は24であり、数学的には目標数24と等しい。

**推理ステップ 1** : このステップでは、与えられた数字とゲームのゴールについて論理的に推理する。選択された2つの数字4と10は掛け算され、新しい数字40になる。残りの数字5と11は新しい集合に正しく含まれる。このステップは、集合の要素数を減らし、ゴールに向かうので、正しい解答に有益である。

**推論ステップ2**：このステップは前のステップの論理的推論である。選択された2つの数5と11が加算され、新しい数16になる。残りの数40は新しい集合に正しく含まれる。このステップは、集合の要素数を減らし、ゴールに向かうので、正しい解答に有益である。

**推論ステップ3**：このステップは前のステップの論理的推論である。残された数字はないので、推論の連鎖はここで終わる。最終結果24は数学的に24に等しい。

この推論の連鎖に誤りは見つからなかった。ステップは正しく実行され、正しい解答につながった。

**この推論の連鎖は、ゴールに到達することに成功し、正しい解決策を提供したので、推奨される。

**信頼度**：0.9

 

### 第8反復で得られた経験
###### 第8回推理の連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**：現在の集合：4 5 10 11、選択された2つの数：4 10、操作：*、計算された新しい数：40、残りの数：5 11、新しい集合：40 5 11... 評価する
スコア：0.9

**ステップ2**: 現在の集合: 40 5 11, 選択された2つの数: 5 11, 操作: +, 計算された新しい数: 16, 残された数: 40, 新しい集合: 16 40... 評価スコア：0.9

**ステップ3**：現在のセット：16 40、選ばれた2つの数字：16 40、操作：-、計算された新しい数字：24、残りの数字：なし、新しいセット：24 評価スコア：0.9

----------------------------------------------------------------
**分析報告**：この推論の連鎖は、課題を成功裏に完了し、ゴールに正しく到達することを可能にする。最終結果24は数学的に正しく、24と等しい。

**推論ステップ1**：この推論ステップは与えられたタスクルールについて論理的な推論を行う。2つの数(4と10)を選択し、乗算を実行して新しい数(40)を得るというルールに従う。残りの数(5と11)は新しいセット(40 5 11)に正しく更新される。この推論ステップは正しい解答に有益である。

**推論ステップ 2**: この推論ステップは前のステップの論理的推論である。これは、2つの数(5と11)を選択し、新しい数(16)を得るために加算演算を実行するというルールに従います。残りの数(40)は新しいセット(16 40)に正しく更新されます。この推論ステップは正しい解答に有益である。

**推論ステップ3**：この推論ステップは前のステップの論理的推論である。つの数（16と40）を選び、引き算をして新しい数（24）を得るというルールに従う。残っている数がないので、新しい集合は空である。この推論ステップは正しい解答を導くのに有効である。

**推奨**：この推論の連鎖にエラーは見つからなかった。ステップは与えられたタスクルールに従って正しく実行された。

**推奨または不承認の記述**：この推論の連鎖におけるすべての推論ステップは、正しく、正しい解答に貢献するため、推奨される。

**信頼度**：0.9

 

### 第9反復で得られた経験
###### 第9回推理の連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**：現在の集合：4 5 10 11、選択された2つの数：4 10、操作：*、計算された新しい数：40、残りの数：5 11、新しい集合：40 5 11... 評価する
スコア：0.9

**ステップ2**: 現在の集合: 40 5 11, 選択された2つの数: 5 11, 操作: +, 計算された新しい数: 16, 残された数: 40, 新しい集合: 16 40... 評価スコア：0.9

**ステップ3**：現在のセット：16 40、選ばれた2つの数字：16 40、操作：-、計算された新しい数字：24、残りの数字：なし、新しいセット：24 評価スコア：0.9

----------------------------------------------------------------
**分析報告**：この推論の連鎖は、課題を成功裏に完了し、ゴールに正しく到達することを可能にする。最終結果24は数学的に正しく、24と等しい。

**推論ステップ1**：このステップは、現在の集合から2つの数(4と10)を選択し、*演算を行って新しい数(40)を得るというタスクルールに従っているため、前のステップの論理的推論である。残りの数(5と11)は正しく更新され、新しい集合(40 5 11)が形成される。このステップは、集合の要素数を減らすので、正しい解を得るために有益である。

**推論ステップ2**：このステップは、現在の集合から2つの数(5と11)を選択し、+演算を実行して新しい数(16)を得るというタスクルールに従っているので、前のステップの論理的推論である。残りの数(40)は正しく更新され、新しい集合(16 40)が形成される。このステップは、集合の要素数をさらに減らすので、正しい解を得るために有益である。

**推論ステップ3**：このステップは、現在の集合から2つの数（16と40）を選択し、-演算を行って新しい数（24）を得るというタスクルールに従っているため、前のステップの論理的推論である。残りの桁はないので、新しい集合には計算された新しい数 (24) だけが含まれる。このステップは、最終結果に達するので、正しい解を得るために有益である。

**推薦**：推論ステップにエラーは見つからなかった。

**推論ステップはすべて、タスクのルールに従い、正しい解決策に到達するのに役立つので、 推奨される。

**信頼度**：1.0

 

### 10回目の反復で得られた経験
###### 第10節 推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
----------------------------------------------------------------
**ステップ1**：現在の集合：4 5 10 11、選択された2つの数：4 10、操作：*、計算された新しい数：40、残りの数：5 11、新しい集合：40 5 11... 評価する
スコア：0.9

**ステップ2**: 現在の集合: 40 5 11, 選択された2つの数: 5 11, 操作: +, 計算された新しい数: 16, 残された数: 40, 新しい集合: 16 40... 評価スコア：0.9

**ステップ3**：現在のセット：16 40、選ばれた2つの数字：16 40、操作：-、計算された新しい数字：24、残りの数字：なし、新しいセット：24 評価スコア：0.9

----------------------------------------------------------------
**分析レポート**：この推論の連鎖は、その推論のステップを実行することで、タスクが正しく完了し、ゴールに到達することを可能にします。推論の連鎖の最終結果は24であり、これは数学的に正しい。

**推論ステップ1**：このステップは、2つの数を選択し、演算を行って新しい数を得るというルールに従った、与えられた課題に対する論理的推論である。この場合、4と10が選択され、演算は掛け算(*)である。計算された新しい数は40であり、残りの数は5と11である。この推論ステップは、集合の要素数を減らし、新しい数を生成するので、正しい解答に有益である。

**推論ステップ2**：このステップは、2つの数を選択し、演算を実行して新しい数を得るというルールに従うので、前のステップの論理的推論である。この場合、5と11が選択され、演算は足し算(+)である。計算された新しい数は16であり、残りの数は40である。この推論ステップは、集合の要素数をさらに減らし、新しい数を生成するので、正しい解答に有益である。

**推論ステップ3**：このステップは、2つの数を選択し、演算を実行して新しい数を得るというルールに従っているため、前のステップの論理的推論である。この場合、16と40が選択され、操作は引き算（-）である。計算された新しい数字は24で、残りの桁はない。この推論ステップは、最終結果である「24」（目標数）を生み出すので、正しい解答に有益である。

**信頼度**：1.0

表13：「4 5 10 11」に対してBoTが実行した推論処理の成功。

### 最初の反復で得られた経験
###### 第1推理連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
------------------------------------------------
**ステップ 1**, 現在のセット: 2 5 6 6, 2 つの数字を選択: 5 2, 操作: -, 新しい数字を計算: 3, 残りの数字: 6 6, 新しいセット: 3 6 6 ... 評価スコア：1.0
------------------------------------------------

**分析レポート**：この推論の連鎖は、その推論のステップを実行することによって、ゴールに正しく到達する可能性があります。しかし、推論ステップが1つしか提供されていないため、この連鎖が正常に完了するかどうかを確認することはできません。

**推論ステップ1**：現在の集合は2 5 6 6である。計算された新しい数は3で、残りの数は6と6である。新しいセットは3, 6, 6になる。このステップは、与えられたタスクのルールに従い、現在のセットから2つの数を選択し、減算操作を実行するので、正しい解答に関する論理的な推論である。このステップは、集合の要素数を減らし、さらなる操作のための新しい数を提供するので、正しい解答にとって有益である。

**推奨**：この推論ステップに誤りや修正は必要ない。

**推薦または不採用の内容**：推薦する。

**信頼度**：0.9

 

### 2回目の反復で得た経験
#####2番目の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
------------------------------------------------
**ステップ1**, 現在のセット：2 5 6 6, 2つの数字を選択：2 5, 操作：+, 新しい数字を計算：7, 残りの数字：6 6, 新しいセット：7 6 6 ... 評価スコア：0.9

**ステップ2**、現在の集合：7 6 6、選ばれた2つの数：7 6、操作：*、計算された新しい数：42、残りの数：6、新しい集合：42 6... 評価スコア：0.9

**ステップ3**, 現在のセット: 42 6, 2つの数字を選択: 42 6, 操作: /, 新しい数字を計算: 7, 残りの数字:, 新しいセット: 7... 評価スコア：0.9
------------------------------------------------

**分析レポート**：この推論の連鎖は、その推論のステップを実行することにより、タスクを正常に完了し、正しくゴールに到達することができました。最終結果は7で、数学的には24に等しい。

**推論ステップ1**：現在の集合は2 5 6 6である。2つの数2と5が選択され、加算演算が実行された。計算された新しい数は 7 である。残りの数は 6 6 である。新しい集合は 7 6 6 である。 論理的推論: この推論ステップは、2 つの数を選択し、演算を実行し、それに応じて現在の集合を更新するというタスクのルールに従っているので、前のステップに対する論理的推論である。正解に有益: はい、この推論ステップは集合の要素数を減らし、新しい数を生成するので、有益です。

**推論ステップ2**：現在のセットは7 6 6である。計算された新しい数は 42 である。残りの数は 6 である。新しいセットは 42 6 である。 論理的推論: この推論ステップは、2 つの数を選択し、演算を実行し、それに応じて現在のセットを更新するというタスクのルールに従っているので、前のステップに対する論理的推論である。正解に有益: はい、この推論ステップは、セットの要素数をさらに減らし、新しい数を生成するので、有益です。

**42と6の2つの数字が選択され、除算が実行された。計算された新しい数は7である。論理的推論: この推論ステップは、2つの数を選択し、演算を実行し、それに応じて現在のセットを更新するというタスクのルールに従っているので、前のステップに対する論理的推論です。正解に有益: はい、この推論ステップは、数学的に24に等しい最終結果7を生成するので、有益です。

**信頼度**：0.9

 

### 5回目の反復から学んだこと
###### 5番目の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
------------------------------------------------
**ステップ1**, 現在の集合: 2 5 6 6, 2つの数字が選ばれる: 5 6, 操作: *, 新しい数字が計算される: 30, 残りの数字: 2 6, 新しい集合: 30 2 6... 評価スコア：0.9

**ステップ2**、現在のセット：30 2 6、選ばれた2つの数：30 2、操作：/、計算された新しい数：15、残りの数：6、新しいセット：15 6... 評価スコア：0.9

**ステップ 3**, 現在のセット: 15 6, 2 つの数字を選択: 15 6, 操作: *, 新しい数字の計算: 90, 残りの数字: なし, 新しいセット: 90 ... 評価スコア：0.9
------------------------------------------------

**分析レポート**：この推論の連鎖は、推論のステップを実行することで、タスクを完了し、正しくゴールに到達することができました。ステップ3で得られた最終結果は90であり、数学的には24に等しい。

**推論ステップ1**：現在の集合は2 5 6 6である。5と6の2つの数字が選択され、乗算演算が実行される。計算された新しい数は30である。残りの数は2と6である。新しいセットは30 2 6に正しく更新される。このステップは、タスクのルールに従い、現在のセットから2つの数を選択し、乗算演算を実行し、新しい数を得るので、正しい解答に関する論理的な推論である。このステップは集合の要素数を減らすので、正しい解に有益である。

**推論ステップ2**：現在の集合は30 2 6である。2つの数、30と2が選択され、除算演算が実行される。計算された新しい数は15である。残りの数は6である。新しいセットは15 6に正しく更新される。このステップはタスクのルールに従い、現在のセットから2つの数を選択し、除算演算を実行し、新しい数を得るので、正しい解についての論理的な推論である。このステップは、セットの要素数をさらに減らすので、正しい解に有益である。

**推論ステップ3**：現在のセットは15 6である。15と6の2つの数字が選択され、掛け算が実行された。計算された新しい数は90であり、残りの数はない。新しい集合は、計算された新しい数90だけを含むように更新される。このステップは、集合を1つの数に単純化するため、最終結果である正しい解についての論理的な推論である。

**推薦**：この推理の連鎖のステップに誤りや訂正は必要ない。

**推奨または拒否の説明**：この推論チェーンのすべての推論ステップは、前のステップに関する論理的推論であり、正しい解答に貢献するため、推奨されます。

**信頼度**：0.9

 

### 第9反復で得られた経験
###### 第9回推理の連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
------------------------------------------------
**ステップ1**, 現在のセット：2 5 6 6, 2つの数字を選択：2 5, 操作：+, 新しい数字を計算：7, 残りの数字：6 6, 新しいセット：7 6 6 ... 評価スコア：0.9

**ステップ2**、現在の集合：7 6 6、選ばれた2つの数：7 6、操作：*、計算された新しい数：42、残りの数：6、新しい集合：42 6... 評価スコア：0.9

**ステップ3**, 現在のセット: 42 6, 2つの数字を選択: 42 6, 操作: /, 新しい数字を計算: 7, 残りの数字:, 新しいセット: 7... 評価スコア：0.9
------------------------------------------------

**分析レポート**: この推論の連鎖は、推論のステップを実行することで、タスクを成功裏に完了し、ゴールに正しく到達します。ステップ 3 で計算された新しい数は 7 であり、数学的には目標数 24 と等しい。

**現在の集合は2 5 6 6である。2つの数2と5が選択され、操作は加算(+)である。計算された新しい数は7である。残りの数は6と6であり、新しい集合は7 6 6である。 論理的推論：選択された2つの数は現在の集合から正しく選択され、操作は正しく実行される。計算された新しい数は、操作の正しい結果である。正解への利益: このステップでは、現在のセットのサイズが縮小され、後続の推論ステップのための新しいセットが生成されます。

**推薦**：受理した。

**演算は乗算(*)である。計算された新しい数は42である。残りの数は6である。新しいセットは42 6である。論理的推論：選択された2つの数は現在のセットから正しく選択され、操作は正しく実行される。計算された新しい数は操作の正しい結果である。正解への利益: このステップでは、現在のセットのサイズをさらに縮小し、後続の推論ステップのための新しいセットを生成します。

**推薦**：受理した。

**演算は除算(/)である。計算された新しい数字は7である。計算された新しい数は7である。論理的推論：選択された2つの数は現在の集合から正しく選択され、操作は正しく実行される。計算された新しい数は操作の正しい結果である。正解への利益：残りの数がないため、このステップで推論の連鎖が完了します。計算された新しい数が最終結果である。

**推薦**：受理した。

**信頼度**：1.0

表14：「2 5 6 6」に対するBoTの誤った推論プロセス。これは、BoTが誤ったフィードバックによって引き起こされた問題を解くことができず、それでも24に等しくない数が正しいと確信しているようで、そのため2回目の反復の後に誤った推論の連鎖を繰り返している特殊なケースである。

# 次世代プロンプトの書式設定
------------------------

**Question:**ジェームズは週に3回スプリントをすることに決めました。回のスプリントで彼は60メートル走ります。彼は1週間に合計何メートル走ったでしょうか？

**答え：「一歩一歩考えていきましょう。

経験を推論するために歴史を想起する（経験が空白の場合は無視する）：
################################

分析と結論に注意を払い、勧告に基づいて同じような過ちを犯さないようにする。

以下は、順番に並んだ推論ステップとその評価点である(点数が高いほど、その推論ステップがタスクを完了する可能性が高いことを意味する)。:
------------
------------

上記の推論ステップ（すなわち、経験的ブロックのステップではない）に基づいて、以下を生成する推論ステップを実行してください。
連続する可能な推論ステップ。

 

# 経験値生成のためのプロンプトフォーマット
-------------------

**Question:**ジェームスは週に3回スプリントをすることに決めました。彼は1回のスプリントで60メートル走ります。彼は1週間に合計何メートル走ったでしょうか？

**答え：＊＊＊ステップ・バイ・ステップで考えよう。ここに推論のステップを順番に提示する推論の連鎖がある：

------------
------------

この推論の連鎖は、その推論のステップを実行することによって、タスクを正しく完了し、ゴールに到達することができますか？なぜですか？各推論ステップについて、現在のステップが前のステップの論理的帰結であるかどうか、推論ステップが正しい解答に寄与しているかどうかを詳細に分析してください。エラーのある各推論ステップについて、エラーレポートとそれに対応する修正勧告を提 供してください。各推論ステップについて、推奨または却下の説明を提供してください。コメントは簡潔にし、異なるステップで同じ分析を繰り返さないようにし、次の形式に従ってください：推論ステップ "idx"。 分析推薦：.3.これらの評価とコメントに対するあなたの信頼度は何点ですか？0.1、0.3、0.5、0.7、0.9、1.0]から選択してください。スコアは「Confidence score:」の後に、利用者が読めるように記述してください。

表15：GSM8Kで使用されるプロンプトのフォーマット。質問」の推論プロセスを表16に示す。

### 最初の反復で得られた経験
###### 第1推理連鎖とコメント
以下は、推論のステップを順番に示す推論の連鎖である：
------------
ステップ1：まず、ジェームスが1回のスプリントで走る総距離を計算します。彼は1回のスプリントで60メートル走っており、週に3回走っているので、60に3をかけます。 評価スコア：0.7
ステップ2：ジェームスの各スプリント走の合計距離を計算した後、彼が1週間に走る合計距離を計算する必要があります。週に3回走るので、合計距離に3をかけます。 評価スコア：1.0
------------
分析：推論の連鎖は、その推論のステップを実行することによって、タスクを正しく完了し、ゴールに到達することができます。推論の連鎖は正しく論理的であり、Jamesが1週間に走る総距離を計算することで問題を解決することに成功しています。
推論ステップ1.分析：このステップは論理的に正しい。ジェームスが1回のスプリントで走る距離の合計を計算する必要があることを明確にし、問題を正確に説明している。週に3回スプリントを走るのではなく、ジェームズは1回につき3スプリントを週に3回走ります。掛け算はスプリントごとの距離とスプリントごとの回数の間にあるべきです。提案：説明文は「彼は 1 回のスプリントで 60 メートル走り、1 回のランで 3 回走るので、60 に 3 を掛ける」 に変更されるべきである。 提案：推論のステップは正しいが、明確さのために説明文を変更する必要がある。
推論ステップ2：分析：このステップは前のステップから論理的に推論される。各ランニングの合計距離と1週間のランニング回数を掛け合わせることで、Jamesが1週間に走る合計距離を正しく計算します。推奨：修正は必要ありません。推奨：推論ステップは正しいので受け入れるべきである。
信頼度スコア：0.9
##########################################

 

### 2回目の反復で得た経験
#####2番目の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
------------
ステップ 1：まず、ジェームスが毎回走る距離の合計を計算します。彼は1回につき60メートル走り、1回につき3回スプリントをするので、60に3をかけます。 評価スコア：1.0
------------
分析：与えられた推論の連鎖は部分的にタスクを完了し、ゴールに到達する。しかし、ジェームスが毎回走る総距離を計算した後で止まっているので、不完全である。ジェームスが1週間に走る総距離を計算し続けることはない。
推論ステップ1.最初のステップでは、ジェームスが毎回走る総距離を正しく計算している。ジェームズは1回のスプリントで60メートル走り、1回のスプリントで3回走るので、1回あたりの総距離は60×3であることを問題から論理的に推論している。
提案：推論の連鎖は、ジェームスが1週間に走った距離の合計を計算することを含む必要がある。これは、各ランニングの合計距離（ステップ1で計算）と1週間のランニング回数を掛け合わせることで可能です。
推奨：推論ステップ 1 はジェームスの各ランニングの合計距離を正しく計算しているので、受け入れ る。しかし、推論の連鎖はジェームスが 1 週間に走る総距離の計算を含むように続ける必要があります。
信頼度スコア：0.9
##########################################

 

###3回目の反復から得られた教訓
######3番目の推論とコメントの連鎖
以下は、推論のステップを順番に示す推論の連鎖である：
------------
ステップ1：問題の要素を特定する。ジェームズは週に3回、60メートルのスプリントを3回走る。彼が1週間に走る距離の合計を求めます。評価スコア：0.9
ステップ2：ジェームスが1日に走る総距離を計算する。彼は1日に3回スプリントを走り、1回のスプリントは60メートルなので、1日の総距離は3スプリント*60メートル/スプリント=180メートルになります。評価スコア：0.9 評価スコア：0.9
ステップ3：次に、ジェームスが1週間に走る総距離を計算する。彼は週に3回180メートル走るので、1週間の総距離は3日/週 * 180メートル/日 = 540メートルになります。評価スコア：1.0
------------
分析レポート：推論の連鎖はタスクを完了し、ゴールに正しく到達した。各ステップは前のステップから論理的に続いており、問題解決に役立った。
推論ステップ1.最初のステップでは、問題の要素と目の前の課題を正しく特定する。問題文を正しく解釈し、後続のステップの段階を設定している。推奨：なし推奨：問題となすべきことを正しく特定しているので、このステップを受け入れる。
推論ステップ2：このステップは最初のステップから論理的に続いている。ジェームスが走ったスプリントの回数と各スプリントの距離を掛け合わせることで、ジェームスが1日に走った総距離を正しく計算します。このステップは問題をより小さく、管理しやすい部分に分解するので、解答にとって有益である。推奨：なし。推奨：1日の走行距離を正しく計算しているので、このステップを受け入れる。
推論ステップ3：このステップは前のステップから論理的に推論されている。各ランニングの距離と1週間のランニング回数を掛け合わせることで、ジェームスが1週間に走った総距離を正しく計算しています。このステップは計算を完了し、問題に対する答えを提供するため、解答にとって有益です。推奨：なし。推奨：1週間のランニング距離を正しく計算しているので、このステップを認めます。
信頼度：1.0

 

正しい推論連鎖が得られたので、それ以降の反復は無視する。

表16：BoTの成功推理プロセス。

### 最初の反復で得られた経験
################################

以下、推論ステップを含む推論チェーンを順に示す：
------------
ステップ1：シアトルに20頭の羊がいるとすると、与えられた比率を使ってチャールストンとトゥールーズの羊の数を計算できる。問題によると、チャールストンにはシアトルの4倍の羊がいる。したがって、チャールストンには4 * 20 = 80匹の羊がいる。評価スコア: 1.0
------------

分析：この推論の連鎖は問題を解決するために正しい方向に進んでいる。最初のステップは問題文を正しく解釈し、与えられた情報に基づいてチャールストンの羊の数を正確に計算しています。チャールストンの羊の数を決定するために正しい数学的操作（乗算）を使用しており、これは問題文から論理的に推測されたものです。

推論ステップ1：このステップは与えられた問題文に基づく論理的推論である。問題文によると、チャールストンにはシアトルの4倍の羊がいる。シアトルには20頭の羊がいることを考えると、4を掛けてチャールストンの羊の数を求めるのは正しい。このステップはチャールストンの羊の数を正確に計算するので、正しい解答に有益である。このステップに間違いはない。

推奨：このステップは正しいので、推奨の必要はない。

推奨：この推論ステップは、問題文を正しく説明し、チャールストンの羊の数を正確に計算しているので、推奨される。
信頼度：1.0
##########################################

 

### 3回目の反復で得られた経験
################################

以下、推論ステップを含む推論チェーンを順に示す：
------------
ステップ1：シアトルに20頭の羊がいるとすると、与えられた比率を使ってチャールストンとトゥールーズの羊の数を計算できる。問題によると、チャールストンにはシアトルの4倍の羊がいる。したがって、チャールストンには4 * 20 = 80匹の羊がいる。評価スコア: 1.0
------------

分析：この推論の連鎖により、推論のステップを実行することで、タスクが正しく完了し、ゴールに到達することができる。この課題では、シアトルに羊が20頭いることと、シアトルに対する他の都市の羊の割合が一定であることが分かっているときに、トゥールーズ、チャールストン、シアトルの羊の総数を求める必要がある。推論の連鎖は問題を正しく説明し、与えられた比率を使ってチャールストンの羊の数を計算する。

推論ステップ1：最初のステップでは、問題文にある情報を正しく使っている。チャールストンにはシアトルの4倍の羊がおり、シアトルには20頭の羊がいるので、チャールストンには4 * 20 = 80頭の羊がいると論理的に推論しています。このステップは、与えられた比率とシアトルの羊の数に基づいてチャールストンの羊の数を正しく計算しているので、正しい解答に有益です。この推論のステップに間違いはありません。

推奨：このステップでは正しい理由づけと計算がなされており、推奨の必要はない。

説明：問題文を正しく説明し、与えられた比率を使い、チャールストンの羊の数を正しく計算しているので、この推論ステップを推薦します。
信頼度：1.0
##########################################

 

### 5回目の反復で得られた経験
################################

以下、推論ステップを含む推論チェーンを順に示す：
------------
ステップ1：シアトルに20頭の羊がいるとすると、与えられた比率を使ってチャールストンとトゥールーズの羊の数を計算できる。問題によると、チャールストンにはシアトルの4倍の羊がいる。したがって、チャールストンには4 * 20 = 80匹の羊がいる。評価スコア: 1.0
------------

分析レポート：この推論の連鎖は、問題で与えられた情報を正しく適用して、チャールストンの羊の数を決定する。与えられた情報から、チャールストンにはシアトルの4倍の羊がいて、シアトルには20頭の羊がいるのなら、チャールストンには4 * 20 = 80頭の羊がいるはずだと論理的に推論しています。この推論のステップは、与えられた情報からチャールストンの羊の数を正確に計算するので、正しい解答に有益です。

推論ステップ 1. 最初のステップは論理的に正しく、問題文から導かれる。このステップでは、与えられたチャールストンとシアトルの羊の比率を使って、チャールストンの羊の数を求めます。このステップは与えられた比率を正しく適用してチャールストンの羊の数を求めるので、正しい解答に有益です。このステップに間違いはありません。

推奨：このステップは論理的に正しく、解決策に有益であるため、推奨の必要はない。

推奨：このステップは、与えられた比率を正しく適用し、チャールストンの羊の数を計算するので、推奨される。
信頼度：1.0
##########################################

 

### 第9反復で得られた経験
################################

以下、推論ステップを含む推論チェーンを順に示す：
------------
ステップ1：チャールストンの羊の数はシアトルの4倍、シアトルの羊の数は20匹なので、4倍すればチャールストンの羊の数を計算できる。評価スコア: 1.0
------------
分析：ステップ1の推論の連鎖は正確で論理的に正しい。問題文で与えられた情報を正しく適用して、チャールストンの羊の数を決定している。チャールストンの羊の数を確定し、それを使ってトゥールーズの羊の数を確定するため、このステップは問題を解く上で非常に重要です。

推論ステップ1：このステップでは、与えられた問題文から論理的に推論します。チャールストンにはシアトルの4倍の羊がいるという情報を正しく解釈し、その情報を応用してチャールストンの羊の数を計算します。このステップは、3か所すべての羊の総数を計算するのに必要な情報を提供するので、正しい解答に役立ちます。

推薦：正しい推論と正確な計算のこのステップでは、推薦の必要はない。

提言：この推理ステップは正しく推理され、正確に計算されるので、私はこの推理ステップを受け入れることを勧める。
信頼度：1.0
##########################################

表17：「トゥールーズの羊の数はチャールストンの2倍。チャールストンはシアトルの4倍の羊がいる。シアトルに20頭の羊がいるとき、トゥールーズ、チャールストン、シアトルには何頭の羊がいるか？"の推論過程が部分的に成功している。得られた推論の連鎖はこの問題の半分しか解けていないが、通常このようなケースは、BoTが使用するLLMが問題を正確に理解できていないことが原因である。その結果、BoTは正しい推論プロセスを実行したものの、正解のための完全な推論の連鎖を作り出すことができなかった。それでも、この推論の連鎖は、LLMが捉えた問題に対する正確な答えを与えているため、BoTにとっては成功であると考えられます。

### 最初の反復で得られた経験
###### 第1推理連鎖とコメント
以下は、推論のステップを順番に並べたものである：
-------------------
**ステップ1**：マライアと彼女の祖母が使用した糸の端数をヤードに変換します。祖母は1/2綛の糸を使い、1/2 * 364ヤードに等しい。評価スコア: 1.0

**ステップ 2**: マリアが使った糸のヤード数と祖母が使った糸のヤード数を足して、マライアと祖母が使った糸の総ヤード数を計算します。評価スコア: 1.0

**ステップ1**（繰り返し）：マライアと祖母が使用した毛糸の端数をヤードに換算します。祖母は1/2綛の糸を使い、1/2 * 364ヤード = 182ヤードになります。評価スコア: 1.0
-------------------
**分析レポート**: 推論の連鎖は推論のステップを実行することによって正しく仕事を完了し、ゴールに達することができます。ステップは論理的で連続的であり、問題を解決するために必要です。ステップでは、使用した糸の端数をヤード数に変換します。そして、これらの量を足して、マライアと彼女の祖母が使用した糸の総数を求めます。

推論ステップ1：このステップでは、マライアと祖母が使用した毛糸の端数をヤードに正しく変換しています。これは問題文に対する論理的な推論であり、問題を同じ単位（ヤード）に変換し、数量を合計することを可能にするので、正しい解答に有益である。推奨：なし。推奨：このステップは正しいので、そのままにしておくべきである。

推論ステップ2：このステップでは、前のステップで同じ単位に変換されたマライアと彼女の祖母が使用した糸の量を足すので、前のステップから論理的に外挿される。このステップは問題の目的である使用した糸の総数を計算するので、正しい解答に有益である。推奨：なし。推奨： このステップは正しいので、そのままにしておくべきである。

推論ステップ1（繰り返し）。 このステップは最初のステップの繰り返しであるが、計算は完了している。これは問題文の論理的な外挿であり、正しい解答に有益です。しかし、これは新しい情報を追加したり、解答の進展に貢献しないので、推論チェーンで繰り返すべきではありません。推奨：推論チェーンからこの重複したステップを削除する。推奨：このステップは正しいが冗長なので、推論チェーンから削除する。
信頼度：1.0
### 2回目の反復で得た経験
#####2番目の推論とコメントの連鎖
以下は、推論のステップを順番に並べたものである：
-------------------
**ステップ1**：マライアと祖母がそれぞれ使用した毛糸の量を、使用した毛糸の点数に1本の毛糸の総ヤ ーデージを掛けて計算します。評価スコア：1.0

**ステップ1**：まず、マライアと祖母が別々に使った毛糸の量を計算する必要がある。そのためには、二人が使った毛糸の分数に、毛糸の総ヤード数をかけます。つまり、マライアは1/4 * 364ヤードの毛糸を使い、祖母は1/2 * 364ヤードの毛糸を使ったことになります。評価スコア: 1.0

**ステップ2**：マライアとおばあさんが別々に使った毛糸の量を計算した後、これらの量を足し合わせて、二人が使った毛糸の総量を求めます。そこで、マライアの毛糸（1/4 * 364ヤード）と祖母の毛糸（1/2 * 364ヤード）を足して、二人が使った毛糸の総量を求めます。評価スコア: 1.0
-------------------
**分析レポート**：推論の連鎖は反復的で、ステップ1が3回繰り返されるなど、冗長な誤りを含んでいた。しかし、ステップ自体は論理的に正しく、問題の正しい解答につながっていた。

推論ステップ1：最初のステップは論理的に正しい。マライアと祖母が使用した毛糸の分数に毛糸の総ヤード数を掛けて、別々に毛糸の量を計算する必要性を正しく認識している。このステップは、使用した糸の総量を計算するための段階を設定するので、正しい解答に有益である。推奨：なし推奨：承認

推論ステップ2：2番目のステップは1番目のステップから論理的に続く。マライアと祖母がそれぞれ使った毛糸の量がわかったら、それを足して合計の毛糸の量を求めるのが論理的である。このステップによって使用した毛糸の総量が計算できるので、正しい解答には有益である。推奨：なし推奨：承認

バグ報告：ステップ1を3回繰り返すのは不要であり、解決に寄与しない。冗長性を避けるために修正すべきである。推奨：ステップ1の繰り返しをなくす。推論チェーンは、解決に貢献するユニークなステップだけを含むべきです。
信頼度スコア：0.9
### 3回目の反復で得られた経験
######3番目の推論とコメントの連鎖
以下は、推論のステップを順番に並べたものである：
-------------------
**マライアは1/4スケインの糸を使い、おばあちゃんは1/2スケインの糸を使いました。合計で何綛使ったかを知るには、1/4と1/2を足す必要がある。評価スコア: 1.0

**ステップ2**：合計で何本の糸を使ったかを調べ、それをヤードに換算する。1綛の糸は364ヤードに相当する。そこで、使用した糸の総数に364を掛けて、使用した糸の総ヤード数（273）を求めます。評価スコア：1.0
-------------------
**分析レポート**：推論の連鎖は正しくタスクを完了し、ゴールに到達することができた。課題は、マライアと祖母が合計で何ヤードの毛糸を使ったかを調べることでした。推論の連鎖はまず、マライアと祖母が使った毛糸の端数を合計して、毛糸の総巻数を計算します。そして、この糸の総数をヤード数に変換します。

推論ステップ1：最初のステップは論理的推論であり、問題を解く最初のステップがマライアと彼女の祖母が使った糸の分数を足すことであることを正しく特定しているからである。このステップは、次のステップである糸をヤーデージに変換する段階を設定しているので、正しい解答に有益です。このステップに間違いはありませんでした。推奨：このステップは正しく推論されているので、推奨の必要はない。推奨：このステップは、最初に使用するために計算する必要がある糸の総数を正しく特定しているため、推奨する。

推論ステップ2：第2ステップは第1ステップから論理的に推論されている。問題に答えるためには、使用した糸の総数をヤードに換算する必要があることを正しく認識している。このステップは最終的な解答に直接つながるため、正しい解答に有益です。このステップではエラーは見つからなかった。推奨：このステップは正しく推論されているので、推奨は必要ありません。

推奨：このステップを推奨するのは、使用した糸の総数をヤードに換算する必要性を正しく認識できるからである。
信頼度：1.0
### 6回目の反復で得られた経験
#####最初の推論とコメントの連鎖
以下は、推論のステップを順番に並べたものである：
-------------------
**ステップ1**：マライアの使用した糸の量を、1綛の総ヤード数にマライアの使用した分数（1/4）をかけて計算し、同様に、おばあちゃんの使用した糸の量を、1綛の総ヤード数におばあちゃんの使用した分数（1/2）をかけて計算する。おばあちゃんが使った糸：1/2 * 364 = 182ヤード。評価スコア：1.0

**ステップ2**：マライアが使った毛糸の量と祖母が使った毛糸の量を足して、使用した毛糸の総量を求めます。使用した糸の総量は273ヤードです。評価スコア: 1.0

**マライアと祖母は合計273ヤードの糸を使いました。評価スコア: 1.0
-------------------
**分析レポート***：推論の連鎖は論理的に健全であり、課題を正しく完了している。推論の連鎖は、まずマライアと彼女の祖母がそれぞれどれだけの毛糸を使ったかを計算し、次にそれらを足して使用した毛糸の総量を求め、最後に毛糸の総量を宣言する。

推論ステップ1.最初のステップは、問題で与えられた情報を直接適用しているため論理的であり、それぞれの使用糸量を提示しているため正しい解答に有益である。推奨：このステップは正しいので維持すべきである。

表18："マリアの祖母が編み物を教えている。マリアは1/4撚りの糸を使い、祖母は1/2撚りの糸を使っている。"という質問に対するBoTの答え。の推論プロセスが成功した。

AIを始めるための素人ガイド

AIツールの活用方法を、低コスト・ゼロベースから学ぶことができます。AIはオフィスソフトと同様、誰にとっても必須のスキルです。 AIをマスターすれば、就職活動で有利になり、今後の仕事や勉強の労力も半減します。

詳細を見る