Problèmes difficiles de niveau olympique : examen de 7 critères de performance en mathématiques chinoises pour le LLM

Les capacités mathématiques, qui englobent la dérivation de formules, la construction de chaînes logiques et la pensée abstraite, sont depuis longtemps considérées comme un domaine clé pour tester les capacités de l'intelligence artificielle (IA), en particulier les modèles de langage à grande échelle (LLM). En effet, il ne s'agit pas seulement de tester la puissance de calcul, mais aussi d'approfondir la capacité du modèle à raisonner, à comprendre et à résoudre des problèmes complexes.

Toutefois, les conclusions récentes d'une équipe de l'ETH Zurich montrent que même les meilleurs grands modèles linguistiques (LLM) obtiennent généralement de mauvais résultats lorsqu'ils sont confrontés à des questions mathématiques difficiles, telles que les défis au niveau des Olympiades américaines de mathématiques, ce qui a suscité un débat sur les capacités réelles des LLM actuels en termes de raisonnement mathématique rigoureux.

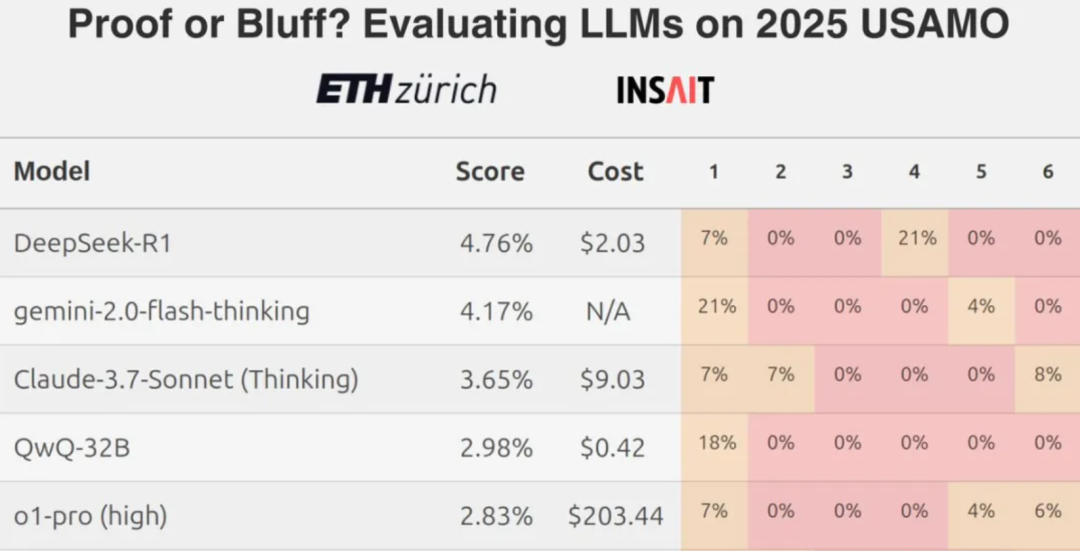
Dans ce contexte, une question naturelle se pose : quelles sont les performances de ces modèles lorsqu'ils traitent des problèmes mathématiques formulés en chinois ? Dans cette étude, un total de sept modèles linguistiques à grande échelle courants ou émergents, nationaux et étrangers, ont été sélectionnés pour une comparaison côte à côte de leurs capacités mathématiques à l'aide de problèmes tirés de l'Alibaba Global Maths Competition et des Olympiades chinoises de mathématiques.

Les modèles concernés par le test sont les suivants :

• Modèles nationaux :DeepSeek R1,Hunyuan T1,Tongyi Qwen-32B (texte original) 通义QwQ-32B),YiXin-Distill-Qwen-72B
• Modélisation internationale :Grok 3 beta,Gemini 2.0 Flash Thinking,o3-mini

Évaluation globale des performances

L'évaluation consiste en 10 questions d'un niveau de difficulté élevé, avec un total de 13 questions de notation. Les critères de notation étaient les suivants : 1 point pour une réponse entièrement correcte, 0,5 point pour une réponse partiellement correcte et aucun point pour les erreurs.

L'exactitude globale de chaque modèle dans ce test est la suivante :

La répartition détaillée des scores montre les différences de performance entre les modèles :

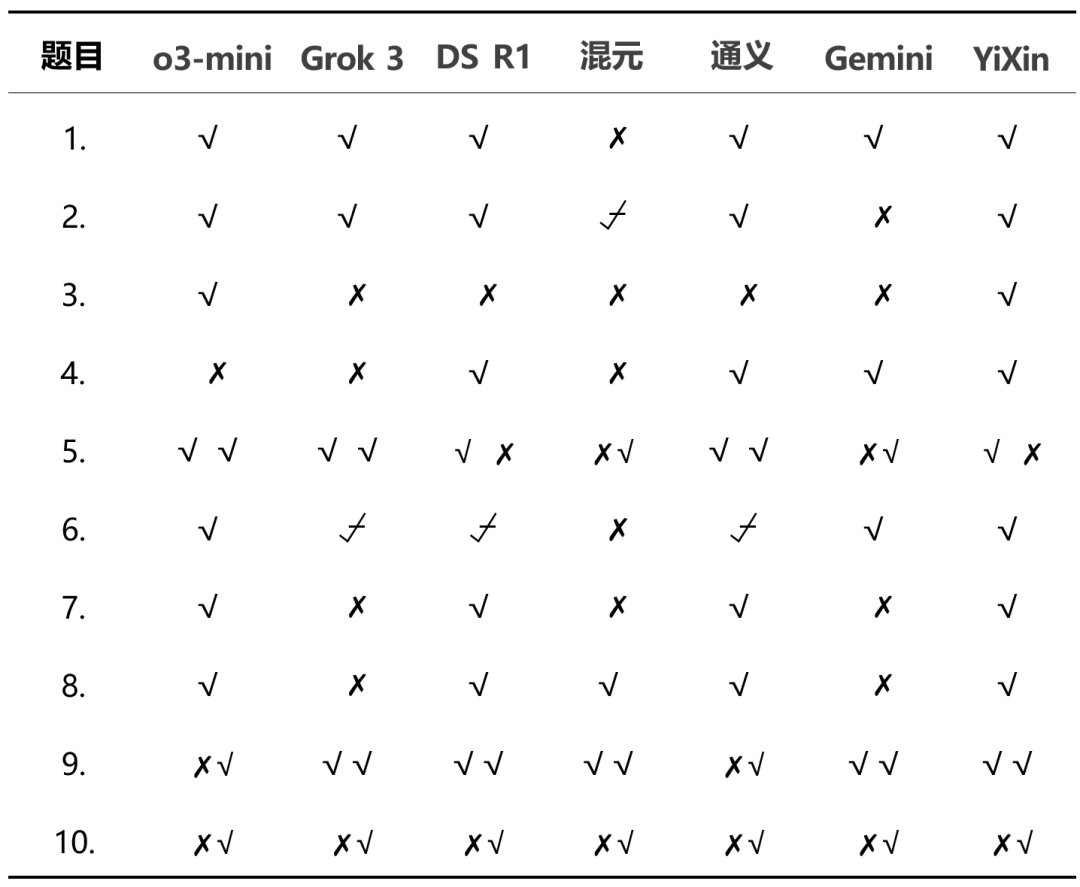
D'après les résultats globaux.o3-mini répondre en chantant YiXin-Distill-Qwen-72B a obtenu de bons résultats lors de ce test, démontrant de solides compétences en matière de résolution de problèmes mathématiques. Les performances des autres modèles ont été variables.

Les réponses spécifiques à certaines des questions du test sont présentées ci-dessous.

Détails de la mesure

Cycle 1 : Le problème du changement

Question : Grand-père a 60 dollars et se rend au supermarché pour acheter 20 dollars de légumes. Comment le caissier pourrait-il rendre la monnaie à Grand-père ?

Analyse : Il s'agit d'une question d'application de l'arithmétique de base qui examine la compréhension du modèle des scénarios de la vie et les compétences de base en matière de calcul de l'argent.

Résultats :
o3-mini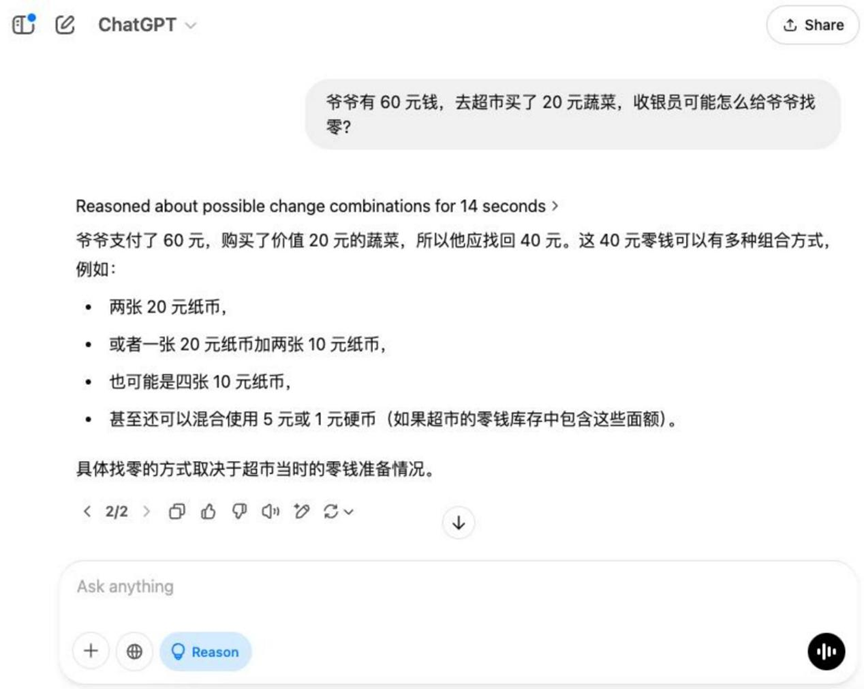

Grok 3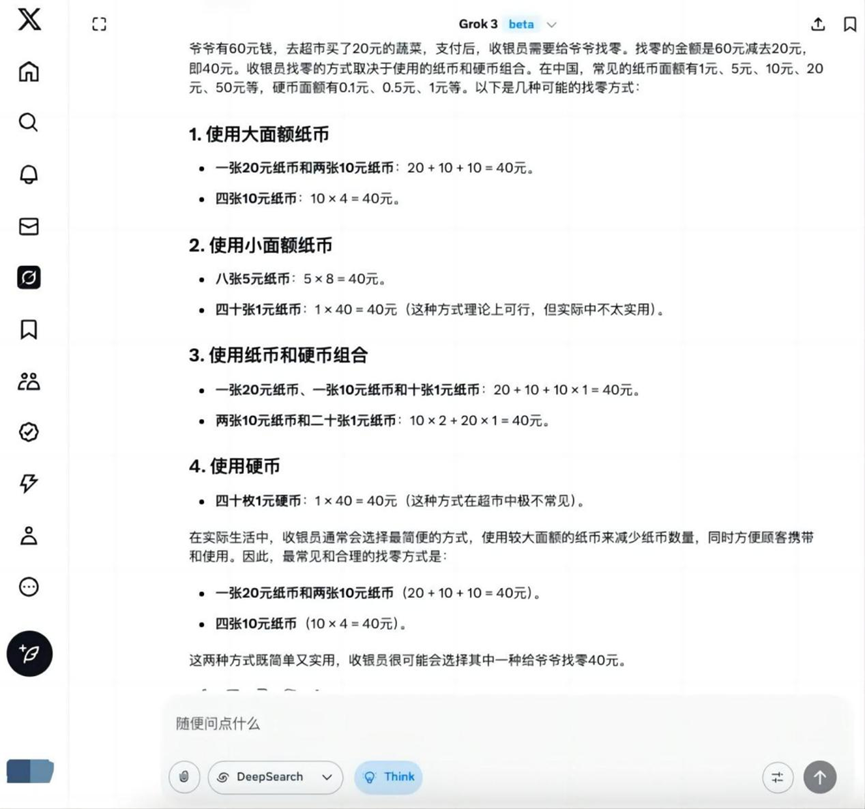

DeepSeek R1

Hunyuan T1

Gemini 2.0 Flash Thinking

YiXin-Distill-Qwen-72B

Sur ce sujet de base, en plus de Hunyuan T1 En dehors de cela, les autres modèles donnent la bonne solution pour trouver le zéro.

Cycle 2 : Calcul des distances de marche et jugements méthodologiques

Question : Xiao Ming et Xiao Hua se rendent chaque jour à l'école à pied. Ming marche 48 mètres par minute et Hua marche 55 mètres par minute. La maison de Xiaoming est située à 384 mètres de l'école. Xiaohua met 4 minutes de plus que Ming pour aller de la maison à l'école. Quelle est la distance entre la maison de Xiaohua et l'école ? Laquelle des méthodes suivantes est incorrecte, et pourquoi ?

Méthode 1 : 55 × 4 = 220 (mètres), 384 + 220 = 604 (mètres)
Méthode 2 : 384 / 48 = 8 (minutes), 55 × (8 + 4) = 660 (mètres)

Analyse : Cette question combine le calcul de problèmes de déplacement et le jugement logique, exigeant du modèle qu'il soit capable non seulement de calculer la réponse correcte, mais aussi d'analyser la justesse ou l'inexactitude de la solution donnée, en examinant le raisonnement en plusieurs étapes et le discernement logique.

Résultats :
DeepSeek R1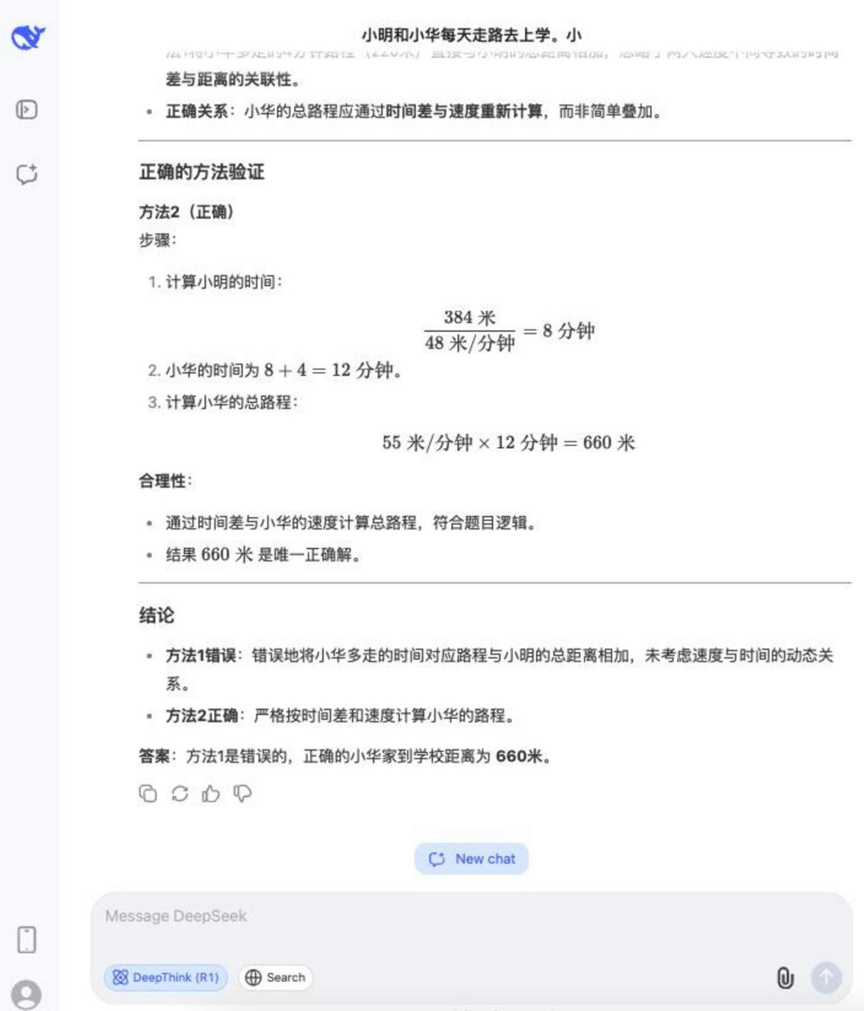

Tongyi Qwen-32B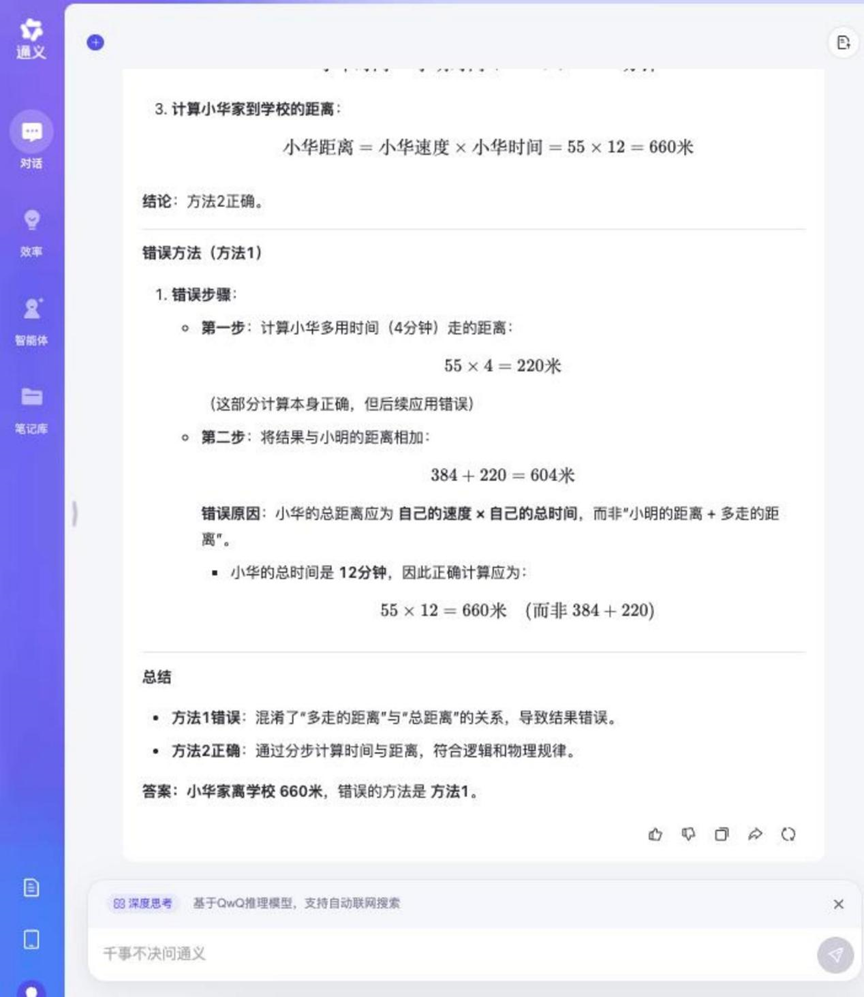

YiXin-Distill-Qwen-72B

Le processus de raisonnement pour cette question était relativement long, mais la plupart des modèles impliqués dans le test ont pu y répondre correctement et déterminer la méthode incorrecte.

Round 3 : Problème d'occlusion géométrique (tours invisibles)

Question : Dans une ville, il y a 6 tours situées aux points A, B, C, D, E et F. Plusieurs étudiants forment un groupe de voyageurs pour partir en excursion gratuite dans la ville. Après un certain temps, chacun des étudiants se rend compte qu'il ne peut voir que les 4 tours situées aux points A, B, C et D, mais pas les tours situées aux points E et F. On sait que les positions des élèves et des tours sont considérées comme des points du même plan, que ces points ne coïncident pas entre eux et que 3 des points A, B, C, D, E et F ne partagent pas une même ligne. La seule possibilité de ne pas voir la tour est que la ligne de vue soit bloquée par une autre tour. Par exemple, si un élève se trouve à un point P situé en même temps que A et B et que A se trouve sur le segment de droite PB, il ne peut pas voir la tour située en B. Demandez : quel est le nombre maximum d'élèves pouvant faire partie de ce groupe de voyageurs ? a. 3 b. 4 c. 6 d. 12

Analyse : Il s'agit d'une question complexe de géométrie et de raisonnement logique impliquant des problèmes de visibilité, d'occlusion et de configuration des points, qui nécessite un niveau élevé d'imagination spatiale et de raisonnement logique dans le modèle.

Résultats :
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B

La difficulté des questions a augmenté de manière significative. Dans cette série de tests, seuls o3-mini répondre en chantant YiXin-Distill-Qwen-72B a été résolu avec succès, les autres modèles n'ont pas donné de réponse correcte.

Tour 4 : Problèmes de probabilité (Tigres et Tigres)

Question : À l'occasion de la fête du printemps, une entreprise de lait a lancé une activité de boîtes aveugles pour le Nouvel An chinois : chaque boîte de lait est accompagnée d'un "paquet rouge" contenant "Tiger" "Sheng"" Wei", l'un des trois motifs. En réunissant deux "Tiger", un "Sheng" et un "Wei", on peut épeler le portrait de famille "Tiger Tiger Sheng Wei". Une fois l'activité lancée, elle est devenue un succès Netflix et a attiré de nombreuses personnes à y participer. Les conditions connues sont les suivantes : les motifs sur les paquets rouges sont distribués de manière aléatoire et indépendante et ne peuvent pas être distingués les uns des autres. La probabilité d'apparition des trois motifs "Tiger", "Sheng" et "Wei" est de 1/3. Q : Afin de collecter un jeu complet de "Tiger Tiger Sheng Wei", combien de cartons de lait doivent être collectés ? Q : Combien de briques de lait devez-vous acheter en moyenne pour avoir un jeu complet de photos de famille "Tigre, Tigre, Puissant" ?

Analyse : Il s'agit d'un problème de collectionneur typique (variante du problème de collectionneur de Coupon), qui nécessite l'utilisation de la théorie des probabilités et des calculs d'espérance, et qui examine la capacité du modèle à traiter des modèles de probabilité et à effectuer des calculs d'espérance mathématique.

Résultats :
DeepSeek R1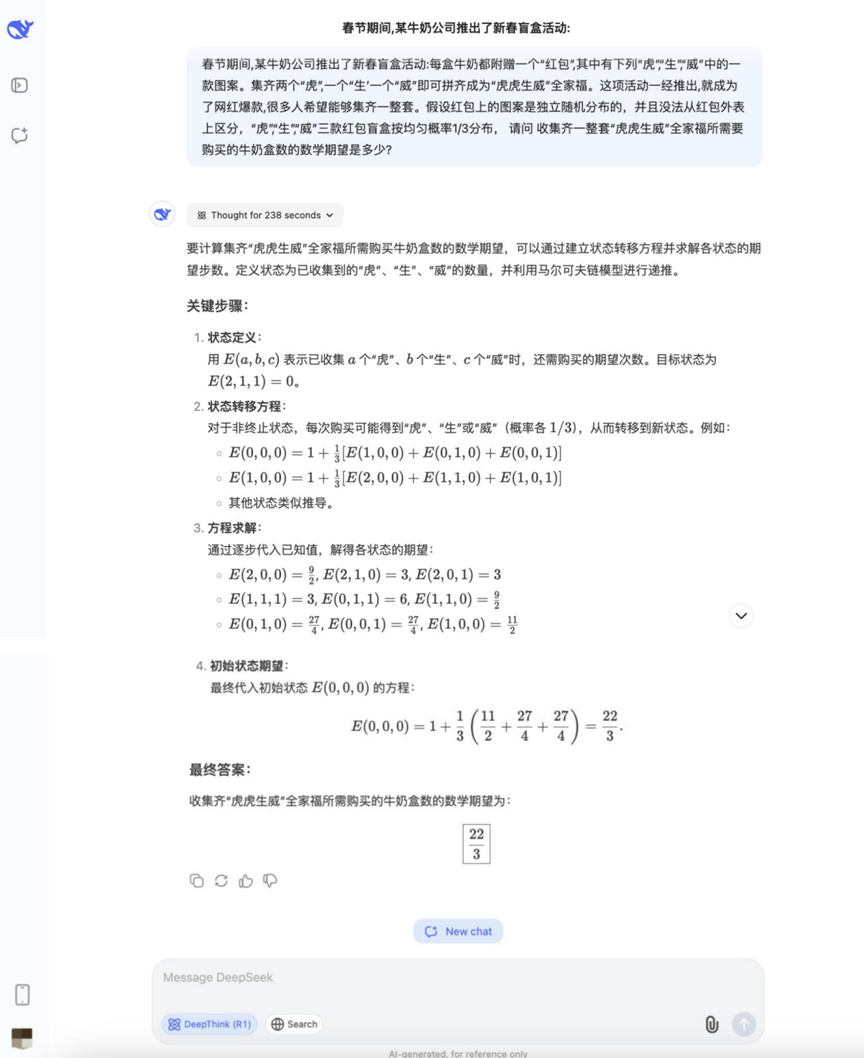

Hunyuan T1
 

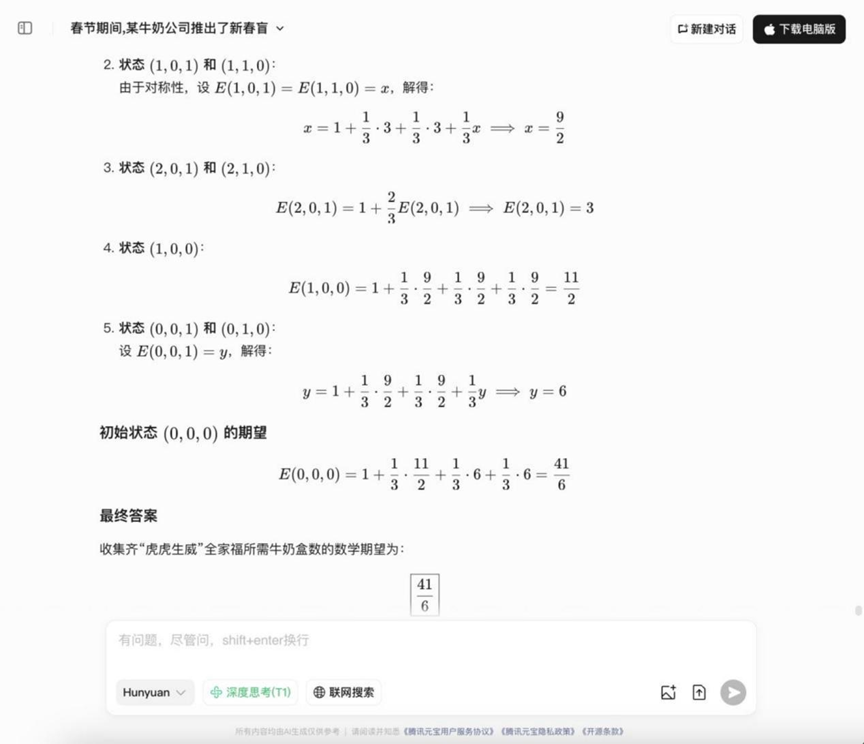
YiXin-Distill-Qwen-72B

Les réponses aux questions sur les probabilités ont commencé à diverger, certains modèles étant capables d'énumérer correctement les idées et de les calculer.

Tour 5 : Géométrie et planification des chemins (jeux de combat)

Description du problème Image :

Analyse : Il s'agit d'un problème qui combine la géométrie, les systèmes de coordonnées ou de grille, le chemin le plus court et les stratégies optimales, et qui peut nécessiter que le modèle comprenne les informations graphiques et effectue un raisonnement et une planification spatiaux.

Résultats :
o3-miniRésolution réussie : Résolution réussie

YiXin-Distill-Qwen-72B: Partiellement correct
 

Cette série de tests nécessite un degré plus élevé d'intégration du modèle, environ la moitié des modèles testés étant traités de manière totalement correcte.

Tour 6 : Problèmes de preuve en théorie des nombres (recherche de non-facteurs minimaux)

Description du problème Image :

Analyse : Les questions de preuve, qui exigent une déduction logique rigoureuse et une compréhension approfondie des concepts de la théorie des nombres, constituent un test direct de la capacité de raisonnement abstrait du modèle.

Résultats :
o3-mini

YiXin-Distill-Qwen-72B
 

Dans la modélisation domestique, leYiXin-Distill-Qwen-72B Meilleures performances dans cette série de questions sur les preuves. Les questions de preuve ont été beaucoup plus difficiles pour le modèle.

Cycle 7 : Fonctions et problèmes de cartographie (cartographie sur le cercle des unités)

Description du problème Image :

Analyse : Cette question porte sur les concepts de fonctions, de mappings et de cercle unitaire dans les mathématiques supérieures et examine la capacité du modèle à comprendre et à appliquer des définitions mathématiques abstraites.

Résultats :
o3-mini

YiXin-Distill-Qwen-72B
 

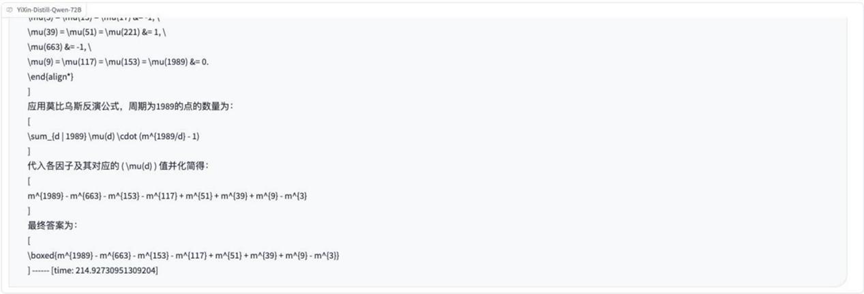
Environ la moitié des modèles ont été en mesure de traiter correctement ce problème impliquant des correspondances abstraites.

Cycle 8 : Problèmes d'optimisation combinatoire (triangle maximum)

Question : Il y a 1989 points dans l'espace, dont trois quelconques ne partagent pas une ligne. Ces points sont divisés en 30 groupes, chacun ayant un nombre différent de points. Un triangle peut être formé en prenant un point comme sommet dans trois groupes différents. Q : Comment le nombre de points dans chaque groupe peut-il être réparti de manière à maximiser le nombre de triangles formés ?

Analyse : Il s'agit d'un problème d'optimisation en mathématiques combinatoires qui exige que le modèle comprenne les principes du comptage combinatoire et trouve la stratégie d'allocation optimale, ce qui implique une modélisation mathématique plus complexe et des idées d'optimisation.

Résultats :
o3-mini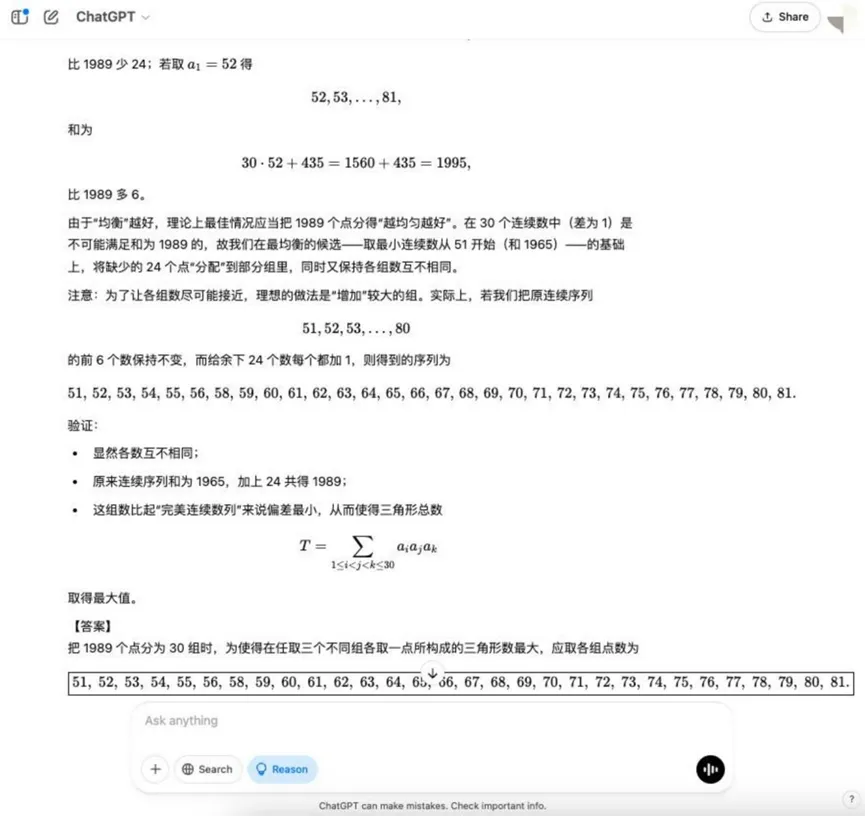

YiXin-Distill-Qwen-72B
 

Les problèmes d'optimisation combinatoire augmentent encore la difficulté et imposent des exigences plus élevées aux stratégies mathématiques et aux compétences informatiques du modèle.

Tour 9 : Problèmes de théorie des nombres (chaînes de facteurs)

Description du problème Image :

Analyse : Une fois de plus, les concepts de la théorie des nombres sont impliqués, examinant la compréhension et l'application par le modèle de relations telles que les factoriels et l'intégralité, qui peuvent nécessiter des preuves constructives ou des comptages.

Résultats :
o3-mini: Partiellement correct

YiXin-Distill-Qwen-72B: C'est tout à fait exact.
 

YiXin-Distill-Qwen-72B Une performance solide sur ce sujet de comptage.

Tour 10 : Problèmes géométriques (points de surface égale)

Description du problème Image :

Analyse : La dernière question était une question géométrique impliquant des calculs d'aires, des trajectoires de points ou des preuves d'existence, testant l'intuition géométrique du modèle, les opérations algébriques et le raisonnement logique.

Résultats :
o3-mini

DeepSeek R1

YiXin-Distill-Qwen-72B
 

Les questions finales de géométrie ont également montré des différences entre les modèles dans leur capacité à traiter des problèmes géométriques complexes.

Observation et analyse

Ce test de la capacité mathématique des Chinois sur un certain nombre de grands modèles linguistiques permet de faire les observations suivantes :

1. La modélisation des compétences mathématiques de base s'améliore considérablement : Par rapport aux modèles précédents, la génération actuelle de LLM montre une amélioration significative dans le traitement des problèmes mathématiques impliquant un raisonnement en plusieurs étapes, tels que la géométrie, les probabilités et certains problèmes d'application ouverts. Cela peut être attribué à l'augmentation de la taille du modèle, à l'abondance des données de formation et à l'application de techniques d'amélioration du raisonnement telles que le "chaînage de pensées".
2. Il existe des différences dans les styles de résolution de problèmes : Les différents modèles se comportent différemment en termes de niveau de détail du processus de solution.
   • o3-mini, Grok 3 beta, Tongyi Qwen-32B Le résultat est relativement concis et les étapes de l'inférence sont simples.
   • DeepSeek R1, Hunyuan T1, YiXin-Distill-Qwen-72B La tendance à montrer des processus de réflexion plus détaillés, incluant parfois des étapes de réflexion et de révision, est plus "verbeuse", mais cela peut aider à retracer la logique de leur raisonnement.
   • Gemini 2.0 Flash Thinking Le processus de résolution de problèmes de l'utilisateur est non seulement long, mais il utilise aussi principalement des résultats en anglais, ce qui suggère qu'il peut être relativement mal formé sur le corpus mathématique chinois.
3. Robustesse aux erreurs d'entrée : Le test montre que même en cas d'erreurs mineures de notation ou d'irrégularités de présentation dans les descriptions des problèmes, certains modèles sont toujours capables de comprendre correctement le sens des questions et d'y répondre, ce qui témoigne d'une certaine robustesse. Cependant, cela ne signifie pas que les modèles peuvent toujours ignorer les erreurs, et des erreurs dans des informations critiques peuvent toujours conduire à un échec de la réponse.
4. Améliorations futures : spécialisation et intégration des outils : Malgré les progrès évidents, la précision du LLM actuel peut encore être améliorée lorsqu'il s'agit de traiter des problèmes mathématiques complexes, en particulier dans les questions de concours difficiles et les scénarios nécessitant des preuves rigoureuses. Les voies d'amélioration futures peuvent inclure :
   • Intégration de moteurs informatiques externes : Les lacunes du LLM en termes de calcul exact et d'opérations symboliques sont compensées par l'utilisation d'outils de calcul symbolique tels que Wolfram Alpha.
   • Réglage fin exclusif du domaine : Construire des ensembles de données de haute qualité pour la logique mathématique, des branches spécifiques des mathématiques (par exemple, l'algèbre, la géométrie, la théorie des probabilités), et renforcer les modèles pour le raisonnement des experts et l'étendue des connaissances.
   • Apprentissage interactif et révision : Développer des mécanismes qui permettent à l'utilisateur de guider le processus de solution, de signaler les erreurs et de permettre au modèle d'ajuster dynamiquement la stratégie de solution.
5. Recommandations aux utilisateurs :
   • Les étudiants : Le LLM peut être utilisé pour faciliter l'apprentissage en vérifiant rapidement les solutions et les réponses aux questions de base. Toutefois, pour les problèmes complexes ou créatifs, il convient de se méfier du potentiel du modèle pour les "graves absurdités" (c'est-à-dire le fait de donner en toute confiance la mauvaise réponse).
   • Éducateurs : Lors de l'utilisation de l'enseignement assisté par l'IA, il est nécessaire de concevoir des questions qui sont plus susceptibles de tester la compréhension approfondie et les capacités de réflexion indépendante des étudiants, de sorte que les étudiants ne s'appuient pas sur des modèles pour parvenir à des réponses superficielles.
   • Développeur : Lors de l'application de la LLM à la résolution de problèmes mathématiques, les limites du problème et les exigences de la solution doivent être clarifiées en optimisant l'ingénierie des invites afin de réduire le raisonnement inefficace ou le "remue-méninges" par le modèle en raison d'une compréhension floue.

En conclusion, l'application de modèles linguistiques à grande échelle en mathématiques passe progressivement du stade exploratoire au stade pratique. L'orientation future du développement des modèles consistera à rechercher un meilleur équilibre entre la simulation de la flexibilité de la pensée humaine et la garantie de la rigueur de la logique mathématique.

Notes :
Les plus performants dans cette revue YiXin-Distill-Qwen-72B Les informations sur le modèle sont les suivantes :

• Version standard : https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B
• AWQ Quantitative Edition : https://huggingface.co/YiXin-AILab/YiXin-Distill-Qwen-72B-AWQ
• Ressources nécessaires au déploiement local : 72B Standard Edition nécessite environ 8 cartes graphiques NVIDIA 4090 ; AWQ Quantitative Edition peut fonctionner avec 2 cartes de la même classe.