La mise à jour de l'évaluation comparative de Claude 3.5 Sonnet Chinese est disponible ! La capacité de codage dépasse le GPT-4o, le raisonnement d'ordre supérieur n'est pas aussi bon que l'o1

Les résultats de cette évaluation ne seront utilisés qu'à des fins de recherche universitaire.

Le 22 octobre, Anthropic a officiellement lancé le grand modèle Claude 3.5 Sonnet ainsi que le nouveau modèle Claude 3.5 Haiku.

Claude

Selon les responsables d'Anthropic, Claude 3.5 Sonnet surpasse la version précédente dans tous les domaines, avec des améliorations significatives des performances, en particulier dans les tâches de codage du corps intelligent et d'utilisation d'outils.Sur le banc d'essai SWE Verified, ses performances d'encodage passent de 33,41 TP3T à 49,01 TP3T, surpassant tous les modèles publiquement disponibles, y compris OpenAI o1-preview.

Anthropic introduit également une nouvelle fonctionnalité révolutionnaire : l'utilisation de l'ordinateur. Les développeurs peuvent contrôler Claude pour qu'il utilise l'ordinateur de la même manière qu'un humain via une API, mais cette fonctionnalité est actuellement au stade expérimental.

En réponse aux préoccupations du public concernant les performances de Claude 3.5 Sonnet upgrade, en termes de raisonnement et de code dans des scénarios chinois, SuperCLUE, une organisation d'évaluation professionnelle tierce, a mené une évaluation approfondie de Claude 3.5 Sonnet upgrade.

environnement d'évaluation

Standards de référence : SuperCLUE-Reasoning Chinese Higher Order Reasoning Assessment Benchmark, SuperCLUE-Code3 Chinese Code Assessment Benchmark.

Modèles d'évaluation Claude 3.5 Sonnet (1022, POE dernier modèle snapshot)

Configuration de la génération de modèles :

• Se référer au document Claude Detailed Instructions : https://www.anthropic.com/news/3-5-models-and-computer-use

Épisode de la revue :

1) SuperCLUE - Raisonnement chinois - Tâches complexes - Ensemble d'examen de raisonnement d'ordre supérieur. Un total de 302 questions, y compris le raisonnement en plusieurs étapes, le raisonnement numérique, les calculs de raisonnement, l'analyse de marché et les problèmes d'optimisation, cinq tâches de raisonnement difficiles.

2. l'ensemble d'évaluation du code natif chinois SuperCLUE-Code3, la version chinoise améliorée de HumanEval, un total de 195 questions, y compris 1 560 cas de test, divisés en trois catégories de niveau de difficulté : primaire, intermédiaire et avancé.

Méthodologie: :

1) Raisonnement d'ordre supérieur : pour chaque question de raisonnement, nous fournissons des réponses de référence et des processus de raisonnement après calibration et vérification manuelles ; ensuite, le modèle arbitre évalue les réponses des modèles candidats conformément au processus d'évaluation défini, aux critères d'évaluation et aux règles de notation (de 1 à 5 points). Les critères d'évaluation définis comprennent : la conformité aux exigences de base, la précision du raisonnement et la vraisemblance des conclusions.

2) Code SC-Code3 : spécifiquement conçu pour évaluer et améliorer les capacités essentielles du Chinese Big Model en matière de génération de code par le biais de tests unitaires fonctionnels.

SuperCLUE-Code3 : Critères d'évaluation des compétences en code des natifs chinois

Commençons par les conclusions

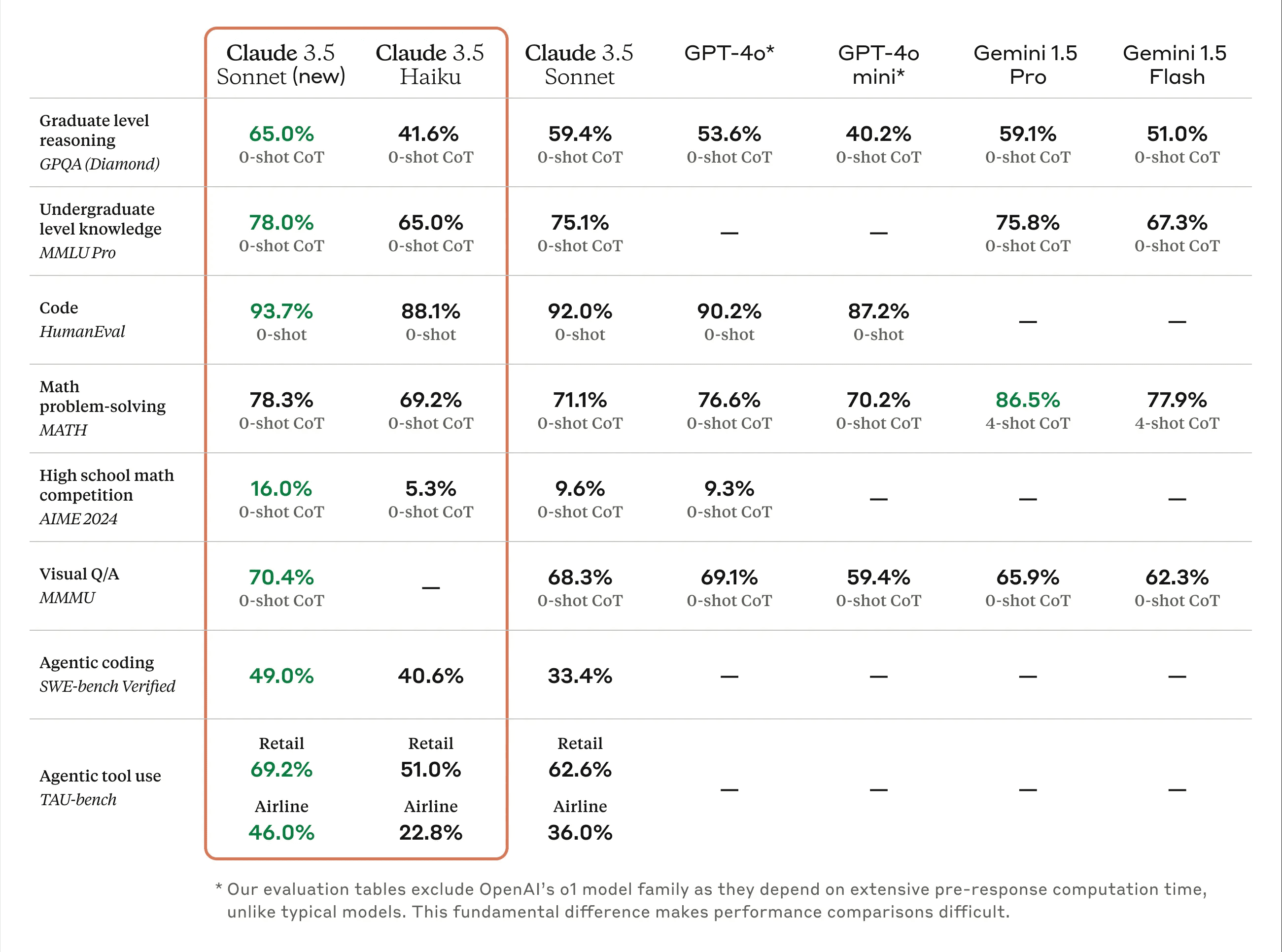
Conclusion 1 : Claude 3.5 Le sonnet (1022) obtient de bons résultats en termes de capacité de codage chinois (SC-Code3). Le score total a atteint 84,85, soit 1,52 point de plus que le GPT-4o-0513. soit 4,54 points de moins que o1-preview. En particulier, il a obtenu d'excellents résultats dans les tâches de codage avancé, avec un score de 69,23, à égalité avec o1-preview.

Conclusion 2 : Claude 3.5 Sonnet (1022) a obtenu un score de 74,54 à la tâche chinoise de raisonnement d'ordre supérieur. Proche de ChatGPT-4o-latest, avec un écart important par rapport à o1-preview (-10.73 points) . Parmi eux, la capacité de raisonnement en plusieurs étapes est relativement remarquable, avec des performances supérieures à celles du ChatGPT-4o-latest.

**Conclusion 3:** Par rapport à la version précédente Claude 3.5 Sonnet (0621). Claude 3.5 Sonnet (1022) a gagné 4,57 points sur la tâche de raisonnement. et des progrès significatifs dans les tâches secondaires telles que le raisonnement numérique et le raisonnement computationnel.

Résultats de l'évaluation

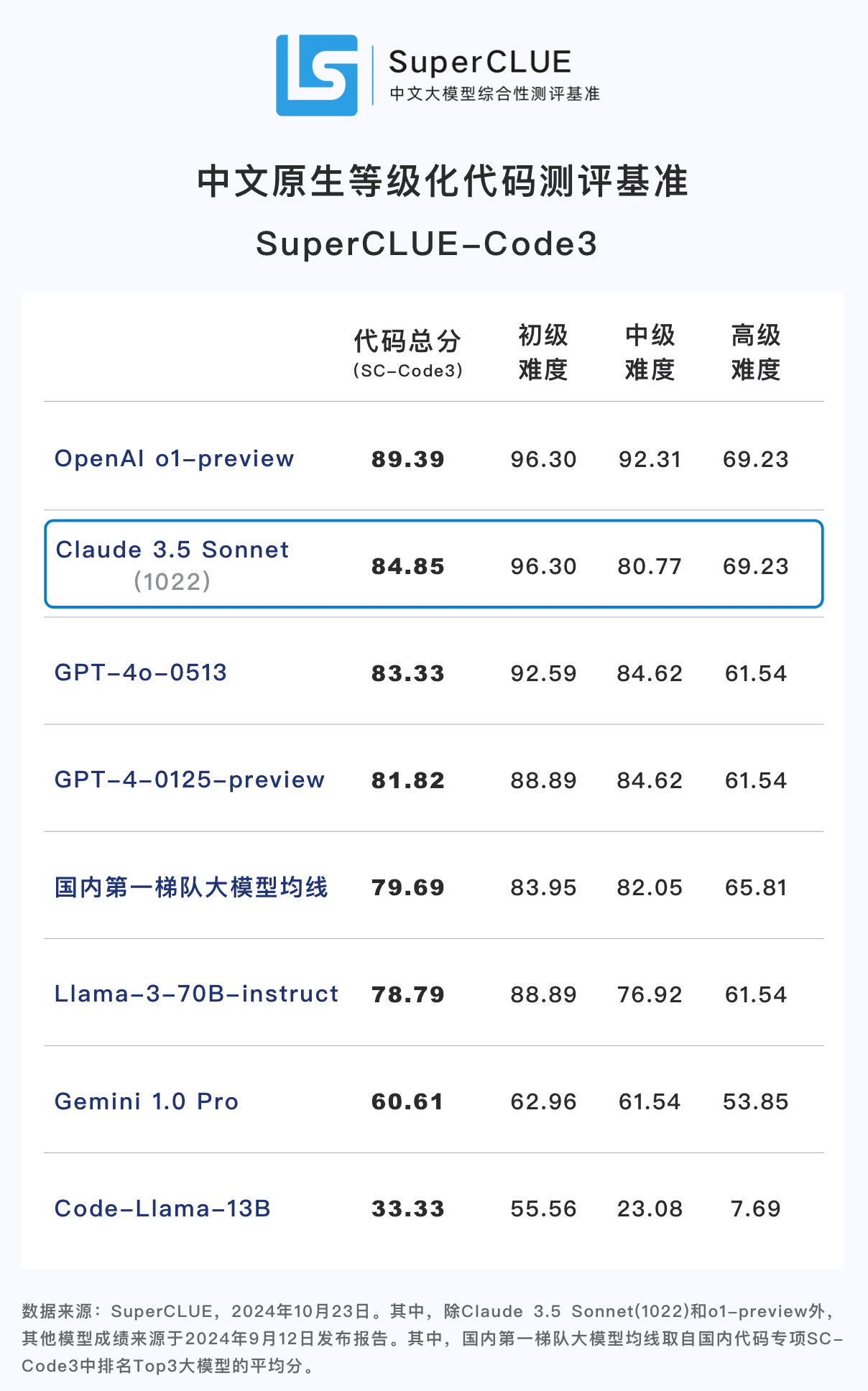
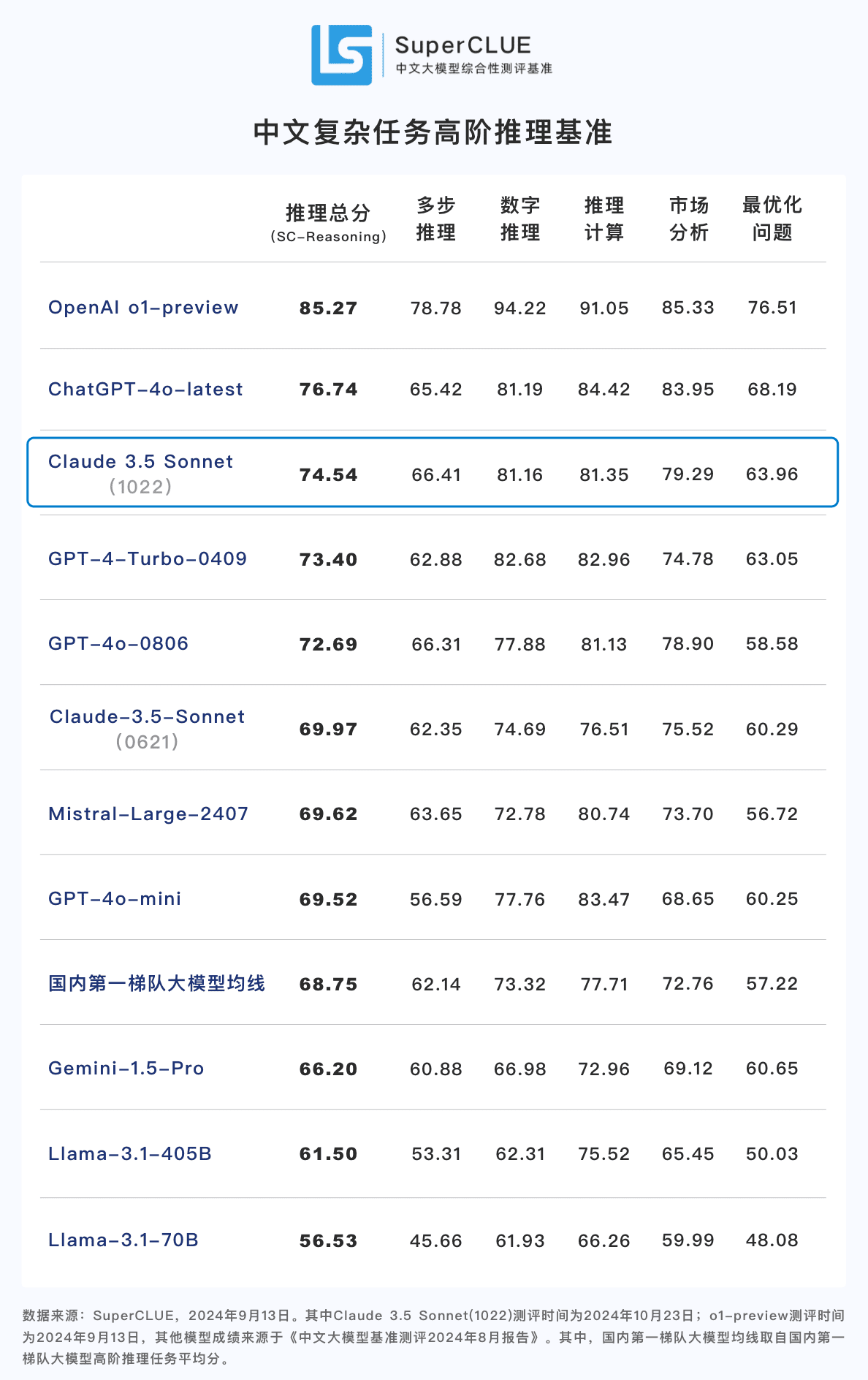
analyse comparative

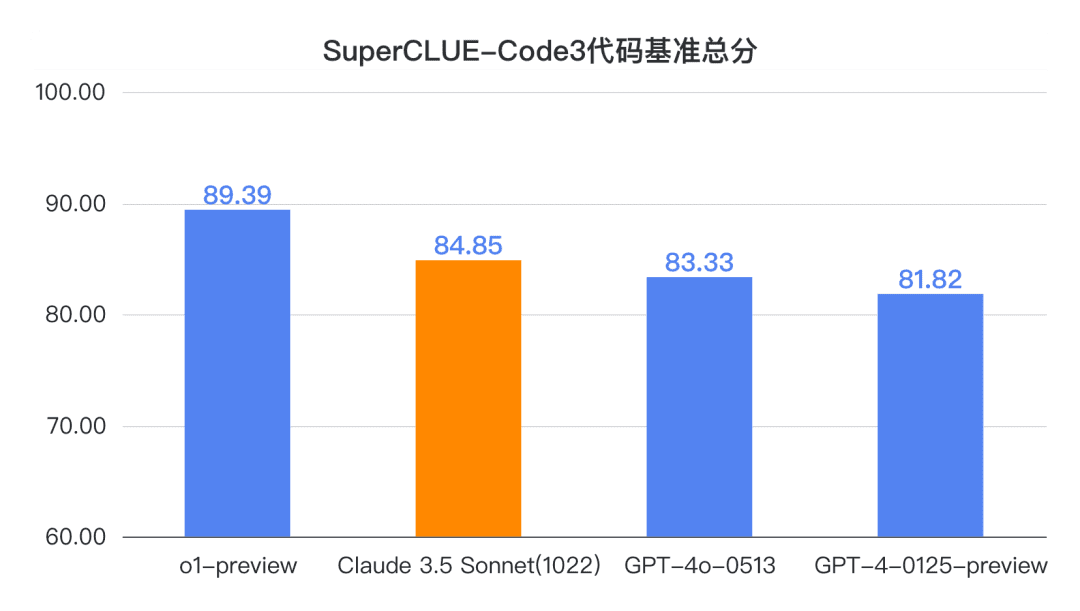
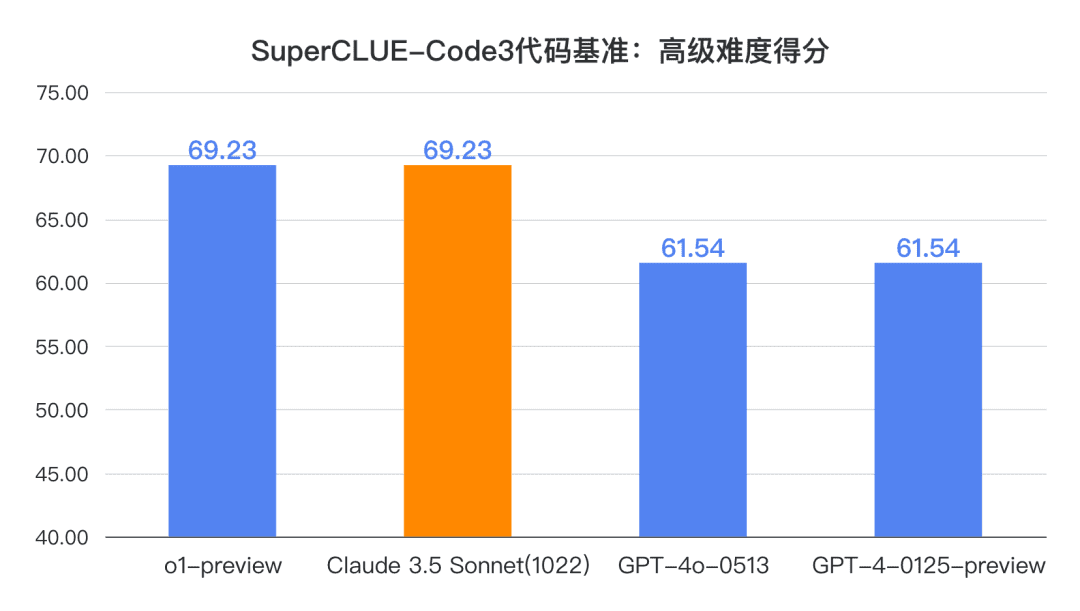
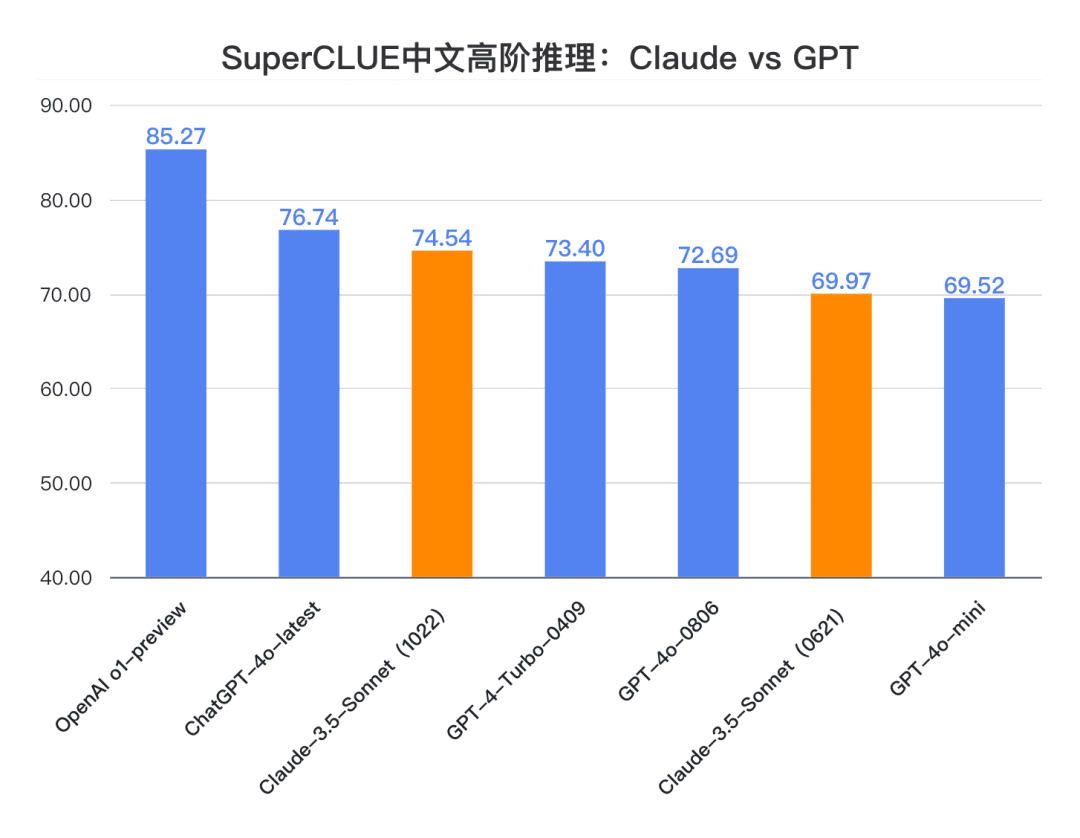
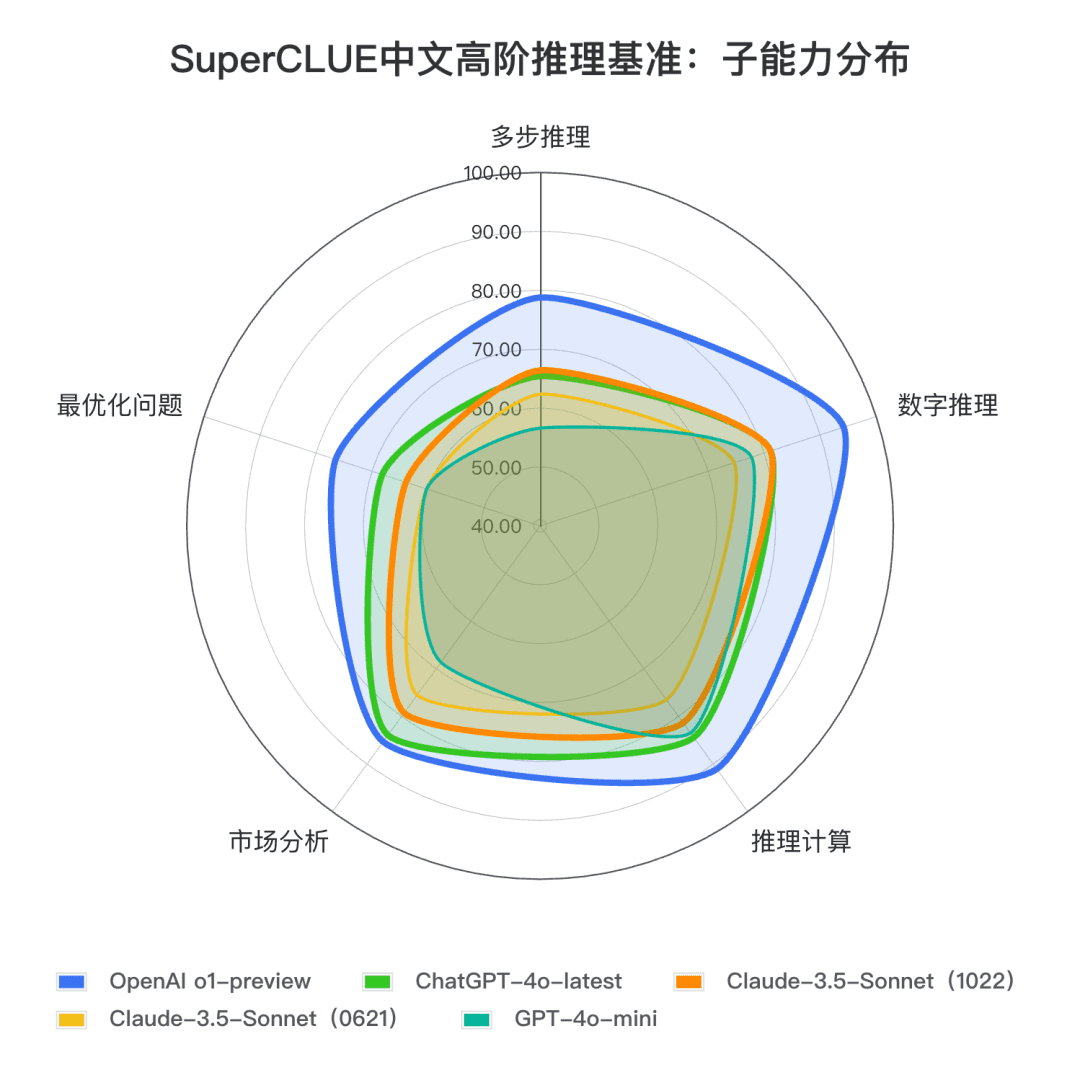
Exemple de mesure de code

Exemple 1

Prompt.

from typing import List


def longest_peak_sequence(nums: List[int]) -> int:
    """
    在一个整数数组中找出最长的"峰"序列的长度。
    所谓"峰"序列，是指先严格递增然后严格递减的序列，且峰顶（即最大值）唯一。
    至少包括三个数以上才能构成一个"峰"序列（即包含递增和递减的部分）。

    返回数组中最长"峰"序列的长度。如果没有"峰"序列，则返回0。


    示例:
    >>> longest_peak_sequence([2, 1, 4, 7, 3, 2, 5])
    5  # 最长的"峰"序列是 [1, 4, 7, 3, 2]


    >>> longest_peak_sequence([5, 4, 3, 2, 1])
    0  # 不存在"峰"序列，因为没有严格递增的部分

    提示:
    - 数组 `nums` 的长度范围为 [0, 10000]。
    - 数组中的每个元素范围为 [-10000, 10000]。
    """

Claude 3.5 Sonnet (1022) Réponse.

from typing import List


def longest_peak_sequence(nums: List[int]) -> int:
    if len(nums) < 3:
        return 0

    max_length = 0

    # 从第二个元素遍历到倒数第二个元素
    for i in range(1, len(nums) - 1):
        # 检查当前位置是否是峰顶
        if nums[i] > nums[i-1] and nums[i] > nums[i+1]:
            # 找到一个峰顶，向两边扩展
            left = i - 1
            right = i + 1

            # 向左扩展，寻找严格递增序列
            while left > 0 and nums[left-1] < nums[left]:
                left -= 1

            # 向右扩展，寻找严格递减序列
            while right < len(nums) - 1 and nums[right+1] < nums[right]:
                right += 1

            # 更新最长峰序列长度
            current_length = right - left + 1
            max_length = max(max_length, current_length)

    return max_length

Cas de test.

def check(candidate):
    assert candidate( [1, 2, 3, 4, 5, 6])==0
    assert candidate([1, 3, 5, 6, 4, 2, 0])==7
    assert candidate( [5, 4, 3, 2, 1, 2, 3, 4, 1])==5
    assert candidate([1, 3, 5, 3, 1])==5
    assert candidate([1, 2, 3, 3, 2, 1])==0
    assert candidate([2, 1, 3, 1, 2, 1, 3])==3
    assert candidate([1, 3, 5, 4, 3, 2, 1])==7

if_passed**(Adopté ou non):**Adopté.

Exemple 2

Prompt.

from typing import List


def longest_increasing_path(matrix: List[List[int]]) -> int:
    """
    给定一个整数矩阵，找到最长严格递增路径的长度。
    路径被定义为从矩阵中的任意单元格开始，每次可以向上、下、左、右移动到相邻的单元格上，如果递增的话。
    你不能在路径中移动到矩阵外面，也不能移动到不满足递增条件的单元格上。
    路径的长度是路径上的单元格总数。

    示例:
    >>> longest_increasing_path([
            [9, 9, 4],
            [6, 6, 8],
            [2, 1, 1]
        ])
    4  # 最长递增路径是 [1, 2, 6, 9]


    >>> longest_increasing_path([
            [3, 4, 5],
            [3, 2, 6],
            [2, 2, 1]
        ])
    4  # 最长递增路径是 [3, 4, 5, 6]或 [2, 4, 5, 6]


    提示:
    - 矩阵 `matrix` 的维度为 m x n。
    - 矩阵 `matrix` 的每个元素是一个非负整数。


    """

Claude 3.5 Sonnet (1022) Réponse.

from typing import List


def longest_increasing_path(matrix: List[List[int]]) -> int:
    if not matrix or not matrix[0]:
        return 0

    m, n = len(matrix), len(matrix[0])
    # 缓存，用于存储每个位置的最长递增路径长度
    cache = [[0] * n for _ in range(m)]

    def dfs(i: int, j: int) -> int:
        # 如果已经计算过，直接返回缓存结果
        if cache[i][j] != 0:
            return cache[i][j]

        # 四个方向：上、下、左、右
        directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]

        # 当前位置的最长路径至少为1
        max_length = 1

        # 遍历四个方向
        for di, dj in directions:
            ni, nj = i + di, j + dj

            # 检查是否在矩阵范围内且满足递增条件
            if (0 <= ni < m and 0 <= nj < n and 
                matrix[ni][nj] > matrix[i][j]):
                # 递归计算邻居位置的最长路径
                curr_length = 1 + dfs(ni, nj)
                max_length = max(max_length, curr_length)

        # 存入缓存
        cache[i][j] = max_length
        return max_length

    # 遍历矩阵中的每个位置，找到最长路径
    result = 0
    for i in range(m):
        for j in range(n):
            result = max(result, dfs(i, j))

    return result

Cas de test.

def check(candidate):
    assert candidate([[1, 1], [1, 1]]) == 1
    assert candidate([
    [9, 9, 4],
    [6, 6, 8],
    [2, 1, 1]
]) == 4
    assert candidate([
    [3, 4, 5],
    [3, 2, 6],
    [2, 2, 1]
]) == 4
    assert candidate([
        [1, 2, 3, 4],
        [5, 6, 7, 8],
        [9, 10, 11, 12],
        [13, 14, 15, 16]
]) == 7
    assert candidate([
        [-1, -2, -3, 0],
        [5, -6, 7, -8],
        [-9, 0, -11, -12],
        [13, 0, 15, -16]
]) == 4
    assert candidate([
    [5, 10, 6, 7, 9],
    [6, 10, 2, 2, 3], 
    [4, 9, 8, 2, 8],
    [3, 3, 3, 8, 8]
])==4
    assert candidate([
    [1, 3, 1, 4],
    [1, 5, 1, 7],
    [4, 2, 1, 1],
    [1, 3, 2, 1]
])==3
    assert candidate([
    [1, 9, 2, 4], 
    [9, 6, 5, 3],
])==4

if_passed(Adoptés ou non) :Adopté.

Exemples de raisonnement d'ordre supérieur

Exemple 1 : Raisonnement en plusieurs étapes

demander

Une entreprise compte sept employés nommés A, B, C, D, E, F et G. L'entreprise a organisé un exercice de notation et, sur la base des notes des employés et des conditions suivantes, en a déduit le classement exact de chaque employé :

1. Le score de A est supérieur à celui de B, mais inférieur à celui de C.
2. La note D est supérieure aux notes E et G, mais inférieure à la note A.
3. G a obtenu le score le plus bas.
4. La note B est plus élevée que les notes E et F.
5. La note F est supérieure à la note E.
6. La note C est la plus élevée.
7. Chaque employé obtient une note différente, la note D se situant à l'extrême centre.

Veuillez déduire le score spécifique de chaque employé sur la base des conditions susmentionnées.

Claude 3.5 Sonnet (1022) répond :

Extrapolons le classement de chaque employé par une analyse logique :

1. Connu de la condition 3 : G est à la dernière place (7ème)
2. Connu de la condition 6 : C est au sommet (1ère place)
3. Connu de la condition 7 : D est classé 4ème (position médiane)
4. Nous savons, d'après la condition 2, que le D est plus élevé que le E et le G, mais plus bas que le A. Donc, le D est plus élevé que le E et le G, mais plus bas que le A :
   • E doit être classé après D (5ème ou 6ème)
   • A doit être classé avant D (2ème ou 3ème)
5. Nous savons, d'après la condition 1, que A est plus élevé que B mais plus bas que C. Combinez cela avec l'analyse précédente :
   • 2ème place au rang A
   • B doit être classé 3ème
6. Nous savons d'après les conditions 4 et 5 que B est plus élevé que E et F, et que F est plus élevé que E. Donc :
   • 5ème place au rang F
   • E 6ème place

Le classement final est le suivant :

1. C (1ère place)
2. A (2ème place)
3. B (3ème place)
4. D (4ème)
5. F (5ème)
6. E (6ème)
7. G (7ème)

Voulez-vous que je vous montre le processus de raisonnement détaillé ?

Exemple 2 : problème d'optimisation

demander

Une ville possède cinq grands centres de transport et le service d'urbanisme souhaite optimiser la couverture des lignes de bus pour s'assurer que chaque centre est relié par au moins une ligne. Les coûts de construction entre les pôles sont connus et l'objectif est de relier tous les pôles à un coût minimum.

Données :

• Coûts de connectivité entre les hubs (en millions de dollars)
• Hub 1 et Hub 2 : 100 000
• Hub 1 et Hub 3 : 150 000
• Hub 2 et Hub 4 : 200 000
• Hub 3 et Hub 4 : 250 000
• Hub 3 et Hub 5 : 300 000
• Hub 4 et Hub 5 : 180 000

Objectif : Identifier les nœuds à connecter les uns aux autres afin de minimiser le coût total de la construction et de s'assurer que tous les nœuds sont interconnectés.

Claude 3.5 Sonnet (1022) répond :

Il s'agit d'un problème d'arbre minimum que je vais résoudre à l'aide de l'algorithme de Kruskal. Analysons-le pas à pas :

1. Tout d'abord, triez toutes les connexions du coût le plus faible au coût le plus élevé :
   • Pôle 1-2 : 100 000
   • Pôles 1 à 3 : 150 000
   • Hub 4-5 : 180 000
   • Carrefours 2-4 : 200 000
   • Pôle 3-4 : 250 000
   • Pôles 3 à 5 : 300 000
2. La connexion la moins coûteuse est sélectionnée afin d'éviter la formation d'un anneau :
   • Select Hub 1-2 (100 000 $)
   • Select Hub 1-3 (150 000 $)
   • Select Hub 4-5 (180 000 $)
   • Select Hub 2-4 (200 000 $)

Programme optimal :

• Connexion du Hub 1 et du Hub 2
• Connexion du Hub 1 et du Hub 3
• Connexion du Hub 4 et du Hub 5
• Connexion du Hub 2 et du Hub 4

Coût total : 10 + 15 + 18 + 20 = 630 000

Ce programme garantit que

1. Tous les concentrateurs sont connectés
2. Aucune boucle formée
3. Coût total de possession minimal

Souhaitez-vous que je génère pour vous une visualisation de cette solution ?

# Rejoindre la communauté

Pour plus d'informations sur le Claude 3.5 latest big model review, vous pouvez rejoindre le groupe d'échange SuperCLUE-Claude.