Qu'est-ce que la quantification de modèle : explication des types de données FP32, FP16, INT8, INT4

guide (par exemple, livre ou autre matériel imprimé)

Dans le vaste ciel étoilé de la technologie de l'IA, les modèles d'apprentissage profond stimulent l'innovation et le développement dans de nombreux domaines grâce à leurs excellentes performances. Cependant, l'expansion continue de l'échelle des modèles est comme une épée à double tranchant, qui entraîne une forte augmentation de la demande arithmétique et de la pression de stockage tout en améliorant les performances. Le déploiement et le fonctionnement des modèles sont confrontés à de sérieux défis, en particulier dans les scénarios d'application où les ressources sont limitées.

Face à ce dilemme, une technologie appelée "quantification" est apparue, qui, tel un scalpel délicat, réduit intelligemment la taille du modèle, améliore la vitesse de calcul et réduit de manière significative la consommation d'énergie dans la plage acceptable de précision du modèle. La technique de quantification peut convertir les données FP32 de haute précision du modèle en données INT4 de faible précision, ce qui permet de "mincir" et d'"accélérer" le modèle. Dans cet article, nous analyserons les principes et les méthodes de quantification et leur application dans le domaine de l'apprentissage profond, afin que même les débutants puissent facilement en comprendre l'essence.

1. les fondements de la représentation numérique

1.1 Conversion binaire-décimale

En informatique, pierre angulaire du monde numérique, toutes les données sont stockées sous forme binaire. Le système binaire ne comporte que deux nombres, 0 et 1, alors que le système décimal, que nous utilisons dans notre vie quotidienne, comporte dix nombres de 0 à 9. La conversion entre ces deux systèmes, comme la traduction entre différentes langues, est la clé pour comprendre la représentation des données dans les ordinateurs.

Le nombre décimal 13, par exemple, est converti en binaire sous la forme 1101. Le processus de conversion est similaire à la décomposition du "tout" décimal en ses "composants" binaires. Les étapes sont les suivantes :

13 Divisé par 2, le quotient est 6 et le reste est 1 (chiffre binaire le plus bas)
6 divisé par 2 donne un quotient de 3 et un reste de 0.
3 divisé par 2, quotient 1, reste 1
1 divisé par 2, le quotient est 0, le reste est 1 (chiffre binaire le plus élevé)

Les résidus sont énumérés de bas en haut :
↑1
↑0
↑1
↑1
Obtenir le résultat binaire : 1101

Inversement, reconvertir le binaire 1101 en décimal revient à réassembler les "pièces" pour obtenir le "tout". De droite à gauche, le poids de chaque bit augmente par puissance de deux, le bit le plus à droite ayant un poids de , , et ainsi de suite vers la gauche. Par conséquent, le nombre binaire 1101 est converti en décimal comme suit : 1× + 1× + 0× + 1× = 8 + 4 + 0 + 1 = 13.

1.2 Différence entre les nombres à virgule flottante et les entiers

(i) Types d'entiers (INT)

INT est l'abréviation de Integer, qui désigne le type de nombre entier. Les entiers, comme leur nom l'indique, sont des nombres qui ne contiennent pas de partie décimale, tels que 1, 2, 3, etc.

INT4 signifie qu'un nombre binaire de 4 bits est utilisé pour représenter un nombre entier, tandis que INT8 utilise un nombre binaire de 8 bits pour représenter un nombre entier. Le nombre de bits détermine la plage de représentation des nombres entiers.

La gamme d'entiers pouvant être représentés par INT4 est limitée, car un nombre binaire de 4 bits peut représenter jusqu'à un nombre différent. Pour les INT4 signés, la plage est généralement comprise entre -8 et 7, et pour les INT4 non signés, entre 0 et 15. Il en va de même pour les INT8, qui vont de -128 à 127, et les INT8 non signés, qui vont de 0 à 255, puisqu'un nombre binaire de 8 bits peut représenter = 256 nombres différents.

(ii) Type à virgule flottante (FP)

FP signifie Floating Point (point flottant), le type de point flottant. Les nombres à virgule flottante, par opposition aux nombres entiers, sont utilisés pour représenter les nombres comportant des parties fractionnaires.

Les nombres à virgule flottante se composent d'un bit de signe, d'un bit d'exposant et d'un bit de mantisse. Un nombre à virgule flottante de 32 bits (FP32), par exemple, se compose d'un bit de signe, de 8 bits d'exposant et de 23 bits de mantisse. Cette conception astucieuse permet aux nombres à virgule flottante de représenter une gamme extrêmement large de valeurs, depuis les très petits nombres jusqu'aux très grands nombres, comme un mètre ruban.

Par exemple, FP32 peut représenter de très petits nombres (approximativement) et de très grands nombres (approximativement). INT8 (entiers de 8 bits) ne peut représenter que les entiers compris entre -128 et 127. Cette différence est analogue à la mesure d'une longueur avec une règle de longueur fixe (nombres entiers) par rapport à un mètre ruban évolutif (nombres à virgule flottante), les nombres à virgule flottante étant de loin supérieurs aux nombres entiers en termes de flexibilité et d'étendue de la représentation numérique.

(iii) Types de données couramment utilisés

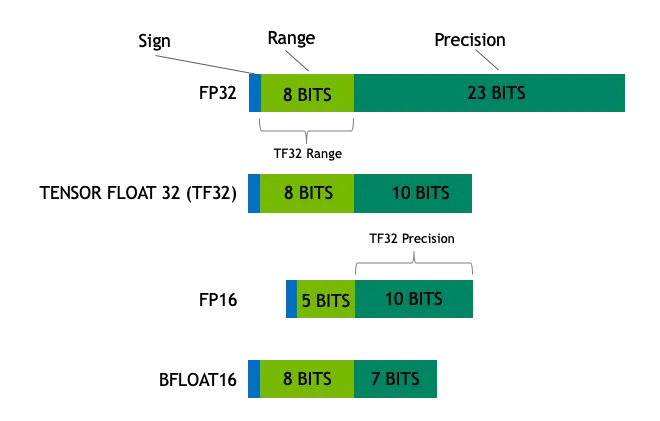
Les types de données courants dans l'apprentissage profond et l'informatique générale sont les suivants :

• Float32 (FP32)Les opérations FP32 dominent l'apprentissage et l'inférence des modèles en raison de leur polyvalence, qui est largement prise en charge par un large éventail de matériel.
• Float16 (FP16)FP16 : FP16 est un nombre à virgule flottante de demi-précision de 16 bits, dont la précision est réduite par rapport à FP32, mais dont l'empreinte mémoire est considérablement réduite et la vitesse de calcul nettement plus rapide.FP16 a une gamme relativement étroite de représentations numériques, qui peut être exposée à un risque de débordement et de sous-débordement. Cependant, dans les pratiques d'apprentissage profond telles queMise à l'échelle des pertes L'application de techniques telles que celles-ci peut atténuer efficacement ces problèmes.
• BFloat16 (BF16)BF16 : BF16 est un autre format à virgule flottante de 16 bits. Il est unique en ce sens que BF16 conserve le même bit d'exposant de 8 bits que FP32, et a donc la même plage dynamique que FP32, mais le bit de fin n'est que de 7 bits, ce qui est moins précis que FP16. Le BF16 donne de bons résultats dans les scénarios comportant une large gamme de valeurs, mais il peut y avoir des compromis dans les tâches sensibles à la précision.
• Int8L'INT8 est principalement utilisé dans les techniques de quantification de modèles, où la conversion des paramètres de modèle de FP32 ou FP16 de haute précision en INT8 réduit considérablement l'espace de stockage requis et la complexité de calcul du modèle, ouvrant ainsi la voie à un déploiement efficace du modèle sur des dispositifs à ressources limitées.

2) Concepts quantitatifs

2.1 Définitions quantitatives

La quantification fait référence à la conversion des données d'un modèle d'une représentation de haute précision à une représentation de faible précision, comme dans le cas de laCompromis entre la qualité de l'image et la taille du fichierDans le domaine de l'apprentissage profond, la quantification est le processus de compression d'une image de haute précision en une image JPEG de faible précision, ce qui réduit considérablement la taille du fichier tout en conservant les principales informations de l'image. Dans le domaine de l'apprentissage profond, la quantification fait généralement référence à la réduction des poids du modèle et des valeurs d'activation de FP32 (virgule flottante de 32 bits) à FP16 (virgule flottante de 16 bits) ou même à INT8 (entier de 8 bits) ou à une précision inférieure.

FP32 est un format de virgule flottante de haute précision qui représente avec précision les valeurs en binaire 32 bits (1 bit de signe, 8 bits d'exposant et 23 bits de mantisse). FP32 est une échelle de précision qui peut mesurer des valeurs petites à grandes, mais sa nature de haute précision s'accompagne d'une surcharge de stockage élevée et d'une vitesse de calcul relativement lente.

Le FP16 est un format de virgule flottante de demi-précision qui ne nécessite que 16 bits binaires (1 bit de signe, 5 bits d'exposant, 10 bits de mantisse) pour représenter une valeur. Par rapport au FP32, le FP16 sacrifie la précision pour la moitié de l'espace de stockage et une meilleure efficacité de calcul, et ressemble à une échelle légèrement plus épaisse, ce qui constitue un bon équilibre entre précision et efficacité.

INT8 est un type d'entier de 8 bits qui ne peut représenter que des entiers compris entre -128 et 127. INT8 présente l'avantage d'une empreinte mémoire très faible et d'une vitesse de calcul très élevée, mais il a également la précision numérique la plus faible. INT8 est similaire à un simple compteur qui ne compte que des entiers, mais il est rapide et pratique.

2.2 Objectif quantitatif

L'objectif principal de la quantification est deRéduction des besoins de stockage et de la complexité informatique des modèleset cherche en même temps à maintenir la perte de précision dans des limites acceptables. Plus précisément, la quantification vise à atteindre les objectifs suivants :

Réduction des besoins de stockage: Les modèles modernes d'apprentissage profond, en particulier les modèles à grande échelle avec des paramètres énormes, ont souvent des centaines de millions ou même des centaines de milliards de paramètres, ce qui exerce une pression énorme sur l'espace de stockage. Si l'on prend l'exemple du modèle FP32, chaque paramètre occupe 4 octets d'espace de stockage. Si le modèle est quantifié en FP16, chaque paramètre ne nécessite que 2 octets, ce qui réduit de moitié l'espace de stockage nécessaire. Si le modèle est quantifié en INT8, chaque paramètre ne nécessite qu'un octet et l'espace de stockage peut être réduit de 75%.

Améliorer l'efficacité des calculsLe modèle quantifié est nettement moins gourmand en calculs lors de la phase d'inférence, ce qui permet d'augmenter la vitesse d'inférence. Par exemple, lorsque le modèle FP32 est exécuté sur un GPU, la vitesse de calcul peut être limitée par la bande passante de la mémoire. En revanche, pour les modèles FP16 ou INT8, grâce à l'accélération optimisée du matériel pour les calculs de faible précision, la vitesse de calcul peut être considérablement augmentée. L'amélioration des performances apportée par la quantification est particulièrement significative dans les scénarios où les ressources informatiques sont limitées, tels que les appareils périphériques ou les appareils mobiles.

réduire la consommation d'énergieLa réduction des besoins en ressources informatiques des modèles se traduit directement par une réduction de la consommation d'énergie. Pour les appareils mobiles et les systèmes embarqués, la consommation d'énergie est une considération essentielle. Les techniques de quantification peuvent réduire efficacement la consommation d'énergie des modèles, prolonger la durée de vie des appareils et réduire les besoins de dissipation thermique.

Réduction des besoins en bande passante: Dans les systèmes informatiques distribués, la réduction de la taille des modèles signifie également la réduction de la bande passante de transmission des données. Dans un scénario multiserveur, les modèles quantitatifs peuvent être distribués et synchronisés plus rapidement, ce qui améliore l'efficacité globale du transfert de données.

3) INT4, INT8 Quantification

3.1 Plage de représentation des INT4 et INT8

INT4 et INT8 sont tous deux des méthodes de quantification de type entier qui stockent les données sous forme binaire dans les systèmes informatiques, mais qui diffèrent par l'étendue et la précision de la représentation numérique.

• INT8INT8 est un type d'entier de 8 bits dont la plage est comprise entre -128 et 127. Il peut être assimilé à un compteur de 8 bits, où chaque bit peut être un 0 ou un 1, et où différentes valeurs entières peuvent être représentées par différentes combinaisons 0/1. Par exemple, dans lenotée INT8 signifie moyen, allant de -128 à 127, et 11111111 en binaire signifie -1 en décimal. S'il estnon signé (c'est-à-dire la valeur absolue, sans tenir compte du signe plus ou moins) INT8, allant de 0 à 255, auquel cas 11111111 représente 255 en décimal, est suffisant pour répondre aux besoins de nombreux scénarios d'application, tels que les valeurs de pixels dans le traitement d'images, qui sont généralement comprises entre 0 et 255, et peuvent être efficacement représentées par INT8.
• INT4INT4 est un type d'entier de 4 bits dont la plage de représentation de -8 à 7 est plus petite que celle d'INT8. INT4 sacrifie la plage numérique au profit d'une empreinte mémoire plus petite et d'un calcul plus rapide. INT4 est comme un compteur plus petit, avec une plage numérique limitée mais une "empreinte" plus petite, ce qui est plus efficace en termes de ressources. Il est plus économe en ressources. Dans certains scénarios d'application avec des exigences de précision relativement faibles, comme certaines couches de réseaux neuronaux légers, l'utilisation de la quantification INT4 peut réduire de manière significative les coûts de stockage et de calcul.Par exemple, lors du déploiement d'un modèle léger de classification d'images sur mobile, les paramètres du modèle et les résultats des calculs intermédiaires peuvent être stockés et calculés à l'aide du format INT4 afin de réduire l'empreinte mémoire et d'accélérer l'inférence.

3.2 Formules quantitatives et exemples

Le processus de quantification est essentiellement la conversion d'une table de nombres à virgule flottante de haute précision en un nombre entier de basse précision. Si l'on prend l'exemple de la quantification de FP32 en INT8, la formule de quantification est la suivante :

est le nombre à virgule flottante d'origine.

est un entier quantifié.

est le facteur d'échelle, utilisé pour faire correspondre les nombres à virgule flottante à la plage des nombres entiers.

Indique l'arrondi au nombre entier le plus proche.

Indique que le résultat est limité à la plage de INT8, c'est-à-dire [-128, 127].

Calcul du facteur d'échelle

Le facteur d'échelle est généralement calculé comme le maximum de la valeur absolue du nombre à virgule flottante. En supposant qu'il existe un ensemble de nombres à virgule flottante, la procédure est la suivante :

1. Trouvez la valeur absolue maximale du groupe de nombres à virgule flottante :
2. Calculer le facteur d'échelle : .

Dans la pratique, il existe plusieurs façons de calculer le facteur d'échelle, telles que la quantification maximale, la quantification moyenne-standard, etc. La quantification maximale utilise la valeur absolue maximale du tenseur pour calculer le facteur d'échelle, ce qui est simple à mettre en œuvre mais peut être sensible aux valeurs aberrantes. La quantification moyenne-étalon utilise les informations relatives à la moyenne et à l'écart-type des données pour déterminer le facteur d'échelle d'une manière plus robuste, mais la complexité de calcul est légèrement plus élevée. Le choix de la méthode appropriée de calcul du facteur d'échelle nécessite un compromis entre la précision et la charge de calcul.

exemple typique

En supposant que nous disposions d'un ensemble de nombres à virgule flottante [-0,5, 0,3, 1,2, -2,1], voici une démonstration étape par étape du processus de quantification :

1) Calculer la valeur absolue maximale :

2. le calcul du facteur d'échelle :

3) Quantifier chaque nombre à virgule flottante :

• Pour -0,5.
• Pour 0.3.
• Pour 1.2.
• Pour -2.1.

La représentation INT8 quantifiée finale est [-1, 1, 4, -7].

Les étapes ci-dessus montrent clairement comment la technique de quantification convertit les nombres à virgule flottante en nombres entiers. Bien que le processus de quantification introduise inévitablement une certaine perte de précision, en choisissant judicieusement le facteur d'échelle, le niveau de performance du modèle peut être maximisé tout en réduisant de manière significative les coûts de stockage et de calcul. Pour réduire davantage les erreurs de quantification, la quantification en virgule zéro peut également être introduite. La quantification en virgule zéro ajoute un décalage en virgule zéro à la formule de quantification, ce qui permet de convertir avec précision les zéros en virgule flottante en zéros entiers, améliorant ainsi la précision de la quantification, en particulier si la valeur d'activation comporte un grand nombre de zéros.

4. quantification du FP8, du FP16 et du FP32

4.1 Représentations FP8, FP16 et FP32

FP8, FP16 et FP32 sont des nombres à virgule flottante qui sont stockés sous forme binaire dans l'ordinateur, mais avec des largeurs de bits différentes et donc des plages et une précision différentes.

FP32

FP32, en tant que format standard à virgule flottante de 32 bits, se compose des trois parties suivantes :

• Bit de signe (1 bit): Utilisé pour identifier les valeurs positives et négatives, 0 représentant un nombre positif et 1 un nombre négatif.
• Chiffres exponentiels (8 chiffres): est utilisé pour définir la plage de taille d'une valeur, ce qui permet à FP32 de représenter des valeurs allant de très petites à très grandes.
• Dernier chiffre (23 bits): Permet de déterminer la précision d'une valeur ; plus il y a de chiffres à la fin, plus la précision est élevée.

Avec une large gamme de valeurs allant d'environ à , et une précision d'environ 6 décimales, le FP32 est comme un mètre ruban de haute précision qui peut mesurer des échelles aussi petites qu'un grain de poussière et des distances aussi grandes qu'une montagne. FP32 est un type de données indispensable dans le calcul scientifique, la modélisation financière et d'autres domaines qui requièrent un haut degré de précision.

16ÈME PCRD

FP16 est un format de virgule flottante de demi-précision qui n'occupe que 16 bits de mémoire, soit la moitié de la taille de FP32 :

• Bit de signe (1 bit)Les valeurs positives et négatives : Identifie les valeurs positives et négatives.
• Chiffre exponentiel (5 chiffres): Définit une gamme de tailles de valeurs.
• Dernier chiffre (10 chiffres): Détermine la précision numérique.

La plage de FP16 est d'environ à, et la précision est réduite à environ 3 décimales par rapport à FP32. FP16 est comme une règle avec une échelle légèrement plus épaisse, qui a une précision plus faible, mais il a plus d'avantages en termes d'espace de stockage et d'efficacité de calcul. Le FP16 est couramment utilisé pour l'entraînement et l'inférence de modèles d'apprentissage profond, ce qui nécessite une vitesse de calcul et une bande passante mémoire élevées. En particulier dans les scénarios accélérés par le GPU, le FP16 peut utiliser pleinement les unités d'accélération matérielle telles que Tensor Core pour obtenir des améliorations de performance significatives.

FP8

FP8 est un format émergent de nombres à virgule flottante de faible précision, principalement utilisé dans le domaine de l'apprentissage profond, visant à un calcul efficace.La structure typique de FP8 est la suivante :

• Bit de signe (1 bit)Les valeurs positives et négatives : Identifie les valeurs positives et négatives.
• Chiffres exponentiels (3 ou 4 chiffres)Définir une gamme de tailles de valeurs (il existe deux variantes de FP8).
• Dernier chiffre (4 ou 3 chiffres): Détermine la précision numérique (correspond au nombre de chiffres de l'index).

La portée et la précision de la représentation numérique du FP8 sont encore réduites, mais les avantages sont une empreinte mémoire plus petite et des vitesses de calcul plus rapides. Si le FP32 est un mètre ruban de précision et le FP16 une règle avec une échelle légèrement plus épaisse, le FP8 est un mètre ruban plus précis. Il s'agit d'une simple règle graduée en centimètres.En outre, la portée et la précision sont encore réduites, mais la tâche de mesure peut toujours être effectuée rapidement dans une situation donnée. En tant que type de données de très faible précision, le FP8 présente un grand potentiel dans les scénarios où les exigences en matière de latence et de débit sont extrêmes, tels que l'inférence en temps réel, l'informatique de pointe, etc. Cependant, l'application du FP8 impose également des exigences plus élevées au matériel et aux algorithmes, nécessitant un support matériel spécial et des stratégies de quantification pour garantir la précision.

4.2 Processus de quantification et formules

La quantification est le processus de conversion d'un nombre à virgule flottante de haute précision en un nombre à virgule flottante de basse précision ou en un nombre entier. Si l'on prend l'exemple de la quantification de FP32 en FP16, la formule de quantification est la suivante :

est le nombre à virgule flottante d'origine.

est un nombre quantifié à virgule flottante de faible précision.

est le facteur d'échelle, utilisé pour faire correspondre les nombres à virgule flottante à des plages de précision inférieure.

Indique l'arrondi à la valeur la plus proche.

Calcul du facteur d'échelle

Le facteur d'échelle est généralement calculé comme le maximum de la valeur absolue du nombre à virgule flottante. En supposant qu'il existe un ensemble de nombres à virgule flottante, la procédure est la suivante :

1. Trouvez la valeur absolue maximale du groupe de nombres à virgule flottante :
2. Calculer le facteur d'échelle : , où est le maximum du format de basse précision ciblePeut être exprimée en valeur absolue. Pour le FP16, cette valeur est d'environ 65504.

Comme pour la quantification INT8, les facteurs d'échelle de la quantification FP16 peuvent être calculés de différentes manières, qui peuvent être choisies en fonction de différentes exigences en matière de précision et de performance. En outre, la quantification FP16 est souvent utilisée en conjonction avec l'apprentissage de la précision mixte (MPT). Au cours du processus d'apprentissage du modèle, le FP16 est utilisé pour certaines opérations à forte intensité de calcul (par exemple, la multiplication de la matrice, la convolution), tandis que le FP32 est utilisé pour les opérations nécessitant une plus grande précision (par exemple, le calcul de la perte, la mise à jour du gradient), afin d'accélérer le processus d'apprentissage et de réduire la consommation de mémoire tout en garantissant l'exactitude du modèle.

exemple typique

En supposant que nous disposions d'un ensemble de nombres à virgule flottante FP32 [-0,5, 0,3, 1,2, -2,1], voici une démonstration étape par étape de la quantification de FP32 en FP16 :

1) Calculer la valeur absolue maximale :

2. le calcul du facteur d'échelle :

3) Quantifier chaque nombre à virgule flottante :

• Pour -0,5.
• Pour 0.3.
• Pour 1.2.
• Pour -2.1.

Le FP16 final, quantifié, est exprimé comme suit : [-0,5, 0,3, 1,2, -2,1].

Les étapes ci-dessus permettent d'observer comment les techniques de quantification convertissent des nombres à virgule flottante de haute précision en nombres à virgule flottante de basse précision. La quantification entraîne certes une perte de précision, mais en choisissant judicieusement le facteur d'échelle, la performance du modèle peut être maintenue autant que possible tout en réduisant les coûts de stockage et de calcul. Afin d'améliorer encore la précision de la quantification FP16, il est possible d'utiliser la quantification dynamique. La quantification dynamique ajuste dynamiquement le facteur d'échelle en fonction de la plage réelle des données d'entrée pendant le processus d'inférence, afin de mieux s'adapter aux changements dans la distribution des données et de réduire l'erreur de quantification.

5. applications quantitatives et avantages

5.1 Applications dans le domaine de l'apprentissage profond

Les techniques quantitatives ont un large éventail d'applications prometteuses dans l'apprentissage profond, en particulier dans les phases d'apprentissage et d'inférence des modèles, où elles sont de plus en plus précieuses. Voici quelques applications majeures des techniques de quantification dans l'apprentissage profond :

Accélération de la formation au modèle

Le calcul avec des types de données de faible précision (par exemple, FP16 ou FP8) pendant la phase d'apprentissage du modèle peut accélérer considérablement le processus d'apprentissage. Par exemple, les GPU NVIDIA Hopper supportent les opérations Tensor Core en précision FP8. L'apprentissage en FP8 peut être 2 à 3 fois plus rapide que l'apprentissage traditionnel en FP32. Cette accélération de l'apprentissage est particulièrement importante pour les modèles comportant des paramètres de grande taille, car elle permet de réduire considérablement le temps d'apprentissage et la consommation de ressources informatiques. Par exemple, lors de l'apprentissage de modèles linguistiques à grande échelle tels que le GPT-3, l'utilisation de l'apprentissage en précision mixte FP16 ou BF16 permet de réduire considérablement le temps d'apprentissage et d'économiser beaucoup de ressources informatiques.

afin de Inflexion AI Inflection-2, par exemple, a été entraîné sur 5 000 GPU NVIDIA Hopper à l'aide d'une stratégie d'entraînement en précision mixte FP8, totalisant FLOPs d'opérations en virgule flottante, et dans un certain nombre de tests de performance standard en IA, Inflection-2 a démontré des performances supérieures à celles du modèle phare de Google, PaLM 2, qui se trouve également dans la catégorie des calculs d'entraînement. Dans un certain nombre de tests de performance standard en IA, Inflection-2 a démontré un avantage significatif en termes de performances par rapport au modèle phare de Google, PaLM 2, dans la même catégorie de calcul d'apprentissage.

Optimisation de l'inférence des modèles

Au stade de l'inférence du modèle, les techniques de quantification peuvent réduire de manière significative les besoins de stockage et la complexité de calcul du modèle, et donc améliorer l'efficacité de l'inférence. Par exemple, en quantifiant un modèle FP32 en INT8, l'espace de stockage du modèle peut être réduit de 75% et la vitesse d'inférence peut être multipliée par plusieurs fois. Cet aspect est essentiel pour le déploiement de modèles d'apprentissage profond sur des appareils mobiles ou de périphérie, qui sont souvent confrontés à des ressources de calcul et à un espace de stockage limités. Par exemple, lors du déploiement de modèles de reconnaissance d'images sur des téléphones mobiles, la quantification du modèle en INT8 peut réduire efficacement la taille du modèle, réduire la consommation de mémoire, accélérer la vitesse d'inférence et améliorer l'expérience de l'utilisateur.

Par exemple, Google a travaillé en étroite collaboration avec l'équipe de NVIDIA pour appliquer la technique d'optimisation TensorRT-LLM au modèle Gemma et l'a associée à la technologie FP8 pour accélérer l'inférence. Les résultats expérimentaux montrent que le FP8 multiplie par plus de trois le débit par rapport au FP16 lorsque les GPU Hopper sont utilisés pour l'inférence.

Compression et déploiement de modèles

Les techniques de quantification peuvent également être utilisées pour la compression et le déploiement de modèles. En quantifiant les modèles de haute précision en modèles de faible précision, la taille du modèle peut être efficacement réduite, ce qui permet de облегчить déployer le modèle dans des environnements où les ressources sont limitées. Par exemple, le modèle zéro-un-toututiliser La pile de technologies matérielles et logicielles de NVIDIA a achevé la formation et la validation de grands modèles FP8, avec un débit de formation de grands modèles multiplié par 1,3 par rapport à BF16. Outre la quantification INT8 et FP16/FP8, il existe également des techniques de quantification INT4 et même de bits inférieurs, telles que le réseau neuronal binaire (BNN) et le réseau neuronal ternaire (TNN). Ces techniques de quantification à très faible nombre de bits peuvent comprimer le modèle à l'extrême, mais généralement avec une grande perte de précision, et conviennent aux scénarios présentant des exigences extrêmes en matière de taille et de vitesse du modèle.

En outre, le modèle quantifié peut être amélioré à l'aide de techniques d'accélération matérielle spécifiques. Par exemple, NVIDIA Transformateur Engine a été intégré dans les principaux cadres d'apprentissage profond tels que PyTorch, JAX, PaddlePaddle, etc., fournissant un support matériel efficace pour l'inférence de modèles quantitatifs. Outre les GPU NVIDIA, d'autres plates-formes matérielles, telles que les CPU d'architecture ARM et les NPU mobiles, sont également optimisées et accélérées pour le calcul quantitatif, fournissant ainsi une base matérielle pour le déploiement à grande échelle de modèles quantitatifs.

5.2 Atouts et limites

tranchant

Amélioration de l'efficacité du calculLa quantification de faible précision peut accélérer considérablement le calcul et réduire la consommation de ressources informatiques. Le FP16 et le FP8 ont un débit de calcul plusieurs fois supérieur à celui du FP32. Cet effet d'accélération est particulièrement important pour l'apprentissage et l'inférence de modèles à grande échelle.

Des besoins de stockage moins importantsLes techniques de quantification peuvent réduire de manière significative les besoins de stockage des modèles. Par exemple, la quantification d'un modèle FP32 en INT8 réduit l'espace de stockage de 75%, ce qui est important pour le déploiement de modèles dans des environnements aux ressources de stockage limitées.

Réduction de la consommation d'énergie: Le calcul de faible précision nécessite moins de ressources de calcul, ce qui réduit la consommation d'énergie des appareils. Dans les appareils mobiles et les systèmes embarqués, la consommation d'énergie est un élément clé de la conception. Les modèles quantifiés permettent de prolonger la durée de vie des batteries et de réduire les besoins de dissipation thermique.

Optimisation du modèleLes techniques de quantification permettent d'optimiser et de comprimer les modèles pendant la formation et l'inférence, ce qui réduit encore les coûts de déploiement. Par exemple, l'application du FP8 permet aux modèles d'explorer des stratégies de quantification plus raffinées pendant la phase de formation, améliorant ainsi l'efficacité globale des modèles.

limitations

Perte de précision: Le processus de quantification s'accompagne inévitablement d'une perte de précision, qui peut être importante, en particulier lorsque des formats à très faible précision (par exemple, FP8) sont utilisés, et peut entraîner une dégradation de la performance du modèle pour une tâche donnée. Bien que la perte de précision puisse être atténuée dans une certaine mesure, par exemple par un choix judicieux des facteurs d'échelle, il est souvent difficile d'éliminer complètement la perte de précision. Afin d'atténuer la perte de précision causée par la quantification, il est possible d'utiliser l'apprentissage conscient de la quantification (QAT). Le QAT simule l'opération de quantification pendant le processus de formation du modèle et prend en compte l'erreur de quantification dans la formation, afin de former un modèle plus robuste à la quantification. Le QAT peut généralement améliorer de manière significative la précision des modèles de quantification, mais le coût de la formation augmentera en conséquence.

Support matérielLes plates-formes matérielles ne prennent pas toutes en charge les calculs de basse précision. Par exemple, les calculs FP8 et FP16 nécessitent souvent un matériel spécifique (par exemple, les GPU NVIDIA Hopper). Si la plate-forme matérielle n'est pas optimisée pour le calcul en basse précision, les avantages de la quantification ne seront pas pleinement exploités. Avec la popularité de l'informatique de basse précision, de plus en plus de plates-formes matérielles commencent à prendre en charge les types de données de basse précision tels que FP16, BF16 et même FP8, ce qui constitue une base matérielle plus solide pour l'application étendue des techniques de quantification.

Complexité accrue: Le processus de quantification lui-même peut ajouter de la complexité à l'élaboration du modèle. Par exemple, le processus de quantification exige un calcul précis des facteurs d'échelle et peut nécessiter un calibrage supplémentaire et une mise au point du modèle. Cela ajoute indéniablement à la difficulté du développement et du déploiement du modèle. Afin de réduire la complexité du déploiement de la quantification, de nombreux outils et plateformes de quantification automatisés sont apparus dans l'industrie, tels que NVIDIA TensorRT, Qualcomm AI Engine, etc., qui aident les développeurs à quantifier et à déployer rapidement et facilement des modèles sur des plateformes matérielles cibles.

scénario d'application: Les techniques de quantification ne conviennent pas à tous les scénarios d'application. Dans les tâches qui exigent une très grande précision (par exemple, le calcul scientifique, la modélisation financière, etc.), la quantification peut entraîner une perte de précision inacceptable. Pour les tâches sensibles à la précision, il est possible d'essayer une stratégie de quantification à précision mixte, dans laquelle différentes précisions de quantification sont appliquées à différentes couches ou paramètres du modèle, par exemple FP32 ou FP16 pour les couches ou paramètres clés, et INT8 ou moins pour d'autres couches ou paramètres, afin de parvenir à un meilleur équilibre entre précision et efficacité.

En résumé, les techniques de quantification, en tant que technologie clé dans le domaine de l'apprentissage profond, présentent un grand potentiel dans l'amélioration de l'efficacité des calculs, la réduction des besoins de stockage et de la consommation d'énergie. Toutefois, les techniques de quantification présentent également des limites, telles que la perte de précision et la dépendance à l'égard du matériel. Par conséquent, dans les applications pratiques, les stratégies de quantification doivent être soigneusement sélectionnées en fonction des exigences spécifiques de l'application et des caractéristiques du scénario, afin d'atteindre un équilibre optimal entre la performance et l'efficacité du modèle. À l'avenir, avec le développement continu du matériel et des algorithmes, la technologie quantitative jouera un rôle plus important dans le domaine de l'apprentissage en profondeur et favorisera l'application de l'intelligence artificielle dans un plus grand nombre de scénarios.