CoRAG : Modélisation dynamique de RAG enchaînés à l'aide de MCTS (Monte Carlo Trees)
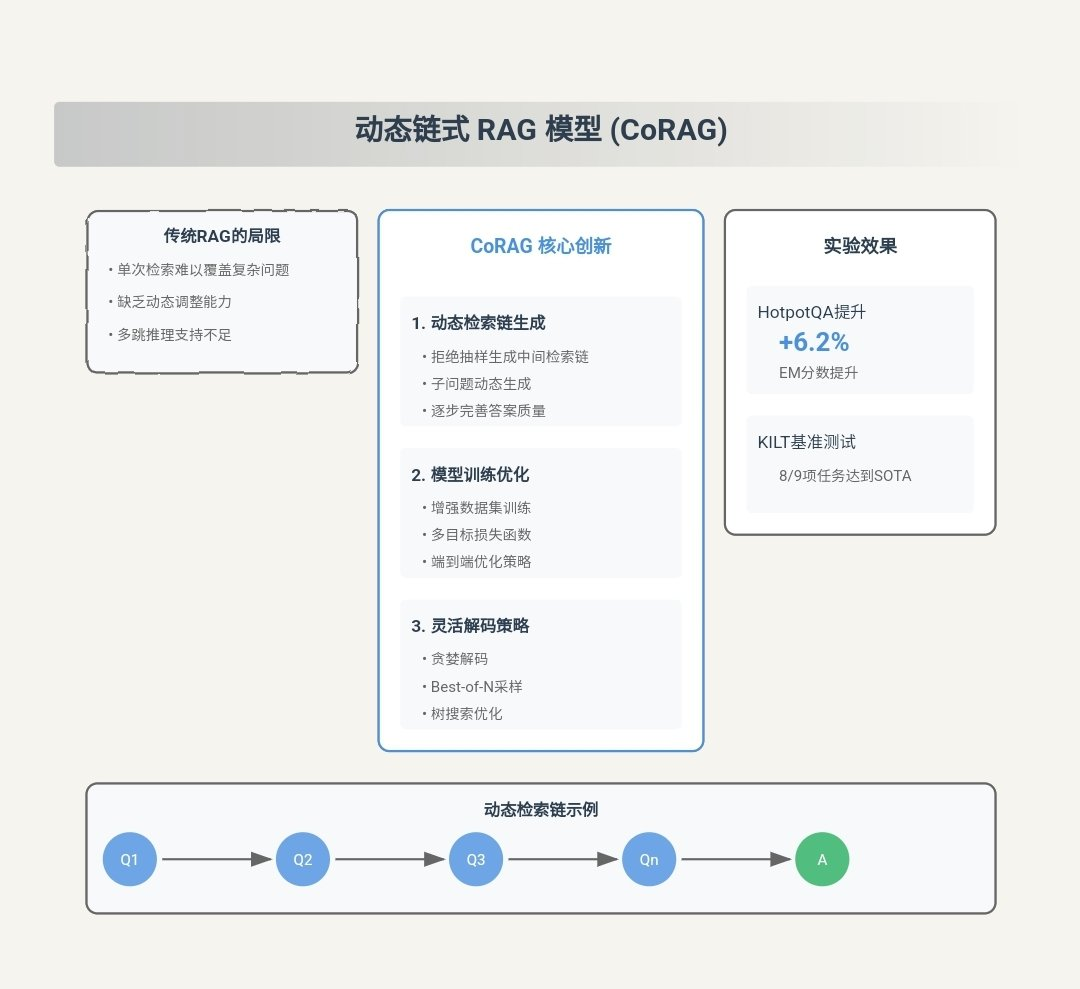
Résumé des principales contributions du CORAG
CORAG (coût limité) Récupération Optimisation for Retrieval-Augmented Generation) est un système innovant de Génération Augmentée de Récupération (RAG) conçu pour répondre aux besoins existants en matière d'information et de communication. RAG Les principaux défis de la méthodologie. Les principales contributions de CORAG sont les suivantes :
- Prise en compte globale des associations inter-blocs: :
- point d'innovationCORAG est le premier cadre à introduire l'optimisation de l'ordre de combinaison des blocs dans la tâche RAG. Contrairement aux approches traditionnelles, CORAG ne traite plus chaque bloc de texte indépendamment ou ne considère les blocs qu'au niveau du regroupement. Recherche arborescente de Monte Carlo (MCTS) pour rechercher séquentiellement l'ordre optimal des combinaisons de blocs. Cette approche permet de saisir pleinement les associations complexes entre les blocs, d'éviter les informations redondantes et de garantir que les combinaisons de blocs sélectionnées répondent pleinement à la requête de l'utilisateur.
- tranchantLe CORAG est ainsi en mesure de produire des réponses plus précises et plus pertinentes, ce qui améliore la qualité de la production.
- Résolution du problème de non-monotonicité de l'utilité des blocs: :
- point d'innovationLe CORAG contrainte budgétaire intégrée dans le processus d'optimisation du portefeuille de blocs, plutôt que de considérer l'épuisement du budget comme une condition d'arrêt. Cette approche prend en compte l'utilité du bloc nonmonotonicitéEn d'autres termes, l'ajout de blocs n'améliore pas toujours la qualité du résultat final.
- tranchantEn ajustant dynamiquement l'utilisation du budget au cours du processus d'optimisation, CORAG est en mesure d'éviter l'inclusion excessive de blocs non pertinents ou redondants, améliorant ainsi la précision et la pertinence des réponses générées.
- Adaptation aux différents domaines d'enquête: :
- point d'innovationLe CORAG a introduit un Configuration de l'agentL'agent utilise le Apprentissage comparatif pour adapter dynamiquement la configuration des SCTM à différents domaines d'interrogation. L'agent recommande la configuration optimale des Modèle de réarrangeur répondre en chantant Configuration des SCTM.
- tranchantCette approche confère à CORAG la souplesse nécessaire pour traiter un large éventail de types de requêtes, depuis les simples requêtes par mot clé jusqu'aux problèmes de raisonnement complexes, en garantissant des réponses de haute qualité dans une grande variété de scénarios d'application.
- Stratégies de recherche efficaces et évolutives: :
- point d'innovationCORAG emploie le système MCTS pour la recherche de nœuds avec le système technique d'expansion parallèle Accélère le processus de recherche. Cette approche réduit l'espace de recherche exponentiel à un espace linéaire et équilibre efficacement le processus de recherche. explorations répondre en chantant utiliser.
- tranchantCORAG est capable de traiter des ensembles de données à grande échelle tout en maintenant une recherche efficace et en trouvant un équilibre entre le coût de calcul et la qualité de la recherche.
- Des gains de performance significatifs: :
- vérification expérimentaleLes résultats expérimentaux montrent que CORAG surpasse les méthodes de base existantes sur plusieurs ensembles de données de référence, en améliorant les scores ROUGE d'environ 30%. CORAG excelle également en matière d'efficacité, en fournissant des réponses de haute qualité dans le cadre de contraintes de coûts très strictes.
Exemple de flux de travail CORAG
Pour aider le lecteur à comprendre rapidement le fonctionnement de CORAG, voici un exemple complet de flux de travail montrant comment CORAG traite une requête d'utilisateur et génère la réponse finale. Chaque étape contient des entrées et des sorties pour représenter le va-et-vient du flux de travail.
Étape 1 : Entrée de la requête de l'utilisateur
- importationLe système CORAG : Un utilisateur soumet une requête en langage naturel au système CORAG, par exemple :
"请解释光合作用的过程,并列出影响其效率的因素。" - exportations: La requête est transmise à l'outil Module d'intégration des requêtes Traitement.
Étape 2 : Génération de l'intégration de la requête
- importationTexte de la requête de l'utilisateur.
- traiter avec: Utilisation d'un système pré-entraîné Intégration de modèles(par exemple BGE-M3) convertit le texte de la requête en une représentation vectorielle.
- exportations: Interroge le vecteur d'intégration (par exemple, un vecteur à 1024 dimensions).
Query Embedding: [0.123, -0.456, 0.789, ..., -0.012]
Étape 3 : Configurer la prédiction des agents
- importationvecteur d'intégration de la requête
[0.123, -0.456, 0.789, ..., -0.012]. - traiter avec: :
- extraction de caractéristiquesLe vecteur d'intégration est introduit dans le Configuration de l'agent (utilisé comme expression nominale) réseau de codage L'extraction des caractéristiques est effectuée dans le
- Prédiction du réarrangeurLa prédiction de la sortie du réseau codé du système optimal de gestion de l'information. Modèle de réarrangeurPar exemple
bge-reranker-large. - Prévision de la configuration des SCTMEn même temps, le réseau de codage prédit les SCTM optimaux. Paramètres de configurationtels que le nombre d'itérations, le facteur de coût et le facteur d'exploration.
- exportations: :
- Modèle de réarrangeur optimal: :
bge-reranker-large - Paramètres de configuration des SCTM: :
- Nombre d'itérations: : 15
- facteur de coût: 0.2
- Facteur d'exploration: 2.5
Optimal Reranker: bge-reranker-large MCTS Configuration: - Iterations: 15 - Cost Coefficient: 0.2 - Exploration Coefficient: 2.5 - Modèle de réarrangeur optimal: :
Étape 4 : Récupération des blocs de texte potentiels
- importation: :
- Vecteur d'intégration des requêtes
[0.123, -0.456, 0.789, ..., -0.012]. - base de données vectorielles(par exemple, contenant des blocs de texte pré-segmentés et leurs vecteurs d'intégration).
- Vecteur d'intégration des requêtes
- traiter avec: Utiliser le vecteur d'intégration de la requête pour Recherche de similitudeLes cinq premiers blocs de texte sont extraits de la base de données vectorielles. Voici des exemples des cinq premiers blocs de texte récupérés :Bloc de texte 1: :
光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。Bloc de texte 2: :
光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。Bloc de texte 3: :
影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。Bloc de texte 4: :
光照强度对光合作用的影响呈正相关,但过强的光照会导致光抑制现象,降低光合作用效率。Bloc de texte 5: :
二氧化碳是光合作用的原料之一,其浓度直接影响光合作用的速率。 - exportations: liste des blocs de texte potentiels et de leurs vecteurs d'intégration.
Retrieved Chunks: - Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。" - Chunk 2: "光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。" - Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。" - Chunk 4: "光照强度对光合作用的影响呈正相关,但过强的光照会导致光抑制现象,降低光合作用效率。" - Chunk 5: "二氧化碳是光合作用的原料之一,其浓度直接影响光合作用的速率。"
Étape 5 : Recherche arborescente des SCTM
- importation: :
- Liste des blocs de texte potentiels: :
- Chunk 1 : ...
- Chunk 2 : ...
- Chunk 3 : ...
- Chunk 4 : ...
- Élément 5 : ...
- Paramètres de configuration des SCTM: :
- Nombre d'itérations: : 15
- facteur de coût: 0.2
- Facteur d'exploration: 2.5
- Modèle de réarrangeur: :
bge-reranker-large
- Liste des blocs de texte potentiels: :
- traiter avec: :
- Initialisation du nœud racineLe nœud racine représente un état vide où aucun bloc de texte n'est sélectionné.
- Expansion itérative: :
- option: Utilisation Algorithme UCB Sélectionnez le nœud dont l'utilité actuelle est la plus élevée. Par exemple, le morceau 3 est choisi pour la première itération parce qu'il est le plus pertinent par rapport à la requête.
- extensionsGénérer tous les nœuds enfants possibles (nouvelles combinaisons de morceaux de texte). Par exemple, les enfants du morceau 3 peuvent être le morceau 1, le morceau 2, le morceau 4 et le morceau 5.
- évaluation: Utilisation Modèle de réarrangeur
bge-reranker-largeÉvaluez l'utilité de toutes les nouvelles combinaisons en parallèle. Par exemple, évaluez l'utilité de combinaisons telles que le morceau 3 + le morceau 1, le morceau 3 + le morceau 2, etc. - mise à jourMise à jour de l'utilité des nœuds et du nombre d'accès, et propagation des mises à jour vers le haut.
- itérerRépéter les étapes de sélection, d'expansion, d'évaluation et de mise à jour jusqu'à ce que le nombre maximum d'itérations (15) soit atteint.
- Conditions de résiliation: Nombre maximum d'itérations atteint.
- exportationsLa Commission européenne a adopté une recommandation sur l'ordre optimal d'association des blocs de texte.
Optimal Chunk Combination: - Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。" - Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。" - Chunk 2: "光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。"prendre notePendant le processus des SCTM, CORAG ajuste dynamiquement l'ordre de combinaison en fonction de l'utilité et sélectionne finalement l'ordre de combinaison optimal.
Étape 6 : Générer la réponse finale
- importation: :
- Ordre optimal de combinaison des blocs de texte: :
- Chunk 3 : "Les facteurs affectant l'efficacité de la photosynthèse comprennent l'intensité lumineuse, la concentration en dioxyde de carbone, la température et la disponibilité de l'eau".
- Extrait 1 : "La photosynthèse est le processus par lequel les plantes, les algues et certaines bactéries utilisent l'énergie lumineuse pour convertir le dioxyde de carbone et l'eau en glucose et en oxygène".
- Chunk 2 : "La photosynthèse se produit principalement dans les chloroplastes des feuilles des plantes et se divise en deux phases : la réaction à la lumière et la réaction au carbone".
- demande d'information de l'utilisateur: "Expliquez le processus de la photosynthèse et énumérez les facteurs qui influencent son efficacité".
- Ordre optimal de combinaison des blocs de texte: :
- traiter avec: :
- Conseils de constructionLa recherche de l'ordre optimal de combinaison des blocs de texte avec les requêtes de l'utilisateur afin de construire la base de données de l'utilisateur. LLM de l'invite de saisie. Exemple :
用户查询:请解释光合作用的过程,并列出影响其效率的因素。 相关信息: 1. 影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。 2. 光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。 3. 光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。 - Générer une réponse: Utilisation LLM(par exemple, Llama3) Générer une réponse finale à l'invitation.
- Conseils de constructionLa recherche de l'ordre optimal de combinaison des blocs de texte avec les requêtes de l'utilisateur afin de construire la base de données de l'utilisateur. LLM de l'invite de saisie. Exemple :
- exportationsLa réponse finale en langage naturel : La réponse finale en langage naturel.
Final Response: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。它主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。"
Étape 7 : Sortie de la réponse
- importationLa réponse finale en langage naturel : La réponse finale en langage naturel.
- traiter avecLa réponse est présentée à l'utilisateur.
- exportationsL'interface utilisateur affiche le résultat de la réponse.
résumés
Avec l'exemple de flux de travail ci-dessus, le principe de fonctionnement de CORAG peut être résumé dans les étapes suivantes :
- Génération de l'intégration des requêtes: Convertir une requête d'utilisateur en une représentation vectorielle.
- Configuration de la prédiction des agentsLa recherche d'un modèle optimal de réarrangeur et des paramètres de configuration des SCTM.
- Récupérer les blocs de texte potentiels: Récupérer le bloc de texte le plus pertinent dans la base de données vectorielles.
- Recherche arborescente des SCTMLes blocs de texte peuvent être combinés dans un ordre optimal à l'aide du système de gestion des connaissances et des technologies (MCTS).
- Générer la réponse finaleLe texte de la réponse finale doit être composé d'une combinaison optimale de blocs de texte et doit être généré à l'aide de la méthode LLM.
- résultat de la réponseLa réponse est présentée à l'utilisateur.
Ces étapes montrent comment CORAG combine efficacement les trois phases d'extraction, d'amélioration et de génération pour fournir des réponses en langage naturel de haute qualité. Grâce à des exemples de données détaillés, les lecteurs peuvent mieux comprendre le processus de traitement des données de CORAG et son fonctionnement.
texte original: : https://arxiv.org/pdf/2411.00744
légende: : CORAG : Un système d'optimisation de la recherche avec des contraintes de coût pour la génération d'améliorations de la recherche.
auteurZiting Wang, Haitao Yuan, Wei Dong (Université technologique de Nanyang), Gao Cong (Université technologique de Nanyang), Feifei Li (Groupe Alibaba)
résumés
Les grands modèles de langage (LLM) ont démontré d'excellentes capacités dans les tâches génératives, mais il est souvent difficile d'accéder à des informations actualisées, ce qui peut conduire à une certaine désillusion. La génération améliorée par récupération (RAG) s'attaque à ce problème en intégrant des connaissances provenant de bases de données externes afin d'obtenir des réponses plus précises et plus pertinentes. En raison de la limitation de la fenêtre contextuelle des LLM, il n'est pas pratique d'introduire directement l'ensemble du contexte de la base de données externe dans le modèle. Au lieu de cela, seules les informations les plus pertinentes, c'est-à-dire les "morceaux" (chunks), sont récupérées de manière sélective. Cependant, la recherche actuelle sur les RAG est confrontée à trois défis majeurs. Premièrement, les solutions existantes sélectionnent généralement chaque morceau de manière indépendante, en ignorant les associations potentielles entre eux. Deuxièmement, dans la pratique, l'utilité des morceaux est "non monotone", ce qui signifie que l'ajout de morceaux supplémentaires peut réduire l'utilité globale. Les approches traditionnelles mettent l'accent sur la maximisation du nombre de blocs inclus, ce qui peut involontairement nuire aux performances. Troisièmement, chaque type de requête d'utilisateur présente des caractéristiques uniques qui nécessitent un traitement sur mesure, que les solutions actuelles ne prennent pas suffisamment en compte.
Pour surmonter ces difficultés, nous proposons CORAG, un système d'optimisation de la recherche avec des contraintes de coût, pour la génération d'améliorations de la recherche. Nous adoptons un cadre stratégique basé sur la recherche arborescente de Monte Carlo (MCTS) pour trouver les combinaisons de blocs optimales de manière séquentielle, ce qui permet de prendre en compte de manière exhaustive les associations entre les blocs. En outre, au lieu de considérer l'épuisement du budget comme une condition de terminaison, nous intégrons les contraintes budgétaires dans le processus d'optimisation des combinaisons de blocs, ce qui résout efficacement le problème de la non-monotonicité de l'utilité des blocs. En outre, en concevant des agents de configuration, notre système prédit la configuration optimale pour chaque type de requête, améliorant ainsi l'adaptabilité et l'efficacité. Les résultats expérimentaux montrent que notre cadre améliore les performances de 301 TP3T par rapport au modèle de base, ce qui met en évidence l'efficacité, l'évolutivité et l'applicabilité du cadre pour les applications à contexte long.
Format de référence PVLDB.
Ziting Wang, Haitao Yuan, Wei Dong, Gao Cong et Feifei Li. CORAG : A Cost-Constrained Retrieval Optimisation System for Retrieval-Augmented Generation (Système d'optimisation de la recherche sous contrainte de coût pour la génération augmentée de la recherche). . pvldb, 14(1) : xxx-xxx, 2020.
doi:XX.XX/XXX.XX
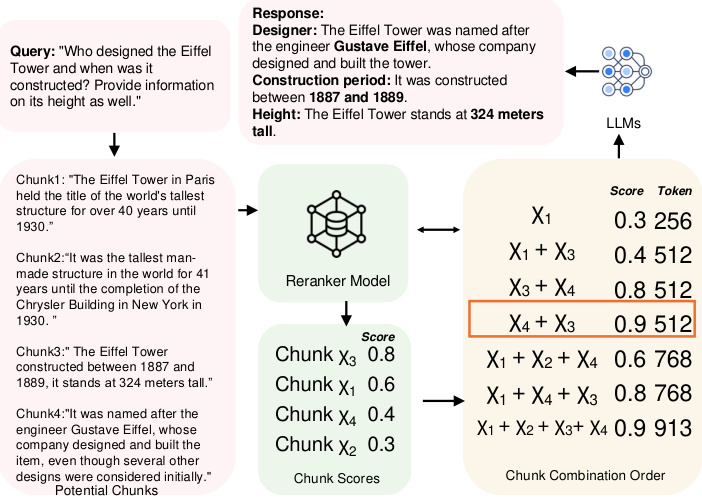
Figure 1 : Exemple d'ordre de combinaison de blocs de données.
1 Introduction
Bien que les LLM aient démontré d'excellentes capacités dans les tâches génératives, ils rencontrent souvent des difficultés dans l'acquisition d'informations actualisées, ce qui peut conduire à des hallucinations [10, 38]. Pour relever ces défis, RAG est apparu comme une solution clé. En intégrant des sources de données externes dans le LLM, le RAG peut fournir des informations plus précises, plus pertinentes et plus récentes. Aujourd'hui, la RAG est largement étudiée dans le contexte des LLM, en particulier dans les tâches qui nécessitent des connaissances externes actualisées, telles que les tâches de question et de réponse [2, 22, 29], la recherche d'informations médicales [1, 32] et l'analyse de séries temporelles [12, 26, 40]. Les sources de données externes sont généralement si importantes qu'il n'est pas pratique de les introduire directement dans le LLM. Pour résoudre ce problème, les données sont généralement divisées en morceaux qui ne se chevauchent pas et stockées dans une base de données vectorielle, puis l'utilisateur interroge les morceaux les plus utiles pour construire des indices pour le LLM. Par conséquent, la conception de structures et d'algorithmes de recherche efficaces et précis pour trouver les morceaux les plus pertinents est devenue un sujet de recherche important et a été largement étudiée dans les communautés des bases de données [39, 48] et de l'apprentissage automatique [2, 35, 43].
Cependant, les approches existantes posent trois problèmes majeurs.
Défi 1 : Liens entre les blocs. Il existe actuellement deux approches principales pour identifier les blocs les plus pertinents. La première formule le problème sous la forme d'une tâche AKNN (Approximate k-Nearest Neighbours) [41, 45], où chaque bloc se voit attribuer un score et où les k premiers blocs approximatifs classés par score sont sélectionnés. La seconde approche regroupe les blocs et renvoie tous les blocs du groupe le plus pertinent en réponse à une requête [22, 29]. Cependant, les deux méthodes ignorent les associations potentielles entre les blocs : la première méthode ignore totalement les associations, tandis que la seconde méthode ne prend en compte que superficiellement tous les blocs de chaque groupe en les considérant comme également pertinents. Par conséquent, ces méthodes introduisent une redondance substantielle dans les blocs sélectionnés lorsque plusieurs blocs transmettent des informations similaires ou redondantes.
Par exemple, comme le montre la figure 1, lors d'une requête sur la hauteur et l'histoire de la Tour Eiffel, si chaque bloc est traité indépendamment, la méthode gourmande sélectionne les blocs χ3 et χ1 parce qu'ils ont les deux premiers scores les plus élevés. Cependant, ces deux blocs ne fournissent que des informations sur l'historique, ce qui n'est pas suffisant pour répondre complètement à la requête. Afin de mieux répondre à la requête, il est nécessaire d'inclure des blocs contenant le nom du constructeur, par exemple χ4. D'autre part, l'approche de regroupement renverra tous les χ1, χ2, χ3 et χ4, ce qui entraînera une redondance. La solution optimale choisira χ3 et χ4 car ils fournissent les informations requises sans redondance. De plus, des études [11, 19, 42] ont montré que l'ordre des blocs affecte la performance du LLM, un facteur qui est également ignoré par les méthodes existantes. Dans le cas de la Tour Eiffel, par exemple, lors du choix des blocs χ3 et χ4, placer χ4 en première position donne un meilleur score que l'ordre inverse. Cependant, la détermination de l'ordre optimal des combinaisons de blocs est une tâche difficile car les deux requièrent que l'espace de recherche croisse de manière exponentielle avec le nombre de blocs disponibles. Dans le présent document, nous démontrons en outre que ce problème est NP-hard (voir section 2.1).
Défi 2 : Non-monotonicité de l'utilité. La solution actuelle repose sur l'hypothèse que l'inclusion d'un plus grand nombre de blocs produit toujours un meilleur résultat final. Plus précisément, dans l'approche AKNN, exactement k blocs sont sélectionnés de manière déterministe à chaque fois. Dans l'approche basée sur le clustering, un seuil de distance entre les clusters et les requêtes est fixé et tous les clusters compris dans ce seuil sont renvoyés. Les deux approches renvoient autant de blocs que possible. Toutefois, dans la pratique, l'utilité des blocs n'est pas monotone. Plus précisément, un trop grand nombre de blocs dilue les informations clés en ajoutant du contenu lié aux bords, produisant un bruit qui réduit la clarté. En outre, les conflits ou les différences subtiles entre les blocs peuvent perturber le modèle et réduire la qualité de la réponse. Par exemple, comme le montre la figure 1, l'ajout du bloc χ1 réduit l'utilité lorsque χ3 et χ4 sont sélectionnés, ce qui souligne le fait que les scores d'utilité ne sont généralement pas monotones dans la pratique.
Défi 3 : Diversité des requêtes. Il existe différents types de requêtes d'utilisateurs, chacune nécessitant une stratégie de classement différente en fonction de ses caractéristiques uniques [47]. Dans les systèmes RAG actuels, le score d'utilité d'un bloc est généralement déterminé par le modèle de reclassement attribué. À ce jour, il existe plusieurs modèles de reclassement, mais nous observons que leurs performances varient considérablement d'un type de requête à l'autre, et qu'aucun modèle de reclassement fixe n'est systématiquement plus performant que les autres pour toutes les variantes de requête (voir les expériences de la section 6.3.4 pour plus de détails). Les approches actuelles [20, 46] s'appuient généralement sur des modèles de reclassement statiques pour le classement des blocs et manquent de flexibilité pour s'adapter aux différents contextes des requêtes.
Énoncé du problème : Existe-t-il un système RAG qui tienne pleinement compte des associations entre blocs et de la non-monotonicité des utilités, tout en étant capable de répondre à tous les types de requêtes ?
1.1 Notre contribution
Dans cet article, nous répondons à cette question par l'affirmative en proposant un nouveau cadre d'arbre de politique basé sur les SCTM pour optimiser la recherche de blocs dans les systèmes RAG. Globalement, notre contribution peut être résumée comme suit :
- Nous présentons le premier cadre RAG qui prend en compte l'ordre des combinaisons de blocs dans une tâche RAG. Au lieu de considérer chaque bloc indépendamment ou à un niveau de regroupement, nous utilisons MCTS pour aider à rechercher l'ordre optimal de combinaison des blocs de manière séquentielle. L'idée de haut niveau est la suivante : nous initialisons d'abord le nœud racine. Ensuite, au cours des itérations, nous développons l'arbre en sélectionnant le nœud ayant l'utilité la plus élevée et en calculant l'utilité de ses nœuds d'expansion. Après chaque expansion, nous mettons à jour l'utilité de l'ensemble de l'arbre politique. Dans ce processus, la décision de chaque itération dépend des blocs qui ont été sélectionnés, ce qui nous permet de prendre pleinement en compte les associations entre les blocs. En outre, les MCTS réduisent l'espace de recherche exponentiel à un espace linéaire, et nous appliquons des techniques d'expansion parallèle pour améliorer encore l'efficacité des calculs. Grâce à cette conception, nous relevons le défi 1.
- Contrairement aux cadres RAG précédents qui considèrent l'épuisement du budget comme une condition de terminaison, nous proposons une nouvelle formulation dans laquelle les contraintes budgétaires sont intégrées dans le processus d'optimisation des combinaisons de blocs afin de tenir pleinement compte de la non-monotonicité de l'utilité des blocs, ce qui permet de relever le deuxième défi. coût de calcul.
- Nous proposons un agent basé sur l'apprentissage comparatif qui adapte dynamiquement la configuration des SCTM à la requête, en adaptant le modèle de reclassement et la configuration au domaine spécifique de la requête. Cette approche offre flexibilité et robustesse pour les requêtes dynamiques et spécifiques à un domaine, en s'adaptant au défi 3.
- En outre, nous avons mené des expériences complètes comparant notre cadre à plusieurs méthodes de pointe. Les résultats valident l'efficacité, l'efficience et l'évolutivité de notre approche et améliorent les performances de 30% par rapport à la référence.
2 Connaissances préparatoires
Dans cette section, nous commençons par introduire les définitions de certains concepts clés, tels que l'ordre des blocs et l'ordre de combinaison des blocs, dans la section 2.1. Ensuite, nous donnons une preuve NP-hard du problème d'optimisation de l'ordre des blocs. Enfin, nous discutons des travaux connexes à la section 2.3.
2.1 Concepts clés
RAG & Chunks. RAG est une méthode efficace pour améliorer les performances des modèles génératifs en récupérant le contexte pertinent d'un corpus externe. Dans cette approche, le corpus est d'abord divisé en unités plus petites et plus faciles à gérer, appelées blocs, qui sont stockées dans une base de données vectorielle. Ainsi, nous pouvons donner une définition formelle d'un bloc comme suit :
Définition 2.1 (Bloc). Soit C un corpus de documents et un bloc χ est défini comme un bloc continu de texte extrait de C. Formellement, un bloc χ consiste en une séquence de jetons (t1, t2, .... , tn), où chaque ti est un token dans C et la taille n est fixée par l'utilisateur.
Dans un système RAG, chaque bloc est intégré dans une représentation vectorielle à l'aide d'un modèle d'intégration qui saisit la signification sémantique du bloc et permet la recherche de contenu contextuellement similaire. Lorsqu'une nouvelle requête est reçue, la base de données vectorielle effectue une recherche de similarité afin d'identifier les blocs les plus pertinents d'un point de vue sémantique par rapport à la requête. Ces blocs récupérés sont ensuite transmis à un générateur (par exemple, un modèle de langage étendu) pour générer une réponse finale basée sur le contenu récupéré. Plus précisément, plus un bloc contient de tokens, plus le coût supporté par le générateur est élevé. Nous définissons donc le coût d'un bloc comme cost(χ) = |χ|, qui est égal au nombre de tokens dans le bloc.
Ordre de combinaison de blocs. Dans un système RAG, les résultats d'une recherche dans une base de données vectorielle peuvent comprendre plusieurs blocs. Cependant, en raison des contraintes d'entrée du modèle génératif, il n'est pas pratique d'utiliser tous ces blocs. Il est donc nécessaire de sélectionner le sous-ensemble optimal de blocs, appelé combinaison de blocs, pour respecter un budget de coûts donné. En outre, l'ordre des blocs dans la combinaison a un impact significatif sur la performance du modèle génératif. L'objectif est d'identifier l'ordre des combinaisons de blocs avec l'ordre optimal, défini formellement comme suit :
Définition 2.2 (sélection de l'ordre optimal de combinaison de blocs). Soit {χ1, χ2, ... , χk} un ensemble de blocs potentiels, ℛ un budget de coûts, Φ = ⟨χφ1, ... , χφm⟩ représente un ordre de combinaisons de blocs potentiels, où chaque χφi est un bloc et l'indice φi indique sa position dans Φ. Soit U(Φ) le score d'utilité attribué par le modèle de reclassement, qui peut être arbitraire ou composite. Notre objectif est de trouver l'ordre de combinaison des blocs qui maximise les scores d'utilité sous la contrainte du coût de leur introduction dans les LLM pour générer la réponse finale, c'est-à-dire la recherche de l'ordre de combinaison le plus approprié.
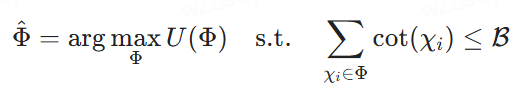
2.2 Preuves de la difficulté NP
Pour montrer que la sélection séquentielle de combinaisons de blocs est NP-difficile, nous généralisons le problème de l'hypergroupe pondéré maximal (MWHP). Puisque le MWHP est NP-hard, nous montrons que toute instance MWHP peut être convertie en une instance d'optimisation de combinaison de blocs en temps polynomial.
2.2.1 Définition du problème de la MWHP
Étant donné un hypergraphe ℋ = (V, E, w1, w2), où V est l'ensemble des sommets et E l'ensemble des hyper-anges, et où chaque hyper-ange contient un sous-ensemble de V. w1 : v → ℝ et w2 : e → ℝ sont les fonctions de poids, qui attribuent un poids à chaque sommet et à chaque hyper-ange respectivement. Étant donné un sous-ensemble de sommets V' ⊆ V, nous disons qu'un hyper-échantillon e appartient à V', c'est-à-dire que e ∈ V', si V' couvre tous les sommets de e. Le but est de trouver k sommets et de maximiser la somme des poids de ces sommets et des hypercordes qu'ils couvrent :
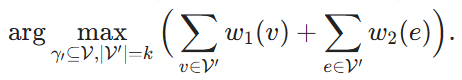
2.2.2 Processus de normalisation
Nous construisons maintenant une instance correspondante du problème d'optimisation de la combinaison de blocs à partir d'une instance MWHP donnée. Pour chaque nœud v ∈ V, nous créons un bloc correspondant Xv. Nous définissons son coût cost(Xv) ≡ 1. Un ordre de combinaison de blocs Φ correspond alors à un sous-ensemble de sommets de V désigné par V(Φ) ⊆ V. Nous définissons son utilité comme suit
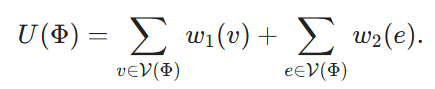
Enfin, nous fixons B = k et nous visons à
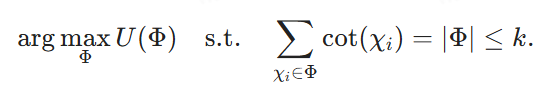
En utilisant Φdésigne la solution de (4), alors il est clair que V(Φ) est une solution de (2) et la réduction peut être effectuée en O(|V|-|E|) temps.
Il convient de noter que cette induction présuppose que, dans notre problème d'optimisation de la combinaison de blocs, nous autorisons un reclassement arbitraire, ce qui signifie que les scores d'utilité peuvent également être attribués de manière arbitraire. La complexité de la recherche de l'ordre optimal de combinaison de blocs peut être considérablement réduite si certaines hypothèses sont formulées au sujet du reclassement. Par exemple, si le reclasseur ne prend pas en compte les associations et se contente de faire la somme linéaire des scores d'utilité de chaque bloc, chaque bloc peut être évalué indépendamment. Toutefois, dans le présent document, nous traitons le cas le plus général et n'émettons aucune hypothèse sur le modèle de reclassement.
2.3 Travaux connexes
2.3.1 Génération de l'amélioration de l'extraction
Le RAG [14, 20] est largement utilisé pour traiter les tâches de NLP à forte intensité de connaissances. Dans un processus RAG typique, un extracteur basé sur l'intégration dense recherche des informations pertinentes dans des bases de données externes, qui sont ensuite utilisées par le LLM pendant le processus de génération. Pour améliorer ce processus, plusieurs études [5, 18, 22, 35] se sont concentrées sur l'adaptation des extracteurs pour mieux répondre aux besoins de génération des LLM, sur le développement de méthodes d'extraction en plusieurs étapes et sur le filtrage des informations non pertinentes. Bien qu'il existe de nombreux extracteurs de pointe [8, 9, 15, 16, 27, 34], l'optimisation des extracteurs et des LLM dans un processus de bout en bout [25, 31] est plus prometteuse. Par exemple, la recherche [30] se concentre sur le co-entraînement du récupérateur et du LLM simultanément ou par étapes. Cependant, cela nécessite une perte d'agent pour l'optimisation et complique le processus d'entraînement, en particulier lorsque les bases de données intégrées doivent être réindexées fréquemment, ce qui entraîne des coûts de calcul élevés. C'est pourquoi des approches telles que [5] décomposent les requêtes complexes à plusieurs étapes en sous-intensités plus petites afin d'améliorer l'exhaustivité de la réponse sans réindexation fréquente. Cependant, ces approches ignorent généralement le rôle crucial de l'ordre de combinaison des blocs, qui peut affecter de manière significative la qualité globale de la réponse du LLM. À notre connaissance, cet article est la première approche à prendre en compte l'ordre de combinaison des blocs dans une tâche RAG.
2.3.2 Reclassement du RAG
Les méthodes de reclassement sont essentielles pour améliorer les performances de recherche dans le processus RAG [43, 44, 51]
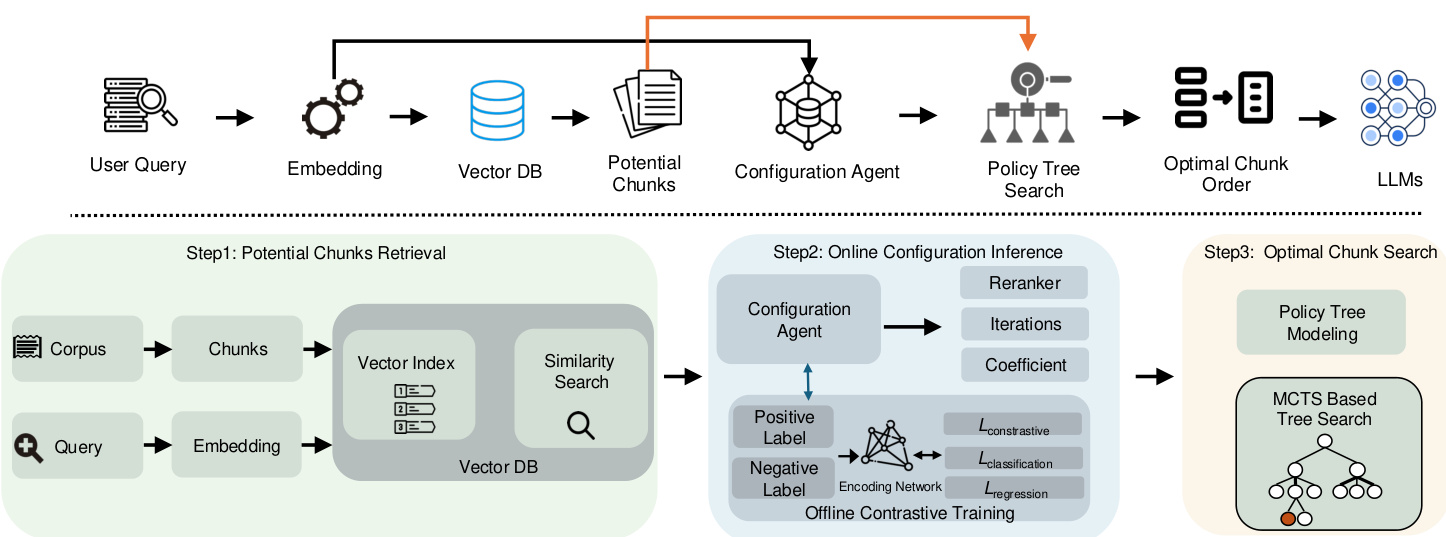
Figure 2 : Vue d'ensemble de l'architecture du système CORAG
Les méthodes traditionnelles de reclassement [33, 50] s'appuient généralement sur des modèles linguistiques de taille moyenne, tels que BERT ou T5, pour classer les contextes récupérés. Cependant, ces modèles ont généralement du mal à capturer les relations sémantiques entre les requêtes et les contextes, en particulier dans des contextes à zéro ou petit échantillon. Par conséquent, des recherches récentes [43] ont mis en évidence le potentiel des LLM ajustés aux commandes pour améliorer le reclassement des contextes, même en présence d'informations bruyantes ou non pertinentes. Malgré ces progrès, les capacités de reclassement du LLM dans les systèmes RAG restent sous-utilisées. En particulier, il a été démontré que le classement des blocs affecte les performances du LLM [19], ce qui souligne la nécessité de prendre en compte l'ordre des combinaisons de blocs dans les tâches RAG. Toutefois, les modèles existants ne sont pas adaptés aux situations dans lesquelles une séquence ou une combinaison spécifique de blocs est requise pour une extraction optimale, plutôt que des blocs isolés. Par conséquent, les recherches futures doivent mieux utiliser le LLM pour séquencer plus efficacement les blocs en réponse aux requêtes dans le cadre du RAG.
2.3.3 Apprentissage par renforcement pour les grands modèles linguistiques
Récemment, l'apprentissage par renforcement (RL) a été de plus en plus utilisé pour une variété de tâches de gestion de données et de RAG. Les techniques RL peuvent permettre à de grands modèles de langage d'améliorer leurs capacités de génération en exploitant des sources de connaissances externes telles que les moteurs de recherche [13, 23]. En particulier, le retour d'information humain [4, 36, 37] peut être intégré pour aider les modèles à générer des réponses plus précises et plus pertinentes sur le plan contextuel par le biais du cadre RL. En outre, un certain nombre d'approches d'optimisation des requêtes [17, 21, 49] améliorent encore le processus de recherche en permettant à la performance du modèle d'informer le réglage de la requête et, en fin de compte, d'améliorer les résultats pour les tâches en aval. Dans ce travail, nous appliquons une technique RL légère, MCTS, pour optimiser le processus de recherche séquentielle par combinaison de blocs dans les systèmes RAG. Nous introduisons également un agent de configuration pour guider le processus de recherche MCTS. À notre connaissance, il s'agit de la première approche de ce problème particulier.
3 Vue d'ensemble du système
Comme indiqué précédemment, les cadres RAG existants sont confrontés à trois défis majeurs : comment prendre en compte de manière adéquate les associations entre les blocs et la non-monotonicité de l'utilité séquentielle des combinaisons de blocs, et comment s'adapter à différents domaines d'interrogation. Ces défis entraînent une réduction de la pertinence des résultats. Pour résoudre ces problèmes, nous présentons CORAG, un système conçu pour extraire des combinaisons de blocs optimales, en tenant compte à la fois des domaines d'interrogation et des budgets des utilisateurs. La composante la plus importante de notre système est le modèle de recherche de combinaisons de blocs optimales. Le modèle utilise un arbre de politique basé sur le MCTS pour la recherche séquentielle des ordres de combinaison de blocs, ce qui nous permet de prendre pleinement en compte les associations entre les blocs (défi 1) ainsi que la non-monotonicité de l'utilité de l'ordre de combinaison de blocs (défi 2). En outre, nous proposons un module d'inférence de configuration qui recommande les configurations optimales des SCTM et les reclassements pour divers domaines de requête, ce qui permet de relever le défi n° 3. Nous décrivons brièvement ces deux modules ci-dessous.
Recherche de combinaisons optimales de blocs : Une approche directe de la prise en compte des associations de blocs consiste à extraire les blocs potentiels d'une base de données vectorielle (comme indiqué à l'étape 1), puis à explorer de manière exhaustive toutes les combinaisons de blocs possibles. Cependant, cette approche entraîne des temps de latence et des coûts de calcul importants. Pour y remédier, nous construisons un arbre stratégique (voir l'étape 2) qui recadre la recherche de la combinaison optimale de blocs comme un problème de recherche de nœuds dans l'arbre. Plus précisément, le nœud racine de l'arbre stratégique représente un état initial vide, et chaque nœud enfant correspond à une combinaison particulière de blocs. Par exemple, si le nœud racine a des nœuds enfants représentant les blocs χ1, l'un de ses enfants peut représenter la combinaison χ1+χ2, tandis qu'un autre peut représenter χ1+χ3
Nous concevons un algorithme de recherche basé sur les SCTM pour résoudre ce problème. Contrairement aux SCTM traditionnels, notre approche développe le nœud le plus utile à chaque itération tout en évaluant tous les nœuds enfants possibles. En outre, nous prenons en compte les contraintes de coût et de budget pendant la recherche de l'arbre stratégique. Les utilités des nœuds sont calculées en équilibrant l'exploration et le contrôle des coûts, en optimisant l'efficacité et la précision.
Raisonnement de configuration : Une solution simple pour le réglage de la configuration consisterait à énumérer toutes les configurations ou reclassements possibles, à calculer les résultats en parallèle, puis à choisir la meilleure configuration. Toutefois, cela entraînerait un coût irréaliste pour le système RAG. Afin d'optimiser les configurations (c'est-à-dire le nombre d'itérations, le facteur de coût et le facteur d'exploration) pour le processus de recherche par arbre de politique, nous introduisons un agent de configuration qui génère dynamiquement des configurations basées sur le domaine de la requête. Pour garantir l'efficacité du modèle, nous employons une approche d'apprentissage comparative en utilisant des paires d'étiquettes positives et négatives : les étiquettes positives correspondent à des encastrements de requêtes provenant du même meilleur reclassement, tandis que les étiquettes négatives proviennent d'un meilleur reclassement différent. La fonction de perte conjointe est utilisée pour optimiser simultanément la régression (pour le réglage des paramètres) et l'apprentissage par contraste (pour améliorer la discrimination des étiquettes).
Résumé. Le flux de notre cadre est illustré à la figure 2. Nous commençons par générer des encastrements pour la requête d'entrée, puis nous les utilisons pour extraire des blocs potentiels de la base de données vectorielle. Ces encastrements de la requête sont également introduits dans un agent de configuration qui génère dynamiquement une configuration optimale des SCTM basée sur le champ de la requête. En utilisant cette configuration optimale, nous pouvons rechercher dans l'arbre des politiques la combinaison et l'ordre de blocs optimaux à partir des blocs potentiels récupérés. Enfin, cette combinaison de blocs optimale est utilisée pour construire les indices finaux pour les LLM.
4 Recherche de combinaisons de blocs
Comme mentionné précédemment, l'ordre des combinaisons de blocs a un impact significatif sur l'efficacité de la construction d'indices pour les LLM. En raison du nombre considérable de combinaisons potentielles, en particulier lorsqu'un grand nombre de blocs est impliqué, l'énumération de tous les ordres de combinaison de blocs possibles n'est pas réalisable. Dans cette section, nous proposons une nouvelle approche qui réalise un bon équilibre entre l'efficacité et la précision dans le problème de la recherche de l'ordre optimal de combinaison de blocs. Dans la section 4.1, nous modélisons le problème comme la recherche de nœuds optimaux dans un arbre de politique (section 4.1). Nous proposons ensuite un algorithme basé sur les SCTM pour résoudre ce problème de recherche de nœuds (section 4.2).
4.1 Modélisation de la recherche d'arbres stratégiques
Afin de trouver l'ordre combinatoire optimal, la première étape consiste à trouver une structure de données capable d'énumérer efficacement tous les ordres combinatoires possibles. Un choix naturel est un arbre, où en parcourant les nœuds de la racine à la feuille, nous pouvons explorer toutes les réponses potentielles.
Arbre stratégique. Comme le montre la figure 3, nous construisons un arbre stratégique pour représenter l'ordre de toutes les combinaisons de blocs possibles extraites de la base de données vectorielle. Plus précisément, le nœud racine symbolise l'état initial sans aucun bloc, et chaque nœud suivant représente un bloc sélectionné parmi les blocs potentiels. Ainsi, un nœud enfant est généré à partir de son nœud parent en sélectionnant le prochain bloc disponible dans la file d'attente des blocs potentiels et en le fusionnant dans la séquence établie par le nœud ancêtre. Par exemple, si un nœud représente la séquence de combinaison de blocs {χ1}, un nœud enfant peut contenir des séquences de combinaison ultérieures telles que {χ1, χ2}, {χ1, χ3} ou {χ1, χ4}. Par conséquent, nous définissons formellement l'arbre stratégique comme suit :
Définition 4.1 (arbre stratégique). Étant donné une requête q et un ensemble de blocs potentiels {χ1, χ2, ..., χn}, nous construisons un arbre de politique T. Le nœud racine T représente l'état initial sans aucun bloc. , χn}, nous construisons un arbre de politique T. Le nœud racine de T représente l'état initial sans aucun bloc. Chaque nœud non racine suivant contient un ensemble de blocs en fusionnant les blocs nouvellement sélectionnés parmi les blocs potentiels restants dans la séquence de ses nœuds parents. Ce processus construit séquentiellement une combinaison ordonnée de blocs dans chaque nœud non racine, et nous cherchons à trouver le nœud ayant le score d'utilité le plus élevé.
Dans un arbre stratégique, notre objectif est de sélectionner un nœud contenant des blocs ordonnés qui offrent le maximum d'avantages pour le minimum de coûts. Pour y parvenir, nous devons concevoir une fonction de calcul de l'utilité afin d'évaluer le compromis entre les avantages et les coûts. Cette fonction est quantifiée par ce que nous définissons comme "l'utilité du nœud", comme décrit ci-dessous.
Utilité nodale. La mesure de l'utilité se compose de deux éléments : l'avantage dérivé de la sélection d'une combinaison de blocs et le coût de l'utilisation des blocs en tant qu'invites pour les LLM. Plus précisément, les avantages sont quantifiés par les LLM, qui mesurent la similarité entre les blocs sélectionnés et la requête. En particulier, nous les désignons par les valeurs de nœud V. Ensuite, nous utilisons l'algorithme Upper Confidence Bound (UCB) [3] pour équilibrer l'exploitation (valeurs de nœud V(vi)) et l'exploration (comptes de recherche N(vi)) des valeurs de nœud V(vi) et des comptes de recherche N(vi). Pour un nœud donné vi, en ce qui concerne le coût, nous considérons le coût d'étiquetage défini à la section 2 et mesuré par le ratio du coût de la combinaison de blocs actuelle par rapport au budget total alloué B. L'utilité du nœud est donc définie comme suit :
Définition 4.2 (utilité nodale). Compte tenu d'un arbre stratégique et d'un budget de coûts B, l'utilité d'un nœud non racine est définie comme suit :
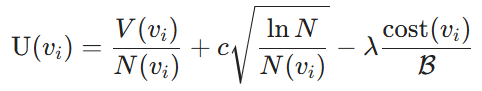
où V(vi) est la valeur estimée du bénéfice de la combinaison de blocs au nœud vi, déterminée par le modèle d'apprentissage, N(vi) est le nombre de visites au nœud vi, qui favorise l'exploration des nœuds moins visités, et N est le nombre total de visites à tous les nœuds de l'arbre de politique pour assurer un équilibre entre l'exploration et l'exploitation. En outre, cost(vi) représente le coût d'étiquetage du nœud vi, B est le budget total d'étiquetage, c régule le compromis exploration-exploitation, et λ sert de facteur de pénalisation des coûts pour améliorer l'efficacité des coûts.
Modélisation de la sélection optimale des nœuds. Sur la base des utilités définies pour les nœuds, la tâche de sélection de l'ordre optimal de combinaison de blocs, telle que décrite à la section 2, est reformulée comme la sélection du nœud optimal dans l'arbre de politique T . Sous une contrainte budgétaire donnée B, l'objectif est d'identifier les nœuds vi ⊆ T pour maximiser l'utilité U(vi) tout en veillant à ce que le coût total associé à vi ne dépasse pas B. Formellement, cela s'exprime comme suit :
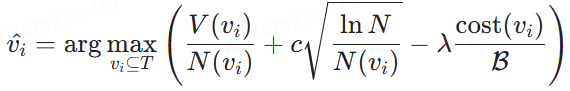
où V(vi) est le bénéfice estimé de la combinaison de blocs au nœud vi et cost(vi) représente son coût associé. Cette formule permet de choisir le bloc qui maximise l'utilité dans un budget donné.
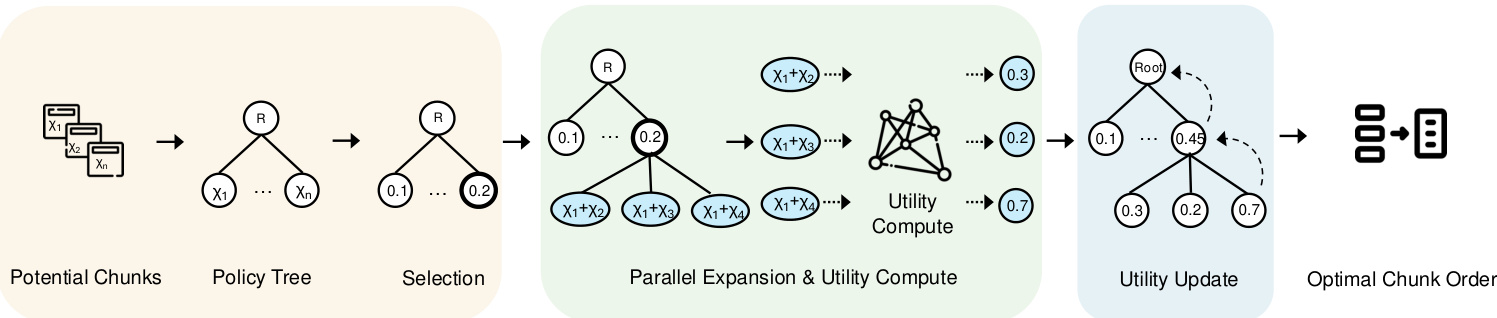
Figure 3 : Processus d'optimisation des blocs basé sur les SCTM

Algorithme 1 Recherche d'arbres stratégiques basée sur les SCTM
4.2 Recherche d'arbres de politique basée sur les SCTM
Motivation. L'énumération de tous les nœuds de l'arbre des politiques permettra de trouver le nœud optimal, mais entraînera un coût de calcul élevé. Pour résoudre ce problème, une approche simple consiste à appliquer une stratégie gourmande qui navigue dans l'arbre de manière itérative en commençant par le nœud racine. À chaque itération, on sélectionne le nœud enfant qui présente le plus grand avantage et on continue jusqu'à ce que le budget soit épuisé. Cependant, cette approche est susceptible de conduire à des résultats sous-optimaux. Par exemple, χ1 peut avoir un avantage légèrement supérieur à χ2, mais χ2 + χ3 peut avoir un avantage significativement supérieur à χ1 + χ3. Dans ce cas, une approche gourmande peut conduire à des résultats sous-optimaux. Il est donc nécessaire de réexaminer le nœud parent à haute efficacité. Dans le même temps, nous devons réduire l'exploration des nœuds à faible bénéfice.
Pour atteindre notre objectif, nous proposons une méthode de recherche par arbre stratégique basée sur les SCTM, conçue pour sélectionner et classer efficacement les combinaisons de blocs. Cette approche explore de manière itérative l'espace des séquences de blocs potentielles, en optimisant une requête donnée dans le cadre d'une contrainte budgétaire spécifiée.
Vue d'ensemble. Les politiques basées sur les SCTM sont décrites dans l'algorithme 1. Nous commençons par initialiser le nœud racine de l'arbre de politique en utilisant des requêtes d'entrée. Lorsque le budget de calcul n'est pas épuisé, nous procédons de manière itérative à deux étapes clés : la sélection des nœuds et la mise à jour de l'utilité. Lorsque la limite d'itération ou le budget est atteint, nous arrêtons le processus et effectuons une recherche récursive dans l'arbre pour trouver le nœud ayant l'utilité la plus élevée. Contrairement aux stratégies MCTS traditionnelles qui se concentrent généralement sur le nœud racine, notre approche prend également en compte les nœuds intermédiaires prometteurs afin de maximiser l'utilité de la combinaison de blocs.
Explication détaillée des principales caractéristiques. Nous expliquons ces deux fonctions clés comme suit :
- Sélection des nœuds (algorithme 2). Nous sélectionnons récursivement le nœud ayant la valeur d'utilité la plus élevée qui est le plus susceptible de conduire à la combinaison de blocs optimale. Plus précisément :

Algorithme 2 Sélection de nœuds

Algorithme 3 UtilityUpdate
- Sélectionner. Nous identifions le nœud ayant la valeur d'utilité maximale. Si 𝑣 n'est pas encore développé, nous générons tous les nœuds descendants possibles et les incluons dans l'arbre stratégique. Si 𝑣 a été développé, nous sélectionnons le nœud descendant ayant l'utilité la plus élevée pour poursuivre l'exploration.
- Extensions. Après avoir sélectionné le nœud présentant l'utilité la plus élevée, nous l'étendons en générant tous les nœuds enfants potentiels. Chaque nœud enfant représente un nouvel ordre de combinaisons de blocs possibles. Notre approche utilise l'expansion parallèle, qui calcule et évalue plusieurs sous-nœuds simultanément. Ce parallélisme exploite la capacité du réseau de valeurs à gérer de multiples combinaisons à un coût de calcul similaire à celui d'un seul nœud, ce qui améliore l'efficacité de la recherche.
- Utilité calculée. Nous calculons la valeur d'utilité de chaque nouveau nœud enfant à l'aide de la formule d'utilité. Le modèle de reclassement R traite plusieurs combinaisons de blocs en parallèle pour générer.

5 Configuration de l'agent
Après avoir examiné l'efficacité du traitement des associations de blocs dans le cadre du budget de l'utilisateur, la tâche restante consiste à concevoir un système adapté au domaine de chaque requête. Le processus des SCTM implique plusieurs configurations clés, notamment la sélection du reclassement, le nombre d'itérations, le facteur d'exploration et le facteur de coût. L'optimisation de ces configurations pour différents types de requêtes est particulièrement difficile. Pour résoudre ce problème, nous proposons un cadre d'agent de configuration qui prédit le reclasseur et la configuration optimaux pour chaque requête. Dans cette section, nous présentons d'abord le cadre de l'agent dans la section 5.1, puis nous décrivons le processus d'apprentissage du modèle dans la section 5.2.
5.1 Cadre de modélisation
Motivation. Pour relever le défi 3, qui consiste à s'adapter au domaine de chaque requête et à recommander des configurations optimales, une solution simple consiste à utiliser un classificateur MLP pour affecter chaque requête à son meilleur reclassement. Cependant, les premières expériences montrent que la classification MLP est peu performante. Après une analyse plus approfondie, nous observons que les types de requêtes similaires ont tendance à partager les mêmes meilleurs reclasseurs et les mêmes configurations. Par conséquent, l'utilisation du réseau siamois avec l'apprentissage par contraste pour rapprocher les requêtes de la même catégorie tout en éloignant les requêtes de catégories différentes est une approche plus réalisable.
La figure 4 donne un aperçu de notre agent configuré, qui se compose de deux modules principaux chargés de transformer l'entrée en un graphe de caractéristiques. Tout d'abord, le module d'intégration de l'entrée génère des intégrations de la requête d'entrée. Ensuite, le réseau d'encodage traite ces encastrements pour produire des cartes de caractéristiques, qui sont ensuite utilisées pour dériver diverses configurations des paramètres des SCTM.
Les sections suivantes décrivent chaque élément en détail et expliquent la raison d'être de sa conception.
(1) Saisir la requête intégrée dans. Afin de capturer efficacement les facteurs des différentes requêtes, étant donné la diversité des types de requêtes tels que les faits explicites, les faits implicites, la rationalité interprétable et la rationalité cachée [47], nous utilisons le modèle d'intégration BGE-M3 [6] pour générer des intégrations pour chaque requête. Ces encastrements améliorent le cadre d'apprentissage en associant des types de requêtes similaires à la même catégorie de reclassement. Représentés dans un espace à 1024 dimensions, les enchâssements capturent les caractéristiques sémantiques sous-jacentes, ce qui permet au réseau de codage de les comparer et de les classer efficacement. Cette étape permet d'améliorer la pertinence de l'extraction des différents types de requêtes. En outre, l'utilisation du même modèle d'intégration génère également des intégrations annotées par le reclassement optimal, y compris leurs caractéristiques uniques et les métadonnées associées, ce qui permet au modèle d'aligner les requêtes sur le reclassement optimal.
(2) Génération de cartes de caractéristiques à l'aide de réseaux codés : la Pour optimiser la tâche de sélection des reclasseurs et recommander le meilleur reclasseur pour chaque requête pour différents types de requêtes, nous utilisons des réseaux de codage pour apprendre efficacement des représentations qui sont utiles à la fois pour la classification et la prédiction de la configuration. Nous utilisons un réseau siamois composé de trois couches entièrement connectées pour cette tâche. Il traite les encastrements de requêtes d'entrée de dimension d = 1024 et apprend les résultats de la classification et les prédictions de configuration des SCTM (c'est-à-dire le nombre d'itérations et λ). Les branches du réseau d'encodage partagent des poids, et chaque branche applique une transformation linéaire suivie d'une activation RELU. La couche de sortie finale fournit des prédictions de classification qui spécifient le meilleur reclassement pour chaque requête, ainsi que des résultats de régression qui sont utilisés pour prédire les configurations MCTS les plus efficaces pour guider le processus de recherche. La sortie de classification identifie le meilleur reclassement pour chaque requête, tandis que la sortie de régression détermine les meilleurs paramètres de configuration des SCTM.
5.2 Formation commune
Dans cette section, nous décrivons le processus de formation pour le développement d'agents de configuration. Comme le montre la figure 4, nous avons mis en œuvre trois tâches de formation conjointes pour améliorer l'efficacité de la formation du modèle. Les deux premières tâches impliquent la classification et la régression pour sélectionner le meilleur reclassement et prédire les meilleures valeurs des hyperparamètres des SCTM, respectivement. En outre, nous avons intégré une approche d'apprentissage comparatif pour améliorer encore le processus d'apprentissage.
5.2.1 Pertes de classification et de régression.
Étant donné l'étiquette de reclassement prédite Y(pred) et son reclassement optimal réel correspondant Y(true), la perte de classification L(cla) est calculée comme suit.
![]()
où F(cla) représente la perte d'entropie croisée entre les étiquettes de reclassement prédites et réelles. Cette fonction de perte permet de classer avec précision le reclasseur optimal pour chaque requête. De même, la perte de régression L(reg) est définie comme suit.
où 𝐹reg est l'erreur quadratique moyenne (EQM) entre le paramètre prédit des SCTM 𝑝pred et le paramètre réel des SCTM 𝑝true. Cette métrique garantit une prédiction précise de la configuration des SCTM en termes de nombre d'itérations et de 𝜆.
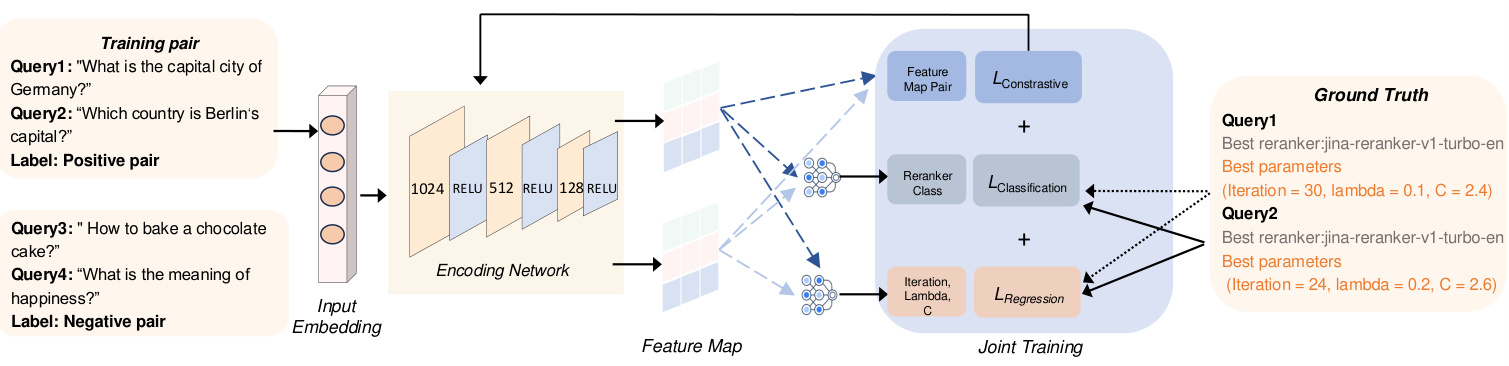
Figure 4 : Présentation de l'agent de configuration
5.2.2 Apprentissage contrastif.
Afin de distinguer efficacement les différents domaines de requête et de recommander la meilleure configuration pour chaque requête, nous utilisons l'apprentissage comparatif pour rapprocher les requêtes d'un même domaine tout en repoussant les enregistrements de différentes classes de reclassement.
Préparation de la comparaison. Afin de préparer l'ensemble de données d'entraînement, nous devons déterminer le reclasseur et la configuration optimaux pour chaque requête. Dans cette étude, les reclasseurs optimaux et les configurations correspondantes pour chaque requête ont été déterminés par des expériences approfondies avec différents paramètres. Par la suite, des paires de requêtes sont générées sur la base de ces annotations de reclassement optimales. Les paires positives sont constituées de requêtes partageant le même reclasseur optimal, ce qui facilite la minimisation de leur intégration dans l'espace des caractéristiques. Au contraire, les paires négatives sont constituées de requêtes ayant des reclasseurs différents, l'objectif étant de maximiser la distance d'intégration entre elles. Étant donné que certains reclasseurs ont des performances similaires pour certaines requêtes, nous ne sélectionnons que les cas où ROUGE-L diffère de plus de 10% pour constituer notre ensemble de données d'entraînement.
Perte de contraste. Comme le montre la figure 4, pour une paire positive donnée (𝑥𝑖, 𝑥+𝑖) et la paire négative (𝑥𝑗, 𝑥-𝑗), nous utilisons d'abord le modèle de codage pour générer les cartes de caractéristiques correspondantes. Ces cartes sont ensuite utilisées pour calculer la perte de contraste 𝐿con. Plus précisément, ce processus peut être représenté comme suit :
Parmi eux.𝑓𝜃(𝑥) désigne la fonction d'intégration.𝐹con est une fonction de similarité appliquée à deux types de paires : les paires positives (avec des reorderers similaires) et les paires négatives (avec des reorderers différents). Cette fonction de perte est conçue pour garantir que les requêtes avec le même reorderer sont plus proches dans l'espace d'intégration et que les requêtes avec des reorderers différents sont plus éloignées.
5.2.3 L'ensemble du processus de formation.
Enfin, la fonction de perte totale L(total) est la somme des pertes de comparaison, de classification et de régression comme suit.
En particulier, la perte de contraste Lcon(θ) incite à rapprocher les enregistrements des requêtes ayant le même reclasseur optimal, tout en éloignant les enregistrements des requêtes ayant des reclasseurs différents. La perte de classification Lcla(θ) aide le modèle à identifier correctement les reclasseurs à l'aide de l'entropie croisée, tandis que la perte de régression Lreg(θ) minimise l'erreur de prédiction de la configuration optimale des SCTM.
Remarques. Une fois la perte totale Ltotal calculée, les paramètres du réseau θ sont mis à jour par descente de gradient à un taux d'apprentissage η. Ce processus d'optimisation est répété sur plusieurs cycles E et lots, ce qui permet d'améliorer à la fois le classificateur et les prédictions des paramètres au fil du temps.
6 expériences
L'étude expérimentale vise à répondre aux questions suivantes.
- RQ1 Comment notre CORAG se compare-t-il à d'autres méthodes dans les pipelines RAG à coûts limités ?
- Quelle est l'efficacité de RQ2 CORAG avec différentes tailles de blocs ?
- QR3 Quels sont les goulets d'étranglement actuels dans le système RAG ?
- Quels sont les goulets d'étranglement dans le système RAG ?
- RQ4 Quelle est l'évolutivité de CORAG en fonction de la taille des ensembles de données ?
- RQ5 Quelle est l'efficacité de chaque modèle dans CORAG ?
6.1 Dispositif expérimental
Environnement. Nous avons intégré notre système au cadre RAG populaire LlamaIndex. Les expériences ont été réalisées sur un serveur Linux équipé d'un CPU Intel Core i7-13700K (12 cœurs, 24 threads, 5,3 GHz), 64 Go de RAM et 1 TiB NVMe SSD. Le module Configuration Agent a été implémenté sur un GPU NVIDIA RTX 4090 équipé de 24 Go de VRAM en utilisant PyTorch 2.0.
Tableau 1 : Données statistiques utilisées dans l'expérience.
| ensemble de données | #rain | #dev | #est | #p |
| MSMARCO | 502,939 | 6,980 | 6,837 | 8,841,823 |
| Wiki | 3,332 | 417 | 416 | 244,136 |
Ensemble de données.Afin d'évaluer les performances de CORAG dans différents scénarios, nous avons mené des expériences sur deux ensembles de données différents axés sur des tâches différentes : (1) WikiPassageQA [7] est un benchmark de questions-réponses contenant 4 165 questions et plus de 100 000 morceaux de texte visant à évaluer la récupération au niveau du paragraphe. (2) MARCO [24] est un ensemble de données complet dédié aux tâches de traitement du langage naturel, avec un accent particulier sur les questions-réponses et la recherche d'informations. Comme le montre le tableau 1, WikiPassageQA et MARCO fournissent tous deux des questions et des annotations de paragraphe de haute qualité, ce qui les rend adaptés à l'évaluation de l'efficacité de la recherche d'informations. Dans nos expériences, nous demandons aux LLM de générer des réponses de référence pour chaque ensemble de données. Par exemple, si nous utilisons Llama3 pour évaluer la performance de CORAG, nous utilisons également Llama3 pour générer des vérités de terrain dans la même configuration expérimentale afin de maintenir l'équité et l'alignement avec les caractéristiques des LLM.
Base de référence.Nous comparons les performances de CORAG à celles de deux modèles de référence de RAG :
- RAPTOR [29] : RAPTOR construit un arbre hiérarchique de résumé de documents en intégrant, en regroupant et en résumant de manière récursive des blocs de texte afin d'obtenir une abstraction à plusieurs niveaux. Cette approche est cohérente avec l'approche basée sur le regroupement décrite à la section 1. Nous achevons la construction de l'arbre en respectant des contraintes budgétaires approximatives.
- NaiveRAG : il s'agit d'une méthode de base pour récupérer les blocs pertinents. Tout d'abord, les blocs candidats sont extraits de la base de données vectorielles sur la base d'une recherche de similarité vectorielle, puis ils sont classés à l'aide du modèle de reclassement. Cette méthode est la méthode AKNN mentionnée à la section 1. Pour satisfaire la contrainte de coût, nous utilisons une stratégie d'allocation de budget avide pour récupérer les blocs jusqu'à ce que le budget soit complètement épuisé.
En outre, nous supprimons l'agent de configuration de notre approche comme référence pour évaluer son impact sur les performances de CORAG, en appelant cette version CORAG sans agent. Enfin, nous mettons en œuvre une approche appelée CORAG Upper, qui établit une limite supérieure en explorant toutes les combinaisons possibles de blocs et en sélectionnant le meilleur ordre. En raison du grand nombre de combinaisons potentielles, dans le cas de CORAG Upper, nous limitons l'exploration aux combinaisons de moins de six blocs.
Remarques.D'autres approches, telles que GraphRAG [22], s'appuient fortement sur des appels fréquents aux LLM pour résumer les blocs et construire des index, ce qui entraîne des coûts énormes (par exemple, des milliards de jetons) qui dépassent nos contraintes strictes en matière de coûts. Par conséquent, ces approches ne sont pas réalisables pour résoudre notre problème. Pour une comparaison équitable, nous avons exclu ces types d'approches RAG de nos expériences.
Paramétrage des hyperparamètres : les hyperparamètres pour CORAG sont déterminés automatiquement par l'agent de configuration, tandis que NaiveRAG ne requiert aucun hyperparamètre. Pour les autres méthodes de base, nous assurons la cohérence en utilisant les mêmes hyperparamètres pour des comparaisons équitables. Plus précisément, nous avons fixé le facteur d'exploration à 2,4, le nombre d'itérations à 10 et le facteur de coût λ à 0,1. Nous mènerons également d'autres études d'ablation pour valider ces paramètres.
Paramètres d'apprentissage. Dans notre approche, l'agent de configuration est formé à l'aide de l'apprentissage par contraste. Les hyperparamètres utilisés dans ce processus comprennent la perte de contraste (margin=1,0), le taux d'apprentissage (lr=0,001), la taille du lot (32), le nombre de cycles (num_epochs=60) et le modèle d'intégration (c.-à-d. BAAI/bge-m3 [6]).
Mesures d'évaluation. Nous évaluons l'efficacité en comparant les scores Rouge des réponses réelles et des réponses générées, en utilisant Rouge-1, Rouge-2 et Rouge-L comme mesures d'évaluation. Pour évaluer l'efficacité, nous mesurons le temps de latence nécessaire pour répondre aux requêtes en utilisant différentes méthodes.
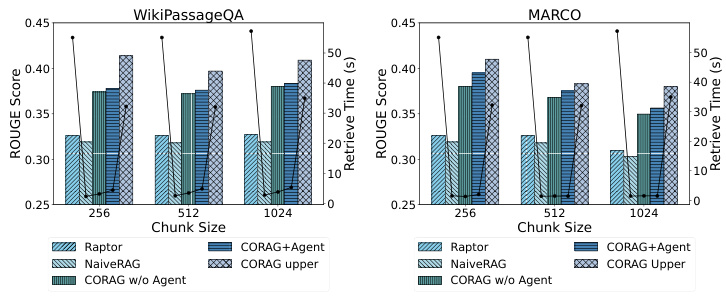
Figure 5 : Comparaison de l'efficacité
6.2 Comparaison des performances
6.2.1 QR1 : Comparaison des rouges.
Comme le montre la Fig. 2, nous comparons la performance de CORAG avec plusieurs baselines sur différents ensembles de données, principalement en utilisant WikiPassageQA et MARCO. l'évaluation est effectuée à trois tailles de blocs différentes, en utilisant les métriques Rouge-1, Rouge-2, et Rouge-L pour évaluer l'amélioration des réponses générées par LLM en raison de notre méthode de recherche. corag se compare aux méthodes RAG traditionnelles (par exemple, NaiveRAG et RAPTOR) par une amélioration significative d'environ 251 TP3 T. Sans surprise, CORAG ne dépasse pas la limite supérieure, ce qui représente un cas extrême de notre méthode de recherche. CORAG se compare aux méthodes RAG traditionnelles (par exemple, NaiveRAG et RAPTOR) avec une amélioration significative d'environ 251 TP3 T. Sans surprise, CORAG ne dépasse pas la limite supérieure, qui représente un cas extrême où tous les ordres de combinaison possibles sont énumérés de manière exhaustive, ce qui est clairement inefficace et impraticable. En conclusion, CORAG est plus performant que la solution de base, améliorant la pertinence de la recherche tout en élaguant efficacement l'espace de recherche.
6.2.2 QR2 : évaluation de l'efficacité.
Comme le montre la figure 5, CORAG étant basé sur un algorithme de recherche arborescente, l'agent aide à prédire le meilleur reclassement et les meilleurs paramètres pour une requête donnée. Il est donc essentiel d'évaluer l'impact des différentes tailles de blocs et des différents ensembles de données sur l'efficacité de la tâche d'optimisation de la recherche. Nous avons testé l'efficacité en utilisant différents ensembles de données et tailles de blocs et nous avons observé que NaiveRAG, qui utilise des méthodes de recherche traditionnelles, permet d'obtenir des temps de recherche plus courts, mais des scores de Rouge plus faibles. De même, RAPTOR utilise un LLM externe pour le résumé et fait preuve d'une efficacité médiocre. En revanche, notre approche CORAG réalise un compromis efficace entre l'efficacité et la pertinence de la recherche.
6.2.3 QR3 : Décomposition des performances.
Nous présentons une décomposition des performances de la base NaiveRAG afin de mettre en évidence les goulets d'étranglement des systèmes RAG actuels. Pour relever le défi de la recherche de l'ordre optimal des combinaisons de blocs, la mise en œuvre à l'aide de NaiveRAG nécessite les étapes suivantes : a) l'obtention de l'intégration des requêtes, b) la récupération des combinaisons de blocs potentielles, c) le reclassement des combinaisons de blocs potentielles et d) l'affinement de l'indice. La figure 6 indique la latence moyenne de chaque étape, dans la configuration expérimentale précédente.
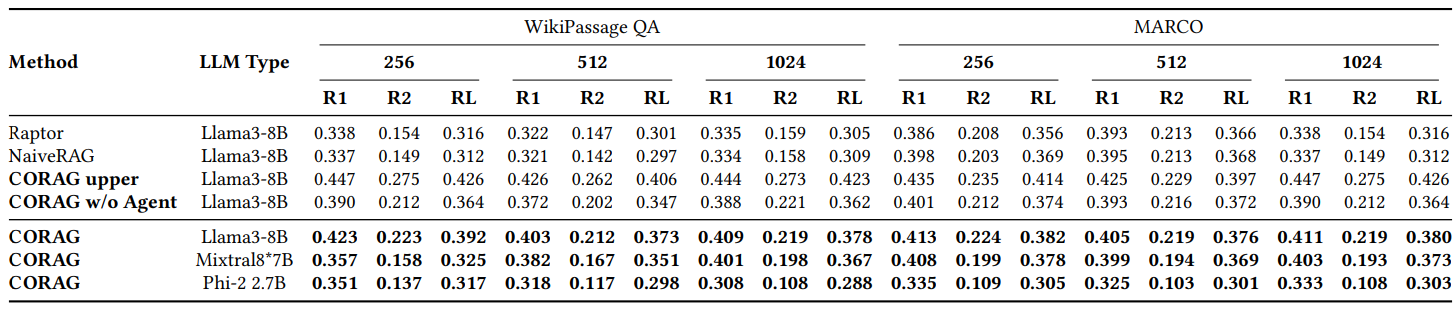
Tableau 2 : Comparaison de Rouge sur les ensembles de données WikiPassage QA et MARCO
6.2.4 QR4 : évaluation de l'évolutivité
CORAG présente une excellente évolutivité, en particulier lorsqu'il travaille avec de grands ensembles de données (tels que WikiPassageQA et MARCO) qui contiennent un grand nombre de paragraphes. Le nombre de morceaux peut être facilement porté à 100 000 ou plus en divisant chaque paragraphe en 256 morceaux étiquetés. Malgré l'augmentation significative du volume de données, notre temps de recherche n'augmente que de 101 TP3T par rapport à l'approche traditionnelle, ce qui démontre l'efficacité de notre système dans la gestion des tâches de recherche à grande échelle. Notamment, notre système surpasse l'approche CORAG Upper, ne nécessitant qu'un dixième du temps de recherche tout en fournissant des scores ROUGE compétitifs. Cet équilibre efficace entre les performances et la charge de calcul met en évidence la capacité du système à élaguer efficacement l'espace de recherche, garantissant ainsi une recherche rapide, même dans des ensembles de données très vastes. Notre approche est donc bien adaptée aux scénarios nécessitant le traitement de données à grande échelle et une grande précision de recherche.
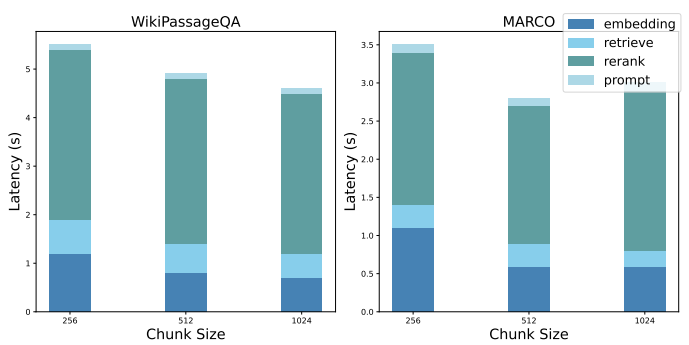
Figure 6 : Décomposition des performances
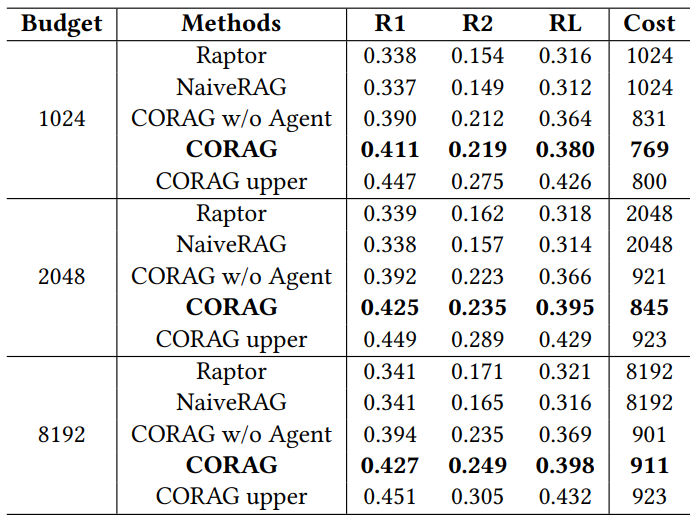
Tableau 3 : Comparaison des performances pour différents budgets
6.3 QR5 : études d'ablation
6.3.1 Études d'ablation avec différents budgets
Comme le montre le tableau 3, nous avons évalué CORAG en tant que système à coût limité et étudié l'impact de différents budgets sur les performances globales. En utilisant l'ensemble de données MARCO, nous avons fixé les limites budgétaires à 1024, 2048 et 8192 jetons et évalué les résultats à l'aide de ROUGE. Notamment, le coût moyen de marquage de CORAG reste inférieur à chaque limite budgétaire, ce qui suggère que l'utilité des blocs n'est pas monotone, comme cela a été mis en évidence dans le défi 2. Au fur et à mesure que le budget augmente, CORAG bénéficie d'un espace de recherche élargi et est capable d'inclure plus d'informations pertinentes, plutôt que d'augmenter simplement le nombre de blocs.
6.3.2 Études d'ablation avec différents coefficients d'exploration
Comme le montre la figure 7, nous avons mené une étude d'ablation pour évaluer l'impact de différents coefficients d'exploration sur les performances du système, en testant en particulier des valeurs de C de 0, 1, 2 et 3. Les résultats montrent qu'un coefficient d'exploration d'environ 2 fournit les meilleures performances, en atteignant un équilibre optimal entre l'exploration et l'exploitation au cours du processus de recherche. Cet équilibre permet au système de découvrir efficacement des informations pertinentes tout en se concentrant sur les blocs à fort potentiel, ce qui permet d'améliorer la réponse du RAG. En revanche, des coefficients d'exploration plus faibles ont conduit à des résultats sous-optimaux en raison d'une sous-exploration, tandis que des coefficients d'exploration plus élevés ont conduit à des résultats sous-optimaux en raison d'un détournement excessif de l'attention. Ces résultats soulignent le rôle critique du coefficient d'exploration dans la performance du processus de recherche CORAG et mettent en évidence l'importance d'un réglage minutieux des paramètres.
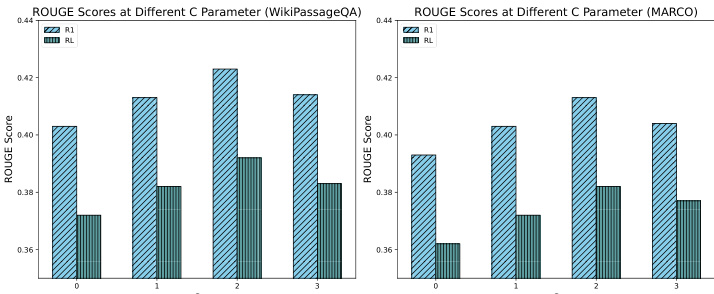
Figure 7 : Comparaison de ROUGE entre différentes valeurs de C
6.3.3 Études d'ablation avec différents facteurs de coût
Comme le montre la figure 8, une étude d'ablation a été menée pour évaluer l'impact de différents coefficients de coût sur les performances du système, en testant en particulier les valeurs 0, 0,1, 0,2 et 0,3. Cette diminution est due au fait qu'en l'absence de contrainte de coût, CORAG a tendance à produire des résultats plus longs, bien qu'au détriment de la rentabilité. Cependant, malgré la légère diminution des scores ROUGE, la diminution reste dans les 51 TP3T, ce qui est acceptable. Ces résultats soulignent l'importance d'un réglage efficace des coefficients de coût pour équilibrer la richesse des résultats et les contraintes de coût, ce qui met encore plus en évidence le rôle de notre agent de configuration pour permettre un réglage efficace de la configuration afin d'optimiser les performances de CORAG.
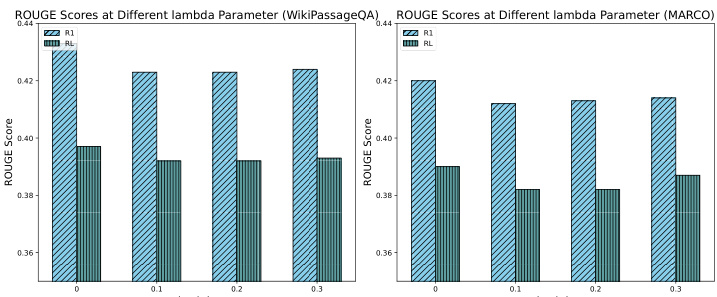
Figure 8 : Comparaison de ROUGE pour différentes valeurs de lambda
6.3.4 Études d'ablation avec différents réarrangeurs
Afin d'évaluer l'impact des différents réarrangeurs sur les performances de récupération, nous avons mené une étude d'ablation en utilisant six modèles de réarrangeurs largement reconnus : jina-reranker-v1-turbo-en, jina-reranker-v2-base-multilingue, bge-reranker-v2-m3, bge- reranker-large, bge-reranker-base et gte-multilingual-reranker-base. ces réarrangeurs ont été évalués sur l'ensemble de données MARCO à l'aide du modèle llama3-8B configuré avec un facteur de coût fixe de 0,1, un facteur d'exploration de 2,4 et une contrainte budgétaire de 1024.
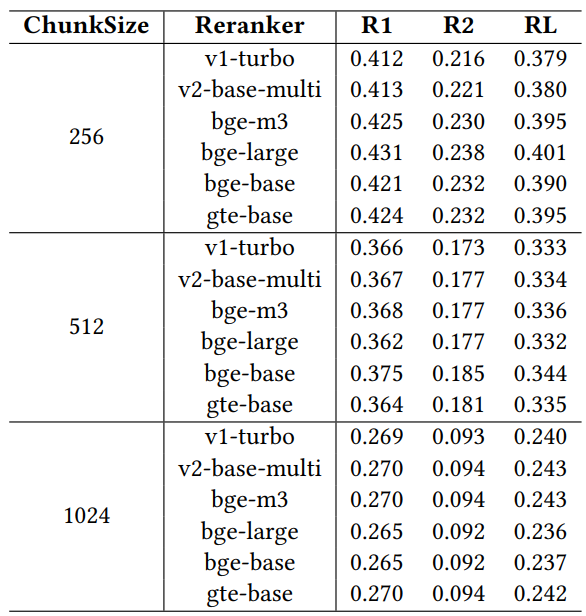
Tableau 4 : Comparaison des performances avec différents réorganisateurs
Les résultats du tableau 4 montrent qu'il existe des différences de performance entre les différents réarrangeurs, ce qui souligne l'importance d'une sélection minutieuse des réarrangeurs pour optimiser la performance du système RAG dans le cadre de contraintes opérationnelles spécifiques. Parmi les réarrangeurs, gte-multilingual-reranker-base et bge-reranker-large affichent des performances constamment élevées pour la tâche d'assurance qualité, ce qui suggère que ces modèles de réarrangement sont très efficaces pour capturer les informations pertinentes pour les différentes requêtes d'assurance qualité. Nous observons qu'au fur et à mesure que la taille du bloc augmente dans l'étude d'ablation, chaque reclassement individuel est moins performant que l'agent en termes de reclassements recommandés pour différentes requêtes. Cela suggère que l'agent de configuration exploite efficacement la diversité des réorganisateurs en ajustant dynamiquement la configuration pour améliorer les résultats de recherche. La capacité de l'agent de configuration à recommander de meilleurs choix de réarrangement et de meilleures configurations de paramètres met en évidence son rôle dans l'optimisation des performances du système RAG, en particulier sous des contraintes telles qu'un budget limité.
6.4 Études de cas
La figure 9 montre trois exemples comparant la qualité d'extraction de CORAG et de l'approche traditionnelle NaiveRAG, en soulignant pourquoi notre approche est plus performante que l'approche de base. En raison de sa simple recherche top-k et de son réordonnancement, NaiveRAG passe souvent à côté d'informations importantes relatives à l'intention de la requête, car il récupère généralement des morceaux sur la base de la correspondance des mots-clés plutôt que sur la pertinence par rapport à la requête. Par exemple, pour la requête "Les fleurs à feuilles sont-elles des arbustes ?" NaiveRAG récupère le contenu qui contient les mots-clés correspondants, mais ne fournit pas la classification réelle de la fleur feuillue. En revanche, la stratégie de combinaison de blocs de CORAG récupère un contexte qui inclut la catégorie de la fleur à feuilles, ce qui permet à LLM de donner une réponse plus précise. Dans un autre cas, NaiveRAG a récupéré des termes et des clauses juridiques comprenant "oxyfluorfen" mais n'a pas compris l'intention de la requête, alors que CORAG a fourni un contenu liant l'oxyfluorfen à des cas d'utilisation dans le coton, ce qui a nécessité une recherche que la stratégie de combinaison de blocs de NaiveRAG n'a pas permis d'effectuer. La recherche de similarité vectorielle de NaiveRAG ne pouvait pas saisir les relations logiques entre les blocs. Enfin, pour la question "D'où viennent les bactéries ? NaiveRAG retrouve les blocs contenant le mot-clé "bactéries" mais n'aborde pas leur origine, alors que CORAG fournit une réponse plus complète, incluant la source des bactéries et leurs conditions de reproduction. Ces cas illustrent le fait que CORAG excelle dans la récupération d'informations logiquement connectées, ce qui le rend plus adapté que NaiveRAG pour les requêtes qui nécessitent plus qu'une simple correspondance de mots-clés.

Figure 9 : Étude de cas CORAG
7 Aperçu du RAG et des options de conception futures
7.1 Insuffisances du système RAG actuel
Nous fournissons une analyse du système RAG actuel, révélant les défis de performance rencontrés pendant les phases de recherche (S1), d'amélioration (S2) et de génération (S3).
S1 : Frais généraux de recherche Les systèmes RAG actuels utilisent généralement des LLM pour les structures de résumé et d'indexation, en ignorant les coûts de calcul associés aux LLM externes, ce qui augmente les frais généraux de calcul. Les réorganisateurs basés sur des modèles, tout en améliorant la pertinence lors de la recherche, introduisent un temps de latence important, ce qui peut entraver l'efficacité contextuelle sensible à la latence. La construction d'index rentables et les optimisations de réordonnancement sont essentielles pour équilibrer l'efficacité et la performance.
S2 : Amélioration des frais généraux Les techniques de post-récupération, telles que l'optimisation de l'ordre des combinaisons de blocs, améliorent la pertinence contextuelle mais nécessitent des calculs supplémentaires. Les stratégies d'élagage qui minimisent l'espace de recherche et optimisent l'ordre des combinaisons sont essentielles pour équilibrer les coûts de calcul et améliorer la pertinence contextuelle. L'optimisation des combinaisons de blocs en mettant l'accent sur l'ordre et la cohérence est essentielle pour réduire les coûts et améliorer les performances de recherche.
S3 : Frais généraux de génération L'ingénierie efficace des indices pour les combinaisons de blocs optimales nécessite des ressources informatiques considérables. Le raffinement et la compression des indices spécifiques aux requêtes sont essentiels pour réduire les frais généraux tout en maintenant la pertinence et la concision des entrées. Des stratégies adaptatives permettant de gérer différents types de requêtes et d'exigences spécifiques à un domaine garantissent l'efficacité des messages-guides sans compromettre la qualité des résultats.
7.2 Options de conception
Pour relever les défis susmentionnés, les choix de conception suivants visent à optimiser les performances du système RAG :
P1 : Co-conception des processus de recherche et de réorganisation Dans CORAG, l'extension parallèle de la recherche arborescente accélère le traitement des requêtes et réduit considérablement le temps de latence en permettant la recherche et le réordonnancement simultanés. Les optimisations futures peuvent s'attaquer au goulot d'étranglement en éliminant les retards spécifiques aux étapes et en améliorant encore l'efficacité du classement. Cette approche de co-conception gère efficacement l'ordre de combinaison des blocs afin d'améliorer le processus de classement et la notation associée.
P2 : Optimisation des structures arborescentes et des itérations de recherche Les résultats montrent que des stratégies plus courtes améliorent l'efficacité de la recherche en réduisant les frais généraux de calcul, ce qui est particulièrement bénéfique pour les grands ensembles de données. La minimisation de la hauteur de l'arbre dans la recherche arborescente améliore la vitesse de recherche des blocs contextuellement pertinents, en réduisant de manière significative la latence et les coûts de calcul. Cette approche d'optimisation améliore les performances du système RAG sur les grands ensembles de données.
P3 : Projet de pointe dynamique La sélection du réarrangeur en fonction du type de requête et l'utilisation de modèles d'indices adaptatifs peuvent améliorer la pertinence de la recherche de LLM. Les structures de repères dynamiques alignées sur l'intention de la requête et le contexte spécifique au domaine peuvent maintenir la qualité de la sortie dans les limites des ressources. Cette approche d'ingénierie adaptative des indices permet d'atteindre un équilibre efficace entre l'efficience et la qualité de la recherche, en tenant compte de la nature dynamique des requêtes dans les systèmes RAG.
8 Conclusion
Compte tenu de la non-monotonicité de l'utilité des blocs, de la corrélation entre les blocs et de la diversité des différents domaines de recherche, nous proposons CORAG, un système d'optimisation de la recherche basé sur l'apprentissage.Initialement, nous modélisons l'ordre des combinaisons de blocs comme un arbre de politiques et explorons cet arbre à l'aide de MCTS, dans le but de trouver l'ordre optimal des combinaisons de blocs. Nous introduisons un agent de configuration qui prédit avec précision la configuration et le réarrangeur optimaux pour une requête donnée. En outre, nous concevons une stratégie d'expansion parallèle des requêtes afin d'étendre plusieurs nœuds à chaque itération. Les résultats expérimentaux montrent que notre approche est nettement plus performante que les approches de pointe dans le respect des contraintes de coût et qu'elle excelle également en termes d'efficacité.
© déclaration de droits d'auteur
Article copyright Cercle de partage de l'IA Tous, prière de ne pas reproduire sans autorisation.
Articles connexes

Pas de commentaires...