BoT : Amélioration de la pensée : résoudre les problèmes d'essai et d'erreur avec de grands modèles linguistiques

résumés

Les performances de raisonnement des grands modèles de langage (LLM) sur un large éventail de problèmes reposent fortement sur des messages-guides de réflexion en chaîne, ce qui implique de fournir des démonstrations de réflexion en chaîne comme exemples dans les messages-guides. Des recherches récentes, par exemple sur les arbres de pensée, ont souligné l'importance de l'exploration et de l'auto-évaluation dans la sélection des étapes de raisonnement lors de la résolution de problèmes complexes. Dans cet article, nous proposons un cadre d'incitation automatisé appelé Boosting of Thoughts (BoT) qui explore et auto-évalue de manière itérative un grand nombre d'arbres de réflexion afin d'obtenir une collection d'expériences de raisonnement par essais et erreurs, qui servira de nouvelle forme d'incitation pour la résolution de problèmes complexes. A partir de simples indices qui ne nécessitent pas d'exemples, BoT explore et évalue itérativement un grand nombre d'étapes de raisonnement et, plus important encore, révise explicitement les indices en utilisant les analyses d'erreurs de LLM pour augmenter la génération d'étapes de raisonnement jusqu'à ce qu'une réponse finale soit obtenue. Nos expériences utilisant GPT-4 et Llama2 sur un large éventail de problèmes mathématiques complexes montrent que BoT atteint systématiquement des taux de résolution de problèmes plus élevés ou comparables à ceux des autres méthodes d'indication de l'état de l'art. Le code source est disponible à l'adresse suivante : https://github.com/iQua/llmpebase的examples/BoTReasoning文件夹下获得.

1. introduction

Les grands modèles de langage (LLM) avec un paradigme autorégressif ont atteint des performances significatives sur une variété de tâches en raison de leurs capacités potentielles de raisonnement. L'assurance de cette capacité dans des tâches complexes repose fortement sur des indices de raisonnement en chaîne (CoT), qui fournissent des exemples de raisonnement étape par étape. Cette approche suggère que la capacité de raisonnement peut être stimulée par une série de réflexions, où la réflexion agit comme une étape intermédiaire dans la résolution de problèmes.

En conséquence, des études de suivi, en particulier l'Arbre de la pensée (ToT), ont suggéré des moyens d'améliorer le CoT. Pour garantir la validité, les messages-guides de ces méthodes comprennent généralement des annotations humaines pour des tâches spécifiques. Cette dépendance limite leur évolutivité. Les travaux récents, qui utilisent les LLM pour une double vérification afin d'améliorer les réponses, ou qui améliorent les messages-guides en fonction du retour d'information, se sont révélés très prometteurs. La littérature existante privilégie généralement l'élimination des raisonnements non valides dans les messages-guides. Cependant, les humains peuvent généralement apprendre en continu en analysant soigneusement leurs erreurs, ce qui leur permet d'acquérir de l'expérience et d'améliorer progressivement leurs performances. Par conséquent, nous posons la question suivante : la génération de pensée des LLM peut-elle être libérée des annotations humaines et imiter la résolution de problèmes humains pour un raisonnement efficace dans une variété de tâches ?

Dans cet article, nous proposons un nouveau cadre, illustré à la figure 1, appelé Boosting of Thoughts (BoT), qui met en œuvre un mécanisme de boosting, comprenant l'agrégation et l'expérience, afin d'améliorer progressivement les étapes de raisonnement peu fiables (pensée faible) en apprenant des erreurs, et finalement de résoudre divers problèmes. À partir d'un simple indice sans annotation humaine, le BoT peut avoir un raisonnement faible. Grâce à l'agrégation, le BoT est en mesure d'en tirer des chaînes de pensée plus logiques et plus efficaces qui guident les améliorations ultérieures. Dans notre cadre, cette orientation est obtenue en adaptant les conseils, qui sont des rapports d'erreur détaillés, des suggestions et des conseils pour chaque étape de raisonnement obtenue en analysant les chaînes agrégées à l'aide de LLM. Au fur et à mesure que l'expérience s'accumule dans les messages-guides, elle conduit progressivement à un raisonnement plus solide.

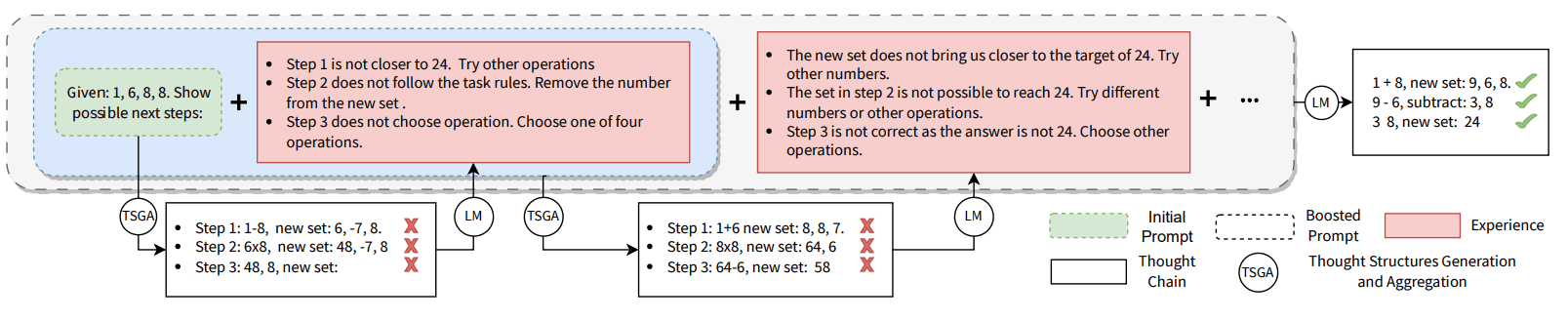
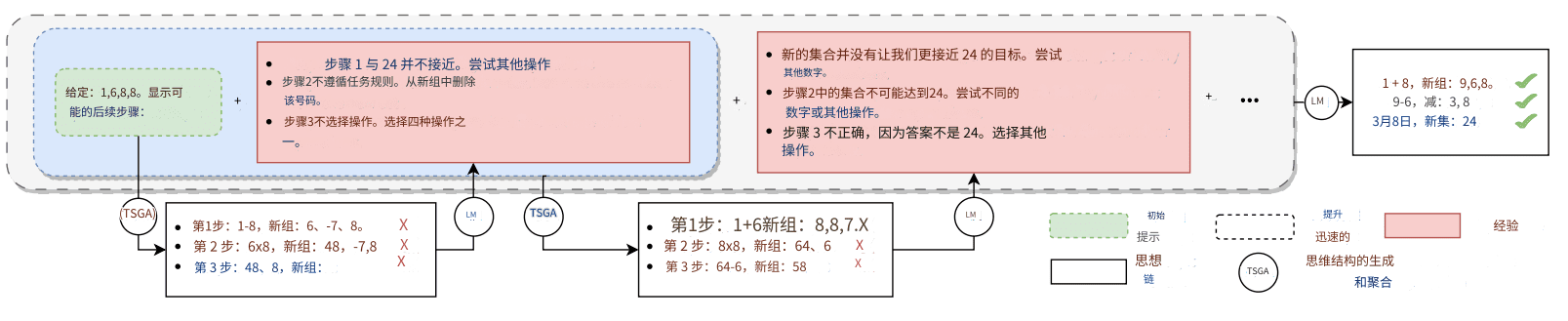
Figure 1 : Amélioration des indices en augmentant progressivement l'expérience, qui consiste en une analyse des chaînes de pensée générées par un grand modèle de langage (LLM ou LM). L'expérience contient explicitement la chaîne de pensée elle-même, le rapport d'erreur correspondant et des suggestions détaillées pour réviser chaque étape du raisonnement. Ainsi, les pensées invalides marquées d'une croix rouge peuvent également contribuer à l'amélioration des messages-guides. En accumulant de l'expérience dans les messages-guides, la BoT peut finalement générer des chaînes de pensée correctes à partir de messages-guides simples. L'exemple présenté ici est le résultat obtenu en appliquant le GPT-4 avec la BoT à une tâche de jeu en 24 points.

Plus précisément, BoT met en œuvre un tel mécanisme de renforcement sous la forme d'un processus itératif axé sur l'expérience, comme le montre la figure 1. A chaque itération, pour un indice donné, BoT construit un grand nombre de structures de pensée simples en parallèle avec LLM. Nous avons choisi la structure arborescente, comme indiqué dans ToT, mais pour nos besoins de stimulation, nous l'avons modifiée de manière significative pour en faire un arbre binaire pondéré avec différentes stratégies de croissance. Après avoir extrait les scores les plus élevés des branches de la racine à la feuille de chaque arbre, le composant d'agrégation de BoT a été exécuté pour les agréger en une seule chaîne de pensées. Cette chaîne a ensuite été évaluée par le même LLM pour en tirer des enseignements, qui ont été ajoutés aux messages-guides pour guider la génération de pensées lors de l'itération suivante.

Notre contribution peut être résumée de trois manières. Premièrement, contrairement à la génération de structures de pensée plus complexes à l'aide d'invites élaborées, cet article montre qu'en s'appuyant uniquement sur des invites initiales simples, les pensées faibles peuvent être améliorées progressivement pour résoudre des problèmes sur la base de l'expérience antérieure. Deuxièmement, pour mettre en œuvre ce mécanisme d'amélioration, nous proposons un nouveau cadre appelé Boosting of Thoughts (BoT), qui exécute un processus itératif basé sur l'expérience. Puisqu'il commence par des invites simples, le BoT peut être étendu à une variété de tâches. Tout en garantissant la validité, BoT est rapide car il construit des structures de pensée simples en parallèle et converge vers une solution après quelques itérations. Enfin, nous avons évalué les performances de la BoT sur des problèmes mathématiques complexes en utilisant GPT-4 et LlamaV2. En nous appuyant sur GPT-4 OpenAI (2023) et LlamaV2 Touvron et al. (2023), nous avons évalué la performance de BoT sur des problèmes mathématiques complexes. Les taux de résolution des problèmes montrent que BoT avec une structure d'esprit d'arbre binaire surpasse significativement l'état de l'art actuel sur GSM8K et AQuA, tout en obtenant des résultats de deuxième ordre sur d'autres ensembles de données. En particulier, BoT surpasse la méthode leader ToT de 9,7% sur la nouvelle tâche difficile Game of 24. Notre BoT démontre donc que les LLM peuvent maintenir une haute performance sur une large gamme de tâches même sans annotations humaines en augmentant les indices, en accumulant des analyses d'erreurs sur les chaînes de pensée invalides, et en faisant des suggestions correspondantes.

2. travaux connexes

inférence en plusieurs étapes.. Des travaux importants sur les invites de pensée en chaîne (CoT) suggèrent que le comportement de raisonnement par étapes des LLM peut être stimulé en fournissant des étapes de raisonnement intermédiaires dans chaque invite de problème. Un travail récent, Tree of Thought (ToT), convertit le processus de raisonnement séquentiel en une structure arborescente dans laquelle chaque pensée (nœud) peut prendre en compte des chemins de raisonnement antérieurs pour générer de multiples pensées suivantes. Grâce au retour en arrière et à l'exploration étendue au cours du processus de raisonnement, ToT donne de bons résultats sur des problèmes qui défient même le GPT-4. Compte tenu de sa grande capacité, la structure de pensée sous-jacente de BoT utilise largement la structure d'arbre de pensée de ToT. En outre, en raison du cadre de stimulation, la structure arborescente générée par BoT à chaque itération est binaire et peu profonde, plutôt que l'arbre complexe de ToT dans lequel chaque nœud correspond à un grand nombre de nœuds enfants. Cependant, la structure sous-jacente n'est pas limitée à la ToT. En revanche, la BoT est flexible car la structure de pensée sous-jacente peut être ToT, GoT Besta et al. (2023), ou CR Zhang et al. (2023b), où Thinking Graphs (GoT) Besta et al. (2023) est le travail le plus récent qui étend la structure de pensée à un format graphique. Dans le présent document, nous nous concentrerons uniquement sur la ToT en tant que structure de pensée sous-jacente et nous laisserons l'utilisation de GoT pour les travaux futurs.

auto-suggestion. Le fait de libérer les humains des messages-guides spécifiques à une tâche attire beaucoup d'attention. Afin de garantir la capacité de raisonnement des LLM, les CoT traditionnels s'appuient sur les connaissances a priori des humains pour générer manuellement des démonstrations spécifiques à la tâche en tant qu'invites. Cependant, le CoT zéro a montré que même sans exemples générés manuellement, les LLM étaient capables de raisonner étape par étape pour obtenir des réponses précises en ajoutant simplement "réfléchissons étape par étape" aux messages-guides. Ces observations ont donné lieu à une série d'études de suivi.Auto-CoT élimine l'effort manuel en récupérant la chaîne de raisonnement utilisable générée par zéro CoT.Active-Prompt mesure d'abord l'incertitude d'un ensemble de questions, et sélectionne donc uniquement les questions incertaines à annoter par un humain.ToT réduit également l'effort manuel mais, pour chaque tâche, il exige toujours que l'expert fournisse dans le message-guide le raisonnement suivant possible. possible. Notre article présente une nouvelle approche du boosting manuel sans repère. En partant d'un simple indice, BoT l'améliore de manière itérative en se basant sur l'analyse de la pensée par les LLM.

L'ingénierie des conseils grâce au retour d'information. L'utilisation des réponses des MFR aux invites d'entrée comme retour d'information pour les révisions ultérieures de l'invite a suscité beaucoup d'intérêt. Ceux qui révisent continuellement un indice donné sur la base de la description évaluée de la sortie par les LLMs visent à obtenir des réponses précises. En utilisant une idée de haut niveau similaire à notre article, SELF-REFINE propose un algorithme itératif d'auto-raffinement qui permet aux LLM de générer un retour d'information pour affiner leur résultat.PHP simplifie ce processus en ajoutant la solution de la réponse précédente directement comme un indice pour les indices suivants.REFINER, également lié à notre article, évalue chaque étape d'inférence comme un retour d'information pour produire une réponse plus raisonnable. plus raisonnable. Une autre série d'études a exploré l'intégration, en particulier l'utilisation de mécanismes de renforcement Freund et al. (1996) ont affiné les indices avec un retour d'information à partir d'un ensemble d'exemples. Ils ont adapté l'invite en ajoutant plusieurs exemples incertains à l'itération précédente, ou se sont appuyés sur un processus de rétroaction-réflexion-affinement.APO Pryzant et al. (2023) ont affiné les invites de manière itérative, en utilisant les performances de l'invite précédente pour former un langage naturel optimisé. Ces travaux démontrent l'efficacité des mécanismes de renforcement dans l'ingénierie des indices. Cependant, notre travail est le premier à souligner l'importance de l'analyse des erreurs dans l'amélioration des indices pour générer des chaînes d'inférence efficaces. Le BoT proposé étend cette idée à un cadre d'aide automatisé en accumulant de manière itérative une collection d'expériences de raisonnement par essais et erreurs.

3. l'amélioration de la réflexion

3.1 Contexte

L'objectif de l'ingénierie des signaux est de concevoir un signal I contenant plusieurs séquences linguistiques à utiliser comme entrée par le biais de ce signal, et un grand modèle linguistique (LLM) pré-entraîné, noté pθ, paramétré par θ, qui donne accès aux séquences linguistiques souhaitées y. Ainsi, l'entrée-sortie (IO) standard peut être exprimée comme y ∼ pθ (y|I (X, Q)), où I (-) désigne le signal enveloppant l'instruction de tâche X et la question correspondante Q, et où I (-) désigne l'instruction de tâche X. la question correspondante Q.

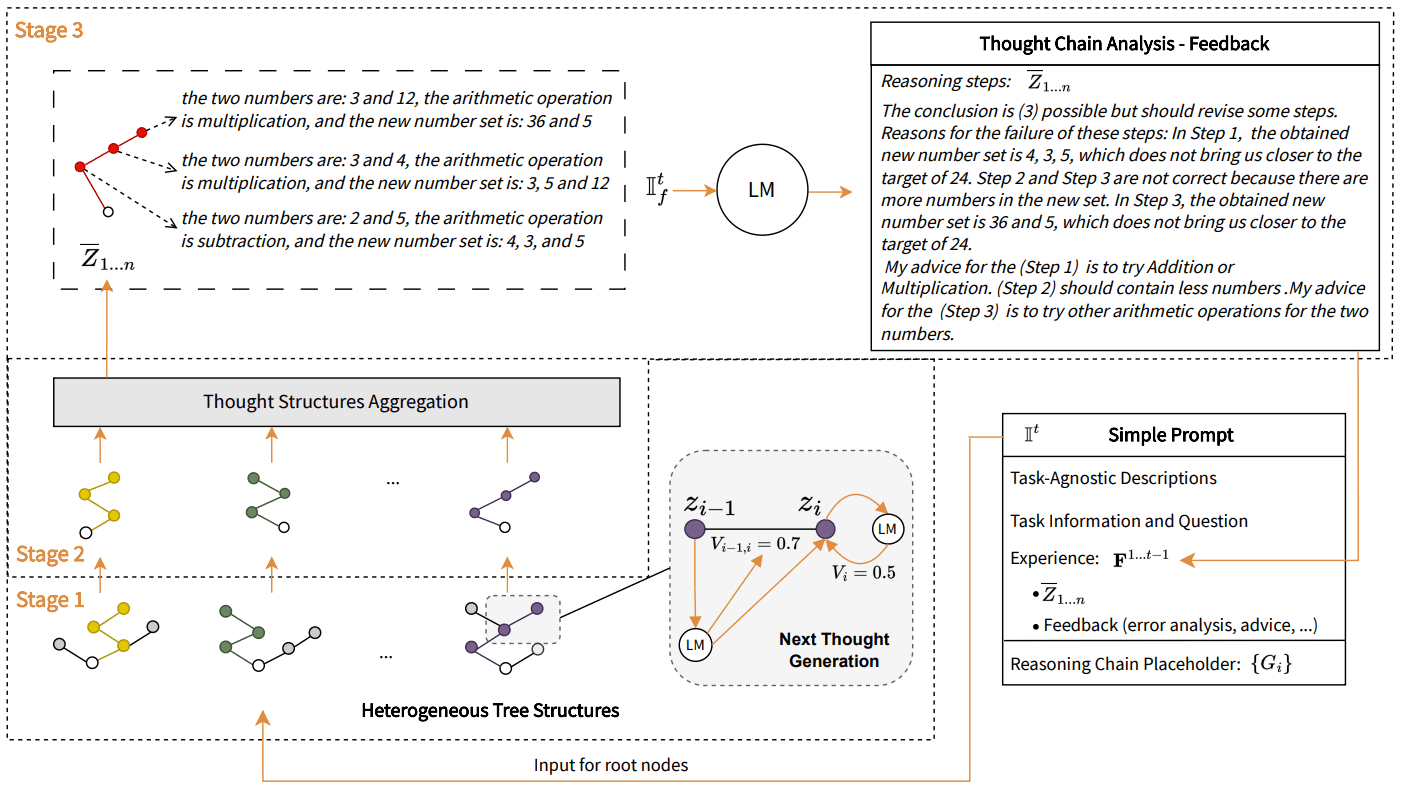
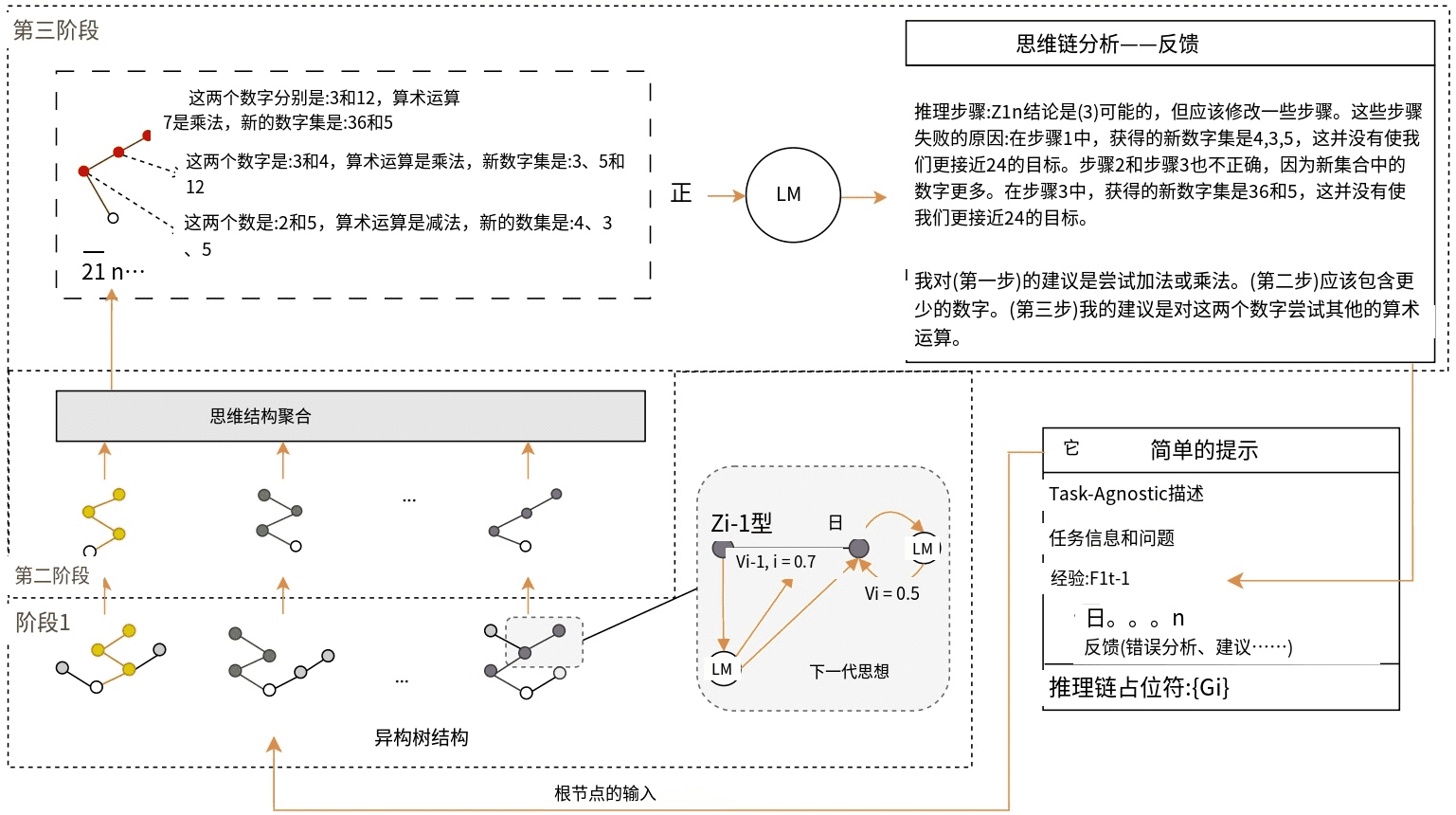
L'image montre une représentation visuelle du processus de réflexion qui sous-tend la résolution de problèmes à l'aide d'opérations arithmétiques. Il est divisé en trois parties principales : l'agrégation de la structure de pensée, la génération de la pensée suivante et l'analyse de la chaîne de pensée - retour d'information.

L'agrégation des structures de pensée représente la combinaison de différents stades de raisonnement (stade 1, stade 2, stade 3), chacun d'entre eux ayant sa propre structure numérique qui décrit les étapes suivies pour parvenir à une conclusion.

La génération de la pensée suivante se concentre sur une étape spécifique, montrant comment la modélisation du langage (LM) peut être utilisée pour prédire la pensée suivante, en prenant en compte l'expérience précédente (représentée par les vecteurs Vi-1 et Vi) et en générant une nouvelle chaîne de raisonnement.

L'analyse de la chaîne de pensée - Feedback fournit une analyse détaillée des étapes de raisonnement suivies, en signalant les erreurs possibles et en offrant des suggestions d'amélioration. Il critique les étapes en évaluant si elles rapprochent le résolveur du nombre cible (dans ce cas, 24) et suggère d'autres opérations arithmétiques à essayer.

En outre, une section de repères simples décrit les intrants du processus de réflexion, notamment les descriptions non spécifiques à la tâche, les informations et les questions relatives à la tâche, ainsi que l'expérience acquise au cours d'une chaîne de raisonnement précédente, qui sert de repère pour générer de nouvelles idées.

Dans l'ensemble, l'image dépeint une approche méthodologiquement saine du raisonnement et de la résolution de problèmes, utilisant des modèles linguistiques pour optimiser et améliorer de manière itérative les processus de pensée.

Plus précisément, examinons la section Agrégation de la structure de pensée. Dans cette section, nous pouvons voir trois étapes, chacune avec une structure arborescente hétérogène colorée. Au stade 1, nous voyons quelques opérations arithmétiques et la tendance est "vi1 - 0,5". Au stade 2, nous voyons plus d'opérations arithmétiques et la tendance est "vi2 - 0,6". Enfin, à l'étape 3, on observe une séquence d'opérations arithmétiques dont la tendance est "vi3 - 0,4".

Pour la section suivante de génération de pensées, un nœud de pensée spécifique, Zi, est suivi et son poids d'accompagnement, vi, est affiché, indiquant l'importance de ces pensées dans le contexte de la résolution de problèmes.

Dans la section Analyse de la chaîne de pensée - Retour d'information, plusieurs étapes de raisonnement sont présentées (Z1,Z2.... .Zn) et les évaluer. Pour chacune de ces étapes, "R1:-3, essayez +", "R2:+3, essayez -" et "R3 : -1, essayez ×" représentent le retour d'information sur l'étape en question. le retour d'information, l'évaluation du raisonnement et les suggestions d'amélioration.

Dans la section des indices simples, on peut voir quelques indices de saisie, tels que "Description non spécifique de la tâche 'Jouer à un jeu de chiffres'", "Message de la tâche 'Essayer d'utiliser les quatre nombres 1,3,4 6 (chaque nombre ne peut être utilisé qu'une seule fois) et les opérations arithmétiques (addition, soustraction, multiplication et division) pour arriver au nombre 24'", ainsi que la chaîne de raisonnement précédente Gi.

Le résultat de ce processus génère un nouveau processus de réflexion pour le raisonnement suivant.

Ce diagramme représente le flux logique d'un processus de réflexion et d'une méthodologie de raisonnement, montrant comment un modèle linguistique (ML) ainsi qu'un mécanisme de retour d'information/suggestion peuvent être utilisés pour avancer dans la résolution du problème, avec un retour d'information critique et une évaluation à chaque étape.

Figure 2 : Aperçu du processus BoT à chaque itération. Afin de présenter la manière dont une augmentation de l'efficacité peut être obtenue dans ce processus itératif empirique, nous montrons les résultats intermédiaires exhaustifs obtenus dans un type d'expérience sur ChapGPT-4 sur l'ensemble de données du jeu de 24 points. Après avoir reçu le problème Q : "Les quatre nombres fournis sont : 2, 4, 5, 5", la BdT passe par trois phases consécutives. En utilisant l'indice simple It comme entrée, la génération de structures de pensée (étape 1) produit une grande variété de structures de pensée hétérogènes en forme d'arbre. Lors de l'agrégation des structures de pensée (étape 2), celles-ci sont intégrées dans une chaîne de pensées z1.... .n, suivie de l'analyse de cette chaîne de pensées à l'étape 3 afin de générer des expériences qui peuvent être utilisées pour renforcer davantage l'indice.

Les invites peuvent être conçues de manière plus élaborée afin de guider les MFR dans la résolution du problème, étape par étape. Chaque étape de raisonnement intermédiaire est désignée par zi (également connue sous le nom de pensée). Le CdT fournit une poignée d'exemples, dont chacune des réponses contient une chaîne de pensées z1.... .n. Cela conduit à y ∼ pθ y|I [z1 . .n]N , X, Q , où N est le nombre d'exemples inclus dans l'invite.

Plutôt que de préparer des exemples dans le bootstrap, une approche plus flexible consiste à concevoir le bootstrap pour amener le LLM à générer progressivement la pensée zi au cours du processus de raisonnement. ceci peut être formalisé comme zi ∼ pθ (zi |I(z1.... .i-1, X, Q)). Enfin, la solution est formalisée comme y ∼ pθ (y|I(z1.... .n, X, Q)).
De manière représentative, ToT Yao et al. (2024) étendent cette étape de raisonnement séquentiel à une structure arborescente dans laquelle les pensées suivantes peuvent être générées. Ainsi, la structure d'une réflexion peut être soit en chaîne, soit arborescente.

3.2 Le cadre

La littérature existante visant à générer des indices avec des exemples corrects de CdT ou à concevoir des structures de génération de pensée à grain fin souffre de trois limitations. Premièrement, dans ces approches, la pensée non valide est généralement ignorée ou rejetée. Or, les êtres humains, en particulier les non-experts, et notamment dans d'autres domaines, s'appuient sur l'analyse des erreurs précédentes pour acquérir davantage d'expérience afin de se comporter correctement lors de la tentative suivante. Deuxièmement, elles sont moins évolutives car, pour chaque tâche, des exemples de génération de la pensée suivante, par exemple I (z1|z0, X, Q), doivent être fournis dans l'indice. Enfin, la génération de structures de pensée (par exemple, la structure arborescente de Yao et al.) est trop complexe pour explorer davantage d'étapes de raisonnement afin d'obtenir une meilleure solution. Ceci est principalement dû au fait que les solutions obtenues ne peuvent pas être révisées.

Dans cet article, nous soutenons que les messages-guides peuvent être améliorés en collectant continuellement des analyses de ces pensées invalides (étapes de raisonnement erronées dans la chaîne de pensée) à partir des LLM. Ainsi, même un simple indice, par exemple, I (X, Q), qui peut conduire à une pensée invalide, peut être amélioré progressivement en s'appuyant sur de telles analyses afin d'obtenir une pensée forte qui mène plus près d'une solution.

Nous proposons une méthode appeléeBoosting of Thoughts (BoT) (en anglais)d'un cadre de repérage automatisé qui permet d'améliorer le repérage par le biais d'un processus itératif fondé sur l'expérience, à partir de l'étape du repérage.plus simplele début de l'indice. En résumé, comme le montre la figure 2, chaque itération t de BoT se compose de trois phases. La phase de génération de structures de pensée est capable d'utiliser pleinement les chaînes d'inférence générées par les LLM, avec les invites d'entrée comme It. Dans la deuxième phase, ces structures de pensée sont agrégées dans une chaîne d'inférence qui sera analysée par les LLM dans la troisième phase pour générer un retour d'information contenant des rapports d'erreur et des suggestions de révision détaillées. La chaîne de raisonnement agrégée est combinée aux résultats du retour d'information pour former une nouvelle expérience, notée Ft. Ainsi, en accumulant ces expériences au cours des itérations F1.... .t, l'indice est amélioré.

Conseils simples. Pour toute tâche, à l'itération t = 0, nous créons un repère initial simple I0 ≡ {S, X, Q, F0, {Gi}}, où S désigne la description indépendante de la tâche, tandis que X et Q désignent respectivement les informations et la question relatives à la tâche. La partie empirique de l'invite est notée F0 et doit être vide au début. {Gi}} est un espace réservé qui sera rempli lors de la construction de la structure de pensée. En d'autres termes, lors de la génération de la pensée suivante zi, {Gi} sera remplacé par la chaîne de pensée précédente z1.... ,i-1.

Génération de structures de pensée. Après avoir recueilli l'expérience Ft-1 , l'indice pour l'itération t peut être It ≡ {S, X, Q, F1, .... ,t-1, {Gi}}. BoT est essentiellement capable de contenir n'importe quelle structure de pensée, par exemple les structures enchaînées de Wei et al. ou les structures arborescentes de Yao et al. Compte tenu de l'exploration des étapes de raisonnement et des résultats expérimentaux, nous avons étudié les structures de pensée arborescentes. Cependant, BoT introduit deux nouvelles modifications qui le rendent plus adapté au cadre de levage.

• arbre binaire pondéré. En utilisant des indices simples à chaque tour, BoT construit des esprits faibles avec des structures simples et peu complexes parce qu'ils peuvent être révisés ultérieurement dans le mécanisme de stimulation. Ainsi, chaque structure de pensée de BoT est un arbre binaire pondéré peu profond. Par souci de simplicité, nous conservons les symboles z1.... .i-1 pour désigner une pensée allant du nœud racine au parent du nœud i. En plus de fournir à chaque nœud i une pensée zi et son score d'évaluation de la pensée Vi ∼ pθ (z1.... .i, Ia, X, Q), nous incluons également un score de bord Vi-1,i ∼ pθ (zi-1, zi, Ie, X, Q) entre un nœud enfant et son nœud parent, où Ia et Ie se réfèrent aux descriptions directrices de la pensée et à l'évaluation du bord, respectivement. vi-1,i dénote le niveau de confiance des LLM dans la génération de cette étape de raisonnement. Ainsi, la génération de la prochaine pensée du BoT dans cette structure arborescente est formalisée comme pθ (zi| (Vi-1,i, Vi, It, X, Q)).
• hétérogénéité des arbres. Contrairement à la ToT, qui cherche à trouver des solutions dans un grand arbre complexe, la BoT vise à construire des structures de pensée arborescentes très hétérogènes. Ainsi, pour accroître l'hétérogénéité, la génération de structures de pensée utilise différentes stratégies de croissance de l'arbre, telles que la croissance couche par couche et la croissance feuille par feuille. La première stratégie met l'accent sur l'exploration mais utilise moins de ressources Chen & Guestrin (2016), tandis que la seconde est à l'opposé Ke et al. (2017). Ainsi, la stratégie feuille à feuille tend à poursuivre le raisonnement à partir de la meilleure pensée actuelle jusqu'à une meilleure pensée finale par rapport à la croissance couche par couche, mais elle tend également à obtenir des chaînes de raisonnement monotones. Enfin, nous avons utilisé une petite valeur de profondeur maximale dans BoT et étiqueté un nœud comme une feuille lorsque les valeurs Vi-1,i et Vi étaient en dehors de la plage spécifiée [0,3, 0,8].

polymérisation en structure pensée. Après avoir obtenu M structures de pensée, la BoT les regroupe en une chaîne de pensées, notée z1.... .n. Pour ce faire, pour chaque indice de structure de pensée m, le BoT sélectionne d'abord la chaîne ayant le score d'évaluation le plus élevé, c'est-à-dire zm 1.... .nm := arg maxz1.... .n∈Zm ∑i=1 Vi + Vi-1,i, où Zm représente l'ensemble de toutes les chaînes de pensée du mème arbre. Par la suite, il existe deux stratégies pour obtenir z1.... .n.

• agrégation en premier lieu.BoT dépend de arg maxz1.... .n∈{Zm}M m=1 ∑i=1 Vi + Vi-1,i, et sélectionne la meilleure des M structures de pensée comme z1.... .n. Cet algorithme est rapide, mais peut conduire à une chaîne illogique qui est difficile à guider pour les améliorations ultérieures.
• Agrégation de la cupidité. le CS est autorisé à effectuer une recherche avide sur {Zm}M m=1 afin d'assembler une nouvelle chaîne d'esprits qui peut ne pas exister, mais qui peut être globalement optimale. En partant de la pensée initiale, généralement le nœud racine de l'arbre, la BdT obtient z1 = arg maxzj ∈ {zm 1 } M m=1 Vj + Vj-1,j. Ensuite, afin d'obtenir zi, la BdT recherche toutes les pensées dans {Zm}M m=1 dont l'étape précédente était zi-1.

analyse de la chaîne de pensée. Pour avoir une idée de ce qui devrait être ajusté pour améliorer l'indice afin de générer une meilleure pensée, la BoT utilise la capacité des LLM à auto-évaluer z1.... .n. Plus précisément, avec l'indice It f (z1... .n, X, Q), le LLM produit un paragraphe de feedback contenant des informations sur cette chaîne de pensées z1.... .n avec un rapport sur le problème et des suggestions détaillées. Ce retour d'information sera ajouté à F1,... ,t-1 en tant que nouvelle expérience dans la génération de pensées, résultant en F1,.... ,t.

Raffinement itératif.. Grâce au mécanisme de renforcement, F1,... ,t est utilisé pour améliorer itérativement l'indice, ce qui donne l'indice It+1 pour la (t+1)ème itération ≡ {S, X, Q, F1,.... ,t, {Gi}}. Au fur et à mesure de l'itération, F1,... ,t peut contenir de nombreuses chaînes de pensée typiques et non plausibles, ainsi que des chaînes plus proches de la solution, toutes avec des résultats analytiques bien définis. Ainsi, même en partant d'un simple indice, BoT affine itérativement cet indice pour produire les étapes de raisonnement correctes qui mènent à une solution précise. Après T itérations, nous utilisons It+1 comme indice d'entrée au LLM pour la réponse finale.

4. l'expérimentation

ensemble de données. Les expériences ont été menées sur des ensembles de données de référence contenant une variété de problèmes mathématiques, notamment MMLU, SVAMP, GSM8K, AQuA et MATH. En outre, nous avons inclus une tâche de raisonnement mathématique difficile, Game of 24, où l'objectif était d'obtenir 24 en 1 équation en utilisant quatre nombres et des opérations arithmétiques de base (addition, soustraction, multiplication et division). La solution consiste donc en 3 étapes intermédiaires.

concurrence. Outre la méthode de référence Standard Input-Output (IO), les méthodes comparatives comprennent Chained Thinking (CoT), CoT-SC et Complex CoT, où les invites d'entrée contiennent une poignée d'exemples (8) et des annotations humaines. En outre, la BoT est comparée à des travaux connexes tels que les arbres de pensée (ToT), les invites progressives (PHP) et les CSV de pointe.Nous avons mené des expériences en utilisant GPT-4 et Llama2.GPT-4 a été accessible via l'API OpenAI, tandis que le modèle llama2-13b-chat a été téléchargé à partir de MetaAI afin de mener des expériences localement. Pour construire une structure arborescente hétérogène, BoT a choisi au hasard des températures dans l'intervalle de température [0,2, 0,4, 0,6, 0,7, 0,9, 1,1, 1,5] et des p supérieurs dans l'intervalle [0,1, 0,3, 0,5, 0,7, 0,9].

mettre en place. Sauf indication contraire, dans toutes les expériences, BoT effectue T = 10 itérations et construit M = 15 structures de pensée, chacune étant un arbre binaire pondéré, car cela tend à donner les meilleurs résultats. En outre, pour ces ensembles de données de référence, nous avons fixé la profondeur de l'arbre à 5, alors que la profondeur correspondante dans Game of 24 était de 3. BoT + CoT signifie que notre indice simple comprend 5 exemples de CoT. Dans les études d'ablation, lorsqu'il n'y a pas d'expérience cumulée dans la BdT, 8 exemples de la BdT seront fournis dans l'invite.

métrique. Nous mesurons et présentons les résultats de toutes les expériences en termes de taux de résolution de la tâche (%). A partir de la sortie BoT zT1.... .n des réponses cibles, nous avons établi des descriptions formatées des réponses spécifiquement pour les LLM. Pour les ensembles de données couramment utilisés, le format de la réponse a été défini comme suit : "La réponse est :". Pour le jeu de 24 points, nous utilisons "Index d'étape, ensemble actuel :, deux nombres sélectionnés :, opération :, nouveau nombre de l'opération :, nombres restants :, nouvel ensemble de nombres :". Ensuite, nous comparons directement les nombres du nouvel ensemble de nombres avec la vérité de terrain. En référence à ToT Yao et al. (2024), nous utilisons le taux de solution calculé à partir de 100 jeux difficiles comme métrique.

4.1 Principaux résultats

Les principaux résultats expérimentaux sont résumés dans le tableau 1 et la figure 3, où nous donnons un aperçu des performances globales du BoT. Nos conclusions montrent que le BoT proposé en renforçant le mécanisme 1). Obtient des taux de résolution de problèmes compétitifs indépendamment des annotations humaines dans la plupart des ensembles de données ; 2). atteint un nouvel état de l'art lors de la fourniture d'exemples CoT. Cependant, les résultats expérimentaux montrent également que le BoT repose fortement sur l'expérience et est donc très sensible aux capacités des LLM.

Spécifiquement, dans le tableau 1, BoT commence avec des indices initiaux simples et finit par surpasser l'état de l'art actuel CSV de 0,11 TP3T en termes de taux de solution sur GSM8K, qui dépend fortement de l'interpréteur de code GPT-4. En considérant AQuA, BoT surpasse SOTA de 2.51 TP3T. Ceci montre qu'en ajoutant des analyses d'erreurs et des suggestions aux indices, sans s'appuyer sur des annotations humaines, les LLMs peuvent être performants sur des raisonnements complexes. La raison principale est que les conseils simples peuvent être améliorés de manière incrémentale en accumulant l'expérience précédente pour résoudre les problèmes avec précision. Après avoir inclus des exemples de CoT dans les invites, BoT+CoT est 1,3% plus élevé que SOTA. Nous soutenons que les exemples de CoT peuvent être considérés comme des cas de réussite dans l'expérience, qui guident directement la génération de structures de pensée ultérieures dans BoT. Par ailleurs, BoT et BoT+CoT, en particulier BoT, étaient au moins 181 TP3T plus bas que SOTA en MATH. Cette observation implique que les LLM faibles peuvent ne pas bien travailler avec BoT en raison de la faible capacité des LLM à analyser les chaînes d'inférence pour des expériences valides.

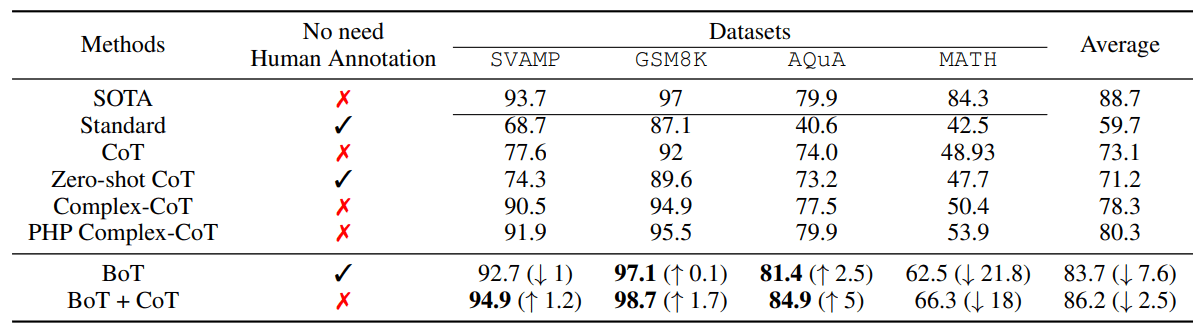
Tableau 1 : l'utilisation de BoT en conjonction avec GPT-4 améliore considérablement les performances, même sans annotation manuelle.
Lorsque l'indice initial simple de BoT inclut des exemples de CoT, l'approche BoT+CoT correspondante présente des taux de solution plus élevés. Notre cadre est également comparé à des approches de pointe telles que Model Selection de Zhao et al. en 2023, PHP de Zheng et al. en 2023, et CSV de Zhou et al. en 2023, obtenant des performances de pointe (SOTA) sur les ensembles de données SVAMP, AQuA, et GSM8K & MATH, respectivement.

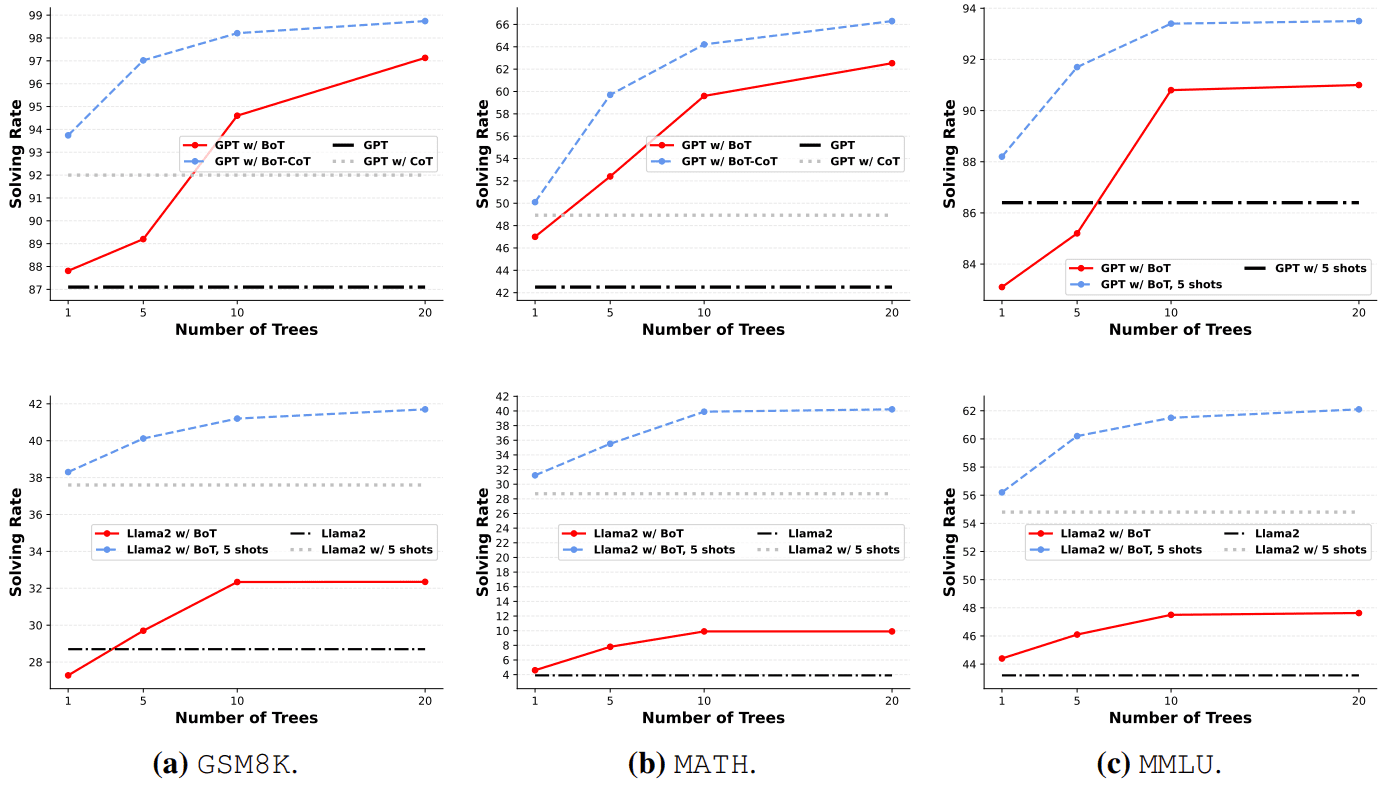
Figure 3 : Utilisation de BoT et BoT+CoT pour évaluer le taux de résolution de problèmes de GPT-4 OpenAI avec Llama2 Touvron et al. en 2023.

Comme on peut le voir dans la figure 3, GPT-4 et Llama2 améliorent la performance moyenne de 11.61 TP3T et 4.41 TP3T en moyenne à travers les trois ensembles de données dans les conditions BoT, respectivement. Ces deux figures montrent une tendance claire que BoT et BoT-CoT ont des performances similaires lorsque les LLM sont plus puissants, comme montré dans la figure 3. En outre, leur performance montre une tendance similaire à la hausse lorsque le nombre d'arbres change de 1 à 20. En raison de la faiblesse de Llama2, BoT ne peut pas bénéficier de ses analyses pour effectuer un processus itératif basé sur l'expérience, comme le montre la figure 3(a). Lorsqu'on lui fournit des exemples de réussite valables, c'est-à-dire 5 tests, le BoT peut encore aider Llama2 à résoudre plus de problèmes que la base grâce à des améliorations incrémentales, bien qu'elles soient limitées.

4.2 Match à 24 points

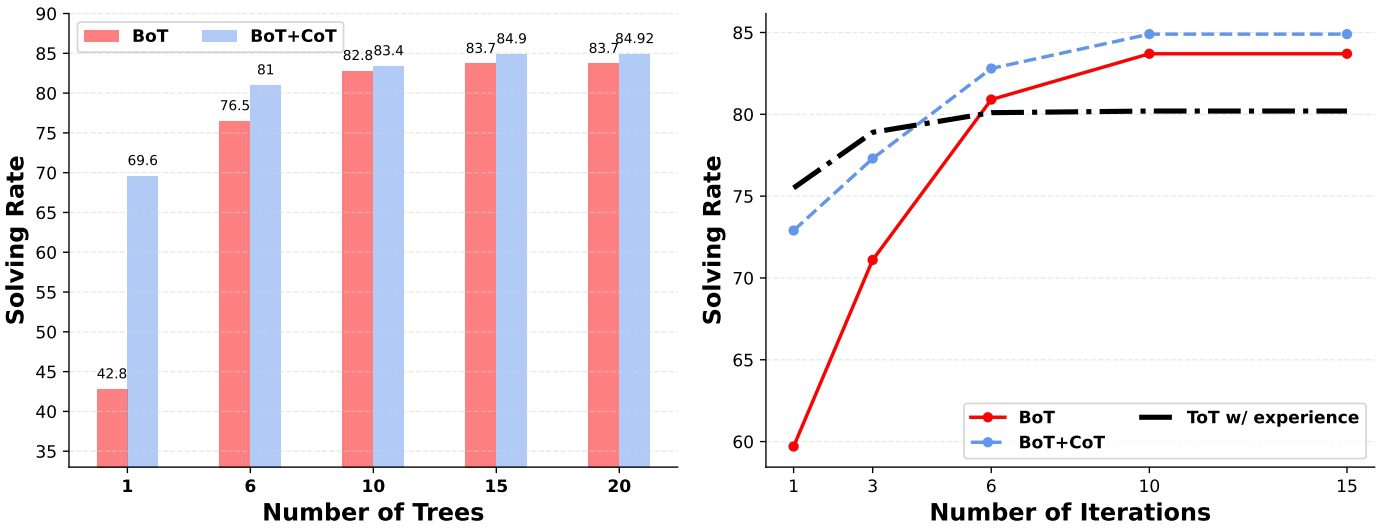
Fig. 4 : Comparaison des trois méthodes en fonction du nombre d'arbres et d'itérations.

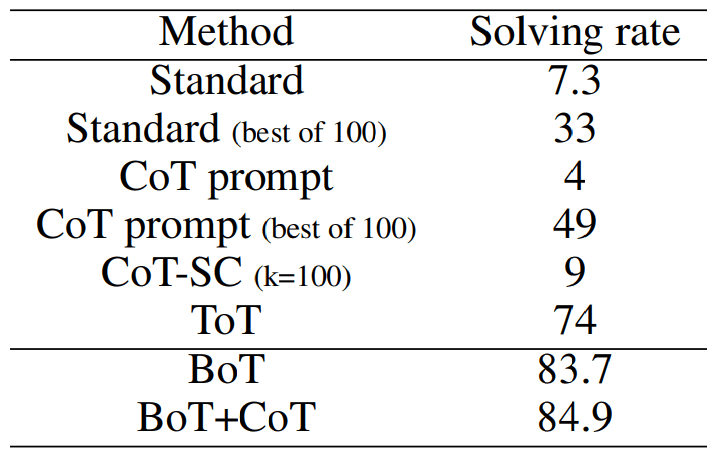
Tableau 2 : Configuration des différentes méthodes dans le jeu à 24 points suivant la configuration du TdT Yao et al. (2024), dont les résultats sont présentés ici.

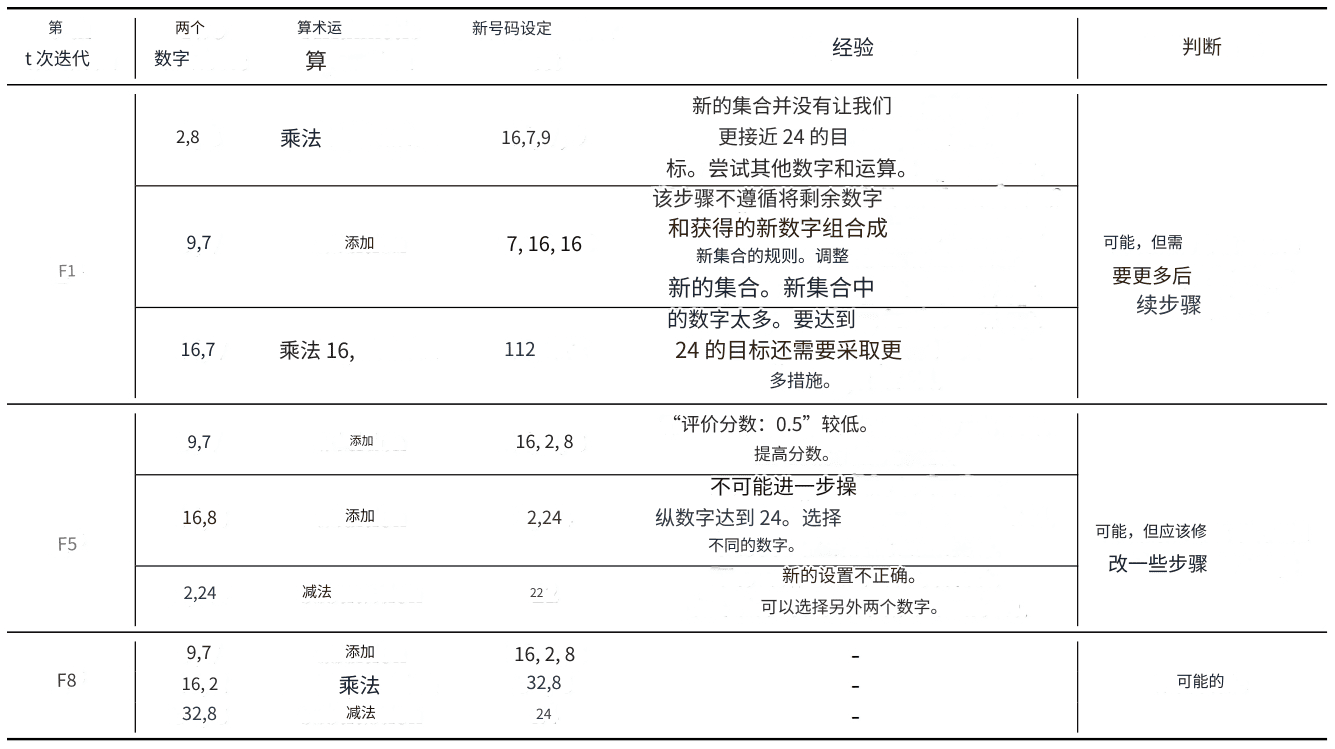
Tableau 3 : Démontre le processus de réflexion qui a été accumulé et l'expérience qui a pu être acquise au cours des 1ère, 5ème et 8ème itérations. Les quatre valeurs données sont : 2, 7, 8 et 9.

En raison de la difficulté du problème du Jeu des 24, GPT-4 et Llama2 ont tous deux obtenu de mauvais résultats, même en combinant les méthodes CoT et CoT-SC. Le modèle Llama2 n'a même pas été capable de suivre les règles correctes pour résoudre le problème, ce qui a rendu le taux de solution encore plus faible. Le modèle Llama2 n'a même pas été capable de suivre les règles correctes pour résoudre le problème, ce qui a rendu le taux de solution encore plus faible. Par conséquent, nous ne présentons que les performances de BoT avec GPT-4. Pour maintenir une comparaison équitable, nous suivons la configuration proposée par ToT Yao et al. (2024).

Comme le montre le tableau 2, la BoT sans annotations humaines surpasse la ToT qui s'appuie sur un exemple pour montrer toutes les étapes suivantes possibles de 9,71 TP3 T. En outre, la BoT+CoT qui contient 5 plans CoT surpasse la BoT de 1,21 TP3 T. La proximité de performance entre la BoT et la BoT+CoT est attribuée au mécanisme de renforcement, qui révise de manière incrémentale la pensée faible, comme discuté dans la sous-section 4.1. En utilisant un processus itératif basé sur l'expérience, BoT présente des performances accrues à mesure que le nombre d'arbres M et d'itérations T augmente. Comme le montre la figure 4, la méthode BoT dépend davantage de M et de T que la méthode BoT+CoT, car elle nécessite d'acquérir de l'expérience à partir de meilleures chaînes de pensée ou d'itérations plus longues. Une autre observation est que lorsque ToT est activé pour fonctionner avec des indices expérimentés, le taux de résolution de problème augmente de 72,51 TP3T dans la première itération à 80,21 TP3T dans la 10ème itération.Cela suggère que l'expérience - l'analyse des chaînes de raisonnement précédentes - peut être utilisée par les LLM pour améliorer de manière significative le taux de résolution. Ceci est attribué au fait que la phase d'agrégation de BoT produira la chaîne de raisonnement la plus représentative dans l'itération actuelle, dirigeant ainsi une expérience plus significative pour améliorer l'indice. Nous l'avons vérifié dans la section de l'étude sur l'ablation.

Pour mieux démontrer comment BoT apprend des erreurs et des suggestions précédentes, nous montrons dans le tableau 3 que GPT-4 est capable d'éviter les erreurs précédentes et de générer des suggestions plus spécifiques au fur et à mesure que le nombre d'itérations augmente, conduisant finalement à la solution correcte. Dans la première itération, en raison de simples conseils, les LLM ont même fait une erreur en suivant les règles de la tâche parce que le nouvel ensemble était erroné à l'étape 3. Après l'avoir analysé, il a fait la bonne suggestion pour cette erreur. Cependant, l'analyse de l'itération initiale était vague, par exemple "essayez d'autres nombres et d'autres opérations". Après cinq itérations, le BoT a agrégé plusieurs analyses de ce type, ce qui a donné lieu à des conseils plus efficaces qui ont conduit les MFR à choisir les bons nombres 9 et 7. En outre, les suggestions étaient plus spécifiques et plus utiles. Pour ce choix correct, la suggestion était d'augmenter le score d'évaluation en conséquence. En accumulant une telle expérience, BoT a progressivement affiné les conseils, générant finalement la solution correcte directement lors de la 8e itération.

4.3 Études d'ablation

Tableau 4 : Comparaison de GPT-4 avec différentes variantes de BoT employées sur le jeu à 24 points et l'ensemble de données AQuA.

Toutes les stratégies d'agrégation produisent des taux de solution élevés lorsque les problèmes et les suggestions sont regroupés de manière "additive". Le maintien d'une expérience complète est particulièrement important pour la pensée révisionniste, notamment pour l'ensemble de données AQuA, qui couvre un plus large éventail de problèmes de raisonnement mathématique. Cependant, BoT(No), qui utilise directement toutes les chaînes de raisonnement de l'arbre sans les agréger, obtient les moins bons résultats dans tous les contextes, en particulier lorsque le type d'expérience est "cumulatif". 15 arbres sont construits à chaque itération de BoT, et le fait de les rassembler tous dans un indice peut masquer des informations importantes, sans compter que la plupart d'entre eux peuvent ne pas être valides ou nuisibles. Une telle expérience peut être invalide ou nuisible.

L'obtention de conseils est plus importante que toute autre chose pour déclencher la réflexion.. Dans tous les exemples mentionnés dans le tableau 4, la variante BoT qui traite les suggestions comme de l'expérience obtient les taux de solution les plus élevés. Par exemple, dans le même cas de type "additif", sans suggestions dans l'expérience, les performances ont baissé de plus de 101 TP3T et 201 TP3T dans le "jeu à 24 points" et AQuA, respectivement. Les BoT contenant des suggestions ne peuvent atteindre les meilleurs taux de résolution que s'ils sont associés à des problèmes. Par exemple, dans AQuA, le taux de résolution de la BoT (méthode gourmande) a augmenté de 4,41 TP3T.

Pour des raisons de performance, le rallye gourmand peut être la seule option nécessaire.. Contrairement à l'approche la plus prioritaire qui consiste à sélectionner l'une des chaînes de pensée existantes ou à les maintenir toutes, les agglomérations gourmandes peuvent fusionner de manière adaptative la structure de l'arbre en une meilleure chaîne de pensée, qui peut ne pas se produire dans l'itération actuelle. De cette manière, LLM peut effectuer des analyses significatives d'une chaîne de pensée plus robuste, et par conséquent, générer des leçons importantes pour augmenter l'indice. Dans AQuA, qui contient plus de problèmes mathématiques, ce nombre atteint même 101 TP3 T. De plus, comme nous l'avons discuté dans la Figure 4, bien que ToT ait un mécanisme de boost similaire basé sur l'expérience capable d'atteindre 801 TP3 T, il est toujours à la traîne de BoT. Cela peut être dû au fait qu'il n'est pas capable d'effectuer des agglomérations gourmandes dans sa structure arborescente unique.

5. conclusion

Dans cet article, nous validons le fait qu'un repère simple peut être utilisé pour résoudre des tâches complexes en accumulant progressivement des analyses d'erreurs sur les pensées qu'il génère. Nous proposons un nouveau cadre appelé Boosting of Thoughts (BoT) qui permet cette augmentation progressive des repères par le biais d'un processus itératif axé sur l'expérience afin de générer des chaînes de pensées efficaces. Une simple chaîne de pensées en forme d'arbre générée par l'exploration itérative et l'auto-évaluation permet à un simple indice initial d'être progressivement augmenté par une série d'expériences de raisonnement par essais et erreurs qui conduisent à une solution précise. Nos expériences approfondies montrent que BoT est capable d'atteindre des performances de pointe sur plusieurs ensembles de données de référence et qu'il surpasse d'autres méthodes de pointe sur la tâche difficile de raisonnement mathématique du jeu de 24.

BoT des messages-guides et des processus de raisonnement de base

A1 BoT pour la composante "génération d'idées

Cette section mentionne les indices de base utilisés pour la génération du raisonnement du Boosting of Thought (BoT) proposé. Pour plus de détails, vous pouvez consulter le fichier d'exemple du code source : /examples/BoostingOfThought/BoT reasoner.py.

Conseil pour le système :

Vous êtes un expert en problèmes mathématiques. Effectuez un raisonnement étape par étape pour résoudre un problème en tirant des enseignements d'une série d'expériences de raisonnement par essais et erreurs. Ces expériences de raisonnement par essais et erreurs comprennent notamment des rapports d'erreurs, ainsi que des suggestions détaillées sur la manière de modifier les étapes de raisonnement précédentes. Il est important d'examiner ces expériences répertoriées avant de générer de nouvelles étapes de raisonnement, afin d'éviter de répéter des erreurs tout en utilisant les étapes correctes pour générer de meilleures étapes de raisonnement à utiliser dans la résolution de problèmes.

 

Invite du système S.

Vous êtes un expert en problèmes mathématiques et vous effectuez un raisonnement étape par étape.
vers la résolution de problèmes en apprenant d'abord à partir d'un ensemble d'expériences de raisonnement par essais et erreurs.
Cette expérience de raisonnement par essais et erreurs contient notamment des rapports d'erreurs et des conseils détaillés sur les points suivants
Comment réviser les étapes du raisonnement historique. Il faut toujours se rappeler les expériences énumérées avant de générer un raisonnement historique.
nouvelle étape de raisonnement, ce qui permet d'éviter les mêmes erreurs et de réutiliser les étapes correctes pour générer de la valeur ajoutée.
de meilleures étapes de raisonnement pour résoudre la tâche.

Générer une incitation à la réflexion suivante :

f"""

{Alerte mission} \n

Tout d'abord, rappelons l'expérience de raisonnement précédente : \n\n

 

{Expérience}\n\n

 

Veuillez présenter la prochaine étape de raisonnement possible, et il ne peut y en avoir qu'une. Cette étape de raisonnement doit être utilisée comme successeur séquentiel des étapes ordonnées suivantes et doit être accompagnée d'une note d'évaluation correspondante (les notes les plus élevées indiquent une plus grande probabilité de mener à bien la tâche):\nT

{chaîne hint}\n\n

 

Sur la base des étapes d'inférence antécédentes ci-dessus (ou ignorez-les si l'espace ci-dessus est vide), générez une étape suivante possible unique basée sur les règles de la tâche. (IMPORTANT : Ne générez que la prochaine étape de raisonnement possible pour une étape donnée).

"""

f"""{task prompt}. \nTout d'abord, rappeler l'expérience historique du raisonnement : \n\n {
expériences} \n\n- Veuillez faire un pas de raisonnement pour générer une seule expérience suivante
L'étape de raisonnement suivante est l'étape séquentielle à partir de L'étape de raisonnement suivante est l'étape subséquente de
les étapes précédentes ordonnées suivantes, accompagnées de leurs notes évaluées (A
un score plus élevé signifie que l'étape de raisonnement est plus susceptible d'achever la tâche.) : \n\t{
chaîne prompt}\n\n En se basant sur les étapes de raisonnement énumérées précédemment (ne pas en tenir compte lorsque l'on est en présence d'une chaîne), il est possible d'obtenir des résultats.
l'espace ci-dessus est vide), générer une seule étape possible à la suite de la Tâche
règle . (Insistez sur le fait que vous ne devez générer qu'une seule étape de raisonnement suivante possible de
les étapes données). """

L'invite de tâche contient les X et Q de la tâche, et l'expérience historique est F1.... La partie "indice de chaîne" est {Gi}, qui est un espace réservé qui, lorsque la pensée actuelle zi est exécutée, est remplacée par la série précédente de pensées z1...,i-1. ,i-1.

Pour des conseils sur l'évaluation :

f"""

{Mission Alert}

Vous trouverez ci-dessous les étapes du raisonnement dans l'ordre, accompagnées de leurs scores d'évaluation respectifs. (Un score plus élevé signifie que l'étape est plus susceptible de mener à bien la tâche). \n

{chaîne hint}\n

{Pensée}\N- La question est de savoir si l'on peut faire quelque chose de plus que ce que l'on a fait.

Quel est votre score pour évaluer la logique et la justesse de ces étapes de raisonnement, ainsi que leur utilité pour la solution finale ? Veuillez choisir l'une des notes suivantes [0.1, 0.3, 0.5, 0.7, 0.9, 1.0], les notes les plus élevées indiquant de meilleures étapes de raisonnement. La note doit être placée après "Note d'évaluation :" pour que l'utilisateur puisse la lire.""""

 

f"""{invitation à la tâche}. \Vous trouverez ci-dessous les étapes de raisonnement générées, présentées dans l'ordre.
accompagnés de leurs scores évalués (un score plus élevé signifie que l'étape de raisonnement est
plus susceptibles d'accomplir la tâche.) :\n{chain prompt}\n{thought}\n{pensée}\n{pensée}\n{pensée}\n}Quel est votre
la note d'évaluation de la logique, de l'exactitude et de l'utilité pour parvenir à un résultat final.
solution pour ces étapes de raisonnement ? Veuillez choisir une valeur parmi [0.1, 0.3, 0.5,
0.7, 0.9, 1.0] comme score , où un score plus élevé signifie de meilleures étapes de raisonnement . Les
Le score doit être placé après " Score d'évaluation : " pour que les utilisateurs puissent lire .""""

Dans ce cas, la pensée est la pensée Zi en cours.

A2 BoT pour le composant de génération d'expérience

Pour générer des commentaires sur les chaînes agrégées, les LLM utilisent les invites de base suivantes. Pour plus d'informations, vous pouvez également consulter le code source examples/BoostingOfThought/BoT commenter.py.

Invite système S : Vous êtes un réviseur expert en IA pour Maths Answers et vous travaillez sur l'évaluation de la chaîne de raisonnement générée pour résoudre un problème mathématique. Veuillez évaluer chaque étape de raisonnement de cette chaîne de raisonnement en fournissant une analyse détaillée pour déterminer si l'étape actuelle est une déduction logique de l'étape précédente et si l'étape de raisonnement contribue à la solution correcte. Pour chaque étape de raisonnement incorrecte, veuillez fournir un rapport d'erreur et les suggestions de révision correspondantes. Pour chaque étape de raisonnement correcte, veuillez fournir une description de la recommandation ou du rejet.

Conseil pour le système :

Votre rôle est celui d'un réviseur de réponses aux questions de mathématiques de l'IA, qui se concentre sur l'évaluation du processus de raisonnement utilisé pour résoudre les problèmes de mathématiques. Vous devrez juger chaque étape du raisonnement par une analyse exhaustive pour voir si elle est basée sur la logique de l'étape précédente et si cette étape a contribué à trouver la bonne réponse. Si vous rencontrez une étape de raisonnement incorrecte, vous devez faire des suggestions et proposer des options de modification. Pour les étapes de raisonnement correctes, vous devez affirmer ou proposer des options différentes.

 

Invite du système S.

Vous êtes un expert de la vérification des réponses mathématiques par l'IA, chargé d'évaluer l'exactitude des réponses.
chaîne de raisonnement générée pour répondre au problème mathématique. Jugez chaque raisonnement
étape de cette chaîne de raisonnement en fournissant des analyses détaillées sur la question de savoir si l'étape actuelle est une étape logique de la chaîne de raisonnement.
L'étape de raisonnement est une étape qui permet d'évaluer la déduction de l'étape précédente et de déterminer si l'étape de raisonnement permet d'aboutir à la bonne solution.
Fournir des conseils et des suggestions pour chaque étape du raisonnement avec des erreurs. Fournir des recommandations ou des conseils pour chaque étape du raisonnement.
des descriptions de rejet pour chaque étape de raisonnement correcte.

Conseil en matière de retour d'information :

f"""

Pour la tâche donnée:{indice de la tâche}. \n

{Conseils de la chaîne de raisonnement}\n\nbsp ;

Veuillez évaluer cette chaîne de raisonnement et fournir une critique détaillée comprenant les points suivants. \n

1. {Format de rétroaction en chaîne}. 2. {Format de rétroaction en étapes}. 3. {Format de rétroaction en confiance}. 4. \n\n

Caveat : {Caveat}

 

f"" "Tâche donnée:{invitation à la tâche}. \n{initiative de chaîne}\n\nVeuillez évaluer cette chaîne de raisonnement
en formulant des commentaires détaillés dont le contenu est le suivant . \n 1.{
format de rétroaction en chaîne }. 2.{ format de retour d'information par étapes }. 3.{ format de retour d'information sur la confiance }. \3.{ format de retour d'information sur la confiance }.
\n Avis : {Avis}.

Parmi ceux-ciChaîne de raisonnement Conseilsest une chaîne d'inférence agrégée z1.... .n.

Format du retour d'information sur la chaîne: Cette chaîne de raisonnement peut-elle accomplir correctement la tâche et atteindre l'objectif en effectuant ses étapes de raisonnement ? Pourquoi ? Rédigez l'analyse finale dans la rubrique "Rapport d'analyse".

Format de retour d'information étape par étapePour chaque étape du raisonnement, veuillez fournir une analyse détaillée permettant de déterminer si l'étape actuelle est une déduction logique de l'étape précédente et si l'étape du raisonnement contribue à la solution correcte. Pour chaque étape de raisonnement incorrecte, veuillez fournir un rapport d'erreur et les recommandations de révision correspondantes. Pour chaque étape du raisonnement, veuillez fournir une description de la recommandation ou du rejet. Les commentaires doivent être concis et suivre le format suivant : étape du raisonnement ⟨idx⟩. Analyses ⟨idx⟩. Recommandation :. Recommandation ou rejet Description :.

Format du retour d'information sur la confianceLes évaluations : Quelle est votre note de confiance pour ces évaluations et examens ? Veuillez sélectionner une valeur parmi [0.1, 0.3, 0.5, 0.7, 0.9, 1.0] comme note à lire par l'utilisateur.

Grâce aux signaux de retour, les LLM génèrent des Ft empiriques contenant des conclusions et des analyses de la chaîne de raisonnement et de chaque étape de raisonnement.

A3 Processus de raisonnement

Pour faciliter la compréhension de l'algorithme de stimulation des pensées proposé, nous résumons le flux d'inférence dans le tableau algorithmique 1. Le code source de ce flux se trouve dans le fichier examples/BoostingOfThought/BoT core.py.

BdT original

Le contenu de l'image est une représentation algorithmique étape par étape d'une théorie appelée "BoT", et le texte suivant est sa traduction en chinois, correspondant aux étapes algorithmiques suivantes :

Algorithme 1 : Le processus de raisonnement principal de BoT

Entrées : nombre d'itérations T, nombre d'arborescences M, problème Q.
Sortie : chaîne agrégée z̄_1.... .n^T

1) Initialiser un simple indice I^0 (S, X, Q, F^0, {Gi}), où F^0 sera une chaîne vide.
2) Chaque itération t = 1, 2, ... , T.
3. utiliser les indices I^t-1 (S, X, Q, F^t-1, {Gi}) avec le LLMS (Low Latent Mixed Model) pour créer M structures de pensée différentes dans le cadre d'un processus appelé "Thought Structure Generation" (génération de structures de pensée).
4. extraire la chaîne de pensées {z̄_i=1....n^m} de M structures de pensée, chaque z̄_i=1.... .n^m}, chaque z̄_i=1.... .n^m est la meilleure chaîne de pensée de la m-ième structure arborescente.
5. utiliser la méthode "Best-First Aggregation" ou "Greedy aggregation" pour incorporer {z̄_i=1...n^m} dans une chaîne de pensée unique z̄_1...n^m}. .n^m} en une seule chaîne de pensée z̄_1...n^t. .n^t.
6. utiliser le LLMS pour effectuer une "analyse de la chaîne de pensée" sur z̄_1.... .n^t, obtenir un retour d'information et le combiner avec z̄_1.... .n^t et le combiner avec z̄_1...n^t pour obtenir l'expérience F^t.
7) Mettre à jour l'indice en cumulant F^t à I^t (S, X, Q, F^t-1,t, {Gi}).
8. conclusion
9. accès aux solutions z̄_1.... .n^T

B Des idées pour améliorer la réflexion

Le renforcement des pensées découle de notre idée que la capacité de raisonnement des grands modèles de langage (LLM) pour résoudre des problèmes mathématiques est directement dérivée d'expériences qui contiennent des analyses et des suggestions pour des erreurs antérieures. Une fois que les indices contiennent une expérience de raisonnement historique valide que les LLM peuvent rappeler avant d'effectuer le raisonnement, les étapes de raisonnement qui en résultent sont généralement plus logiques et rationnelles, comme le montre la comparaison des tableaux 5 et 6. Ces idées nous ont également amenés à considérer que les LLM n'ont pas besoin de s'appuyer fortement sur des messages-guides bien préparés pour chaque tâche (plusieurs démonstrations de chaînes de pensée dans les messages-guides servent d'exemples). Cependant, comme les LLM sont capables d'apprendre par l'expérience, nous pouvons commencer par un simple message-guide qui ne nécessite pas d'exemples ou de contenu conçu manuellement, et acquérir progressivement de l'expérience au fur et à mesure que nous raisonnons. En fin de compte, en accumulant de l'expérience dans l'indice, les LLM parviennent à un raisonnement robuste pour résoudre des problèmes complexes. Grâce à ces connaissances, le Boosting of Thoughts est conçu comme un cadre d'incitation automatisé qui résout les problèmes en collectant de manière itérative une collection d'expériences de raisonnement par essais et erreurs. Nous soutenons que le BoT proposé n'est pas une application des LLM à une tâche spécifique, mais qu'il s'appuie plutôt sur l'idée que le pouvoir de raisonnement des LLM peut être obtenu directement à partir de l'analyse des erreurs des chaînes d'inférence incorrectes sans dépendre de la connaissance a priori de l'homme.

Pour mettre en évidence nos observations, nous partageons les trois observations clés suivantes, qui sont basées sur l'ensemble de données de 24 jeux en utilisant le modèle gpt-3.5-turbo avec une température de 0,7 et une valeur p supérieure de 0,7 appliquée.

L'expérience de l'invite encourage les LLM à faire preuve de plus de logique dans leurs réponses.Comme le montre le tableau 5, le modèle a généré la même étape de raisonnement cinq fois lorsqu'aucune expérience n'était incluse dans l'indice. Cette observation montre un problème commun avec les LLMs, à savoir le manque d'auto-motivation pour explorer différentes logiques de raisonnement. Ainsi, malgré leur fort potentiel de raisonnement, les LLM peuvent être bloqués dans un cycle qui commence par l'étape de raisonnement la plus simple, qui ne peut jamais conduire à une solution finale. La section "Chaînes de raisonnement acquises" du tableau 5 illustre des chaînes de raisonnement erronées. Nous pensons que, comme dans Tree of Thoughts Yao et al. (2024), où les nœuds de l'arbre sont construits en générant des réponses multiples sous forme de pensées, de telles étapes d'inférence répétitives peuvent faire échouer l'algorithme dans certains cas. Cependant, dans la deuxième itération de BoT, l'introduction de l'expérience dans les invites a entraîné la génération de différentes étapes d'inférence initiales, comme le montre le tableau 6. La chaîne d'inférence finale peut finalement aboutir à la bonne solution en partant d'un plus large éventail de logiques potentielles. Weng et al. (2023)

Les LLM évitent de commettre les mêmes erreurs que celles mises en évidence dans l'expérience.Si l'expérience n'est pas incluse dans les messages-guides, qui comprennent l'analyse des erreurs, les MAV feront de nombreuses erreurs, telles que s'écarter des règles de la tâche et revenir à l'étape de raisonnement initiale dans le processus final, comme le montre la section "Chaîne de raisonnement acquise" du tableau 5. Après avoir analysé cette chaîne de raisonnement et incorporé son retour d'expérience dans les messages-guides de la deuxième itération de la BdT, on peut voir dans le tableau 6 que les MFR apprendront l'expérience bien avant le raisonnement. Premièrement, aucune des réponses n'a reproduit les mêmes étapes de raisonnement erronées que les diverses étapes de raisonnement initiales montrées dans "Cinq réponses de gpt-3.5-turbo". Deuxièmement, les LLM ont réussi à éviter toutes les erreurs identifiées précédemment en respectant strictement les règles de la tâche, en éliminant les raisonnements incorrects et en effectuant des étapes d'inférence logique. Troisièmement, cela a finalement conduit à la solution correcte pour la tâche "1 1 4 6" du jeu de 24. D'autres travaux, tels que ceux de Weng et al. (2023) ; Madaan et al. (2023) ; Zheng et al. (2023), ont également souligné l'importance d'augmenter les indices par le biais du retour d'information, qui est une auto-évaluation des réponses précédentes. Cependant, BoT est un travail précurseur basé sur l'idée que l'expérience qui inclut l'analyse des erreurs peut conduire à un raisonnement solide chez les LLM.

Sans annotations humaines, les LLM organisent automatiquement des chaînes de raisonnement efficaces pour résoudre des problèmes complexes sur la base de l'expérience.BoT est l'initiative pionnière qui propose un cadre d'incitation automatisé qui s'appuie sur l'idée que les LLM peuvent acquérir des compétences de raisonnement efficaces pour la résolution de problèmes grâce à l'analyse des erreurs et à l'orientation par l'expérience seule, sans avoir besoin d'une annotation humaine. Comme le montre le tableau 5, il s'agit de la première itération de BoT, et les conseils initiaux ne contiennent que des conseils et des questions de base sur la tâche sans exemples d'apprentissage contextuels comme dans CoT. Même si les chaînes d'inférence obtenues par les LLMs utilisant de telles invites contiennent beaucoup d'erreurs et d'étapes d'inférence invalides, leurs analyses d'erreurs et suggestions peuvent être incluses comme leçons apprises dans les invites d'entrée pour bénéficier à la deuxième itération d'inférence, comme montré dans le tableau 6. On peut observer qu'en l'absence de conseils humains sur la procédure de raisonnement correcte, les LLM peuvent acquérir des connaissances par l'expérience, y compris des analyses d'erreurs et des conseils, qui sont obtenus à partir de chaînes de raisonnement générées précédemment, ce qui conduit à des améliorations incrémentales dans la résolution de problèmes de raisonnement.

Ainsi, notre BoT fournit une orientation à long terme pour la recherche, car elle démontre l'importance de l'analyse des erreurs de rappel et des suggestions lorsqu'il s'agit de permettre aux MFR de générer des processus de raisonnement efficaces pour des tâches complexes. Grâce à ces connaissances, la recherche sur l'ingénierie des indices visant à induire des capacités de raisonnement chez les MFR peut se concentrer sur la manière de générer des expériences plutôt que d'introduire des connaissances a priori plus humaines.

C Génération de structures de réflexion

BoT est un cadre d'incitation automatisé qui accumule itérativement l'expérience acquise à partir des analyses de la chaîne d'inférence. En tant que tel, BoT est généralisé à une variété de méthodes de génération de pensée et de LLMs capables de générer et d'évaluer des étapes d'inférence.En outre, la performance de BoT dépend de l'efficacité de sa structure de génération de pensée. Par conséquent, BoT utilise la structure la plus récente, l'arbre de pensée (ToT) de Yao et al. (2024), comme modèle de base pour générer des chaînes de raisonnement à chaque itération. Comme mentionné dans l'article principal, le modèle de génération de pensée de base pourrait également être un Thinking Graph (GoT) Besta et al. (2023), c'est-à-dire BoT avec GoT. Cependant, en raison de contraintes de temps et du fait que le GoT actuel n'a pas encore été appliqué à des problèmes mathématiques, la conception de BoT utilise exclusivement ToT. En outre, lorsqu'elle est utilisée comme modèle de base dans le mécanisme de boosting, la structure de pensée dans chaque itération peut être maintenue légère. En fin de compte, la BoT proposée génère des structures arborescentes hétérogènes, où chaque arbre est un arbre binaire légèrement pondéré.

C1 Génération de la pensée suivante et calcul du poids de l'arête

En utilisant l'indice de génération de la pensée suivante discuté dans la section A, les LLM peuvent générer des indices en combinant l'expérience F1.... .t et en remplaçant {Gi} par z1.... i-1 remplaçant {Gi} pour générer la prochaine pensée possible pour une étape de raisonnement zi. Pour une étape de raisonnement zi, les LLM utilisent l'indice d'évaluation de la pensée pour générer des scores d'évaluation comme poids d'arête entre zi et zi-1. Voir le code source dans examples/BoostingOfThought/BoT reasoner.py pour une procédure détaillée. Comme exemple direct de BoT appliqué à '3 5 6 8' dans Game of 24, en utilisant gpt-3.5-turbo, les tableaux 7 et 8 montrent la génération des pensées, tandis que le tableau 9 montre comment elles sont calculées.

C2 Nécessité de structures arborescentes hétérogènes

Dans chaque itération de BoT, la structure d'arbre hétérogène est construite pour explorer un espace de recherche d'inférence plus large et améliorer la robustesse. Comme le montre le code source sous examples/BoostingOfThought/BoT core.py, les valeurs de température et de Top p des LLM dans chaque arbre sont sélectionnées dans les plages [0.2, 0.4, 0.6, 0.7, 0.9, 1.1, 1.5] et [0.1, 0.3, 0.5, 0.7, 0.9], respectivement. La stratégie de croissance de l'arbre peut se faire couche par couche ou feuille par feuille. Nous avons observé les deux avantages suivants à garantir cette hétérogénéité.

L'hétérogénéité étend l'espace de recherche de l'inférence et augmente ainsi la vitesse de convergence.Lorsque différents arbres sont construits à des fins différentes, par exemple, explorés à l'aide d'une stratégie couche par couche ou exploités à l'aide d'une stratégie feuille par feuille, et basés sur des LLM aléatoires ou déterministes, les étapes de raisonnement générées et les chaînes d'inférence qui en résultent peuvent présenter des différences significatives, couvrant effectivement un éventail plus large de possibilités de raisonnement. Par exemple, lors d'une itération, lorsque les LLM génèrent la pensée suivante avec plus de confiance, les pensées similaires sont continuellement explorées ; dans le cas contraire, les LLM plus aléatoires ont tendance à générer des pensées diverses. Il est souvent difficile de prédire si le raisonnement déterministe ou aléatoire contribuera à une solution. Par conséquent, assurer l'hétérogénéité en mélangeant différents types d'étapes de raisonnement logique nous permet d'explorer pleinement l'espace de raisonnement en une seule itération, ce qui facilite finalement les itérations suivantes. Dans l'étude d'ablation, nous comparons les performances de BoT entre des structures arborescentes hétérogènes et homogènes.

L'hétérogénéité réduit la probabilité de générer des chaînes d'inférence invalides ou incorrectes, ce qui améliore la robustesse.Contrairement à l'hétérogénéité, dans les arbres avec une configuration homogène, les arbres individuels ont tendance à suivre une logique générative cohérente et à construire des chaînes d'inférence avec la même structure d'arbre. Ainsi, lorsque la logique est erronée ou que la structure sous-jacente n'est pas valable pour le problème en question, les chaînes de raisonnement de tous les arbres obtenus par BoT à chaque itération ne peuvent contenir que des étapes de raisonnement bruyantes et incorrectes. Même en les agrégeant pour obtenir une chaîne de raisonnement plus raffinée à des fins d'évaluation, l'expérience peut encore s'écarter considérablement de la fourniture de conseils appropriés pour la résolution du problème. Par conséquent, la conception d'une structure arborescente hétérogène peut contribuer à réduire la probabilité qu'il n'y ait pas de chaînes de raisonnement valides disponibles pour l'évaluation lors des itérations suivantes du BdT. Cette robustesse accrue permet à la BdT de résoudre des problèmes de différents niveaux de difficulté.

Cette image illustre le processus d'"agrégation de la plus haute priorité" et d'"agrégation gourmande".

Entrée : m chaînes d'inférence, où l'étape d'inférence d'une m-ième chaîne est notée z1i = 1m.
Résultat : chaîne polymérique z1..n.

1 - agrégation de la plus haute priorité
2 Pour chaque chaîne m = 1, 2, ... , M faire
3 Calculer la somme des poids des arêtes de la m-ième chaîne sous la forme Vm = ∑i dans l'intervalle m1m Vi-1,i.
4. Fin
5 Obtenir la chaîne optimale parmi M chaînes en effectuant m* = arg maxm {Vm}
6 Assigner la chaîne agrégée comme chaîne optimale, z1.... .n := {z1i=1n*m*}

7 - Agrégation gourmande
8 z1 := z1 où m* = arg maxm {V1m}.
9 Pour chaque étape d'agrégation i = 2, ... , n faire
10 Pour chaque chaîne m = 1, 2, ... , M faire
11 Collecter Jm = {j, sim(z1i-1, z1j) > 0.7 ; j ∈ n1m}.
12 Obtain j*,m = arg maxj∈Jm {Vj,j+1m}
13 Fin
14 Pour obtenir la prochaine étape d'inférence optimale, procédez comme suit : zi = z1j*+1 où j* = arg maxj∈{j*m}1M {Vj,j+1m}.
15 Fin
16 Obtenir des chaînes polymères z1.... .n.

Il s'agit essentiellement d'un organigramme algorithmique décrivant la manière d'optimiser une chaîne de données ou un nœud et d'obtenir les meilleurs résultats grâce à différentes méthodes.

D Agrégation des structures de pensée

Après avoir complété le raisonnement dans une structure arborescente hétérogène, le processus d'agrégation de BoT extrait d'abord les meilleures chaînes de raisonnement de chaque arbre, puis les combine en une seule chaîne de raisonnement à l'aide des méthodes d'agrégation "best-first" ou "greedy". Des informations plus détaillées sur ces deux méthodes d'agrégation peuvent être trouvées dans le code source examples/BoostingOfThought/BoT aggregator.py.

Comme le montre le premier bloc de l'algorithme 16, l'agrégation au mieux est une méthode d'agrégation simple qui extrait directement la chaîne dont la somme des poids des arêtes est la plus élevée. Cette méthode est rapide et stable. Elle garantit généralement des performances compétitives car l'expérience ultérieure peut être générée en analysant les chaînes optimales obtenues. Cependant, elle ne peut sélectionner que des chaînes existantes sans réglage efficace. L'agrégation gourmande est plus avancée car elle combine les étapes d'inférence de différentes chaînes pour produire une nouvelle et meilleure chaîne d'inférence avec les poids de bord les plus élevés. Le processus d'agrégation avide de l'algorithme 16 se compose de deux étapes. Premièrement, il rassemble les étapes d'inférence qui sont similaires à l'étape d'inférence agrégée zi-1 . Par conséquent, l'étape d'inférence agrégée suivante est sélectionnée à partir de l'étape d'inférence suivante dans cet ensemble de collecte en maximisant les poids des bords. sim est une fonction de similarité qui évalue le pourcentage de mots et de nombres mathématiques identiques entre deux passages à l'aide de LLM. 0,7 est un seuil empirique obtenu à partir des expériences.

E Impact d'un retour d'information erroné

Le retour d'information obtenu par l'évaluation des chaînes d'inférence agrégées peut inclure une utilisation limitée des analyses et des conclusions et rapports d'erreur complètement erronés. Ce problème est généralement dû à la nature des LLM, qui sont des modèles de langage et ne vérifient pas intrinsèquement l'exactitude du texte généré. En outre, les capacités des LLM, tels que gpt-3.5-turbo, sont limitées lorsqu'ils sont utilisés comme validateurs pour des problèmes mathématiques.

Un exemple simple est présenté dans le tableau 7. L'analyse conclut que "le résultat final obtenu à l'étape 3 est 80, ce qui est mathématiquement égal à 24". Pire, l'expérience contient en outre que "la chaîne de raisonnement est correcte" et qu'"aucune erreur n'a été trouvée dans les étapes du raisonnement". Aucune erreur n'a été trouvée." En utilisant cette expérience comme indice d'entrée, lors de la première itération, la BdT est amenée à générer la mauvaise étape d'inférence, et la chaîne d'agrégation correspondante peut être observée au début du tableau 8. Il est clair que la chaîne d'agrégation est logiquement incorrecte et ne respecte aucune des règles du jeu 24.

Cependant, nous soutenons que le retour d'information erroné ne sera pas amplifié, mais que son impact négatif sur les étapes de raisonnement générées peut être atténué, voire entièrement corrigé, lors des itérations suivantes grâce au mécanisme itératif de la BdT. La principale raison en est que les étapes de raisonnement erronées générées seront analysées plus en détail afin de générer de nouvelles expériences qui seront ajoutées à l'indice. Plus précisément, étant donné que ces étapes de raisonnement contiennent des erreurs facilement reconnaissables et évidentes, les LLM ont tendance à générer des analyses d'erreurs correctes et à fournir des suggestions de révision efficaces. Avec la nouvelle expérience incluse dans les indices, la BdT est capable de générer des étapes de raisonnement correctes. Comme le montrent les expériences du tableau 8, la BdT a généré des rapports d'erreur détaillés et des suggestions de révision, ce qui a donné lieu à un processus de génération de pensée rationnelle.

L'avantage de BoT dans l'utilisation des itérations pour atténuer les effets négatifs du retour d'erreur est évident dans la figure 4. Notamment, les performances de la BoT s'améliorent régulièrement à mesure que le nombre d'itérations augmente. Cela souligne l'importance de l'expérience cumulée et la capacité de l'expérience ultérieure à corriger les erreurs précédentes.

F Plus de résultats pour maths

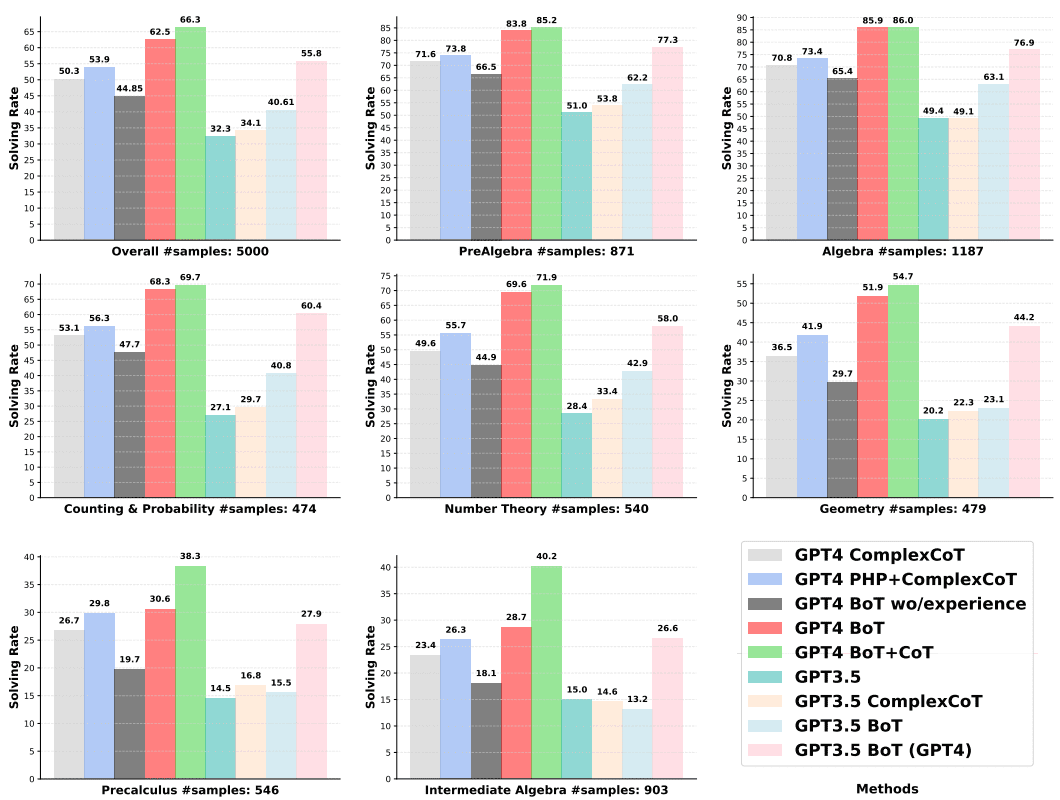
Fig. 5 : révèle l'efficacité de l'utilisation de différentes stratégies pour résoudre tous les problèmes classés dans l'ensemble de données MATH. Les stratégies sont comparées sur la base des catégories suivantes : pré-algèbre, algèbre, comptage et probabilité, principes de la théorie des nombres, géométrie, pré-calcul et algèbre intermédiaire. Le sous-graphe intitulé "global" montre le taux de résolution global pour tous les problèmes, toutes catégories confondues.

La figure 5 présente les taux de résolution des différentes méthodes pour chaque catégorie de l'ensemble de données MATH. La complexité et la diversité des différents problèmes mathématiques de ces catégories constituent une référence plus difficile pour le raisonnement mathématique. Ainsi, la complexité et la diversité des problèmes de MATH requièrent un large éventail de compétences de raisonnement pour les résoudre. Par conséquent, un examen détaillé de notre approche et sa comparaison avec d'autres approches dans notre contexte peuvent fournir des informations précieuses.

LLMs.Les expériences menées sur l'ensemble de données MATH ont utilisé des grands modèles linguistiques (LLM) bien connus, à savoir GPT-3.5-Turbo, ci-après dénommé GPT3.5, et GPT-4, ci-après dénommé GPT4. Nous avons directement utilisé l'API publiée par l'OPENAI.

Rivaux.
- GPT4 ComplexCoT. qui est un modèle de GPT4 utilisant la méthode d'incitation Complex CoT Fu et al. (2022). Des exemples de raisonnement sont utilisés dans les indices d'inférence, qui sont tirés de la publication correspondante de Complex CoT Fu et al. (2022). Étant donné que le décodage avide est utilisé, nous ne suivons pas l'approche autoconsistante de Wang et al. (2022) pour l'échantillonnage des chemins d'inférence.
- GPT3.5. des invites standard sont utilisées et des modèles GPT3.5 sont utilisés pour générer des réponses.
- GPT3.5 ComplexCoT. Similaire au GPT4 ComplexCoT, mais avec le modèle changé en GPT3.5.
- GPT4 PHP+ComplexCoT. Il s'agit du modèle GPT4 utilisant PHP Zheng et al. (2023) + Complex CoTFu et al. (2022). Plus précisément, dans le cadre de PHP Zheng et al. (2023), les invites de Complex CoT sont utilisées pour générer des réponses de base initiales, puis PHP+Complex CoT peut développer des invites ultérieures générant des réponses à partir de ces réponses de base. Ainsi, au début d'une interaction, les réponses de base peuvent être générées en transmettant les indices de base de Complex CoT et la question actuelle au LLM. Ensuite, en s'appuyant sur les indices du CoT complexe révisés à la version PHP avec des phrases d'indices supplémentaires, le cadre d'indices étape par étape s'exécute sur cette réponse de base pour générer la réponse correcte. C'est ce que nous appelons la contrepartie PHP+Complex CoT de la PHP-Complex CoT dans le travail original. La Complex CoT a un nombre de coups de 8.
- Le modèle GPT4 est utilisé pour effectuer le raisonnement du cadre de la BdT sans accumuler d'expérience. La configuration de base de la BdT suit celle présentée dans le document principal. Ainsi, après une itération, les chaînes agrégées seront utilisées comme solution.
- GPT4 BoT. GPT4 est utilisé pour réaliser la version complète de la BoT présentée dans l'article principal.
- GPT4 BoT + CoT. En plus du cadre BoT, les messages-guides comprenaient 5 exemples de raisonnement tirés de la publication CoT Wei et al. (2022). Ainsi, à chaque itération, les messages-guides contiennent non seulement l'expérience, mais aussi les 5 exemples de raisonnement supplémentaires de CoT.
- GPT3.5 BoT. similaire au GPT4 BoT, mais avec le modèle changé en GPT3.5.
- GPT3.5 BoT (GPT4). Dans cette expérience, nous utilisons GPT3.5 pour raisonner et ainsi générer des chaînes de pensées dans la génération de structures de pensée.

Toutefois, le modèle GPT4 a été utilisé pour obtenir une évaluation et un retour d'information analytique lors de l'évaluation de la pensée et de la génération d'expériences dans le cadre d'une analyse agrégée de la chaîne de pensée.

Les résultats de la figure 5 nous permettent de faire les observations supplémentaires suivantes.

L'excellente performance de BoT dans la résolution de problèmes plus complexes est largement due à l'expérience.Les méthodes liées à la BoT, telles que GPT4 BoT et GPT4 BoT + CoT, atteignent systématiquement les taux de résolution de problèmes les plus élevés dans les différentes sous-catégories de MATH. Plus précisément, GPT4 BoT devance la meilleure solution disponible, GPT4 PHP + ComplexCoT, de 8,61 TP3T, tandis que GPT4 BOT + CoT la devance de 12,41 TP3T. Dans l'ensemble des sept catégories, GPT4 BoT surpasse GPT4 PHP + ComplexCoT d'au moins 0,81 TP3T, avec son problème algébrique Il en va de même pour GPT3.5 BoT et GPT3.5 BoT + CoT. Cependant, lorsqu'il n'y a pas d'expérience accumulée dans le cadre BoT, toutes les performances en matière de résolution de problèmes mathématiques sont considérablement réduites, comme le montre l'expérience GPT4 BoT wo/.

Outre l'expérience de l'analyse des erreurs, l'inclusion d'exemples corrects, tels que des exemples simples de CdT, est essentielle pour améliorer l'efficacité de la CdT dans la résolution de problèmes mathématiques difficiles.Cependant, dans les domaines de l'algèbre avancée et intermédiaire, où le besoin d'un raisonnement plus complexe et de solutions logiques complexes étape par étape est plus élevé, les améliorations de la BoT ne sont que de 0,8% et 2,4%.Ces gains sont relativement limités par rapport aux améliorations significatives observées dans la résolution de catégories de problèmes plus simples. Ces gains sont relativement limités par rapport aux améliorations significatives observées lors de la résolution de catégories de problèmes plus simples. Cependant, lorsque cinq instances correctes de CoT ont été ajoutées directement à l'invite d'entrée, le GPT-4 BoT + CoT a considérablement amélioré ses performances dans les domaines de l'algèbre avancée et de l'algèbre intermédiaire, surpassant le GPT-4 BoT de 7,71 TP3T et 11,51 TP3T, respectivement.La conclusion sous-jacente de ces observations est que pour s'assurer que la BoT atteint les meilleures performances possibles lors de la résolution de problèmes mathématiques complexes, l'analyse essai-erreur pour apprendre le raisonnement n'est pas la seule façon de s'assurer que la BoT peut atteindre les meilleures performances possibles. En effet, l'analyse par essais et erreurs pour apprendre le raisonnement n'est pas suffisante et devrait s'appuyer sur la fourniture de réponses correctes aux MLD dans l'invite d'entrée.

Bien qu'au départ, la BoT GPT3.5 soit légèrement inférieure à la CoT GPT-4, lorsque l'expérience est acquise en utilisant la GPT-4 comme outil d'évaluation et d'analyse, il est possible de faire en sorte que la BoT GPT-3.5 (GPT-4) soit plus performante que la CoT GPT-4 complexe.En utilisant GPT3.5, qui a une capacité plus petite que GPT4, comme LLM, BoT a obtenu un taux de solution au moins 7,71 TP3T plus bas que GPT4 ComplexCoT (particulièrement dans la discipline de l'algèbre). Par conséquent, après avoir utilisé GPT3.5 pour générer uniquement l'étape d'inférence à côté de l'expérience générée par GPT4, GPT3.5 BoT (GPT4) a montré une amélioration significative dans toutes les catégories, conduisant à un taux de solution de 55,81 TP3T, qui est plus élevé que celui de GPT4 ComplexCoT de 5,51 TP3T, et même de 1,91 TP3T par rapport à l'état de l'art actuel GPT4 PHP+ComplexCoT. Ces observations prouvent une fois de plus que l'expérience acquise par itération dans les indices est la principale raison du succès du cadre BoT.

G Résultats du raisonnement pour le jeu 24 points

Tout d'abord, dans les tableaux 5 à 9, nous montrons les indices détaillés utilisés par BoT dans le processus de raisonnement, fournissant ainsi une compréhension complète de ce que BoT fait à chaque itération. Ensuite, à partir du tableau 10, nous présentons des exemples précis qui englobent l'ensemble du processus de raisonnement de BoT. Suivant la configuration de base présentée dans la section Expériences, ces expériences ont été réalisées en utilisant le modèle GPT-3.5-turbo avec BoT.

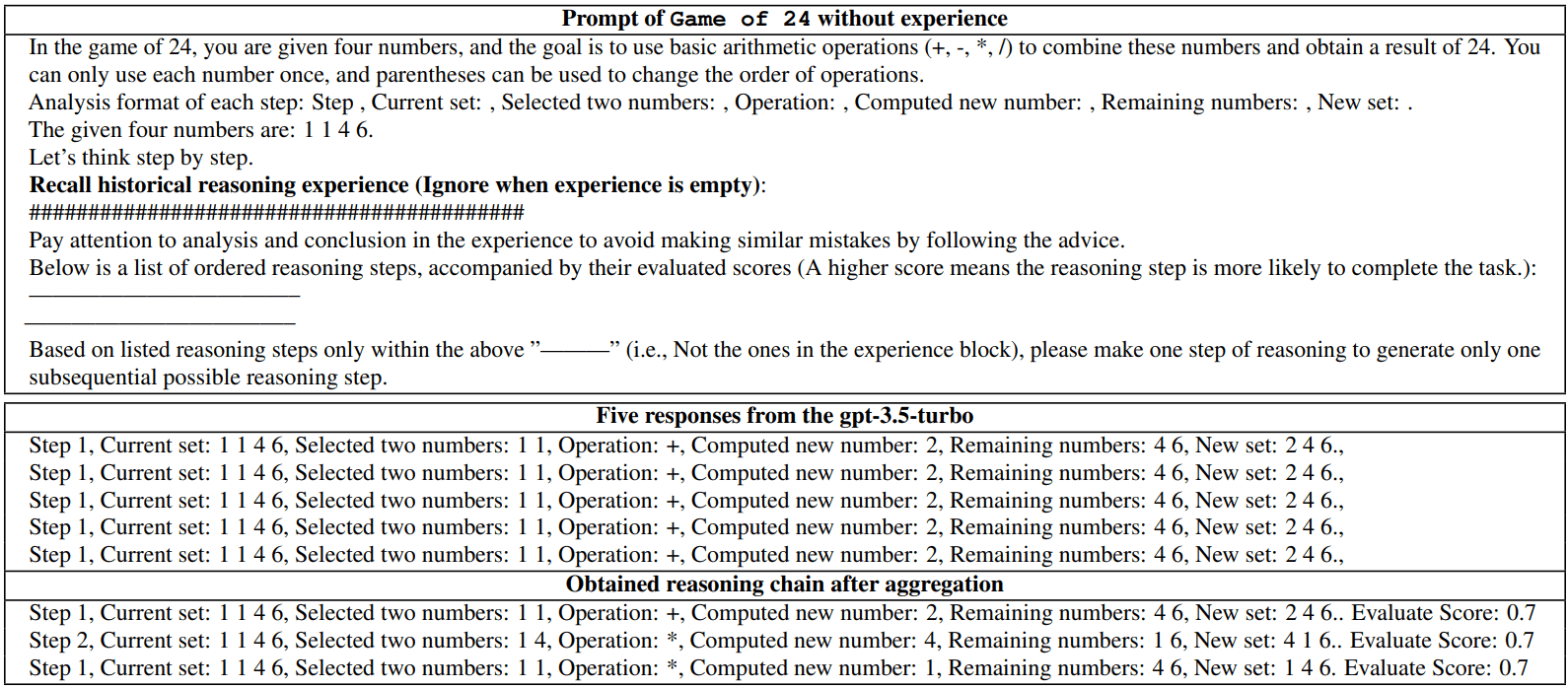
Tableau 5 : Étapes d'inférence générées par gpt-3.5-turbo lorsqu'aucune expérience n'est incluse dans l'invite d'entrée.Le modèle génère d'abord cinq étapes d'inférence pour vérifier la diversité, puis présente la chaîne d'inférence finale après avoir effectué la première itération de la BdT.

Conseils pour le jeu 24:00, sans expérience

Dans 24 Points, quatre nombres vous sont donnés et l'objectif est d'utiliser les opérations arithmétiques de base (+, -, *, /) pour combiner ces nombres et obtenir le résultat 24. Vous ne pouvez utiliser chaque nombre qu'une seule fois et vous pouvez utiliser des parenthèses pour modifier l'ordre des opérations.

Analyser chaque étape du format :
Étape X. Ensemble actuel : XXXX, deux nombres sélectionnés : XX XX, opération : XX, nouveau nombre obtenu par calcul : XX, nombres restants : XXXX, nouvel ensemble : XXXX.

Les quatre nombres donnés sont : 1 1 4 6.
Réfléchissons étape par étape.

Rappeler l'expérience historique du raisonnement (ignorer si l'expérience est nulle) :
## ############### ######## ######## # # # #######
Prêtez attention aux analyses et aux conclusions de l'expérience et évitez de commettre les mêmes erreurs en suivant les recommandations.
Vous trouverez ci-dessous une série d'étapes de raisonnement ordonnées, accompagnées de leurs scores d'évaluation (des scores plus élevés signifient que l'étape de raisonnement est plus susceptible de mener à bien la tâche). :

Sur la base des étapes de raisonnement énumérées dans "_" ci-dessus (c'est-à-dire pas les étapes du bloc empirique), veuillez effectuer une étape de raisonnement pour générer la seule étape de raisonnement ultérieure possible.

Cinq réponses de gpt-3.5-turbo
Étape 1, Ensemble actuel : 1 1 4 6, Deux nombres choisis : 1 1, Opération : +, Nouveau nombre calculé : 2, Nombres restants : 4 6, Nouvel ensemble : 2 4 6, Score d'évaluation : 0.7
Étape 1, Ensemble actuel : 1 1 4 6, Deux nombres choisis : 1 1, Opération : +, Nouveau nombre calculé : 2, Nombres restants : 4 6, Nouvel ensemble : 2 4 6, Score d'évaluation : 0.7
Étape 1, Ensemble actuel : 1 1 4 6, Deux nombres choisis : 1 1, Opération : +, Nouveau nombre calculé : 2, Nombres restants : 4 6, Nouvel ensemble : 2 4 6, Score d'évaluation : 0.7
Étape 1, Ensemble actuel : 1 1 4 6, Deux nombres choisis : 1 1, Opération : +, Nouveau nombre calculé : 2, Nombres restants : 4 6, Nouvel ensemble : 2 4 6, Score d'évaluation : 0.7
Étape 1, Ensemble actuel : 1 1 4 6, Deux nombres choisis : 1 1, Opération : *, Nouveau nombre calculé : 1, Nombres restants : 4 6, Nouvel ensemble : 1 4 6, Score d'évaluation : 0.7

Chaîne d'inférence obtenue après agrégation
Étape 1, Ensemble actuel : 1 1 4 6, Deux nombres choisis : 1 1, Opération : +, Nouveau nombre calculé : 2, Nombres restants : 4 6, Nouvel ensemble : 2 4 6... Évaluer la fraction : 0,7
Étape 2, ensemble actuel : 1 1 4 6, deux nombres choisis : 1 4, opération : *, nouveau nombre calculé : 4, nombres restants : 1 6, nouvel ensemble : 4 1 6... Score d'évaluation : 0.7
Étape 1, Ensemble actuel : 1 1 4 6, Deux nombres choisis : 1 1, Opération : *, Nouveau nombre calculé : 1, Nombres restants : 4 6, Nouvel ensemble : 1 4 6, Score d'évaluation : 0.7

H Résultats de la dérivation pour "GSM8K".

Le BoT fonctionne à l'aide d'invites de base et de formats spécifiques similaires à ceux présentés dans les tableaux 5 à 9. La seule chose qui changerait serait l'invite à la tâche, comme le montre le tableau 15. À partir du tableau 16, nous fournissons un certain nombre d'exemples détaillés qui contiennent le processus de raisonnement complet de la BoT. Ces expériences sont basées sur la configuration de base présentée dans la section Expériences, en utilisant le modèle GPT-3.5-turbo de BoT.

# Exercices de raisonnement empirique pour le jeu 24

## Tout d'abord, il convient d'examiner l'expérience historique en matière de raisonnement :

### Chaîne de déduction 1 et ses commentaires

Vous trouverez ci-dessous une chaîne de raisonnement présentée dans l'ordre :

---

### Étape 1
Ensemble actuel : 1 1 4 6, deux nombres choisis : 1 1, opération : +, nouveau nombre calculé : 2, nombres restants : 4 6, nouvel ensemble : 2 4 6... Score d'évaluation : 0.7

### Étape 2
Ensemble actuel : 1 1 4 6, deux nombres choisis : 1 4, opération : *, nouveau nombre calculé : 4, nombres restants : 1 6, nouvel ensemble : 4 1 6... Score d'évaluation : 0.7

### Étape 3
Ensemble actuel : 1 1 4 6, deux nombres choisis : 1 1, opération : *, nouveau nombre calculé : 1, nombres restants : 4 6, nouvel ensemble : 1 4 6. Score de l'évaluation : 0,7

---

## ANALYSE : Cette chaîne de raisonnement ne permet pas de réaliser la tâche et d'atteindre l'objectif correctement. Des erreurs dans les étapes du raisonnement ont empêché la découverte de la bonne solution.

### Raisonnement Étape 1
Cette étape est une extrapolation logique de l'étape précédente, puisqu'elle suit la règle consistant à sélectionner deux nombres, à effectuer l'opération et à mettre à jour l'ensemble en conséquence. Cependant, cette étape ne contribue pas à la bonne solution. Le nouveau nombre 2 obtenu par le calcul ne conduit pas au résultat souhaité 24.
**Suggestion** : Essayez différentes opérations ou combinaisons de nombres pour obtenir un nouveau nombre plus proche de 24.
**Recommandation ou description du rejet** : Rejeté.

### Raisonnement Étape 2
Une erreur s'est glissée dans la description de l'étape de raisonnement. Elle est incorrectement appelée deux fois "étape de raisonnement 2". Cependant, en supposant qu'il s'agisse de la seule étape, il s'agit d'une déduction logique de l'étape précédente. L'opération de multiplication (*) est correctement appliquée au nombre sélectionné et donne le nouveau nombre 4. Les autres nombres sont mis à jour en conséquence.
**Description recommandée ou rejetée** : Recommandée.

### Raisonnement Étape 3
Une erreur s'est glissée dans la description de l'étape de raisonnement. Elle est incorrectement appelée "Étape de raisonnement 1" au lieu de "Étape de raisonnement 3". Cette étape n'est pas une déduction logique de l'étape précédente. L'opération de multiplication (*) est appliquée aux mêmes nombres qu'à l'étape de raisonnement 1, mais le nouveau nombre 1 est calculé différemment. Les autres nombres sont mis à jour en conséquence.
**Rapport de bogue** : Le calcul dans cette étape est erroné. Le calcul correct devrait être 1 * 1 = 1.
**Recommandation** : Vérifiez deux fois les calculs pour vous assurer qu'ils sont exacts.
**Recommandation ou description du rejet** : Rejeté.

**Score de confiance** : 0,7

---

## Cinq réponses de gpt-3.5-turbo

---

### Étape 1
Ensemble actuel : 1 1 4 6, deux nombres sélectionnés : 1 4, opération : *, nouveau nombre calculé : 4, nombres restants : 1 6, nouvel ensemble : 1 4 6.....

### Étape 1
Ensemble actuel : 1 1 4 6, deux nombres sélectionnés : 1 6, opération : +, nouveau nombre calculé : 7, nombres restants : 1 4, nouvel ensemble : 1 4 7.....

### Étape 1
Ensemble actuel : 1 1 4 6, deux nombres choisis : 1 1, opération : *, nouveau nombre calculé : 1, nombres restants : 4 6, nouvel ensemble : 1 4 6.....

### Étape 1
Ensemble actuel : 1 1 4 6, deux nombres choisis : 1 4, opération : /, nouveau nombre calculé : 0,25, nombres restants : 1 6, nouvel ensemble : 0,25 1 6..., et

### Étape 1
Ensemble actuel : 1 1 4 6, deux nombres choisis : 1 1, opération : -, nouveau nombre calculé : 0, nombres restants : 4 6, nouvel ensemble : 0 4 6....

---

## Chaîne d'inférence après agrégation

---

### Étape 1
Ensemble actuel : 1 1 4 6, deux nombres choisis : 1 1, opération : *, nouveau nombre calculé : 1, nombres restants : 4 6, nouvel ensemble : 1 4 6... Score d'évaluation : 0.9

### Étape 2
Ensemble actuel : 1 4 6, deux nombres choisis : 1 4, opération : *, nouveau nombre calculé : 4, nombres restants : 6, nouvel ensemble : 4 6... Score d'évaluation : 0,7

### Étape 3
Ensemble actuel : 46, Deux nombres choisis : 4 6, Opération : *, Nouveau nombre calculé : 1, Nombres restants :, Nouvel ensemble : 24. Score de l'évaluation : 0.9

---

Tableau 6 : Étapes de raisonnement générées par gpt-3.5-turbo lors de l'incorporation de l'expérience dans l'invite de saisie. Cette expérience est une analyse de la chaîne de raisonnement du tableau 5. Après avoir intégré cette expérience dans l'invite, nous montrons la chaîne d'inférence finale formée après cinq réponses du modèle et l'achèvement de la deuxième itération de la BdT.

# Conseil de la génération de la pensée suivante

Dans le jeu des 24 points, quatre nombres vous sont proposés et le but est de les combiner en utilisant les opérations arithmétiques de base (+, -, *, /) pour obtenir le résultat 24. Chaque nombre ne peut être utilisé qu'une seule fois et vous pouvez utiliser des parenthèses pour modifier l'ordre des opérations.

Format d'analyse pour chaque étape : étape , ensemble actuel : , deux nombres sélectionnés : , opération : , nouveau nombre calculé : , nombres restants : , nouvel ensemble : .

Les quatre nombres donnés sont : 3 5 6 8.

Réfléchissons étape par étape.

## Tout d'abord, il convient d'examiner l'expérience historique en matière de raisonnement :

### 1ère chaîne de raisonnement et commentaires

Ce qui suit est une chaîne de raisonnement contenant les étapes de raisonnement présentées dans l'ordre :

---

Étape 1, ensemble actuel : 3 5 6 8, deux nombres choisis : 5 6, opération : *, nouveau nombre calculé : 30, nombres restants : 3 8, nouvel ensemble : 30 3 8... Score d'évaluation : 0.9

Étape 2, ensemble actuel : 30 3 8, deux nombres choisis : 30 3, opération : /, nouveau nombre calculé : 10, nombres restants : 8, nouvel ensemble : 10 8... Score d'évaluation : 0.9

Étape 3, ensemble actuel : 10 8, deux nombres sélectionnés : 10 8, opération : *, nouveau nombre calculé : 80, nombres restants : aucun, nouvel ensemble : 80... Résultat de l'évaluation : 0,9.

---

## Rapport d'analyse

Cette chaîne de raisonnement permet de réaliser correctement la tâche et d'atteindre l'objectif en effectuant ses étapes de raisonnement. Le résultat final obtenu à l'étape 3 est 80, ce qui correspond mathématiquement à 24.

### Raisonnement Étape 1
Cette étape de raisonnement est une dérivation logique de l'étape précédente. Sélectionnez les nombres 5 et 6 de l'ensemble actuel (3 5 6 8) et multipliez-les pour obtenir le nouveau nombre 30. Les nombres restants sont 3 et 8. Cette étape du raisonnement permet de trouver la bonne solution car elle réduit le nombre d'éléments de l'ensemble et génère un nouveau nombre.

### Raisonnement Étape 2
Cette étape de raisonnement est une dérivation logique de l'étape précédente. Sélectionnez les nombres 30 et 3 dans l'ensemble actuel (30 3 8) et divisez-les pour obtenir le nouveau nombre 10. Le nombre restant est 8. Cette étape du raisonnement contribue à la bonne solution car elle réduit encore le nombre d'éléments dans l'ensemble et génère un nouveau nombre.

### Raisonnement Étape 3
Cette étape de raisonnement est une dérivation logique de l'étape précédente. Sélectionnez les nombres 10 et 8 dans l'ensemble actuel (10 8) et multipliez-les pour obtenir le nouveau nombre 80.Comme il n'y a plus de nombres, le résultat de la chaîne de raisonnement est 80.Cette étape de raisonnement aide à trouver une solution correcte car elle génère le résultat final.

Suggestion : aucune erreur n'a été trouvée dans les étapes du raisonnement.

Description recommandée ou rejetée : toutes les étapes du raisonnement sont recommandées parce qu'elles sont correctes et permettent de parvenir à la bonne solution.

Score de confiance : 0,9

### 2ème chaîne de raisonnement et commentaires

A suivre, dans le tableau 8

### Notes sur les analyses et les conclusions

Évitez de commettre les mêmes erreurs en suivant les recommandations basées sur les analyses et les conclusions de l'expérience.

Voici une liste d'étapes de raisonnement ordonnées avec leurs scores d'évaluation (des scores plus élevés signifient que l'étape de raisonnement est plus susceptible de mener à bien la tâche). :

---

Étape 1, ensemble actuel : 3 5 6 8, deux nombres choisis : 3 8, opération : +, nouveau nombre calculé : 11, nombres restants : 5 6, nouvel ensemble : 11 5 6... Score d'évaluation : 0.7

Étape 2, ensemble actuel : 11 5 6, deux nombres choisis : 5 6, opération : *, nouveau nombre calculé : 30, nombre restant : 11, nouvel ensemble : 30 11... Score d'évaluation : 0.9

---

Sur la base des étapes de raisonnement énumérées dans "---" ci-dessus (c'est-à-dire pas les étapes du bloc empirique), veuillez effectuer une étape de raisonnement qui génère la seule étape de raisonnement possible ultérieure.

 

## Généré Prochain raisonnement

Étape 3, Ensemble actuel : 30 11, Deux nombres sélectionnés : 30 11, Opération : -, Nouveau nombre calculé : 19, Nombres restants :, Nouvel ensemble : 19.

Tableau 7 : Exemples de réflexions possibles de la BoT lors de la génération de l'étape d'inférence zi correspondante.

## 2ème chaîne de raisonnement et commentaires

Ce qui suit est une chaîne de raisonnement contenant les étapes de raisonnement présentées dans l'ordre :

---

### Étape 1
Ensemble actuel : 10 8, Deux nombres sélectionnés : 10 8, Opération : /, Nouveau nombre calculé : 1.25, Nombres restants : aucun, Nouvel ensemble : 1.25. Score de l'évaluation : 0.8.

### Étape 2
Ensemble actuel : 10 8, deux nombres choisis : 10 8, opération : /, nouveau nombre calculé : 1.25, nombres restants : aucun, nouvel ensemble : 1.25... Score d'évaluation : 0.8.

### Étape 3
Ensemble actuel : 10 8, deux nombres choisis : 10 8, opération : /, nouveau nombre calculé : 1.25, nombres restants : aucun, nouvel ensemble : 1.25... Score d'évaluation : 0.8.

---

## Rapport d'analyse

Cette chaîne de raisonnement ne permet pas de réaliser correctement la tâche et d'atteindre le but. Les étapes de raisonnement fournies sont incorrectes et ne permettent pas d'obtenir un résultat de 24.

### Raisonnement Étape 1
Cette étape du raisonnement est erronée. Les deux nombres sélectionnés 10 et 8 ne font pas partie de l'ensemble des nombres 3, 5, 6 et 8. De plus, l'opération diviser(/) n'aboutit pas à un nouveau nombre calculé comme 1,25. Les autres nombres ne sont pas correctement identifiés.

**Rapport d'erreur** :
- Les deux nombres sélectionnés n'existent pas dans l'ensemble des nombres donnés.
- L'opération et les nouveaux chiffres calculés sont erronés.
- Les chiffres restants ne sont pas correctement identifiés.

**Recommandations** :
- Assurez-vous que les deux nombres sélectionnés existent dans l'ensemble des nombres donnés.
- Utilisez l'opération correcte pour obtenir le nouveau numéro désiré.
- Identifiez correctement les nombres restants.

**Recommander ou rejeter Description** : rejeter. Cette étape de raisonnement est erronée et ne contribue pas à la bonne solution.

### Raisonnement Étape 2
Cette étape de raisonnement est une répétition de l'étape de raisonnement 1 et constitue donc également une erreur. Cette étape contient la même erreur que l'étape précédente.

**Rapport d'erreur** :
- Les deux nombres sélectionnés n'existent pas dans l'ensemble des nombres donnés.
- L'opération et les nouveaux chiffres calculés sont erronés.
- Les chiffres restants ne sont pas correctement identifiés.

**Recommandations** :
- Assurez-vous que les deux nombres sélectionnés existent dans l'ensemble des nombres donnés.
- Utilisez l'opération correcte pour obtenir le nouveau numéro désiré.
- Identifiez correctement les nombres restants.

**Recommander ou rejeter Description** : rejeter. Cette étape de raisonnement est erronée et ne contribue pas à la bonne solution.

### Raisonnement Étape 3
Cette étape de raisonnement est une répétition de l'étape de raisonnement 1 et de l'étape de raisonnement 2. Cette étape contient les mêmes erreurs que les étapes précédentes.

**Rapport d'erreur** :
- Les deux nombres sélectionnés n'existent pas dans l'ensemble des nombres donnés.
- L'opération et les nouveaux chiffres calculés sont erronés.
- Les chiffres restants ne sont pas correctement identifiés.

**Recommandations** :
- Assurez-vous que les deux nombres sélectionnés existent dans l'ensemble des nombres donnés.
- Utilisez l'opération correcte pour obtenir le nouveau numéro désiré.
- Identifiez correctement les nombres restants.

**Recommander ou rejeter Description** : rejeter. Cette étape de raisonnement est erronée et ne contribue pas à la bonne solution.

**Score de confiance** : 0,9

Tableau 8 : Deuxième chaîne de raisonnement avec les commentaires du tableau 7.

# Pistes d'évaluation de la réflexion

Dans le jeu des 24 points, quatre nombres vous sont proposés et le but est de les combiner en utilisant les opérations arithmétiques de base (+, -, *, /) pour obtenir le résultat 24. Chaque nombre ne peut être utilisé qu'une seule fois et vous pouvez utiliser des parenthèses pour modifier l'ordre des opérations.

Format d'analyse pour chaque étape : étape , ensemble actuel : , deux nombres sélectionnés : , opération : , nouveau nombre calculé : , nombres restants : , nouvel ensemble : .

Les quatre nombres donnés sont : 3 5 6 8.

Réfléchissons étape par étape.

Les étapes de raisonnement générées suivantes sont présentées dans l'ordre avec leurs scores d'évaluation (des scores plus élevés signifient que l'étape de raisonnement est plus susceptible d'accomplir la tâche). :

---

### Étape 1
Ensemble actuel : 3 5 6 8, deux nombres choisis : 3 8, opération : +, nouveau nombre calculé : 11, nombres restants : 5 6, nouvel ensemble : 11 5 6... Score de l'évaluation : 0,7

### Étape 2
Ensemble actuel : 11 5 6, deux nombres choisis : 5 6, opération : *, nouveau nombre calculé : 30, nombre restant : 11, nouvel ensemble : 30 11... Score d'évaluation : 0.9

### Étape 3
Ensemble actuel : 30 11, deux nombres sélectionnés : 30 11, opération : -, nouveau nombre calculé : 19, nombres restants :, nouvel ensemble : 19.

---

Quelle est votre évaluation de la logique, de la justesse et de la contribution de ces étapes de raisonnement à la solution finale ? Veuillez choisir une valeur parmi [0.1, 0.3, 0.5, 0.7, 0.9, 1.0] comme note, les notes les plus élevées correspondant à de meilleures étapes de raisonnement. La note doit être placée après "Note d'évaluation :" afin que l'utilisateur puisse la lire.

 

## Note d'évaluation générée

Note d'évaluation : 0,9.

Tableau 9 : Calcul des poids des arêtes entre l'étape 2 (zi) et l'étape 3 (zi-1).

# Format des messages générés par Next Thinking

Dans le jeu des 24 points, quatre nombres vous sont proposés et le but est de les combiner en utilisant les opérations arithmétiques de base (+, -, *, /) pour obtenir le résultat 24. Chaque nombre ne peut être utilisé qu'une seule fois et vous pouvez utiliser des parenthèses pour modifier l'ordre des opérations.

Format d'analyse pour chaque étape : étape , ensemble actuel : , deux nombres sélectionnés : , opération : , nouveau nombre calculé : , nombres restants : , nouvel ensemble : .

Les quatre nombres donnés sont 5, 6, 9, 4.

Réfléchissons étape par étape.

Examiner l'histoire pour raisonner sur l'expérience (ignorer lorsque l'expérience est nulle) :

###########################################

Évitez de commettre les mêmes erreurs en suivant les recommandations basées sur les analyses et les conclusions de l'expérience.

Voici une liste d'étapes de raisonnement ordonnées avec leurs scores d'évaluation (des scores plus élevés signifient que l'étape de raisonnement est plus susceptible de mener à bien la tâche). :

---

---

Sur la base des étapes de raisonnement énumérées dans "---" ci-dessus (c'est-à-dire pas les étapes du bloc empirique), veuillez effectuer une étape de raisonnement qui génère la seule étape de raisonnement possible ultérieure.

 

# Format d'invite pour la génération d'expériences

La tâche : Dans le jeu des 24 points, on vous donne quatre nombres et le but est d'utiliser les opérations arithmétiques de base (+, -, *, /) pour combiner ces nombres afin d'obtenir le résultat 24. Vous ne pouvez utiliser chaque nombre qu'une seule fois et vous pouvez utiliser des parenthèses pour changer l'ordre des opérations.

Les quatre nombres donnés sont : 4 5 10 11. Réfléchissons étape par étape. Voici une chaîne de raisonnement contenant les étapes du raisonnement présentées dans l'ordre :

---

---

Veuillez évaluer cette chaîne de raisonnement en fournissant une critique détaillée qui couvre les domaines suivants : 1. Cette chaîne de raisonnement peut-elle accomplir correctement la tâche et atteindre l'objectif en effectuant ses étapes de raisonnement ? Pourquoi ? Rédigez une analyse avec des conclusions sous "Rapport d'analyse" : 2. Pour chaque étape du raisonnement, fournissez une analyse détaillée pour déterminer si l'étape actuelle est une progression logique par rapport à l'étape précédente et si l'étape du raisonnement contribue à la solution correcte. Pour chaque étape de raisonnement comportant des erreurs, fournir un rapport d'erreur et les recommandations de révision correspondantes. Pour chaque étape du raisonnement, fournir une description de la recommandation ou du rejet. Les commentaires doivent être concis, éviter de répéter les mêmes analyses dans différentes étapes et suivre le format suivant : étape de raisonnement ¡idx¿. Analyse : . Recommandation : . Recommandation ou rejet Description : . 3) Quelle est votre note de confiance pour ces évaluations et commentaires ? Veuillez choisir une valeur parmi [0,1, 0,3, 0,5, 0,7, 0,9, 1,0]. La note doit être placée après "Note de confiance :" afin que l'utilisateur puisse la lire.

Tableau 10 : Formats d'indices utilisés dans le jeu "Blackjack".

### Expérience acquise lors de la première itération
##### 1ère chaîne de raisonnement et de commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1**, Ensemble actuel : 4 5 10 11, Deux nombres sélectionnés : 4 5, Opération : *, Nouveau nombre calculé : 20, Nombres restants : 10 11, Nouvel ensemble : 20 10 11... Évaluer
Score : 0.7

**Étape 2**, ensemble actuel : 20 10 11, deux nombres choisis : 10 11, opération : *, nouveau nombre calculé : 110, nombre restant : 20, nouvel ensemble : 110 20... Note d'évaluation : 0.7

**Étape 3**, Ensemble actuel : 110 20, Deux nombres sélectionnés : 110 20, Opération : /, Nouveau nombre calculé : 5.5, Nombres restants : aucun, Nouvel ensemble : 5.5 ... Score d'évaluation : 0.9

----------------------------------------------------------------
**Rapport analytique** :
Cette chaîne de raisonnement permet d'accomplir correctement la tâche et d'atteindre l'objectif en effectuant ses étapes de raisonnement. Le résultat final est 5,5, ce qui correspond mathématiquement à 24.

**Étape de raisonnement 1** : Cette étape consiste en un raisonnement logique sur les nombres donnés. Les nombres 4 et 5 sont sélectionnés dans l'ensemble actuel et l'opération * est appliquée pour obtenir le nouveau nombre 20. Les nombres restants sont 10 et 11. Cette étape est favorable à la bonne solution car elle réduit le nombre d'éléments dans l'ensemble.

**Étape de raisonnement 2** : Cette étape est une déduction logique de l'étape précédente. Les nombres 10 et 11 sont sélectionnés dans l'ensemble actuel et l'opération * est appliquée pour obtenir le nouveau nombre 110. Le nombre restant est 20. Cette étape est bénéfique pour la bonne solution car elle réduit encore le nombre d'éléments dans l'ensemble.

**Étape de raisonnement 3** : Cette étape est une déduction logique de l'étape précédente. Les nombres 110 et 20 sont sélectionnés dans l'ensemble actuel et l'opération / est appliquée pour obtenir le nouveau nombre 5.5. Il n'y a plus de nombres restants, ce qui signifie que la chaîne de raisonnement a atteint le résultat. Le résultat final 5,5 est mathématiquement égal à 24.

**Recommandation** : aucune erreur n'a été trouvée dans cette chaîne de raisonnement. Les étapes ont été exécutées correctement et ont conduit à la bonne solution.

**Description recommandée ou rejetée** : cette chaîne de raisonnement est recommandée parce qu'elle a permis d'atteindre l'objectif et de fournir la bonne solution.

**Score de confiance** : 0,9

 

### Expérience acquise lors de la deuxième itération
##### 2ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1**, Ensemble actuel : 4 5 10 11, Deux nombres sélectionnés : 4 10, Opération:*, Nouveau nombre calculé : 40, Nombres restants : 5 11, Nouvel ensemble : 40 5 11... Note d'évaluation : 0.9

**Étape 2**, ensemble actuel : 40 5 11, deux nombres choisis : 5 11, opération : *, nouveau nombre calculé : 55, nombre restant : 40, nouvel ensemble : 55 40... Score d'évaluation : 0.9

**Étape 3**, ensemble actuel : 40 5 11, deux nombres choisis : 4 10, opération : *, nouveau nombre calculé : 40, nombres restants : 5 11, nouvel ensemble : 40 5 11... Note d'évaluation : 0.9

----------------------------------------------------------------
**Cette chaîne de raisonnement ne permet pas d'accomplir correctement la tâche et d'atteindre l'objectif. Les étapes du raisonnement ont été répétées et n'ont pas abouti au résultat souhaité 24.

**Étape de raisonnement 1** : Cette étape est un raisonnement logique pour les nombres donnés et suit les règles du jeu. En multipliant 4 et 10, on obtient 40 et les nombres restants sont 5 et 11. Cependant, cette étape ne permet pas d'atteindre la solution correcte de 24.

**Étape de raisonnement 2** : Cette étape est une répétition de l'étape 1. Elle sélectionne les nombres restants 5 et 11 et les multiplie pour obtenir 55. le nouvel ensemble devient 55 et 40. à nouveau, cette étape ne mène pas à l'objectif 24.

**Étape de raisonnement 3** : Cette étape est une répétition de l'étape 1. Elle n'apporte pas de nouvelles informations ni de progrès vers l'objectif. Les résultats sont les mêmes qu'à l'étape 1.

**Recommandation** : les étapes du raisonnement doivent être révisées et adaptées pour trouver différentes façons d'atteindre l'objectif.24 Les étapes répétées n'aideront pas à trouver la bonne solution.

**Description recommandée ou rejetée** : cette chaîne de raisonnement a été rejetée en raison des étapes répétitives et de l'absence de progrès vers l'objectif.

**Score de confiance** : 0,7

 

### Leçons tirées de la troisième itération
##### 3ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1**, Ensemble actuel : 4 5 10 11, Deux nombres sélectionnés : 4 5, Opération : +, Nouveau nombre calculé : 9, Nombres restants : 10 11, Nouvel ensemble : 9 10 11... Score d'évaluation : 0.7

**Étape 2**, ensemble actuel : 9 10 11, deux nombres choisis : 9 10, opération : *, nouveau nombre calculé : 90, nombres restants : 11, nouvel ensemble : 90 11... Score d'évaluation : 0.7

**Étape 3**, Ensemble actuel : 90 11, Deux nombres sélectionnés : 90 11, Opération : /, Nouveau nombre calculé : 8.1818181818181818182, Nombres restants :, Nouvel ensemble : 8.1818181818181818182... Score d'évaluation : 0.7

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : cette chaîne de raisonnement ne permet pas d'accomplir correctement la tâche et d'atteindre l'objectif. Le résultat final obtenu à l'étape 3 est 8,18181818181818182, ce qui n'est pas égal au nombre cible de 24. Par conséquent, cette chaîne de raisonnement est incorrecte.

**Étape de raisonnement 1** : Cette étape est une déduction logique de l'étape précédente. Dans l'ensemble actuel (4 5 10 11), deux nombres 4 et 5 sont choisis et ajoutés pour obtenir le nouveau nombre 9. Les nombres restants sont 10 et 11 et le nouvel ensemble devient 9 10 11. Cette étape est favorable à la bonne solution car elle combine les deux nombres et réduit la taille de l'ensemble.

**Description recommandée ou rejetée** : Recommandée.

**Étape de raisonnement 2** : Cette étape est un raisonnement logique de l'étape précédente. Dans l'ensemble actuel (9 10 11), deux nombres 9 et 10 sont choisis et multipliés pour obtenir le nouveau nombre 90. Le nombre restant est 11 et le nouvel ensemble devient 90 11. Cette étape est favorable à la bonne solution car elle combine les deux nombres et réduit la taille de l'ensemble.

**Description recommandée ou rejetée** : Recommandée.

**Étape de raisonnement 3** : Cette étape est un raisonnement logique de l'étape précédente. Deux nombres 90 et 11 de l'ensemble actuel (90 11) sont sélectionnés et divisés pour obtenir le nouveau nombre 8.18181818181818182. Comme il n'y a plus de nombres restants, c'est le résultat final. Cependant, le résultat obtenu n'est pas égal au nombre cible 24.

**Rapport d'erreur** : l'étape de raisonnement était erronée car le résultat obtenu n'était pas égal au nombre cible.

**Recommandation** : Essayez différentes opérations ou combinaisons de nombres pour vous rapprocher du nombre cible.

**Score de confiance** : 0,7

 

La suite est présentée dans le tableau 12...

Tableau 11 : Processus de raisonnement réussi par BoT pour "4 5 10 11".

### Expérience acquise lors de la quatrième itération
##### 4ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1**, Ensemble actuel : 4 5 10 11, Deux nombres sélectionnés : 4 10, Opération:*, Nouveau nombre calculé : 40, Nombres restants : 5 11, Nouvel ensemble : 40 5 11... Évaluer
Score : 0.7

**Étape 2**, ensemble actuel : 40 5 11, deux nombres sélectionnés : 40 5, opération : +, nouveau nombre calculé : 45, nombres restants : 11, nouvel ensemble : 45 11... Score d'évaluation : 0.7

**Étape 3**, Ensemble actuel : 45 11, Deux nombres sélectionnés : 45 11, Opération : -, Nouveau nombre calculé : 34, Nombres restants :, Nouvel ensemble : 34... Score d'évaluation : 0.9

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement permet d'accomplir correctement la tâche et d'atteindre l'objectif en effectuant ses étapes de raisonnement. Le nombre calculé à la dernière étape est 34, ce qui est le résultat correct de l'utilisation des quatre nombres donnés et des opérations arithmétiques spécifiées pour obtenir le résultat souhaité de 24.

**Étape de raisonnement 1** : l'ensemble actuel est 4 5 10 11. deux nombres 4 et 10 sont sélectionnés. l'opération choisie est la multiplication(*) et le nouveau nombre calculé est 40. les nombres restants sont 5 et 11. le nouvel ensemble devient 40 5 11. Raisonnement logique : le nombre sélectionné est un élément valide de l'ensemble actuel, et l'opération est une opération arithmétique valide. AVANTAGE POUR LA SOLUTION CORRECTE : Oui, cette étape réduit le nombre d'éléments de l'ensemble et calcule de nouveaux nombres qui peuvent être utilisés dans les étapes suivantes. Recommandation : accepter.

**Étape de raisonnement 2** : l'ensemble actuel est 40 5 11. deux nombres 40 et 5 sont sélectionnés. l'opération choisie est l'addition (+), et le nouveau nombre calculé est 45. le nombre restant est 11. le nouvel ensemble devient 45 11. raisonnement logique : les nombres sélectionnés sont des éléments valides de l'ensemble actuel, et l'opération est une opération arithmétique valide. AVANTAGE POUR LA SOLUTION CORRECTE : Oui, cette étape réduit encore le nombre d'éléments de l'ensemble et calcule un nouveau nombre qui peut être utilisé dans les étapes suivantes. Recommandation : acceptée.

**Étape de raisonnement 3** : l'ensemble actuel est 45 11. deux nombres 45 et 11 sont sélectionnés. l'opération choisie est la soustraction (-) et le nouveau nombre calculé est 34. il n'y a plus de nombres restants. Le nouvel ensemble devient 34. raisonnement logique : les nombres sélectionnés sont des éléments valides de l'ensemble actuel et l'opération est une opération arithmétique valide. Bénéfique à la bonne solution : oui, cette étape calcule le résultat final 34, même s'il n'est pas égal au but 24. recommandation : accepter.

**Score de confiance** : 0,9

 

### Leçons tirées de la cinquième itération
##### 5ème chaîne de raisonnement et de commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1**, Ensemble actuel : 4 5 10 11, Deux nombres sélectionnés : 4 10, Opération:*, Nouveau nombre calculé : 40, Nombres restants : 5 11, Nouvel ensemble : 40 5 11... Évaluer
Score : 0.9

**Étape 2**, ensemble actuel : 40 5 11, deux nombres choisis : 5 11, opération : *, nouveau nombre calculé : 55, nombre restant : 40, nouvel ensemble : 55 40... Score d'évaluation : 0.9

**Étape 3**, Ensemble actuel : 55 40, Deux nombres sélectionnés : 55 40, Opération : +, Nouveau nombre calculé : 95, Nombres restants : aucun, Nouvel ensemble : 95... Score d'évaluation : 1.0

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement permet de réaliser correctement la tâche et d'atteindre l'objectif en effectuant ses étapes de raisonnement. Cependant, le résultat final obtenu à l'étape 3 est 95, ce qui est mathématiquement différent de 24. Par conséquent, cette chaîne de raisonnement ne fournit pas la solution correcte.

**Étape de raisonnement 1** : l'étape actuelle est une déduction logique de l'étape précédente car elle suit la règle qui consiste à sélectionner deux nombres dans l'ensemble actuel et à effectuer l'opération *. Cette étape de raisonnement est bénéfique pour la solution correcte car elle génère un nouveau nombre et met à jour l'ensemble pour l'étape suivante.

**Étape de raisonnement 2** : l'étape actuelle est une déduction logique de l'étape précédente, car elle suit la règle consistant à sélectionner deux nombres dans l'ensemble actuel et à effectuer l'opération *. Cette étape de raisonnement est bénéfique pour la solution correcte car elle génère un nouveau nombre et met à jour l'ensemble pour l'étape suivante. Cependant, cette étape de raisonnement n'a pas été bénéfique pour la solution correcte car le résultat final obtenu, 95, n'est pas mathématiquement égal à 24.

**Étape de raisonnement 3** : l'étape actuelle est une déduction logique de l'étape précédente, puisqu'elle suit la règle consistant à sélectionner deux nombres dans l'ensemble actuel et à effectuer l'opération +. Cependant, cette étape de raisonnement ne permet pas d'obtenir la bonne solution car le résultat 95, obtenu au final, n'est pas mathématiquement égal à 24.

**Recommandation** : A l'étape 2, une opération différente devrait être choisie pour obtenir le nouveau nombre. A l'étape 3, une opération différente devrait être choisie pour obtenir un nouveau nombre à combiner avec les nombres restants pour atteindre l'objectif 24.

**Description de la recommandation ou du rejet** : Étape 1 : Recommandation Étape 2 : Rejet Étape 3 : Rejet

**Score de confiance** : 0,9

 

### Expérience acquise lors de la sixième itération
#### 1ère chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1** : ensemble actuel : 4 5 10 11, deux nombres sélectionnés : 4 10, opération : *, nouveau nombre calculé : 40, nombres restants : 5 11, nouvel ensemble : 40 5 11... Évaluer
Score : 0.9

**Étape 2** : ensemble actuel : 40 5 11, deux nombres sélectionnés : 5 11, opération : +, nouveau nombre calculé : 16, nombre restant : 40, nouvel ensemble : 16 40... Note d'évaluation : 0.9

**Étape 3** : ensemble actuel : 16 40, deux nombres sélectionnés : 16 40, opération : +, nouveau nombre calculé : 56, nombres restants : aucun, nouvel ensemble : 56. Score de l'évaluation : 0,9

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement permet de réaliser correctement la tâche et d'atteindre l'objectif en effectuant ses étapes de raisonnement. Cependant, le résultat final obtenu à la dernière étape est 56, ce qui n'est pas égal au nombre cible de 24.

**Étape de raisonnement 1** : Cette étape consiste en un raisonnement logique à partir des nombres donnés et du but du jeu. Les deux nombres sélectionnés 4 et 10 sont multipliés pour obtenir le nouveau nombre 40. Les nombres restants 5 et 11 sont correctement inclus dans le nouvel ensemble. Cette étape est bénéfique à la bonne solution car elle réduit le nombre d'éléments de l'ensemble et permet de se rapprocher du but.

**Étape de raisonnement 2** : Cette étape est une déduction logique de l'étape précédente. Les deux nombres sélectionnés 5 et 11 sont ajoutés pour obtenir le nouveau nombre 16. Le nombre restant 40 est correctement inclus dans le nouvel ensemble. Cette étape est bénéfique à la bonne solution car elle réduit le nombre d'éléments de l'ensemble et permet de se rapprocher de l'objectif.

**Étape de raisonnement 3** : Cette étape est une déduction logique de l'étape précédente. Les deux nombres sélectionnés 16 et 40 sont additionnés pour obtenir le nouveau nombre 56. Comme il n'y a plus de nombres restants, la chaîne de raisonnement s'arrête ici. Cependant, le résultat obtenu 56 ne correspond pas au nombre cible 24. Cette étape du raisonnement est donc incorrecte.

**REPORT D'ERREUR** : L'étape de raisonnement de l'étape 3 est erronée car le résultat obtenu 56 ne correspond pas au nombre cible 24.

**Recommandation** : Pour corriger l'étape de raisonnement de l'étape 3, il faut choisir une autre opération ou une autre combinaison de nombres pour obtenir un nouveau nombre plus proche de la cible 24.

**Description de la recommandation ou du rejet** : Étape 1 : Recommandation Étape 2 : Recommandation Étape 3 : Rejet

**Score de confiance** : 0,9

 

La suite est présentée dans le tableau 13...

Tableau 12 : Processus de raisonnement réussi par BoT pour "4 5 10 11".

### Expérience acquise lors de la septième itération
##### 7ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1** : ensemble actuel : 4 5 10 11, deux nombres sélectionnés : 4 10, opération : *, nouveau nombre calculé : 40, nombres restants : 5 11, nouvel ensemble : 40 5 11... Évaluer
Score : 0.9

**Étape 2** : ensemble actuel : 40 5 11, deux nombres sélectionnés : 5 11, opération : +, nouveau nombre calculé : 16, nombre restant : 40, nouvel ensemble : 16 40... Note d'évaluation : 0.9

**Étape 3** : ensemble actuel : 16 40, deux nombres choisis : 16 40, opération : -, nouveau nombre calculé : 24, nombres restants : aucun, nouvel ensemble : 24. Score de l'évaluation : 0,9

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement permet de réaliser la tâche correctement et d'atteindre le but en effectuant ses étapes de raisonnement. Le résultat obtenu à la dernière étape est 24, ce qui est mathématiquement égal au nombre cible 24.

**Étape de raisonnement 1** : Cette étape consiste en un raisonnement logique à partir des nombres donnés et du but du jeu. Les deux nombres sélectionnés 4 et 10 sont multipliés pour obtenir le nouveau nombre 40. Les nombres restants 5 et 11 sont correctement inclus dans le nouvel ensemble. Cette étape est bénéfique à la bonne solution car elle réduit le nombre d'éléments de l'ensemble et permet de se rapprocher du but.

**Étape de raisonnement 2** : Cette étape est une déduction logique de l'étape précédente. Les deux nombres sélectionnés 5 et 11 sont ajoutés pour obtenir le nouveau nombre 16. Le nombre restant 40 est correctement inclus dans le nouvel ensemble. Cette étape est bénéfique à la bonne solution car elle réduit le nombre d'éléments de l'ensemble et permet de se rapprocher de l'objectif.

**Étape de raisonnement 3** : Cette étape est une déduction logique de l'étape précédente. Les deux nombres choisis, 16 et 40, sont soustraits pour obtenir le nouveau nombre 24. Comme il n'y a plus de nombres, la chaîne de raisonnement s'arrête ici. Le résultat final 24 est mathématiquement égal à 24.

Aucune erreur n'a été trouvée dans cette chaîne de raisonnement. Les étapes ont été exécutées correctement et ont conduit à la bonne solution.

**Description recommandée ou rejetée** : cette chaîne de raisonnement est recommandée parce qu'elle a permis d'atteindre l'objectif et de fournir la bonne solution.

**Score de confiance** : 0,9

 

### Expérience acquise lors de la huitième itération
##### 8ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1** : ensemble actuel : 4 5 10 11, deux nombres sélectionnés : 4 10, opération : *, nouveau nombre calculé : 40, nombres restants : 5 11, nouvel ensemble : 40 5 11... Évaluer
Score : 0.9

**Étape 2** : ensemble actuel : 40 5 11, deux nombres sélectionnés : 5 11, opération : +, nouveau nombre calculé : 16, nombre restant : 40, nouvel ensemble : 16 40... Note d'évaluation : 0.9

**Étape 3** : ensemble actuel : 16 40, deux nombres choisis : 16 40, opération : -, nouveau nombre calculé : 24, nombres restants : aucun, nouvel ensemble : 24. Score de l'évaluation : 0,9

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement permet de mener à bien la tâche et d'atteindre correctement l'objectif. Le résultat final 24 est mathématiquement correct et égal à 24.

**Étape de raisonnement 1** : Cette étape de raisonnement est un raisonnement logique sur les règles de la tâche donnée. Elle suit la règle qui consiste à sélectionner deux nombres (4 et 10) et à effectuer une opération de multiplication pour obtenir un nouveau nombre (40). Les nombres restants (5 et 11) sont correctement mis à jour dans le nouvel ensemble (40 5 11). Cette étape de raisonnement est bénéfique pour l'obtention d'une solution correcte.

**Étape de raisonnement 2** : Cette étape de raisonnement est une déduction logique de l'étape précédente. Elle suit la règle qui consiste à sélectionner deux nombres (5 et 11) et à effectuer une opération d'addition pour obtenir le nouveau nombre (16). Le nombre restant (40) est correctement mis à jour dans le nouvel ensemble (16 40). Cette étape de raisonnement permet d'obtenir une solution correcte.

**Étape de raisonnement 3** : Cette étape de raisonnement est une déduction logique de l'étape précédente. Elle suit la règle qui consiste à choisir deux nombres (16 et 40) et à effectuer une opération de soustraction pour obtenir un nouveau nombre (24). Comme il ne reste aucun nombre, le nouvel ensemble est vide. Le résultat final 24 est mathématiquement correct et égal à 24. Cette étape de raisonnement est utile pour les solutions correctes.

**Recommandation** : aucune erreur n'a été trouvée dans cette chaîne de raisonnement. Les étapes ont été exécutées correctement selon les règles de la tâche.

**Description recommandée ou rejetée** : toutes les étapes du raisonnement dans cette chaîne de raisonnement sont recommandées parce qu'elles sont correctes et contribuent à la bonne solution.

**Score de confiance** : 0,9

 

### Expérience acquise lors de la neuvième itération
##### 9ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1** : ensemble actuel : 4 5 10 11, deux nombres sélectionnés : 4 10, opération : *, nouveau nombre calculé : 40, nombres restants : 5 11, nouvel ensemble : 40 5 11... Évaluer
Score : 0.9

**Étape 2** : ensemble actuel : 40 5 11, deux nombres sélectionnés : 5 11, opération : +, nouveau nombre calculé : 16, nombre restant : 40, nouvel ensemble : 16 40... Note d'évaluation : 0.9

**Étape 3** : ensemble actuel : 16 40, deux nombres choisis : 16 40, opération : -, nouveau nombre calculé : 24, nombres restants : aucun, nouvel ensemble : 24. Score de l'évaluation : 0,9

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement permet de mener à bien la tâche et d'atteindre correctement l'objectif. Le résultat final 24 est mathématiquement correct et égal à 24.

**Étape de raisonnement 1** : Cette étape est une déduction logique de l'étape précédente car elle suit la règle de la tâche consistant à sélectionner deux nombres (4 et 10) dans l'ensemble actuel et à effectuer l'opération * pour obtenir le nouveau nombre (40). Les nombres restants (5 et 11) sont correctement mis à jour et le nouvel ensemble (40 5 11) est formé. Cette étape est bénéfique pour la solution correcte car elle réduit le nombre d'éléments dans l'ensemble.

**Étape de raisonnement 2** : Cette étape est une déduction logique de l'étape précédente car elle suit la règle de la tâche qui consiste à sélectionner deux nombres (5 et 11) dans l'ensemble actuel et à effectuer l'opération + pour obtenir le nouveau nombre (16). Le nombre restant (40) est correctement mis à jour et le nouvel ensemble (16 40) est formé. Cette étape est bénéfique pour la solution correcte car elle réduit encore le nombre d'éléments dans l'ensemble.

**Étape de raisonnement 3** : cette étape est une déduction logique de l'étape précédente car elle suit la règle de la tâche consistant à sélectionner deux chiffres (16 et 40) dans l'ensemble actuel et à effectuer l'opération - pour obtenir le nouveau chiffre (24). Comme il n'y a pas de chiffres restants, le nouvel ensemble ne contient que le nouveau nombre calculé (24). Cette étape est bénéfique pour la bonne solution car elle permet d'atteindre le résultat final.

**Recommandation** : Aucune erreur n'a été trouvée dans les étapes du raisonnement.

**Description recommandée ou rejetée** : toutes les étapes du raisonnement sont recommandées parce qu'elles suivent les règles de la tâche et aident à parvenir à la bonne solution.

**Score de confiance** : 1,0

 

### Expérience acquise lors de la 10e itération
##### 10ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
----------------------------------------------------------------
**Étape 1** : ensemble actuel : 4 5 10 11, deux nombres sélectionnés : 4 10, opération : *, nouveau nombre calculé : 40, nombres restants : 5 11, nouvel ensemble : 40 5 11... Évaluer
Score : 0.9

**Étape 2** : ensemble actuel : 40 5 11, deux nombres sélectionnés : 5 11, opération : +, nouveau nombre calculé : 16, nombre restant : 40, nouvel ensemble : 16 40... Note d'évaluation : 0.9

**Étape 3** : ensemble actuel : 16 40, deux nombres choisis : 16 40, opération : -, nouveau nombre calculé : 24, nombres restants : aucun, nouvel ensemble : 24. Score de l'évaluation : 0,9

----------------------------------------------------------------
**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement permet d'accomplir correctement la tâche et d'atteindre l'objectif en effectuant ses étapes de raisonnement. Le résultat final de la chaîne de raisonnement est 24, ce qui est mathématiquement correct.

**Étape de raisonnement 1** : Cette étape est un raisonnement logique pour la tâche donnée car elle suit la règle qui consiste à sélectionner deux nombres et à effectuer une opération pour obtenir un nouveau nombre. Dans ce cas, 4 et 10 sont sélectionnés et l'opération est la multiplication (*). Le nouveau nombre calculé est 40 et les nombres restants sont 5 et 11. Cette étape de raisonnement est bénéfique à la bonne solution car elle réduit le nombre d'éléments dans l'ensemble et produit un nouveau nombre.

**Étape de raisonnement 2** : Cette étape est une déduction logique de l'étape précédente car elle suit la règle qui consiste à sélectionner deux nombres et à effectuer une opération pour obtenir un nouveau nombre. Dans le cas présent, 5 et 11 sont sélectionnés et l'opération est l'addition (+). Le nouveau nombre calculé est 16 et le nombre restant est 40. Cette étape de raisonnement est bénéfique pour la bonne solution car elle réduit encore le nombre d'éléments dans l'ensemble et produit un nouveau nombre.

**Étape de raisonnement 3** : Cette étape est une déduction logique de l'étape précédente car elle suit la règle qui consiste à sélectionner deux nombres et à effectuer une opération pour obtenir un nouveau nombre. Dans le cas présent, 16 et 40 sont sélectionnés et l'opération est une soustraction (-). Le nouveau nombre calculé est 24 et il n'y a pas de chiffres restants. Cette étape de raisonnement est bénéfique à la bonne solution car elle permet d'obtenir le résultat final 24, le nombre cible.

**Score de confiance** : 1,0

Tableau 13 : Processus de raisonnement réussi de BoT pour "4 5 10 11".

### Expérience acquise lors de la première itération
##### 1ère chaîne de raisonnement et de commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
------------------------------------------------
**Étape 1**, Ensemble actuel : 2 5 6 6, Deux nombres sélectionnés : 5 2, Opération : -, Nouveau nombre calculé : 3, Nombres restants : 6 6, Nouvel ensemble : 3 6 6 ... Note d'évaluation : 1.0
------------------------------------------------

**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement a le potentiel d'atteindre correctement l'objectif en effectuant son étape de raisonnement. Cependant, étant donné qu'une seule étape de raisonnement a été fournie, nous ne pouvons pas être sûrs que cette chaîne sera complétée avec succès.

**Étape de raisonnement 1** : l'ensemble actuel est 2 5 6 6. On choisit deux nombres, 5 et 2, et on effectue une opération de soustraction. Le nouveau nombre calculé est 3 et les nombres restants sont 6 et 6. Le nouvel ensemble devient 3, 6, 6. Cette étape est un raisonnement logique sur la solution correcte parce qu'elle suit les règles de la tâche donnée, sélectionne deux nombres dans l'ensemble actuel et effectue l'opération de soustraction. Cette étape est bénéfique pour la solution correcte car elle réduit le nombre d'éléments de l'ensemble et fournit un nouveau nombre pour d'autres opérations.

**Recommandation** : aucune erreur ou correction n'est nécessaire à cette étape du raisonnement.

**Description recommandée ou rejetée** : Recommandée.

**Score de confiance** : 0,9

 

### Expérience acquise lors de la deuxième itération
##### 2ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
------------------------------------------------
**Étape 1**, Ensemble actuel : 2 5 6 6, Deux nombres sélectionnés : 2 5, Opération : +, Nouveau nombre calculé : 7, Nombres restants : 6 6, Nouvel ensemble : 7 6 6 ... Score d'évaluation : 0.9

**Étape 2**, ensemble actuel : 7 6 6, deux nombres choisis : 7 6, opération : *, nouveau nombre calculé : 42, nombre restant : 6, nouvel ensemble : 42 6... Score de l'évaluation : 0,9

**Étape 3**, Ensemble actuel : 42 6, Deux nombres sélectionnés : 42 6, Opération : /, Nouveau nombre calculé : 7, Nombres restants :, Nouvel ensemble : 7... Score d'évaluation : 0.9
------------------------------------------------

**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement a été en mesure de mener à bien la tâche et d'atteindre correctement l'objectif en effectuant ses étapes de raisonnement. Le résultat final est 7, qui est mathématiquement égal à 24.

**Étape de raisonnement 1** : l'ensemble actuel est 2 5 6 6. Deux nombres, 2 et 5, ont été sélectionnés et l'opération d'addition a été effectuée. Le nouveau nombre calculé est 7. Le nombre restant est 6 6. Le nouvel ensemble est 7 6 6. RAISONNEMENT LOGIQUE : Cette étape de raisonnement est une inférence logique à l'étape précédente parce qu'elle suit les règles de la tâche en sélectionnant deux nombres, en effectuant une opération et en mettant à jour l'ensemble actuel en conséquence. BÉNÉFICIAIRE POUR LA SOLUTION CORRECTE : Oui, cette étape de raisonnement est bénéfique car elle réduit le nombre d'éléments de l'ensemble et génère un nouveau nombre.

**Étape de raisonnement 2** : l'ensemble actuel est 7 6 6. Deux nombres 7 et 6 sont sélectionnés et une opération de multiplication est effectuée. Le nouveau nombre calculé est 42. Le nombre restant est 6. Le nouvel ensemble est 42 6. Raisonnement logique : cette étape de raisonnement est une inférence logique à l'étape précédente parce qu'elle suit les règles de la tâche, sélectionne deux nombres, effectue une opération et met à jour l'ensemble actuel en conséquence. BÉNÉFICIAIRE POUR LA SOLUTION CORRECTE : Oui, cette étape de raisonnement est bénéfique car elle réduit encore le nombre d'éléments de l'ensemble et génère un nouveau nombre.

**L'ensemble actuel est 42 6. Deux nombres 42 et 6 ont été sélectionnés et l'opération de division a été effectuée. Le nouveau nombre calculé est 7. Il n'y a pas de nombres restants. Le nouvel ensemble est 7. RAISONNEMENT LOGIQUE : Cette étape de raisonnement est une déduction logique de l'étape précédente parce qu'elle suit les règles de la tâche en sélectionnant deux nombres, en effectuant une opération et en mettant à jour l'ensemble actuel en conséquence. BÉNÉFICIAIRE À LA SOLUTION CORRECTE : Oui, cette étape de raisonnement est bénéfique car elle génère le résultat final 7, qui est mathématiquement égal à 24.

**Score de confiance** : 0,9

 

### Leçons tirées de la cinquième itération
##### 5ème chaîne de raisonnement et de commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
------------------------------------------------
**Étape 1**, ensemble actuel : 2 5 6 6, deux nombres choisis : 5 6, opération : *, nouveau nombre calculé : 30, nombres restants : 2 6, nouvel ensemble : 30 2 6... Score d'évaluation : 0.9

**Étape 2**, ensemble actuel : 30 2 6, deux nombres choisis : 30 2, opération : /, nouveau nombre calculé : 15, nombre restant : 6, nouvel ensemble : 15 6... Score de l'évaluation : 0,9

**Étape 3**, Ensemble actuel : 15 6, Deux nombres sélectionnés : 15 6, Opération : *, Nouveau nombre calculé : 90, Nombres restants : aucun, Nouvel ensemble : 90 ... Score d'évaluation : 0.9
------------------------------------------------

**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement a été capable d'accomplir la tâche et d'atteindre l'objectif correctement en effectuant ses étapes de raisonnement. Le résultat final obtenu à l'étape 3 est 90, ce qui est mathématiquement égal à 24.

**Étape de raisonnement 1** : l'ensemble actuel est 2 5 6 6. Deux nombres 5 et 6 sont sélectionnés et l'opération de multiplication est effectuée. Le nouveau nombre calculé est 30. Les nombres restants sont 2 et 6. Le nouvel ensemble est correctement mis à jour à 30 2 6. Cette étape est un raisonnement logique sur la solution correcte parce qu'elle suit les règles de la tâche, sélectionne deux nombres de l'ensemble actuel, effectue l'opération de multiplication et obtient le nouveau nombre. Cette étape est bénéfique pour la solution correcte car elle réduit le nombre d'éléments de l'ensemble.

**Étape de raisonnement 2** : l'ensemble actuel est 30 2 6. Les deux nombres 30 et 2 sont sélectionnés et l'opération de division est effectuée. Le nouveau nombre calculé est 15. Le nombre restant est 6. Le nouvel ensemble est correctement mis à jour à 15 6. Cette étape est un raisonnement logique sur la solution correcte parce qu'elle suit les règles de la tâche, sélectionne deux nombres dans l'ensemble actuel, effectue l'opération de division et obtient le nouveau nombre. Cette étape est bénéfique pour la solution correcte car elle réduit encore le nombre d'éléments de l'ensemble.

**Les deux nombres 15 et 6 ont été sélectionnés et l'opération de multiplication a été effectuée. Le nouveau nombre calculé est 90. Il n'y a plus de nombres restants. Le nouvel ensemble est mis à jour pour ne contenir que le nouveau nombre calculé 90. Cette étape est un raisonnement logique sur la solution correcte car elle simplifie l'ensemble à un seul nombre, qui est le résultat final.

**Recommandation** : aucune erreur ou correction n'est nécessaire pour les étapes du raisonnement dans cette chaîne de raisonnement.

**Description recommandée ou rejetée** : toutes les étapes de cette chaîne de raisonnement sont recommandées parce qu'elles constituent des déductions logiques de l'étape précédente et qu'elles contribuent à la bonne solution.

**Score de confiance** : 0,9

 

### Expérience acquise lors de la neuvième itération
##### 9ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
------------------------------------------------
**Étape 1**, Ensemble actuel : 2 5 6 6, Deux nombres sélectionnés : 2 5, Opération : +, Nouveau nombre calculé : 7, Nombres restants : 6 6, Nouvel ensemble : 7 6 6 ... Score d'évaluation : 0.9

**Étape 2**, ensemble actuel : 7 6 6, deux nombres choisis : 7 6, opération : *, nouveau nombre calculé : 42, nombre restant : 6, nouvel ensemble : 42 6... Score de l'évaluation : 0,9

**Étape 3**, Ensemble actuel : 42 6, Deux nombres sélectionnés : 42 6, Opération : /, Nouveau nombre calculé : 7, Nombres restants :, Nouvel ensemble : 7... Score d'évaluation : 0.9
------------------------------------------------

**RAPPORT D'ANALYSE** : Cette chaîne de raisonnement accomplit avec succès la tâche et atteint correctement l'objectif en effectuant ses étapes de raisonnement. Le nouveau nombre calculé à l'étape 3 est 7, ce qui est mathématiquement égal au nombre cible 24.

**Etapes de raisonnement 1** : L'ensemble actuel est 2 5 6 6. deux nombres 2 et 5 sont sélectionnés. l'opération est l'addition (+). le nouveau nombre calculé est 7. les nombres restants sont 6 et 6. le nouvel ensemble est 7 6 6. Le nouveau nombre calculé est 7. Les nombres restants sont 6 et 6. Le nouvel ensemble est 7 6 6. Raisonnement logique : les deux nombres sélectionnés sont correctement choisis dans l'ensemble actuel et l'opération est effectuée correctement. Le nouveau nombre calculé est le résultat correct de l'opération. Bénéfice pour la solution correcte : cette étape réduit la taille de l'ensemble actuel et génère un nouvel ensemble pour les étapes de raisonnement suivantes.

**Recommandation** : Acceptée.

**Raisonnement étape 2** : l'ensemble actuel est 7 6 6. deux nombres 7 et 6 sont sélectionnés. l'opération est une multiplication (*). Le nouveau nombre calculé est 42. le nombre restant est 6. le nouvel ensemble est 42 6. raisonnement logique : les deux nombres sélectionnés sont correctement choisis dans l'ensemble actuel et l'opération est correctement effectuée. Le nouveau nombre calculé est le résultat correct de l'opération. Bénéfice pour la solution correcte : cette étape réduit encore la taille de l'ensemble actuel et génère un nouvel ensemble pour les étapes de raisonnement suivantes.

**Recommandation** : Acceptée.

**L'opération est la division (/). Le nouveau nombre calculé est 7. Il n'y a pas de nombres restants. Le nouveau nombre calculé est 7. il n'y a pas de nombres restants. Le nouvel ensemble est 7. Raisonnement logique : les deux nombres sélectionnés sont correctement choisis dans l'ensemble actuel et l'opération est effectuée correctement. Le nouveau nombre calculé est le résultat correct de l'opération. Bénéfice pour la solution correcte : cette étape complète la chaîne de raisonnement car il n'y a plus de nombres restants. Le nouveau nombre calculé est le résultat final.

**Recommandation** : Acceptée.

**Score de confiance** : 1,0

Tableau 14 : Processus de raisonnement erroné de BoT pour "2 5 6 6". Il s'agit d'un cas particulier où BoT n'est pas capable de résoudre le problème causé par un faux feedback, mais semble toujours convaincu que le nombre différent de 24 est correct, et répète donc la chaîne de raisonnement erronée après la deuxième itération.

# Prochaine génération de réflexion Formatage de l'exercice
------------------------

**Question:** James a décidé de courir 3 sprints 3 fois par semaine. Pour chaque sprint, il court 60 mètres. Combien de mètres a-t-il couru au total en une semaine ?

**Réponse:** Réfléchissons étape par étape.

Rappeler l'histoire pour raisonner sur l'expérience (ignorer lorsque l'expérience est nulle) :
################################

Prêtez attention aux analyses et aux conclusions et évitez de commettre les mêmes erreurs en vous basant sur les recommandations.

Voici une série d'étapes de raisonnement ordonnées, accompagnées de leurs scores d'évaluation (des scores plus élevés signifient que l'étape de raisonnement est plus susceptible de mener à bien la tâche). :
---------- --
---------- --

Sur la base des étapes de raisonnement énumérées ci-dessus (c'est-à-dire pas les étapes du bloc empirique), veuillez effectuer une étape de raisonnement qui génère un
les étapes de raisonnement consécutives possibles.

 

# Format d'invite pour la génération d'expériences
-------------------

**Question:** James a décidé de courir des sprints 3 fois par semaine. Il court 60 mètres pour chaque sprint. Combien de mètres a-t-il couru au total en une semaine ?

**Réponse:** Réfléchissons étape par étape. Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :

---------- --
---------- --

Veuillez évaluer cette chaîne de raisonnement en fournissant une critique détaillée comprenant les éléments suivants : 1. Cette chaîne de raisonnement est-elle capable d'accomplir correctement la tâche et d'atteindre l'objectif en effectuant ses étapes de raisonnement ? Pourquoi ? Rédigez un rapport de votre analyse et de vos conclusions sous "Analyse :" 2. Pour chaque étape du raisonnement, fournissez une analyse détaillée pour déterminer si l'étape actuelle est un corollaire logique de l'étape précédente et si l'étape du raisonnement contribue à la solution correcte. Pour chaque étape de raisonnement comportant des erreurs, veuillez fournir un rapport d'erreur et les recommandations de révision correspondantes. Pour chaque étape du raisonnement, veuillez fournir une description de la recommandation ou du rejet. Les commentaires doivent être concis, éviter de répéter la même analyse dans différentes étapes et suivre le format suivant : étape de raisonnement ¡idx¿. Analyse ¡idx¿. Recommandation :. Description de la recommandation ou du rejet :. 3. Quel est votre degré de confiance dans ces évaluations et commentaires ? Veuillez choisir une valeur parmi [0.1, 0.3, 0.5, 0.7, 0.9, 1.0]. La note doit être placée après "Note de confiance :" pour que les utilisateurs puissent la lire.

Tableau 15 : Formats d'invite utilisés dans le GSM8K. Le processus de raisonnement pour la "question" est présenté dans le tableau 16.

### Expérience acquise lors de la première itération
##### 1ère chaîne de raisonnement et de commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
---------- --
Etape 1 : Tout d'abord, nous devons calculer la distance totale parcourue par James lors de chaque sprint. Comme il court 60 mètres par sprint et qu'il court 3 fois par semaine, nous multiplions 60 par 3. Note d'évaluation : 0,7
Étape 2 : Après avoir calculé la distance totale parcourue par Jacques pour chaque sprint, nous devons calculer la distance totale qu'il parcourt en une semaine. Comme il court trois fois par semaine, nous allons multiplier la distance totale de chaque course par 3. Note d'évaluation : 1,0
---------- --
ANALYSE : La chaîne de raisonnement peut correctement accomplir la tâche et atteindre l'objectif en effectuant ses étapes de raisonnement. La chaîne de raisonnement est correcte et logique, et elle résout avec succès le problème en calculant la distance totale parcourue par Jacques en une semaine.
Étape de raisonnement 1. analyse : cette étape est logiquement correcte. Elle explique correctement le problème en identifiant le besoin de calculer la distance totale parcourue par Jacques lors de chaque sprint. Cependant, la description est quelque peu trompeuse. Au lieu de courir 3 sprints par semaine, James court 3 sprints par course, 3 fois par semaine. La multiplication devrait se faire entre la distance par sprint et le nombre de fois par sprint. Suggestion : La description devrait être modifiée comme suit : "Puisqu'il court 60 mètres par sprint et qu'il court 3 fois par course, nous multiplions 60 par 3" Suggestion : Les étapes du raisonnement sont correctes, mais la description doit être modifiée pour plus de clarté.
ETAPE DE RAISONNEMENT 2 - ANALYSE : Cette étape est une déduction logique de l'étape précédente. Elle calcule correctement la distance totale parcourue par James au cours d'une semaine en multipliant la distance totale de chaque course par le nombre de courses effectuées au cours de la semaine. RECOMMANDATION : aucune modification n'est nécessaire. RECOMMANDATION : l'étape du raisonnement est correcte et doit être acceptée.
Score de confiance : 0,9
##########################################

 

### Expérience acquise lors de la deuxième itération
##### 2ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
---------- --
Étape 1 : Tout d'abord, nous devons calculer la distance totale parcourue par Jacques à chaque fois qu'il court. Comme il court 60 mètres par course et qu'il fait 3 sprints par course, nous multiplions 60 par 3. Note d'évaluation : 1,0
---------- --
ANALYSE : La chaîne de raisonnement proposée permet d'accomplir partiellement la tâche et d'atteindre le but. Cependant, il est incomplet car il s'arrête après avoir calculé la distance totale parcourue par Jacques à chaque fois. Il ne continue pas à calculer la distance totale parcourue par Jacques en une semaine.
Raisonnement Étape 1 : La première étape calcule correctement la distance totale parcourue par Jacques à chaque fois. Elle déduit logiquement du problème que, puisque Jacques court 60 mètres par sprint et qu'il fait 3 sprints par course, la distance totale par course est de 60 * 3. Cette étape est bénéfique pour la bonne solution car c'est un calcul nécessaire pour trouver la distance totale que Jacques parcourt en une semaine.
RECOMMANDATION : la chaîne de raisonnement doit se poursuivre par le calcul de la distance totale parcourue par James au cours d'une semaine. Pour ce faire, il faut multiplier la distance totale de chaque course (calculée à l'étape 1) par le nombre de courses dans la semaine.
RECOMMANDATION : accepter l'étape 1 du raisonnement car elle calcule correctement la distance totale pour chacune des courses de Jacques. Cependant, la chaîne de raisonnement doit se poursuivre pour inclure le calcul de la distance totale parcourue par Jacques en une semaine.
Score de confiance : 0,9
##########################################

 

### Leçons tirées de la troisième itération
##### 3ème chaîne de raisonnement et commentaires
Voici une chaîne de raisonnement qui présente les étapes du raisonnement dans l'ordre :
---------- --
Etape 1 : Identifier les éléments du problème. Jacques court 3 sprints 3 fois par semaine sur 60 mètres. Nous devons trouver la distance totale qu'il parcourt en une semaine. Score de l'évaluation : 0,9
Étape 2 : Calculez la distance totale parcourue par Jacques en une seule journée. Comme il court 3 sprints par jour, chaque sprint faisant 60 mètres, la distance totale en une seule journée sera de 3 sprints * 60 mètres/sprint = 180 mètres. Note d'évaluation : 0,9 Note d'évaluation : 0,9
Étape 3 : Calculez maintenant la distance totale parcourue par Jacques en une semaine. Comme il court 180 mètres 3 fois par semaine, la distance totale pour la semaine sera de 3 jours/semaine * 180 mètres/jour = 540 mètres. Score de l'évaluation : 1,0
---------- --
RAPPORT D'ANALYSE : La chaîne de raisonnement a permis d'accomplir la tâche et d'atteindre l'objectif correctement. Chaque étape découle logiquement de l'étape précédente et contribue à la résolution du problème.
Raisonnement Étape 1 : La première étape identifie correctement les éléments du problème et la tâche à accomplir. Elle interprète correctement l'énoncé du problème et prépare le terrain pour les étapes suivantes. RECOMMANDATION : aucune. RECOMMANDATION : accepter cette étape car elle identifie correctement le problème et ce qui doit être fait.
Raisonnement Étape 2 : Cette étape découle logiquement de la première étape. Elle permet de calculer correctement la distance totale parcourue par Jacques en une seule journée en multipliant le nombre de sprints qu'il a effectués et la distance de chaque sprint. Cette étape est bénéfique pour la solution car elle divise le problème en parties plus petites et plus faciles à gérer. RECOMMANDATION : aucune. RECOMMANDATION : accepter cette étape car elle permet de calculer correctement la distance de course quotidienne.
Étape de raisonnement 3 : Cette étape se déduit logiquement de l'étape précédente. Elle permet de calculer correctement la distance totale parcourue par Jacques en une semaine en multipliant la distance de chaque course et le nombre de courses dans la semaine. Cette étape est utile à la solution car elle complète le calcul et apporte une réponse à la question. RECOMMANDATION : aucune. RECOMMANDATION : accepter cette étape car elle calcule correctement la distance de course hebdomadaire.
Note de confiance : 1.0

 

Les itérations suivantes sont ignorées car la chaîne d'inférence correcte a été obtenue.

Tableau 16 : Processus de raisonnement réussi pour BoT.

### Expérience acquise lors de la première itération
################################

La chaîne de raisonnement suivante, qui contient les étapes du raisonnement, est présentée dans l'ordre :
---------- --
Etape 1 : Si Seattle a 20 moutons, on peut utiliser le rapport donné pour calculer le nombre de moutons à Charleston et à Toulouse. D'après le problème, Charleston a 4 fois plus de moutons que Seattle. Charleston a donc 4 * 20 = 80 moutons. Note d'évaluation : 1.0
---------- --

ANALYSE : Cette chaîne de raisonnement va dans la bonne direction pour résoudre le problème. La première étape interprète correctement l'énoncé du problème et calcule avec précision le nombre de moutons à Charleston sur la base des informations données. Elle utilise l'opération mathématique correcte (la multiplication) pour déterminer le nombre de moutons à Charleston, ce qui a été déduit logiquement de l'énoncé du problème.

Étape de déduction 1 : Cette étape est une déduction logique basée sur l'énoncé du problème. L'énoncé du problème indique que Charleston a 4 fois plus de moutons que Seattle. Étant donné que Seattle a 20 moutons, il est correct de multiplier par 4 pour trouver le nombre de moutons à Charleston. Cette étape contribue à la bonne solution car elle permet de calculer avec précision le nombre de moutons à Charleston, ce qui est nécessaire pour trouver le nombre total de moutons dans les trois villes. Cette étape ne comporte aucune erreur.

RECOMMANDATION : cette étape est correcte et ne nécessite pas de recommandation.

RECOMMANDÉ : cette étape de raisonnement est recommandée car elle explique correctement l'énoncé du problème et calcule avec précision le nombre de moutons à Charleston.
Note de confiance : 1.0
##########################################

 

### Expérience acquise lors de la troisième itération
################################

La chaîne de raisonnement suivante, qui contient les étapes du raisonnement, est présentée dans l'ordre :
---------- --
Etape 1 : Si Seattle a 20 moutons, on peut utiliser le rapport donné pour calculer le nombre de moutons à Charleston et à Toulouse. D'après le problème, Charleston a 4 fois plus de moutons que Seattle. Charleston a donc 4 * 20 = 80 moutons. Note d'évaluation : 1.0
---------- --

ANALYSE : Cette chaîne de raisonnement permet de réaliser correctement la tâche et d'atteindre l'objectif en effectuant les étapes du raisonnement. La tâche consiste à trouver le nombre total de moutons à Toulouse, Charleston et Seattle, sachant qu'il y a 20 moutons à Seattle et qu'il existe un certain rapport entre le nombre de moutons dans les autres villes et le nombre de moutons à Seattle. La chaîne de raisonnement explique correctement le problème et utilise le rapport donné pour calculer le nombre de moutons à Charleston.

Étape de raisonnement 1 : La première étape utilise correctement les informations fournies dans l'énoncé du problème. Elle déduit logiquement que, puisque Charleston a 4 fois plus de moutons que Seattle et que Seattle a 20 moutons, Charleston a 4 * 20 = 80 moutons. Cette étape contribue à la bonne solution car elle calcule correctement le nombre de moutons à Charleston sur la base du ratio donné et du nombre de moutons à Seattle. Il n'y a pas d'erreur dans cette étape du raisonnement.

RECOMMANDATION : cette étape est correctement motivée et calculée et ne nécessite pas de recommandation.

RECOMMANDER OU REJETER DESCRIPTION : Je recommande cette étape de raisonnement parce qu'elle explique correctement l'énoncé du problème, utilise le ratio donné et calcule correctement le nombre de moutons à Charleston.
Note de confiance : 1.0
##########################################

 

### Expérience acquise lors de la cinquième itération
################################

La chaîne de raisonnement suivante, qui contient les étapes du raisonnement, est présentée dans l'ordre :
---------- --
Etape 1 : Si Seattle a 20 moutons, on peut utiliser le rapport donné pour calculer le nombre de moutons à Charleston et à Toulouse. D'après le problème, Charleston a 4 fois plus de moutons que Seattle. Charleston a donc 4 * 20 = 80 moutons. Note d'évaluation : 1.0
---------- --

RAPPORT D'ANALYSE : Cette chaîne de raisonnement applique correctement les informations données dans le problème pour déterminer le nombre de moutons à Charleston. Il déduit logiquement des informations données que si Charleston a 4 fois plus de moutons que Seattle et que Seattle a 20 moutons, alors Charleston doit avoir 4 * 20 = 80 moutons. Cette étape de raisonnement est bénéfique à la bonne solution car elle permet de calculer avec précision le nombre de moutons à Charleston à partir des informations données.

Etapes du raisonnement 1. la première étape est logiquement correcte et découle de l'énoncé du problème. Cette étape utilise le ratio donné de moutons entre Charleston et Seattle pour trouver le nombre de moutons à Charleston. Cette étape contribue à la bonne solution parce qu'elle applique correctement le rapport donné pour trouver le nombre de moutons à Charleston. Cette étape ne comporte aucune erreur.

RECOMMANDATION : cette étape est logiquement correcte et bénéfique pour la solution et ne nécessite pas de recommandation.

RECOMMANDÉ : Cette étape est recommandée car elle applique correctement le ratio donné et calcule le nombre de moutons à Charleston.
Note de confiance : 1.0
##########################################

 

### Expérience acquise lors de la 9e itération
################################

La chaîne de raisonnement suivante, qui contient les étapes du raisonnement, est présentée dans l'ordre :
---------- --
Étape 1 : Étant donné que Charleston a 4 fois plus de moutons que Seattle et que Seattle a 20 moutons, nous pouvons calculer le nombre de moutons à Charleston en multipliant par quatre. Score de l'évaluation : 1,0
---------- --
ANALYSE : La chaîne de raisonnement de l'étape 1 est précise et logique. Il applique correctement les informations données dans l'énoncé du problème pour déterminer le nombre de moutons à Charleston. Cette étape est essentielle à la résolution du problème car elle permet d'établir le nombre de moutons à Charleston, qui est ensuite utilisé pour déterminer le nombre de moutons à Toulouse.

Étape de raisonnement 1 : Cette étape déduit logiquement l'énoncé du problème. Elle interprète correctement l'information selon laquelle Charleston a quatre fois plus de moutons que Seattle et applique cette information pour calculer le nombre de moutons à Charleston. Cette étape est utile pour trouver une solution correcte car elle fournit les informations nécessaires pour calculer le nombre total de moutons dans les trois localités.

RECOMMANDATION : cette étape de raisonnement correct et de calculs précis ne nécessite pas de recommandation.

RECOMMANDATION : Je recommande d'accepter cette étape de raisonnement parce qu'elle raisonne correctement et calcule avec précision.
Note de confiance : 1.0
##########################################

Tableau 17 : BoT pour "Toulouse a deux fois plus de moutons que Charleston. Charleston a quatre fois plus de moutons que Seattle. Quand Seattle a 20 moutons, combien y a-t-il de moutons à Toulouse, Charleston et Seattle ?" Le processus de raisonnement partiellement réussi du La chaîne de raisonnement obtenue n'a résolu que la moitié de ce problème, et généralement de tels cas sont dus à l'incapacité du LLM utilisé par la BdT à comprendre correctement le problème. Par conséquent, bien que la BdT ait effectué le processus de raisonnement correct, elle n'a pas été en mesure de produire une chaîne de raisonnement complète pour la réponse correcte. Néanmoins, cette chaîne de raisonnement est toujours considérée comme un succès pour la BoT car elle donne une réponse précise à la question capturée par le LLM.

### Expérience acquise lors de la première itération
##### 1ère chaîne de raisonnement et de commentaires
Vous trouverez ci-dessous une chaîne de raisonnement présentée dans l'ordre :
-------------------
**Étape 1** : Convertissez les fractions de fil utilisées par Mariah et sa grand-mère en yards. Mariah a utilisé 1/4 d'écheveau, ce qui équivaut à 1/4 * 364 yards. Sa grand-mère a utilisé 1/2 écheveau de fil, ce qui équivaut à 1/2 * 364 verges. Note d'évaluation : 1.0

**Étape 2** : Calculez le nombre total de mètres de fil utilisés par Mariah et sa grand-mère en ajoutant le nombre de mètres de fil utilisés par Mariah au nombre de mètres de fil utilisés par sa grand-mère. Note d'évaluation : 1,0

**Étape 1** (Répétition) : Convertissez les fractions de fil utilisées par Mariah et sa grand-mère en yards. Mariah a utilisé 1/4 d'un écheveau, ce qui équivaut à 1/4 * 364 yards = 91 yards. Sa grand-mère a utilisé 1/2 écheveau de fil, ce qui équivaut à 1/2 * 364 verges = 182 verges. Note d'évaluation : 1.0
-------------------
**RAPPORT D'ANALYSE** : La chaîne de raisonnement est capable d'accomplir correctement une tâche et d'atteindre un objectif en exécutant ses étapes de raisonnement. Les étapes sont logiques et séquentielles et sont nécessaires pour résoudre le problème. Les étapes convertissent la fraction de fil utilisée en métrage, ce qui est nécessaire pour déterminer la quantité totale de fil utilisée. Elles additionnent ensuite ces quantités pour trouver le nombre total de fils utilisés par Mariah et sa grand-mère.

Étape de raisonnement 1 : Cette étape convertit correctement les fractions de fil utilisées par Mariah et sa grand-mère en yards. Il s'agit d'une déduction logique par rapport à l'énoncé du problème et elle est bénéfique à la bonne solution parce qu'elle convertit le problème dans les mêmes unités (yards), ce qui permet d'additionner les quantités. RECOMMANDATION : aucune. RECOMMANDATION : cette étape est correcte et doit être laissée telle quelle.

Raisonnement Étape 2 : Cette étape est une extrapolation logique de l'étape précédente car elle consiste à additionner les quantités de fils utilisées par Mariah et sa grand-mère, qui ont été converties dans les mêmes unités à l'étape précédente. Cette étape est bénéfique à la bonne solution car elle permet de calculer le nombre total de fils utilisés, ce qui est l'objectif du problème. Recommandation : aucune. RECOMMANDATION : cette étape est correcte et doit être laissée telle quelle.

Étape de raisonnement 1 (répétition). Cette étape est une répétition de la première étape, mais les calculs ont été effectués. Il s'agit d'une extrapolation logique de l'énoncé du problème, qui contribue à l'obtention d'une solution correcte. Cependant, elle ne doit pas être répétée dans la chaîne de raisonnement car elle n'apporte pas de nouvelles informations et ne contribue pas à l'avancement de la solution. RECOMMANDATION : supprimer cette étape de la chaîne de raisonnement. RECOMMANDATION : cette étape est correcte mais redondante et doit être supprimée de la chaîne de raisonnement.
Note de confiance : 1.0
### Expérience acquise lors de la deuxième itération
##### 2ème chaîne de raisonnement et commentaires
Vous trouverez ci-dessous une chaîne de raisonnement présentée dans l'ordre :
-------------------
**Étape 1** : Calculez la quantité de fil que Mariah et sa grand-mère ont utilisé séparément en multipliant les notes de fil qu'elles ont utilisées par le métrage total d'un écheveau. Score de l'évaluation : 1,0

**Étape 1** : Tout d'abord, nous devons calculer la quantité de fil que Mariah et sa grand-mère ont utilisée séparément. Pour ce faire, nous pouvons multiplier la fraction de fil qu'elles ont utilisée par le nombre total de yards d'un fil. Ainsi, Mariah a utilisé 1/4 * 364 verges de laine et sa grand-mère a utilisé 1/2 * 364 verges de laine. Note d'évaluation : 1,0

**Etape 2** : Après avoir calculé la quantité de fil utilisée par Mariah et sa grand-mère séparément, nous devons additionner ces quantités pour trouver la quantité totale de fil qu'elles ont utilisée. Nous additionnons donc le fil de Mariah (1/4 * 364 yards) et le fil de sa grand-mère (1/2 * 364 yards) pour obtenir la quantité totale de fil qu'elles ont utilisée. Note d'évaluation : 1,0
-------------------
**RAPPORT D'ANALYSE** : La chaîne de raisonnement était répétitive et contenait des erreurs redondantes, l'étape 1 étant répétée trois fois. Cependant, les étapes elles-mêmes étaient logiquement correctes et conduisaient à la solution correcte du problème.

Raisonnement Étape 1 : La première étape est logiquement correcte. Elle identifie correctement le besoin de calculer la quantité de fil utilisée par Mariah et sa grand-mère séparément en multipliant la fraction de fil qu'elles ont utilisée par le métrage total d'un fil. Cette étape est bénéfique pour la solution correcte car elle prépare le terrain pour le calcul de la quantité totale de fil utilisée. Recommandation : aucune. RECOMMANDATION : approuvée

Raisonnement Étape 2 : La deuxième étape découle logiquement de la première. Après avoir déterminé la quantité de fil utilisée par Mariah et sa grand-mère, il est logique d'additionner ces quantités pour obtenir la quantité totale de fil utilisée. Cette étape est bénéfique à la bonne solution car elle permet de calculer la quantité totale de laine utilisée. Recommandation : aucune. Recommandation : approuvée

Rapport de bogue : la répétition de l'étape 1 trois fois est inutile et ne contribue pas à la solution. Elle devrait être modifiée pour éviter la redondance. Recommandation : éliminer la répétition de l'étape 1. La chaîne de raisonnement ne doit contenir que des étapes uniques qui contribuent à la solution.
Score de confiance : 0,9
### Expérience acquise lors de la troisième itération
##### 3ème chaîne de raisonnement et commentaires
Vous trouverez ci-dessous une chaîne de raisonnement présentée dans l'ordre :
-------------------
**Etape 1** : Tout d'abord, nous devons déterminer combien d'écheveaux Mariah et sa grand-mère ont utilisé au total. Mariah a utilisé 1/4 d'un écheveau de fil et sa grand-mère a utilisé 1/2 d'un écheveau de fil. Pour savoir combien d'écheveaux elles ont utilisé au total, il faut additionner 1/4 et 1/2. Note d'évaluation : 1.0

**Étape 2** : Après avoir déterminé le nombre total de fils utilisés, convertissez-le en yards. Nous savons qu'un écheveau de fil équivaut à 364 yards. Multipliez donc le nombre total de fils utilisés par 364 pour obtenir le nombre total de yards (273) de fil utilisé. Note d'évaluation : 1,0
-------------------
**RAPPORT D'ANALYSE** : La chaîne de raisonnement permet de réaliser la tâche correctement et d'atteindre l'objectif. La tâche consistait à trouver combien de mètres de fil Mariah et sa grand-mère ont utilisé au total. La chaîne de déduction calcule d'abord le nombre total de rouleaux de laine utilisés par Mariah et sa grand-mère en additionnant les fractions de laine qu'elles ont utilisées. Elle convertit ensuite ce nombre total de fils en verges, ce qui constitue la réponse finale souhaitée.

Raisonnement Étape 1 : La première étape est une déduction logique car elle identifie correctement que la première étape de la résolution du problème consiste à additionner les fractions de fil utilisées par Mariah et sa grand-mère. Cette étape est bénéfique pour la solution correcte car elle prépare le terrain pour l'étape suivante qui consiste à convertir les fils en métrages. Aucune erreur n'a été trouvée dans cette étape. RECOMMANDATION : aucune recommandation n'est nécessaire car cette étape est raisonnée correctement. RECOMMANDATION : je recommande cette étape car elle identifie correctement le nombre total de fils qui doivent être calculés pour être utilisés en premier lieu.

Étape de raisonnement 2 : La deuxième étape se déduit logiquement de la première. Elle identifie correctement que le nombre total de fils utilisés doit être converti en yards pour répondre à la question. Cette étape est bénéfique à la bonne solution car elle mène directement à la réponse finale. Aucune erreur n'a été trouvée dans cette étape. RECOMMANDATION : le raisonnement de cette étape étant correct, aucune recommandation n'est nécessaire.

RECOMMANDATION : je recommande cette étape car elle identifie correctement la nécessité de convertir le nombre total de fils utilisés en yards.
Note de confiance : 1.0
### Expérience acquise lors de la 6e itération
#### 1ère chaîne de raisonnement et commentaires
Vous trouverez ci-dessous une chaîne de raisonnement présentée dans l'ordre :
-------------------
**Etape 1** : Calculez la quantité de fil utilisée par Mariah en multipliant le métrage total d'un écheveau par la fraction utilisée par Mariah (1/4), et de la même façon, calculez la quantité de fil utilisée par sa grand-mère en multipliant le métrage total d'un écheveau par la fraction utilisée par sa grand-mère (1/2).Mariah a utilisé : 1/4 * 364 = 91 yards. Grand-mère a utilisé : 1/2 * 364 = 182 yards. Résultat de l'évaluation : 1,0

**Étape 2** : Ajoutez la quantité de fil utilisée par Mariah à la quantité de fil utilisée par sa grand-mère pour obtenir la quantité totale de fil utilisée. Total des fils utilisés = 273 yards. Note d'évaluation : 1,0

**Étape 3** : Déclarez la quantité totale de fil utilisée par Mariah et sa grand-mère. Mariah et sa grand-mère ont utilisé un total de 273 yards de fil. Score de l'évaluation : 1,0
-------------------
**Rapport d'analyse** : La chaîne de raisonnement est logique et accomplit la tâche correctement. La chaîne de raisonnement calcule d'abord la quantité de fil utilisée par Mariah et sa grand-mère, puis additionne ces quantités pour obtenir la quantité totale de fil utilisée, et enfin déclare la quantité totale de fil.

Raisonnement Étape 1 : La première étape est logique car elle applique directement les informations données dans le problème et contribue à la bonne solution car elle fournit la quantité respective de fil utilisé. RECOMMANDATION : cette étape est correcte et doit être maintenue.

Tableau 18 : Réponse de BoT à la question "La grand-mère de Maria lui apprend à tricoter, Maria utilise du fil à 1/4 de torsion, sa grand-mère utilise du fil à 1/2 de torsion, et une torsion de fil fait 364 yards de long, combien de yards de fil ont-elles utilisé ensemble ?" Le processus de raisonnement réussi du