Qué es el descenso gradual (Gradient Descent), un artículo para leer y entender

Definición de descenso por gradiente

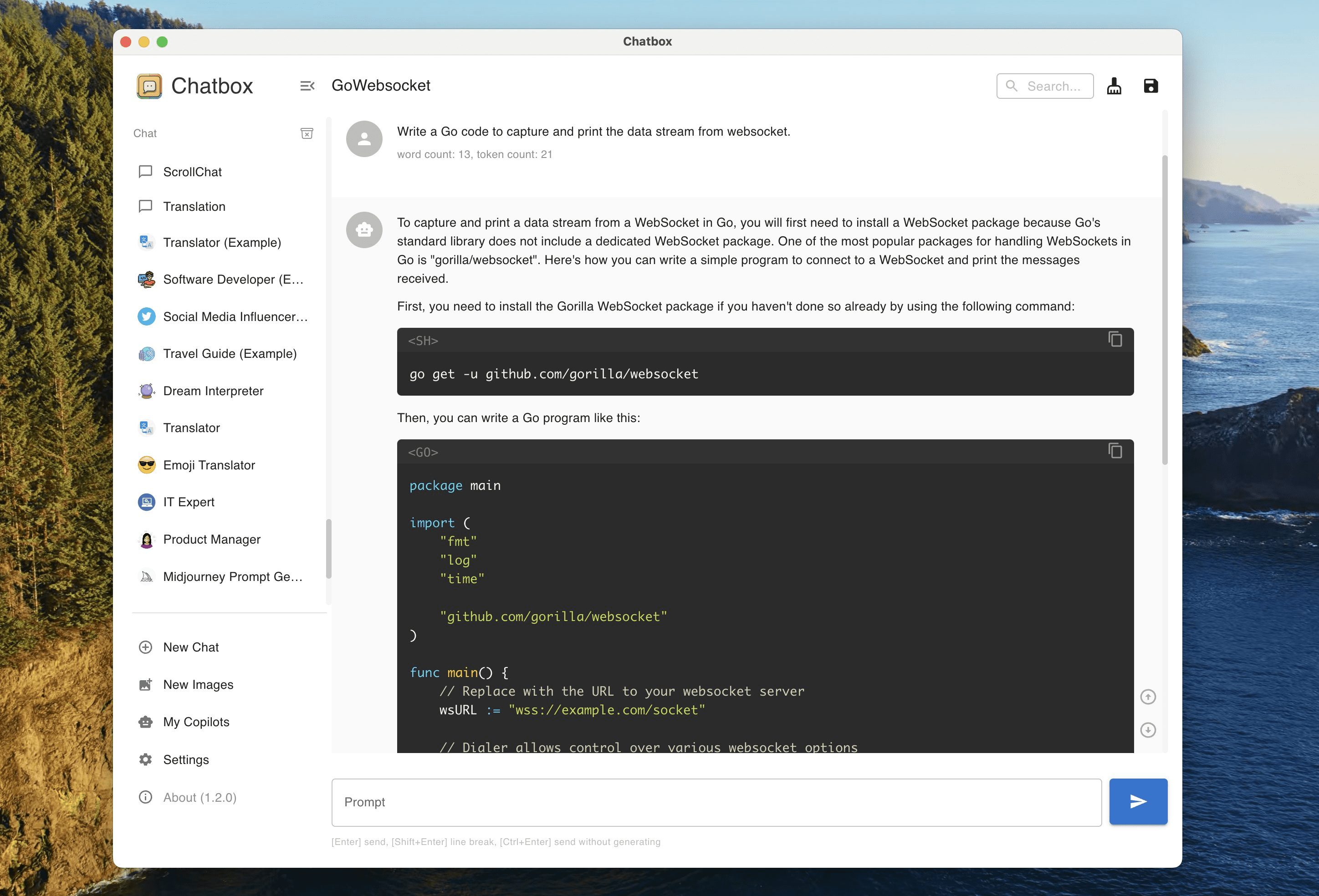
El Descenso Gradiente es el algoritmo central de optimización para resolver el mínimo de una función, y es similar en principio al proceso de descenso de una montaña: uno continúa moviéndose en la dirección de descenso más empinada hasta alcanzar el punto más bajo. El algoritmo determina la dirección de descenso calculando el gradiente de la función (el vector formado por cada derivada parcial) y actualizando iterativamente los parámetros según la regla θ = θ - η - ∇J(θ). La tasa de aprendizaje η controla el tamaño del paso y afecta directamente al rendimiento de la convergencia. Dependiendo de cómo se utilicen los datos, el descenso de gradiente se divide en tres variantes principales: batch, estocástico y small batch. En el campo del aprendizaje automático, el algoritmo se ha convertido en la piedra angular del entrenamiento de redes neuronales al minimizar la función de pérdida para entrenar los parámetros del modelo. Aunque puede caer en un óptimo local para funciones no convexas, su sencillez y eficacia lo convierten en uno de los métodos de optimización más utilizados.

Comprensión intuitiva del descenso por gradiente

• la parábola de los ciegos que bajan del monteImagínese a un ciego que se encuentra en la ladera de una colina y sólo puede detectar la pendiente a sus pies con un bastón. Cada vez que da un paso en la dirección del descenso más pronunciado, acaba llegando al fondo de algún valle. Esta analogía ilustra vívidamente la idea básica del descenso por pendiente.
• Analogía de la regulación de la temperaturaCuando ajuste la temperatura del calentador de agua, reduzca la potencia de calefacción si la temperatura del agua es demasiado alta y aumente la potencia si es demasiado baja. El descenso gradual es similar a este proceso de ajuste continuo, con el objetivo de encontrar el ajuste de temperatura más confortable.
• Mecanismo de corrección de erroresEl descenso gradual es similar a aprender a montar en bicicleta ajustando constantemente el equilibrio y girando el manillar en sentido contrario según la dirección de la inclinación del cuerpo. El descenso gradual se aproxima gradualmente a la solución óptima corrigiendo repetidamente los errores.
• Perspectivas mundial y localLa vista global: como en la búsqueda del punto más bajo de un mapa, una vista global ve todo el terreno y una vista local sólo ve una pequeña zona a su alrededor. El descenso gradual es un método de optimización local.
• Filosofía de mejora incrementalEn lugar de seguir un enfoque de un solo paso, el objetivo se alcanza a través de pequeñas mejoras continuas. Esta idea tiene un amplio valor de aplicación en la ingeniería y en la vida.

La idea central del descenso por gradiente

• dirección del gradiente negativoSiga siempre la dirección en la que la función decrece más rápidamente, que viene determinada por el gradiente negativo. La dirección del gradiente es la dirección en la que la función crece más rápido, y la dirección opuesta es el camino de declive más rápido.
• Estrategias de optimización iterativaAproximación gradual a la solución óptima actualizándola en muchos pasos pequeños, en lugar de intentar encontrar la solución exacta de una vez. Mejora continua de la calidad de la solución durante el proceso de iteración.
• aproximación lineal localEl problema se simplifica en cada paso utilizando las propiedades lineales locales de la función. Esta aproximación tiene suficiente precisión en una región suficientemente pequeña.
• El arte de controlar el ritmoLa elección de la velocidad de aprendizaje requiere un equilibrio entre estabilidad y eficacia. Un tamaño de paso demasiado grande es propenso a la oscilación, un tamaño de paso demasiado pequeño converge lentamente.
• condición de garantía de convergencia (matem.)Se garantiza que el algoritmo converge al óptimo global en condiciones tales como que la función satisfaga la convexidad. En la práctica, a menudo sólo es posible alcanzar un óptimo local.

Flujo de trabajo del descenso gradual

• Punto de partida de la inicializaciónValores iniciales de los parámetros: Los valores iniciales de los parámetros se eligen al azar o se fijan basándose en un conocimiento a priori. Diferentes puntos de partida pueden conducir a diferentes resultados de convergencia, especialmente para funciones no convexas.
• Pasos para calcular el gradienteCalcula el gradiente de la función en el parámetro actual para determinar la dirección de descenso óptima. La precisión del cálculo del gradiente afecta directamente al rendimiento del algoritmo.
• Operación de actualización de parámetrosActualiza los parámetros en función de la dirección del gradiente y del tamaño de la tasa de aprendizaje. La fórmula de actualización es sencilla pero eficaz y constituye el paso central del algoritmo.
• Lógica de juicio convergente: Comprueba si el paradigma del gradiente o la variación de los parámetros está por debajo de un umbral. Un criterio de parada adecuado evita cálculos innecesarios al tiempo que garantiza la calidad de la solución.
• Fase de salida de resultadosSalida de los valores finales de los parámetros y registro del proceso de optimización. Esta información ayuda a analizar el comportamiento del algoritmo y a depurar problemas.

Una familia de algoritmos para el descenso de gradiente

• Disminución del gradiente por lotesCalcular el gradiente utilizando todos los datos cada vez, preciso en la dirección pero grande en el cálculo. Adecuado para situaciones en las que la cantidad de datos no es grande o en las que se requiere una actualización precisa.
• descenso por gradiente estocásticoCalcula el gradiente seleccionando aleatoriamente una sola muestra cada vez, cálculo rápido pero dirección inestable. Adecuado para datos a gran escala y entornos de aprendizaje en línea.
• Disminución de gradiente en lotes pequeñosUna solución de compromiso que equilibra la estabilidad de la eficiencia utilizando tamaños de muestra pequeños. El enfoque de optimización más popular en el aprendizaje profundo.
• algoritmo de la fuerza motrizLa introducción de un término de impulso reduce las oscilaciones y acelera el proceso de convergencia. Modelización de la inercia física para ayudar a atravesar regiones planas.
• Ritmo de aprendizaje adaptativoAjustar la tasa de aprendizaje basándose en la historia del gradiente, p. ej. Adam, Adagrad. Reducir la dificultad de ajuste de hiperparámetros.

Características ventajosas del descenso por gradiente

• Simplicidad de aplicaciónLos algoritmos subyacentes pueden implementarse en unas pocas líneas de código y son fáciles de entender y modificar. Esta sencillez lo convierte en el caso preferido para la enseñanza.
• integridad teóricaSe ofrecen pruebas matemáticas rigurosas en el marco de la optimización convexa, que proporcionan una sólida base teórica para las aplicaciones. Se analizan explícitamente la convergencia y la tasa de convergencia.
• versatilidad: Del aprendizaje automático tradicional al aprendizaje profundo, de la investigación académica a la práctica industrial. Se ha convertido casi en una solución estándar para los problemas de optimización.
• EscalabilidadEs fácil de combinar con otras técnicas para producir versiones mejoradas, como métodos de impulso, tasas de aprendizaje adaptativas, etc. Esta escalabilidad mantiene vivo el algoritmo.
• Potencial de paralelizaciónEl modelo de paralelismo de datos es compatible con el paralelismo de modelos para entornos informáticos distribuidos. Los marcos informáticos modernos proporcionan implementaciones paralelas eficientes.

Desafiando las limitaciones del descenso por gradiente

• dilema del óptimo localEn el caso de funciones no convexas, es fácil caer en óptimos locales, y no puede garantizarse la optimalidad global. Los efectos de punto de silla son más significativos en problemas de gran dimensión.
• Problema de velocidad de convergenciaConvergencia lenta en problemas patológicamente condicionados, que requieren un gran número de pasos iterativos. El fenómeno de los dientes de sierra en el terreno de los cañones consume recursos informáticos.
• Alta sensibilidad a los parámetrosLos hiperparámetros, como la tasa de aprendizaje, deben ajustarse cuidadosamente, y cada problema requiere una configuración diferente. El método de ajuste automático está aún poco desarrollado.
• Requisitos estrictos de pendienteLa función requerida es diferenciable en todas partes y no puede tratar directamente el problema no degradable. Los métodos de subgradiente amplían la gama de aplicaciones, pero su eficacia es limitada.

Aplicaciones prácticas del descenso por gradiente

• Formación en aprendizaje profundoLas redes neuronales calculan los gradientes por retropropagación y actualizan los pesos por descenso de gradiente. Desde la visión por ordenador hasta el procesamiento del lenguaje natural se basan en esta técnica.
• Ajuste convencional del modeloEl modelo de regresión: Los modelos estadísticos como la regresión lineal y la regresión logística utilizan el descenso de gradiente para resolver los parámetros. Estos modelos básicos se utilizan mucho en la industria.
• Optimización del sistema recomendadaLa descomposición matricial y el filtrado colaborativo para aprender las características potenciales de los usuarios y los artículos mediante el descenso de gradiente. Una de las tecnologías clave para el comercio electrónico y las plataformas de streaming.
• Diseño de sistemas de controlLa optimización de los parámetros de los controladores es necesaria en ámbitos como el control de robots y el filtrado adaptativo. El descenso gradiente ofrece soluciones eficaces de aprendizaje en línea.
• Calibración del modelo financieroEstimación de parámetros para problemas financieros como la valoración de opciones y la modelización del riesgo. El descenso gradiente ayuda a encontrar los parámetros óptimos del modelo.

Ajuste de parámetros para el descenso por gradiente

• Opciones de tasas de aprendizaje: Aumente gradualmente a partir de valores pequeños y observe el cambio en el comportamiento de convergencia. Las estrategias de programación de la tasa de aprendizaje, como el recocido del coseno, pueden mejorar el rendimiento.
• Determinación del tamaño del loteEl equilibrio entre el uso de memoria y la estabilidad de la convergencia se suele utilizar en lotes de entre 32 y 256. Las características del hardware también influyen en la mejor elección. Las características del hardware también influyen en la mejor elección.
• Ajuste del factor de impulso: Normalmente toma valores en torno a 0,9 para ayudar a suavizar la dirección de actualización. El impulso Nesterov proporciona estrategias de actualización más inteligentes.
• Diseño de los criterios de paradaControlar el momento de las paradas tempranas en el conjunto de validación para evitar el sobreajuste. El número máximo de iteraciones debe ser suficiente para garantizar la convergencia.

Consejos para aplicar el descenso por gradiente

• Método de comprobación del gradiente: Utiliza gradientes numéricos para verificar que el gradiente de análisis es correcto y evitar errores de implementación. Esta comprobación es extremadamente importante durante la fase de desarrollo.
• Normalización de datosLa normalización de las características de entrada a media cero y varianza unitaria acelera el proceso de convergencia. Las características a diferentes escalas pueden plantear dificultades de optimización.
• visualizaciónGráfico de curvas de descenso de funciones de pérdida y trayectorias de actualización de parámetros. Las pantallas intuitivas ayudan a diagnosticar problemas algorítmicos y ajustar parámetros.
• Reiniciar la aplicación de la estrategiaReinicialice los parámetros cuando el progreso se estanque en un intento de escapar del óptimo local. La reinicialización periódica puede mejorar significativamente los resultados.
• Diseño de estrategia mixtaCombine las ventajas de distintos optimizadores, por ejemplo, Adam para una convergencia rápida y SGD para el ajuste fino. Esta combinación suele dar mejores resultados.