Qué es la cuantificación de modelos: explicación de los tipos de datos FP32, FP16, INT8, INT4

guía (por ejemplo, libro u otro material impreso)

En el vasto cielo estrellado de la tecnología de IA, los modelos de aprendizaje profundo impulsan la innovación y el desarrollo en muchos campos con su excelente rendimiento. Sin embargo, la continua expansión de la escala de los modelos es como un arma de doble filo, que conlleva un fuerte aumento de la demanda aritmética y de la presión de almacenamiento al tiempo que mejora el rendimiento. Especialmente en escenarios de aplicaciones con recursos limitados, el despliegue y el funcionamiento de los modelos se enfrentan a graves desafíos.

Ante este dilema, ha surgido una tecnología llamada "cuantificación", que es como un delicado bisturí, reduce inteligentemente el tamaño del modelo, mejora la velocidad de cálculo y reduce significativamente el consumo de energía dentro del rango aceptable de precisión del modelo. La técnica de cuantificación puede convertir los datos FP32 de alta precisión del modelo en datos INT4 de baja precisión, con lo que se consigue "adelgazar" y "acelerar" el modelo. En este artículo, analizaremos los principios y métodos de la cuantización y su aplicación en el campo del aprendizaje profundo, para que incluso los principiantes puedan comprender fácilmente su esencia.

1. Fundamentos de la representación numérica

1.1 Conversión de binario a decimal

En informática, piedra angular del mundo digital, todos los datos se almacenan en forma binaria. El sistema binario consta de sólo dos números, 0 y 1, mientras que el sistema decimal, que utilizamos en nuestra vida cotidiana, tiene diez números del 0 al 9. La conversión entre estos dos sistemas, como la traducción entre diferentes idiomas, es la clave para entender la representación de datos en los ordenadores. La conversión entre estos dos sistemas, como la traducción entre distintos idiomas, es la clave para entender la representación de datos en los ordenadores.

El número decimal 13, por ejemplo, se convierte a forma binaria como 1101. El proceso de conversión es similar a descomponer el "todo" decimal en sus "componentes" binarios. Los pasos son los siguientes:

13 Dividido por 2, el cociente es 6 y el resto es 1 (dígito binario más bajo)
6 dividido por 2 da un cociente de 3 y un resto de 0.
3 dividido por 2, cociente 1, resto 1
1 dividido por 2, el cociente es 0, el resto es 1 (dígito binario más alto)

Los residuos se enumeran de abajo arriba:
↑1
↑0
↑1
↑1
Obtener resultado binario: 1101

A la inversa, convertir el binario 1101 de nuevo a decimal es como volver a montar las "partes" para hacer el "todo". De derecha a izquierda, el peso de cada bit aumenta en potencias de dos, teniendo el bit situado más a la derecha un peso de , , y así sucesivamente hacia la izquierda. Por tanto, el 1101 binario se convierte a decimal de la siguiente manera: 1× + 1× + 0× + 1× = 8 + 4 + 0 + 1 = 13.

1.2 Diferencia entre números enteros y números en coma flotante

(i) Tipos enteros (INT)

INT es la abreviatura de Integer, que representa el tipo de número entero. Los números enteros, como su nombre indica, son números que no contienen partes decimales, como 1, 2, 3, etc.

INT4 significa que se utiliza un número binario de 4 bits para representar un número entero, mientras que INT8 utiliza un número binario de 8 bits para representar un número entero. El número de bits determina el rango de representación de enteros.

El rango de enteros que puede representar INT4 es limitado, ya que un número binario de 4 bits puede representar hasta un número diferente. Para INT4 con signo, el rango suele ser de -8 a 7, y para INT4 sin signo, el rango es de 0 a 15. Lo mismo ocurre con INT8, que va de -128 a 127, y con INT8 sin signo, que va de 0 a 255, ya que un número binario de 8 bits puede representar = 256 números diferentes.

(ii) Tipo de coma flotante (FP)

FP son las siglas de Floating Point, el tipo de punto flotante. Los números de coma flotante, a diferencia de los enteros, se utilizan para representar números con partes fraccionarias.

Los números de coma flotante constan de un bit de signo, un bit de exponente y un bit de mantisa. Un número de coma flotante de 32 bits (FP32), por ejemplo, consta de 1 bit de signo, 8 bits de exponente y 23 bits de mantisa. Este ingenioso diseño permite que los números de coma flotante representen una amplísima gama de valores, desde números muy pequeños hasta números muy grandes, como una cinta métrica.

Por ejemplo, FP32 puede representar números muy pequeños (aproximadamente) y números muy grandes (aproximadamente). INT8 (enteros de 8 bits), por otro lado, sólo puede representar enteros entre -128 y 127. Esta diferencia es análoga a medir la longitud con una regla de longitud fija (números enteros) frente a una cinta métrica escalable (números de coma flotante), donde los números de coma flotante son muy superiores a los enteros en términos de flexibilidad y rango de representación numérica.

(iii) Tipos de datos más utilizados

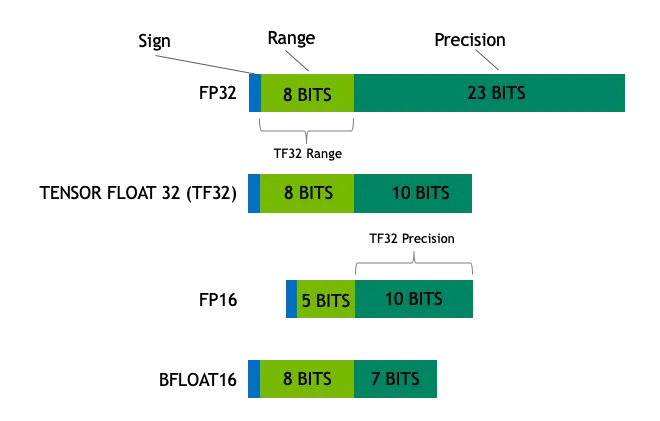
Los tipos de datos comunes en el aprendizaje profundo y la computación de propósito general incluyen:

• Float32 (FP32)FP32 : Es el formato estándar de coma flotante de 32 bits, conocido por su gran precisión y su amplia gama de valores.Las operaciones FP32 dominan el entrenamiento y la inferencia de modelos debido a su versatilidad, que es ampliamente soportada por una amplia gama de hardware.
• Float16 (FP16)FP16: FP16 es un número de coma flotante de 16 bits de media precisión, que tiene una precisión reducida en comparación con FP32, pero tiene una huella de memoria significativamente reducida y una velocidad de cálculo sustancialmente más rápida.FP16 tiene un rango relativamente estrecho de representaciones numéricas, que pueden estar en riesgo de desbordamiento y subdesbordamiento. Sin embargo, en prácticas de aprendizaje profundo comoEscalado de pérdidas La aplicación de técnicas como éstas puede paliar eficazmente estos problemas.
• BFloat16 (BF16)BF16: BF16 es otro formato de coma flotante de 16 bits. Es único en el sentido de que BF16 conserva el mismo bit de exponente de 8 bits que FP32, y por lo tanto tiene el mismo rango dinámico que FP32, sin embargo, el bit de arrastre es de sólo 7 bits, lo que es menos preciso que FP16. Sin embargo, BF16 sólo tiene 7 bits de salida, lo que es menos preciso que FP16. BF16 funciona bien en escenarios con un amplio rango de valores, pero puede haber compensaciones en tareas sensibles a la precisión.
• Int8INT8 es un tipo de número entero de 8 bits con una gama limitada de representación numérica, pero que ocupa muy poca memoria. INT8 se utiliza principalmente en técnicas de cuantificación de modelos, en las que la conversión de los parámetros del modelo de FP32 o FP16 de alta precisión a INT8 reduce significativamente el espacio de almacenamiento necesario y la complejidad computacional del modelo, allanando el camino para la implantación eficiente del modelo en dispositivos con recursos limitados.

2. Conceptos cuantitativos

2.1 Definiciones cuantitativas

La cuantificación se refiere a la conversión de los datos de un modelo de una representación de alta precisión a otra de baja precisión, como en el caso de laCompromisos entre calidad de imagen y tamaño de archivoEn el aprendizaje profundo, la cuantificación es el proceso de comprimir una imagen de alta precisión en una imagen JPEG de baja precisión, lo que reduce significativamente el tamaño del archivo sin perder la información principal de la imagen. En el campo del aprendizaje profundo, la cuantificación suele referirse a la reducción de los pesos del modelo y los valores de activación de FP32 (coma flotante de 32 bits) a FP16 (coma flotante de 16 bits) o incluso INT8 (entero de 8 bits) o de menor precisión.

FP32 es un formato de coma flotante de alta precisión que representa con exactitud valores en binario de 32 bits (1 bit de signo, 8 bits de exponente y 23 bits de mantisa). FP32 es una escala de precisión que puede medir valores pequeños y grandes, pero su naturaleza de alta precisión conlleva una elevada sobrecarga de almacenamiento y una velocidad de cálculo relativamente lenta.

FP16 es un formato de coma flotante de media precisión que sólo requiere 16 bits binarios (1 bit de signo, 5 bits de exponente, 10 bits de mantisa) para representar un valor. En comparación con FP32, FP16 sacrifica precisión a cambio de la mitad de espacio de almacenamiento y una mayor eficiencia computacional, y es una escala ligeramente más gruesa que consigue un buen equilibrio entre precisión y eficiencia.

INT8 es un tipo de entero de 8 bits que sólo puede representar enteros en el rango de -128 a 127. INT8 tiene la ventaja de ocupar muy poca memoria y tener una velocidad de cálculo muy alta, pero también tiene la precisión numérica más baja. INT8 es similar a un contador simple que sólo cuenta enteros, pero es rápido y cómodo.

2.2 Objetivo cuantitativo

El objetivo central de la cuantificación esReducción de los requisitos de almacenamiento y de la complejidad computacional de los modelosy, al mismo tiempo, trata de mantener la pérdida de precisión dentro de límites aceptables. Concretamente, la cuantificación pretende alcanzar los siguientes objetivos:

Reducción de las necesidades de almacenamientoEl modelo FP32: Los modelos modernos de aprendizaje profundo, especialmente los modelos a gran escala con parámetros de gran tamaño, a menudo tienen cientos de millones o incluso cientos de miles de millones de parámetros, lo que ejerce una enorme presión sobre el espacio de almacenamiento. Si tomamos como ejemplo un modelo FP32, cada parámetro ocupa 4 bytes de espacio de almacenamiento. Si el modelo se cuantifica a FP16, cada parámetro requiere sólo 2 bytes, lo que reduce a la mitad las necesidades de almacenamiento. Si el modelo se cuantifica además a INT8, cada parámetro sólo necesita 1 byte, y el espacio de almacenamiento puede reducirse en 75%.

Aumentar la eficiencia computacionalEl modelo cuantificado es significativamente menos intensivo desde el punto de vista computacional en la fase de inferencia, con lo que se consigue un aumento de la velocidad de inferencia. Por ejemplo, cuando el modelo FP32 se ejecuta en una GPU, la velocidad de cálculo puede verse limitada por el ancho de banda de la memoria. En cambio, en los modelos FP16 o INT8, gracias a la aceleración optimizada del hardware para el cálculo de baja precisión, la velocidad de cálculo puede aumentar considerablemente. La mejora del rendimiento que aporta la cuantificación es especialmente significativa en escenarios en los que los recursos informáticos son limitados, como los dispositivos periféricos o los dispositivos móviles.

reducir el consumo de energíaEl objetivo es reducir el consumo de energía: la reducción de los requisitos de recursos informáticos del modelo se traduce directamente en una reducción del consumo de energía. Para los dispositivos móviles y los sistemas empotrados, el consumo de energía es una consideración crítica. Las técnicas de cuantificación pueden reducir eficazmente el consumo de energía de los modelos, prolongar la vida útil de los dispositivos y reducir las necesidades de disipación de calor.

Reducción de las necesidades de ancho de banda:: En los sistemas informáticos distribuidos, la reducción del tamaño de los modelos implica también la reducción del ancho de banda de transmisión de datos. En un escenario multiservidor, los modelos cuantitativos pueden distribuirse y sincronizarse a mayor velocidad, mejorando así la eficiencia global de la transferencia de datos.

3. Cuantificación INT4, INT8

3.1 Rango de representación INT4 e INT8

INT4 e INT8 son métodos de cuantificación de tipo entero que almacenan datos en forma binaria en sistemas informáticos, pero difieren en el rango y la precisión de la representación numérica.

• INT8INT8 es un tipo de entero de 8 bits con un rango de representación de -128 a 127. Puede analogizarse a un contador de 8 bits, en el que cada bit puede ser 0 ó 1, y diferentes valores enteros pueden representarse mediante distintas combinaciones de 0/1. Por ejemplo, en elanotado INT8 significa medio, que va de -128 a 127, y 11111111 en binario significa -1 en decimal. Si essin signo (es decir, el valor absoluto, independientemente del signo más o menos) INT8, que va de 0 a 255, en cuyo caso 11111111 representa 255 en decimal, es suficiente para satisfacer las necesidades de muchos escenarios de aplicación, como los valores de píxel en el procesamiento de imágenes, que suelen estar en el rango de 0 a 255, y pueden ser representados eficazmente por INT8.
• INT4INT4 es un tipo de entero de 4 bits con un rango de representación más pequeño de -8 a 7 que INT8. INT4 sacrifica el rango numérico por una huella de almacenamiento más pequeña y un cálculo más rápido. INT4 es como un contador más pequeño, con un rango numérico limitado pero una "huella" más pequeña, que es más eficiente en recursos. Es más eficiente en cuanto a recursos. En algunos escenarios de aplicación con requisitos de precisión relativamente laxos, como algunas capas de redes neuronales ligeras, el uso de la cuantificación INT4 puede reducir significativamente los costes de almacenamiento y cálculo.Por ejemplo, cuando se despliega un modelo ligero de clasificación de imágenes en un móvil, los parámetros del modelo y los resultados de los cálculos intermedios pueden almacenarse y calcularse utilizando el formato INT4 para reducir la huella de memoria y acelerar la inferencia.

3.2 Fórmulas cuantitativas y ejemplos

El proceso de cuantificación es esencialmente la conversión de un mapa numérico de coma flotante de alta precisión a un número entero de baja precisión. Tomando como ejemplo la cuantificación de FP32 a INT8, la fórmula de cuantificación es la siguiente:

es el número original en coma flotante.

es un número entero cuantificado.

es el factor de escala, utilizado para asignar números de coma flotante al rango de enteros.

Indica el redondeo al número entero más próximo.

Indica que el resultado está limitado al rango de INT8, es decir, [-128, 127].

Cálculo del factor de escala

El factor de escala suele calcularse como el máximo del valor absoluto del número en coma flotante. Suponiendo que existe un conjunto de números de coma flotante, el procedimiento es el siguiente:

1. Hallar el valor absoluto máximo del grupo de números en coma flotante:
2. Calcular el factor de escala: .

En la práctica, hay varias formas de calcular el factor de escala, como la cuantificación máxima, la cuantificación media-estándar, etc. La cuantificación máxima utiliza el valor absoluto máximo del tensor para calcular el factor de escala. La Cuantización Max utiliza el valor absoluto máximo del tensor para calcular el factor de escala, lo que es sencillo de aplicar pero puede ser sensible a los valores atípicos. La Cuantización Media-Std utiliza la información sobre la media y la desviación típica de los datos para determinar el factor de escala de una forma más sólida, pero la complejidad computacional es ligeramente mayor. La elección del método de cálculo del factor de escala adecuado requiere un compromiso entre la precisión y la carga computacional.

ejemplo típico

Suponiendo que tenemos un conjunto de números en coma flotante [-0,5, 0,3, 1,2, -2,1], a continuación se muestra paso a paso el proceso de cuantificación:

1. Calcula el valor absoluto máximo:

2. Cálculo del factor de escala:

3. Cuantificar cada número en coma flotante:

• Para -0.5.
• Para 0,3.
• Para 1.2.
• Para -2.1.

La representación final cuantificada INT8 es [-1, 1, 4, -7].

A través de los pasos anteriores, podemos ver claramente cómo la técnica de cuantificación convierte los números de coma flotante en enteros. Aunque el proceso de cuantificación introduce inevitablemente una cierta pérdida de precisión, si se elige bien el factor de escalado, el nivel de rendimiento del modelo puede mantenerse al máximo, al tiempo que se reducen significativamente los costes de almacenamiento y cálculo. Para reducir aún más los errores de cuantificación, también se puede introducir la cuantificación de punto cero. La cuantificación de punto cero añade un desplazamiento de punto cero a la fórmula de cuantificación, lo que permite que los ceros de punto flotante se asignen con precisión a ceros enteros, mejorando así la precisión de la cuantificación, especialmente si hay un gran número de ceros en los valores de activación.

4. Cuantificación FP8, FP16, FP32

4.1 Representaciones FP8, FP16, FP32

FP8, FP16 y FP32 son números en coma flotante que se almacenan en forma binaria en el ordenador, pero con diferentes anchos de bits y, por tanto, diferentes rangos y precisión.

FP32

FP32, como formato estándar de coma flotante de 32 bits, consta de las tres partes siguientes:

• Bit de signo (1 bit): Se utiliza para identificar valores positivos y negativos, con 0 representando un número positivo y 1 representando un número negativo.
• Dígitos exponenciales (8 dígitos): se utiliza para definir el rango de tamaño de un valor, permitiendo a FP32 representar valores desde muy pequeños a muy grandes.
• Último dígito (23 bits): Se utiliza para determinar la precisión de un valor; cuantos más dígitos finales, mayor precisión.

Con una amplia gama de valores, desde aproximadamente hasta , y una precisión de unos 6 decimales, el FP32 es como una cinta métrica de alta precisión que puede medir escalas tan pequeñas como una mota de polvo y distancias tan vastas como una montaña. FP32 es un tipo de datos indispensable en la informática científica, la modelización financiera y otros campos que requieren un alto grado de precisión.

FP16

FP16 es un formato de coma flotante de media precisión que ocupa sólo 16 bits de memoria, la mitad que FP32.La estructura de FP16 es la siguiente:

• Bit de signo (1 bit): Identifica valores positivos y negativos.
• Dígito exponencial (5 dígitos): Define un rango de tamaños de valor.
• Última cifra (10 dígitos): Determina la precisión numérica.

El rango de FP16 es de aproximadamente a, y la precisión se reduce a unos 3 decimales en comparación con FP32. FP16 es como una regla con una escala ligeramente más gruesa, que tiene una precisión menor, pero tiene más ventajas en espacio de almacenamiento y eficiencia computacional. FP16 se utiliza habitualmente para el entrenamiento y la inferencia de modelos de aprendizaje profundo, lo que requiere una gran velocidad de cálculo y ancho de banda de memoria. Especialmente en escenarios acelerados por GPU, FP16 puede aprovechar al máximo las unidades de aceleración de hardware como Tensor Core para lograr mejoras significativas en el rendimiento.

FP8

FP8 es un formato emergente de números de coma flotante de baja precisión, utilizado principalmente en el campo del aprendizaje profundo, con el objetivo de lograr un cálculo eficiente.La estructura típica de FP8 es la siguiente:

• Bit de signo (1 bit): Identifica valores positivos y negativos.
• Dígitos exponenciales (3 ó 4 dígitos): Define un rango de tamaños de valor (existen dos variantes FP8).
• Última cifra (4 ó 3 dígitos)Determina la precisión numérica (corresponde al número de dígitos del índice).

El rango y la precisión de la representación numérica de la FP8 se reducen aún más, pero las ventajas son una menor huella de memoria y velocidades de cálculo más rápidas. Si FP32 es una cinta métrica de precisión y FP16 es una regla con una escala ligeramente más gruesa, entonces FP8 es una cinta métrica más precisa. Es como una simple regla con escala centimétrica.Además, el alcance y la precisión se reducen aún más, pero la tarea de medición puede seguir realizándose rápidamente en una situación determinada. Como tipo de datos de precisión extremadamente baja, el FP8 muestra un gran potencial en escenarios con requisitos extremos de latencia y rendimiento, como la inferencia en tiempo real, la computación de borde, etc. Sin embargo, el FP8 también impone mayores exigencias al hardware y a los algoritmos. Sin embargo, la aplicación de FP8 también impone mayores exigencias al hardware y los algoritmos, lo que requiere un soporte de hardware especial y estrategias de cuantificación para garantizar la precisión.

4.2 Proceso de cuantificación y fórmulas

La cuantificación es el proceso de convertir un número de coma flotante de alta precisión en un número de coma flotante de baja precisión o entero. Tomando como ejemplo la cuantificación de FP32 a FP16, la fórmula de cuantificación es la siguiente:

es el número original en coma flotante.

es un número cuantificado de coma flotante de baja precisión.

es el factor de escala, utilizado para asignar números de coma flotante a rangos de menor precisión.

Indica el redondeo al valor más próximo.

Cálculo del factor de escala

El factor de escala suele calcularse como el máximo del valor absoluto del número en coma flotante. Suponiendo que existe un conjunto de números de coma flotante, el procedimiento es el siguiente:

1. Hallar el valor absoluto máximo del grupo de números en coma flotante:
2. Calcular el factor de escala: , donde es el máximo del formato de baja precisión objetivoPuede expresarse en valor absoluto. Para FP16, este valor es aproximadamente 65504.

De forma similar a la cuantificación INT8, los factores de escala en la cuantificación FP16 pueden calcularse de diversas formas, que pueden elegirse en función de los distintos requisitos de precisión y rendimiento. Además, la cuantificación FP16 se utiliza a menudo junto con el entrenamiento de precisión mixta (MPT). Durante el proceso de entrenamiento del modelo, FP16 se utiliza para algunas operaciones de cálculo intensivo (por ejemplo, multiplicación de matrices, convolución), mientras que FP32 se utiliza para operaciones que requieren una mayor precisión (por ejemplo, cálculo de pérdidas, actualización de gradientes), con el fin de acelerar el proceso de entrenamiento y reducir el consumo de memoria, garantizando al mismo tiempo la precisión del modelo.

ejemplo típico

Suponiendo que tenemos un conjunto de números en coma flotante FP32 [-0.5, 0.3, 1.2, -2.1], a continuación se muestra paso a paso la cuantificación de FP32 a FP16:

1. Calcula el valor absoluto máximo:

2. Cálculo del factor de escala:

3. Cuantificar cada número en coma flotante:

• Para -0.5.
• Para 0,3.
• Para 1.2.
• Para -2.1.

El FP16 final cuantificado se expresa como [-0,5, 0,3, 1,2, -2,1].

A través de los pasos anteriores, es posible observar cómo las técnicas de cuantificación convierten números de coma flotante de alta precisión en números de coma flotante de baja precisión. Sin duda, la cuantificación conlleva cierta pérdida de precisión, pero si se elige bien el factor de escalado, se puede mantener el rendimiento del modelo en la medida de lo posible, al tiempo que se reducen los costes de almacenamiento y cálculo. Para mejorar aún más la precisión de la cuantificación FP16, puede utilizarse la cuantificación dinámica. La cuantificación dinámica ajusta dinámicamente el factor de escala según el rango real de los datos de entrada durante el proceso de inferencia, para adaptarse mejor a los cambios en la distribución de los datos y reducir el error de cuantificación.

5. Aplicaciones y ventajas cuantitativas

5.1 Aplicaciones en el aprendizaje profundo

Las técnicas cuantitativas tienen una amplia gama de aplicaciones prometedoras en el aprendizaje profundo, especialmente en las fases de entrenamiento e inferencia de modelos, donde son cada vez más valiosas. A continuación se exponen algunas de las principales aplicaciones de las técnicas de cuantificación en el aprendizaje profundo:

Aceleración de la formación de modelos

La computación con tipos de datos de baja precisión (por ejemplo, FP16 o FP8) durante la fase de entrenamiento del modelo puede acelerar significativamente el proceso de entrenamiento. Por ejemplo, las GPU de arquitectura NVIDIA Hopper admiten operaciones Tensor Core con precisión FP8. El entrenamiento en FP8 puede ser de 2 a 3 veces más rápido que el entrenamiento tradicional en FP32. Esta aceleración del entrenamiento es especialmente crítica para modelos con parámetros de gran tamaño, ya que reduce significativamente el tiempo de entrenamiento y el consumo de recursos computacionales. Por ejemplo, al entrenar modelos lingüísticos a gran escala como GPT-3, el uso de FP16 o BF16 de precisión mixta puede acortar significativamente el tiempo de entrenamiento y ahorrar muchos recursos computacionales.

para Inflexión IA Inflection-2, por ejemplo, se entrenó en 5.000 GPU de arquitectura NVIDIA Hopper utilizando una estrategia de entrenamiento de precisión mixta FP8, con un total de FLOPs de operaciones de coma flotante, y en una serie de pruebas de rendimiento de IA estándar Inflection-2 demostró un rendimiento superior al modelo PaLM 2, buque insignia de Google, que también se encuentra en la categoría de cálculo de entrenamiento. En una serie de pruebas de rendimiento de IA estándar, Inflection-2 demostró una ventaja de rendimiento significativa sobre el modelo PaLM 2, buque insignia de Google, en la misma categoría de computación de entrenamiento.

Optimización de la inferencia de modelos

En la fase de inferencia del modelo, las técnicas de cuantificación pueden reducir significativamente los requisitos de almacenamiento y la complejidad computacional del modelo, mejorando así la eficacia de la inferencia. Por ejemplo, al cuantificar un modelo FP32 a INT8, el espacio de almacenamiento del modelo puede reducirse en 75% y la velocidad de inferencia puede aumentar varias veces. Esto es fundamental para desplegar modelos de aprendizaje profundo en dispositivos periféricos o móviles, que a menudo se enfrentan a la limitación de recursos informáticos y espacio de almacenamiento. Por ejemplo, al desplegar modelos de reconocimiento de imágenes en teléfonos móviles, cuantificar el modelo como INT8 puede reducir eficazmente el tamaño del modelo, reducir el consumo de memoria, acelerar la velocidad de inferencia y mejorar la experiencia del usuario.

Por ejemplo, Google ha trabajado en estrecha colaboración con el equipo de NVIDIA para aplicar la técnica de optimización TensorRT-LLM al modelo Gemma y combinarla con la tecnología FP8 para conseguir acelerar la inferencia. Los resultados experimentales muestran que FP8 consigue más de 3 veces más rendimiento que FP16 cuando se utilizan las GPU Hopper para la inferencia.

Compresión y despliegue de modelos

Las técnicas de cuantificación también pueden utilizarse para la compresión y el despliegue de modelos. Cuantificando modelos de alta precisión en modelos de baja precisión, se puede reducir eficazmente el tamaño del modelo, lo que облегчить su despliegue en entornos con recursos limitados. Por ejemplo, cero-uno-todoutilice La tecnología combinada de hardware y software de NVIDIA ha completado el entrenamiento y la validación de modelos FP8 de gran tamaño, con un aumento de 1,3 veces en el rendimiento del entrenamiento de modelos de gran tamaño en comparación con BF16. Además de la cuantificación INT8 y FP16/FP8, también existen técnicas de cuantificación INT4 e incluso de bits más bajos, como la red neuronal binaria (BNN) y la red neuronal ternaria (TNN). Estas técnicas de cuantificación de bits muy bajos pueden comprimir el modelo hasta el extremo, pero normalmente con una gran pérdida de precisión, y son adecuadas para escenarios con requisitos extremos de tamaño y velocidad del modelo.

Además, el modelo cuantificado puede mejorarse aún más con la ayuda de técnicas específicas de aceleración por hardware. Por ejemplo, NVIDIA Transformador Engine se ha integrado en los principales marcos de aprendizaje profundo, como PyTorch, JAX, PaddlePaddle, etc., proporcionando un soporte eficiente a nivel de hardware para la inferencia de modelos cuantitativos. Además de las GPU NVIDIA, otras plataformas de hardware, como las CPU de arquitectura ARM y las NPU móviles, también están optimizadas y aceleradas para el cálculo cuantitativo, lo que proporciona una base de hardware para la implantación generalizada de modelos cuantitativos.

5.2 Puntos fuertes y limitaciones

vanguardia

Mejora de la eficiencia computacionalLa cuantificación de baja precisión puede acelerar considerablemente el cálculo y reducir el consumo de recursos informáticos. tanto FP16 como FP8 tienen un rendimiento informático varias veces superior a FP32. este efecto de aceleración es especialmente importante en el entrenamiento y la inferencia de modelos a gran escala.

Menores necesidades de almacenamientoLas técnicas de cuantificación pueden reducir significativamente los requisitos de almacenamiento de los modelos. Por ejemplo, cuantificar un modelo FP32 a INT8 reduce el espacio de almacenamiento en 75%, lo que es importante para desplegar modelos en entornos con recursos de almacenamiento limitados.

Menor consumo de energía:: La computación de baja precisión requiere menos recursos computacionales, lo que reduce el consumo de energía de los dispositivos. En los dispositivos móviles y los sistemas integrados, el consumo de energía es un aspecto clave del diseño. Los modelos cuantificados ayudan a prolongar la duración de la batería del dispositivo y a reducir las necesidades de disipación de calor.

Optimización de modelosLas técnicas de cuantificación impulsan la optimización y compresión de los modelos durante el entrenamiento y la inferencia, lo que reduce aún más los costes de despliegue. Por ejemplo, la aplicación del FP8 permite a los modelos explorar estrategias de cuantificación más refinadas durante la fase de entrenamiento, mejorando así la eficiencia global del modelo.

limitaciones

Pérdida de precisiónEl proceso de cuantificación va inevitablemente acompañado de una pérdida de precisión, que puede ser significativa, especialmente cuando se utilizan formatos de muy baja precisión (por ejemplo, FP8), y puede provocar una degradación del rendimiento del modelo en una tarea determinada. Aunque la pérdida de precisión puede atenuarse en cierta medida, por ejemplo, mediante una elección cuidadosa de los factores de escala, a menudo es difícil eliminar por completo la pérdida de precisión. Para mitigar la pérdida de precisión causada por la cuantificación, puede utilizarse el entrenamiento consciente de la cuantificación (QAT). QAT simula la operación de cuantificación durante el proceso de entrenamiento del modelo y tiene en cuenta el error de cuantificación en el entrenamiento, para entrenar un modelo más resistente a la cuantificación. Por lo general, QAT puede mejorar significativamente la precisión de los modelos de cuantificación, pero el coste de formación aumentará en consecuencia.

Soporte de hardwareCaracterísticas: No todas las plataformas de hardware son totalmente compatibles con el cálculo de baja precisión. Por ejemplo, los cálculos FP8 y FP16 suelen requerir hardware específico (por ejemplo, GPU de arquitectura NVIDIA Hopper). Si la plataforma de hardware no está optimizada para el cálculo de baja precisión, no se aprovecharán plenamente las ventajas de la cuantificación. Con la popularidad de la computación de baja precisión, cada vez más plataformas de hardware empiezan a admitir tipos de datos de baja precisión como FP16, BF16 e incluso FP8, lo que proporciona una base de hardware más sólida para la amplia aplicación de técnicas de cuantificación.

Mayor complejidadEl proceso de cuantificación en sí puede añadir complejidad al desarrollo del modelo. Por ejemplo, el proceso de cuantificación requiere un cálculo detallado de los factores de escala y puede requerir una calibración y un ajuste adicionales del modelo. Sin duda, esto aumenta la dificultad del desarrollo y la implantación del modelo. Con el fin de reducir la complejidad del despliegue de la cuantificación, han surgido en el sector numerosas herramientas y plataformas de cuantificación automatizada, como NVIDIA TensorRT, Qualcomm AI Engine, etc., que ayudan a los desarrolladores a cuantificar e implantar modelos de forma rápida y sencilla en las plataformas de hardware de destino.

escenario de aplicaciónLas técnicas de cuantificación no son adecuadas en todos los escenarios de aplicación. En tareas que requieren una precisión muy alta (por ejemplo, cálculo científico, modelización financiera, etc.), la cuantización puede provocar una pérdida de precisión inaceptable. Para tareas sensibles a la precisión, puede probarse una estrategia de cuantificación de precisión mixta, en la que se aplican diferentes precisiones de cuantificación a diferentes capas o parámetros del modelo, por ejemplo, FP32 o FP16 para capas o parámetros clave, e INT8 o inferior para otras capas o parámetros, con el fin de lograr un mejor equilibrio entre precisión y eficiencia.

En resumen, las técnicas de cuantificación, como tecnología clave en el campo del aprendizaje profundo, muestran un gran potencial en la mejora de la eficiencia computacional, la reducción de los requisitos de almacenamiento y el consumo de energía. Sin embargo, las técnicas de cuantificación también tienen limitaciones, como la pérdida de precisión y la dependencia del hardware. Por lo tanto, en aplicaciones prácticas, las estrategias de cuantificación deben seleccionarse cuidadosamente en función de los requisitos específicos de la aplicación y las características del escenario, con el fin de lograr un equilibrio óptimo entre el rendimiento y la eficiencia del modelo. En el futuro, con el desarrollo continuo de hardware y algoritmos, la tecnología cuantitativa desempeñará un papel más importante en el campo del aprendizaje profundo, y promoverá el arraigo de la aplicación de la inteligencia artificial en una gama más amplia de escenarios.