Goedel-Prover-V2 - Modelo de demostración de teoremas de código abierto de Princeton en colaboración con Tsinghua y NVIDIA, entre otros.

¿Qué es Goedel-Prover-V2?

Goedel-Prover-V2 es un modelo de demostración de teoremas de código abierto creado por instituciones tan importantes como la Universidad de Princeton, la Universidad de Tsinghua y NVIDIA. El modelo se basa en técnicas innovadoras como la síntesis jerárquica de datos, la autocorrección guiada por el verificador y el promediado de modelos para mejorar significativamente el rendimiento de las pruebas formales automatizadas. El modelo Goedel-Prover-V2 está disponible en dos versiones, 32B y 8B, y ofrece muy buenos resultados en una serie de pruebas comparativas. Por ejemplo, el modelo 32B alcanza una puntuación de 90,41 TP3T para Pass@32 en la prueba MiniF2F, superando al DeepSeek-Prover, que es mucho mayor. Por ejemplo, en la prueba MiniF2F, el modelo 32B obtuvo una puntuación Pass@32 de 90,4%, superando al mucho más grande DeepSeek-Prover-V2. El modelo es capaz de generar automáticamente pruebas para problemas matemáticos complejos, y se autocorrige basándose en la retroalimentación del compilador Lean para mejorar la calidad de las pruebas, y la naturaleza de código abierto de Goedel-Prover-V2 proporciona una base para que los investigadores realicen nuevos desarrollos y mejoras.

Principales características de Goedel-Prover-V2

• Generación automática de certificadosGenerar procesos formales de demostración de problemas matemáticos complejos para ayudar a resolver enigmas matemáticos complejos.
• Capacidad de autocorrecciónGracias a la retroalimentación del compilador Lean, el modelo puede revisar iterativamente sus pruebas para mejorar su precisión y calidad.
• Formación y optimización eficacesEl método de síntesis jerárquica de datos y de promediado de modelos mejora la eficacia de la formación y el rendimiento de los modelos, lo que les permite obtener buenos resultados en múltiples pruebas comparativas.
• Código abierto y escalabilidadProporcionar modelos y conjuntos de datos de código abierto para facilitar su desarrollo y mejora por parte de los investigadores.

Rendimiento de Goedel-Prover-V2

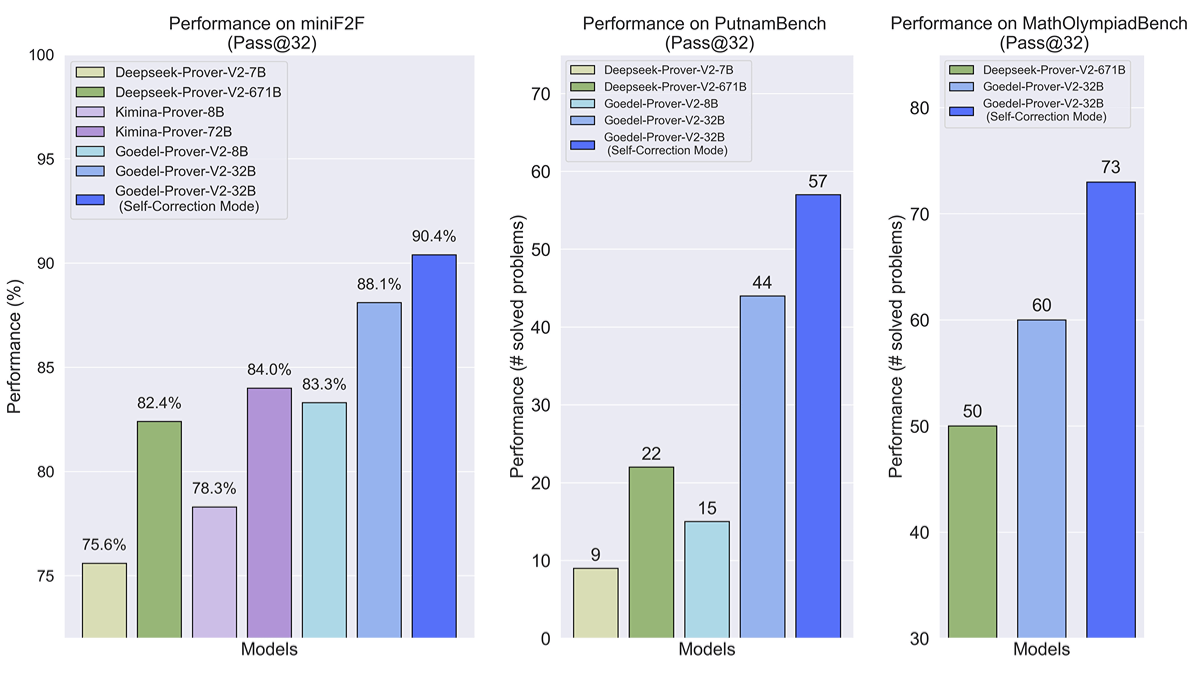
• MiniF2F Evaluación comparativa::
  • La puntuación Pass@32 para el modelo 32B es de 90,41 TP3T, muy superior a la de DeepSeek-Prover-V2 (82,41 TP3T) para 671B.
  • El modelo 8B obtiene una puntuación Pass@32 de 83,3%, comparable al rendimiento de DeepSeek-Prover-V2, aunque el número de parámetros es sólo 1/100 del de DeepSeek-Prover-V2.
• Puntos de referencia PutnamBench::
  • El modelo 32B supera las métricas Pass@64, resolviendo 64 problemas.
  • En la métrica Pass@32, el modelo 32B resuelve 57 problemas, superando significativamente a DeepSeek-Prover-V2-671B con 47 problemas.
  • El modelo 8B también funciona muy bien y es comparable al DeepSeek-Prover-V2-671B.
• MathOlympiadBench Puntos de referencia::
  • El modelo 32B resuelve 73 problemas, significativamente mejor que DeepSeek-Prover-V2-671B con 50 problemas.
  • El modelo 8B también obtiene buenos resultados, acercándose al nivel del modelo 32B y mostrando una gran capacidad para demostrar teoremas.

Dirección del sitio web oficial de Goedel-Prover-V2

• Página web del proyecto:: https://blog.goedel-prover.com/
• Biblioteca de modelos HuggingFace::
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-8B
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-32B

Cómo utilizar Goedel-Prover-V2

• Acceso a los recursos del proyectoAcceso a la biblioteca de modelos de HuggingFace, descarga de los archivos de modelos de HuggingFace y selección de la versión adecuada (por ejemplo, 8B o 32B).
• requisitos de hardwareSe recomiendan GPUs o clusters de GPUs de alto rendimiento.
• entorno de softwareInstalación de Python y marcos de aprendizaje profundo como PyTorch para garantizar que el entorno admite la inferencia de modelos de gran tamaño.
• Cuestiones de entradaConvertir problemas matemáticos que requieran demostración en un formato compatible con el modelo (por ejemplo, lenguaje Lean).
• Preprocesamiento de datosCodificación y formato de las preguntas según los requisitos del modelo.
• Modelos de cargaCarga el modelo preentrenado con las herramientas proporcionadas por HuggingFace.
• Prueba de generaciónEl problema se introduce en el modelo, que genera automáticamente pruebas que se verifican y corrigen utilizando el compilador Lean.
• certificado de verificación: Comprueba que las pruebas generadas son correctas con el compilador Lean.
• Corrección iterativaSi la prueba es incorrecta, el modelo se autocorrige basándose en la retroalimentación hasta que se genera la prueba correcta.

Principales ventajas de Goedel-Prover-V2

• Excelente rendimientoGoedel-Prover-V2: Goedel-Prover-V2 obtiene buenos resultados en varias pruebas comparativas; por ejemplo, el modelo de 32B alcanza una precisión de 90,4% en la prueba Pass@32 de MiniF2F, lo que supone una ventaja significativa con respecto a otros modelos similares.
• Arquitectura técnica innovadoraBasado en la síntesis jerárquica de datos, la autocorrección guiada por el validador y las técnicas de promediado de modelos para mejorar eficazmente la eficacia de la formación de modelos y la calidad de las pruebas.
• Código abierto y escalabilidadProporcionar modelos y conjuntos de datos de código abierto a los que los investigadores puedan acceder, utilizar y desarrollar libremente para mejorarlos.
• Amplia gama de aplicacionesAplicable a una amplia gama de campos, como la investigación matemática, la validación de software y hardware, las ayudas educativas, la inteligencia artificial y el aprendizaje automático, y la investigación científica y la ingeniería.
• Formación y optimización eficacesFormación eficiente y optimización del rendimiento basada en técnicas de síntesis jerárquica de datos y promediado de modelos para mejorar la robustez de los modelos.

Personas para las que está indicado Goedel-Prover-V2

• Matemáticos e investigadores matemáticos: Se utiliza para verificar conjeturas matemáticas, generar pruebas de problemas complejos y acelerar la exploración y el estudio de teorías matemáticas.
• Informáticos e ingenieros de software: Se utiliza en el desarrollo de software y hardware para verificar la corrección de algoritmos, lógica de programas y diseño de circuitos, y para mejorar la fiabilidad y seguridad de los sistemas.
• investigador en inteligencia artificialValidar los fundamentos matemáticos y la lógica algorítmica de los modelos de aprendizaje automático para garantizar la fiabilidad y precisión del modelo.
• Educadores y estudiantes: Servir de ayuda a la enseñanza de las matemáticas, ayudando a los estudiantes a comprender y dominar mejor los conceptos y teoremas matemáticos mediante ejemplos de demostraciones formales.
• Investigadores e ingenierosValidar modelos y teorías matemáticas en la investigación científica y el diseño de ingeniería para garantizar la viabilidad y fiabilidad de las soluciones de diseño.