CoRAG: modelización dinámica encadenada de GAR mediante MCTS (árboles de Montecarlo)
Base de conocimientos de IAPublicado hace 1 año Círculo de intercambio de inteligencia artificial 55.6K 00
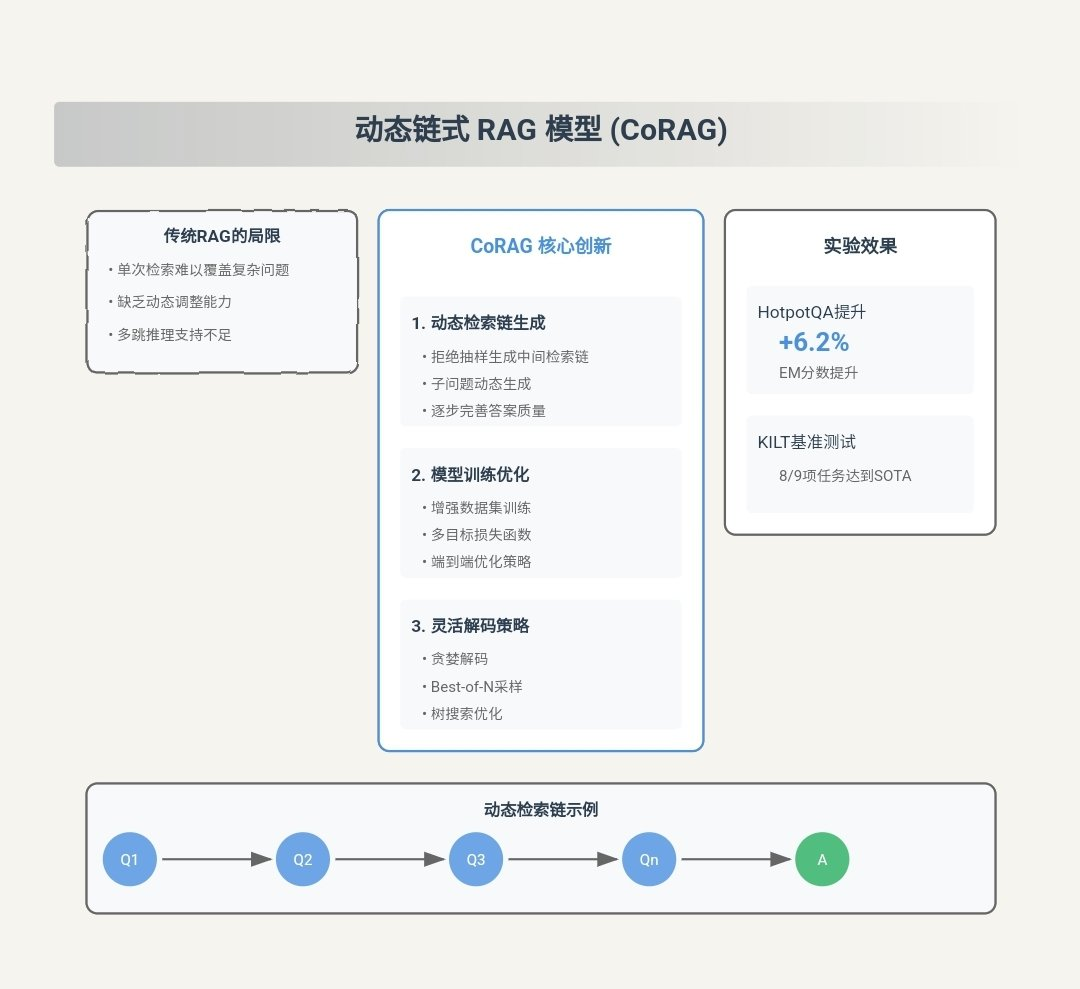
Resumen de las principales contribuciones del CORAG
CORAG (Costes limitados) Recuperación Optimisation for Retrieval-Augmented Generation) es un innovador sistema de Generación Aumentada de Recuperación (RAG, por sus siglas en inglés) diseñado para hacer frente a la actual RAG Principales retos de la metodología. A continuación se exponen las principales aportaciones del CORAG:
- Consideración exhaustiva de las asociaciones entre bloques::
- punto de innovaciónCORAG es el primer marco que introduce la optimización del orden de combinación de bloques en la tarea RAG. A diferencia de los enfoques tradicionales, CORAG ya no trata cada bloque de texto de forma independiente ni considera los bloques solo a nivel de agrupación, sino que utiliza la Búsqueda en árbol Monte Carlo (MCTS) para buscar secuencialmente el orden óptimo de las combinaciones de bloques. Este enfoque capta plenamente las complejas asociaciones entre bloques, evita la información redundante y garantiza que las combinaciones de bloques seleccionadas respondan plenamente a la consulta del usuario.
- vanguardia: De este modo, CORAG puede generar respuestas más precisas y pertinentes, mejorando la calidad de la generación.
- Resolver el problema de no monotonicidad de la utilidad en bloque::
- punto de innovación: CORAG restricción presupuestaria integrado en el proceso de optimización de la cartera de bloques, en lugar de considerar el agotamiento del presupuesto como una condición de terminación. Este planteamiento considera la utilidad por bloques de no monotonicidades decir, añadir más bloques no siempre mejora la calidad del resultado final.
- vanguardiaLa función de CORAG: al ajustar dinámicamente el uso del presupuesto durante el proceso de optimización, CORAG es capaz de evitar la inclusión excesiva de bloques irrelevantes o redundantes, mejorando así la precisión y pertinencia de las respuestas generadas.
- Adaptación a distintos campos de consulta::
- punto de innovación: CORAG introdujo un Configuración del AgenteEl agente utiliza el Aprendizaje comparativo para adaptar dinámicamente la configuración del MCTS a diferentes dominios de consulta. El agente recomienda la Modelo de reordenador responder cantando Configuración MCTS.
- vanguardiaEste enfoque proporciona a CORAG la flexibilidad necesaria para gestionar una amplia gama de tipos de consulta, desde simples consultas de palabras clave hasta complejos problemas de razonamiento, garantizando respuestas de alta calidad en una gran variedad de escenarios de aplicación.
- Estrategias de búsqueda eficientes y escalables::
- punto de innovaciónCORAG emplea MCTS para la búsqueda de nodos con la función técnica de expansión paralela Acelera el proceso de búsqueda. Este enfoque reduce el espacio de búsqueda exponencial a lineal y equilibra eficazmente el exploraciones responder cantando utilice.
- vanguardiaCORAG es capaz de manejar conjuntos de datos a gran escala manteniendo una recuperación eficiente y logrando un equilibrio entre el coste computacional y la calidad de la recuperación.
- Aumento significativo del rendimiento::
- verificación experimentalLos resultados experimentales demuestran que CORAG supera a los métodos de referencia existentes en varios conjuntos de datos de referencia, mejorando las puntuaciones ROUGE en cerca de 2.000 puntos. 30%. CORAG también destaca por su eficiencia, ya que ofrece respuestas de alta calidad dentro de unas estrictas limitaciones de costes.
Ejemplo de flujo de trabajo CORAG
Para ayudar al lector a comprender rápidamente cómo funciona CORAG, a continuación se muestra un ejemplo de flujo de trabajo completo que muestra cómo CORAG procesa una consulta de usuario y genera la respuesta final. Cada paso contiene entradas y salidas para representar las idas y venidas del flujo de trabajo.
Paso 1: Consulta del usuario
- importaciónUn usuario envía una consulta en lenguaje natural al sistema CORAG, por ejemplo:
"请解释光合作用的过程,并列出影响其效率的因素。" - exportacionesLa consulta se pasa a la función Módulo de incrustación de consultas Procesando.
Paso 2: Generación de consultas incrustadas
- importación: Texto de consulta del usuario.
- tratar con: Utilización de Modelos de incrustación(por ejemplo, BGE-M3) convierte el texto de la consulta en una representación vectorial.
- exportacionesConsulta el vector de incrustación (por ejemplo, un vector de 1024 dimensiones).
Query Embedding: [0.123, -0.456, 0.789, ..., -0.012]
Paso 3: Configurar la predicción del agente
- importaciónvector de incrustación de la consulta
[0.123, -0.456, 0.789, ..., -0.012]. - tratar con::
- extracción de características: El vector de incrustación se introduce en el Configuración del Agente (utilizado como expresión nominal) red de codificación La extracción de características se realiza en el
- Predicción del reordenadorpredicción de la salida de la red codificada de la Modelo de reordenadorPor ejemplo
bge-reranker-large. - Pronóstico de configuración MCTS: Al mismo tiempo, la red de codificación predice el MCTS óptimo Parámetros de configuracióncomo el número de iteraciones, el factor de coste y el factor de exploración.
- exportaciones::
- Modelo óptimo de reordenación::
bge-reranker-large - Parámetros de configuración MCTS::
- Número de iteraciones:: 15
- factor coste: 0.2
- Factor de exploración: 2.5
Optimal Reranker: bge-reranker-large MCTS Configuration: - Iterations: 15 - Cost Coefficient: 0.2 - Exploration Coefficient: 2.5 - Modelo óptimo de reordenación::
Paso 4: Recuperar posibles bloques de texto
- importación::
- Vector de incrustación de consultas
[0.123, -0.456, 0.789, ..., -0.012]. - base de datos vectorial(por ejemplo, que contengan bloques de texto presegmentados y sus vectores de incrustación).
- Vector de incrustación de consultas
- tratar conUtiliza el vector de incrustación de la consulta para Búsqueda por similitudrecupera los posibles bloques de texto más relevantes de la base de datos vectorial. A continuación se muestran ejemplos de los cinco primeros bloques de texto recuperados:Bloque de texto 1::
光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。Bloque de texto 2::
光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。Bloque de texto 3::
影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。Bloque de texto 4::
光照强度对光合作用的影响呈正相关,但过强的光照会导致光抑制现象,降低光合作用效率。Bloque de texto 5::
二氧化碳是光合作用的原料之一,其浓度直接影响光合作用的速率。 - exportacionesLista de posibles bloques de texto y sus vectores de incrustación.
Retrieved Chunks: - Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。" - Chunk 2: "光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。" - Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。" - Chunk 4: "光照强度对光合作用的影响呈正相关,但过强的光照会导致光抑制现象,降低光合作用效率。" - Chunk 5: "二氧化碳是光合作用的原料之一,其浓度直接影响光合作用的速率。"
Paso 5: Búsqueda en árbol MCTS
- importación::
- Lista de posibles bloques de texto::
- Trozo 1: ...
- Chunk 2: ...
- Trozo 3: ...
- Chunk 4: ...
- Chunk 5: ...
- Parámetros de configuración MCTS::
- Número de iteraciones:: 15
- factor coste: 0.2
- Factor de exploración: 2.5
- Modelo de reordenador::
bge-reranker-large
- Lista de posibles bloques de texto::
- tratar con::
- Inicialización del nodo raízEl nodo raíz representa un estado vacío en el que no hay ningún bloque de texto seleccionado.
- Expansión iterativa::
- opción: Uso Algoritmo UCB Seleccione el nodo con la utilidad actual más alta. Por ejemplo, el trozo 3 se elige para la primera iteración porque tiene la mayor relevancia para la consulta.
- extensionesGenerar todos los posibles nodos hijos (nuevas combinaciones de trozos de texto). Por ejemplo, los hijos del trozo 3 pueden ser el trozo 1, el trozo 2, el trozo 4 y el trozo 5.
- valoración: Uso Modelo de reordenador
bge-reranker-largeEvalúe la utilidad de todas las combinaciones nuevas en paralelo. Por ejemplo, evalúe la utilidad de combinaciones como Trozo 3 + Trozo 1, Trozo 3 + Trozo 2, etc. - actualización: Actualiza la utilidad de los nodos y los recuentos de acceso y propaga las actualizaciones hacia arriba.
- iterar: Repita los pasos de selección, expansión, evaluación y actualización hasta alcanzar el número máximo de iteraciones (15).
- Condiciones de rescisiónNúmero máximo de iteraciones alcanzado.
- exportaciones: Orden óptimo de combinación de bloques de texto.
Optimal Chunk Combination: - Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。" - Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。" - Chunk 2: "光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。"tenga en cuentaDurante el proceso MCTS, CORAG ajusta dinámicamente el orden de combinación en función de la utilidad, y finalmente selecciona el orden de combinación óptimo.
Paso 6: Generar la respuesta final
- importación::
- Orden óptimo de combinación de los bloques de texto::
- Trozo 3: "Los factores que afectan a la eficiencia fotosintética incluyen la intensidad de la luz, la concentración de dióxido de carbono, la temperatura y la disponibilidad de agua".
- Fragmento 1: "La fotosíntesis es el proceso por el cual las plantas, las algas y algunas bacterias utilizan la energía luminosa para convertir el dióxido de carbono y el agua en glucosa y oxígeno".
- Fragmento 2: "La fotosíntesis se produce principalmente en los cloroplastos de las hojas de las plantas y se divide en dos fases: la reacción de la luz y la reacción del carbono".
- consulta de usuario:: "Explica el proceso de fotosíntesis y enumera los factores que afectan a su eficiencia".
- Orden óptimo de combinación de los bloques de texto::
- tratar con::
- Consejos de construcción: Combinar el orden óptimo de combinación de bloques de texto con las consultas del usuario para construir el LLM de la solicitud de entrada. Ejemplo:
用户查询:请解释光合作用的过程,并列出影响其效率的因素。 相关信息: 1. 影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。 2. 光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。 3. 光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。 - Generar una respuesta: Uso LLM(por ejemplo, Llama3) Genera una respuesta final a la pregunta.
- Consejos de construcción: Combinar el orden óptimo de combinación de bloques de texto con las consultas del usuario para construir el LLM de la solicitud de entrada. Ejemplo:
- exportacionesLa respuesta final en lenguaje natural.
Final Response: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。它主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。"
Paso 7: Respuesta
- importaciónLa respuesta final en lenguaje natural.
- tratar con: Presenta la respuesta al usuario.
- exportacionesLa interfaz de usuario muestra el resultado de la respuesta.
resúmenes
Con el ejemplo de flujo de trabajo anterior, el principio de funcionamiento de CORAG puede resumirse en los siguientes pasos:
- Generación de consultas incrustadas: Convierte una consulta de usuario en una representación vectorial.
- Configuración de la predicción de agentesPredicción del modelo óptimo de reordenación y de los parámetros de configuración del MCTS.
- Recuperar posibles bloques de textoRecupera el bloque de texto más relevante de la base de datos vectorial.
- MCTS Búsqueda en árbol: Utiliza MCTS para buscar el orden óptimo de combinación de los bloques de texto.
- Generar respuesta final: Utiliza LLM para generar la respuesta final basada en la combinación óptima de bloques de texto.
- salida de respuesta: Presenta la respuesta al usuario.
Estos pasos demuestran cómo CORAG combina eficazmente las tres fases de recuperación, mejora y generación para ofrecer respuestas en lenguaje natural de alta calidad. Con ejemplos de datos detallados, los lectores pueden comprender mejor el proceso de tratamiento de datos de CORAG y su funcionamiento.
texto original:: https://arxiv.org/pdf/2411.00744
leyenda:: CORAG: Un sistema de optimización de la recuperación con restricciones de costes para la generación de mejoras de la recuperación
autorZiting Wang, Haitao Yuan, Wei Dong (Universidad Tecnológica de Nanyang), Gao Cong (Universidad Tecnológica de Nanyang), Feifei Li (Alibaba Group)
resúmenes
Los grandes modelos lingüísticos (LLM) han demostrado excelentes capacidades en tareas generativas, pero a menudo resulta difícil acceder a información actualizada, lo que puede llevar a la desilusión. La generación mejorada por recuperación (RAG) aborda este problema integrando conocimientos de bases de datos externas para lograr respuestas más precisas y pertinentes. Debido a la limitación de la ventana de contexto de los LLM, no resulta práctico introducir directamente en el modelo todo el contexto de la base de datos externa. En su lugar, sólo se recupera selectivamente la información más relevante, es decir, los "trozos" (chunks). Sin embargo, la investigación actual sobre GAR se enfrenta a tres retos fundamentales. En primer lugar, las soluciones existentes suelen seleccionar cada "chunk" de forma independiente, ignorando posibles asociaciones entre ellos. En segundo lugar, en la práctica, la utilidad de los trozos es "no monotónica", lo que significa que añadir más trozos puede reducir la utilidad global. Los enfoques tradicionales hacen hincapié en maximizar el número de bloques incluidos, lo que puede perjudicar inadvertidamente el rendimiento. En tercer lugar, cada tipo de consulta de usuario tiene unas características únicas que requieren un tratamiento a medida, algo que las soluciones actuales no tienen suficientemente en cuenta.
Para superar estos retos, proponemos CORAG, un sistema de optimización de la recuperación con restricciones de costes, para la generación de mejoras en la recuperación. Adoptamos un marco estratégico basado en la búsqueda en árbol Monte Carlo (MCTS) para encontrar secuencialmente las combinaciones óptimas de bloques, considerando así de forma exhaustiva las asociaciones entre bloques. Además, en lugar de considerar el agotamiento del presupuesto como condición de terminación, integramos las restricciones presupuestarias en el proceso de optimización de las combinaciones de bloques, lo que resuelve eficazmente el problema de la no monotonicidad de la utilidad de los bloques. Además, mediante el diseño de agentes de configuración, nuestro sistema predice la configuración óptima para cada tipo de consulta, lo que mejora la adaptabilidad y la eficiencia. Los resultados experimentales muestran que nuestro marco mejora el rendimiento hasta en 301 TP3T en comparación con el modelo de referencia, lo que pone de manifiesto la eficacia, escalabilidad y aplicabilidad del marco para aplicaciones de contexto largo.
Formato de referencia PVLDB.
Ziting Wang, Haitao Yuan, Wei Dong, Gao Cong y Feifei Li. CORAG: A Cost-Constrained Retrieval Optimisation System for Retrieval-Augmented Generation. . pvldb, 14(1): xxx-xxx, 2020.
doi:XX.XX/XXX.XX
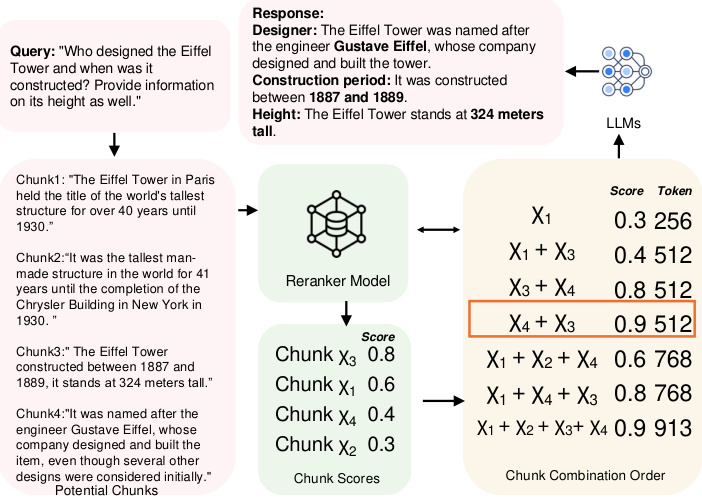
Figura 1: Ejemplo de orden de combinación de bloques de datos.
1 Introducción
Aunque los LLM han demostrado excelentes capacidades en tareas generativas, a menudo encuentran dificultades para obtener información actualizada, lo que puede dar lugar a alucinaciones [10, 38]. Para hacer frente a estos retos, la RAG ha surgido como una solución clave. Al integrar fuentes de datos externas en el LLM, la RAG puede proporcionar información más precisa, relevante y actualizada. En la actualidad, la GAR se ha estudiado ampliamente en el contexto de los LLM, especialmente en tareas que requieren conocimiento externo actualizado, como las tareas de preguntas y respuestas [2, 22, 29], la recuperación de información médica [1, 32] y el análisis de series temporales [12, 26, 40]. Las fuentes de datos externas suelen ser tan grandes que no resulta práctico introducirlas directamente en el LLM. Para resolver este problema, los datos suelen dividirse en fragmentos no solapados y almacenarse en una base de datos vectorial, y después el usuario consulta los fragmentos más útiles para construir pistas para el LLM. Por lo tanto, el diseño de estructuras y algoritmos de búsqueda eficientes y precisos para encontrar los trozos más relevantes se ha convertido en un tema de investigación destacado y ha sido ampliamente estudiado en las comunidades de bases de datos [39, 48] y aprendizaje automático [2, 35, 43].
Sin embargo, los planteamientos actuales plantean tres retos fundamentales.
Reto 1: Enlaces entre bloques. En la actualidad, existen dos enfoques principales para identificar los bloques más relevantes. El primero formula el problema como una tarea AKNN (Approximate k Nearest Neighbours) [41, 45], en la que a cada bloque se le asigna una puntuación y se seleccionan aproximadamente los k bloques mejor clasificados según su puntuación. El segundo enfoque agrupa los bloques y devuelve todos los bloques del grupo más relevante en respuesta a una consulta [22, 29]. Sin embargo, ambos métodos ignoran las posibles asociaciones entre bloques: el primer método ignora por completo las asociaciones, mientras que el segundo sólo considera superficialmente todos los bloques de cada clúster al tratarlos como igualmente relevantes. Como resultado, estos métodos introducen una redundancia sustancial en los bloques seleccionados cuando varios bloques transmiten información similar o redundante.
Por ejemplo, como se muestra en la Fig. 1, al consultar la altura y la historia de la Torre Eiffel, si cada bloque se trata de forma independiente, el método codicioso selecciona los bloques χ3 y χ1 porque tienen las dos primeras puntuaciones más altas. Sin embargo, estos dos bloques sólo proporcionan información histórica, lo que no es suficiente para responder completamente a la consulta. Para responder mejor a la consulta, es necesario incluir bloques que contengan el nombre del constructor, por ejemplo, χ4. Por otro lado, el enfoque de agrupación devolverá todos los χ1, χ2, χ3 y χ4, lo que provocará redundancia. La solución óptima elegirá χ3 y χ4, ya que proporcionan la información necesaria sin redundancia. Además, los estudios [11, 19, 42] han demostrado que el orden de los bloques afecta al rendimiento del LLM, un factor que también ignoran los métodos existentes. En el caso de la Torre Eiffel, por ejemplo, a la hora de elegir los bloques χ3 y χ4, colocar χ4 en la primera posición arroja una mayor puntuación en comparación con el orden inverso. Sin embargo, determinar el orden óptimo de las combinaciones de bloques es una tarea difícil, ya que ambas requieren que el espacio de búsqueda crezca exponencialmente con el número de bloques disponibles. En este documento, demostramos además que este problema es NP-difícil (véase la sección 2.1).
Reto 2: No monotonicidad de la utilidad. La solución actual se basa en el supuesto de que incluir más bloques siempre produce un mejor resultado final. En concreto, en el enfoque basado en AKNN, se seleccionan exactamente k bloques de forma determinista cada vez. En el enfoque basado en la agrupación, se establece un umbral de distancia entre las agrupaciones y las consultas, y se devuelven todas las agrupaciones que se encuentren dentro de este umbral. Ambos métodos devuelven tantos bloques como sea posible. Sin embargo, en la práctica, la utilidad de los bloques no es monótona. Más concretamente, demasiados bloques diluyen la información clave al añadir contenido relacionado con los bordes, produciendo ruido que reduce la claridad. Además, los conflictos o las diferencias sutiles entre bloques pueden confundir al modelo y reducir la calidad de la respuesta. Por ejemplo, como se muestra en la figura 1, añadir el bloque χ1 reduce la utilidad cuando se seleccionan χ3 y χ4, lo que pone de relieve el hecho de que las puntuaciones de utilidad no suelen ser monótonas en la práctica.
Reto 3: Diversidad de consultas. Existen diferentes tipos de consultas de usuario, cada una de las cuales requiere una estrategia de clasificación diferente basada en sus características únicas [47]. En los sistemas RAG actuales, la puntuación de utilidad de un bloque suele venir determinada por el modelo re-ranker asignado. Hasta la fecha, existen varios modelos de re-ranker, pero observamos que su rendimiento varía mucho según el tipo de consulta, y no hay ningún modelo de re-ranker fijo que supere sistemáticamente a los demás en todas las variaciones de consulta (para más detalles, véanse los experimentos de la Sección 6.3.4). Los enfoques actuales [20, 46] suelen basarse en modelos de reordenación estáticos para la clasificación por bloques y carecen de la flexibilidad necesaria para adaptarse a diferentes contextos de consulta.
Planteamiento del problema: ¿Existe un sistema de GAR que tenga plenamente en cuenta las asociaciones entre bloques y la no monotonicidad de las utilidades, al tiempo que sea capaz de dar cabida a todo tipo de consultas?
1.1 Nuestra contribución
En este artículo, respondemos afirmativamente a esta pregunta proponiendo un novedoso marco de árbol de políticas basado en MCTS para optimizar la recuperación de bloques en sistemas RAG. En general, nuestra contribución puede resumirse como sigue:
- Presentamos el primer marco RAG que tiene en cuenta el orden de las combinaciones de bloques en una tarea RAG. En lugar de considerar cada bloque de forma independiente o a nivel de agrupación, utilizamos MCTS para ayudar a buscar el orden óptimo de combinación de bloques de forma secuencial. La idea de alto nivel es la siguiente: en primer lugar, inicializamos el nodo raíz. A continuación, durante las iteraciones, expandimos el árbol seleccionando el nodo con la utilidad más alta y calculando la utilidad de sus nodos de expansión. Después de cada expansión, actualizamos la utilidad en todo el árbol de políticas. En este proceso, la decisión de cada iteración depende de los bloques que se hayan seleccionado, lo que nos permite considerar plenamente las asociaciones entre bloques. Además, MCTS reduce el espacio de búsqueda exponencial a lineal, y aplicamos técnicas de expansión paralela para mejorar aún más la eficiencia computacional. Con este diseño, abordamos el reto 1.
- A diferencia de los marcos RAG anteriores que consideran el agotamiento del presupuesto como una condición de finalización, proponemos una nueva formulación en la que las restricciones presupuestarias se integran en el proceso de optimización de las combinaciones de bloques para tener plenamente en cuenta la no monotonicidad de la utilidad de los bloques, abordando así el Desafío 2. Además, al dar prioridad a los bloques altamente correlacionados y de bajo coste y tener en cuenta la longitud de las fichas, reducimos aún más el coste computacional de la optimización. el coste computacional.
- Proponemos un agente basado en el aprendizaje comparativo que adapta dinámicamente la configuración MCTS a la consulta, adaptando el modelo re-ranker y la configuración al dominio específico de la consulta. Este enfoque proporciona flexibilidad y robustez para consultas dinámicas y específicas del dominio, adaptándose al Desafío 3.
- Además, realizamos experimentos exhaustivos comparando nuestro marco con varios métodos de vanguardia. Los resultados validan la eficacia, eficiencia y escalabilidad de nuestro enfoque y mejoran el rendimiento en 30% en comparación con la línea de base.
2 Conocimientos preparatorios
En esta sección, primero introducimos las definiciones de algunos conceptos clave, como orden de bloque y combinación de bloques, en la Sección 2.1. A continuación, damos una prueba NP-hard del problema de optimización del orden de bloques. A continuación, presentamos una prueba NP-hard del problema de optimización del orden de los bloques. Por último, en la sección 2.3 se analizan trabajos relacionados.
2.1 Conceptos clave
RAG & Chunks. La RAG es un método eficaz para mejorar el rendimiento de los modelos generativos recuperando el contexto pertinente de un corpus externo. En este enfoque, el corpus se divide primero en unidades más pequeñas y manejables, denominadas bloques, que se almacenan en una base de datos vectorial. Así, podemos dar una definición formal de un bloque de la siguiente manera:
Definición 2.1 (Bloque). Supongamos que C representa un corpus de documentos y que un bloque χ se define como un bloque continuo de texto extraído de C. Formalmente, un bloque χ consiste en una secuencia de tokens (t1, t2, ... , tn), donde cada ti es un token en C y el tamaño n lo fija el usuario.
En un sistema RAG, cada bloque se incrusta en una representación vectorial mediante un modelo de incrustación que capta el significado semántico del bloque y permite recuperar contenidos contextualmente similares. Cuando se recibe una nueva consulta, la base de datos vectorial realiza una búsqueda de similitudes para identificar los bloques semánticamente más relevantes para la consulta. Estos trozos recuperados se pasan entonces a un generador (por ejemplo, un gran modelo de lenguaje) para generar una respuesta final basada en el contenido recuperado. En concreto, cuantos más tokens contenga un bloque, mayor será el coste en que incurra el generador. Así, definimos el coste de un bloque como cost(χ) = |χ|, que es igual al número de tokens del bloque.
Orden de combinación de bloques. En un sistema GAR, los resultados de una búsqueda en una base de datos vectorial pueden incluir varios bloques. Sin embargo, debido a las restricciones de entrada del modelo generativo, no resulta práctico utilizar todos estos bloques. Por lo tanto, es necesario seleccionar el subconjunto óptimo de bloques, denominado combinación de bloques, para ajustarse a un presupuesto de costes determinado. Además, el orden de los bloques dentro de la combinación tiene un impacto significativo en el rendimiento del modelo generativo. El objetivo es identificar el orden de las combinaciones de bloques con un orden óptimo, definido formalmente como sigue:
Definición 2.2 (Selección óptima del orden de combinación de bloques). Sea {χ1, χ2, ... , χk} es un conjunto de bloques potenciales, ℛ es un presupuesto de costes, Φ = ⟨χφ1, ... , χφm⟩ representa un orden de combinaciones potenciales de bloques, donde cada χφi es un bloque y el índice φi denota su posición en Φ. Sea U(Φ) la puntuación de utilidad asignada por el modelo re-ranker, que puede ser arbitraria o compuesta. Nuestro objetivo es encontrar el orden de combinación de los bloques que maximice las puntuaciones de utilidad bajo la restricción del coste de introducirlos en los LLM para generar la respuesta final, es decir, buscar el
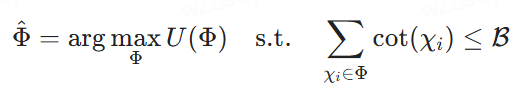
2.2 Pruebas de la dificultad NP
Para demostrar que la selección secuencial de la combinación de bloques es NP-difícil, generalizamos el Problema del Hipergrupo Máximamente Ponderado (MWHP). Dado que el MWHP es NP-duro, demostramos que cualquier instancia MWHP se puede convertir en una instancia de optimización de combinación de bloques en tiempo polinómico.
2.2.1 Definición del problema del MWHP
Dado un hipergrafo ℋ = (V, E, w1, w2), donde V es el conjunto de vértices y E es el conjunto de hiperborde, y cada hiperborde contiene un subconjunto de V. w1: v → ℝ y w2: e → ℝ son las funciones de peso, que asignan un peso a cada vértice e hiperborde respectivamente. Dado un subconjunto de vértices V' ⊆ V, decimos que un hiperborde e pertenece a V', es decir, e ∈ V', si V' cubre todos los vértices de e. El objetivo es encontrar k vértices y maximizar la suma de los pesos de estos vértices y de los hiperborde que cubren:
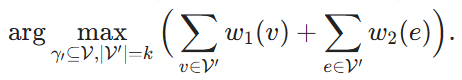
2.2.2 Proceso de normalización
Ahora construimos una instancia correspondiente del problema de optimización de combinación de bloques a partir de una instancia MWHP dada. Para cada nodo v ∈ V, creamos un bloque correspondiente Xv. Definimos su coste cost(Xv) ≡ 1. Un orden de combinación de bloques Φ corresponde entonces a un subconjunto de vértices de V denotado como V(Φ) ⊆ V. Definimos su utilidad como
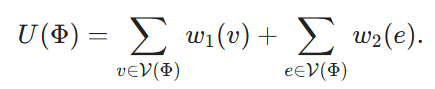
Por último, fijamos B = k y nos proponemos
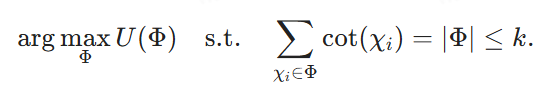
con Φdenota la solución de (4), entonces está claro que V(Φ) es una solución de (2) y la reducción puede hacerse en tiempo O(|V|-|E|).
Nótese que esta inducción presupone que en nuestro problema de optimización de combinación de bloques permitimos que el re-ranker sea arbitrario, lo que significa que las puntuaciones de utilidad también pueden asignarse arbitrariamente. La complejidad de encontrar el orden óptimo de combinación de bloques puede reducirse significativamente si se hacen ciertas suposiciones sobre el reclasificador. Por ejemplo, si el re-ranker no tiene en cuenta las asociaciones y sólo suma linealmente las puntuaciones de utilidad de cada bloque, cada bloque puede evaluarse de forma independiente. Sin embargo, en este artículo nos ocupamos del caso más general y no hacemos ninguna suposición sobre el modelo del re-ranker.
2.3 Trabajos relacionados
2.3.1 Generación de mejoras de recuperación
La RAG [14, 20] se utiliza ampliamente para manejar tareas de PLN intensivas en conocimiento. En un proceso típico de RAG, un recuperador basado en incrustación densa busca información relevante en bases de datos externas, que luego utiliza el LLM durante el proceso de generación. Para mejorar este proceso, varios estudios [5, 18, 22, 35] se han centrado en adaptar los recuperadores para que se ajusten mejor a las necesidades de generación de los LLM, desarrollar métodos de recuperación multipaso y filtrar la información irrelevante. Aunque existen muchos recuperadores de última generación [8, 9, 15, 16, 27, 34], la optimización conjunta de recuperadores y LLM en un proceso integral [25, 31] es más prometedora. Por ejemplo, la investigación [30] se centra en el co-entrenamiento del recuperador y el LLM simultáneamente o por etapas. sin embargo, esto requiere la pérdida de agentes para la optimización y complica el proceso de entrenamiento, especialmente cuando las bases de datos incrustadas necesitan ser reindexadas con frecuencia, lo que incurre en altos costes computacionales. Por ello, enfoques como [5] descomponen las consultas complejas de varios pasos en subintentos más pequeños para mejorar la exhaustividad de la respuesta sin necesidad de reindexación frecuente. Sin embargo, estos enfoques suelen ignorar el papel crucial del orden de combinación de bloques, que puede afectar significativamente a la calidad general de la respuesta de LLM. Hasta donde sabemos, este trabajo es el primer enfoque que tiene en cuenta el orden de combinación de bloques en una tarea RAG.
2.3.2 Nueva clasificación RAG
Los métodos de reordenación son esenciales para mejorar el rendimiento de la recuperación en el proceso GAR [43, 44, 51].
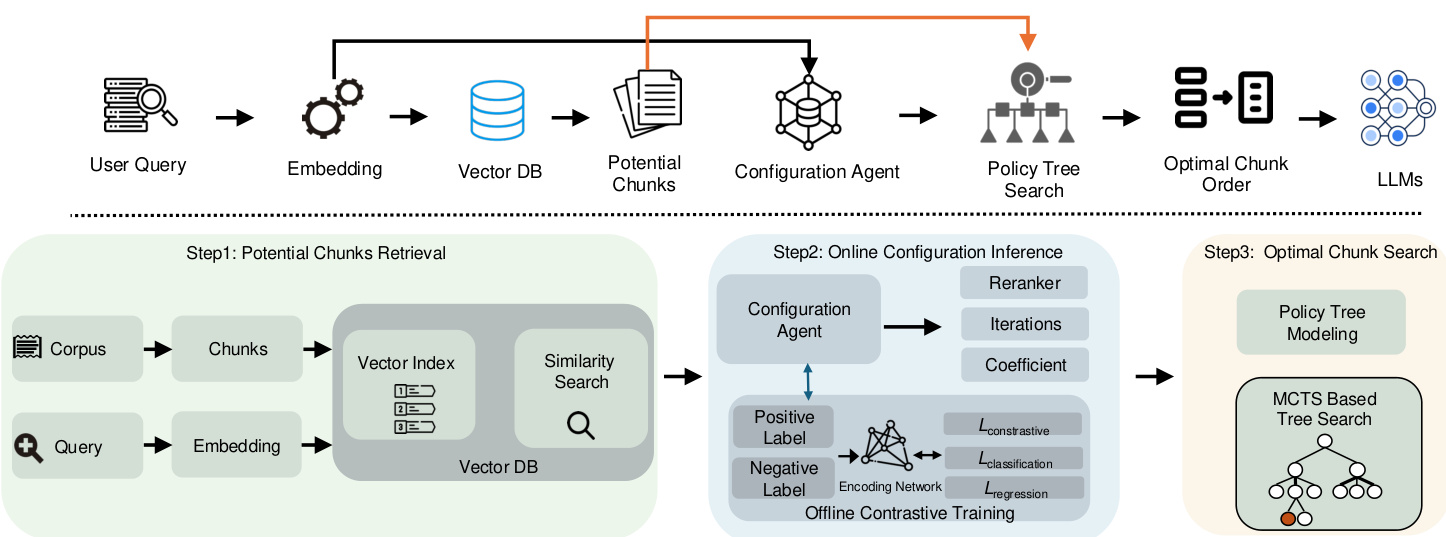
Figura 2: Visión general de la arquitectura del sistema CORAG
Los métodos tradicionales de reordenación [33, 50] suelen basarse en modelos lingüísticos de tamaño medio, como BERT o T5, para ordenar los contextos recuperados. Sin embargo, estos modelos suelen tener dificultades para captar las relaciones semánticas entre las consultas y los contextos, especialmente en contextos de muestra cero o pequeña. Por ello, investigaciones recientes [43] han destacado el potencial de los LLM ajustados a comandos para mejorar la reclasificación de contextos, incluso en presencia de información ruidosa o irrelevante. A pesar de estos avances, las capacidades de reordenación de los LLM en los sistemas GAR siguen estando infrautilizadas. En concreto, se ha demostrado que la clasificación por bloques afecta al rendimiento del LLM [19], lo que subraya la necesidad de tener en cuenta el orden de las combinaciones de bloques en las tareas GAR. Sin embargo, los modelos existentes no son adecuados para situaciones en las que se requiere una secuencia o combinación específica de bloques para una recuperación óptima, en lugar de bloques aislados. Por lo tanto, la investigación futura debe hacer un mejor uso del LLM para secuenciar de forma más eficiente los bloques en respuesta a las consultas dentro del marco RAG.
2.3.3 Aprendizaje por refuerzo para grandes modelos lingüísticos
Recientemente, el aprendizaje por refuerzo (RL) se ha utilizado cada vez más para diversas tareas de gestión de datos y GAR. Las técnicas de RL pueden permitir que grandes modelos lingüísticos mejoren sus capacidades generativas explotando fuentes de conocimiento externas, como los motores de búsqueda [13, 23]. En particular, se puede integrar la retroalimentación humana [4, 36, 37] para ayudar a los modelos a generar respuestas más precisas y contextualmente relevantes a través del marco de la RL. Además, una serie de enfoques de optimización de consultas [17, 21, 49] mejoran aún más el proceso de recuperación al permitir que el rendimiento del modelo informe el ajuste de la consulta y, en última instancia, mejore los resultados de las tareas posteriores. En este trabajo, aplicamos una técnica ligera de RL, MCTS, para optimizar el proceso de búsqueda secuencial de combinación de bloques en sistemas RAG. También introducimos un agente de configuración para guiar el proceso de búsqueda MCTS. Hasta donde sabemos, se trata de la primera aproximación a este problema concreto.
3 Descripción general del sistema
Como ya se ha mencionado, los marcos RAG existentes se enfrentan a tres retos fundamentales: cómo tener en cuenta adecuadamente las asociaciones entre bloques y la no monotonicidad de la utilidad secuencial de las combinaciones de bloques, y adaptarse a distintos dominios de consulta. Estos problemas reducen la relevancia de los resultados. Para resolver estos problemas, presentamos CORAG, un sistema diseñado para recuperar combinaciones de bloques óptimas, teniendo en cuenta tanto los dominios de consulta como los presupuestos de los usuarios. El componente más importante de nuestro sistema es el modelo de búsqueda de combinaciones óptimas de bloques. El modelo emplea un árbol de políticas basado en MCTS para la búsqueda secuencial de órdenes de combinación de bloques, lo que nos permite considerar plenamente las asociaciones entre bloques (Desafío 1), así como la no monotonicidad de la utilidad del orden de combinación de bloques (Desafío 2). Además, proponemos un módulo de inferencia de configuración que recomienda configuraciones MCTS óptimas y reordenadores para varios dominios de consulta, abordando así el Desafío 3. A continuación, ofrecemos una breve descripción de estos dos módulos.
Búsqueda de combinaciones óptimas de bloques: Un enfoque sencillo para considerar las asociaciones de bloques consiste en recuperar posibles bloques de una base de datos vectorial (como se muestra en el paso 1) y, a continuación, explorar exhaustivamente todas las combinaciones de bloques posibles. Sin embargo, este método conlleva una latencia y un coste computacional considerables. Para mitigarlo, construimos un árbol de estrategias (paso 2) que reformula la búsqueda de la combinación óptima de bloques como un problema de búsqueda en los nodos del árbol. En concreto, el nodo raíz del árbol estratégico representa un estado inicial vacío, y cada nodo hijo corresponde a una combinación concreta de bloques. Por ejemplo, si el nodo raíz tiene nodos hijos que representan los bloques χ1, uno de sus hijos puede representar la combinación χ1+χ2, mientras que otro puede representar χ1+χ3
Diseñamos un algoritmo de búsqueda basado en MCTS para resolver este problema. A diferencia del MCTS tradicional, nuestro enfoque expande el nodo de mayor utilidad en cada iteración mientras evalúa todos los posibles nodos hijos. Además, tenemos en cuenta las restricciones de costes y presupuesto durante la búsqueda en el árbol estratégico. Las utilidades de los nodos se calculan equilibrando la exploración con el control de costes, optimizando la eficiencia y la precisión.
Razonamiento de la configuración: Una solución sencilla al ajuste de configuraciones sería enumerar todas las configuraciones o reordenadores posibles, calcular los resultados en paralelo y, a continuación, elegir la mejor configuración. Sin embargo, esto supondría un coste poco realista para el sistema GAR. Con el fin de optimizar las configuraciones (es decir, el número de iteraciones, el factor de coste y el factor de exploración) para el proceso de búsqueda del árbol de políticas, introducimos un agente de configuración que genera dinámicamente configuraciones basadas en el dominio de consulta. Para garantizar la eficacia del modelo, empleamos un enfoque de aprendizaje comparativo utilizando pares etiquetados positivos y negativos: las etiquetas positivas corresponden a incrustaciones de consultas del mismo mejor re-ranqueador, mientras que las etiquetas negativas proceden de otro mejor re-ranqueador. La función de pérdida conjunta se utiliza para optimizar simultáneamente la regresión (para ajustar los parámetros) y el aprendizaje por contraste (para mejorar la discriminación de etiquetas).
Resumen. El flujo de nuestro marco se muestra en la Figura 2. En primer lugar, generamos incrustaciones para la consulta de entrada y, a continuación, las utilizamos para recuperar posibles bloques de la base de datos de vectores. Estas incrustaciones de consulta también se introducen en un agente de configuración que genera dinámicamente una configuración MCTS óptima basada en el campo de consulta. A partir de esta configuración óptima, podemos buscar en el árbol de políticas para determinar la combinación y el orden óptimos de los bloques potenciales recuperados. Por último, esta combinación óptima de bloques se utiliza para construir las pistas finales para los LLM.
4 Búsqueda de combinaciones de bloques
Como se ha mencionado anteriormente, el orden de las combinaciones de bloques tiene un impacto significativo en la eficacia de la construcción de pistas para los LLM. Debido al enorme número de combinaciones posibles, especialmente cuando se trata de un gran número de bloques, no es factible enumerar todos los posibles órdenes de combinación de bloques. En esta sección, proponemos un enfoque novedoso que consigue un buen equilibrio entre eficiencia y precisión en el problema de la búsqueda del orden óptimo de combinación de bloques. En la sección 4.1, modelamos el problema como la búsqueda de nodos óptimos en un árbol de políticas (sección 4.1). A continuación, proponemos un algoritmo basado en MCTS para resolver este problema de búsqueda de nodos (Sección 4.2).
4.1 Modelización de la búsqueda estratégica en árbol
Para encontrar el orden combinatorio óptimo, el primer paso es encontrar una estructura de datos que pueda enumerar de forma eficiente todos los órdenes combinatorios posibles. Una opción natural es un árbol, en el que, recorriendo los nodos de raíz a hoja, podemos explorar todas las posibles respuestas.
Árbol estratégico. Como se muestra en la Fig. 3, construimos un árbol estratégico para representar el orden de todas las posibles combinaciones de bloques extraídas de la base de datos de vectores. En concreto, el nodo raíz simboliza el estado inicial sin ningún bloque, y cada nodo posterior representa un bloque seleccionado de entre los bloques potenciales. Así, los nodos hijos se generan a partir de sus nodos padres seleccionando el siguiente bloque disponible de la cola de bloques potenciales y fusionándolo en la secuencia establecida por el nodo antecesor. Por ejemplo, si un nodo representa la secuencia de combinación de bloques {χ1}, un nodo hijo puede contener secuencias de combinación posteriores como {χ1, χ2}, {χ1, χ3} o {χ1, χ4}. Por lo tanto, definimos formalmente el árbol de estrategias de la siguiente manera:
Definición 4.1 (Árbol de estrategias). Dada una consulta q y un conjunto de bloques potenciales {χ1, χ2, ... . , χn}, construimos un árbol de políticas T. El nodo raíz de T representa el estado inicial sin ningún bloque. Cada nodo no raíz posterior contiene un conjunto de bloques mediante la fusión de los bloques recién seleccionados de los bloques potenciales restantes en la secuencia de sus nodos padre. Este proceso construye secuencialmente una combinación ordenada de bloques en cada nodo no raíz, y nuestro objetivo es encontrar el nodo con la mayor puntuación de utilidad.
En un árbol estratégico, nuestro objetivo es seleccionar un nodo que contenga bloques ordenados que proporcionen el máximo beneficio con el mínimo coste. Para lograrlo, tenemos que diseñar una función de cálculo de la utilidad para evaluar el equilibrio entre beneficios y costes. Esta función se cuantifica mediante lo que definimos como "utilidad del nodo", tal y como se describe a continuación.
Utilidad nodal. La métrica de utilidad consta de dos componentes: el beneficio derivado de seleccionar una combinación de bloques y el coste de utilizar los bloques como indicadores de los LLM. En concreto, los beneficios se cuantifican mediante los LLM, que miden la similitud entre los bloques seleccionados y la consulta. En concreto, los denotamos como valores de nodo V. A continuación, utilizamos el algoritmo Upper Confidence Bound (UCB) [3] para equilibrar la balanza entre la explotación (valores de nodo V(vi)) y la exploración (recuentos de búsqueda N(vi)) de los valores de nodo V(vi) y los recuentos de búsqueda N(vi). Para un nodo vi dado, con respecto al coste, consideramos el coste de etiquetado definido en la Sección 2 y medido por el cociente del coste de la combinación de bloques actual con respecto al presupuesto total asignado B. Así, la utilidad del nodo se define de la siguiente manera:
Definición 4.2 (Utilidad nodal). Dado un árbol estratégico y un presupuesto de costes B, la utilidad de un nodo no raíz se define como:
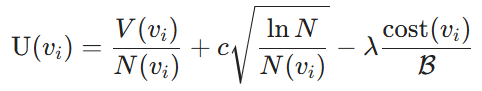
donde V(vi) es el valor de beneficio estimado de la combinación de bloques en el nodo vi, determinado por el modelo de entrenamiento, N(vi) es el número de visitas al nodo vi, que promueve la exploración de los nodos menos visitados, y N es el número total de visitas a todos los nodos del árbol de políticas para garantizar un equilibrio entre exploración y explotación. Además, cost(vi) denota el coste de etiquetado del nodo vi, B es el presupuesto total de etiquetado, c regula el equilibrio entre exploración y explotación, y λ sirve como factor de penalización de costes para mejorar la eficiencia de costes.
Modelización de la selección óptima de nodos. A partir de las utilidades de los nodos definidas, la tarea de seleccionar el orden óptimo de combinación de bloques, descrita en la sección 2, se reformula como la selección del nodo óptimo en el árbol de políticas T . Con una determinada restricción presupuestaria B, el objetivo es identificar los nodos vi ⊆ T para maximizar la utilidad U(vi), garantizando al mismo tiempo que el coste total asociado a vi no supere B. Formalmente, esto se expresa como:
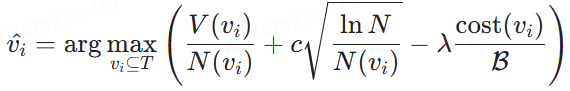
donde V(vi) es la utilidad estimada de la combinación de bloques en el nodo vi y cost(vi) representa su coste asociado. Esta fórmula permite elegir el bloque que maximiza la utilidad dentro de un presupuesto determinado.
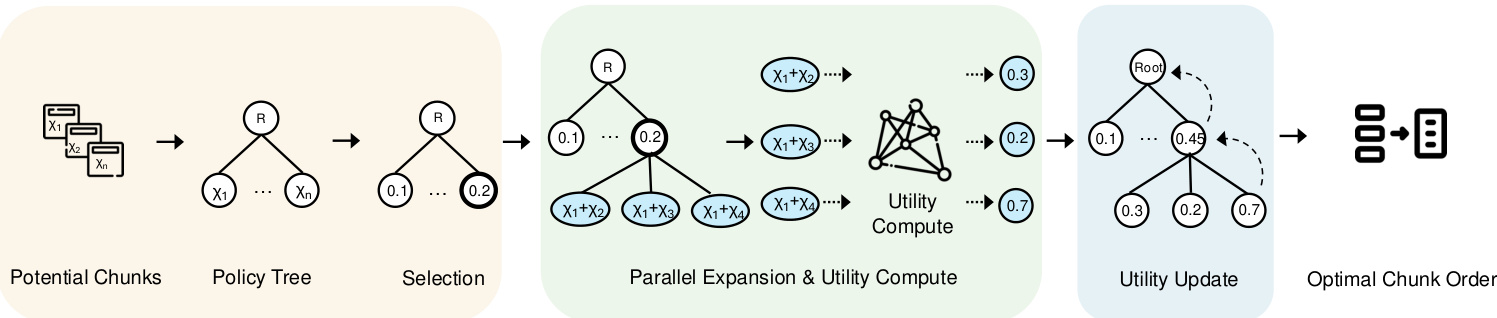
Figura 3: Flujo de trabajo de optimización de bloques basado en MCTS

Algoritmo 1 Búsqueda en árbol de estrategias basada en MCTS
4.2 Búsqueda de árboles de políticas basada en MCTS
Motivación. Enumerar todos los nodos del árbol de políticas permitirá encontrar el nodo óptimo, pero supondrá un elevado coste computacional. Para resolver este problema, un enfoque sencillo consiste en aplicar una estrategia codiciosa que recorra el árbol de forma iterativa empezando por el nodo raíz. En cada iteración, selecciona el nodo hijo con el mayor beneficio y continúa hasta agotar el presupuesto. Sin embargo, es probable que este enfoque conduzca a resultados subóptimos. Por ejemplo, χ1 puede tener un beneficio ligeramente mayor que χ2, pero χ2 + χ3 pueden tener un beneficio significativamente mayor que χ1 + χ3. En este caso, un enfoque codicioso puede conducir a resultados subóptimos. Por lo tanto, es necesario volver a visitar el nodo padre de alta eficiencia. Al mismo tiempo, hay que reducir la exploración de los nodos de baja eficiencia.
Para lograr nuestro objetivo, proponemos un método de búsqueda en árbol de estrategias basado en MCTS y diseñado para seleccionar y clasificar eficazmente combinaciones de bloques. Este enfoque explora iterativamente el espacio de secuencias de bloques potenciales, optimizando una consulta dada dentro de una restricción presupuestaria especificada.
Visión general. Las políticas basadas en MCTS se describen en el algoritmo 1. Primero inicializamos el nodo raíz del árbol de políticas utilizando consultas de entrada. Cuando el presupuesto computacional no se agota, realizamos iterativamente dos pasos clave: selección de nodos y actualización de utilidades. Una vez alcanzado el límite de iteración o el presupuesto, detenemos el proceso y buscamos recursivamente en el árbol hasta encontrar el nodo con la utilidad más alta. A diferencia de las estrategias MCTS tradicionales, que suelen centrarse sólo en el nodo raíz, nuestro enfoque también tiene en cuenta los nodos prometedores de nivel intermedio para maximizar la utilidad de la combinación de bloques.
Explicación detallada de las principales características. A continuación explicamos con más detalle estas dos funciones clave:
- Selección de nodos (algoritmo 2). Seleccionamos recursivamente el nodo con el valor de utilidad más alto que tenga más probabilidades de conducir a la combinación óptima de bloques. Específicamente:

Algoritmo 2 Selección de nodos

Algoritmo 3 UtilityUpdate
- Selecciona. Identificamos el nodo con el máximo valor de utilidad. Si 𝑣 aún no se ha expandido, generamos todos los posibles nodos descendientes y los incluimos en el árbol estratégico. Si 𝑣 se ha expandido, seleccionamos el nodo descendiente con la utilidad más alta para seguir explorando.
- Extensiones. Tras seleccionar el nodo con mayor utilidad, lo ampliamos generando todos los posibles nodos hijos. Cada nodo hijo representa un nuevo orden de posibles combinaciones de bloques. Nuestro enfoque utiliza la expansión paralela, que computa y evalúa múltiples subnodos simultáneamente. Este paralelismo explota la capacidad de la red de valores para manejar múltiples combinaciones con un coste computacional similar al de un único nodo, mejorando la eficiencia de la búsqueda.
- Utilidad calculada. Calculamos el valor de utilidad de cada nuevo nodo hijo utilizando la fórmula de utilidad. El modelo de re-ranker R procesa múltiples combinaciones de bloques en paralelo para generar.

5 Configuración del Agente
Tras abordar la eficiencia del procesamiento de asociaciones de bloques dentro del presupuesto del usuario, la tarea restante consiste en diseñar un sistema que se adapte al dominio de cada consulta.El proceso MCTS implica varias configuraciones clave, como la selección del re-ranker, el número de iteraciones, el factor de exploración y el factor de coste. Optimizar estas configuraciones en función del tipo de consulta resulta especialmente complicado. Para resolver este problema, proponemos un marco de agentes de configuración que predice el reordenador y la configuración óptimos para cada consulta. En esta sección, presentamos primero el marco de agentes en la sección 5.1 y, a continuación, esbozamos el proceso de aprendizaje del modelo en la sección 5.2.
5.1 Marco de modelización
Motivación. Para abordar el reto 3, que requiere adaptarse al dominio de cada consulta y recomendar configuraciones óptimas, una solución directa es utilizar un clasificador MLP para asignar cada consulta a su mejor reclasificador. Sin embargo, los experimentos iniciales demostraron que la clasificación MLP no funciona bien. Tras un análisis más detallado, observamos que tipos similares de consultas tienden a compartir los mismos mejores reclasificadores y configuraciones. Por tanto, utilizar la red siamesa con aprendizaje por contraste para acercar las consultas de la misma categoría y separar las de categorías diferentes es un enfoque más viable.
La figura 4 ofrece una visión general de nuestro agente configurado, que consta de dos módulos principales responsables de transformar la entrada en un grafo de características. En primer lugar, el módulo de incrustación de entrada genera incrustaciones de la consulta de entrada. A continuación, la red de codificación procesa estas incrustaciones para producir mapas de características, que luego se utilizan para derivar varias configuraciones de los ajustes MCTS.
Las secciones siguientes describen detalladamente cada componente y explican su justificación de diseño.
(1) Introduzca la consulta incrustada en. Para captar eficazmente los factores de varias consultas, dada la diversidad de tipos de consultas como hechos explícitos, hechos implícitos, racionalidad interpretable y racionalidad oculta [47], utilizamos el modelo de incrustación BGE-M3 [6] para generar incrustaciones para cada consulta. Estas incrustaciones mejoran el marco de aprendizaje asignando tipos similares de consultas a la misma categoría de re-ranker. Representadas en un espacio de 1024 dimensiones, las incrustaciones capturan las características semánticas subyacentes, lo que permite a la red de codificación compararlas y clasificarlas con eficacia. Este paso ayuda a mejorar la relevancia de recuperación de los distintos tipos de consulta. Además, el uso del mismo modelo de incrustación también genera incrustaciones anotadas por el reclasificador óptimo, incluidas sus características únicas y los metadatos asociados, lo que permite al modelo alinear las consultas con el reclasificador óptimo.
(2) Generación de mapas de características mediante redes codificadas: el Para optimizar la tarea de selección de re-ranker y recomendar el mejor re-ranker para cada consulta para distintos tipos de consulta, utilizamos redes de codificación para aprender de forma eficiente representaciones que sean útiles tanto para la clasificación como para la predicción de configuraciones. Para esta tarea utilizamos una red siamesa formada por tres capas totalmente conectadas. Procesa incrustaciones de consulta de entrada de dimensión d = 1024 y aprende resultados de clasificación y predicciones de configuración MCTS (es decir, número de iteraciones y λ). Las ramas de la red de codificación comparten pesos, y cada rama aplica una transformación lineal seguida de una activación RELU. Secuencialmente, la primera capa oculta reduce la dimensionalidad a 512, la segunda a 256 y la tercera a 128. La última capa de salida proporciona predicciones de clasificación que especifican el mejor re-ranker para cada consulta, así como resultados de regresión que se utilizan para predecir las configuraciones MCTS más eficientes para guiar el proceso de búsqueda. El resultado de la clasificación identifica el mejor re-ranker para cada consulta, mientras que el resultado de la regresión determina la mejor configuración MCTS.
5.2 Formación conjunta
En esta sección, esbozamos el proceso de entrenamiento para desarrollar agentes de configuración. Como se muestra en la Fig. 4, implementamos tres tareas de entrenamiento conjuntas para mejorar la eficacia del modelo. Las dos primeras tareas implican clasificación y regresión para seleccionar el mejor re-ranker y predecir los mejores valores de los hiperparámetros MCTS, respectivamente. Además, incorporamos un enfoque de aprendizaje comparativo para mejorar aún más el proceso de aprendizaje.
5.2.1 Pérdidas por clasificación y regresión.
Dada la etiqueta re-ranker predicha Y(pred) y su correspondiente re-ranker óptimo real Y(true), la pérdida de clasificación L(cla) se calcula como sigue.
![]()
donde F(cla) representa la pérdida de entropía cruzada entre las etiquetas predichas y las reales del re-ranker. Esta función de pérdida ayuda a clasificar con precisión el reclasificador óptimo para cada consulta. Del mismo modo, la pérdida por regresión L(reg) se define como.
donde 𝐹reg es el error cuadrático medio (MSE) entre el parámetro MCTS predicho 𝑝pred y el parámetro MCTS real 𝑝true. Esta métrica garantiza una predicción precisa de la configuración MCTS en términos de número de iteraciones y 𝜆.
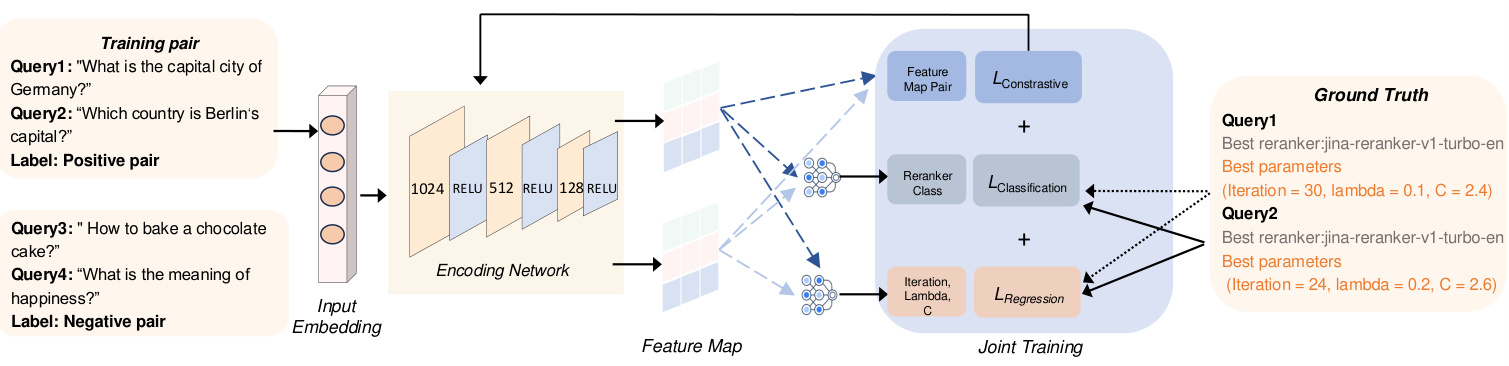
Figura 4: Visión general del Agente de Configuración
5.2.2 Aprendizaje contrastivo.
Con el fin de distinguir eficazmente los distintos dominios de consulta y recomendar la mejor configuración para cada consulta, utilizamos el aprendizaje comparativo para acercar las consultas de un mismo dominio al tiempo que expulsamos las incrustaciones de distintas clases de re-ranker.
Preparación de la comparación. Para preparar el conjunto de datos de entrenamiento, debemos determinar el reclasificador y la configuración óptimos para cada consulta. En este estudio, los reordenadores óptimos y las configuraciones correspondientes para cada consulta se determinaron mediante experimentos exhaustivos con diversas configuraciones. A continuación, se generan pares de consultas a partir de estas anotaciones óptimas de los reordenadores. Los pares positivos consisten en consultas que comparten el mismo reordenador óptimo, lo que facilita la minimización de su incrustación en el espacio de características. Por el contrario, los pares negativos consisten en consultas con diferentes re-rankers con el objetivo de maximizar la distancia de incrustación entre ellos. Dado que algunos reordenadores tienen un rendimiento similar en determinadas consultas, sólo seleccionamos los casos en los que ROUGE-L difiere en más de 10% para formar nuestro conjunto de datos de entrenamiento.
Pérdida de contraste. Como se muestra en la Fig. 4, para un par positivo dado (𝑥𝑖, 𝑥+𝑖) y el par negativo (𝑥𝑗, 𝑥-𝑗), primero utilizamos el modelo de codificación para generar sus correspondientes mapas de características. A continuación, estos mapas de características se utilizan para calcular la pérdida de contraste 𝐿con. En concreto, este proceso puede representarse de la siguiente manera:
Entre ellas.𝑓𝜃(𝑥) denota la función de incrustación.𝐹con es una función de similitud aplicada a dos tipos de pares: pares positivos (con reordenadores similares) y pares negativos (con reordenadores diferentes). Esta función de pérdida está diseñada para garantizar que las consultas con el mismo reordenador estén más cerca en el espacio de incrustación y las consultas con reordenadores diferentes estén más lejos.
5.2.3 Todo el proceso de formación.
Por último, la función de pérdida total L(total) es la suma de las pérdidas por comparación, clasificación y regresión, como se indica a continuación.
En concreto, la pérdida por contraste Lcon(θ) fomenta que las incrustaciones de las consultas con el mismo re-ranker óptimo estén más próximas, mientras que aleja las incrustaciones de las consultas con diferentes re-rankers. La pérdida por clasificación Lcla(θ) ayuda al modelo a identificar correctamente los reclasificadores utilizando la entropía cruzada, mientras que la pérdida por regresión Lreg(θ) minimiza el error de predicción de la configuración MCTS óptima.
Observaciones. Una vez calculada la pérdida total Ltotal, los parámetros de la red θ se actualizan mediante descenso gradiente a una tasa de aprendizaje η. Este proceso de optimización se repite a lo largo de múltiples ciclos E y lotes, asegurando que tanto el clasificador como las predicciones de los parámetros mejoran con el tiempo.
6 Experimentos
El estudio experimental pretende responder a las siguientes preguntas.
- RQ1 ¿Cómo se compara nuestro CORAG con otros métodos en conducciones RAG de costes limitados?
- ¿Cuál es la eficiencia de RQ2 CORAG con distintos tamaños de bloque?
- RQ3 ¿Cuáles son los cuellos de botella actuales del GAR?
- ¿Cuáles son los cuellos de botella del GAR?
- RQ4 ¿Cuál es la escalabilidad de CORAG con conjuntos de datos de distintos tamaños?
- RQ5 ¿Cuál es la eficacia de cada diseño en CORAG?
6.1 Montaje experimental
Entorno. Integramos nuestro sistema con el popular framework RAG LlamaIndex. Los experimentos se ejecutaron en un servidor Linux equipado con una CPU Intel Core i7-13700K (12 núcleos, 24 hilos, 5,3 GHz), 64 GB de RAM y 1 TiB NVMe SSD. El módulo Configuration Agent se implementó en una GPU NVIDIA RTX 4090 equipada con 24 GB de VRAM utilizando PyTorch 2.0.
Tabla 1: Datos estadísticos utilizados en el experimento.
| conjunto de datos | #ren | #dev | #est | #p |
| MSMARCO | 502,939 | 6,980 | 6,837 | 8,841,823 |
| Wiki | 3,332 | 417 | 416 | 244,136 |
Conjunto de datos.Para evaluar el rendimiento de CORAG en distintos escenarios, realizamos experimentos con dos conjuntos de datos diferentes centrados en distintas tareas:(1) WikiPassageQA [7] es una referencia de preguntas y respuestas que contiene 4.165 preguntas y más de 100.000 trozos de texto destinados a evaluar la recuperación a nivel de párrafo. (2) MARCO [24] es un amplio conjunto de datos dedicado a tareas de procesamiento del lenguaje natural, con especial énfasis en las preguntas y respuestas y la recuperación de información. Como se muestra en la Tabla 1, tanto WikiPassageQA como MARCO proporcionan preguntas y anotaciones de párrafos de alta calidad, lo que los hace adecuados para evaluar la eficacia de la recuperación. En nuestros experimentos, pedimos a los LLM que generen respuestas reales para cada conjunto de datos. Por ejemplo, si utilizamos Llama3 para evaluar el rendimiento de CORAG, también utilizamos Llama3 para generar verdades básicas en la misma configuración experimental para mantener la imparcialidad y la alineación con las características de los LLM.
Línea de base.Comparamos el rendimiento de CORAG con dos líneas de base típicas de RAG:
- RAPTOR [29]: RAPTOR construye un árbol jerárquico de resúmenes de documentos incrustando, agrupando y resumiendo recursivamente bloques de texto para lograr una abstracción multinivel. Este planteamiento es coherente con el basado en la agrupación que se expone en la sección 1. Completamos la construcción del árbol dentro de unos límites presupuestarios aproximados.
- NaiveRAG: se trata de un método básico para recuperar bloques relevantes. En primer lugar, los bloques candidatos se recuperan de la base de datos de vectores basándose en la búsqueda de similitud de vectores y, a continuación, se clasifican utilizando el modelo re-ranker. Este método es el método AKNN mencionado en la sección 1. Para satisfacer la restricción de costes, utilizamos una estrategia codiciosa de asignación de presupuesto para recuperar bloques hasta que el presupuesto se agota por completo.
Además, eliminamos el agente de configuración en nuestro enfoque como línea de base para evaluar su impacto en el rendimiento de CORAG, refiriéndonos a esta versión como CORAG sin agente.Por último, implementamos un enfoque denominado CORAG Superior, que establece un límite superior explorando todas las combinaciones posibles de bloques y seleccionando el mejor orden. Debido al gran número de combinaciones posibles, en el caso de CORAG Upper limitamos la exploración a combinaciones de menos de seis bloques.
Observaciones.Otros enfoques, como GraphRAG [22], dependen en gran medida de llamadas frecuentes a LLMs para resumir bloques y construir índices, incurriendo en enormes costes (por ejemplo, miles de millones de tokens) que exceden nuestras estrictas restricciones de costes. Por tanto, estos enfoques no son viables para resolver nuestro problema. Para que la comparación sea justa, hemos excluido este tipo de enfoques RAG de nuestros experimentos.
Configuración de hiperparámetros: los hiperparámetros de CORAG los determina automáticamente el agente de configuración, mientras que NaiveRAG no requiere ningún hiperparámetro. Para los demás métodos de referencia, garantizamos la coherencia utilizando los mismos hiperparámetros para realizar comparaciones equitativas. En concreto, fijamos el factor de exploración en 2,4, el número de iteraciones en 10 y el factor de coste λ en 0,1. Los experimentos preliminares muestran que esta configuración optimiza el rendimiento de la línea de base. También realizaremos más estudios de ablación para validar estos ajustes.
Configuración de los parámetros de aprendizaje. En nuestro enfoque, el agente de configuración se entrena utilizando el aprendizaje por contraste. Los hiperparámetros utilizados en este proceso incluyen la pérdida por contraste (margin=1,0), la tasa de aprendizaje (lr=0,001), el tamaño del lote (32), el número de ciclos (num_epochs=60) y el modelo de incrustación (es decir, BAAI/bge-m3 [6]).
Métricas de evaluación. Evaluamos la eficacia comparando las puntuaciones Rouge de las respuestas reales y las respuestas generadas, utilizando Rouge-1, Rouge-2 y Rouge-L como métricas de evaluación. Para evaluar la eficiencia, medimos la latencia necesaria para responder a las consultas utilizando distintos métodos.
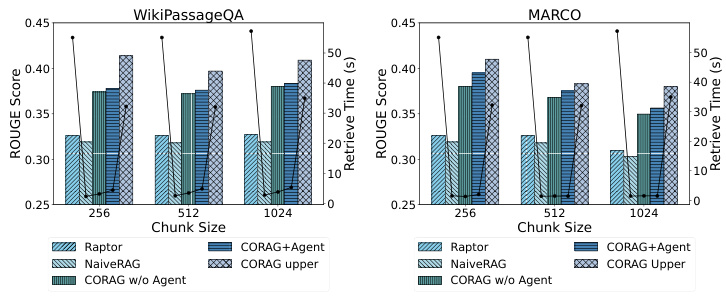
Figura 5: Comparación de la eficiencia
6.2 Comparación de resultados
6.2.1 RQ1: Comparación de Rouge.
Como se muestra en la Fig. 2, comparamos el rendimiento de CORAG con varias líneas de base en diferentes conjuntos de datos, utilizando principalmente WikiPassageQA y MARCO. la evaluación se realiza en tres tamaños de bloque diferentes, utilizando las métricas Rouge-1, Rouge-2 y Rouge-L para evaluar la mejora de las respuestas generadas por LLM debido a nuestro método de recuperación. corag se compara con los principales métodos RAG (por ejemplo, NaiveRAG y RAPTOR) en una mejora significativa de alrededor de 251 TP3 T. Como era de esperar, CORAG no supera el límite superior, lo que representa el límite extremo de los métodos RAG. (por ejemplo, NaiveRAG y RAPTOR) con una mejora significativa de aproximadamente 251 TP3 T. Como era de esperar, CORAG no supera el límite superior, que representa un caso extremo en el que se enumeran exhaustivamente todos los órdenes de combinación posibles, lo que resulta claramente ineficaz y poco práctico. En conclusión, CORAG supera a la línea de base, mejorando la relevancia de la búsqueda al tiempo que poda eficazmente el espacio de búsqueda.
6.2.2 RQ2: Evaluación de la eficiencia.
Como se muestra en la Fig. 5, dado que CORAG se basa en un algoritmo de búsqueda en árbol, el agente ayuda a predecir el mejor reordenador y los mejores parámetros para una consulta determinada. Por lo tanto, es crucial evaluar el impacto de diferentes tamaños de bloque y conjuntos de datos en la eficiencia de la tarea de optimización de la recuperación. Probamos la eficacia utilizando diferentes conjuntos de datos y tamaños de bloque y observamos que NaiveRAG, utilizando métodos de recuperación tradicionales, consigue tiempos de recuperación más cortos pero puntuaciones Rouge más bajas.CORAG obtiene buenos resultados en términos de Rouge pero es significativamente menos eficaz ya que explora todo el espacio de búsqueda. Del mismo modo, RAPTOR utiliza un LLM externo para resumir y muestra una eficiencia deficiente. En cambio, nuestro enfoque CORAG logra un equilibrio eficaz entre eficacia y relevancia de la búsqueda.
6.2.3 RQ3: Descomposición del rendimiento.
Mostramos una descomposición del rendimiento del NaiveRAG de referencia para destacar los cuellos de botella de los sistemas RAG actuales. Para abordar el reto de buscar el orden óptimo de las combinaciones de bloques, su aplicación mediante NaiveRAG requiere los siguientes pasos: a) obtención de la incrustación de la consulta, b) recuperación de las posibles combinaciones de bloques, c) reordenación de las posibles combinaciones de bloques y d) refinamiento de las pistas. La figura 6 muestra la latencia media de cada paso en la configuración experimental anterior.
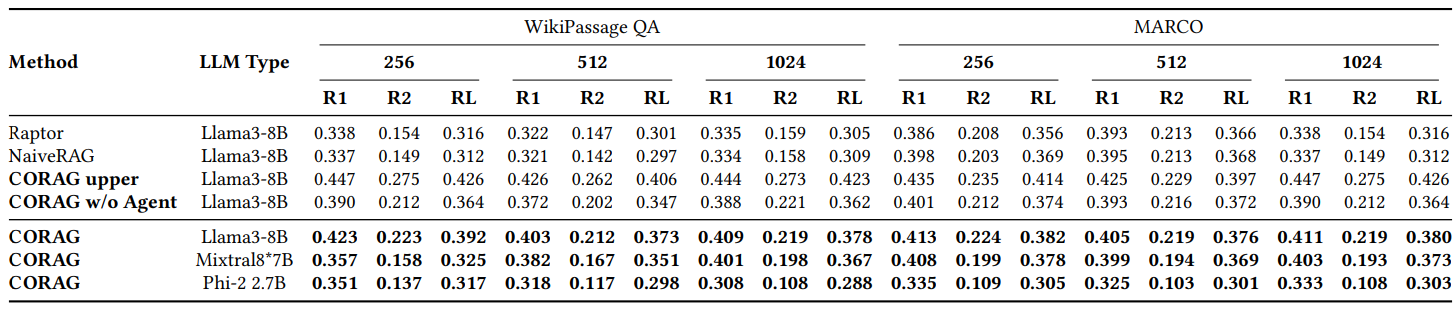
Tabla 2: Comparación de Rouge en los conjuntos de datos WikiPassage QA y MARCO
6.2.4 RQ4: Evaluación de la escalabilidad
CORAG presenta una excelente escalabilidad, especialmente cuando se trabaja con grandes conjuntos de datos (como WikiPassageQA y MARCO) que contienen un gran número de párrafos. El número de trozos puede ampliarse fácilmente a 100.000 o más dividiendo cada párrafo en 256 trozos etiquetados. A pesar del considerable aumento del volumen de datos, nuestro tiempo de recuperación sólo se incrementó en 101 TP3T con respecto al método tradicional, lo que demuestra la eficacia de nuestro sistema a la hora de gestionar tareas de recuperación a gran escala. En particular, nuestro sistema supera al método CORAG Upper, ya que requiere sólo una décima parte del tiempo de recuperación y, al mismo tiempo, proporciona puntuaciones ROUGE competitivas. Este equilibrio eficaz entre rendimiento y sobrecarga computacional pone de manifiesto la capacidad del sistema para podar eficazmente el espacio de búsqueda, garantizando una recuperación rápida incluso en conjuntos de datos enormes. Así pues, nuestro planteamiento es idóneo para situaciones que requieran el procesamiento de datos a gran escala y una gran precisión en la recuperación.
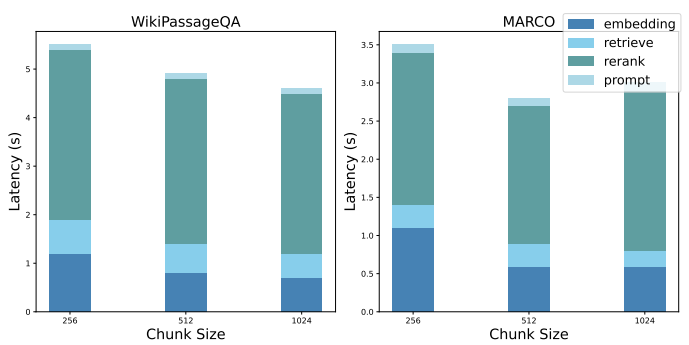
Figura 6: Descomposición del rendimiento
Cuadro 3: Comparación del rendimiento con distintos presupuestos
6.3 RQ5: Estudios de ablación
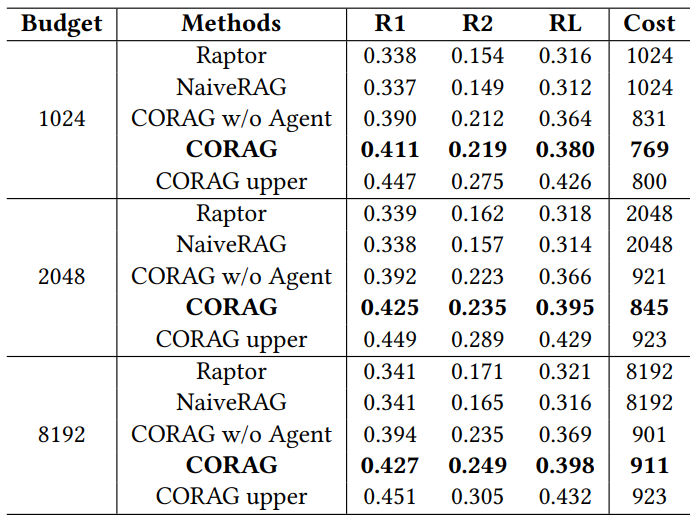
6.3.1 Estudios de ablación con diferentes presupuestos
Como se muestra en la Tabla 3, evaluamos CORAG como un sistema de costes limitados e investigamos el impacto de diferentes presupuestos en el rendimiento general. Utilizando el conjunto de datos MARCO, fijamos los límites presupuestarios en 1024, 2048 y 8192 tokens y evaluamos los resultados con ROUGE. Cabe destacar que el coste medio de etiquetado de CORAG se mantiene por debajo de cada límite presupuestario, lo que sugiere que la utilidad de los bloques no es monótona, como se puso de manifiesto en el Desafío 2. A medida que aumenta el presupuesto, CORAG se beneficia de un mayor número de bloques. A medida que aumenta el presupuesto, CORAG se beneficia de un espacio de búsqueda ampliado y es capaz de incluir más información relevante, en lugar de limitarse a aumentar el número de bloques.
6.3.2 Estudios de ablación con diferentes coeficientes de exploración
Como se muestra en la Fig. 7, realizamos un estudio de ablación para evaluar el impacto de diferentes coeficientes de exploración en el rendimiento del sistema, probando concretamente valores de C de 0, 1, 2 y 3. Los resultados muestran que un coeficiente de exploración de aproximadamente 2 proporciona el mejor rendimiento, logrando un equilibrio óptimo entre exploración y explotación durante el proceso de búsqueda. Este equilibrio permite que el sistema descubra información relevante de forma eficaz y, al mismo tiempo, se centre en los bloques de alto potencial, lo que, en última instancia, se traduce en una mejora de la respuesta del GAR. Por el contrario, los coeficientes de exploración más bajos condujeron a resultados subóptimos debido a la subexploración, mientras que los coeficientes de exploración más altos condujeron a resultados subóptimos debido a la desviación excesiva de la atención. Estos resultados ponen de relieve el papel fundamental del coeficiente de exploración en el rendimiento del proceso de búsqueda CORAG y subrayan la importancia de ajustar cuidadosamente los parámetros.
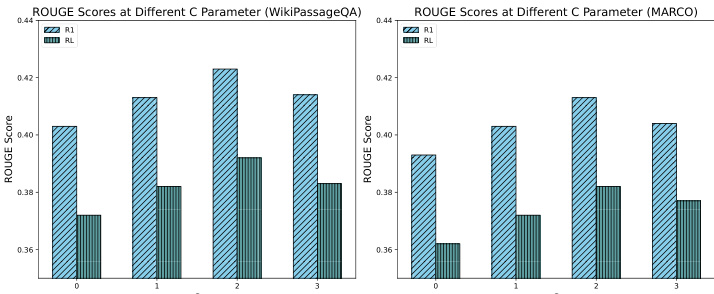
Figura 7: Comparación de ROUGE entre distintos valores de C
6.3.3 Estudios de ablación con diferentes factores de coste
Como se muestra en la Fig. 8, se realizó un estudio de ablación para evaluar el impacto de distintos coeficientes de coste en el rendimiento del sistema, concretamente se probaron los valores 0, 0,1, 0,2 y 0,3. Los resultados muestran que la introducción de coeficientes de coste en la utilidad provoca una ligera disminución de la puntuación ROUGE. Esta disminución se debe al hecho de que, en ausencia de una restricción de costes, CORAG tiende a producir outputs más largos, aunque a costa de la eficiencia de costes. Sin embargo, a pesar del ligero descenso en la puntuación ROUGE, la disminución se mantiene dentro de 51 TP3T, lo cual es aceptable. Estos resultados ponen de relieve la importancia de ajustar eficazmente los coeficientes de coste para equilibrar la riqueza de los resultados y las restricciones de coste, lo que subraya aún más el papel de nuestro agente de configuración a la hora de permitir un ajuste eficaz de la configuración para optimizar el rendimiento de CORAG.
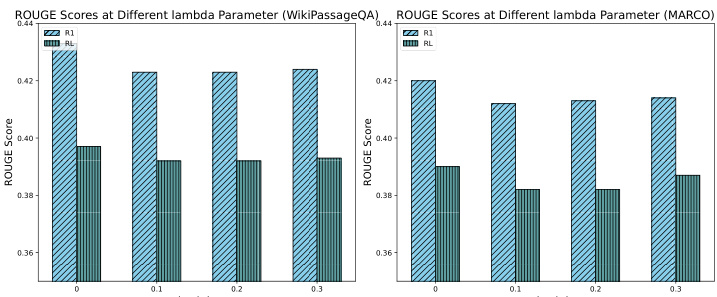
Figura 8: Comparación de ROUGE para distintos valores de lambda
6.3.4 Estudios de ablación con diferentes reordenadores
Para evaluar el impacto de los distintos reordenadores en el rendimiento de la recuperación, realizamos un estudio de ablación utilizando seis modelos de reordenadores ampliamente reconocidos: jina-reranker-v1-turbo-en, jina-reranker-v2-base-multilingüe, bge-reranker-v2-m3, bge-reranker-large y gte-multilingüe-reranker-base. reranker-large, bge-reranker-base y gte-multilingual-reranker-base. Estos reordenadores se evaluaron en el conjunto de datos MARCO utilizando el modelo llama3-8B configurado con un factor de coste fijo de 0,1, un factor de exploración de 2,4 y una restricción presupuestaria de 1024.
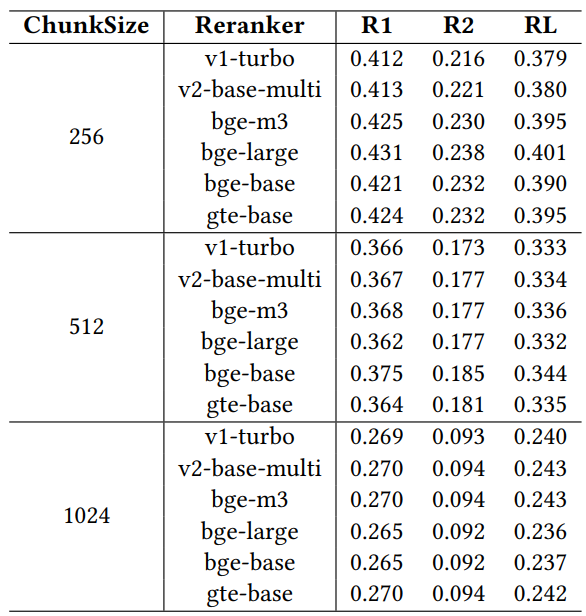
Tabla 4: Comparación del rendimiento con distintos reordenadores
Los resultados de la Tabla 4 muestran que existen diferencias de rendimiento entre los distintos reordenadores, lo que pone de relieve la importancia de seleccionar cuidadosamente los reordenadores para optimizar el rendimiento del sistema GAR bajo restricciones operativas específicas. Entre los reordenadores, gte-multilingual-reranker-base y bge-reranker-large muestran un rendimiento consistentemente alto en la tarea de GC, lo que sugiere que estos modelos de reordenación son muy eficientes a la hora de capturar información relevante para diferentes consultas de GC. Observamos que, a medida que aumenta el tamaño del bloque en el estudio de ablación, cada reordenador individual obtiene peores resultados que el agente en términos de reordenadores recomendados para diferentes consultas. Esto sugiere que el agente de configuración explota eficazmente la diversidad de reordenadores ajustando dinámicamente la configuración para mejorar los resultados de recuperación. La capacidad del agente de configuración para recomendar mejores opciones de reordenación y configuraciones de parámetros pone de relieve su papel a la hora de maximizar el rendimiento del sistema RAG, especialmente con restricciones como un presupuesto limitado.
6.4 Casos prácticos
La Figura 9 muestra tres ejemplos en los que se compara la calidad de recuperación de CORAG con la del método tradicional NaiveRAG, lo que pone de manifiesto por qué nuestro método supera al método de referencia. Debido a su simple búsqueda top-k y a su reordenación, NaiveRAG a menudo pasa por alto información importante para la intención de la consulta, ya que suele recuperar trozos basándose en la coincidencia de palabras clave y no en la relevancia de la consulta. Por ejemplo, para la consulta "¿Las flores de hojas son arbustos?" NaiveRAG recupera contenidos que contienen palabras clave coincidentes, pero no proporciona la clasificación real de la flor de hoja. En cambio, la estrategia de combinación de bloques de CORAG recupera un contexto que incluye la categoría de la flor de hoja, lo que permite a LLM dar una respuesta más precisa. En otro caso, NaiveRAG recuperó términos y cláusulas legales que incluían "oxifluorfeno", pero no comprendía la intención de la consulta, mientras que CORAG proporcionó contenido que relacionaba el oxifluorfeno con casos de uso en el algodón, lo que requería una búsqueda que la estrategia de búsqueda por similitud vectorial de NaiveRAG no podía captar. de NaiveRAG no podía captar las relaciones lógicas entre los bloques. Por último, para la consulta "¿De dónde vienen las bacterias?" NaiveRAG recupera los chunks que contienen la palabra clave "bacteria" pero no aborda su origen, mientras que CORAG proporciona una respuesta más completa, que incluye el origen de las bacterias y sus condiciones de reproducción. Estos casos ilustran que CORAG destaca en la recuperación de información conectada lógicamente, lo que lo hace más adecuado que NaiveRAG para consultas que requieren algo más que una simple coincidencia de palabras clave.

Figura 9: Estudio de caso CORAG
7 Perspectivas del GAR y futuras opciones de diseño
7.1 Deficiencias del actual GAR
Analizamos el actual sistema GAR y descubrimos los problemas de rendimiento a los que se enfrenta durante las fases de recuperación (S1), mejora (S2) y generación (S3).
S1: Gastos generales de búsqueda Los sistemas GAR actuales suelen utilizar LLM para las estructuras de resumen e indexación, ignorando los costes computacionales asociados a los LLM externos, lo que aumenta la sobrecarga computacional. Los reordenadores basados en modelos, aunque mejoran la pertinencia durante la recuperación, introducen una latencia significativa, que puede obstaculizar la eficacia contextual sensible a la latencia. La construcción de índices rentables y la optimización de la reordenación son esenciales para equilibrar la eficiencia y el rendimiento.
S2: Aumento de los gastos generales Las técnicas posteriores a la recuperación, como la ordenación optimizada de combinaciones de bloques, mejoran la relevancia contextual, pero requieren cálculos adicionales. Las estrategias de poda que minimizan el espacio de búsqueda y optimizan el orden de las combinaciones son esenciales para equilibrar el coste computacional y mejorar la relevancia contextual. Una optimización eficaz de las combinaciones de bloques que haga hincapié en el orden y la coherencia es esencial para reducir los costes y mejorar el rendimiento de la recuperación.
S3: Gastos generales de generación La ingeniería eficiente de sugerencias para combinaciones óptimas de bloques requiere importantes recursos informáticos. El perfeccionamiento y la compresión de sugerencias específicas para cada consulta son esenciales para reducir los gastos generales y mantener al mismo tiempo la pertinencia y la concisión de los datos de entrada. Las estrategias adaptativas para tratar distintos tipos de consultas y requisitos específicos del dominio garantizan la eficacia de las sugerencias sin comprometer la calidad del resultado.
7.2 Opciones de diseño
Para hacer frente a estos retos, las siguientes opciones de diseño pretenden optimizar el rendimiento del sistema GAR:
P1: Co-diseño de los procesos de recuperación y reordenación En CORAG, la extensión paralela en la búsqueda en árbol acelera el procesamiento de las consultas y reduce significativamente la latencia al permitir la recuperación y reordenación concurrentes. Futuras optimizaciones pueden abordar el cuello de botella eliminando los retrasos específicos de cada etapa y mejorando aún más la eficacia de la clasificación. Este enfoque de codiseño gestiona eficazmente el orden de combinación de bloques para mejorar el proceso de clasificación y la puntuación asociada.
P2: Optimización de estructuras de árbol e iteraciones de búsqueda Los resultados demuestran que las estrategias con árboles de menor altura mejoran la eficiencia de la búsqueda al reducir los gastos generales de cálculo, lo que resulta especialmente beneficioso en el caso de grandes conjuntos de datos. Minimizar la altura del árbol en la búsqueda basada en árboles mejora la velocidad de búsqueda de bloques contextualmente relevantes, reduciendo significativamente la latencia y el coste computacional. Este enfoque de optimización mejora el rendimiento del sistema RAG en conjuntos de datos a gran escala.
P3: Proyecto Punta Dinámica La selección del reordenador en función del tipo de consulta y el uso de plantillas de sugerencias adaptativas pueden mejorar la relevancia de la recuperación de LLM. Las estructuras de pistas dinámicas alineadas con la intención de la consulta y el contexto específico del dominio pueden mantener la calidad del resultado dentro de las limitaciones de recursos. Este enfoque de ingeniería de pistas adaptativas logra un equilibrio eficaz entre la eficiencia y la calidad de la recuperación, abordando la naturaleza dinámica de las consultas en los sistemas GAR.
8 Conclusiones
Teniendo en cuenta la no monotonicidad de la utilidad de los bloques, la correlación entre bloques y la diversidad de dominios de consulta, proponemos CORAG, un sistema de optimización de la recuperación basado en el aprendizaje. Introducimos un agente de configuración que predice con precisión la configuración y el reordenador óptimos para una consulta determinada. Además, ideamos una estrategia paralela de expansión de consultas para expandir múltiples nodos en cada iteración. Los resultados experimentales demuestran que nuestro método supera con creces a los métodos más avanzados en cuanto a costes y eficiencia.
© declaración de copyright
Derechos de autor del artículo Círculo de intercambio de inteligencia artificial Todos, por favor no reproducir sin permiso.
Artículos relacionados

Sin comentarios...




