I read an interesting paper today called "TheLarge Language Models as Analogical Reasoners A new method of Prompting is mentioned - "Analogical Prompting.
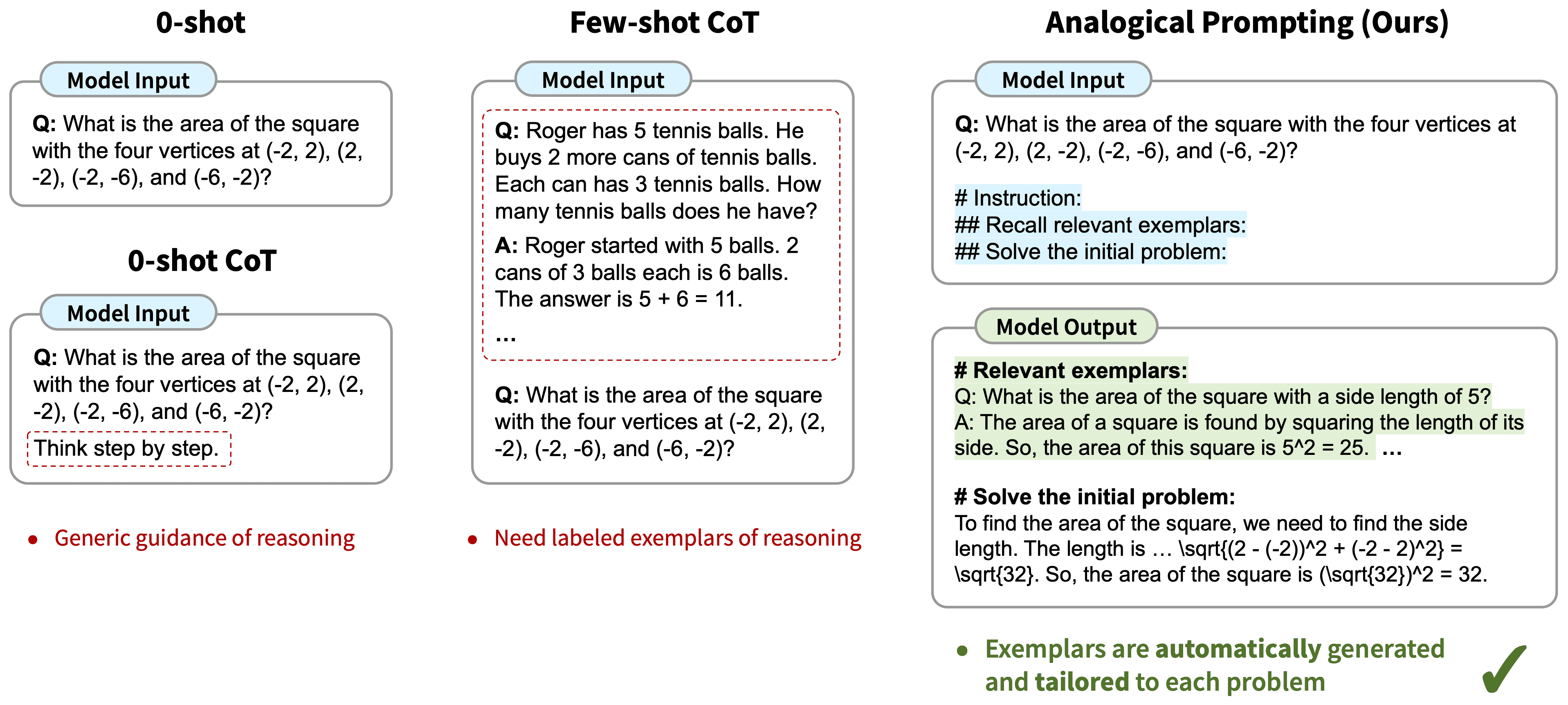
If you are familiar with cue engineering, you must have heard of CoT (Chain of Thought), which can significantly improve the reasoning ability of Large Language Models (LLMs). However, when using CoT, we need to provide relevant guidance or reasoning examples to guide the model.
The two commonly used CoT methods are: "0-shot CoT" and "few-shot CoT". 0-shot CoT is to explicitly give the inference steps in the Prompt and let the LLM refer to the steps to complete the inference. 0-shot CoT is to give the reasoning steps explicitly in the Prompt and let the LLM refer to the steps to complete the reasoning. few-shot CoT is to give a small number of examples and let the LLM refer to the examples to complete the reasoning.
Comparison of three cueing methods
For example, there is now a math problem: "There is a square whose four vertices are (-2, 2), (2, -2), (-2, -6) and (-6, -2), find what is the area of this square? "
If you don't use CoT, then you are just throwing the problem at the LLM and letting it come up with the answer. This problem should be solvable for GPT-4, but is likely to be wrong for GPT-3.5, and even more so for other models with weaker reasoning.
If you use 0-shot CoT, then it's a matter of giving the inference steps explicitly inside the Prompt, for example:
Please follow the steps below to calculate:
1, first calculate the distance between any two neighboring vertices as the length of the side of the square
2、Calculate the square of the side length to get the square area
Following these steps should yield correct results for an LLM with a GPT of 3.5.
If you use few-shot CoT, then it is giving a small number of examples, for example:
Q: Here is a square whose four vertices are (0, 0), (1, 1), (0, 1), and (1, 0).What is the area of this square?
A: We choose two neighboring vertices from it, say (0, 0) and (1, 1), compute their distances to get an edge length of 1, and then compute the square of the edge length to get an area of 1.
Q: There is a square whose four vertices are (-2, 2), (2, -2), (-2, -6), and (-6, -2).What is the area of the square?
We explicitly give an example in the Prompt, telling the LLM to follow the steps in the example, so that it should also give the correct result for an LLM like GPT-3.5.
So what is "analogical cueing"?
Think about when we learn math in school, if we do a math problem like this, we will think about whether we have ever done a similar problem, especially for a small town doer like me, I don't know how many papers I did back then, and when I see the problem at the back, I can remember that I have done a similar problem before, and then I can come up with the answer very quickly.
For LLM, its knowledge reserve is stronger than that of human beings, and it has accumulated all kinds of knowledge and cases during training, so what we need to do is to "stimulate" LLM to find out the knowledge and cases related to the problem, and then use them to reason and solve the problem.
So the "analogical hint method" is to let the LLM not rush to solve the problem, but first list a number of examples related to the problem, and then use these examples to reason to solve the problem. This is equivalent to letting the LLM help you to write a few-shot, to help you generate a chain of thought.
It's similar to when you get a math problem and have it first follow that math problem to find similar examples and reference answers, and then have it follow those examples and reference answers to solve the original problem.
The structure of Prompt is as follows:
Initial question: \
Related Problems: Think back to three related and unique problems and describe each problem and its solution.
Solve the initial problem:
Have the LLM, upon receiving the problem, recall three related and unique problems and list each problem and solution (preferably with steps), and be sure to print out the intermediate processes. When the LLM has finished outputting these relevant examples, print out the original problem again (to prevent forgetfulness), so that the LLM can use these relevant examples to reason about the original problem.
A complete reference to Prompt using analogous hinting:
Your task is to solve math problems. When presented with a math problem, recall some related topics as examples. Then, go back and solve the very first one.
# The very first question:
One airline provides dinner for every passenger on the plane, and passengers can choose either steak or fish. Three of the six crew members can choose steak and three can choose fish. If the food is randomly assigned, what is the probability that both pilots get the fish?
# Operating Guide:
The following points must be included in your answer:
## Related Questions:
Think of three math problems related to the very first problem as examples. Note that each problem should be different from the others, including from the very first problem (e.g., involving different numbers and names). Each problem should follow the format below:
- "Q:" followed by a description of the problem
- "A:" Followed by the solution to the problem and write the final answer in \boxed.
## Solve the problem at the very beginning:
Say, "Let's solve the following math problem." Then answer in the following format:
Q: Copy and paste the very first question here.
A: Explain the solution and write the final answer in \boxed.
LLM will output the following:
## Related Questions:
### Question 1:
- **Q:** At a party, everyone has the choice of eating either apple pie or vanilla ice cream. Five of the ladies have the choice of apple pie and five of the ladies have the choice of vanilla ice cream. If the desserts are randomly assigned, what is the probability that both ladies get vanilla ice cream?
- **A:** Use combinatorial computation to solve this problem. The total way is to choose two out of five ladies who can choose ice cream, which is \( \binom{5}{2} = 10 \) ways. And the total distribution is to choose two out of ten ladies, which is \( \binom{10}{2} = 45 \) ways. So the probability is \( \frac{10}{45} = \frac{2}{9} \). The final answer is \( \boxed{\frac{2}{9}} \).
### Question 2:
- **Q:** At a dinner party, each person has a choice of red or white wine. There are four men who can choose red wine and four men who can choose white wine. If the wines are randomly assigned, what is the probability that all three men will get white wine?
- **A:** Using a similar method, three men are chosen from the four men who have a choice of white wine in \( \binom{4}{3} = 4 \) ways. And the total distribution is made by choosing three out of eight men, i.e. \( \binom{8}{3} = 56 \) ways. So the probability is \( \frac{4}{56} = \frac{1}{14} \). The final answer is \( \boxed{\frac{1}{14}} \).
### Question 3:
- **Q:** In the café, each person can choose either a latte or a cappuccino. Three customers can choose a latte and three customers can choose a cappuccino. If the coffees are randomly assigned, what is the probability that one customer will get a cappuccino?
- **A:** In this case, there are \( \binom{3}{1} = 3 \) ways of choosing one customer who can have a cappuccino. The total allocation is to choose one customer from six, i.e. \( \binom{6}{1} = 6 \) ways. So the probability is \( \frac{3}{6} = \frac{1}{2} \). The final answer is \( \boxed{\frac{1}{2}} \).
## Let's solve the following math problem.
### Q: An airline provides dinner for every passenger on an airplane, who can choose either steak or fish. Three of the six crew members can choose steak and three can choose fish. If the food is randomly assigned, what is the probability that both pilots get the fish?
### A: We can use a similar solution for this problem. We have three pilots who can choose the fish, and we want to choose two of them. This is done in \( \binom{3}{2} = 3 \) ways. The total distribution is two from six pilots, which is \( \binom{6}{2} = 15 \) ways. So the probability is \( \frac{3}{15} = \frac{1}{5} \). The final answer is \( \boxed{\frac{1}{5}} \).
