Goedel-Prover-V2 - Princeton's open-source theorem proving model in conjunction with Tsinghua and NVIDIA, among others

What is Goedel-Prover-V2?

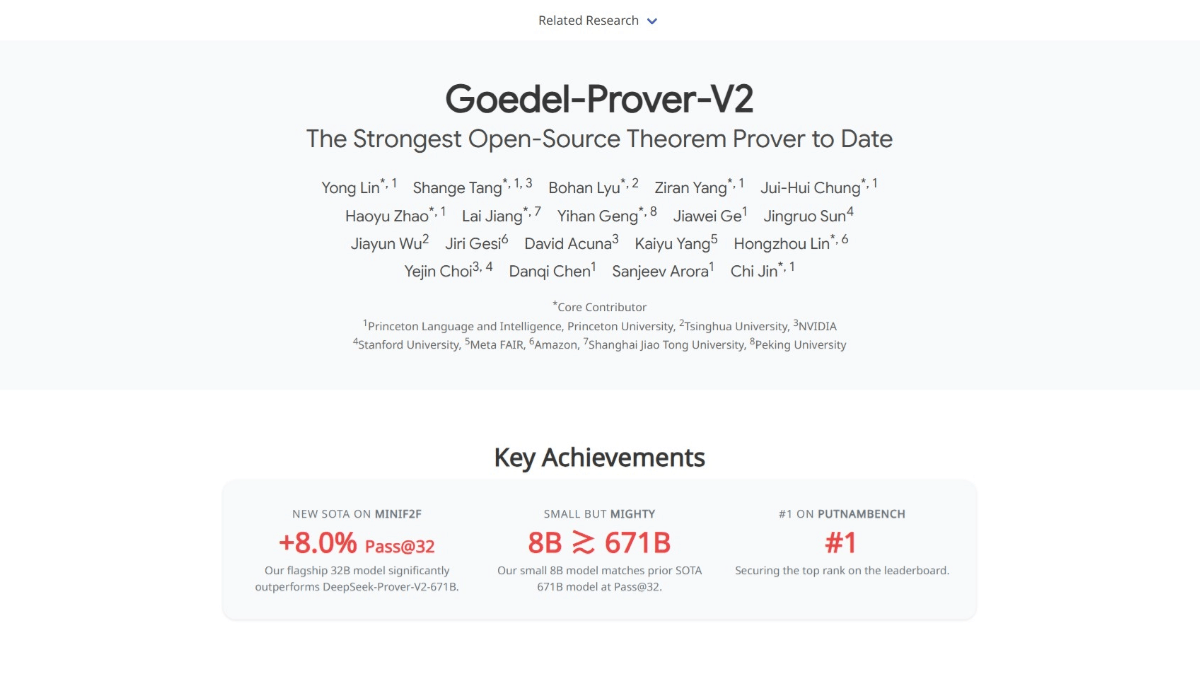
Goedel-Prover-V2 is an open-source theorem proving model from leading organizations such as Princeton University, Tsinghua University, and NVIDIA. The model is based on innovative techniques such as hierarchical data synthesis, verifier-guided self-correction, and model averaging to significantly improve the performance of automated formal proofs.The Goedel-Prover-V2 model is available in two versions, 32B and 8B, and the model excels in several benchmarks, such as the MiniF2F test, where the 32B model scores up to 90.41 TP3T for Pass@32, outperforming the much larger DeepSeek-Prover. For example, in the MiniF2F test, the 32B model achieved a Pass@32 score of 90.4%, outperforming the much larger DeepSeek-Prover-V2. The model is able to automatically generate proofs for complex mathematical problems, and self-corrects itself based on feedback from the Lean compiler, improving the quality of the proofs.

Main features of Goedel-Prover-V2

• Automatic generation of certificates: Generate formal proof processes for complex mathematical problems to help solve complex mathematical puzzles.
• Capacity for self-correction: With feedback from the Lean compiler, the model can iteratively revise its proofs to improve their accuracy and quality.
• Efficient training and optimization: Based on hierarchical data synthesis and model averaging techniques, it improves training efficiency and enhances model performance, enabling it to excel in multiple benchmark tests.
• Open Source and Scalability: Provide open source models and datasets to facilitate further development and improvement by researchers.

Performance of the Goedel-Prover-V2

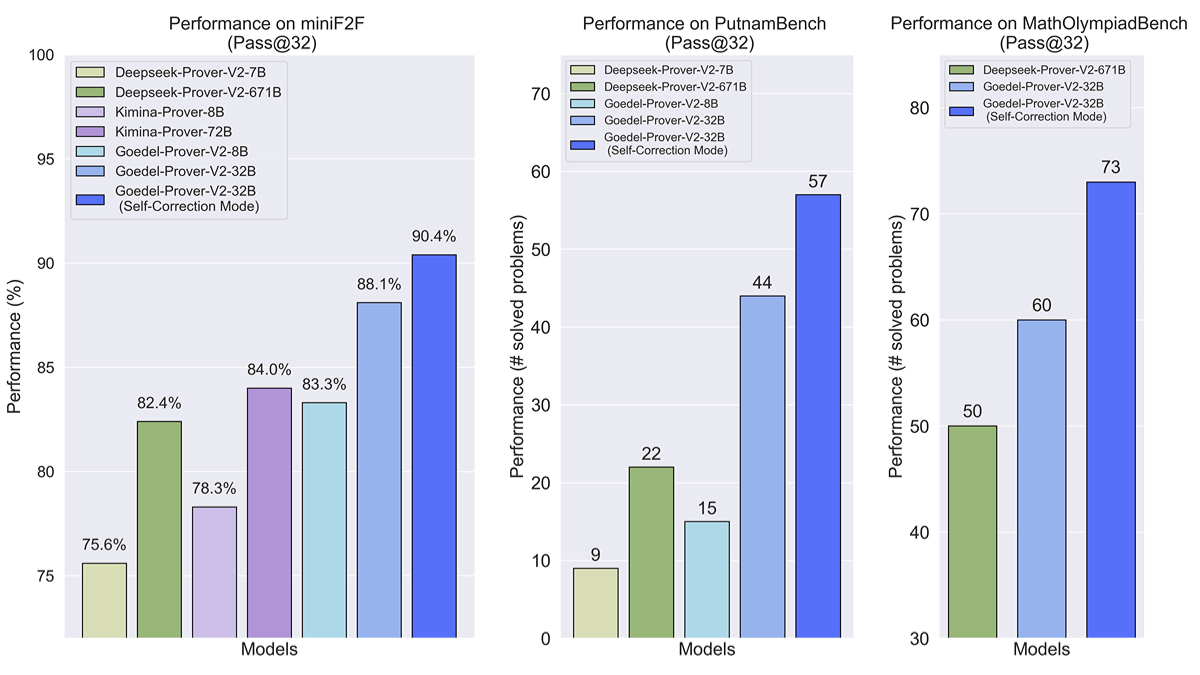
• MiniF2F Benchmark::
  • The Pass@32 score for the 32B model is as high as 90.41 TP3T, which is significantly ahead of DeepSeek-Prover-V2 (82.41 TP3T) for the 671B.
  • The 8B model achieves a Pass@32 score of 83.3%, which is a comparable performance despite the number of parameters being only about 1/100 of DeepSeek-Prover-V2.
• PutnamBench Benchmarks::
  • The 32B model tops the Pass@64 metrics, solving 64 problems.
  • On the Pass@32 metric, the 32B model solves 57 problems, significantly outperforming DeepSeek-Prover-V2-671B with 47 problems.
  • The 8B model also performed very well and was comparable to DeepSeek-Prover-V2-671B.
• MathOlympiadBench Benchmarking::
  • The 32B model solves 73 problems, significantly outperforming DeepSeek-Prover-V2-671B with 50 problems.
  • The 8B model also performs well, approaching the level of the 32B model, showing strong theorem proving ability.

Goedel-Prover-V2 official website address

• Project website:: https://blog.goedel-prover.com/
• HuggingFace Model Library::
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-8B
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-32B

How to use Goedel-Prover-V2

• Access to project resources: Access the HuggingFace model library, download the model files from HuggingFace, and select the appropriate version (e.g., 8B or 32B).
• hardware requirement: High-performance GPUs or GPU clusters are recommended.
• software environment: Install Python and deep learning frameworks such as PyTorch to ensure that the environment supports large model inference.
• Input Issues: Convert mathematical problems requiring proofs into a format supported by the model (e.g., the Lean language).
• Data preprocessing: Coding and formatting questions according to model requirements.
• Loading Models: Load the pre-trained model with the tools provided by HuggingFace.
• Proof of generation: The problem is fed into the model, which automatically generates proofs and verifies and corrects them with the Lean compiler.
• verification certificate: Check that the generated proofs are correct with the Lean compiler.
• Iterative correction: If the proof is incorrect, the model self-corrects based on feedback until the correct proof is generated.

Core benefits of Goedel-Prover-V2

• Excellent performance: Goedel-Prover-V2 performs well in several benchmarks, for example, the 32B model achieves an accuracy of 90.4% in MiniF2F's Pass@32 test, which is significantly ahead of other similar models.
• Innovative technical architecture: Hierarchical data synthesis, validator-guided self-correction and model averaging techniques based on hierarchical data synthesis, effectively improving the efficiency of model training and the quality of proofs.
• Open Source and Scalability: Provide open-source models and datasets that can be freely accessed, used and further developed by researchers for improvement.
• Wide range of application scenarios: Applicable to a wide range of fields such as math research, software and hardware validation, educational assistance, artificial intelligence and machine learning, and scientific research and engineering.
• Efficient training and optimization: Efficient training and performance optimization for enhanced model robustness based on hierarchical data synthesis and model averaging techniques.

People for whom Goedel-Prover-V2 is indicated

• Mathematicians and mathematical researchers: Used in verifying mathematical conjectures, generating proofs for complex problems, and accelerating the exploration and study of mathematical theories.
• Computer scientists and software engineers: Used in software and hardware development to verify the correctness of algorithms, program logic, and circuit design, and to enhance system reliability and safety.
• artificial intelligence researcher: Validate the mathematical foundations and algorithmic logic of machine learning models to ensure model reliability and accuracy.
• Educators and students: To serve as an aid to mathematics education, helping students to better understand and master mathematical concepts and theorems by providing examples of formal proofs.
• Researchers and engineers: In scientific research and engineering design, verify mathematical models and theories to ensure the feasibility and reliability of design solutions.