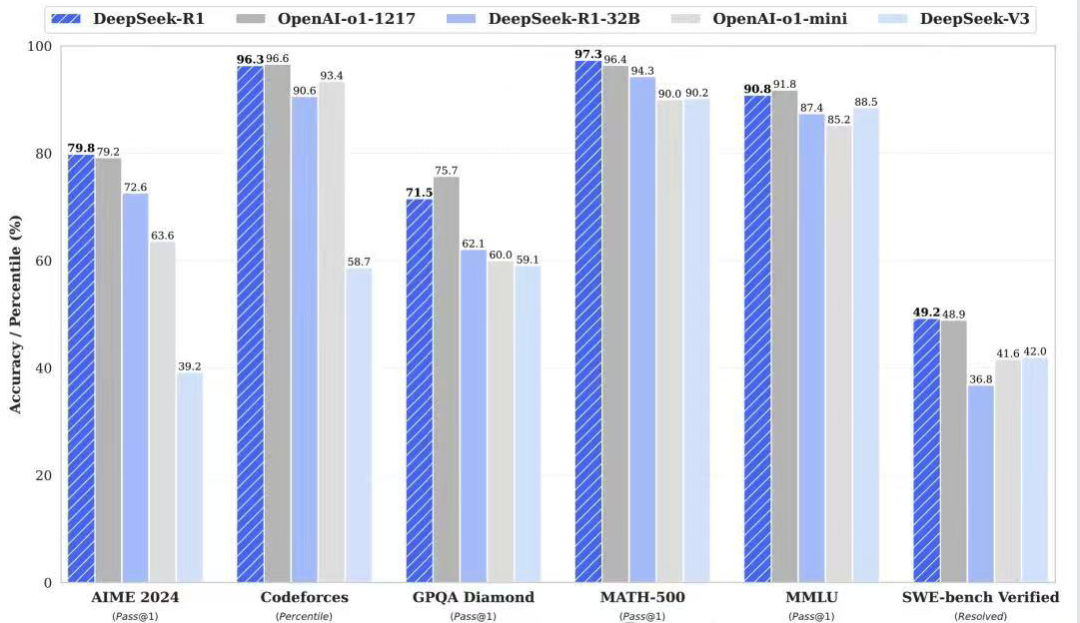
Die aktualisierte Claude 3.5 Sonnet Chinese Benchmark Auswertung ist da! Code-Fähigkeit übertrifft GPT-4o, logisches Denken höherer Ordnung ist nicht so gut wie o1

Die Ergebnisse dieser Bewertung werden ausschließlich für die akademische Forschung verwendet.

Am 22. Oktober stellte Anthropic offiziell das aktualisierte große Modell Claude 3.5 Sonnet sowie das neue Modell Claude 3.5 Haiku vor.

Claude

Nach Angaben von Anthropic übertrifft Claude 3.5 Sonnet die Vorgängerversion in jeder Hinsicht, insbesondere bei der Codierung von intelligenten Körpern und bei der Verwendung von Werkzeugen wurden erhebliche Leistungssteigerungen erzielt.Im SWE-Bench Verified verbessert sich die Codierleistung von 33,41 TP3T auf 49,01 TP3T und übertrifft damit alle öffentlich verfügbaren Modelle, einschließlich OpenAI o1-preview.

Anthropic führt auch eine bahnbrechende neue Funktion ein: die Computernutzung. Entwickler können Claude über eine API so steuern, dass er den Computer auf dieselbe Weise wie ein Mensch benutzt, aber diese Funktion befindet sich derzeit noch im Versuchsstadium.

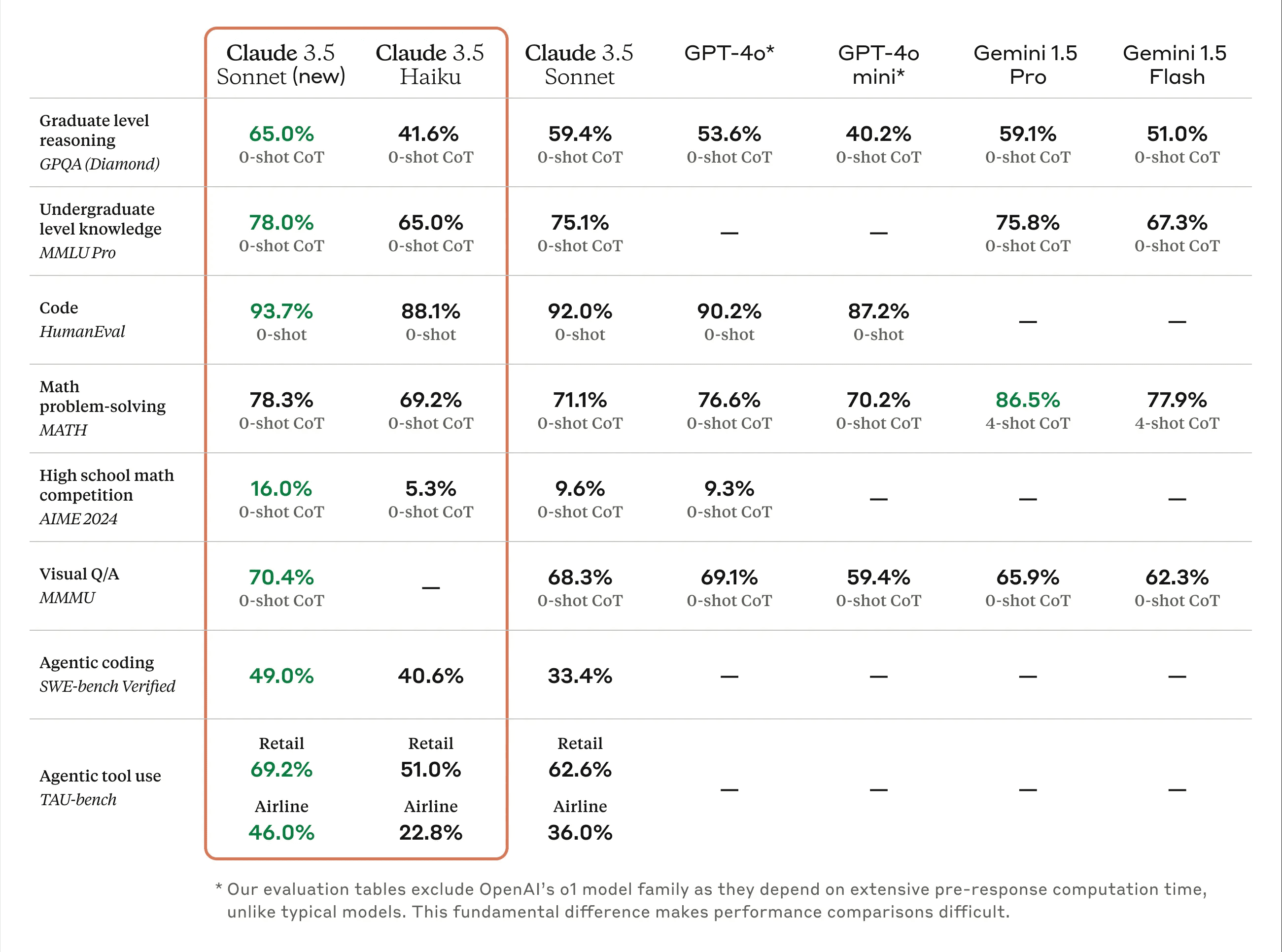
Als Reaktion auf die öffentliche Besorgnis über die Leistung des Claude 3.5 Sonnet-Upgrades in Bezug auf Argumentation und Code in chinesischen Szenarien hat SuperCLUE, ein professionelles externes Bewertungsunternehmen, eine eingehende Bewertung des Claude 3.5 Sonnet-Upgrades durchgeführt.

Bewertungsumfeld

Referenzstandards: SuperCLUE-Reasoning Chinese Higher Order Reasoning Assessment Benchmark, SuperCLUE-Code3 Chinese Code Assessment Benchmark.

Bewertungsmodelle Claude 3.5 Sonnet (1022, POE letztes Modell Snapshot)

Modell GenerationConfig-Konfiguration:

• Siehe das Dokument Claude Detailed Instructions: https://www.anthropic.com/news/3-5-models-and-computer-use

Rückblick auf die Episode:

1. SuperCLUE-Reasoning Chinese Complex Tasks Higher Order Reasoning Review Set. Insgesamt 302 Fragen, darunter mehrstufiges Denken, numerisches Denken, logische Berechnungen, Marktanalyse und Optimierungsprobleme - fünf schwierige logische Aufgaben.

2.SuperCLUE-Code3 Chinese native code evaluation set.HumanEval's Chinese upgraded version, insgesamt 195 Fragen, darunter 1.560 Testfälle, unterteilt in primären, mittleren und fortgeschrittenen drei Kategorien von Schwierigkeitsgrad.

Methodik::

1. übergeordnete Argumentation: Für jede Argumentationsfrage stellen wir Referenzantworten und Argumentationsprozesse nach manueller Kalibrierung und Überprüfung bereit; dann bewertet das Schiedsrichtermodell die Antworten der Kandidatenmodelle gemäß dem festgelegten Bewertungsprozess, den Bewertungskriterien und den Bewertungsregeln (1-5 Punkte). Zu den festgelegten Bewertungskriterien gehören: Einhaltung der Grundanforderungen, Genauigkeit der Argumentation und Angemessenheit der Schlussfolgerungen.

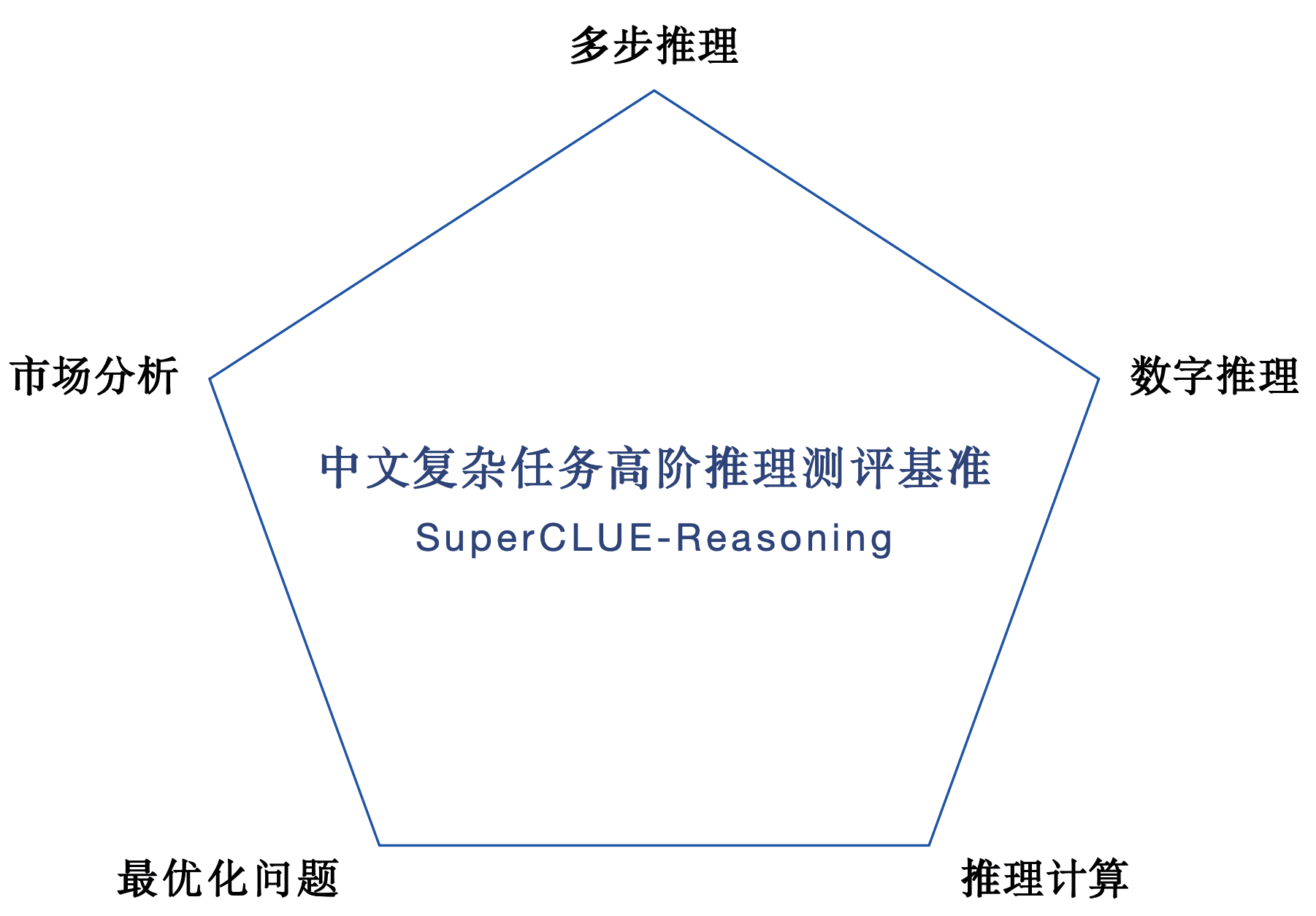
2) Code SC-Code3: speziell entwickelt, um die Kernfunktionen des Chinese Big Model bei der Codegenerierung durch funktionale Einheitstests zu bewerten und zu verbessern.

SuperCLUE-Code3: Benchmarks für die Code-Kenntnisse chinesischer Muttersprachler

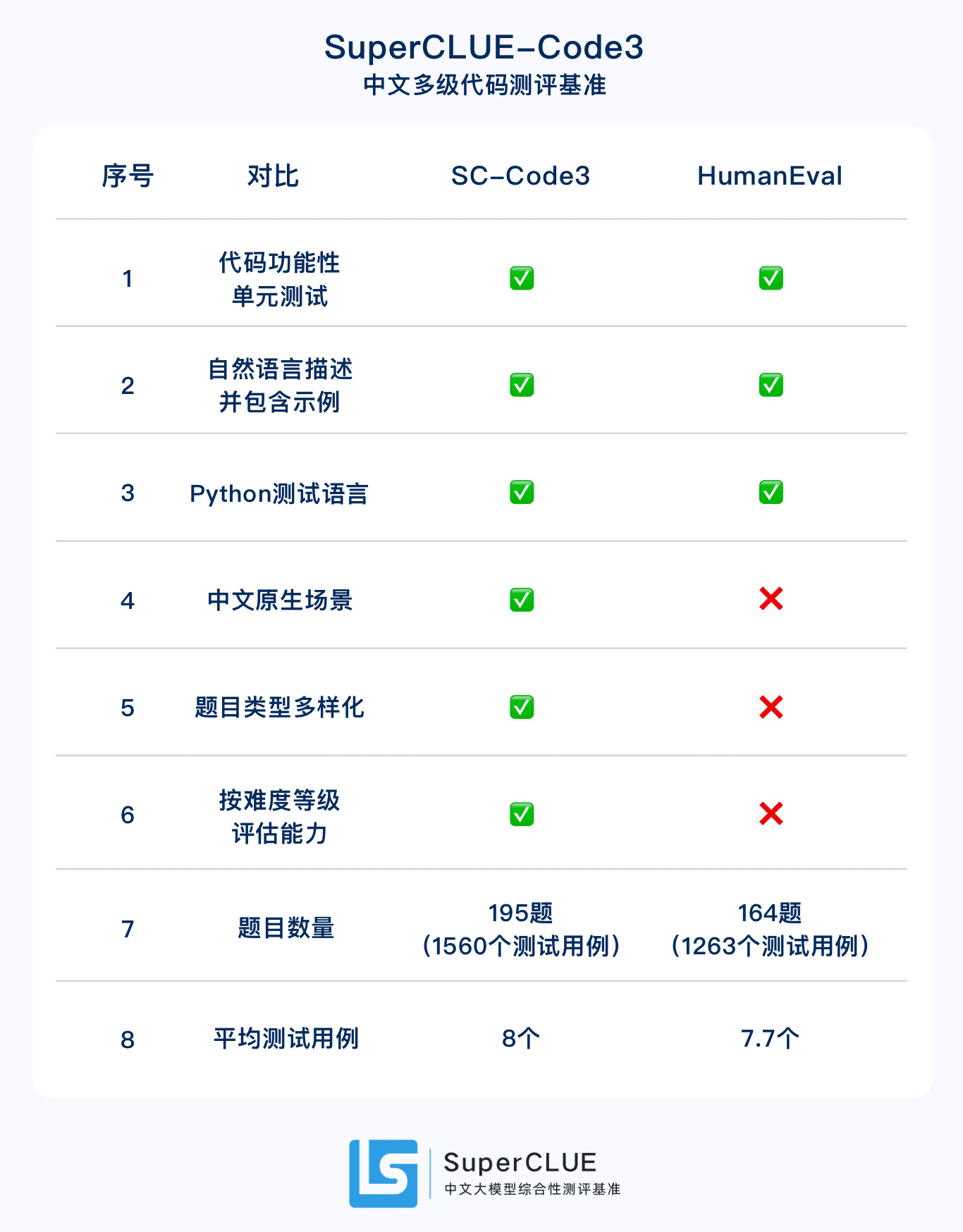
Beginnen wir mit den Schlussfolgerungen

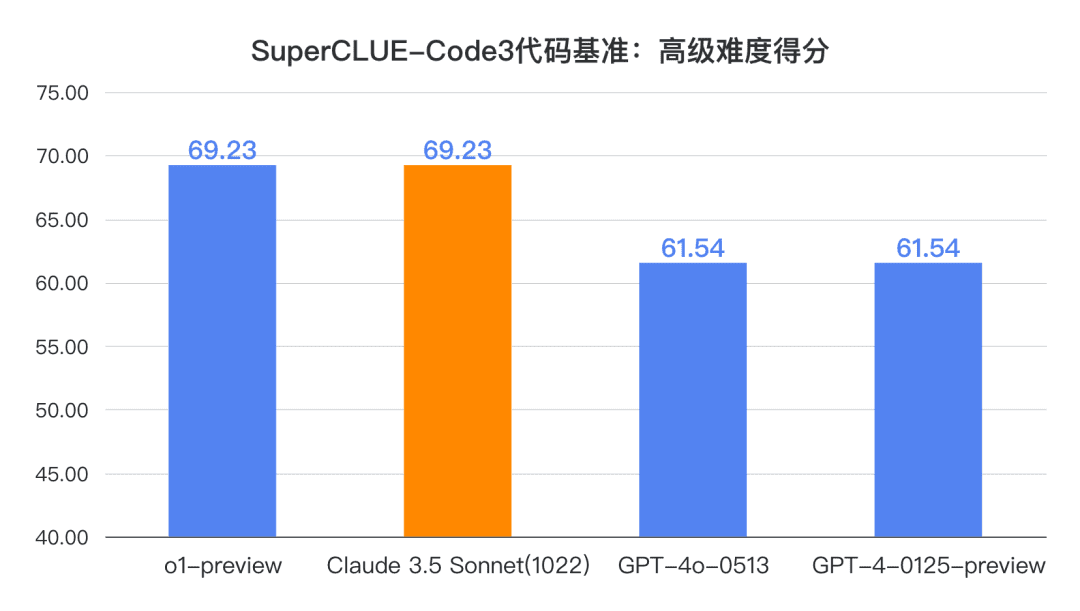
Schlussfolgerung 1: Claude 3.5 Sonnet (1022) schneidet in Bezug auf die chinesische Codefähigkeit (SC-Code3) gut ab. Die Gesamtpunktzahl erreichte 84,85, 1,52 Punkte mehr als GPT-4o-0513 das sind 4,54 Punkte weniger als o1-preview. Vor allem bei den fortgeschrittenen Code-Aufgaben schnitt es mit 69,23 Punkten erstaunlich gut ab und lag damit gleichauf mit o1-preview.

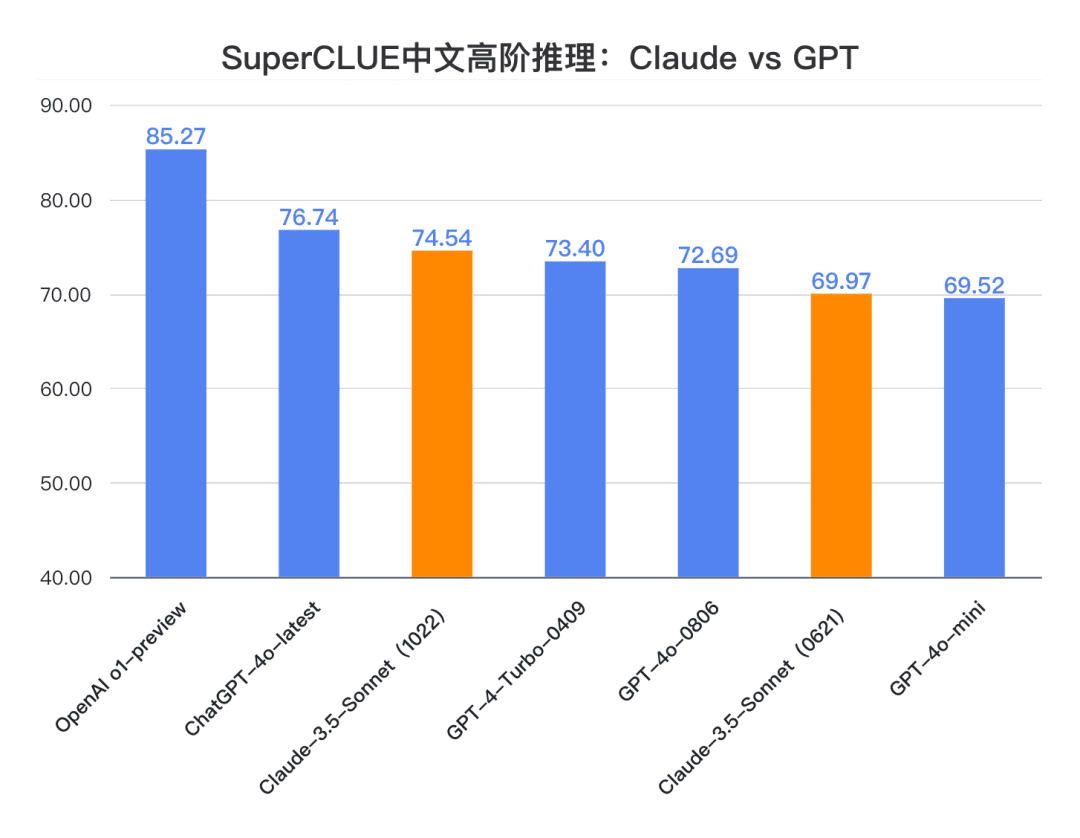
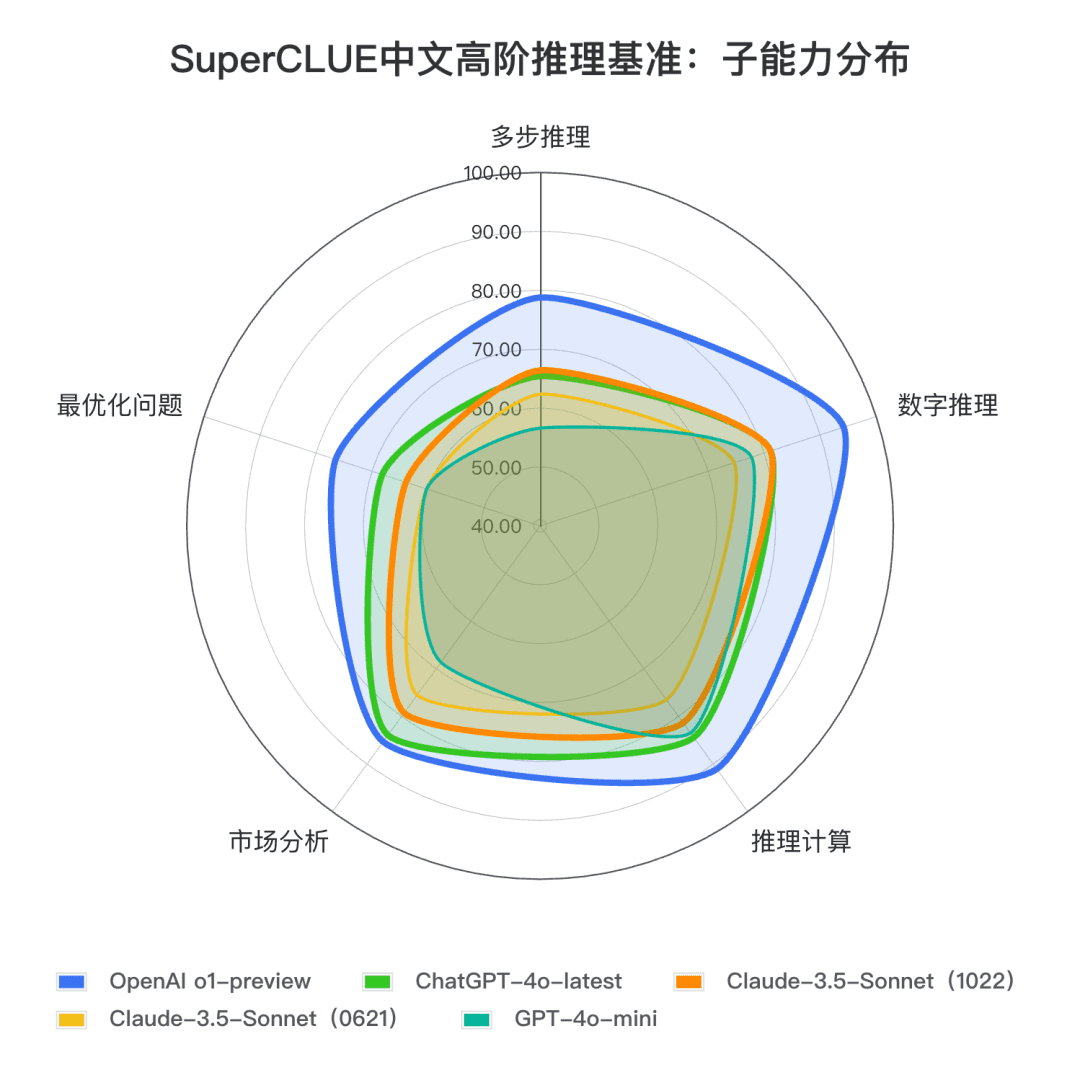
Schlussfolgerung 2: Claude 3.5 Sonnet (1022) erzielte 74,54 Punkte bei der chinesischen Aufgabe zum logischen Denken höherer Ordnung. Nahe an ChatGPT-4o-latest, mit einem großen Abstand zu o1-preview (-10,73 Punkte) . Unter ihnen ist die mehrstufige Argumentation Fähigkeit relativ hervorragend, mit einer Leistung, die die ChatGPT-4o-latest.

**Schlussfolgerung 3:** Im Vergleich zur vorherigen Version Claude 3.5 Sonnet (0621). Claude 3.5 Sonnet (1022) verbesserte sich um 4,57 Punkte bei der Argumentationsaufgabe und signifikante Fortschritte bei sekundären Aufgaben, wie z. B. Zahlenverständnis und rechnerisches Denken.

Ergebnisse der Bewertung

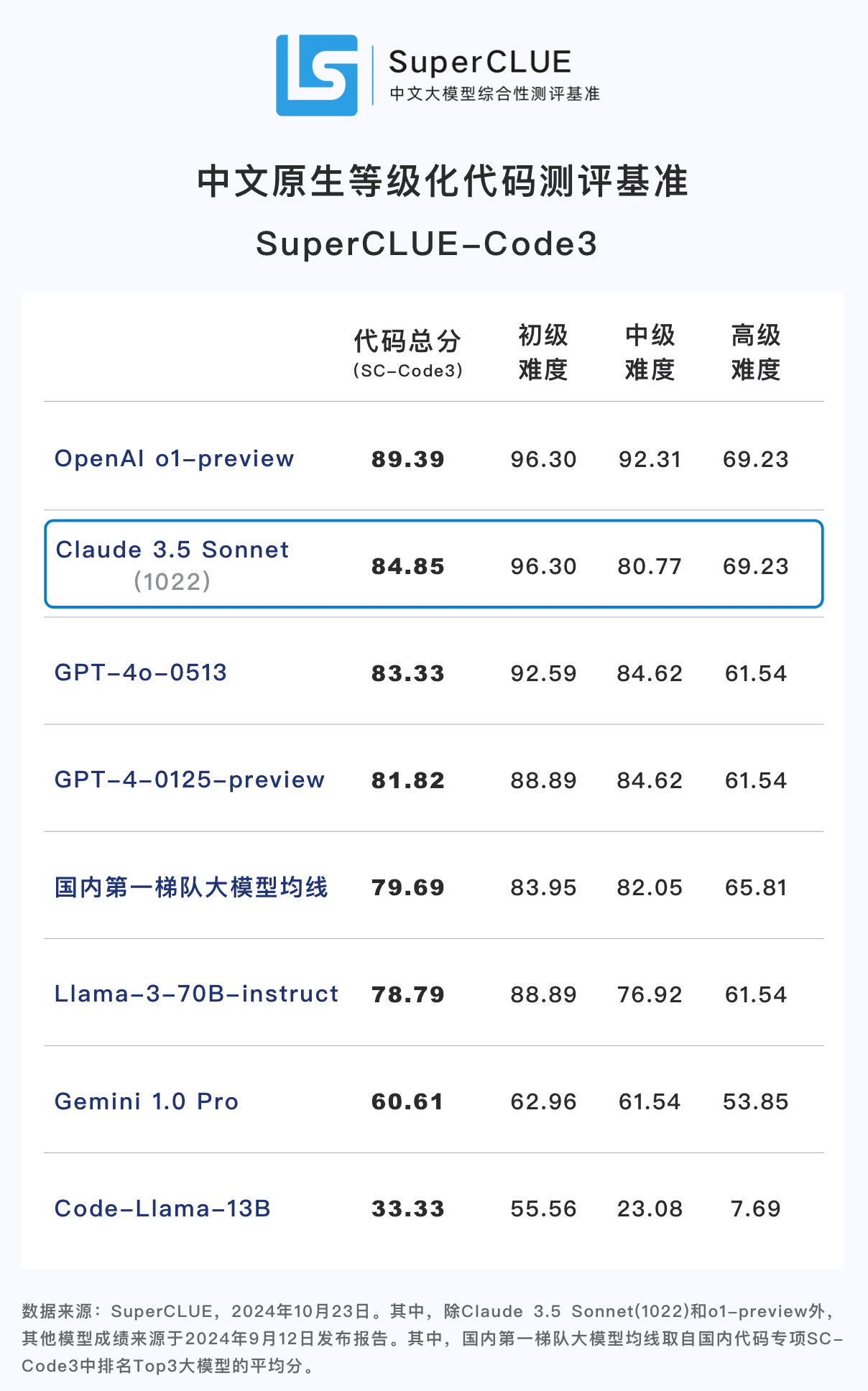
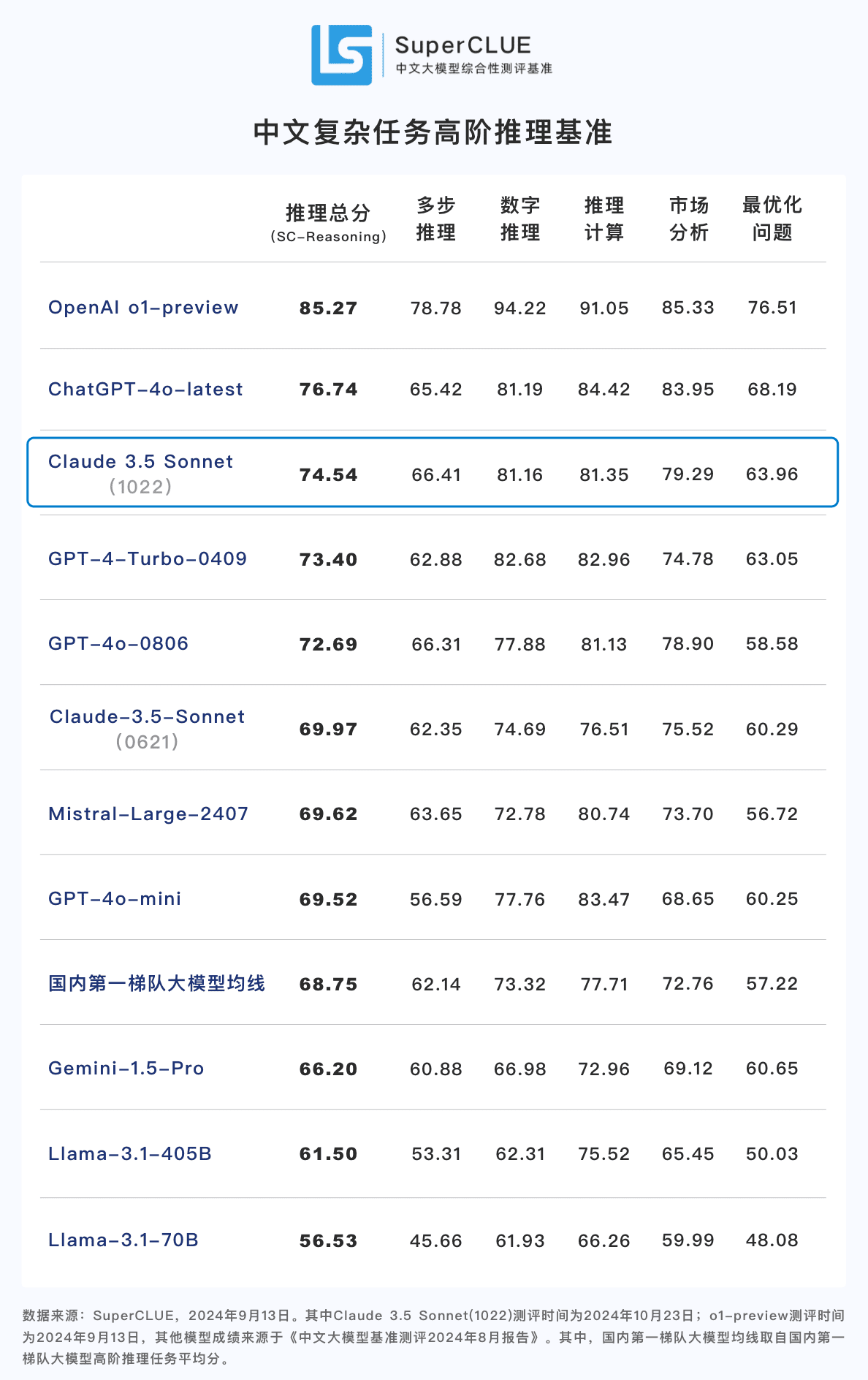
vergleichende Analyse

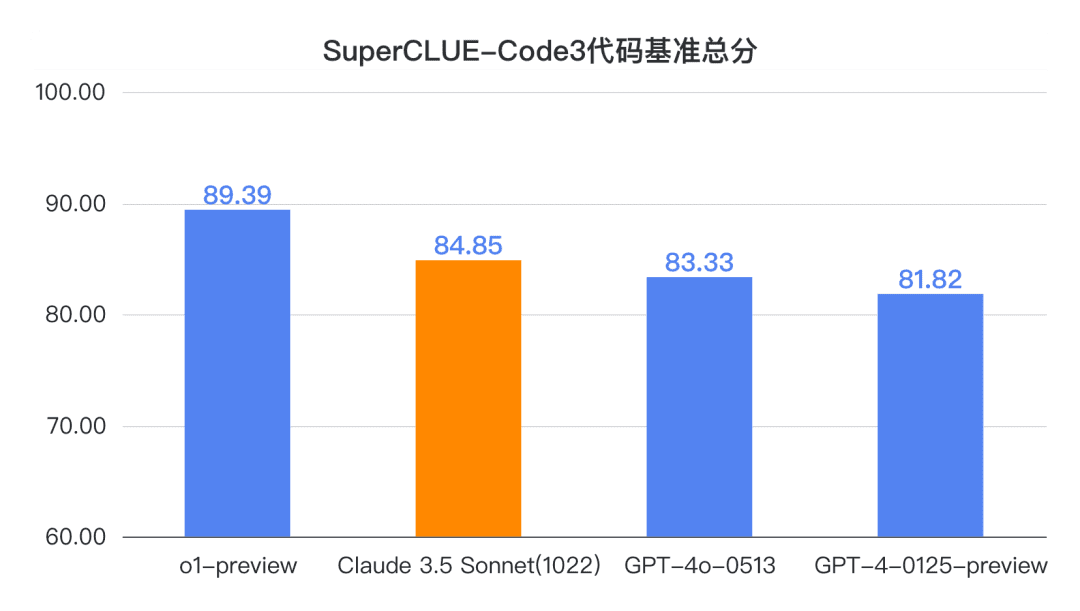
Beispiel für eine Code-Messung

Beispiel 1

Aufforderung.

from typing import List

def longest_peak_sequence(nums: List[int]) -> int:
    """
    在一个整数数组中找出最长的"峰"序列的长度。
    所谓"峰"序列，是指先严格递增然后严格递减的序列，且峰顶（即最大值）唯一。
    至少包括三个数以上才能构成一个"峰"序列（即包含递增和递减的部分）。

    返回数组中最长"峰"序列的长度。如果没有"峰"序列，则返回0。

    示例:
    >>> longest_peak_sequence([2, 1, 4, 7, 3, 2, 5])
    5  # 最长的"峰"序列是 [1, 4, 7, 3, 2]

    >>> longest_peak_sequence([5, 4, 3, 2, 1])
    0  # 不存在"峰"序列，因为没有严格递增的部分

    提示:
    - 数组 `nums` 的长度范围为 [0, 10000]。
    - 数组中的每个元素范围为 [-10000, 10000]。
    """

Claude 3.5 Sonett (1022) Antwort.

from typing import List

def longest_peak_sequence(nums: List[int]) -> int:
    if len(nums) < 3:
        return 0

    max_length = 0

    # 从第二个元素遍历到倒数第二个元素
    for i in range(1, len(nums) - 1):
        # 检查当前位置是否是峰顶
        if nums[i] > nums[i-1] and nums[i] > nums[i+1]:
            # 找到一个峰顶，向两边扩展
            left = i - 1
            right = i + 1

            # 向左扩展，寻找严格递增序列
            while left > 0 and nums[left-1] < nums[left]:
                left -= 1

            # 向右扩展，寻找严格递减序列
            while right < len(nums) - 1 and nums[right+1] < nums[right]:
                right += 1

            # 更新最长峰序列长度
            current_length = right - left + 1
            max_length = max(max_length, current_length)

    return max_length

Testfall.

def check(candidate):
    assert candidate( [1, 2, 3, 4, 5, 6])==0
    assert candidate([1, 3, 5, 6, 4, 2, 0])==7
    assert candidate( [5, 4, 3, 2, 1, 2, 3, 4, 1])==5
    assert candidate([1, 3, 5, 3, 1])==5
    assert candidate([1, 2, 3, 3, 2, 1])==0
    assert candidate([2, 1, 3, 1, 2, 1, 3])==3
    assert candidate([1, 3, 5, 4, 3, 2, 1])==7

wenn_bestanden**(Angenommen oder nicht):**Verabschiedet.

Beispiel 2

Aufforderung.

from typing import List

def longest_increasing_path(matrix: List[List[int]]) -> int:
    """
    给定一个整数矩阵，找到最长严格递增路径的长度。
    路径被定义为从矩阵中的任意单元格开始，每次可以向上、下、左、右移动到相邻的单元格上，如果递增的话。
    你不能在路径中移动到矩阵外面，也不能移动到不满足递增条件的单元格上。
    路径的长度是路径上的单元格总数。

    示例:
    >>> longest_increasing_path([
            [9, 9, 4],
            [6, 6, 8],
            [2, 1, 1]
        ])
    4  # 最长递增路径是 [1, 2, 6, 9]

    >>> longest_increasing_path([
            [3, 4, 5],
            [3, 2, 6],
            [2, 2, 1]
        ])
    4  # 最长递增路径是 [3, 4, 5, 6]或 [2, 4, 5, 6]

    提示:
    - 矩阵 `matrix` 的维度为 m x n。
    - 矩阵 `matrix` 的每个元素是一个非负整数。

    """

Claude 3.5 Sonett (1022) Antwort.

from typing import List

def longest_increasing_path(matrix: List[List[int]]) -> int:
    if not matrix or not matrix[0]:
        return 0

    m, n = len(matrix), len(matrix[0])
    # 缓存，用于存储每个位置的最长递增路径长度
    cache = [[0] * n for _ in range(m)]

    def dfs(i: int, j: int) -> int:
        # 如果已经计算过，直接返回缓存结果
        if cache[i][j] != 0:
            return cache[i][j]

        # 四个方向：上、下、左、右
        directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]

        # 当前位置的最长路径至少为1
        max_length = 1

        # 遍历四个方向
        for di, dj in directions:
            ni, nj = i + di, j + dj

            # 检查是否在矩阵范围内且满足递增条件
            if (0 <= ni < m and 0 <= nj < n and 
                matrix[ni][nj] > matrix[i][j]):
                # 递归计算邻居位置的最长路径
                curr_length = 1 + dfs(ni, nj)
                max_length = max(max_length, curr_length)

        # 存入缓存
        cache[i][j] = max_length
        return max_length

    # 遍历矩阵中的每个位置，找到最长路径
    result = 0
    for i in range(m):
        for j in range(n):
            result = max(result, dfs(i, j))

    return result

Testfall.

def check(candidate):
    assert candidate([[1, 1], [1, 1]]) == 1
    assert candidate([
    [9, 9, 4],
    [6, 6, 8],
    [2, 1, 1]
]) == 4
    assert candidate([
    [3, 4, 5],
    [3, 2, 6],
    [2, 2, 1]
]) == 4
    assert candidate([
        [1, 2, 3, 4],
        [5, 6, 7, 8],
        [9, 10, 11, 12],
        [13, 14, 15, 16]
]) == 7
    assert candidate([
        [-1, -2, -3, 0],
        [5, -6, 7, -8],
        [-9, 0, -11, -12],
        [13, 0, 15, -16]
]) == 4
    assert candidate([
    [5, 10, 6, 7, 9],
    [6, 10, 2, 2, 3], 
    [4, 9, 8, 2, 8],
    [3, 3, 3, 8, 8]
])==4
    assert candidate([
    [1, 3, 1, 4],
    [1, 5, 1, 7],
    [4, 2, 1, 1],
    [1, 3, 2, 1]
])==3
    assert candidate([
    [1, 9, 2, 4], 
    [9, 6, 5, 3],
])==4

wenn_bestanden(Angenommen oder nicht):Verabschiedet.

Beispiele für logisches Denken höherer Ordnung

Beispiel 1: Mehrstufiges Reasoning

fragen Sie

Ein Unternehmen hat sieben Mitarbeiter mit den Namen A, B, C, D, E, F und G. Das Unternehmen hat eine Einstufung vorgenommen und auf der Grundlage der Noten der Mitarbeiter und der folgenden Bedingungen die genaue Rangfolge jedes Mitarbeiters ermittelt:

1. A hat eine höhere Punktzahl als B, aber eine niedrigere als C.
2. D schneidet besser ab als E und G, aber schlechter als A.
3. G erhielt die niedrigste Punktzahl.
4. B hat eine höhere Punktzahl als E und F.
5. F hat eine höhere Punktzahl als E.
6. C erhielt die höchste Punktzahl.
7. Jeder Arbeitnehmer erhält unterschiedliche Noten, wobei D in der Mitte liegt.

Bitte leiten Sie die spezifische Punktzahl für jeden Arbeitnehmer auf der Grundlage der oben genannten Bedingungen ab.

Claude 3.5 Sonnet (1022) antwortet:

Lassen Sie uns die Rangfolge der einzelnen Mitarbeiter durch eine logische Analyse extrapolieren:

1. Bekannt aus Bedingung 3: G ist auf dem letzten Platz (7.)
2. Bekannt aus Bedingung 6: C ist an der Spitze (Platz 1)
3. Bekannt aus Bedingung 7: D ist auf Platz 4 (mittlere Position)
4. Wir wissen aus Bedingung 2: D ist höher als E und G, aber niedriger als A. Also:
   • E muss nach D eingestuft werden (5. oder 6.)
   • A muss vor D platziert sein (2. oder 3.)
5. Wir wissen aus Bedingung 1: A ist höher als B, aber niedriger als C. Kombinieren Sie dies mit der vorherigen Analyse:
   • 2. Platz in Reihe A
   • B muss auf Platz 3 liegen
6. Wir wissen aus den Bedingungen 4 und 5: B ist höher als E und F, und F ist höher als E. Also:
   • 5. Platz in Reihe F
   • E 6. Platz

Die endgültige Rangliste sieht wie folgt aus:

1. C (1. Platz)
2. A (2. Platz)
3. B (3. Platz)
4. D (4.)
5. F (5. Platz)
6. E (6.)
7. G (7.)

Möchten Sie, dass ich Ihnen den detaillierten Argumentationsprozess zeige?

Beispiel 2: Optimierungsproblem

fragen Sie

Eine Stadt hat fünf große Verkehrsknotenpunkte, und die Stadtplanungsabteilung möchte die Abdeckung der Buslinien optimieren, um sicherzustellen, dass jeder Knotenpunkt durch mindestens eine Linie verbunden ist. Die Baukosten zwischen den Knotenpunkten sind bekannt und das Ziel ist es, alle Knotenpunkte zu minimalen Kosten zu verbinden.

Daten:

• Konnektivitätskosten zwischen Knotenpunkten (in Mio. $)
• Drehkreuz 1 und Drehkreuz 2: 100.000 $
• Hub 1 und Hub 3: 150.000 $
• Hub 2 und Hub 4: 200.000 $
• Hub 3 und Hub 4: 250.000 $
• Hub 3 und Hub 5: 300.000 $
• Hub 4 und Hub 5: 180.000 $

Ziel: Ermittlung, welche Knotenpunkte miteinander verbunden werden sollten, um die Gesamtbaukosten zu minimieren und sicherzustellen, dass alle Knotenpunkte miteinander verbunden sind.

Claude 3.5 Sonnet (1022) antwortet:

Es handelt sich um ein minimales Spannbaumproblem, das ich mit dem Algorithmus von Kruskal lösen werde. Analysieren wir es Schritt für Schritt:

1. Sortieren Sie zunächst alle Verbindungen von den kleinsten zu den größten Kosten:
   • Drehscheibe 1-2: 100.000 $
   • Drehkreuze 1-3: 150.000 $
   • Nabe 4-5: 180.000 $
   • Drehkreuze 2-4: 200.000 $
   • Nabe 3-4: 250.000 $
   • Drehkreuze 3-5: 300.000 $
2. Es wird die Verbindung mit den geringsten Kosten gewählt, um eine Ringbildung zu vermeiden:
   • Wählen Sie Hub 1-2 ($100.000)
   • Hub 1-3 auswählen ($150.000)
   • Wählen Sie Hub 4-5 ($180.000)
   • Hub 2-4 auswählen ($200.000)

Optimales Programm:

• Verbinden von Hub 1 und Hub 2
• Verbinden von Hub 1 und Hub 3
• Verbinden von Hub 4 und Hub 5
• Verbinden von Hub 2 und Hub 4

Gesamtkosten: 10 + 15 + 18 + 20 = 630.000 $

Dieses Programm stellt sicher, dass:

1. Alle Hubs sind verbunden
2. Keine Schleife gebildet
3. Minimale Gesamtbetriebskosten

Soll ich Ihnen eine Visualisierung erstellen, die diese Lösung zeigt?

# Mitglied der Gemeinschaft

Für weitere detaillierte Claude 3.5 neuesten großen Modell Überprüfung Details, können Sie sich SuperCLUE-Claude Austausch Gruppe.