BoT: Verbessertes Denken: Lösen von Problemen durch Versuch und Irrtum mit großen Sprachmodellen

Abstracts

Die Denkleistung von Large Language Models (LLMs) bei einem breiten Spektrum von Problemen hängt in hohem Maße von verketteten Denkaufforderungen ab, bei denen einige verkettete Denkdemonstrationen als Beispiele in den Aufforderungen enthalten sind. Jüngste Forschungsarbeiten, z.B. zu Denkbäumen, haben auf die Bedeutung von Exploration und Selbsteinschätzung bei der Auswahl von Denkschritten beim Lösen komplexer Probleme hingewiesen. In diesem Beitrag schlagen wir ein automatisiertes Prompting-System namens Boosting of Thoughts (BoT) vor, das eine große Anzahl von Thinking Trees iterativ erforscht und selbst bewertet, um eine Sammlung von Trial-and-Error-Erfahrungen zu erhalten, die als neue Form des Promptens beim Lösen komplexer Probleme dienen. Ausgehend von einfachen Hinweisen, die keine Beispiele erfordern, untersucht und bewertet BoT iterativ eine große Anzahl von Argumentationsschritten und, was noch wichtiger ist, revidiert die Hinweise explizit unter Verwendung der LLM-Fehleranalysen, um die Generierung von Argumentationsschritten zu erweitern, bis eine endgültige Antwort erreicht ist. Unsere Experimente mit GPT-4 und Llama2 an einer Vielzahl komplexer mathematischer Probleme zeigen, dass BoT durchgängig höhere oder vergleichbare Problemlösungsraten erzielt als andere moderne Hinweismethoden. Der Quellcode ist unter https://github.com/iQua/llmpebase的examples/BoTReasoning文件夹下获得 verfügbar.

1. einleitung

Große Sprachmodelle (Large Language Models, LLMs) mit einem autoregressiven Paradigma haben aufgrund ihrer potenziellen Argumentationsfähigkeiten bei einer Vielzahl von Aufgaben erhebliche Leistungen erzielt. Die Sicherstellung dieser Fähigkeit bei komplexen Aufgaben stützt sich stark auf Chained Thinking (CoT)-Hinweise, die Schritt-für-Schritt-Denkbeispiele liefern. Dieser Ansatz legt nahe, dass die Fähigkeit zum schlussfolgernden Denken durch eine Reihe von Denkschritten stimuliert werden kann, wobei das Denken als Zwischenschritt bei der Problemlösung fungiert.

Folglich haben Folgestudien, insbesondere der Tree of Thought (ToT), Wege zur Verbesserung des CoT vorgeschlagen. Um die Validität zu gewährleisten, enthalten die Prompts dieser Methoden in der Regel menschliche Anmerkungen für bestimmte Aufgaben. Diese Abhängigkeit schränkt ihre Skalierbarkeit ein. Neuere Arbeiten, die entweder LLMs zur doppelten Überprüfung der Antworten nutzen oder die Aufforderungen auf der Grundlage von Rückmeldungen verbessern, sind sehr vielversprechend. In der vorhandenen Literatur wird in der Regel empfohlen, ungültiges Denken in Aufforderungen zu verwerfen. Menschen können jedoch in der Regel kontinuierlich lernen, indem sie Fehler sorgfältig analysieren, dadurch Erfahrungen sammeln und ihre Leistung schrittweise verbessern. Daher stellen wir die Frage: Kann die Gedankengenerierung von LLMs von menschlichen Anmerkungen befreit werden und das menschliche Problemlösungsverhalten nachahmen, um eine effektive Argumentation in einer Vielzahl von Aufgaben zu ermöglichen?

In diesem Papier schlagen wir einen neuartigen Rahmen vor, der in Abb. 1 dargestellt ist und Boosting of Thoughts (BoT) genannt wird. Dieser implementiert einen Boosting-Mechanismus, der Aggregation und Erfahrung einschließt, um unzuverlässige Argumentationsschritte (schwaches Denken) durch Lernen aus Fehlern schrittweise zu verbessern und schließlich verschiedene Probleme zu lösen. Ausgehend von einem einfachen Hinweis ohne menschliche Kommentierung kann BoT schwaches Denken entwickeln. Durch Aggregation kann das BoT daraus logischere und effektivere Gedankenketten ableiten, die zu weiteren Verbesserungen führen. Eine solche Anleitung wird in unserem Rahmen durch die Anpassung von Hinweisen erreicht, bei denen es sich um detaillierte Fehlermeldungen, Vorschläge und Anleitungen für jeden Argumentationsschritt handelt, die durch die Analyse der aggregierten Ketten unter Verwendung von LLMs gewonnen werden. Wenn solche Erfahrungen in den Hinweisen gesammelt werden, führt dies allmählich zu einem besseren Denken.

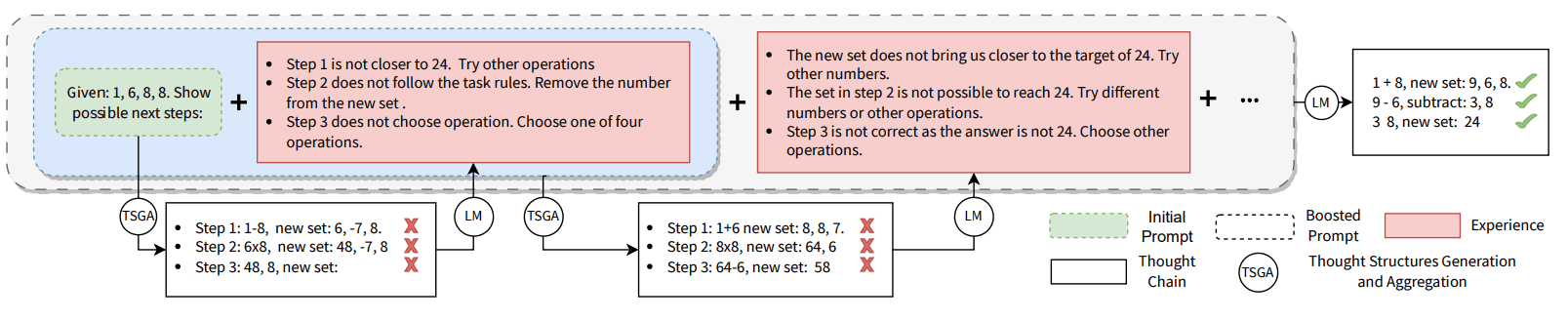
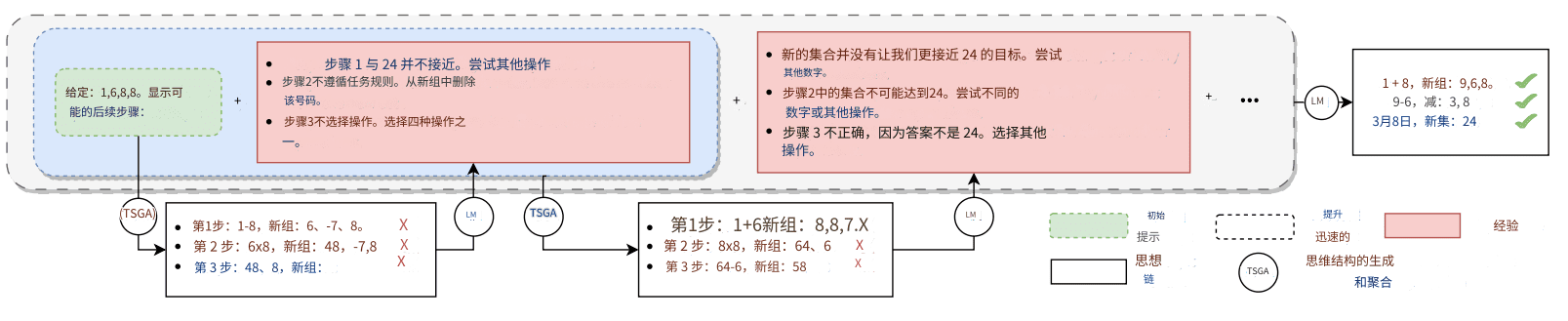
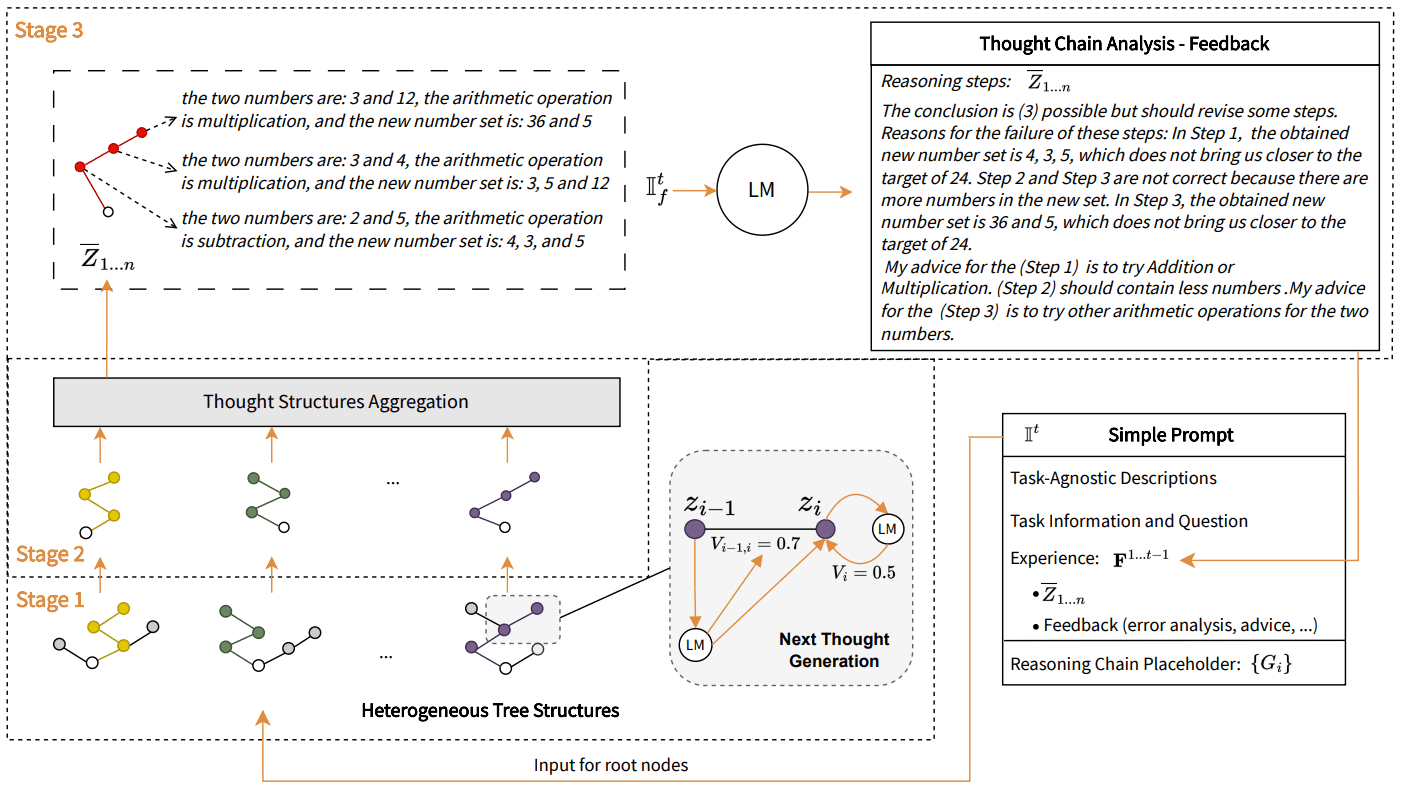
Abbildung 1: Verbesserung von Hinweisen durch schrittweise Erweiterung der Erfahrung, die aus einer Analyse der generierten Gedankenketten durch ein großes Sprachmodell (LLM oder LM) besteht. Die Erfahrung enthält explizit die Gedankenkette selbst, den entsprechenden Fehlerbericht und detaillierte Vorschläge zur Überarbeitung der einzelnen Argumentationsschritte. So können auch jene ungültigen Gedanken, die mit einem roten Kreuz markiert sind, zur Verfeinerung der Prompts beitragen. Durch das Sammeln von Erfahrungen mit den Prompts kann das BoT schließlich korrekte Gedankenketten ausgehend von einfachen Prompts generieren. Das hier vorgestellte Beispiel ist das Ergebnis der Anwendung von GPT-4 mit BoT auf eine 24-Punkte-Spielaufgabe.

Konkret implementiert BoT einen solchen Verstärkungsmechanismus als erfahrungsgesteuerten iterativen Prozess, wie in Abbildung 1 dargestellt. In jeder Iteration baut BoT für einen gegebenen Hinweis eine große Anzahl von einfachen Gedankenstrukturen parallel zum LLM auf. Wir haben uns für die Baumstruktur entschieden, wie sie in ToT gezeigt wird, aber für unsere Boosting-Zwecke haben wir sie erheblich modifiziert, um sie zu einem gewichteten binären Baum mit verschiedenen Wachstumsstrategien zu machen. Nach der Extraktion der höchsten Punktzahlen für die Wurzel-zu-Blatt-Zweige jedes Baums wurde die Aggregationskomponente von BoT ausgeführt, um sie zu einer einzigen Gedankenkette zusammenzufassen. Diese Kette wurde dann von demselben LLM bewertet, um daraus Lehren zu ziehen, die den Prompts als Leitfaden für die Gedankengenerierung in der nächsten Iteration hinzugefügt wurden.

Unser Beitrag lässt sich auf drei Arten zusammenfassen. Erstens: Im Gegensatz zur Generierung komplexerer Denkstrukturen mit Hilfe ausgefeilter Eingabeaufforderungen zeigt diese Arbeit, dass schwache Gedanken, die sich nur auf einfache anfängliche Eingabeaufforderungen stützen, schrittweise verbessert werden können, um Probleme auf der Grundlage früherer Erfahrungen zu lösen. Zweitens schlagen wir zur Umsetzung dieses Verbesserungsmechanismus ein neuartiges System namens Boosting of Thoughts (BoT) vor, das einen erfahrungsgesteuerten iterativen Prozess durchführt. Da es mit einfachen Aufforderungen beginnt, kann BoT auf eine Vielzahl von Aufgaben erweitert werden. Bei gleichzeitiger Gewährleistung der Validität ist BoT schnell, da es einfache Gedankenstrukturen parallel aufbaut und nach wenigen Iterationen zu einer Lösung konvergiert. Schließlich haben wir die Leistung von BoT bei komplexen mathematischen Problemen mit GPT-4 und LlamaV2 evaluiert. Auf der Grundlage von GPT-4 OpenAI (2023) und LlamaV2 Touvron et al. (2023) haben wir die Leistung von BoT bei komplexen mathematischen Problemen evaluiert. Die Problemlösungsraten zeigen, dass BoT mit einer binären Baumstruktur den aktuellen Stand der Technik bei GSM8K und AQuA deutlich übertrifft und bei anderen Datensätzen zweitbeste Ergebnisse erzielt. Insbesondere übertrifft BoT die führende Methode ToT um 9,7% bei der neuen anspruchsvollen Aufgabe Game of 24. Unser BoT zeigt somit, dass LLMs auch ohne menschliche Annotationen eine hohe Leistung über ein breites Spektrum von Aufgaben beibehalten können, indem sie Hinweise ergänzen, Fehleranalysen von ungültigen Gedankenketten akkumulieren und entsprechende Vorschläge machen.

2. verwandte Arbeiten

mehrstufiger Rückschluss.. Prominente Arbeiten zu Aufforderungen zum verketteten Denken (Chained Thinking, CoT) legen nahe, dass das schrittweise Denkverhalten von LLMs durch die Bereitstellung von Zwischenschritten in jeder Problemaufforderung stimuliert werden kann. Neuere Arbeiten, Tree of Thought (ToT), wandeln den sequentiellen Denkprozess in eine Baumstruktur um, in der jeder Gedanke (Knoten) frühere Denkwege berücksichtigen kann, um mehrere nächste Gedanken zu generieren. Durch Backtracking und erweiterte Exploration während des Denkprozesses ist ToT auch bei Problemen leistungsfähig, die selbst GPT-4 herausfordern. In Anbetracht der hohen Kapazität nutzt die zugrundeliegende Denkstruktur von BoT weitgehend die Denkbaumstruktur von ToT. Aufgrund des Boosting-Frameworks ist die von BoT bei jeder Iteration erzeugte Baumstruktur binär und flach, im Gegensatz zum komplexen Baum von ToT, bei dem jeder Knoten einer großen Anzahl von Kindknoten entspricht. Die zugrundeliegende Struktur ist jedoch nicht auf ToT beschränkt. Im Gegensatz dazu ist BoT flexibel, da die zugrundeliegende Denkstruktur ToT, GoT Besta et al. (2023) oder CR Zhang et al. (2023b) sein kann, wobei Thinking Graphs (GoT) Besta et al. (2023) die jüngste Arbeit ist, die die Struktur des Denkens auf ein grafisches Format erweitert. In dieser Arbeit werden wir uns nur auf ToT als zugrundeliegende Denkstruktur konzentrieren und die Verwendung von GoT als zukünftige Arbeit betrachten.

Autosuggestion. Die Entlastung des Menschen von aufgabenspezifischen Aufforderungen zieht viel Aufmerksamkeit auf sich. Um die Schlussfolgerungsfähigkeit von LLMs zu gewährleisten, verlassen sich traditionelle CoTs auf menschliches a priori Wissen, um manuell aufgabenspezifische Demonstrationen als Aufforderungen zu generieren. Zero CoT zeigte jedoch, dass LLMs auch ohne manuell erstellte Beispiele in der Lage waren, Schritt für Schritt zu denken, um genaue Antworten zu erhalten, indem sie der Aufforderung einfach den Satz "Lass uns Schritt für Schritt denken" hinzufügten. Diese Erkenntnisse führten zu einer Reihe von Folgestudien: Auto-CoT eliminiert den manuellen Aufwand, indem es die von Zero-CoTs erzeugte Kette brauchbarer Schlussfolgerungen abruft.Active-Prompt misst zunächst die Unsicherheit einer Reihe von Fragen und wählt so nur unsichere Fragen aus, die von einem Menschen kommentiert werden.ToT reduziert ebenfalls den manuellen Aufwand, erfordert aber für jede Aufgabe immer noch, dass der Experte in der Eingabeaufforderung die möglichen nächsten Gedanken. Unser Beitrag stellt einen neuen Ansatz für manuelles cue-free boosting vor. Ausgehend von einem einfachen Hinweis, verbessert BoT diesen iterativ auf der Grundlage von LLMs Analyse des Denkens.

Tip Engineering durch Feedback. Die Verwendung der Antworten von LLMs auf Eingabeaufforderungen als Feedback für weitere Überarbeitungen von Aufforderungen hat viel Aufmerksamkeit erregt. Diejenigen, die einen gegebenen Hinweis auf der Grundlage der von den LLMs bewerteten Beschreibung der Ausgabe kontinuierlich überarbeiten, zielen darauf ab, genaue Antworten zu erhalten. SELF-REFINE schlägt einen iterativen Selbstverfeinerungsalgorithmus vor, der es LLMs ermöglicht, Feedback zu generieren, um ihre Ausgabe weiter zu verfeinern. PHP vereinfacht diesen Prozess, indem es die Lösung der vorherigen Antwort direkt als Hinweis zu den nachfolgenden Hinweisen hinzufügt.REFINER, das sich ebenfalls auf unsere Arbeit bezieht, wertet jeden Inferenzschritt als Feedback aus, um eine vernünftigere Antwort zu erzeugen. vernünftigere Lösung. Eine andere Reihe von Studien hat sich mit der Integration befasst, insbesondere mit der Verwendung von Boosting-Mechanismen. Freund et al. (1996) verfeinerten Hinweise mit Feedback aus einer Reihe von Beispielen. Sie passten den Prompt an, indem sie mehrere unsichere Beispiele zur vorherigen Iteration hinzufügten, oder sie stützten sich auf einen Feedback-Reflexions-Verfeinerungsprozess.APO Pryzant et al. (2023) verfeinerten Prompts iterativ, indem sie die Leistung des vorherigen Prompts nutzten, um eine optimierte natürliche Sprache zu bilden. Diese Arbeiten zeigen die Effektivität von Boosting-Mechanismen im Cue Engineering. Unsere Arbeit ist jedoch die erste, die die Bedeutung der Fehleranalyse bei der Verbesserung von Hinweisen zur Generierung effektiver Inferenzketten hervorhebt. Die vorgeschlagene BoT erweitert diese Einsicht auf einen automatisierten Prompting-Rahmen, indem sie iterativ eine Sammlung von Versuch-und-Irrtum-Erfahrungen sammelt.

3. verstärktes Denken

3.1 Hintergrund

Das Ziel des Cue-Engineering ist es, einen Cue I zu entwerfen, der mehrere Sprachsequenzen enthält, so dass durch die Verwendung dieses Cue als Input ein vortrainiertes Large Language Model (LLM), bezeichnet als pθ, parametrisiert durch θ, die gewünschten Sprachsequenzen y erhalten werden können. Somit kann der Standard-Input-Output (IO) als y ∼ pθ (y|I (X, Q)) formuliert werden, wobei I (-) den Cue bezeichnet, der die Aufgabenanweisung X und die die entsprechende Frage Q.

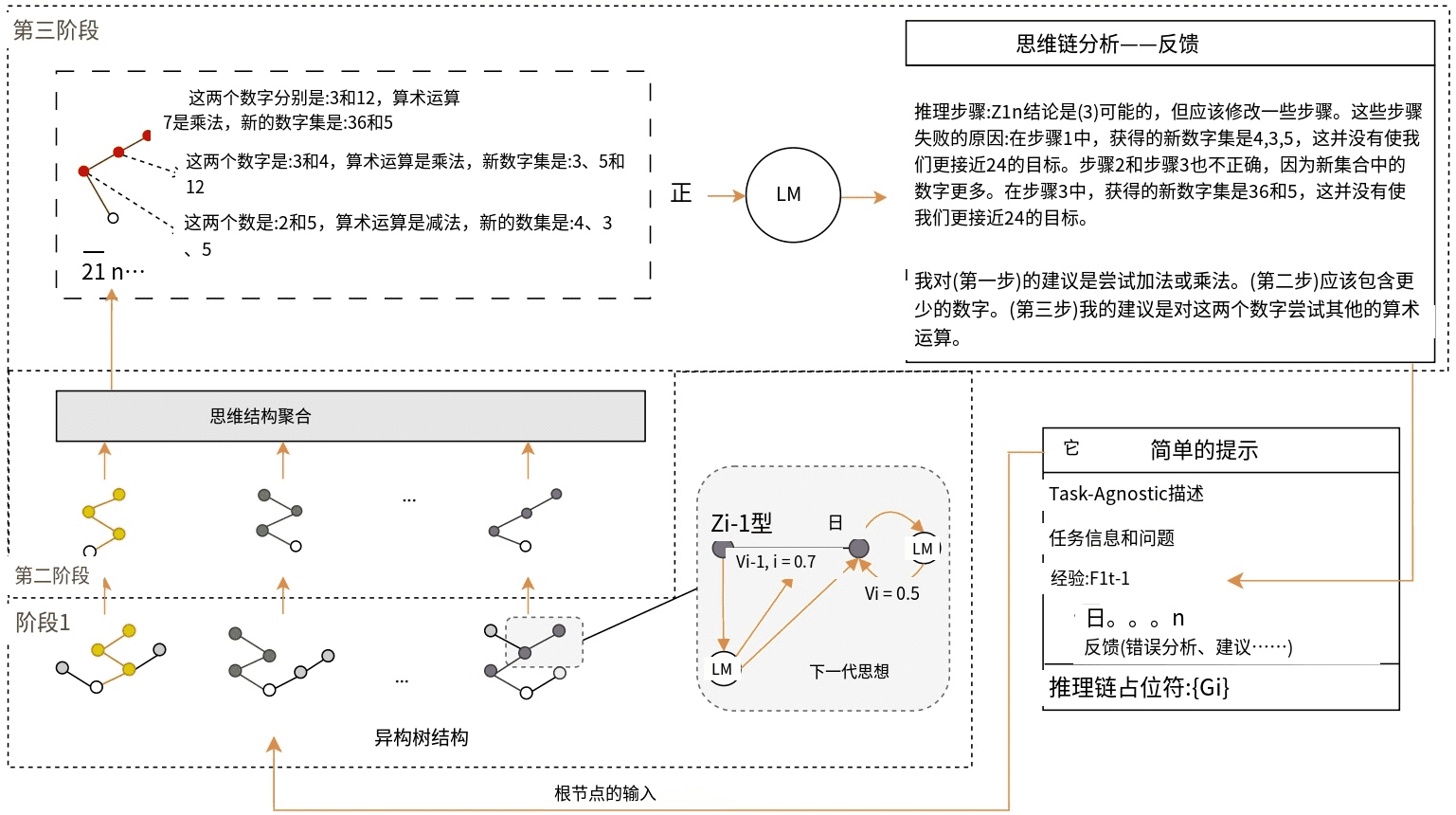
Das Bild zeigt eine visuelle Darstellung des Denkprozesses beim Lösen von Problemen mit Hilfe von Rechenoperationen. Er ist in drei Hauptteile unterteilt: Aggregation der Gedankenstruktur, Generierung des nächsten Gedankens und Analyse der Gedankenkette - Feedback.

Die Aggregation von Denkstrukturen stellt die Kombination verschiedener Stufen des Denkens dar (Stufe 1, Stufe 2 und Stufe 3), von denen jede ihre eigene Zahlenstruktur hat, die die Schritte beschreibt, die unternommen werden, um zu einer Schlussfolgerung zu gelangen.

Next Thought Generation konzentriert sich auf eine bestimmte Phase und zeigt, wie Language Modelling (LM) zur Vorhersage des nächsten Gedankens verwendet werden kann, wobei frühere Erfahrungen (dargestellt durch die Vektoren Vi-1 und Vi) berücksichtigt werden und eine neue Argumentationskette entsteht.

Gedankenkettenanalyse - Feedback bietet eine detaillierte Analyse der durchgeführten Rechenschritte, weist auf mögliche Fehler hin und bietet Verbesserungsvorschläge. Sie kritisiert die Schritte, indem sie bewertet, ob sie den Löser näher an die Zielzahl (in diesem Fall 24) bringen, und schlägt andere Rechenoperationen vor, die er ausprobieren sollte.

Dazu gehören aufgabenunspezifische Beschreibungen, Informationen und Fragen zur Aufgabe sowie Erfahrungen aus einer vorangegangenen Denkkette, die als Platzhalter für die Generierung neuer Gedanken dient.

Insgesamt zeigt das Bild einen methodisch fundierten Ansatz für das Denken und die Problemlösung, bei dem Sprachmodelle zur iterativen Optimierung und Verbesserung von Denkprozessen eingesetzt werden.

Schauen wir uns insbesondere den Abschnitt Aggregation der Denkstruktur an. In diesem Abschnitt sehen wir drei Stufen, jede mit einer farbigen heterogenen Baumstruktur. In Stufe 1 sehen wir einige arithmetische Operationen, und der Trend ist "vi1 - 0,5". In Stufe zwei sehen wir mehr arithmetische Operationen und die Tendenz ist "vi2 - 0,6". In der dritten Stufe schließlich sehen wir eine Reihe von arithmetischen Operationen mit einem Trend von "vi3 - 0,4".

Für den nächsten Abschnitt der Gedankengenerierung wird ein bestimmter Gedankenknoten, Zi, verfolgt und sein zugehöriges Gewicht, vi, angezeigt, das die Bedeutung dieser Gedanken im Kontext der Problemlösung angibt.

Im Abschnitt Gedankenkettenanalyse - Feedback werden mehrere Argumentationsschritte dargestellt (Z1,Z2.... .Zn) und bewertet sie. Für jeden dieser Schritte geben "R1:-3, versuche +", "R2:+3, versuche -" und "R3: -1, versuche ×" ein Feedback zu dem jeweiligen Schritt Feedback, Bewertung der Argumentation und Vorschläge zur Verbesserung.

Im Abschnitt Einfache Hinweise sind einige Eingabehinweise zu sehen, wie z. B. "Aufgabenbeschreibung unspezifisch 'Spielen Sie ein Zahlenspiel'", "Aufgabenmeldung 'Versuchen Sie, mit den vier Zahlen 1,3,4 ,6 (jede Zahl kann nur einmal verwendet werden) und arithmetische Operationen (Addition, Subtraktion, Multiplikation und Division) zu verwenden, um die Zahl 24 zu erhalten'" sowie die vorherige Argumentationskette Gi.

Das Ergebnis dieser Pipeline erzeugt einen neuen Denkprozess für die nächste Argumentation.

Dieses Diagramm stellt den logischen Ablauf eines Denkprozesses und einer Argumentationsmethodik dar und zeigt, wie ein Sprachmodell (LM) sowie ein Feedback-/Vorschlagsmechanismus verwendet werden können, um mit dem Problem voranzukommen, mit kritischem Feedback und Bewertung bei jedem Schritt.

Abbildung 2: Zeigt einen Überblick über den BoT-Prozess in jeder Iteration. Um zu zeigen, wie eine Steigerung der Effektivität in diesem empirisch basierten iterativen Prozess erreicht werden kann, zeigen wir die erschöpfenden Zwischenergebnisse, die in einer Art von Experiment mit ChapGPT-4 auf dem 24-Punkte-Spiel-Datensatz erzielt wurden. Nachdem das BoT die Aufgabe Q: "Die vier vorgegebenen Zahlen sind: 2, 4, 5, 5" erhalten hat, durchläuft es drei aufeinanderfolgende Phasen. Unter Verwendung des einfachen Hinweises It als Eingabe gibt die Gedankenstruktur-Generierung (Phase 1) eine große Vielfalt an heterogenen baumförmigen Gedankenstrukturen aus. In der Gedankenstruktur-Aggregation (Stufe 2) werden sie zu einer Gedankenkette z1.... .n integriert und diese Gedankenkette anschließend in Stufe 3 analysiert, um Erfahrungen zu generieren, die zur weiteren Verstärkung des Hinweises genutzt werden können.

Die Aufforderungen können ausführlicher gestaltet werden, um LLMs anzuleiten, das Problem Schritt für Schritt zu lösen. Jeder Zwischenschritt wird als zi (auch als Gedanke bezeichnet) bezeichnet. Der CoT liefert eine Handvoll Beispiele, deren Antworten jeweils eine Kette von Gedanken z1.... .n. Dies führt zu y ∼ pθ y|I [z1 . .n]N , X, Q , wobei N die Anzahl der in der Aufforderung enthaltenen Beispiele ist.

Anstatt Beispiele im Bootstrap vorzubereiten, besteht ein flexiblerer Ansatz darin, den Bootstrap so zu gestalten, dass er den LLM dazu bringt, den Gedanken zi während des Argumentationsprozesses allmählich zu generieren. Dies kann als zi ∼ pθ (zi |I(z1.... .i-1, X, Q)). Schließlich wird die Lösung formalisiert als y ∼ pθ (y|I(z1.... .n, X, Q)).
Stellvertretend dafür erweitern ToT Yao et al. (2024) diesen sequentiellen Denkschritt zu einer Baumstruktur, in der C nächste Gedanken generiert werden können. Die Struktur einer Überlegung kann also entweder verkettet oder baumartig sein.

3.2 Rahmen

Die vorhandene Literatur, die darauf abzielt, Hinweise mit korrekten CoT-Beispielen zu generieren oder feinkörnige Denkstrukturen zu entwerfen, leidet unter drei Einschränkungen. Erstens wird ungültiges Denken bei diesen Ansätzen in der Regel ignoriert oder verworfen. Menschen, vor allem Nicht-Experten, und insbesondere in anderen Bereichen, sind jedoch darauf angewiesen, frühere Fehler zu analysieren, um mehr Erfahrung zu sammeln, damit sie beim nächsten Versuch richtig handeln. Zweitens sind sie weniger skalierbar, da für jede Aufgabe Beispiele für die Generierung des nächsten Gedankens, z. B. I (z1|z0, X, Q), im Hinweis gegeben werden müssen. Schließlich ist die Generierung von Denkstrukturen (z.B. die Baumstruktur von Yao et al.) zu komplex, um weitere Denkschritte zu erforschen, um eine bessere Lösung zu erhalten. Dies ist vor allem darauf zurückzuführen, dass die erhaltenen Lösungen möglicherweise nicht weiter überarbeitet werden können.

In diesem Beitrag argumentieren wir, dass Aufforderungen verbessert werden können, indem kontinuierlich Analysen dieser ungültigen Gedanken (fehlerhafte Argumentationsschritte in der Gedankenkette) von LLMs gesammelt werden. So kann sogar ein einfacher Hinweis, z. B. I (X, Q), der zu ungültigem Denken führen kann, schrittweise verbessert werden, indem man sich auf solche Analysen stützt, um ein starkes Denken zu erhalten, das näher an eine Lösung führt.

Wir schlagen eine Methode vor, dieVerstärkung der Gedanken (BoT)eines automatisierten Cueing-Frameworks, das Cueing-Verbesserungen durch einen erfahrungsgesteuerten iterativen Prozess ermöglicht, vonEinfacherden Beginn des Hinweises. Wie in Abbildung 2 dargestellt, besteht jede Iteration t von BoT aus drei Phasen. In der zweiten Phase werden diese Gedankenstrukturen zu einer Schlussfolgerungskette aggregiert, die von den LLMs in der dritten Phase analysiert wird, um ein Feedback mit Fehlerberichten und detaillierten Änderungsvorschlägen zu generieren. Die aggregierte Schlussfolgerungskette wird mit den Feedback-Ergebnissen zu einer neuen Erfahrung kombiniert, die mit Ft bezeichnet wird. Durch die Akkumulation dieser Erfahrungen über die Iterationen F1.... .t, wird der Hinweis verbessert.

Einfache Tipps. Für jede Aufgabe wird bei der Iteration t = 0 ein einfacher Anfangshinweis I0 ≡ {S, X, Q, F0, {Gi}} erstellt, wobei S die aufgabenunabhängige Beschreibung bezeichnet, während X und Q die Aufgabeninformation bzw. die Frage bezeichnen. Der empirische Teil des Prompts wird mit F0 bezeichnet und sollte zu Beginn leer sein. {Gi}} ist ein Platzhalter, der bei der Konstruktion der Gedankenstruktur ausgefüllt wird. Mit anderen Worten: Bei der Generierung des nächsten Gedankens zi wird {Gi} durch die vorherige Gedankenkette z1.... ,i-1.

Generierung von Gedankenstrukturen. Nach dem Sammeln der Erfahrung Ft-1 kann der Hinweis für Iteration t It ≡ {S, X, Q, F1, ... ,t-1, {Gi}}. Auf der Grundlage dieses Hinweises generiert BoT parallel M Gedankenstrukturen, wobei BoT im Prinzip jede beliebige Gedankenstruktur enthalten kann, z. B. verkettete Strukturen von Wei et al. oder baumartige Strukturen von Yao et al. In Anbetracht der Erforschung von Argumentationsschritten und experimentellen Ergebnissen haben wir baumartige Gedankenstrukturen untersucht. BoT führt jedoch zwei neue Modifikationen ein, die es für den Lifting-Rahmen besser geeignet machen.

• gewichteter Binärbaum. Durch die Verwendung einfacher Stichwörter in jeder Runde konstruiert BoT schwache Gedanken mit einfachen Strukturen und geringer Komplexität, da sie durch den Boosting-Mechanismus weiter überarbeitet werden können. Somit ist jede Gedankenstruktur von BoT ein flacher gewichteter Binärbaum. Der Einfachheit halber behalten wir die Symbole z1.... .i-1, um einen Gedanken vom Wurzelknoten zum Elternteil des Knotens i zu bezeichnen. Zusätzlich zur Ausstattung jedes Knotens i mit einem Gedanken zi und seiner Gedankenbewertungsnote Vi ∼ pθ (z1.... .i, Ia, X, Q), sondern auch eine Kantenbewertung Vi-1,i ∼ pθ (zi-1, zi, Ie, X, Q) zwischen einem Kindknoten und seinem Elternknoten, wobei sich Ia und Ie auf die Leitbeschreibungen des Gedankens bzw. die Kantenbewertung beziehen. vi-1,i bezeichnet das Vertrauensniveau der LLMs bei der Generierung dieses Argumentationsschritts. Somit ist die nächste Gedankengenerierung des BoT in dieser Baumstruktur formalisiert als pθ (zi| (Vi-1,i, Vi, It, X, Q)).
• Heterogenität der Bäume. Im Gegensatz zu ToT, bei dem Lösungen in einem großen, komplexen Baum gefunden werden sollen, zielt BoT darauf ab, sehr heterogene, baumartige Gedankenstrukturen aufzubauen. Um die Heterogenität zu erhöhen, werden bei der Generierung von Denkstrukturen verschiedene Baumwachstumsstrategien verwendet, wie z. B. schichtweises und blattweises Wachstum. Erstere betont die Exploration, nutzt aber weniger Chen & Guestrin (2016), während letztere das Gegenteil ist Ke et al. (2017). So neigt die Blatt-für-Blatt-Strategie im Vergleich zum Schicht-für-Schicht-Wachstum dazu, die Argumentation vom aktuell besten Gedanken bis zu einem besseren Endgedanken fortzusetzen, aber sie neigt auch dazu, monotone Argumentationsketten zu erhalten. Darüber hinaus wurden LLMs mit unterschiedlichen Temperatur- und Top p-Einstellungen angewandt. Schließlich verwendeten wir einen kleinen maximalen Tiefenwert in BoT und kennzeichneten einen Knoten als Blatt, wenn die Werte von Vi-1,i und Vi außerhalb des angegebenen Bereichs [0,3, 0,8] lagen.

Gedankenstrukturpolymerisation. Nachdem er M Gedankenstrukturen erhalten hat, fasst der BoT diese zu einer Gedankenkette zusammen, die mit z1.... .n. Um dies zu erreichen, wählt der BoT für jeden Gedankenstrukturindex m zunächst die Kette mit der höchsten Bewertungszahl aus, d. h. zm 1.... .nm := arg maxz1... .n∈Zm ∑i=1 Vi + Vi-1,i, wobei Zm die Menge aller Gedankenketten des m-ten Baums bezeichnet. Anschließend gibt es zwei Strategien, um z1.... .n.

• Best-First-Aggregation.BoT hängt von arg maxz1.... .n∈{Zm}M m=1 ∑i=1 Vi + Vi-1,i, und wählt die beste der M Gedankenstrukturen als z1... .n. Dieser Algorithmus ist schnell, kann aber zu einer unlogischen Kette führen, die es schwierig macht, spätere Verbesserungen zu steuern.
• Aggregation der Gier. kann das BoT eine gierige Suche auf {Zm}M m=1 durchführen, um eine neue Gedankenkette zusammenzustellen, die möglicherweise nicht existiert, aber global optimal sein kann. Ausgehend vom Anfangsgedanken, in der Regel dem Wurzelknoten des Baums, erhält der BoT z1 = arg maxzj ∈ {zm 1 } M m=1 Vj + Vj-1,j. Um zi zu erhalten, sucht der BoT anschließend nach allen Gedanken in {Zm}M m=1, deren vorheriger Schritt zi-1 war.

Analyse der Gedankenkette. Um Erkenntnisse darüber zu gewinnen, was angepasst werden sollte, um den Hinweis zu verbessern und besseres Denken zu erzeugen, nutzt der BoT die Fähigkeit der LLMs, z1.... .n. Genauer gesagt, mit dem Hinweis It f (z1.. .n, X, Q) als Eingabe, gibt das LLM einen Feedback-Absatz aus, der Informationen über diese Gedankenkette z1.... .n mit einem Problembericht und detaillierten Vorschlägen. Dieses Feedback wird zu F1,... ,t-1 als eine neue Erfahrung in der Gedankengenerierung hinzugefügt, was zu F1,... ,t.

Iterative Verfeinerung.. Durch den Boosting-Mechanismus wird F1,... ,t verwendet, um den Hinweis iterativ zu verbessern, was zu dem Hinweis It+1 für die (t+1)-te Iteration ≡ {S, X, Q, F1,... ,t, {Gi}}. Im weiteren Verlauf der Iteration kann F1,... ,t viele typische, unlogische Gedankenketten enthalten, aber auch solche, die näher an der Lösung liegen, und zwar alle mit wohldefinierten analytischen Ergebnissen. Selbst wenn man mit einem einfachen Hinweis beginnt, verfeinert BoT diesen Hinweis iterativ, um die richtigen Denkschritte zu erzeugen, die zu einer genauen Lösung führen. Nach T Iterationen verwenden wir It+1 als Eingabehinweis für den LLM, um die endgültige Antwort zu erhalten.

4) Experimente

Datensatz. Die Experimente wurden mit Benchmark-Datensätzen durchgeführt, die eine Vielzahl von mathematischen Problemen enthielten, darunter MMLU, SVAMP, GSM8K, AQuA und MATH. Zusätzlich haben wir eine anspruchsvolle mathematische Denkaufgabe, Game of 24, einbezogen, bei der das Ziel darin bestand, 24 in einer Gleichung mit vier Zahlen und grundlegenden arithmetischen Operationen (Addition, Subtraktion, Multiplikation und Division) zu erhalten. besteht also aus 3 Zwischenschritten.

Wettbewerb. Neben der Benchmark-Methode Standard Input-Output (IO) werden die Methoden Chained Thinking (CoT), CoT-SC und Complex CoT verglichen, bei denen die Eingabeaufforderungen eine Handvoll Beispiele (8) und menschliche Annotationen enthalten. Darüber hinaus wird BoT mit verwandten Arbeiten wie Thinking Trees (ToT), Progressive Prompts (PHP) und State-of-the-Art-CSVs verglichen. Wir haben Experimente mit GPT-4 und Llama2 durchgeführt. GPT-4 wurde über die OpenAI-API aufgerufen, während das Llama2-13b-Chat-Modell von MetaAI heruntergeladen wurde, um Experimente lokal durchzuführen. Um eine heterogene Baumstruktur zu konstruieren, wählte BoT zufällig Temperaturen im Temperaturbereich [0.2, 0.4, 0.6, 0.7, 0.9, 1.1, 1.5] und den oberen p-Bereich [0.1, 0.3, 0.5, 0.7, 0.9].

aufstellen. Sofern nicht ausdrücklich angegeben, führt BoT in allen Experimenten T = 10 Iterationen durch und konstruiert M = 15 Gedankenstrukturen, von denen jede ein gewichteter Binärbaum ist, da dies tendenziell die besten Ergebnisse liefert. Darüber hinaus haben wir für diese Benchmark-Datensätze die Tiefe des Baums auf 5 festgelegt, während die entsprechende Tiefe in Game of 24 3 betrug. BoT + CoT bedeutet, dass unser einfacher Hinweis 5 Beispiele aus CoT enthält. In Ablationsstudien, in denen es keine kumulative Erfahrung im BoT gibt, werden 8 CoT-Beispiele im Prompt bereitgestellt.

metrisch. Wir messen und berichten die Ergebnisse aller Experimente in Bezug auf die Lösungsrate der Aufgabe (%). Aus der BoT-Ausgabe zT1.... .n der Zielantworten haben wir formatierte Beschreibungen der Antworten speziell für die LLMs erstellt. Für häufig verwendete Datensätze wurde das Format der Antwort auf "Die Antwort ist:" festgelegt. Für das Spiel mit 24 Punkten verwenden wir "Schrittindex, aktuelle Menge:, zwei ausgewählte Zahlen:, Operation:, neue Zahl aus der Operation:, verbleibende Zahlen:, neue Zahlenmenge:". Dann vergleichen wir die Zahlen in der neuen Zahlenmenge direkt mit der Grundwahrheit. In Anlehnung an ToT Yao et al. (2024) verwenden wir die aus 100 schwierigen Spielen ermittelte Lösungsrate als Metrik.

4.1 Wichtigste Ergebnisse

Die wichtigsten experimentellen Ergebnisse sind in Tabelle 1 und Abbildung 3 zusammengefasst, wo wir einen Einblick in die Gesamtleistung des BoT geben. Unsere Ergebnisse zeigen, dass die vorgeschlagene BoT durch Verstärkung des Mechanismus 1). wettbewerbsfähige Problemlösungsraten unabhängig von menschlichen Annotationen in den meisten Datensätzen erzielt; 2). einen neuen Stand der Technik bei der Bereitstellung von CoT-Beispielen erreicht. Die experimentellen Ergebnisse zeigen jedoch auch, dass BoT stark auf Erfahrung beruht und daher sehr empfindlich auf die Fähigkeiten von LLMs reagiert.

In Tabelle 1 beginnt BoT mit einfachen anfänglichen Hinweisen und übertrifft schließlich den aktuellen Stand der Technik CSV um 0,11 TP3T in Bezug auf die Lösungsrate auf GSM8K, die sich stark auf den GPT-4 Code-Interpreter stützt. In Bezug auf AQuA übertrifft BoT SOTA um 2,51 TP3T. Dies zeigt, dass LLMs durch das Hinzufügen von Fehleranalysen und Vorschlägen zu den Hinweisen, ohne sich auf menschliche Annotationen zu verlassen, in der Lage sind, bei komplexen Schlussfolgerungen gut abzuschneiden. Der Hauptgrund dafür ist, dass einfache Hinweise schrittweise verbessert werden können, indem frühere Erfahrungen gesammelt werden, um Probleme korrekt zu lösen. Nach der Einbeziehung von CoT-Beispielen in die Eingabeaufforderungen ist BoT+CoT um 1,3% höher als SOTA. Wir argumentieren, dass CoT-Beispiele als erfolgreiche Erfahrungsfälle betrachtet werden können, die die Generierung nachfolgender Denkstrukturen in BoT direkt anleiten. Durch die iterative Verbesserung erreichte BoT+CoT eine neue SOTA.Währenddessen waren BoT und BoT+CoT, insbesondere BoT, mindestens 181 TP3T niedriger als SOTA in MATH.Diese Beobachtung impliziert, dass schwache LLMs aufgrund der geringen Fähigkeit von LLMs, Schlussfolgerungsketten für gültige Erfahrungen zu analysieren, möglicherweise nicht gut mit BoT funktionieren.

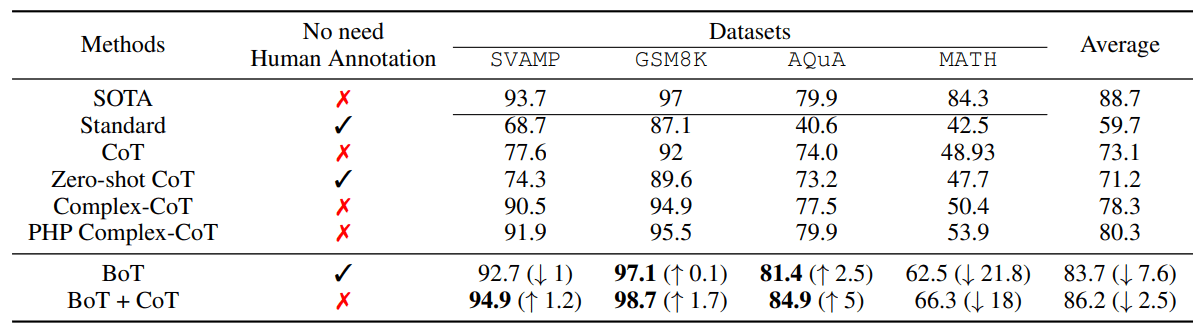
Tabelle 1: Die Verwendung von BoT in Verbindung mit GPT-4 verbessert die Leistung auch ohne manuelle Annotation erheblich.
Wenn der einfache BoT-Anfangshinweis CoT-Beispiele enthält, weist der entsprechende BoT+CoT-Ansatz höhere Lösungsraten auf. Unser Rahmenwerk wird auch mit führenden Ansätzen wie Model Selection von Zhao et al. 2023, PHP von Zheng et al. 2023 und CSV von Zhou et al. 2023 verglichen, die jeweils eine State-of-the-Art-Leistung (SOTA) auf den Datensätzen SVAMP, AQuA und GSM8K & MATH erzielen.

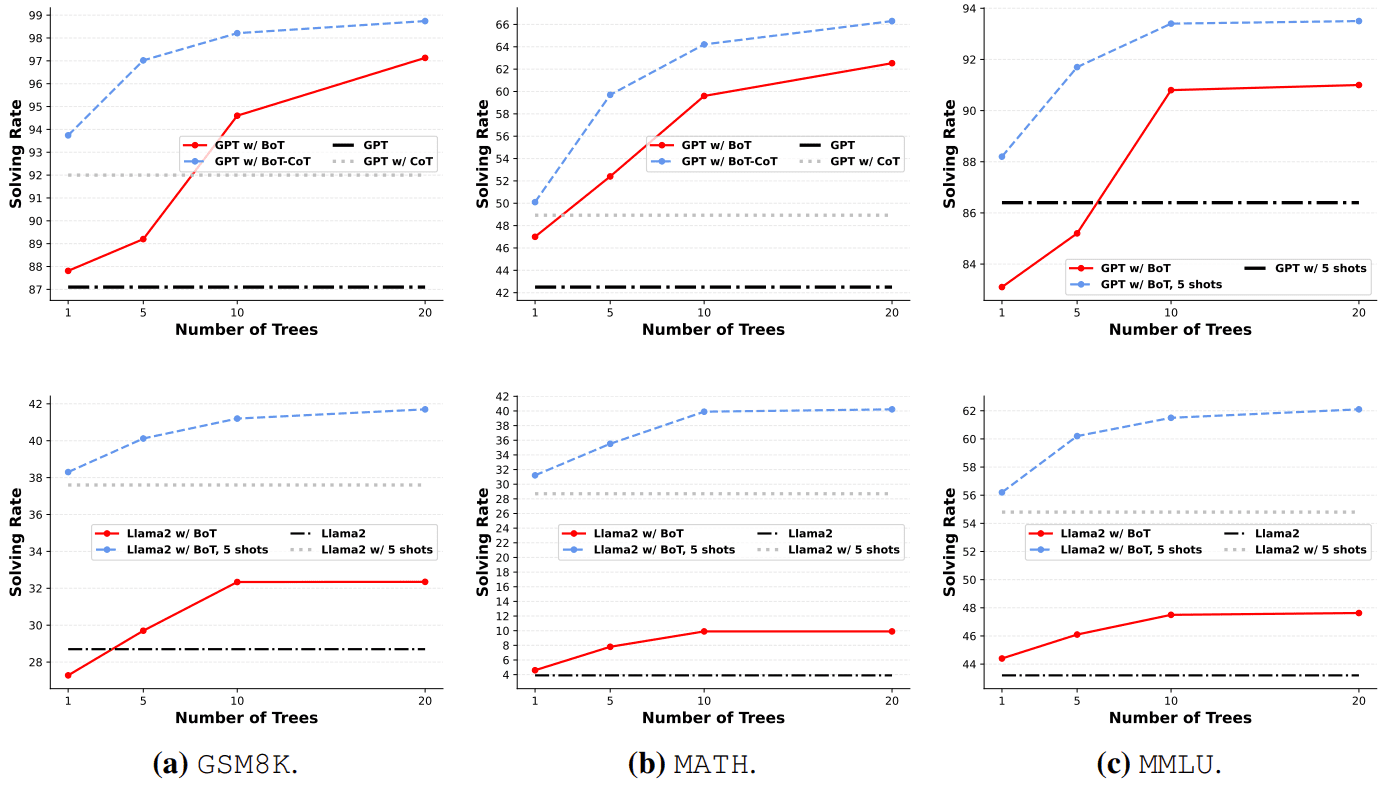
Abbildung 3: Verwendung von BoT und BoT+CoT zur Bewertung der Problemlösungsrate von GPT-4 OpenAI mit Llama2 Touvron et al. im Jahr 2023.

Wie in Abb. 3 zu sehen ist, verbessern GPT-4 und Llama2 die durchschnittliche Leistung von 11,61 TP3T bzw. 4,41 TP3T in den drei Datensätzen unter BoT-Bedingungen. Diese beiden Zahlen zeigen einen klaren Trend, dass BoT und BoT-CoT ähnlich gut abschneiden, wenn die LLMs leistungsfähiger sind, wie in Abbildung 3 dargestellt. Wenn sich die Anzahl der Bäume von 1 auf 20 ändert, zeigt sich außerdem ein ähnlicher Aufwärtstrend der Leistung. Aufgrund des schwächeren Llama2 kann BoT nicht von seinen Analysen profitieren, um einen erfahrungsgesteuerten iterativen Prozess durchzuführen, wie insbesondere in Abb. 3(a) gezeigt wird. Wenn gültige Erfolgsgeschichten vorliegen, d.h. 5 Tests, kann das BoT Llama2 immer noch helfen, mehr Probleme als die Baseline durch inkrementelle Verbesserungen zu lösen, wenn auch mit begrenzten Verbesserungen.

4.2 24-Punkte-Spiel

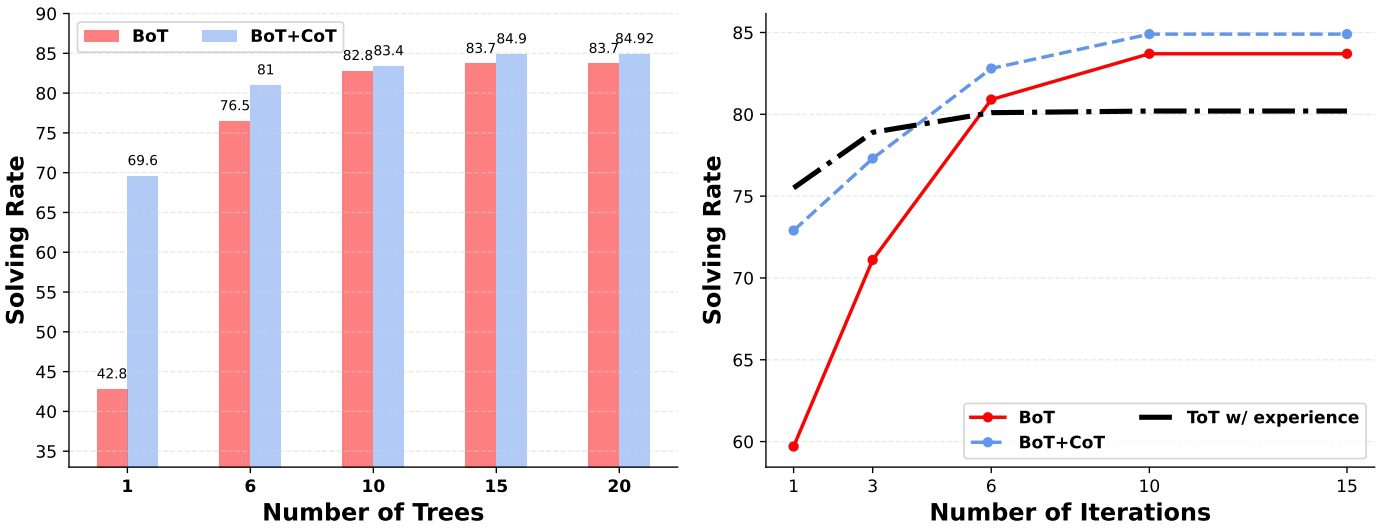
Abb. 4: Vergleich der drei Methoden bei unterschiedlicher Anzahl von Bäumen und Iterationen.

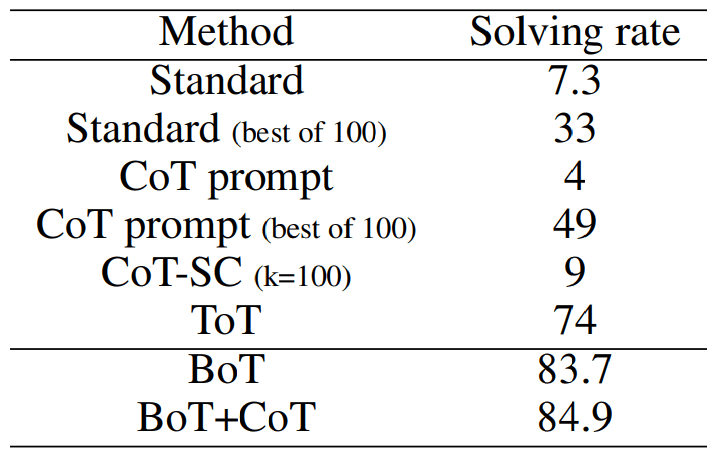
Tabelle 2: Aufbau der verschiedenen Methoden im 24-Punkte-Spiel in Anlehnung an den Aufbau in ToT Yao et al. (2024), deren Ergebnisse hier gezeigt werden.

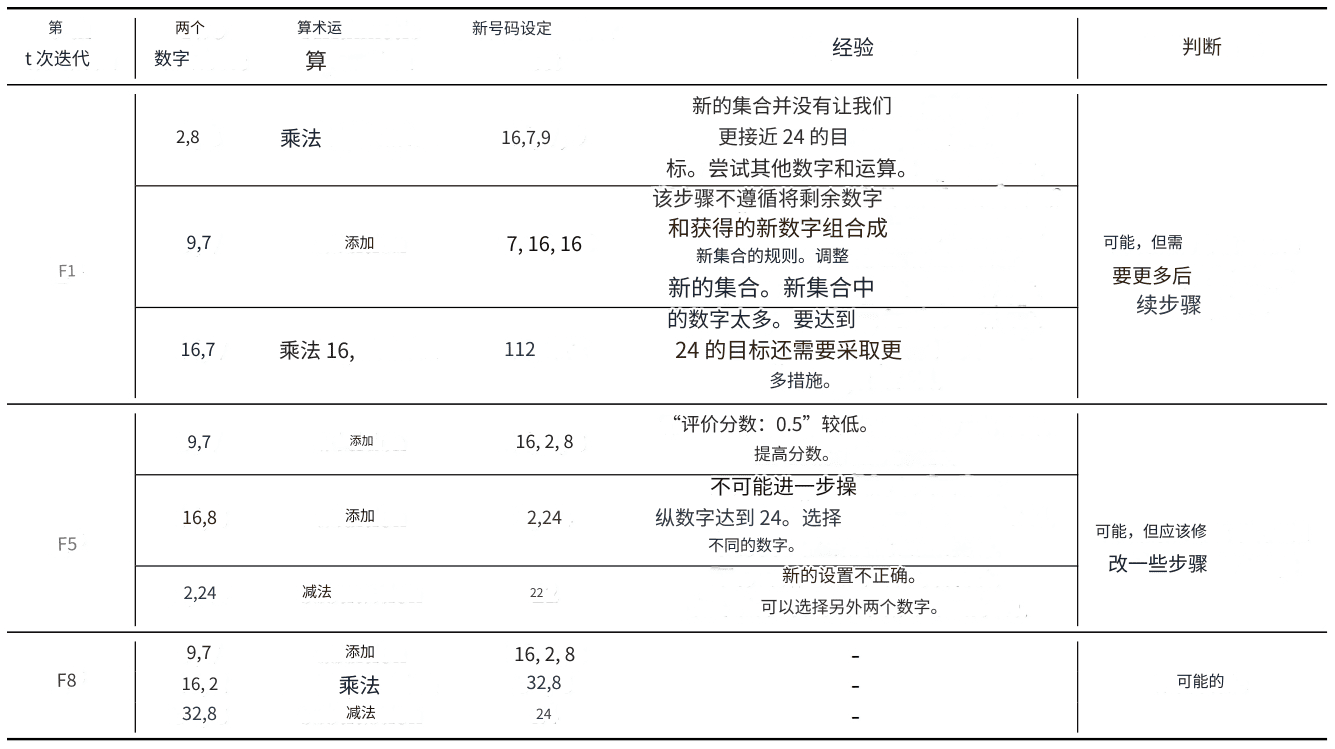
Tabelle 3: Zeigt den Denkprozess und die Erfahrungen, die während der ersten, fünften und achten Iteration gesammelt werden konnten. Die vier angegebenen Werte sind: 2, 7, 8 und 9.

Aufgrund der Schwierigkeit des Game of 24-Problems schnitten sowohl GPT-4 als auch Llama2 bei dieser Aufgabe schlecht ab, selbst bei der Kombination der Methoden CoT und CoT-SC. Das Llama2-Modell war nicht einmal in der Lage, die richtigen Regeln zur Lösung des Problems zu befolgen, was die Lösungsrate noch weiter senkte. Insbesondere bei der Anwendung von BoT, die auf Erfahrung beruht, sind alle Ergebnisse von Llama2 niedriger als 5%, ohne dass eine signifikante Verbesserung erzielt wird. Daher berichten wir nur über die Leistung von BoT mit GPT-4. Um einen fairen Vergleich zu erhalten, folgen wir dem von ToT Yao et al. (2024) vorgeschlagenen Aufbau.

Wie in Tabelle 2 gezeigt, übertrifft die BoT ohne menschliche Anmerkungen die ToT, die sich auf ein Beispiel verlässt, um alle möglichen nächsten Schritte zu zeigen, um 9,71 TP3 T. Zusätzlich übertrifft die BoT+CoT, die 5 CoT-Shots enthält, die BoT um 1,21 TP3 T. Die Leistungsnähe zwischen der BoT und der BoT+CoT ist auf den Boosting-Mechanismus zurückzuführen, der das schwache Denken inkrementell überarbeitet, wie in Unterabschnitt 4.1 diskutiert. Mit Hilfe eines erfahrungsgesteuerten iterativen Prozesses zeigt BoT eine verbesserte Leistung, wenn die Anzahl der Bäume M und der Iterationen T steigt. Wie in Abb. 4 zu sehen ist, ist BoT stärker von M und T abhängig als BoT+CoT, weil es Erfahrungen aus einer besseren Gedankenkette oder längeren Iterationen sammeln muss. Eine weitere Beobachtung ist, dass die Problemlösungsrate von 72,51 TP3T in der ersten Iteration auf 80,21 TP3T in der zehnten Iteration ansteigt, wenn ToT mit erfahrenen Hinweisen arbeiten kann, was darauf hindeutet, dass Erfahrung - die Analyse früherer Gedankenketten - von LLMs genutzt werden kann, um die Lösungsrate deutlich zu verbessern. Dies ist auf die Tatsache zurückzuführen, dass die Aggregationsphase von BoT die repräsentativste Argumentationskette in der aktuellen Iteration hervorbringt und somit mehr bedeutungsvolle Erfahrung zur Verbesserung des Hinweises liefert. Wir haben dies im Abschnitt über die Ablationsstudie überprüft.

Um besser zu demonstrieren, wie BoT aus Fehlern und früheren Vorschlägen lernt, zeigen wir in Tabelle 3, dass GPT-4 in der Lage ist, frühere Fehler zu vermeiden und spezifischere Vorschläge zu generieren, wenn die Anzahl der Iterationen steigt, was schließlich zur richtigen Lösung führt. In der ersten Iteration machten die LLMs aufgrund einfacher Hinweise sogar einen Fehler bei der Befolgung der Aufgabenregeln, weil die neue Menge in Schritt 3 falsch war. Nach der Analyse machte es den richtigen Vorschlag für diesen Fehler. Die Analyse der ersten Iteration war jedoch vage, z. B. "versuchen Sie andere Zahlen und Operationen". Nach fünf Iterationen fasste der BoT mehrere solcher Analysen zusammen, was zu effektiveren Hinweisen führte, die die LLMs dazu brachten, die richtigen Zahlen 9 und 7 zu wählen. Außerdem waren die Vorschläge spezifischer und nützlicher. Für die richtige Wahl wurde vorgeschlagen, die Bewertungsnote entsprechend zu erhöhen. Durch das Sammeln solcher Erfahrungen verfeinerte BoT schrittweise die Hinweise und generierte schließlich in der 8. Iteration direkt die richtige Lösung.

4.3 Studien zur Ablation

Tabelle 4: Vergleich von GPT-4 mit verschiedenen BoT-Varianten, die auf dem 24-Punkte-Spiel und dem AQuA-Datensatz verwendet wurden.

Alle Aggregationsstrategien führen zu hohen Lösungsraten, wenn Probleme und Vorschläge in einer "additiven" Weise zusammengefasst werden. Die Beibehaltung einer vollständigen Erfahrung ist besonders wichtig für revisionistisches Denken, vor allem für den AQuA-Datensatz, der ein breiteres Spektrum an mathematischen Argumentationsproblemen abdeckt. BoT(No), bei dem alle Argumentationsketten des Spannbaums direkt und ohne Aggregation verwendet werden, schneidet jedoch in allen Kontexten am schlechtesten ab, vor allem, wenn die kumulative Art der Erfahrung "kumulativ" ist. 15 Bäume werden in jeder Iteration von BoT konstruiert, und wenn man alle in einem Hinweis zusammenfasst, können wichtige Informationen verschleiert werden, ganz zu schweigen davon, dass die meisten von ihnen möglicherweise ungültig oder schädlich sind. Solche Erfahrungen können ungültig oder schädlich sein.

Die Einholung von Ratschlägen ist für den Anstoß zum Nachdenken entscheidender als alles andere.. In allen in Tabelle 4 genannten Beispielen erreicht die BoT-Variante, die Vorschläge als Erfahrung behandelt, die höchsten Lösungsraten. Im gleichen Fall des "additiven" Typs, ohne Vorschläge in der Erfahrung, sinkt die Leistung beispielsweise um mehr als 101 TP3T und 201 TP3T im "24-Punkte-Spiel" bzw. AQuA. BoTs mit Vorschlägen können nur dann die besten Lösungsraten erzielen, wenn sie mit Problemen gepaart sind. In AQuA zum Beispiel stieg die Lösungsrate von BoT (gierige Methode) um 4,41 TP3T.

Aus Leistungsgründen kann die Greedy Rallye die einzige Option sein, die notwendig ist. Im Gegensatz zum Ansatz der höchsten Priorität, bei dem eine der bestehenden Gedankenketten ausgewählt oder alle beibehalten werden, können gierige Agglomerationen die Baumstruktur adaptiv zu einer besseren Gedankenkette zusammenfügen, die in der aktuellen Iteration möglicherweise nicht vorkommt. Auf diese Weise kann LLM aussagekräftige Analysen einer robusteren Gedankenkette durchführen und als Ergebnis wichtige Lehren zur Ergänzung des Hinweises generieren. In AQuA, das mehr mathematische Probleme enthält, erreicht diese Zahl sogar 101 TP3 T. Wie in Abbildung 4 dargestellt, verfügt ToT zwar über einen ähnlichen erfahrungsgesteuerten Boosting-Mechanismus, der 801 TP3 T erreichen kann, liegt aber immer noch hinter BoT zurück, was darauf zurückzuführen sein könnte, dass es nicht in der Lage ist, gierige Agglomerationen in seiner Einzelbaumstruktur durchzuführen.

5. schlussfolgerung

In diesem Beitrag bestätigen wir, dass ein einfacher Hinweis zur Lösung komplexer Aufgaben verwendet werden kann, indem wir schrittweise Fehleranalysen der von ihm generierten Gedanken anhäufen. Wir schlagen ein neuartiges Rahmenwerk namens Boosting of Thoughts (BoT) vor, das diese allmähliche Erweiterung des Hinweises durch einen erfahrungsgesteuerten iterativen Prozess zur Erzeugung effektiver Gedankenketten ermöglicht. Eine einfache baumartige Gedankenkette, die durch iterative Erkundung und Selbsteinschätzung erzeugt wird, ermöglicht es, einen einfachen anfänglichen Hinweis schrittweise durch eine Reihe von Versuch-und-Irrtum-Erfahrungen zu erweitern, die zu einer genauen Lösung führen. Unsere umfangreichen Experimente zeigen, dass BoT in der Lage ist, bei mehreren Benchmark-Datensätzen Spitzenleistungen zu erzielen und andere führende Methoden bei der anspruchsvollen mathematischen Denkaufgabe Game of 24 zu übertreffen.

Ein BoT mit grundlegenden Aufforderungen und Argumentationsprozessen

A1 BoT für die Komponente Gedankengenerierung

In diesem Abschnitt werden die grundlegenden Hinweise erwähnt, die für die Generierung von Argumenten für das vorgeschlagene Boosting of Thought (BoT) verwendet werden. Für spezifische Details können Sie die Beispieldatei des Quellcodes besuchen: /examples/BoostingOfThought/BoT reasoner.py.

System-Tipp:

Sie sind ein Experte für mathematische Probleme. Führen Sie schrittweises Problemlösen durch, indem Sie aus einer Reihe von Versuch-und-Irrtum-Problemlösungen lernen. Zu diesen Versuch-und-Irrtum-Erfahrungen gehören insbesondere Fehlerberichte sowie detaillierte Vorschläge zur Änderung früherer Argumentationsschritte. Es ist wichtig, diese aufgelisteten Erfahrungen zu überprüfen, bevor man neue Argumentationsschritte entwickelt, um die Wiederholung von Fehlern zu vermeiden und gleichzeitig die richtigen Schritte zu verwenden, um bessere Argumentationsschritte für die Lösung von Problemen zu entwickeln.

 

System-Eingabeaufforderung S.

Sie sind ein Experte für mathematische Probleme und können Schritt für Schritt argumentieren.
zur Problemlösung, indem sie zunächst aus einer Reihe von Versuch-und-Irrtum-Erfahrungen lernen.
Eine solche Trial-and-Error-Erfahrung beinhaltet insbesondere Fehlerberichte und detaillierte Hinweise zu
Wie man die Schritte des historischen Denkens überarbeitet. Erinnern Sie sich immer an diese aufgelisteten Erfahrungen, bevor Sie eine
neuen Argumentationsschritt, wodurch dieselben Fehler vermieden und korrekte Schritte wiederverwendet werden, um die
bessere Argumentationsschritte zur Lösung der Aufgabe.

Erzeugen Sie eine Aufforderung für den nächsten Gedanken:

f"""

{Mission Alert} \n

Erinnern Sie sich zunächst an die vorherige Argumentationserfahrung: \n\n

 

{Erfahrung}

 

Bitte stellen Sie den nächsten möglichen Argumentationsschritt vor, wobei es nur einen geben kann. Dieser Argumentationsschritt sollte als sequentieller Nachfolger der folgenden geordneten Schritte verwendet werden und sollte mit einer entsprechenden Bewertungspunktzahl versehen werden (höhere Punktzahlen bedeuten eine höhere Wahrscheinlichkeit, die Aufgabe zu lösen):\n\t

(chain hint)

 

Erzeugen Sie auf der Grundlage der obigen Schritte der Vorgeschichte (oder ignorieren Sie sie, wenn der obige Bereich leer ist) einen eindeutigen nächstmöglichen Schritt auf der Grundlage der Aufgabenregeln. (WICHTIG: Erzeugen Sie bitte nur den nächstmöglichen Folgerungsschritt für einen bestimmten Schritt).

"""

f"""{Aufgabenstellung}. \n Zunächst einmal, erinnern Sie sich an historische Argumentationserfahrungen: \n\n {
Erfahrungen} \n\n Bitte machen Sie einen Schritt der Argumentation, um nur einen nächsten
Dieser nächste Argumentationsschritt ist der Folgeschritt von Dieser nächste Argumentationsschritt ist der Folgeschritt von
die folgenden geordneten vorherigen Schritte , zusammen mit ihren bewerteten Noten (A
Eine höhere Punktzahl bedeutet, dass die Aufgabe mit größerer Wahrscheinlichkeit gelöst werden kann). : \n\t{
Kette prompt}\n\n Auf der Grundlage der aufgelisteten vorherigen Argumentationsschritte (ignorieren Sie diese, wenn die
obiges Feld leer ist), erzeugen Sie einen einzigen möglichen nächsten Schritt nach der Aufgabe
Regel . (Hervorgehoben: Bitte erzeugen Sie nur einen einzigen möglichen nächsten Argumentationsschritt von
die angegebenen Schritte). """

Die Aufgabenaufforderung enthält das X und Q der Aufgabe, und die historische Erfahrung ist F1.... Der Teil "Kettenhinweis" ist {Gi}, der ein Platzhalter ist, der beim Ausführen des aktuellen Gedankens zi durch die vorherige Gedankenreihe z1...,i-1 ersetzt wird. ,i-1.

Tipps zum Nachdenken über die Bewertung:

f"""

{Mission Alert} \n\n

Nachfolgend sind die Argumentationsschritte in der richtigen Reihenfolge aufgeführt, zusammen mit den jeweiligen Bewertungsergebnissen. (Eine höhere Punktzahl bedeutet, dass der Schritt eher geeignet ist, die Aufgabe zu lösen). \n

{Ketten-Hinweis

{Das Denken}

Mit welcher Punktzahl bewerten Sie, wie logisch und korrekt diese Argumentationsschritte sind und wie hilfreich sie für die endgültige Lösung sind? Bitte wählen Sie eine von [0.1, 0.3, 0.5, 0.7, 0.9, 1.0] als Punktzahl, wobei höhere Punktzahlen für bessere Argumentationsschritte stehen. Die Punktzahl sollte für den Benutzer lesbar hinter "Bewertungspunktzahl:" stehen. """"

 

f"""{Aufgabenstellung}. \n\n Nachfolgend sind die generierten Argumentationsschritte in der Reihenfolge aufgeführt.
zusammen mit ihrer Bewertung (eine höhere Punktzahl bedeutet, dass der Argumentationsschritt
die Aufgabe wahrscheinlicher zu erledigen). Was ist Ihr Gedanke?
Bewertungspunkte für die Logik, die Korrektheit und den Nutzen, um zu einer endgültigen
Lösung für diese Argumentationsschritte? Bitte wählen Sie einen Wert aus [0.1, 0.3, 0.5,
0,7, 0,9, 1,0] als Punktzahl, wobei eine höhere Punktzahl bessere Argumentationsschritte bedeutet. Die
score sollte nach " Evaluation score :" stehen, damit die Benutzer es lesen können .""""

In diesem Fall ist das Denken das Denken Zi, das gerade im Gange ist.

A2 BoT für die Komponente Erlebnispädagogik

Um Feedback zu aggregierten Ketten zu erzeugen, verwenden LLMs die folgenden grundlegenden Aufforderungen. Weitere Informationen finden Sie auch im Quellcode examples/BoostingOfThought/BoT commenter.py.

System Prompt S: Sie sind ein KI-Experte für Maths Answers und arbeiten an der Bewertung der Argumentationskette, die zur Lösung eines mathematischen Problems erstellt wurde. Bitte bewerten Sie jeden Argumentationsschritt dieser Argumentationskette, indem Sie eine detaillierte Analyse erstellen, um festzustellen, ob der aktuelle Schritt eine logische Schlussfolgerung aus dem vorherigen Schritt ist und ob der Argumentationsschritt zur richtigen Lösung beiträgt. Geben Sie bitte für jeden fehlerhaften Argumentationsschritt einen Fehlerbericht und entsprechende Änderungsvorschläge an. Geben Sie für jeden korrekten Argumentationsschritt eine Beschreibung der Empfehlung oder Ablehnung.

System-Tipp:

Ihre Rolle ist die eines geschickten AI Maths Answer Reviewers, der sich darauf konzentriert, den Denkprozess beim Lösen von Matheaufgaben zu bewerten. Sie müssen jeden Argumentationsschritt durch eine erschöpfende Analyse beurteilen, um zu sehen, ob er auf der Logik des vorherigen Schritts basiert und ob dieser Schritt dazu beigetragen hat, die richtige Antwort zu finden. Wenn Sie auf einen falschen Rechenschritt stoßen, müssen Sie Vorschläge und Möglichkeiten zur Änderung machen. Bei korrekten Argumentationsschritten müssen Sie diese bejahen oder andere Optionen angeben.

 

System-Eingabeaufforderung S.

Sie sind ein Experte für AI-Checker für mathematische Antworten, der sich der Bewertung der
Argumentationskette zur Lösung des mathematischen Problems. Beurteilen Sie jede Argumentation
Schritt dieser Argumentationskette, indem er detaillierte Analysen darüber liefert, ob der aktuelle Schritt ein logischer ist
Schlussfolgerung des vorangegangenen Schritts und ob der Schlussfolgerungsschritt der richtigen Lösung zuträglich ist.
Geben Sie Ratschläge und Vorschläge für jeden Argumentationsschritt mit Fehlern. Geben Sie eine Empfehlung oder
Ablehnungsbeschreibungen für jeden korrekten Argumentationsschritt.

Feedback-Tipp:

f"""

Für die gegebene Aufgabe:{Task hint}. \n

{Grundlagenketten-Hinweise}

Bitte bewerten Sie diese Argumentationskette und formulieren Sie eine ausführliche Kritik, die die folgenden Punkte umfasst. \n

1. {Ketten-Feedback-Format}. 2. {Schritt-Feedback-Format}. 3. {Vertrauens-Feedback-Format}. 4. \n\n

Caveat: {Caveat}

 

f"""Gegebene Aufgabe:{Aufgabenaufforderung}. \n{chain prompt}\n\n Bitte bewerten Sie diese Argumentationskette
indem sie ausführliche Kommentare mit folgendem Inhalt abgeben. \n 1.{
Format der Kettenrückmeldung }. 2.{ Format der Schrittrückmeldung }. 3.{ Format der Vertrauensrückmeldung }. \n
\n Hinweis: {Notice}.

darunter auchHinweise zur Argumentationsketteist eine aggregierte Inferenzkette z1.... .n.

Format der KettenrückmeldungKann diese Argumentationskette die Aufgabe korrekt erfüllen und das Ziel erreichen, indem sie ihre Argumentationsschritte ausführt? Warum? Schreiben Sie die abschließende Analyse unter "Analysebericht:" auf.

Schritt-für-Schritt-Feedback-FormatFür jeden Argumentationsschritt geben Sie bitte eine detaillierte Analyse, ob der aktuelle Schritt eine logische Ableitung aus dem vorherigen Schritt ist und ob der Argumentationsschritt zur richtigen Lösung beiträgt. Geben Sie bitte für jeden fehlerhaften Argumentationsschritt einen Fehlerbericht und entsprechende Empfehlungen zur Überarbeitung an. Geben Sie für jeden Argumentationsschritt eine Beschreibung der Empfehlung oder Ablehnung. Die Kommentare sollten prägnant sein und folgendem Format folgen: Argumentationsschritt ⟨idx⟩. Analysen ⟨idx⟩. Empfehlung:. Empfehlung oder Ablehnung Beschreibung:.

Format des VertrauensfeedbacksWie hoch ist Ihr Vertrauen in diese Bewertungen und Rezensionen? Bitte wählen Sie einen Wert aus [0,1, 0,3, 0,5, 0,7, 0,9, 1,0] als Wert, den der Benutzer lesen kann.

Mit Hilfe von Feedback-Hinweisen erzeugen LLMs empirische Ft, die Schlussfolgerungen und Analysen der Argumentationskette und jedes Argumentationsschritts enthalten.

A3 Begründungsprozess

Um das Verständnis des vorgeschlagenen Boosting of Thoughts zu erleichtern, fassen wir den Inferenzfluss in Algorithmus-Tabelle 1 zusammen. Der Quellcode dieses Flusses ist in der Datei examples/BoostingOfThought/BoT core.py zu finden.

BoT Original

Der Inhalt des Bildes ist eine schrittweise algorithmische Darstellung einer Theorie, die "BoT" genannt wird, und das Folgende ist ihre chinesische Übersetzung, die den folgenden algorithmischen Schritten entspricht:

Algorithmus 1: Der Hauptschlussfolgerungsprozess von BoT

Eingaben: Anzahl der Iterationen T, Anzahl der Baumstrukturen M, Problem Q.
Ausgabe: aggregierte Kette z̄_1.... .n^T

1. einen einfachen Hinweis I^0 (S, X, Q, F^0, {Gi}) initialisieren, wobei F^0 eine leere Zeichenkette sein wird.
2. jede Iteration t = 1, 2, ... , T.
3. die Stichwörter I^t-1 (S, X, Q, F^t-1, {Gi}) mit dem LLMS (Low Latent Mixed Model) zu verwenden, um M verschiedene Gedankenstrukturen in einem Prozess namens Thought Structure Generation zu erzeugen.
4. extrahiere die Gedankenkette {z̄_i=1....n^m} aus M Gedankenstrukturen, jede z̄_i=1.... .n^m}, jedes z̄_i=1... .n^m ist die beste Gedankenkette der m-ten Baumstruktur.
5. die Methode der "Best-First-Aggregation" oder "Greedy-Aggregation" anwenden, um {z̄_i=1...n^m} in eine einzige Gedankenkette z̄_1...n^m} zu überführen. .n^m} in eine einzige Gedankenkette z̄_1...n^t. .n^t.
6. verwenden Sie LLMS, um eine "Gedankenkettenanalyse" für z̄_1.... .n^t durchzuführen, eine Rückmeldung zu erhalten und diese mit z̄_1.... .n^t und kombinieren sie mit z̄_1...n^t, um die Erfahrung F^t zu erhalten.
7. den Hinweis durch Akkumulation von F^t zu I^t aktualisieren (S, X, Q, F^t-1,t, {Gi}).
8. schlussfolgerung
9. der Zugang zu Lösungen z̄_1.... .n^T

B Einblicke zur Förderung des Denkens

Die Verstärkung der Gedanken beruht auf unserer Erkenntnis, dass die Fähigkeit von Large Language Models (LLMs), mathematische Probleme zu lösen, direkt von Erfahrungen abgeleitet ist, die Analysen und Vorschläge für frühere Fehler enthalten. Sobald die Hinweise gültige historische Argumentationserfahrungen enthalten, an die sich LLMs vor der Durchführung der Argumentation erinnern können, sind die resultierenden Argumentationsschritte typischerweise logischer und rationaler, wie der Vergleich der Tabellen 5 und 6 zeigt. Diese Erkenntnisse führten uns auch zu der Überlegung, dass LLMs sich nicht in hohem Maße auf gut vorbereitete Prompts für jede Aufgabe verlassen müssen (mehrere Gedankenketten-Demonstrationen in den Prompts dienen als Beispiele). Da LLMs jedoch in der Lage sind, aus Erfahrung zu lernen, können wir mit einer einfachen Aufforderung beginnen, die keine Beispiele oder manuell gestalteten Inhalte erfordert, und nach und nach Erfahrungen sammeln, während wir argumentieren. Letztendlich erreichen LLMs durch das Sammeln von Erfahrungen mit dem Hinweis eine robuste Argumentation zur Lösung komplexer Probleme. Auf der Grundlage dieser Erkenntnisse wurde Boosting of Thoughts als automatisierter Prompting-Rahmen entwickelt, der Probleme durch iteratives Sammeln einer Sammlung von Versuch-und-Irrtum-Erfahrungen löst. Wir argumentieren, dass das vorgeschlagene BoT keine Anwendung von LLMs auf eine spezifische Aufgabe ist, sondern vielmehr auf der Einsicht aufbaut, dass die Argumentationskraft von LLMs direkt aus der Analyse der Fehleranalyse von fehlerhaften Inferenzketten gewonnen werden kann, ohne sich auf menschliches a priori Wissen zu verlassen.

Um unsere Erkenntnisse hervorzuheben, teilen wir die folgenden drei Schlüsselbeobachtungen mit, die auf dem folgenden Datensatz von 24 Spielen basieren, der aus einer Anwendung mit dem gpt-3.5-Turbomodell mit einer Temperatur von 0,7 und einem Top-P-Wert von 0,7 stammt.

Die Erfahrungen in den Prompts ermutigen die LLMs, ihre Antworten logischer zu gestalten.Wie aus Tabelle 5 hervorgeht, generierte das Modell fünfmal denselben Argumentationsschritt, wenn keine Erfahrung im Hinweis enthalten war. Diese Beobachtung zeigt ein häufiges Problem bei LLMs, nämlich die fehlende Eigenmotivation, verschiedene Argumentationslogiken zu erkunden. So kann es sein, dass LLMs trotz ihres starken Denkpotenzials in einem Zyklus stecken bleiben, der mit dem einfachsten Denkschritt beginnt, der möglicherweise nie zu einer endgültigen Lösung führt. Der Abschnitt "Acquired Reasoning Chains" in Tabelle 5 zeigt fehlerhafte Schlussfolgerungsketten. Wir gehen davon aus, dass solche sich wiederholenden Schlussfolgerungsschritte, wie in Tree of Thoughts Yao et al. (2024), wo die Knoten des Baums durch die Generierung mehrerer Antworten als Gedanken konstruiert werden, den Algorithmus in einigen Fällen zum Scheitern bringen können. In der zweiten Iteration von BoT führte die Einführung von Erfahrung in die Prompts jedoch zur Generierung verschiedener anfänglicher Inferenzschritte, wie in Tabelle 6 dargestellt. Die endgültige Inferenzkette kann schließlich zur richtigen Lösung führen, wenn sie von einer größeren Bandbreite möglicher Logiken ausgeht.Weng et al. (2023)

LLMs vermeiden es, ähnliche Fehler zu machen, die in der Erfahrung hervorgehoben wurden.Wenn die Erfahrung nicht in die Aufforderungen einbezogen wird, die eine Fehleranalyse beinhalten, werden die LLMs viele Fehler machen, wie z.B. das Abweichen von den Aufgabenregeln und das Zurückfallen auf den anfänglichen Argumentationsschritt im endgültigen Prozess, wie im Abschnitt "Erworbene Argumentationskette" in Tabelle 5 gezeigt. Nach der Analyse dieser Argumentationskette und der Einbeziehung des Feedbacks als Erfahrung in die Prompts für die zweite Iteration des BoT ist aus Tabelle 6 ersichtlich, dass die LLMs die Erfahrung gut lernen, bevor sie argumentieren. Erstens wiederholte keine der Antworten die gleichen fehlerhaften Argumentationsschritte wie die verschiedenen anfänglichen Argumentationsschritte, die in "Fünf Antworten von gpt-3.5-turbo" gezeigt werden. Zweitens konnten die LLMs alle zuvor identifizierten Fehler erfolgreich vermeiden, indem sie sich strikt an die Aufgabenregeln hielten, falsche Schlussfolgerungen ausschlossen und logische Schlussfolgerungsschritte durchführten. Drittens führte dies schließlich zur korrekten Lösung der Aufgabe "1 1 4 6" (Game of 24). Andere Arbeiten, wie Weng et al. (2023); Madaan et al. (2023); Zheng et al. (2023), haben ebenfalls die Bedeutung der Ergänzung von Hinweisen durch Feedback, d. h. eine Selbsteinschätzung früherer Antworten, hervorgehoben. BoT ist jedoch eine bahnbrechende Arbeit, die auf der Einsicht beruht, dass Erfahrung, die eine Fehleranalyse einschließt, zu einer starken Argumentation bei LLMs führen kann.

Ohne menschliche Anmerkungen organisieren LLMs automatisch effektive Argumentationsketten, um komplexe Probleme auf der Grundlage von Erfahrungen zu lösen.BoT ist die bahnbrechende Initiative, die ein automatisiertes Prompting-Rahmenwerk vorschlägt, das die Einsicht nutzt, dass LLMs effektive Argumentationsfähigkeiten zur Problemlösung durch Fehleranalyse und Anleitung allein durch Erfahrung erwerben können, ohne dass eine menschliche Kommentierung erforderlich ist. Wie in Tabelle 5 gezeigt, ist dies die erste Iteration von BoT, und die anfänglichen Hinweise enthalten nur grundlegende Aufgabenanleitungen und Fragen ohne kontextbezogene Lernbeispiele wie in CoT. Obwohl die Inferenzketten, die von LLMs unter Verwendung solcher Eingabeaufforderungen erhalten wurden, viele Fehler und ungültige Inferenzschritte enthalten, können ihre Fehleranalysen und Vorschläge als gelernte Lektionen in die Eingabeaufforderungen aufgenommen werden, um von der zweiten Iteration der Inferenz zu profitieren, wie in Tabelle 6 gezeigt. Es kann beobachtet werden, dass LLMs ohne menschliche Anleitung zum korrekten Schlussfolgern Wissen aus Erfahrung gewinnen können, einschließlich Fehleranalysen und Anleitungen, die aus zuvor generierten Schlussfolgerungsketten gewonnen werden, was zu inkrementellen Verbesserungen beim Lösen von Schlussfolgern führt.

Somit bietet unser BoT eine langfristige Orientierung für die Forschung, da es die Bedeutung der Analyse von Erinnerungsfehlern und Vorschlägen aufzeigt, wenn LLMs in die Lage versetzt werden, effektive Denkprozesse für komplexe Aufgaben zu entwickeln. Mit diesen Erkenntnissen kann sich die Cue-Engineering-Forschung zur Induktion von Argumentationsfähigkeiten bei LLMs darauf konzentrieren, wie man Erfahrungen generiert, anstatt mehr menschliches A-priori-Wissen einzuführen.

C Generierung von Denkstrukturen

BoT ist ein automatisiertes Prompting-System, das iterativ Erfahrungen aus Inferenzkettenanalysen sammelt. Als solches ist BoT auf eine Vielzahl von Methoden zur Gedankengenerierung und LLMs verallgemeinerbar, die in der Lage sind, Schlussfolgerungsschritte zu generieren und zu bewerten.Darüber hinaus hängt die Leistung von BoT von der Effektivität seiner Gedankengenerierungsstruktur ab. Daher verwendet BoT die neueste Struktur, den Tree of Thought (ToT) Yao et al. (2024), als Basismodell für die Generierung von Argumentationsketten in jeder Iteration. Wie im Hauptbeitrag erwähnt, könnte das Basismodell für die Generierung von Gedanken auch ein Thinking Graph (GoT) Besta et al. (2023) sein, d. h. BoT mit GoT. Aufgrund von Zeitbeschränkungen und der Tatsache, dass der aktuelle GoT noch nicht auf mathematische Probleme angewendet wurde, verwendet das BoT-Design jedoch ausschließlich ToT. Letztendlich erzeugt die vorgeschlagene BoT heterogene Baumstrukturen, von denen jede ein leicht gewichteter Binärbaum ist.

C1 Next Thinking Generation und Kantengewichtsberechnung

Unter Verwendung des in Abschnitt A besprochenen Hinweises zur Generierung des nächsten Gedankens können LLMs Hinweise generieren, indem sie die Erfahrung F1.... .t und Ersetzen von {Gi} durch z1... ,i-1 ersetzt {Gi}, um den nächsten möglichen Gedanken für einen Argumentationsschritt zi zu generieren. Für einen Argumentationsschritt zi verwenden LLMs den Gedankenbewertungshinweis, um Bewertungswerte als Kantengewichte zwischen zi und zi-1 zu erzeugen. Der Quellcode in examples/BoostingOfThought/BoT reasoner.py enthält eine detaillierte Beschreibung des Verfahrens. Als direktes Beispiel für die Anwendung von BoT auf "3 5 6 8" in Game of 24 unter Verwendung von gpt-3.5-turbo zeigen die Tabellen 7 und 8 die Generierung des Gedankens, während Tabelle 9 zeigt, wie er berechnet wird.

C2 Der Bedarf an heterogenen Baumstrukturen

In jeder Iteration von BoT wird die heterogene Baumstruktur aufgebaut, um einen größeren Suchraum für Inferenzen zu erkunden und die Robustheit zu verbessern. Wie im Quellcode unter examples/BoostingOfThought/BoT core.py zu sehen ist, werden die Temperatur- und Top p-Werte der LLMs in jedem Baum aus den Bereichen [0.2, 0.4, 0.6, 0.7, 0.9, 1.1, 1.5] bzw. [0.1, 0.3, 0.5, 0.7, 0.9] ausgewählt. Die Baumwachstumsstrategie kann Schicht für Schicht oder Blatt für Blatt erfolgen. Wir haben die folgenden zwei Vorteile dieser Heterogenität festgestellt.

Die Heterogenität erweitert den Suchraum für die Inferenz und erhöht somit die Konvergenzgeschwindigkeit.Wenn verschiedene Bäume für unterschiedliche Zwecke konstruiert werden, z. B. unter Verwendung einer Schicht-für-Schicht-Strategie oder unter Verwendung einer Blatt-für-Blatt-Strategie und basierend auf zufälligen oder deterministischen LLMs, können die generierten Schlussfolgerungsschritte und die daraus resultierenden Schlussfolgerungsketten signifikante Unterschiede aufweisen, die effektiv eine größere Bandbreite an Schlussfolgerungsmöglichkeiten abdecken. Wenn LLMs beispielsweise in einer Iteration den nächsten Gedanken mit größerer Zuversicht generieren, werden kontinuierlich ähnliche Gedanken erforscht; andernfalls neigen LLMs mit größerer Zufälligkeit dazu, verschiedene Gedanken zu generieren. Es ist oft schwer vorherzusagen, ob deterministisches Denken oder Zufälligkeit zu einer Lösung beitragen wird. Die Gewährleistung von Heterogenität durch die Mischung verschiedener Arten von logischen Denkschritten ermöglicht es uns daher, den Denkraum in einer einzigen Iteration vollständig zu erforschen, was letztlich die nachfolgenden Iterationen erleichtert. In der Ablationsstudie vergleichen wir die BoT-Leistung zwischen heterogenen und homogenen Baumstrukturen.

Heterogenität verringert die Wahrscheinlichkeit, ungültige oder falsche Schlussfolgerungsketten zu erzeugen, und erhöht damit die Robustheit.Im Gegensatz zur Heterogenität neigen die einzelnen Bäume bei einem homogenen Aufbau dazu, einem konsistenten logisch-generativen Denken zu folgen und Schlussfolgerungsketten mit der gleichen Baumstruktur zu bilden. Wenn dann die Logik falsch ist oder die zugrunde liegende Struktur für das vorliegende Problem nicht gültig ist, können die Schlussfolgerungsketten aller Bäume, die durch BoT in jeder Iteration erhalten werden, nur verrauschte und falsche Schlussfolgerungsschritte enthalten. Selbst wenn man sie aggregiert, um eine verfeinerte Argumentationskette für die Auswertung zu erhalten, kann die Erfahrung immer noch erheblich von der Bereitstellung geeigneter Problemlösungsvorschläge abweichen. Daher kann eine heterogene Baumstruktur dazu beitragen, die Wahrscheinlichkeit zu verringern, dass in nachfolgenden BoT-Iterationen keine gültigen Argumentationsketten zur Bewertung zur Verfügung stehen. Diese erhöhte Robustheit ermöglicht es dem BoT, Probleme mit unterschiedlichen Schwierigkeitsgraden zu lösen.

Dieses Bild zeigt den Prozess der "Aggregation mit höchster Priorität" und der "gierigen Aggregation".

Eingabe: m Inferenzketten, wobei der Inferenzschritt der m-ten Kette mit z1i = 1m bezeichnet wird.
Ausgabe: Polymerkette z1..n.

1 - Aggregation mit höchster Priorität
2 Für jede Kette m = 1, 2, ... , M tun
3 Berechnen Sie die Summe der Kantengewichte der m-ten Kette als Vm = ∑i im Bereich m1m Vi-1,i.
4 Ende
5 Ermitteln Sie die optimale Kette unter M Ketten, indem Sie m* = arg maxm {Vm}
6 Weisen Sie die aggregierten Ketten als optimal zu, z1.... .n := {z1i=1n*m*}

7 - Gierige Aggregation
8 z1 := z1 wobei m* = arg maxm {V1m}.
9 Für jeden Aggregationsschritt i = 2, ... , n tun
10 Für jede Kette m = 1, 2, ... , M tun
11 Sammeln Sie Jm = {j, sim(z1i-1, z1j) > 0,7; j ∈ n1m}.
12 Behalten j*,m = arg maxj∈Jm {Vj,j+1m}
13 Ende
14 Führen Sie Folgendes durch, um den optimalen nächsten Inferenzschritt zu erhalten: zi = z1j*+1 mit j* = arg maxj∈{j*m}1M {Vj,j+1m}.
15 Ende
16 Erhalt von Polymerketten z1.... .n.

Dabei handelt es sich im Wesentlichen um ein algorithmisches Flussdiagramm, das beschreibt, wie eine Datenkette oder ein Knotenpunkt optimiert werden kann, um mit verschiedenen Methoden die besten Ergebnisse zu erzielen.

D Gedankenstruktur-Aggregation

Nach Abschluss der Argumentation in einer heterogenen Baumstruktur extrahiert der BoT-Aggregationsprozess zunächst die besten Argumentationsketten aus jedem Baum und kombiniert sie dann zu einer einzigen Argumentationskette, indem er entweder die Best-First- oder die Greedy-Aggregationsmethode verwendet. Detailliertere Informationen zu diesen beiden Aggregationsmethoden finden Sie im Quellcode examples/BoostingOfThought/BoT aggregator.py.

Wie im ersten Block von Algorithmus 16 gezeigt, ist die Best-First-Aggregation eine unkomplizierte Aggregationsmethode, die direkt die Kette mit der höchsten Summe der Kantengewichte extrahiert. Diese Methode ist schnell und stabil. Sie garantiert in der Regel eine wettbewerbsfähige Leistung, da durch die Analyse der erhaltenen optimalen Ketten weitere Erfahrungen gesammelt werden können. Sie kann jedoch nur bestehende Ketten ohne effiziente Abstimmung auswählen. Die Greedy-Aggregation ist fortschrittlicher, weil sie die Inferenzschritte in verschiedenen Ketten kombiniert, um eine neue und bessere Inferenzkette mit den höchsten Kantengewichten zu erzeugen. Der Greedy-Aggregationsprozess in Algorithmus 16 besteht aus zwei Schritten. Zunächst werden die Inferenzschritte gesammelt, die dem aggregierten Inferenzschritt zi-1 ähnlich sind. Daher wird der nächste aggregierte Inferenzschritt aus dem nächsten Inferenzschritt in dieser Sammlung ausgewählt, indem die Kantengewichte maximiert werden. sim ist eine Ähnlichkeitsfunktion, die den Prozentsatz der gleichen Wörter und mathematischen Zahlen zwischen zwei Passagen unter Verwendung von LLMs bewertet. 0,7 ist ein empirischer Schwellenwert, der aus den Experimenten gewonnen wurde.

E Auswirkungen einer fehlerhaften Rückmeldung

Die Rückmeldungen, die man durch die Auswertung der aggregierten Inferenzkette erhält, können eine eingeschränkte Nutzung der Analysen und völlig falsche Schlussfolgerungen und Fehlermeldungen beinhalten. Dieses Problem wird in der Regel durch die Natur von LLMs verursacht, die Sprachmodelle sind und die Genauigkeit des generierten Textes nicht von sich aus überprüfen. Außerdem sind die Fähigkeiten von LLMs, wie gpt-3.5-turbo, begrenzt, wenn sie als Validatoren für mathematische Probleme verwendet werden.

Ein einfaches Beispiel ist in Tabelle 7 dargestellt. Die Analyse kommt zu dem Schluss, dass "das in Schritt 3 erhaltene Endergebnis 80 ist, was mathematisch gleich 24 ist. "Schlimmer noch, die Erfahrung beinhaltet weiterhin, dass "die Argumentationskette korrekt ist" und dass "keine Fehler in den Argumentationsschritten gefunden wurden". Es wurden keine Fehler gefunden." Unter Verwendung dieser Erfahrung als Eingabehinweis wird das BoT in der ersten Iteration dazu verleitet, den falschen Schlussfolgerungsschritt zu erzeugen, und die entsprechende Aggregationskette ist am Anfang von Tabelle 8 zu sehen. Es ist klar, dass die Aggregationskette logisch falsch ist und keiner der Regeln des Game of 24 entspricht.

Wir argumentieren jedoch, dass fehlerhafte Rückmeldungen nicht verstärkt werden, sondern dass ihre negativen Auswirkungen auf die generierten Argumentationsschritte in nachfolgenden Iterationen durch den iterativen Mechanismus der BoT abgeschwächt oder sogar vollständig korrigiert werden können. Der Hauptgrund dafür ist, dass die erzeugten fehlerhaften Argumentationsschritte weiter analysiert werden, um neue Erfahrungen zu generieren, die dem Hinweis hinzugefügt werden. Da diese Argumentationsschritte leicht erkennbare und offensichtliche Fehler enthalten, neigen LLMs dazu, korrekte Fehleranalysen zu erstellen und effektive Revisionsvorschläge zu liefern. Mit der neuen Erfahrung, die in den Hinweisen enthalten ist, ist der BoT in der Lage, korrekte Argumentationsschritte zu generieren. Wie die Erfahrungen in Tabelle 8 zeigen, generierte der BoT detaillierte Fehlerberichte und Revisionsvorschläge, was zu einem rationalen Gedankengenerierungsprozess führte.

Der Vorteil von BoT bei der Nutzung von Iterationen zur Abschwächung der nachteiligen Auswirkungen von Fehlerrückmeldungen ist in Abbildung 4 ersichtlich. Bemerkenswert ist, dass sich die Leistung von BoT mit zunehmender Anzahl der Iterationen stetig verbessert. Dies unterstreicht die Bedeutung der kumulativen Erfahrung und die Fähigkeit der nachfolgenden Erfahrung, frühere Fehler zu korrigieren.

F Weitere Ergebnisse für Mathe

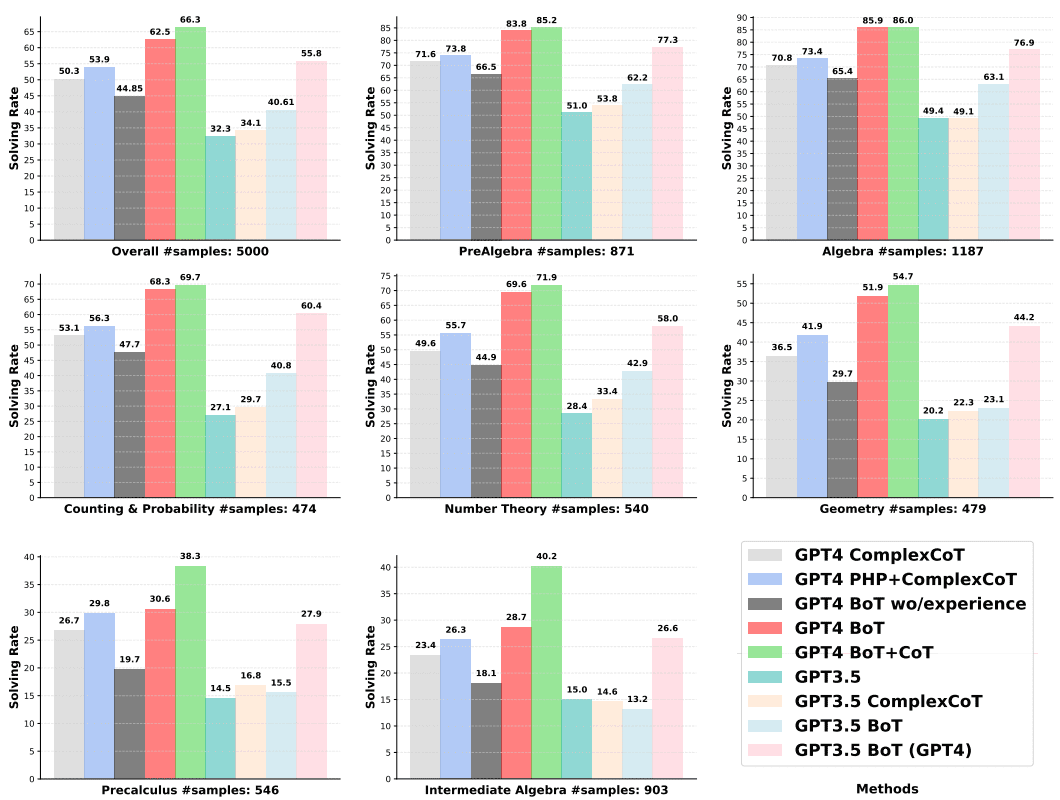
Abb. 5: Zeigt die Effektivität der Verwendung verschiedener Strategien zur Lösung aller im MATH-Datensatz kategorisierten Probleme. Die Strategien werden auf der Grundlage der Kategorien Voralgebra, Algebra, Zählen und Wahrscheinlichkeit, Grundlagen der Zahlentheorie, Geometrie, Vorkalkül und mittlere Algebra verglichen. Die Teilgrafik mit der Bezeichnung "insgesamt" zeigt die Gesamtlösungsrate für alle Probleme in allen Kategorien.

In Abbildung 5 sind die Lösungsraten der verschiedenen Methoden für jede Kategorie des MATH-Datensatzes dargestellt. Die Komplexität und Vielfalt der verschiedenen mathematischen Probleme in diesen Kategorien stellen eine größere Herausforderung für das mathematische Denken dar. Die Komplexität und die Vielfalt der Probleme in MATH erfordern ein breites Spektrum an logischen Fähigkeiten, um sie zu lösen. Daher kann eine detaillierte Untersuchung unseres Ansatzes und sein Vergleich mit anderen Ansätzen in unserem Kontext wertvolle Erkenntnisse liefern.

LLMs.Bei den Experimenten, die mit dem MATH-Datensatz durchgeführt wurden, kamen bekannte Large Language Models (LLMs) zum Einsatz, nämlich GPT-3.5-Turbo (im Folgenden als GPT3.5 bezeichnet) und GPT-4 (im Folgenden als GPT4 bezeichnet). Wir verwendeten direkt die von OPENAI veröffentlichte API.

Rivalen.
- GPT4 ComplexCoT. ist ein Modell von GPT4 unter Verwendung der Complex CoT Fu et al. (2022) Prompting-Methode. In den Schlussfolgerungshinweisen werden Argumentationsbeispiele verwendet, die aus der entsprechenden Complex CoT-Veröffentlichung Fu et al. (2022) stammen. Da greedy decoding verwendet wird, folgen wir nicht dem selbstkonsistenten Ansatz von Wang et al. (2022) für das Sampling von Inferenzpfaden.
- GPT3.5. werden Standardabfragen verwendet und GPT3.5-Modelle zur Generierung von Antworten eingesetzt.
- GPT3.5 ComplexCoT. Ähnlich wie GPT4 ComplexCoT, aber mit einem anderen Modell als GPT3.5.
- GPT4 PHP+ComplexCoT. Dies ist das GPT4-Modell mit PHP Zheng et al. (2023) + Complex CoTFu et al. (2022). Konkret werden im Rahmen von PHP Zheng et al. (2023) Complex CoT-Prompts verwendet, um anfängliche Basisantworten zu generieren, und dann kann PHP+Complex CoT aus diesen Basisantworten weitere Prompts entwickeln, die Antworten generieren. So können zu Beginn einer Interaktion Basisantworten generiert werden, indem die Complex CoT-Basishinweise und die aktuelle Frage an das LLM übergeben werden. Auf der Grundlage der Complex CoT-Hinweise, die in der PHP-Version mit zusätzlichen Hinweissätzen überarbeitet wurden, wird dann das schrittweise Hinweissystem auf dieser Basisantwort ausgeführt, um die richtige Antwort zu generieren. Wir bezeichnen dies als das PHP+Komplexe CoT-Gegenstück zum PHP-Komplexen CoT in der ursprünglichen Arbeit. Der Komplexe CoT hat eine Schusszahl von 8.
- GPT4 BoT ohne Erfahrung. Das GPT4-Modell wird verwendet, um die Argumentation des BoT-Rahmens durchzuführen, ohne Erfahrungen zu sammeln. Der grundlegende Aufbau des BoT folgt den im Hauptbeitrag vorgestellten. Nach einer Iteration werden also aggregierte Ketten als Lösung verwendet.
- GPT4 BoT: GPT4 wird verwendet, um die vollständige Version des BoT aus dem Hauptbeitrag durchzuführen.
- GPT4 BoT + CoT.Zusätzlich zum BoT-Rahmenwerk enthielten die Prompts 5 Argumentationsbeispiele aus der CoT-Veröffentlichung von Wei et al. (2022). Somit enthalten die Prompts in jeder Iteration nicht nur die Erfahrung, sondern auch die zusätzlichen 5 CoT-Beispiele.
- GPT3.5 BoT. Ähnlich wie GPT4 BoT, aber das Modell wurde in GPT3.5 geändert.
- GPT3.5 BoT (GPT4). In diesem Experiment verwenden wir GPT3.5, um zu schlussfolgern und so Gedankenketten in der Gedankenstrukturgenerierung zu erzeugen.

Das GPT4-Modell wurde jedoch verwendet, um ein Bewertungs- und Analysefeedback zu erhalten, wenn es um die Bewertung von Gedanken und die Generierung von Erfahrungen in einer aggregierten Denkkettenanalyse ging.

Aus den Ergebnissen in Abbildung 5 lassen sich die folgenden zusätzlichen Beobachtungen ableiten.

Die herausragende Leistung von BoT bei der Lösung schwierigerer Probleme ist weitgehend auf Erfahrung zurückzuführen.BoT-verwandte Methoden wie GPT4 BoT und GPT4 BoT + CoT erreichen durchgängig die höchsten Problemlösungsraten in den verschiedenen Unterkategorien von MATH. Insbesondere führt GPT4 BoT die beste verfügbare Lösung, GPT4 PHP + ComplexCoT, um 8,61 TP3T, während GPT4 BOT + CoT um 12,41 TP3T führt. In den insgesamt sieben Kategorien übertrifft GPT4 BoT GPT4 PHP + ComplexCoT um mindestens 0,81 TP3T, wobei das algebraische Problem Das Gleiche gilt für GPT3.5 BoT und GPT3.5 BoT + CoT. Wenn jedoch keine gesammelte Erfahrung im BoT-Rahmen vorhanden ist, sinkt die Leistung beim Lösen aller mathematischen Probleme drastisch, wie das GPT4 BoT wo/ experience zeigt.

Neben der Erfahrung mit der Fehleranalyse ist die Einbeziehung von korrekten Beispielen, wie z. B. einfachen CoT-Beispielen, von wesentlicher Bedeutung, um die Effektivität des BoT bei der Lösung anspruchsvoller mathematischer Probleme zu verbessern.GPT4 BoT übertrifft GPT4 PHP+ComplexCoT signifikant bei der Lösung der ersten fünf Unterkategorien des MATH-Problems. In den Bereichen der fortgeschrittenen und mittleren Algebra, in denen komplexere Überlegungen und komplexe logische Schritt-für-Schritt-Lösungen erforderlich sind, betragen die Verbesserungen von BoT jedoch nur 0,8% und 2,4%. Diese Gewinne sind relativ begrenzt im Vergleich zu den signifikanten Verbesserungen, die bei der Lösung einfacherer Problemkategorien beobachtet wurden. Diese Verbesserungen sind relativ begrenzt im Vergleich zu den signifikanten Verbesserungen, die beim Lösen von einfacheren Problemkategorien beobachtet wurden. Als jedoch fünf korrekte Instanzen von CoT direkt zur Eingabeaufforderung hinzugefügt wurden, verbesserte das GPT-4 BoT + CoT seine Leistung in den Bereichen Fortgeschrittene Algebra und Mittlere Algebra erheblich und übertraf das GPT-4 BoT um 7,71 TP3T bzw. 11,51 TP3T.Die zugrundeliegende Schlussfolgerung aus diesen Beobachtungen ist, dass die Trial-and-Error-Analyse zum Erlernen des logischen Denkens nicht die einzige Möglichkeit ist, um sicherzustellen, dass das BoT die bestmögliche Leistung beim Lösen komplexer mathematischer Probleme erzielen kann. Die Fehleranalyse zum Erlernen des schlussfolgernden Denkens ist nicht ausreichend und sollte sich auf die korrekte Beantwortung der LLMs in der Eingabeaufforderung verlassen.

Obwohl der GPT3.5 fit BoT anfangs dem GPT-4 CoT leicht unterlegen sein kann, ist es möglich, dass der GPT-3.5 BoT (GPT-4) den GPT-4 Complex CoT übertrifft, wenn Erfahrungen mit dem GPT-4 als Bewertungs- und Analyseinstrument gesammelt wurden.Bei Verwendung von GPT3.5, das eine geringere Kapazität als GPT4 hat, als LLM, erhielt BoT eine Lösungsrate, die mindestens 7,71 TP3T niedriger war als GPT4 ComplexCoT (insbesondere in der Disziplin Algebra). Es ist klar, dass BoT GPT4 ComplexCoT nicht übertreffen kann, wenn die leistungsschwächeren LLMs qualitativ schlechtere Trial-and-Error-Analysen produzieren. Nachdem GPT3.5 daher nur den Inferenzschritt neben der von GPT4 generierten Erfahrung generiert hatte, zeigte GPT3.5 BoT (GPT4) eine signifikante Verbesserung in allen Kategorien, was zu einer Lösungsrate von 55,81 TP3T führte, die um einen Faktor von 10 höher ist als die von GPT4 ComplexCoT um 5,51 TP3T und sogar um 1,91 TP3T höher als der aktuelle Stand der Technik GPT4 PHP+ComplexCoT. Diese Beobachtungen sind ein weiterer Beweis dafür, dass die durch Iteration in Hints gewonnene Erfahrung der Hauptgrund für den Erfolg des BoT-Rahmens ist.

G Reasoning-Ergebnisse für das Spiel 24 Punkte

Zunächst zeigen wir in den Tabellen 5 bis 9 die detaillierten Hinweise, die von BoT im Argumentationsprozess verwendet werden, und vermitteln so ein umfassendes Verständnis dessen, was BoT in jeder Iteration tut. Dann, beginnend mit Tabelle 10, zeigen wir genaue Beispiele, die den gesamten Argumentationsprozess von BoT umfassen. Diese Experimente wurden unter Verwendung des GPT-3.5-Turbo-Modells mit BoT durchgeführt und folgen dem im Abschnitt "Experimente" beschriebenen Grundaufbau.

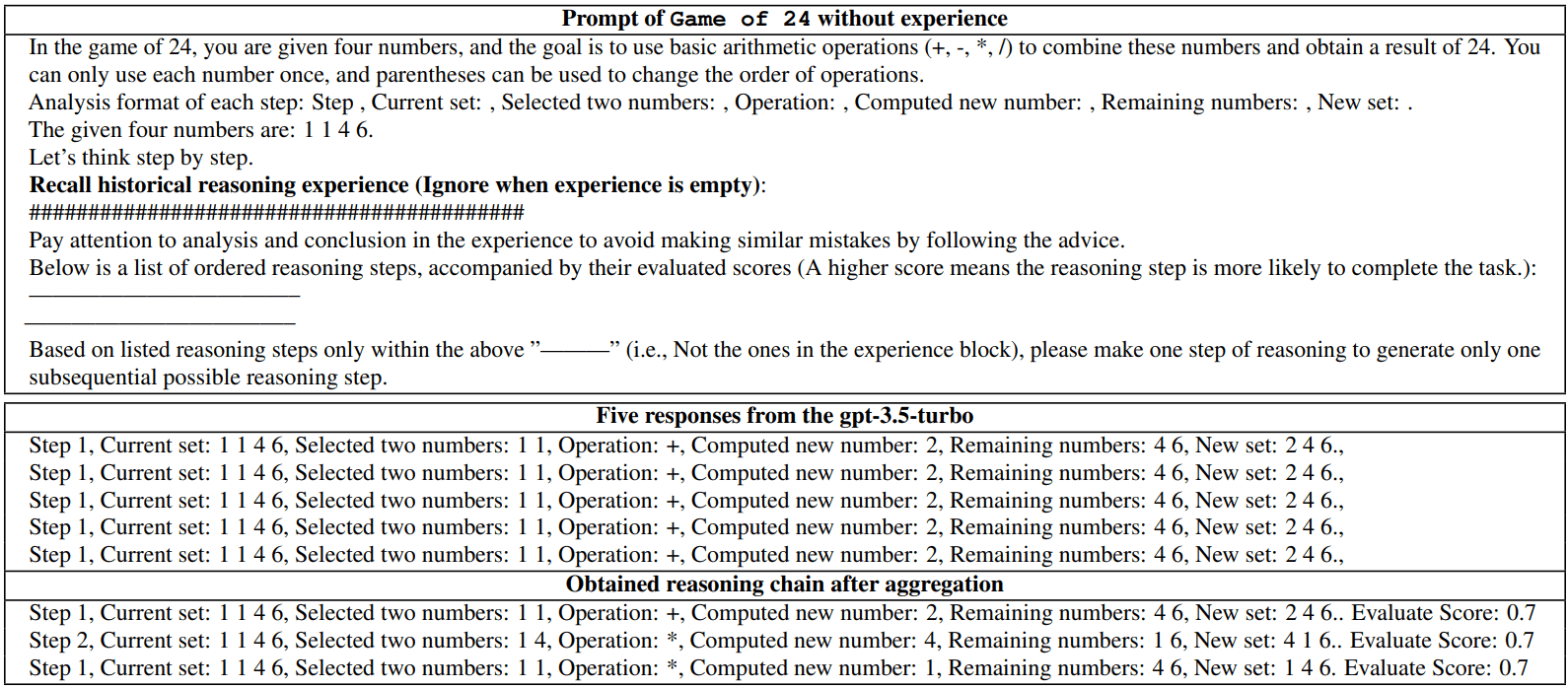
Tabelle 5: Von gpt-3.5-turbo generierte Inferenzschritte, wenn in der Eingabeaufforderung keine Erfahrung angegeben wird.Wir lassen das Modell zunächst fünf Inferenzschritte generieren, um die Diversität zu prüfen, und präsentieren dann die endgültige Inferenzkette nach Abschluss der ersten Iteration der BoT.

Tipps für das Spiel 24:00, keine Erfahrung

In 24 Punkte erhalten Sie vier Zahlen, die Sie mit Hilfe der Grundrechenarten (+, -, *, /) kombinieren müssen, um das Ergebnis 24 zu erhalten. Sie dürfen jede Zahl nur einmal verwenden und können die Reihenfolge der Operationen durch Klammern ändern.

Analysieren Sie jeden Schritt des Formats:
Schritt X. Derzeitige Menge: XXXX, zwei ausgewählte Zahlen: XX XX, Operation: XX, neue, durch Berechnung erhaltene Zahl: XX, verbleibende Zahlen: XXXX, neue Menge: XXXX.

Die vier Zahlen lauten: 1 1 4 6.
Lassen Sie uns Schritt für Schritt denken.

Erinnern Sie sich an historische Argumentationserfahrungen (ignorieren, wenn die Erfahrung null ist):
## ############### ######## ######## # # # #######
Achten Sie auf die Analysen und Schlussfolgerungen in den Erfahrungsberichten und vermeiden Sie ähnliche Fehler, indem Sie die Empfehlungen befolgen.
Nachfolgend finden Sie eine Reihe von geordneten Argumentationsschritten, begleitet von ihren Bewertungspunkten (höhere Punkte bedeuten, dass der Argumentationsschritt eher geeignet ist, die Aufgabe zu lösen). :

Führen Sie auf der Grundlage der oben unter "_" aufgeführten Argumentationsschritte (d. h. nicht der Schritte im empirischen Block) einen Argumentationsschritt aus, um den einzig möglichen nachfolgenden Argumentationsschritt zu erzeugen.

Fünf Antworten von gpt-3.5-turbo
Schritt 1, Aktuelle Menge: 1 1 4 6, Zwei Zahlen ausgewählt: 1 1, Operation: +, Neue Zahl berechnet: 2, Verbleibende Zahlen: 4 6, Neue Menge: 2 4 6, Bewertungspunktzahl: 0,7
Schritt 1, Aktuelle Menge: 1 1 4 6, Zwei Zahlen ausgewählt: 1 1, Operation: +, Neue Zahl berechnet: 2, Verbleibende Zahlen: 4 6, Neue Menge: 2 4 6, Bewertungspunktzahl: 0,7
Schritt 1, Aktuelle Menge: 1 1 4 6, Zwei Zahlen ausgewählt: 1 1, Operation: +, Neue Zahl berechnet: 2, Verbleibende Zahlen: 4 6, Neue Menge: 2 4 6, Bewertungspunktzahl: 0,7
Schritt 1, Aktuelle Menge: 1 1 4 6, Zwei Zahlen ausgewählt: 1 1, Operation: +, Neue Zahl berechnet: 2, Verbleibende Zahlen: 4 6, Neue Menge: 2 4 6, Bewertungspunktzahl: 0,7
Schritt 1, Aktuelle Menge: 1 1 4 6, Zwei Zahlen ausgewählt: 1 1, Operation: *, Neue Zahl berechnet: 1, Verbleibende Zahlen: 4 6, Neue Menge: 1 4 6, Bewertungspunktzahl: 0,7

Nach der Aggregation erhaltene Inferenzkette
Schritt 1, Aktuelle Menge: 1 1 4 6, Zwei Zahlen ausgewählt: 1 1, Operation: +, Neue Zahl berechnet: 2, Übrige Zahlen: 4 6, Neue Menge: 2 4 6... Berechne den Bruch: 0.7
Schritt 2, aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 4, Operation: *, neue Zahl berechnet: 4, verbleibende Zahlen: 1 6, neue Menge: 4 1 6... Bewertung: 0,7
Schritt 1, Aktuelle Menge: 1 1 4 6, Zwei Zahlen ausgewählt: 1 1, Operation: *, Neue Zahl berechnet: 1, Verbleibende Zahlen: 4 6, Neue Menge: 1 4 6, Bewertungspunktzahl: 0,7

H Ableitungsergebnisse für "GSM8K".

BoT arbeitet mit grundlegenden Eingabeaufforderungen und spezifischen Formaten, die denen in den Tabellen 5 bis 9 ähneln. Das einzige, was sich ändert, ist die Aufgabenaufforderung, wie in Tabelle 15 gezeigt. Ab Tabelle 16 finden Sie eine Reihe von detaillierten Beispielen, die den gesamten Argumentationsprozess von BoT enthalten. Diese Experimente basieren auf dem im Abschnitt Experimente gezeigten Basis-Setup unter Verwendung des GPT-3.5-Turbomodells von BoT.

# Empirische Argumentation - Aufgaben für Spiel 24

## Zunächst ein Blick auf die historische Argumentationserfahrung:

### Inferenzkette 1 und ihre Kommentare

Im Folgenden wird eine Kette von Argumentationsschritten in der richtigen Reihenfolge dargestellt:

---

### Schritt 1
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 1, Operation: +, neue Zahl berechnet: 2, verbleibende Zahlen: 4 6, neue Menge: 2 4 6... Bewertung: 0,7

### Schritt 2
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 4, Operation: *, neue Zahl berechnet: 4, verbleibende Zahlen: 1 6, neue Menge: 4 1 6... Bewertungsnote: 0,7

### Schritt 3
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 1, Operation: *, neue Zahl berechnet: 1, verbleibende Zahlen: 4 6, neue Menge: 1 4 6. Bewertung: 0,7

---

## ANALYSE: Diese Argumentationskette ist nicht in der Lage, die Aufgabe zu lösen und das Ziel richtig zu erreichen. Es gab Fehler in den Argumentationsschritten, die die Entdeckung der richtigen Lösung verhinderten.

### Argumentation Schritt 1
Dieser Schritt ist eine logische Fortführung des vorherigen Schritts, da er der Regel folgt, zwei Zahlen auszuwählen, die Operation durchzuführen und die Menge entsprechend zu aktualisieren. Allerdings trägt dieser Schritt nicht zur richtigen Lösung bei. Die durch die Berechnung erhaltene neue Zahl 2 führt nicht zu dem gewünschten Ergebnis 24.
**Vorschlag**: Probiere verschiedene Operationen oder Zahlenkombinationen aus, um eine neue Zahl zu erhalten, die näher an 24 liegt.
**Empfehlung oder Ablehnung Beschreibung**: Abgelehnt.

### Argumentation Schritt 2
Es gibt einen Fehler in der Beschreibung des Argumentationsschritts. Er wird fälschlicherweise zweimal als "Argumentationsschritt 2" bezeichnet. Wenn man jedoch davon ausgeht, dass dies der einzige Schritt ist, handelt es sich um eine logische Ableitung aus dem vorherigen Schritt. Die Multiplikation (*) wird korrekt auf die ausgewählte Zahl angewandt und ergibt die neue Zahl 4. Die übrigen Zahlen werden entsprechend aktualisiert.
**Empfohlene oder abgelehnte Beschreibung**: Empfohlen.

### Argumentation Stufe 3
Es gibt einen Fehler in der Beschreibung des Argumentationsschritts. Er wird fälschlicherweise als "Argumentationsschritt 1" statt als "Argumentationsschritt 3" bezeichnet. Dieser Schritt ist keine logische Ableitung aus dem vorherigen Schritt. Die Multiplikation (*) wird auf dieselben Zahlen angewandt wie in Argumentationsschritt 1, aber die neue Zahl 1 wird anders berechnet. Die übrigen Zahlen werden entsprechend aktualisiert.
**Fehlerbericht**: Die Berechnung in diesem Schritt ist falsch. Die richtige Berechnung sollte 1 * 1 = 1 sein.
**Empfehlung**: Überprüfen Sie die Berechnungen, um sicherzustellen, dass sie korrekt sind.
**Empfehlung oder Ablehnung Beschreibung**: Abgelehnt.

**Konfidenzniveau**: 0,7

---

## Fünf Antworten von gpt-3.5-turbo

---

### Schritt 1
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 4, Operation: *, neue Zahl berechnet: 4, verbleibende Zahlen: 1 6, neue Menge: 1 4 6.....

### Schritt 1
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 6, Operation: +, neue Zahl berechnet: 7, verbleibende Zahlen: 1 4, neue Menge: 1 4 7.....

### Schritt 1
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 1, Operation: *, neue Zahl berechnet: 1, verbleibende Zahlen: 4 6, neue Menge: 1 4 6.....

### Schritt 1
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 4, Operation: /, neue Zahl berechnet: 0,25, verbleibende Zahlen: 1 6, neue Menge: 0,25 1 6..., und

### Schritt 1
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 1, Operation: -, neue Zahl berechnet: 0, verbleibende Zahlen: 4 6, neue Menge: 0 4 6.....

---

## Schlussfolgerungskette nach Aggregation

---

### Schritt 1
Aktuelle Menge: 1 1 4 6, zwei Zahlen ausgewählt: 1 1, Operation: *, neue Zahl berechnet: 1, verbleibende Zahlen: 4 6, neue Menge: 1 4 6... Bewertungsnote: 0,9

### Schritt 2
Aktuelle Menge: 1 4 6, zwei Zahlen ausgewählt: 1 4, Operation: *, neue Zahl berechnet: 4, verbleibende Zahlen: 6, neue Menge: 4 6... Bewertungsnote: 0,7

### Schritt 3
Aktuelle Menge: 46, Zwei Zahlen ausgewählt: 4 6, Operation: *, Neue Zahl berechnet: 1, Verbleibende Zahlen:, Neue Menge: 24.

---

Tabelle 6: Von gpt-3.5-turbo generierte Argumentationsschritte bei Einbeziehung von Erfahrungen in die Eingabeaufforderung. Diese Erfahrung ist eine Analyse der Argumentationskette in Tabelle 5. Nachdem diese Erfahrung in die Eingabeaufforderung eingefügt wurde, zeigen wir die endgültige Schlussfolgerungskette, die nach fünf Antworten des Modells und dem Abschluss der zweiten Iteration des BoT gebildet wurde.

# Next Thought Generation Tipp

Bei dem Spiel 24 Punkte werden Ihnen vier Zahlen vorgegeben, die Sie mit Hilfe der Grundrechenarten (+, -, *, /) kombinieren müssen, um das Ergebnis 24 zu erhalten. Jede Zahl kann nur einmal verwendet werden, und Sie können Klammern verwenden, um die Reihenfolge der Operationen zu ändern.

Analyseformat für jeden Schritt: Schritt , aktuelle Menge: , zwei ausgewählte Zahlen: , Operation: , neu berechnete Zahl: , verbleibende Zahlen: , neue Menge: .

Die vier Zahlen lauten: 3 5 6 8.

Lassen Sie uns Schritt für Schritt denken.

## Zunächst ein Blick auf die historische Argumentationserfahrung:

### 1. Argumentationskette und Kommentare

Es folgt eine Argumentationskette, in der die einzelnen Argumentationsschritte nacheinander aufgeführt sind:

---

Schritt 1, aktuelle Menge: 3 5 6 8, zwei Zahlen ausgewählt: 5 6, Operation: *, neue Zahl berechnet: 30, verbleibende Zahlen: 3 8, neue Menge: 30 3 8... Bewertung: 0,9

Schritt 2, aktuelle Menge: 30 3 8, zwei Zahlen ausgewählt: 30 3, Operation: /, neue Zahl berechnet: 10, verbleibende Zahlen: 8, neue Menge: 10 8... Bewertung: 0,9

Schritt 3, aktuelle Menge: 10 8, zwei Zahlen ausgewählt: 10 8, Operation: *, neue Zahl berechnet: 80, verbleibende Zahlen: keine, neue Menge: 80... Bewertungspunktzahl: 0,9.

---

## Analysebericht

Diese Argumentationskette ermöglicht es, die Aufgabe richtig zu lösen und das Ziel zu erreichen, indem man ihre Argumentationsschritte ausführt. Das Endergebnis von Schritt 3 ist 80, was mathematisch gleich 24 ist.

### Argumentation Schritt 1
Dieser Argumentationsschritt ist eine logische Ableitung des vorherigen Schritts. Wähle die Zahlen 5 und 6 aus der aktuellen Menge (3 5 6 8) und multipliziere sie, um die neue Zahl 30 zu erhalten. Die übrigen Zahlen sind 3 und 8.

### Argumentation Schritt 2
Dieser Argumentationsschritt ist eine logische Ableitung des vorherigen Schritts. Wähle die Zahlen 30 und 3 aus der aktuellen Menge (30 3 8) und teile sie, um die neue Zahl 10 zu erhalten. Die verbleibende Zahl ist 8. Dieser Argumentationsschritt trägt zur richtigen Lösung bei, da er die Anzahl der Elemente in der Menge weiter reduziert und eine neue Zahl ergibt.

### Argumentation Schritt 3
Dieser Argumentationsschritt ist eine logische Ableitung des vorherigen Schritts. Wähle die Zahlen 10 und 8 aus der aktuellen Menge (10 8) und multipliziere sie, um die neue Zahl 80 zu erhalten. Da keine Zahlen mehr übrig sind, ist das Ergebnis der Argumentationskette 80.

Vorschlag: Bei den Begründungsschritten wurden keine Fehler gefunden.

Empfohlene oder abgelehnte Beschreibung: Alle Argumentationsschritte werden empfohlen, weil sie richtig sind und zur richtigen Lösung führen.

Konfidenzniveau: 0,9

### 2. Argumentationskette und Kommentare

Fortsetzung folgt in Tabelle 8

### Anmerkungen zu den Analysen und Schlussfolgerungen

Vermeiden Sie ähnliche Fehler, indem Sie Empfehlungen befolgen, die auf Analysen und Schlussfolgerungen aus Erfahrungen beruhen.

Nachfolgend finden Sie eine Liste der geordneten Argumentationsschritte mit ihren Bewertungspunkten (höhere Werte bedeuten, dass der Argumentationsschritt mit größerer Wahrscheinlichkeit zur Lösung der Aufgabe führt). :

---

Schritt 1, aktuelle Menge: 3 5 6 8, zwei Zahlen ausgewählt: 3 8, Operation: +, neue Zahl berechnet: 11, verbleibende Zahlen: 5 6, neue Menge: 11 5 6... Bewertung: 0,7

Schritt 2, aktuelle Menge: 11 5 6, zwei Zahlen ausgewählt: 5 6, Operation: *, neue Zahl berechnet: 30, verbleibende Zahl: 11, neue Menge: 30 11... Bewertung: 0,9

---

Führen Sie auf der Grundlage der oben unter "---" aufgeführten Argumentationsschritte (d. h. nicht der Schritte im empirischen Block) einen Argumentationsschritt durch, der den einzig möglichen nachfolgenden Argumentationsschritt erzeugt.

 

## Generierte nächste Argumentation

Schritt 3, Aktueller Satz: 30 11, Zwei Nummern ausgewählt: 30 11, Operation: -, Neue Nummer berechnet: 19, Verbleibende Nummern:, Neuer Satz: 19.

Tabelle 7: Beispiele für mögliche Reflexionen von BoT bei der Generierung des entsprechenden Inferenzschritts zi.

## 2. Argumentationskette und Kommentare

Es folgt eine Argumentationskette, in der die einzelnen Argumentationsschritte nacheinander aufgeführt sind:

---

### Schritt 1
Aktueller Satz: 10 8, Zwei Zahlen ausgewählt: 10 8, Operation: /, Neue Zahl berechnet: 1,25, Verbleibende Zahlen: keine, Neuer Satz: 1,25. Bewertungspunktzahl: 0,8.

### Schritt 2
Aktuelle Menge: 10 8, zwei Zahlen ausgewählt: 10 8, Operation: /, neue Zahl berechnet: 1.25, verbleibende Zahlen: keine, neue Menge: 1.25... Bewertungsnote: 0,8.

### Schritt 3
Aktuelle Menge: 10 8, zwei Zahlen ausgewählt: 10 8, Operation: /, neue Zahl berechnet: 1.25, verbleibende Zahlen: keine, neue Menge: 1.25... Bewertungsnote: 0,8.

---

## Analysebericht

Mit dieser Argumentationskette wird die Aufgabe nicht richtig gelöst und das Ziel nicht erreicht. Die angegebenen Argumentationsschritte sind falsch und führen nicht zu einem Ergebnis von 24.

### Argumentation Schritt 1
Dieser Argumentationsschritt ist falsch. Die beiden ausgewählten Zahlen 10 und 8 sind nicht in der gegebenen Zahlenmenge 3, 5, 6 und 8 enthalten. Außerdem führt die Operation divide(/) nicht zu einer neuen Zahl, die als 1,25 berechnet wird. Die übrigen Zahlen werden nicht richtig erkannt.

**Fehlerbericht**:
- Die beiden ausgewählten Zahlen sind in der gegebenen Zahlenmenge nicht vorhanden.
- Der Vorgang und die neu berechneten Zahlen sind falsch.
- Die übrigen Ziffern werden nicht richtig erkannt.

**Empfehlungen**:
- Vergewissern Sie sich, dass die beiden ausgewählten Zahlen in der gegebenen Zahlenmenge vorhanden sind.
- Verwenden Sie die richtige Operation, um die gewünschte neue Nummer zu erhalten.
- Bestimmen Sie die übrigen Zahlen genau.

**Empfehlen oder Ablehnen Beschreibung**: Ablehnen. Dieser Argumentationsschritt ist falsch und trägt nicht zur richtigen Lösung bei.

### Argumentation Schritt 2
Dieser Argumentationsschritt ist eine Wiederholung von Argumentationsschritt 1 und daher ebenfalls ein Fehler. Dieser Schritt enthält denselben Fehler wie der vorherige Schritt.

**Fehlerbericht**:
- Die beiden ausgewählten Zahlen sind in der gegebenen Zahlenmenge nicht vorhanden.
- Der Vorgang und die neu berechneten Zahlen sind falsch.
- Die übrigen Ziffern werden nicht richtig erkannt.

**Empfehlungen**:
- Vergewissern Sie sich, dass die beiden ausgewählten Zahlen in der gegebenen Zahlenmenge vorhanden sind.
- Verwenden Sie die richtige Operation, um die gewünschte neue Nummer zu erhalten.
- Bestimmen Sie die übrigen Zahlen genau.

**Empfehlen oder Ablehnen Beschreibung**: Ablehnen. Dieser Argumentationsschritt ist falsch und trägt nicht zur richtigen Lösung bei.

### Argumentation Schritt 3
Dieser Argumentationsschritt ist eine Wiederholung von Argumentationsschritt 1 und Argumentationsschritt 2. Dieser Schritt enthält die gleichen Fehler wie die vorherigen Schritte.

**Fehlerbericht**:
- Die beiden ausgewählten Zahlen sind in der gegebenen Zahlenmenge nicht vorhanden.
- Der Vorgang und die neu berechneten Zahlen sind falsch.
- Die übrigen Ziffern werden nicht richtig erkannt.

**Empfehlungen**:
- Vergewissern Sie sich, dass die beiden ausgewählten Zahlen in der gegebenen Zahlenmenge vorhanden sind.
- Verwenden Sie die richtige Operation, um die gewünschte neue Nummer zu erhalten.
- Bestimmen Sie die übrigen Zahlen genau.

**Empfehlen oder Ablehnen Beschreibung**: Ablehnen. Dieser Argumentationsschritt ist falsch und trägt nicht zur richtigen Lösung bei.

**Konfidenzniveau**: 0,9

Tabelle 8: Zweite Argumentationskette mit Kommentaren aus Tabelle 7.

# Aufgaben zur Bewertung des Denkens

Bei dem Spiel 24 Punkte werden Ihnen vier Zahlen vorgegeben, die Sie mit Hilfe der Grundrechenarten (+, -, *, /) kombinieren müssen, um das Ergebnis 24 zu erhalten. Jede Zahl kann nur einmal verwendet werden, und Sie können Klammern verwenden, um die Reihenfolge der Operationen zu ändern.

Analyseformat für jeden Schritt: Schritt , aktuelle Menge: , zwei ausgewählte Zahlen: , Operation: , neu berechnete Zahl: , verbleibende Zahlen: , neue Menge: .

Die vier Zahlen lauten: 3 5 6 8.

Lassen Sie uns Schritt für Schritt denken.

Die folgenden generierten Argumentationsschritte werden in der Reihenfolge ihrer Bewertungsergebnisse dargestellt (höhere Werte bedeuten, dass der Argumentationsschritt die Aufgabe mit größerer Wahrscheinlichkeit erfüllt). :

---

### Schritt 1
Aktuelle Menge: 3 5 6 8, zwei Zahlen ausgewählt: 3 8, Operation: +, neue Zahl berechnet: 11, verbleibende Zahlen: 5 6, neue Menge: 11 5 6... Bewertungsnote: 0,7

### Schritt 2
Aktuelle Menge: 11 5 6, zwei Zahlen ausgewählt: 5 6, Operation: *, neue Zahl berechnet: 30, verbleibende Zahl: 11, neue Menge: 30 11... Bewertung: 0,9

### Schritt 3
Aktuelle Menge: 30 11, zwei Zahlen ausgewählt: 30 11, Operation: -, neue Zahl berechnet: 19, verbleibende Zahlen:, neue Menge: 19.

---

Wie bewerten Sie die Logik, die Korrektheit und den Beitrag dieser Argumentationsschritte zum Erreichen der endgültigen Lösung? Bitte wählen Sie als Punktzahl einen Wert aus [0,1, 0,3, 0,5, 0,7, 0,9, 1,0], wobei höhere Punktzahlen bessere Argumentationsschritte bedeuten. Die Punktzahl sollte hinter "Evaluation Score:" stehen, damit sie vom Benutzer gelesen werden kann.

 

## Erstellte Bewertungsnote

Bewertungsnote: 0,9.

Tabelle 9: Berechnung der Kantengewichte zwischen Schritt 2 (zi) und Schritt 3 (zi-1).

# Das Format der von Next Thinking generierten Prompts

Bei dem Spiel 24 Punkte werden Ihnen vier Zahlen vorgegeben, die Sie mit Hilfe der Grundrechenarten (+, -, *, /) kombinieren müssen, um das Ergebnis 24 zu erhalten. Jede Zahl kann nur einmal verwendet werden, und Sie können Klammern verwenden, um die Reihenfolge der Operationen zu ändern.

Analyseformat für jeden Schritt: Schritt , aktuelle Menge: , zwei ausgewählte Zahlen: , Operation: , neu berechnete Zahl: , verbleibende Zahlen: , neue Menge: .

Die vier angegebenen Zahlen sind 5, 6, 9, 4.

Lassen Sie uns Schritt für Schritt denken.

Überprüfen Sie die Geschichte, um über die Erfahrung nachzudenken (ignorieren Sie, wenn die Erfahrung nichtig ist):

###########################################

Vermeiden Sie ähnliche Fehler, indem Sie Empfehlungen befolgen, die auf Analysen und Schlussfolgerungen aus Erfahrungen beruhen.

Nachfolgend finden Sie eine Liste der geordneten Argumentationsschritte mit ihren Bewertungspunkten (höhere Werte bedeuten, dass der Argumentationsschritt mit größerer Wahrscheinlichkeit zur Lösung der Aufgabe führt). :

---

---

Führen Sie auf der Grundlage der oben unter "---" aufgeführten Argumentationsschritte (d. h. nicht der Schritte im empirischen Block) einen Argumentationsschritt durch, der den einzig möglichen nachfolgenden Argumentationsschritt erzeugt.

 

# Aufforderungsformat für die Erzeugung von Erfahrungen

Aufgabenstellung: Im Spiel um 24 Punkte werden Ihnen vier Zahlen vorgegeben, die Sie mit Hilfe der Grundrechenarten (+, -, *, /) so kombinieren sollen, dass das Ergebnis 24 lautet. Sie dürfen jede Zahl nur einmal verwenden und können die Reihenfolge der Operationen durch Klammern ändern.

Die vier gegebenen Zahlen sind: 4 5 10 11. Denken wir Schritt für Schritt. Im Folgenden finden Sie eine Argumentationskette, in der die einzelnen Schritte der Reihe nach aufgeführt sind:

---

---

Bitte bewerten Sie diese Argumentationskette, indem Sie eine detaillierte Kritik abgeben, die die folgenden Bereiche abdeckt: 1. Kann diese Argumentationskette die Aufgabe korrekt erfüllen und das Ziel erreichen, indem sie ihre Argumentationsschritte ausführt? Warum? Schreiben Sie eine Analyse mit Schlussfolgerungen unter "Analysebericht": 2. Analysieren Sie für jeden Argumentationsschritt detailliert, ob der aktuelle Schritt eine logische Fortsetzung des vorherigen Schrittes ist und ob der Argumentationsschritt zur richtigen Lösung beiträgt. Geben Sie für jeden Argumentationsschritt, der einen Fehler aufweist, einen Fehlerbericht und entsprechende Empfehlungen zur Überarbeitung. Geben Sie für jeden Argumentationsschritt eine Beschreibung der Empfehlung oder Ablehnung. Die Kommentare sollten prägnant sein, die Wiederholung derselben Analysen in verschiedenen Schritten vermeiden und dem folgenden Format folgen: Argumentationsschritt ¡idx¿. Analyse: . Empfehlung: . Empfehlung oder Ablehnung Beschreibung: . 3. wie hoch ist Ihr Vertrauen in diese Bewertungen und Kommentare? Bitte wählen Sie einen Wert aus [0,1, 0,3, 0,5, 0,7, 0,9, 1,0]. Die Punktzahl sollte nach "Vertrauenspunktzahl:" stehen, damit sie vom Benutzer gelesen werden kann.

Tabelle 10: Im Spiel "Blackjack" verwendete Tippformate.

### Erfahrungen aus der ersten Iteration
####1T# 1. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**, Aktuelle Menge: 4 5 10 11, Zwei Zahlen ausgewählt: 4 5, Operation:*, Neue Zahl berechnet: 20, Verbleibende Zahlen: 10 11, Neue Menge: 20 10 11... Auswerten
Punktzahl: 0,7

**Schritt 2**, aktuelle Menge: 20 10 11, zwei Zahlen ausgewählt: 10 11, Operation: *, neue Zahl berechnet: 110, verbleibende Zahl: 20, neue Menge: 110 20... Bewertung: 0,7

**Schritt 3**, Aktuelle Menge: 110 20, Zwei Zahlen ausgewählt: 110 20, Operation: /, Neue Zahl berechnet: 5.5, Verbleibende Zahlen: keine, Neue Menge: 5.5 ... Bewertung Note: 0.9

----------------------------------------------------------------
**Analytischer Bericht**:
Diese Argumentationskette ermöglicht es, die Aufgabe richtig zu lösen und das Ziel zu erreichen, indem man ihre Argumentationsschritte ausführt. Das Endergebnis ist 5,5, was mathematisch gleich 24 ist.

**Begründungsschritt 1** : Dieser Schritt ist eine logische Überlegung über die gegebenen Zahlen. Die Zahlen 4 und 5 werden aus der aktuellen Menge ausgewählt und die Operation * wird angewandt, um die neue Zahl 20 zu erhalten. Die verbleibenden Zahlen sind 10 und 11. Dieser Schritt ist günstig für die richtige Lösung, da er die Anzahl der Elemente in der Menge reduziert.

**Begründungsschritt 2** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts. Die Zahlen 10 und 11 werden aus der aktuellen Menge ausgewählt und die Operation * wird angewendet, um die neue Zahl 110 zu erhalten. die verbleibende Zahl ist 20. dieser Schritt ist für die richtige Lösung von Vorteil, da er die Anzahl der Elemente in der Menge weiter reduziert.

**Schlussfolgernder Schritt 3**: Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts. Die Zahlen 110 und 20 werden aus der aktuellen Menge ausgewählt und die Operation / wird angewendet, um die neue Zahl 5,5 zu erhalten. Es gibt keine verbleibenden Zahlen, was bedeutet, dass die Schlussfolgerungskette das Ergebnis erreicht hat. Das Endergebnis 5,5 ist mathematisch gleich 24.

**Empfehlung**: In dieser Argumentationskette wurden keine Fehler gefunden. Die Schritte wurden korrekt ausgeführt und führten zur richtigen Lösung.

**Empfohlene oder abgelehnte Beschreibung**: Diese Argumentationskette wird empfohlen, weil sie das Ziel erreicht und die richtige Lösung liefert.

**Konfidenzniveau**: 0,9

 

### Erfahrungen aus der zweiten Iteration
####1T# 2. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**, Aktuelle Menge: 4 5 10 11, Zwei Zahlen ausgewählt: 4 10, Operation:*, Neue Zahl berechnet: 40, Verbleibende Zahlen: 5 11, Neue Menge: 40 5 11... Bewertung: 0.9

**Schritt 2**, aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 5 11, Operation: *, neue Zahl berechnet: 55, verbleibende Zahl: 40, neue Menge: 55 40... Bewertung: 0.9

**Schritt 3**, aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 4 10, Operation: *, neue Zahl berechnet: 40, verbleibende Zahlen: 5 11, neue Menge: 40 5 11... Bewertung: 0,9

----------------------------------------------------------------
**ANALYSEBERICHT**: Mit dieser Argumentationskette wird die Aufgabe nicht korrekt gelöst und das Ziel nicht erreicht. Die Argumentationsschritte wurden wiederholt und führten nicht zu dem gewünschten Ergebnis 24.

**Begründungsschritt 1** : Dieser Schritt ist eine logische Begründung für die gegebenen Zahlen und folgt den Regeln des Spiels. Die Multiplikation von 4 und 10 ergibt 40 und die verbleibenden Zahlen sind 5 und 11. Dieser Schritt hilft jedoch nicht, die richtige Lösung von 24 zu finden.

**Begründungsschritt 2**: Dieser Schritt ist eine Wiederholung von Schritt 1. Er wählt die verbleibenden Zahlen 5 und 11 und multipliziert sie, um 55 zu erhalten. Die neue Menge wird 55 und 40. Auch dieser Schritt führt nicht zum Ziel 24.

**Begründungsschritt 3**: Dieser Schritt ist eine Wiederholung von Schritt 1. Er liefert keine neuen Informationen oder Fortschritte auf dem Weg zum Ziel. Die Ergebnisse sind die gleichen wie in Schritt 1.

**Empfehlung**: Die Argumentationsschritte müssen überarbeitet und angepasst werden, um verschiedene Wege zum Ziel zu finden.24 Wiederholte Schritte werden nicht dazu beitragen, die richtige Lösung zu finden.

**Empfohlene oder abgelehnte Beschreibung**: Diese Argumentationskette wurde aufgrund von sich wiederholenden Schritten und mangelndem Fortschritt in Richtung des Ziels abgelehnt.

**Konfidenzniveau**: 0,7

 

### Lehren aus der dritten Iteration
####1T# 3. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**, Aktuelle Menge: 4 5 10 11, Zwei Zahlen ausgewählt: 4 5, Operation: +, Neue Zahl berechnet: 9, Verbleibende Zahlen: 10 11, Neue Menge: 9 10 11... Bewertung: 0,7

**Schritt 2**, aktuelle Menge: 9 10 11, zwei Zahlen ausgewählt: 9 10, Operation: *, neue Zahl berechnet: 90, verbleibende Zahl: 11, neue Menge: 90 11... Bewertung: 0.7

**Schritt 3**, Aktuelle Menge: 90 11, Zwei Zahlen ausgewählt: 90 11, Operation: /, Neue Zahl berechnet: 8.1818181818181818182, Verbleibende Zahlen:, Neue Menge: 8.1818181818181818182... Bewertungsnote: 0.7

----------------------------------------------------------------
**ANALYSEBERICHT**: Mit dieser Argumentationskette wird die Aufgabe nicht korrekt gelöst und das Ziel nicht erreicht. Das in Schritt 3 erhaltene Endergebnis ist 8.18181818181818182, was nicht der Zielzahl 24 entspricht. daher ist diese Argumentationskette falsch.

**Begründungsschritt 1** : Dieser Schritt ist eine logische Schlussfolgerung aus dem vorherigen Schritt. Aus der aktuellen Menge (4 5 10 11) werden zwei Zahlen 4 und 5 ausgewählt und zu der neuen Zahl 9 addiert. Die verbleibenden Zahlen sind 10 und 11 und die neue Menge wird zu 9 10 11. Dieser Schritt begünstigt die richtige Lösung, da er die beiden Zahlen kombiniert und die Größe der Menge reduziert.

**Empfohlene oder abgelehnte Beschreibung**: Empfohlen.

**Begründungsschritt 2** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts. Aus der aktuellen Menge (9 10 11) werden zwei Zahlen 9 und 10 ausgewählt und multipliziert, um die neue Zahl 90 zu erhalten. Die verbleibende Zahl ist 11 und die neue Menge wird zu 90 11. Dieser Schritt begünstigt die richtige Lösung, da er die beiden Zahlen kombiniert und die Größe der Menge reduziert.

**Empfohlene oder abgelehnte Beschreibung**: Empfohlen.

**Begründungsschritt 3** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts. Zwei Zahlen 90 und 11 aus der aktuellen Menge (90 11) werden ausgewählt und geteilt, um die neue Zahl 8 zu erhalten.18181818181818182. Da es keine restlichen Zahlen gibt, ist dies das Endergebnis. Das erhaltene Ergebnis ist jedoch nicht gleich der Zielzahl 24.

**Fehlermeldung**: Der Argumentationsschritt war falsch, weil das erhaltene Ergebnis nicht gleich der Zielzahl war.

**Empfehlung**: Probieren Sie verschiedene Operationen oder Zahlenkombinationen aus, um der Zielzahl näher zu kommen.

**Konfidenzniveau**: 0,7

 

Dies wird in der nächsten Tabelle 12 fortgesetzt...

Tabelle 11: Erfolgreicher Argumentationsprozess durch BoT für "4 5 10 11".

### Erfahrungen aus der vierten Iteration
####1T# 4. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**, Aktuelle Menge: 4 5 10 11, Zwei Zahlen ausgewählt: 4 10, Operation:*, Neue Zahl berechnet: 40, Verbleibende Zahlen: 5 11, Neue Menge: 40 5 11... Auswerten
Punktzahl: 0,7

**Schritt 2**, aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 40 5, Operation: +, neue Zahl berechnet: 45, verbleibende Zahlen: 11, neue Menge: 45 11... Bewertung: 0,7

**Schritt 3**, Aktuelle Menge: 45 11, Zwei Zahlen ausgewählt: 45 11, Operation: -, Neue Zahl berechnet: 34, Verbleibende Zahlen:, Neue Menge: 34... Bewertungsnote: 0.9

----------------------------------------------------------------
**ANALYSEBERICHT**: Diese Argumentationskette ermöglicht es, die Aufgabe richtig zu lösen und das Ziel zu erreichen, indem man ihre Argumentationsschritte ausführt. Die im letzten Schritt berechnete Zahl ist 34, was das korrekte Ergebnis der Verwendung der vier vorgegebenen Zahlen und der angegebenen Rechenoperationen ist, um das gewünschte Ergebnis von 24 zu erhalten.

**Begründung Schritt 1**: die aktuelle Menge ist 4 5 10 11. zwei Zahlen 4 und 10 werden ausgewählt. die gewählte Operation ist Multiplikation (*) und die neu berechnete Zahl ist 40. die verbleibenden Zahlen sind 5 und 11. die neue Menge wird 40 5 11. Logische Begründung: die ausgewählte Zahl ist ein gültiges Element der aktuellen Menge und die Operation ist eine gültige arithmetische Operation. NUTZEN FÜR DIE RICHTIGE LÖSUNG: Ja, dieser Schritt reduziert die Anzahl der Elemente in der Menge und berechnet neue Zahlen, die in den folgenden Schritten verwendet werden können. Empfehlung: Annehmen.

**Begründungsschritt 2**: die aktuelle Menge ist 40 5 11. zwei Zahlen 40 und 5 werden ausgewählt. die gewählte Operation ist Addition (+), und die neu berechnete Zahl ist 45. die verbleibende Zahl ist 11. die neue Menge wird 45 11. logische Schlussfolgerung: die ausgewählten Zahlen sind gültige Elemente der aktuellen Menge und die Operation ist eine gültige arithmetische Operation. VORTEIL ZUR RICHTIGEN LÖSUNG: Ja, dieser Schritt reduziert die Anzahl der Elemente in der Menge weiter und berechnet eine neue Zahl, die in den folgenden Schritten verwendet werden kann. Empfehlung: akzeptiert.

**Begründung Schritt 3**: die aktuelle Menge ist 45 11. zwei Zahlen 45 und 11 werden ausgewählt. die gewählte Operation ist Subtraktion (-) und die neu berechnete Zahl ist 34. es sind keine Zahlen übrig. Die neue Menge wird 34. Logische Schlussfolgerung: Die ausgewählten Zahlen sind gültige Elemente der aktuellen Menge und die Operation ist eine gültige arithmetische Operation. Vorteilhaft für die richtige Lösung: ja, dieser Schritt berechnet das Endergebnis 34, auch wenn es nicht gleich dem Ziel 24 ist. empfehlung: akzeptieren.

**Konfidenzniveau**: 0,9

 

### Lehren aus der fünften Iteration
####1T# 5. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**, Aktuelle Menge: 4 5 10 11, Zwei Zahlen ausgewählt: 4 10, Operation:*, Neue Zahl berechnet: 40, Verbleibende Zahlen: 5 11, Neue Menge: 40 5 11... Auswerten
Wertung: 0,9

**Schritt 2**, aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 5 11, Operation: *, neue Zahl berechnet: 55, verbleibende Zahl: 40, neue Menge: 55 40... Bewertung: 0.9

**Schritt 3**, Aktuelle Menge: 55 40, Zwei Zahlen ausgewählt: 55 40, Operation: +, Neue Zahl berechnet: 95, Verbleibende Zahlen: keine, Neue Menge: 95... Bewertungsnote: 1,0

----------------------------------------------------------------
**ANALYSEBERICHT**: Diese Argumentationskette ermöglicht die korrekte Erfüllung der Aufgabe und das Erreichen des Ziels durch die Durchführung ihrer Argumentationsschritte. Das in Schritt 3 erhaltene Endergebnis ist jedoch 95, was mathematisch nicht gleich 24 ist. Daher liefert diese Argumentationskette nicht die richtige Lösung.

**Überlegungsschritt 1**: Der aktuelle Schritt ist eine logische Schlussfolgerung aus dem vorherigen Schritt, da er der Regel folgt, zwei Zahlen aus der aktuellen Menge auszuwählen und die *-Operation durchzuführen. Dieser Schlussfolgerungsschritt ist für die richtige Lösung von Vorteil, da er eine neue Zahl erzeugt und die Menge für den nächsten Schritt aktualisiert.

**Überlegungsschritt 2**: Der aktuelle Schritt ist eine logische Schlussfolgerung aus dem vorherigen Schritt, da er der Regel folgt, zwei Zahlen aus der aktuellen Menge auszuwählen und die Operation * durchzuführen. Dieser Schlussfolgerungsschritt ist für die richtige Lösung von Vorteil, da er eine neue Zahl erzeugt und die Menge für den nächsten Schritt aktualisiert. Allerdings hat dieser Schritt nicht zur korrekten Lösung beigetragen, da das Endergebnis, 95, mathematisch nicht gleich 24 ist.

**Überlegungsschritt 3**: Der aktuelle Schritt ist eine logische Folgerung aus dem vorherigen, da er der Regel folgt, zwei Zahlen aus der aktuellen Menge auszuwählen und die Operation + durchzuführen. Allerdings führt dieser Schritt nicht zur richtigen Lösung, da das Endergebnis, 95, mathematisch nicht gleich 24 ist.

**Empfehlung**: In Schritt 2 sollte eine andere Operation gewählt werden, um die neue Zahl zu erhalten. In Schritt 3 sollte eine andere Operation gewählt werden, um eine neue Zahl zu erhalten, die mit den übrigen Zahlen kombiniert wird, um das Ziel 24 zu erreichen.

**Beschreibung der Empfehlung oder Ablehnung**: Schritt 1: Empfehlung Schritt 2: Ablehnung Schritt 3: Ablehnung

**Konfidenzniveau**: 0,9

 

### Erfahrungen aus der sechsten Iteration
#### 1. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**: aktuelle Menge: 4 5 10 11, zwei Zahlen ausgewählt: 4 10, Operation: *, neue Zahl berechnet: 40, verbleibende Zahlen: 5 11, neue Menge: 40 5 11... Auswerten
Wertung: 0,9

**Schritt 2**: aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 5 11, Operation: +, neue Zahl berechnet: 16, verbleibende Zahl: 40, neue Menge: 16 40... Bewertung: 0.9

**Schritt 3**: aktuelle Menge: 16 40, zwei Zahlen ausgewählt: 16 40, Operation: +, neue Zahl berechnet: 56, verbleibende Zahlen: keine, neue Menge: 56. Bewertung: 0,9

----------------------------------------------------------------
**ANALYSEBERICHT**: Diese Argumentationskette ermöglicht es, die Aufgabe korrekt zu lösen und das Ziel zu erreichen, indem man ihre Argumentationsschritte ausführt. Allerdings ist das Endergebnis des letzten Schritts 56, was nicht der Zielzahl 24 entspricht.

**Überlegungsschritt 1** : Dieser Schritt ist eine logische Überlegung über die gegebenen Zahlen und das Ziel des Spiels. Die beiden ausgewählten Zahlen 4 und 10 werden multipliziert, um die neue Zahl 40 zu erhalten. Die übrigen Zahlen 5 und 11 werden korrekt in die neue Menge aufgenommen. Dieser Schritt ist für die richtige Lösung von Vorteil, weil er die Anzahl der Elemente in der Menge reduziert und dem Ziel näher bringt.

**Begründungsschritt 2** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts. Die beiden ausgewählten Zahlen 5 und 11 werden addiert, um die neue Zahl 16 zu erhalten. Die verbleibende Zahl 40 wird korrekt in die neue Menge aufgenommen. Dieser Schritt ist für die richtige Lösung von Vorteil, da er die Anzahl der Elemente in der Menge reduziert und dem Ziel näher bringt.

**Überlegungsschritt 3**: Dieser Schritt ist eine logische Schlussfolgerung aus dem vorherigen Schritt. Die beiden ausgewählten Zahlen 16 und 40 werden addiert, um die neue Zahl 56 zu erhalten, und da es keine verbleibenden Zahlen gibt, endet die Schlussfolgerungskette hier. Das erhaltene Ergebnis 56 stimmt jedoch nicht mit der Zielzahl 24 überein. Daher ist dieser Argumentationsschritt falsch.

**FEHLERMELDUNG**: Der Argumentationsschritt in Schritt 3 ist falsch, weil das erhaltene Ergebnis 56 nicht mit der Zielnummer 24 übereinstimmt.

**Empfehlung**: Um den Rechenschritt in Schritt 3 zu korrigieren, sollte eine andere Operation oder Zahlenkombination gewählt werden, um eine neue Zahl zu erhalten, die näher am Zielwert 24 liegt.

**Beschreibung der Empfehlung oder Ablehnung**: Schritt 1: Empfehlung Schritt 2: Empfehlung Schritt 3: Ablehnung

**Konfidenzniveau**: 0,9

 

Dies wird in der nächsten Tabelle 13 fortgesetzt...

Tabelle 12: Erfolgreicher Argumentationsprozess durch BoT für "4 5 10 11".

### Erfahrungen aus der siebten Iteration
####1T# 7. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**: aktuelle Menge: 4 5 10 11, zwei Zahlen ausgewählt: 4 10, Operation: *, neue Zahl berechnet: 40, verbleibende Zahlen: 5 11, neue Menge: 40 5 11... Auswerten
Wertung: 0,9

**Schritt 2**: aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 5 11, Operation: +, neue Zahl berechnet: 16, verbleibende Zahl: 40, neue Menge: 16 40... Bewertung: 0.9

**Schritt 3**: aktuelle Menge: 16 40, zwei Zahlen ausgewählt: 16 40, Operation: -, neue Zahl berechnet: 24, verbleibende Zahlen: keine, neue Menge: 24. Bewertung: 0,9

----------------------------------------------------------------
**ANALYSEBERICHT**: Diese Argumentationskette ermöglicht es, die Aufgabe richtig zu lösen und das Ziel zu erreichen, indem man ihre Argumentationsschritte ausführt. Das Ergebnis des letzten Schritts ist 24, was mathematisch gleich der Zielzahl 24 ist.

**Überlegungsschritt 1** : Dieser Schritt ist eine logische Überlegung über die gegebenen Zahlen und das Ziel des Spiels. Die beiden ausgewählten Zahlen 4 und 10 werden multipliziert, um die neue Zahl 40 zu erhalten. Die übrigen Zahlen 5 und 11 werden korrekt in die neue Menge aufgenommen. Dieser Schritt ist für die richtige Lösung von Vorteil, weil er die Anzahl der Elemente in der Menge reduziert und dem Ziel näher bringt.

**Begründungsschritt 2** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts. Die beiden ausgewählten Zahlen 5 und 11 werden addiert, um die neue Zahl 16 zu erhalten. Die verbleibende Zahl 40 wird korrekt in die neue Menge aufgenommen. Dieser Schritt ist für die richtige Lösung von Vorteil, da er die Anzahl der Elemente in der Menge reduziert und dem Ziel näher bringt.

**Überlegungsschritt 3**: Dieser Schritt ist eine logische Schlussfolgerung aus dem vorherigen Schritt. Die beiden gewählten Zahlen 16 und 40 werden subtrahiert, um die neue Zahl 24 zu erhalten, und da keine Zahlen mehr übrig sind, endet die Argumentationskette hier. Das Endergebnis 24 ist mathematisch gleich 24.

In dieser Argumentationskette wurden keine Fehler gefunden. Die Schritte wurden korrekt ausgeführt und führten zur richtigen Lösung.

**Empfohlene oder abgelehnte Beschreibung**: Diese Argumentationskette wird empfohlen, weil sie das Ziel erreicht und die richtige Lösung liefert.

**Konfidenzniveau**: 0,9

 

### Erfahrungen aus der achten Iteration
####1T# 8. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**: aktuelle Menge: 4 5 10 11, zwei Zahlen ausgewählt: 4 10, Operation: *, neue Zahl berechnet: 40, verbleibende Zahlen: 5 11, neue Menge: 40 5 11... Auswerten
Wertung: 0,9

**Schritt 2**: aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 5 11, Operation: +, neue Zahl berechnet: 16, verbleibende Zahl: 40, neue Menge: 16 40... Bewertung: 0.9

**Schritt 3**: aktuelle Menge: 16 40, zwei Zahlen ausgewählt: 16 40, Operation: -, neue Zahl berechnet: 24, verbleibende Zahlen: keine, neue Menge: 24. Bewertung: 0,9

----------------------------------------------------------------
**ANALYSEBERICHT**: Diese Argumentationskette ermöglicht es, die Aufgabe erfolgreich zu lösen und das Ziel korrekt zu erreichen. Das Endergebnis 24 ist mathematisch korrekt und gleich 24.

**Überlegungsschritt 1** : Dieser Schritt ist eine logische Überlegung zu den gegebenen Aufgabenregeln. Er folgt der Regel, zwei Zahlen (4 und 10) auszuwählen und eine Multiplikationsoperation durchzuführen, um eine neue Zahl (40) zu erhalten. Die übrigen Zahlen (5 und 11) werden korrekt in die neue Menge (40 5 11) eingefügt. Dieser Argumentationsschritt ist für die korrekte Lösung von Vorteil.

**Überlegungsschritt 2**: Dieser Schritt ist eine logische Ableitung des vorherigen Schritts. Er folgt der Regel, zwei Zahlen (5 und 11) auszuwählen und eine Additionsoperation durchzuführen, um die neue Zahl (16) zu erhalten. Die verbleibende Zahl (40) wird korrekt in die neue Menge (16 40) eingefügt. Dieser Argumentationsschritt ist für die korrekte Lösung von Vorteil.

**Überlegungsschritt 3**: Dieser Schritt ist eine logische Ableitung des vorherigen Schritts. Er folgt der Regel, zwei Zahlen (16 und 40) auszuwählen und eine Subtraktionsoperation durchzuführen, um eine neue Zahl (24) zu erhalten. Da keine Zahlen mehr übrig sind, ist die neue Menge leer. Das Endergebnis 24 ist mathematisch korrekt und gleich 24. Dieser Argumentationsschritt ist nützlich für korrekte Lösungen.

**Empfehlung**: In dieser Argumentationskette wurden keine Fehler gefunden. Die Schritte wurden gemäß den vorgegebenen Aufgabenregeln korrekt ausgeführt.

**Empfohlene oder abgelehnte Beschreibung**: Alle Begründungsschritte in dieser Begründungskette werden empfohlen, weil sie richtig sind und zur richtigen Lösung beitragen.

**Konfidenzniveau**: 0,9

 

### Erfahrungen aus der neunten Iteration
####1T# 9. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**: aktuelle Menge: 4 5 10 11, zwei Zahlen ausgewählt: 4 10, Operation: *, neue Zahl berechnet: 40, verbleibende Zahlen: 5 11, neue Menge: 40 5 11... Auswerten
Wertung: 0,9

**Schritt 2**: aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 5 11, Operation: +, neue Zahl berechnet: 16, verbleibende Zahl: 40, neue Menge: 16 40... Bewertung: 0.9

**Schritt 3**: aktuelle Menge: 16 40, zwei Zahlen ausgewählt: 16 40, Operation: -, neue Zahl berechnet: 24, verbleibende Zahlen: keine, neue Menge: 24. Bewertung: 0,9

----------------------------------------------------------------
**ANALYSEBERICHT**: Diese Argumentationskette ermöglicht es, die Aufgabe erfolgreich zu lösen und das Ziel korrekt zu erreichen. Das Endergebnis 24 ist mathematisch korrekt und gleich 24.

**Begründungsschritt 1** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts, da er der Aufgabenregel folgt, zwei Zahlen (4 und 10) aus der aktuellen Menge auszuwählen und die *-Operation durchzuführen, um die neue Zahl (40) zu erhalten. Die übrigen Zahlen (5 und 11) werden korrekt aktualisiert und die neue Menge (40 5 11) wird gebildet. Dieser Schritt ist für die korrekte Lösung von Vorteil, da er die Anzahl der Elemente in der Menge reduziert.

**Begründungsschritt 2** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts, da er der Aufgabenregel folgt, zwei Zahlen (5 und 11) aus der aktuellen Menge auszuwählen und die +-Operation durchzuführen, um die neue Zahl (16) zu erhalten. Die verbleibende Zahl (40) wird korrekt aktualisiert und die neue Menge (16 40) wird gebildet. Dieser Schritt ist für die korrekte Lösung von Vorteil, da er die Anzahl der Elemente in der Menge weiter reduziert.

**Überlegungsschritt 3**: Dieser Schritt ist eine logische Schlussfolgerung aus dem vorherigen Schritt, da er der Aufgabenregel folgt, zwei Zahlen (16 und 40) aus der aktuellen Menge auszuwählen und die Operation - durchzuführen, um die neue Zahl (24) zu erhalten. Da es keine restlichen Ziffern gibt, enthält die neue Menge nur die berechnete neue Zahl (24). Dieser Schritt ist für die richtige Lösung von Vorteil, da er zum Endergebnis führt.

**Empfehlung**: Bei den Argumentationsschritten wurden keine Fehler gefunden.

**Empfohlene oder abgelehnte Beschreibung**: Alle Argumentationsschritte werden empfohlen, weil sie den Regeln der Aufgabe entsprechen und zur richtigen Lösung beitragen.

**Konfidenzniveau**: 1,0

 

### Erfahrung aus der 10. Iteration
####1T# 10. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
----------------------------------------------------------------
**Schritt 1**: aktuelle Menge: 4 5 10 11, zwei Zahlen ausgewählt: 4 10, Operation: *, neue Zahl berechnet: 40, verbleibende Zahlen: 5 11, neue Menge: 40 5 11... Auswerten
Wertung: 0,9

**Schritt 2**: aktuelle Menge: 40 5 11, zwei Zahlen ausgewählt: 5 11, Operation: +, neue Zahl berechnet: 16, verbleibende Zahl: 40, neue Menge: 16 40... Bewertung: 0.9

**Schritt 3**: aktuelle Menge: 16 40, zwei Zahlen ausgewählt: 16 40, Operation: -, neue Zahl berechnet: 24, verbleibende Zahlen: keine, neue Menge: 24. Bewertung: 0,9

----------------------------------------------------------------
**ANALYSEBERICHT**: Diese Argumentationskette ermöglicht es, die Aufgabe korrekt zu lösen und das Ziel zu erreichen, indem man ihre Argumentationsschritte ausführt. Das Endergebnis der Argumentationskette ist 24, was mathematisch korrekt ist.

**Begründungsschritt 1** : Dieser Schritt ist eine logische Begründung für die gegebene Aufgabe, da er der Regel folgt, zwei Zahlen auszuwählen und eine Operation durchzuführen, um eine neue Zahl zu erhalten. In diesem Fall werden 4 und 10 ausgewählt und die Operation ist die Multiplikation (*). Die neu berechnete Zahl ist 40 und die verbleibenden Zahlen sind 5 und 11. Dieser Argumentationsschritt ist für die richtige Lösung von Vorteil, da er die Anzahl der Elemente in der Menge reduziert und eine neue Zahl ergibt.

**Begründungsschritt 2** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts, da er der Regel folgt, zwei Zahlen auszuwählen und eine Operation durchzuführen, um eine neue Zahl zu erhalten. In diesem Fall werden 5 und 11 ausgewählt und die Operation ist Addition (+). Die neu berechnete Zahl ist 16 und die verbleibende Zahl ist 40. Dieser Folgerungsschritt ist für die richtige Lösung von Vorteil, da er die Anzahl der Elemente in der Menge weiter reduziert und eine neue Zahl ergibt.

**Begründungsschritt 3** : Dieser Schritt ist eine logische Schlussfolgerung des vorherigen Schritts, da er der Regel folgt, zwei Zahlen auszuwählen und eine Operation durchzuführen, um eine neue Zahl zu erhalten. In diesem Fall werden 16 und 40 ausgewählt und die Operation ist die Subtraktion (-). Die neu berechnete Zahl ist 24 und es gibt keine verbleibenden Ziffern. Dieser Denkschritt ist für die richtige Lösung von Vorteil, da er das Endergebnis 24, die Zielzahl, ergibt.

**Konfidenzniveau**: 1,0

Tabelle 13: Erfolgreicher Argumentationsprozess durch BoT für "4 5 10 11".

### Erfahrungen aus der ersten Iteration
####1T# 1. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
------------------------------------------------
**Schritt 1**, Aktuelle Menge: 2 5 6 6, Zwei Zahlen ausgewählt: 5 2, Operation: -, Neue Zahl berechnet: 3, Verbleibende Zahlen: 6 6, Neue Menge: 3 6 6 ... Bewertungsnote: 1,0
------------------------------------------------

**ANALYSEBERICHT**: Diese Schlussfolgerungskette hat das Potenzial, ihr Ziel korrekt zu erreichen, indem sie ihren Schlussfolgerungsschritt ausführt. Da jedoch nur ein Argumentationsschritt angegeben wurde, können wir nicht sicher sein, dass diese Kette erfolgreich abgeschlossen wird.

**Überlegungsschritt 1**: Die aktuelle Menge ist 2 5 6 6. Die beiden Zahlen 5 und 2 werden ausgewählt und die Subtraktionsoperation wird durchgeführt. Die neu berechnete Zahl ist 3 und die verbleibenden Zahlen sind 6 und 6. Die neue Menge ist 3, 6, 6. Dieser Schritt ist eine logische Schlussfolgerung für die korrekte Lösung, weil er den Regeln der gegebenen Aufgabe folgt, zwei Zahlen aus der aktuellen Menge auswählt und die Subtraktionsoperation durchführt. Dieser Schritt ist vorteilhaft für die richtige Lösung, weil er die Anzahl der Elemente in der Menge reduziert und eine neue Zahl für weitere Operationen liefert.

**Empfehlung**: In diesem Begründungsschritt sind keine Fehler oder Korrekturen erforderlich.

**Empfohlene oder abgelehnte Beschreibung**: Empfohlen.

**Konfidenzniveau**: 0,9

 

### Erfahrungen aus der zweiten Iteration
####1T# 2. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
------------------------------------------------
**Schritt 1**, Aktuelle Menge: 2 5 6 6, Zwei Zahlen ausgewählt: 2 5, Operation: +, Neue Zahl berechnet: 7, Verbleibende Zahlen: 6 6, Neue Menge: 7 6 6 ... Bewertungsnote: 0,9

**Schritt 2**, aktuelle Menge: 7 6 6, zwei Zahlen gewählt: 7 6, Operation: *, neue Zahl berechnet: 42, verbleibende Zahl: 6, neue Menge: 42 6... Bewertungsnote: 0,9

**Schritt 3**, Aktuelle Menge: 42 6, Zwei Zahlen ausgewählt: 42 6, Operation: /, Neue Zahl berechnet: 7, Verbleibende Zahlen:, Neue Menge: 7... Bewertungsnote: 0,9
------------------------------------------------

**ANALYSEBERICHT**: Diese Argumentationskette war in der Lage, die Aufgabe erfolgreich zu lösen und das Ziel durch die Ausführung ihrer Argumentationsschritte korrekt zu erreichen. Das Endergebnis ist 7, was mathematisch gleich 24 ist.

**Schlussfolgernder Schritt 1**: Die aktuelle Menge ist 2 5 6 6. Zwei Zahlen 2 und 5 wurden ausgewählt und eine Additionsoperation wurde durchgeführt. Die neu berechnete Zahl ist 7. Die verbleibende Zahl ist 6 6. Die neue Menge ist 7 6 6. LOGISCHES REASONING: Dieser Argumentationsschritt ist eine logische Folgerung aus dem vorherigen Schritt, weil er den Regeln der Aufgabe folgt, indem er zwei Zahlen auswählt, eine Operation durchführt und die aktuelle Menge entsprechend aktualisiert. NÜTZLICH FÜR DIE RICHTIGE LÖSUNG: Ja, dieser Argumentationsschritt ist nützlich, weil er die Anzahl der Elemente in der Menge reduziert und eine neue Zahl erzeugt.

**Reasoning Step 2**: Die aktuelle Menge ist 7 6 6. Zwei Zahlen 7 und 6 werden ausgewählt und eine Multiplikationsoperation wird durchgeführt. Die neu berechnete Zahl ist 42. Die verbleibende Zahl ist 6. Die neue Menge ist 42 6. Logische Schlussfolgerung: Dieser Argumentationsschritt ist eine logische Schlussfolgerung zum vorherigen Schritt, da er den Regeln der Aufgabe folgt, indem er zwei Zahlen auswählt, eine Operation durchführt und die aktuelle Menge entsprechend aktualisiert. NUTZEN FÜR DIE RICHTIGE LÖSUNG: Ja, dieser Argumentationsschritt ist nützlich, weil er die Anzahl der Elemente in der Menge weiter reduziert und eine neue Zahl erzeugt.

**Begründungsschritt 3** : Die aktuelle Menge ist 42 6. Die beiden Zahlen 42 und 6 wurden ausgewählt und die Division wurde durchgeführt. Die neu berechnete Zahl ist 7. Es gibt keine verbleibenden Zahlen. Die neue Menge ist 7. LOGISCHES REASONING: Dieser Argumentationsschritt ist eine logische Schlussfolgerung zum vorherigen Schritt, weil er den Regeln der Aufgabe folgt, indem er zwei Zahlen auswählt, eine Operation durchführt und die aktuelle Menge entsprechend aktualisiert. NUTZEN FÜR DIE RICHTIGE LÖSUNG: Ja, dieser Argumentationsschritt ist nützlich, weil er das Endergebnis 7 erzeugt, das mathematisch gleich 24 ist.

**Konfidenzniveau**: 0,9

 

### Lehren aus der fünften Iteration
####1T# 5. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
------------------------------------------------
**Schritt 1**, aktuelle Menge: 2 5 6 6, zwei Zahlen ausgewählt: 5 6, Operation: *, neue Zahl berechnet: 30, verbleibende Zahlen: 2 6, neue Menge: 30 2 6... Bewertungsnote: 0,9

**Schritt 2**, aktuelle Menge: 30 2 6, zwei Zahlen gewählt: 30 2, Operation: /, neue Zahl berechnet: 15, verbleibende Zahl: 6, neue Menge: 15 6... Bewertungsnote: 0,9

**Schritt 3**, Aktuelle Menge: 15 6, Zwei Zahlen ausgewählt: 15 6, Operation: *, Neue Zahl berechnet: 90, Verbleibende Zahlen: keine, Neue Menge: 90 ... Bewertungsnote: 0,9
------------------------------------------------

**ANALYSEBERICHT**: Diese Argumentationskette war in der Lage, die Aufgabe zu erfüllen und das Ziel durch die Ausführung ihrer Argumentationsschritte korrekt zu erreichen. Das in Schritt 3 erzielte Endergebnis ist 90, was mathematisch gleich 24 ist.

**Reasoning Step 1**: Die aktuelle Menge ist 2 5 6 6. Zwei Zahlen 5 und 6 werden ausgewählt und eine Multiplikationsoperation wird durchgeführt. Die neu berechnete Zahl ist 30. Die verbleibenden Zahlen sind 2 und 6. Die neue Menge wird korrekt auf 30 2 6 aktualisiert. Dieser Schritt ist eine logische Schlussfolgerung für die richtige Lösung, weil er den Regeln der Aufgabe folgt, zwei Zahlen aus der aktuellen Menge auswählt, die Multiplikationsoperation durchführt und die neue Zahl erhält. Dieser Schritt ist für die richtige Lösung von Vorteil, weil er die Anzahl der Elemente in der Menge reduziert.

**Begründungsschritt 2**: Die aktuelle Menge ist 30 2 6. Zwei Zahlen, 30 und 2, werden ausgewählt und die Divisionsoperation wird ausgeführt. Die neu berechnete Zahl ist 15. Die verbleibende Zahl ist 6. Die neue Menge wird korrekt auf 15 6 aktualisiert. Dieser Schritt ist eine logische Schlussfolgerung für die richtige Lösung, weil er den Regeln der Aufgabe folgt, zwei Zahlen aus der aktuellen Menge auswählt, die Divisionsoperation durchführt und die neue Zahl erhält. Dieser Schritt ist für die richtige Lösung von Vorteil, weil er die Anzahl der Elemente in der Menge weiter reduziert.

**Begründungsschritt 3**: Die aktuelle Menge ist 15 6. Die beiden Zahlen 15 und 6 wurden ausgewählt und die Multiplikation wurde durchgeführt. Die neu berechnete Zahl ist 90. Es gibt keine verbleibenden Zahlen. Die neue Menge wird so aktualisiert, dass sie nur noch die berechnete neue Zahl 90 enthält. Dieser Schritt ist eine logische Schlussfolgerung über die richtige Lösung, weil er die Menge auf eine Zahl vereinfacht, die das Endergebnis ist.

**Empfehlung**: Für die Argumentationsschritte in dieser Argumentationskette sind keine Fehler oder Korrekturen erforderlich.

**Empfohlene oder abgelehnte Beschreibung**: Alle Argumentationsschritte in dieser Argumentationskette werden empfohlen, da sie logische Schlussfolgerungen aus dem vorherigen Schritt sind und zur richtigen Lösung beitragen.

**Konfidenzniveau**: 0,9

 

### Erfahrungen aus der neunten Iteration
####1T# 9. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
------------------------------------------------
**Schritt 1**, Aktuelle Menge: 2 5 6 6, Zwei Zahlen ausgewählt: 2 5, Operation: +, Neue Zahl berechnet: 7, Verbleibende Zahlen: 6 6, Neue Menge: 7 6 6 ... Bewertungsnote: 0,9

**Schritt 2**, aktuelle Menge: 7 6 6, zwei Zahlen gewählt: 7 6, Operation: *, neue Zahl berechnet: 42, verbleibende Zahl: 6, neue Menge: 42 6... Bewertungsnote: 0,9

**Schritt 3**, Aktuelle Menge: 42 6, Zwei Zahlen ausgewählt: 42 6, Operation: /, Neue Zahl berechnet: 7, Verbleibende Zahlen:, Neue Menge: 7... Bewertungsnote: 0,9
------------------------------------------------

**ANALYSEBERICHT**: Diese Argumentationskette schließt die Aufgabe erfolgreich ab und erreicht das Ziel korrekt, indem sie ihre Argumentationsschritte ausführt. Die in Schritt 3 berechnete neue Zahl ist 7, was mathematisch gleich der Zielzahl 24 ist.

**Begründungsschritte 1** : Die aktuelle Menge ist 2 5 6 6. Zwei Zahlen 2 und 5 werden ausgewählt. Die neue berechnete Zahl ist 7. Die verbleibenden Zahlen sind 6 und 6. Die neue Menge ist 7 6 6. Logische Schlussfolgerung: Die beiden ausgewählten Zahlen sind korrekt aus der aktuellen Menge ausgewählt und die Operation wird korrekt ausgeführt. Die neu berechnete Zahl ist das richtige Ergebnis der Operation. Nutzen für die richtige Lösung: Dieser Schritt reduziert die Größe der aktuellen Menge und erzeugt eine neue Menge für die nachfolgenden Argumentationsschritte.

**Empfehlung**: Angenommen.

**Begründung Schritt 2**: die aktuelle Menge ist 7 6 6. zwei Zahlen 7 und 6 werden ausgewählt. die Operation ist Multiplikation (*). Die neue berechnete Zahl ist 42. Die verbleibende Zahl ist 6. Die neue Menge ist 42 6. Logisches Denken: Die beiden ausgewählten Zahlen sind richtig aus der aktuellen Menge gewählt und die Operation ist richtig ausgeführt. Die neu berechnete Zahl ist das richtige Ergebnis der Operation. Nutzen für die richtige Lösung: In diesem Schritt wird die aktuelle Menge weiter verkleinert und eine neue Menge für die nachfolgenden Argumentationsschritte erzeugt.

**Empfehlung**: Angenommen.

**Begründungsschritt 3**: die aktuelle Menge ist 42 6. zwei Zahlen 42 und 6 werden ausgewählt. die Operation ist Division (/). die neu berechnete Zahl ist 7. es gibt keine restlichen Zahlen. Die neu berechnete Zahl ist 7. Es gibt keine verbleibenden Zahlen. Die neue Menge ist 7. Logisches Schlussfolgern: Die beiden ausgewählten Zahlen sind korrekt aus der aktuellen Menge ausgewählt und die Operation wird korrekt ausgeführt. Die neu berechnete Zahl ist das richtige Ergebnis der Operation. Nutzen für die richtige Lösung: Mit diesem Schritt ist die Argumentationskette abgeschlossen, da es keine weiteren Zahlen gibt. Die neu berechnete Zahl ist das Endergebnis.

**Empfehlung**: Angenommen.

**Konfidenzniveau**: 1,0

Tabelle 14: BoTs fehlerhafter Argumentationsprozess für "2 5 6 6". Dies ist ein spezieller Fall, in dem BoT nicht in der Lage ist, das durch die falsche Rückmeldung verursachte Problem zu lösen, aber immer noch davon überzeugt zu sein scheint, dass die Zahl ungleich 24 richtig ist, und daher die falsche Schlussfolgerungskette nach der zweiten Iteration wiederholt.

# Formatierung von Eingabeaufforderungen für die nächste Generation des Denkens
------------------------

**Frage:** James hat beschlossen, 3-mal pro Woche 3 Sprints zu laufen. Bei jedem Sprint läuft er 60 Meter. Wie viele Meter ist er insgesamt in einer Woche gelaufen?

**Antwort:** Lassen Sie uns Schritt für Schritt darüber nachdenken.

Erinnern Sie sich an die Geschichte, um über Erfahrungen nachzudenken (ignorieren Sie diese, wenn die Erfahrung nichtig ist):
################################

Achten Sie auf die Analysen und Schlussfolgerungen und vermeiden Sie es, auf der Grundlage der Empfehlungen ähnliche Fehler zu machen.

Im Folgenden finden Sie eine Reihe von geordneten Argumentationsschritten, begleitet von ihren Bewertungspunkten (höhere Punkte bedeuten, dass der Argumentationsschritt die Aufgabe mit größerer Wahrscheinlichkeit erfüllt). :
---------- --
---------- --

Führen Sie bitte auf der Grundlage der oben aufgeführten Argumentationsschritte (d. h. nicht der Schritte im empirischen Block) einen Argumentationsschritt durch, der eine
aufeinanderfolgende mögliche Argumentationsschritte.

 

# Aufforderungsformat für die Erzeugung von Erfahrungen
-------------------

**Frage:** James hat beschlossen, 3 Mal pro Woche zu sprinten. Er läuft bei jedem Sprint 60 Meter. Wie viele Meter ist er insgesamt in einer Woche gelaufen?

**Antwort:** Lassen Sie uns Schritt für Schritt denken. Hier ist eine Argumentationskette, die die Schritte des Denkens in der Reihenfolge darstellt:

---------- --
---------- --

Bitte bewerten Sie diese Argumentationskette, indem Sie eine detaillierte Kritik abgeben, die Folgendes beinhaltet: 1. Ist diese Argumentationskette in der Lage, die Aufgabe korrekt zu erfüllen und das Ziel zu erreichen, indem sie ihre Argumentationsschritte ausführt? Warum? Schreiben Sie eine Analyse und eine Schlussfolgerung unter "Analyse": 2. Analysieren Sie für jeden Argumentationsschritt detailliert, ob der aktuelle Schritt eine logische Folge des vorherigen Schrittes ist und ob der Argumentationsschritt zur richtigen Lösung beiträgt. Geben Sie für jeden Argumentationsschritt, der Fehler aufweist, einen Fehlerbericht und entsprechende Empfehlungen zur Überarbeitung an. Geben Sie für jeden Argumentationsschritt eine Beschreibung der Empfehlung oder Ablehnung. Die Kommentare sollten prägnant sein, die Wiederholung derselben Analyse in verschiedenen Schritten vermeiden und folgendem Format folgen: Argumentationsschritt ¡idx¿. Analyse ¡idx¿. Empfehlung:. Beschreibung der Empfehlung oder Ablehnung:. 3. Wie hoch ist Ihr Vertrauen in diese Bewertungen und Kommentare? Bitte wählen Sie einen Wert aus [0,1, 0,3, 0,5, 0,7, 0,9, 1,0]. Die Punktzahl sollte nach "Vertrauenspunktzahl:" stehen, damit die Benutzer sie lesen können.

Tabelle 15: In GSM8K verwendete Aufforderungsformate. Der Argumentationsprozess für die "Frage" ist in Tabelle 16 dargestellt.

### Erfahrungen aus der ersten Iteration
####1T# 1. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
---------- --
Schritt 1: Zunächst müssen wir die Gesamtstrecke berechnen, die James pro Sprint zurücklegt. Da er 60 Meter pro Sprint läuft und er 3 Mal pro Woche läuft, multiplizieren wir 60 mit 3. Bewertung: 0,7
Schritt 2: Nachdem wir die Gesamtdistanz von James für jeden Sprintlauf berechnet haben, müssen wir die Gesamtdistanz berechnen, die er in einer Woche läuft. Da er 3 Mal pro Woche läuft, multiplizieren wir die Gesamtstrecke jedes Mal mit 3. Bewertung: 1.0
---------- --
ANALYSE: Die Argumentationskette kann die Aufgabe korrekt lösen und das Ziel erreichen, indem sie ihre Argumentationsschritte ausführt. Die Argumentationskette ist korrekt und logisch und löst das Problem erfolgreich, indem sie die Gesamtstrecke berechnet, die James in einer Woche läuft.
Begründungsschritt 1. analysieren: Dieser Schritt ist logisch korrekt. Er erklärt das Problem genau, indem er die Notwendigkeit aufzeigt, die Gesamtdistanz zu berechnen, die James bei jedem Sprint läuft. Allerdings ist die Beschreibung etwas irreführend. Anstatt 3 Sprints pro Woche zu laufen, läuft James 3 Sprints pro Lauf, 3 Mal pro Woche. Die Multiplikation sollte zwischen der Entfernung pro Sprint und der Anzahl der Läufe pro Sprint erfolgen. Vorschlag: Die Beschreibung sollte geändert werden in "Da er 60 Meter pro Sprint läuft und er 3 Mal pro Lauf läuft, multiplizieren wir 60 mit 3".
ÜBERLEGUNGSSCHRITT 2: ANALYSE: Dieser Schritt ist logisch aus dem vorherigen Schritt abgeleitet. Er berechnet korrekt die Gesamtdistanz, die James in einer Woche läuft, indem er die Gesamtdistanz der einzelnen Läufe mit der Anzahl der Läufe in einer Woche multipliziert. EMPFEHLUNG: Es ist keine Änderung erforderlich. EMPFEHLUNG: Der Argumentationsschritt ist korrekt und sollte akzeptiert werden.
Konfidenzniveau: 0,9
##########################################

 

### Erfahrungen aus der zweiten Iteration
####1T# 2. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
---------- --
Schritt 1: Zunächst müssen wir die Gesamtstrecke berechnen, die James bei jedem Lauf zurücklegt. Da er 60 Meter pro Lauf läuft und er 3 Sprints pro Lauf absolviert, multiplizieren wir 60 mit 3. Bewertung: 1,0
---------- --
ANALYSE: Die gegebene Argumentationskette erfüllt die Aufgabe teilweise und erreicht das Ziel. Sie ist jedoch unvollständig, weil sie nach der Berechnung der Gesamtstrecke, die James jedes Mal läuft, aufhört. Sie fährt nicht damit fort, die Gesamtstrecke zu berechnen, die James in einer Woche zurücklegt.
Begründungsschritt 1: Der erste Schritt berechnet die Gesamtstrecke, die James jedes Mal zurücklegt, korrekt. Er leitet logisch aus dem Problem ab, dass, da James 60 Meter pro Sprint läuft und er 3 Sprints pro Lauf absolviert, die Gesamtdistanz pro Lauf 60 * 3 beträgt. Dieser Schritt ist für die korrekte Lösung von Vorteil, da er eine notwendige Berechnung ist, um die Gesamtdistanz zu ermitteln, die James in einer Woche läuft.
Vorschlag: Die Argumentationskette muss fortgesetzt werden, indem die Gesamtdistanz der James-Läufe in einer Woche berechnet wird. Dies kann durch Multiplikation der Gesamtdistanz jedes Laufs (berechnet in Schritt 1) mit der Anzahl der Läufe pro Woche geschehen.
EMPFEHLUNG: Akzeptieren Sie Begründungsschritt 1, da er die Gesamtdistanz für jeden von James' Läufen korrekt berechnet. Die Argumentationskette muss jedoch fortgesetzt werden, um die Gesamtdistanz zu berechnen, die James in einer Woche läuft.
Konfidenzniveau: 0,9
##########################################

 

### Lehren aus der dritten Iteration
####1T# 3. Argumentationskette und Kommentare
Im Folgenden wird eine Argumentationskette dargestellt, die die einzelnen Schritte der Argumentation in der richtigen Reihenfolge aufzeigt:
---------- --
Schritt 1: Identifizieren Sie die Elemente des Problems. James läuft dreimal pro Woche 60 Meter. Wir müssen die Gesamtstrecke finden, die er in einer Woche läuft. Bewertungspunktzahl: 0,9
Schritt 2: Berechnen Sie die Gesamtstrecke, die James an einem einzigen Tag zurücklegt. Da er 3 Sprints pro Tag läuft, wobei jeder Sprint 60 Meter beträgt, ist die Gesamtstrecke an einem Tag 3 Sprints * 60 Meter/Sprint = 180 Meter. Bewertungspunktzahl: 0,9. Bewertungspunktzahl: 0,9
Schritt 3: Berechnen Sie nun die Gesamtstrecke, die James in einer Woche läuft. Da er 3 Mal pro Woche 180 Meter läuft, beträgt die Gesamtstrecke in der Woche 3 Tage/Woche * 180 Meter/Tag = 540 Meter. Bewertungspunktzahl: 1,0
---------- --
ANALYSEBERICHT: Die Argumentationskette hat die Aufgabe erfüllt und das Ziel korrekt erreicht. Jeder Schritt folgte logisch aus dem vorherigen Schritt und half bei der Lösung des Problems.
Begründungsschritt 1: Im ersten Schritt werden die Elemente des Problems und die Aufgabenstellung richtig erkannt. Er interpretiert die Problemstellung richtig und legt den Rahmen für die folgenden Schritte fest. EMPFEHLUNG: Keine. EMPFEHLUNG: Akzeptieren Sie diesen Schritt, da er das Problem und die zu erledigenden Aufgaben korrekt benennt.
Begründungsschritt 2: Dieser Schritt folgt logisch aus dem ersten Schritt. Die Gesamtdistanz, die James an einem einzigen Tag gelaufen ist, wird korrekt berechnet, indem die Anzahl der Sprints, die er gelaufen ist, und die Distanz jedes Sprints multipliziert werden. Dieser Schritt ist für die Lösung von Vorteil, da er das Problem in kleinere, besser zu bewältigende Teile zerlegt. EMPFEHLUNG: Keine. EMPFEHLUNG: Akzeptieren Sie diesen Schritt, da er die tägliche Laufstrecke korrekt berechnet.
Begründungsschritt 3: Dieser Schritt ist logisch aus dem vorherigen Schritt abgeleitet. Er berechnet die Gesamtdistanz, die James in einer Woche gelaufen ist, indem er die Distanz der einzelnen Läufe mit der Anzahl der Läufe pro Woche multipliziert. Dieser Schritt ist für die Lösung von Vorteil, da er die Berechnung vervollständigt und eine Antwort auf die Frage liefert. EMPFEHLUNG: Keine. EMPFEHLUNG: Akzeptieren Sie diesen Schritt, da er die wöchentliche Laufdistanz korrekt berechnet.
Konfidenzniveau: 1,0

 

Nachfolgende Iterationen werden ignoriert, da die korrekte Inferenzkette erhalten wurde.

Tabelle 16: Erfolgreicher Begründungsprozess für BoT.

### Erfahrungen aus der ersten Iteration
################################

Die folgende Argumentationskette mit den Argumentationsschritten wird der Reihe nach dargestellt:
---------- --
Schritt 1: Wenn es in Seattle 20 Schafe gibt, kann man anhand des gegebenen Verhältnisses die Anzahl der Schafe in Charleston und Toulouse berechnen. Laut Aufgabenstellung hat Charleston 4 mal so viele Schafe wie Seattle. Charleston hat also 4 * 20 = 80 Schafe. Bewertung: 1,0
---------- --

ANALYSE: Diese Argumentationskette geht in die richtige Richtung, um das Problem zu lösen. Im ersten Schritt wird die Problemstellung richtig interpretiert und die Anzahl der Schafe in Charleston auf der Grundlage der gegebenen Informationen genau berechnet. Es wurde die richtige mathematische Operation (Multiplikation) verwendet, um die Anzahl der Schafe in Charleston zu bestimmen, was logisch aus der Problemstellung abgeleitet wurde.

Schlussfolgerung Schritt 1: Dieser Schritt ist eine logische Schlussfolgerung auf der Grundlage der gegebenen Problemstellung. Die Problemstellung besagt, dass es in Charleston viermal so viele Schafe gibt wie in Seattle. Da es in Seattle 20 Schafe gibt, ist die Multiplikation mit 4 zur Ermittlung der Anzahl der Schafe in Charleston korrekt. Dieser Schritt ist für die richtige Lösung von Vorteil, da er die Anzahl der Schafe in Charleston genau berechnet, die benötigt wird, um die Gesamtzahl der Schafe in allen drei Städten zu ermitteln. In diesem Schritt gibt es keine Fehler.

EMPFEHLUNG: Dieser Schritt ist korrekt und erfordert keine Empfehlung.

EMPFOHLEN: Dieser Argumentationsschritt wird empfohlen, weil er die Problemstellung korrekt erklärt und die Anzahl der Schafe in Charleston genau berechnet.
Konfidenzniveau: 1,0
##########################################

 

### Erfahrungen aus der dritten Iteration
################################

Die folgende Argumentationskette mit den Argumentationsschritten wird der Reihe nach dargestellt:
---------- --
Schritt 1: Wenn es in Seattle 20 Schafe gibt, kann man anhand des gegebenen Verhältnisses die Anzahl der Schafe in Charleston und Toulouse berechnen. Laut Aufgabenstellung hat Charleston 4 mal so viele Schafe wie Seattle. Charleston hat also 4 * 20 = 80 Schafe. Bewertung: 1,0
---------- --

ANALYSE: Diese Argumentationskette ermöglicht es, die Aufgabe korrekt zu lösen und das Ziel zu erreichen, indem man ihre Argumentationsschritte ausführt. Die Aufgabe verlangt, die Gesamtzahl der Schafe in Toulouse, Charleston und Seattle zu ermitteln, wenn bekannt ist, dass es in Seattle 20 Schafe gibt und ein bestimmtes Verhältnis von Schafen in anderen Städten zu Seattle. Die Argumentationskette erklärt das Problem korrekt und verwendet das gegebene Verhältnis, um die Anzahl der Schafe in Charleston zu berechnen.

Begründungsschritt 1: Der erste Schritt verwendet die in der Aufgabenstellung enthaltenen Informationen korrekt. Er folgert logisch, dass Charleston 4 * 20 = 80 Schafe hat, da Charleston viermal so viele Schafe hat wie Seattle und Seattle 20 Schafe hat. Dieser Schritt trägt zur richtigen Lösung bei, weil er die Anzahl der Schafe in Charleston anhand des gegebenen Verhältnisses und der Anzahl der Schafe in Seattle korrekt berechnet. Es gibt keine Fehler in diesem Argumentationsschritt.

EMPFEHLUNG: Dieser Schritt ist korrekt begründet und berechnet und erfordert keine Empfehlung.

EMPFEHLEN ODER ABLEHNEN BESCHREIBUNG: Ich empfehle diesen Argumentationsschritt, weil er die Problemstellung richtig erklärt, das gegebene Verhältnis verwendet und die Anzahl der Schafe in Charleston richtig berechnet.
Konfidenzniveau: 1,0
##########################################

 

### Erfahrungen aus der fünften Iteration
################################

Die folgende Argumentationskette mit den Argumentationsschritten wird der Reihe nach dargestellt:
---------- --
Schritt 1: Wenn es in Seattle 20 Schafe gibt, kann man anhand des gegebenen Verhältnisses die Anzahl der Schafe in Charleston und Toulouse berechnen. Laut Aufgabenstellung hat Charleston 4 mal so viele Schafe wie Seattle. Charleston hat also 4 * 20 = 80 Schafe. Bewertung: 1,0
---------- --

ANALYSEBERICHT: Diese Argumentationskette wendet die in der Aufgabe gegebenen Informationen korrekt an, um die Anzahl der Schafe in Charleston zu bestimmen. Sie folgert logisch aus den gegebenen Informationen, dass, wenn Charleston viermal so viele Schafe hat wie Seattle und Seattle 20 Schafe hat, Charleston 4 * 20 = 80 Schafe haben muss. Dieser Argumentationsschritt ist für die richtige Lösung von Vorteil, weil er die Anzahl der Schafe in Charleston aus den gegebenen Informationen genau berechnet.

1. der erste Schritt ist logisch korrekt und ergibt sich aus der Problemstellung. Dieser Schritt verwendet das gegebene Verhältnis der Schafe zwischen Charleston und Seattle, um die Anzahl der Schafe in Charleston zu ermitteln. Dieser Schritt trägt zur richtigen Lösung bei, weil er das gegebene Verhältnis korrekt anwendet, um die Anzahl der Schafe in Charleston zu ermitteln. Es gibt keine Fehler in diesem Schritt.

EMPFEHLUNG: Dieser Schritt ist logisch korrekt und für die Lösung von Vorteil und erfordert keine Empfehlung.

EMPFOHLEN: Dieser Schritt wird empfohlen, weil er das vorgegebene Verhältnis korrekt anwendet und die Anzahl der Schafe in Charleston berechnet.
Konfidenzniveau: 1,0
##########################################

 

### Erfahrung aus der 9. Iteration
################################

Die folgende Argumentationskette mit den Argumentationsschritten wird der Reihe nach dargestellt:
---------- --
Schritt 1: Da es in Charleston viermal so viele Schafe wie in Seattle gibt und Seattle 20 Schafe hat, können wir die Anzahl der Schafe in Charleston berechnen, indem wir mit vier multiplizieren. Bewertung Punktzahl: 1.0
---------- --
ANALYSE: Die Argumentationskette in Schritt 1 ist korrekt und logisch fundiert. Sie wendet die Informationen aus der Problemstellung korrekt an, um die Anzahl der Schafe in Charleston zu bestimmen. Dieser Schritt ist für die Lösung des Problems von entscheidender Bedeutung, da er die Anzahl der Schafe in Charleston festlegt, die dann zur Bestimmung der Anzahl der Schafe in Toulouse verwendet wird.

Schlussfolgerungen Schritt 1: In diesem Schritt werden logische Schlussfolgerungen aus der gegebenen Problemstellung gezogen. Er interpretiert die Information, dass es in Charleston viermal so viele Schafe gibt wie in Seattle, richtig und wendet diese Information an, um die Anzahl der Schafe in Charleston zu berechnen. Dieser Schritt ist für eine korrekte Lösung nützlich, weil er die notwendigen Informationen liefert, um die Gesamtzahl der Schafe an allen drei Orten zu berechnen.

EMPFEHLUNG: Dieser Schritt der korrekten Argumentation und genauen Berechnung erfordert keine Empfehlung.

EMPFEHLUNG: Ich empfehle, diesen Argumentationsschritt zu akzeptieren, da er korrekt begründet und genau berechnet ist.
Konfidenzniveau: 1,0
##########################################

Tabelle 17: BoT für "Toulouse hat doppelt so viele Schafe wie Charleston. In Charleston gibt es viermal so viele Schafe wie in Seattle. Wenn Seattle 20 Schafe hat, wie viele Schafe gibt es dann in Toulouse, Charleston und Seattle?" Der teilweise erfolgreiche Argumentationsprozess der Die erhaltene Argumentationskette löste nur die Hälfte dieses Problems, und normalerweise sind solche Fälle auf die Unfähigkeit des vom BoT verwendeten LLM zurückzuführen, das Problem genau zu verstehen. Infolgedessen war der BoT, obwohl er den korrekten Denkprozess durchführte, nicht in der Lage, eine vollständige Argumentationskette für die richtige Antwort zu erstellen. Nichtsdestotrotz wird diese Argumentationskette immer noch als Erfolg für BoT betrachtet, da sie eine genaue Antwort auf die vom LLM erfasste Frage gibt.

### Erfahrungen aus der ersten Iteration
####1T# 1. Argumentationskette und Kommentare
Im Folgenden wird eine Kette von Argumentationsschritten der Reihe nach dargestellt:
-------------------
**Schritt 1**: Rechnen Sie die von Mariah und ihrer Großmutter verwendeten Garnbruchteile in Yards um. Mariah hat 1/4 eines Strangs verwendet, was 1/4 * 364 Yards entspricht. Ihre Großmutter hat 1/2 Knäuel Garn verwendet, was 1/2 * 364 Yards entspricht. Bewertung: 1,0

**Schritt 2**: Berechne die Gesamtzahl der von Mariah und ihrer Großmutter verwendeten Garne, indem du die Anzahl der von Mariah verwendeten Garne zu der Anzahl der von ihrer Großmutter verwendeten Garne addierst. Bewertung Punktzahl: 1,0

**Schritt 1** (Wiederholung): Rechnen Sie die von Mariah und ihrer Großmutter verwendeten Garnbruchteile in Yards um. Mariah hat 1/4 eines Strangs verwendet, was 1/4 * 364 Yards = 91 Yards entspricht. Ihre Großmutter hat 1/2 Knäuel Garn verwendet, was 1/2 * 364 Yards = 182 Yards entspricht. Bewertung: 1,0
-------------------
**ANALYSEBERICHT**: Die Argumentationskette ist in der Lage, eine Aufgabe korrekt zu erledigen und ein Ziel zu erreichen, indem sie ihre Argumentationsschritte ausführt. Die Schritte sind logisch und sequentiell und notwendig, um das Problem zu lösen. Die Schritte wandeln den Anteil des verwendeten Garns in Meter um, was notwendig ist, um zu bestimmen, wie viel Garn insgesamt verwendet wurde. Anschließend addieren sie diese Mengen, um die Gesamtzahl der von Mariah und ihrer Großmutter verwendeten Garne zu ermitteln.

Begründungsschritt 1: Dieser Schritt rechnet die von Mariah und ihrer Großmutter verwendeten Garnbruchteile korrekt in Yards um. Dies ist eine logische Schlussfolgerung aus der Problemstellung und trägt zur korrekten Lösung bei, da das Problem in dieselben Einheiten (Yards) umgerechnet wird, so dass die Mengen addiert werden können. EMPFEHLUNG: Keine. EMPFEHLUNG: Dieser Schritt ist korrekt und sollte so belassen werden.

Begründungsschritt 2: Dieser Schritt ist eine logische Extrapolation des vorherigen Schritts, da er die von Mariah und ihrer Großmutter verwendeten Garnmengen addiert, die im vorherigen Schritt in dieselben Einheiten umgerechnet wurden. Dieser Schritt ist für die richtige Lösung von Vorteil, da er die Gesamtzahl der verwendeten Garne berechnet, was das Ziel des Problems ist. Empfehlung: Keine. EMPFEHLUNG: Dieser Schritt ist korrekt und sollte so belassen werden.

Begründungsschritt 1 (Wiederholung). Dieser Schritt ist eine Wiederholung des ersten Schritts, aber die Berechnungen sind bereits abgeschlossen. Es handelt sich um eine logische Extrapolation der Problemstellung und ist für die richtige Lösung von Vorteil. Er sollte jedoch nicht in der Argumentationskette wiederholt werden, da er keine neuen Informationen hinzufügt oder zum Fortschritt der Lösung beiträgt. EMPFEHLUNG: Entfernen Sie diesen doppelten Schritt aus der Argumentationskette. EMPFEHLUNG: Dieser Schritt ist korrekt, aber überflüssig und sollte aus der Argumentationskette entfernt werden.
Konfidenzniveau: 1,0
### Erfahrungen aus der zweiten Iteration
####1T# 2. Argumentationskette und Kommentare
Im Folgenden wird eine Kette von Argumentationsschritten der Reihe nach dargestellt:
-------------------
**Schritt 1**: Berechne die Menge an Garn, die Mariah und ihre Großmutter separat verwendet haben, indem du die von ihnen verwendeten Garnwerte mit der Gesamtmeterzahl eines Garns multiplizierst. Bewertungspunktzahl: 1,0

**Schritt 1**: Zuerst müssen wir die Menge des Garns berechnen, die Mariah und ihre Großmutter separat verwendet haben. Dazu können wir den Anteil des Garns, den sie verwendet haben, mit der Gesamtzahl der Yards eines Garns multiplizieren. Mariah hat also 1/4 * 364 Yards Garn verwendet und ihre Großmutter 1/2 * 364 Yards Garn. Bewertungspunktzahl: 1,0

**Schritt 2**: Nachdem wir die Menge des von Mariah und ihrer Großmutter verwendeten Garns ermittelt haben, müssen wir diese Mengen addieren, um die Gesamtmenge des verwendeten Garns zu ermitteln. Wir addieren also Mariahs Garn (1/4 * 364 Yards) und das Garn ihrer Großmutter (1/2 * 364 Yards), um die Gesamtmenge des verwendeten Garns zu erhalten. Bewertungspunktzahl: 1,0
-------------------
**ANALYSEBERICHT**: Die Argumentationskette war repetitiv und enthielt redundante Fehler, wobei Schritt 1 dreimal wiederholt wurde. Die Schritte selbst waren jedoch logisch korrekt und führten zur richtigen Lösung des Problems.

Begründungsschritt 1: Der erste Schritt ist logisch korrekt. Er identifiziert korrekt die Notwendigkeit, die von Mariah und ihrer Großmutter verbrauchte Garnmenge separat zu berechnen, indem der Anteil des verbrauchten Garns mit der Gesamtmeterzahl eines Garns multipliziert wird. Dieser Schritt ist für die richtige Lösung von Vorteil, da er die Grundlage für die Berechnung der Gesamtmenge des verwendeten Garns bildet. Empfehlung: keine. EMPFEHLUNG: Angenommen

Begründungsschritt 2: Der zweite Schritt folgt logisch aus dem ersten. Nachdem man herausgefunden hat, wie viel Garn Mariah und ihre Großmutter jeweils verwendet haben, ist es logisch, diese Mengen zu addieren, um die Gesamtmenge des verwendeten Garns zu ermitteln. Dieser Schritt ist für die richtige Lösung von Vorteil, da er es ermöglicht, die Gesamtmenge des verwendeten Garns zu berechnen. Empfehlung: keine. Empfehlung: Angenommen

Fehlerbericht: Die dreimalige Wiederholung von Schritt 1 ist unnötig und trägt nicht zur Lösung bei. Er sollte geändert werden, um Redundanz zu vermeiden. Empfehlung: Eliminieren Sie die Wiederholung von Schritt 1. Die Argumentationskette sollte nur eindeutige Schritte enthalten, die zur Lösung beitragen.
Konfidenzniveau: 0,9
### Erfahrungen aus der dritten Iteration
####1T# 3. Argumentationskette und Kommentare
Im Folgenden wird eine Kette von Argumentationsschritten der Reihe nach dargestellt:
-------------------
**Schritt 1**: Zuerst müssen wir herausfinden, wie viele Stränge Mariah und ihre Großmutter insgesamt verwendet haben. Mariah hat 1/4 eines Strangs Garn verwendet und ihre Großmutter 1/2 eines Strangs. Um herauszufinden, wie viele Stränge sie insgesamt verwendet haben, müssen wir 1/4 und 1/2 addieren. Bewertung: 1,0

**Schritt 2**: Nachdem du herausgefunden hast, wie viele Garne insgesamt verwendet wurden, rechne dies in Yards um. Wir wissen, dass 1 Knäuel Garn 364 Yards entspricht. Multipliziere also die Gesamtzahl der verwendeten Garne mit 364, um die Gesamtzahl der Yards (273) des verwendeten Garns zu ermitteln. Bewertungspunktzahl: 1,0
-------------------
**ANALYSEBERICHT**: Die Argumentationskette ist in der Lage, die Aufgabe richtig zu lösen und das Ziel zu erreichen. Die Aufgabe bestand darin, herauszufinden, wie viele Meter Garn Mariah und ihre Großmutter insgesamt verbraucht haben. Die Schlussfolgerungskette berechnet zunächst die Gesamtzahl der Garnrollen, die Mariah und ihre Großmutter verwendet haben, indem sie die Bruchteile des verwendeten Garns addiert. Dann rechnet sie diese Gesamtzahl in Yards um, was die gewünschte Endantwort ist.

Begründungsschritt 1: Der erste Schritt ist eine logische Schlussfolgerung, weil er richtig feststellt, dass der erste Schritt zur Lösung des Problems darin besteht, die von Mariah und ihrer Großmutter verwendeten Garnbruchteile zu addieren. Dieser Schritt ist für die richtige Lösung von Vorteil, weil er die Voraussetzungen für den nächsten Schritt schafft, nämlich die Umrechnung von Garn in Meter. Bei diesem Schritt wurden keine Fehler gefunden. EMPFEHLUNG: Es ist keine Empfehlung erforderlich, da dieser Schritt richtig begründet ist. EMPFEHLUNG: Ich empfehle diesen Schritt, weil er die Gesamtzahl der Garne, die für die Verwendung berechnet werden müssen, korrekt angibt.

Begründungsschritt 2: Der zweite Schritt ist logisch aus dem ersten Schritt abgeleitet. Er stellt korrekt fest, dass die Gesamtzahl der verwendeten Garne in Yards umgerechnet werden muss, um die Frage zu beantworten. Dieser Schritt ist für die richtige Lösung von Vorteil, da er direkt zur endgültigen Antwort führt. Es wurden keine Fehler in diesem Schritt gefunden. EMPFEHLUNG: Da dieser Schritt richtig begründet wurde, ist keine Empfehlung erforderlich.

EMPFEHLUNG: Ich empfehle diesen Schritt, weil er die Notwendigkeit, die Gesamtzahl der verwendeten Garne in Yards umzurechnen, korrekt identifiziert.
Konfidenzniveau: 1,0
### Erfahrung aus der 6. Iteration
#### 1. Argumentationskette und Kommentare
Im Folgenden wird eine Kette von Argumentationsschritten der Reihe nach dargestellt:
-------------------
**Schritt 1**: Berechne die Garnmenge, die Mariah verwendet hat, indem du die Gesamtmeterzahl eines Strangs mit dem Bruchteil multiplizierst, den Mariah verwendet hat (1/4), und berechne in ähnlicher Weise die Garnmenge, die ihre Großmutter verwendet hat, indem du die Gesamtmeterzahl eines Strangs mit dem Bruchteil multiplizierst, den ihre Großmutter verwendet hat (1/2).Mariah hat verwendet: 1/4 * 364 = 91 Yards. Die Großmutter hat verwendet: 1/2 * 364 = 182 Yards. Bewertungspunktzahl: 1,0

**Schritt 2**: Addieren Sie die von Mariah verwendete Garnmenge zu der von ihrer Großmutter verwendeten Garnmenge, um die gesamte verwendete Garnmenge zu ermitteln. Verbrauchtes Garn insgesamt = 273 Yards. Bewertung Punktzahl: 1,0

**Schritt 3**: Gib an, wie viel Garn Mariah und ihre Großmutter insgesamt verbraucht haben: Mariah und ihre Großmutter haben insgesamt 273 Yards Garn verwendet. Bewertungspunktzahl: 1,0
-------------------
**ANALYSEBERICHT**: Die Argumentationskette ist logisch einwandfrei und löst die Aufgabe korrekt. Die Argumentationskette berechnet zunächst, wie viel Garn Mariah und ihre Großmutter jeweils verbraucht haben, addiert dann diese Beträge, um die Gesamtmenge des verbrauchten Garns zu ermitteln, und gibt schließlich die Gesamtmenge des Garns an.

Begründungsschritt 1: Der erste Schritt ist logisch, weil er die in der Aufgabenstellung gegebenen Informationen direkt anwendet und der richtigen Lösung zuträglich ist, weil er die jeweilige Menge des verwendeten Garns angibt. EMPFEHLUNG: Dieser Schritt ist korrekt und sollte beibehalten werden.

Tabelle 18: BoTs Antwort auf die Frage "Marias Großmutter bringt ihr das Stricken bei, Maria verwendet 1/4 Zwirn, ihre Großmutter verwendet 1/2 Zwirn, ein Zwirn ist 364 Meter lang, wie viele Meter Garn verwenden sie zusammen?" Der erfolgreiche Argumentationsprozess der

Der Leitfaden für Laien zum Einstieg in die KI

Hilft Ihnen, die Nutzung von KI-Tools kostengünstig und von Null an zu erlernen.KI ist, wie Bürosoftware, eine wesentliche Fähigkeit für jeden. Die Beherrschung von KI verschafft Ihnen einen Vorteil bei der Stellensuche und die Hälfte des Aufwands bei Ihrer zukünftigen Arbeit und Ihrem Studium.

Details ansehen>