HuggingFace stellt die technischen Details von o1 vor und stellt sie als Open Source zur Verfügung!

Wenn kleinen Modellen mehr Zeit zum Nachdenken gegeben wird, können sie größere Modelle übertreffen.

In jüngster Zeit hat sich in der Branche eine noch nie dagewesene Begeisterung für kleine Modelle entwickelt, die mit einigen "praktischen Tricks" größere Modelle in ihrer Leistung übertreffen können.

Es kann argumentiert werden, dass es eine logische Konsequenz ist, sich auf die Verbesserung der Leistung kleinerer Modelle zu konzentrieren. Bei großen Sprachmodellen hat die Skalierung der Trainingszeit die Entwicklung dieser Modelle dominiert. Dieses Paradigma hat sich zwar als sehr effektiv erwiesen, aber die für das Pre-Training immer größerer Modelle erforderlichen Ressourcen sind unerschwinglich geworden, und es sind Multimilliarden-Dollar-Cluster entstanden.

Infolgedessen hat dieser Trend ein großes Interesse an einem anderen, ergänzenden Ansatz geweckt, nämlich der Skalierung von Testzeitberechnungen. Anstatt sich auf immer größere Pre-Training-Budgets zu verlassen, verwenden Testzeit-Methoden dynamische Inferenzstrategien, die es den Modellen ermöglichen, bei schwierigeren Problemen "länger zu denken". Ein bekanntes Beispiel ist das o1-Modell von OpenAI, das bei schwierigen mathematischen Problemen mit zunehmender Testzeitberechnung beständige Fortschritte erzielt hat.

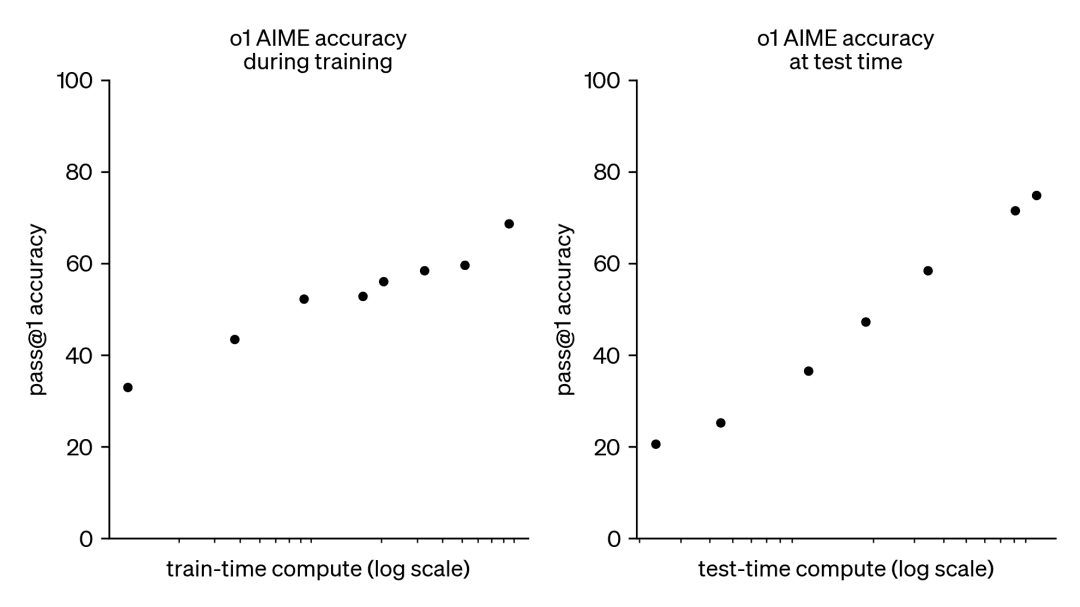
Wir wissen zwar nicht genau, wie o1 trainiert wird, aber neuere Forschungen von DeepMind deuten darauf hin, dass eine optimale Skalierung der Testzeitberechnung durch Strategien wie iterative Selbstverbesserung oder die Suche im Lösungsraum mithilfe eines Belohnungsmodells erreicht werden kann. Durch die adaptive Zuteilung von Testzeitberechnungen auf einer Prompt-by-Prompt-Basis können kleinere Modelle mit größeren, ressourcenintensiven Modellen mithalten und diese manchmal sogar übertreffen. Die Skalierung der Berechnungszeit ist besonders dann von Vorteil, wenn der Speicher begrenzt ist und die verfügbare Hardware nicht ausreicht, um größere Modelle auszuführen. Dieser vielversprechende Ansatz wurde jedoch anhand eines Closed-Source-Modells demonstriert, und es wurden keine Implementierungsdetails oder Code veröffentlicht.

DeepMind-Papier: https://arxiv.org/pdf/2408.03314

In den letzten Monaten hat HuggingFace versucht, diese Ergebnisse nachzuvollziehen und zu reproduzieren. Sie werden sie in diesem Blogbeitrag vorstellen:

• Rechneroptimale Skalierung (compute-optimal scaling):Verbessern Sie die mathematische Leistung offener Modelle zur Testzeit durch die Implementierung von DeepMind-Tricks.
• Diversity Validator Tree Search (DVTS):Es handelt sich um eine Erweiterung, die für die Bootstrap-Baumsuchtechnik des Validators entwickelt wurde. Dieser einfache und effiziente Ansatz erhöht die Diversität und bietet eine bessere Leistung, insbesondere bei Tests mit einem großen Rechenbudget.
• Suchen und lernen:Ein leichtgewichtiges Toolkit für die Implementierung von Suchstrategien unter Verwendung von LLM mit dem vLLM Erzielen Sie höhere Geschwindigkeiten.

Wie gut funktioniert also die rechnerisch optimale Skalierung in der Praxis? In der nachstehenden Grafik übertreffen die sehr kleinen 1B- und 3B-Llama-Instruct-Modelle die viel größeren 8B- und 70B-Modelle beim anspruchsvollen MATH-500-Benchmark, wenn man ihnen genügend "Denkzeit" gibt.

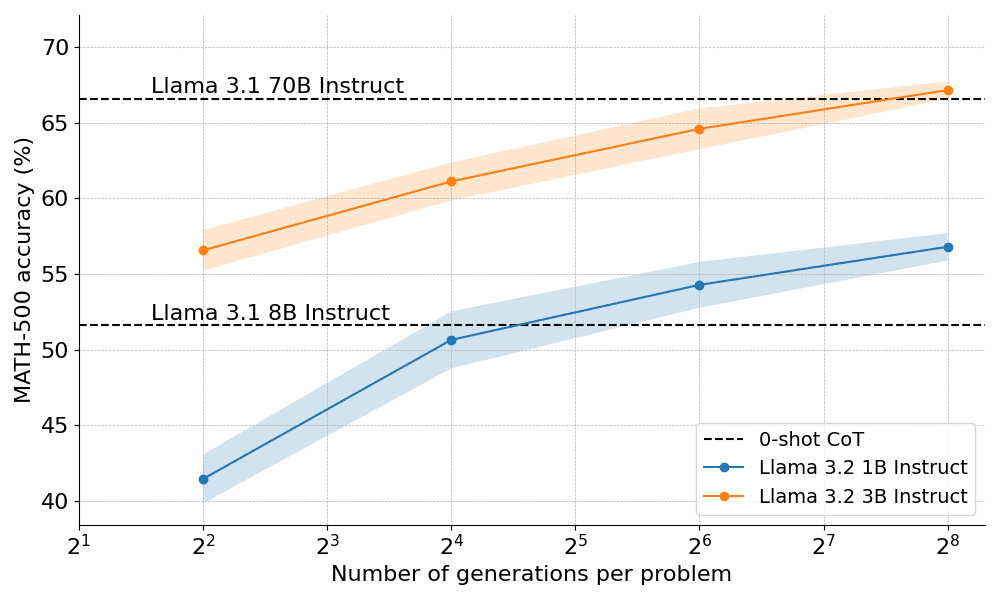
Nur 10 Tage nach dem öffentlichen Debüt von OpenAI o1 freuen wir uns, eine Open-Source-Version der bahnbrechenden Technologie zu enthüllen, die hinter dem Erfolg steht: Extended Test-Time Computing", sagt Clem Delangue, Mitbegründer und CEO von HuggingFace. Indem man dem Modell eine längere "Denkzeit" einräumt, kann das 1B-Modell 8B schlagen und das 3B-Modell 70B. Natürlich ist das gesamte Rezept quelloffen.

Netizens aus allen Bereichen des Lebens sind nicht ruhig, wenn sie diese Ergebnisse sehen, nennen es unglaublich und betrachten es als einen Sieg für die Miniaturen.

Anschließend geht HuggingFace auf die Gründe für diese Ergebnisse ein und hilft den Lesern, praktische Strategien für die Umsetzung der rechnerischen Skalierung beim Testen zu verstehen.

Erweiterte Strategie für die Berechnung der Testzeit

Es gibt zwei Hauptstrategien zur Erweiterung der Testzeitberechnung:

• Selbstverbesserung: Das Modell verbessert iterativ seinen Output oder seine "Idee", indem es in nachfolgenden Iterationen Fehler identifiziert und korrigiert. Diese Strategie ist zwar bei einigen Aufgaben wirksam, setzt aber in der Regel voraus, dass das Modell über einen eingebauten Selbstverbesserungsmechanismus verfügt, was seine Anwendbarkeit einschränken kann.
• Suche anhand eines Validators: Dieser Ansatz konzentriert sich auf die Generierung mehrerer Antwortkandidaten und die Verwendung eines Validators zur Auswahl der besten Antwort. Validatoren können auf fest kodierten Heuristiken oder erlernten Belohnungsmodellen basieren. In diesem Beitrag konzentrieren wir uns auf gelernte Validatoren, zu denen Techniken wie Best-of-N-Sampling und Baumsuche gehören. Solche Suchstrategien sind flexibler und können an die Schwierigkeit des Problems angepasst werden, obwohl ihre Leistung durch die Qualität des Validators begrenzt ist.

HuggingFace hat sich auf suchbasierte Methoden spezialisiert, die praktische und skalierbare Lösungen für die rechnergestützte Optimierung zur Testzeit darstellen. Hier sind drei Strategien:

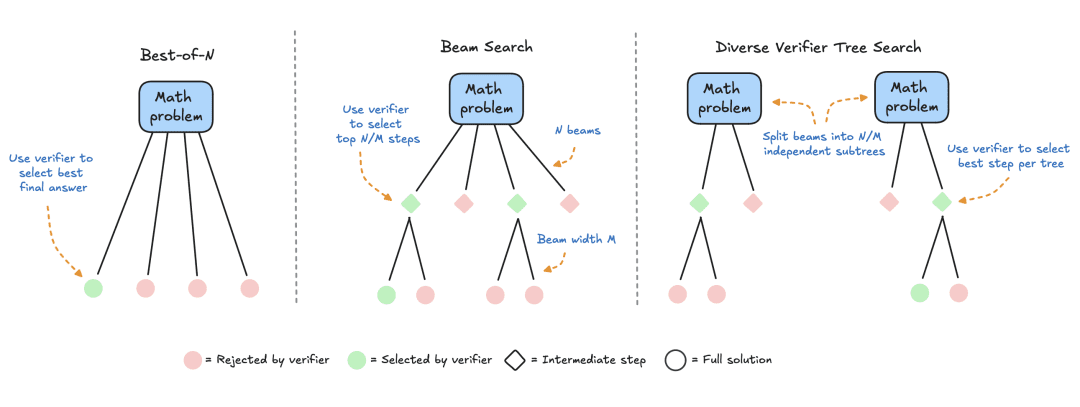
• Best-of-N: In der Regel wird ein Belohnungsmodell verwendet, um mehrere Antworten für jede Frage zu generieren, und jeder Antwortkandidatin bzw. jedem Antwortkandidaten wird eine Punktzahl zugewiesen; anschließend wird die Antwort mit der höchsten Belohnung ausgewählt (oder eine gewichtete Variante, wie später erläutert). Bei diesem Ansatz steht die Qualität der Antworten im Vordergrund und nicht die Häufigkeit.
• Clustersuche: eine systematische Suchmethode zur Erkundung des Lösungsraums, die häufig in Verbindung mit Prozess-Belohnungsmodellen (PRMs) verwendet wird, um die Auswahl und Bewertung von Zwischenschritten bei der Problemlösung zu optimieren. Im Gegensatz zu herkömmlichen Belohnungsmodellen, die eine einzige Punktzahl für die endgültige Antwort liefern, liefern PRMs eine Reihe von Punktzahlen, eine für jeden Schritt des Denkprozesses. Diese feinkörnige Feedback-Fähigkeit macht PRMs zu einer natürlichen Wahl für LLM-Suchmethoden.
• Diversity Validator Tree Search (DVTS): eine von HuggingFace entwickelte Erweiterung der Clustersuche, die den ursprünglichen Cluster in separate Teilbäume aufteilt und diese Teilbäume dann mithilfe von PRM gierig erweitert. Dieser Ansatz verbessert die Diversität und die Gesamtleistung der Lösung, insbesondere wenn das Rechenbudget zum Zeitpunkt der Prüfung groß ist.

Experimenteller Aufbau

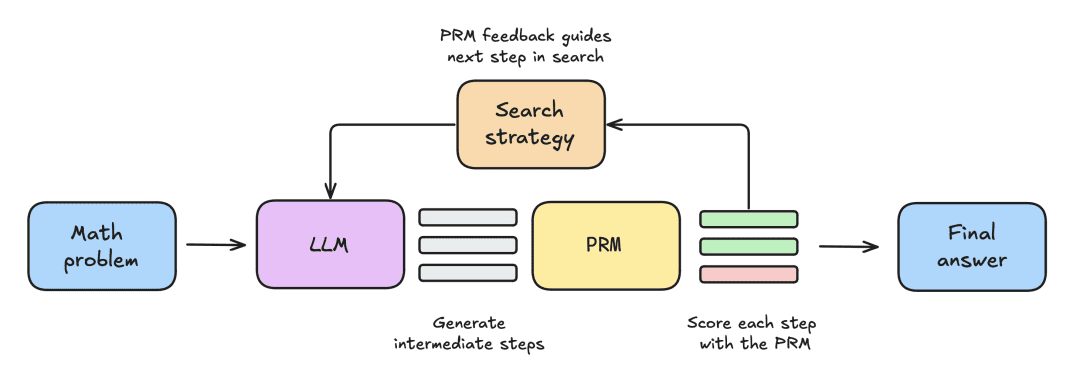
Der Versuchsaufbau bestand aus den folgenden Schritten:

• Dem LLM wird zunächst ein mathematisches Problem gestellt, um N Teillösungen zu generieren, z. B. Zwischenschritte im Ableitungsprozess.
• Jeder Schritt wird von einem PRM bewertet, das die Wahrscheinlichkeit schätzt, dass jeder Schritt mit der richtigen Antwort endet.
• Sobald die Suchstrategie abgeschlossen ist, werden die endgültigen Lösungsvorschläge vom PRM sortiert, um die endgültige Antwort zu erhalten.

Um verschiedene Suchstrategien zu vergleichen, werden in dieser Arbeit die folgenden Open-Source-Modelle und -Datensätze verwendet:

• Modelle: Verwenden Sie meta-llama/Llama-3.2-1B-Instruct als primäres Modell für erweiterte Testzeitberechnungen;
• Process Reward Model PRM: Zur Steuerung der Suchstrategie wird in dieser Arbeit RLHFlow/Llama3.1-8B-PRM-Deepseek-Data verwendet, ein prozessüberwachtes trainiertes 8-Milliarden-Reward-Modell. Bei der Prozessüberwachung handelt es sich um eine Trainingsmethode, bei der das Modell bei jedem Schritt des Argumentationsprozesses Feedback erhält, nicht nur beim Endergebnis;
• Datensatz: Diese Arbeit wurde mit dem MATH-500-Teilsatz bewertet, einem MATH-Benchmark-Datensatz, der von OpenAI als Teil einer prozessüberwachten Studie veröffentlicht wurde. Diese mathematischen Probleme umfassen sieben Themen und sind sowohl für Menschen als auch für die meisten Modelle großer Sprachen eine Herausforderung.

In diesem Artikel wird mit einer einfachen Basislinie begonnen und dann schrittweise weitere Techniken zur Verbesserung der Leistung eingeführt.

Mehrheitsbeschluss

Die Mehrheitswahl ist der einfachste Weg, die Ergebnisse des LLM zusammenzufassen. Für ein gegebenes mathematisches Problem werden N Lösungsvorschläge generiert und die Antwort mit der höchsten Häufigkeit des Auftretens wird ausgewählt. In allen Experimenten werden bis zu N=256 Lösungsvorschläge mit einem Temperaturparameter T=0,8 ausgewählt und bis zu 2048 Token für jedes Problem erzeugt.

Hier sehen Sie, wie die Mehrheit der Stimmen bei der Anwendung auf den Llama 3.2 1B Instruct abschneidet:

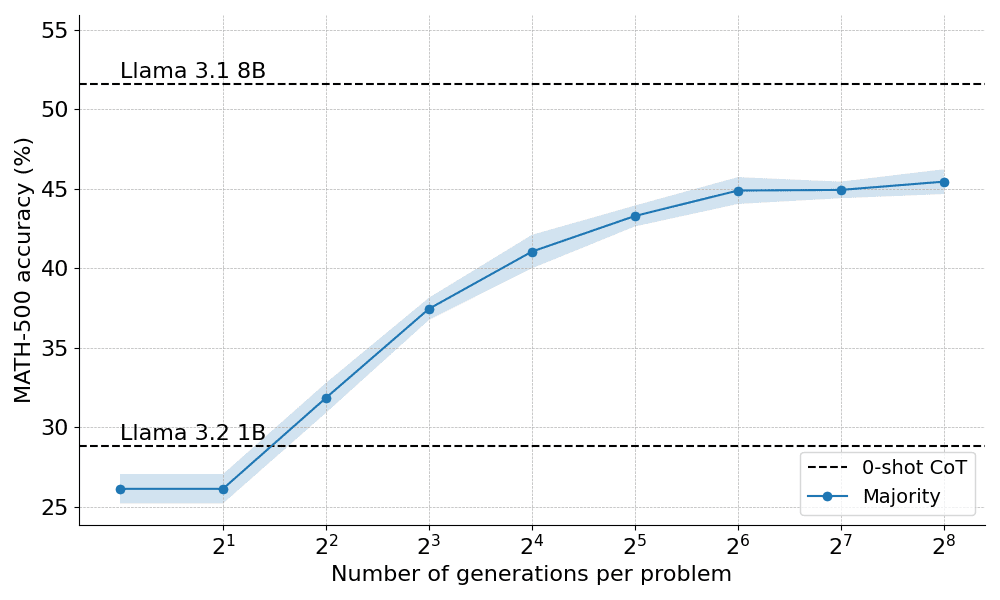
Die Ergebnisse zeigen, dass die Mehrheitsentscheidung eine signifikante Verbesserung gegenüber der Basisvariante der gierigen Dekodierung darstellt, aber ihre Gewinne beginnen nach etwa N=64 Generationen abzuflachen. Diese Einschränkung ergibt sich daraus, dass das Mehrheitswahlverfahren Schwierigkeiten hat, Probleme zu lösen, die eine sorgfältige Argumentation erfordern.

Ausgehend von den Einschränkungen der Mehrheitsentscheidung wollen wir sehen, wie wir ein Belohnungsmodell zur Verbesserung der Leistung einführen können.

Jenseits der Mehrheit: Best-of-N

Best-of-N ist eine einfache und effiziente Erweiterung des Mehrheitsabstimmungsalgorithmus, die ein Belohnungsmodell verwendet, um die vernünftigste Antwort zu bestimmen. Es gibt zwei Hauptvarianten der Methode:

Gewöhnliches Best-of-N: Es werden N unabhängige Antworten generiert und diejenige mit der höchsten RM-Belohnung wird als endgültige Antwort ausgewählt. Dies stellt sicher, dass die Antwort mit dem höchsten Vertrauen gewählt wird, berücksichtigt aber nicht die Konsistenz zwischen den Antworten.

Gewichtetes Best-of-N: Fasst die Punktzahlen aller identischen Antworten zusammen und wählt diejenige mit der höchsten Gesamtbelohnung aus. Bei dieser Methode werden Antworten von hoher Qualität bevorzugt, indem die Punktzahl durch wiederholtes Auftreten erhöht wird. Mathematisch werden die Antworten mit a_i gewichtet:

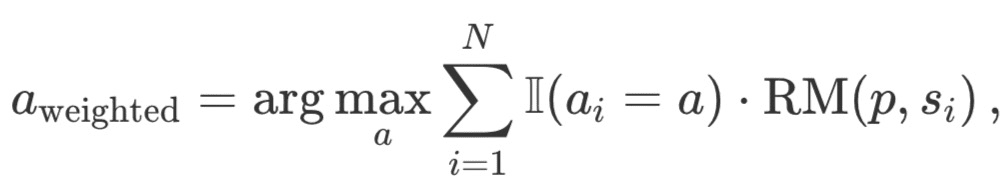
wobei RM (p,s_i) der Reward Model Score für die i-te Lösung s_i des Problems p ist.

In der Regel wird das Outcome Reward Model (ORM) verwendet, um individuelle Bewertungen auf Lösungsebene zu erhalten. Um jedoch einen fairen Vergleich mit anderen Suchstrategien zu ermöglichen, wird dasselbe PRM zur Bewertung von Best-of-N-Lösungen verwendet. Wie in der nachstehenden Abbildung gezeigt, erzeugt das PRM eine kumulative Folge von Bewertungen auf Schrittsebene für jede Lösung, und daher müssen die Schritte statistisch (reduktiv) bewertet werden, um individuelle Bewertungen auf Lösungsebene zu erhalten:

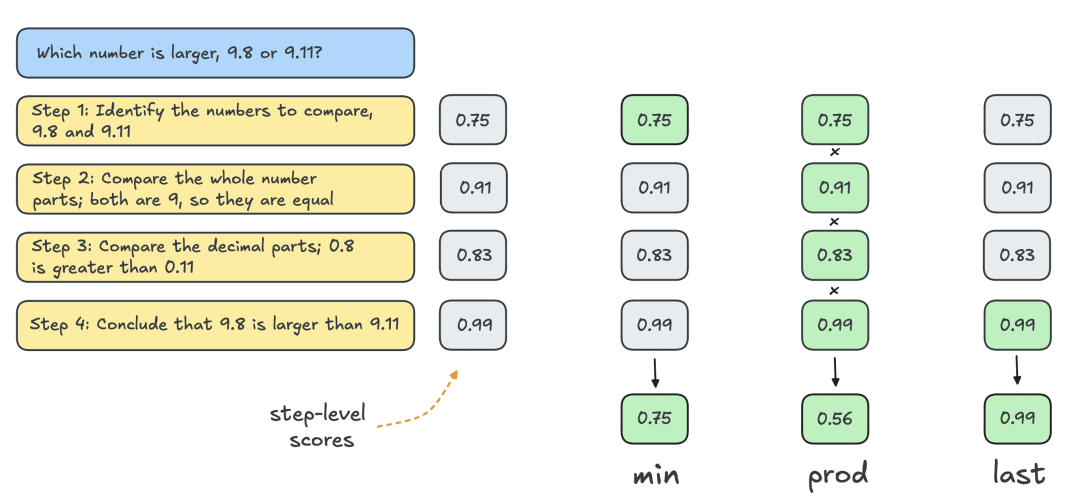
Die gängigsten Statuten sind im Folgenden aufgeführt:

• Min: Verwenden Sie die niedrigste Punktzahl aus allen Schritten.
• Prod: Verwenden Sie das Produkt der Stufenbrüche.
• Zuletzt: Verwenden Sie die Endbewertung des Schritts. Diese Punktzahl enthält kumulative Informationen aus allen vorangegangenen Schritten, so dass der PRM effektiv wie ein ORM behandelt wird, der Teillösungen bewerten kann.

Nachfolgend sind die Ergebnisse der beiden Varianten von Best-of-N aufgeführt:

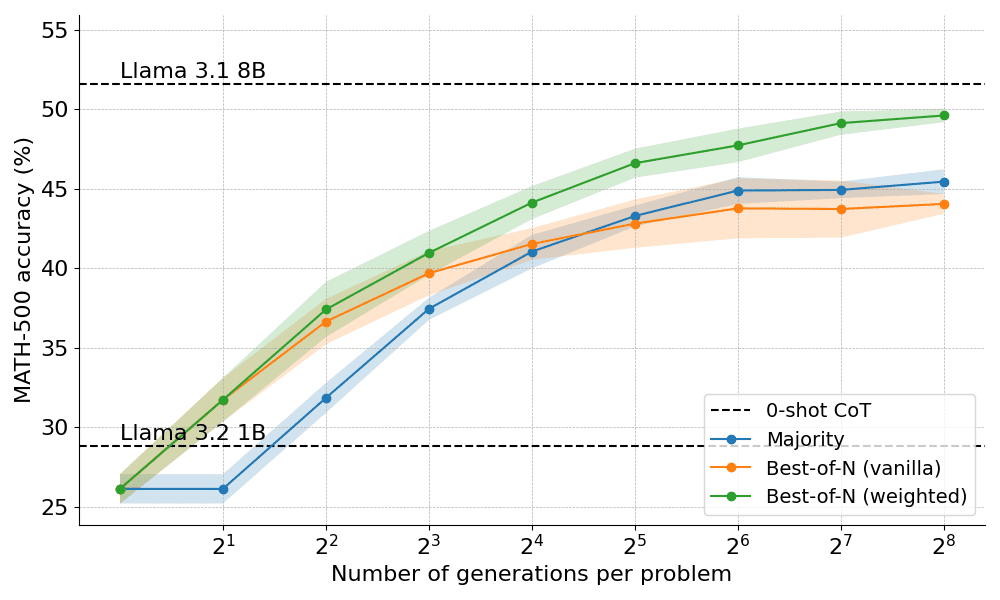
Die Ergebnisse zeigen einen klaren Vorteil: gewichtetes Best-of-N übertrifft durchweg das reguläre Best-of-N, insbesondere bei größeren Generierungsbudgets. Seine Fähigkeit, die Punktzahlen identischer Antworten zu aggregieren, stellt sicher, dass auch weniger häufige, aber qualitativ hochwertigere Antworten effektiv priorisiert werden.

Trotz dieser Verbesserungen bleibt sie jedoch hinter der Leistung des Modells Llama 8B zurück, und die Best-of-N-Methode beginnt sich bei N=256 zu stabilisieren.

Lassen sich die Grenzen durch eine schrittweise Überwachung des Suchprozesses weiter verschieben?

Clustersuche mit PRM

Als strukturierte Suchmethode ermöglicht die Clustersuche die systematische Erkundung des Lösungsraums und ist damit ein leistungsfähiges Instrument zur Verbesserung der Modellergebnisse zur Testzeit. In Verbindung mit PRM kann die Clustersuche die Generierung und Auswertung von Zwischenschritten bei der Problemlösung optimieren. Die Clustersuche funktioniert auf folgende Weise:

1. Mehrere Lösungsvorschläge werden iterativ erzeugt, indem eine feste Anzahl von "Clustern" oder aktiven Pfaden N beibehalten wird.
2. In der ersten Iteration werden N unabhängige Schritte aus dem LLM mit der Temperatur T genommen, um Vielfalt in die Antworten zu bringen. Diese Schritte werden in der Regel durch ein Stoppkriterium definiert, z. B. Beendigung bei neuer Zeile n oder doppelter neuer Zeile nn.
3. Jeder Schritt wird mit PRM bewertet und die besten N/M Schritte werden als Kandidaten für die nächste Generierungsrunde ausgewählt. Dabei bezeichnet M die "Clusterbreite" eines bestimmten Aktivitätspfads. Wie bei Best-of-N wird das "letzte" Statut verwendet, um Teillösungen für jede Iteration zu bewerten.
4. Erweitern Sie die in Schritt (3) ausgewählten Schritte, indem Sie M nachfolgende Schritte in die Lösung aufnehmen.
5. Wiederholen Sie die Schritte (3) und (4), bis EOS erreicht ist. Token oder die maximale Suchtiefe überschreitet.

Indem das PRM die Korrektheit von Zwischenschritten bewerten kann, kann die Clustersuche vielversprechende Pfade früh im Prozess identifizieren und priorisieren. Diese schrittweise Bewertungsstrategie ist besonders nützlich für komplexe logische Aufgaben wie Mathematik, da die Validierung von Teillösungen das Endergebnis erheblich verbessern kann.

Einzelheiten der Durchführung

In den Experimenten folgte HuggingFace der Hyperparameterauswahl von DeepMind und führte die Clustersuche wie folgt durch:

• Berechnung von N Clustern bei Skalierung auf 4, 16, 64, 256
• Feste Clusterbreite M=4
• Probenahme bei Temperatur T=0,8
• Bis zu 40 Iterationen, d. h. ein Baum mit einer maximalen Tiefe von 40 Schritten

Wie in der Abbildung unten zu sehen ist, sind die Ergebnisse verblüffend: Bei einem Testzeitbudget von N=4 erreicht die Clustersuche die gleiche Genauigkeit wie Best-of-N mit N=16, d.h. eine vierfache Verbesserung der Berechnungseffizienz! Darüber hinaus ist die Leistung der Clustersuche vergleichbar mit der von Llama 3.1 8B, das nur N=32 Lösungen pro Problem benötigt. Die durchschnittliche Leistung von Informatik-Doktoranden in Mathematik liegt bei 40%, für das 1B-Modell sind also fast 55% gut genug!

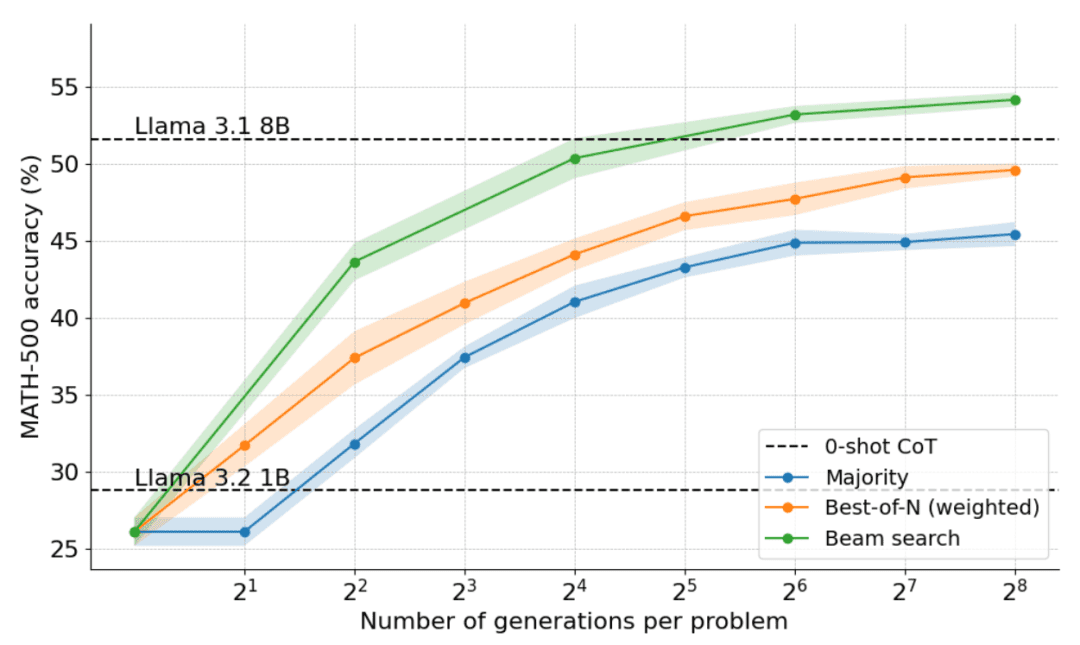
Welche Probleme lassen sich am besten durch Clustersuche lösen?

Während es insgesamt klar ist, dass die Clustersuche eine bessere Suchstrategie ist als Best-of-N oder die Mehrheitsentscheidung, zeigt das DeepMind-Papier, dass es für jede Strategie Kompromisse gibt, die von der Schwierigkeit des Problems und dem Rechenbudget zum Zeitpunkt der Prüfung abhängen.

Um zu verstehen, welche Probleme für welche Strategie am besten geeignet sind, berechnete DeepMind die Verteilung der geschätzten Problemschwierigkeit und teilte die Ergebnisse in Quintile ein. Mit anderen Worten: Jedes Problem wurde einer von fünf Stufen zugeordnet, wobei Stufe 1 für leichtere Probleme und Stufe 5 für die schwierigsten Probleme steht. Um die Schwierigkeit des Problems abzuschätzen, generierte DeepMind 2048 Lösungsvorschläge für jedes Problem mit Standardstichproben und schlug dann die folgenden Heuristiken vor:

• Oracle: Schätzen Sie die pass@1-Punkte für jede Frage unter Verwendung von grundlegenden Faktenbezeichnungen und klassifizieren Sie die Verteilung der pass@1-Punkte, um Quintile zu bestimmen.
• Modellierung: Die Quintile werden anhand der Verteilung der mittleren PRM-Punktzahlen für jedes Problem bestimmt. Die Intuition dabei ist, dass schwierigere Fragen niedrigere Punktzahlen haben werden.

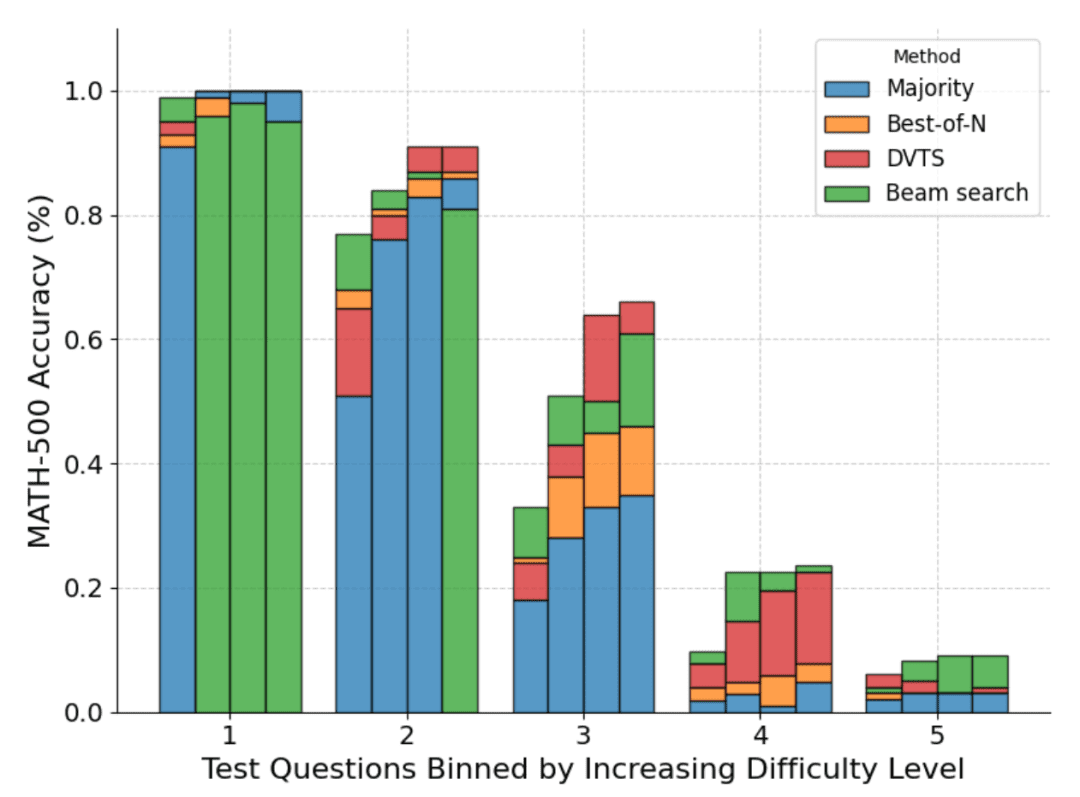
Die folgende Abbildung zeigt eine Aufschlüsselung der verschiedenen Methoden auf der Grundlage der pass@1-Punktzahl und des für die vier Tests berechneten Budgets N=[4,16,64,256]:

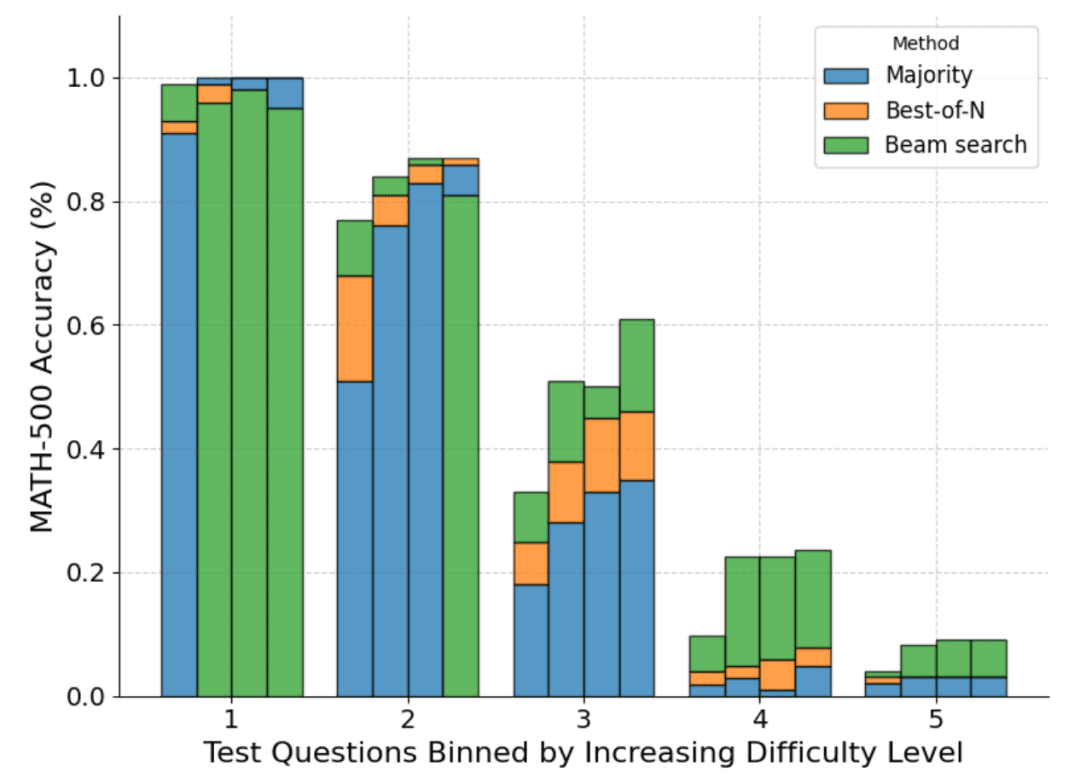
Wie zu sehen ist, stellt jeder Balken das zum Zeitpunkt der Prüfung berechnete Budget dar, und die relative Genauigkeit jeder Methode ist innerhalb jedes Balkens angegeben. Zum Beispiel, in den vier Balken für den Schwierigkeitsgrad 2:

Die Mehrheitsabstimmung ist die schlechteste Methode aller Berechnungsbudgets, mit Ausnahme von N=256 (die Clustersuche schneidet am schlechtesten ab).

Die Clustersuche ist am besten für N=[4,16,64], aber Best-of-N ist am besten für N=256.

Es ist anzumerken, dass die Clustersuche bei Problemen mit mittlerem und hohem Schwierigkeitsgrad (Level 3 bis 5) beständige Fortschritte gemacht hat, aber bei einfacheren Problemen tendenziell schlechter abschneidet als Best-of-N (oder sogar Mehrheitsbeschlüsse), insbesondere bei größeren Berechnungsbudgets.

Bei der Betrachtung des durch die Clustersuche erzeugten Ergebnisbaums stellte HuggingFace fest, dass, wenn einem einzelnen Schritt eine hohe Belohnung zugewiesen wurde, der gesamte Baum auf dieser Trajektorie zusammenbrach, was die Vielfalt beeinträchtigte. Dies motivierte sie dazu, eine Erweiterung der Clustersuche zu erforschen, die die Diversität maximiert.

DVTS: Leistungssteigerung durch Vielfalt

Wie oben gezeigt, bietet die Clustersuche eine bessere Leistung als Best-of-N, neigt aber dazu, bei einfachen Problemen und großen Berechnungsbudgets zum Zeitpunkt des Tests schlecht abzuschneiden.

Um dieses Problem zu lösen, hat HuggingFace eine Erweiterung namens "Diversity Validator Tree Search" (DVTS) entwickelt, die darauf abzielt, die Vielfalt zu maximieren, wenn N groß ist.

DVTS funktioniert ähnlich wie die Clustersuche mit den folgenden Änderungen:

• Für ein gegebenes N und M wird die Ausgangsmenge in N/M unabhängige Teilbäume zerlegt.
• Wählen Sie für jeden Teilbaum den Schritt mit der höchsten PRM-Punktzahl.
• Erzeugen Sie M neue Schritte aus dem in Schritt (2) ausgewählten Knoten und wählen Sie den Schritt mit der höchsten PRM-Punktzahl.
• Wiederholen Sie Schritt (3), bis das EOS-Token oder die maximale Baumtiefe erreicht ist.

Die folgende Grafik zeigt die Ergebnisse der Anwendung von DVTS auf Llama 1B:

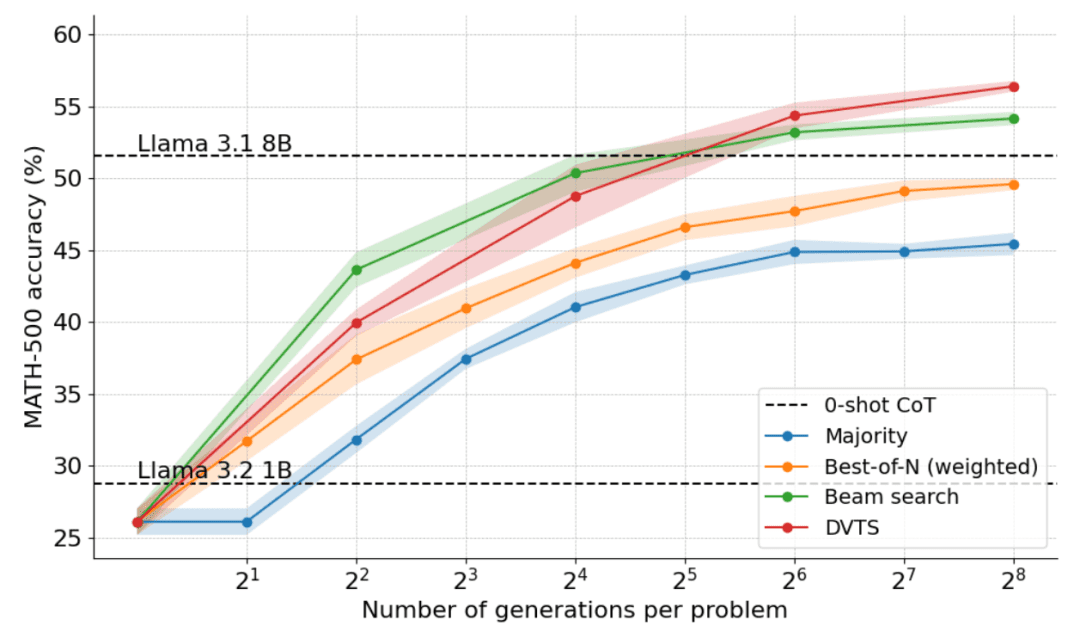
Es zeigt sich, dass DVTS eine komplementäre Strategie zur Clustersuche darstellt: Bei kleinen N ist die Clustersuche effektiver bei der Suche nach der richtigen Lösung, aber bei größeren N kommt die Vielfalt der DVTS-Kandidaten ins Spiel und es kann eine bessere Leistung erzielt werden.

Auch bei der Aufschlüsselung der Problemschwierigkeiten verbessert DVTS die Leistung bei einfachen/mittleren Problemen mit großem N, während die Clustersuche bei kleinen N am besten abschneidet.

Rechenoptimale Skalierung (rechenoptimale Skalierung)

Bei einer Vielzahl von Suchstrategien stellt sich natürlich die Frage, welche die beste ist. In dem Papier von DeepMind (verfügbar als Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters ) wird eine rechnerisch optimale Skalierungsstrategie vorgeschlagen, die die Suchmethode und den Hyper Parameter θ auswählt, um eine optimale Leistung für ein gegebenes Berechnungsbudget N zu erreichen:

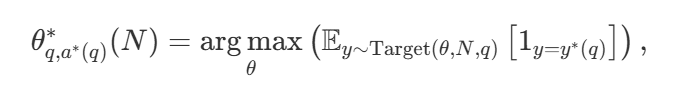
darunter auch 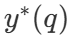ist die richtige Antwort auf Frage q. 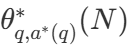Repräsentationsberechnungen - Die optimale Skalierungsstrategie. Da es einfach ist, zu berechnen 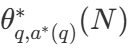DeepMind schlägt eine Annäherung vor, die auf der Schwierigkeit des Problems basiert, d. h. die Zuweisung von Rechenressourcen während des Tests basiert darauf, welche Suchstrategie bei einem bestimmten Schwierigkeitsgrad die beste Leistung erzielt.

Bei einfacheren Problemen und geringem Rechenaufwand ist es beispielsweise besser, Strategien wie Best-of-N zu verwenden, während bei schwierigeren Problemen die Set-Shu-Suche eine bessere Wahl ist. Die folgende Abbildung zeigt die Berechnungs-Optimierungskurve!

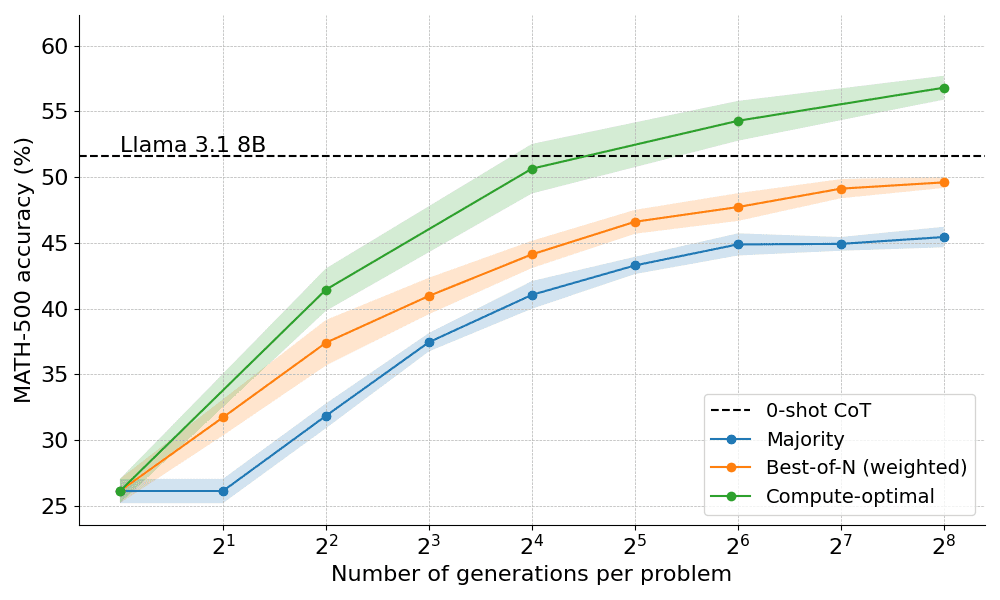
Erweiterung auf größere Modelle

In diesem Papier wird auch die Erweiterung des rechenoptimalen Ansatzes auf das Llama 3.2 3B Instruct Modell untersucht, um zu sehen, an welchem Punkt die PRM im Vergleich zur Kapazität der Politik selbst zu schwächeln beginnt. Die Ergebnisse zeigen, dass die rechenoptimale Erweiterung sehr gut funktioniert, wobei das 3B Modell das Llama 3.1 70B Instruct Modell übertrifft (das 22 mal so groß ist wie das erste!). .

Was kommt als Nächstes?

Die Untersuchung der rechnerischen Skalierung während der Testzeit zeigt das Potenzial und die Herausforderungen der Verwendung von suchbasierten Ansätzen. Mit Blick auf die Zukunft schlägt dieses Papier mehrere spannende Richtungen vor:

• Starke Validatoren: Starke Validatoren spielen eine Schlüsselrolle bei der Verbesserung der Leistung, und die Verbesserung der Robustheit und Vielseitigkeit der Validatoren ist entscheidend für die Weiterentwicklung dieser Ansätze;
• Selbstvalidierung: Das ultimative Ziel ist die Selbstvalidierung, d. h. das Modell kann seine eigenen Ergebnisse selbständig validieren. Dieser Ansatz scheint das zu sein, was Modelle wie o1 tun, ist aber in der Praxis immer noch schwierig zu erreichen. Im Gegensatz zur standardmäßigen überwachten Feinabstimmung (SFT) erfordert die Selbstvalidierung eine differenziertere Strategie;
• (a) Integration des Denkens in den Prozess: Die Einbeziehung expliziter Zwischenschritte oder des Denkens in den generativen Prozess kann die Argumentation und Entscheidungsfindung weiter verbessern. Durch die Einbeziehung strukturierten Denkens in den Suchprozess kann eine bessere Leistung bei komplexen Aufgaben erzielt werden;
• Suche als Datengenerierungswerkzeug: Die Methode kann auch als leistungsfähiger Datengenerierungsprozess dienen, um qualitativ hochwertige Trainingsdatensätze zu erstellen. So kann beispielsweise die Feinabstimmung eines Modells wie Llama 1B auf der Grundlage der durch die Suche erzeugten korrekten Trajektorien erhebliche Vorteile bringen. Dieser strategiebasierte Ansatz ähnelt Techniken wie ReST oder V-StaR, jedoch mit dem zusätzlichen Vorteil der Suche, die eine vielversprechende Richtung für iterative Verbesserungen bietet;
• Aufruf zu mehr PRMs: Es gibt relativ wenige PRMs, was ihre breitere Anwendung einschränkt. Die Entwicklung und Verbreitung weiterer PRM für verschiedene Bereiche ist ein Schlüsselbereich, in dem die Gemeinschaft einen wichtigen Beitrag leisten kann.