Uma nova abordagem para o Prompting - Analogical Prompting

Li hoje um artigo interessante chamado "TheModelos de linguagem grandes como raciocinadores analógicos Uma nova abordagem para Prompts é mencionada - "Analogical Prompts".

Se você está familiarizado com a engenharia de dicas, deve ter ouvido falar da CoT (Chain of Thought), que pode melhorar significativamente a capacidade de raciocínio dos LLMs (Large Language Models). No entanto, ao usar a CoT, precisamos fornecer orientações relevantes ou exemplos de raciocínio para guiar o modelo.

Os dois métodos de CoT comumente usados são: "0-shot CoT" e "few-shot CoT". 0-shot CoT consiste em fornecer explicitamente as etapas de inferência no Prompt e deixar que o LLM consulte as etapas para concluir a inferência. A 0-shot CoT consiste em fornecer as etapas de raciocínio explicitamente no Prompt e deixar que o LLM se refira às etapas para concluir o raciocínio. few-shot CoT consiste em fornecer um pequeno número de exemplos e deixar que o LLM se refira aos exemplos para concluir o raciocínio.

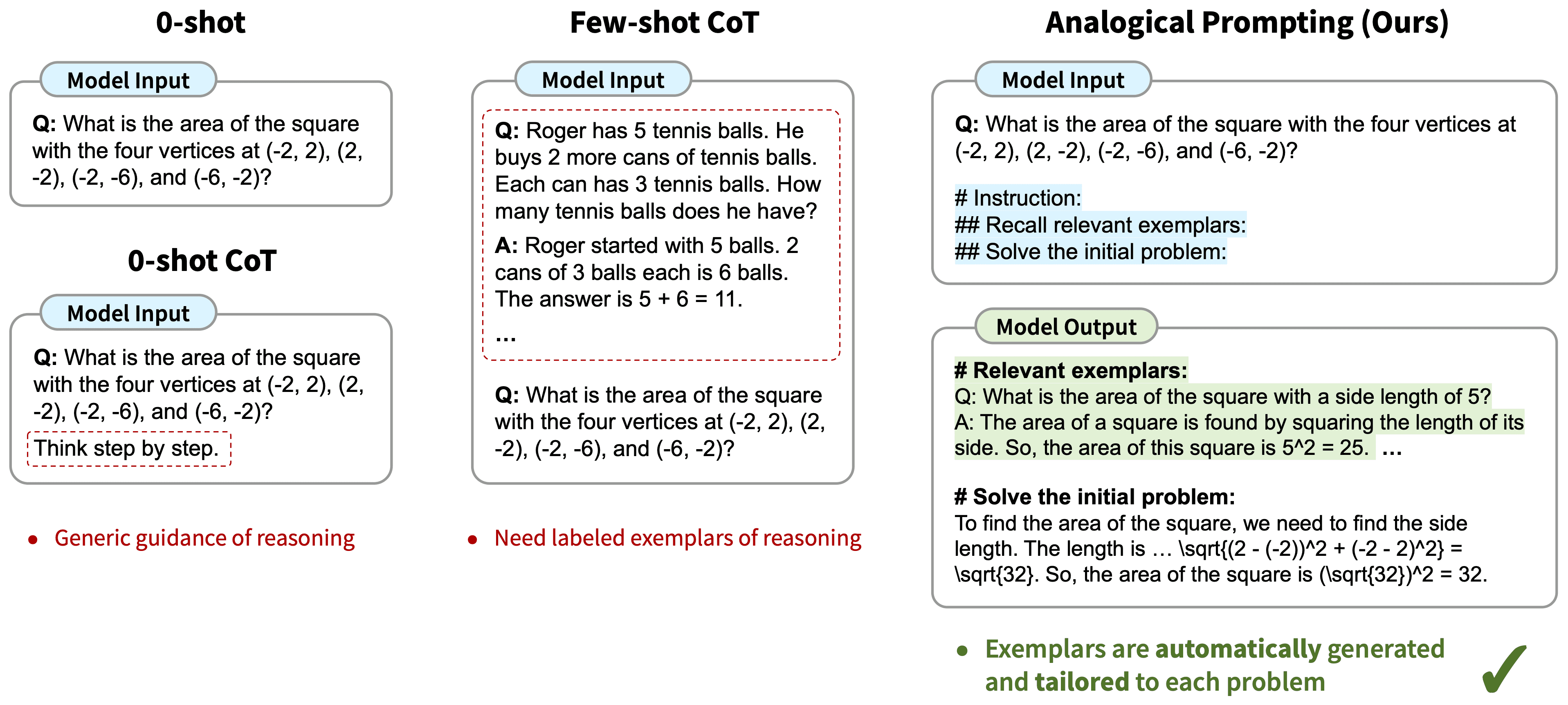
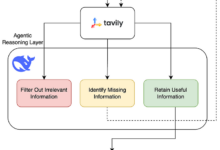
Comparação de três métodos de estímulo

Por exemplo, agora há uma pergunta de matemática: "Há um quadrado cujos quatro vértices são (-2, 2), (2, -2), (-2, -6) e (-6, -2), descubra qual é a área desse quadrado? "

Se você não usar a CoT, estará apenas lançando o problema para o LLM e deixando que ele dê a resposta. Esse problema deve ser solucionável para o GPT-4, mas é provável que esteja errado para o GPT-3.5, e ainda mais para outros modelos com raciocínio mais fraco.

Se você usar um CoT de 0 disparo, é possível fornecer as etapas de inferência explicitamente dentro do Prompt, por exemplo:

Siga as etapas abaixo para fazer o cálculo:
1, primeiro calcule a distância entre quaisquer dois vértices adjacentes como o comprimento do lado do quadrado
2、Calcule o quadrado do comprimento lateral para obter a área quadrada

Seguir essas etapas deve produzir resultados corretos para um LLM com um GPT de 3,5.

Se você usar o CoT de poucos disparos, ele estará fornecendo um pequeno número de exemplos, por exemplo:

P: Aqui está um quadrado cujos quatro vértices são (0, 0), (1, 1), (0, 1) e (1, 0). Qual é a área desse quadrado?
R: Escolhemos dois vértices vizinhos, digamos (0, 0) e (1, 1), calculamos suas distâncias para obter um comprimento de borda de 1 e, em seguida, calculamos o quadrado do comprimento da borda para obter uma área de 1.
P: Há um quadrado cujos quatro vértices são (-2, 2), (2, -2), (-2, -6) e (-6, -2). Qual é a área do quadrado?

Damos explicitamente um exemplo no Prompt, informando ao LLM que ele deve seguir as etapas do exemplo, para que possa obter o resultado correto para um LLM como o GPT-3.5.

Então, o que é "analogical cueing"?

Pense em quando aprendemos matemática na escola. Se fizermos uma pergunta de matemática como essa, pensaremos se já fizemos perguntas semelhantes, especialmente para os solucionadores de problemas de cidades pequenas como eu, que não sei quantos trabalhos fiz naquela época.

Para o LLM, sua reserva de conhecimento é mais forte do que a dos seres humanos, e ele acumulou todos os tipos de conhecimento e casos durante o treinamento, portanto, o que precisamos fazer é "estimular" o LLM a descobrir o conhecimento e os casos relacionados ao problema e, em seguida, usá-los para raciocinar e resolver o problema.

Portanto, o "método de dica analógica" é permitir que o LLM não se apresse em resolver o problema primeiro, mas primeiro liste uma série de exemplos relacionados ao problema e, em seguida, use esses exemplos para raciocinar para resolver o problema. Isso equivale a deixar que o LLM o ajude a escrever algumas frases, ajudando-o a gerar uma cadeia de raciocínio.

É semelhante a quando você obtém um problema de matemática e pede que ele primeiro siga esse problema de matemática para encontrar exemplos semelhantes e respostas de referência e, em seguida, pede que ele siga esses exemplos e respostas de referência para resolver o problema original.

A estrutura do Prompt é a seguinte:

Pergunta inicial: \
Problemas relacionados: Pense em três problemas relacionados e únicos e descreva cada problema e sua solução.
Resolva o problema inicial:

Faça com que o LLM, ao receber o problema, lembre-se de três problemas relacionados e únicos e liste cada problema e solução (de preferência com etapas), e não se esqueça de imprimir os processos intermediários. Quando o LLM tiver terminado de produzir esses exemplos relevantes, imprima o problema original novamente (para evitar o esquecimento), de modo que ele possa usar esses exemplos relevantes para raciocinar sobre o problema original.

Uma referência completa ao Prompt usando dicas análogas:

Sua tarefa é resolver problemas de matemática. Quando lhe for apresentado um problema de matemática, lembre-se de alguns tópicos relacionados como exemplos. Em seguida, volte e resolva o primeiro problema.

# A primeira pergunta:

Uma companhia aérea oferece jantar a todos os passageiros do avião, que podem escolher entre bife ou peixe. Três dos seis membros da tripulação podem escolher bife e três podem escolher peixe. Se a comida for atribuída aleatoriamente, qual é a probabilidade de que ambos os pilotos recebam peixe?

Guia de operação do #:

Os seguintes pontos devem ser incluídos em sua resposta:

Perguntas relacionadas ao ##:

Pense em três problemas de matemática relacionados ao primeiro problema como exemplos. Observe que cada problema deve ser diferente dos outros, inclusive do primeiro problema (por exemplo, envolvendo números e nomes diferentes). Cada problema deve seguir o formato abaixo:

- "Q:" seguido de uma descrição do problema

- "A:" Seguido da solução do problema e escreva a resposta final em \boxed.

## Resolva o problema logo no início:

Diga: "Vamos resolver o seguinte problema de matemática". Em seguida, responda no seguinte formato:

P: Copie e cole a primeira pergunta aqui.

A: Explique a solução e escreva a resposta final em \boxed.

O LLM produzirá o seguinte:

Perguntas relacionadas ao ##:

### Pergunta 1:

- P:** Em uma festa, todos podem escolher entre comer torta de maçã ou sorvete de baunilha. Cinco das damas podem escolher torta de maçã e cinco das damas podem escolher sorvete de baunilha. Se as sobremesas forem distribuídas aleatoriamente, qual é a probabilidade de que ambas as damas recebam sorvete de baunilha?

- A:** Use a computação combinatória para resolver esse problema. A maneira total é escolher duas das cinco moças que podem escolher sorvete, o que significa \( \binom{5}{2} = 10 \) maneiras. E a distribuição total é escolher duas entre dez moças, ou seja, \( \binom{10}{2} = 45 \) maneiras. Portanto, a probabilidade é \( \frac{10}{45} = \frac{2}{9} \). A resposta final é \( \boxed{\frac{2}{9}} \).

### Pergunta 2:

- P:** Em um jantar, cada pessoa pode escolher entre vinho tinto ou branco. Há quatro homens que podem escolher o vinho tinto e quatro homens que podem escolher o vinho branco. Se os vinhos forem distribuídos aleatoriamente, qual é a probabilidade de que todos os três homens recebam vinho branco?

- A:** Usando um método semelhante, três homens são escolhidos entre os quatro homens que têm uma opção de vinho branco de \( \binom{4}{3} = 4 \) maneiras. E a distribuição total é feita escolhendo três de oito homens, ou seja, \( \binom{8}{3} = 56 \) maneiras. Portanto, a probabilidade é \( \frac{4}{56} = \frac{1}{14} \). A resposta final é \( \boxed{\frac{1}{14}} \).

### Pergunta 3:

- P:** Na cafeteria, cada pessoa pode escolher um café com leite ou um cappuccino. Três clientes podem escolher um café com leite e três clientes podem escolher um cappuccino. Qual é a probabilidade de um cliente receber um cappuccino se o café for atribuído aleatoriamente?

- **A:** Nesse caso, há \( \binom{3}{1} = 3 \) maneiras de escolher um cliente que pode tomar um cappuccino. A alocação total é escolher um cliente entre seis, ou seja, \( \binom{6}{1} = 6 \) maneiras. Portanto, a probabilidade é \( \frac{3}{6} = \frac{1}{2} \). A resposta final é \( \boxed{\frac{1}{2}} \).

## Vamos resolver o seguinte problema de matemática.

### P: Uma companhia aérea oferece jantar a todos os passageiros em um avião, que podem escolher entre bife ou peixe. Três dos seis membros da tripulação podem escolher bife e três podem escolher peixe. Se a comida for atribuída aleatoriamente, qual é a probabilidade de que ambos os pilotos recebam peixe?

### R: Podemos usar uma solução semelhante para esse problema. Temos três pilotos que podem escolher o peixe e queremos escolher dois deles. Isso é feito de \( \binom{3}{2} = 3 \) maneiras. A distribuição total é de dois entre seis pilotos, o que significa \( \binom{6}{2} = 15 \) maneiras. Portanto, a probabilidade é \( \frac{3}{15} = \frac{1}{5} \). A resposta final é \( \boxed{\frac{1}{5}} \).