Uma alternativa ao Transformer na modelagem de linguagem
A arquitetura Transformer é um componente essencial para o sucesso dos modelos de linguagem grandes (LLMs). Quase todos os modelos de linguagem grandes em uso atualmente empregam a arquitetura, desde modelos de código aberto, como o Mistral para modelos de código fechado, como o ChatGPT.
Para aprimorar ainda mais o modelo de linguagem grande, foram desenvolvidas novas arquiteturas que podem até mesmo ir além da arquitetura Transformer. Uma dessas abordagens é a Mambaum tipo de modelo de espaço de estado.
Mamba no jornal Mamba: modelagem de sequência de tempo linear com espaços de estado seletivos1 em que foi apresentado. Você pode saber mais sobre ele em seu repositório Encontre sua implementação oficial e os pontos de verificação do modelo em.
Nesta postagem, apresentarei o campo da modelagem de espaço de estado no contexto da modelagem de linguagem e explorarei passo a passo vários conceitos para ajudar a entender o campo. Em seguida, discutiremos como o Mamba pode desafiar a arquitetura do Transformer.
Como um guia visual, este artigo apresentará várias visualizações para ajudar a entender o Mamba e os modelos de espaço de estado!
Parte 1:Problemas com Transformers
Para ilustrar a arquitetura interessante do Mamba, vamos primeiro analisar brevemente o Transformers e explorar uma de suas deficiências.
O Transformer trata qualquer entrada de texto como se fosse uma entrada de texto do tokens constituinte sequência.
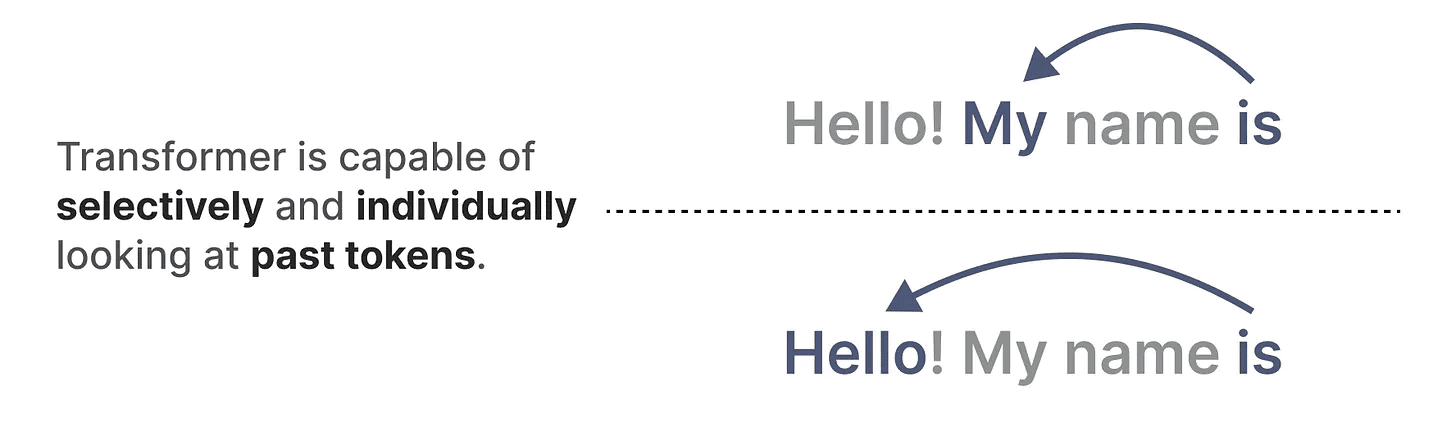
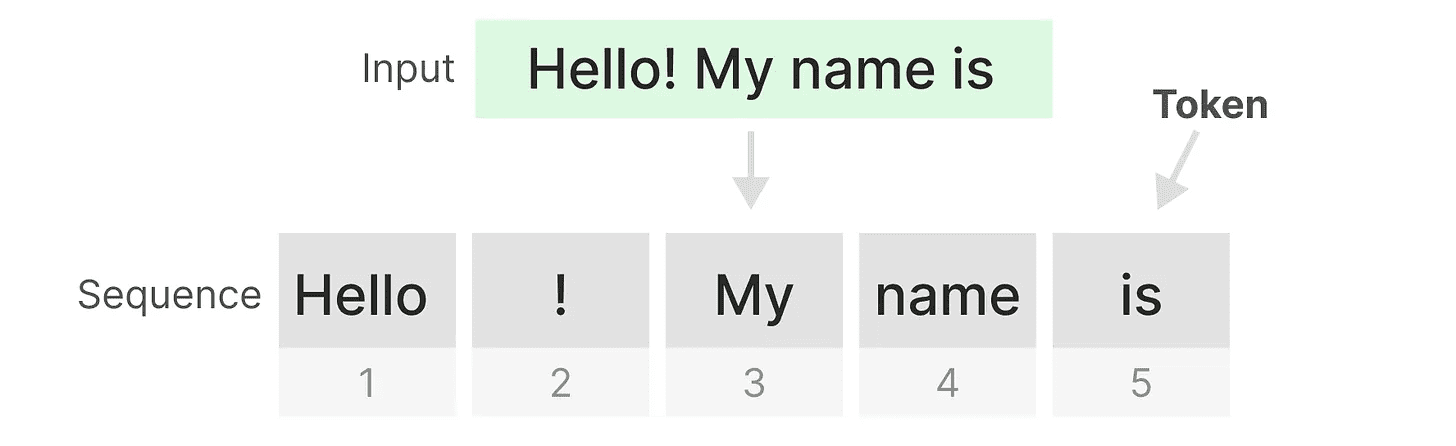Uma das principais vantagens dos Transformers é que, independentemente da entrada recebida, ele pode voltar a quaisquer tokens anteriores na sequência para derivar sua representação.
Componentes principais dos transformadores
Lembre-se de que o Transformer consiste em duas estruturas, um conjunto de blocos codificadores para representar texto e um conjunto de blocos decodificadores para gerar texto. Combinadas, essas estruturas podem ser usadas para várias tarefas, inclusive a tradução.
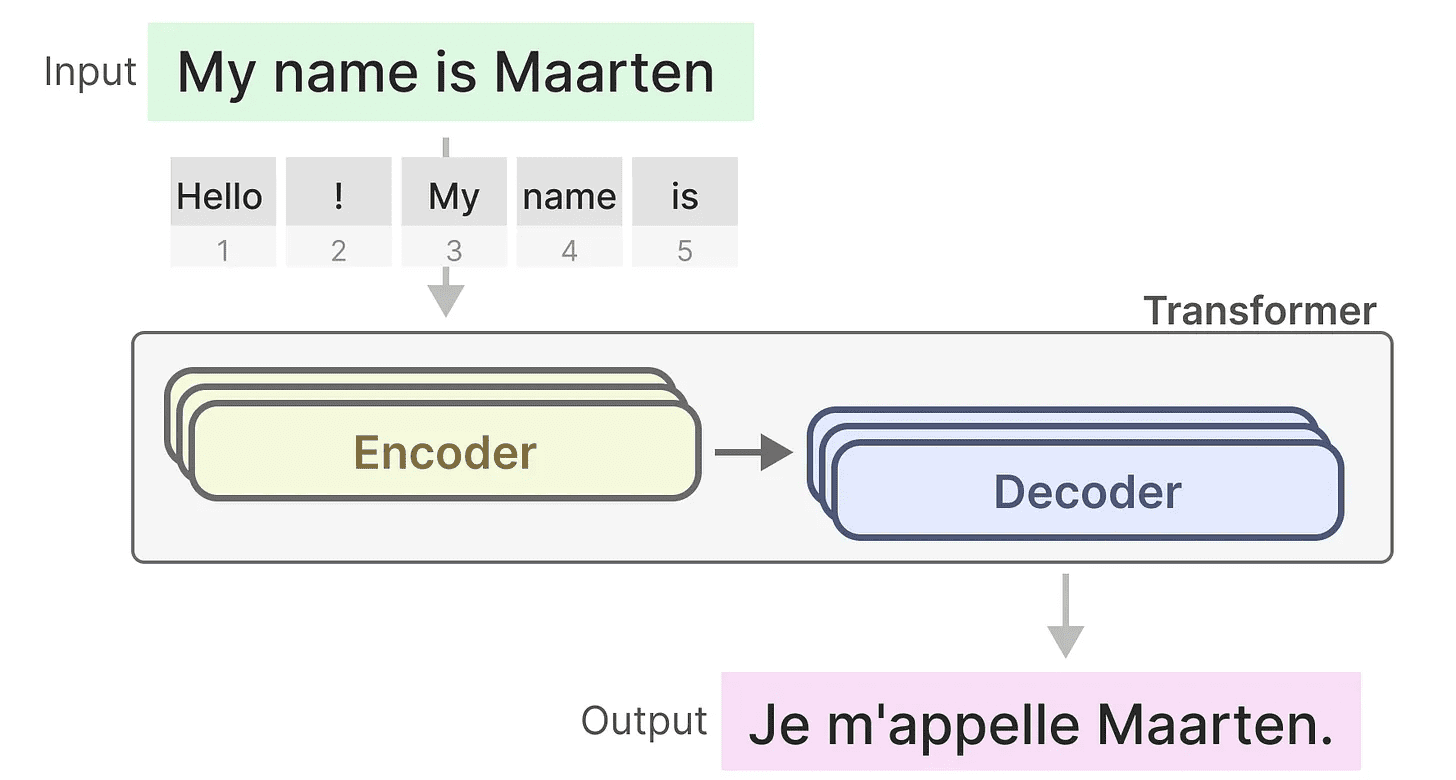Podemos usar essa estrutura e criar modelos generativos usando apenas decodificadores. Esse modelo baseado no Transformer, oTransformador de pré-treinamento generativo(GPT) que usa blocos de decodificador para completar parte do texto de entrada.
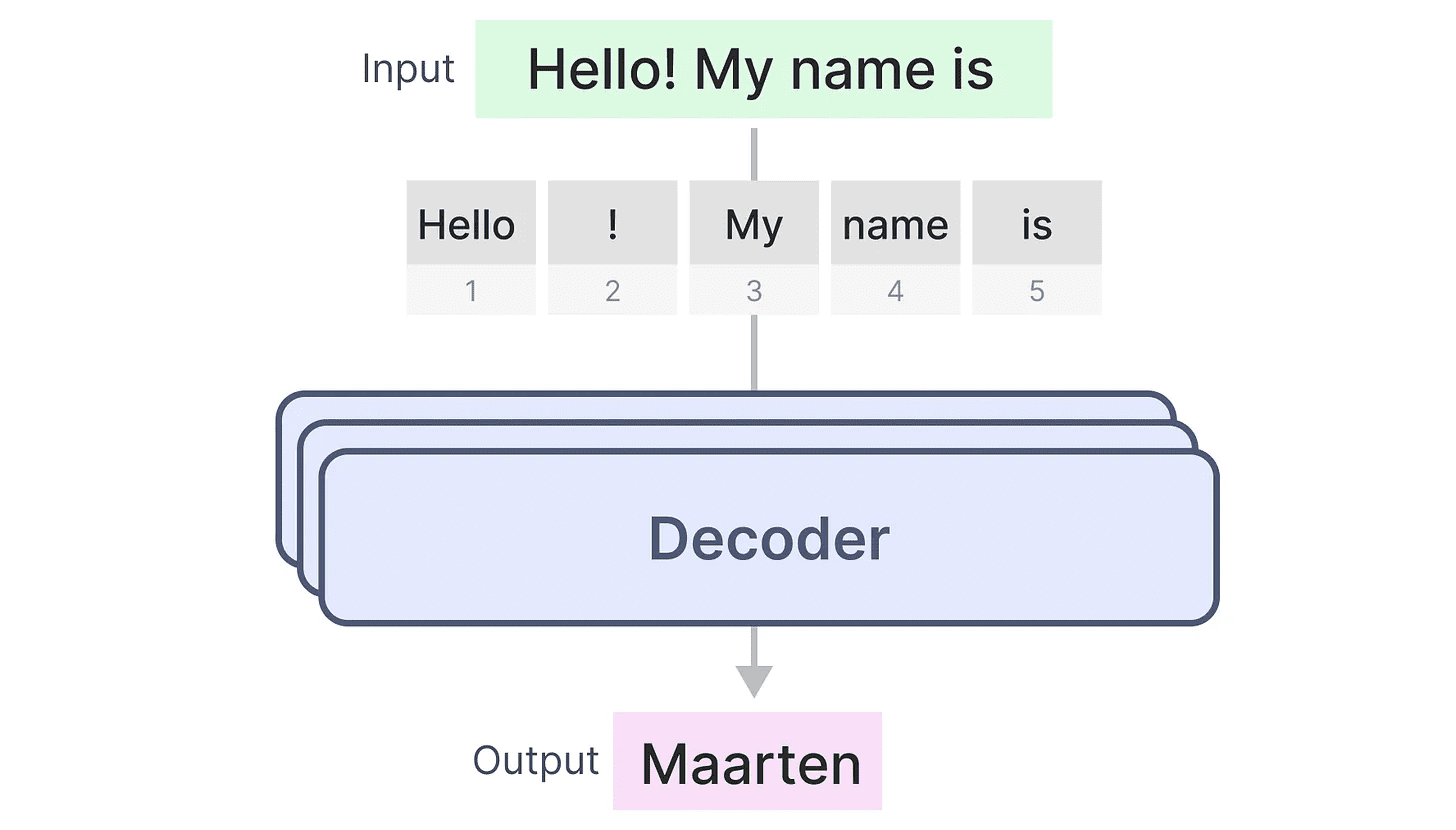Vamos ver como isso funciona!
Bênçãos no treinamento...
Um único bloco de decodificador consiste em dois componentes principais, o mecanismo de autoatenção mascarado e a rede neural feedforward.
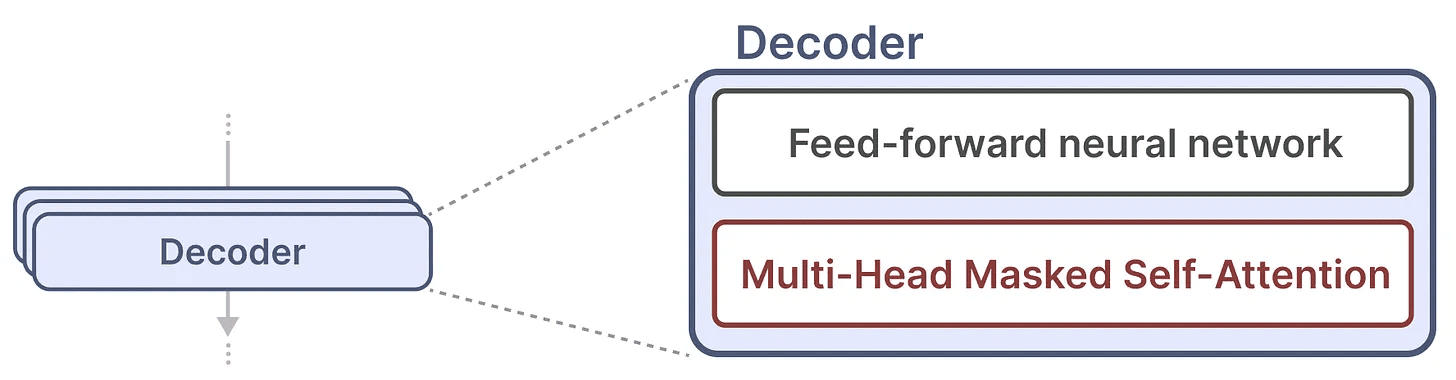O mecanismo de autoatenção é um motivo importante pelo qual esses modelos funcionam tão bem. Ele permite uma visão descompactada de toda a sequência e é rápido de treinar.
Então, como isso funciona?
Ele cria uma matriz que leva cada Token Compare-o com cada token anterior. Os pesos na matriz dependem da relevância dos pares de tokens entre si.
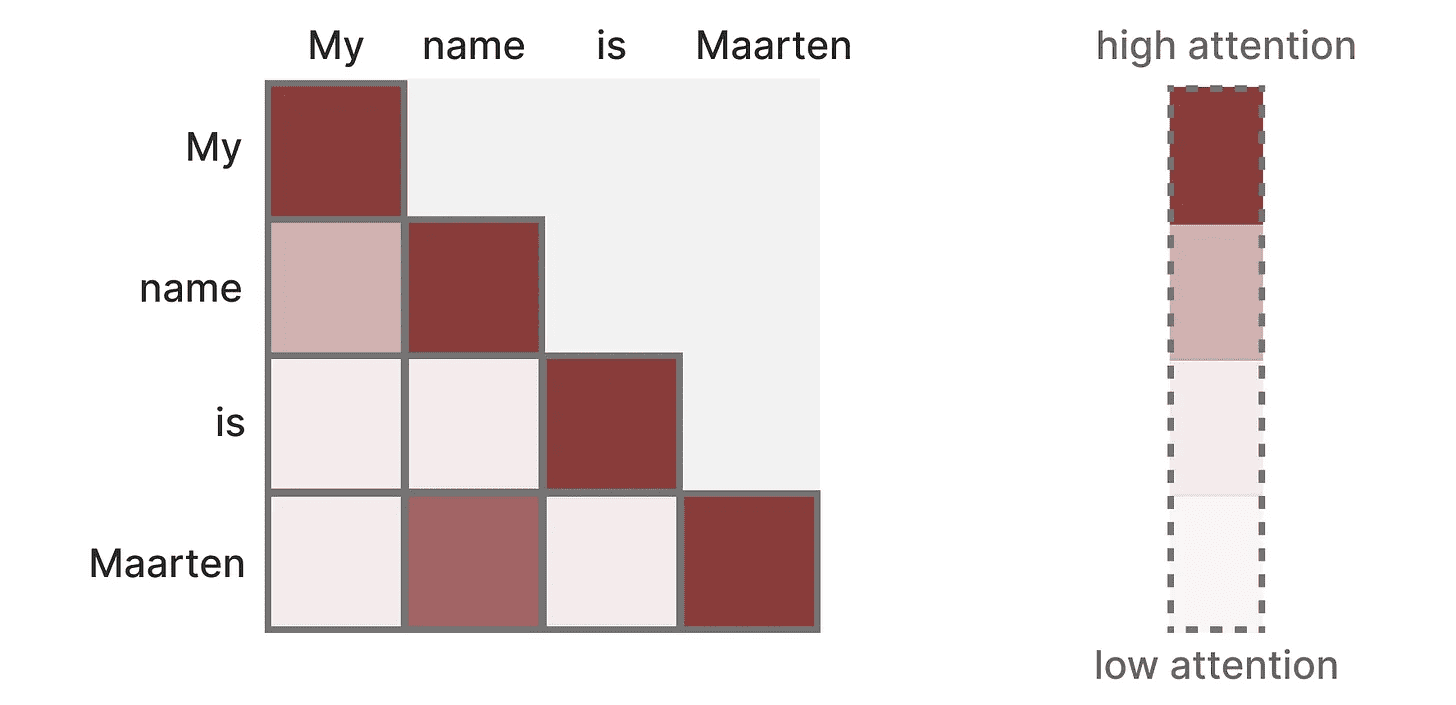Essa matriz é criada de uma só vez durante o treinamento. "Minhas"e"nome"A atenção entre não precisa ser calculada antes de poder ser calculada."nome"e"é"Atenção entre.
Ele percebeparalelizaçãoo que acelera muito o treinamento!
Problemas de raciocínio!
No entanto, há uma desvantagem. Ao gerar o próximo token, precisamos recalcular osequência completaatenção, mesmo que já tenhamos gerado algum Token.
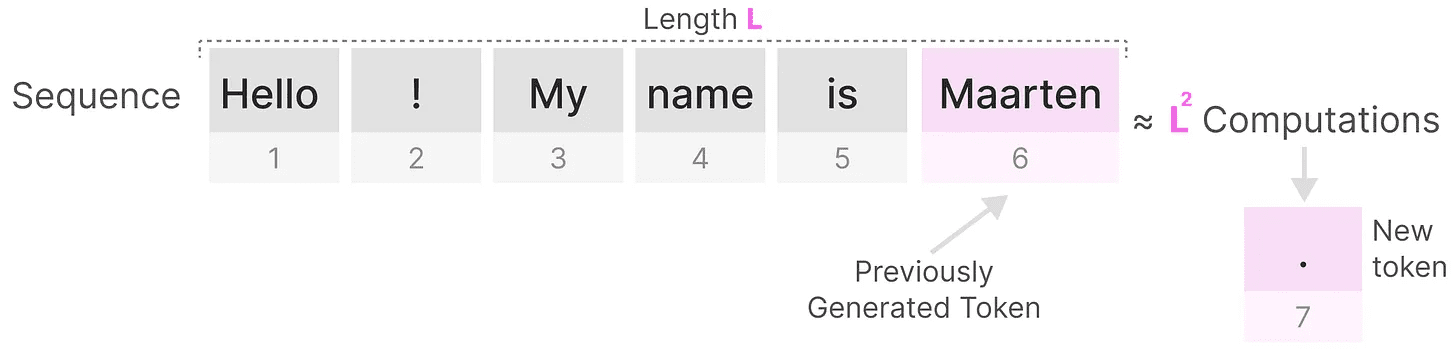Gerar o comprimento doLA sequência requer cerca deL²vezes, o que pode ser computacionalmente caro se o comprimento da sequência aumentar.
Essa necessidade de recomputar a sequência inteira é um dos principais gargalos da arquitetura do Transformer.
Vamos ver como uma técnica "clássica", as redes neurais recorrentes (RNN), resolve esse problema de inferência lenta.
A RNN é a solução?
A Rede Neural Recorrente (RNN) é uma rede baseada em sequência. Ela recebe duas entradas em cada etapa de tempo, ou seja, etapa de tempote a etapa de tempo anteriort-1do estado oculto é usado para gerar o próximo estado oculto e prever a saída.
A RNN tem um mecanismo de looping que permite que ela passe informações de uma etapa para a seguinte. Podemos "expandir" esse processo de visualização para torná-lo mais explícito.
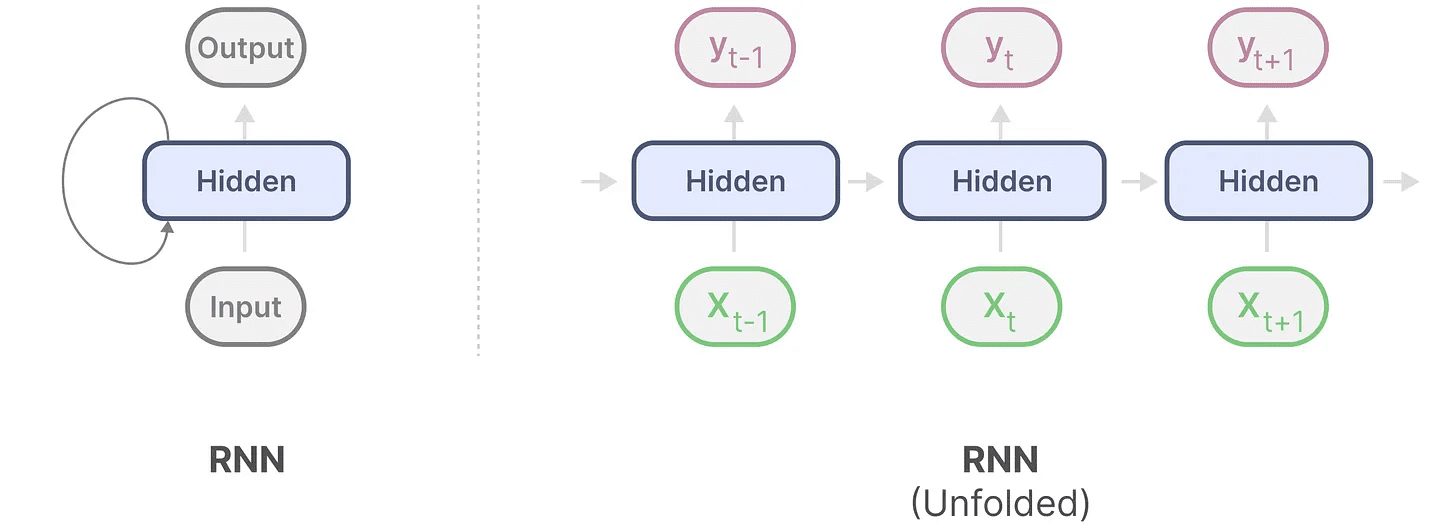Ao gerar a saída, o RNN só precisa considerar o estado oculto anterior e a entrada atual. Isso evita o problema de recalcular todos os estados ocultos anteriores exigidos pelo Transformer.
Em outras palavras, uma RNN é capaz de fazer inferências rápidas porque é escalonada linearmente com o comprimento da sequência! Em teoria, ela poderia até terComprimento ilimitado do contexto.
Para ilustrar isso, vamos aplicar o RNN ao texto de entrada que usamos anteriormente.
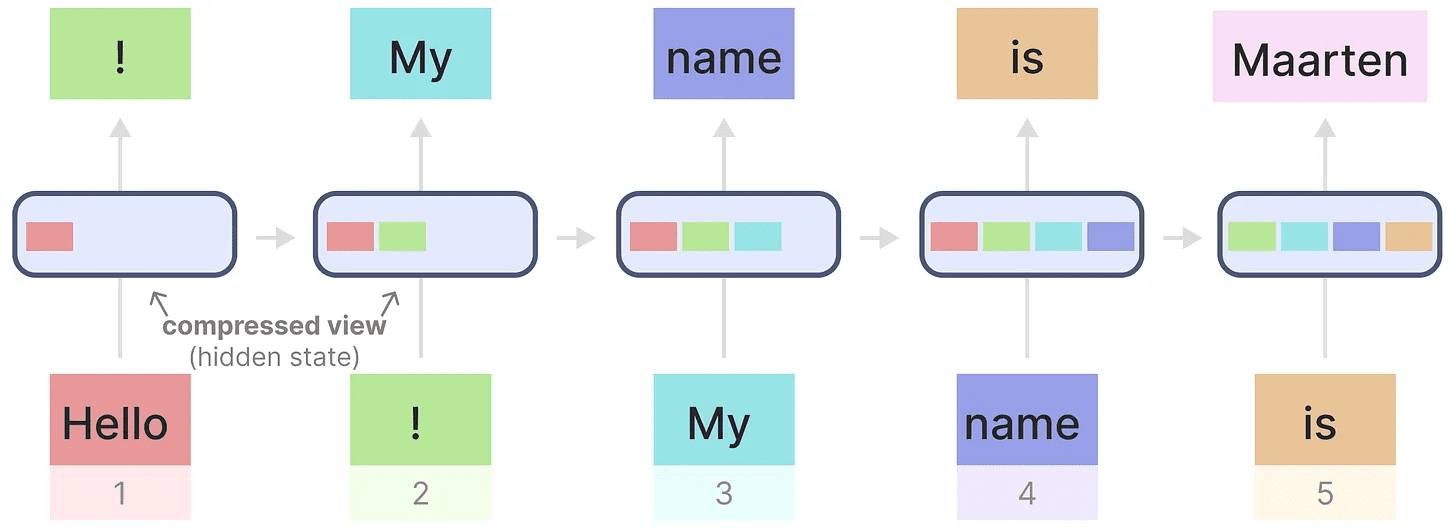Cada estado oculto é uma agregação de todos os estados ocultos anteriores, geralmente uma visualização compactada.
Entretanto, há um problema aqui ......
Observe que, ao gerar o nome "Maarten" quando o último estado oculto não contiver mais informações sobre a palavra "Olá"Os RNNs tendem a esquecer as informações ao longo do tempo porque consideram apenas o último estado.
Embora os RNNs sejam mais rápidos em termos de treinamento e inferência, eles não têm a precisão que os modelos Transformer podem oferecer.
Portanto, estudamos modelos de espaço de estado para usar RNNs (e, às vezes, convolução) de forma eficiente.
Parte 2:Modelagem de espaço de estado (SSM)
Os modelos de espaço de estado (SSMs), como transformadores e RNNs, lidam com sequências de informações, como texto e sinais. Nesta seção, apresentamos os conceitos básicos dos SSMs e como eles se relacionam com dados textuais.
O que é espaço de estado?
Um espaço de estado contém o número mínimo de variáveis necessárias para descrever completamente um sistema. É uma forma de representar matematicamente um problema, definindo os possíveis estados de um sistema.
Vamos simplificar. Imagine que estamos viajando por um labirinto. "espaço de estado"É um mapa de todos os locais (estados) possíveis. Cada ponto representa um local exclusivo no labirinto com detalhes específicos, como a distância que você está da saída.
"representação do espaço de estado"é uma descrição simplificada desse mapa. Ele mostra sua localização atual (estado atual), o próximo local para o qual você pode viajar (possível estado futuro) e como você pode chegar ao próximo local (movendo-se para a direita ou para a esquerda).
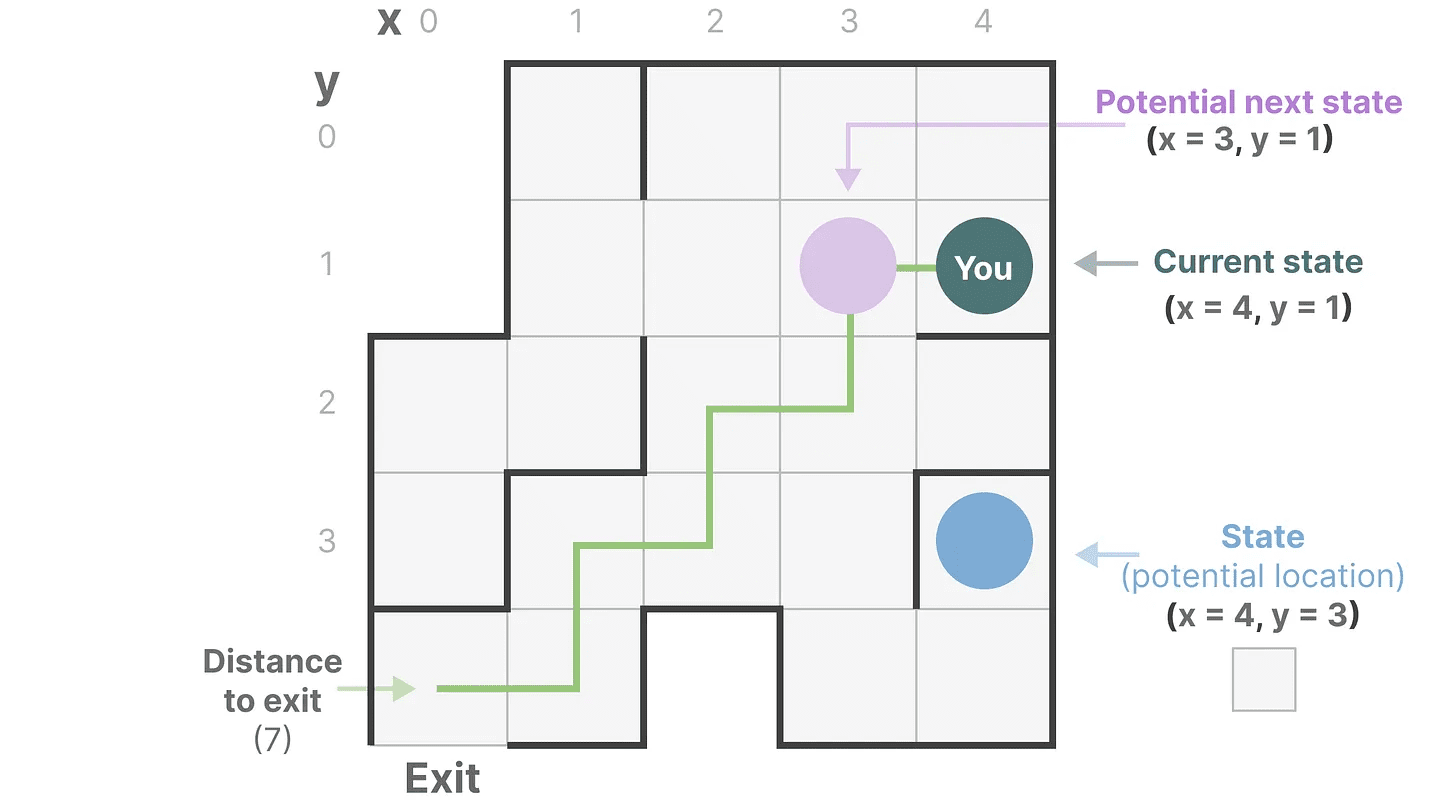Embora o modelo de espaço de estado use equações e matrizes para rastrear esse comportamento, ele é, na verdade, apenas uma forma de rastrear onde você está, para onde pode ir e como chegar lá.
As variáveis descrevem um estado, em nosso caso as coordenadas X e Y, e a distância até a saída, que pode ser expressa como "vetor de estado".
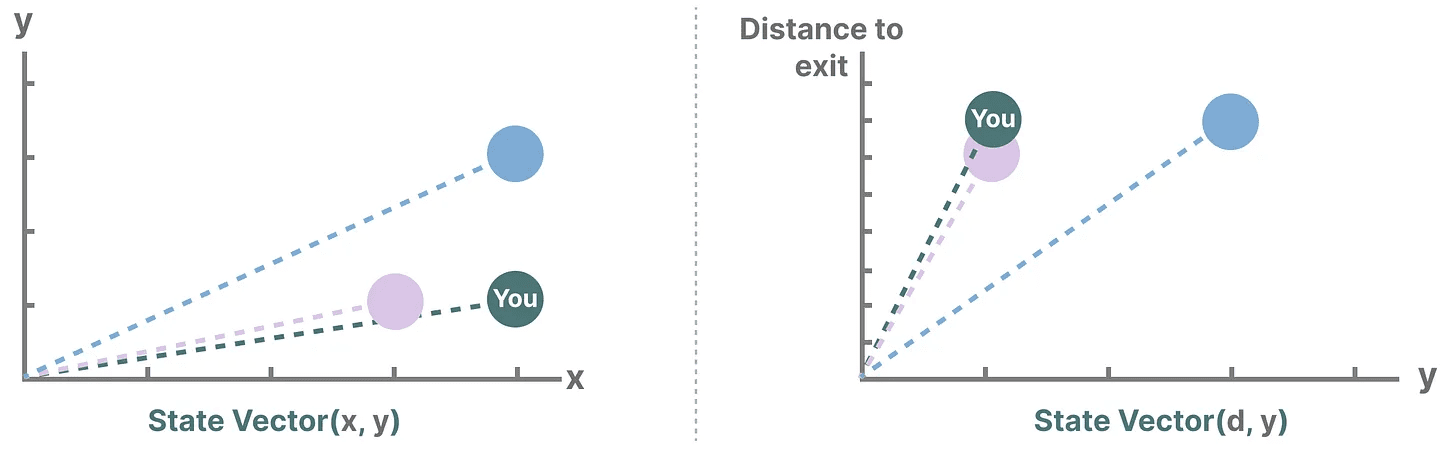Parece familiar? Isso ocorre porque os embeddings ou vetores também são usados com frequência em modelos de linguagem para descrever o "estado" de uma sequência de entrada. Por exemplo, um vetor que descreve sua posição atual (um vetor de estado) pode ter a seguinte aparência:
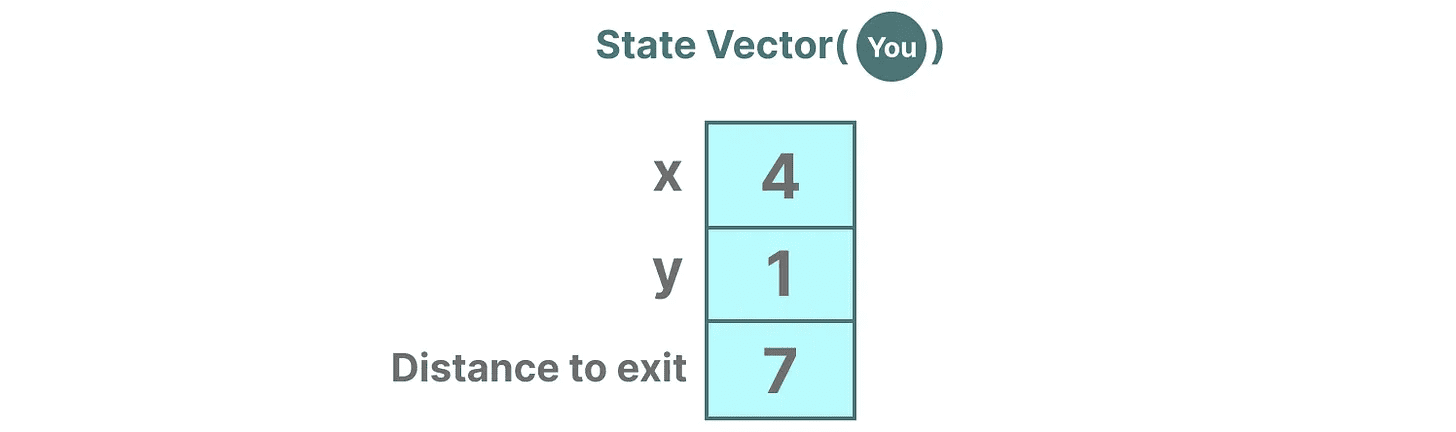Nas redes neurais, "estado" geralmente se refere ao estado oculto do sistema, que é um dos aspectos mais importantes da geração de novos tokens em um modelo de linguagem grande.
O que é um modelo de espaço de estado?
Os SSMs (Modelos de Espaço de Estado) são uma classe de modelos usados para descrever essas representações de estado e prever seu próximo estado, com previsões baseadas em determinadas entradas.
Tradicionalmente, com o tempo tSSM:
- A sequência de entrada será x(t)(por exemplo, mover-se para a esquerda e para baixo em um labirinto) mapeia a representação do estado potencial h(t)(por exemplo, distância até a saída e coordenadas x/y)
- e derivar a sequência de saída prevista y(t)(por exemplo, mover-se novamente para a esquerda para chegar mais rápido à saída)
No entanto, em vez de usar sequências discretas (por exemplo, deslocar uma vez para a esquerda), o SSM aceita sequências contínuas como entrada e prevê a sequência de saída.
O SSM pressupõe que os sistemas dinâmicos (por exemplo, objetos que se movem no espaço 3D) podem ser temporalmente t do estado e duas equações para prever esse estado.
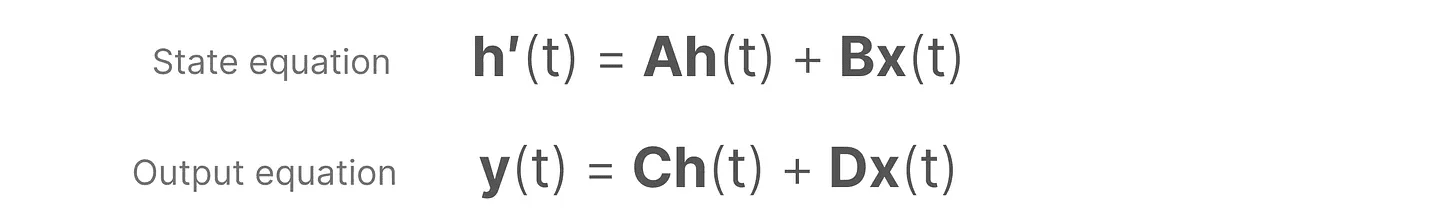Ao resolver essas equações, supomos que podemos revelar princípios estatísticos para prever o estado do sistema com base nos dados observados (sequências de entrada e estados anteriores).
O objetivo é encontrar essa representação de estado h(t)que nos permite passar de sequências de entrada para sequências de saída.
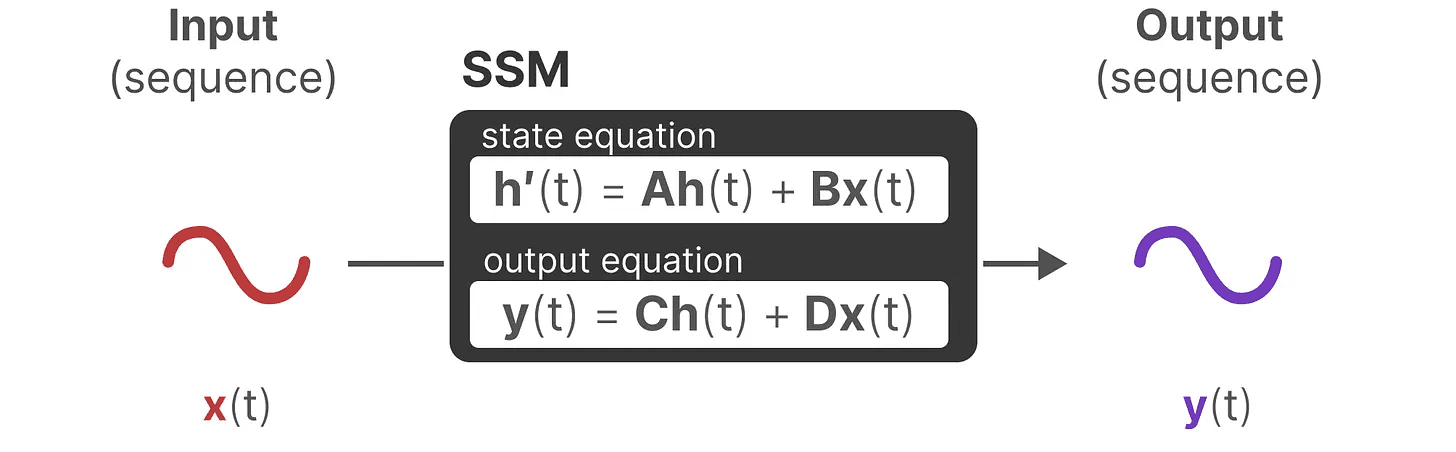Essas duas equações estão no centro do modelo de espaço de estado.
Essas duas equações serão mencionadas ao longo do guia. Para torná-las mais intuitivas, oUsamos código de corespara que você possa citá-los rapidamente.
equação de estado descreve como o estado será alterado de acordo com as entradas (por meio do Matriz B) impactam o estado (via Matriz A) e mudança.
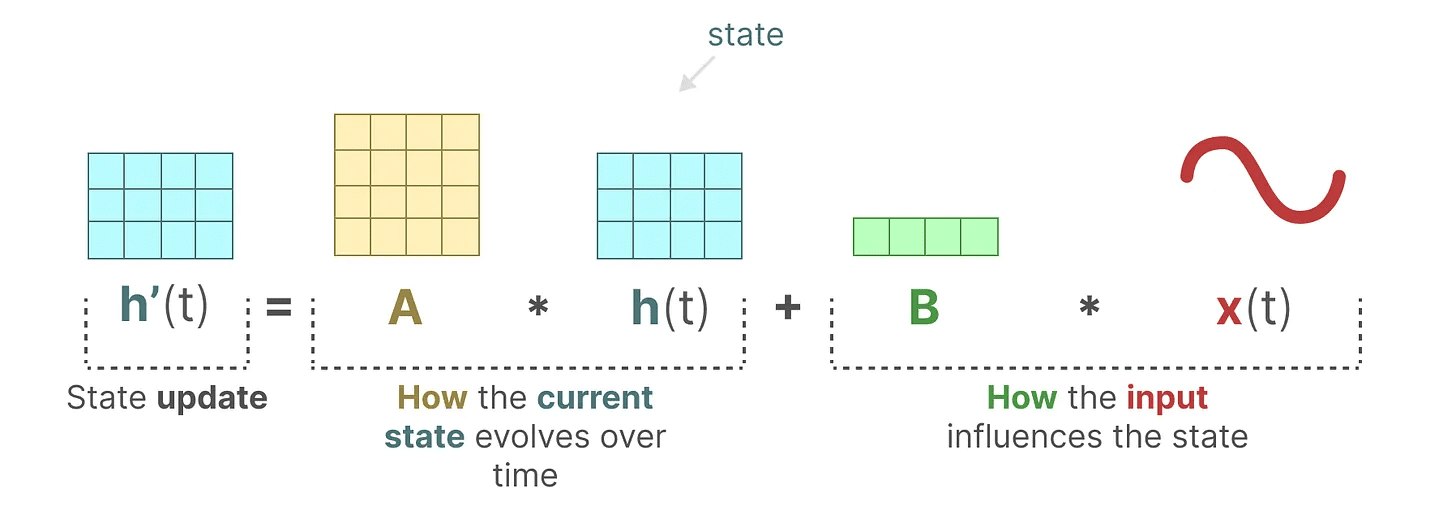Conforme mencionado anteriormente.h(t) refere-se a um determinado momento t A representação do estado potencial dox(t) refere-se a uma determinada entrada.
equação de saída descreve como o estado é transmitido através do Matriz C convertido em saída, e como as entradas são convertidas em saídas pelo Matriz D Afeta a saída.
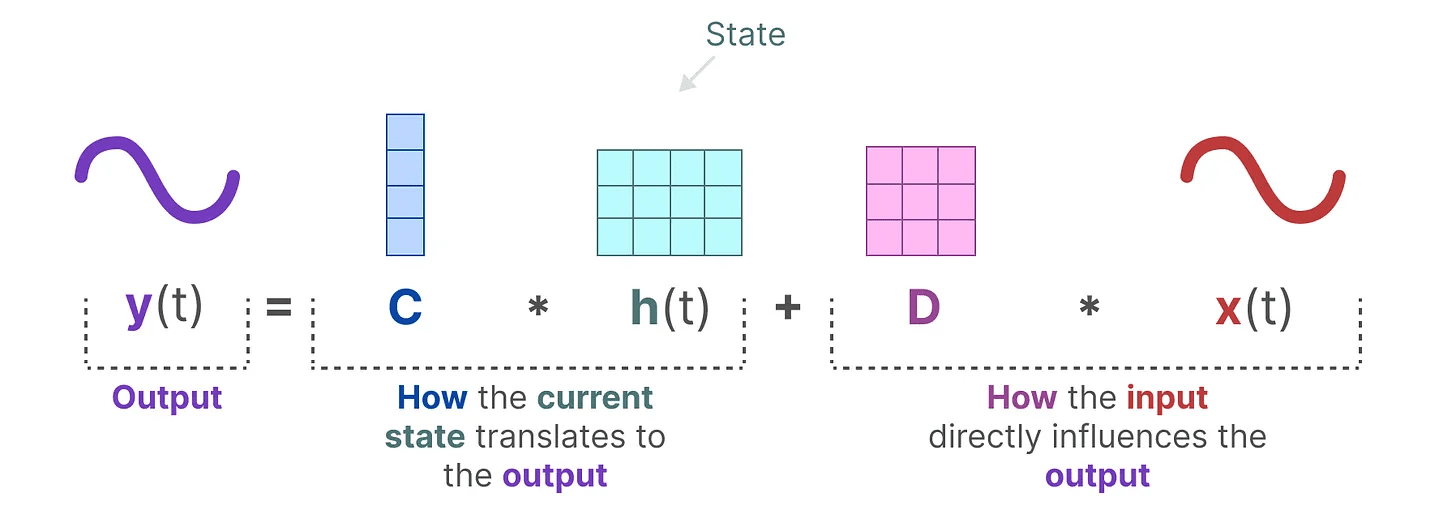
tomar nota de: Matriz AeBeC responder cantando D Também conhecido como parâmetrosporque eles podem ser aprendidos.
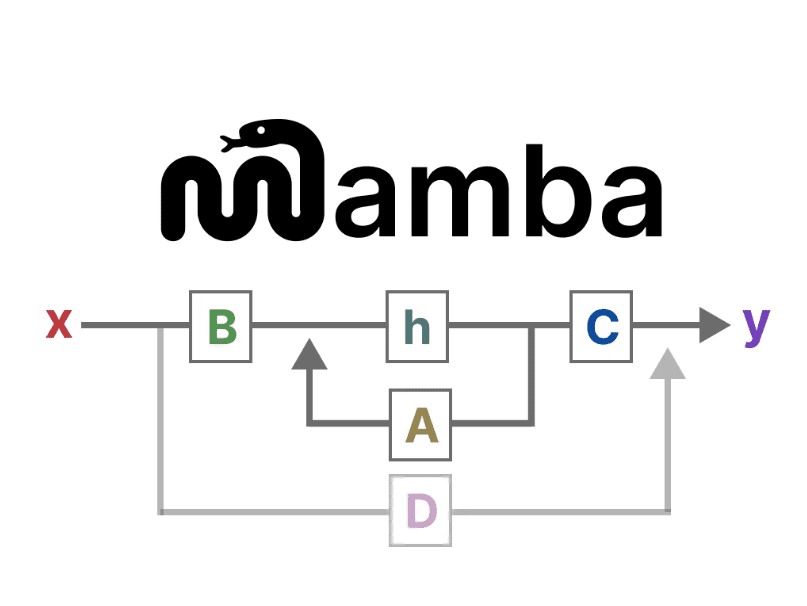
Visualizando essas duas equações, obtemos a seguinte arquitetura:
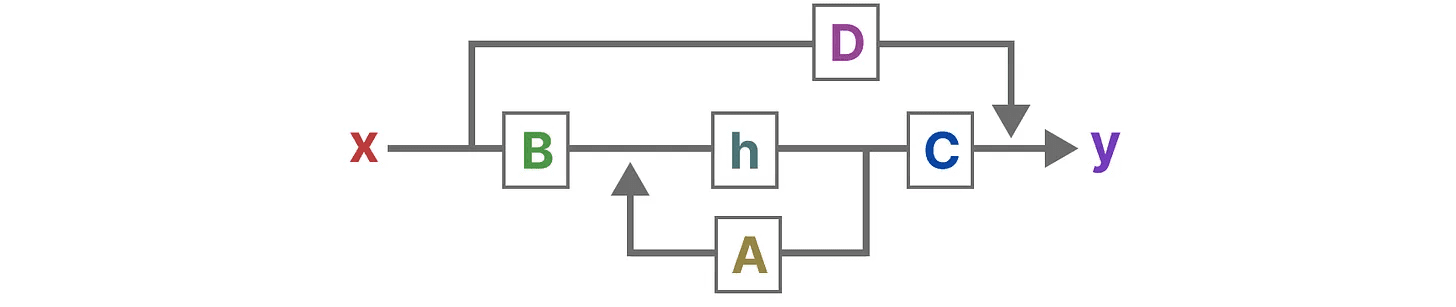Vamos dar uma olhada passo a passo em como essas matrizes afetam o processo de aprendizagem.
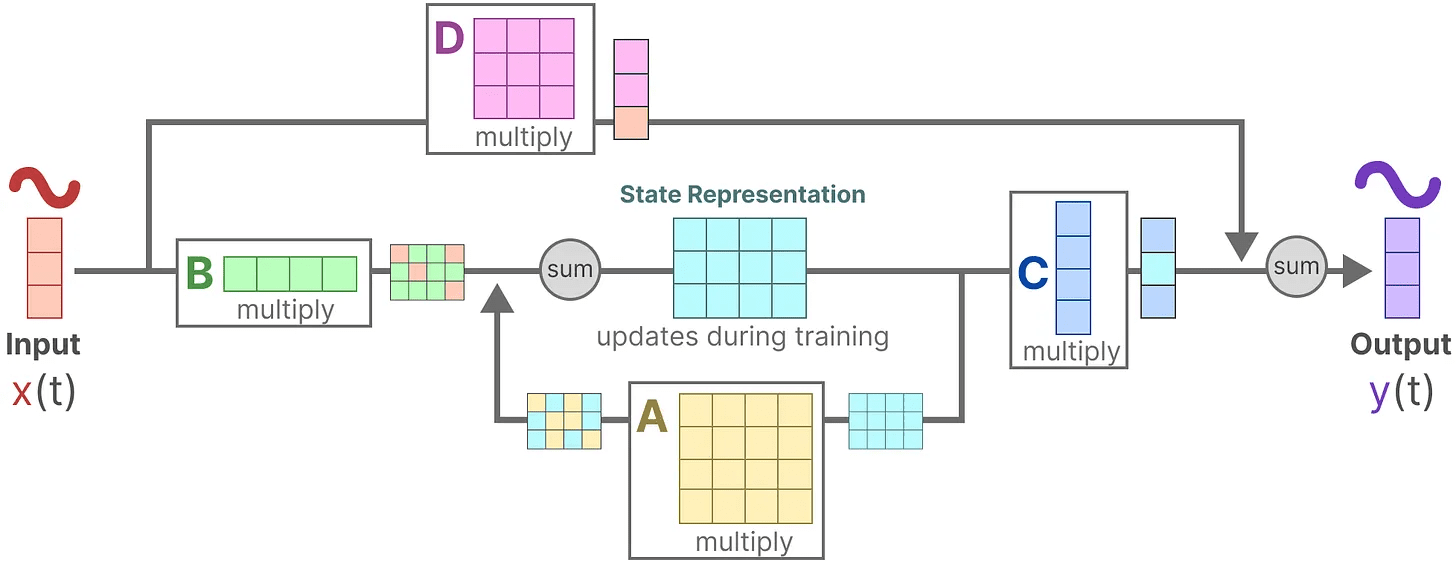
Suponha que tenhamos alguns sinais de entrada x(t)O sinal é conectado primeiro ao Matriz B Multiplicar.Matriz B Descreve como as entradas afetam o sistema.
O estado atualizado (semelhante ao estado oculto de uma rede neural) é um espaço potencial que contém o "conhecimento" central do ambiente. Relacionamos o estado com o Matriz A Multiplicada, essa matriz descreve as associações entre todos os estados internos e representa a dinâmica subjacente do sistema.
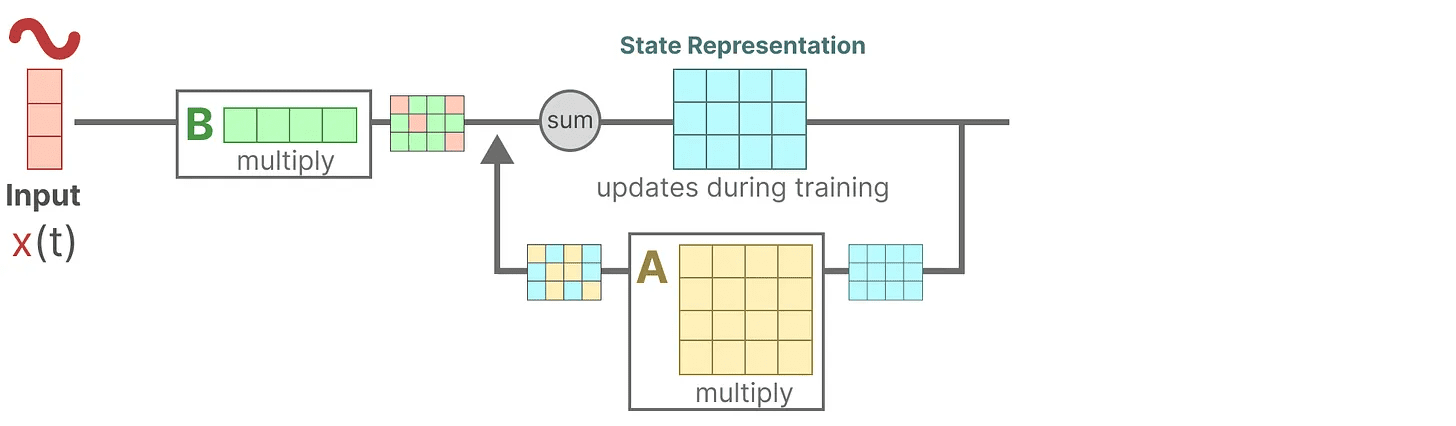Como você deve ter notado.Matriz A Aplicar antes da criação da representação do estado e novamente após a atualização da representação do estado.
Em seguida, usamos o Matriz C para descrever como os estados são convertidos em saídas.
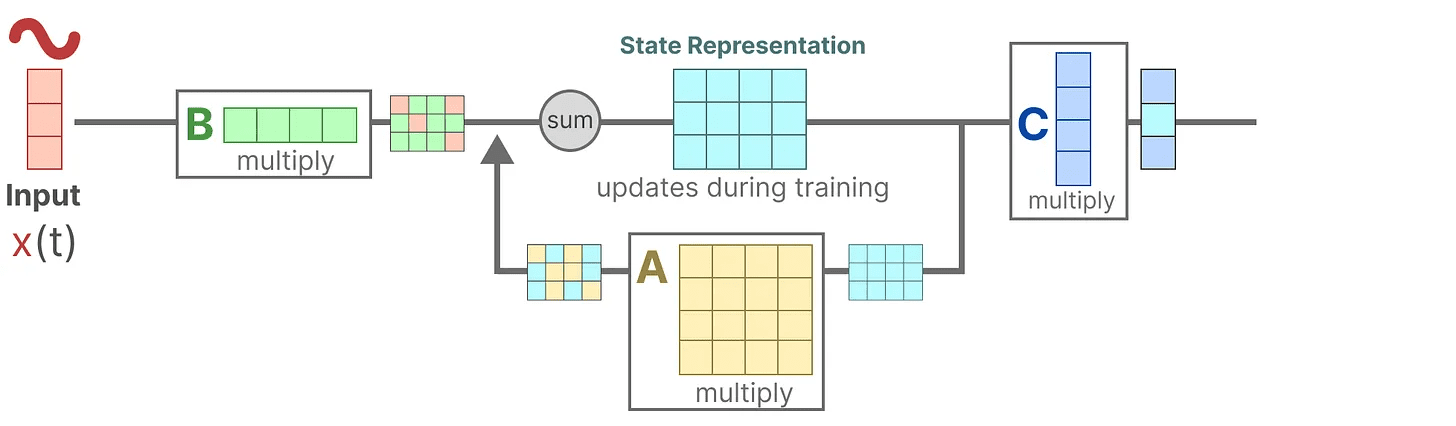Por fim, podemos usar o Matriz D Fornece um sinal direto da entrada para a saída. Isso também é comumente chamado de conexão de salto.
devido a Matriz D Semelhante às conexões de salto, as SSMs são frequentemente consideradas como as seguintes formas que não contêm conexões de salto.
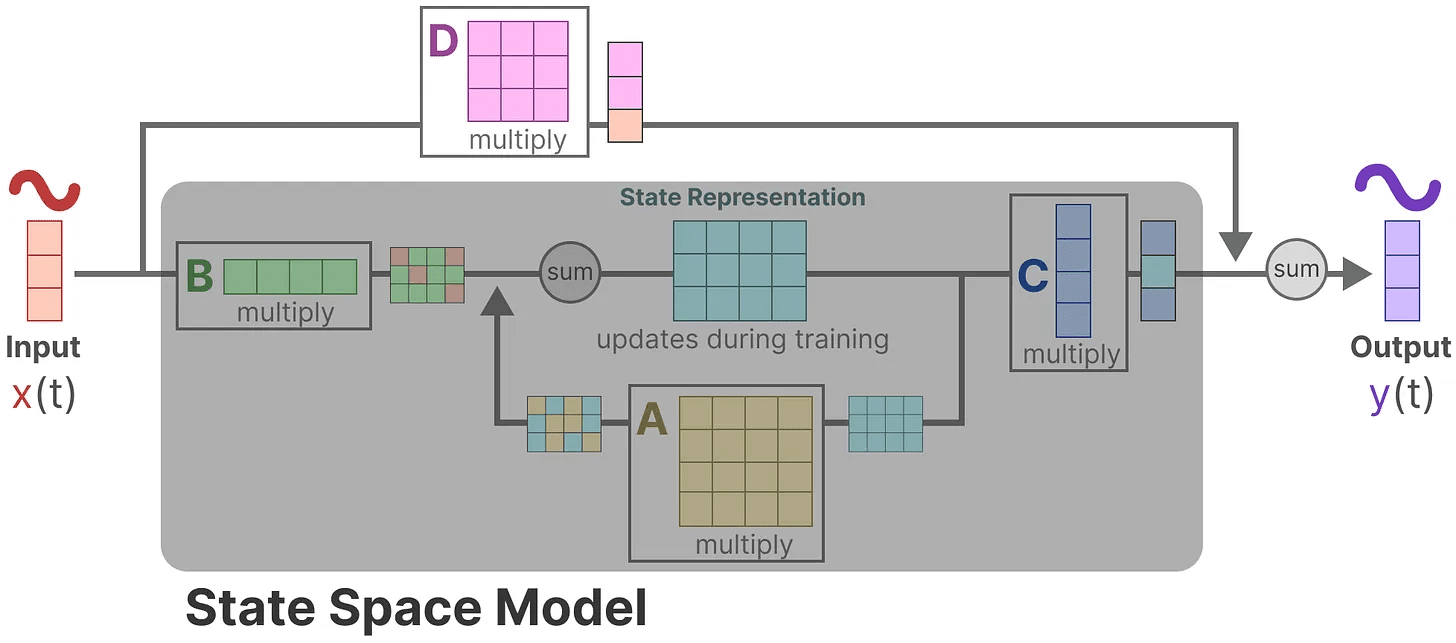Voltando à nossa perspectiva simplificada, podemos agora nos concentrar na matriz AeB responder cantando C como o núcleo do SSM.
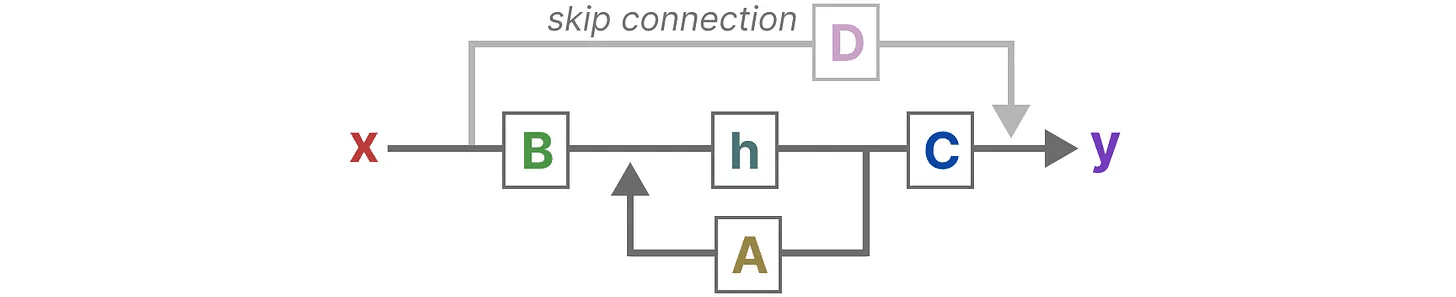Podemos atualizar as equações originais (e adicionar algumas cores bonitas) para marcar para que cada matriz é usada, como fizemos anteriormente.
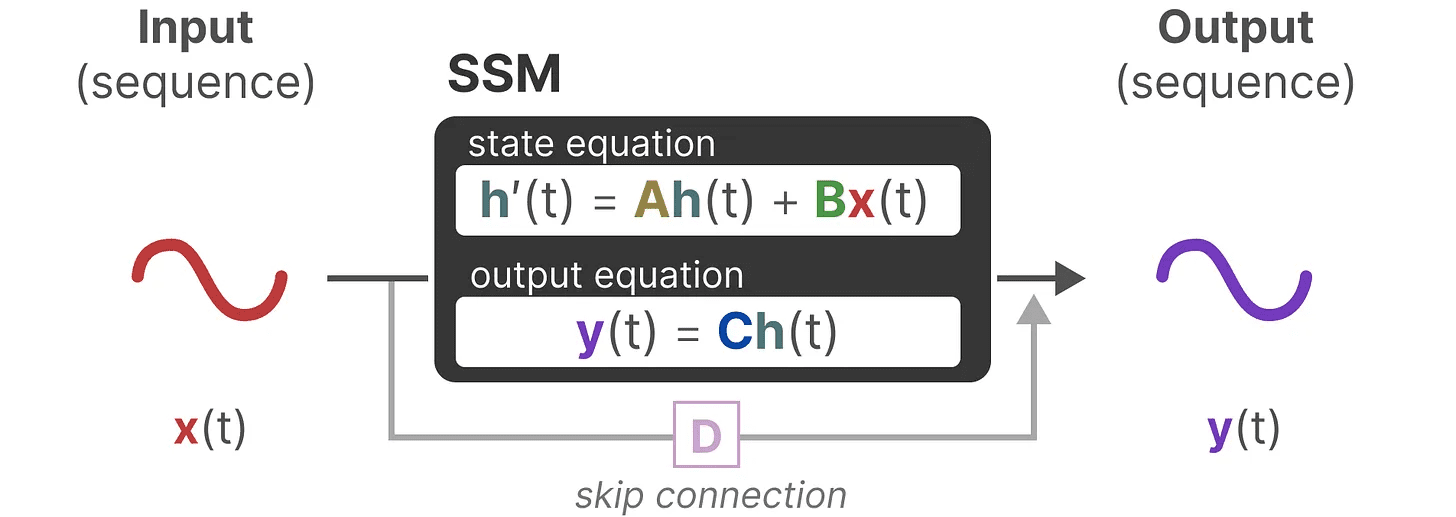Juntos, esses dois conjuntos de equações têm o objetivo de prever o estado do sistema a partir dos dados observados. Como as entradas são contínuas, a representação principal do SSM é escala de tempo contínuo.
De sinais contínuos a discretos
Se você tiver um sinal contínuo, encontre a representação do estado h(t) desafiador de analisar. Além disso, como normalmente temos entradas discretas (por exemplo, sequências de texto), gostaríamos de discretizar o modelo.
Para fazer isso, usamos o técnica de retenção de ordem zero. Ele funciona da seguinte forma: primeiro, sempre que recebemos um sinal discreto, mantemos seu valor até recebermos um novo sinal discreto. Esse processo gera um sinal contínuo para o SSM:
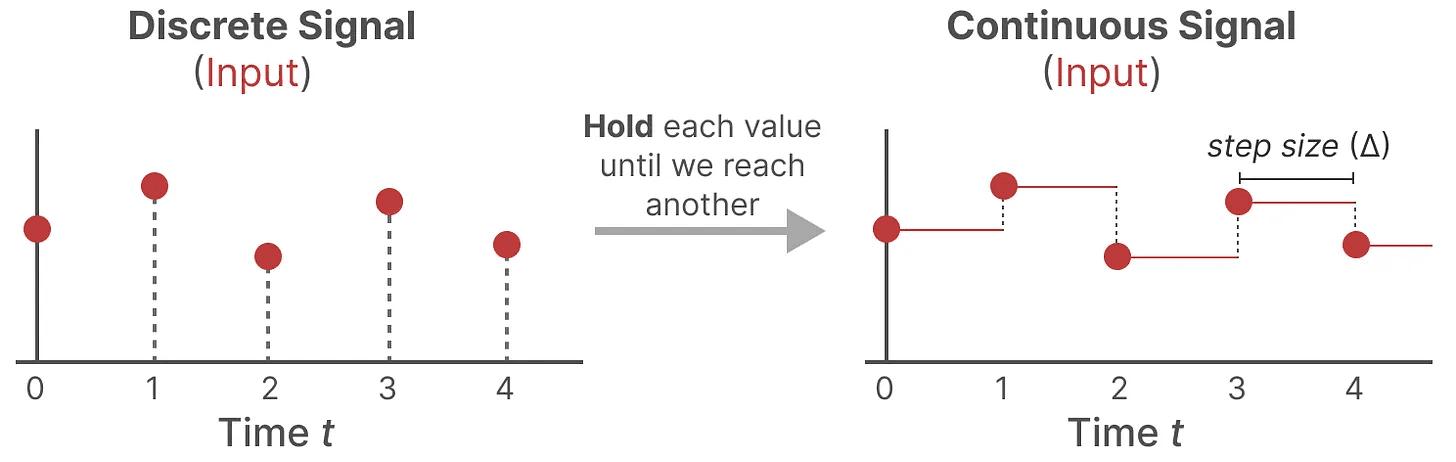Mantemos o valor do tempo por meio de um novo parâmetro que pode ser aprendido marca-passo ∆ Indica. Indica a resolução da entrada.
Agora que geramos um sinal contínuo para a entrada, podemos gerar uma saída contínua e amostrar esses valores com base na etapa de tempo da entrada.
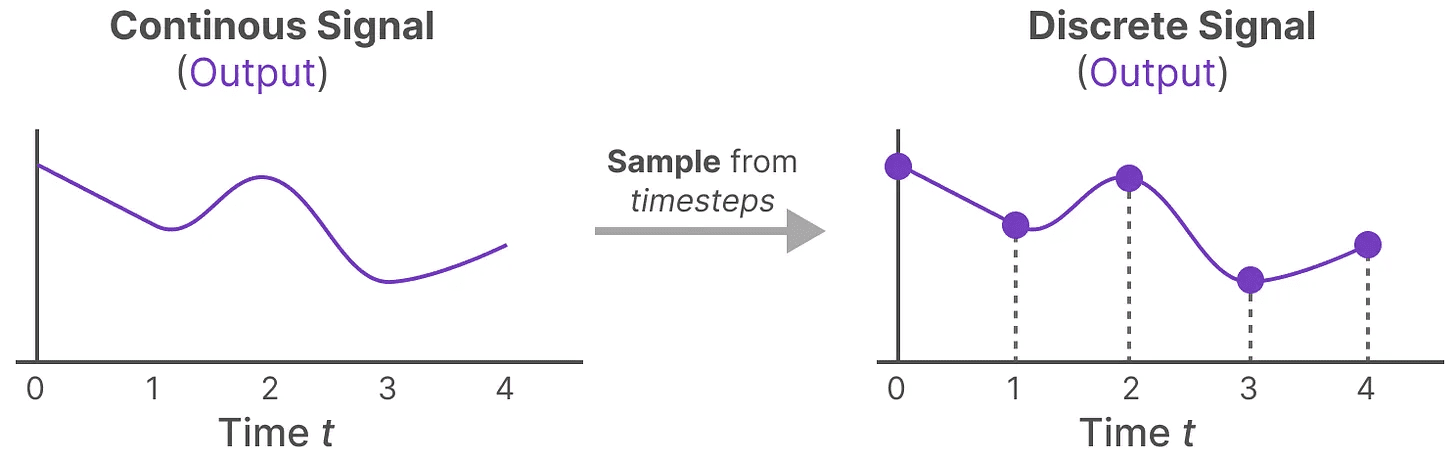Esses valores amostrados são o resultado de nossa discretização!
Matematicamente, podemos aplicar a retenção de ordem zero da seguinte forma:
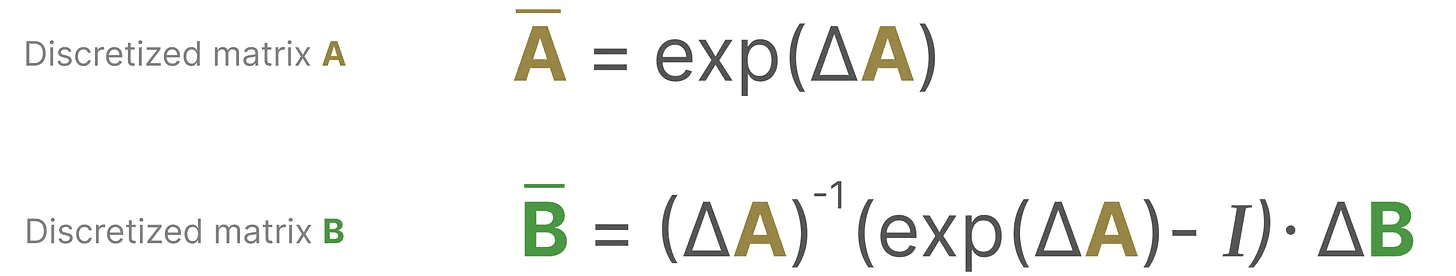Juntos, eles nos permitem fazer a transição de um SSM contínuo para um SSM discreto. Nesse ponto, o modelo não é mais função a função x(t) → y(t)Em vez disso, é sequência para série xₖ → y_ₖ::
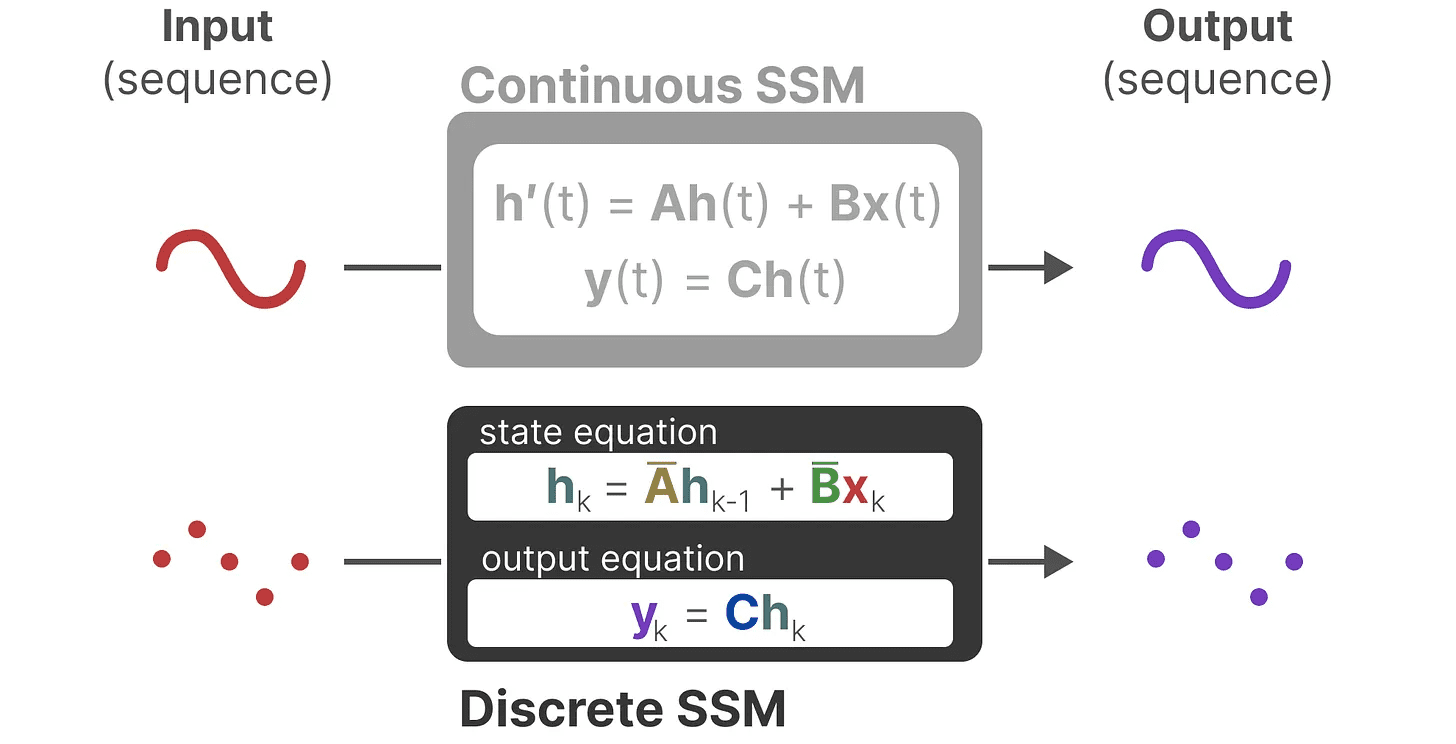Aqui, a matriz A responder cantando B Agora denotamos os parâmetros discretizados do modelo.
Usamos k em vez de tpara distinguir quando estamos falando de SSM contínua e SSM discreta.
Atenção: Durante o treinamento, ainda mantemos Matriz A em sua forma contínua, e não em sua versão discretizada. Durante o treinamento, a representação contínua é discretizada.
Agora que temos uma fórmula para a representação discretizada, vamos explorar como realmente contagem O modelo.
representação recursiva
Nosso SSM discretizado nos permite construir o problema em uma etapa de tempo específica, em vez de em um sinal contínuo. Como vimos anteriormente nas RNNs, os métodos recursivos são muito úteis aqui.
Se considerarmos etapas de tempo discretas em vez de sinais contínuos, poderemos reformular o problema usando etapas de tempo:
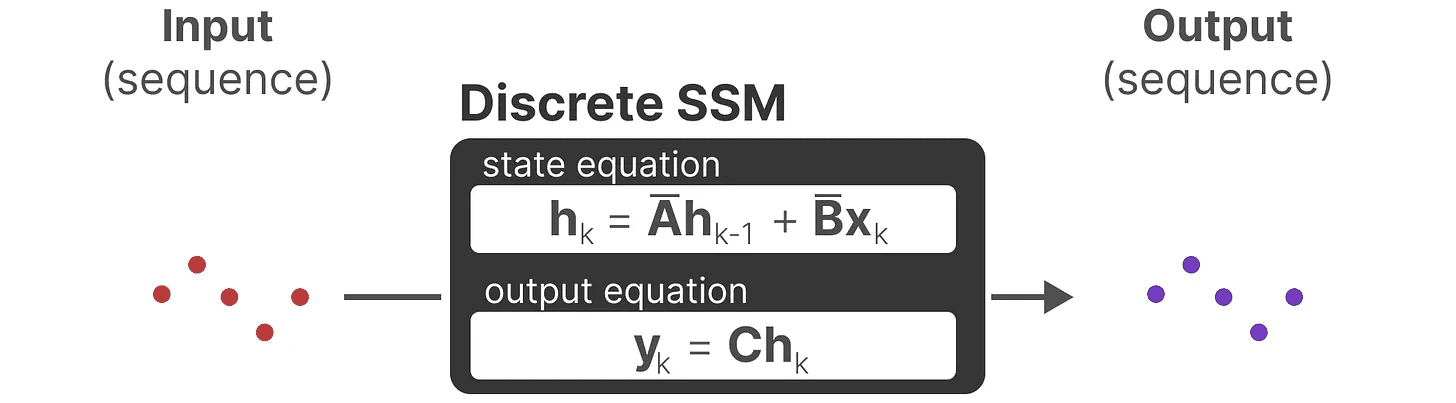Em cada etapa de tempo, calculamos a entrada atual (Bxₖ) como isso afeta o estado anterior (Ahₖ₋₁) e, em seguida, calcular a saída prevista (Chₖ).
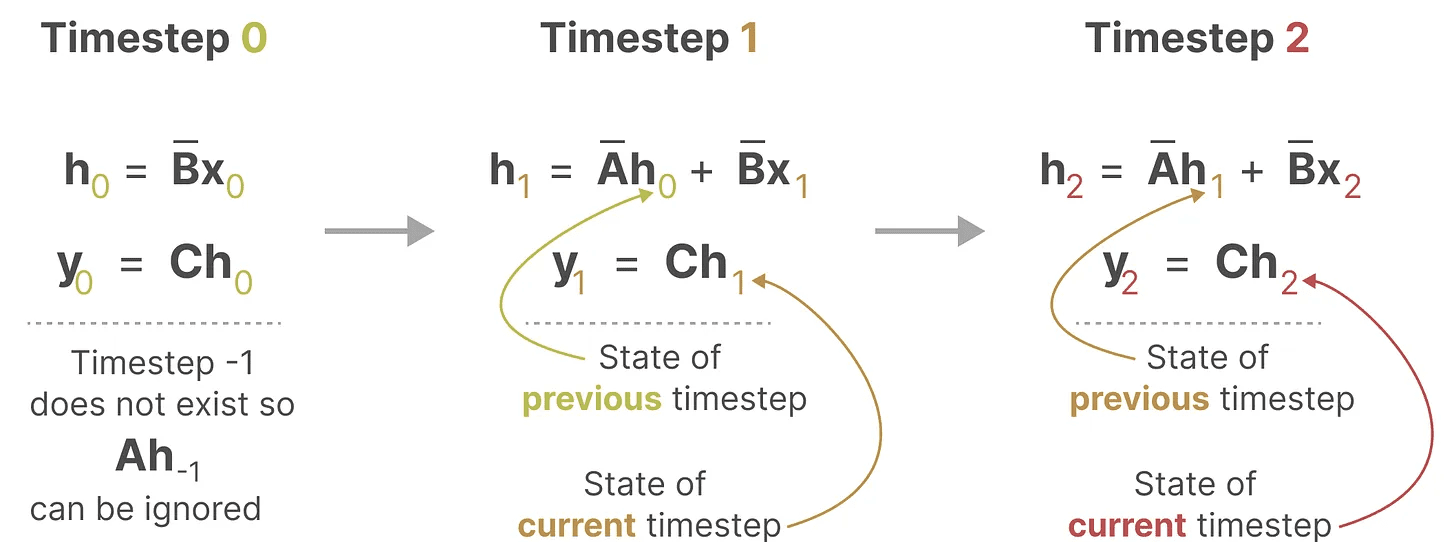Essa representação já deve ser familiar para você! Podemos analisá-la como fizemos com o tratamento anterior dos RNNs.
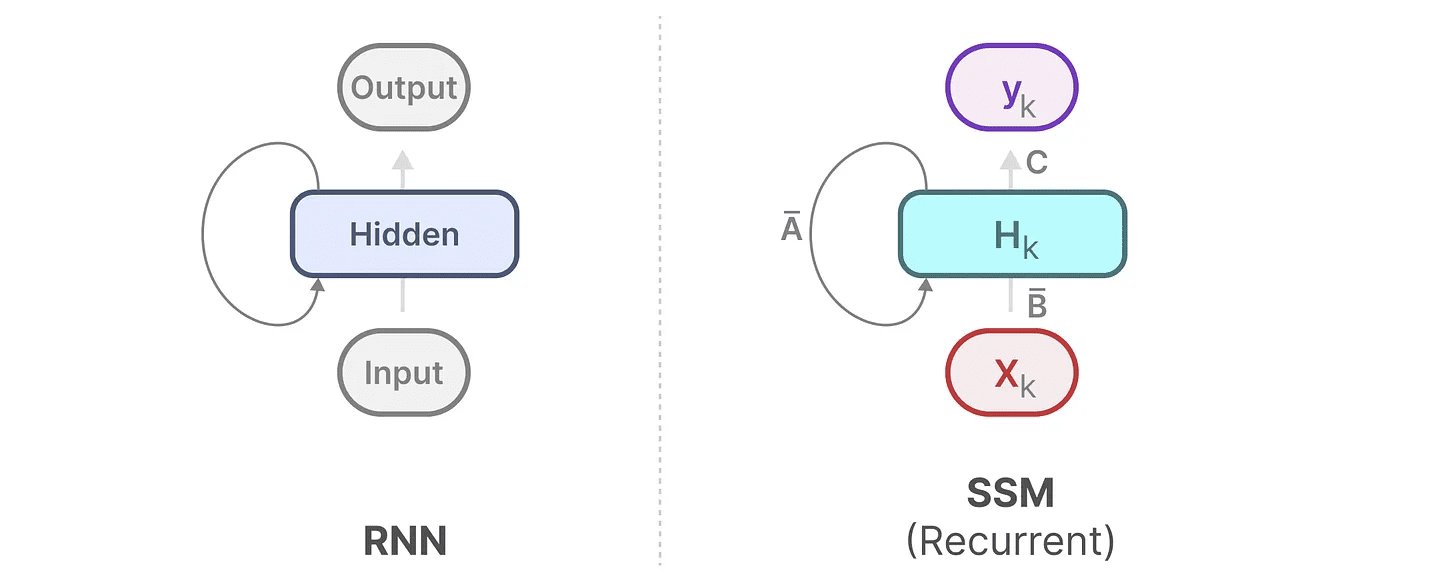Podemos expandir (ou expandir em uma série de etapas de tempo) da seguinte forma:
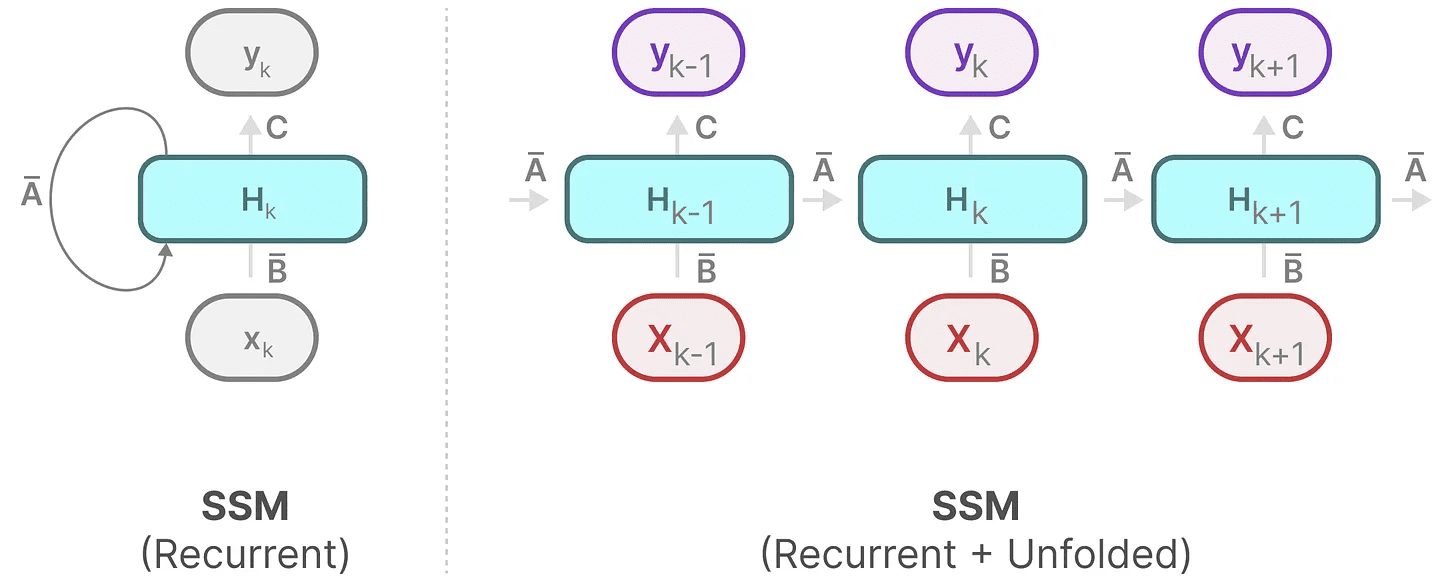Observe que podemos usar uma versão discretizada disso usando a abordagem básica de uma RNN.
representação de convolução (matemática)
Podemos usar a convolução para representar o SSM. Lembre-se de que, nas tarefas clássicas de reconhecimento de imagens, aplicamos filtros (núcleos) para extrair recursos agregados:
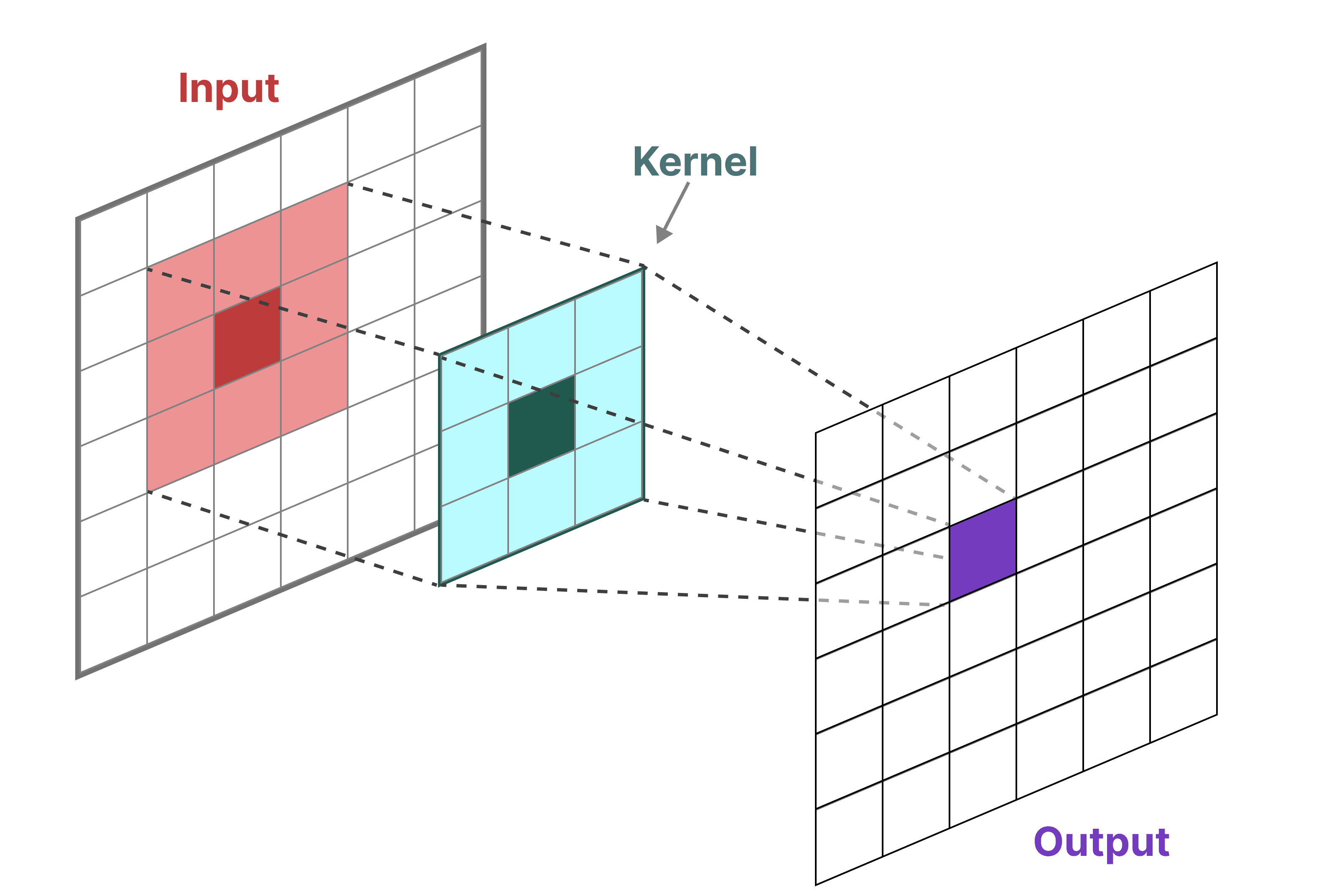Como estamos lidando com texto e não com imagens, precisamos usar uma visualização unidimensional:
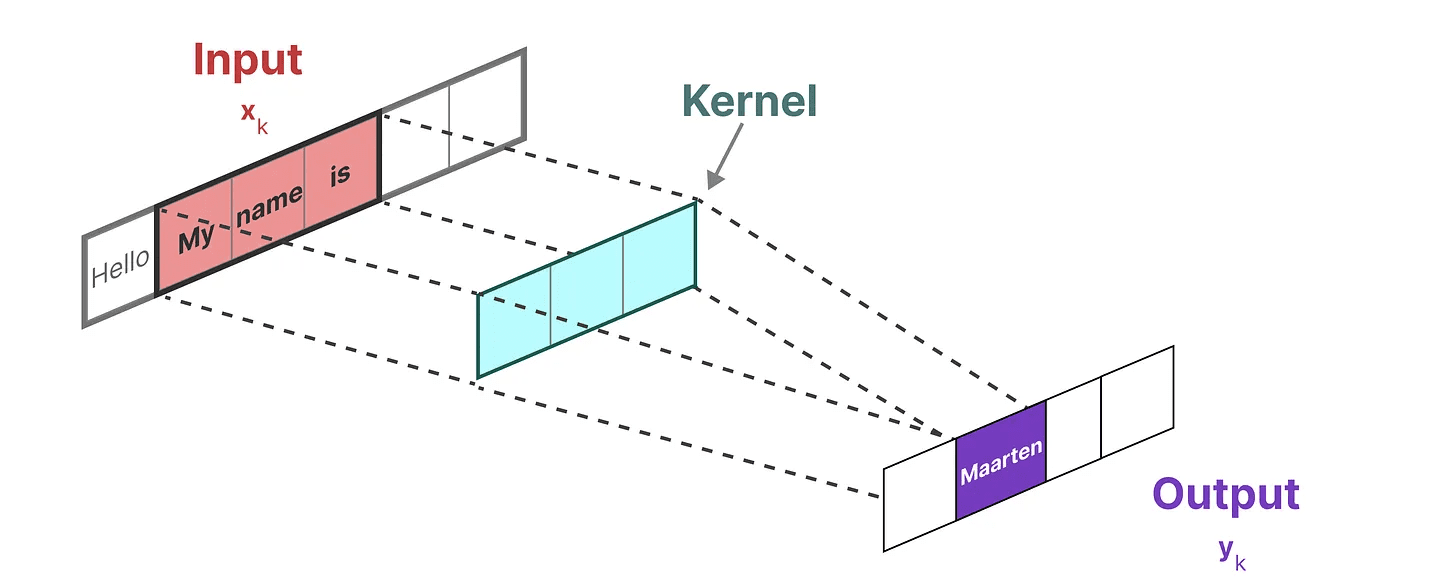O núcleo que usamos para representar esse "filtro" é derivado da fórmula SSM:
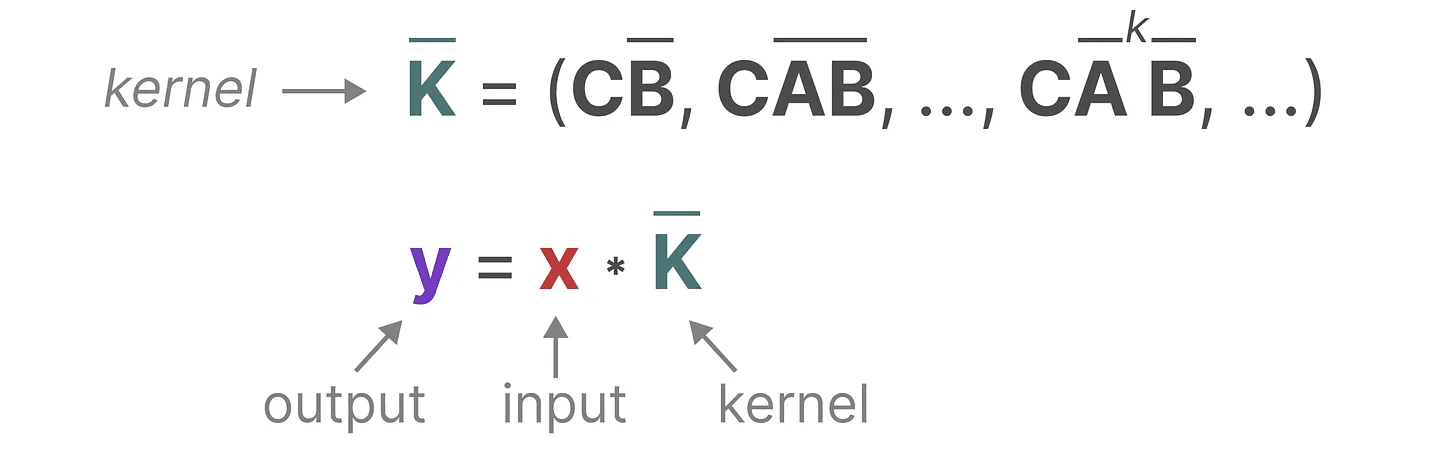Vamos ver o que esse núcleo faz na prática. Assim como a convolução, podemos usar o kernel SSM para percorrer cada conjunto de tokens e calcular a saída:
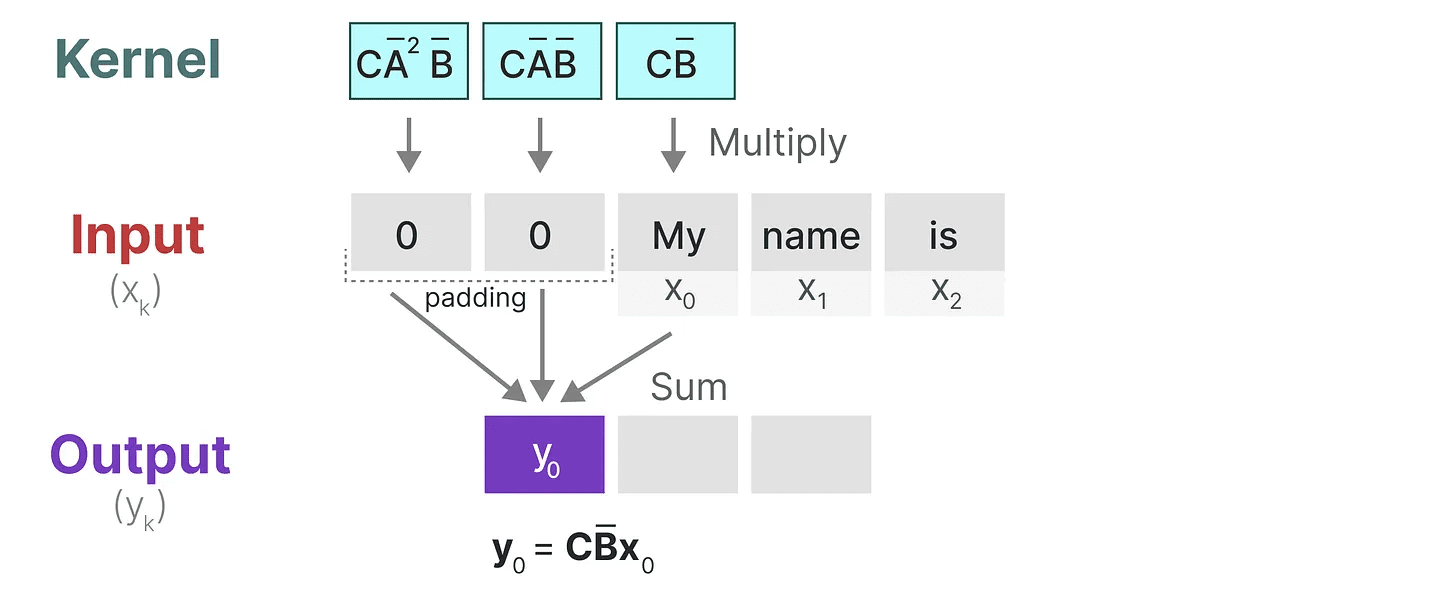Isso também demonstra o efeito que o preenchimento pode ter no resultado. Alterei a ordem do preenchimento para melhorar a visualização, mas normalmente aplicamos o preenchimento no final da frase.
Na próxima etapa, o núcleo se move uma vez para executar a próxima etapa do cálculo:
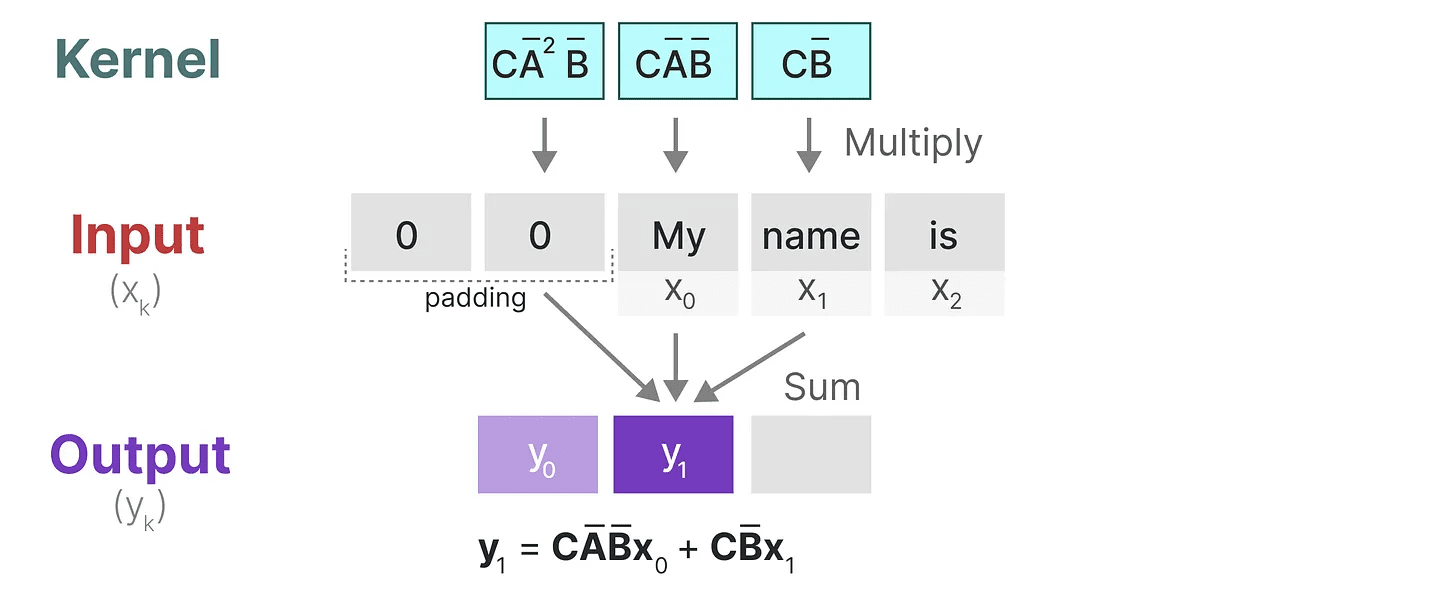Na última etapa, podemos ver o efeito completo do kernel:
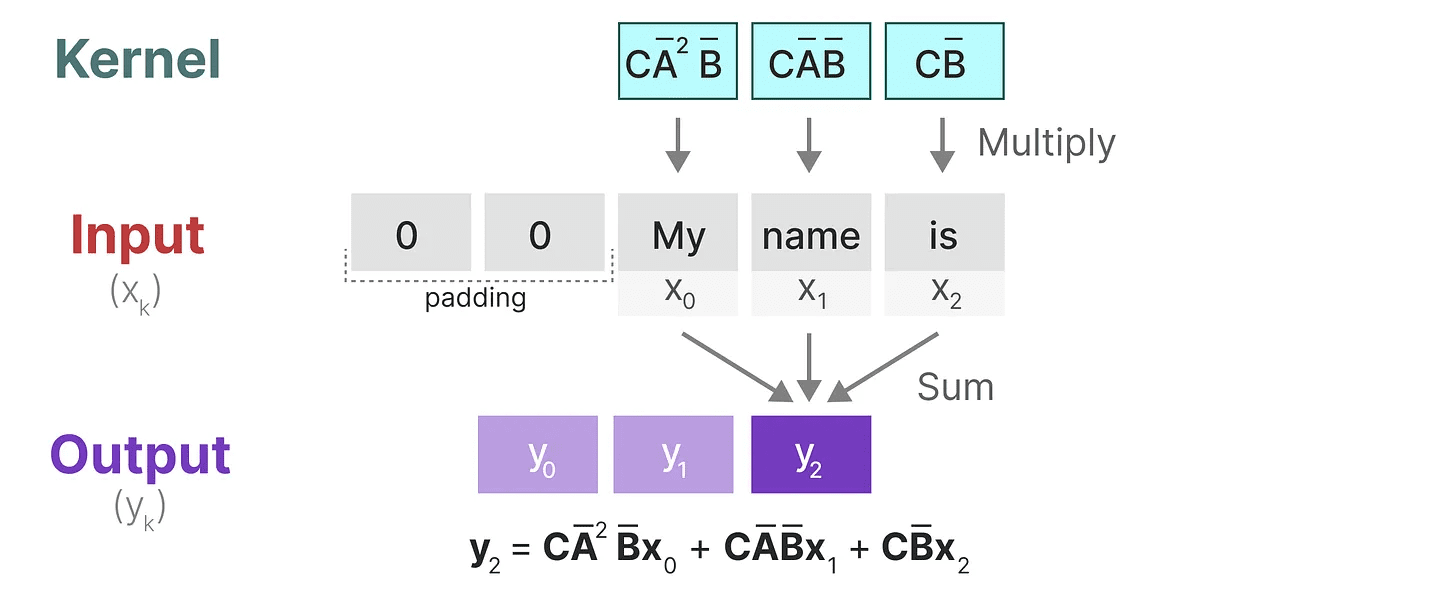Uma das principais vantagens de representar as SSMs como convoluções é que elas podem ser treinadas em paralelo, como as redes neurais convolucionais (CNNs). Entretanto, devido ao tamanho fixo do kernel, sua inferência não é tão rápida e sem restrições quanto as RNNs.
Três tipos de representação
Essas três representações -progressãoerecursivo (cálculo) responder cantando convolução Cada um tem vantagens e desvantagens diferentes:
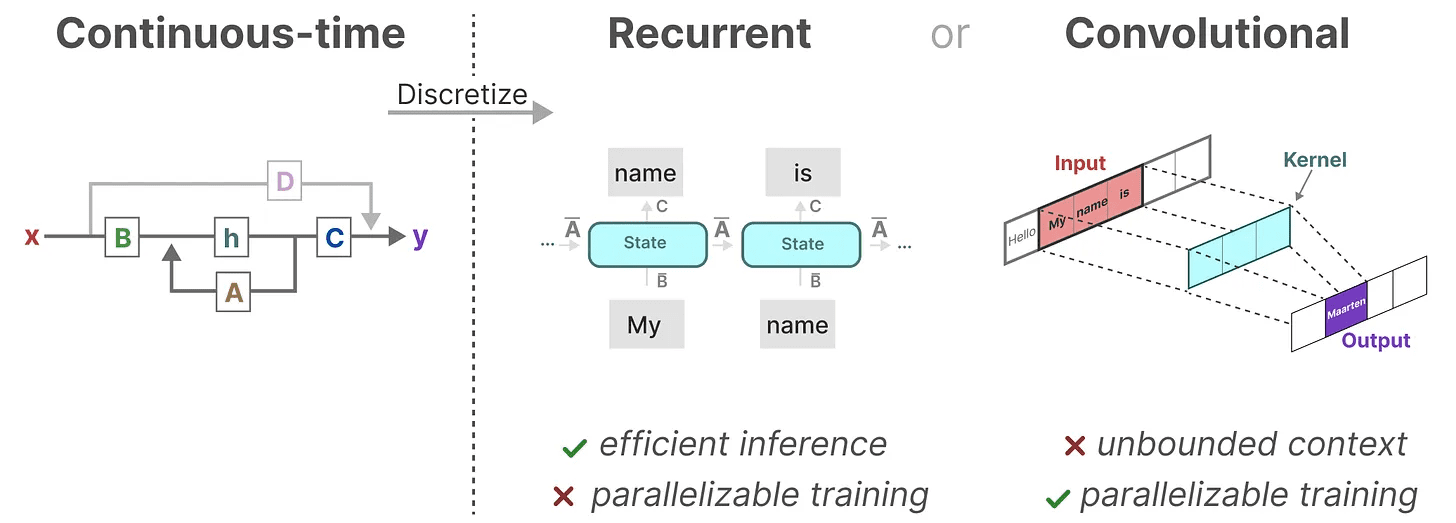É interessante notar que agora podemos usar SSMs recursivos para inferência eficiente enquanto usamos SSMs convolucionais para treinamento paralelo.
Usando essas representações, podemos usar um truque inteligente para escolher uma representação com base na tarefa. Durante o treinamento, usamos uma representação convolucional que pode ser paralelizada, enquanto durante a inferência usamos uma representação recursiva eficiente:
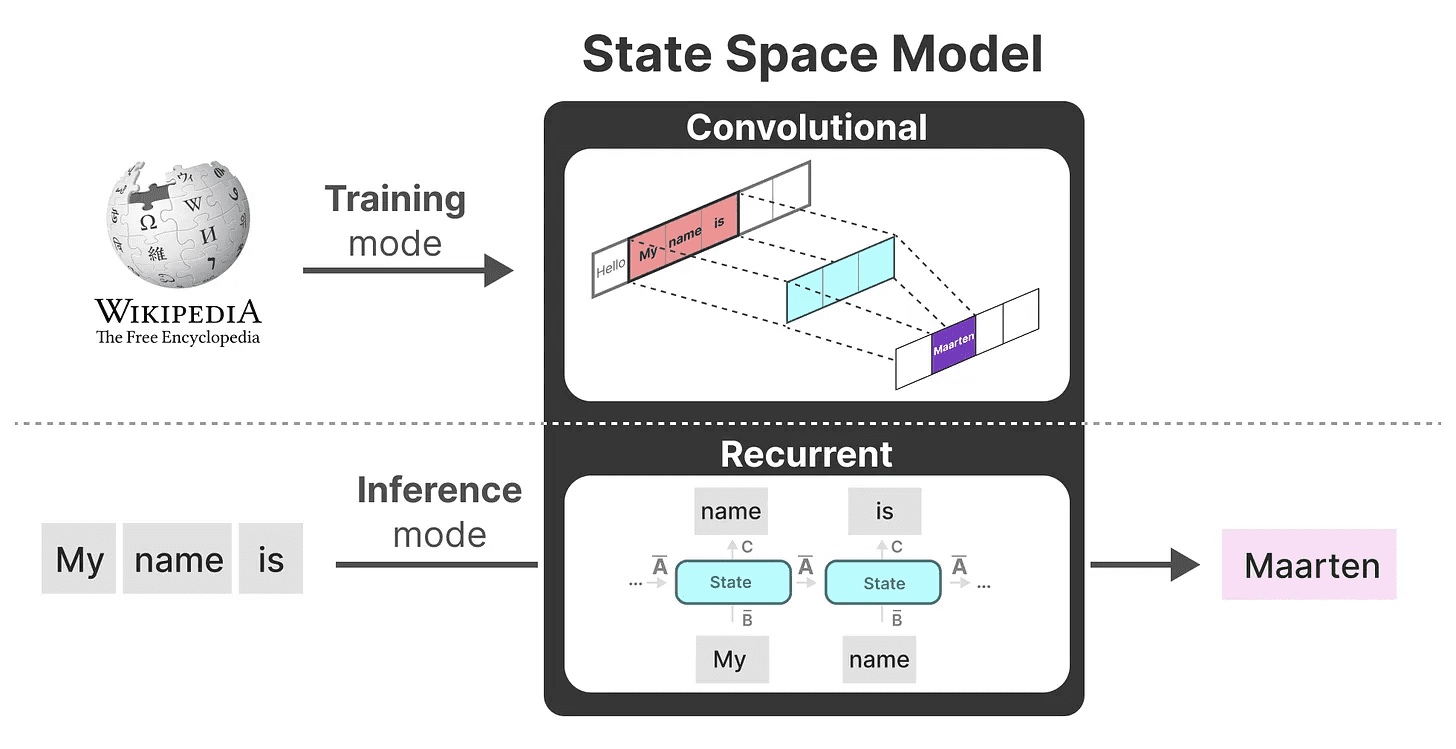Esse modelo é conhecido como Camada de espaço de estado linear (LSSL). 2
Essas representações compartilham uma propriedade importante, a saberinvariante de tempo linear (matemática)（LTI indica os parâmetros do SSM. AeB responder cantando C é fixo em todas as etapas de tempo. Isso significa que a matriz AeB responder cantando C é o mesmo para todos os tokens gerados.
Em outras palavras, qualquer que seja a sequência que você dê ao SSM.AeB responder cantando C Os valores de todos eles permanecem os mesmos. Temos uma representação estática que não se importa com o conteúdo.
Antes de explorar como o Mamba resolve esse problema, vamos explorar a última peça do quebra-cabeça - oMatriz A.
matrizes A importância de
Sem dúvida, um dos aspectos mais importantes da fórmula do SSM é que o Matriz A. Como vimos anteriormente na representação recursiva, ele captura informações sobre o anterior informações sobre o estado para construir o renovado Status.
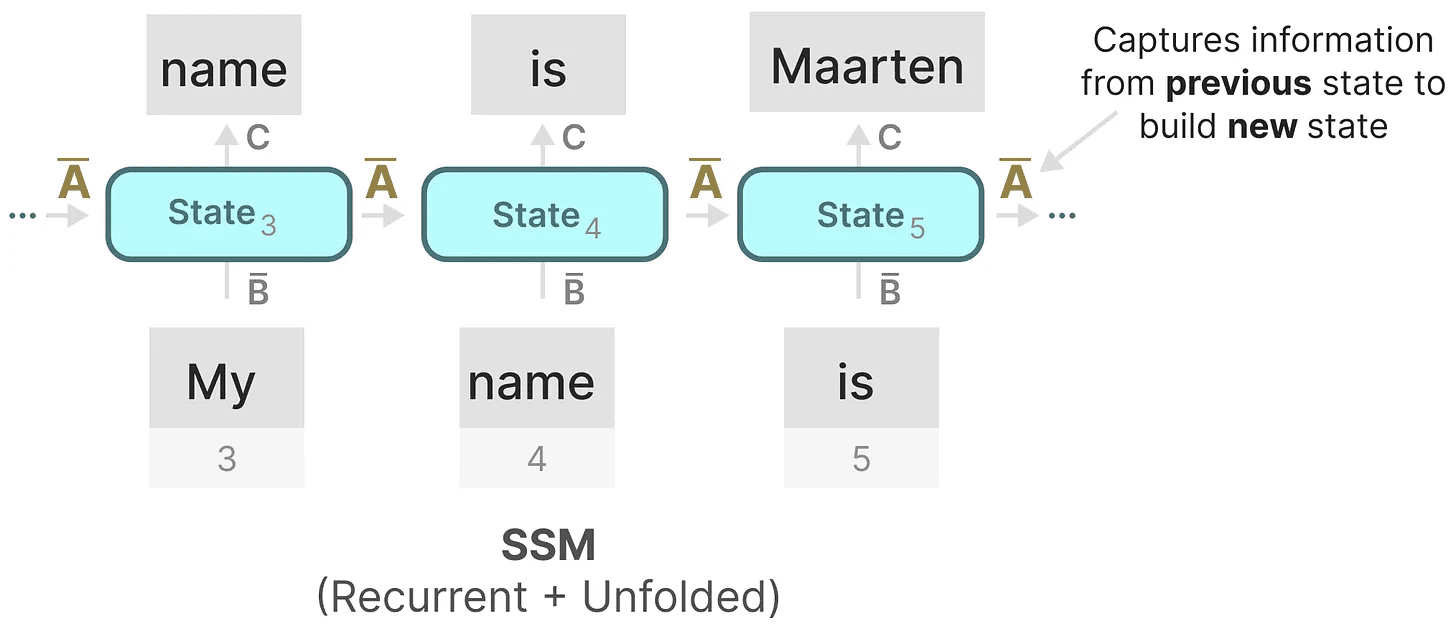Essencialmente.Matriz A Gerar um estado oculto:
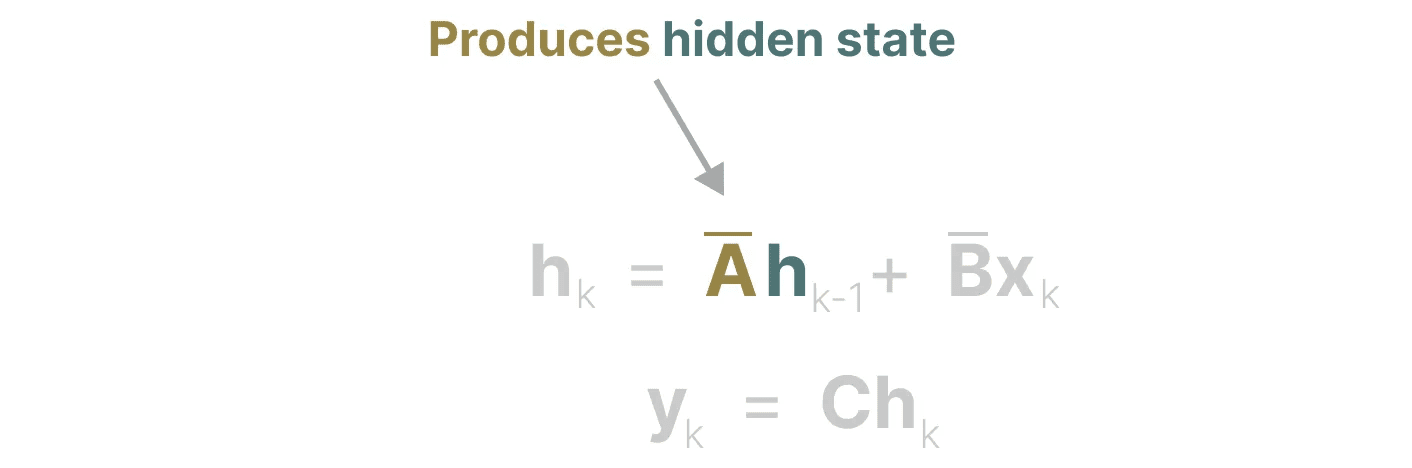Portanto, criar Matriz A pode determinar se podemos nos lembrar de apenas alguns tokens anteriores ou capturar todos os tokens que vimos até o momento. especialmente no contexto da representação recursiva, que apenas lembra que Estado anterior.
Como criar de uma forma que retenha muita memória (tamanho do contexto) matriz A?
Usamos o Hungry Hungry Hippo! ou HiPPO3 para realizaryour (honorífico)escadas como (em que medida)termo (matemática) colocar-se nas mãos defilme sorteO operator.HiPPO tenta compactar todos os sinais de entrada que viu até o momento em um vetor de coeficientes.
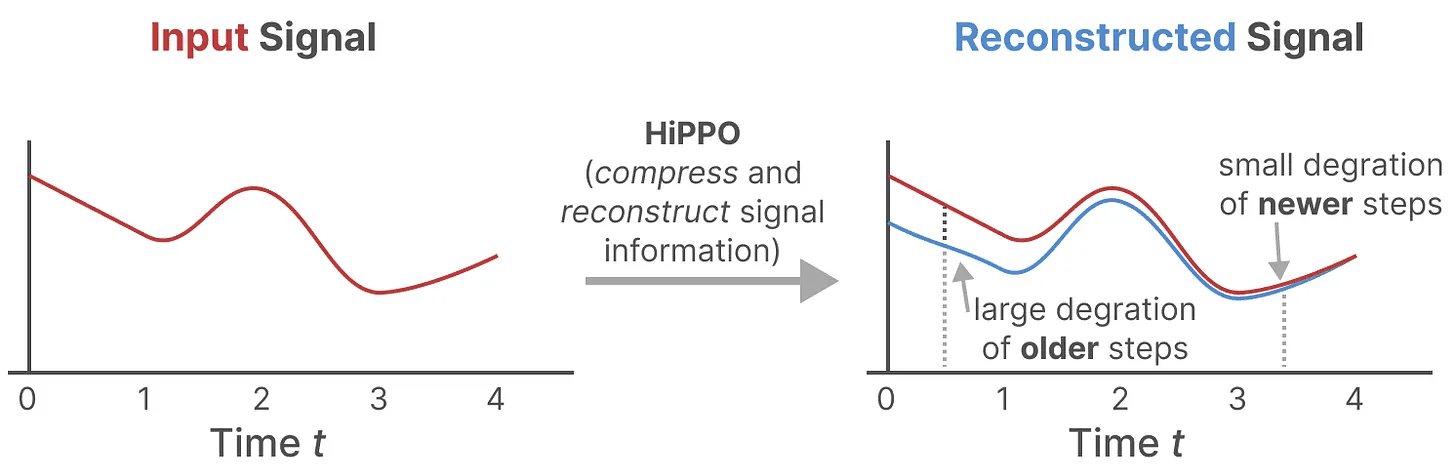Ele usa matriz A para construir uma representação de estado que capture melhor os tokens recentes e diminua os tokens mais antigos:
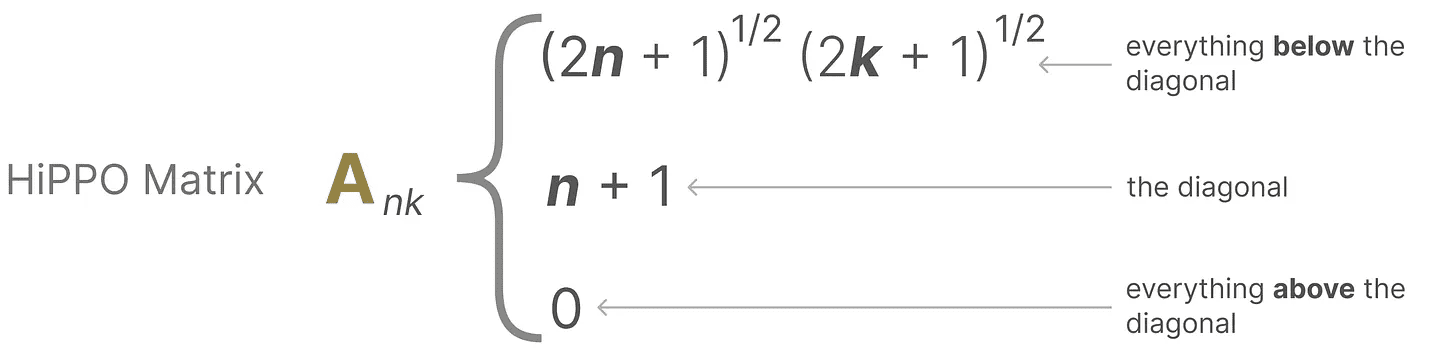Suponha que tenhamos um quadrado matriz AIsso nos dá:
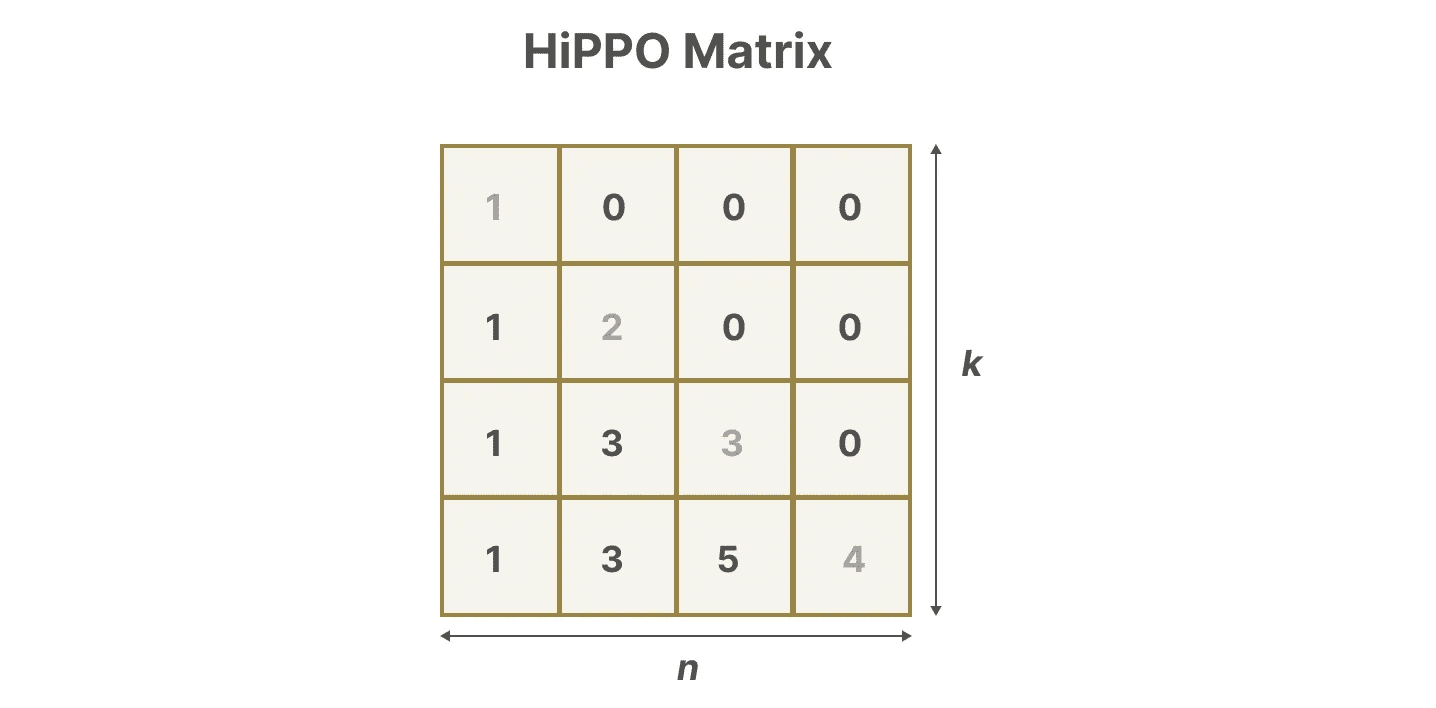Construindo com o HiPPO matriz A provou ser muito melhor do que inicializá-lo em uma matriz aleatória. Portanto, ele é melhor na reconstrução da atualização O aspecto da sinalização (token mais próximo) é mais importante do que mais antigos O sinal (token inicial) é mais preciso.
A ideia central da matriz HiPPO é gerar um estado oculto que se lembre de seu histórico.
Matematicamente, ele faz isso rastreando Polinômio de Legendre para conseguir isso, o que permite que ele se aproxime de todos os registros históricos.4
A HiPPO é então aplicada às representações recursivas e convolucionais que vimos anteriormente para lidar com as dependências de longo alcance. O resultado. Espaço de estado estruturado para sequências (S4)A classe SSM é uma classe de SSM que pode lidar eficientemente com sequências longas.5
Ele consiste em três partes:
- modelo de espaço de estado
- HiPPO para processamento dependência de longa distância
- A discrição é usada para criar recursivo (cálculo) responder cantando convolução indicar
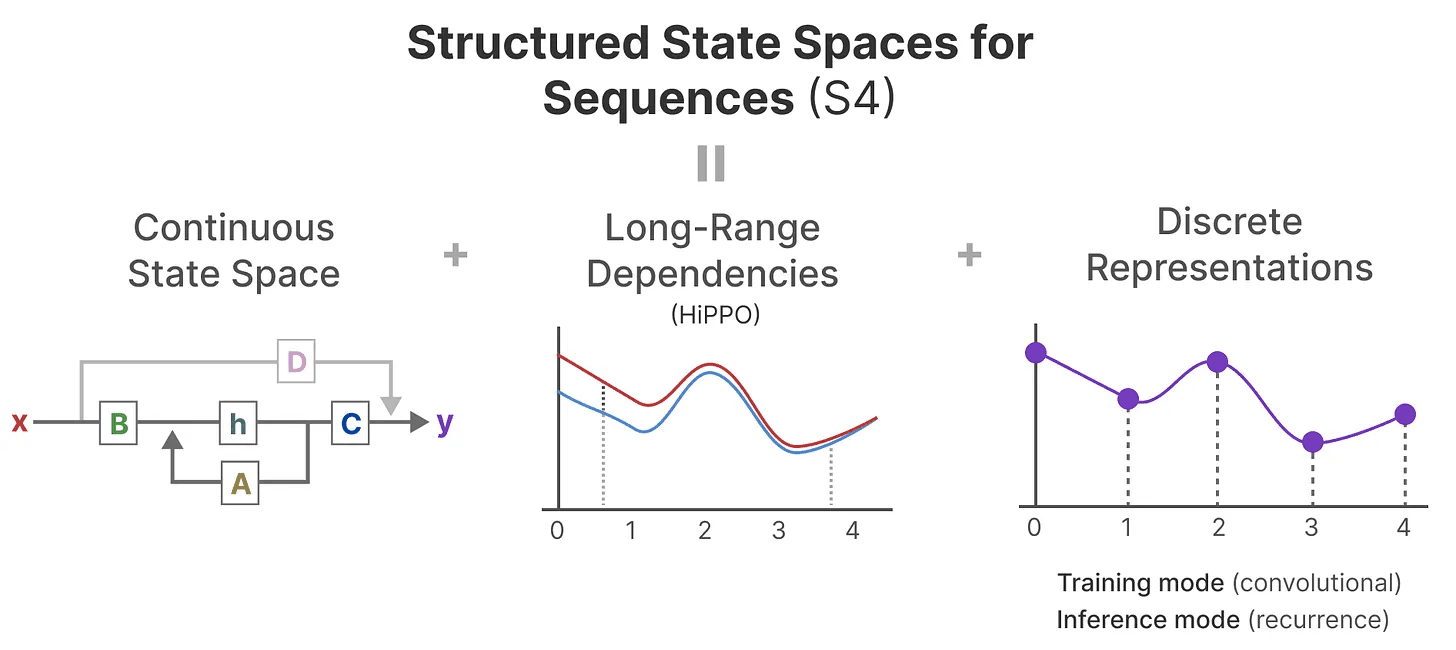Esse tipo de SSM tem várias vantagens, dependendo da representação escolhida (recursiva vs. convolucional). Ele também pode lidar com sequências de texto longas e armazenar memórias de forma eficiente por ser baseado em matrizes HiPPO.
tomar nota deSe você quiser entender melhor como calcular a matriz HiPPO e criar seu próprio modelo S4, recomendo a leitura de S4 anotado.
Parte 3:Mamba - um modelo de espaço de estado seletivo
Finalmente, abordamos todos os conceitos básicos necessários para entender o que torna o Mamba especial. Os modelos de espaço de estado podem ser usados para modelar sequências de texto, mas ainda há várias desvantagens que gostaríamos de evitar.
Nesta seção, discutiremos as duas principais contribuições do Mamba:
- um tipo de Algoritmo de varredura seletivapermitindo que o modelo filtre as informações (in)relevantes
- um tipo de Algoritmos com reconhecimento de hardwarepor varredura paralelaefusão de kernel responder cantando recalcular para armazenar resultados (intermediários) com eficiência.
Juntos, esses dois criam o Modelagem seletiva de espaço de estado talvez S6 modelo que pode ser usado, como a autoatenção, para criar Bloqueio Mamba.
Antes de explorar essas duas principais contribuições, vamos primeiro explorar por que elas são necessárias.
Qual é o problema que está sendo tentado resolver?
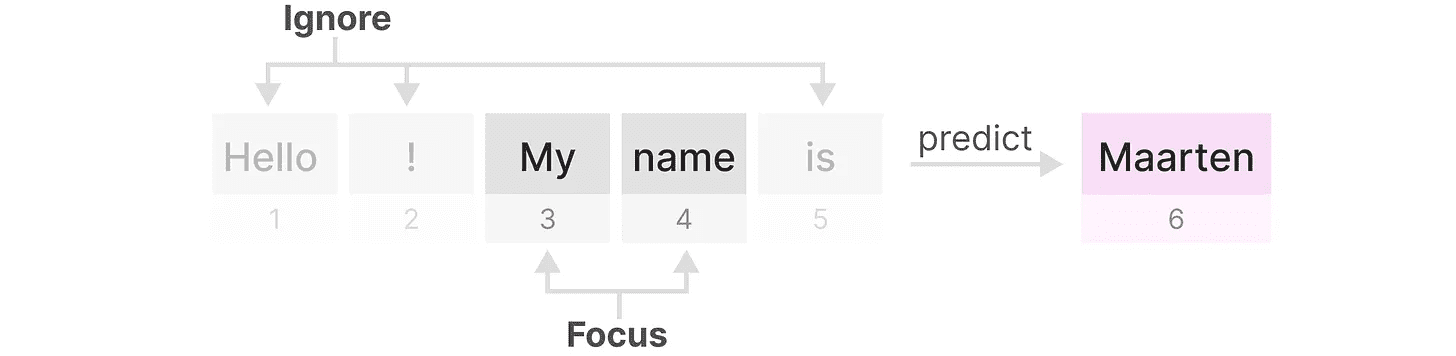
Os modelos de espaço de estado, mesmo os S4 (modelos de espaço de estado estruturado), têm um desempenho ruim em determinadas tarefas importantes na modelagem e geração de linguagem, a saber Capacidade de se concentrar ou ignorar entradas específicas.
Podemos ilustrar isso com duas tarefas sintéticas, a saber cópia seletiva responder cantando cabeçote do indutor.
existir cópia seletiva O objetivo do SSM em uma tarefa é copiar as partes de entrada e produzi-las em ordem:
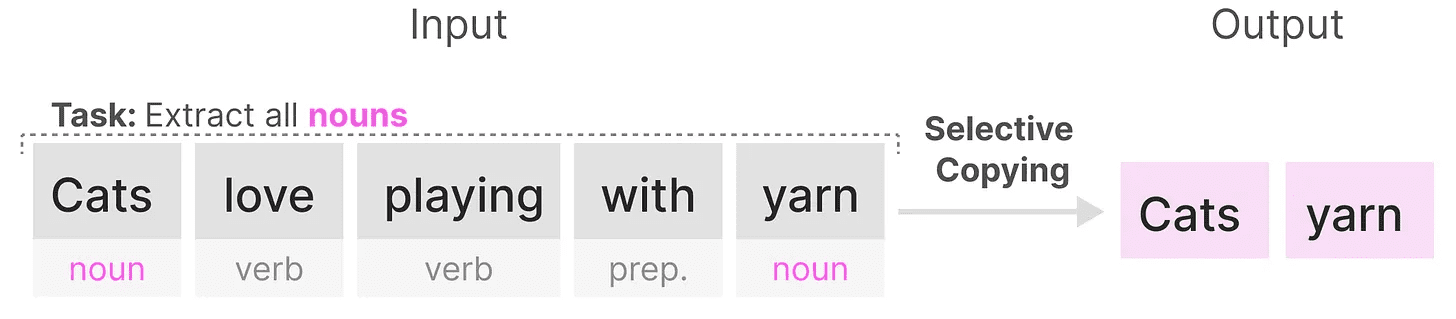Entretanto, como o SSM é Invariante de tempo linear(usado em uma expressão nominal)que ele tem um desempenho ruim nessa tarefa. Como vimos anteriormente, a matriz AeB responder cantando C Cada token gerado é o mesmo para SSM.
Como resultado, o SSM não consegue executar Raciocínio com reconhecimento de conteúdoIsso é um problema porque queremos que o SSM raciocine sobre as entradas (dicas). porque ele trata cada token igualmente devido a uma matriz fixa de A, B e C. Isso é um problema porque queremos que o SSM raciocine sobre as entradas (dicas).
O SSM tem um desempenho ruim em outra tarefa, a de cabeçote do indutorcujo objetivo é reproduzir os padrões encontrados na entrada:
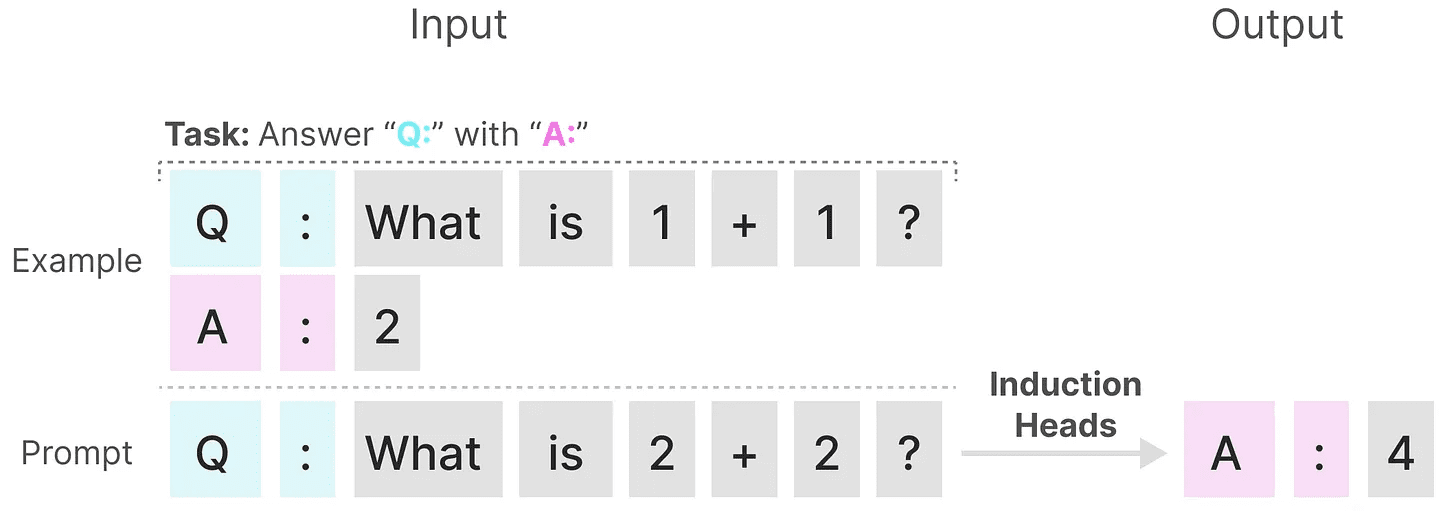No exemplo acima, estamos essencialmente realizando um prompt único no qual tentamos "ensinar" o modelo a usar a mesma dica em cada "Q." depois de fornecer um "A.". No entanto, como o SSM é invariável no tempo, ele não pode escolher quais tokens anteriores serão recuperados do histórico.
Vamos fazer isso concentrando-nos em Matriz B para ilustrar esse ponto. Independentemente da entrada x O que é.Matriz B é sempre o mesmo, portanto, com x Irrelevante:
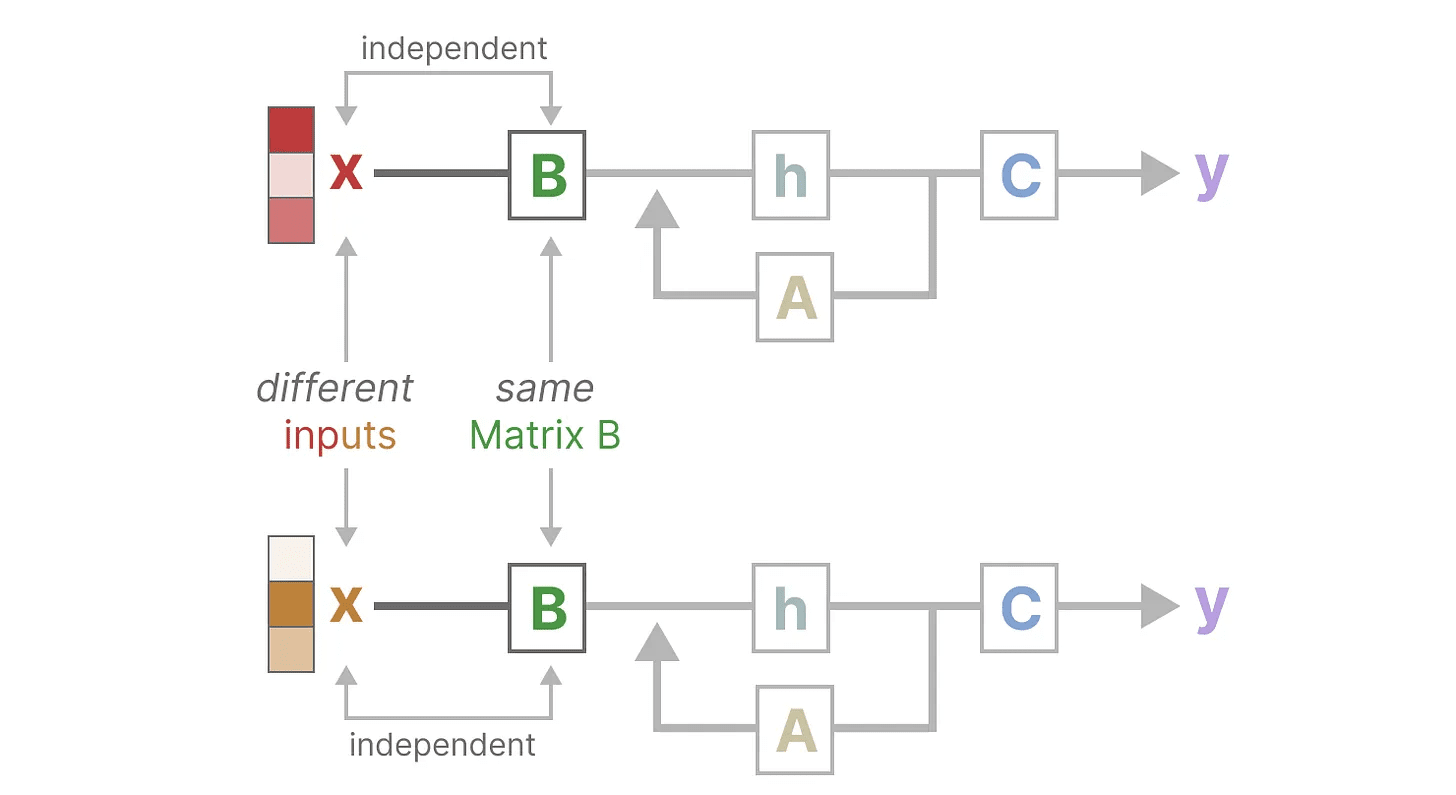Da mesma forma.A responder cantando C também permanece fixo o tempo todo, independentemente da entrada. Isso sugere que o que vimos até agora sobre o SSM estado de não estar funcionando Características.
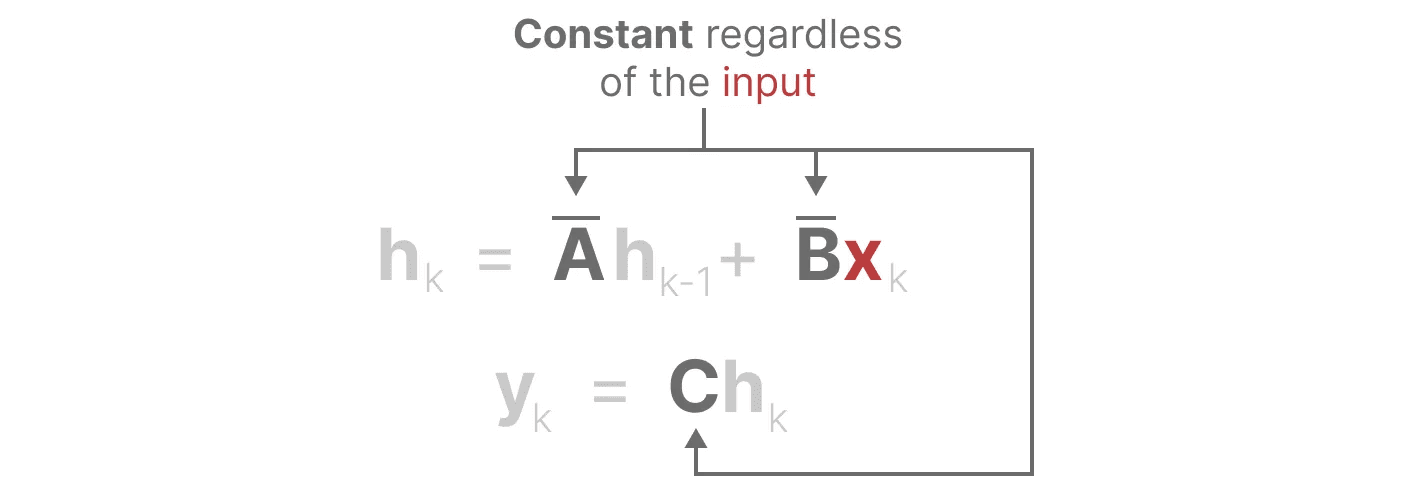Por outro lado, essas tarefas são relativamente simples para o Transformer, pois são baseadas na sequência de entrada dinâmica (ciência) Mudança de atenção. Eles podem "observar" ou "concentrar-se" seletivamente em diferentes partes da sequência.
O desempenho ruim da SSM nessas tarefas ilustra os possíveis problemas da SSM com variação de tempo, matriz AeB responder cantando C A natureza estática do Sentido do conteúdo da questão.
Retenção seletiva de informações
A representação recursiva do SSM cria um estado menor que é muito eficiente porque comprime todo o histórico. Entretanto, comparado ao modelo Transformer, o modelo Transformer não comprime o histórico (por meio da Matriz de Atenção), o que o torna mais capaz.
O objetivo do Mamba é ter o melhor dos dois mundos. Um estado pequeno que seja tão poderoso quanto um estado transformador:
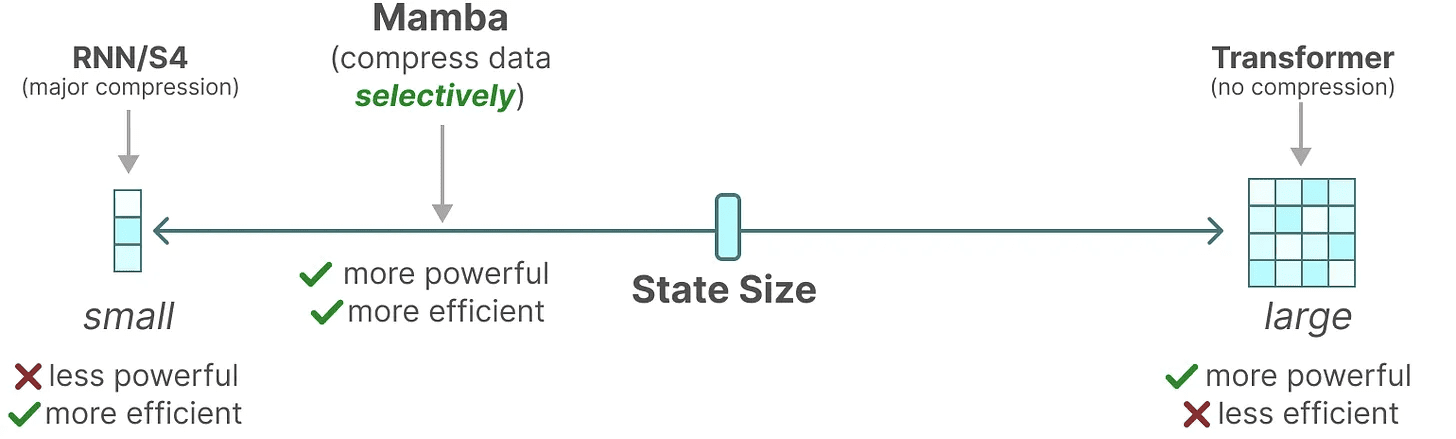Como mencionado acima, ele faz isso compactando seletivamente os dados em estados. Quando você tem uma frase de entrada, geralmente há alguma informação, como uma palavra de parada, que não faz muito sentido.
Para compactar informações de forma seletiva, precisamos que os parâmetros sejam dependentes da entrada. Para isso, vamos primeiro explorar as dimensões das entradas e saídas do SSM durante o treinamento:
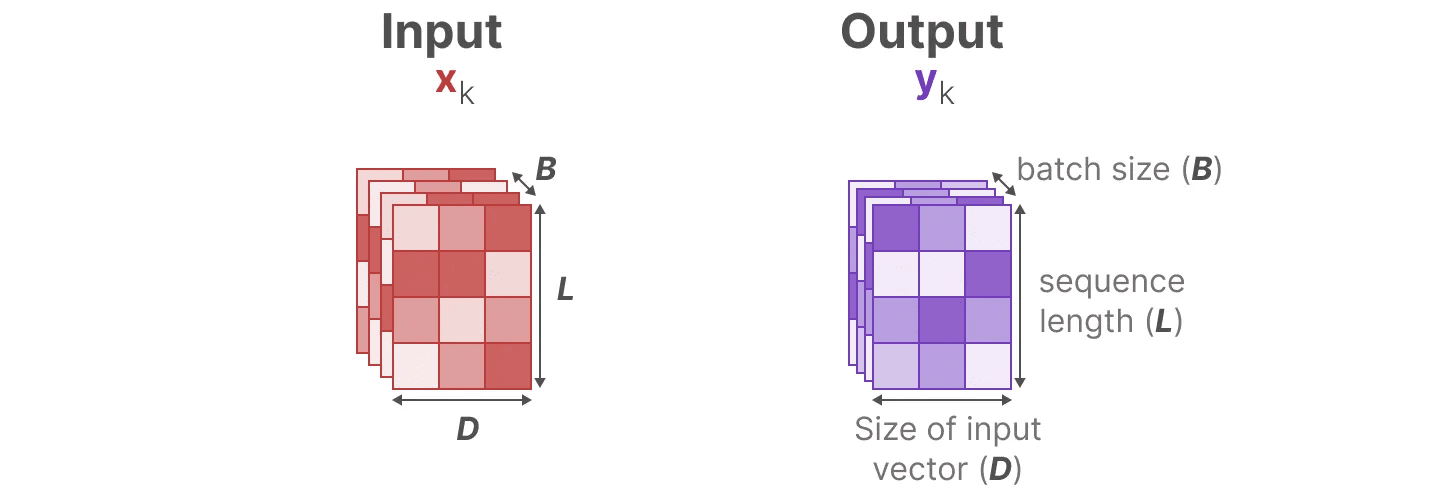No modelo de espaço de estado estruturado (S4), a matriz AeB responder cantando C são independentes dos inputs porque suas dimensões N responder cantando D é estático e não muda.
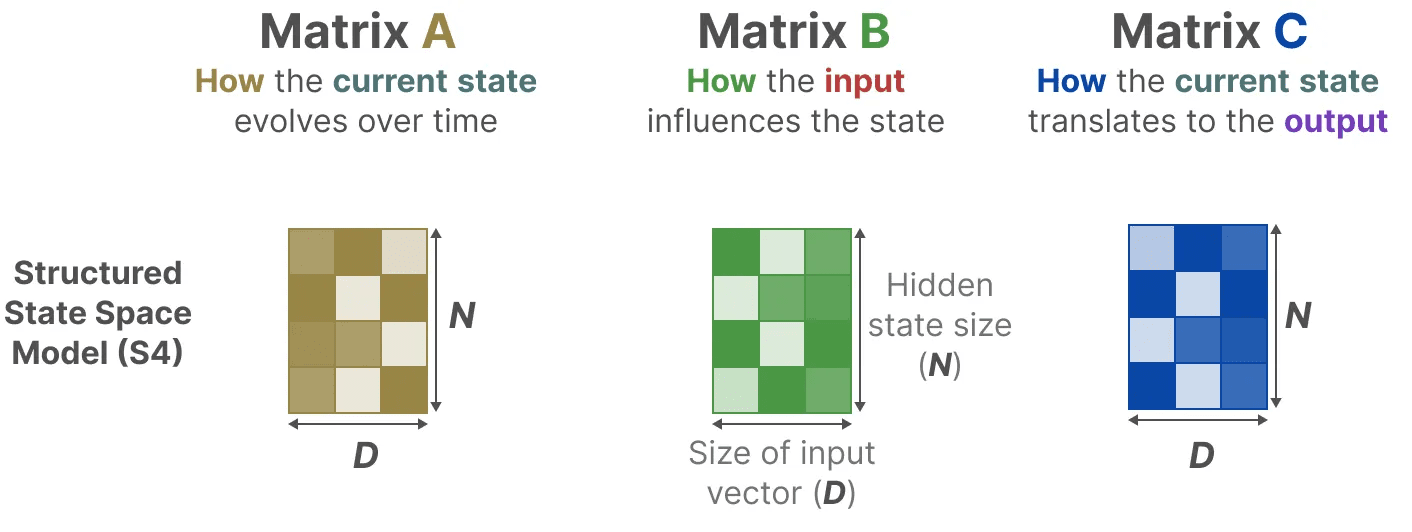Em vez disso, o Mamba, ao combinar o comprimento da sequência de entrada e o tamanho do lote, cria a matriz B responder cantando Cmesmo marca-passo ∆_, dependendo da entrada:
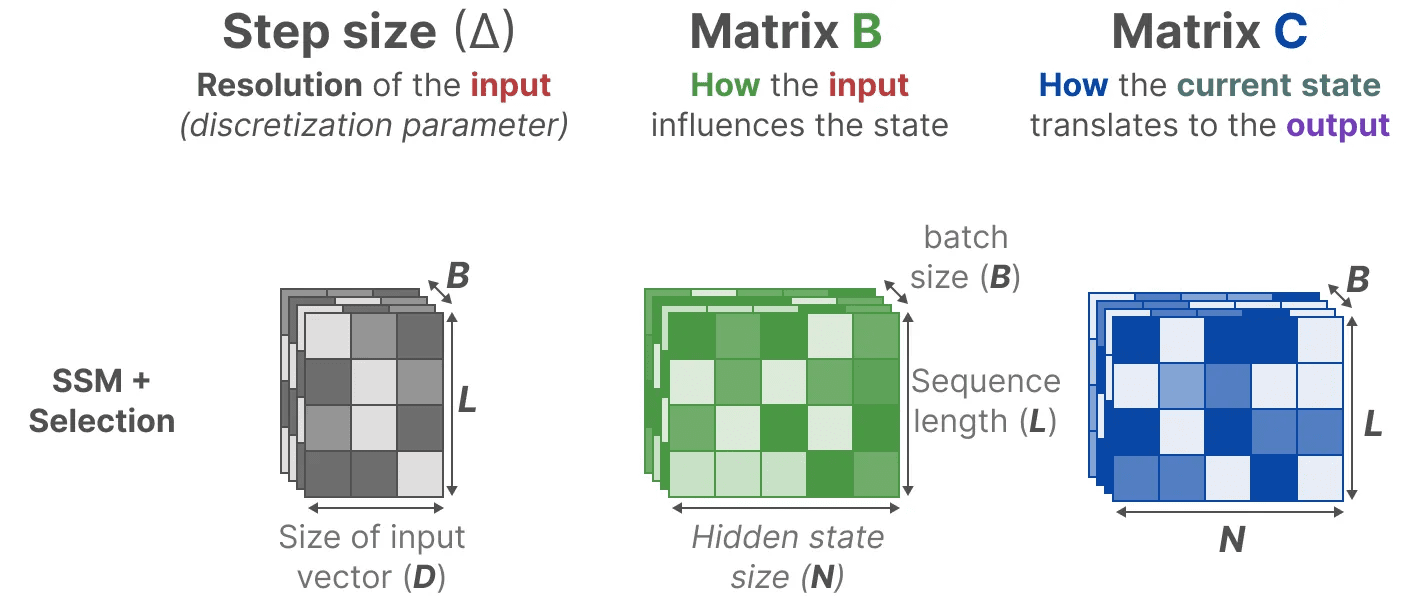Isso significa que, para cada token de entrada, agora temos diferentes B responder cantando C que resolve o problema da percepção do conteúdo!
tomar nota de: Matriz A permanece inalterado porque queremos que o estado em si permaneça estático, mas a maneira como ele é afetado (por meio do B responder cantando C) é dinâmico.
juntos seletivamente Selecione o que deve ser mantido no estado oculto e o que deve ser ignorado, pois agora eles dependem da entrada.
menor marca-passo ∆ leva a ignorar palavras específicas em favor do contexto anterior, enquanto que a maior marca-passo ∆ Em vez disso, o foco está mais no vocabulário de entrada do que no contexto:
operação de escaneamento
Como essas matrizes agora são dinâmica (ciência) s, eles não podem ser computados usando a representação convolucional, que pressupõe um fixação do núcleo de convolução. Só podemos usar representações recursivas, o que perde a vantagem da paralelização proporcionada pela convolução.
Para obter a paralelização, vamos explorar como podemos usar a recursão para calcular a saída:
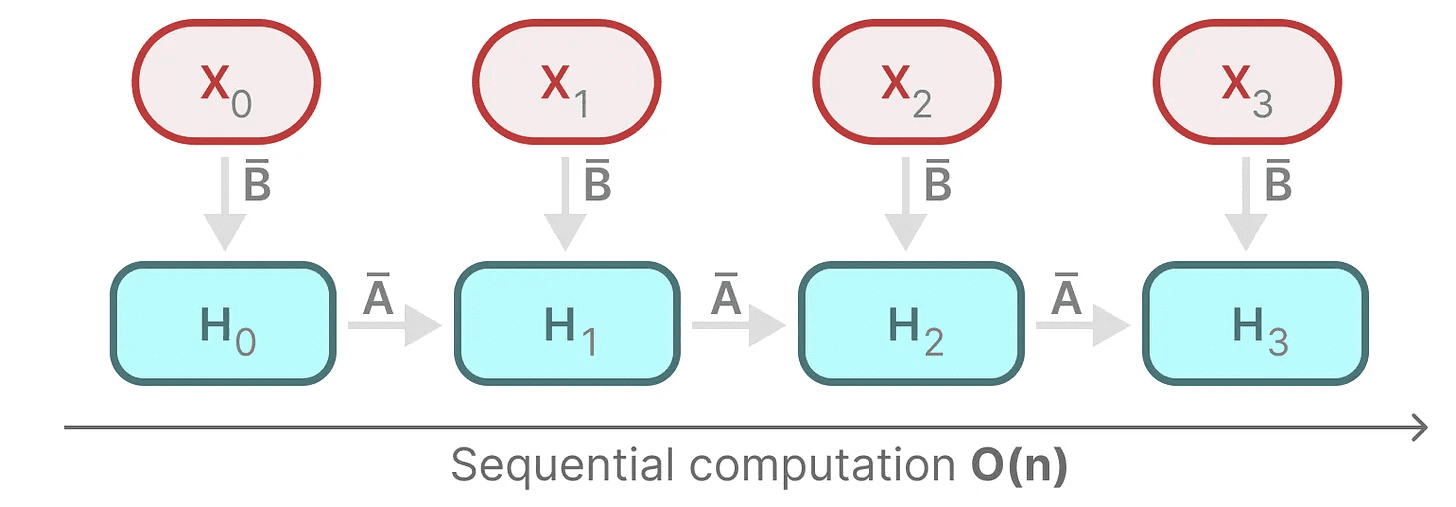Cada estado é o estado anterior (multiplicado por A) com a entrada atual (multiplicada por B) de e. Isso é conhecido como operação de escaneamentoIsso pode ser facilmente calculado com um loop for.
Em contrapartida, a paralelização parece impossível, pois cada estado só pode ser computado depois que um estado anterior estiver disponível. No entanto, o Mamba tornou possível paralelizar o estado de cada estado por meio de varredura paralela Os algoritmos tornam isso possível.
Ele pressupõe que a ordem em que realizamos as operações não é importante, utilizando uma propriedade da lei da união. Assim, podemos calcular a sequência em partes e depois combiná-las iterativamente:
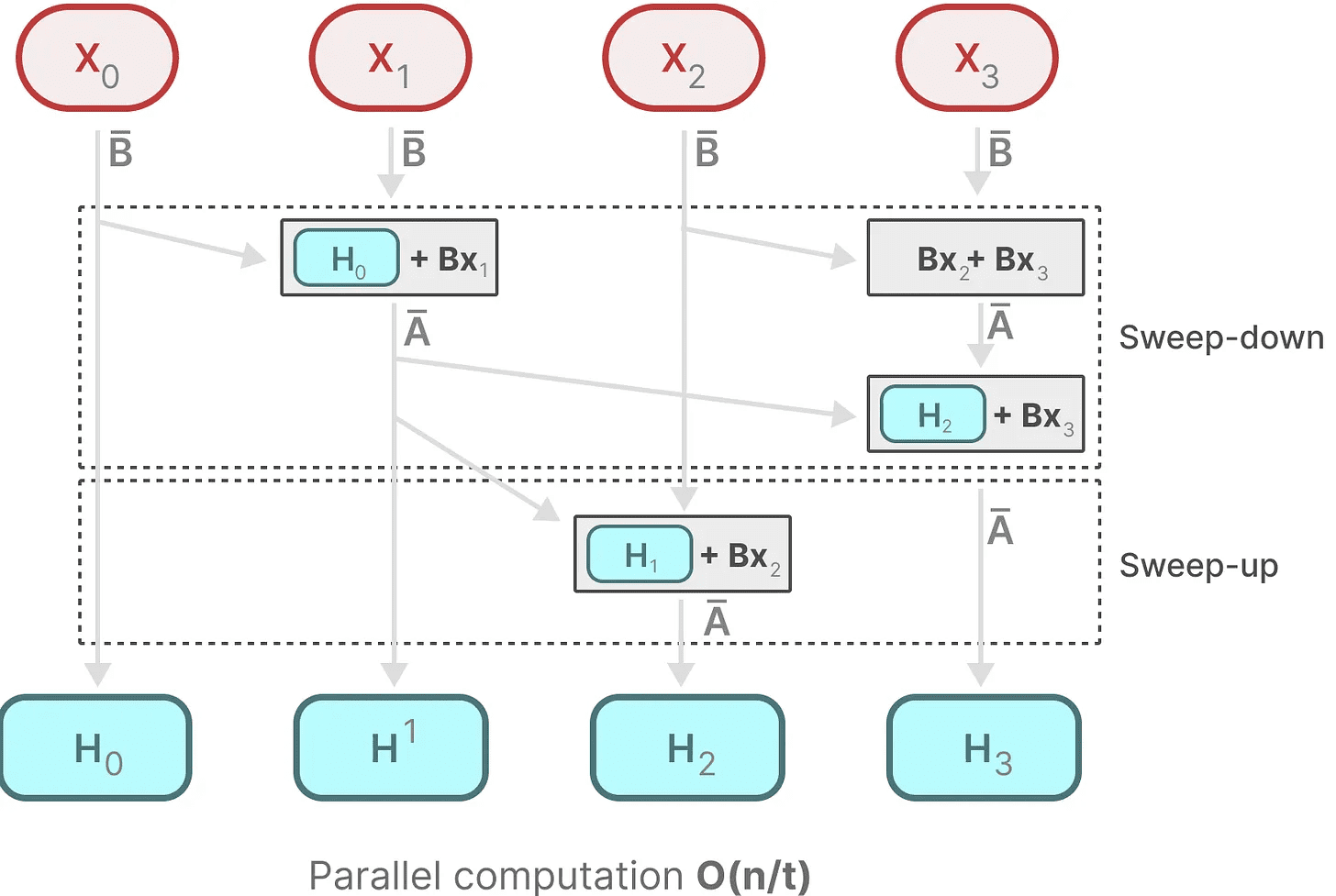matriz dinâmica B responder cantando C e os algoritmos de varredura paralela se unem para criar Algoritmo de varredura seletivapara representar a natureza dinâmica e rápida do uso de representações recursivas.
Algoritmos com reconhecimento de hardware
Uma das desvantagens das GPUs recentes é a velocidade limitada de transferência (IO) entre sua SRAM pequena, mas eficiente, e sua DRAM grande, mas um pouco menos eficiente. A cópia frequente de informações entre a SRAM e a DRAM pode se tornar um gargalo.
O Mamba é semelhante ao Flash Attention, pois tenta limitar o número de viagens da DRAM para a SRAM e vice-versa. Ele faz isso por meio de fusão de kernel A implementação disso permite que o modelo evite a gravação de resultados intermediários e continue realizando o cálculo até que ele seja concluído.
Podemos ver exemplos específicos de alocação de DRAM e SRAM visualizando a arquitetura básica do Mamba:
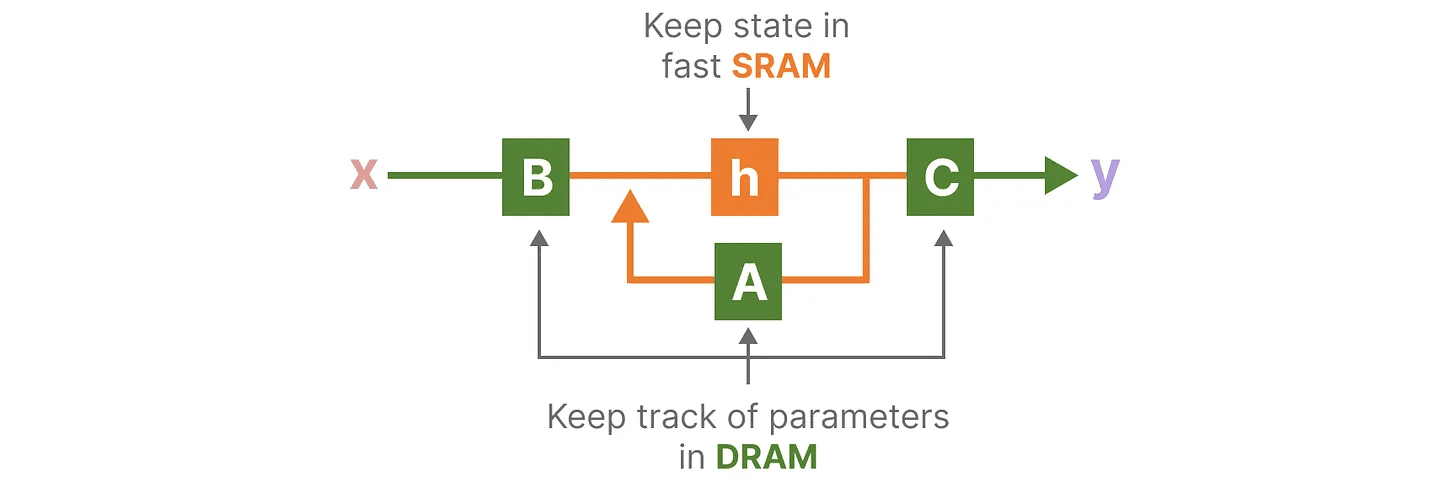Aqui, os seguintes são fundidos em um único kernel:
- A etapa de discretização é a mesma que tamanho do passo ∆
- Algoritmo de varredura seletiva
- junto com C multiplicação
A última parte do algoritmo com reconhecimento de hardware é recomputação.
Os estados intermediários não são salvos, mas são necessários para calcular o gradiente na passagem inversa. Em vez disso, os autores recalculam esses estados intermediários durante a passagem reversa.
Embora isso possa parecer ineficiente, é muito mais barato do que ler todo esse estado intermediário da DRAM relativamente lenta.
Já abordamos todos os componentes de sua arquitetura, que é mostrada abaixo em seu artigo:
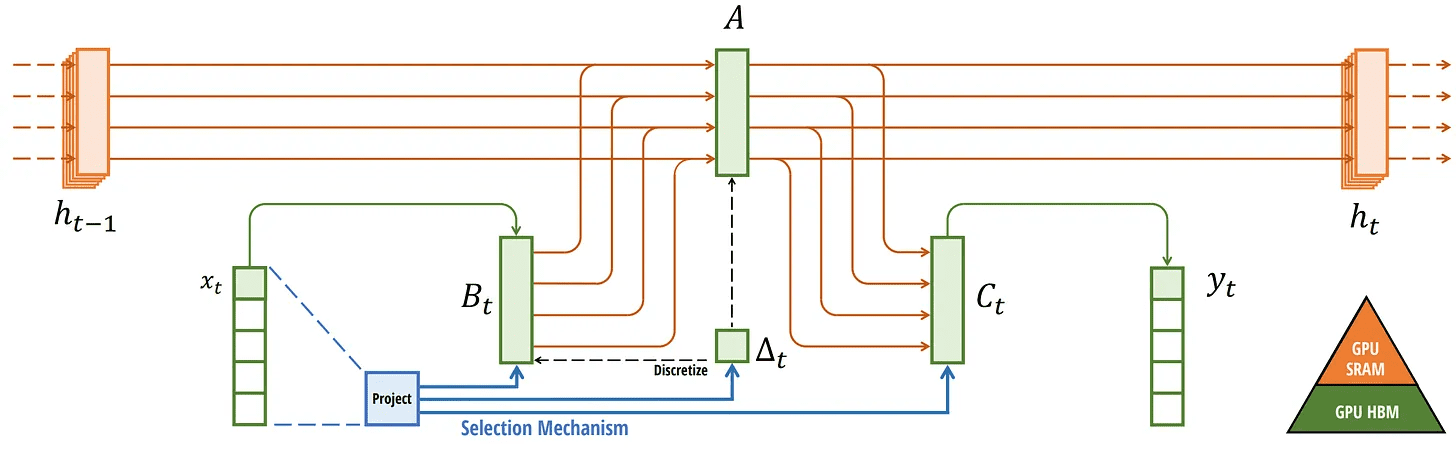SSM seletivo. Recuperado de: Gu, Albert e Tri Dao. "Mamba: modelagem de séries temporais lineares com espaços de estado seletivos". arXiv preprint arXiv:2312.00752 (2023).
Essa arquitetura é frequentemente chamada de SSM seletivo talvez S6 pois é essencialmente um modelo S4 calculado usando o algoritmo de varredura seletiva.
Módulo Mamba
O que exploramos até o momento SSM seletivo pode ser implementado como um módulo, assim como podemos representar a autoatenção em um módulo decodificador.
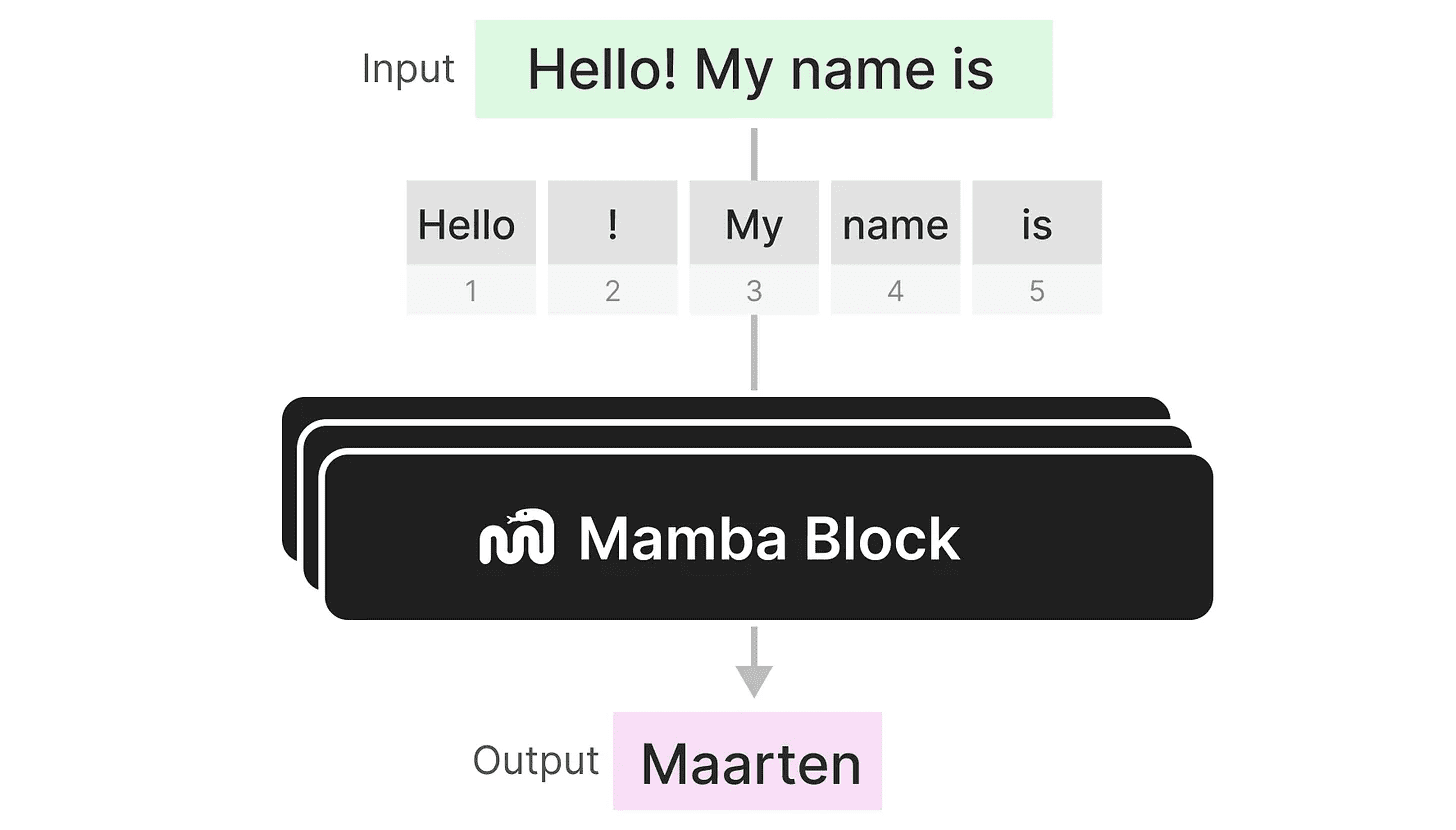Como um decodificador, podemos empilhar vários módulos Mamba e usar sua saída como entrada para o próximo módulo Mamba:
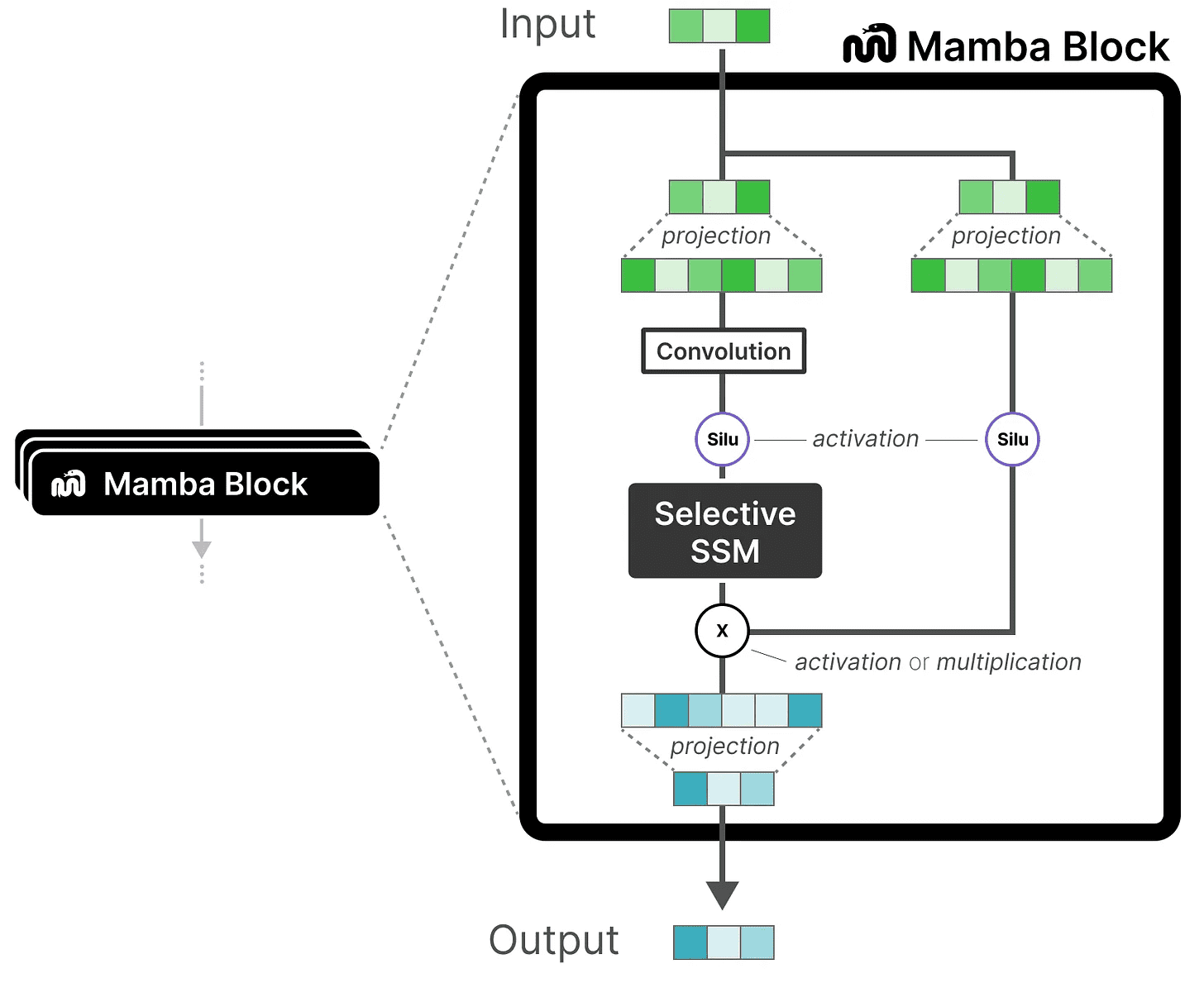Ele começa com uma projeção linear para estender a incorporação de entrada. Em seguida, a SSM seletivo A convolução é aplicada antes para evitar o cálculo de tokens independentes.
SSM seletivo tem as seguintes características:
- aprovar (um projeto de lei ou inspeção etc.) discreto criado SSM recursivo
- matriz A ir em frente HiPPO Inicialização para captura dependência de longo prazo
- Algoritmo de varredura seletiva para comprimir seletivamente as informações
- Algoritmos com reconhecimento de hardware para acelerar os cálculos
Quando analisamos a implementação do código, podemos ampliar ainda mais essa arquitetura e explorar como seria um exemplo de ponta a ponta:
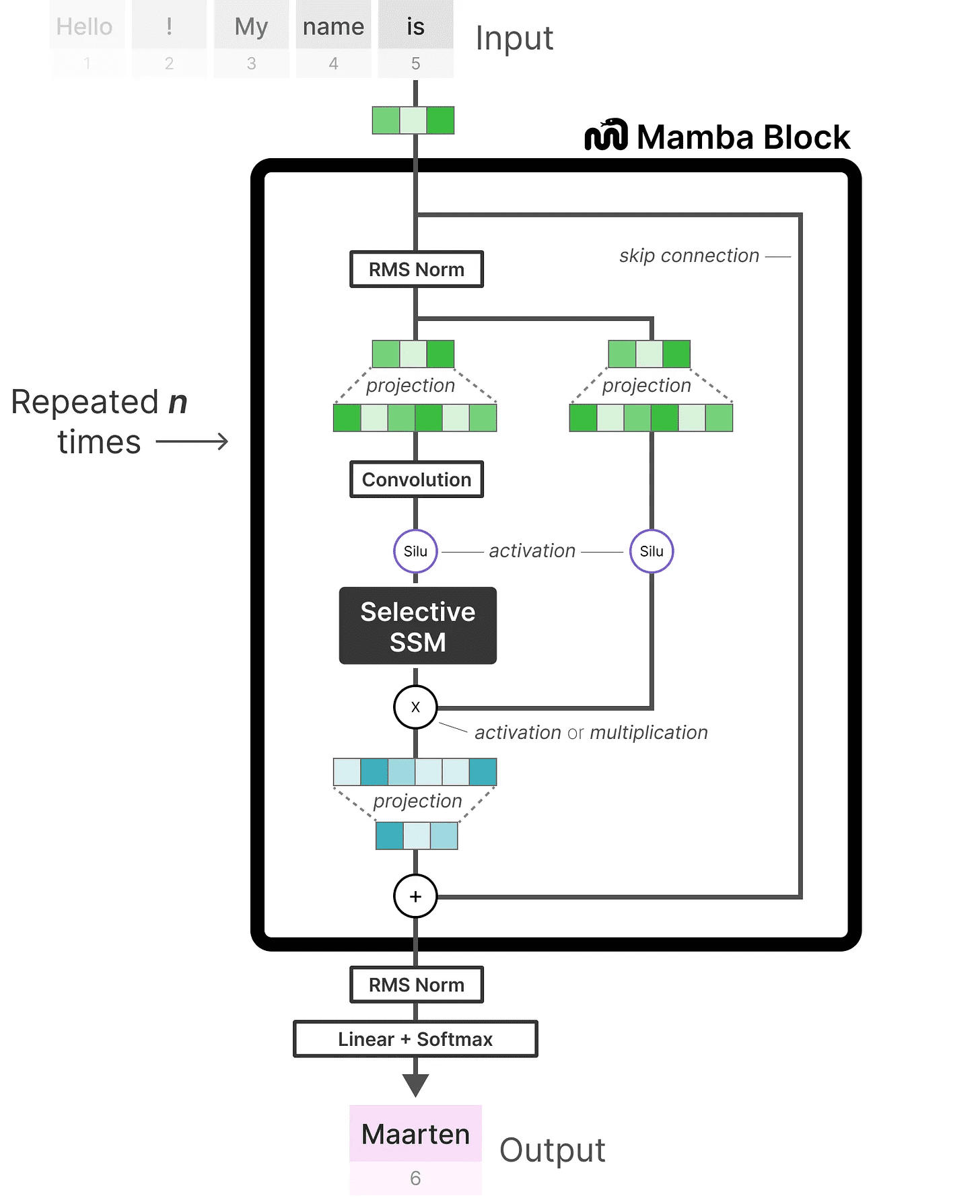Observe algumas alterações, como a adição de uma camada de normalização e um softmax para selecionar tokens de saída.
Quando juntamos tudo isso, obtemos inferência e treinamento rápidos, mesmo com contexto infinito. Usando essa arquitetura, os autores descobriram que seu desempenho se equiparava e, às vezes, excedia o de um modelo Transformer do mesmo tamanho!
chegar a um veredicto
Isso conclui nossa exploração dos modelos de espaço de estado e da incrível arquitetura Mamba usando modelos de espaço de estado seletivo. Esperamos que esta postagem tenha lhe dado uma melhor compreensão do modelo de espaço de estado e do Mamba em particular. Quem sabe se ele substituirá o Transformers, mas, por enquanto, é incrível ver uma arquitetura tão diferente receber a atenção que merece!
Para ver mais visualizações relacionadas à modelagem de big language e para apoiar este boletim informativo, confira o livro do qual sou coautor com Jay Alammar.
