Goedel-Prover-V2 - Modelo de prova de teoremas de código aberto de Princeton em conjunto com Tsinghua e NVIDIA, entre outros

O que é o Goedel-Prover-V2?

O Goedel-Prover-V2 é um modelo de prova de teoremas de código aberto de instituições líderes como a Universidade de Princeton, a Universidade de Tsinghua e a NVIDIA. O modelo baseia-se em técnicas inovadoras, como síntese de dados hierárquicos, autocorreção orientada pelo verificador e média do modelo para melhorar significativamente o desempenho de provas formais automatizadas. O modelo Goedel-Prover-V2 está disponível em duas versões, 32B e 8B, e o modelo tem um desempenho muito bom em vários benchmarks, por exemplo, o modelo 32B tem uma pontuação de 90,41 TP3T para Pass@32 no teste MiniF2F, superando o DeepSeek-Prover, que é muito maior. Por exemplo, no teste MiniF2F, o modelo 32B obteve uma pontuação de 90,41 TP3T para Pass@32, superando o DeepSeek-Prover-V2, que é muito maior. O modelo é capaz de gerar automaticamente provas para problemas matemáticos complexos e se autocorrige com base no feedback do compilador Lean para melhorar a qualidade das provas, e a natureza de código aberto do Goedel-Prover-V2 fornece uma base para que os pesquisadores façam mais desenvolvimentos e melhorias.

Principais recursos do Goedel-Prover-V2

• Geração automática de certificadosGeração de processos de prova formal para problemas matemáticos complexos para ajudar a resolver quebra-cabeças matemáticos complexos.
• Capacidade de autocorreçãoCom o feedback do compilador Lean, o modelo pode revisar iterativamente suas provas para melhorar sua precisão e qualidade.
• Treinamento e otimização eficientesBaseado em síntese de dados hierárquicos e técnicas de média de modelos, ele melhora a eficiência do treinamento e aprimora o desempenho do modelo, permitindo que ele tenha um bom desempenho em vários testes de referência.
• Código aberto e escalabilidadeFornecimento de modelos e conjuntos de dados de código aberto para facilitar o desenvolvimento e o aprimoramento por parte dos pesquisadores.

Desempenho do Goedel-Prover-V2

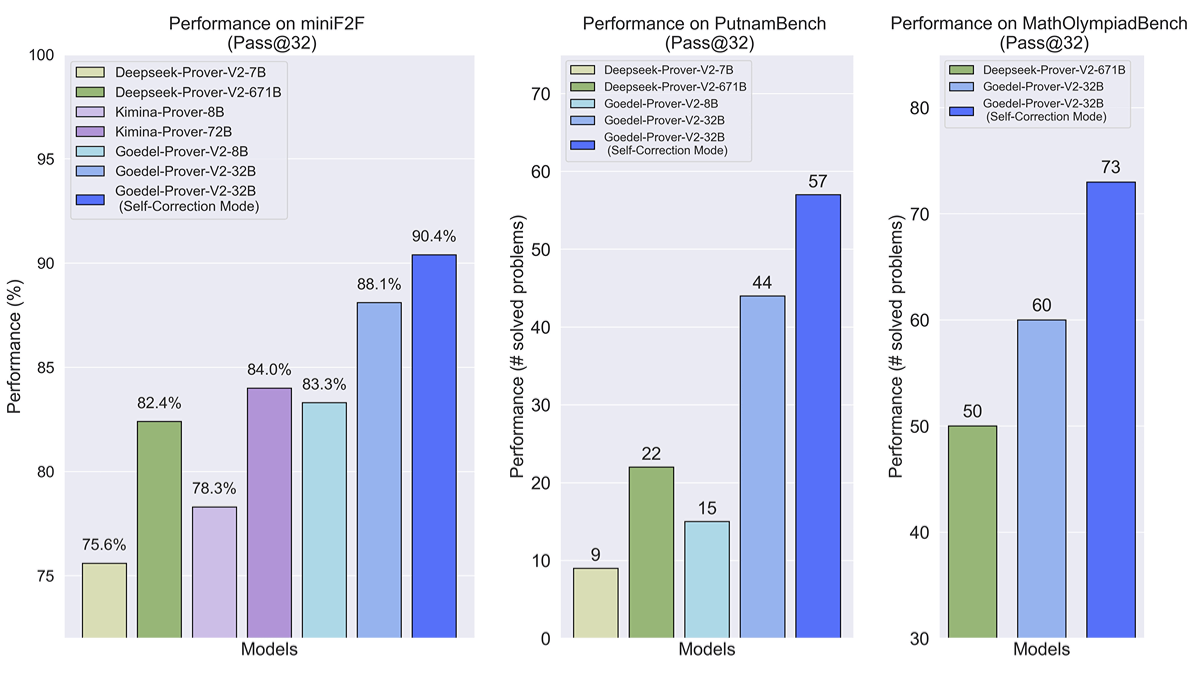
• Benchmarks do MiniF2F::
  • A pontuação Pass@32 para o modelo 32B chega a 90,41 TP3T, o que é significativamente superior ao DeepSeek-Prover-V2 (82,41 TP3T) para o 671B.
  • O modelo 8B alcança uma pontuação Pass@32 de 83,3%, que é comparável ao desempenho do DeepSeek-Prover-V2, embora o número de parâmetros seja apenas cerca de 1/100 do número do DeepSeek-Prover-V2.
• Benchmarks do PutnamBench::
  • O modelo 32B supera a métrica Pass@64, resolvendo 64 problemas.
  • Na métrica Pass@32, o modelo 32B resolve 57 problemas, superando significativamente o DeepSeek-Prover-V2-671B com 47 problemas.
  • O modelo 8B também tem um desempenho muito bom e é comparável ao DeepSeek-Prover-V2-671B.
• Benchmarks do MathOlympiadBench::
  • O modelo 32B resolve 73 problemas, significativamente melhor do que o DeepSeek-Prover-V2-671B com 50 problemas.
  • O modelo 8B também tem um bom desempenho, aproximando-se do nível do modelo 32B, mostrando uma forte capacidade de comprovação de teoremas.

Endereço do site oficial do Goedel-Prover-V2

• Site do projeto:: https://blog.goedel-prover.com/
• Biblioteca do modelo HuggingFace::
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-8B
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-32B

Como usar o Goedel-Prover-V2

• Acesso aos recursos do projetoAcesse a biblioteca de modelos do HuggingFace, baixe os arquivos de modelo do HuggingFace e selecione a versão apropriada (por exemplo, 8B ou 32B).
• Requisitos de hardwareGPUs de alto desempenho ou clusters de GPUs são recomendados.
• ambiente de softwareInstale o Python e estruturas de aprendizagem profunda, como o PyTorch, para garantir que o ambiente ofereça suporte à inferência de modelos grandes.
• Problemas de entradaConversão de problemas matemáticos que exigem provas em um formato compatível com o modelo (por exemplo, linguagem Lean).
• Pré-processamento de dadosCodificação e formatação de perguntas de acordo com os requisitos do modelo.
• Modelos de carregamentoCarregamento do modelo pré-treinado com as ferramentas fornecidas pelo HuggingFace.
• Prova de geraçãoO problema é alimentado no modelo, que gera automaticamente provas que são verificadas e corrigidas usando o compilador Lean.
• certificado de verificaçãoVerificar se as provas geradas estão corretas com o compilador Lean.
• Correção iterativaSe a prova estiver incorreta, o modelo se autocorrige com base no feedback até que a prova correta seja gerada.

Principais benefícios do Goedel-Prover-V2

• Excelente desempenhoGoedel-Prover-V2: o Goedel-Prover-V2 tem um bom desempenho em vários benchmarks; por exemplo, o modelo 32B atinge uma precisão de 90,4% no teste Pass@32 do MiniF2F, o que é significativamente superior a outros modelos semelhantes.
• Arquitetura técnica inovadoraBaseado em síntese hierárquica de dados, autocorreção orientada por validador e técnicas de média de modelos para melhorar efetivamente a eficiência do treinamento de modelos e a qualidade das provas.
• Código aberto e escalabilidadeFornecimento de modelos e conjuntos de dados de código aberto que podem ser livremente acessados, usados e desenvolvidos por pesquisadores para aprimoramento.
• Ampla gama de cenários de aplicaçãoAplicável a uma ampla gama de campos, como pesquisa matemática, validação de software e hardware, auxílios educacionais, inteligência artificial e aprendizado de máquina, além de pesquisa científica e engenharia.
• Treinamento e otimização eficientesTreinamento eficiente e otimização de desempenho com base em síntese de dados hierárquicos e técnicas de média de modelos para aumentar a robustez do modelo.

Pessoas para as quais o Goedel-Prover-V2 é indicado

• Matemáticos e pesquisadores matemáticosUtilizado para verificar conjecturas matemáticas, gerar provas de problemas complexos e acelerar a exploração e o estudo de teorias matemáticas.
• Cientistas da computação e engenheiros de softwareUtilizado no desenvolvimento de software e hardware para verificar a exatidão dos algoritmos, da lógica do programa e do projeto do circuito e para aumentar a confiabilidade e a segurança do sistema.
• pesquisador de inteligência artificialValidação dos fundamentos matemáticos e da lógica algorítmica dos modelos de aprendizado de máquina para garantir a confiabilidade e a precisão do modelo.
• Educadores e alunosDescrição: Servir como auxílio ao ensino de matemática, ajudando os alunos a entender e dominar melhor os conceitos e teoremas matemáticos, fornecendo exemplos de provas formais.
• Pesquisadores e engenheirosValidação de modelos e teorias matemáticas em pesquisa científica e projeto de engenharia para garantir a viabilidade e a confiabilidade das soluções de projeto.