言語モデリングにおけるトランスフォーマーに代わるもの
Transformerアーキテクチャは、大規模言語モデル（LLM）の成功の鍵となる要素である。現在使用されているほとんどの大規模言語モデルは、以下のようなオープンソースのモデルに至るまで、このアーキテクチャを採用しています。 ミストラル ChatGPTのようなクローズドソースのモデルに。
大規模言語モデルをさらに改善するために、Transformerアーキテクチャを超えるような新しいアーキテクチャが開発されている。そのようなアプローチのひとつが マンバ一種類 状態空間モデル.
新聞に掲載されたマンバ Mamba: 選択的状態空間による線形時系列モデリング1 で発表された。これについては リポジトリ 公式な実施要項とモデルのチェックポイントはこちら。
この投稿では、言語モデリングの文脈で状態空間モデリングの分野を紹介し、この分野を理解するのに役立つ様々な概念を段階的に探っていく。その後、MambaがどのようにTransformerアーキテクチャに挑戦するかについて議論する。
ビジュアルガイドとして、この記事ではマンバと状態空間モデルを理解するのに役立つ多くのビジュアライゼーションを紹介する！
パート1：トランスフォーマー問題
マンバがいかに興味深い建築物であるかを説明するために、まず『トランスフォーマー』を簡単におさらいし、その欠点のひとつを探ってみよう。
トランスフォーマーは、あらゆるテキスト入力を、あたかも トークン 構成体 シーケンス.
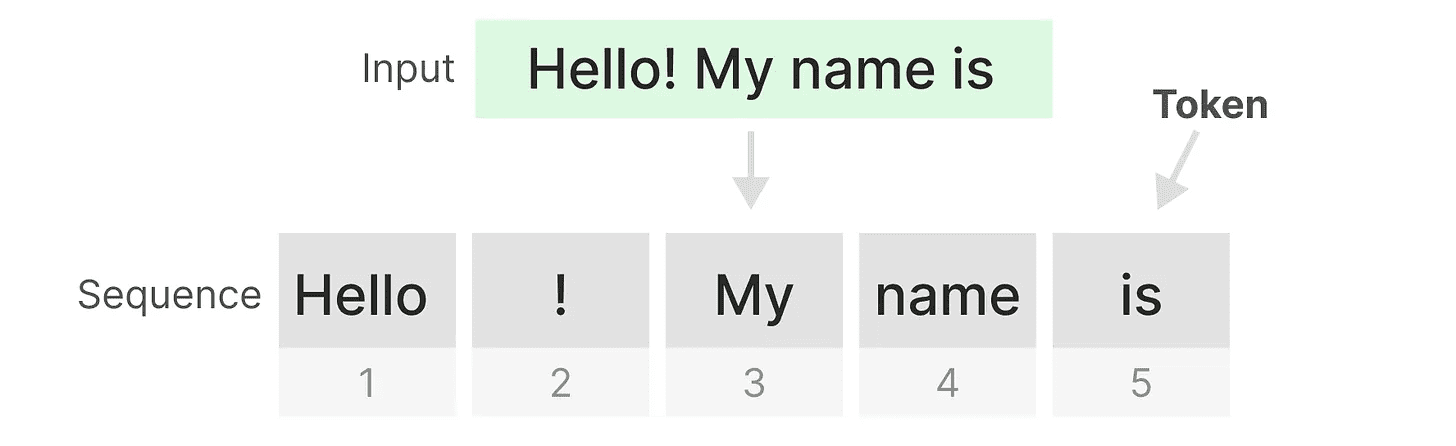トランスフォーマーの主な利点のひとつは、どのような入力を受けても、その表現を導き出すために、シーケンス内の以前のトークンに戻ることができることだ。
トランスのコア部品
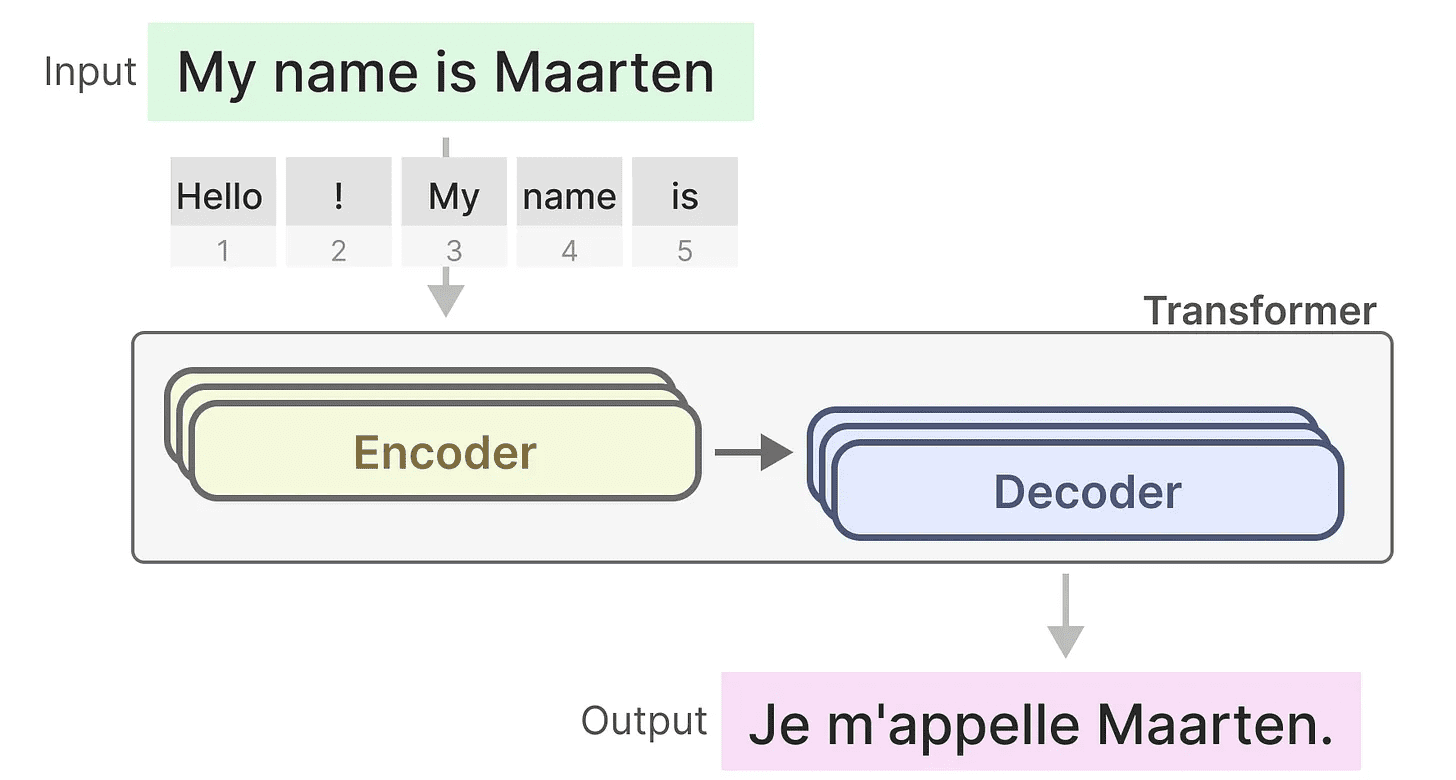
トランスフォーマーは、テキストを表現するためのエンコーダー・ブロックのセットと、テキストを生成するためのデコーダー・ブロックのセットという、2つの構造から構成されていることを覚えておいてほしい。これらの構造を組み合わせることで、翻訳を含む複数のタスクに使用することができる。
この構造を利用して、デコーダだけで生成モデルを作ることができる。このトランスフォーマーに基づくモデルジェネレーティブ・プレトレーニング・トランスフォーマー(GPT）は、デコーダー・ブロックを使って入力テキストの一部を完成させる。
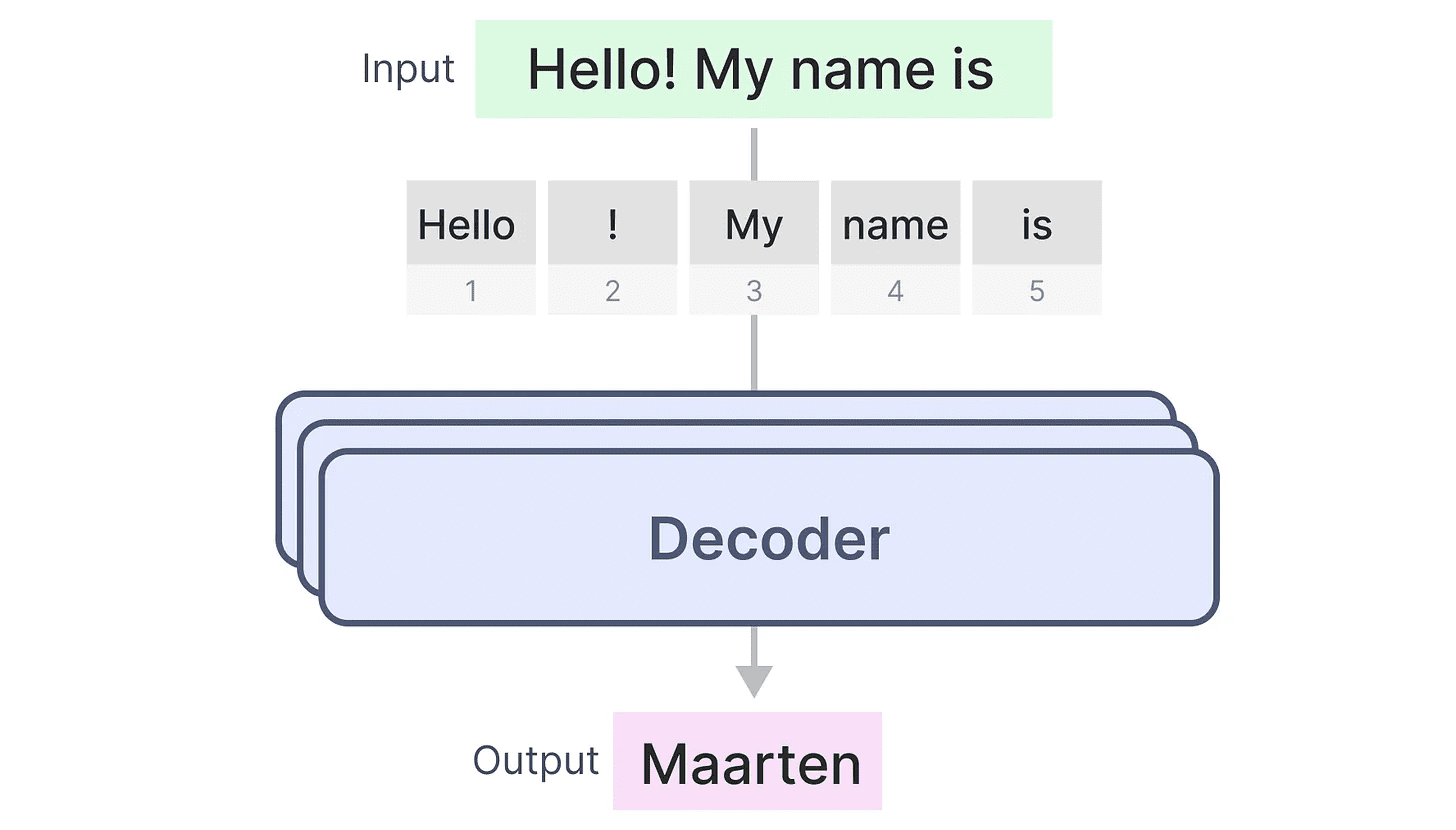どう動くか見てみよう！
トレーニングに祝福を...
1つのデコーダーブロックは、マスクされた自己注意機構とフィードフォワード型ニューラルネットワークの2つの主要コンポーネントで構成されている。
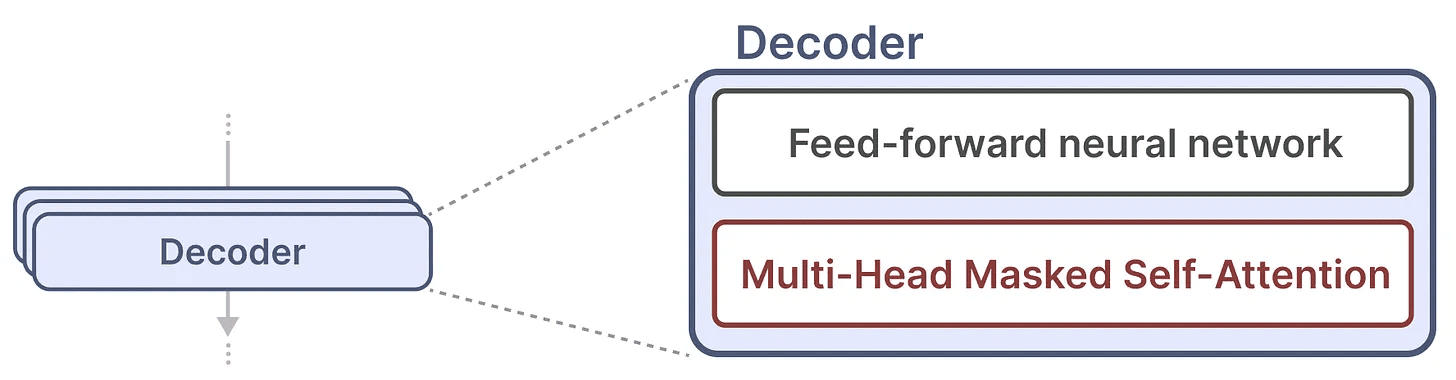自己注意メカニズムは、これらのモデルが非常にうまく機能する重要な理由である。シーケンス全体を圧縮せずに見ることができ、訓練も速い。
では、どのように機能するのか？
このマトリックスは トークン それぞれの前のトークンと比較する。行列の重みは、トークンのペアの関連性に依存する。
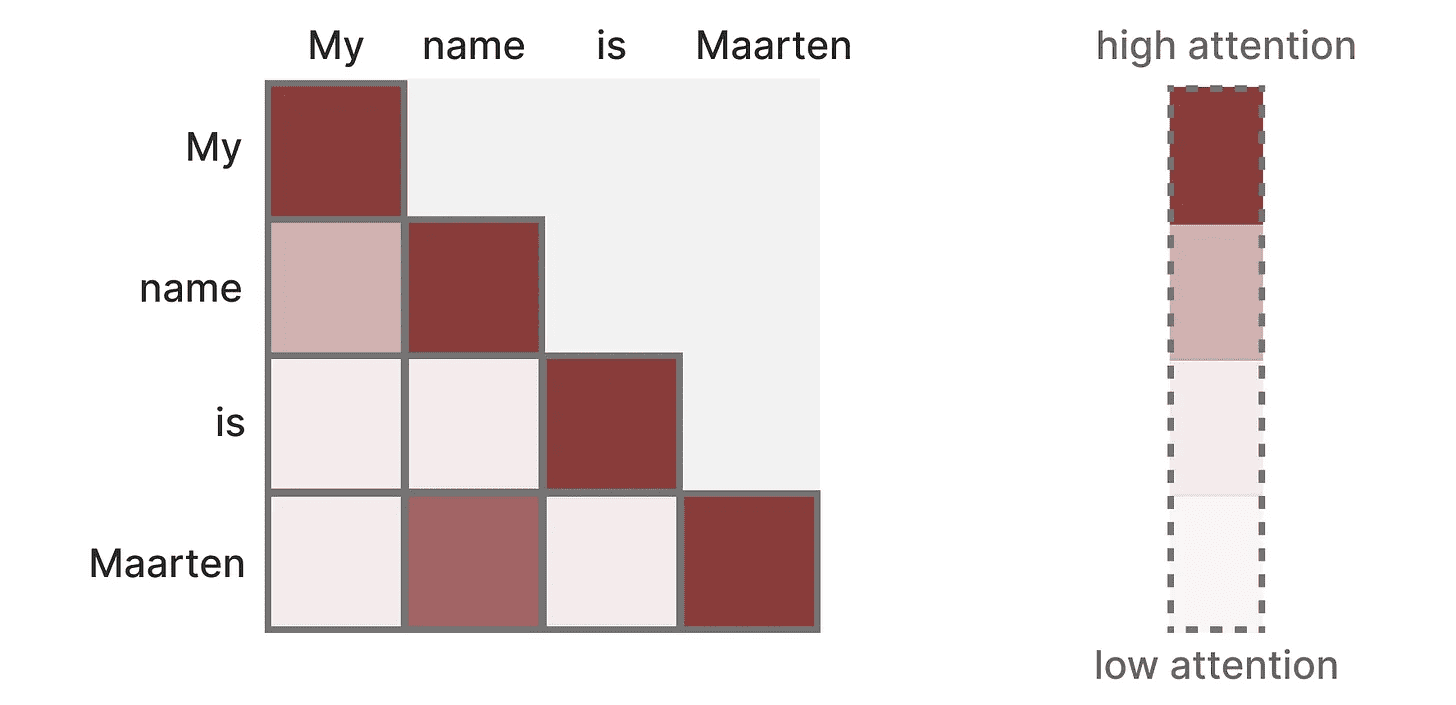このマトリックスはトレーニング中に一気に作られる。"私の「そして名称"アテンション "を計算する前に、"アテンション "を計算する必要はない。名称「そしては"間に注目。
それはへいこうこれにより、トレーニングが大幅にスピードアップする！
推論の問題！
しかし欠点もある。次のトークンを生成する際に全シーケンスすでにトークンを生成していたとしても。
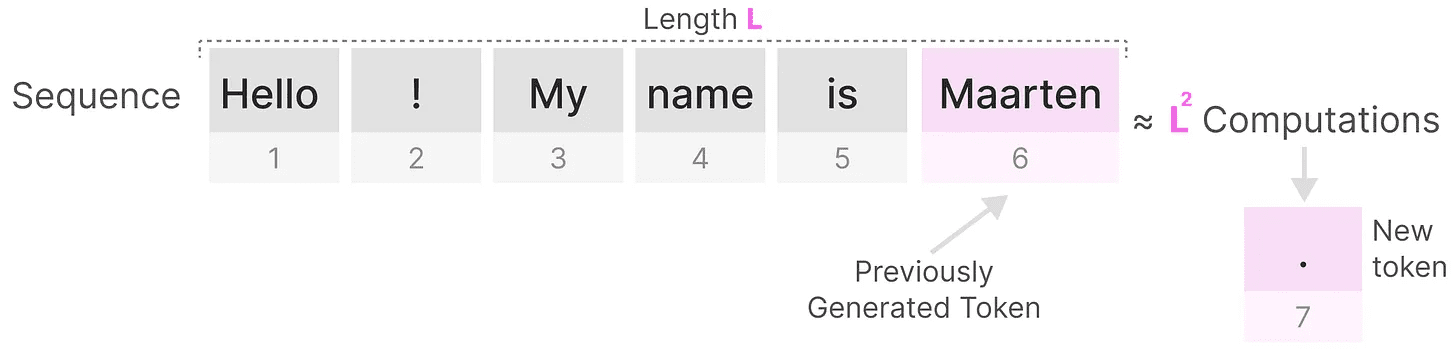の長さを生成する。Lこのシークエンスに必要なのはL²回となり、シーケンスの長さが長くなると計算量が多くなる。
このシーケンス全体を再計算する必要性は、Transformerアーキテクチャの主なボトルネックの1つである。
古典的な」手法であるリカレント・ニューラル・ネットワーク（RNN）が、この遅い推論問題をどのように解決するか見てみよう。
RNNは解決策か？
リカレントニューラルネットワーク(RNN)はシーケンスベースのネットワークである。各時間ステップで2つの入力を受け取る。t入力と前の時間ステップt-1の隠れ状態は、次の隠れ状態を生成し、出力を予測するために使用される。
RNNにはループ機構があり、あるステップから次のステップに情報を渡すことができる。この可視化プロセスを「拡張」することで、より明示的にすることができる。
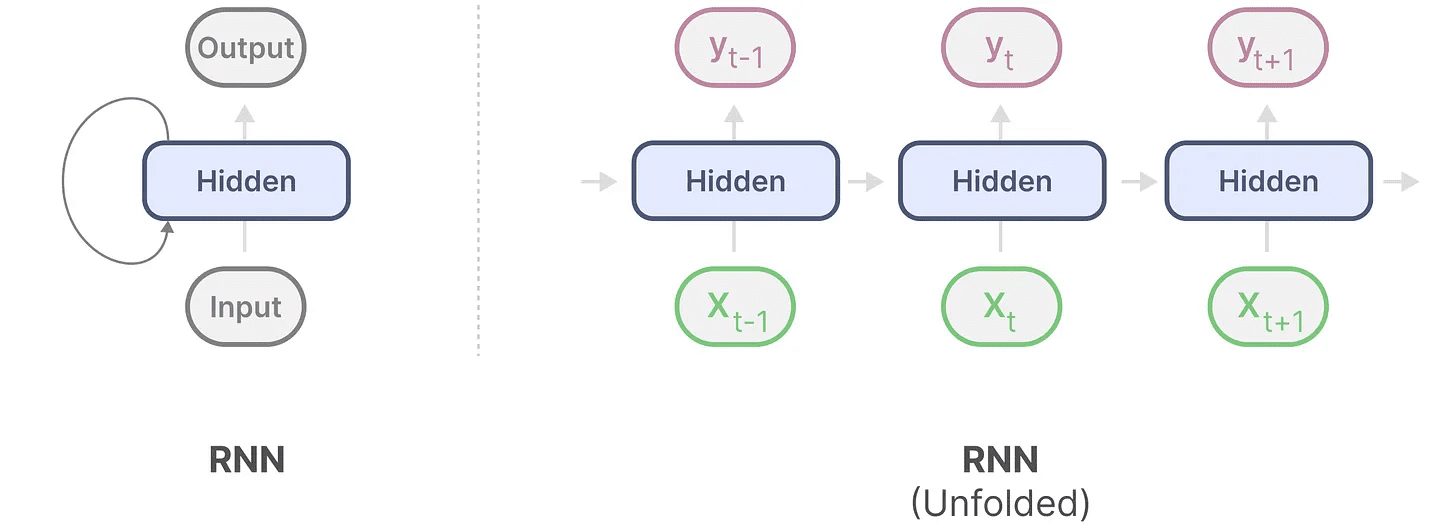出力を生成する際、RNNは前の隠れ状態と現在の入力のみを考慮すればよい。これにより、Transformerが必要とする以前の隠れ状態をすべて再計算する問題を回避できる。
つまり、RNNはシーケンスの長さに応じて線形にスケールするため、高速な推論が可能なのだ！理論的にはコンテキストの長さは無制限.
これを説明するために、先ほど使った入力テキストにRNNを適用してみよう。
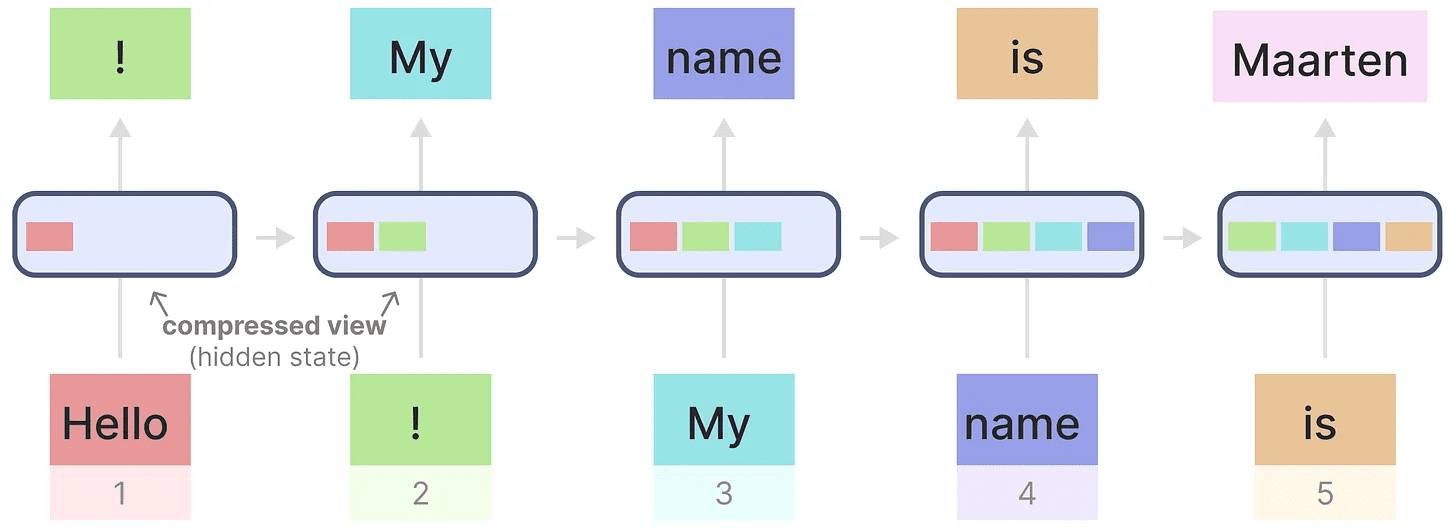各隠れ状態は、以前のすべての隠れ状態の集合体であり、通常は圧縮されたビューである。
しかし、ここで問題がある。
という名前を生成するときに、"マールテン"という単語に関する情報が最後の隠された状態に含まれなくなったとき。こんにちは「RNNは最後の状態しか考慮しないため、時間とともに情報を忘れる傾向がある。
RNNは学習と推論が速い反面、Transformerモデルが提供できる精度に欠ける。
そこで、RNN（時には畳み込み）を効率的に利用するために、状態空間モデルを研究している。
パート2：状態空間モデリング（SSM）
TransformerやRNNのような状態空間モデル（SSM）は、テキストや信号のような情報のシーケンスを扱う。このセクションでは、SSMの基本的な概念と、それらがテキストデータにどのように関係するかを紹介する。
状態空間とは何か？
状態空間は、システムを完全に記述するのに必要な変数の最小数を含む。これは、システムの可能な状態を定義することによって、問題を数学的に表現する方法である。
単純化しよう。私たちが迷路を旅していると想像してください。"状態空間「すべての可能な場所（状態）の地図だ。各ポイントは迷路内の固有の場所を表し、出口までの距離など具体的な詳細が記されている。
"状態空間表現「とは、この地図の簡略化された説明である。現在地（現在の状態）、次に行ける場所（将来の可能性のある状態）、次の場所への行き方（右か左に移動）を示しています。
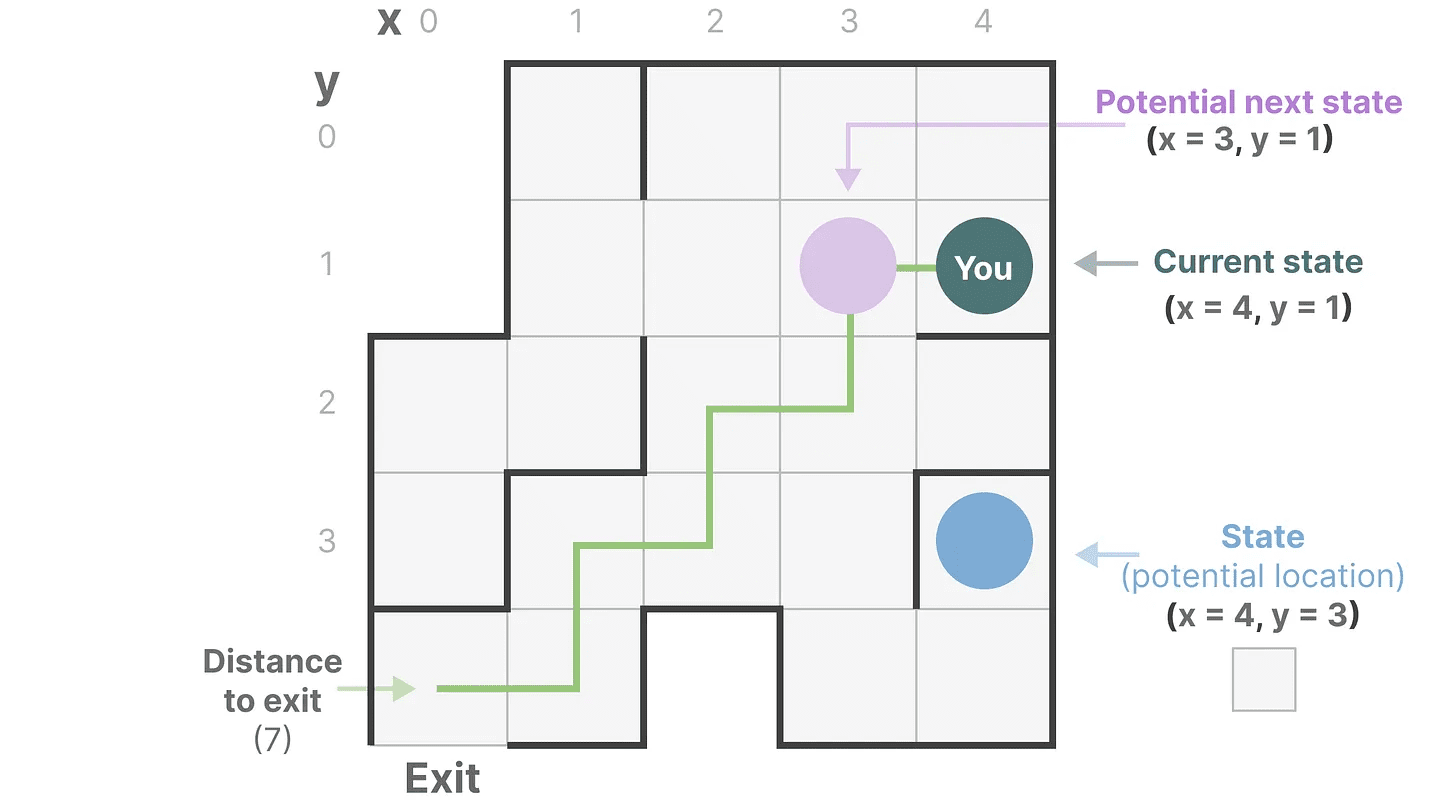状態空間モデルは、方程式と行列を使ってこの挙動を追跡するものだが、実際には、どこにいて、どこに行けるのか、そしてそこに行くにはどうすればいいのかを追跡する方法にすぎない。
変数は状態、この場合はXとYの座標と出口までの距離を表す。状態ベクトル".
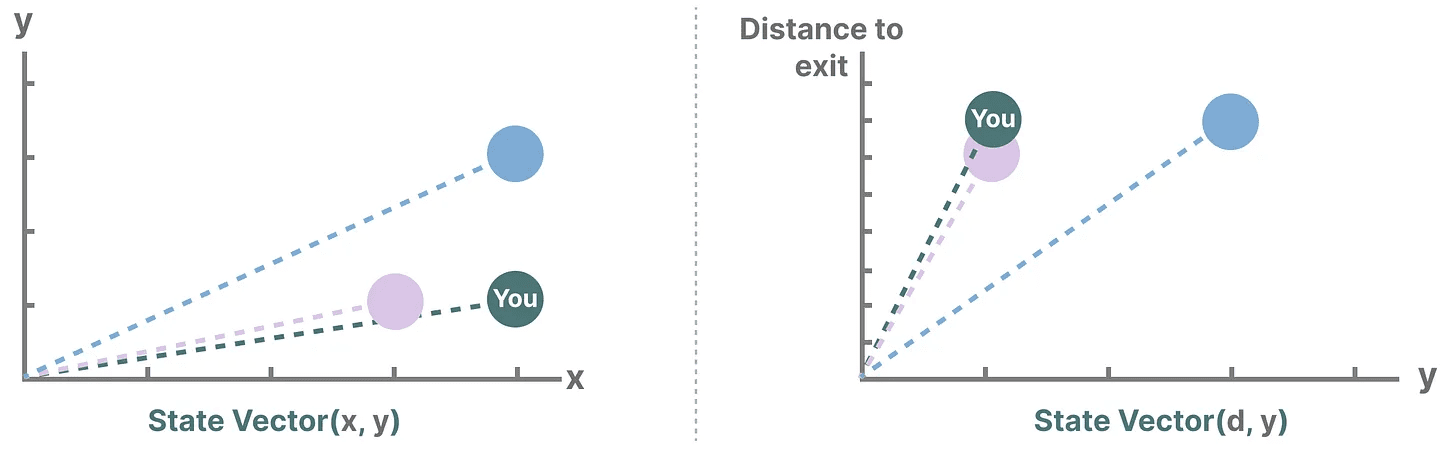聞き覚えがあるだろうか？それは、エンベッディングやベクトルもまた、入力シーケンスの「状態」を記述するために言語モデルでよく使われるからだ。例えば、あなたの現在位置を表すベクトル（状態ベクトル）は次のようなものだ：
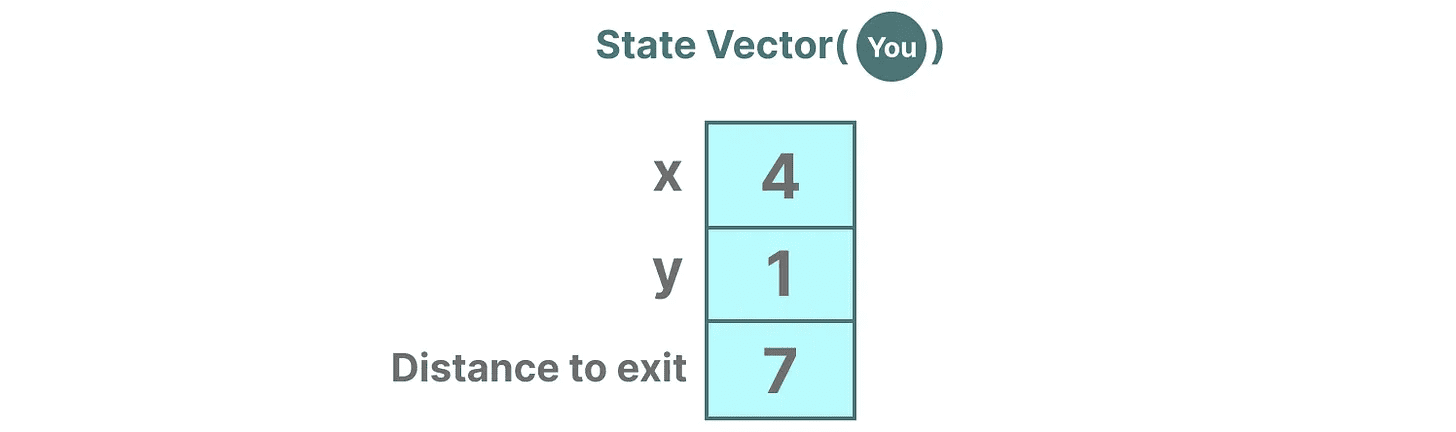ニューラルネットワークでは、「状態」は通常システムの隠れた状態を指し、これは大規模な言語モデルで新しいトークンを生成する上で最も重要な側面の1つである。
状態空間モデルとは何か？
SSM（状態空間モデル）は、これらの状態表現を記述し、特定の入力に基づく予測で、次の状態を予測するために使用されるモデルのクラスである。
伝統的に、そのうちに tSSMだ：
- 入力シーケンスは次のようになる。 x(t)(例えば、迷路で左や下に移動すること）が潜在的な状態表現にマッピングされる。 h(t)(出口までの距離やX/Y座標など）
- そして、予測出力シーケンスを導き出す y(t)(例：出口に早く行くためにもう一度左に移動する）
しかし、SSMは離散的なシーケンス（例えば、1回左にシフトする）を使用する代わりに、連続的なシーケンスを入力として受け入れ、出力シーケンスを予測する。
SSMは、動的システム（例えば、3D空間を移動する物体）が時間的に t の状態と、それを予測する2つの方程式。
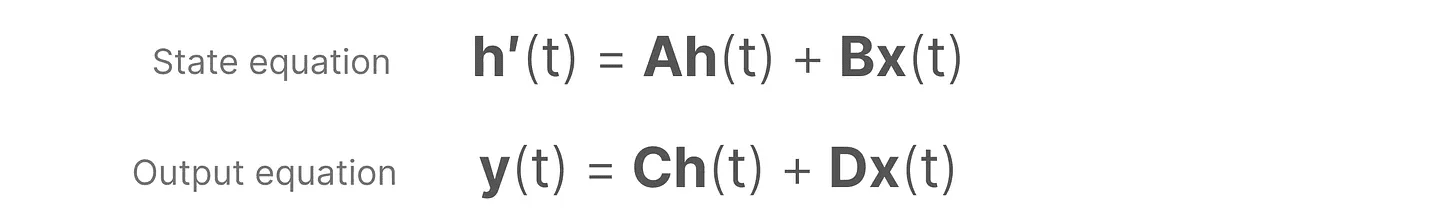これらの方程式を解くことで、観測されたデータ（入力シーケンスと以前の状態）に基づいてシステムの状態を予測するための統計的原理を明らかにすることができる、というのが我々の仮説である。
目標は、この状態の表現を見つけることだ h(t)これは、入力シーケンスから出力シーケンスへの移行を可能にする。
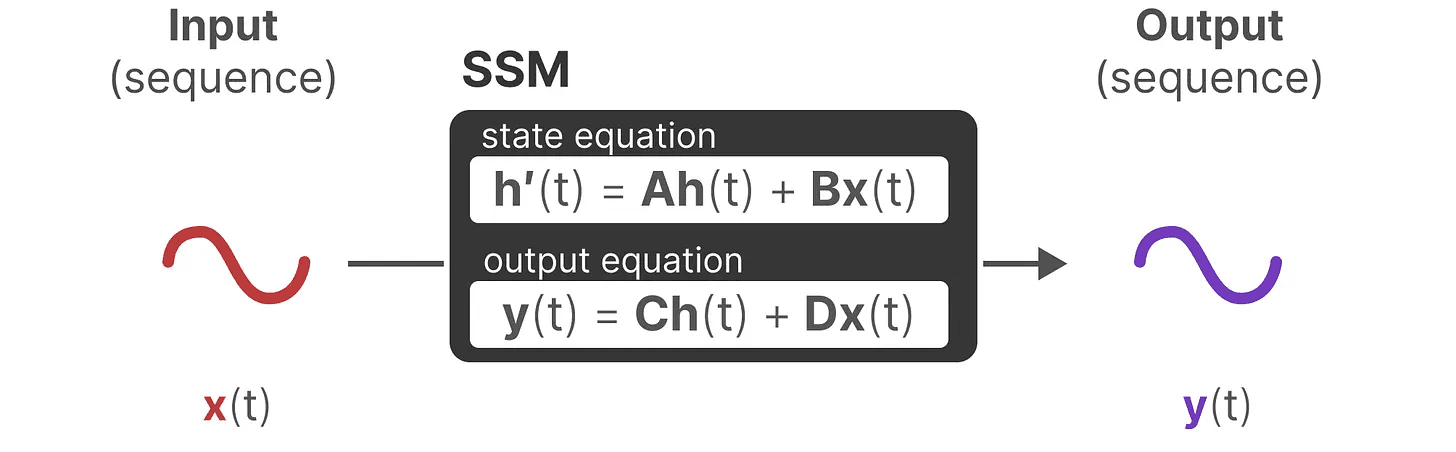この2つの方程式が状態空間モデルの核心である。
この2つの方程式は、本ガイドを通して参照される。より直感的に理解できるように色分けをするすぐに引用できるように。
状態方程式 入力に応じてどのように状態を変化させるかを記述する。 マトリックスBを経由して）に影響を与える。 マトリックスA)と変化する。
前述の通りだ。h(t) 任意の時間を指す t の潜在的な状態表現である。x(t) はある入力を指す。
出力方程式 をどのように通過させるかを説明する。 マトリックスC そして、入力がどのように出力に変換されるのか。 マトリックスD 出力に影響する。
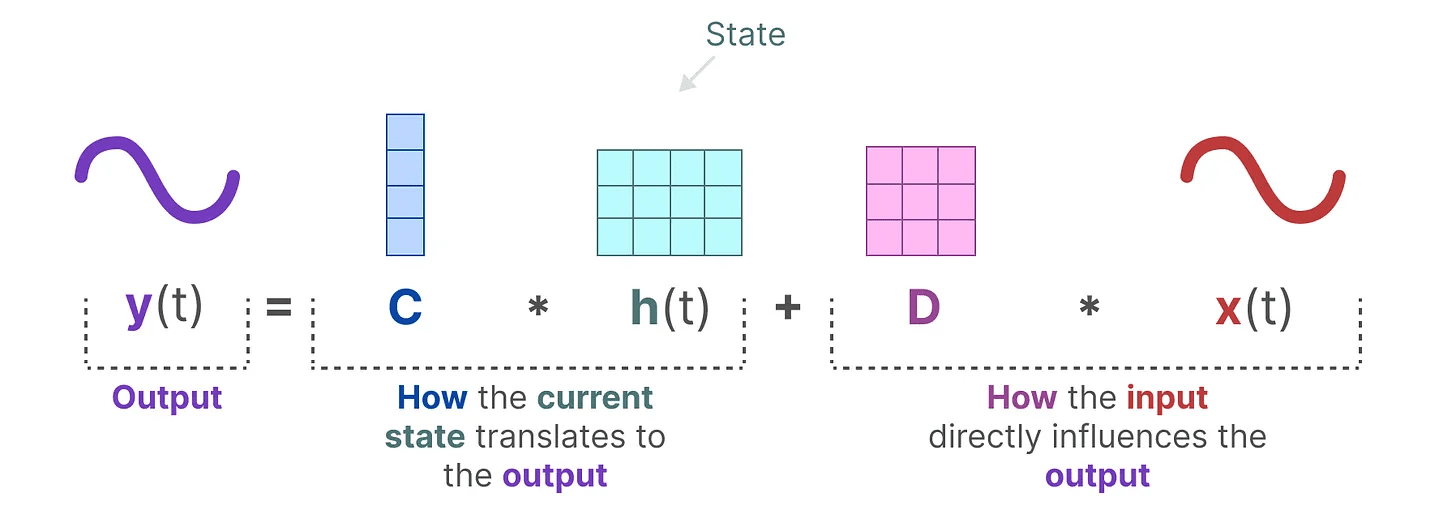
銘記するマトリックス AそしてBそしてC 歌で応える D と呼ばれることもある。 パラメトリック学べるからだ。
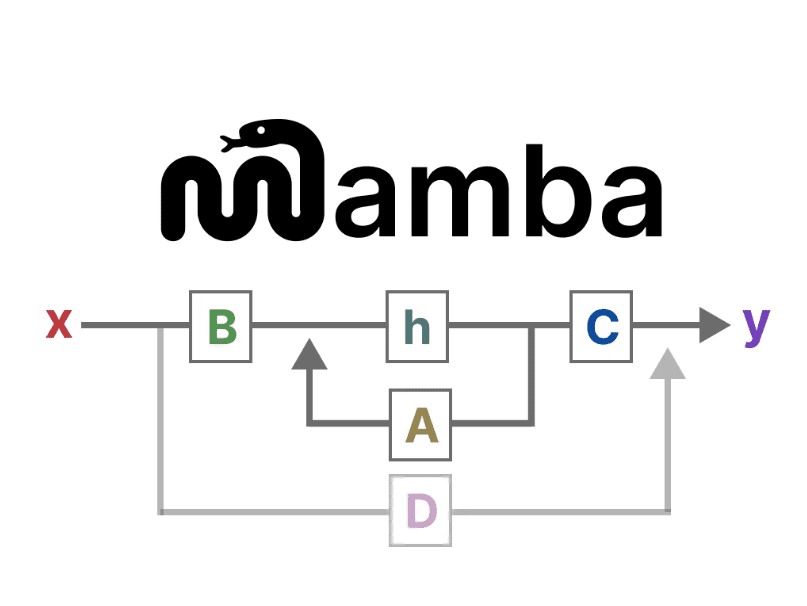
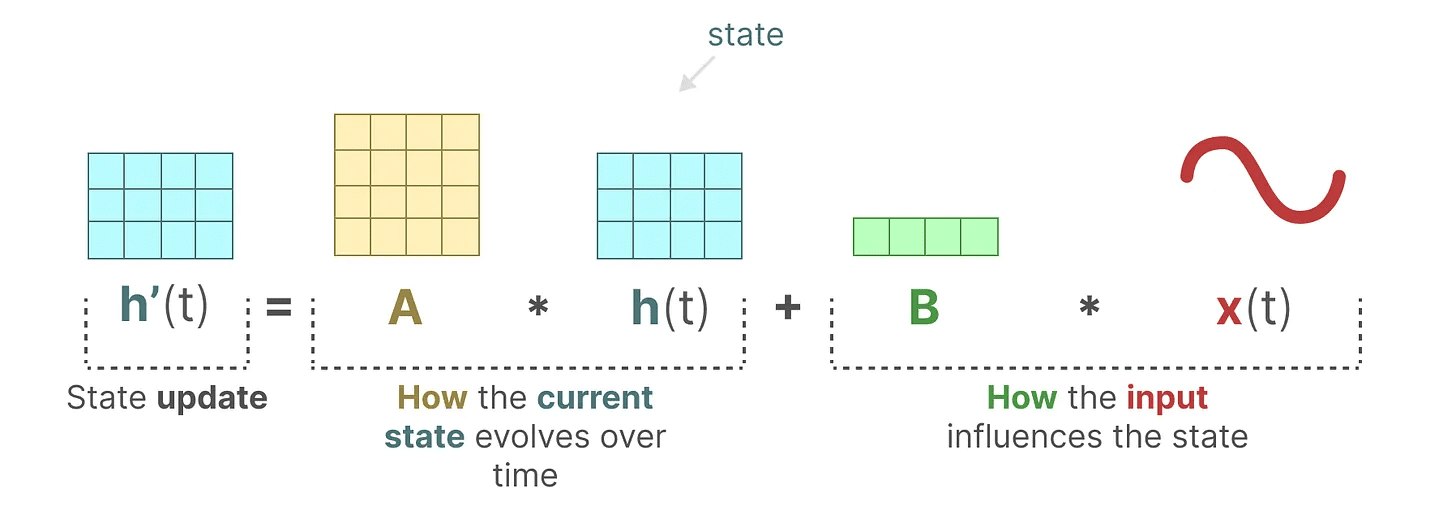
この2つの方程式を視覚化すると、次のようなアーキテクチャが得られる：
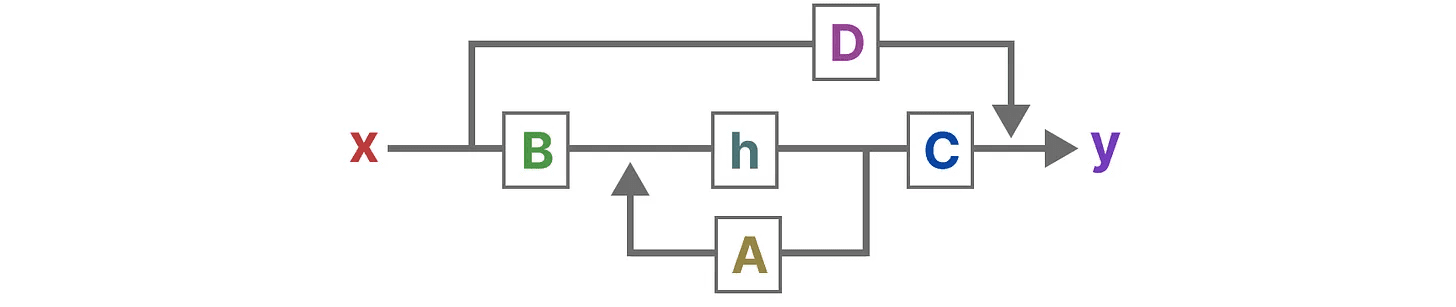これらのマトリックスが学習プロセスにどのような影響を与えるか、順を追って見ていこう。
いくつかの入力信号があるとする。 x(t)信号はまず マトリックスB 掛け算。マトリックスB 入力がシステムにどのような影響を与えるかを説明する。
更新された状態（ニューラルネットワークの隠れ状態に似ている）は、環境の核となる「知識」を含むポテンシャル空間である。この状態を マトリックスA この行列を掛け合わせることで、すべての内部状態間の関連性が記述され、システムの基本的なダイナミクスを表す。
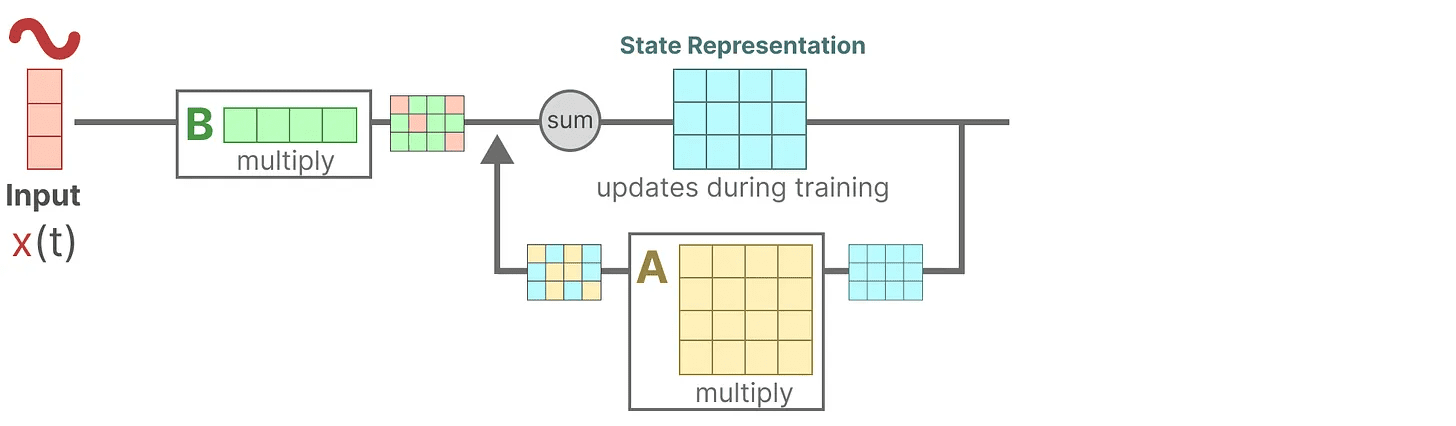お気づきかもしれないが。マトリックスA 状態表現が作成される前に適用し、状態表現が更新された後に再度適用する。
次に マトリックスC 状態をどのように出力に変換するかを記述する。
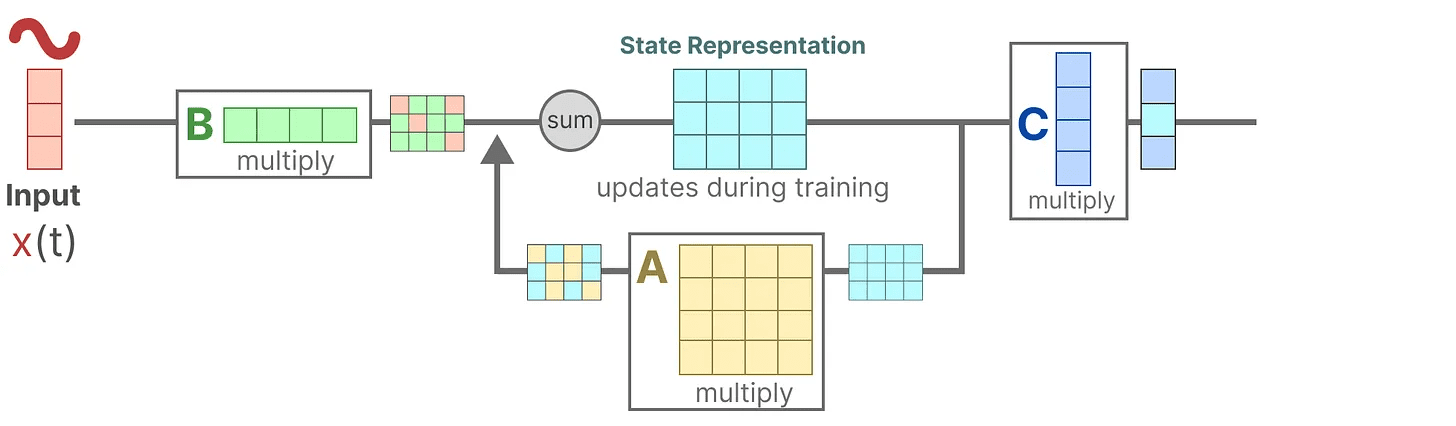最後に マトリックスD 入力から出力へ直接信号を供給する。これは一般に ジャンプ接続.
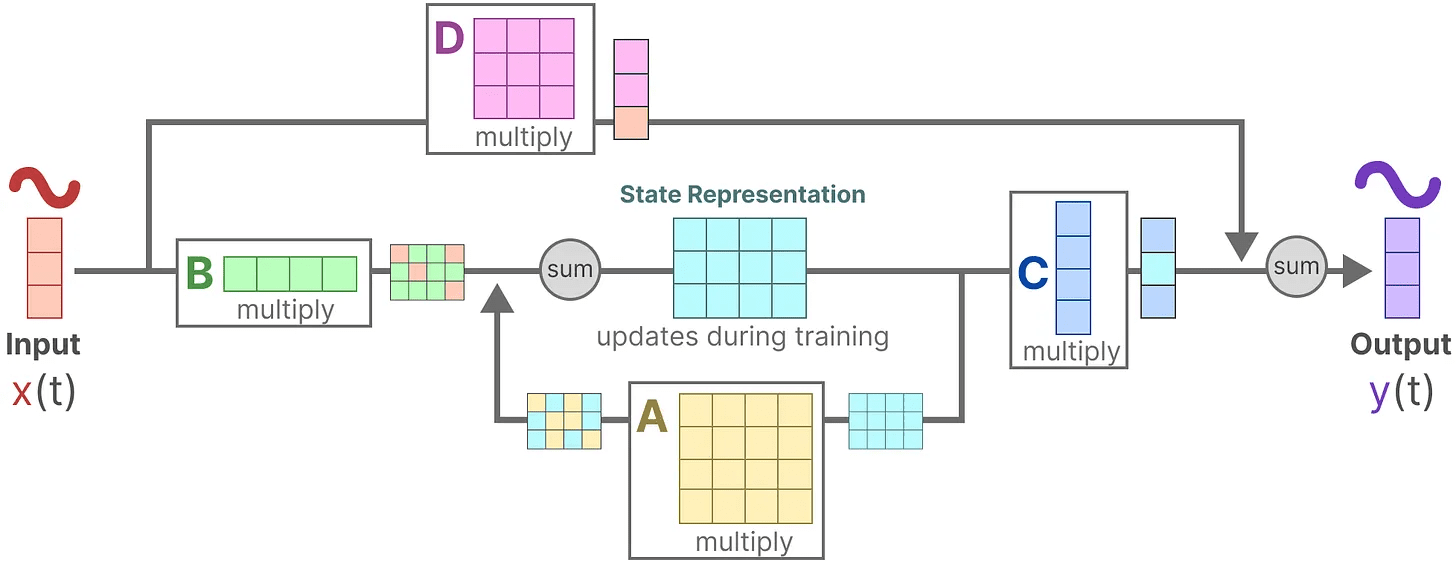により マトリックスD ジャンプコネクションと同様に、SSMもジャンプコネクションを含まない次のような形と考えられることが多い。
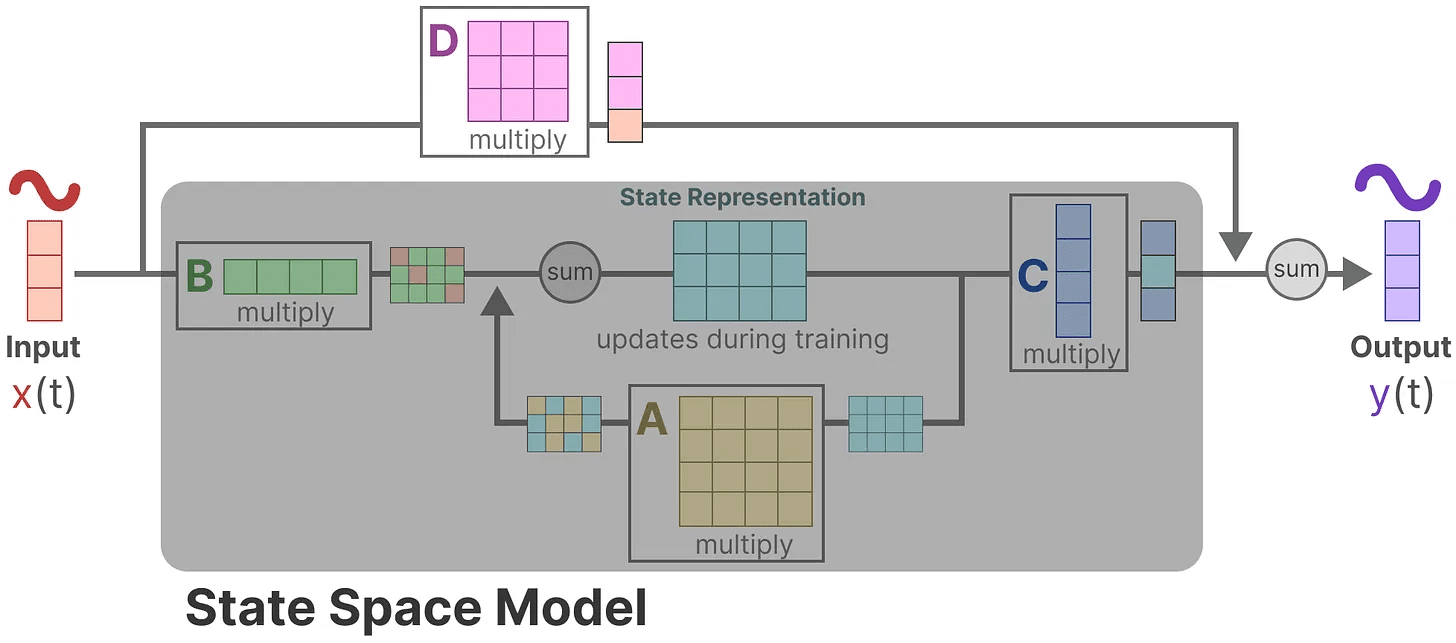単純化した視点に戻り、今度は行列に注目しよう。 AそしてB 歌で応える C をSSMの中核としている。
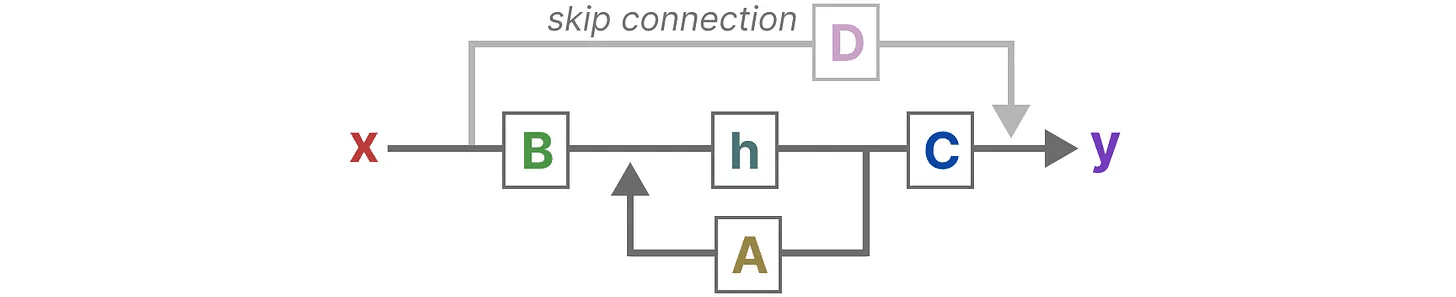前と同じように、それぞれの行列が何に使われるかを示すために、元の方程式を更新することができる（そして素敵な色を追加する）。
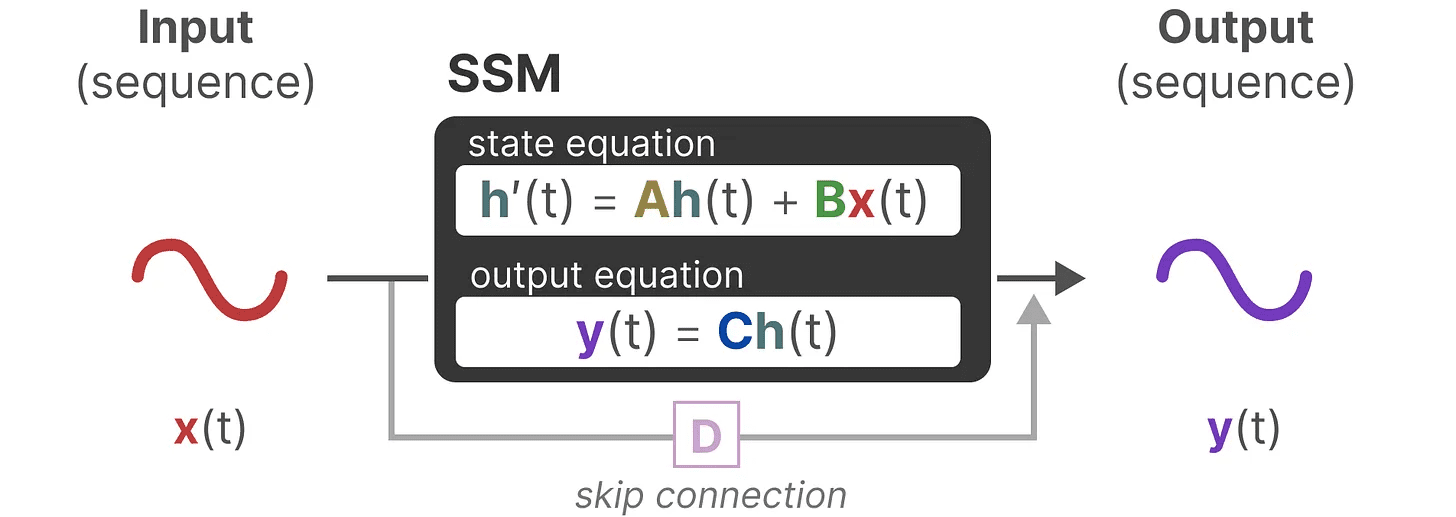これらの2つの方程式は、観測されたデータからシステムの状態を予測することを目的としている。入力は連続的なので、SSMの主な表現は次のようになる。 連続時間スケール.
連続信号から離散信号へ
連続信号がある場合、状態表現を見つける h(t) 解析が難しい。さらに、我々は通常、離散的な入力（例えば、テキストシーケンス）を持っているので、モデルを離散化したい。
そのためには ゼロ・オーダー保持テクニック.まず、離散信号を受信するたびに、新しい離散信号を受信するまでその値を保持する。このプロセスにより、SSM用の連続信号が生成される：
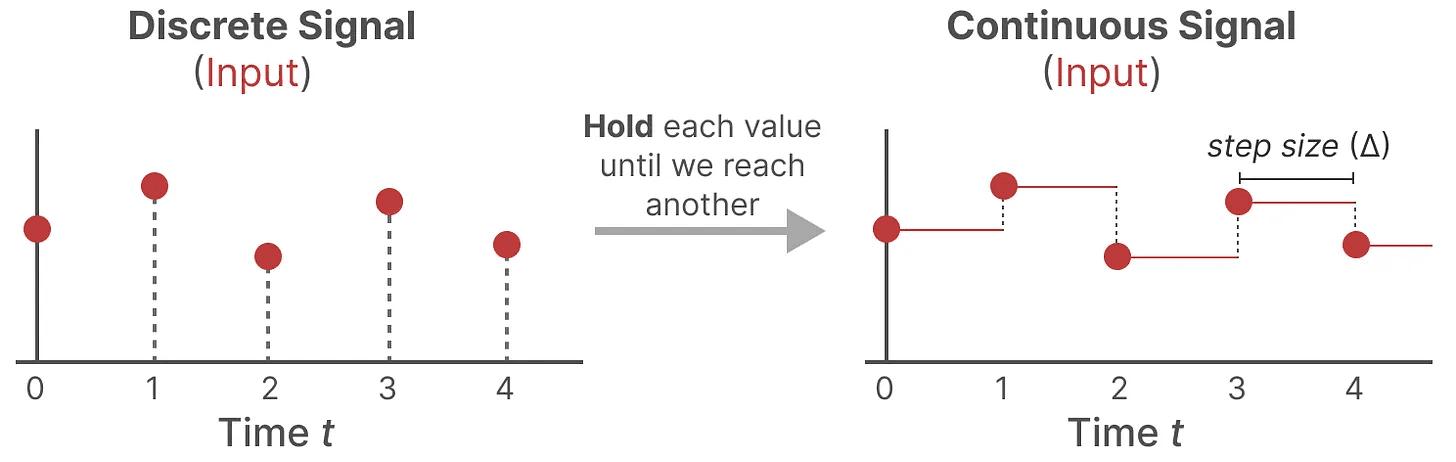我々は、学習可能な新しいパラメータによって時間の値を保持する。 ペースメーカー ∆ 示す。入力の解像度を示す。
入力に対して連続信号を生成できたので、次に連続出力を生成し、入力の時間ステップに従ってこれらの値をサンプリングすることができる。
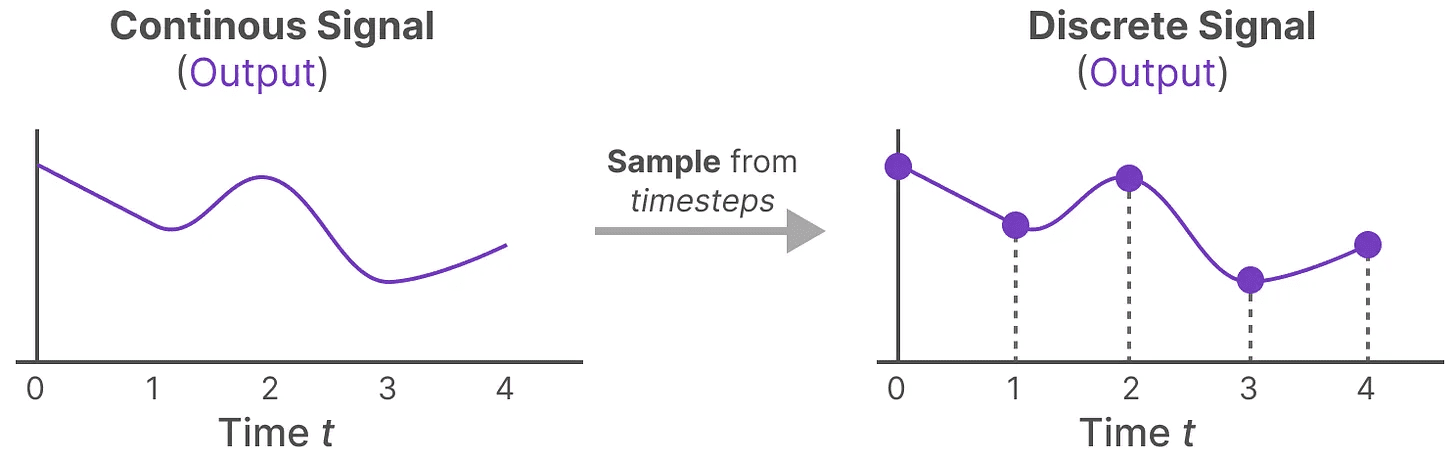これらのサンプリングされた値が離散化の出力となる！
数学的には、次のように0次ホールドを適用することができる：
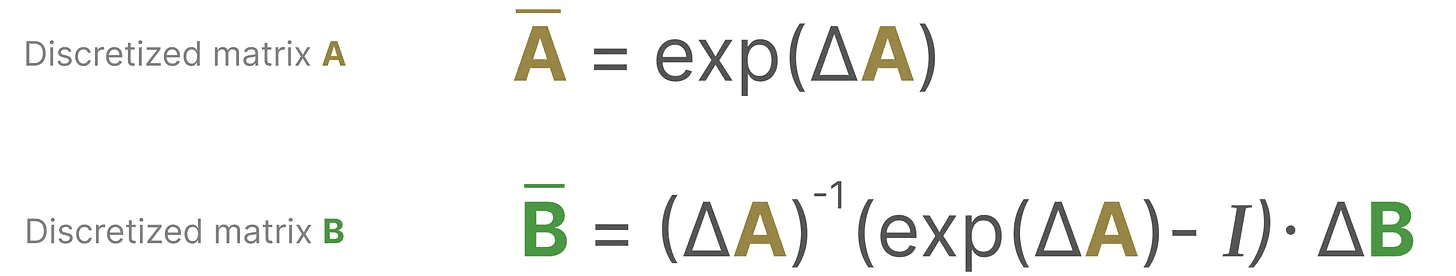これによって、連続的なSSMから離散的なSSMへと移行することができる。 関数間 x(t) → y(t)その代わりに シーケンス間 xₖ → y_ₖ::
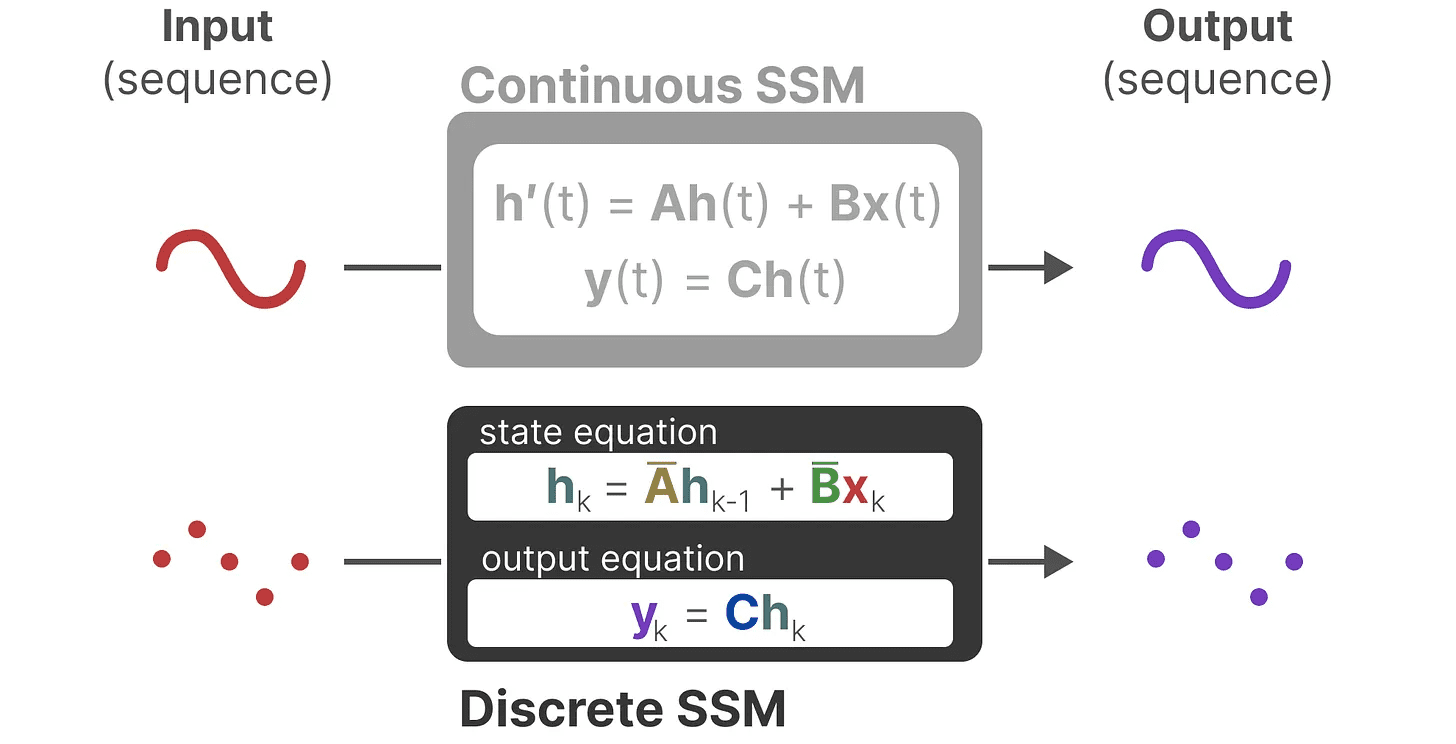ここで、行列 A 歌で応える B ここで、モデルの離散化されたパラメータを示す。
を使用する。 k の代わりに t連続的なSSMと離散的なSSMを区別するためだ。
注目してほしい： トレーニング中、我々はまだ保持している マトリックスA を、離散化された形ではなく、連続的な形で表現する。訓練中、連続的な表現は離散化される。
さて、離散化表現の公式を得たところで、実際にどのように表現するかを探ってみよう。 カウント モデルだ。
再帰的表現
我々の離散化SSMは、連続信号ではなく、特定の時間ステップで問題を構成することを可能にする。以前RNNで見たように、再帰的手法はここで非常に役に立つ。
連続信号の代わりに離散時間ステップを考えれば、時間ステップを使って問題を再定式化できる：
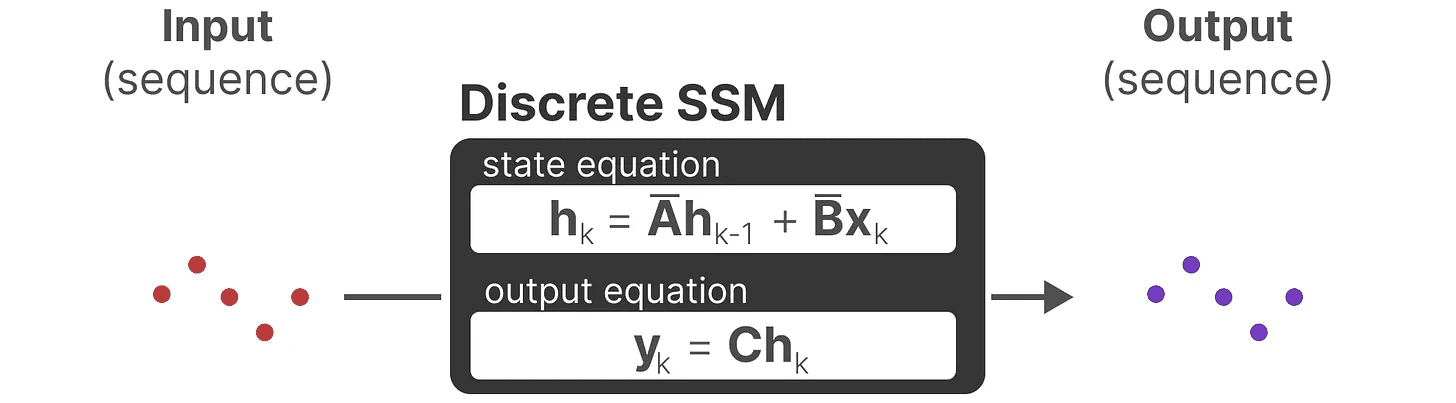各時間ステップで、現在の入力(Bxₖ)前の状態(あ ₖ₋₁₁)を計算し、予測出力(Chₖ).
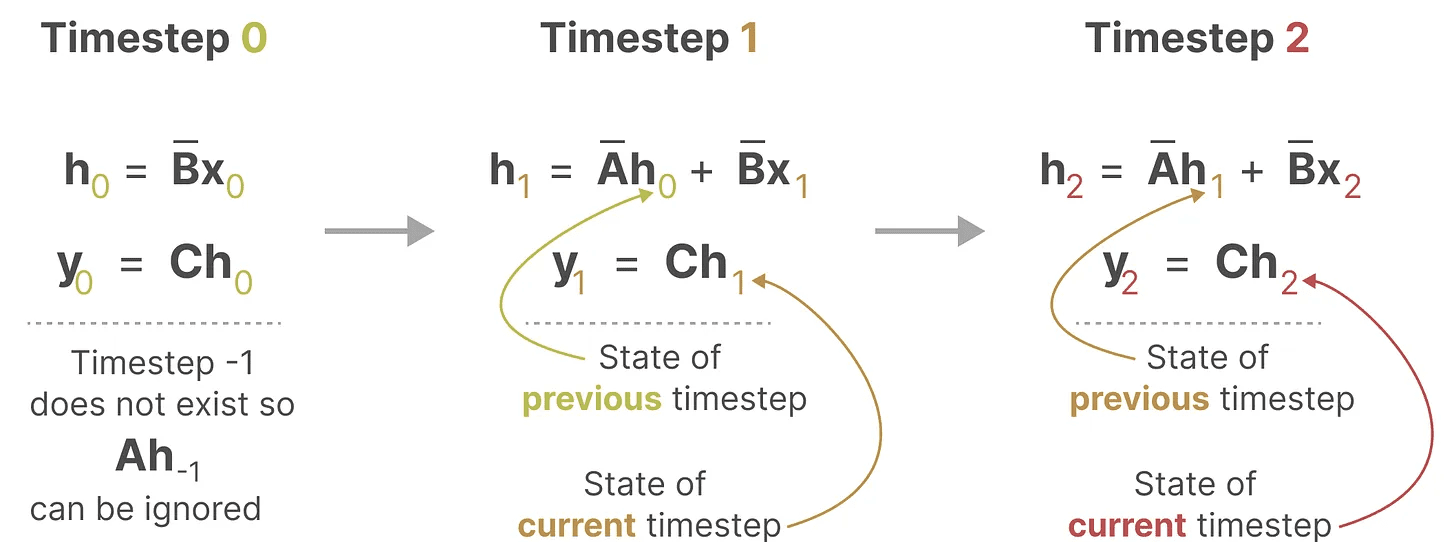この表現はすでにお馴染みかもしれない！前回のRNNの扱いと同じように分析することができる。
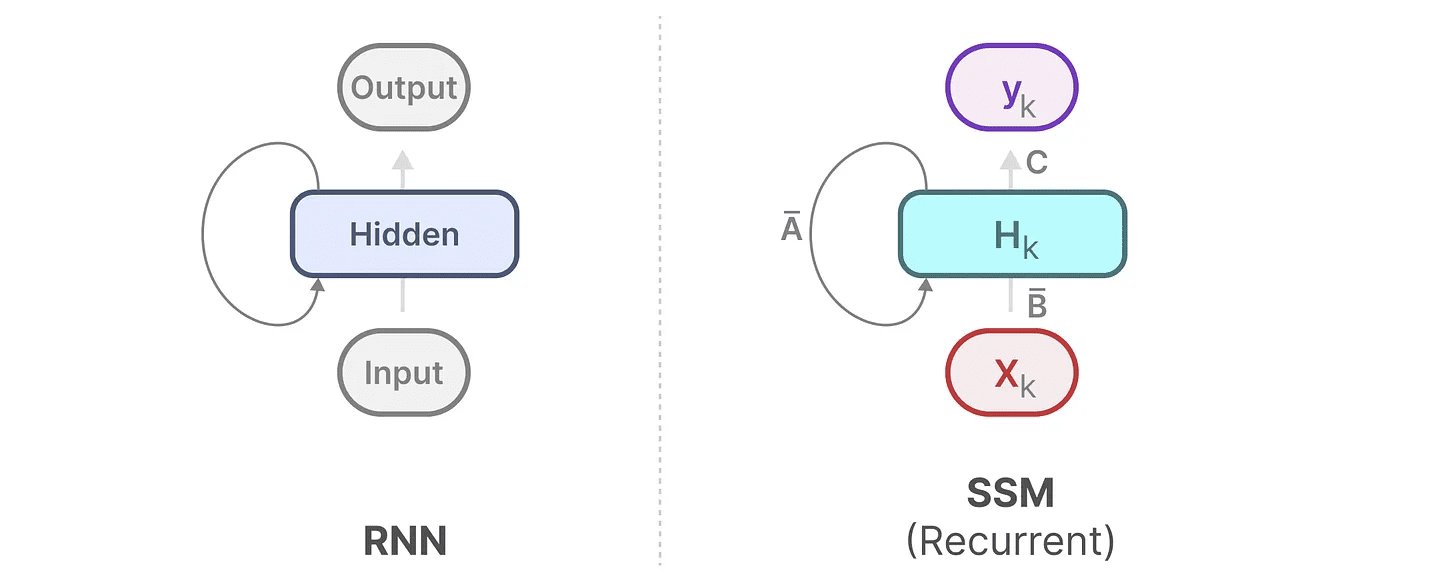次のように展開できる（あるいは一連の時間ステップに展開できる）：
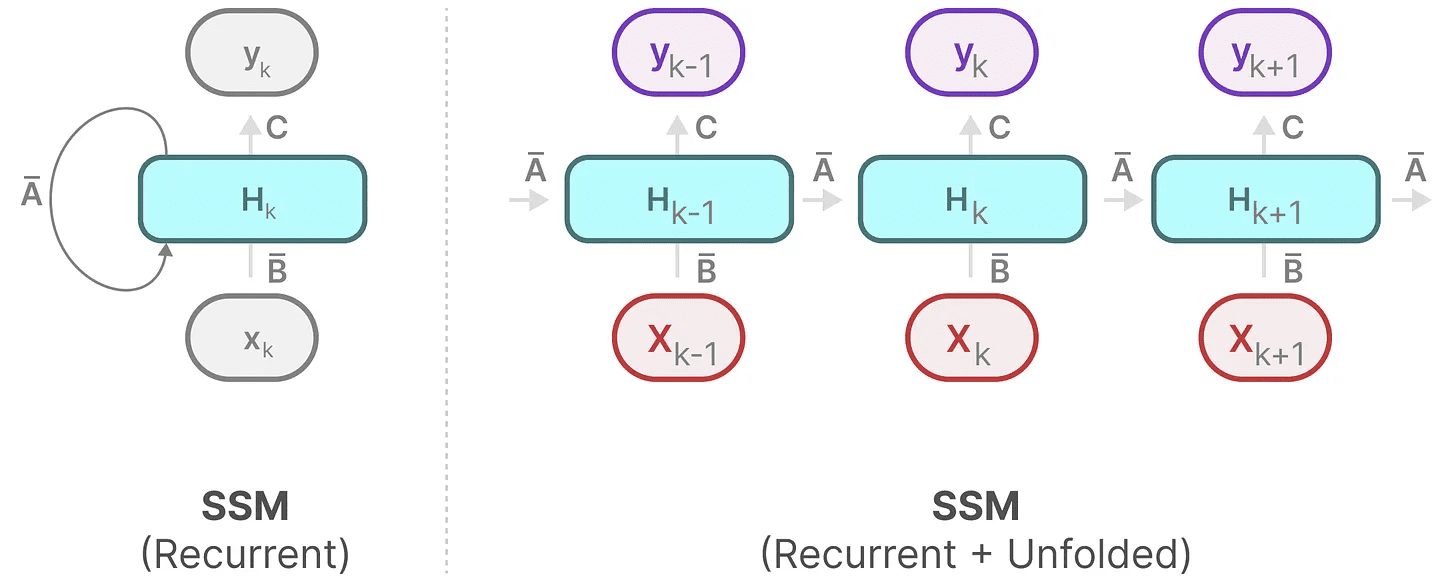なお、RNNの基本的なアプローチを使えば、これを離散化したものを使うこともできる。
畳み込み表現（数学）
古典的な画像認識タスクでは、フィルタ(カーネル)に集約された特徴を抽出する：
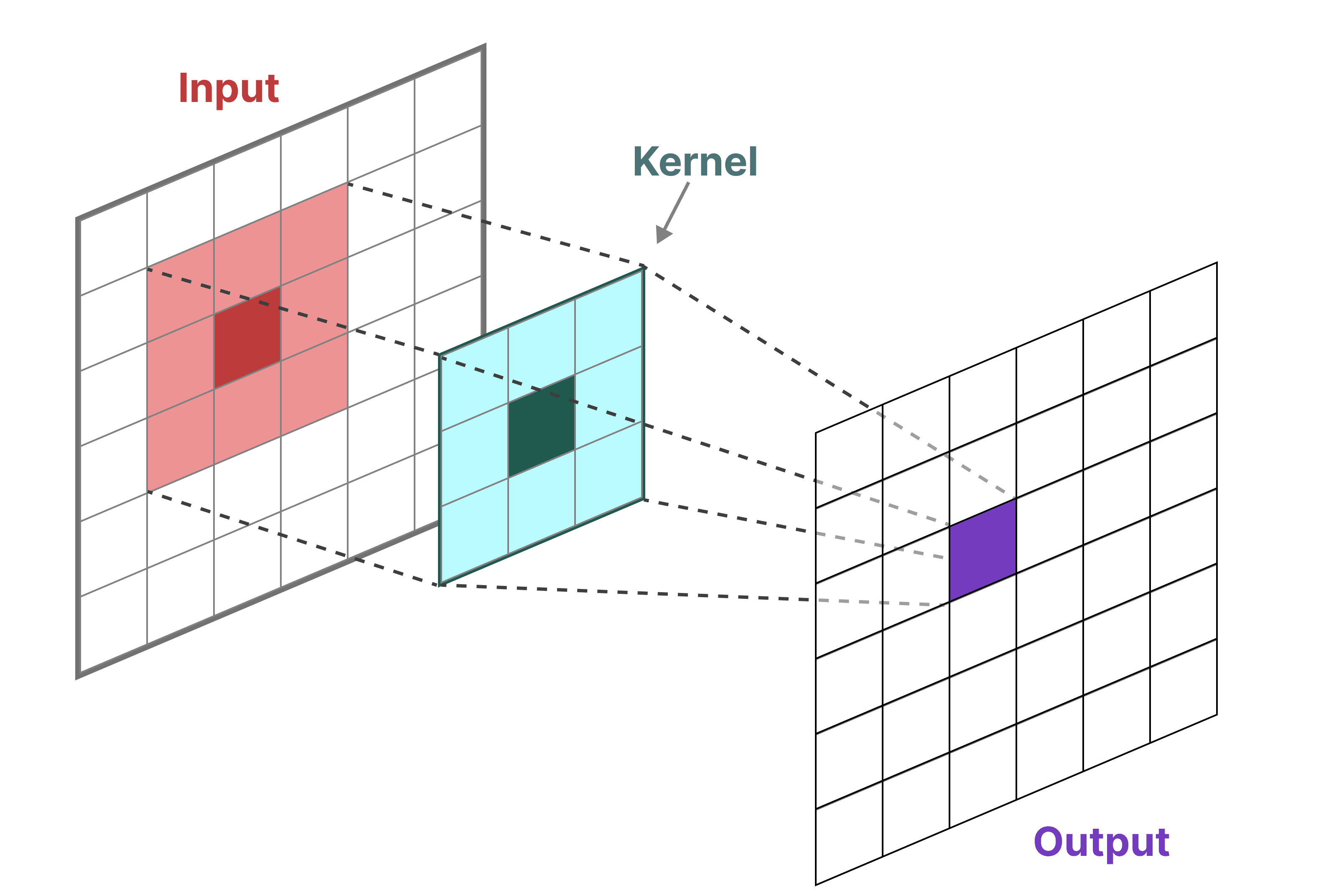画像ではなくテキストを扱っているので、一次元のビューを使う必要がある：
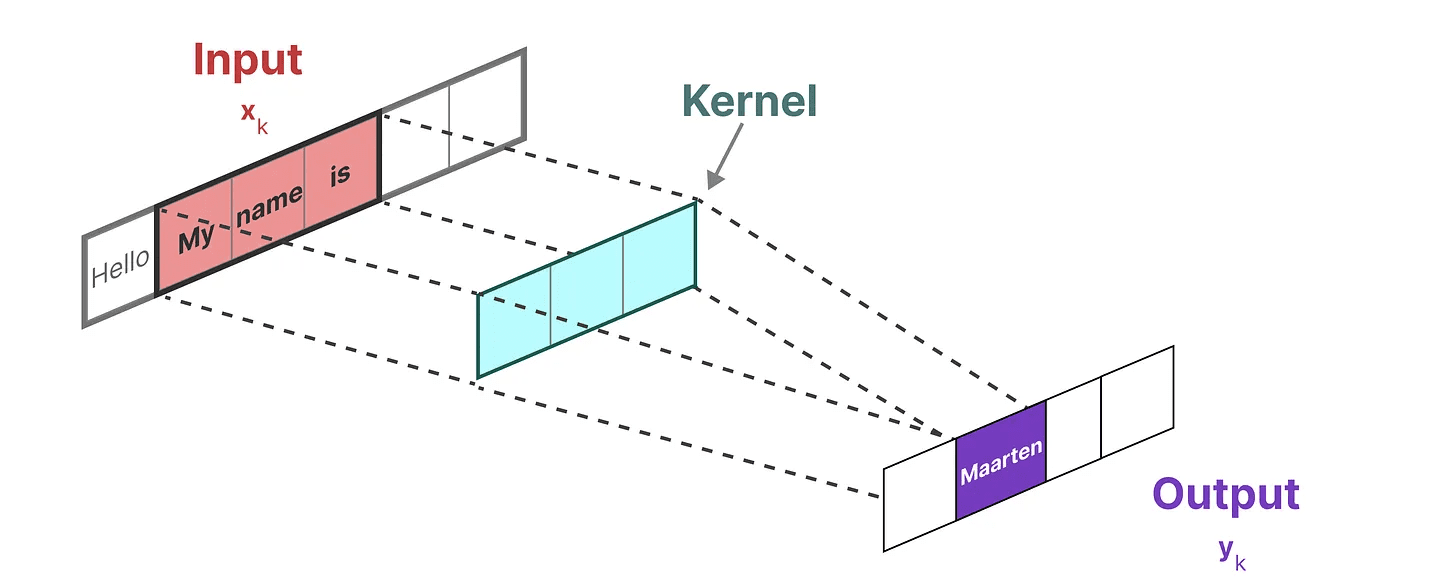この "フィルター "を表すために使用するカーネルは、SSMの公式から導き出される：
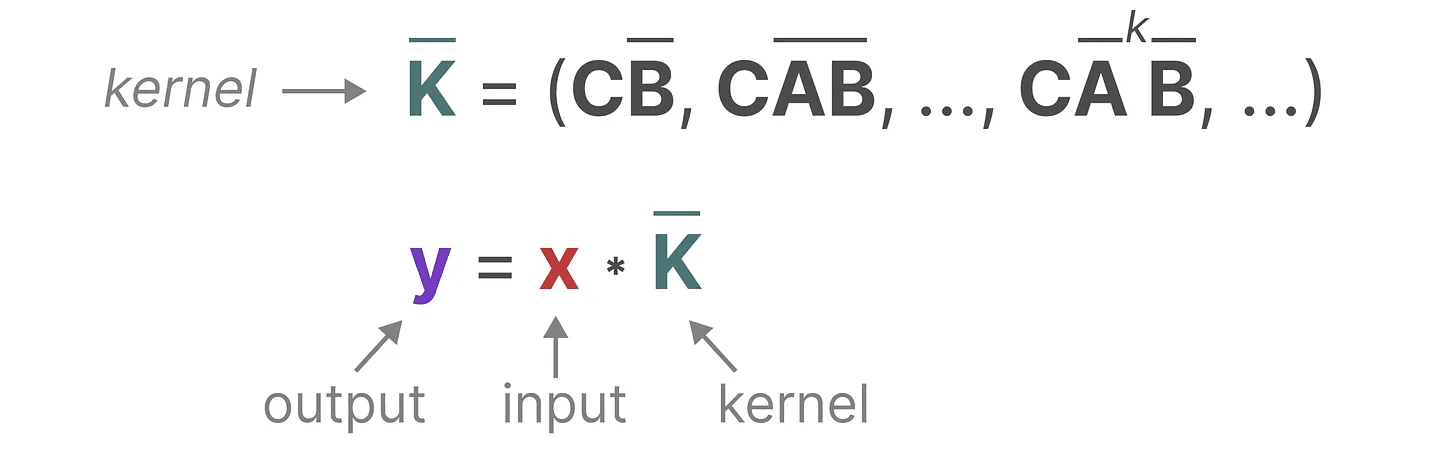このカーネルが実際に何をするのか見てみよう。畳み込みと同様に、SSMカーネルを使ってトークンの各セットをトラバースし、出力を計算することができる：
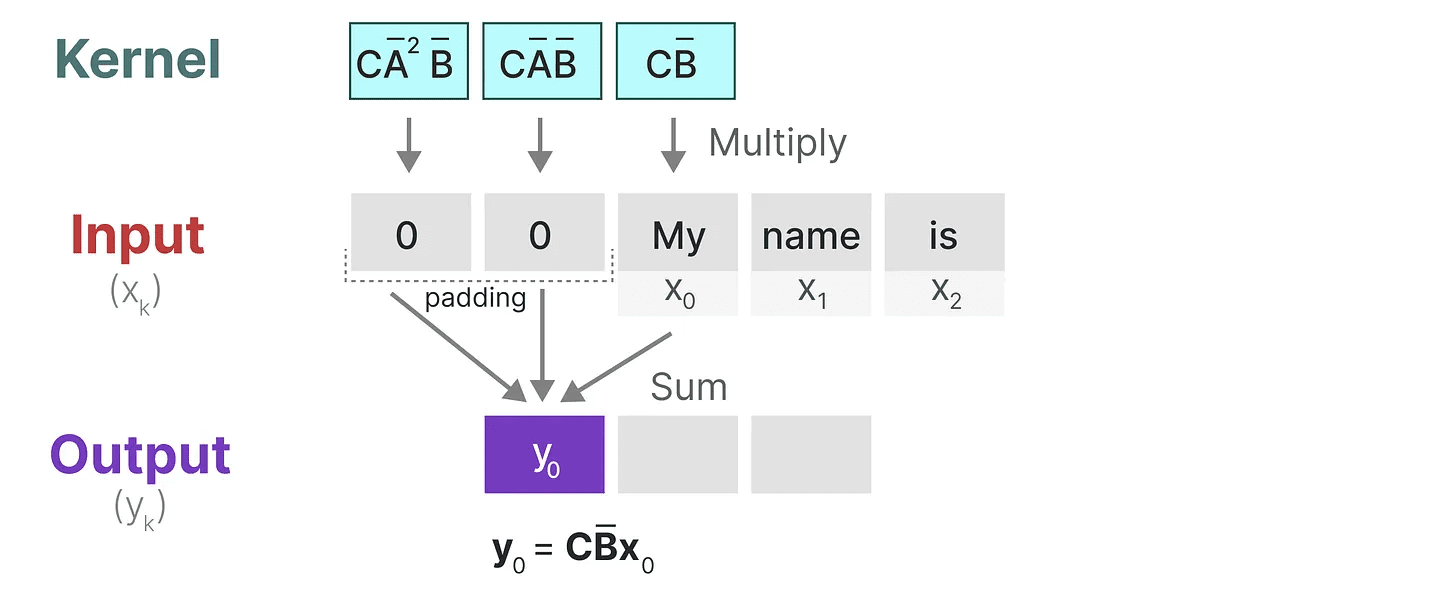これは、パディングが出力に与える影響も示している。見やすくするためにパディングの順番を変えていますが、通常は文末にパディングを適用します。
次のステップでは、カーネルは次のステップの計算を行うために1回移動する：
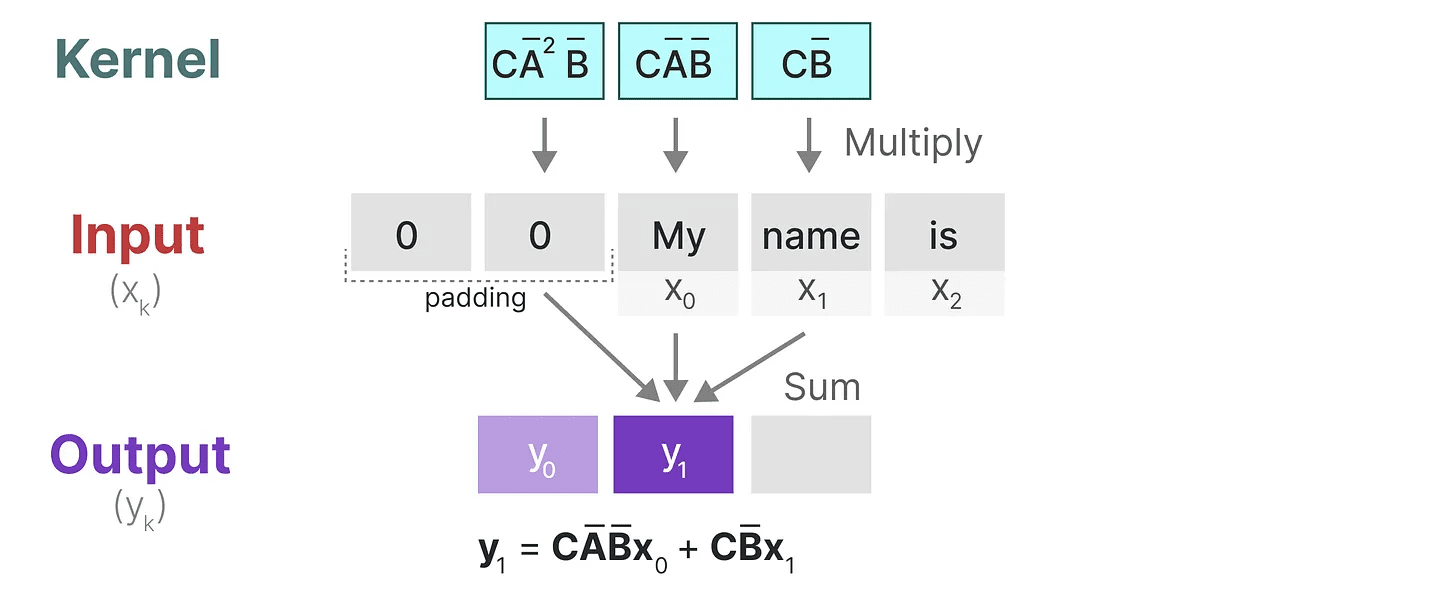最後のステップでは、カーネルの効果を存分に見ることができる：
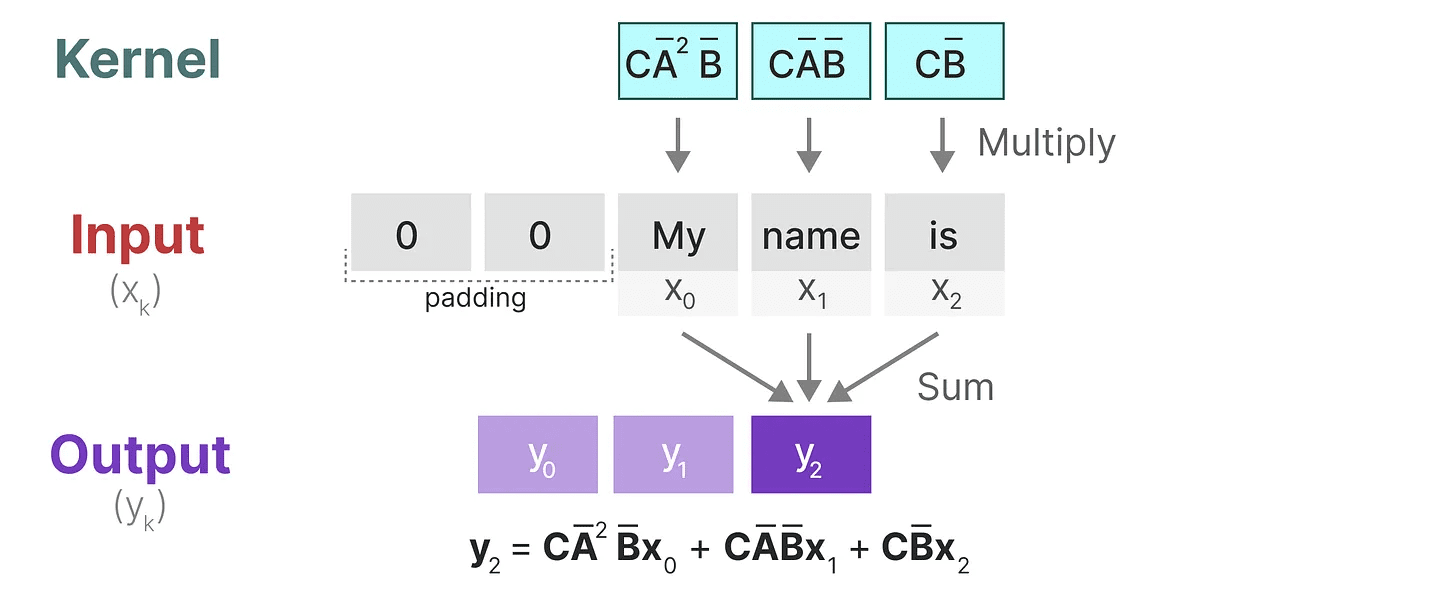SSMを畳み込みとして表現する主な利点の1つは、畳み込みニューラルネットワーク（CNN）のように並列に学習できることである。しかし、カーネルサイズが固定されているため、RNNほど高速で制約のない推論はできない。
3種類の表現
これら3つの表現数列そして再帰的 歌で応える コンヴォリューション それぞれに異なる長所と短所がある：
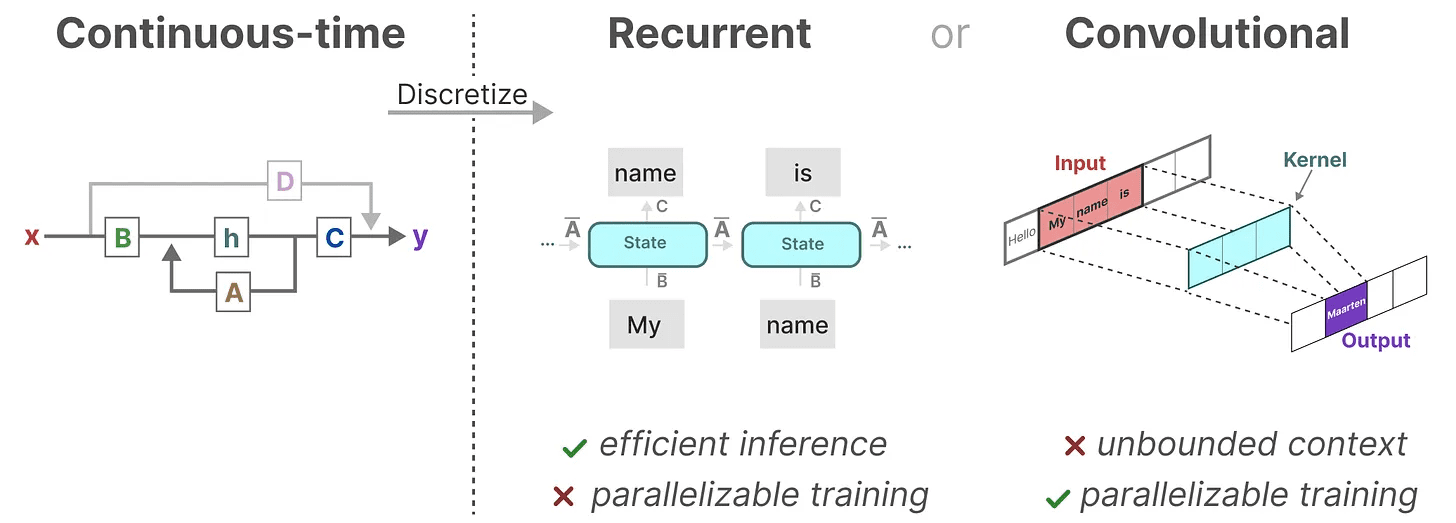興味深いことに、畳み込みSSMを並列学習に使いながら、再帰的SSMを使って効率的な推論ができるようになった。
これらの表現を使って、タスクに応じて表現を選択するという巧妙なトリックを使うことができる。学習時には並列化可能な畳み込み表現を使い、推論時には効率的な再帰的表現を使う：
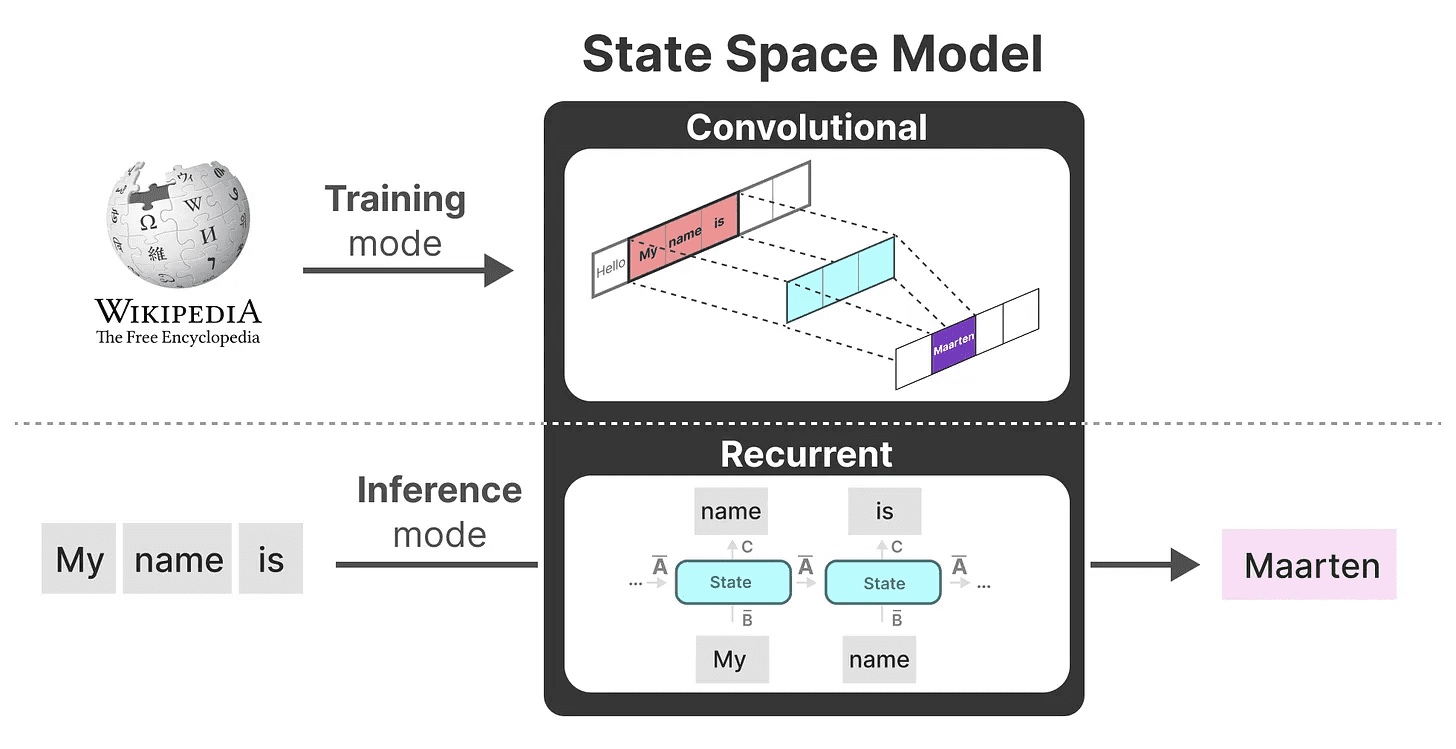このモデルは 線形状態空間層（LSSL）. 2
これらの表現には重要な性質がある。線形時間不変（LTIはSSMのパラメータを示す。 AそしてB 歌で応える C はすべての時間ステップで固定される。これは AそしてB 歌で応える C は、生成されるすべてのトークンに対して同じである。
つまり、SSMにどのような順序を与えてもいい。AそしてB 歌で応える C それらの値はすべて同じままである。中身を気にしない静的な表現をしているのだ。
マンバがこの問題をどのように解決するのかを探る前に、パズルの最後のピースであるマトリックスA.
マトリックス A 重要性
おそらく、SSM方式の最も重要な側面のひとつは マトリックスA.前に再帰的表現で見たように、この表現には 前回 を構築するための状態に関する情報である。 リニューアル ステータス
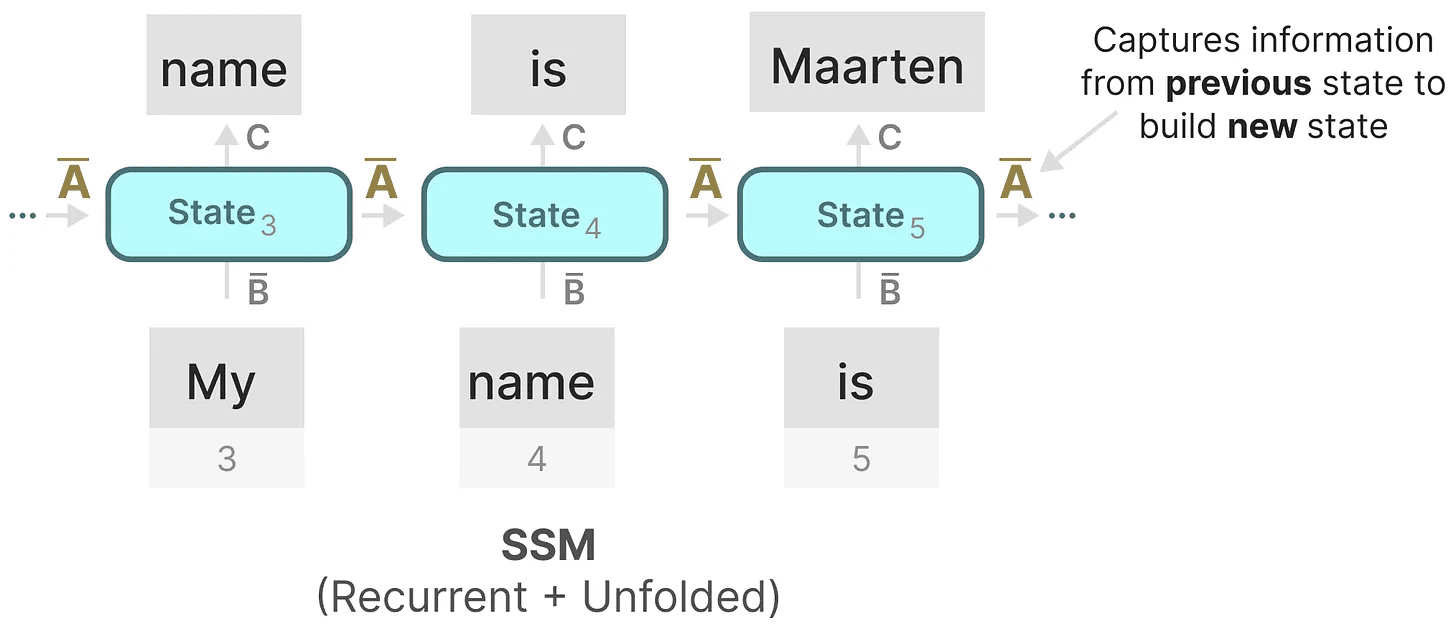本質的なことだ。マトリックスA 隠された状態を生成する：
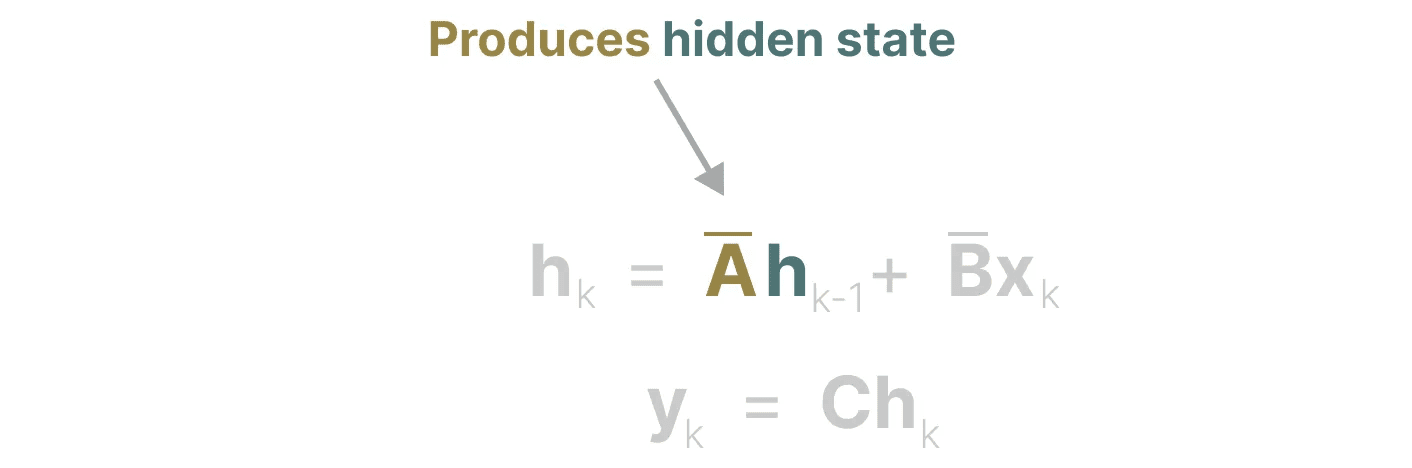従って、次のようなものを作る必要がある。 マトリックスA 特に、再帰的表現の文脈においては、トークンのみを記憶することはできない。 を思い出す。 前の状態.
多くのメモリ（コンテキストサイズ）を保持する方法で作成する方法 行列A?
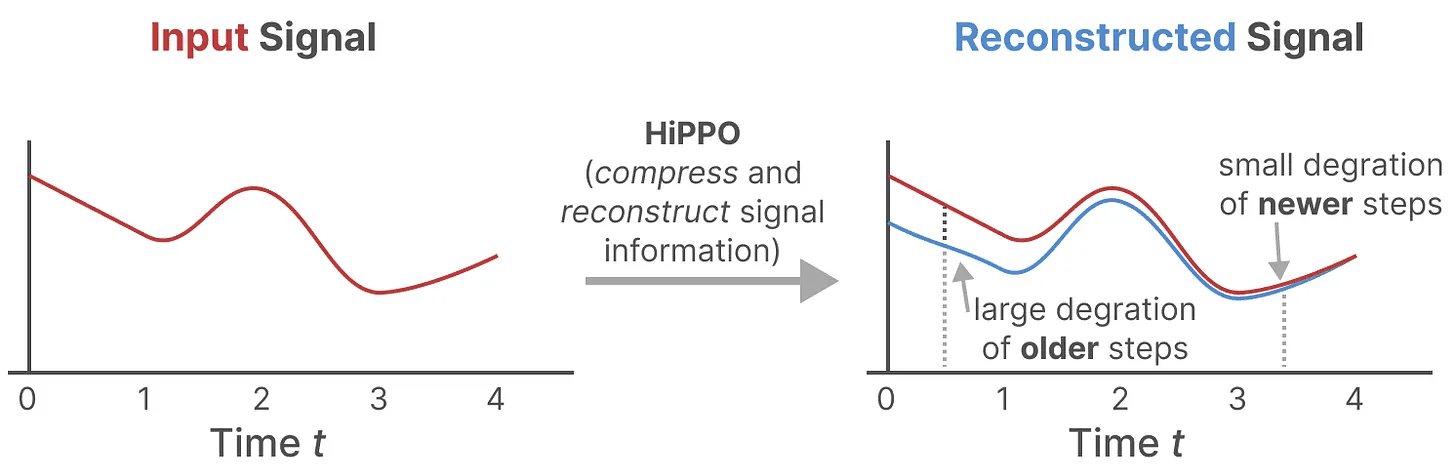
はらぺこヒッポを使うか ハイプポ3 実現するために御前階段 どのように項 身を置くフィルム 運operator.HiPPOは、これまでに見たすべての入力信号を係数のベクトルに圧縮しようとする。
を使用している。 行列A この式は次のように表すことができる：
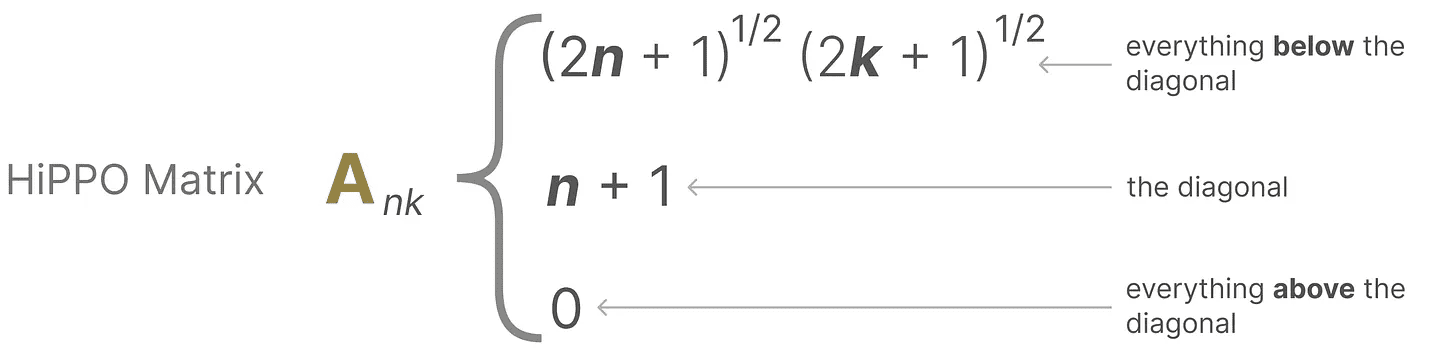正方形があるとする。 行列Aこれによって私たちは
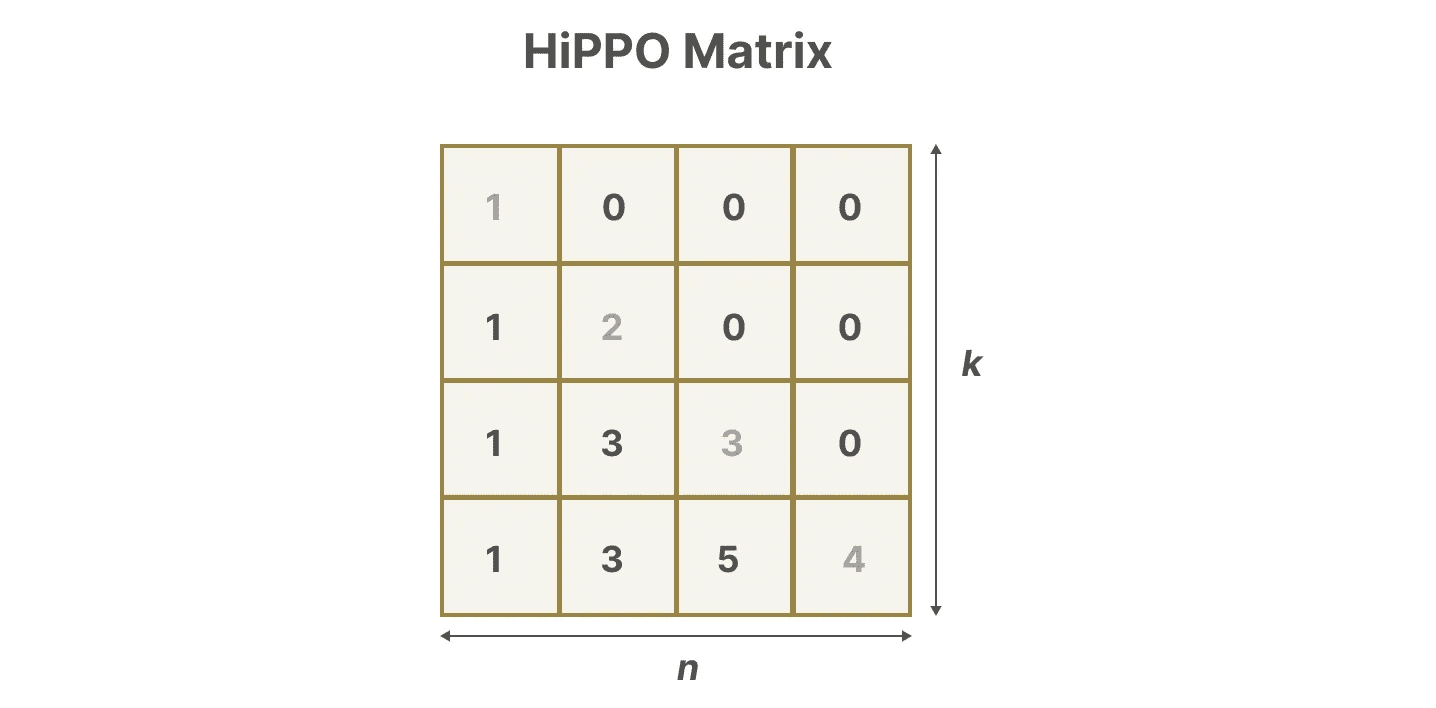HiPPOを使った建築 行列A をランダム行列に初期化するよりもはるかに優れていることが証明された。したがって 更新 信号（最も近いトークン）という側面は、以下のことよりも重要である。 年上 シグナル（イニシャル・トークン）の方が正確だ。
HiPPOマトリックスの核となるアイデアは、履歴を記憶する隠された状態を生成することである。
数学的には、次のようになる。 レジェンド多項式 係数を使用することで、すべての過去の記録を近似することができる。4
HiPPOは次に、長距離依存性を処理するために、前に見た再帰的表現と畳み込み表現に適用される。その結果 シーケンスの構造化状態空間 (S4)SSMは、長いシーケンスを効率的に処理できるSSMのクラスである。5
3つの部分から構成されている：
- 状態空間モデル
- 加工用HiPPO 長距離依存
- ディスクレチゼーションは、次のような目的で使用される。 再帰的 歌で応える コンヴォリューション 示す
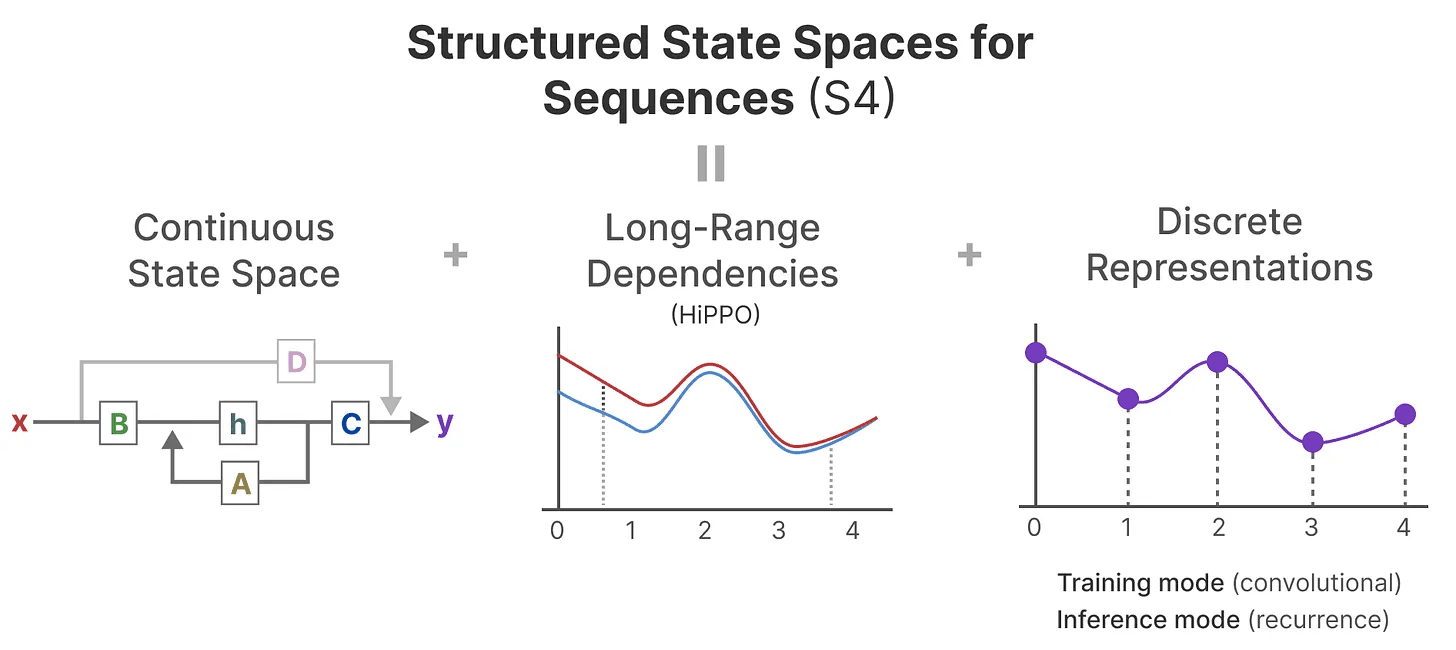このタイプのSSMには、選択する表現（再帰的か畳み込みか）によっていくつかの利点がある。また、HiPPO行列をベースにしているため、長いテキスト列を扱ったり、メモリを効率的に格納したりすることができる。
銘記するHiPPOマトリックスの計算方法やS4モデルの作成方法についてより深く理解したい場合は、以下を読むことを強くお勧めする。 注釈付きS4.
パート3：マンバ - 選択的状態空間モデル
ここまでで、Mambaの特徴を理解するのに必要な基本的なことはすべて終わった。状態空間モデルはテキストシーケンスのモデリングに使うことができるが、まだ避けたい欠点がいくつかある。
このセクションでは、マンバの2つの主な貢献について説明する：
- 一種類 選択的走査アルゴリズムモデルが（関連性のない）情報を選別できるようにする。
- 一種類 ハードウェア対応アルゴリズムを使用する。 パラレルスキャンそしてカーネルフュージョン 歌で応える 再計算 中間）結果を効率的に保存する。
この2つが組み合わさることで 選択的状態空間モデリング もしかしたら S6 このモデルは、セルフ・アテンション・モデルのようなものだ。 マンバ・ブロック.
これら2つの主な貢献を探る前に、まず、なぜそれらが必要なのかを探ってみよう。
解決しようとしている問題は何か？
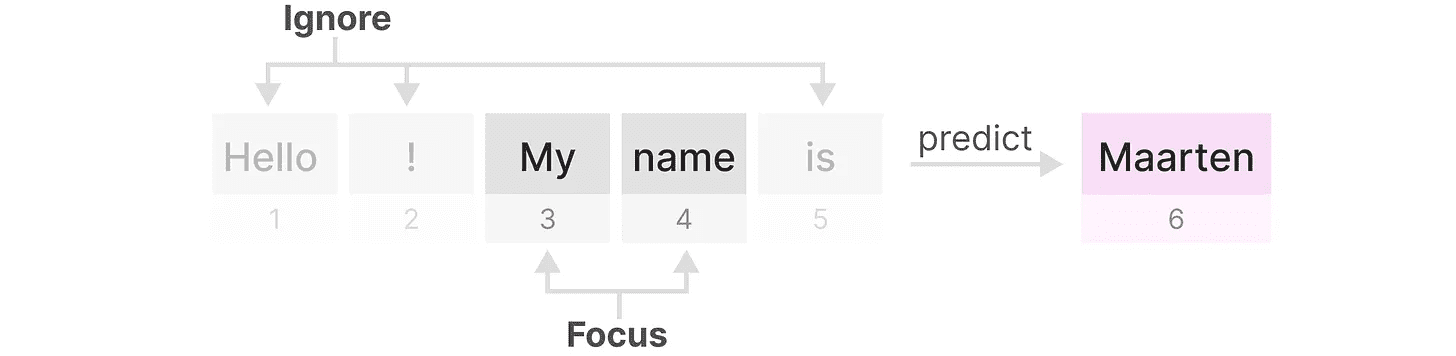
状態空間モデルは、たとえS4（構造化状態空間モデル）であっても、言語モデリングと言語生成における特定の重要なタスク、つまり、以下のようなタスクでは性能が低い。 特定の入力に集中したり無視したりする能力.
これを2つの合成タスクで説明しよう。 選択コピー 歌で応える インデューサーヘッド.
ある 選択コピー タスクにおけるSSMの目的は、入力されたパーツをコピーして順番に出力することである：
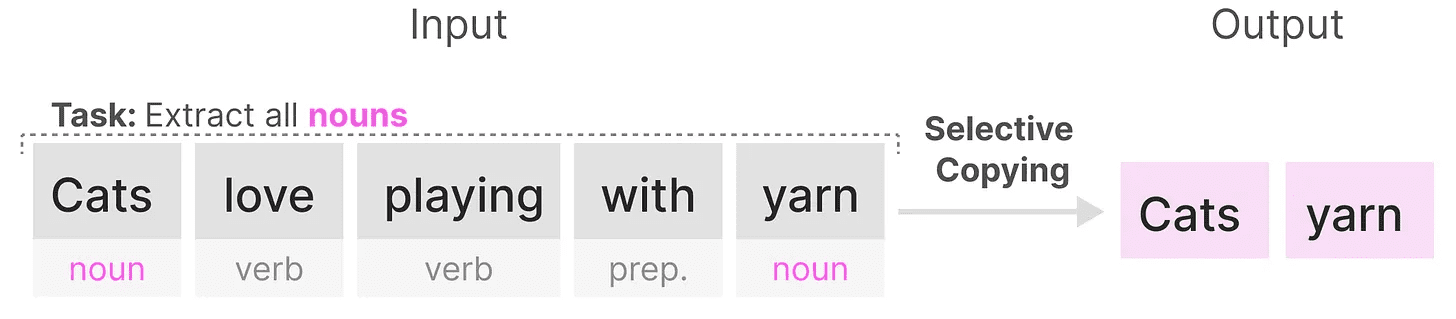しかし、SSMは 線形時間不変なというのは、このタスクではパフォーマンスが低いからである。前に見たように、行列 AそしてB 歌で応える C 生成されるトークンはすべてSSMと同じである。
その結果、SSMが実行できなくなった。 内容を考慮した推論というのも、SSMはA、B、Cの固定マトリックスによって各トークンを平等に扱うからである。
SSMは、もうひとつの課題、つまり、次のような課題では劣っている。 インデューサーヘッドその目的は、入力に見られるパターンを再現することである：
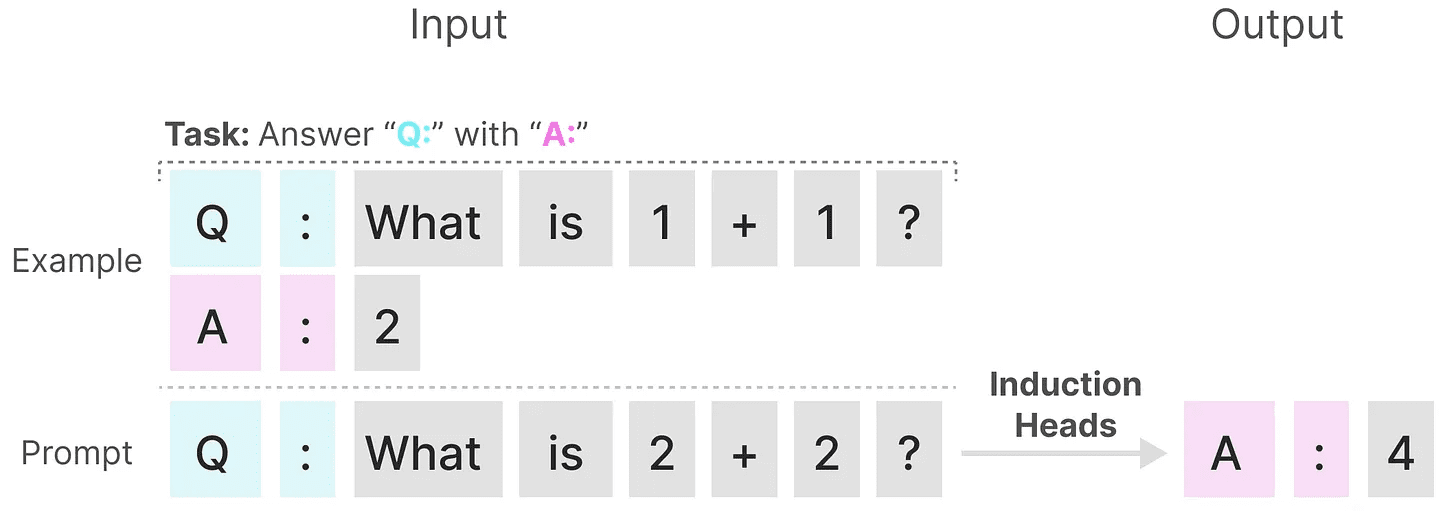上記の例では、基本的に1回限りのプロンプトを実行している。Q.「を提供した後、"A."という応答を返す。しかし、SSMは時間不変であるため、履歴からどの前のトークンを呼び出すかを選択することはできない。
そのためには マトリックスB この点を説明する。入力に関係なく x それが何か。マトリックスB は常に同じである。 x 無関係だ：
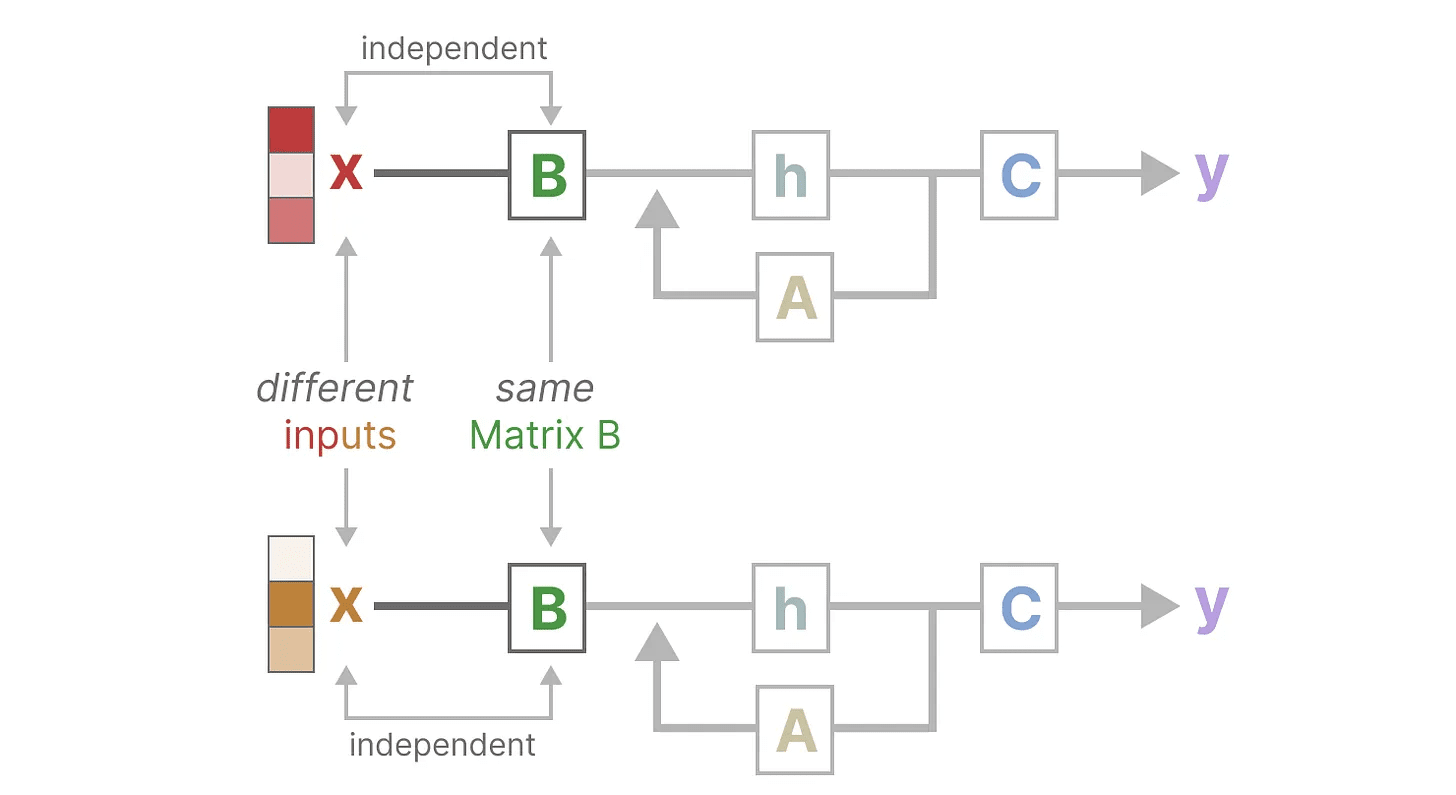同様に。A 歌で応える C も、入力とは無関係に常に固定されたままである。このことは、これまで見てきたSSMの 静電気 特徴
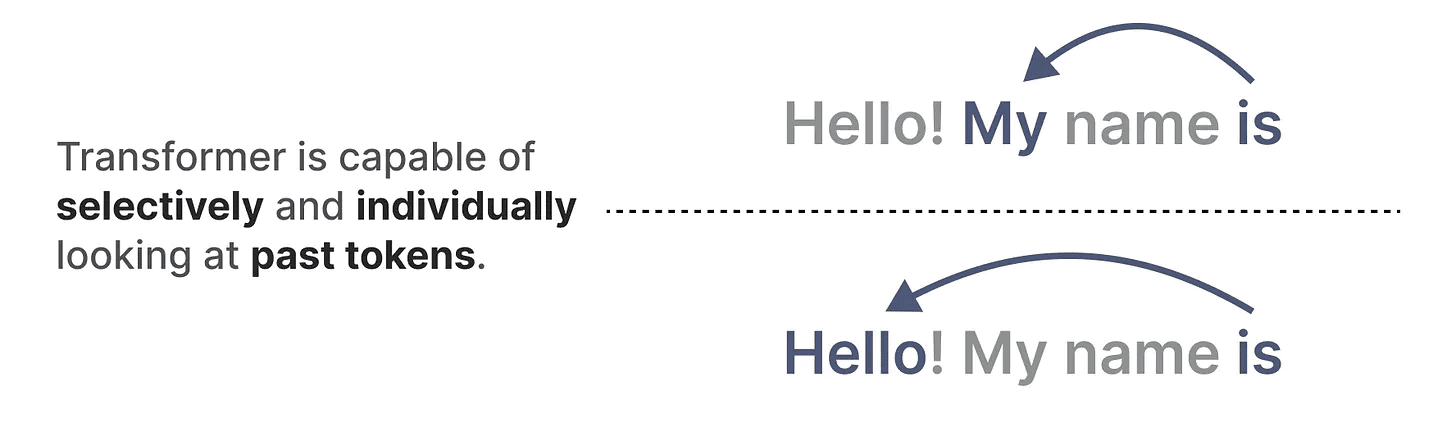
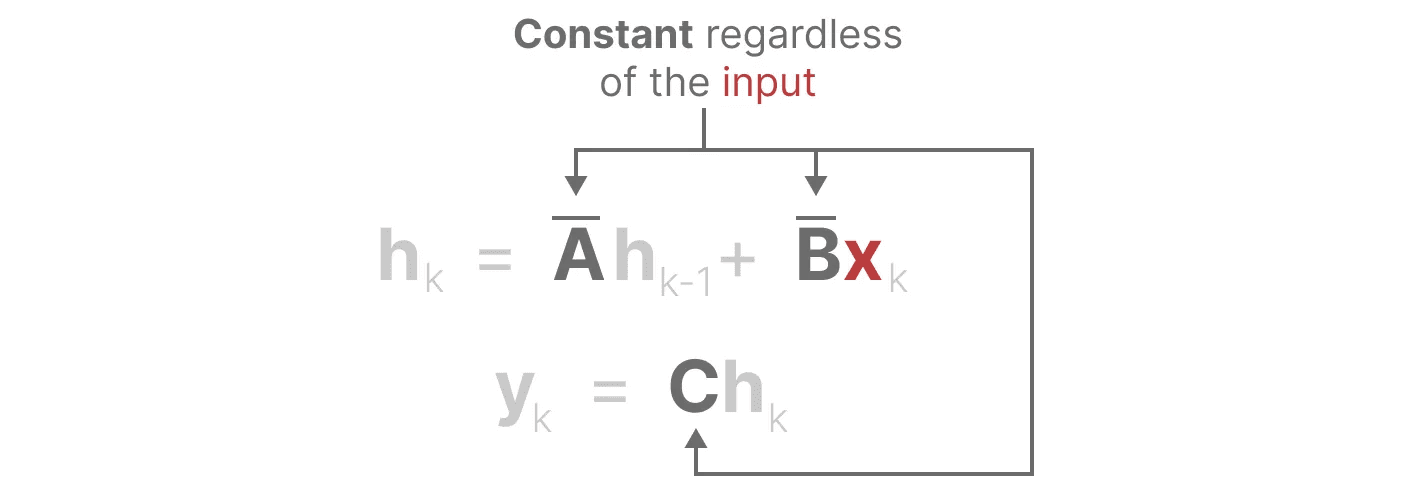対照的に、トランスフォーマーにとってこれらのタスクは比較的単純である。 どうたい 注意を変える。彼らはシークエンスの異なる部分を選択的に「見る」あるいは「集中する」ことができる。
これらのタスクにおけるSSMのパフォーマンスの低さは、時変SSMの潜在的な問題を示している。 AそしてB 歌で応える C の静的な性質 コンテンツ・センス 問題の
情報の選択的保持
SSMの再帰的表現は、履歴全体を圧縮するため、より小さな状態を作り出し、非常に効率的である。しかし、Transformerモデルと比較すると、Transformerモデルは（Attention Matrixを介して）履歴を圧縮しないので、より能力が高い。
マンバは両方の長所を併せ持つことを目指している。トランスフォーマー国家に匹敵するパワーを持つ小さな国家：
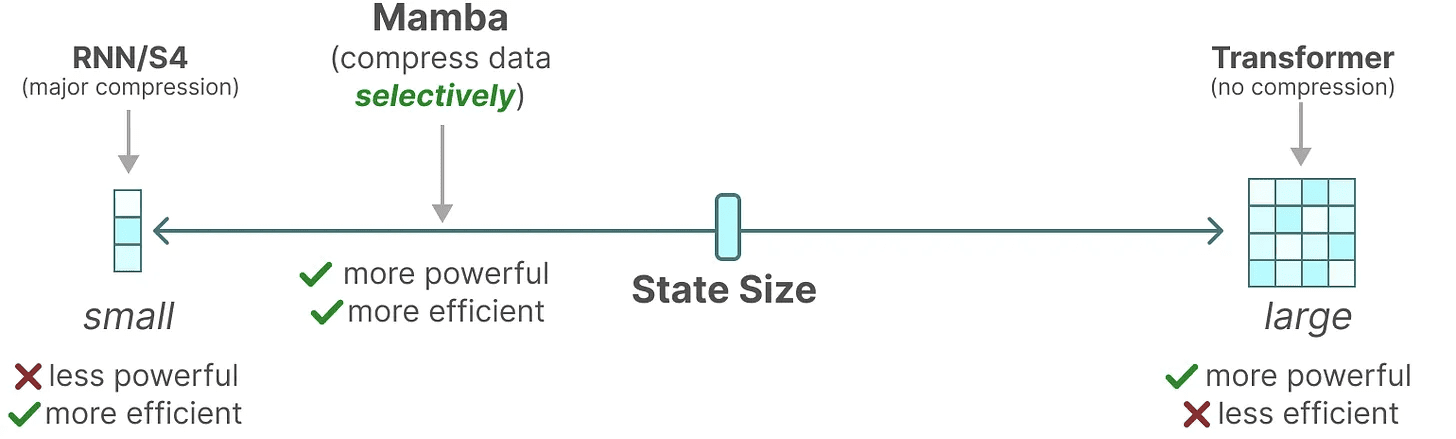前述したように、データを選択的に状態に圧縮することでこれを行う。入力文がある場合、ストップワードなど、あまり意味のない情報があるのが普通だ。
情報を選択的に圧縮するためには、パラメータが入力に依存する必要がある。この目的のために、まず学習中のSSMの入力と出力の次元を探ってみよう：
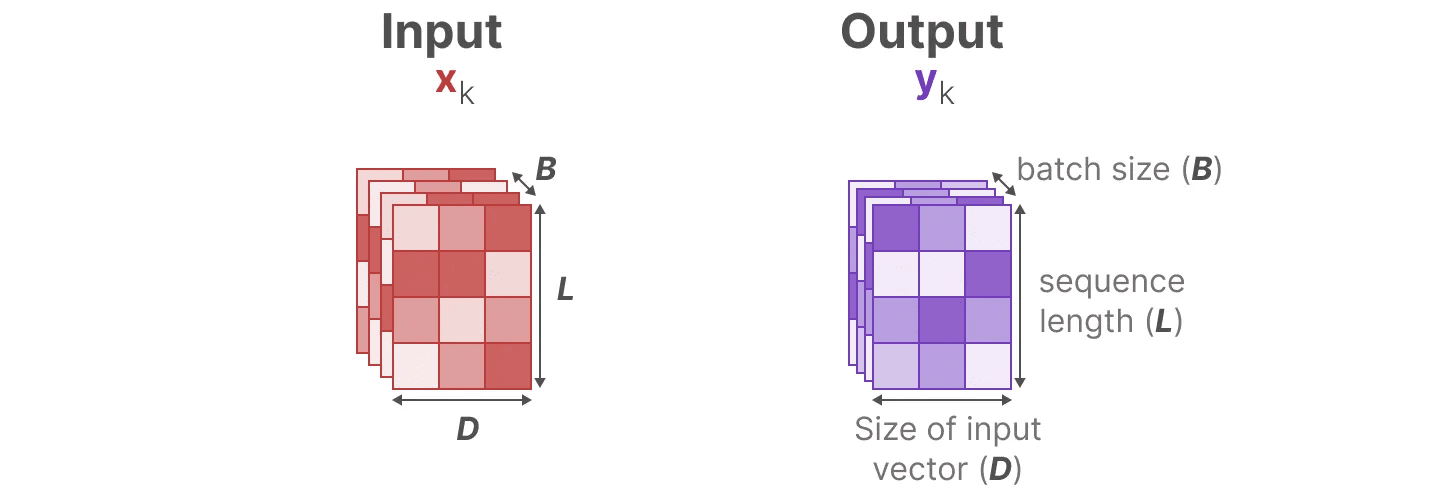構造化状態空間モデル（S4）では、行列 AそしてB 歌で応える C なぜなら、その次元は入力に依存しないからである。 N 歌で応える D は静的で変化しない。
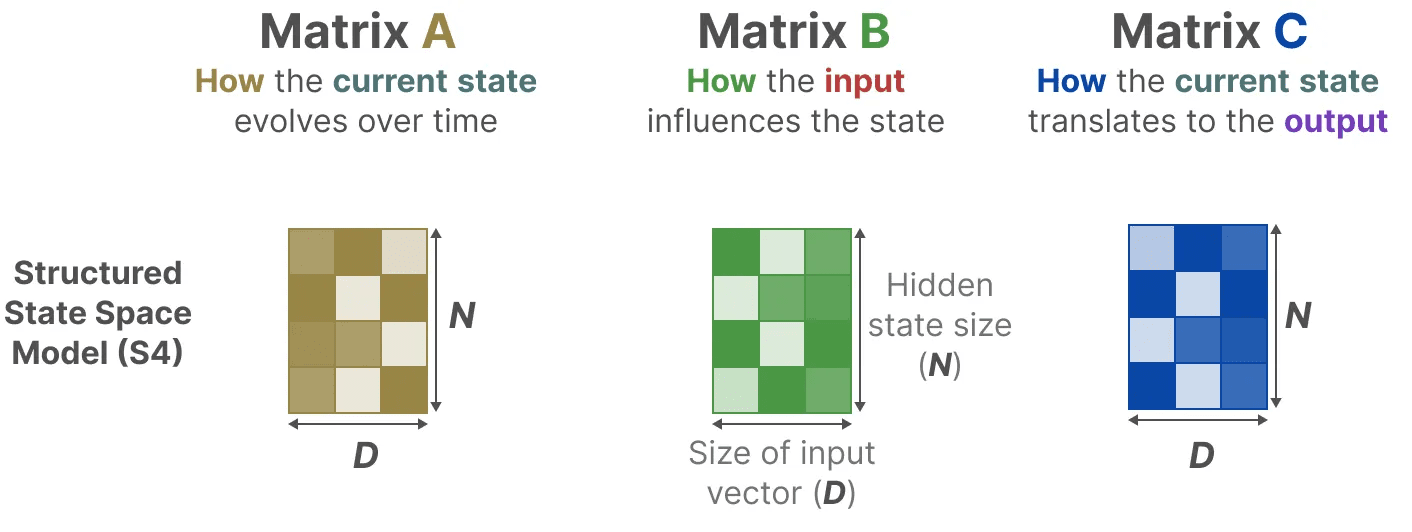その代わりに、Mambaは、入力シーケンスの長さとバッチサイズを組み合わせることで、行列を作る。 B 歌で応える Cでさえ ペースメーカー ∆入力次第：
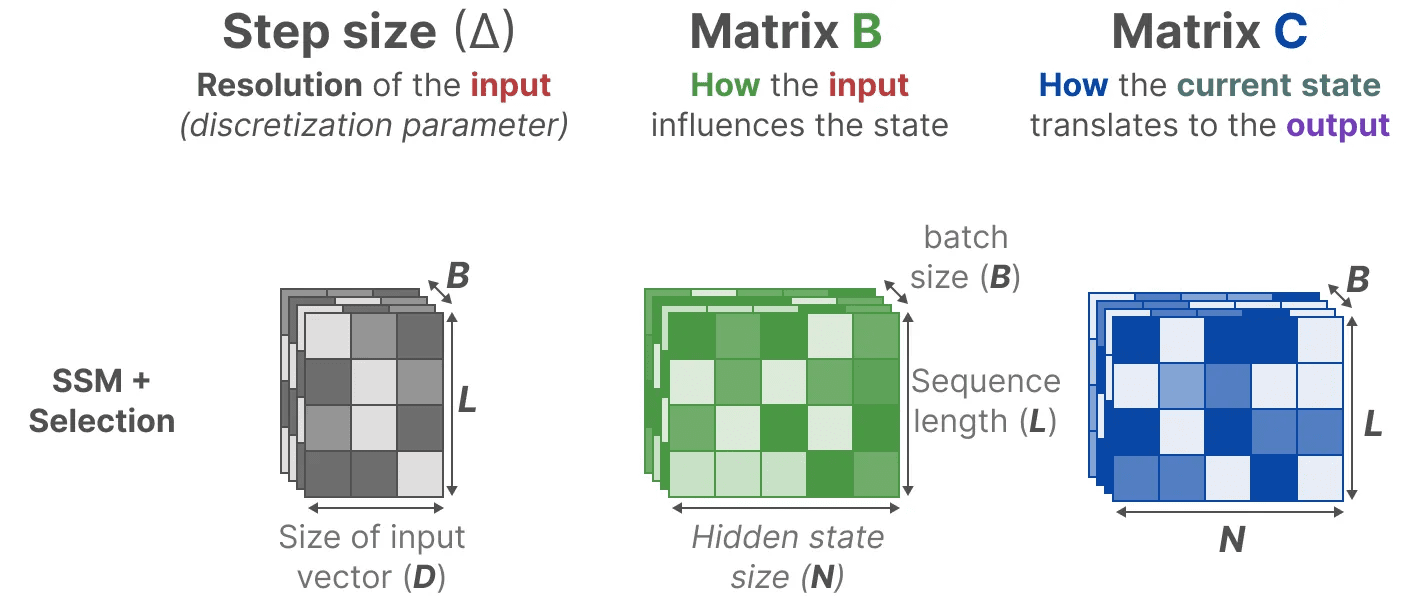つまり、各入力トークンに対して、異なる B 歌で応える C マトリックスで、内容認知の問題を解決する！
銘記するマトリックス A というのも、状態そのものは静止したままにしておきたいからだ。 B 歌で応える C)は動的である。
一緒に 択一的に 非表示の状態を維持するものと、入力に依存するようになったので無視するものを選択する。
より小さい ペースメーカー ∆ が大きくなると、前の文脈を優先して特定の単語を無視するようになる。 ペースメーカー ∆ その代わり、文脈よりも入力語彙に焦点が当てられている：
スキャン操作
これらの行列は現在 どうたい を前提とする畳み込み表現では計算できない。 固定 畳み込みカーネルの再帰的表現しか使えないので、畳み込みが提供する並列化の利点は失われる。
並列化を実現するために、再帰を使って出力を計算する方法を探ってみよう：
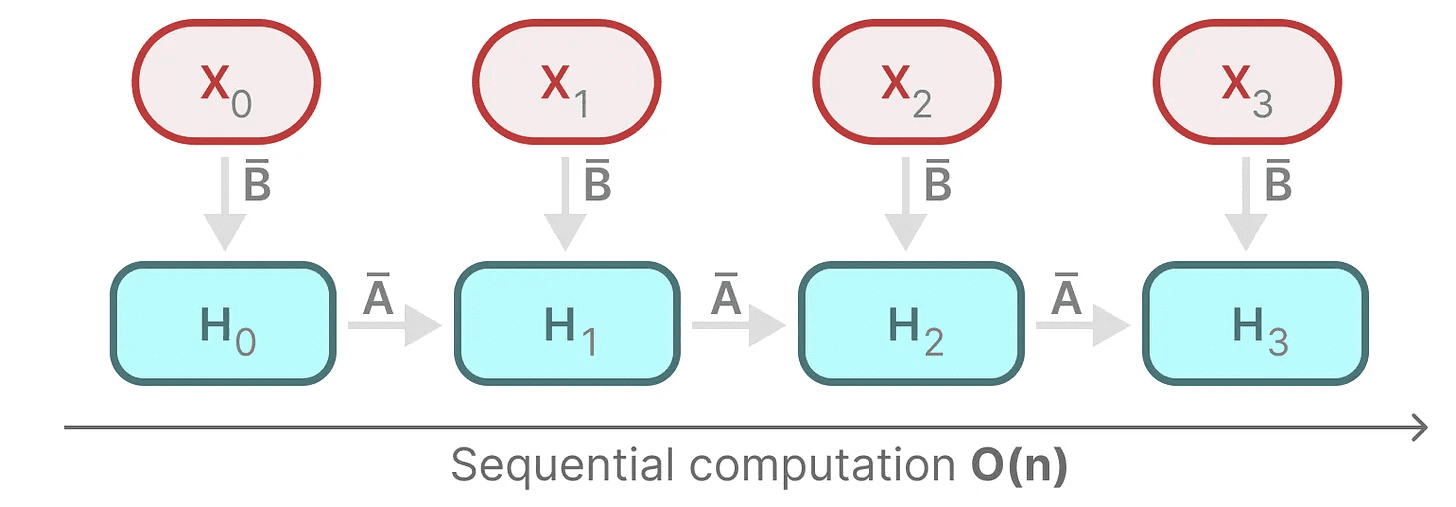各状態は、前の状態（を乗じたもの）である。 Aを乗じたもの）を現在の入力に加える。 B)である。これは スキャン操作これはforループで簡単に計算できる。
対照的に、各状態は前の状態が利用可能になってからしか計算できないため、並列化は不可能に思える。しかし、Mambaは、各状態の並列化を可能にした。 パラレルスキャン アルゴリズムがこれを可能にしている。
これは和の法則の性質を利用したもので、演算の順番は重要でないと仮定している。したがって、部分的にシーケンスを計算し、それらを反復的に結合することができる：
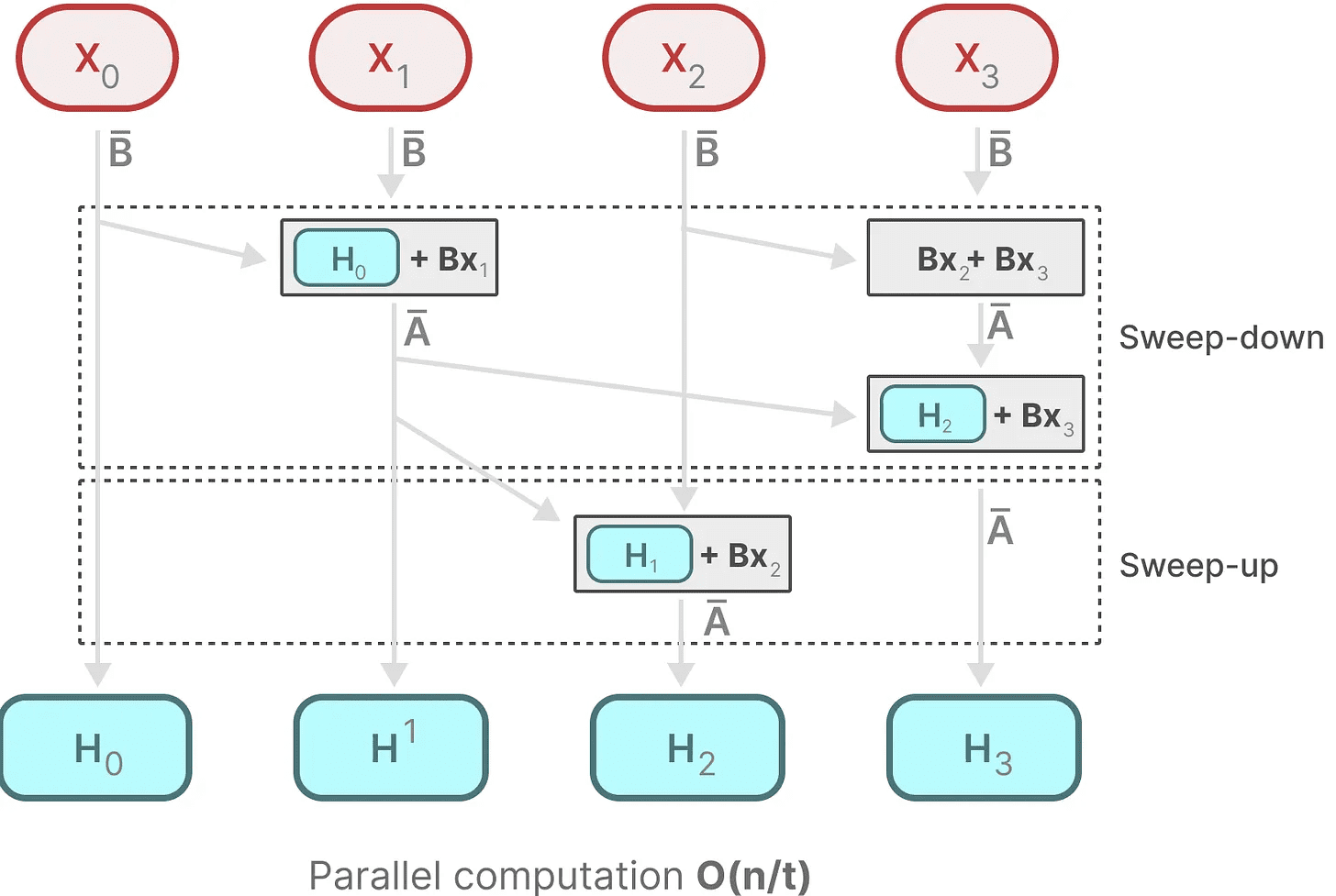ダイナミックマトリクス B 歌で応える C とパラレル・スキャン・アルゴリズムが組み合わさって誕生した。 選択的走査アルゴリズム再帰的表現の動的で高速な性質を表現する。
ハードウェア対応アルゴリズム
最近のGPUの欠点の1つは、小さいが効率的なSRAMと、大きいが効率はやや劣るDRAM間の転送（IO）速度が限られていることだ。SRAMとDRAM間の頻繁な情報のコピーがボトルネックになる可能性があります。
マンバは、DRAMからSRAMへの往復の回数を制限しようとする点で、フラッシュ・アテンションと似ている。そのために カーネルフュージョン これを実装することで、中間結果の書き込みを防ぎ、計算が完了するまで計算を実行し続けることができる。
マンバの基本アーキテクチャを視覚化することで、DRAMとSRAMの割り当ての具体例を見ることができる：
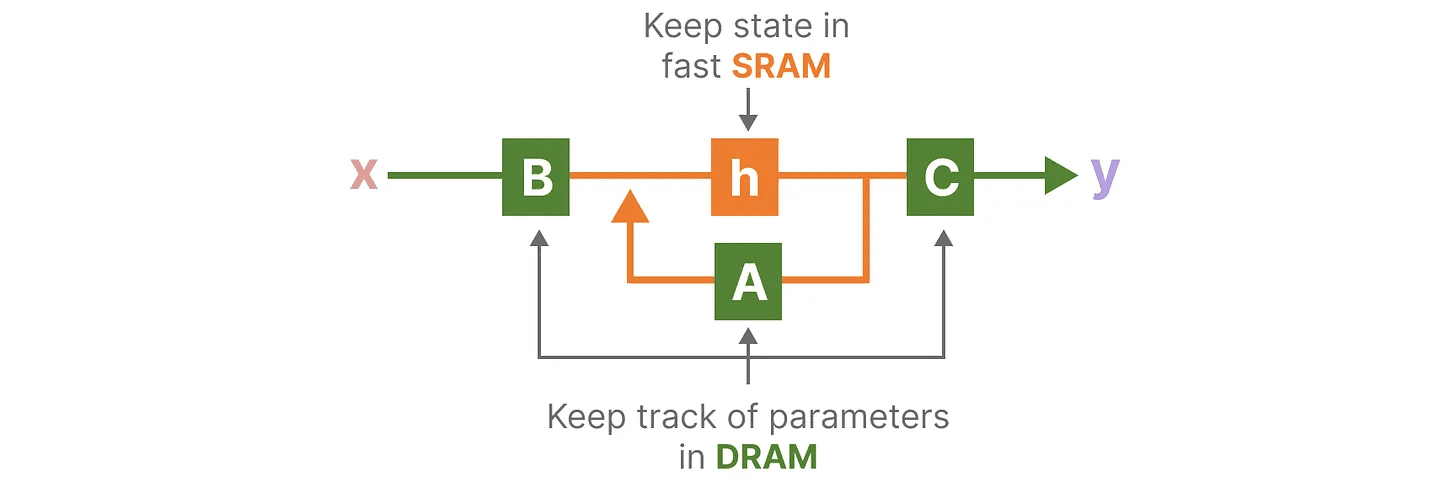ここでは、以下が1つのカーネルに融合されている：
- 離散化のステップは ステップサイズ ∆
- 選択的走査アルゴリズム
- とともに C 乗算
ハードウェア対応アルゴリズムの最後の部分は 再計算.
中間状態は保存されないが、リバースパスで勾配を計算するのに必要である。その代わり、著者らはリバース・パスの間にこれらの中間状態を再計算する。
これは非効率的に見えるかもしれないが、比較的低速のDRAMからこの中間状態をすべて読み出すよりははるかに安上がりだ。
我々は現在、そのアーキテクチャーのすべての構成要素を網羅している：
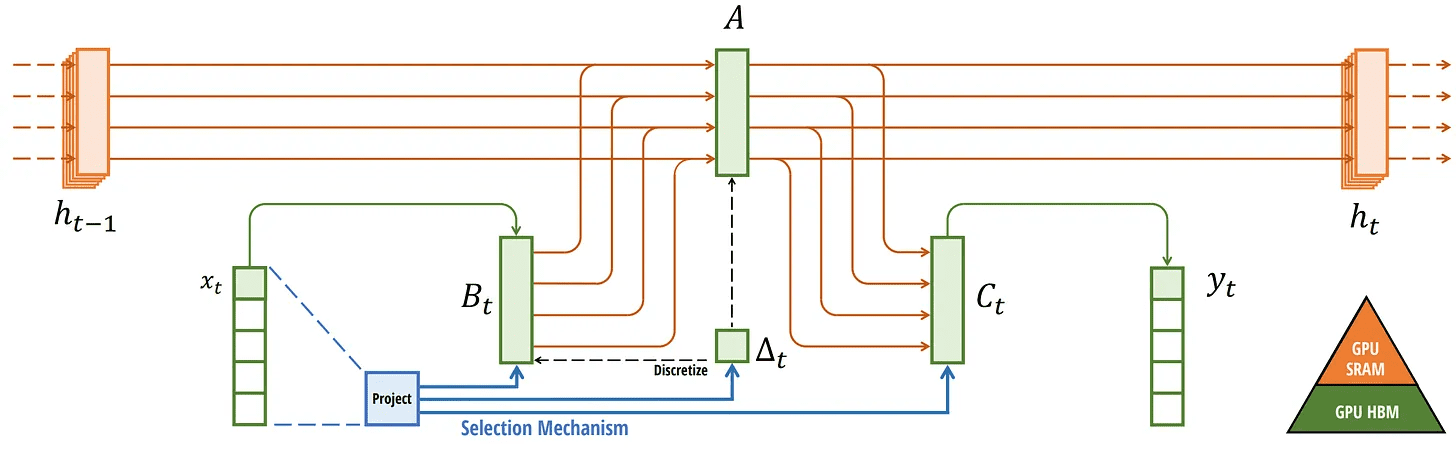選択的SSM。 Mamba: 選択的状態空間による線形時系列モデリング". arXiv preprint arXiv:2312.00752 (2023).
このアーキテクチャはしばしばこう呼ばれる。 選択的SSM もしかしたら S6 このモデルは、基本的に選択的スキャニング・アルゴリズムを使って計算されたS4モデルだからだ。
マンバモジュール
これまで探求してきたこと 選択的SSM デコーダー・モジュールで自己注意を表現できるように、モジュールとして実装することができる。
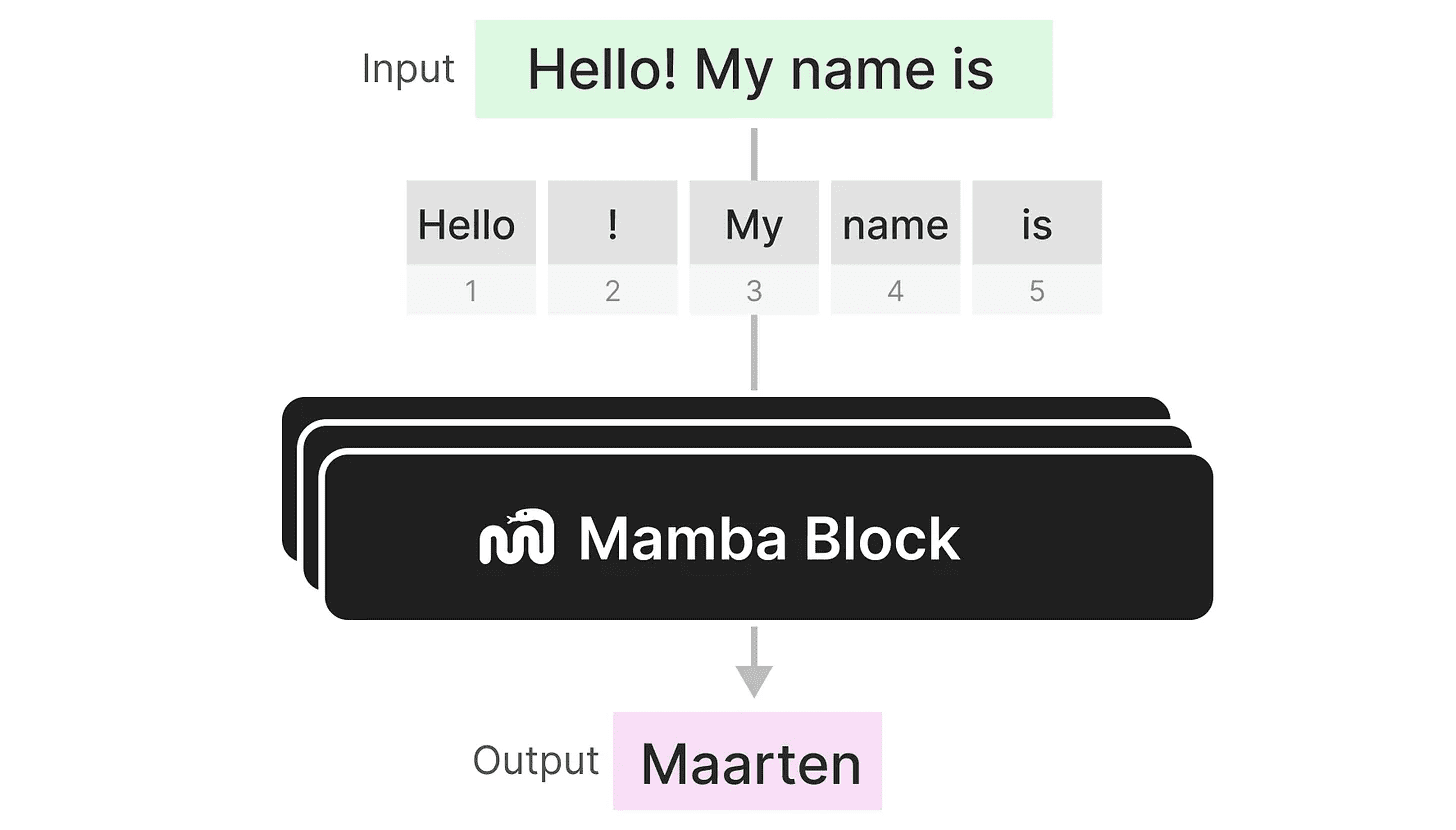デコーダーのように、複数のMambaモジュールをスタックし、その出力を次のMambaモジュールの入力として使うことができる：
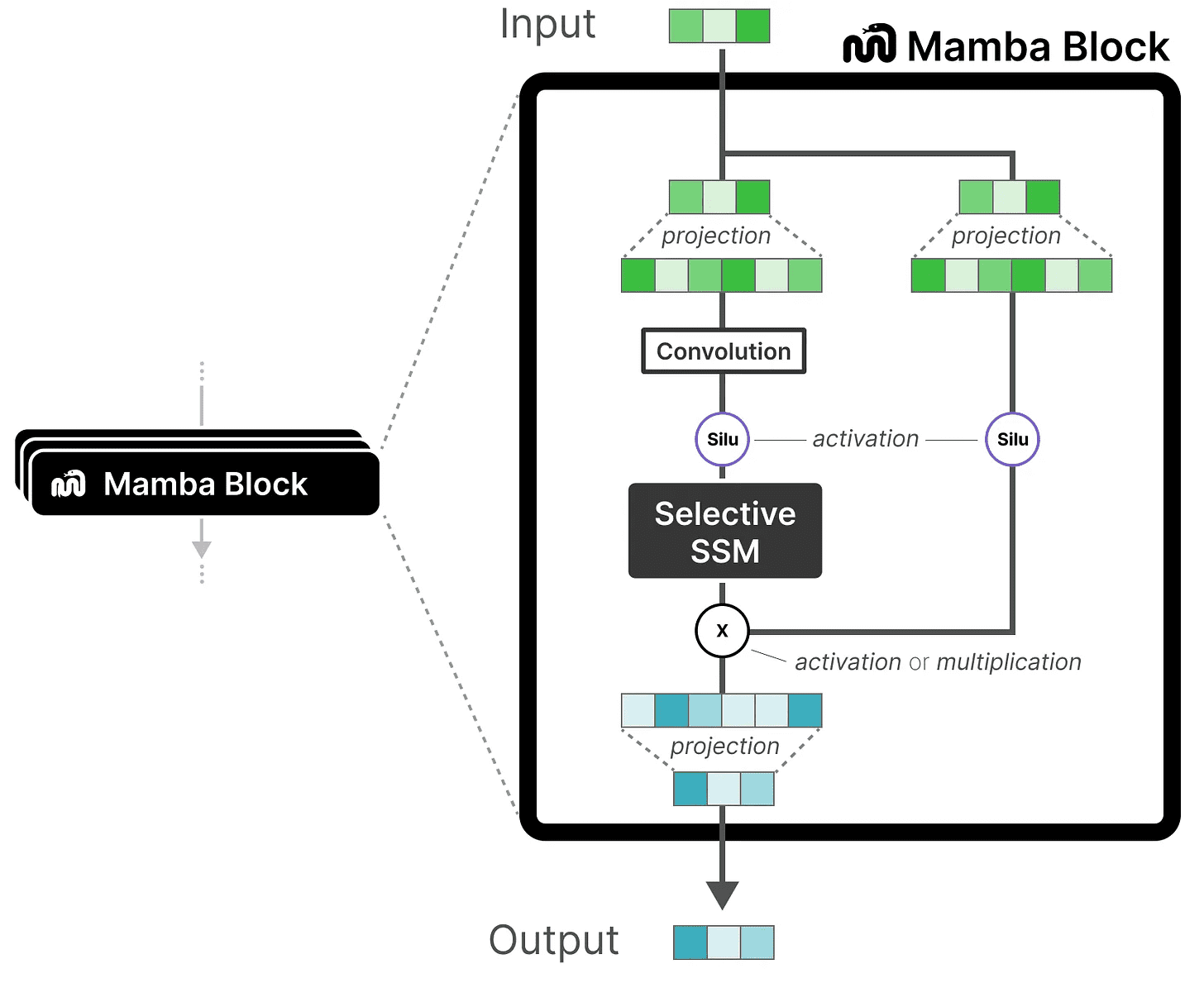入力の埋め込みを拡張するための線形射影から始まる。次に 選択的SSM 独立したトークンの計算を防ぐために、コンボリューションが適用される。
選択的SSM には次のような特徴がある：
- とおす 個別 作成 再帰的SSM
- マトリックス A 進め ハイプポ キャプチャの初期化 ロングレンジ依存
- 選択的走査アルゴリズム 情報を選択的に圧縮する
- ハードウェア対応アルゴリズム 計算速度を上げる
コードの実装を見てみると、このアーキテクチャをさらに拡張し、エンド・ツー・エンドの例がどのようなものかを探ることができる：
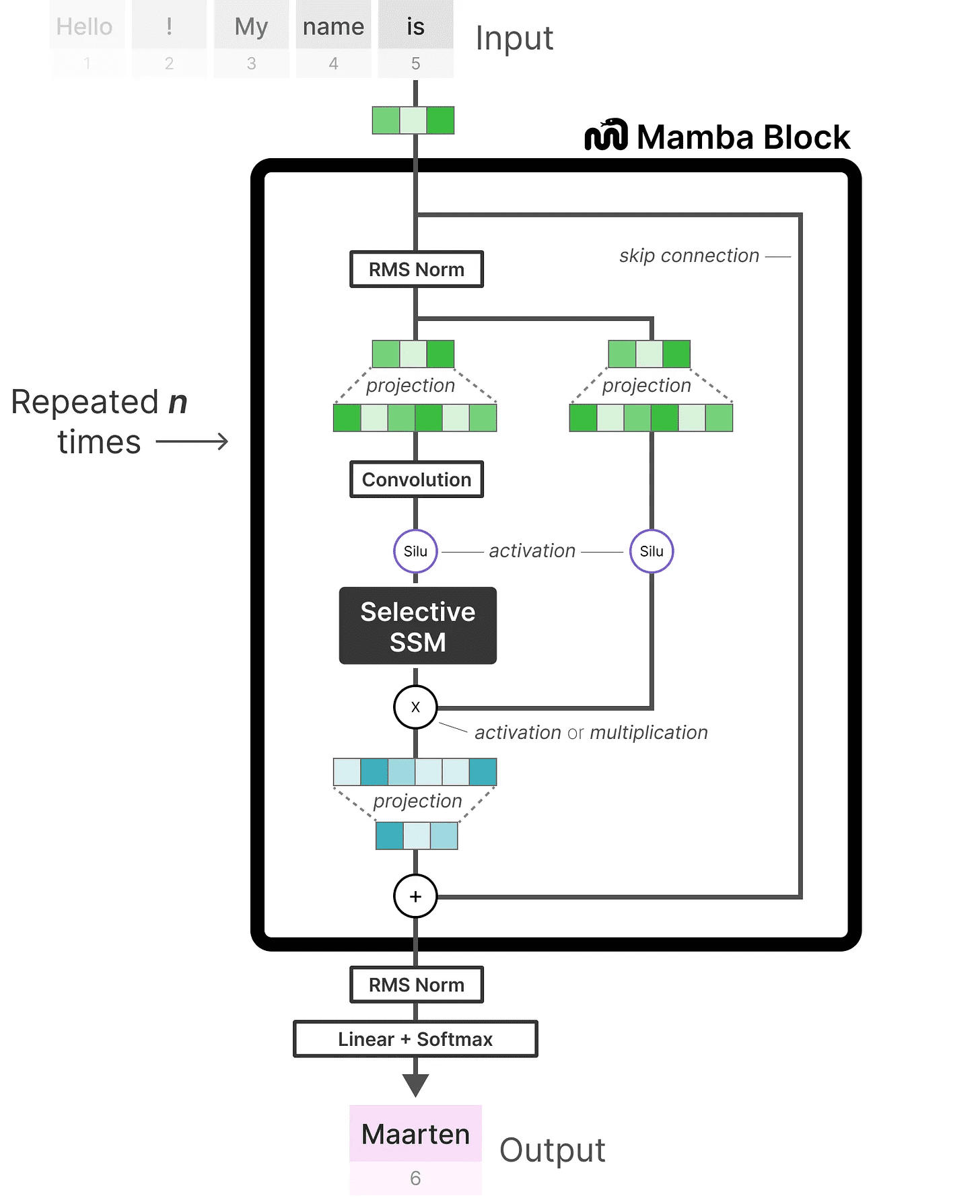正規化レイヤーの追加や、出力トークンを選択するためのソフトマックスの追加など、いくつかの変更点に注意。
これをすべて組み合わせると、無限のコンテキストがあっても、高速な推論と学習が可能になる。このアーキテクチャーを使うことで、同じサイズのTransformerモデルに匹敵し、時にはそれを上回る性能を発揮することがわかった！
評決を下す
これで、状態空間モデルと、選択的状態空間モデルを使用した驚くべきMambaアーキテクチャーの探求を終える。この投稿が、状態空間モデルと特にMambaについて理解を深めてくれたことを願っている。これがTransformersに取って代わるかどうかは誰にもわからないが、今のところ、このような異なるアーキテクチャが注目されるのは素晴らしいことだ！
ビッグ・ランゲージ・モデリングに関連したビジュアライゼーションをもっとご覧になりたい方は、ジェイ・アランマーとの共著をご覧ください。
