Goedel-Prover-V2 - Modèle de preuve de théorème à source ouverte de Princeton, en collaboration avec Tsinghua, NVIDIA et d'autres.

Qu'est-ce que Goedel-Prover-V2 ?

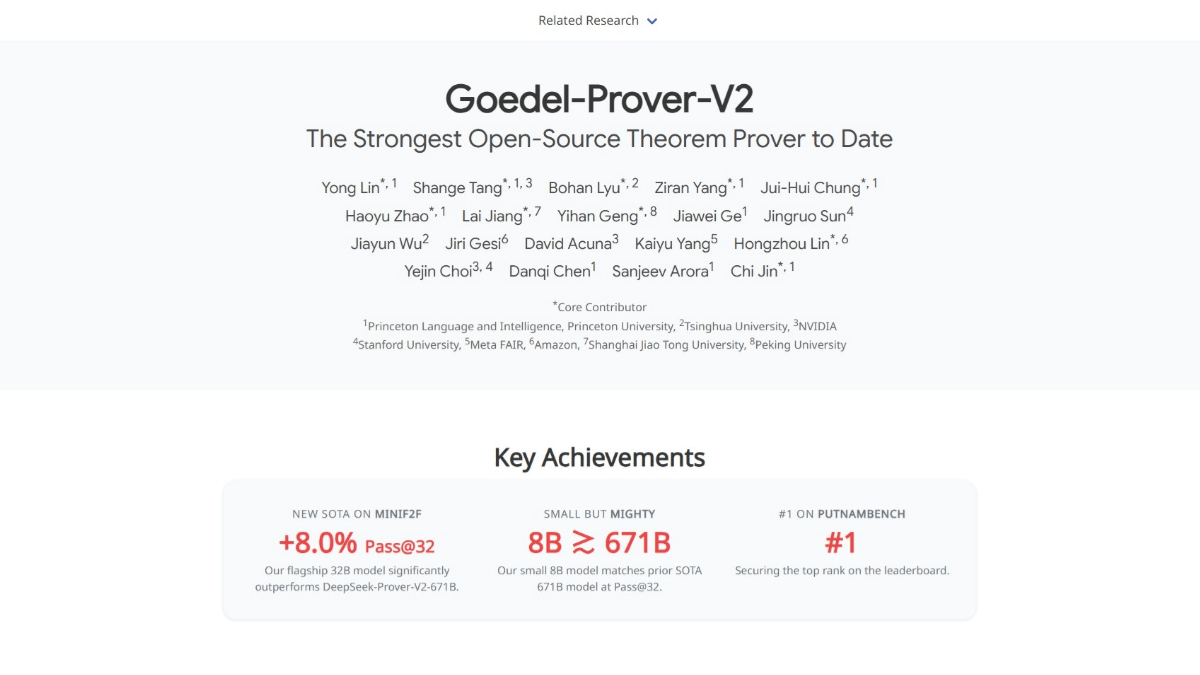
Goedel-Prover-V2 est un modèle de preuve de théorème open source provenant d'institutions de premier plan telles que l'université de Princeton, l'université de Tsinghua et NVIDIA. Le modèle Goedel-Prover-V2 est disponible en deux versions, 32B et 8B, et le modèle donne d'excellents résultats dans un certain nombre de tests de référence, par exemple, le modèle 32B obtient un score de 90,41 TP3T pour Pass@32 dans le test MiniF2F, surpassant le DeepSeek-Prover, beaucoup plus grand. Le modèle est capable de générer automatiquement des preuves pour des problèmes mathématiques complexes, et s'auto-corrige en fonction du feedback du compilateur Lean pour améliorer la qualité des preuves. La nature open-source de Goedel-Prover-V2 fournit une base pour les chercheurs afin d'effectuer des développements et des améliorations supplémentaires.

Principales caractéristiques de Goedel-Prover-V2

• Génération automatique de certificatsLes résultats de l'étude ont été publiés dans un rapport de la Commission européenne sur l'état de la science et de la technologie.
• Capacité d'autocorrectionLe modèle peut réviser ses preuves de manière itérative afin d'améliorer leur précision et leur qualité, grâce au retour d'information du compilateur Lean.
• Une formation et une optimisation efficacesIl améliore l'efficacité de la formation et la performance des modèles, ce qui lui permet d'obtenir de bons résultats dans de nombreux tests de référence.
• Source ouverte et évolutivitéLes chercheurs doivent pouvoir disposer de modèles et d'ensembles de données en libre accès afin de faciliter le développement et l'amélioration par les chercheurs.

Performance de Goedel-Prover-V2

• MiniF2F Benchmarks: :
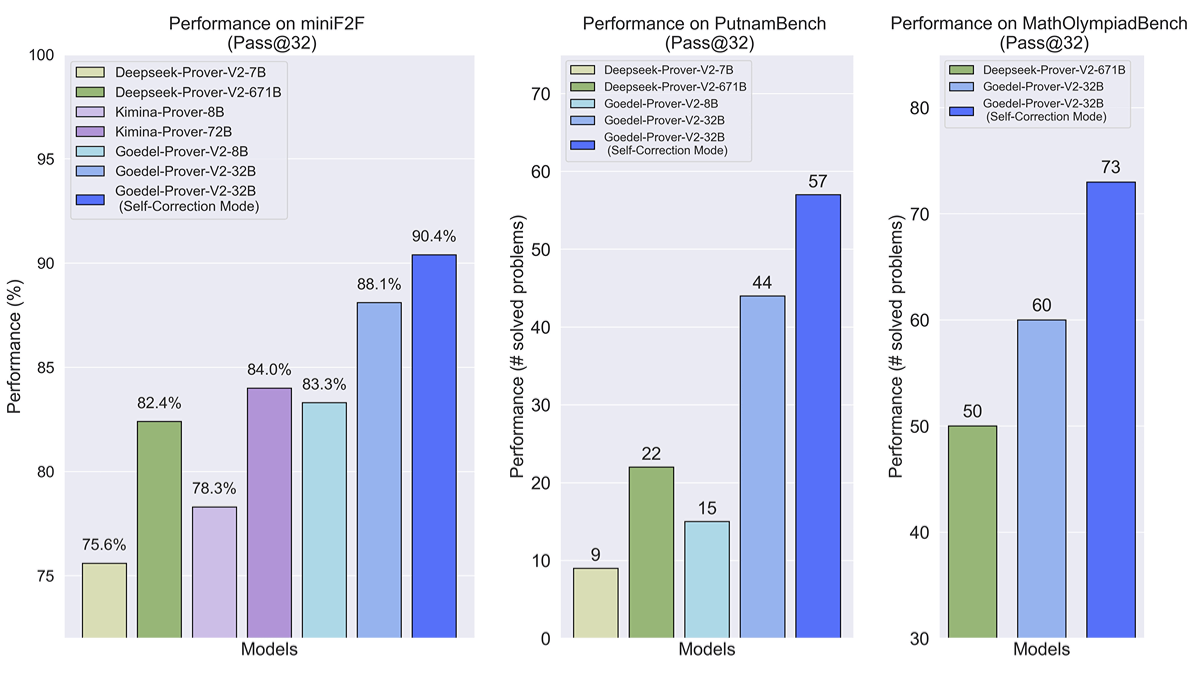
  • Le score Pass@32 pour le modèle 32B atteint 90,41 TP3T, ce qui est nettement supérieur à DeepSeek-Prover-V2 (82,41 TP3T) pour le modèle 671B.
  • Le modèle 8B obtient un score Pass@32 de 83,3%, ce qui est comparable à la performance de DeepSeek-Prover-V2, bien que le nombre de paramètres ne représente qu'environ 1/100 de celui de DeepSeek-Prover-V2.
• Benchmarks PutnamBench: :
  • Le modèle 32B est le plus performant pour les mesures Pass@64, puisqu'il résout 64 problèmes.
  • En ce qui concerne la mesure Pass@32, le modèle 32B résout 57 problèmes, ce qui est nettement supérieur à DeepSeek-Prover-V2-671B, qui en résout 47.
  • Le modèle 8B est également très performant et comparable à DeepSeek-Prover-V2-671B.
• Repères MathOlympiadBench: :
  • Le modèle 32B résout 73 problèmes, ce qui est nettement mieux que DeepSeek-Prover-V2-671B qui en résout 50.
  • Le modèle 8B obtient également de bons résultats, approchant le niveau du modèle 32B et démontrant une forte capacité à prouver des théorèmes.

Adresse du site officiel de Goedel-Prover-V2

• Site web du projet: : https://blog.goedel-prover.com/
• Bibliothèque de modèles HuggingFace: :
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-8B
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-32B

Comment utiliser Goedel-Prover-V2

• Accès aux ressources du projetPour cela, il faut : accéder à la bibliothèque de modèles HuggingFace, télécharger les fichiers de modèles depuis HuggingFace et sélectionner la version appropriée (par exemple, 8B ou 32B).
• exigences en matière de matérielLes GPU à haute performance ou les clusters de GPU sont recommandés.
• environnement logicielInstaller Python et des cadres d'apprentissage profond tels que PyTorch pour s'assurer que l'environnement prend en charge l'inférence de grands modèles.
• Problèmes de saisieLes problèmes mathématiques nécessitant des preuves sont convertis dans un format pris en charge par le modèle (par exemple, le langage Lean).
• Prétraitement des donnéesLes questions de codage et de formatage sont conformes aux exigences du modèle.
• Modèles de chargementChargement du modèle pré-entraîné à l'aide des outils fournis par HuggingFace.
• Preuve de générationLe problème est introduit dans le modèle, qui génère automatiquement des preuves qui sont vérifiées et corrigées à l'aide du compilateur Lean.
• certificat de vérificationLean : Vérifier que les preuves générées sont correctes à l'aide du compilateur Lean.
• Correction itérativeSi la preuve est incorrecte, le modèle s'autocorrige en fonction du retour d'information jusqu'à ce que la preuve correcte soit générée.

Principaux avantages de Goedel-Prover-V2

• Excellente performanceGoedel-Prover-V2 obtient de bons résultats dans plusieurs tests de référence. Par exemple, le modèle 32B atteint une précision de 90,4% dans le test Pass@32 de MiniF2F, ce qui est nettement supérieur à d'autres modèles similaires.
• Architecture technique innovanteLe projet est basé sur la synthèse hiérarchique des données, l'autocorrection guidée par le validateur et les techniques de calcul de la moyenne des modèles afin d'améliorer efficacement l'efficacité de l'apprentissage des modèles et la qualité des preuves.
• Source ouverte et évolutivitéLes modèles et les ensembles de données à source ouverte qui peuvent être librement consultés, utilisés et développés par les chercheurs en vue d'une amélioration.
• Large éventail de scénarios d'applicationLes résultats de l'analyse des données et de l'évaluation de l'impact sur l'environnement peuvent être appliqués à un large éventail de domaines tels que la recherche mathématique, la validation des logiciels et du matériel, les aides pédagogiques, l'intelligence artificielle et l'apprentissage automatique, ainsi que la recherche scientifique et l'ingénierie.
• Une formation et une optimisation efficacesLes résultats de l'étude sont les suivants : une formation efficace et une optimisation des performances basées sur une synthèse hiérarchique des données et des techniques de calcul de la moyenne des modèles afin d'améliorer la robustesse des modèles.

Personnes pour lesquelles Goedel-Prover-V2 est indiqué

• Mathématiciens et chercheurs en mathématiquesLes données de l'enquête sur l'état de l'art sont des données qui permettent de vérifier les conjectures mathématiques, de générer des preuves de problèmes complexes et d'accélérer l'exploration et l'étude des théories mathématiques.
• Informaticiens et ingénieurs en logicielsLes tests sont utilisés dans le développement de logiciels et de matériel pour vérifier l'exactitude des algorithmes, de la logique des programmes et de la conception des circuits, et pour améliorer la fiabilité et la sécurité des systèmes.
• chercheur en intelligence artificielleValider les fondements mathématiques et la logique algorithmique des modèles d'apprentissage automatique afin de garantir la fiabilité et l'exactitude des modèles.
• Éducateurs et étudiantsLe but est de servir de support à l'enseignement des mathématiques, en aidant les étudiants à mieux comprendre et maîtriser les concepts et théorèmes mathématiques en leur fournissant des exemples de preuves formelles.
• Chercheurs et ingénieursLes objectifs sont les suivants : valider les modèles et théories mathématiques dans le cadre de la recherche scientifique et de la conception technique afin d'assurer la faisabilité et la fiabilité des solutions de conception.