What is Model Quantization: FP32, FP16, INT8, INT4 Data Types Explained

guide (e.g. book or other printed material)

In the vast starry sky of AI technology, deep learning models drive innovation and development in many fields with their excellent performance. However, the continuous expansion of model scale is like a double-edged sword, which brings about a sharp increase in arithmetic demand and storage pressure while improving performance. Especially in resource-constrained application scenarios, the deployment and operation of models face severe challenges.

In the face of this dilemma, a technology called "quantization" has emerged, which is like a delicate scalpel, within the acceptable range of model accuracy, subtly reduces the model size, improves the computing speed, and significantly reduces energy consumption. The quantization technology can convert the high-precision FP32 data in the model into low-precision INT4 data, realizing the "slimming" and "acceleration" of the model. In this article, we will analyze the principles and methods of quantization and its application in the field of deep learning, so that even beginners can easily understand its essence.

1. Fundamentals of numerical representation

1.1 Binary to decimal conversion

In computer science, the cornerstone of the digital world, all data is stored in binary form. The binary system contains only two numbers, 0 and 1, while the decimal system, which we use in our daily lives, has ten numbers from 0 to 9. The conversion between these two systems, like translation between different languages, is the key to understanding the representation of computer data.

The decimal number 13, for example, is converted to binary form as 1101. The conversion process is similar to breaking down the decimal "whole" into its binary "components". The steps are as follows:

13 Divided by 2, the quotient is 6 and the remainder is 1 (lowest binary digit)
6 divided by 2 gives a quotient of 3 and a remainder of 0.
3 divided by 2 gives a quotient of 1 and a remainder of 1
1 divided by 2, quotient is 0, remainder is 1 (highest binary digit)

The residuals are listed from bottom to top:
↑1
↑0
↑1
↑1
Get binary result: 1101

Conversely, converting binary 1101 back to decimal is like reassembling the "parts" to make the "whole". From right to left, the weight of each bit increases by powers of two, with the rightmost bit having a weight of , , and so on to the left. Therefore, binary 1101 is converted to decimal as follows: 1× + 1× + 0× + 1× = 8 + 4 + 0 + 1 = 13.

1.2 Difference between Floating Point Numbers and Integers

(i) Integer types (INT)

INT is an abbreviation for Integer, which stands for the type of integer. Integers, as the name suggests, are numbers that do not contain decimal parts, such as 1, 2, 3, etc.

INT4 means that a 4-bit binary number is used to represent an integer, while INT8 uses an 8-bit binary number to represent an integer. The number of bits determines the range of integer representation.

The range of integers that can be represented by INT4 is limited, because a 4-bit binary number can represent up to one different number. For signed INT4, the range is usually -8 to 7, and for unsigned INT4, the range is 0 to 15. The same is true for INT8, which ranges from -128 to 127, and unsigned INT8, which ranges from 0 to 255, since an 8-bit binary number can represent = 256 different numbers.

(ii) Floating point type (FP)

FP stands for Floating Point, the floating point type. Floating point numbers, as opposed to integers, are used to represent numbers with fractional parts.

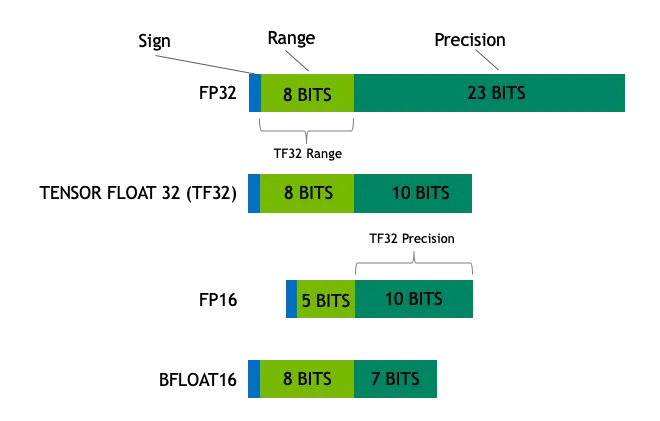
Floating point numbers consist of a sign bit, an exponent bit, and a mantissa bit. A 32-bit floating-point number (FP32), for example, contains 1 sign bit, 8 exponent bits, and 23 mantissa bits. This clever design allows floating-point numbers to represent an extremely wide range of values, from very small numbers to very large numbers, like a tape measure.

For example, FP32 can represent very small numbers (approximately) and very large numbers (approximately). INT8 (8-bit integers), on the other hand, can only represent integers between -128 and 127. This difference is similar to measuring length using a fixed-length ruler (integer) versus a scalable tape measure (floating-point number), where floating-point numbers are far superior to integers in terms of flexibility and range of numerical representation.

(iii) Commonly used data types

Common data types in deep learning and general purpose computing include:

• Float32 (FP32): This is the standard 32-bit floating-point format, known for its high accuracy and wide range of values.FP32 operations dominate model training and inference because of their versatility, which is widely supported by a wide range of hardware.
• Float16 (FP16): FP16 is a 16-bit half-precision floating-point number, which has a reduced precision compared to FP32, but has a significantly reduced memory footprint and a substantially faster computation speed.FP16 has a relatively narrow range of numerical representations, which may be subject to the risk of overflow and underflow. However, in deep learning practices such asLoss Scaling The application of techniques such as these can effectively alleviate these problems.
• BFloat16 (BF16): BF16 is another 16-bit floating point format. It is unique in that BF16 retains the same 8-bit exponent bit as FP32, and thus has the same dynamic range as FP32, however, the trailing bit is only 7 bits, which is less precise than FP16. However, BF16 has only 7 trailing bits, which is less precise than FP16. BF16 performs well in scenarios with a wide range of values, but there may be tradeoffs in precision-sensitive tasks.
• Int8: INT8 is an 8-bit integer type with a limited range of numerical representation but very low memory consumption. INT8 is mainly used in model quantization techniques, and by converting the model parameters from high-precision FP32 or FP16 to INT8, the model storage space requirement and computational complexity can be greatly reduced, paving the way for efficient deployment of the model on resource-constrained devices.

2. Quantitative concepts

2.1 Quantitative definitions

Quantization refers to the conversion of data in a model from a high-precision representation to a low-precision representation, as in the case of theTrade-offs between image quality and file sizeIn deep learning, quantization is the process of compressing a high-precision image into a low-precision JPEG image, which greatly reduces the file size while still retaining the main information of the image. In the field of deep learning, quantization usually refers to the reduction of model weights and activation values from FP32 (32-bit floating point) to FP16 (16-bit floating point) or even INT8 (8-bit integer) or lower precision.

FP32 is a high-precision floating-point format that accurately represents values in 32-bit binary (1 sign bit, 8 exponent bits, and 23 mantissa bits.) FP32 is a precision scale that can measure small to large values, but its high precision comes with a high storage overhead and relatively slow computation speed.

FP16 is a half-precision floating-point format that requires only 16 binary bits (1 sign bit, 5 exponent bits, 10 mantissa bits) to represent a value. Compared to FP32, FP16 sacrifices precision for half the storage space and improved computational efficiency, and is like a slightly thicker scale, striking a good balance between precision and efficiency.

INT8 is an 8-bit integer type that can only represent integers in the range of -128 to 127. INT8 has the advantage of very low memory footprint and very high computational speed, but it also has the lowest numerical precision. INT8 is similar to a simple counter that only counts integers, but it is fast and convenient.

2.2 Quantitative purpose

The central purpose of quantification is toReduced storage requirements and computational complexity of modelsand at the same time seeks to keep the loss of precision within acceptable limits. Specifically, quantization aims to achieve the following objectives:

Reduced storage requirements: Modern deep learning models, especially large-scale models with huge parameter sizes, often have hundreds of millions or even hundreds of billions of parameters, which puts a huge pressure on the storage space. Taking FP32 model as an example, each parameter occupies 4 bytes of storage space. If the model is quantized to FP16, each parameter requires only 2 bytes, which reduces the storage requirement by half. If the model is further quantized to INT8, each parameter only needs 1 byte, and the storage space can be reduced by 75%.

Improve computational efficiency: The quantized model is significantly less computationally intensive in the inference phase, which results in an improvement in inference speed. For example, when FP32 model runs on GPU, the computation speed may be limited by the memory bandwidth. On the other hand, FP16 or INT8 models, thanks to the hardware's optimized acceleration of low-precision computation, the computation speed can be significantly increased. The performance improvement brought by quantization is especially significant in scenarios where computing resources are limited, such as edge devices or mobile devices.

reduce power consumption: A reduction in the model's computational resource requirements translates directly into a reduction in energy consumption. For mobile devices and embedded systems, power consumption is a critical consideration. Quantization techniques can effectively reduce model power consumption, extend device life, and reduce heat dissipation requirements.

Reduced bandwidth requirements:: In distributed computing systems, the reduction of model size also means the reduction of data transmission bandwidth. In a multi-server scenario, quantitative models can be distributed and synchronized with parameters at a faster rate, thus improving the overall data transfer efficiency.

3. INT4, INT8 Quantification

3.1 Range of INT4 and INT8 Indications

INT4 and INT8 are both integer type quantization methods that store data in binary form in a computer system, but differ in the range and precision of numerical representation.

• INT8: INT8 is an 8-bit integer type with a representation range of -128 to 127. It can be likened to an 8-bit counter, where each bit can be either a 0 or a 1, and different integer values can be represented by different 0/1 combinations. For example, in thenotated INT8 means in the range of -128 to 127, and 11111111 in binary means -1 in decimal. If it'sunsigned (i.e. the absolute value, regardless of plus or minus sign) INT8, ranging from 0 to 255, in which case 11111111 represents 255 in decimal, is sufficient to meet the needs of many application scenarios, such as pixel values in image processing, which are usually in the range of 0 to 255, and can be effectively represented by INT8.
• INT4INT4 is a 4-bit integer type with a smaller representation range of -8 to 7 than INT8. INT4 sacrifices numeric range for smaller storage footprint and faster computation. INT4 is like a smaller counter, with a limited numeric range but a smaller "footprint", which is more resource-efficient. It is more resource-efficient. In some application scenarios with relatively loose precision requirements, such as some lightweight neural network layers, the use of INT4 quantization can significantly reduce storage and computation costs.For example, when deploying a lightweight image classification model on mobile, model parameters and intermediate computation results can be stored and computed using the INT4 format to reduce memory footprint and accelerate inference.

3.2 Quantitative formulas and examples

The process of quantization is essentially the conversion of a high-precision floating-point number map to a low-precision integer. Taking FP32 quantization to INT8 as an example, the quantization formula is as follows:

is the original floating point number.

is a quantized integer.

is the scaling factor, used to map floating point numbers to integer ranges.

Indicates rounding to the nearest whole number.

Indicates that the result is limited to the range of INT8, i.e., [-128, 127].

Calculate the scaling factor

The scale factor is usually determined by taking the maximum of the absolute value of the floating point number. Assuming there is a set of floating-point numbers, the procedure is as follows:

1. Find the maximum absolute value of the group of floating point numbers:
2. Calculate the scaling factor: .

In practice, there are several ways to calculate the scaling factor, such as Max Quantization, Mean-Std Quantization, and so on. Max Quantization uses the maximum absolute value of the tensor to calculate the scaling factor, which is simple to implement but may be sensitive to outliers. Mean-Std Quantization uses the mean and standard deviation information of the data to determine the scaling factor more robustly, but the computational complexity is slightly higher. Choosing the appropriate scaling factor calculation method requires a trade-off between accuracy and computational overhead.

typical example

Assuming we have a set of floating point numbers [-0.5, 0.3, 1.2, -2.1], the following step-by-step demonstrates the quantization process:

1. Calculate the maximum absolute value:

2. Calculate the scaling factor:

3. Quantize each floating point number:

• For -0.5.
• For 0.3.
• For 1.2.
• For -2.1.

The final, quantized INT8 representation is [-1, 1, 4, -7].

Through the above steps, we can clearly see how the quantization technique converts floating point numbers to integers. Although the quantization process inevitably introduces a certain loss of precision, by choosing the scaling factor wisely, the performance level of the model can be maintained to the maximum extent while significantly reducing the storage and computation costs. To further minimize quantization errors, zero-point quantization can also be introduced. Zero-point quantization adds a zero-point offset to the quantization equation, which allows floating-point zeros to be accurately mapped to integer zeros, thus improving quantization accuracy, especially if there are a large number of zeros in the activation value.

4. FP8, FP16, FP32 quantification

4.1 FP8, FP16, FP32 Representations

FP8, FP16, and FP32 are floating-point numbers that are stored in binary form in the computer, but with different bit widths and therefore different ranges and precision.

FP32

FP32, as a standard 32-bit floating point format, consists of the following three parts:

• Sign Bit (1 bit): Used to identify positive and negative values, with 0 representing a positive number and 1 representing a negative number.
• Exponential digits (8 digits): is used to define the size range of a value, allowing FP32 to represent values from very small to very large.
• Last digit (23 bits): Used to determine the precision of a value; the more trailing digits, the higher the precision.

With a wide range of values from about to , and an accuracy of about 6 decimal places, the FP32 is like a highly accurate tape measure that can measure scales as small as a speck of dust and distances as vast as a mountain. FP32 is an indispensable data type in scientific computing, financial modeling, and other fields that require a high degree of precision.

FP16

FP16 is a half-precision floating-point number format that occupies only 16 bits of memory, half the size of FP32.The structure of FP16 is as follows:

• Sign Bit (1 bit): Identifies positive and negative values.
• Exponential Digits (5 digits): Defines a range of value sizes.
• Last digit (10 digits): Determines the numerical precision.

The numerical representation of FP16 ranges from about to, and the precision is reduced to about 3 decimal places compared with FP32. FP16 is like a straightedge with a slightly thicker scale, which has a lower precision, but it has more advantages in terms of storage space and computational efficiency. FP16 is commonly used for deep learning model training and inference, which requires high computational speed and memory bandwidth. Especially in GPU-accelerated scenarios, FP16 can make full use of hardware acceleration units such as Tensor Core to achieve significant performance improvements.

FP8

FP8 is an emerging low-precision floating-point number format mainly used in the field of deep learning, aiming at efficient computation.The typical structure of FP8 is as follows:

• Sign Bit (1 bit): Identifies positive and negative values.
• Exponential digits (3 or 4 digits): Define a range of values (two FP8 variants exist).
• Last digit (4 or 3 digits): Determines the numerical precision (corresponds to the number of index digits).

The range and accuracy of the FP8's numerical representation is further reduced, but the advantages are smaller memory footprint and faster computation. If FP32 is a precision tape measure and FP16 is a straightedge with a slightly thicker scale, then FP8 is a more precise tape measure. It's like a simple straightedge with a centimeter scale.In addition, the range and accuracy are further reduced, but the measurement task can still be accomplished quickly in a given situation. As an extremely low precision data type, FP8 shows great potential in scenarios with extreme latency and throughput requirements, such as real-time inference, edge computing, etc. However, FP8 also puts more demands on hardware and algorithms, requiring specialized hardware support and quantization strategies to ensure accuracy. However, the application of FP8 also puts higher requirements on hardware and algorithms, requiring specialized hardware support and quantization strategies to ensure accuracy.

4.2 Quantification process and formulas

Quantization is the process of converting a high precision floating point number to a low precision floating point number or integer. Taking FP32 quantization to FP16 as an example, the quantization formula is as follows:

is the original floating point number.

is a quantized low-precision floating-point number.

is a scaling factor used to map floating point numbers to lower precision ranges.

Indicates rounding to the nearest value.

Calculate the scaling factor

The scale factor is usually determined by taking the maximum of the absolute value of the floating point number. Assuming there is a set of floating-point numbers, the procedure is as follows:

1. Find the maximum absolute value of the group of floating point numbers:
2. Calculate the scaling factor: , where is the maximum for the target low-precision formatCan be expressed as an absolute value. For FP16, this value is approximately 65504The

Similar to INT8 quantization, the scaling factors in FP16 quantization can be calculated in various ways, which can be chosen according to different accuracy and performance requirements. In addition, FP16 quantization is often used in conjunction with Mixed Precision Training (MPT). During the model training process, FP16 is used for some computationally intensive operations (e.g., matrix multiplication, convolution), while FP32 is used for operations requiring higher accuracy (e.g., loss calculation, gradient updating), so as to speed up the training process and reduce the memory consumption while guaranteeing the accuracy of the model.

typical example

Assuming we have a set of FP32 floating point numbers [-0.5, 0.3, 1.2, -2.1], the following is a step-by-step demonstration of quantizing FP32 to FP16:

1. Calculate the maximum absolute value:

2. Calculate the scaling factor:

3. Quantize each floating point number:

• For -0.5.
• For 0.3.
• For 1.2.
• For -2.1.

The final, quantized FP16 is expressed as [-0.5, 0.3, 1.2, -2.1].

Through the above steps, it is possible to observe how quantization techniques can convert high-precision floating-point numbers to low-precision floating-point numbers. Quantization certainly brings some loss of precision, but by choosing the scaling factor wisely, the performance of the model can be maintained as much as possible while reducing the storage and computation cost. In order to further improve the accuracy of FP16 quantization, Dynamic Quantization can be used. Dynamic quantization dynamically adjusts the scaling factor according to the actual range of the input data in the inference process, so as to better adapt to the changes in the distribution of the data and reduce the quantization error.

5. Quantitative applications and advantages

5.1 Applications in Deep Learning

Quantization techniques have a wide range of promising applications in the field of deep learning, especially in the model training and inference phases, where they are increasingly valuable. The following are a few major applications of quantization techniques in deep learning:

Model Training Acceleration

During the model training phase, computation with low-precision data types such as FP16 or FP8 can significantly accelerate the training process. For example, NVIDIA Hopper architecture GPUs support Tensor Core operations at FP8 precision. FP8 training can be 2 to 3 times faster than traditional FP32 training. This training acceleration is especially critical for models with large parameter sizes, dramatically reducing training time and computational resource consumption. For example, when training large-scale language models such as GPT-3, using FP16 or BF16 mixed-precision training can significantly shorten the training time and save a lot of computational resources.

in order to Inflection AI The Inflection-2 model, for example, was trained on 5,000 NVIDIA Hopper architecture GPUs using an FP8 mixed-precision training strategy, totaling FLOPs of floating-point operations, and demonstrated superior performance over Google's flagship PaLM 2 model, which also belongs to the training compute category, in several standard AI performance benchmarks. In a number of standard AI performance benchmarks, Inflection-2 demonstrated a significant performance advantage over Google's flagship model PaLM 2 in the same training computation category.

Model inference optimization

In the model inference stage, the quantization technique can significantly reduce the storage requirement and computational complexity of the model, and thus improve the inference efficiency. For example, by quantizing an FP32 model to INT8, the model storage space can be reduced by 75% and the inference speed can be increased by several times. This is critical for deploying deep learning models on edge or mobile devices, which are often challenged by limited compute resources and storage space. For example, when deploying an image recognition model on the cell phone, quantizing the model as INT8 can effectively reduce the model size, reduce memory consumption, accelerate the inference speed, and improve the user experience.

For example, Google worked closely with the NVIDIA team to apply the TensorRT-LLM optimization technique to the Gemma model and combined it with FP8 technology to achieve inference acceleration. Experimental results show that FP8 achieves more than 3X improvement in throughput compared to FP16 when using Hopper GPUs for inference.

Model Compression and Deployment

Quantization techniques can also be used for model compression and deployment. By quantizing high-precision models into low-precision models, model size can be effectively reduced, thus облегчить model deployment in resource-constrained environments. For example, zero-one-everythingutilization NVIDIA's combined hardware and software technology stack completed large model FP8 training and validation, with a 1.3x increase in large model training throughput compared to BF16. In addition to INT8 and FP16/FP8 quantization, there are also INT4 and even lower bit quantization techniques, such as Binary Neural Network (BNN) and Ternary Neural Network (TNN). These very low-bit quantization techniques can compress the model to the extreme, but usually with a large loss of accuracy, and are suitable for scenarios with extreme requirements on model size and speed.

In addition, the quantized model can be further enhanced with specific hardware acceleration techniques. For example, NVIDIA Transformer Engine has been integrated into mainstream deep learning frameworks such as PyTorch, JAX, PaddlePaddle, etc., providing efficient hardware-level support for inference in quantitative models. In addition to NVIDIA GPUs, other hardware platforms, such as ARM architecture CPUs and mobile NPUs, have also been optimized and accelerated for quantization computation, providing a hardware foundation for the widespread deployment of quantization models.

5.2 Strengths and limitations

dominance

Computational Efficiency Improvement: Low-precision quantization can significantly speed up computation and reduce the consumption of computational resources. both FP16 and FP8 have several times higher computational throughput than FP32. this acceleration effect is especially prominent in large-scale model training and inference.

Lower storage requirements: Quantization techniques can significantly reduce model storage requirements. For example, quantizing an FP32 model to INT8 reduces storage space by 75%, which is important for deploying models in environments with limited storage resources.

Reduced power consumption: Low-precision computing requires fewer computational resources, which reduces device power consumption. In mobile devices and embedded systems, power consumption is a key design consideration. Quantized models help extend device battery life and reduce heat dissipation requirements.

model optimization: Quantization techniques drive model optimization and compression during training and inference, thereby further reducing deployment costs. For example, the application of FP8 enables the model to explore more fine-grained quantization strategies during the training phase, thus improving the overall efficiency of the model.

limitations

Loss of precision:: The quantization process is inevitably accompanied by a loss of precision, which can be significant especially when very low precision formats (e.g., FP8) are used and can lead to degradation of the model's performance on a given task. While the loss of precision can be mitigated to some extent by means such as a careful choice of scaling factors, the complete elimination of the loss of precision is often difficult to achieve. In order to mitigate the accuracy loss caused by quantization, Quantization-Aware Training (QAT) can be used. QAT simulates the quantization operation during the model training process, and takes the quantization error into account in the training, so as to train a model that is more robust to quantization. QAT can usually significantly improve the accuracy of quantization models, but the training cost will be increased accordingly.

Hardware Support: Not all hardware platforms fully support low-precision computation. For example, FP8 and FP16 computations often require specific hardware (e.g., NVIDIA Hopper architecture GPUs). If the hardware platform is not optimized for low-precision computation, the benefits of quantization will not be fully realized. With the popularization of low-precision computing, more and more hardware platforms begin to support low-precision data types such as FP16, BF16, and even FP8, which provides a more solid hardware foundation for the wide application of quantization technology.

Increased complexity:: The quantization process itself can add complexity to model development. For example, the quantization process requires fine-grained calculation of scaling factors and may require additional calibration and fine-tuning of the model. This definitely adds to the difficulty of model development and deployment. In order to reduce the complexity of quantization deployment, many automated quantization tools and platforms have emerged in the industry, such as NVIDIA TensorRT, Qualcomm AI Engine, etc., which can help developers quickly and easily quantize models and deploy them to target hardware platforms.

application scenario:: Quantization techniques are not suitable in all application scenarios. In tasks that require very high precision (e.g., scientific computing, financial modeling, etc.), quantization may lead to unacceptable loss of precision. For accuracy-sensitive tasks, we can try to adopt mixed-precision quantization strategy, which adopts different quantization accuracies for different layers or parameters in the model, e.g., keeping FP32 or FP16 accuracy for key layers or parameters, and adopting INT8 or lower accuracy for other layers or parameters, so as to achieve a better balance between accuracy and efficiency.

In summary, quantization techniques, as a key technology in the field of deep learning, show great potential in improving computational efficiency, reducing storage requirements and power consumption. However, quantization techniques also have limitations such as accuracy loss and hardware dependency. Therefore, in practical applications, quantization strategies should be carefully selected according to specific application requirements and scenario characteristics, in order to achieve an optimal balance between model performance and efficiency. In the future, with the continuous development of hardware and algorithms, quantization technology will play a more important role in the field of deep learning, and promote the application of artificial intelligence in a wider range of scenarios to take root.