CoRAG: Dynamic chained RAG modeling using MCTS (Monte Carlo Trees)
Summary of CORAG's main contributions
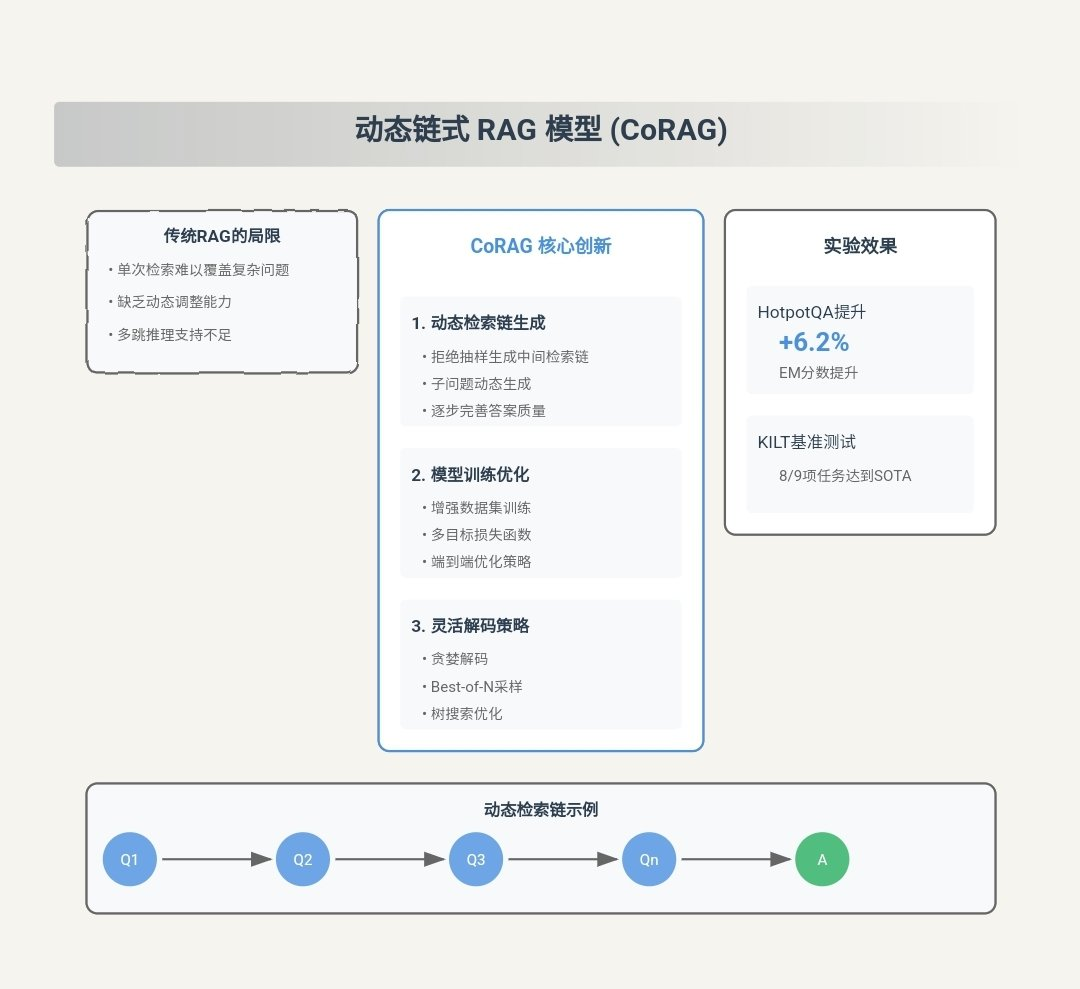
CORAG (Cost-Constrained) Retrieval Optimization for Retrieval-Augmented Generation) is an innovative Retrieval Augmented Generation (RAG) system designed to address existing RAG Key challenges in the methodology. The following are the main contributions of CORAG:
- Comprehensive consideration of inter-block associations::
- innovation point: CORAG is the first framework to introduce block combination order optimization in the RAG task. Unlike traditional approaches, CORAG no longer treats each text block independently or considers blocks only at the clustering level, but instead uses the Monte Carlo Tree Search (MCTS) to sequentially search for the optimal order of block combinations. This approach fully captures the complex associations between blocks, avoids redundant information, and ensures that the selected block combinations fully answer the user query.
- dominance: In this way, CORAG is able to generate more accurate and relevant responses, improving the quality of generation.
- Solving the block utility nonmonotonicity problem::
- innovation point: CORAG will budget constraint integrated into the optimization process of the block portfolio, rather than considering budget exhaustion as a termination condition. This approach considers the block utility of nonmonotonicity (math.), i.e. adding more blocks does not always improve the quality of the end result.
- dominance: By dynamically adjusting budget usage during the optimization process, CORAG is able to avoid over-inclusion of irrelevant or redundant blocks, thus improving the accuracy and relevance of the generated responses.
- Adaptation to different query fields::
- innovation point: CORAG introduced a Configuring the AgentThe agent uses the Comparative learning to dynamically adapt the MCTS configuration to different query domains. The agent recommends the optimal Rearranger model cap (a poem) MCTS ConfigurationThe
- dominance: This approach gives CORAG the flexibility to handle a wide range of query types, from simple keyword queries to complex reasoning problems, and ensures that high quality responses are provided in different application scenarios.
- Efficient and scalable search strategies::
- innovation point: CORAG employs MCTS for node searching with the parallel expansion technique Accelerates the search process. This approach reduces the exponential search space to a linear one and effectively balances the explorations cap (a poem) utilizationThe
- dominance: CORAG is able to handle large-scale datasets while maintaining efficient retrieval and balancing computational cost and retrieval quality.
- Significant performance gains::
- experimental verification: Experimental results show that CORAG outperforms existing baseline methods on several benchmark datasets, improving ROUGE scores by about 30%In addition, CORAG excels in efficiency. CORAG also excels in efficiency, delivering high quality response within tight cost constraints.
CORAG Workflow Example
To help the reader quickly understand how CORAG works, the following is a complete workflow example showing how CORAG processes a user query and generates the final response. Each step contains inputs and outputs to represent the back-and-forth of the workflow.
Step 1: User Query Input
- importation: A user submits a natural language query to the CORAG system, for example:
"请解释光合作用的过程,并列出影响其效率的因素。" - exports: The query is passed to the Query Embedding Module Processing.
Step 2: Query Embedding Generation
- importation: User query text.
- deal with: Using a pre-trained embedding model(e.g., BGE-M3) converts the query text into a vector representation.
- exports: Queries the embedding vector (e.g., a 1024-dimensional vector).
Query Embedding: [0.123, -0.456, 0.789, ..., -0.012]
Step 3: Configure Agent Prediction
- importation: query embedding vector
[0.123, -0.456, 0.789, ..., -0.012]The - deal with::
- feature extraction: The embedding vector is fed into the Configuring the Agent (used form a nominal expression) coding network in which feature extraction is performed.
- Rearranger prediction: Optimization of the output prediction of the coding network Rearranger modelFor example
bge-reranker-largeThe - MCTS Configuration Forecast: At the same time, the coding network predicts the optimal MCTS Configuration parameters, such as the number of iterations, the cost factor, and the exploration factor.
- exports::
- Optimal Rearranger Model::
bge-reranker-large - MCTS Configuration Parameters::
- Number of iterations15
- cost factor: 0.2
- Exploration factor: 2.5
Optimal Reranker: bge-reranker-large MCTS Configuration: - Iterations: 15 - Cost Coefficient: 0.2 - Exploration Coefficient: 2.5 - Optimal Rearranger Model::
Step 4: Retrieve Potential Text Blocks
- importation::
- Query Embedding Vector
[0.123, -0.456, 0.789, ..., -0.012]The - vector database(e.g., containing pre-segmented text blocks and their embedding vectors).
- Query Embedding Vector
- deal with: Use the query embedding vector for Similarity Search, retrieve the most relevant potential text blocks from the vector database. The following are examples of the first five text blocks retrieved:Text block 1::
光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。Text Block 2::
光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。Text Block 3::
影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。Text block 4::
光照强度对光合作用的影响呈正相关,但过强的光照会导致光抑制现象,降低光合作用效率。Text Block 5::
二氧化碳是光合作用的原料之一,其浓度直接影响光合作用的速率。 - exports: A list of potential text blocks and their embedding vectors.
Retrieved Chunks: - Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。" - Chunk 2: "光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。" - Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。" - Chunk 4: "光照强度对光合作用的影响呈正相关,但过强的光照会导致光抑制现象,降低光合作用效率。" - Chunk 5: "二氧化碳是光合作用的原料之一,其浓度直接影响光合作用的速率。"
Step 5: MCTS Tree Search
- importation::
- List of potential text blocks::
- Chunk 1: ...
- Chunk 2: ...
- Chunk 3: ...
- Chunk 4: ...
- Chunk 5: ...
- MCTS Configuration Parameters::
- Number of iterations15
- cost factor: 0.2
- Exploration factor: 2.5
- Rearranger model::
bge-reranker-large
- List of potential text blocks::
- deal with::
- Initialize the root node: The root node represents an empty state where no text block is selected.
- Iterative extensions::
- option: Use UCB Algorithm Select the node with the highest current utility. For example, Chunk 3 is chosen for the first iteration because it has the highest relevance to the query.
- extensions: Generate all possible child nodes (new combinations of text chunks). For example, the child nodes of Chunk 3 might be Chunk 1, Chunk 2, Chunk 4 and Chunk 5.
- valuation: Use Rearranger model
bge-reranker-largeEvaluate the utility of all new combinations in parallel. For example, evaluate the utility of combinations such as Chunk 3 + Chunk 1, Chunk 3 + Chunk 2, and so on. - update: Update node utility and access counts and propagate updates upwards.
- iterate: Repeat the selection, expansion, evaluation, and update steps until the maximum number of iterations (15) is reached.
- Termination conditions: Maximum number of iterations reached.
- exports: Optimal order of combining text blocks.
Optimal Chunk Combination: - Chunk 3: "影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。" - Chunk 1: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。" - Chunk 2: "光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。"take note of: During the MCTS process, CORAG dynamically adjusts the combination order according to the utility, and finally selects the optimal combination order.
Step 6: Generate Final Response
- importation::
- Optimized order of combining text blocks::
- Chunk 3: "Factors that affect photosynthetic efficiency include light intensity, carbon dioxide concentration, temperature, and water availability."
- Chunk 1: "Photosynthesis is the process by which plants, algae, and some bacteria use light energy to convert carbon dioxide and water into glucose and oxygen."
- Chunk 2: "Photosynthesis occurs primarily in the chloroplasts of plant leaves and is divided into two phases: the light reaction and the carbon reaction."
- user search:: "Explain the process of photosynthesis and list the factors that affect its efficiency."
- Optimized order of combining text blocks::
- deal with::
- Build Tips: Combine the optimal order of combining text blocks with user queries to construct the LLM of the input prompt. Example:
用户查询:请解释光合作用的过程,并列出影响其效率的因素。 相关信息: 1. 影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。 2. 光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。 3. 光合作用主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。 - Generating a Response: Use LLM(e.g. Llama3) Generate a final response to the prompt.
- Build Tips: Combine the optimal order of combining text blocks with user queries to construct the LLM of the input prompt. Example:
- exports: The final natural language response.
Final Response: "光合作用是植物、藻类和某些细菌利用光能将二氧化碳和水转化为葡萄糖和氧气的过程。它主要发生在植物叶片的叶绿体中,分为光反应和碳反应两个阶段。影响光合作用效率的因素包括光照强度、二氧化碳浓度、温度和水分供应等。"
Step 7: Response Output
- importation: The final natural language response.
- deal with: Present the response to the user.
- exports: The user interface displays the response result.
summarize
With the above workflow example, the working principle of CORAG can be summarized in the following steps:
- Query Embedding Generation: Convert a user query into a vector representation.
- Configuring Agent Prediction: Predicting the optimal rearranger model and MCTS configuration parameters.
- Retrieve potential text blocks: Retrieve the most relevant block of text from the vector database.
- MCTS Tree Search: Use MCTS to search for the optimal order of combining text blocks.
- Generate Final Response: Use LLM to generate the final response based on the optimal combination of text blocks.
- response output: Present the response to the user.
These steps demonstrate how CORAG effectively combines the three phases of retrieval, enhancement, and generation to deliver high-quality natural language responses. With detailed data examples, readers can gain a clearer understanding of CORAG's data processing process and how it works.
original text:: https://arxiv.org/pdf/2411.00744
caption:: CORAG: A Retrieval Optimization System with Cost Constraints for Retrieval Enhancement Generation
authorZiting Wang, Haitao Yuan, Wei Dong (Nanyang Technological University), Gao Cong (Nanyang Technological University), Feifei Li (Alibaba Group)
summaries
Large Language Models (LLMs) have demonstrated excellent capabilities in generative tasks, but it is often difficult to access up-to-date information, which can lead to disillusionment. Retrieval-enhanced generation (RAG) addresses this problem by integrating knowledge from external databases to achieve more accurate and relevant responses. Due to the context window limitation of LLMs, it is impractical to directly input the entire external database context into the model. Instead, only the most relevant information, i.e., "chunks" (chunks), are selectively retrieved. However, current RAG research faces three key challenges. First, existing solutions usually select each chunk independently, ignoring potential associations between them. Second, in practice, the utility of chunks is "non-monotonic", which means that adding more chunks may reduce the overall utility. Traditional approaches emphasize maximizing the number of blocks included, which may unintentionally hurt performance. Third, each type of user query has unique characteristics that require tailored processing, which current solutions do not adequately account for.
To overcome these challenges, we propose CORAG, a retrieval optimization system with cost constraints, for retrieval enhancement generation. We adopt a Monte Carlo Tree Search (MCTS)-based strategy framework to find the optimal block combinations sequentially, thus comprehensively considering the associations between blocks. In addition, instead of considering budget exhaustion as a termination condition, we integrate budget constraints into the optimization process of block combinations, which effectively solves the problem of non-monotonicity of block utility. In addition, by designing configuration agents, our system predicts the optimal configuration for each query type, improving adaptability and efficiency. Experimental results show that our framework has up to 301 TP3T of performance improvement compared to the baseline model, highlighting the effectiveness, scalability, and applicability of the framework for long-context applications.
PVLDB Reference Format.
Ziting Wang, Haitao Yuan, Wei Dong, Gao Cong, and Feifei Li. CORAG: A Cost-Constrained Retrieval Optimization System for Retrieval-Augmented Generation . pvldb, 14(1): xxx-xxx, 2020.
doi:XX.XX/XXX.XX
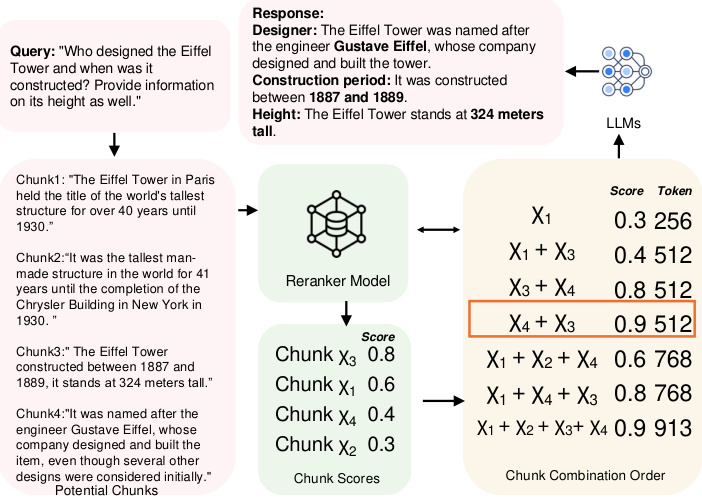
Figure 1: Example of data block combination order.
1 Introduction
Although LLMs have demonstrated excellent capabilities in generative tasks, they often encounter difficulties in obtaining up-to-date information, which can lead to hallucinations [10, 38]. To address these challenges, RAG has emerged as a key solution. By integrating external data sources into LLM, RAG can provide more accurate, relevant and up-to-date information. Nowadays, RAG is widely studied in the context of LLMs, especially in tasks that require updated external knowledge, such as question and answer tasks [2, 22, 29], medical information retrieval [1, 32] and time series analysis [12, 26, 40]. External data sources are usually so large that it is impractical to feed them directly into the LLM. To solve this problem, the data are usually partitioned into non-overlapping chunks and stored in a vector database, and then the user queries the most useful chunks to construct hints for the LLM. Therefore, designing efficient and accurate search structures and algorithms to find the most relevant chunks has become a prominent research topic and has been extensively studied in the database [39, 48] and machine learning communities [2, 35, 43].
However, there are three key challenges with existing approaches.
Challenge 1: Associations between blocks. Currently, there are two main approaches for identifying the most relevant blocks. The first approach formulates the problem as an Approximate k-Nearest Neighbors (AKNN) task [41, 45], where each block is assigned a score and the approximate top k blocks ranked by score are selected. The second approach clusters blocks and returns all blocks in the most relevant cluster in response to a query [22, 29]. However, both methods ignore potential associations between blocks: the first method ignores associations altogether, while the second method only superficially considers all blocks in each cluster by treating them as equally relevant. As a result, these methods introduce substantial redundancy in selected blocks when multiple blocks convey similar or redundant information.
For example, as shown in Fig. 1, when querying the height and history of the Eiffel Tower, if each block is treated independently, the greedy method selects blocks χ3 and χ1 because they have the first two highest scores. However, these two blocks only provide history information, which is not enough to fully answer the query. In order to better answer the query, it is necessary to include blocks containing the name of the builder, e.g., χ4. On the other hand, the clustering approach will return all χ1, χ2, χ3, and χ4, leading to redundancy. The optimal solution will choose χ3 and χ4 as they provide the required information without redundancy. Furthermore, studies [11, 19, 42] have shown that the order of the blocks affects the performance of LLM, a factor that is also ignored by existing methods. In the case of the Eiffel Tower, for example, when choosing blocks χ3 and χ4, placing χ4 in the first position yields a higher score compared to the opposite order. However, determining the optimal order of block combinations is a challenging task since both require the search space to grow exponentially with the number of available blocks. In this paper, we further demonstrate that this problem is NP-hard (see Section 2.1).
Challenge 2: Non-monotonicity of utility. The current solution is based on the assumption that including more blocks always yields better final results. Specifically, in the AKNN-based approach, exactly k blocks are deterministically selected each time. In the clustering-based approach, a distance threshold between clusters and queries is set and all clusters within this threshold are returned. Both return as many blocks as possible. However, in practice, the utility of blocks is not monotonic. More specifically, too many chunks dilute key information by adding edge-related content, producing noise that reduces clarity. In addition, conflicts or subtle differences between blocks may confuse the model and reduce the quality of the response. For example, as shown in Figure 1, adding block χ1 reduces utility when χ3 and χ4 are selected, which highlights the fact that utility scores are typically non-monotonic in practice.
Challenge 3: Variety of queries. There are different types of user queries, each requiring a different ranking strategy based on its unique characteristics [47]. In current RAG systems, the utility score of a block is usually determined by the assigned re-ranker model. To date, various re-ranker models exist, but we observe that their performance varies widely across query types, and no single fixed re-ranker model consistently outperforms others across all query variations (see the experiments in Section 6.3.4 for more details). Current approaches [20, 46] typically rely on static re-ranker models for block ranking and lack the flexibility to adapt to different query contexts.
Problem statement: Does a RAG system exist that takes full account of associations between blocks and the non-monotonicity of utilities, while being able to accommodate all types of queries?
1.1 Our contribution
In this paper, we answer this question affirmatively by proposing a novel MCTS-based policy tree framework to optimize block retrieval in RAG systems. Overall, our contribution can be summarized as follows:
- We present the first RAG framework that considers the order of block combinations in a RAG task. Instead of considering each block independently or at a clustering level, we use MCTS to help search for the optimal block combination order sequentially. The high-level idea is as follows: first, we initialize the root node. Then, during iterations, we expand the tree by selecting the node with the highest utility and computing the utility of its expansion nodes. After each expansion, we update the utility in the entire policy tree. In this process, the decision of each iteration depends on the blocks that have been selected, allowing us to fully consider the associations between blocks. In addition, MCTS reduces the exponential search space to linear, and we apply parallel expansion techniques to further enhance the computational efficiency. With this design, we address Challenge 1.
- Unlike previous RAG frameworks that consider budget exhaustion as a termination condition, we propose a novel formulation in which budget constraints are integrated into the process of optimizing block combinations to fully account for the non-monotonicity of block utility, thus addressing Challenge 2. In addition, by prioritizing highly correlated, low-cost blocks and accounting for token length, we further reduce the computational cost.
- We propose a comparative learning-based agent that dynamically adapts MCTS configurations to queries, adapting the re-ranker model and configurations to specific query domains. This approach provides flexibility and robustness for dynamic, domain-specific queries, adapting to Challenge 3.
- In addition, we conducted comprehensive experiments comparing our framework with several state-of-the-art methods. The results validate the effectiveness, efficiency, and scalability of our approach and improve the performance by 30% compared to the baseline.
2 Preparatory knowledge
In this section, we first introduce the definitions of some key concepts, such as block and block combination order, in Section 2.1. Next, we give an NP-hard proof of the block order optimization problem. Finally, we discuss related work in Section 2.3.
2.1 Key concepts
RAG & Chunks. RAG is an efficient method to improve the performance of generative models by retrieving relevant context from an external corpus. In this approach, the corpus is first partitioned into smaller, more manageable units called chunks, which are stored in a vector database. Thus, we can give a formal definition of a block as follows:
Definition 2.1 (Block). Let C represent a corpus of documents, and a block χ be defined as a continuous block of text extracted from C. Formally, a block χ consists of a sequence of tokens (t1, t2, ... , tn), where each ti is a token in C and the size n is set by the user.
In a RAG system, each block is embedded in a vector representation using an embedding model that captures the semantic meaning of the block and enables the retrieval of contextually similar content. When a new query is received, the vector database performs a similarity search to identify the most semantically relevant blocks to the query. These retrieved chunks are then passed to a generator (e.g., a large language model) to generate a final response based on the retrieved content. Specifically, the more tokens a chunk contains, the higher the cost incurred by the generator. Thus, we define the cost of a block as cost(χ) = |χ|, which is equal to the number of tokens in the block.
Block combination order. In a RAG system, the retrieval results of a vector database may include multiple blocks. However, due to the input constraints of the generative model, it is impractical to use all these blocks. Therefore, it is necessary to select the optimal subset of blocks, called block combination, to fit a given cost budget. In addition, the order of the blocks within the combination has a significant impact on the performance of the generative model. The goal is to identify the order of block combinations with optimal order, formally defined as follows:
Definition 2.2 (Optimal block combination order selection). Let {χ1, χ2, ... , χk} be a set of potential blocks, ℛ be a cost budget, Φ = ⟨χφ1, ... , χφm⟩ represents an order of potential block combinations, where each χφi is a block and the index φi denotes its position in Φ. Let U(Φ) be the utility score assigned by the re-ranker model, which may be arbitrary or composite. Our goal is to find the order of combination of blocks that maximizes the utility scores under the cost constraint of feeding them into LLMs to generate the final response, i.e., searching for the
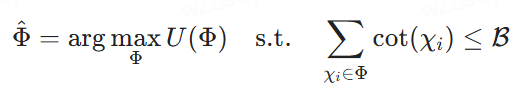
2.2 Proofs of NP-hard
To show that block combination sequential selection is NP-hard, we generalize the Maximum Weighted Hypergroup Problem (MWHP) to it. Since MWHP is NP-hard, we show that any MWHP instance can be converted to a block combination optimization instance in polynomial time.
2.2.1 Problem Definition for MWHP
Given a hypergraph ℋ = (V, E, w1, w2), where V is the set of vertices and E is the set of hyperedges, and each hyperedge contains a subset of V. w1: v → ℝ and w2: e → ℝ are the weight functions, which assigns a weight to each vertex and hyperedge, respectively. Given a subset of vertices V' ⊆ V, we say that a hyperedge e belongs to V', i.e., e ∈ V', if V' covers all the vertices of e. The goal is to find k vertices and maximize the sum of the weights of these vertices and the hyperedges they cover:
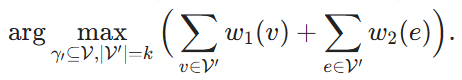
2.2.2 Normalization process
We now construct a corresponding instance of the block combination optimization problem from a given MWHP instance. For each node v ∈ V, we create a corresponding block Xv. We define its cost cost(Xv) ≡ 1. A block combination order Φ then corresponds to a subset of vertices of V denoted as V(Φ) ⊆ V. We define its utility as
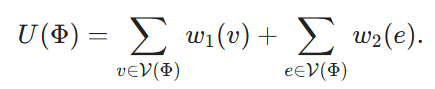
Finally, we set B = k, and we aim at
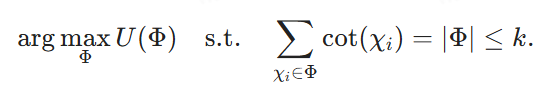
Using Φdenotes the solution of (4), then it is clear that V(Φ) is a solution of (2) and the induction can be done in O(|V|-|E|) time.
Note that this induction presupposes that in our block combination optimization problem, we allow the re-ranker to be arbitrary, which means that the utility scores can also be assigned arbitrarily. The complexity of finding the optimal block combination order can be significantly reduced if certain assumptions are made about the re-ranker. For example, if the re-ranker does not take associations into account and just linearly sums the utility scores of each block, each block can be evaluated independently. However, in this paper, we deal with the most general case and do not make any assumptions about the re-ranker model.
2.3 Related work
2.3.1 Retrieving Enhancement Generation
RAG [14, 20] is widely used to handle knowledge-intensive NLP tasks. In a typical RAG process, a dense embedding-based retriever searches for relevant information from external databases, which is then used by the LLM during the generation process. To improve this process, several studies [5, 18, 22, 35] have focused on adapting retrievers to better fit the generation needs of LLMs, developing multi-step retrieval methods, and filtering out irrelevant information. Although there are many state-of-the-art retrievers [8, 9, 15, 16, 27, 34], optimizing retrievers and LLMs together in an end-to-end process [25, 31] is more promising. For example, research [30] focuses on co-training the retriever and LLM simultaneously or in stages. however, this requires agent loss for optimization and complicates the training process, especially when embedded databases need to be reindexed frequently, which incurs high computational costs. Therefore, approaches like [5] decompose complex multi-step queries into smaller sub-intents to improve the comprehensiveness of the response without frequent re-indexing. However, these approaches usually ignore the crucial role of block combination order, which can significantly affect the overall response quality of LLM. To the best of our knowledge, this paper is the first approach to consider block combination order in a RAG task.
2.3.2 RAG re-ranking
Re-ranking methods are essential to improve retrieval performance in the RAG process [43, 44, 51]
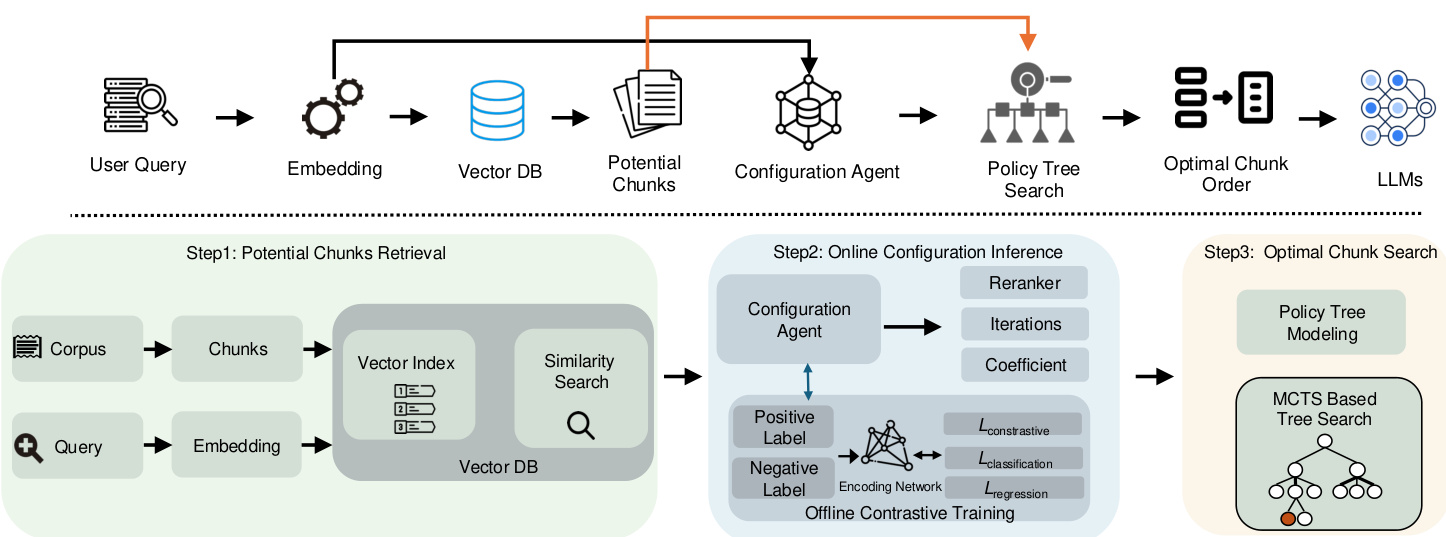
Figure 2: Overview of CORAG system architecture
Traditional re-ranking methods [33, 50] typically rely on medium-sized language models, such as BERT or T5, to rank retrieved contexts. However, these models usually struggle to capture the semantic relationships between queries and contexts, especially in zero- or small-sample settings. Therefore, recent research [43] has emphasized the potential of command-adjusted LLMs to improve context re-ranking, even in the presence of noisy or irrelevant information. Despite these advances, the re-ranking capabilities of LLM in RAG systems remain underutilized. In particular, it has been shown that block ranking affects the performance of LLM [19], emphasizing the need to consider the order of block combinations in RAG tasks. However, the existing models are not suitable for situations where a specific sequence or combination of blocks is required for optimal retrieval, rather than isolated blocks. Therefore, future research needs to better utilize LLM to more efficiently order blocks in response to queries within the RAG framework.
2.3.3 Reinforcement Learning for Large-Scale Language Models
Recently, Reinforcement Learning (RL) has been increasingly used for a variety of data management and RAG tasks.RL techniques can enable large language models to improve their generative capabilities by utilizing external knowledge sources (e.g., search engines) [13, 23]. In particular, human feedback [4, 36, 37] can be integrated to help models generate more accurate and contextually relevant responses through the RL framework. In addition, a number of query optimization approaches [17, 21, 49] further improve the retrieval process by allowing model performance to inform query tuning and ultimately improve results for downstream tasks. In this work, we apply a lightweight RL technique, MCTS, to optimize the block combination sequential search process in RAG systems. We also introduce a configuration agent to guide the MCTS search process. To the best of our knowledge, this is the first approach to this particular problem.
3 System overview
As mentioned earlier, existing RAG frameworks face three key challenges: how to adequately account for the associations between blocks and the non-monotonicity of the sequential utility of block combinations, and to adapt to different query domains. These challenges lead to reduced output relevance. To address these issues, we introduce CORAG, a system designed to retrieve optimal block combinations, taking into account both query domains and user budgets. As the most important component of our system, we introduce the optimal block combination search model. The model employs an MCTS-based policy tree for sequential search of block combination orders, allowing us to fully consider the associations between blocks (Challenge 1) as well as the non-monotonicity of the block combination order utility (Challenge 2). In addition, we propose a configuration inference module that recommends optimal MCTS configurations and re-rankers for various query domains, thus addressing Challenge 3. Below, we provide a brief description of these two modules.
Optimal block combination search: A straightforward approach to considering block associations consists of retrieving potential blocks from a vector database (as shown in Step 1) and then exhaustively exploring all possible block combinations. However, this approach leads to significant latency and computational cost. To mitigate this, we construct a strategy tree (shown in Step 2) that reframes the optimal block combination search as an in-tree node search problem. Specifically, the root node of the strategy tree represents an initial empty state, and each child node corresponds to a particular combination of blocks. For example, if the root node has child nodes representing blocks χ1 , one of its children may represent the combination χ1+χ2 , while another may represent χ1+χ3
We design an MCTS-based search algorithm to solve this problem. Unlike traditional MCTS, our approach expands the highest utility node in each iteration while evaluating all possible sub-nodes. In addition, we consider cost and budget constraints during the strategy tree search. Node utilities are computed by balancing exploration with cost control, optimizing efficiency and accuracy.
Configuration Reasoning: A simple solution to configuration tuning would be to enumerate every possible configuration or re-ranker, compute the results in parallel, and then choose the best configuration. However, this would lead to an unrealistic cost of the RAG system. In order to optimize the configurations (i.e., number of iterations, cost factor, and exploration factor) for the policy tree search process, we introduce a configuration agent that dynamically generates configurations based on the query domain. To ensure the effectiveness of the model, we employ a contrastive learning approach using positive and negative label pairs: positive labels correspond to query embeddings from the same best re-ranker, while negative labels come from a different best re-ranker. The joint loss function is used to simultaneously optimize regression (for parameter tuning) and contrast learning (to enhance label differentiation).
Summary. The flow of our framework is shown in Figure 2. We first generate embeddings for the input query and then use it to retrieve potential blocks from the vector database. These query embeddings are also fed into a configuration agent that dynamically generates an optimal MCTS configuration based on the query domain. Using this optimal configuration, we can search through the policy tree to determine the optimal block combination and order from the retrieved potential blocks. Finally, this optimal block combination is used to construct the final hints for the LLMs.
4 Block combination search
As mentioned earlier, the order of block combinations has a significant impact on the efficiency of hint construction for LLMs. Due to the huge number of potential combinations, especially when a large number of blocks are involved, enumerating all possible block combination orders is not feasible. In this section, we propose a novel approach that achieves a good balance of efficiency and accuracy in the problem of searching for the optimal block combination order. In Section 4.1, we model the problem as searching for optimal nodes in a policy tree (Section 4.1). We then propose an MCTS-based algorithm to solve this node search problem (Section 4.2).
4.1 Strategy Tree Search Modeling
In order to find the optimal combinatorial order, the first step is to find a data structure that can efficiently enumerate all possible combinatorial orders. A natural choice is a tree, where by traversing from root to leaf nodes we can explore all potential answers.
Strategy Tree. As shown in Fig. 3, we construct a strategy tree to represent the order of all possible block combinations extracted from the vector database. Specifically, the root node symbolizes the initial state without any blocks, and each subsequent node depicts a block selected from the potential blocks. Thus, a child node is generated from its parent node by selecting the next available block from the queue of potential blocks and merging it into the sequence established by the ancestor node. For example, if a node represents the block combination sequence {χ1}, then a child node may contain subsequent combination sequences such as {χ1, χ2}, {χ1, χ3}, or {χ1, χ4}. Therefore, we formally define the strategy tree as follows:
Definition 4.1 (Strategy Tree). Given a query q and a set of potential blocks {χ1, χ2, ... , χn}, we construct a policy tree T. The root node of T represents the initial state without any blocks. Each subsequent non-root node contains a set of blocks by merging the newly selected blocks from the remaining potential blocks into the sequence of its parent nodes. This process sequentially constructs an ordered combination of blocks in each non-root node, and we aim to find the node with the highest utility score.
In a strategy tree, our goal is to select a node containing ordered blocks that provide the maximum benefit at the minimum cost. In order to achieve this, we need to design a utility calculation function to evaluate the trade-off between benefits and costs. This function is quantified by what we define as "node utility", as described below.
Nodal utility. The utility metric consists of two components: the benefit derived from selecting a combination of blocks and the cost of using the blocks as prompts for LLMs. Specifically, the benefits are quantified by the LLMs, which measure the similarity between the selected blocks and the query. In particular, we denote them as node values V. Next, we further use the Upper Confidence Bound (UCB) [3] algorithm to balance the balance between utilization (node values V(vi)) and exploration (search counts N(vi)) of node values V(vi) and search counts N(vi). For a given node vi, with respect to the cost, we consider the labeling cost defined in Section 2 and measured by the ratio of the cost of the current block combination relative to the total allocated budget B. Thus, the node utility is defined as follows:
Definition 4.2 (Nodal Utility). Given a strategy tree and a cost budget B, the utility of a non-root node is defined as:
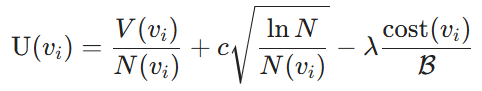
where V(vi) is the estimated benefit value of the block combination at node vi, determined by the training model, N(vi) is the number of visits to node vi, which promotes the exploration of less visited nodes, and N is the total number of visits to all the nodes in the policy tree to ensure the balance between exploration and utilization. In addition, cost(vi) denotes the labeling cost of node vi, B is the total labeling budget, c regulates the exploration-utilization trade-off, and λ serves as a cost penalty factor to improve cost efficiency.
Optimal node selection modeling. Based on the defined node utilities, the task of selecting the optimal block combination order, as described in Section 2, is reformulated as selecting the optimal node in the policy tree T . Under a given budget constraint B, the goal is to identify nodes vi ⊆ T to maximize the utility U(vi) while ensuring that the total cost associated with vi does not exceed B. Formally, this is expressed as:
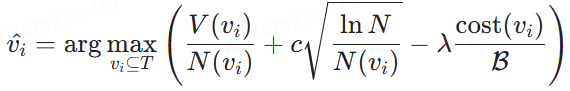
where V(vi) is the estimated benefit of the combination of blocks at node vi and cost(vi) represents its associated cost. This formula makes it possible to choose the block that maximizes utility within a given budget.
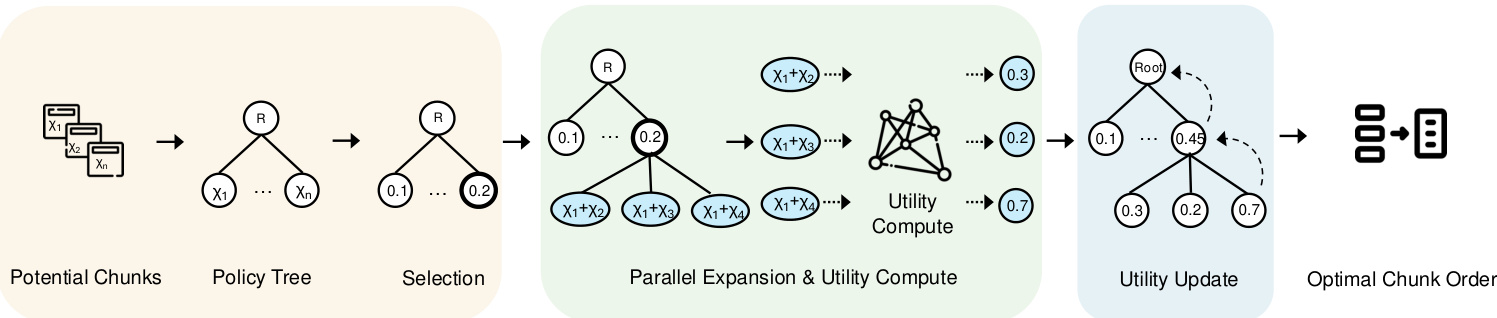
Figure 3: MCTS-based block optimization workflow

Algorithm 1 MCTS-based Strategy Tree Search
4.2 MCTS-based policy tree search
Motivation. Enumerating all nodes in the policy tree will find the optimal node, but will result in high computational cost. To solve this problem, a straightforward approach is to apply a greedy strategy that navigates the tree iteratively starting from the root node. In each iteration, select the child node with the highest benefit and continue until the budget is exhausted. However, this approach is likely to lead to suboptimal results. For example, the benefit of χ1 may be slightly higher than that of χ2, but the benefit of χ2 + χ3 may be substantially higher than that of χ1 + χ3. In this case, a greedy approach may lead to sub-optimal results. Therefore, it is necessary to revisit the high-efficiency parent nodes. At the same time, we need to reduce the exploration of low-benefit nodes.
To achieve our goal, we propose an MCTS-based strategy tree search method designed to efficiently select and rank block combinations. This approach iteratively explores the space of potential block sequences to optimize a given query within a specified budget constraint.
Overview. MCTS-based policies are outlined in Algorithm 1. We first initialize the root node of the policy tree using input queries. When the computational budget is not exhausted, we iteratively perform two key steps: node selection and utility update. Once the iteration limit or budget is reached, we stop the process and recursively search through the tree to find the node with the highest utility. Unlike traditional MCTS strategies that usually focus only on the root node, our approach also considers promising intermediate level nodes to maximize the block combination utility.
Detailed explanation of key features. We further explain these two key features as follows:
- Node selection (Algorithm 2). We recursively select the node with the highest utility value that is most likely to lead to the optimal block combination. Specifically:

Algorithm 2 NodeSelection

Algorithm 3 UtilityUpdate
- Select. We identify the nodes with the maximum utility value. If 𝑣 is not yet expanded, we generate all possible descendant nodes and include them in the strategy tree. If 𝑣 has been expanded, we select the descendant node with the highest utility for further exploration.
- Extensions. After selecting the node with the highest utility, we extend it by generating all potential child nodes. Each child node represents a new order of possible block combinations. Our approach employs parallel expansion, which computes and evaluates multiple sub-nodes simultaneously. This parallelism exploits the ability of the value network to handle multiple combinations at a computational cost similar to that of a single node, enhancing the efficiency of the search.
- Calculated utility. We compute the utility value for each new child node using the utility formula. The re-ranker model R processes multiple block combinations in parallel to generate.

5 Configuring the Agent
After addressing the efficiency of processing block associations within the user's budget, the remaining task is to design a system to fit the domain of each query.The MCTS process involves several key configurations, including the re-ranker selection, the number of iterations, the exploration factor, and the cost factor. Optimizing these configurations across different query types is particularly challenging. To address this problem, we propose a configuration agent framework that predicts the optimal re-ranker and configuration for each query. In this section, we first introduce the agent framework in Section 5.1 and then outline the model learning process in Section 5.2.
5.1 Modeling framework
Motivation. To address Challenge 3, which requires adapting to the domain of each query and recommending optimal configurations, a straightforward solution is to use an MLP classifier to assign each query to its optimal re-ranker. However, initial experiments show that MLP classification performs poorly. Upon further analysis, we observe that similar types of queries tend to share the same best re-rankers and configurations. Therefore, utilizing the Siamese network with contrast learning to bring queries of the same category closer together while pushing queries of different categories apart is a more feasible approach.
Figure 4 provides an overview of our configured agent, which consists of two main modules responsible for transforming the input into a feature graph. First, the input embedding module generates embeddings of the input query. Subsequently, the encoding network processes these embeddings to produce feature maps, which are then used to derive various configurations of the MCTS settings.
The following sections describe each component in detail and explain its design rationale.
(1) Enter the query embedded in. In order to efficiently capture the factors of various queries, given the diversity of query types such as explicit facts, implicit facts, interpretable rationality, and hidden rationality [47], we use the BGE-M3 [6] embedding model to generate embeddings for each query. These embeddings enhance the learning framework by mapping similar types of queries to the same re-ranker category. Represented in a 1024-dimensional space, the embeddings capture the underlying semantic features, enabling the coding network to efficiently compare and categorize them. This step helps to improve the retrieval relevance of different query types. In addition, using the same embedding model also generates optimal re-ranker annotated embeddings, including their unique features and associated metadata, enabling the model to align queries to the optimal re-ranker.
(2) Generating feature maps using coded networks: the To optimize the re-ranker selection task and recommend the best re-ranker for each query for different query types, we use coding networks to efficiently learn representations that are useful for both classification and configuration prediction. We use a Siamese network consisting of three fully connected layers for this task. It processes input query embeddings of dimension d = 1024 and learns classification outputs and MCTS configuration predictions (i.e., number of iterations and λ). The branches of the encoding network share weights, and each branch applies a linear transformation followed by RELU activation. Sequentially, the first hidden layer reduces the dimensionality to 512, the second to 256, and the third to 128.The final output layer provides classification predictions that specify the best re-ranker for each query, as well as regression outputs that are used to predict the most efficient MCTS configurations to guide the search process. The classification output identifies the best re-ranker for each query, while the regression output determines the best MCTS configuration settings.
5.2 Joint training
In this section, we outline the training process for developing configuration agents. As shown in Fig. 4, we implemented three joint training tasks to improve the training efficiency of the model. The first two tasks involve classification and regression for selecting the best re-ranker and predicting the best values of the MCTS hyperparameters, respectively. In addition, we incorporate a comparative learning approach to further improve the learning process.
5.2.1 Classification and regression losses.
Given the predicted re-ranker label Y(pred) and its corresponding actual optimal re-ranker Y(true), the classification loss L(cla) is calculated as follows.
![]()
where F(cla) represents the cross-entropy loss between the predicted and actual re-ranker labels. This loss function helps to accurately classify the optimal re-ranker for each query. Similarly, the regression loss L(reg) is defined as.
where 𝐹reg is the mean square error (MSE) between the predicted MCTS parameter 𝑝pred and the actual MCTS parameter 𝑝true. This metric ensures an accurate prediction of the MCTS configuration in terms of the number of iterations and 𝜆.
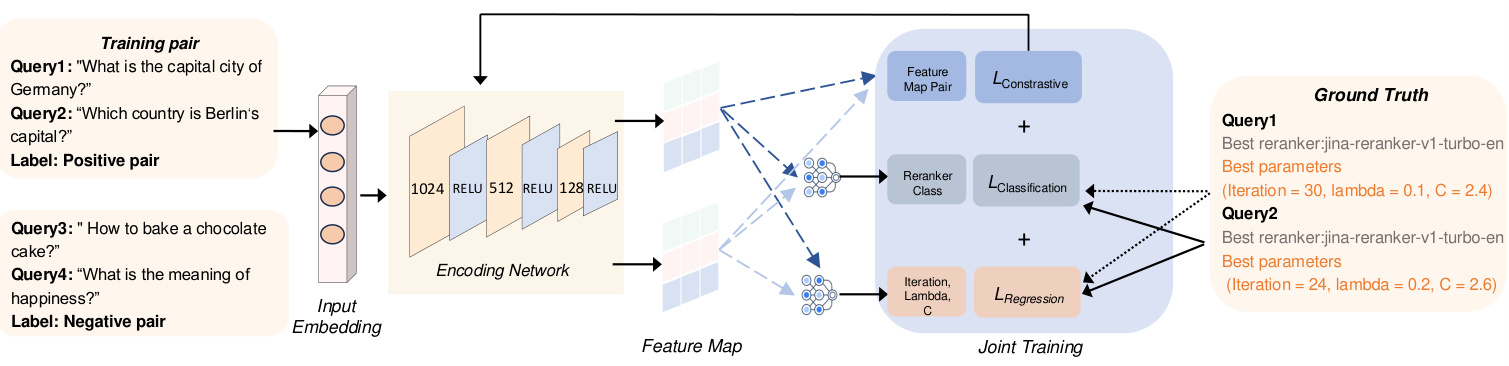
Figure 4: Configuration Agent Overview
5.2.2 Contrastive learning.
In order to efficiently distinguish different query domains and recommend the best configuration for each query, we utilize comparative learning to bring queries in the same domain closer together while pushing out embeddings of different re-ranker classes.
Comparison Preparation. In order to prepare the training dataset, we must determine the optimal re-ranker and configuration for each query. In this study, the optimal re-rankers and corresponding configurations for each query were determined through extensive experiments with various settings. Subsequently, query pairs are generated based on these optimal re-ranker annotations. Positive pairs consist of queries sharing the same optimal re-ranker, facilitating the minimization of their embedding in the feature space. On the contrary, negative pairs consist of queries with different re-rankers with the goal of maximizing the embedding distance between them. Since some re-rankers perform similarly on certain queries, we only select cases where ROUGE-L differs by more than 10% to form our training dataset.
Contrast loss. As shown in Fig. 4, for a given pair of positive pairs (𝑥𝑖, 𝑥+𝑖) and the negative pair (𝑥𝑗, 𝑥-𝑗), we first use the coding model to generate their corresponding feature maps. These feature maps are then used to compute the contrast loss 𝐿con. Specifically, this process can be represented as follows:
Among them.𝑓𝜃(𝑥) denotes the embedding function.𝐹con is a similarity function applied to two types of pairs: positive pairs (with similar reorderers) and negative pairs (with different reorderers). This loss function is designed to ensure that queries with the same reorderer are closer in the embedding space and queries with different reorderers are farther away.
5.2.3 The entire training process.
Finally, the total loss function L(total) is the sum of comparison, classification and regression losses as follows.
In particular, the contrast loss Lcon(θ) encourages the embeddings of queries with the same optimal re-ranker to be closer together while pushing the embeddings of queries with different re-rankers out of the way. The classification loss Lcla(θ) helps the model correctly identify the re-rankers using cross-entropy, while the regression loss Lreg(θ) minimizes the error in predicting the optimal MCTS configuration.
Remarks. Once the total loss Ltotal is computed, the network parameters θ are updated using gradient descent at a learning rate η. This optimization process is repeated over multiple cycles E and batches, ensuring that both the classifier and parameter predictions are improved over time.
6 Experimentation
The experimental study was designed to answer the following questions.
- RQ1 How does our CORAG compare to other methods in cost-constrained RAG pipelines?
- How efficient is RQ2 CORAG with different block sizes?
- RQ3 What are the current bottlenecks in RAG?
- What are the bottlenecks in RAG?
- How scalable is RQ4 CORAG with different dataset sizes?
- RQ5 How effective is each design in CORAG?
6.1 Experimental setup
Environment. We integrated our system with the popular RAG framework LlamaIndex. The experiments were run on a Linux server equipped with an Intel Core i7-13700K CPU (12 cores, 24 threads, 5.3 GHz), 64 GB of RAM and 1 TiB NVMe SSD. The Configuration Agent module was implemented on an NVIDIA RTX 4090 GPU equipped with 24 GB VRAM using PyTorch 2.0.
Table 1: Statistical data used in the experiment.
| data set | #train | #dev | #test | #p |
| MSMARCO | 502,939 | 6,980 | 6,837 | 8,841,823 |
| Wiki | 3,332 | 417 | 416 | 244,136 |
Dataset.To evaluate the performance of CORAG in different scenarios, we conducted experiments on two different datasets with different task foci: (1) WikiPassageQA [7] is a Q&A benchmark containing 4,165 questions and more than 100,000 text chunks aimed at evaluating paragraph-level retrieval. (2) MARCO [24] is a comprehensive dataset dedicated to natural language processing tasks with a major emphasis on Q&A and information retrieval. As shown in Table 1, both WikiPassageQA and MARCO provide high-quality questions and paragraph annotations, making them suitable for evaluating retrieval effectiveness. In our experiments, we prompt LLMs to generate ground truth answers for each dataset. For example, if we use Llama3 to evaluate CORAG performance, we also use Llama3 to generate ground truths in the same experimental setup to maintain fairness and alignment with the LLMs' characteristics.
Baseline.We compare CORAG performance to two typical RAG baselines:
- RAPTOR [29]: RAPTOR constructs a hierarchical document summary tree by recursively embedding, clustering, and summarizing blocks of text to achieve multi-level abstraction. This approach is consistent with the clustering-based approach discussed in Section 1. We complete the tree construction within approximate budget constraints.
- NaiveRAG: This is a basic method for retrieving relevant blocks. First, candidate blocks are retrieved from a vector database based on vector similarity search and then they are ranked using a re-ranker model. This method is the AKNN method mentioned in Section 1. To satisfy the cost constraint, we use a greedy budget allocation strategy to retrieve blocks until the budget is completely exhausted.
In addition, we remove the configuration agent in our approach as a baseline to evaluate its impact on CORAG performance, referring to this version as the CORAG w/o Agent.Finally, we implement an approach called CORAG Upper, which establishes an upper bound by exploring all possible combinations of blocks and selecting the best order. Due to the large number of potential combinations, in the case of CORAG Upper, we limit exploration to combinations of fewer than six blocks.
Remarks.Other approaches, such as GraphRAG [22], rely heavily on frequent calls to LLMs to summarize blocks and construct indexes, incurring huge costs (e.g., billions of tokens) that exceed our strict cost constraints. Therefore, these approaches are not feasible for solving our problem. For a fair comparison, we excluded these types of RAG approaches from our experiments.
Hyperparameter settings: the hyperparameters for CORAG are determined automatically by the configuration agent, while NaiveRAG does not require any hyperparameters. For other baseline methods, we ensure consistency by using the same hyperparameters for fair comparisons. Specifically, we set the exploration factor to 2.4, the number of iterations to 10, and the cost factor λ to 0.1. Preliminary experiments show that this configuration optimizes baseline performance. We will also conduct further ablation studies to validate these settings.
Learning parameter settings. In our approach, the configuration agent is trained using contrast learning. Hyperparameters used in this process include contrast loss (margin=1.0), learning rate (lr=0.001), batch size (32), number of cycles (num_epochs=60), and embedding model (i.e., BAAI/bge-m3 [6]).
Assessment Metrics. We evaluate effectiveness by comparing the Rouge scores of ground-truth answers and generated responses, using Rouge-1, Rouge-2, and Rouge-L as evaluation metrics. To evaluate efficiency, we measure the latency required to answer queries using different methods.
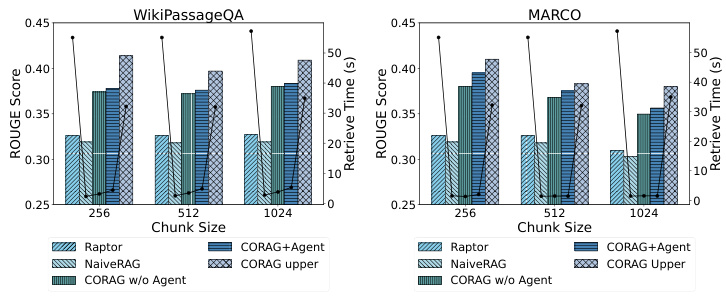
Figure 5: Efficiency Comparison
6.2 Performance comparison
6.2.1 RQ1: Rouge Comparison.
As shown in Figure 2, we compare the performance of CORAG with several baselines on different datasets, mainly using WikiPassageQA and MARCO. the evaluation is performed at three different block sizes, using the Rouge-1, Rouge-2, and Rouge-L metrics to assess the improvement of the responses generated by LLM due to our retrieval method. corag compares favorably with the mainstream RAG methods (e.g., NaiveRAG and RAPTOR) by a significant improvement of about 251 TP3 T. Unsurprisingly, CORAG does not exceed the upper bound, which represents an extreme case where all possible combination orders are exhaustively enumerated, which is clearly inefficient and impractical. In conclusion, CORAG outperforms the baseline, enhancing search relevance while effectively pruning the search space.
6.2.2 RQ2: Efficiency assessment.
As shown in Fig. 5, since CORAG is based on a tree search algorithm, the agent helps to predict the best re-ranker and parameters for a given query. Therefore, it is crucial to evaluate the impact of different block sizes and datasets on the efficiency of the retrieval optimization task. We tested the efficiency using different datasets and block sizes and observed that NaiveRAG using traditional retrieval methods achieves shorter retrieval times but lower Rouge scores.CORAG upper performs well in terms of Rouge but is significantly less efficient as it explores the entire search space. Similarly, RAPTOR utilizes an external LLM for summarization and exhibits poor efficiency. In contrast, our CORAG approach balances efficiency with search relevance, achieving an effective trade-off.
6.2.3 RQ3: Performance Decomposition.
We show a performance decomposition of the baseline NaiveRAG to highlight the bottlenecks of current RAG systems. To address the challenge of searching for the optimal order of block combinations, implementing it using NaiveRAG requires the following steps: a) obtaining the query embedding, b) retrieving the potential block combinations, c) re-ranking the potential block combinations, and d) cue refinement. Figure 6 reports the average latency of each step, in the previous experimental setup.
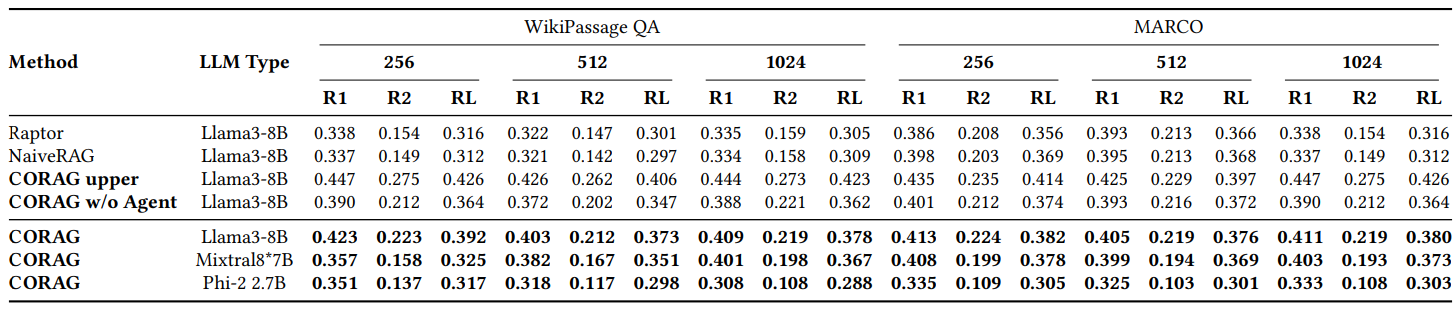
Table 2: Comparison of Rouge on WikiPassage QA and MARCO datasets
6.2.4 RQ4: Scalability assessment
CORAG exhibits excellent scalability, especially when working with large datasets (such as WikiPassageQA and MARCO) that contain a large number of paragraphs. The number of chunks can be easily scaled to 100k or more by splitting each paragraph into 256-tagged chunks. Despite the significant increase in data volume, our retrieval time increases by only 101 TP3T over the traditional approach, demonstrating the efficiency of our system in managing large-scale retrieval tasks. Notably, our system outperforms the CORAG Upper method, requiring only one-tenth of the retrieval time while still providing competitive ROUGE scores. This effective balance between performance and computational overhead highlights the system's ability to efficiently prune the search space, ensuring fast retrieval even in huge datasets. Thus, our approach is well suited for scenarios requiring large-scale data processing and high retrieval accuracy.
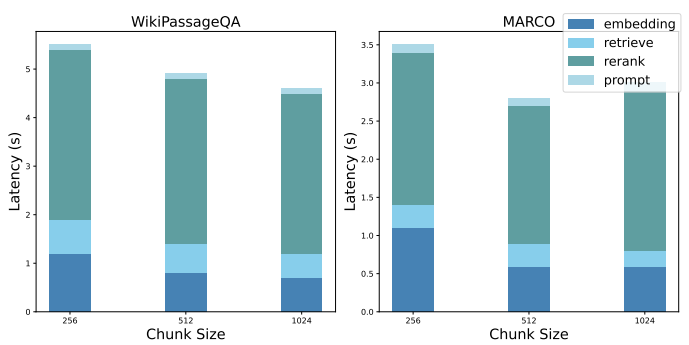
Figure 6: Performance Decomposition
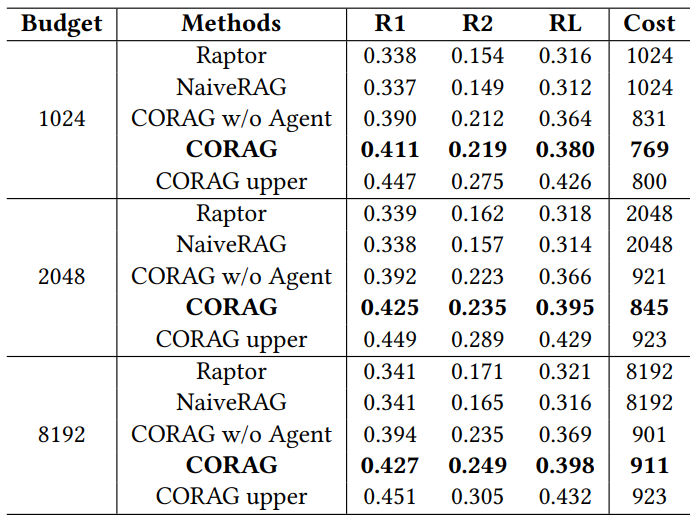
Table 3: Comparison of performance under different budgets
6.3 RQ5: Ablation studies
6.3.1 Ablation studies with different budgets
As shown in Table 3, we evaluated CORAG as a cost-constrained system and investigated the impact of different budgets on overall performance. Using the MARCO dataset, we set the budget limits to 1024, 2048, and 8192 markers and evaluate the results using ROUGE.CORAG consistently outperforms all baselines at these budget levels. Notably, CORAG's average tagging cost stays below each budget limit, suggesting that the utility of the blocks is not monotonic, as emphasized in Challenge 2. As the budget increases, CORAG benefits from an expanded search space and is able to include more relevant information, rather than just increasing the number of blocks.
6.3.2 Ablation studies with different exploration coefficients
As shown in Fig. 7, we conducted an ablation study to evaluate the impact of different exploration coefficients on the system performance, specifically testing values of C of 0, 1, 2, and 3. The results show that an exploration coefficient of approximately 2 provides the best performance, achieving an optimal balance between exploration and exploitation during the search process. This balance allows the system to efficiently discover relevant information while maintaining focus on high potential blocks, ultimately leading to improved RAG response. In contrast, lower exploration coefficients led to sub-optimal results due to under-exploration, while higher exploration coefficients led to sub-optimal results due to over-diversion of focus. These findings emphasize the critical role of the exploration coefficient in the performance of the CORAG search process and highlight the importance of careful parameter tuning.
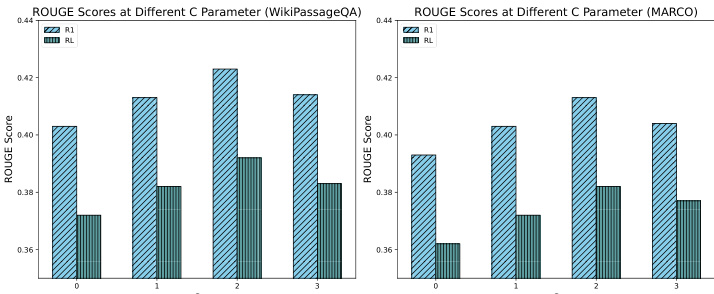
Figure 7: Comparison of ROUGE between different values of C
6.3.3 Ablation studies with different cost factors
As shown in Fig. 8, we conducted an ablation study to evaluate the impact of different cost coefficients on the system performance, specifically testing values 0, 0.1, 0.2, and 0.3. The results show that the introduction of cost coefficients in the utility leads to a slight decrease in the ROUGE score. This decrease is due to the fact that in the absence of a cost constraint, CORAG tends to produce longer outputs, albeit at the cost of cost efficiency. However, despite the slight decrease in ROUGE scores, the decrease stays within 51 TP3T, which is acceptable. These results highlight the importance of efficiently tuning the cost coefficients to balance output richness and cost constraints, further emphasizing the role of our configuration agent in enabling efficient configuration tuning to optimize CORAG performance.
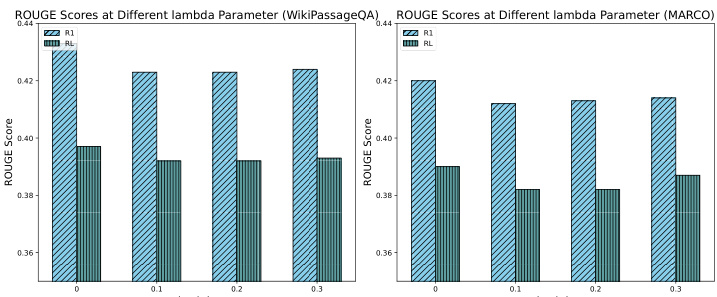
Figure 8: Comparison of ROUGE for different values of lambda
6.3.4 Ablation studies with different rearrangeers
In order to evaluate the impact of different rearrangeers on retrieval performance, we conducted an ablation study using six widely recognized rearrangeer models: jina-reranker-v1-turbo-en, jina-reranker-v2-base-multilingual, bge-reranker-v2-m3, bge- reranker-large, bge-reranker-base, and gte-multilingual-reranker-base. these rearrangeers were evaluated on the MARCO dataset using the llama3-8B model configured with a fixed cost factor of 0.1, an exploration factor of 2.4, and a budget constraint of 1024.
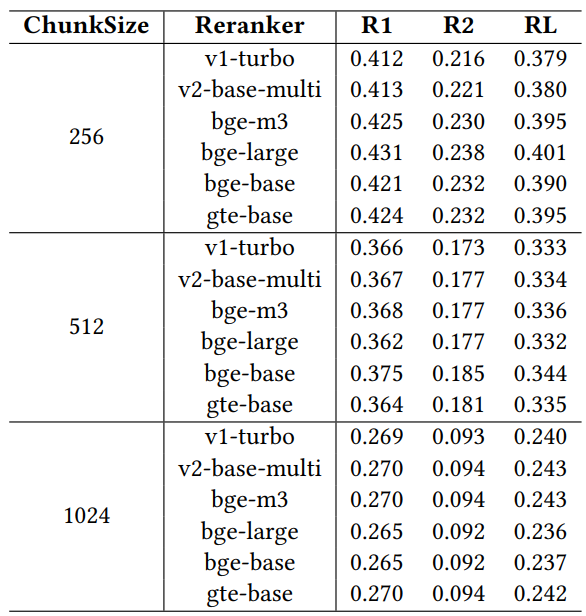
Table 4: Performance comparison with different reorderers
The results in Table 4 show that there are differences in performance between the different rerankers, highlighting the importance of carefully selecting a reranker to optimize the performance of the RAG system under specific operational constraints. Among the rearrangeers, gte-multilingual-reranker-base and bge-reranker-large show consistently strong performance on the QA task, suggesting that these rearrangement models are highly efficient in capturing relevant information for different QA queries. We observe that as the block size increases in the ablation study, each individual re-ranker underperforms the agent in terms of recommended re-rankers for different queries. This suggests that the configuration agent effectively utilizes the diversity of the rearrangeers by dynamically adjusting the configuration to improve the retrieval results. The ability of the configuration agent to recommend better rearrangement choices and parameter configurations highlights its role in maximizing the performance of the RAG system, especially under constraints such as limited budget.
6.4 Case Studies
Figure 9 shows three examples comparing the retrieval quality of CORAG and the traditional NaiveRAG approach, highlighting why our approach outperforms the baseline approach. Due to its simple top-k search and reordering, NaiveRAG often misses important information relevant to the query intent because it usually retrieves chunks based on keyword matching rather than relevance to the query. For example, for the query "Are leafy flowers shrubs?" , NaiveRAG retrieves content that contains matching keywords but fails to provide the actual classification of the leaf flower. In contrast, CORAG's block combination strategy retrieves context that includes the category of the leaf flower, enabling LLM to give a more accurate response. In another case, NaiveRAG retrieved terms and legal clauses that included "oxyfluorfen" but lacked an understanding of the query intent, while CORAG provided content that linked oxyfluorfen to use cases in cotton, which required a search that NaiveRAG's Vector similarity search could not capture the logical relationships between the blocks. Finally, for the query "Where do bacteria come from?" NaiveRAG retrieves chunks containing the keyword "bacteria" but does not address their origin, while CORAG provides a more complete response, including the source of the bacteria and their reproduction conditions. These cases illustrate that CORAG excels in retrieving logically connected information, making it more suitable than NaiveRAG for queries that require more than simple keyword matching.

Figure 9: CORAG case study
7 Insights into the RAG and Future Design Options
7.1 Shortcomings of the current RAG
We provide an analysis of the current RAG system, revealing the performance challenges faced during the retrieval (S1), enhancement (S2) and generation (S3) phases.
S1: Search overhead Current RAG systems typically utilize LLMs for summarization and indexing structures, ignoring the computational costs associated with external LLMs, which increases computational overhead. Model-based reorderers, while improving relevance during retrieval, introduce significant latency, which may hinder latency-sensitive contextual efficiency. Cost-effective index construction and reordering optimizations are essential to balance efficiency and performance.
S2: Enhanced overhead Post-retrieval techniques, such as optimized block combination ordering, enhance context relevance but require additional computation. Pruning strategies that minimize the search space and optimize the combination order are essential to balance computational cost and enhance contextual relevance. Efficient block combination optimization that emphasizes order and coherence is critical for reducing cost and improving retrieval performance.
S3: Generation overhead Efficient hint engineering for optimal block combinations requires significant computational resources. Query-specific hint refinement and compression are essential to reduce overhead while maintaining input relevance and conciseness. Adaptive strategies to handle different query types and domain-specific requirements ensure prompting efficiency without compromising output quality.
7.2 Design Options
To address the above challenges, the following design choices are intended to optimize the performance of the RAG system:
P1: Co-design of retrieval and reordering processes In CORAG, the parallel extension in tree search accelerates query processing and significantly reduces latency by enabling concurrent retrieval and reordering. Future optimizations can address the bottleneck by eliminating stage-specific delays and further improving ranking efficiency. This co-design approach efficiently manages the block combination order to improve the ranking process and associated scoring.
P2: Optimization of tree structures and search iterations The results show that shorter strategy tree heights improve search efficiency by reducing computational overhead, which is especially beneficial for large datasets. Minimizing tree height in tree-based search improves the speed of searching contextually relevant blocks and significantly reduces latency and computational cost. This optimization approach improves the performance of RAG systems on large-scale datasets.
P3: Dynamic Tip Project Selecting the rearranger based on the query type and using adaptive hint templates can improve the retrieval relevance of LLM. The dynamic cueing structure aligned with query intent and domain-specific context can maintain output quality within resource constraints. This adaptive cue engineering approach achieves an effective balance between efficiency and retrieval quality, addressing the dynamic nature of queries in RAG systems.
8 Conclusion
Considering the non-monotonicity of the utility of blocks, the correlation between blocks, and the diversity of different query domains, we propose CORAG, a learning-based retrieval optimization system.Initially, we model the order of block combinations as a tree of policies, and explore this tree using MCTS, aiming to find the optimal order of block combinations. We introduce a configuration agent that accurately predicts the optimal configuration and rearranger for a given query. In addition, we design a parallel query expansion strategy to expand multiple nodes in each iteration. Experimental results show that our approach significantly outperforms state-of-the-art approaches within cost constraints and also excels in efficiency.
© Copyright notes
Article copyright AI Sharing Circle All, please do not reproduce without permission.
Related posts

No comments...