Goedel-Prover-V2 - Princetons quelloffenes Modell zum Beweisen von Theoremen, unter anderem in Zusammenarbeit mit Tsinghua und NVIDIA

Was ist Goedel-Prover-V2?

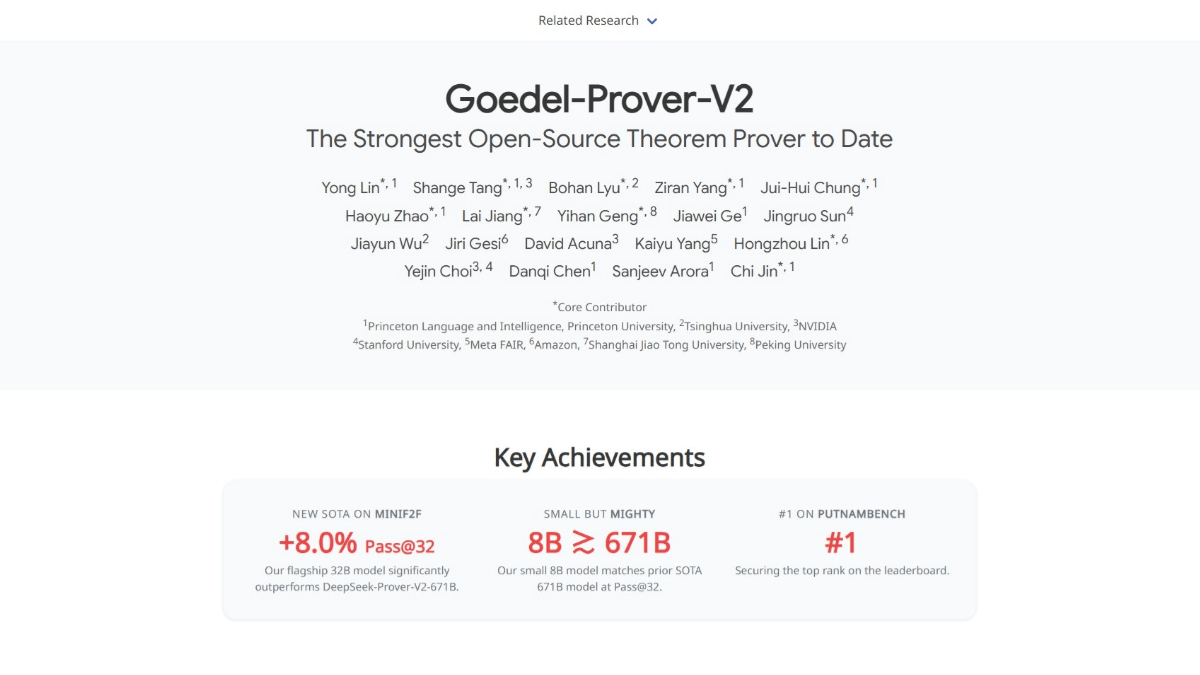
Goedel-Prover-V2 ist ein Open-Source-Theorembeweisungsmodell von führenden Institutionen wie der Princeton University, der Tsinghua University und NVIDIA. Das Modell basiert auf innovativen Techniken wie hierarchischer Datensynthese, verifier-geführter Selbstkorrektur und Modellmittelung, um die Leistung automatisierter formaler Beweise erheblich zu verbessern. Das Goedel-Prover-V2-Modell ist in zwei Versionen verfügbar, 32B und 8B, und das Modell schneidet in einer Reihe von Benchmarks sehr gut ab, z. B. erreicht das 32B-Modell eine Punktzahl von 90,41 TP3T für Pass@32 im MiniF2F-Test und übertrifft damit das größere DeepSeek-Prover-Prover-V2-Modell. So erreichte das 32B-Modell im MiniF2F-Test eine Pass@32-Punktzahl von 90,41 TP3T und übertraf damit das wesentlich größere Modell DeepSeek-Prover-V2. Das Modell ist in der Lage, automatisch Beweise für komplexe mathematische Probleme zu generieren und korrigiert sich selbst auf der Grundlage von Rückmeldungen des Lean-Compilers, um die Qualität der Beweise zu verbessern, und der Open-Source-Charakter von Goedel-Prover-V2 bietet Forschern eine Grundlage für weitere Entwicklungen und Verbesserungen.

Hauptmerkmale von Goedel-Prover-V2

• Automatische Erstellung von ZertifikatenGenerierung formaler Beweisverfahren für komplexe mathematische Probleme, um komplexe mathematische Rätsel zu lösen.
• Fähigkeit zur SelbstkorrekturMit dem Feedback des Lean-Compilers kann das Modell seine Beweise iterativ überarbeiten, um ihre Genauigkeit und Qualität zu verbessern.
• Effiziente Ausbildung und OptimierungBasierend auf hierarchischer Datensynthese und Modellmittelungstechniken verbessert es die Trainingseffizienz und die Modellleistung, so dass es in mehreren Benchmark-Tests gut abschneiden kann.
• Open Source und SkalierbarkeitBereitstellung von Open-Source-Modellen und -Datensätzen zur Erleichterung der weiteren Entwicklung und Verbesserung durch Forscher.

Leistung von Goedel-Prover-V2

• MiniF2F Benchmarks::
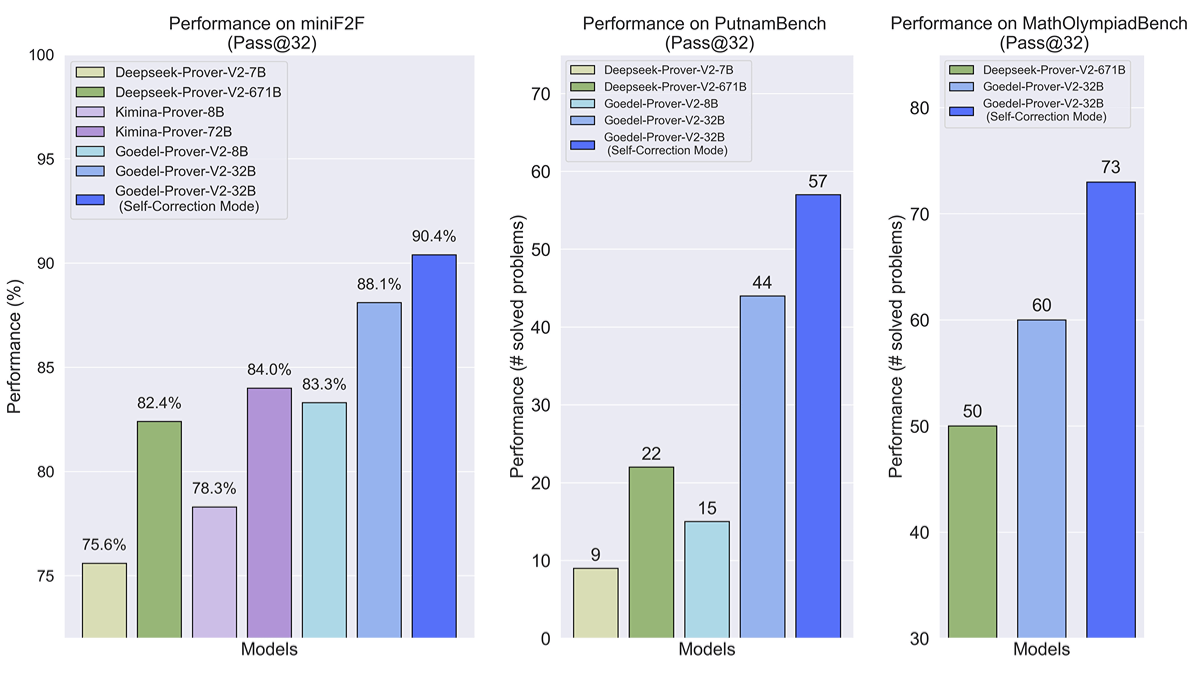
  • Die Pass@32-Punktzahl für das 32B-Modell liegt bei 90,41 TP3T und damit deutlich vor DeepSeek-Prover-V2 (82,41 TP3T) für 671B.
  • Das 8B-Modell erreicht eine Pass@32-Punktzahl von 83,3%, was mit der Leistung von DeepSeek-Prover-V2 vergleichbar ist, obwohl die Anzahl der Parameter nur etwa 1/100 derjenigen von DeepSeek-Prover-V2 beträgt.
• PutnamBench Benchmarks::
  • Das Modell 32B übertrifft die Pass@64-Metriken und löst 64 Probleme.
  • Bei der Pass@32-Metrik löst das 32B-Modell 57 Probleme und übertrifft damit DeepSeek-Prover-V2-671B mit 47 Problemen deutlich.
  • Das Modell 8B schneidet ebenfalls sehr gut ab und ist vergleichbar mit DeepSeek-Prover-V2-671B.
• MathOlympiadBench Benchmarks::
  • Das 32B-Modell löst 73 Probleme, deutlich besser als DeepSeek-Prover-V2-671B mit 50 Problemen.
  • Das 8B-Modell schneidet ebenfalls gut ab und nähert sich dem Niveau des 32B-Modells an und zeigt eine starke Fähigkeit zum Theorembeweis.

Goedel-Prover-V2 offizielle Website-Adresse

• Projekt-Website:: https://blog.goedel-prover.com/
• HuggingFace-Modellbibliothek::
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-8B
  • https://huggingface.co/Goedel-LM/Goedel-Prover-V2-32B

So verwenden Sie Goedel-Prover-V2

• Zugang zu ProjektressourcenZugriff auf die HuggingFace-Modellbibliothek, Herunterladen der Modelldateien von HuggingFace und Auswahl der entsprechenden Version (z. B. 8B oder 32B).
• Hardware-VoraussetzungLeistungsstarke GPUs oder GPU-Cluster werden empfohlen.
• SoftwareumgebungInstallation von Python und Deep-Learning-Frameworks wie PyTorch, um sicherzustellen, dass die Umgebung umfangreiche Modellinferenzen unterstützt.
• Probleme bei der EingabeKonvertieren Sie mathematische Probleme, die Beweise erfordern, in ein vom Modell unterstütztes Format (z. B. Lean-Sprache).
• Vorverarbeitung der DatenKodierung und Formatierung der Fragen gemäß den Musteranforderungen.
• Modelle ladenLaden Sie das vortrainierte Modell mit den von HuggingFace bereitgestellten Tools.
• Nachweis der ErzeugungDas Problem wird in das Modell eingespeist, das automatisch Beweise generiert, die mit Hilfe des Lean-Compilers überprüft und korrigiert werden.
• PrüfbescheinigungÜberprüfen Sie, ob die erzeugten Beweise mit dem Lean-Compiler korrekt sind.
• Iterative KorrekturWenn der Beweis falsch ist, korrigiert sich das Modell auf der Grundlage von Rückmeldungen selbst, bis der korrekte Beweis erstellt ist.

Die wichtigsten Vorteile von Goedel-Prover-V2

• Ausgezeichnete LeistungGoedel-Prover-V2 schneidet in mehreren Benchmarks gut ab. So erreicht das 32B-Modell im Pass@32-Test von MiniF2F eine Genauigkeit von 90,4% und liegt damit deutlich vor anderen ähnlichen Modellen.
• Innovative technische ArchitekturHierarchische Datensynthese, validatorgeführte Selbstkorrektur und Modellmittelungstechniken auf der Grundlage hierarchischer Datensynthese, die die Effizienz des Modelltrainings und die Qualität der Nachweise wirksam verbessern.
• Open Source und SkalierbarkeitBereitstellung von Open-Source-Modellen und -Datensätzen, die frei zugänglich sind und von Forschern zur Verbesserung genutzt und weiterentwickelt werden können.
• Breite Palette von AnwendungsszenarienAnwendbar in einer Vielzahl von Bereichen wie mathematische Forschung, Software- und Hardware-Validierung, Lehrmittel, künstliche Intelligenz und maschinelles Lernen sowie wissenschaftliche Forschung und Ingenieurwesen.
• Effiziente Ausbildung und OptimierungEffizientes Training und Leistungsoptimierung auf der Grundlage hierarchischer Datensynthese und Modellmittelungstechniken zur Verbesserung der Modellrobustheit.

Personen, bei denen Goedel-Prover-V2 angezeigt ist

• Mathematiker und mathematische ForscherVerifiziert mathematische Vermutungen, erstellt Beweise für komplexe Probleme und beschleunigt die Erforschung und das Studium mathematischer Theorien.
• Informatiker und Software-IngenieureWird in der Software- und Hardwareentwicklung eingesetzt, um die Korrektheit von Algorithmen, Programmlogik und Schaltungsdesign zu überprüfen und die Zuverlässigkeit und Sicherheit von Systemen zu verbessern.
• Forscher für künstliche IntelligenzValidierung der mathematischen Grundlagen und der algorithmischen Logik von Modellen des maschinellen Lernens, um die Zuverlässigkeit und Genauigkeit der Modelle zu gewährleisten.
• Lehrkräfte und Studenten: Als Hilfsmittel für den Mathematikunterricht, das Schülern hilft, mathematische Konzepte und Theoreme besser zu verstehen und zu beherrschen, indem es Beispiele für formale Beweise liefert.
• Forscher und IngenieureValidierung mathematischer Modelle und Theorien in der wissenschaftlichen Forschung und im technischen Design, um die Machbarkeit und Zuverlässigkeit von Designlösungen zu gewährleisten.